Open-Circuit Fault-Tolerant Strategy for Interleaved Boost Converters via Filippov Method
Abstract
:1. Introduction
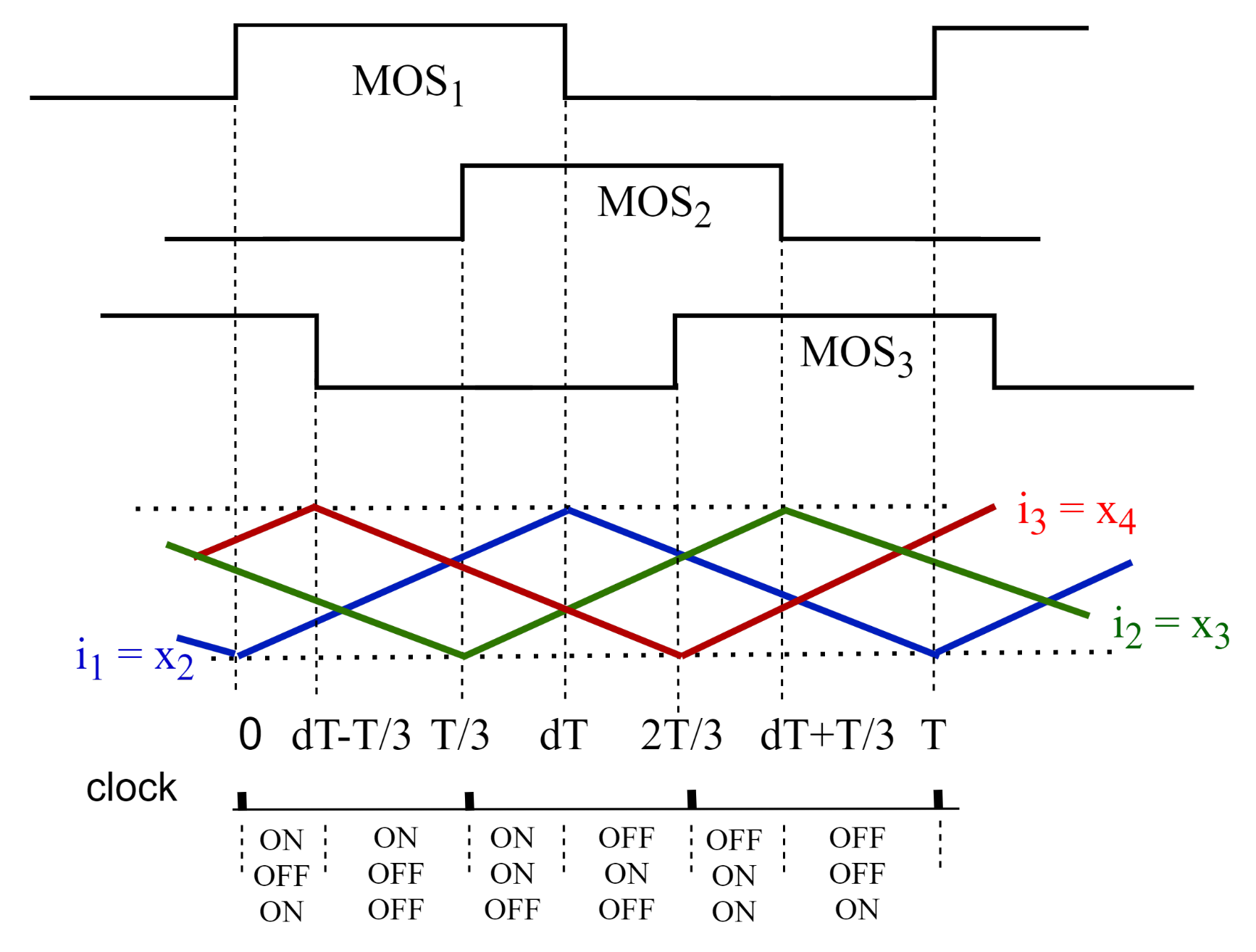
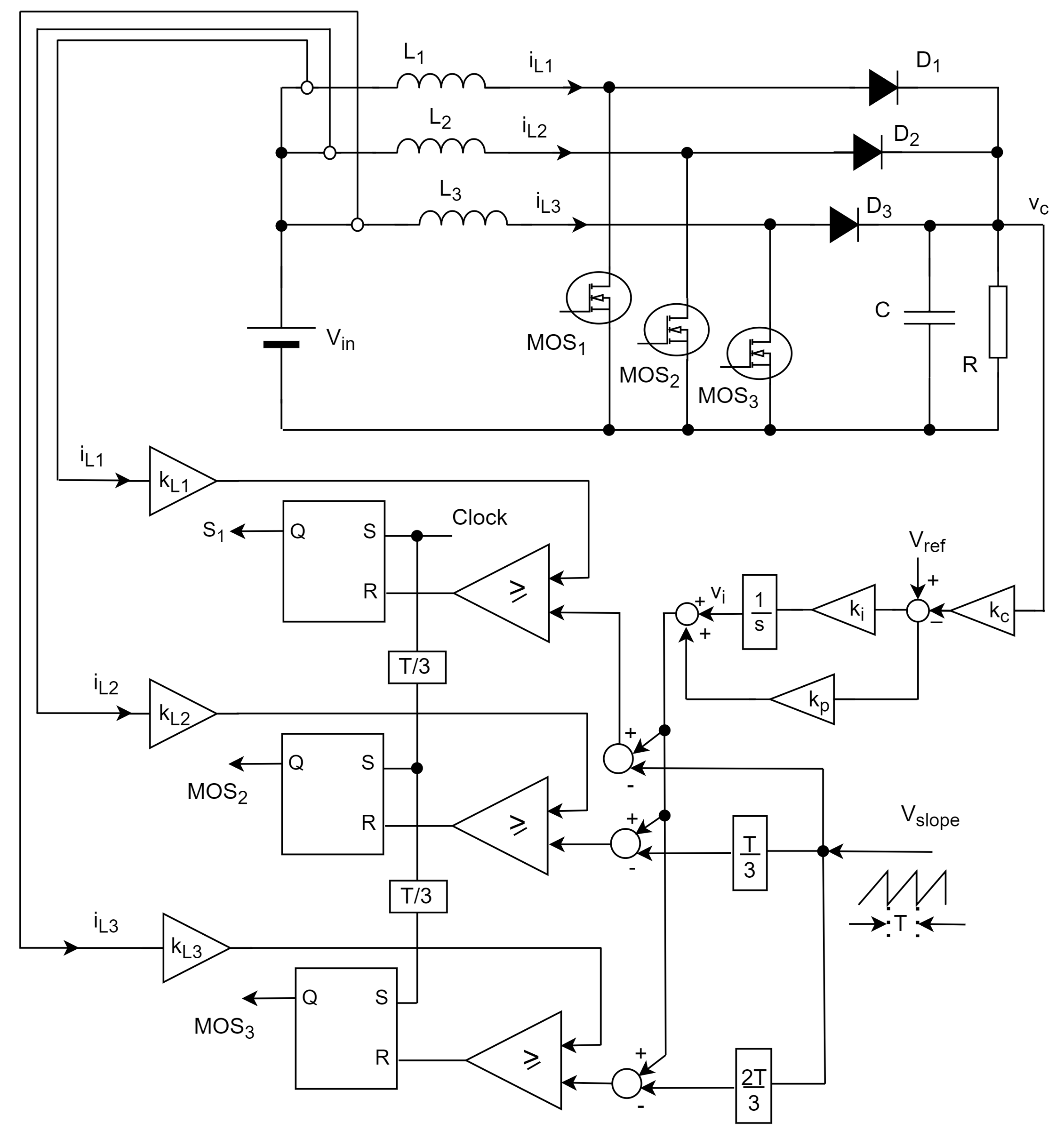
2. The Interleaved Boost Converter with Healthy and One Open-Circuit Faulty Condition
3. Mathematical Model of the Boost Converter under Several Operating Modes
3.1. Mode
3.2. Mode
3.3. Mode
3.4. Mode
3.5. Mode
3.6. Mode
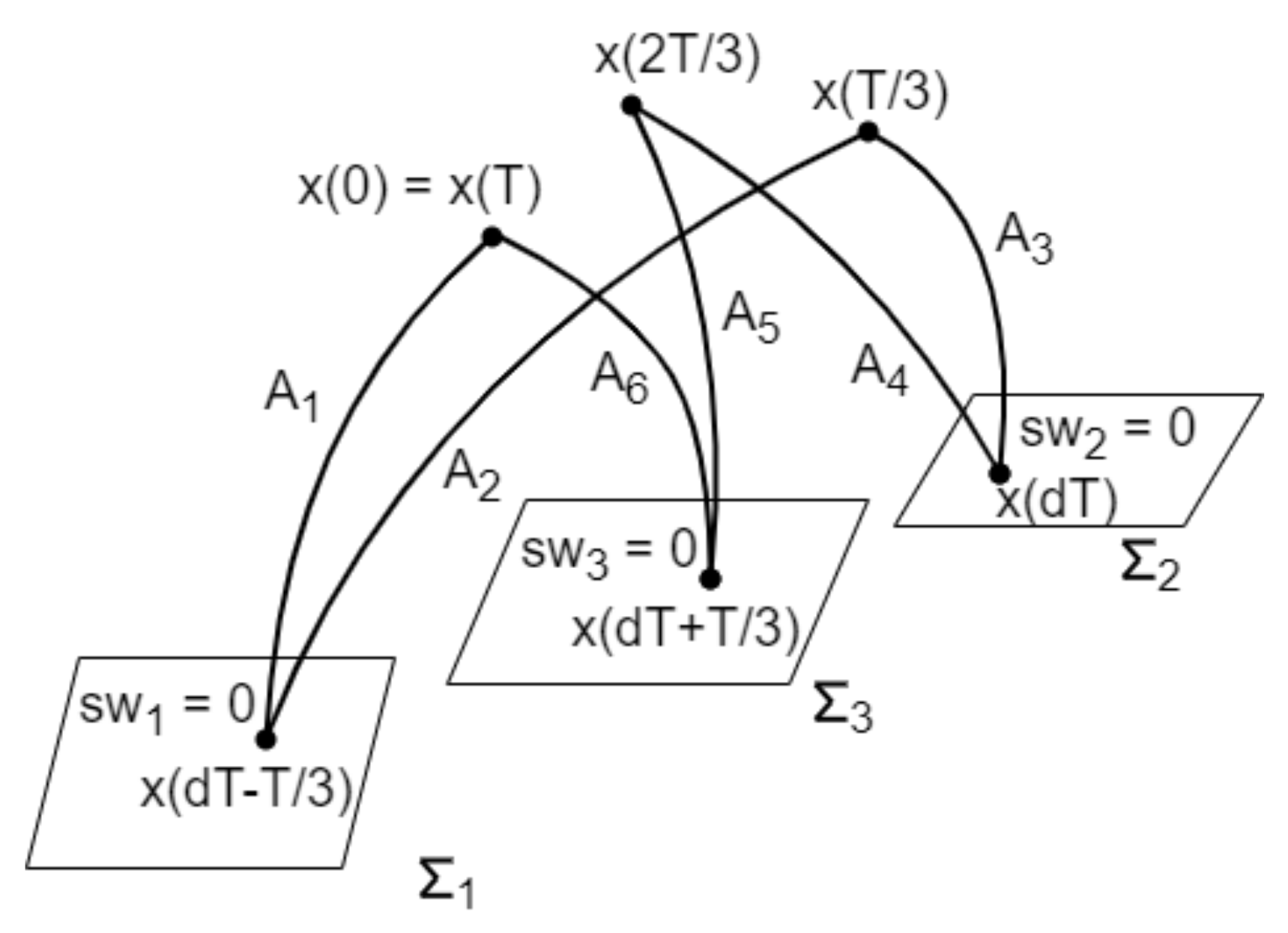
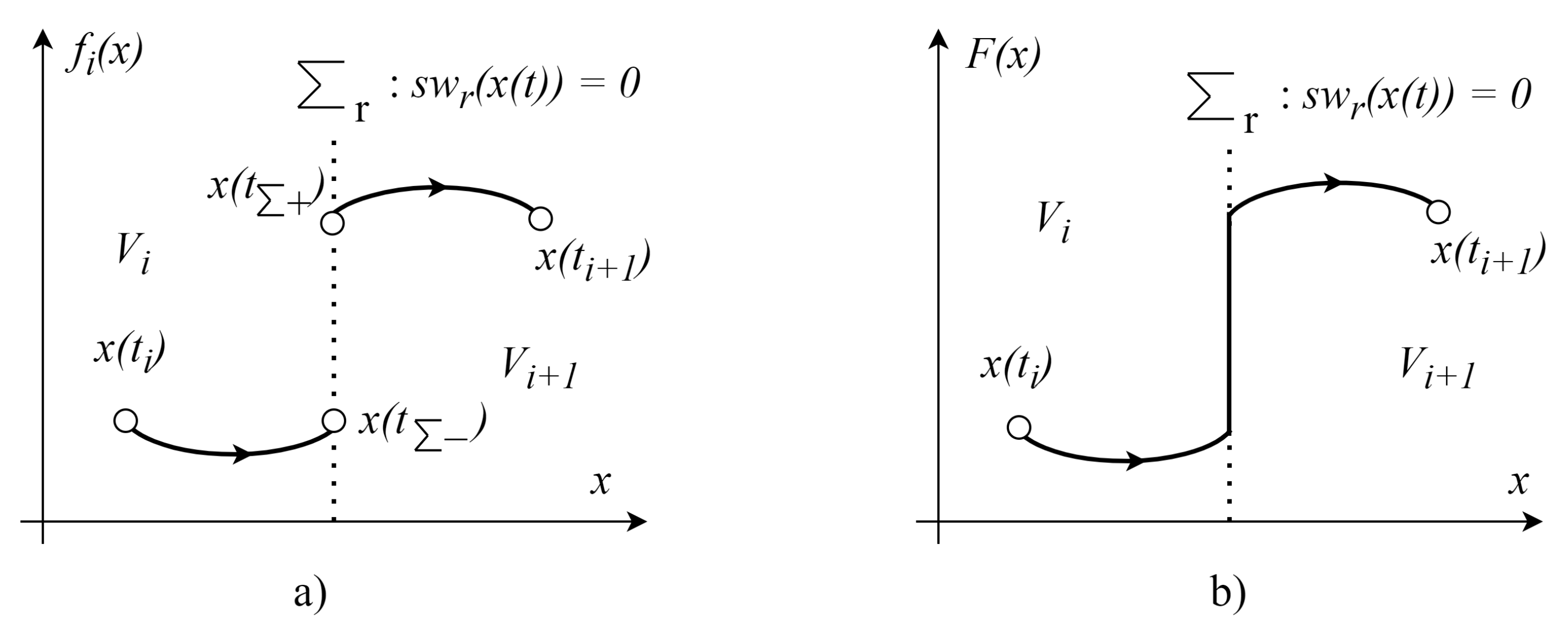
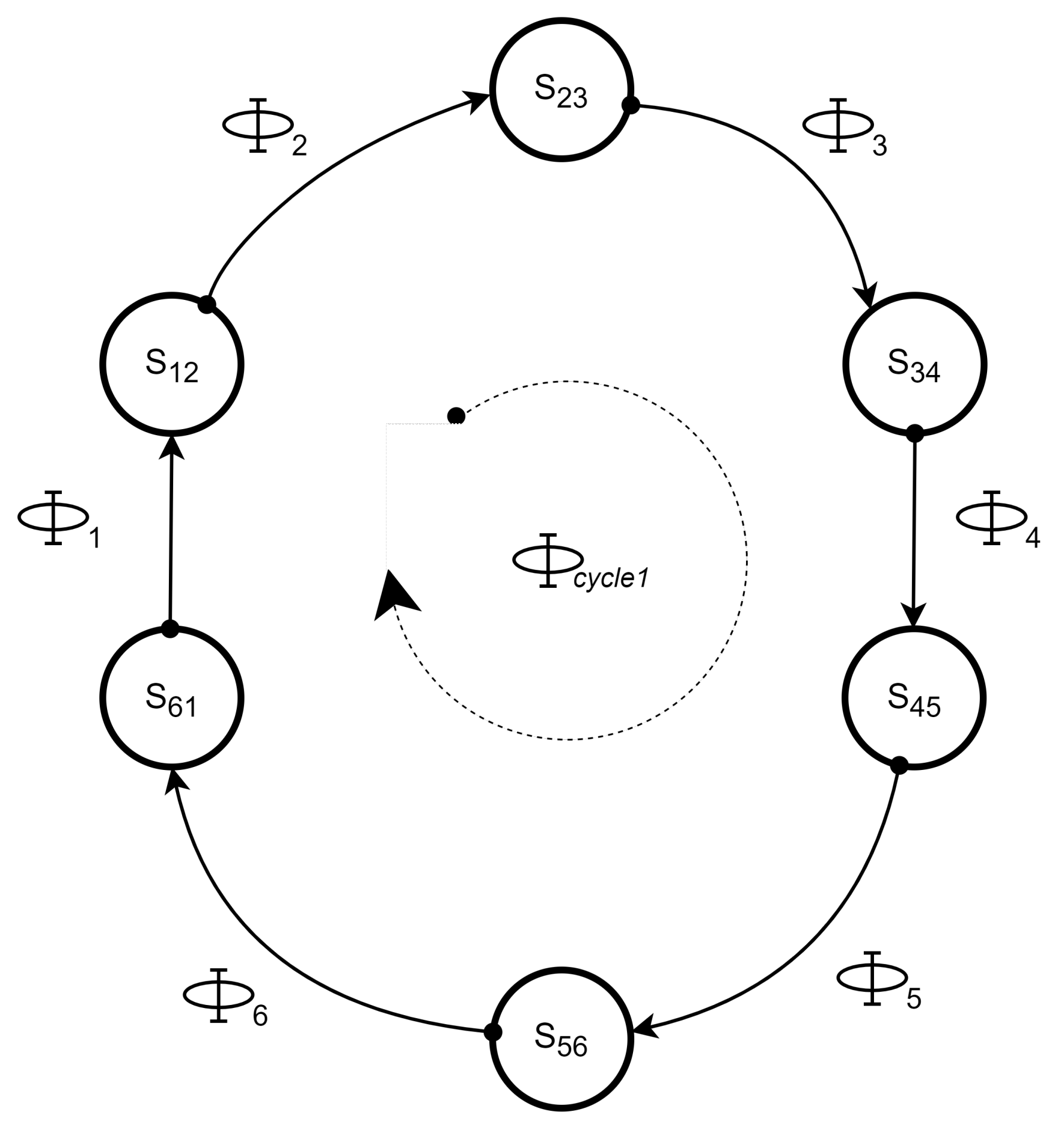
4. Saltation and Monodromy Matrices for the Interleaved Boost Converter
5. Identification of Duty Cycles of the Period-1T Limit Cycle
6. Simulation Results
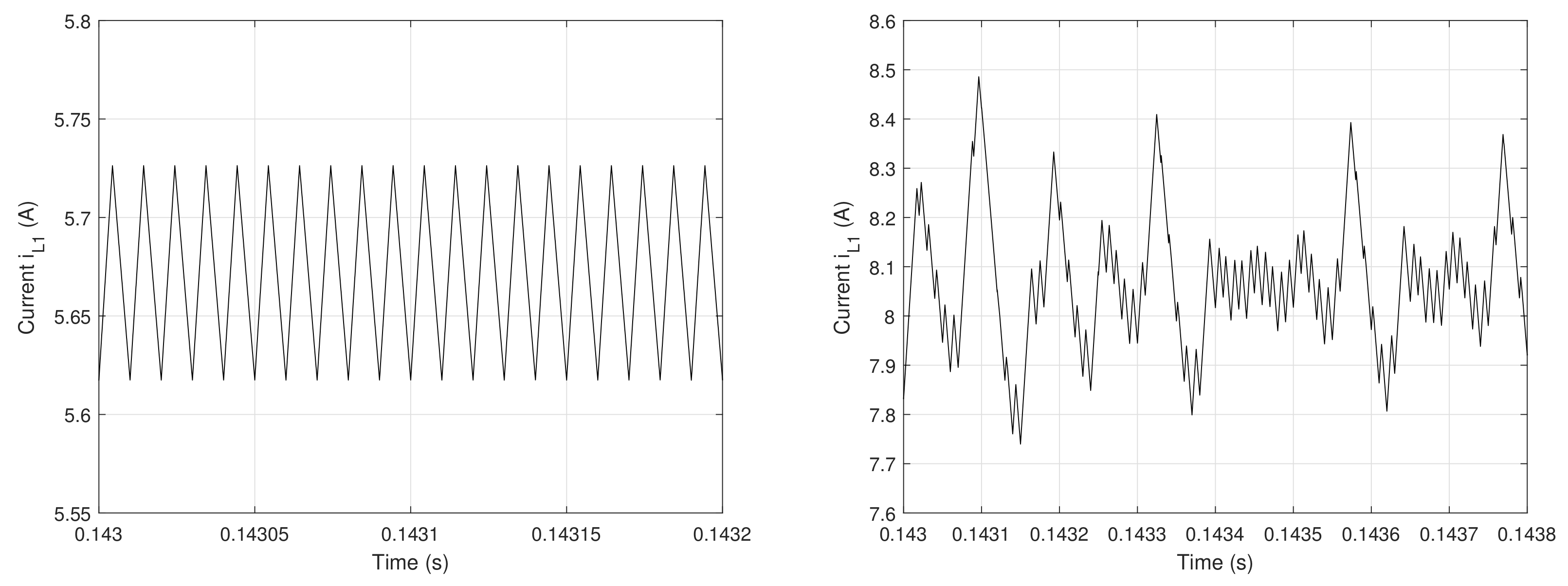
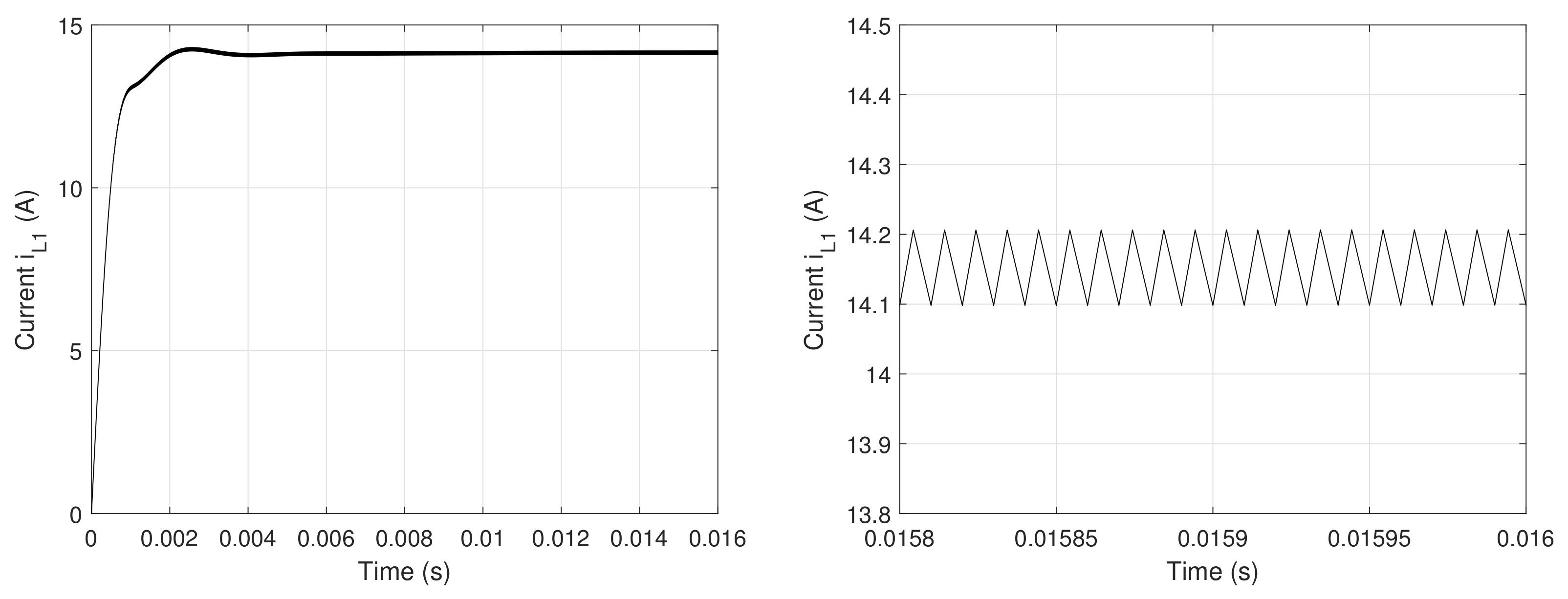
6.1. System Simulation under Healthy Conditions
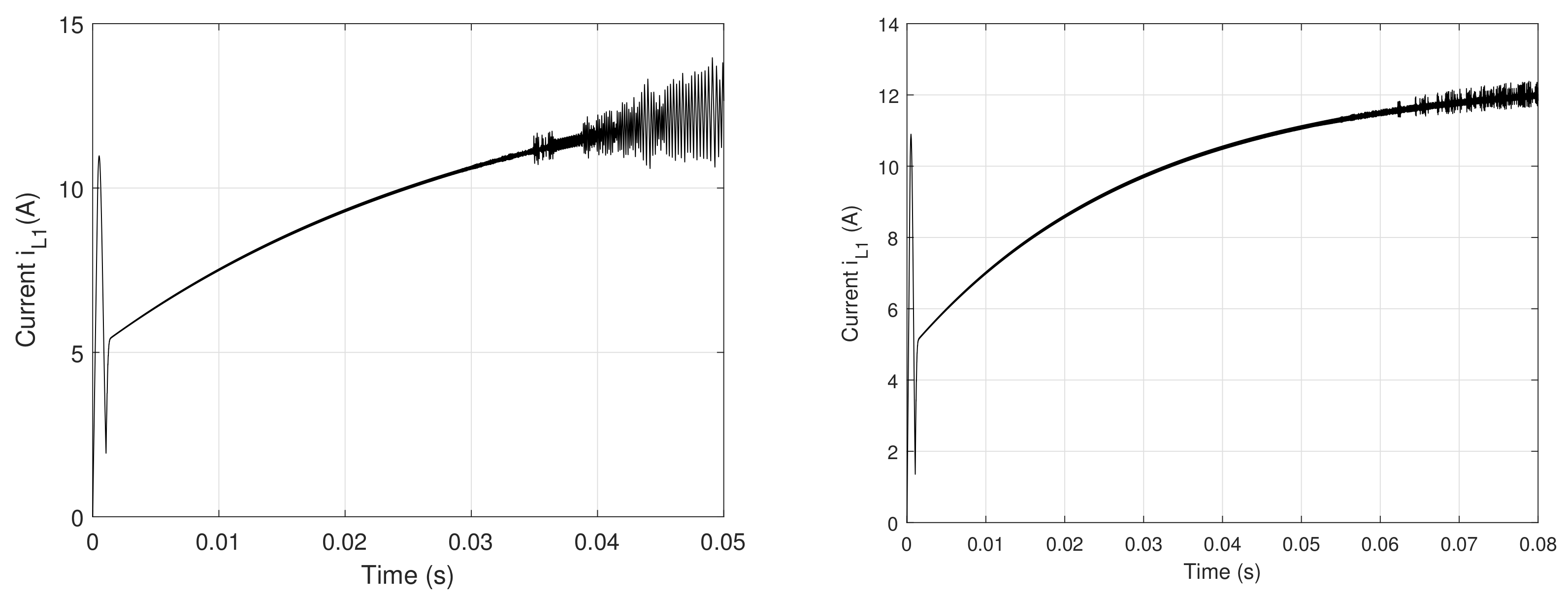
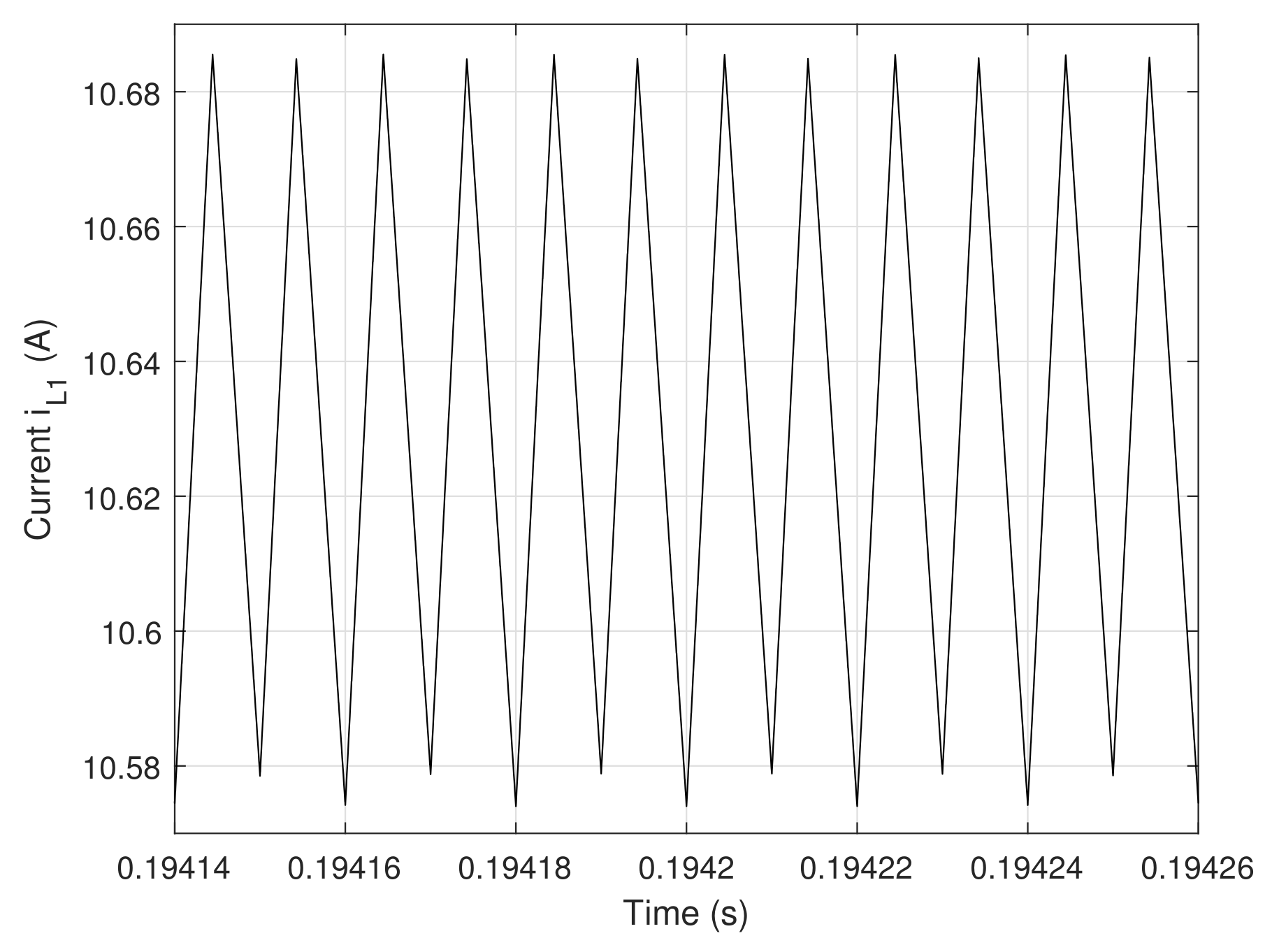
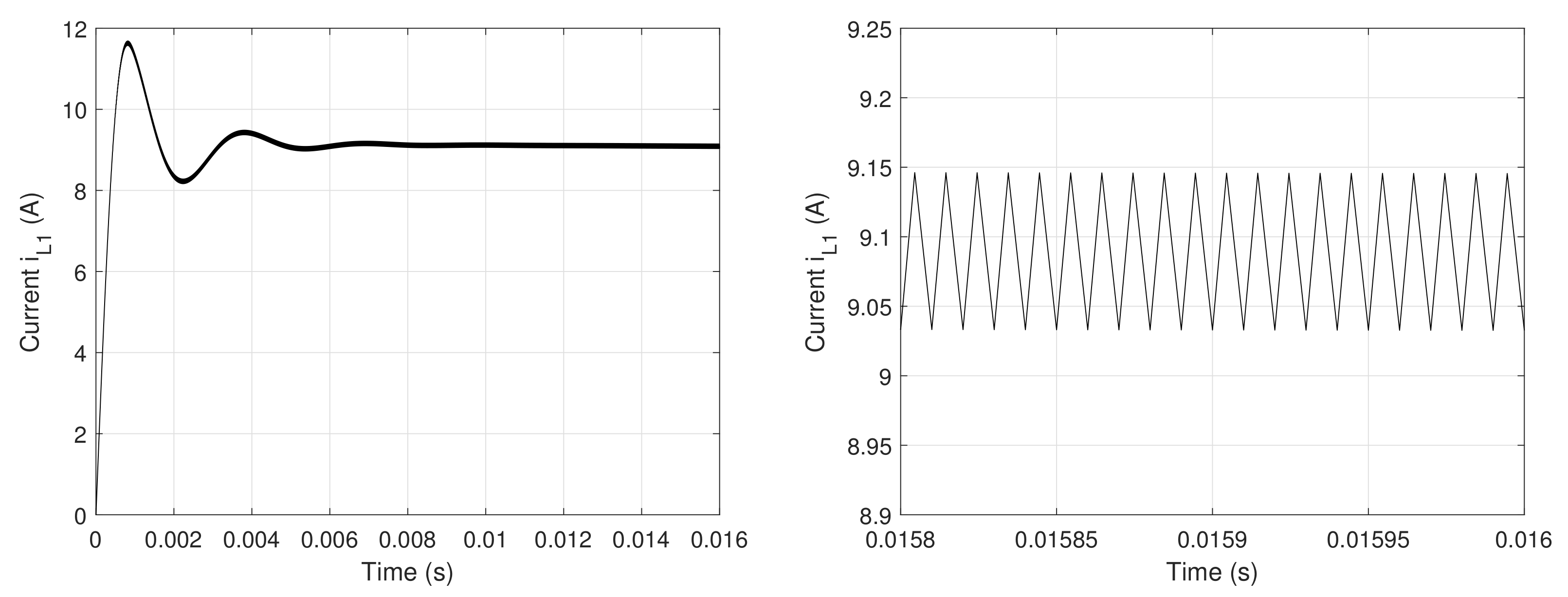
6.2. System Simulation under One Open-Circuit Faulty Condition
6.3. Development of a Fault-Tolerant Strategy with the Slope Compensation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aghdam, F.H.; Abapour, M. Reabilityand cost analysis of multistage boost converters connected to pv panels. IEEE J. Photovoltaics 2016, 6, 981–989. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Gorla, N.B.Y.; Malik, H.; Panda, S.K. A fault diagnosis and postfault reconguration scheme for interleaved boost converter in pv-based system. IEEE Trans. Power Electron 2021, 36, 3769–3780. [Google Scholar] [CrossRef]
- Apablaza, D.; Munoz, J. Laboratory implementation of a boost interleaved converter for pv applications. IEEE Latin Am. 2016, 14, 2738–2743. [Google Scholar] [CrossRef]
- Pei, T.; Hao, X. A fault detection method for photovoltaic systems based on voltage and current observation and evaluation. Energies 2019, 12, 1712. [Google Scholar] [CrossRef] [Green Version]
- Guilbert, D.; N’Diaye, A.; Gaillard, A.; Djerdir, A. Fuel cell systems reliability and availability enhancement by developing a fast and efficient power switch open-circuit fault detection algorithm in interleaved dc-dc boost converter topologies. Int. J. Hydrogen Energy 2016, 41, 15505–15517. [Google Scholar] [CrossRef]
- Seyezhai, R.; Mathur, B.L. A comparison of three-phase uncoupled and directly coupled interleaved boost converter for fuel cell applications. Int. J. Electr. Eng. Informatics 2011, 3, 394–407. [Google Scholar] [CrossRef]
- Marcos-Pastor, M.; Vidal-Idiarte, E.; Cid-Pastor, A.; Martinez-Salamero, L. Interleaved digital power factor correction based on the sliding-mode approach. IEEE Trans. Power Electron. 2016, 31, 4641–4653. [Google Scholar] [CrossRef]
- Garcia, O.; Zumel, P.; de Castro, A.; Cobos, A. Automotive dc-dc bidirectional converter made with many interleaved buck stages. SIAM Rev. 2008, 50, 578–586. [Google Scholar] [CrossRef]
- Garcia, O.; Zumel, P.; de Castro, A.; Cobos, A. An automotive 16 phases dc-dc converter. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; pp. 350–355. [Google Scholar]
- Neugebauer, C.T.; Perreault, J. Computer aided optimisation of dc-dc converters for automotive applications. IEEE Trans. Power Electron. 2003, 18, 775–783. [Google Scholar] [CrossRef]
- Banerjee, S.; Ghosh, A.; Rana, N. Design and fabrication of closed loop two-phase interleaved boost converter with type-iii controller. In Proceedings of the IECON—42th Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; Volume 14, pp. 3331–3336. [Google Scholar]
- Hui, L.; Ke, M.; Poh, L.; Frede, H. Online fault identification based on an adaptive observer for modular multilevel converters applied to wind power generation systems. Energies 2015, 8, 7140–7160. [Google Scholar]
- Ni, L.; Patterson, D.J.; Hudgins, J.L. Maximum power extraction from a small wind turbine using a 4-phase interleaved boost converter. In Proceedings of the IEEE Power Electronics and Machines in Wind Applications, Lincoln, NE, USA; 2009; Volume 11, pp. 1–5. [Google Scholar]
- Givi, H.; Farjah, E.; Ghanbari, T. Switch and diode fault diagnosis in nonisolated dc-dc converters using diode voltage signature. Int. J. Circuit Theory Appl. 2018, 65, 1606–1615. [Google Scholar] [CrossRef]
- Pei, X.; Nie, S.Y.; Chen, Y.; Kang, Y. Open-circuit fault diagnosis and fault-tolerant strategies for full-bridge dc-dc converters. IEEE Trans. Power Electron. 2012, 27, 2550–2565. [Google Scholar] [CrossRef]
- Shahbazi, M.; Jamshidpour, E.; Poure, P.; Saadate, S.; Zolghadri, M.R. Open- and short-circuit switch fault diagnosis for non isolated dc-dc converters using field programmable gate array. IEEE Trans. Ind. Electron 2013, 60, 4136–4146. [Google Scholar] [CrossRef] [Green Version]
- Shahbazi, M.; Zolghadri, M.R.; Ouni, S.; Zolghadri, M.R. Fast and simple open-circuit fault detection method for interleaved dc-dc converters. In Proceedings of the 7th PEDSTC, Tehran, Iran, 16–18 February 2016; pp. 440–445. [Google Scholar]
- Wassinger, N.; Penovi, E.; Retegui, R.G.; Maestri, S. Open-circuit fault identification method for interleaved converters based on time-domain analysis of the state observer residual. IEEE Trans. Power Electron 2019, 34, 3740–3749. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Y.; Yu, L.; Zhang, M. A new diagnostic algorithm for multiple igbts open circuit faults by the phase currents for power inverter in electric vehicles. Energies 2018, 11, 1508. [Google Scholar] [CrossRef] [Green Version]
- Zhuo, S.; Xu, L.; Gaillard, A.; Huangfu, Y.; Gao, F. Robust open-circuit fault diagnosis of multi-phase interleaved dc-dc boost converter based on sliding mode observer. IEEE Trans. Transp. Electrif 2019, 5, 638–649. [Google Scholar] [CrossRef]
- Bento, F.; Marques Cardoso, A.J. A comprehensive survey on fault diagnosis and fault tolerance of dc-dc converters. Chin. J. Electron. 2018, 12, 1–12. [Google Scholar]
- Li, P.; Li, X.; Zeng, T. A fast and simple fault diagnosis method for interleaved dc-dc converters based on output voltage analysis. Electronics 2021, 10, 1451. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, H.; Deng, C.; Song, Q. Multiloop interleaved control for three-level buck converter in solar charging applications. IEICE Electron. Express 2018, 15, 20180369. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, S.; Verghese, G.C. Nonlinear Phenomena in Power Electronics: Attractors, Bifurcations, Chaos, and Nonlinear Control; IEEE Press: New York, NY, USA, 2001. [Google Scholar]
- Tse, C.K. Complex Behavior of Switching Power Converters; CRC Press: New York, NY, USA, 2003. [Google Scholar]
- Giaouris, D.; Banerjee, S.; Zahawi, B.; Pickert, V. Stability analysis of the continuous-conduction-mode Buck converter via Filippovs method. IEEE Trans. Circuits Syst. 2008, 55, 1084–1096. [Google Scholar] [CrossRef] [Green Version]
- Giaouris, D.; Maity, S.; Banerjee, S.; Pickert, V.; Zahawi, B. Application of Filippov’s method for the analysis of subharmonic instability in dc-dc converters. Int. J. Circuit Theory Appl. 2009, 37, 899–919. [Google Scholar] [CrossRef] [Green Version]
- Leine, R.I.; van Campen, D.H. Bifurcation phenomena in nonsmooth dynamical systems. Eur. J. Mech. Solids 2006, 25, 595–6168. [Google Scholar] [CrossRef]
- Leine, R.I.; van Campen, D.H.; van de Vrande, B.L. Bifurcations in nonlinear discontinuous systems. Nonlinear Dyn. 2000, 23, 105–164. [Google Scholar] [CrossRef]
- Morel, C.; Morel, J.-Y.; Petreus, D. Generalization of the Filippov method for systems with a large periodic input. Math. Comput. Simul. 2018, 146, 1–17. [Google Scholar] [CrossRef]
- Di Bernardo, M.; Budd, C.J.; Champneys, A.R.; Kowalczyk, P.; Nordmark, A.B.; Tost, G.O.; Piiroinen, P.T. Bifurcations in nonsmooth dynamical systems. SIAM Rev. 2008, 50, 629–701. [Google Scholar] [CrossRef] [Green Version]
- Kowalczyk, P.; di Bernardo, M. Two parameter degenerated sliding bifurcations in Filippov systems. Phys. D 2005, 20, 204–229. [Google Scholar] [CrossRef]
- Kuznetsov, Y.A.; Rinaldi, S.; Gragnani, A. One-parameter bifurcations in planar Filippov systems. Int. J. Bifurc. Chaos 2003, 13, 2157–2188. [Google Scholar] [CrossRef] [Green Version]
- Morel, C.; Petreus, D.; Rusu, A. Application of the Filippov method for the stability analysis of a photovoltaic system. Adv. Electr. Comput. Eng. 2011, 11, 93–98. [Google Scholar] [CrossRef]
- Wu, H.; Pickert, V.; Giaouris, D.; Ji, B. Nonlinear analysis and control of interleaved boost converter using real-time cycle to cycle variable slope compensation. IEEE Trans. Power Electron. 2017, 32, 7256–7270. [Google Scholar] [CrossRef]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Khaki-Sedigh, A.; Sepehri, N. Observer-based adaptative control of chaos in nonlinear discret-time systems using time-delayed state feedback. Chaos Solitons Fractal 2009, 41, 2448–2455. [Google Scholar] [CrossRef]
- Wang, N.; Lu, G.N.; Peng, X.Z.; Cai, Y.K. A research on time delay feedback control performance in chaotic system of dc-dc inverter. In Proceedings of the 2013 IEEE International Conference on Vehicular Electronics and Safety, Dongguan, China, 28–30 July 2013; pp. 215–218. [Google Scholar]

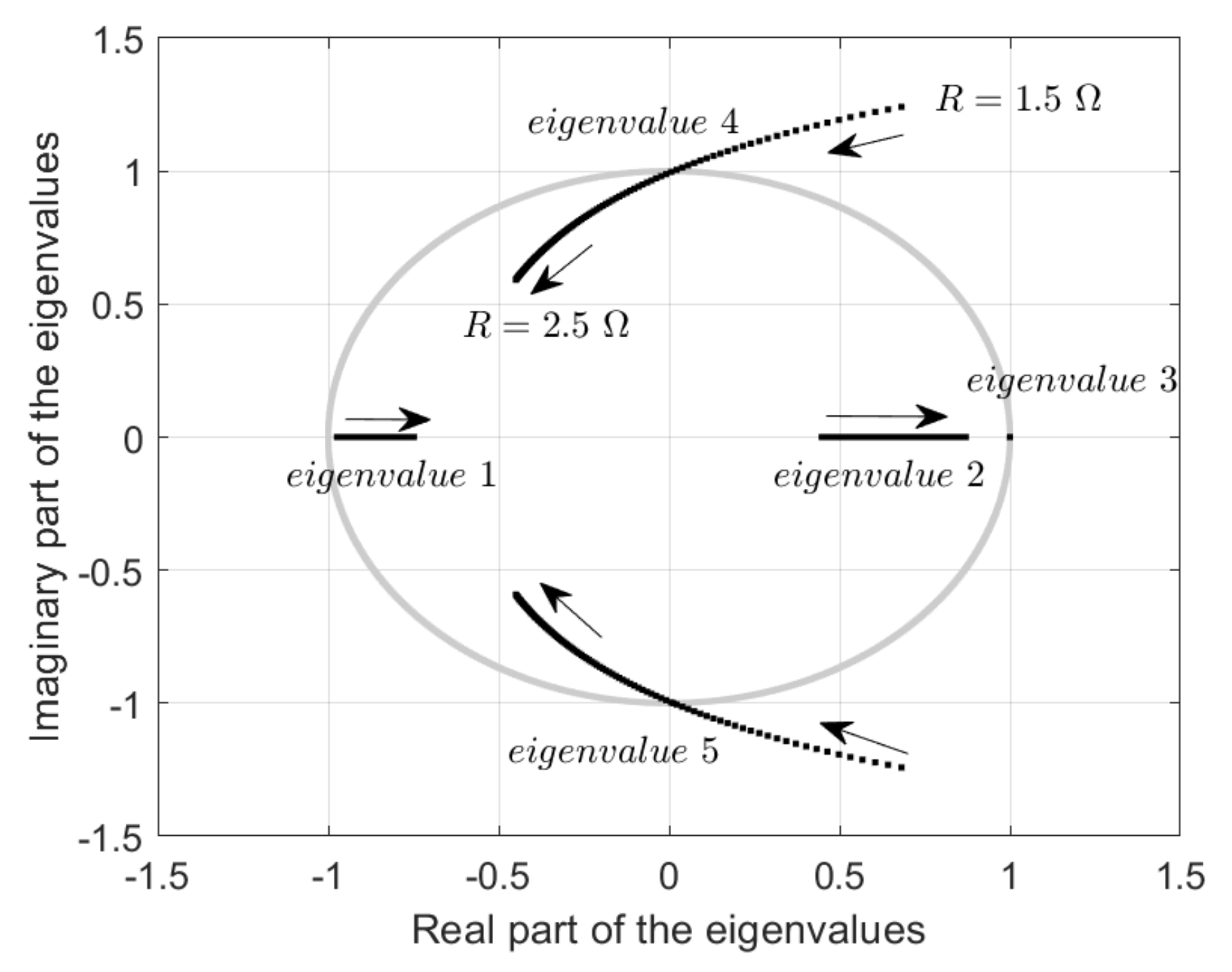
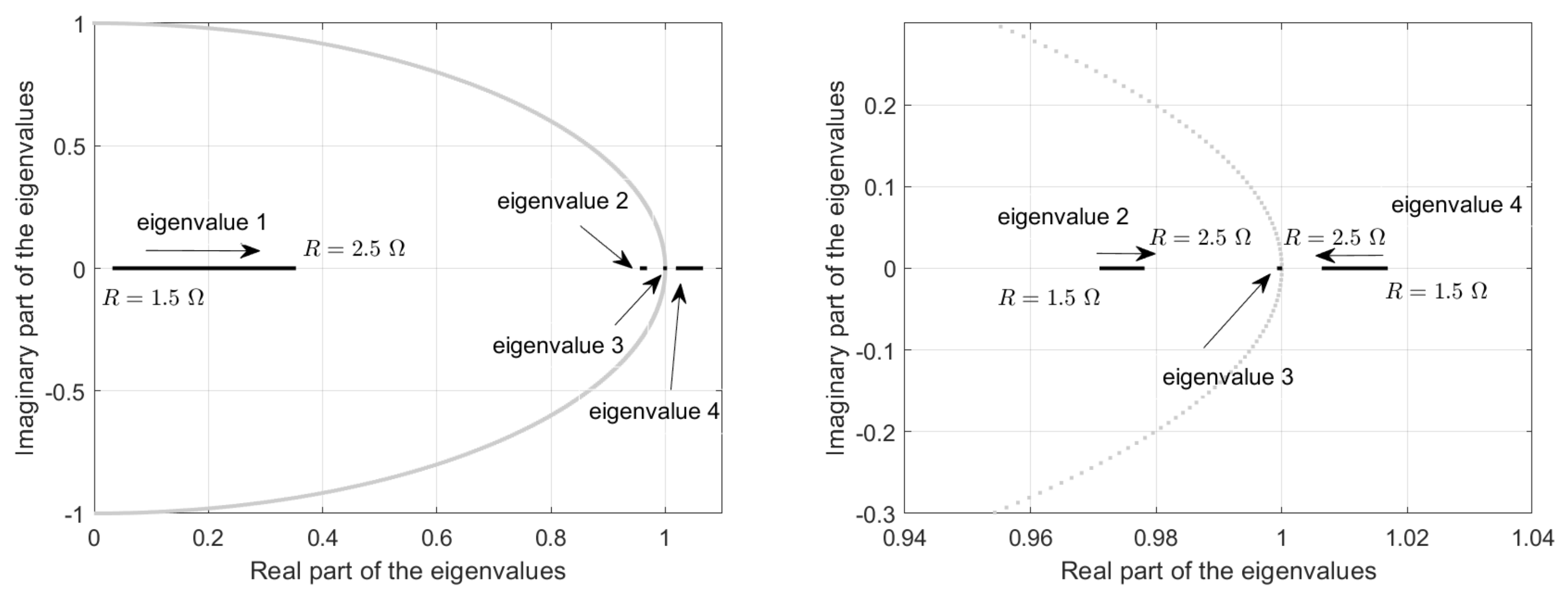
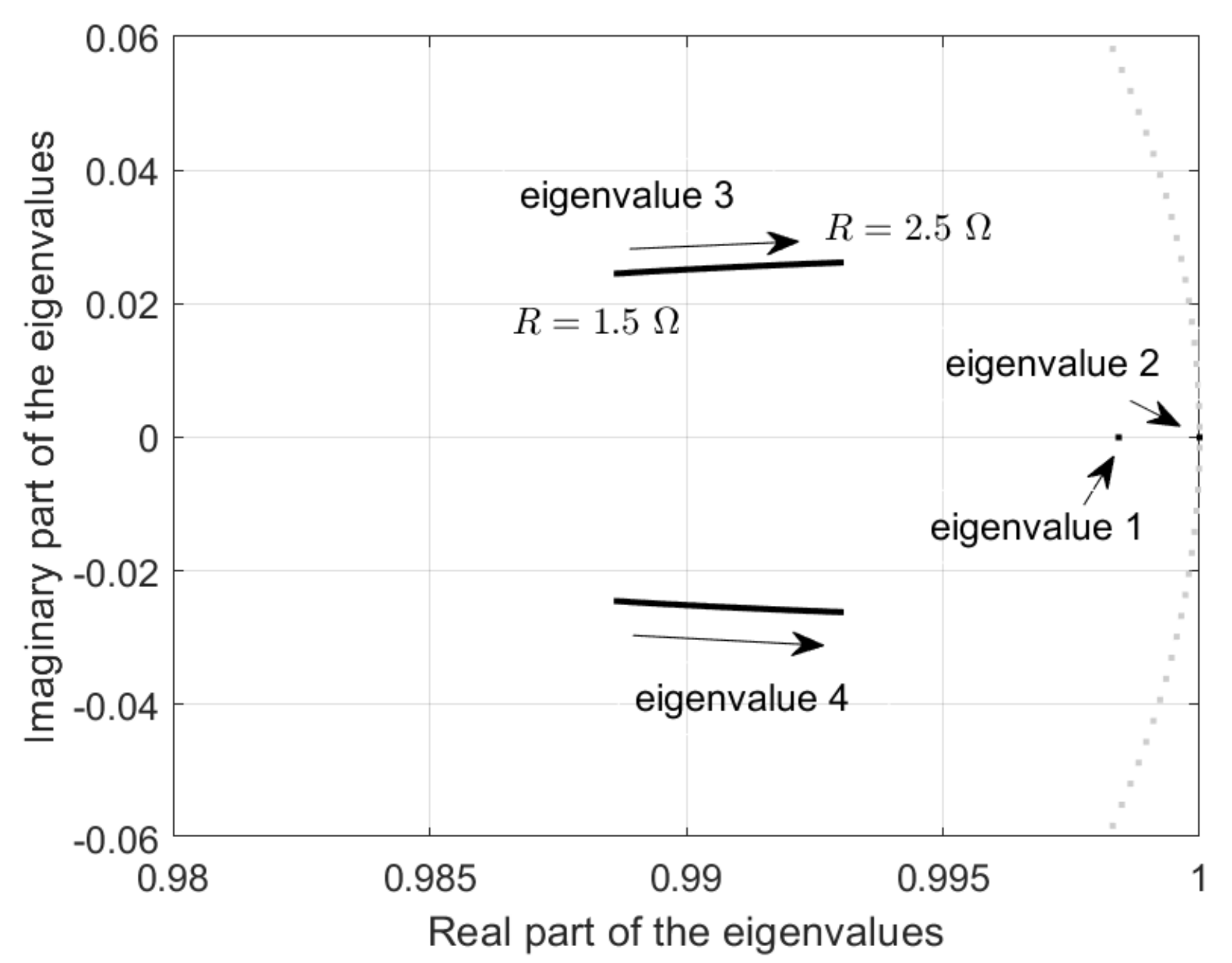
| R | Real Eigenvalue 1 | Real Eigenvalue 2 | Real Eigenvalue 3 | Complex Eigenvalues 45 |
|---|---|---|---|---|
| 2 | ||||
| R | Real Eigenvalue 1 | Real Eigenvalue 2 | Real Eigenvalue 3 | Real Eigenvalues 4 |
|---|---|---|---|---|
| 2 | ||||
| R | Real Eigenvalue 1 | Real Eigenvalue 2 | Complex Eigenvalues 34 |
|---|---|---|---|
| 2 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morel, C.; Akrad, A.; Sehab, R.; Azib, T.; Larouci, C. Open-Circuit Fault-Tolerant Strategy for Interleaved Boost Converters via Filippov Method. Energies 2022, 15, 352. https://doi.org/10.3390/en15010352
Morel C, Akrad A, Sehab R, Azib T, Larouci C. Open-Circuit Fault-Tolerant Strategy for Interleaved Boost Converters via Filippov Method. Energies. 2022; 15(1):352. https://doi.org/10.3390/en15010352
Chicago/Turabian StyleMorel, Cristina, Ahmad Akrad, Rabia Sehab, Toufik Azib, and Cherif Larouci. 2022. "Open-Circuit Fault-Tolerant Strategy for Interleaved Boost Converters via Filippov Method" Energies 15, no. 1: 352. https://doi.org/10.3390/en15010352







