The Effect of Dynamic Cold Storage Packed Bed on Liquid Air Energy Storage in an Experiment Scale
Abstract
:1. Introduction
1.1. Development of Cold Recovery for LAES System
1.2. Development of Experimental Packed Bed
1.3. Objective and Motivation of This Study
2. Methods and Approaches
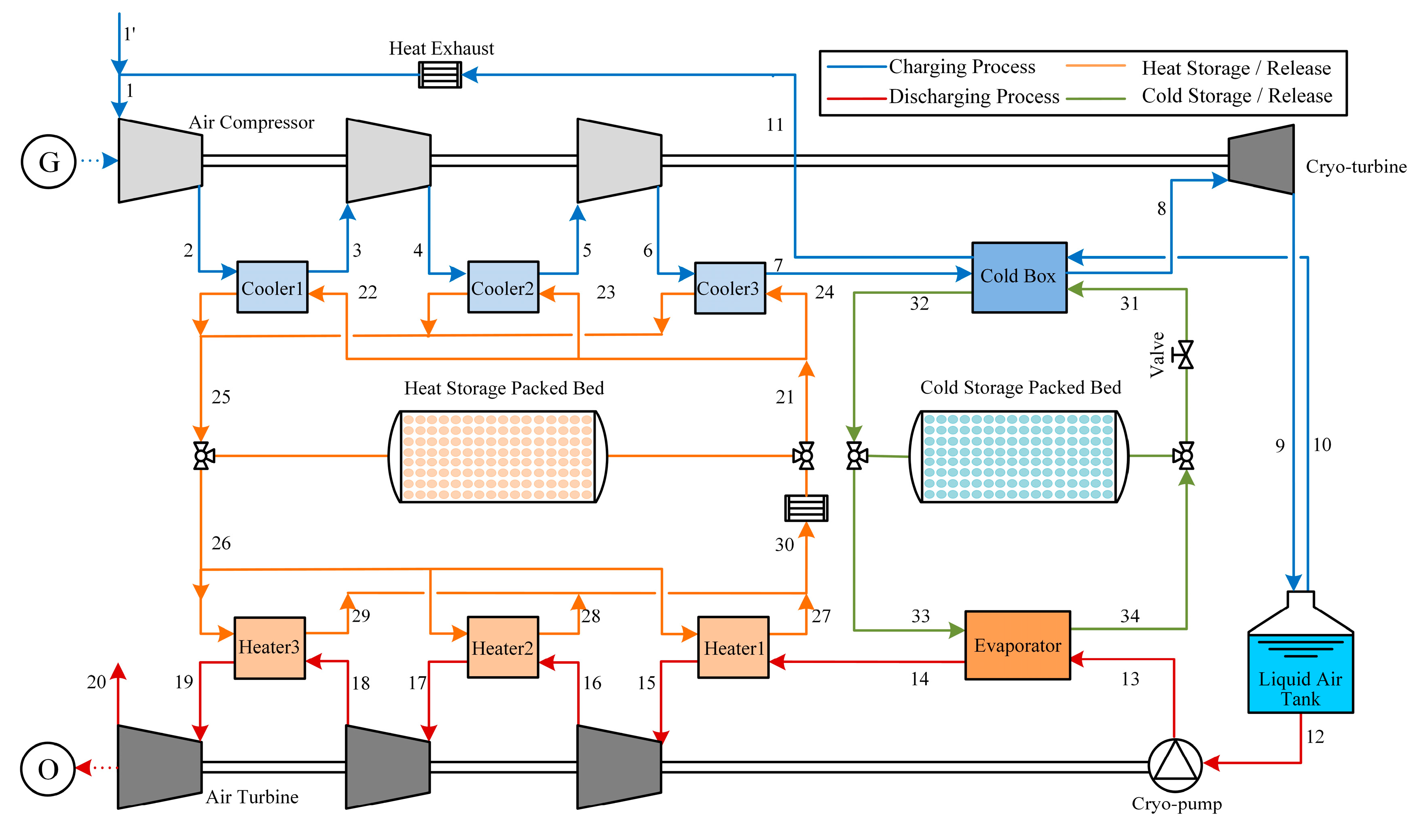
2.1. System Description
2.1.1. Charging and Discharging Process of LAES System
2.1.2. Charge and Discharge Process of the Packed Beds
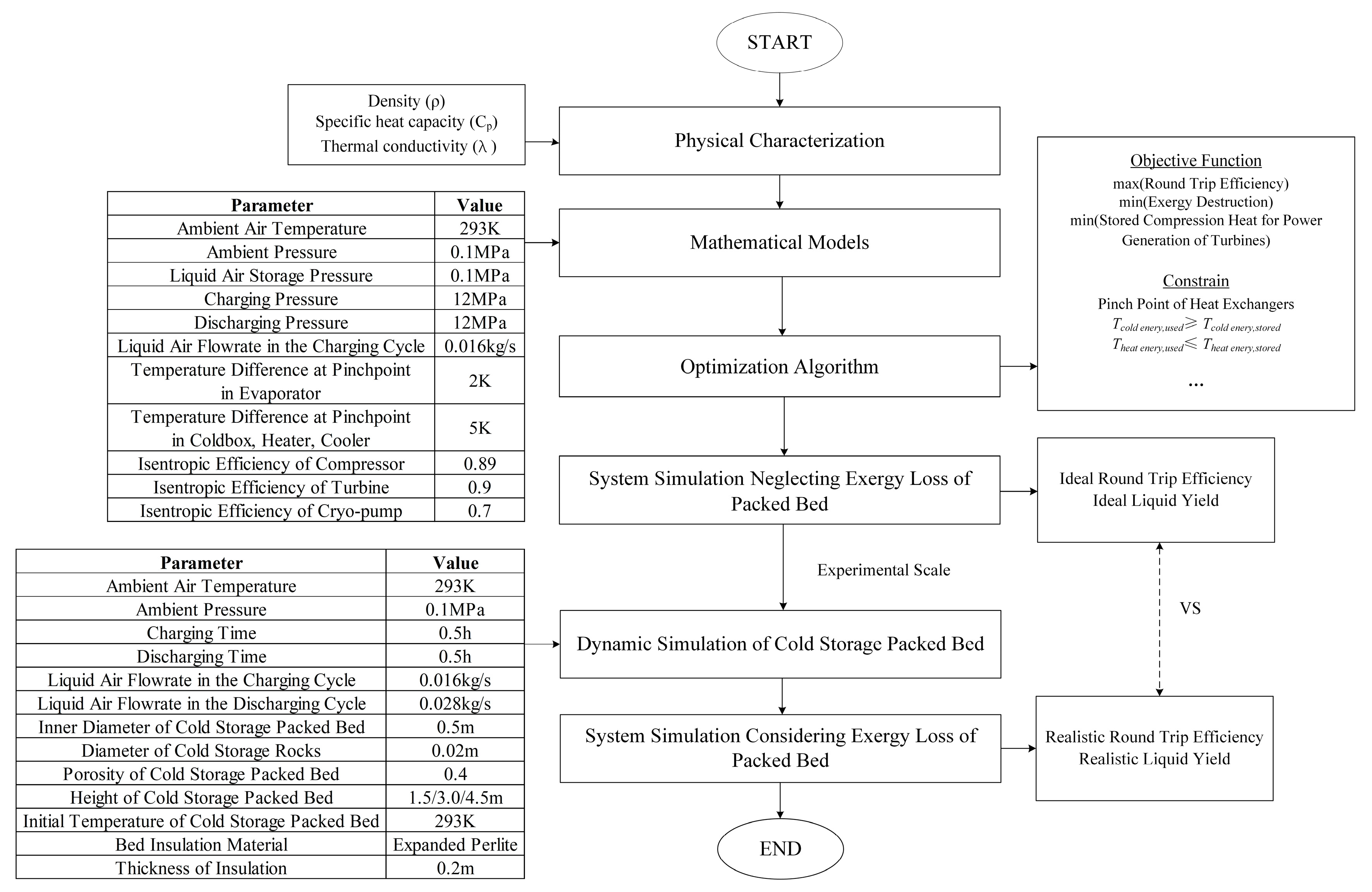
2.2. Methodology
2.3. Mathematical Model
2.3.1. Power Components and Heat Exchangers
2.3.2. Charge and Discharge Processes of Packed Bed
- (1)
- One-dimensional Newton heat transfer, ignoring the radial temperature gradient [30].
- (2)
- It is unidirectional for the fluid to flow in the bed, ignoring the viscous stress and kinetic energy terms.
- (3)
- The specific heat, density, and thermal conductivity of rocks change as the temperature changes; the viscosity, specific heat, density, and thermal conductivity of the fluid change with temperature.
- (4)
- Radiation heat transfer is ignored.
2.4. Thermodynamic Performance Index
2.4.1. Exergy Efficiency of the Cold Storage Packed Bed
2.4.2. Exergy Efficiency of Cold Box and Evaporator
2.4.3. Liquid Yield and Round Trip Efficiency
2.5. Model Validation
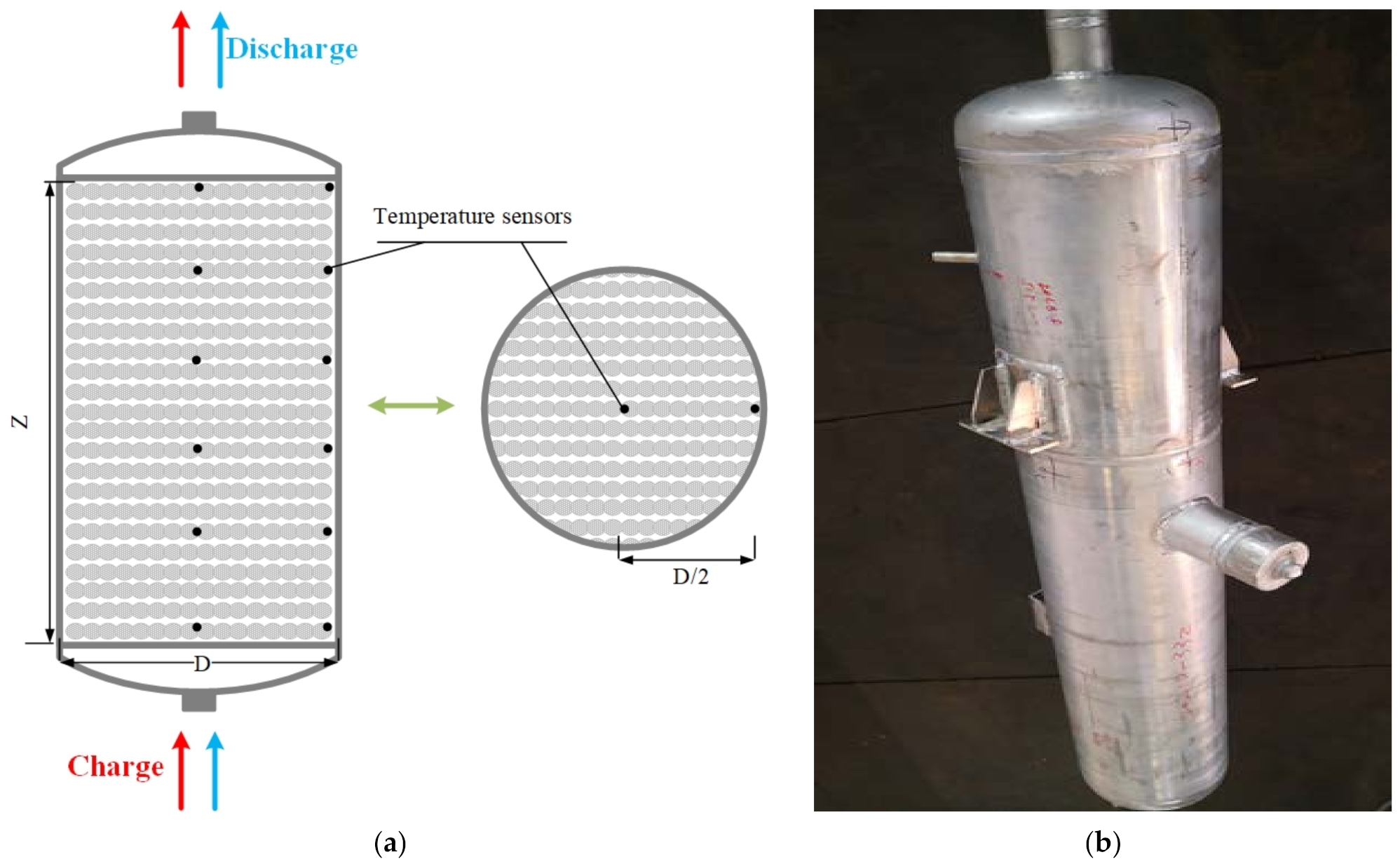
2.5.1. Model Validation of Cold Storage Packed Bed
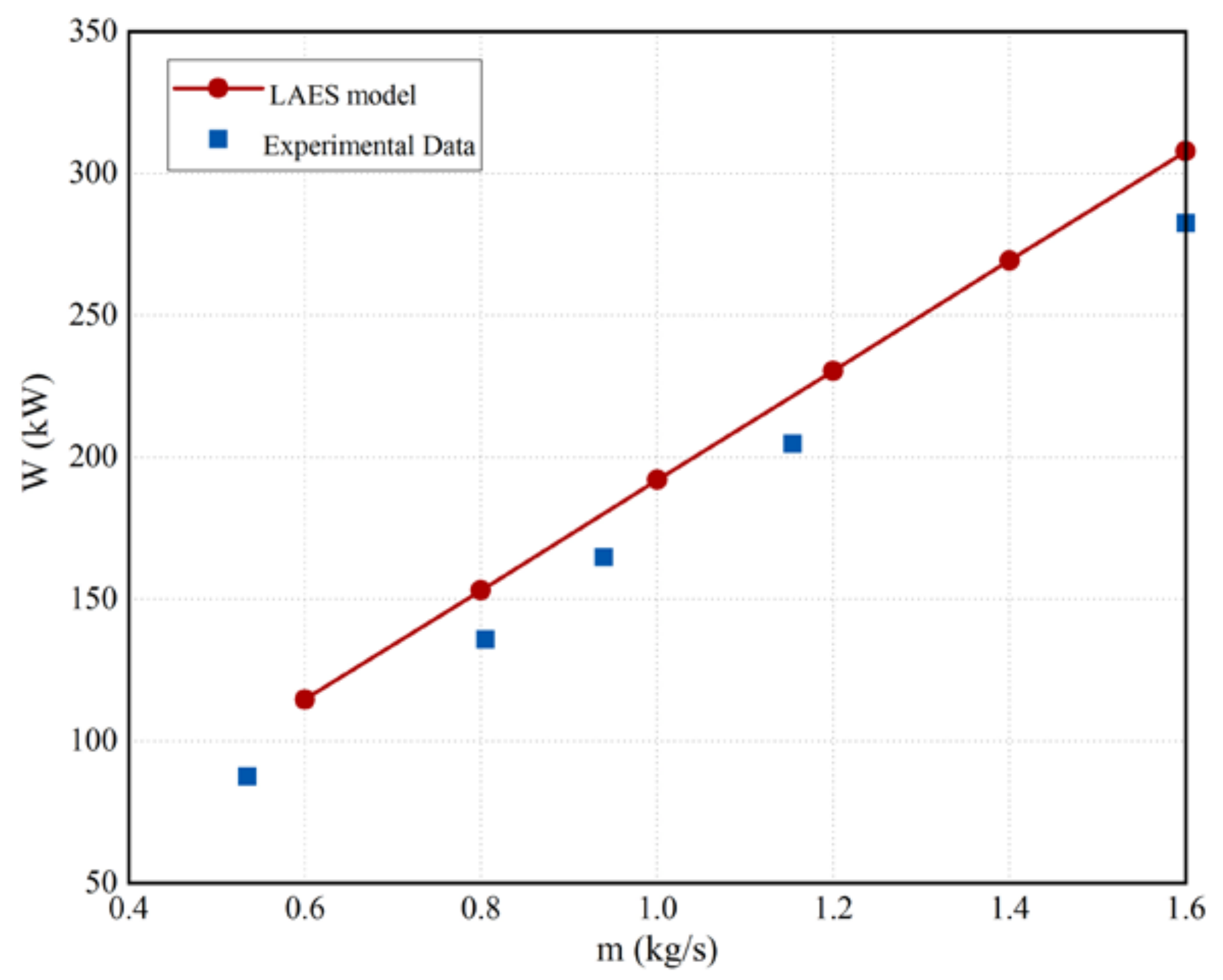
2.5.2. Model Validation of the Proposed LAES System
3. Results and Discussion
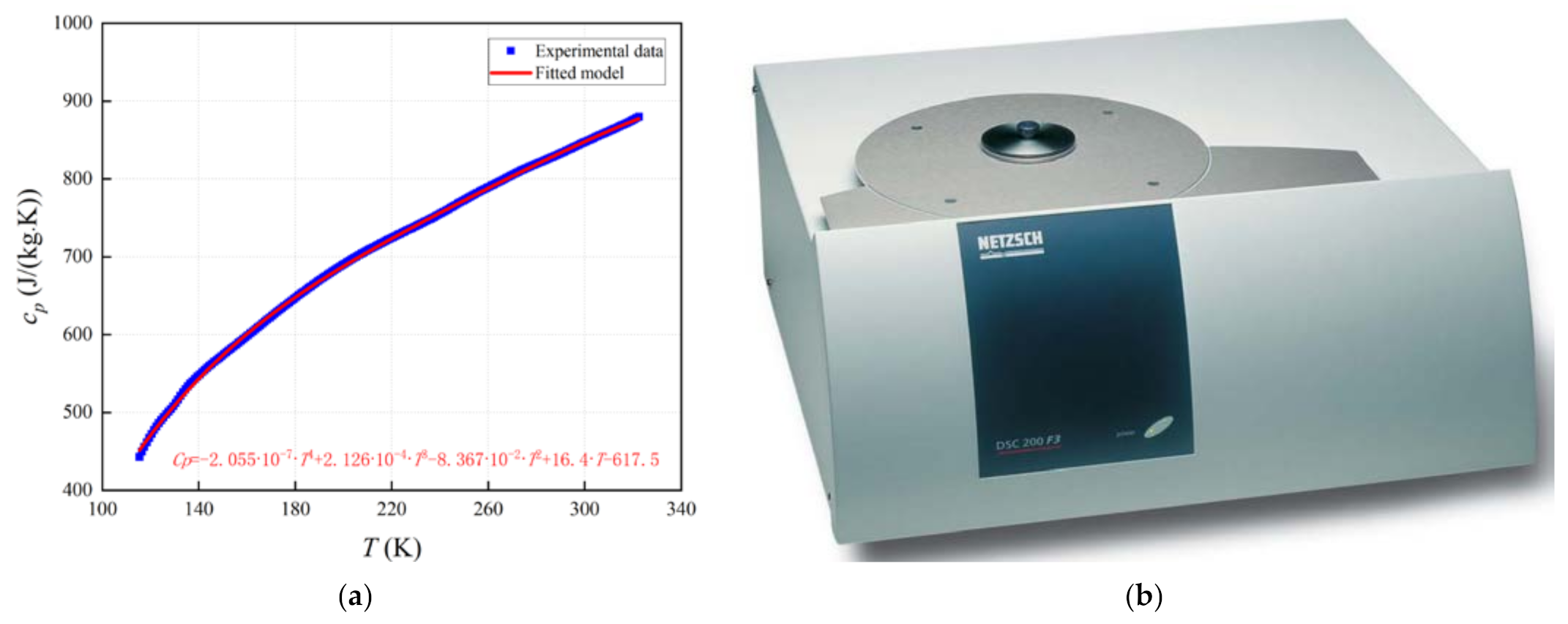
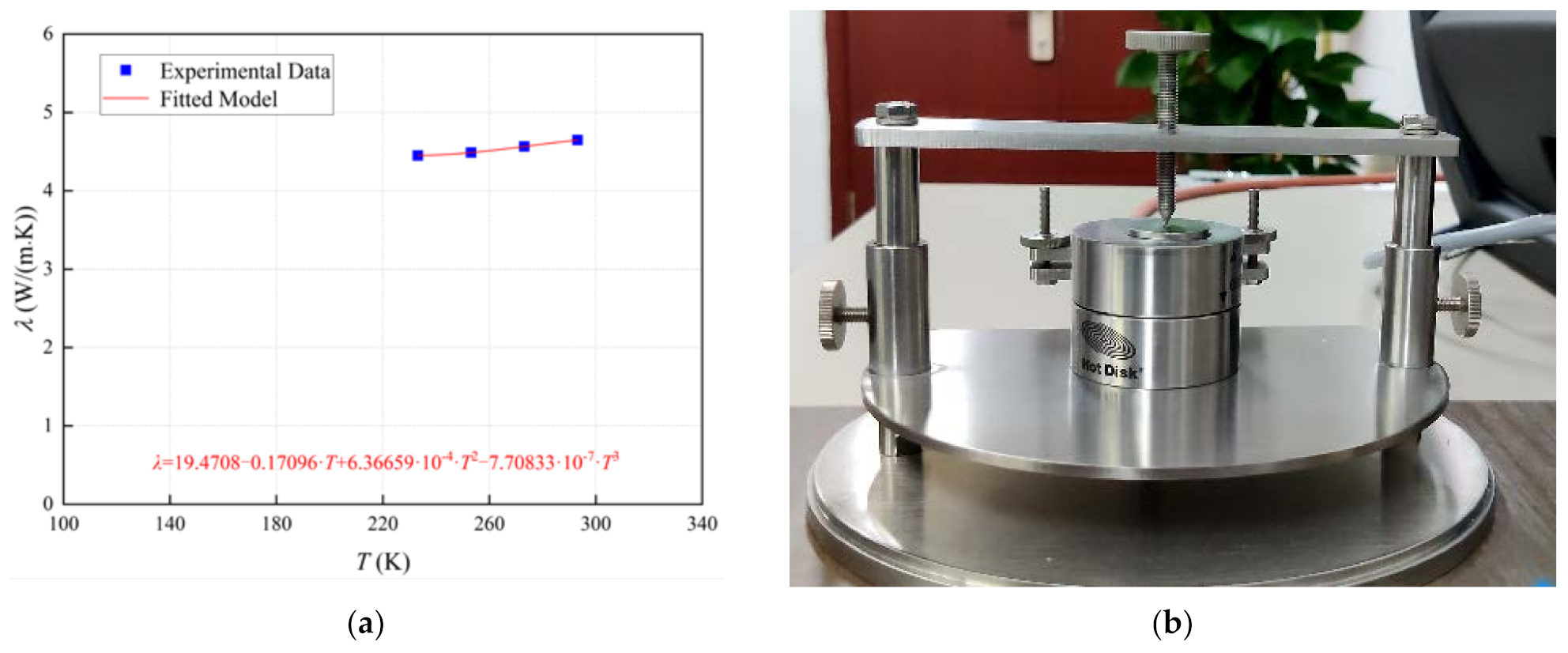
3.1. Physical Characterization of Cold Storage Materials
3.1.1. Density of White Cobbles
3.1.2. Specific Heat Capacity of White Cobbles
3.1.3. Thermal Conductivity of Particles
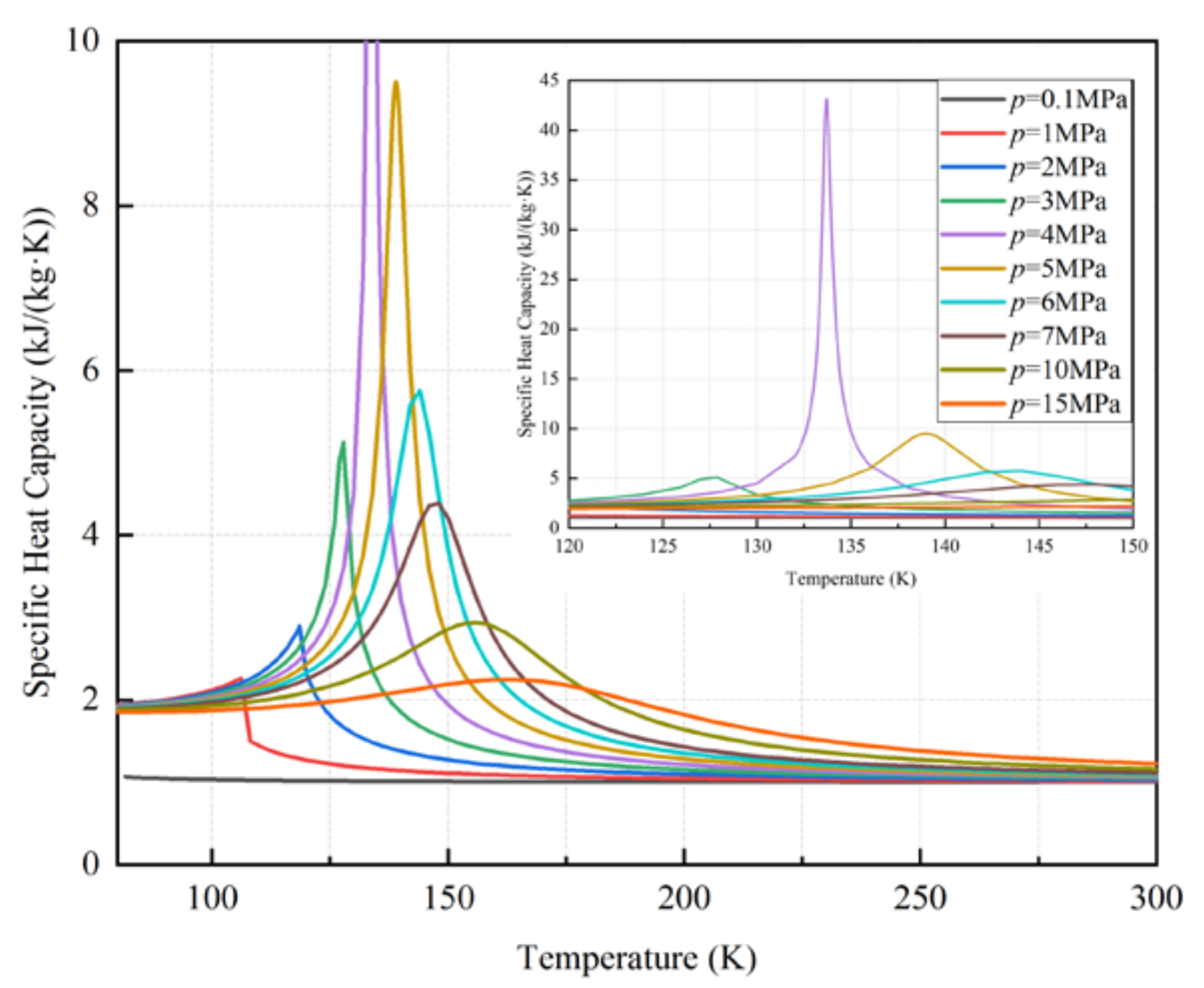
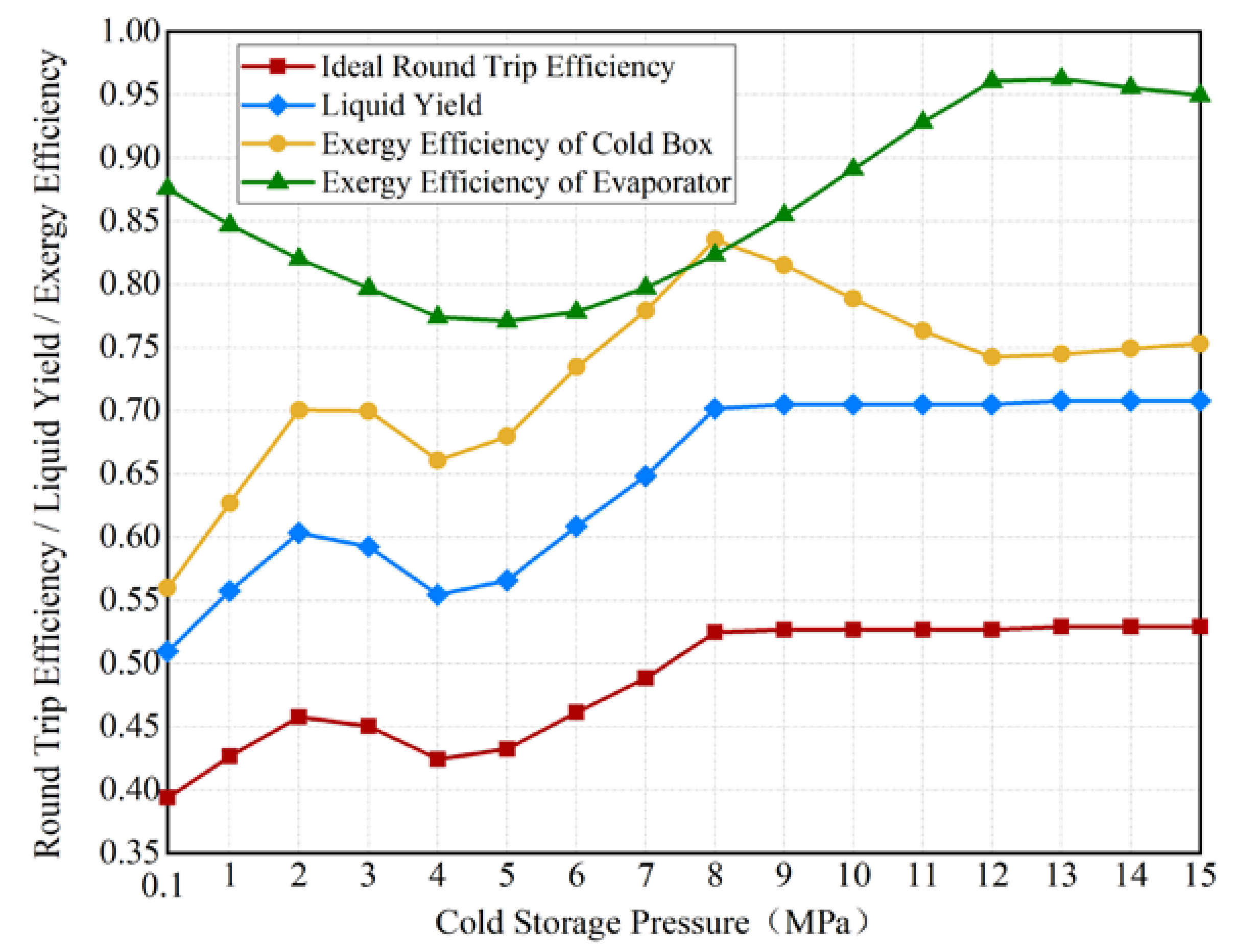
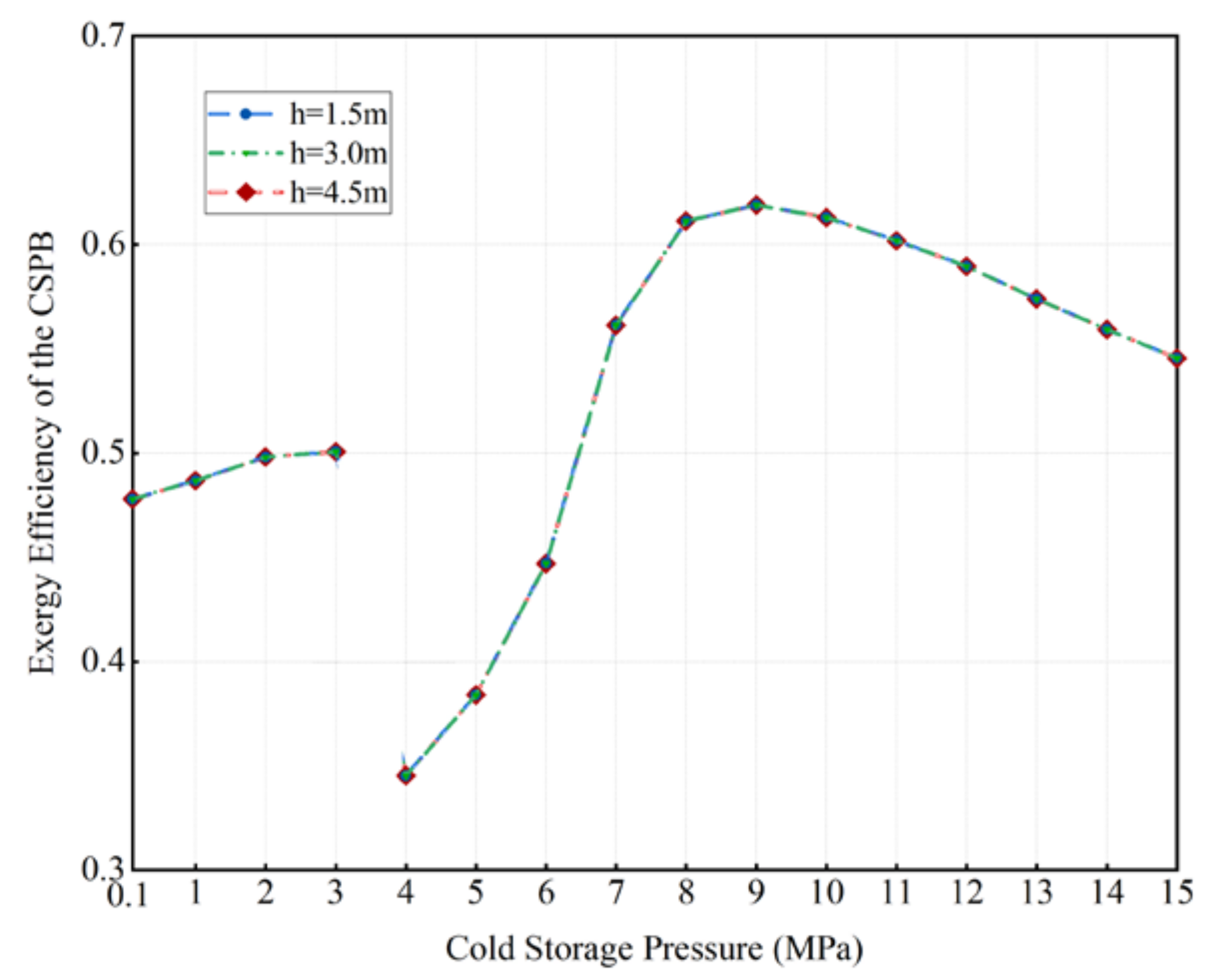
3.2. The Effects of Cold Storage Pressure on the LAES System
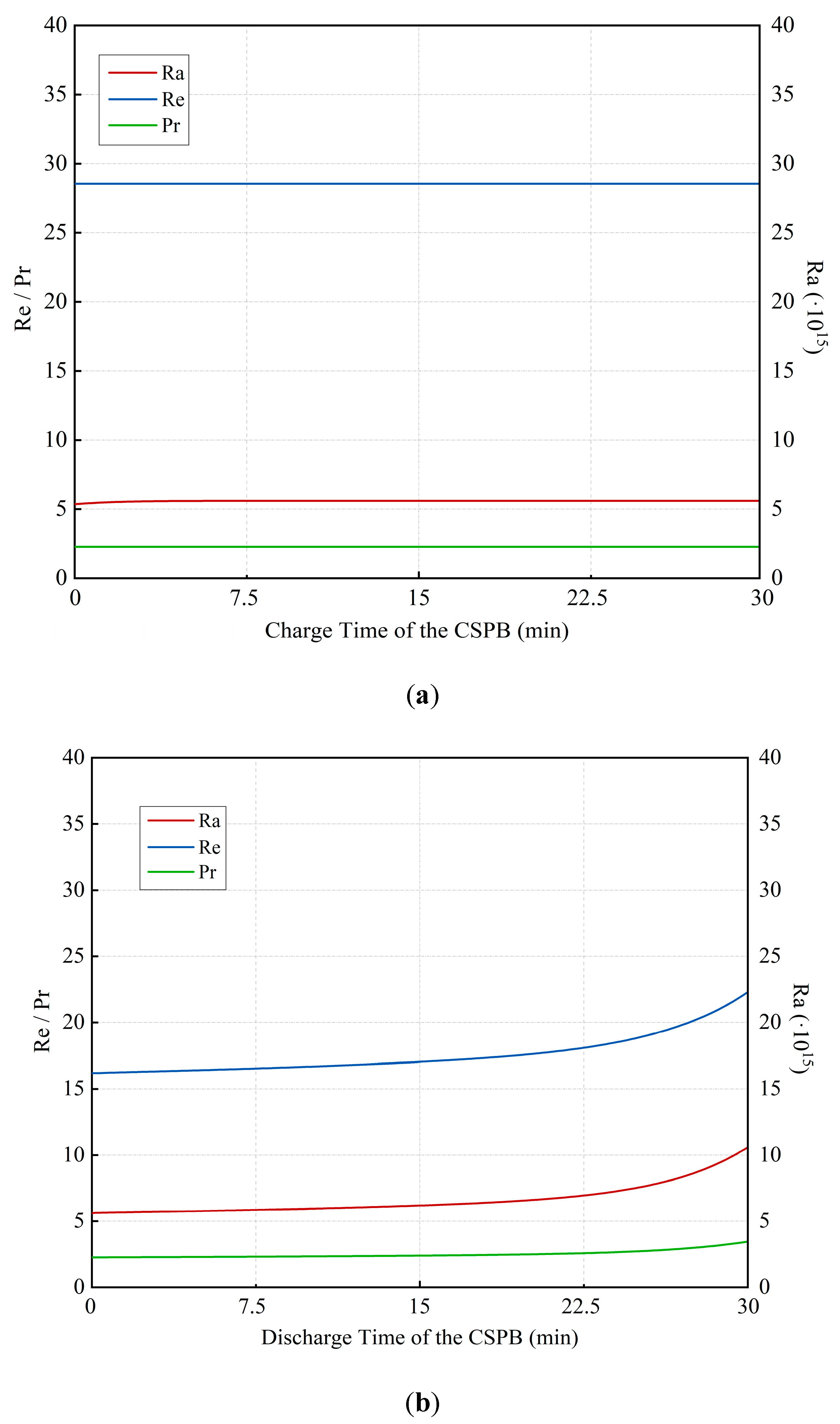
3.3. Dynamic Performance of the Cold Storage Packed Bed
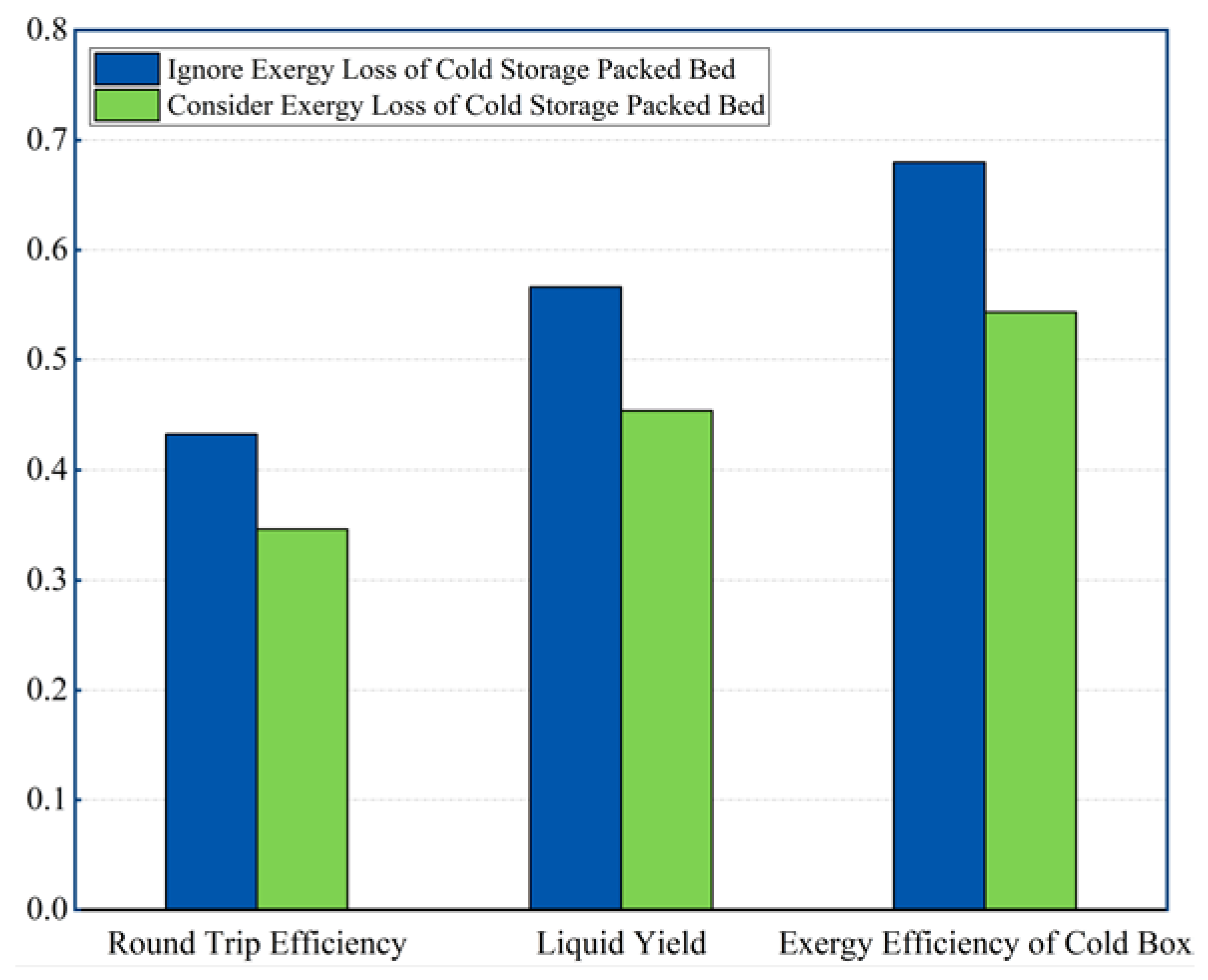
3.4. System Performance Considering the Exergy Loss in the Cold Storage Packed Bed
4. Conclusions
- The cold storage pressure has a significant influence on the thermodynamic performance of the LAES system. The proposed LAES system has an ideal RTE of 39.38–52.91%, without the exergy loss of the CSPB.
- Employed packed bed for cold storage leads to contracted cold contribution to the air liquefaction from liquid air evaporation. The RTE declines by 19.91% considering the exergy loss of the CSPB, compared to the ideal RTE.
- Increasing the cold storage pressure reasonably is beneficial to the exergy efficiency of the CSPB, whether it is non-supercritical air under the pressure of 0.1 MPa–3 MPa or supercritical air under the pressure of 4 MPa–9 MPa.
- The characterizations of the cold storage material are conducted, which indicates that as temperature increases, its specific heat capacity and thermal conductivity both increase.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Δm | mass difference (K) |
| Δt | time step (s) |
| Δz | space step (m) |
| cp | Specific heat (J/(kg·K)) |
| D | diameter of packed bed, i.e., internal diameter of the tank (m) |
| dp | diameter of particles (m) |
| e | specific exergy (J/kg) |
| Gr | Grashof number |
| h | heat transfer coefficient (W/(m2·K)) |
| he | enthalpy (J/kg) |
| m | mass flowrate (kg/s) |
| Nu | Nusselt number |
| P | pressure (MPa) |
| Pr | Prandtl number |
| Q | heat flux (W) |
| Ra | Rayleigh number |
| Re | Reynolds number |
| s | specific entropy (J/(kg·K)) |
| T | temperature (K) |
| t | time (s) |
| u | velocity (m/s) |
| W | power (kW) |
| Y | liquid yield |
| z | height of packed bed (m) |
| Greek symbols | |
| ε | porosity |
| η | efficiency |
| λ | thermal conductivity (W/(m·K)) |
| μ | viscosity (Pa·s) |
| ρ | density (kg/m3) |
| Subscripts | |
| 0 | ambience |
| ave | average |
| charging | charging cycle of the LAES system |
| discharging | discharging cycle of the LAES system |
| f | fluid |
| i | index for cell number |
| in | inlet |
| iso | isentropic |
| out | outlet |
| Pump | cryo-pump |
| s | solid |
| surface | the surface of the bed |
| tra | transient |
| w | wall |
| Acronyms | |
| AC | air compressor |
| AT | air turbine |
| CSPB | cold storage packed bed |
| CT | cryo-turbine |
| EE | exergy efficiency |
| HSPB | heat storage packed bed |
| LA | liquid air |
| LAES | liquid air energy storage |
| PA | pressurized air |
| PC | power consumption |
| PO | power output |
| RTE | round trip efficiency |
References
- IEA Renewable Energy Market Update. 2021. Available online: https://www.iea.org/reports/renewable-energy-market-update-2021 (accessed on 31 July 2021).
- RENEWABLES 2020 GLOBAL STATUS REPORT. Available online: https://www.ren21.net/wp-content/uploads/2019/05/gsr_2020_full_report_en.pdf (accessed on 4 July 2021).
- Denholm, P.; Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 2011, 39, 1817–1830. [Google Scholar] [CrossRef]
- Rodrigues, E.M.G.; Godina, R.; Santos, S.F.; Bizuayehu, A.W.; Contreras, J.; Catalão, J.P.S. Energy storage systems supporting increased penetration of renewables in islanded systems. Energy 2014, 75, 265–280. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, C.; Luo, A.; Liu, Z.; Zhang, X. Molecular dynamics simulation on thermophysics of paraffin/EVA/graphene nanocomposites as phase change materials. Appl. Therm. Eng. 2020, 166, 114639. [Google Scholar] [CrossRef]
- Sun, X.; Mahdi, J.M.; Mohammed, H.I.; Majdi, H.S.; Zixiong, W.; Talebizadehsardari, P. Solidification Enhancement in a Triple-Tube Latent Heat Energy Storage System Using Twisted Fins. Energies 2021, 14, 7179. [Google Scholar] [CrossRef]
- Gao, Y.; Hu, G.; Zhang, Y.; Zhang, X. An experimental study of a hybrid photovoltaic thermal system based on ethanol phase change self-circulation technology: Energy and exergy analysis. Energy 2022, 238, 121663. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Zhang, J. Conjugate solid-liquid phase change heat transfer in heatsink filled with phase change material-metal foam. Int. J. Heat Mass Transf. 2020, 146, 118832. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, D.; Qi, Z.; He, S.; Yang, H.; Zhang, H. Modeling thermal insulation of firefighting protective clothing embedded with phase change material. Heat Mass Transf. 2012, 49, 567–573. [Google Scholar] [CrossRef]
- Li, Y.; Chen, H.; Zhang, X.; Tan, C.; Ding, Y. Renewable energy carriers: Hydrogen or liquid air/nitrogen? Appl. Therm. Eng. 2010, 30, 1985–1990. [Google Scholar] [CrossRef] [Green Version]
- Emiliano, B.; Alessio, T.; Alessandro, R.; Gabriele, C. A review on liquid air energy storage: History, state of the art and recent developments. Renew. Sustain. Energy Rev. 2021, 137, 110572. [Google Scholar]
- Smith, E.M. Storage of electrical energy using supercritical liquid air. Proc. Inst. Mech. Eng. 1977, 191, 289–298. [Google Scholar] [CrossRef]
- Kooichi Chino, H.A. Evaluation of energy storage method using liquid air. Heat Transf. 2000, 29, 347–357. [Google Scholar]
- Morgan, R.; Nelmes, S.; Gibson, E.; Brett, G. Liquid air energy storage—Analysis and first results from a pilot scale demonstration plant. Appl. Energy 2015, 137, 845–853. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Vecchi, A.; Ding, Y. Liquid air energy storage (LAES) with packed bed cold thermal storage—From component to system level performance through dynamic modelling. Appl. Energy 2017, 190, 84–98. [Google Scholar] [CrossRef] [Green Version]
- Legrand, M.; Rodríguez-Antón, L.M.; Martinez-Arevalo, C.; Gutiérrez-Martín, F. Integration of liquid air energy storage into the spanish power grid. Energy 2019, 187, 115965. [Google Scholar] [CrossRef]
- Vecchi, A.; Li, Y.; Mancarella, P.; Sciacovelli, A. Integrated techno-economic assessment of Liquid Air Energy Storage (LAES) under off-design conditions: Links between provision of market services and thermodynamic performance. Appl. Energy 2020, 262, 114589. [Google Scholar] [CrossRef]
- Wang, C.; Bian, Y.; You, Z.; Luo, Y.; Zhang, X.; Peng, H.; Ding, Y.; She, X. Dynamic analysis of a novel standalone liquid air energy storage system for industrial applications. Energy Convers. Manag. 2021, 245, 114537. [Google Scholar] [CrossRef]
- Li, Y.; Cao, H.; Wang, S.; Jin, Y.; Li, D.; Wang, X.; Ding, Y. Load shifting of nuclear power plants using cryogenic energy storage technology. Appl. Energy 2014, 113, 1710–1716. [Google Scholar] [CrossRef]
- She, X.; Peng, X.; Nie, B.; Leng, G.; Zhang, X.; Weng, L.; Tong, L.; Zheng, L.; Wang, L.; Ding, Y. Enhancement of round trip efficiency of liquid air energy storage through effective utilization of heat of compression. Appl. Energy 2017, 206, 1632–1642. [Google Scholar] [CrossRef]
- Peng, X.; She, X.; Cong, L.; Zhang, T.; Li, C.; Li, Y.; Wang, L.; Tong, L.; Ding, Y. Thermodynamic study on the effect of cold and heat recovery on performance of liquid air energy storage. Appl. Energy 2018, 221, 86–99. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Xue, X.; Wang, G.; Mei, S. Thermodynamic Analysis of a Hybrid Power System Combining Kalina Cycle with Liquid Air Energy Storage. Entropy 2019, 21, 220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- She, X.; Zhang, T.; Peng, X.; Wang, L.; Tong, L.; Luo, Y.; Zhang, X.; Ding, Y. Liquid Air Energy Storage for Decentralized Micro Energy Networks with Combined Cooling, Heating, Hot Water and Power Supply. J. Therm. Sci. 2020, 30, 1–17. [Google Scholar] [CrossRef]
- Qi, M.; Park, J.; Kim, J.; Lee, I.; Moon, I. Advanced integration of LNG regasification power plant with liquid air energy storage: Enhancements in flexibility, safety, and power generation. Appl. Energy 2020, 269, 115049.1–115049.18. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, L.; Zhang, X.; Mei, S.; Xue, X.; Zhou, Y. Thermodynamic analysis of a novel hybrid liquid air energy storage system based on the utilization of LNG cold energy. Energy 2018, 155, 641–650. [Google Scholar] [CrossRef]
- Al-Zareer, M.; Dincer, I.; Rosen, M.A. Analysis and assessment of novel liquid air energy storage system with district heating and cooling capabilities. Energy 2017, 141, 792–802. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; You, Z.; Zhang, M.; Huang, S.; She, X. The effect of air purification on liquid air energy storage—An analysis from molecular to systematic modelling. Appl. Energy 2021, 300, 117349. [Google Scholar] [CrossRef]
- Wen, D.; Ding, Y. Heat transfer of gas flow through a packed bed. Chem. Eng. Sci. 2006, 61, 3532–3542. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.; Yang, L.; Yue, L.; Chai, L.; Sheng, Y.; Chen, H.; Tan, C. Experimental study on heat storage and transfer characteristics of supercritical air in a rock bed. Int. J. Heat Mass Transf. 2014, 77, 883–890. [Google Scholar] [CrossRef]
- Chai, L.; Liu, J.; Wang, L.; Yue, L.; Yang, L.; Sheng, Y.; Chen, H.; Tan, C. Cryogenic energy storage characteristics of a packed bed at different pressures. Appl. Therm. Eng. Des. Process. Equip. Econ. 2014, 63, 439–446. [Google Scholar] [CrossRef]
- Ismail, K.A.R.; Stuginsky, R., Jr. A parametric study on possible fixed bed models for pcm and sensible heat storage. Appl. Therm. Eng. 1999, 19, 757–788. [Google Scholar] [CrossRef]
- Esence, T.; Bruch, A.; Fourmigué, J.-F.; Stutz, B. A versatile one-dimensional numerical model for packed-bed heat storage systems. Renew. Energy 2019, 133, 190–204. [Google Scholar] [CrossRef]
- Wakao, N.; Tanisho, S. Chromatographic measurements of particle—Gas mass transfer coefficients at low Reynolds numbers in packed beds. Pergamon 1974, 29, 1991–1994. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Introduction to Conduction. In Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2007; pp. 57–82. [Google Scholar]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Introduction to Convection. In Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2007; pp. 347–387. [Google Scholar]
- Fachlicher Träger VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen. In VDI-Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 2006.
- Lukasz, S.; Piotr, K.; Marcin, W. Exergy Analysis of Adiabatic Liquid Air Energy Storage (A-LAES) System Based on Linde–Hampson Cycle. Energies 2021, 14, 945. [Google Scholar]
- Peng, X.; She, X.; Li, C.; Luo, Y.; Zhang, T.; Li, Y.; Ding, Y. Liquid air energy storage flexibly coupled with LNG regasification for improving air liquefaction. Appl. Energy 2019, 250, 1190–1201. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. Reference fluid thermodynamic and transport properties (REFPROP). In NIST Standard Reference Database 23 Version 9.1; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2013. [Google Scholar]
- Ebrahimi, A.; Ghorbani, B.; Skandarzadeh, F.; Ziabasharhagh, M. Introducing a novel liquid air cryogenic energy storage system using phase change material, solar parabolic trough collectors, and Kalina power cycle (process integration, pinch, and exergy analyses). Energy Convers. Manag. 2021, 228, 113653. [Google Scholar] [CrossRef]
- Nabat, M.H.; Zeynalian, M.; Razmi, A.R.; Arabkoohsar, A.; Soltani, M. Energy, exergy, and economic analyses of an innovative energy storage system; liquid air energy storage (LAES) combined with high-temperature thermal energy storage (HTES). Energy Convers. Manag. 2020, 226, 113486. [Google Scholar] [CrossRef]




| Inner Diameter of Cold Storage Packed Bed | 12 m |
| Height of the Cold Storage Packed Bed | 13.65 m |
| Inlet Air Mass Flow Rate | 406.6 kg/s |
| Pressure of Inlet Air | 0.15 MPa |
| Temperature of Inlet Air | 278.2 K |
| State | m (kg/s) | T (K) | P (kPa) | Medium |
|---|---|---|---|---|
| 1 | 0.028 | 293.000 | 100.000 | Working air |
| 2 | 0.028 | 481.637 | 493.240 | Working air |
| 3 | 0.028 | 299.000 | 493.240 | Working air |
| 4 | 0.028 | 491.925 | 2432.880 | Working air |
| 5 | 0.028 | 299.000 | 2432.880 | Working air |
| 6 | 0.028 | 494.292 | 12,000.000 | Working air |
| 7 | 0.028 | 299.000 | 12,000.000 | Working air |
| 8 | 0.028 | 137.384 | 12,000.000 | Working air |
| 9 | 0.028 | 79.583 | 100.000 | Working air |
| 10 | 0.012 | 81.644 | 100.000 | Working air |
| 11 | 0.012 | 246.317 | 100.000 | Working air |
| 12 | 0.016 | 78.816 | 100.000 | Working air |
| 13 | 0.016 | 84.644 | 12,000.000 | Working air |
| 14 | 0.016 | 273.000 | 12,000.000 | Working air |
| 15 | 0.016 | 441.100 | 12,000.000 | Working air |
| 16 | 0.016 | 293.081 | 2432.880 | Working air |
| 17 | 0.016 | 441.100 | 2432.880 | Working air |
| 18 | 0.016 | 295.522 | 493.240 | Working air |
| 19 | 0.016 | 441.100 | 493.240 | Working air |
| 20 | 0.016 | 296.182 | 100.000 | Working air |
| 21 | 0.067 | 293.000 | 100.000 | Thermal oil |
| 22 | 0.022 | 436.810 | 100.000 | Thermal oil |
| 23 | 0.022 | 446.100 | 100.000 | Thermal oil |
| 24 | 0.022 | 457.605 | 100.000 | Thermal oil |
| 25 | 0.067 | 446.900 | 100.000 | Thermal oil |
| 26 | 0.039 | 446.100 | 100.000 | Thermal oil |
| 27 | 0.013 | 310.295 | 100.000 | Thermal oil |
| 28 | 0.013 | 340.634 | 100.000 | Thermal oil |
| 29 | 0.013 | 344.813 | 100.000 | Thermal oil |
| 30 | 0.039 | 332.200 | 100.000 | Thermal oil |
| 31 | 0.020 | 132.511 | 5000.000 | Pressurized air |
| 32 | 0.020 | 293.000 | 5000.000 | Pressurized air |
| 33 | 0.020 | 293.000 | 5000.000 | Pressurized air |
| 34 | 0.020 | 131.000 | 5000.000 | Pressurized air |
| Type | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Size | Diameter = 0.5 m Height = 1.5 m | Diameter = 3.0 m Height = 1.5 m | Diameter = 4.5 m Height = 1.5 m |
| Charge gas | Pressurized air (0.1–10 MPa) | ||
| Discharge gas | Pressurized air (0.1–10 MPa) | ||
| Charge time | 0.5 h | ||
| Discharge time | 0.5 h | ||
| Charge flowrate | 0.028 kg/s | ||
| Discharge flowrate | 0.016 kg/s | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, Y.; Wang, C.; Wang, Y.; Qin, R.; Song, S.; Qu, W.; Xue, L.; Zhang, X. The Effect of Dynamic Cold Storage Packed Bed on Liquid Air Energy Storage in an Experiment Scale. Energies 2022, 15, 36. https://doi.org/10.3390/en15010036
Bian Y, Wang C, Wang Y, Qin R, Song S, Qu W, Xue L, Zhang X. The Effect of Dynamic Cold Storage Packed Bed on Liquid Air Energy Storage in an Experiment Scale. Energies. 2022; 15(1):36. https://doi.org/10.3390/en15010036
Chicago/Turabian StyleBian, Yong, Chen Wang, Yajun Wang, Run Qin, Shunyi Song, Wenhao Qu, Lu Xue, and Xiaosong Zhang. 2022. "The Effect of Dynamic Cold Storage Packed Bed on Liquid Air Energy Storage in an Experiment Scale" Energies 15, no. 1: 36. https://doi.org/10.3390/en15010036





