RLS-Based Algorithm for Detecting Partial Demagnetization under Both Stationary and Nonstationary Conditions

Abstract

An algorithm was developed detect the partial demagnetization of permanent-magnet synchronous motors (PMSMs) under both stationary and nonstationary conditions. On the basis of the recursive least-squares (RLS) method, the vital component of fault-related harmonics in the current could be extracted on the line, and its proportion to fundamental component could be regarded as the indicator of partial demagnetization faults. The proposed algorithm is fairly easy to realize and could substitute conventional and complicated signal processing methods such as Fourier transform and wavelet transform when detecting partial demagnetization. Experiments with inverter-fed healthy and partially demagnetized PMSMs are carried out to substantiate the effectiveness of proposed algorithm under both stationary and nonstationary conditions. At the end, a way to eliminate the impact of eccentricity fault on the partial demagnetization diagnosis is given.

1. Introduction

1.1. Motivations

Permanent-magnet synchronous motors (PMSMs) are deployed on a large scale for their inherent merits of high torque and power density, and high efficiency [1]. However, the demagnetization of permanent magnets installed in PMSMs has raised major concerns in the academic and industrial fields. Demagnetization occurs in some harsh operation environments such as high temperatures and large currents [2]. In addition, mechanical failures may cause demagnetization faults [3]. In some applications that require high reliability [4,5,6,7], demagnetization faults must be reported early [8].

1.2. Demagnetization Phenomena

In partial demagnetization [9], one or some parts of permanent magnets are demagnetized, which results in the spatial asymmetry of the magnetic field in the air gap. Due to spatial asymmetry, with specific combinations of poles and slots [10,11], back electromotive force (EMF) contains fault-related harmonics that are the source of current harmonics. Many studies proved that this kind of harmonics can be expressed as follows [12,13,14,15,16,17]:

$$f_{fault}=f_e(1\pm n/p)$$

(1)

where f_fault refers to the fault-related harmonic frequency, f_e is the electrical fundamental frequency, p denotes the number of pole pairs, and n is an integer that can be 1, 2, 3, ……

1.3. Related Works

In the literature, many methods emerged to detect partial demagnetization. To directly identify the distribution of magnetic flux, signals measured by the Gaussmeter [18] and Hall sensors [19,20] are analyzed. Since faulted-related harmonics in (1) are introduced in back-EMF, back-EMF could be measured to detect partial demagnetization [21]. However, in most cases, back-EMF cannot be directly measured for PMSMs under operation. Methods based on motor current signature analysis (MCSA) [22,23,24,25,26] were developed and widely commercialized since fault-related harmonics in currents occur simultaneously due to back-EMF harmonics [26]. In addition, information on output torque [27], vibration, and acoustics [28] can also be used to analyze partial demagnetization. In this paper, MCSA was adopted to detect partial online demagnetization due to its feasibility and easy implementation.

According to orders of a fault-related harmonic frequency, partial demagnetization can be recognized by using signal processing methods such as fast Fourier transform (FFT) [22,23], wavelet transform (WT) [24], and Hilbert–Huang transform (HHT) [25]. When PMSMs are operated under stationary conditions, FFT is the most common approach to gain components of fault-related harmonics [26]. However, rigorous conditions must be satisfied when using FFT: (1) integer periods need to be sampled or spectral leakage may happen; (2) sample frequency must be twice higher than the maximal frequency that needs to be analyzed; (3) the number of sample points should be 2N to achieve fast operation of the algorithm [29]. Although the above conditions can be satisfied, there are still some other problems when using FFT, such as complex calculation, and FFT not being suitable when PMSMs are operated under nonstationary conditions since FFT can only reflect the frequency spectrum, but is not able to correlate to time [26]. However, in most applications, such as electrical vehicles and pumps, PMSMs are often operated under nonstationary conditions.

In order to detect partial demagnetization under nonstationary conditions, many time–frequency methods were investigated, including short-time Fourier transform (STFT) [30], continuous and discrete wavelet transform (CWT/DWT) [13,24], and S-transform [21]. The main problem of these time–frequency methods is the resolution of time and frequency [31]. If time resolution is too low, it is difficult to accurately catch the change in frequency during transient processes; if the frequency resolution is too low, the previous frequency cannot be obtained at a specific time. Tme and frequency resolution cannot simultaneously be at a high level according to the Heisenberg uncertainty principle [32]. In order to overcome resolution problems, harmonic order tracking analysis (HOTA) was proposed by means of Gabor transform [33,34,35]. However, this still requires a window of sample data that must be stored in the memory, and needs complex calculation.

In this paper, an RLS-based algorithm to detect the partial demagnetization of PMSMs under both stationary and nonstationary conditions is presented. Some regression models, such as neural networks [36], ADALINE filters [37], convolutional neural networks (CNNs), the support vector regression method (SVRM) [38], and RLS [39] were applied in most applications, but none of these models was utilized in the field of partial demagnetization detection, where they may present sremarkable merits under stationary and nonstationary conditions. Among these regression models, RLS is comparatively easy to realize and was hence used in this paper. Another advantage of methods such as RLS is the fact that the result is physically interpretable, which is not always true with advanced methods. The proposed RLS-based algorithm can be executed in real time, and magnitudes of fault-related harmonics are established to indicate the health of PMSMs. Moreover, there is no need to store previous data in the proposed algorithm, which enables the use of the algorithm in embedding devices with small-capacity memory. The proposed algorithm could substitute conventional and complicated signal-processing methods, such as Fourier transform and wavelet transform, when detecting partial demagnetization. Experiments with inverter-fed healthy and partially demagnetized PMSMs were carried out to substantiate the effectiveness of proposed algorithm under both stationary and nonstationary conditions. Lastly, a specific part of eccentricity faults and its impact is discussed.

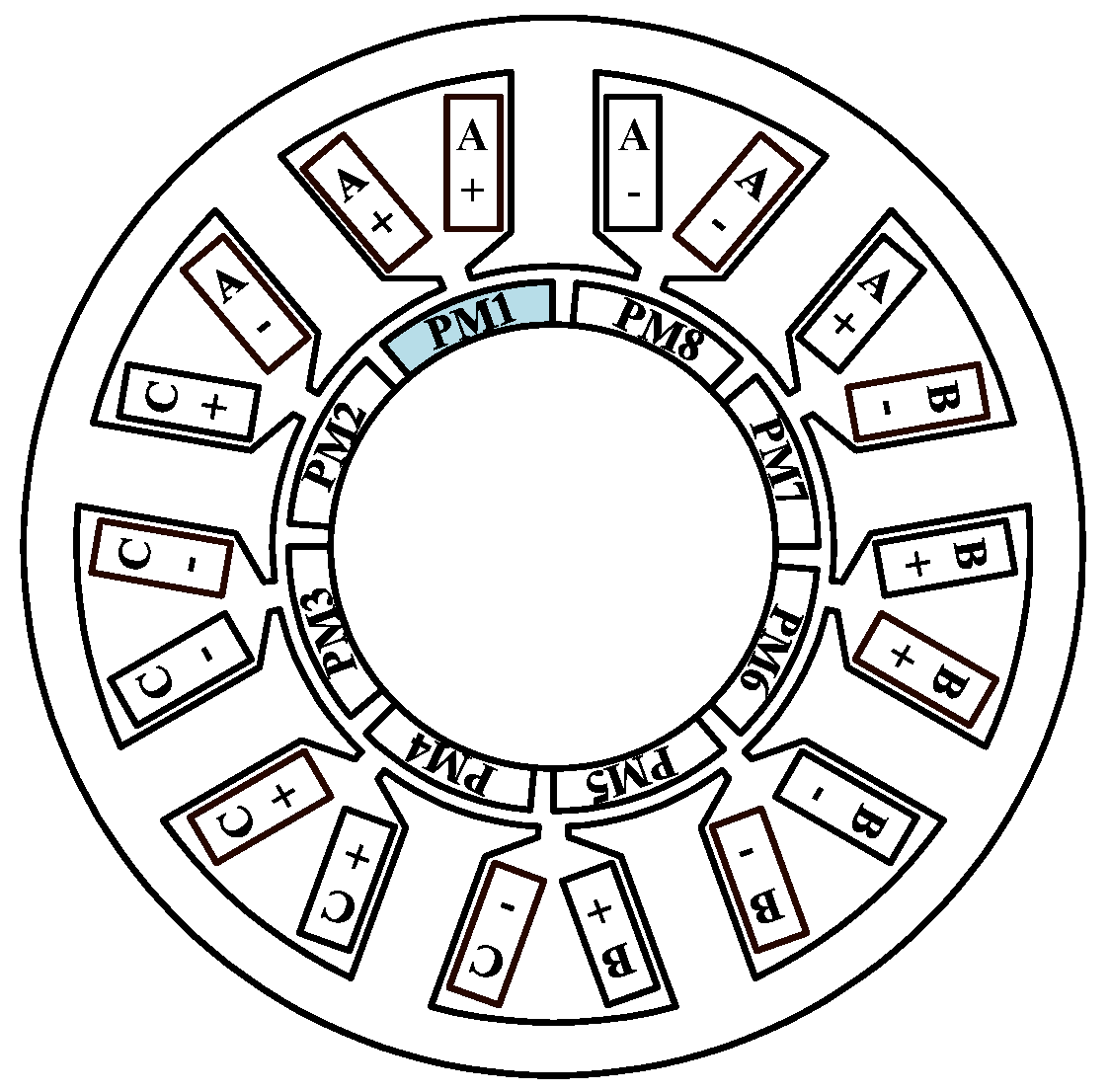
2. Partial Demagnetization Model of PMSMs

To better illustrate the fault-related harmonics introduced in the current due to partial demagnetization, a 9-slot and 8-pole PMSM with star-connected winding, whose structure is presented in Figure 1, is investigated in this paper. The typical frequency spectrum of phase back-EMF when one or more permanent magnets are partially demagnetized is shown in Figure 2, in which magnitude refers to the ratio of the fundamental components. Side frequencies around the fundamental component (2/4th-, 3/4th- and 5/4th-order) were the predominant fault-related harmonics whose magnitudes are major indicators of partial demagnetization faults.

For inverter-fed PMSMs, back-EMF cannot be directly measured, so currents must be sampled and used to detect partial demagnetization faults. To reduce computational resources and use less memory storage, only a few orders of fault-related harmonics are relevant, and phase current i_a when partial demagnetization happens can be written as follows [40]:

$$i_a={\displaystyle \sum _{k=1}^{\infty }{A}_k\sin (2\pi f_{e}t\times k/p)+B_k\cos (2\pi f_{e}t\times k/p)}$$

(2)

When detecting a partial demagnetization fault, specific values of k are adopted instead of all on the basis of the frequency spectrum. For instance, Figure 2 displays that the other frequencies were near to zero except the 2/4th-, 3/4th-, 5/4th-order and fundamental components; values of k in i_a current expression (2) could be set as 2 (for the 2/4th order), 3 (for the 3/4th order), 4 (for the fundamental components), and 5 (for the 5/4th order). However, the real current content was more complicated than the components above. Some odd harmonics such as the 5th and 7th orders were included in the currents due to magnet saturation, the slot effect, and inverter nonlinearity. Inphase fault-related harmonics disappear in a symmetric three-phase winding; for instance, the 3/4th order harmonic existing in phase back-EMF shown in Figure 2 was absent in the line-to-line back-EMF and may not appear in the currents either. Due to the switching frequency of the inverter, components around the switching and double switching frequencies are also involved in the frequency spectrum of currents, but these high-frequency components could be simply eliminated by a low-pass filter (LPF) with a proper cut-off frequency. Hence, phase current i_a in (2) can be expressed as the combination of selected frequencies:

$$\begin{array}{l}{i}_a=A_2\sin (2\pi f_{e}t\times 2/p)+B_2\cos (2\pi f_{e}t\times 2/p)+A_4\sin (2\pi f_{e}t\times 4/p)+B_4\cos (2\pi f_{e}t\times 4/p)\\ \begin{array}{cc}& +A_5\sin (2\pi f_{e}t\times 5/p)+B_5\cos (2\pi f_{e}t\times 5/p)+A_{20}\sin (2\pi f_{e}t\times 20/p)+B_{20}\cos (2\pi f_{e}t\times 20/p)\end{array}\\ \begin{array}{cc}& +A_{28}\sin (2\pi f_{e}t\times 28/p)+B_{28}\cos (2\pi f_{e}t\times 28/p)\end{array}\end{array}$$

(3)

Magnitude M_k of each component could be established as follows:

$$M_k=\sqrt{A_k{}^2+B_k{}^2}$$

(4)

and phase φ_k of each component is calculated with:

$${\phi }_k=\arctan \frac{B_k}{A_k}$$

(5)

The magnitude of fault-related frequency could be deemed to be the indicator of partial demagnetization. The key point is to identify values of A_k and B_k for each selected frequency component, which is discussed in the next sections.

3. Proposed Algorithm of Detecting Partial Demagnetization

The expression of i_a in (3) is the linear combination of selected components; recursive least-squares (RLS) is the simplest way to identify A_k and B_k. Under stationary conditions, motor speed and electrical fundamental frequency f_e are constant, while under nonstationary conditions, motor speed and f_e vary. In order to apply the RLS algorithm, motor speed must be obtained from the position sensors. In this section, RLS is first briefly introduced, and an algorithm of detecting partial demagnetization is proposed that is adaptive to the change in speed and can be utilized under both stationary and nonstationary conditions.

3.1. Recursive Least Squares (RLS)

Consider a system with output that can be expressed as the linear combination of inputs, which is presented in (6):

$$y(i)=w_1(i)x_1(i)+w_2(i)x_2(i)+\dots +w_m(i)x_m(i)=W{(i)}^{T}X(i)$$

(6)

where i is the i-th iteration of RLS algorithm; y is the output of the system; x_m is the m-th input of the system; and w_m is the coefficient of the m-th input that needs to be identified. Auxiliary variable s is inserted to represent the estimated output:

$$s(i)={\widehat{w}}_1(i)x_1(i)+{\widehat{w}}_2(i)x_2(i)+\dots +{\widehat{w}}_m(i)x_m(i)=\widehat{W}{(i)}^{T}X(i)$$

(7)

where ${\widehat{w}}_m$ is the estimated coefficient of the m-th input. The basic principle of RLS is to minimize the error between estimated output s and real output y; hence, a cost function is given by:

$$C=\frac{1}{2}{[y(i)-s(i)]}^2$$

(8)

There are many other selections for cost functions, such as symmetric mean absolute percentage error (SMAPE), given by:

$$C=\frac{|y(i)-s(i)|}{(|y(i)|+|s(i)|)/2}$$

(9)

To simplify the algorithms, the cost function in (8) was selected in this paper.

By using the gradient descent algorithm to minimize the value of C, the operation process of updating the estimated coefficients could be written as:

$$\widehat{W}(i)=\widehat{W}(i-1)+K(i)[y(i)-\widehat{W}{(i-1)}^{T}X(i)]$$

(10)

$$K(i)=\frac{P(i-1)X(i)}{\lambda +X{(i)}^{T}P(i-1)X(i)}$$

(11)

$$P(i)=[I-K(i)X{(i)}^T]\times P(i-1)/\lambda$$

(12)

where λ is the forgetting factor to deal with data saturation; a larger value of λ always needs longer convergence time, while a smaller λ may cause the vibration of the results; hence, the selection of λ is a trade-off between convergence time and vibration.

In the case of the RLS algorithm, the normal equations are as follows [41,42,43]:

$${\displaystyle \sum _{i=1}^n{\lambda }^{n-i}X(i)X^T(i)\widehat{W}(i)}={\displaystyle \sum _{i=1}^n{\lambda }^{n-i}X(i)y(i)}+{\displaystyle \sum _{i=1}^n{\lambda }^{n-i}X(i)v(i)}$$

(13)

where v(i) is system noise. When the value of λ is close to 1, it is assumed that

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{\lambda }^{n-i}X(i)v(i)}\approx E(X(n)v(n))=0$$

(14)

where E is the mathematical expectation. Then,

$${\displaystyle \sum _{i=1}^n{\lambda }^{n-i}X(i)X^T(i)\widehat{W}(i)}={\displaystyle \sum _{i=1}^n{\lambda }^{n-i}X(i)y(i)}={\displaystyle \sum _{i=1}^n{\lambda }^{n-i}X(i)X^T(i)W(i)}$$

(15)

Thus,

$$\widehat{W}(i)=W(i)$$

(16)

which means that the estimated values can be well-converged to the real values when the value of λ is close to 1. When the value of λ is much less than 1,

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{\lambda }^{n-i}X(i)v(i)}\ne 0$$

(17)

Lastly, estimated values are impacted by system noise, leading to the instability of the RLS algorithm.

3.2. Methodology of Partial Demagnetization Detection

By virtue of the RLS algorithm introduced above, the coefficients of each component A_k and B_k can be estimated. Then, their magnitudes can be regarded as indicators of partial demagnetization:

$$y(i)=i_a(i)$$

(18)

$$\begin{array}{ll}X(i)=& [\sin (2\pi f_{e}t\times 2/p),\cos (2\pi f_{e}t\times 2/p),\\ & \sin (2\pi f_{e}t\times 4/p),\cos (2\pi f_{e}t\times 4/p),\\ & \sin (2\pi f_{e}t\times 5/p),\cos (2\pi f_{e}t\times 5/p),\dots {]}^T\end{array}$$

(19)

$$W(i)={[A_2,B_2,A_4,B_4,A_5,B_5,\dots ]}^T$$

(20)

The proposed methodology estimates values of A_k and B_k. Figure 3 shows the flowchart of the proposed methodology.

Figure 3 shows that f_e and t are used to calculate the selected components in (3), and i_a, 0 measured with current sensors, is system output y. After the system initialization of i, λ, P(0) and $\widehat{W}(0)$, the values of K(i), P(i), and $\widehat{W}(i)$, can be established. Through several iterations, the results of A_k and B_k are able to converge to their real values. Then, the magnitude of each fault-related harmonic component and the fundamental component in the currents are identified through Equation (4). The magnitude values of fault-related harmonic components can help in distinguishing healthy PMSMs from partially demagnetized ones by selecting proper threshold value ε.

Under stationary conditions, motor speed and f_e are fixed, and the proposed algorithm functions are the same as in the FFT method to gain the amplitude of each component. Under nonstationary conditions, motor speed and f_e vary and must be obtained from position sensors; hence, the proposed algorithm is adaptive to speed changes, which allows for dealing with nonstationary situations like in methods of time–frequency analysis. In addition, the proposed algorithm focuses on several dominant components that can avoid the resolution problems of existing time–frequency analysis and reduce computational resources.

4. Experimental and Simulation Validation

In order to substantiate the effectiveness of proposed algorithm, experimental validation was carried out and is described in Figure 4. The main parameters of the tested PMSM are listed in

Table 1. Tested PMSM parameters.

Parameter	Value
Number of poles and slots	8 poles and 9 slots
Winding connection	Star-connected winding
Rated speed	1000 rpm
Rated current	2.6A (peak)
Rated voltage	100 V
Stator resistance	2.54 ohm
Stator inductance	7.1 mH
Flux linkage	0.062 Wb

. The details of RLS algorithms are given in

Table 2. Details of RLS algorithms.

Sampling Number	Forgetting Factor λ	Sampling Step
Sampling in each PWM period (0.1 ms)	0.999	0.1 ms

.

The tested PMSM was partially demagnetized while PMSM load was healthy. Moreover, another healthy PMSM was tested in order to compare the current difference between healthy and partially demagnetized PMSMs. The tested healthy and partially demagnetized PMSMs were both driven by commercial inverter box with the TMS320F28335 DSP and controlled with field oriented control (FOC) strategy, the overall control block is shown in Figure 5:

Figure 5 shows that i_a was measured from the terminal of the motor. Additionally, motor speed was monitored by the encoder installed in the rotor, and fundamental frequency f_e could be established. Values of i_a and f_e were used to execute the proposed algorithm, as shown in Figure 3, to detect partial demagnetization in real time. Both the stationary and nonstationary operations of the tested PMSM were analyzed in the experiments.

4.1. Stationary Conditions

First, the case when the tested PMSMs were operated under stationary conditions was examined. PMSMs are maintained at rated speed of 1000 rpm, and rated phase current i_a had a peak value of 2.6 A. Figure 6 shows the waveforms of i_a for both healthy and demagnetized PMSMs.

By using the proposed algorithm in Figure 3, coefficient values of each selected component in (3) A_k and B_k could be established. Through Equation (4), the magnitude of each fault-related harmonic in current i_a can then be calculated. In order to vividly depict the effectiveness of the proposed algorithm and consider the magnitude change of fundamental component, explicit indicator value η of partial demagnetization can be expressed as:

$$\eta =\frac{M_k}{M_4}\times 100\%=\frac{\sqrt{A_k{}^2+B_k{}^2}}{\sqrt{A_4{}^2+B_4{}^2}}\times 100\%$$

(21)

which is the magnitude ratio of the k/4th-order harmonic component to the fundamental component. Figure 7a,b show the ratio comparisons of 2/4th- and 5/4th-order harmonics, respectively, between partially demagnetized and healthy PMSMs under stationary conditions. Figure 7 shows that the fault-related harmonic ratio of the partially demagnetized PMSM was larger than that of the healthy PMSM. Figure 7a shows that the ratio of the 2/4th-order harmonic to the fundamental component for the partially demagnetized PMSM was 1.4%, while the ratio for the healthy PMSM was less than 0.2%. In terms of the 5/4th-order harmonic, as shown in Figure 7b, the ratio was 2.5% for the partially demagnetized PMSM, and 1.0% for the healthy PMSM. The first 0.2 s in Figure 7 is the convergence time of the proposed algorithm that is related to the value of λ. If the forgetting factor is too small, previous data are forgotten faster, leading to possible numerical instability. On the other hand, data saturation may occur with a larger forgetting factor, resulting in a slow convergence rate. Thus, there is a trade-off when selecting the value of the forgetting factor; in this paper, the final value of the forgetting factor was 0.999. Experimental results with different values of forgetting factor (0.999 and 0.9) are presented in Figure 7.

Fault-related harmonics in a healthy PMSM are ideally zero, but due to the inherent spatial asymmetry caused by the mechanical installation of rotor shafts and permanent magnets, some small fault-related harmonics exist in the current for healthy PMSMs, which is why current magnitudes of 2/4th- and 5/4th-order harmonics for healthy PMSMs were not absolutely zero in the experiment.

To evaluate the proposed algorithm against a conventional FFT, the magnitudes of corresponding harmonic components in the current with different motor health conditions were also computed through FFT and are listed in

Table 3. Magnitude of each fault-related harmonic component in current with different algorithms and different health status (unit: A).

Harmonic Order	Demagnetized PMSM (FFT)	Demagnetized PMSM (RLS)	Healthy PMSM (FFT)	Healthy PMSM (RLS)
2/4th	0.0335	0.0375	0.0007	0.0027
4/4th	2.6299	2.6301	2.5171	2.5197
5/4th	0.0699	0.0662	0.0324	0.0325
5th	0.0139	0.0143	0.0167	0.0199
7th	0.0084	0.0086	0.0090	0.0087

. Important points from Table 3 are as follows:

• Comparing Columns 2 and 3, and Columns 4 and 5 shows that the magnitudes of each fault-related harmonic component were similar through different algorithms (FFT and RLS) for the partially demagnetized PMSM. The same was true in comparing Columns 4 and 5 for the healthy PMSM, which means the proposed algorithm with RLS could substitute FFT when analyzing the frequency spectrum in real-world use. Minor errors between FFT and RLS may be due to the spectral leakage of FFT, the data saturation of RLS, and other factors.
• For the partially demagnetized PMSM, the magnitudes of fault-related harmonics components are larger than the ones of healthy PMSM, which can be seen from the column 2 and column 4 as well as the column 3 and column 5 in Table 3. This characteristic can be regarded as the indicator of the partial demagnetization fault.
• Since the proposed algorithm is in the recursive form, the computational resources can be reduced significantly. The execution time of one iteration in the proposed algorithm is 0.2 ms, while under stationary conditions, the execution time of 512-point FFT in the TMS320F28335 DSP is more than 10 ms. In addition, the FFT requires more memory capacity to store the data points.

To prove the robustness of the proposed algorithm when the load changes, the PMSMs are operated at the same speed of 1000 rpm with the different peak current of 0.6A. After implementing the proposed algorithm in Figure 3, the extracted 2/4th and 5/4th harmonics are displayed in Figure 8. Similarly, 2/4th and 5/4th harmonic magnitudes when the PMSM was partially demagnetized were larger than those of the healthy PMSM.

4.2. Nonstationary Conditions

Under nonstationary conditions, PMSM speed is not constant. Normal FFT cannot analyze the content of harmonic components with the change in time, which hinders recognizing partial demagnetization faults. Many time–frequency analyses were investigated to overcome the problem of FFT under nonstationary conditions, but these methods tend to require complicated calculations, and have poor resolution of time and frequency. Using the proposed algorithm in this paper, it is possible to deal with the above problems. To prove that, the tested partially demagnetized PMSM was operated under nonstationary conditions, and current i_a was measured and analyzed with the proposed algorithm in Figure 3. Under nonstationary conditions, motor speed or fundamental frequency f_e is a crucial factor that greatly impacts the accuracy of the proposed algorithm; hence, motor speed should be precisely sampled through speed sensors.

Waveforms of phase current i_a and speed for the partially demagnetized PMSM under nonstationary conditions are given in Figure 9. During the first 3 s, motor speed was maintained at 900 rpm, and peak current was 0.5A. At 3 s, the motor began to decelerate to 450 rpm, and the current was decreased to 0.4 A. After the transient process, the motor speed was held at 450 rpm.

Using the proposed algorithm in Figure 3 under nonstationary conditions, the magnitudes of fundamental and harmonic components in the current could be extracted, and results are presented in Figure 10, showing that the magnitude of the fundamental component in current i_a began to decrease at 3 s. Results in Figure 10 prove that, with the change in time, the proposed algorithm enables gaining the magnitude of each predominant component in the frequency spectrum of the current under nonstationary conditions, just like other methods of time–frequency analyses.

Figure 11 shows the magnitude ratios of the 2/4th-order component to the fundamental component, which uses indicator value η in (15) to evaluate partial demagnetization. In terms of the 2/4th-order harmonic, the ratio to the fundamental component was 1% for the partially demagnetized PMSM, and less than 0.1% for the healthy PMSM. In addition, Figure 12 displays the magnitude ratios of the 5/4th-order component to the fundamental component; the ratio for the partially demagnetized PMSM was much larger than that of the healthy PMSM. Under nonstationary conditions, magnitudes of fundamental and harmonic components vary, as shown in Figure 10, which hinders setting a threshold value for judging the occurrence of demagnetization. To overcome this problem, the ratio of harmonic component to fundamental component can be regarded to be a unified and per-unit value. When the motor is operated under nonstationary conditions, the ratio is on the same or a similar level, and it is convenient to set threshold value ε to recognize partial demagnetization.

4.3. Comparison with Other Time–Frequency Analyses under Nonstationary Conditions

Furthermore, other tools of time–frequency analysis were compared when the PMSM is operated under nonstationary conditions. As mentioned in Section 1, problems of time and frequency resolution are major concerns when using these tools. For instance, Gabor transform possesses the highest resolution and concentration in the time–frequency domain [35], which can be expressed as:

$$G(t,f)=\sqrt[4]{\sigma }{\displaystyle {\int }_{-\infty }^{\infty }{e}^{-\sigma \pi {(\tau -t)}^2}{e}^{-j2\pi f\tau }x(\tau )}d\tau$$

(22)

To describe resolution problems in detail, Gabor transform was adopted to track fault-related harmonics in the nonstationary current in Figure 9. Results when σ = 0.5 and σ = 50 are shown in Figure 13 and Figure 14., respectively.

Figure 13 shows that, when σ was smaller (σ = 0.5), the resolution in the frequency domain was higher, while the resolution in the time domain was not satisfactory, which hindered catching the change in frequency during the transient process in time. Figure 14 shows the opposite: when the value of σ was larger (σ = 50), resolution in the time domain was higher, so the frequency change was clearer under nonstationary conditions. However, the improvement of resolution in the time domain sacrifices resolution in the frequency domain, which obstructs distinguishing fault-related harmonics in the frequency spectrum, for instance, the 5/4th harmonic component can hardly be seen in Figure 14. Therefore, it is crucial to find a proper value of σ when utilizing Gabor transform. For other tools of time–frequency analysis such as wavelet transform, a similar problem also occurs. By using the proposed algorithm in this paper, the resolution problem in the time and frequency domains could be avoided.

There are also other potential merits of our proposed algorithm compared with other existing methods of time–frequency analysis. The execution time of one iteration in the proposed algorithm is 0.2 ms under both stationary and nonstationary conditions. The execution time of other time–frequency analyses is much longer under nonstationary conditions, for instance, it takes more than 2 ms to complete one-point calculation (for one specific time and one specific frequency) on the time–frequency plane. To finish the whole map of the time–frequency plane, it usually takes several hours when the dataset is too large, which hinders using these time–frequency analyses in embedded devices. In addition, other methods of time–frequency analysis require large memory capacity to store data points within the specific window. The proposed algorithm only needs one data point at the current moment, which pronouncedly reduces the memory burden of embedded devices. The merits and demerits of FFT, time–frequency (TF) analyses, and RLS are listed in

Table 4. Merits and demerits of different analytical tools.

Tools	Merits	Demerits
FFT	(1) Most known and mature way to analyze spectrum. (2) No resolution problems, since it can only analyze the frequency domain along with a long stationary time of 0.0335.	(1) Cannot detect the fault under nonstationary conditions. (2) Integer periods need be sampled or spectrum leakage may happen. Sample frequency must be twice higher than the maximal frequency that needs to be analyzed. (3) The number of sample points should be 2N to achieve fast algorithm processing.
TF(Gabor)	(1) Able to detect faults under both stationary and nonstationary conditions.	(1) Resolution problem in time and frequency domains. (2) Complicated calculation (2 ms to complete one-point on time–frequency plane, more time to complete analysis).
RLS	(1) Able to detect faults under both stationary and nonstationary conditions. (2) No resolution problem in time and frequency domains. (3) Execute in recursive form to reduce computational burden (only 0.2 ms for one iteration).	(1) Careful selection of forgetting factor λ. (2) Needs precise speed information.

.

4.4. Elimination of Eccentricity Faults

Eccentricity faults also introduce the fault harmonics presented in (1) [11,13,17,20], which lead to false diagnoses of partial demagnetization. Some measures should be taken to eliminate the impact of eccentricity faults. Hence, two different kinds of eccentricity, namely, static and dynamic eccentricity (SE and DE), are discussed here. Using finite element analysis (FEA), 3-phase back-EMFs are shown in Figure 15 when the 9-slot and 8-pole PMSM was healthy or suffering from partially demagnetization, and with SE and DE faults.

On the one hand, SE causes different distances between 3-phase windings on the stator and permanent magnets on the rotor, which obviously resulted in the unbalance of 3-phase back-EMFs in Figure 15c. For one-phase or line-to-line back-EMF, the fault-related harmonics in (1) would not be present, which the frequency spectrum of E_AB in Figure 16a shows.

On the other hand, a DE fault introduces the fault-related harmonics shown in Figure 16b. However, the rotor is always dynamically decentered to one direction along with time when the DE fault occurs, which causes the back-EMF amplitude to be much larger than that of healthy motors. Hence, a DE fault can be simply excluded by capturing the largest peak value of E_AB in one mechanical period, depicted in Figure 15b,d. As shown in

Table 5. Largest peak value of E_AB in one mechanical period under different conditions (for 9-slot and 8-poles motor at 1000 rpm).

Healthy	DE 25%	DE 100%	Demag 1.78%	Demag 3.57%	Demag 5.35%	Demag 7.14%	Demag 8.92%	Demag 10.71%
58.2 V	65.5 V	88.5 V	58.4 V	58.3 V	58.1 V	58.1 V	58.1 V	58.1 V

, the largest peak value of E_AB in one mechanical period under different conditions is listed. When DE occurs, the largest peak value is larger than that of healthy motors; when partial demagnetization happens, the largest peak value is always near that of a healthy motor. By using this characteristic, the impact of eccentricity could be eliminated from the partial demagnetization fault. Because manufacturing eccentric PMSMs always takes a long time, and the main focus of this paper is the application of RLS algorithm in the field of partial demagnetization, the experimental validation of eccentricity faults is absent.

5. Conclusions

This paper proposed a RLS-based algorithm to detect partial demagnetization under both stationary and nonstationary conditions. With the use of RLS, the proposed algorithm enables extracting the fault-related harmonic components introduced in the current; magnitudes of these fault-related harmonics can be regarded as an indicator of partial demagnetization. To better set the threshold value to evaluate the occurrence of partial demagnetization, a magnitude ratio of fault-related harmonics to fundamental component is given that can also be used when the magnitude of current changes with time. Experimental results show the effectiveness of the proposed algorithm under stationary and nonstationary conditions. Furthermore, comparisons with other existing methods of time–frequency analysis show that the proposed algorithm is an alternative method to detect partial demagnetization while overcoming time- and frequency-domain resolution problems, reducing computational burden and memory storage. Lastly, the impact of eccentricity faults was discussed. Experimental validation of the impact of eccentricity could and the distinction of different faults could future research directions. Although a method was proposed in the paper to eliminate the impact of eccentricity, the method is still not applicable. In addition, it was impossible to apply all faults in one paper; hence, the impacts of other possible faults on the detection of demagnetization still need further investigation.