Characteristic Forced and Spontaneous Imbibition Behavior in Strongly Water-Wet Sandstones Based on Experiments and Simulation
Abstract
:1. Introduction
- -
- Why is most of or all the mobile oil recovered before water breakthrough when flooding SWW media?
- -
- Do end effects prevent water breakthrough significantly or is the displacement piston-like?
- -
- Can capillary forces be detected from the pressure drop profile during flooding?
- -
- How does a change in oil viscosity affect time scale and recovery profile during spontaneous imbibition? What if we change water viscosity instead?
2. Experimental Setup
2.1. Fluids
2.2. Rock Material and Core Preparation
2.3. Establishing Initial Conditions
2.4. Flooding Rig Equipment
2.5. Measurement of End Point Permeabilities
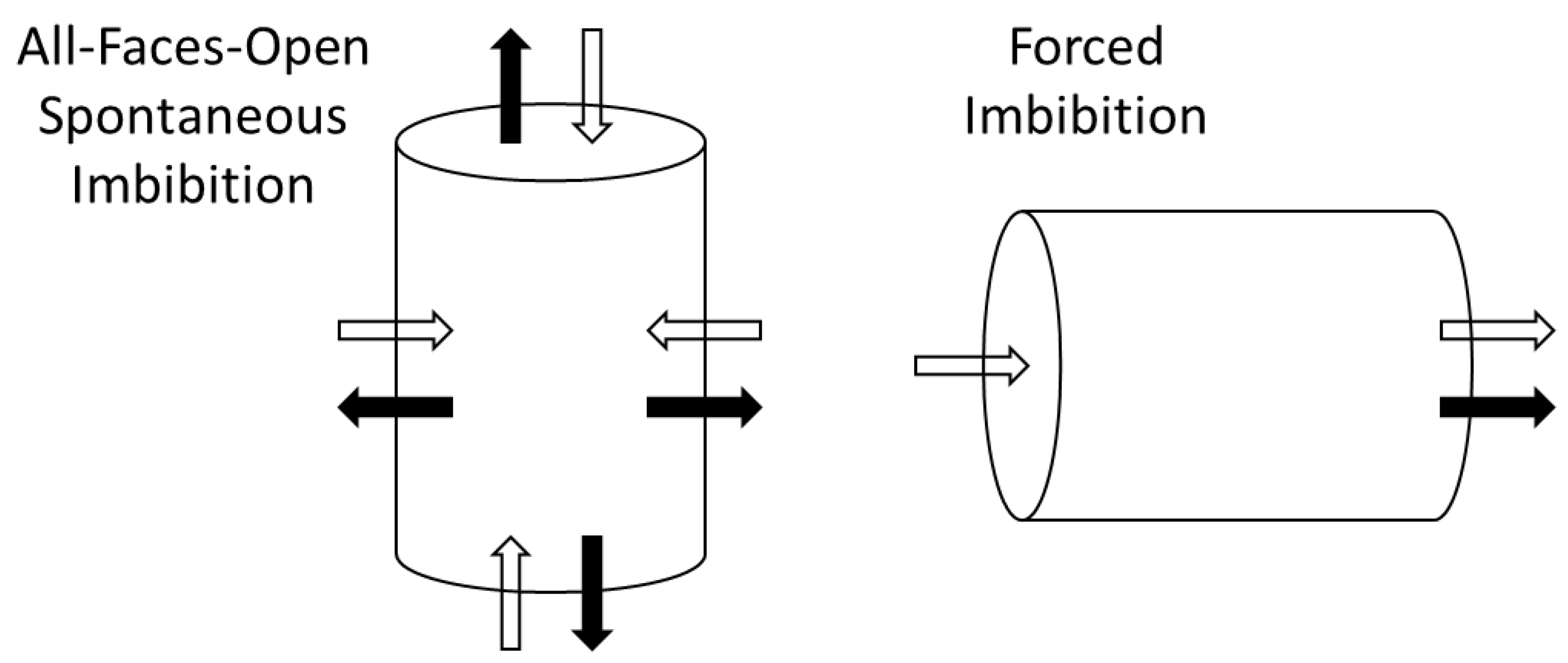
2.6. Spontaneous Imbibition Tests
2.7. Forced Imbibition
2.8. Procedure for Cleaning Cores Using Soxhlet Extractor
3. Theory
3.1. General Description of 1D Two-Phase Flow
3.2. Forced Imbibition
3.3. Counter-Current Spontaneous Imbibition
3.4. Analytical Approximate Solutions
3.4.1. Forced Imbibition
- Assuming negligible capillary forces and a fixed injection rate, increases linearly with time from the defined by the end point mobility of oil (displaced phase) to:
- the defined by the end point mobility of water (displacing phase) if the displacement is piston-like. The scaled pressure drop starts at and ends at one when . It is assumed ;
- the defined by the mobility of the Buckley–Leverett profile , which is less than the water mobility . A higher pressure drop is measured when only water flows and the peak is observed at water breakthrough, . Scaled pressure drop starts at and ends at at breakthrough.
- We can expect negligible capillary effects if the interfacial tension, water mobility and permeability are low and the velocity, length and porosity are high as given by large values of the capillary number
- When capillary forces are significant, they reduce the initial below that which would be expected when only mobile oil flows (scaled pressure drop less than ).
- If the saturation profile (front) does not change shape, increases linearly, also when capillary forces are present but shifted to lower values.
- However, capillary diffusion may smear the front and result in less of a capillary driving force with time. The pressure drop may increase as a result.
- As the front disappears at water breakthrough, we expect the capillary driving force at the front to vanish. Viscous forces must sustain the rate and a jump in is expected. The will not reach as high values as without capillary forces as the positive capillary pressure of the remaining saturation profile still provides a (small) driving force.
- A low initial pressure drop. ‘Low’ means compared to what is expected from the pressure drop, based on the measured oil end point relative permeability with oil flooding;
- A pressure drop that increases accelerating with time. The first period may be expected to be more linear;
- By increasing the factor it is expected that capillary forces will have more effect on the measurements.
3.4.2. Piston-like Counter-Current Spontaneous Imbibition
3.5. Implementation in Numerical Simulator
4. Results and Discussion
4.1. Summary of Experiments
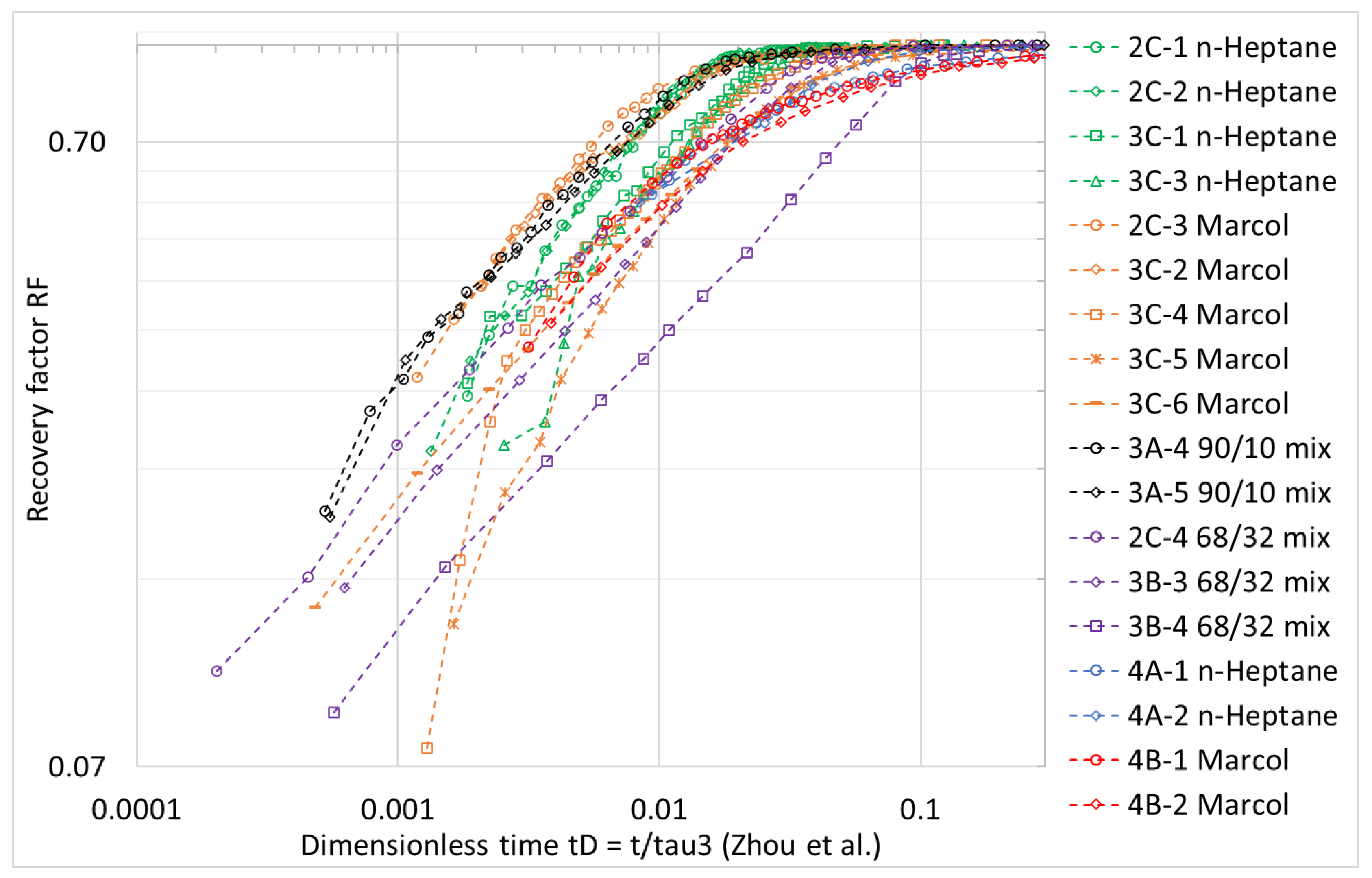
4.2. Spontaneous Imbibition Results
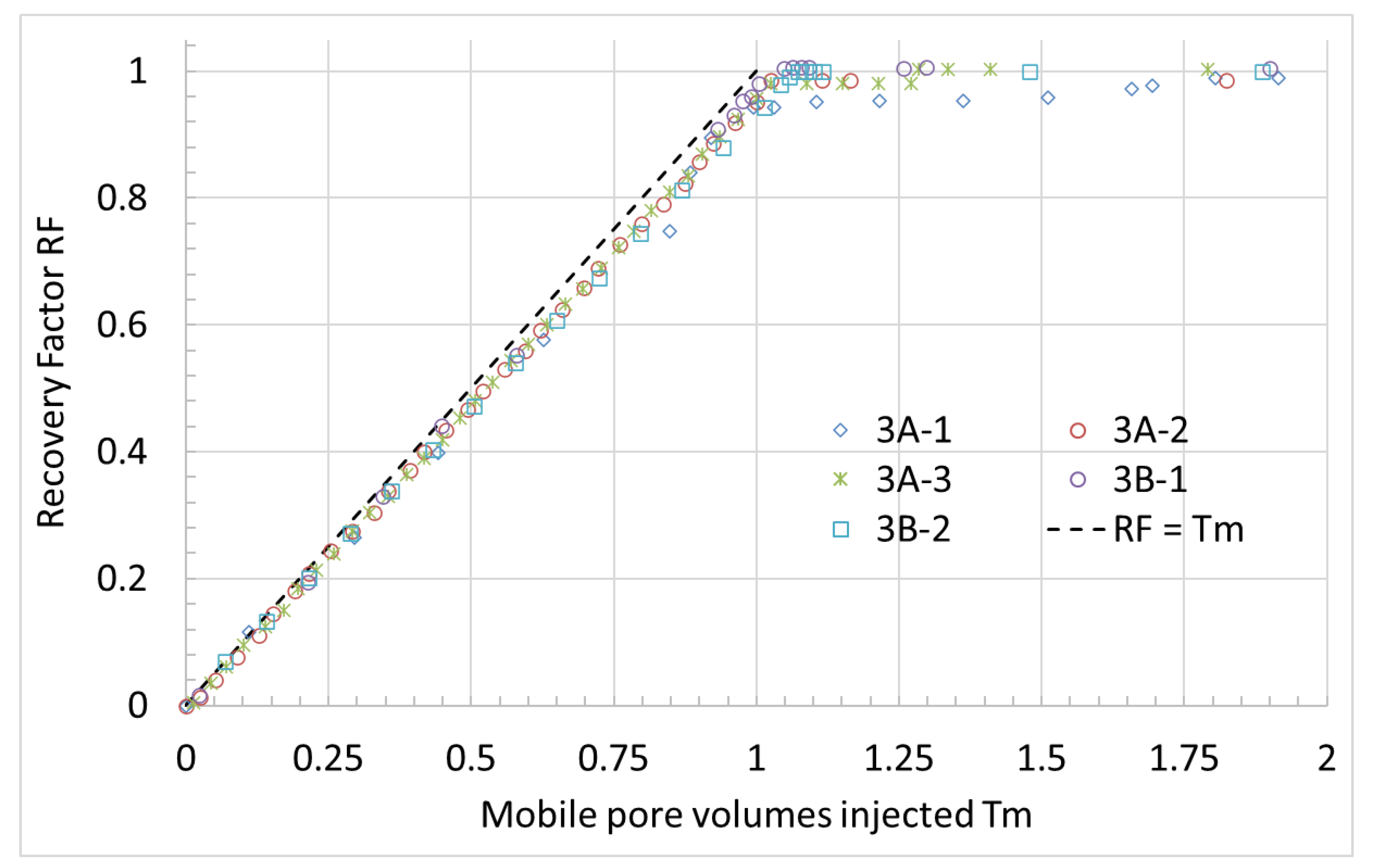
4.3. Forced Imbibition Data
4.4. Matching Experimental Data
4.5. Viscosity Impact on Spontaneous Imbibition Behavior
5. Summary and Conclusions
- During flooding, linear recovery vs. volume injected was observed until all mobile oil was displaced for high and low combinations of rate and viscosity indicating piston-like displacement. This was explained by a favorable mobility ratio even at high oil viscosities. Capillary pressure effects gave less recovery at breakthrough as the effect of capillary diffusion towards the outlet was greater than the capillary water blockage effect.
- Pressure drop should increase linearly with time from the oil end point mobility to the water end point mobility if piston-like displacement occurs. If it is lower than this trend, capillary forces assist the imbibition. The pressure drop increases in a jump at water breakthrough as the capillary pressure contribution, mainly at the front, vanishes.
- Non-piston-like displacement will also give a pressure drop changing linearly with time, but the end point depends on the mobility of the imbibing saturation profile and when it reaches the outlet. Capillary blockage at that time can cause an added resistance with a pressure peak higher than without capillary forces.
- The change in spontaneous imbibition time scale ~3–5 was much less than the change in oil viscosity (a factor ~80), and indicated that oil mobility was much higher than that of water.
- Including relative permeability end points during the scaling of spontaneous imbibition data provided much better results in terms of collecting the imbibition curves than only using the viscosities. That was due to the water relative permeability being very low compared to oil. The scaling was successfully used to estimate the water relative permeability end point for Bentheimer.
- The time scale of spontaneous imbibition is more sensitive to water viscosity than oil viscosity in a SWW system since water has the limiting mobility. When oil mobility becomes increased compared to the water mobility, a higher recovery will be obtained following a square root of time profile, with the entire profile as a limiting case of infinite oil mobility.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman | |
| Diameter: m | |
| Water fractional flow function | |
| Scaled capillary pressure | |
| -function parameters | |
| Phase relative permeability | |
| Absolute permeability, m2 | |
| Core length, m | |
| Characteristic length, m | |
| End point mobility ratio | |
| Phase Corey exponent | |
| Phase Corey exponent end values | |
| Phase pressure, Pa | |
| Capillary pressure, Pa | |
| Recovery factor (of mobile oil) | |
| Phase saturation | |
| Normalized phase saturation | |
| Normalized water saturation, at which capillary pressure is zero | |
| Normalized water saturation averaged over the core | |
| Scaled time | |
| Mobile pore volumes injected | |
| Darcy phase velocity, m/s | |
| Greek | |
| Porosity | |
| Phase viscosity, Pa s | |
| Interfacial tension, N/m | |
| Phase mobility, 1/(Pa s) | |
| Phase pressure drop, Pa | |
| Pressure drop when water flows at residual oil saturation, Pa | |
| Mobile saturation range | |
| Time scale, s | |
| Subscripts | |
| Capillary | |
| Characteristic | |
| Zero capillary pressure condition | |
| Front | |
| Phase index | |
| Oil | |
| Reference (no end effects) | |
| Total | |
| Water | |
| Superscripts | |
| End point or characteristic value |
Appendix A. Forced Imbibition with Buckley–Leverett Profile
References
- Blunt, M.J. Multiphase Flow in Permeable Media: A Pore-Scale Perspective; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Ahmed, T. Reservoir Engineering Handbook; Gulf Professional Publishing: Cambridge, MA, USA, 2018. [Google Scholar]
- Morrow, N.R. Wettability and its effect on oil recovery. J. Pet. Technol. 1990, 42, 1476–1484. [Google Scholar] [CrossRef]
- Johnson, E.F.; Bossler, D.P.; Naumann, V.O. Calculation of relative permeability from displacement experiments. Trans. AIME 1959, 216, 370–372. [Google Scholar] [CrossRef]
- Jones, S.C.; Roszelle, W.O. Graphical techniques for determining relative permeability from displacement experiments. J. Pet. Technol. 1978, 30, 807–817. [Google Scholar] [CrossRef]
- Civan, F.; Donaldson, E.C. Relative permeability from unsteady-state displacements: An analytical interpretation. In SPE Production Operations Symposium; OnePetro: Moscow, Russia, 1987. [Google Scholar]
- Leverett, M. Capillary behavior in porous solids. Trans. AIME 1941, 142, 152–169. [Google Scholar] [CrossRef]
- Andersen, P.Ø.; Walrond, K.; Nainggolan, C.K.; Pulido, E.Y.; Askarinezhad, R. Simulation interpretation of capillary pressure and relative permeability from laboratory waterflooding experiments in preferentially oil-wet porous media. SPE Reserv. Eval. Eng. 2020, 23, 230–246. [Google Scholar] [CrossRef]
- Rapoport, L.A.; Leas, W.J. Properties of linear waterfloods. J. Pet. Technol. 1953, 5, 139–148. [Google Scholar] [CrossRef]
- Gupta, R.; Maloney, D.R. Intercept method—A novel technique to correct steady-state relative permeability data for capillary end effects. SPE Reserv. Eval. Eng. 2016, 19, 316–330. [Google Scholar] [CrossRef]
- Andersen, P.Ø. Analytical modeling and correction of steady state relative permeability experiments with capillary end effects–An improved intercept method, scaling and general capillary numbers. Oil Gas Sci. Technol. Rev. D’ifp Energ. Nouv. 2021, 76, 61. [Google Scholar] [CrossRef]
- Anderson, W.G. Wettability literature survey-part 4: Effects of wettability on capillary pressure. J. Pet. Technol. 1987, 39, 1283–1300. [Google Scholar] [CrossRef]
- Craig, F. The Reservoir Engineering Aspects of Waterflooding; Monograph Series; Society of Petroleum Engineers of AIME: Wilkes-Barre, PA, USA, 1971. [Google Scholar]
- Anderson, W.G. Wettability literature survey-part 6: The effects of wettability on waterflooding. J. Pet. Technol. 1987, 39, 1605–1622. [Google Scholar] [CrossRef]
- Kleppe, J.; Morse, R.A. Oil production from fractured reservoirs by water displacement. In Proceedings of the Fall meeting of the Society of Petroleum Engineers of AIME, Houston, TX, USA, 6–9 October 1974. [Google Scholar]
- Anderson, W.G. Wettability literature survey part 5: The effects of wettability on relative permeability. J. Pet. Technol. 1987, 39, 1453–1468. [Google Scholar] [CrossRef]
- Bourbiaux, B.J.; Kalaydjian, F.J. Experimental study of cocurrent and countercurrent flows in natural porous media. SPE Reserv. Eng. 1990, 5, 361–368. [Google Scholar] [CrossRef]
- Yortsos, Y.C.; Fokas, A.S. An analytical solution for linear waterflood including the effects of capillary pressure. SPE J. 1983, 23, 115–124. [Google Scholar] [CrossRef]
- Odeh, A.S.; Dotson, B.J. A method for reducing the rate effect on oil and water relative permeabilities calculated from dynamic displacement data. J. Pet. Technol. 1985, 37, 2051–2058. [Google Scholar] [CrossRef]
- Morrow, N.R.; Mason, G. Recovery of oil by spontaneous imbibition. Curr. Opin. Colloid Interface Sci. 2001, 6, 321–337. [Google Scholar] [CrossRef]
- Amott, E. Observations relating to the wettability of porous rock. Trans. AIME 1959, 216, 156–162. [Google Scholar] [CrossRef]
- Handy, L.L. Determination of effective capillary pressures for porous media from imbibition data. Trans. AIME 1960, 219, 75–80. [Google Scholar] [CrossRef]
- Mason, G.; Morrow, N.R. Developments in spontaneous imbibition and possibilities for future work. J. Pet. Sci. Eng. 2013, 110, 268–293. [Google Scholar] [CrossRef]
- Andersen, P.Ø.; Brattekås, B.; Nødland, O.; Lohne, A.; Føyen, T.L.; Fernø, M.A. Darcy-Scale simulation of Boundary-Condition effects during Capillary-Dominated flow in high-permeability systems. SPE Reserv. Eval. Eng. 2019, 22, 673–691. [Google Scholar] [CrossRef]
- Haugen, Å.; Fernø, M.A.; Mason, G.; Morrow, N.R. The effect of viscosity on relative permeabilities derived from spontaneous imbibition tests. Transp. Porous Media 2015, 106, 383–404. [Google Scholar] [CrossRef]
- Andersen, P.Ø. Early-and Late-Time Analytical Solutions for Cocurrent Spontaneous Imbibition and Generalized Scaling. SPE J. 2021, 26, 220–240. [Google Scholar] [CrossRef]
- Andersen, P.Ø.; Ahmed, S. Simulation study of wettability alteration enhanced oil recovery during co-current spontaneous imbibition. J. Pet. Sci. Eng. 2021, 196, 107954. [Google Scholar] [CrossRef]
- Mattax, C.C.; Kyte, J.R. Imbibition oil recovery from fractured, water-drive reservoir. SPE J. 1962, 2, 177–184. [Google Scholar] [CrossRef]
- Ma, S.; Morrow, N.R.; Zhang, X. Generalized scaling of spontaneous imbibition data for strongly water-wet systems. J. Pet. Sci. Eng. 1997, 18, 165–178. [Google Scholar]
- Fischer, H.; Morrow, N.R. Scaling of oil recovery by spontaneous imbibition for wide variation in aqueous phase viscosity with glycerol as the viscosifying agent. J. Pet. Sci. Eng. 2006, 52, 35–53. [Google Scholar] [CrossRef]
- Mason, G.; Fischer, H.; Morrow, N.R.; Ruth, D.W. Correlation for the effect of fluid viscosities on counter-current spontaneous imbibition. J. Pet. Sci. Eng. 2010, 72, 195–205. [Google Scholar] [CrossRef]
- Tantciura, S.; Qiao, Y.; Andersen, P.Ø. Simulation of Counter-Current Spontaneous Imbibition Based on Momentum Equations with Viscous Coupling, Brinkman Terms and Compressible Fluids. Transp. Porous Media 2022, 141, 49–85. [Google Scholar] [CrossRef]
- Zhou, X.; Morrow, N.R.; Ma, S. Interrelationship of wettability, initial water saturation, aging time, and oil recovery by spontaneous imbibition and waterflooding. SPE J. 2000, 5, 199–207. [Google Scholar] [CrossRef]
- McWhorter, D.B.; Sunada, D.K. Exact integral solutions for two-phase flow. Water Resour. Res. 1990, 26, 399–413. [Google Scholar] [CrossRef]
- Standnes, D.C. Scaling spontaneous imbibition of water data accounting for fluid viscosities. J. Pet. Sci. Eng. 2010, 73, 214–219. [Google Scholar] [CrossRef]
- Standnes, D.C.; Andersen, P.Ø. Analysis of the impact of fluid viscosities on the rate of countercurrent spontaneous imbibition. Energy Fuels 2017, 31, 6928–6940. [Google Scholar] [CrossRef]
- Zhou, D.; Jia, L.; Kamath, J.; Kovscek, A.R. Scaling of counter-current imbibition processes in low-permeability porous media. J. Pet. Sci. Eng. 2002, 33, 61–74. [Google Scholar] [CrossRef]
- Schmid, K.S.; Geiger, S. Universal scaling of spontaneous imbibition for arbitrary petrophysical properties: Water-wet and mixed-wet states and Handy’s conjecture. J. Pet. Sci. Eng. 2013, 101, 44–61. [Google Scholar] [CrossRef]
- Andersen, P.Ø.; Nesvik, E.K.; Standnes, D.C. Analytical solutions for forced and spontaneous imbibition accounting for viscous coupling. J. Pet. Sci. Eng. 2020, 186, 106717. [Google Scholar] [CrossRef]
- Reis, J.C.; Cil, M. A model for oil expulsion by counter-current water imbibition in rocks: One-dimensional geometry. J. Pet. Sci. Eng. 1993, 10, 97–107. [Google Scholar] [CrossRef]
- Tavassoli, Z.; Zimmerman, R.W.; Blunt, M.J. Analytic analysis for oil recovery during counter-current imbibition in strongly water-wet systems. Transp. Porous Media 2005, 58, 173–189. [Google Scholar] [CrossRef]
- Churcher, P.L.; French, P.R.; Shaw, J.C.; Schramm, L.L. Rock properties of Berea sandstone, Baker dolomite, and Indiana limestone. In Proceedings of the SPE International Symposium on Oilfield Chemistry, Anaheim, CA, USA, 20–22 February 1991. [Google Scholar]
- Peksa, A.E.; Wolf, K.H.A.; Zitha, P.L. Bentheimer sandstone revisited for experimental purposes. Mar. Pet. Geol. 2015, 67, 701–719. [Google Scholar] [CrossRef]
- Hamouda, A.A.; Valderhaug, O.M.; Munaev, R.; Stangeland, H. Possible mechanisms for oil recovery from chalk and sandstone rocks by low salinity water (LSW). In Proceedings of the SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 12–16 April 2014. [Google Scholar]
- Abhishek, R.; Hamouda, A.A.; Murzin, I. Adsorption of silica nanoparticles and its synergistic effect on fluid/rock interactions during low salinity flooding in sandstones. Colloids Surf. A Physicochem. Eng. Asp. 2018, 555, 397–406. [Google Scholar] [CrossRef]
- Andersen, P.Ø.; Qiao, Y.; Standnes, D.C.; Evje, S. Cocurrent spontaneous imbibition in porous media with the dynamics of viscous coupling and capillary backpressure. SPE J. 2019, 24, 158–177. [Google Scholar] [CrossRef]
- Lenormand, R.; Lorentzen, K.; Maas, J.G.; Ruth, D. Comparison of four numerical simulators for SCAL experiments. Petrophysics 2017, 58, 48–56. [Google Scholar]
- Andersen, P.Ø. Early- and late-time prediction of counter-current spontaneous imbibition and estimation of the capillary diffusion coefficient. In Proceedings of the SPE EuropEC, Madrid, Spain, 5–9 June 2022. [Google Scholar]
- Fischer, H.; Wo, S.; Morrow, N.R. Modeling the Effect of Viscosity Ratio on Spontaneous Imbibition. SPE Reserv. Eval. Eng. 2008, 11, 577–589. [Google Scholar] [CrossRef]
- Lohne, A. User’s Manual for BugSim–an MEOR Simulator (V1.2); NORCE: Stavanger, Norway, 2013. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. J. Irrig. Drain. Div. 1966, 92, 61–90. [Google Scholar] [CrossRef]
- Bentsen, R.G.; Anli, J. A new displacement capillary pressure model. J. Can. Pet. Technol. 1976, 15. [Google Scholar] [CrossRef]
- Buckley, S.E.; Leverett, M. Mechanism of fluid displacement in sands. Trans. AIME 1942, 146, 107–116. [Google Scholar] [CrossRef]











| n-Heptane (C7) | C7-M82 Mixture (90/10) | C7-M82 Mixture (68/32) | Marcol 82 (M82) | 1 M NaCl | 0.1 M NaCl | |
|---|---|---|---|---|---|---|
| 1 Viscosity [cP] | 0.408 | 4.04 | 13.82 | 31.77 | 1.098 | 0.965 |
| Viscosity ratio | 0.39 | 3.89 | 13.31 | 30.59 | ||
| 1 Density [g/mL] | 0.684 | 0.800 | 0.833 | 0.850 | 1.0386 | 1.0024 |
| 2 Interfacial tension [mN/m] | 35.40 | 35.05 | 38.20 | 39.51 | - | - |
| Core ID | Source | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [mm] | [mm] | [mm] | [mL] | [mL] | [mL] | [mL] | [%] | [mD] | ||
| 2C | Berea | 59.31 | 37.80 | 12.18 | 66.56 | 53.10 | 13.46 | 13.15 | 19.85 | 152 |
| 3A | 64.94 | 37.82 | 12.36 | 72.95 | 58.64 | 14.31 | 13.93 | 19.19 | 124 | |
| 3B | 64.07 | 37.82 | 12.34 | 71.98 | 57.78 | 14.20 | 13.78 | 19.25 | 126 | |
| 3C | 65.61 | 37.82 | 12.38 | 73.71 | 59.21 | 14.50 | 14.13 | 19.26 | 128 | |
| 4A | Bentheimer | 67.42 | 37.64 | 12.38 | 75.02 | 56.23 | 18.79 | 18.63 | 24.27 | 1989 |
| 4B | 65.94 | 37.62 | 12.33 | 73.30 | 55.10 | 18.20 | 18.07 | 25.58 | 1948 |
| Core ID | Imbibition Type | NW Phase | M [-] | Rate [mL/h] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Berea | ||||||||||
| 2C-1 | SI | C7 | 0.100 | - | - | 0.561 | - | - | - | |
| 2C-2 | SI | C7 | 0.098 | - | - | 0.559 | - | - | - | |
| 2C-3 | SI | M82 | 0.100 | - | - | 0.509 | - | - | - | |
| 2C-4 | SI | 68-32 | 0.102 | 122 | 0.805 | 0.505 | - | - | - | |
| 3A-1 | FI | M82 | 0.104 | 102 | 0.823 | 0.571 | 1.41 | 0.0114 | 0.42 | 2 |
| 3A-2 | FI | M82 | 0.101 | 87.1 | 0.702 | 0.545 | 1.19 | 0.0096 | 0.42 | 15 |
| 3A-3 | FI | M82 | 0.103 | 90.5 | 0.730 | 0.519 | 0.788 | 0.0064 | 0.27 | 2 |
| 3A-4 | SI | 90-10 | 0.100 | - | - | 0.514 | - | - | - | |
| 3A-5 | SI | 90-10 | 0.104 | 100.4 | 0.811 | 0.507 | - | - | - | |
| 3B-1 | FI | C7 | 0.106 | 81.7 | 0.648 | 0.585 | 2.90 | 0.0230 | 0.0138 | 15 |
| 3B-2 | FI | C7 | 0.103 | 83.2 | 0.660 | 0.564 | 1.19 | 0.0094 | 0.0056 | 2 |
| 3B-3 | SI | 68-32 | 0.101 | - | - | 0.521 | - | - | - | |
| 3B-4 | SI | 68-32 | 0.103 | - | 0.677 | 0.521 | - | - | - | |
| 3C-1 | SI | C7 | 0.099 | - | - | 0.594 | - | - | - | |
| 3C-2 | SI | M82 | 0.104 | 111 | 0.867 | 0.515 | - | - | - | |
| 3C-3 | SI | C7 | 0.103 | 100 | 0.781 | 0.557 | - | - | - | |
| 3C-4 | SI | M82 | 0.104 | 103 | 0.805 | 0.612 | - | - | - | |
| 3C-5 | SI | M82 | 0.102 | - | - | 0.528 | - | - | - | |
| 3C-6 | SI | M82 | 0.099 | 94.6 | 0.739 | 0.520 | - | - | - | |
| Average | 0.102 | 97.77 | 0.754 | 0.541 | 1.50 | 0.0120 | ||||
| Rel variation | 0.04 | 0.25 | 0.19 | 0.12 | 1.09 | 1.07 | ||||
| Bentheimer | ||||||||||
| 4A-1 | SI | C7 | 0.105 | - | - | 0.403 | - | - | - | |
| 4A-2 | SI | C7 | 0.104 | 1309 | 0.658 | 0.396 | - | - | - | |
| 4B-1 | SI | M82 | 0.102 | - | - | 0.398 | - | - | - | |
| 4B-2 | SI | M82 | 0.105 | 1499 | 0.770 | 0.446 | - | - | - | |
| Average | 0.104 | 1404 | 0.714 | 0.411 | ||||||
| Rel variation | 0.03 | 0.19 | 0.22 | 0.12 |
| Constant Parameters | Rock Specific Parameters | Saturation Function Parameters | |||||
|---|---|---|---|---|---|---|---|
| Berea | Bentheimer | Tuning | K and M | ||||
| 64.8 mm | 0.54 | 0.41 | 6 | 6 | |||
| 12.3 mm | 0.194 | 0.249 | 3 | 2.5 | |||
| 37.75 mm | 133 mD | 1970 mD | 1.5 | 2 | |||
| 37.0 mN/m | 0.012 | 0.065 | 1.5 | 0.5 | |||
| 1.10 cP | 5.43 × 10−4 h | 2.18 × 10−4 h | 0.14 | 0.3 | |||
| 0.41 cP | 0.014 | 0.03 | |||||
| 32 cP | - | 3 × 10−4 | |||||
| 0.10 | - | 0.75 | |||||
| 0.75 | - | 0.07 | |||||
| 0.0047 | |||||||
| 0.45 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andersen, P.Ø.; Salomonsen, L.; Sleveland, D.S. Characteristic Forced and Spontaneous Imbibition Behavior in Strongly Water-Wet Sandstones Based on Experiments and Simulation. Energies 2022, 15, 3531. https://doi.org/10.3390/en15103531
Andersen PØ, Salomonsen L, Sleveland DS. Characteristic Forced and Spontaneous Imbibition Behavior in Strongly Water-Wet Sandstones Based on Experiments and Simulation. Energies. 2022; 15(10):3531. https://doi.org/10.3390/en15103531
Chicago/Turabian StyleAndersen, Pål Østebø, Liva Salomonsen, and Dagfinn Søndenaa Sleveland. 2022. "Characteristic Forced and Spontaneous Imbibition Behavior in Strongly Water-Wet Sandstones Based on Experiments and Simulation" Energies 15, no. 10: 3531. https://doi.org/10.3390/en15103531






