Static and Dynamic Simulation of an Induction Motor Using Matlab/Simulink
Abstract
:1. Introduction
2. Problem Statement
3. Objectives of the Research
- To contribute to the development of induction motor models and protection systems.
- To simulate an adaptable simulation of a three-phase induction motor in Matlab/Simulink.
- To accurately size the motor parameters and increase performance thereof.
- To implement a dq0-axis reference frame modelling technique of a rotating machine.
- To implement a feeder protection system for the machine during its steady operation.
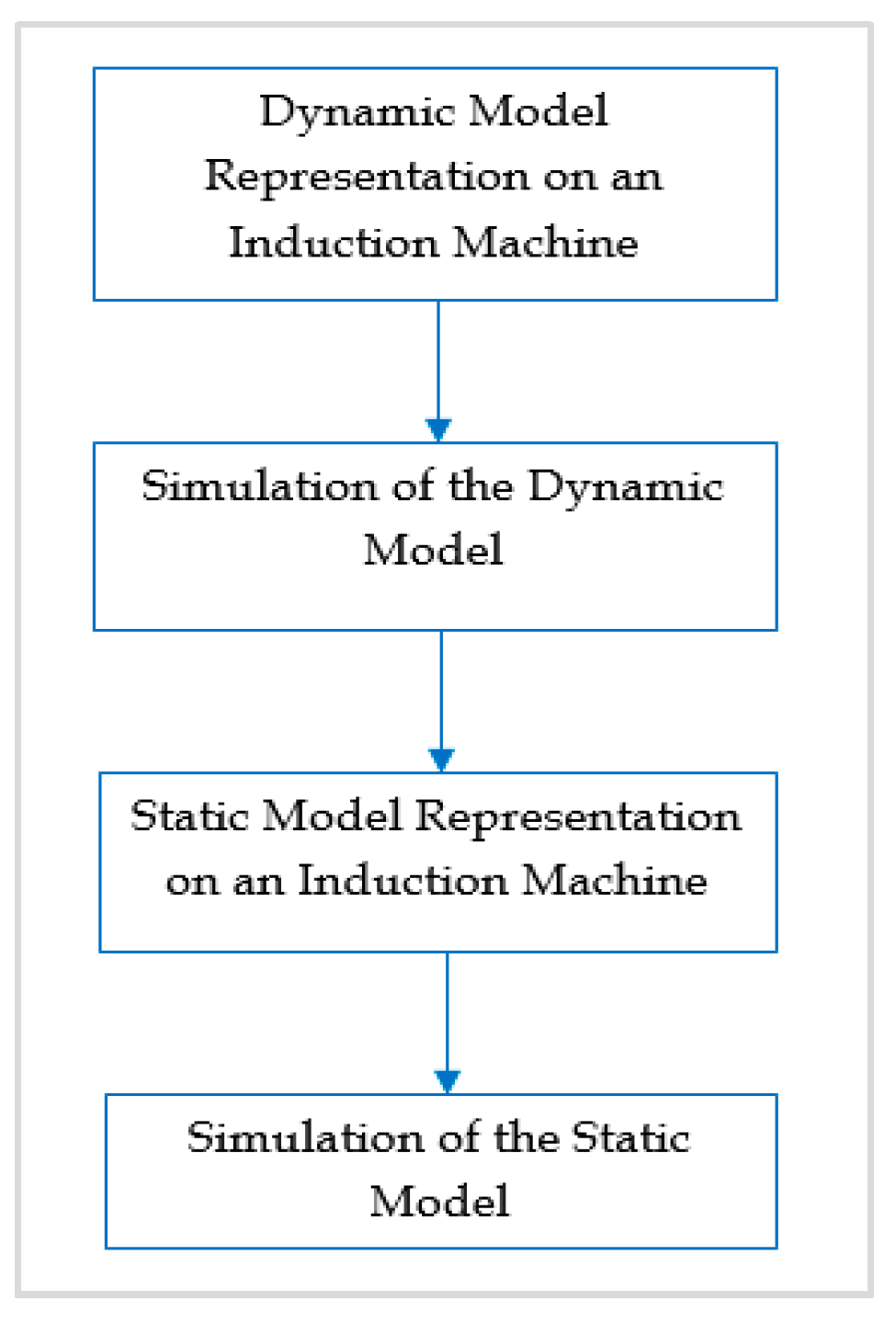
4. Methodology
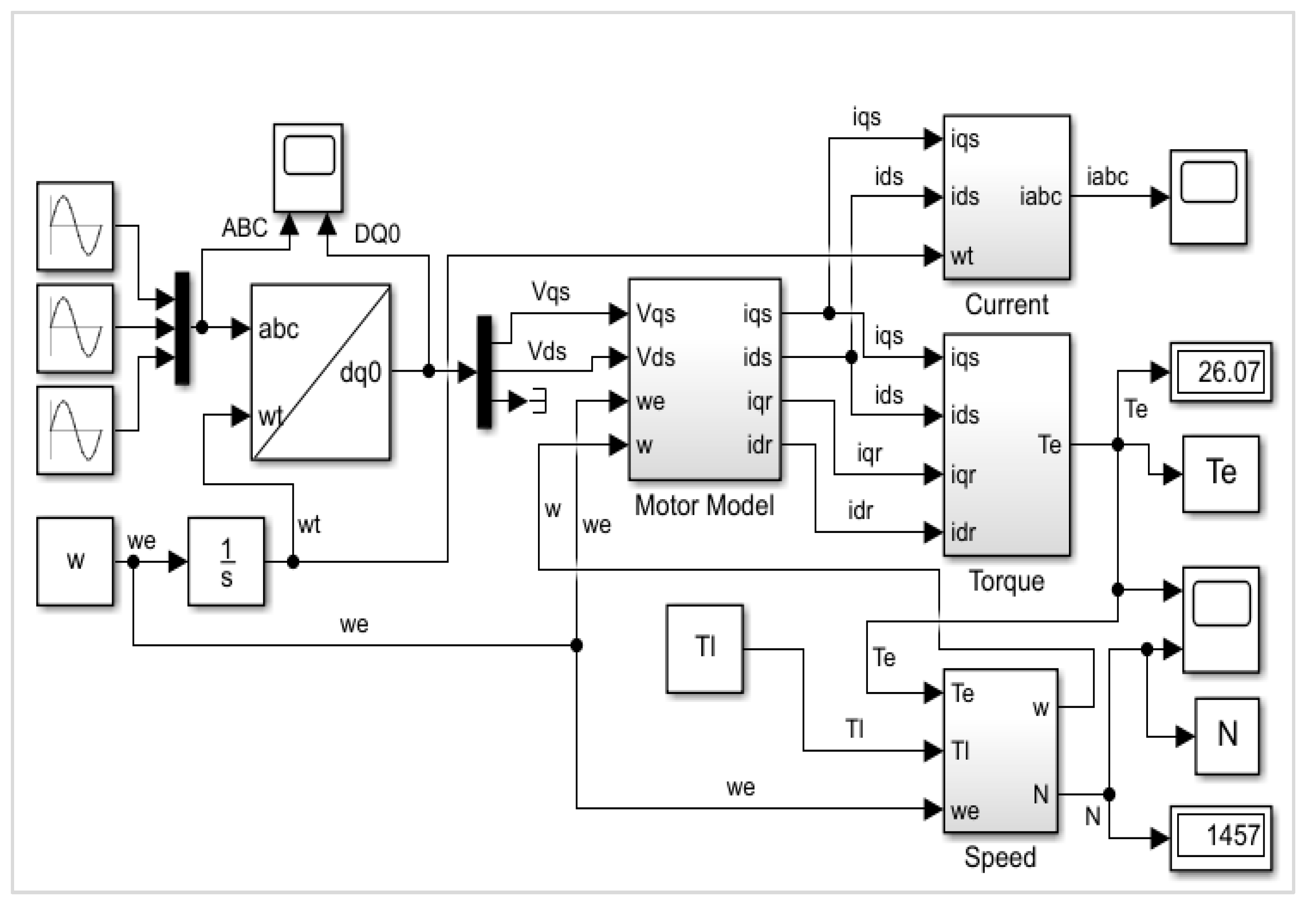
5. Simulations of Induction Motors
- Two-pole, three-phase windings are symmetrical.
- The slotting impacts are considered.
- Iron losses are not disregarded.
- The conductivity of the iron elements is limitless.
- The magnetisation in the airgap is circular.
- The stator and rotor windings are coordinated as a single and multi-turn full-pitch coil located on opposite sides of the air gap.
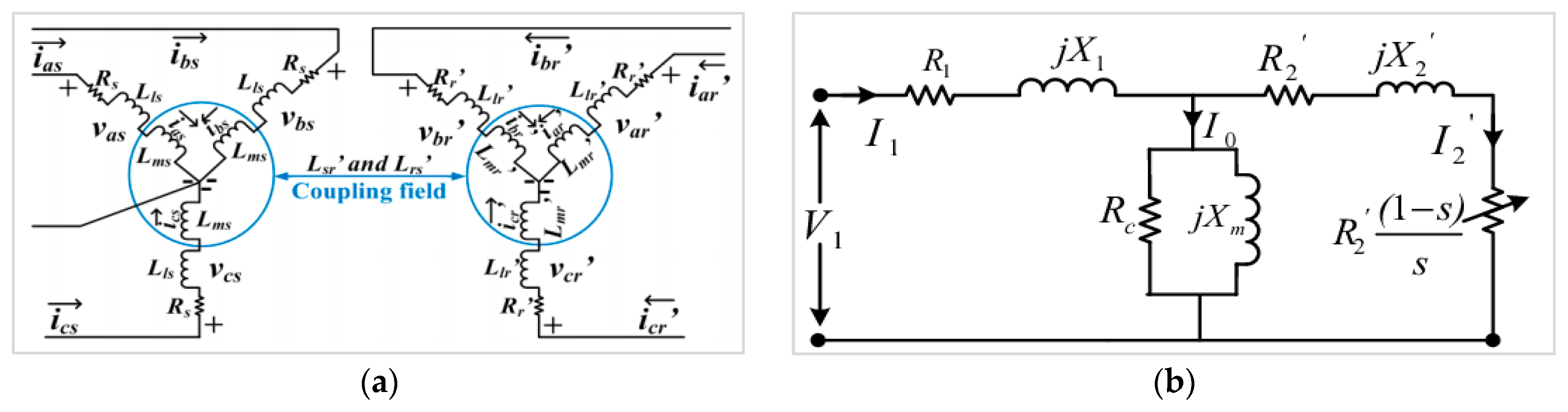
5.1. Model

5.2. Inverse Model
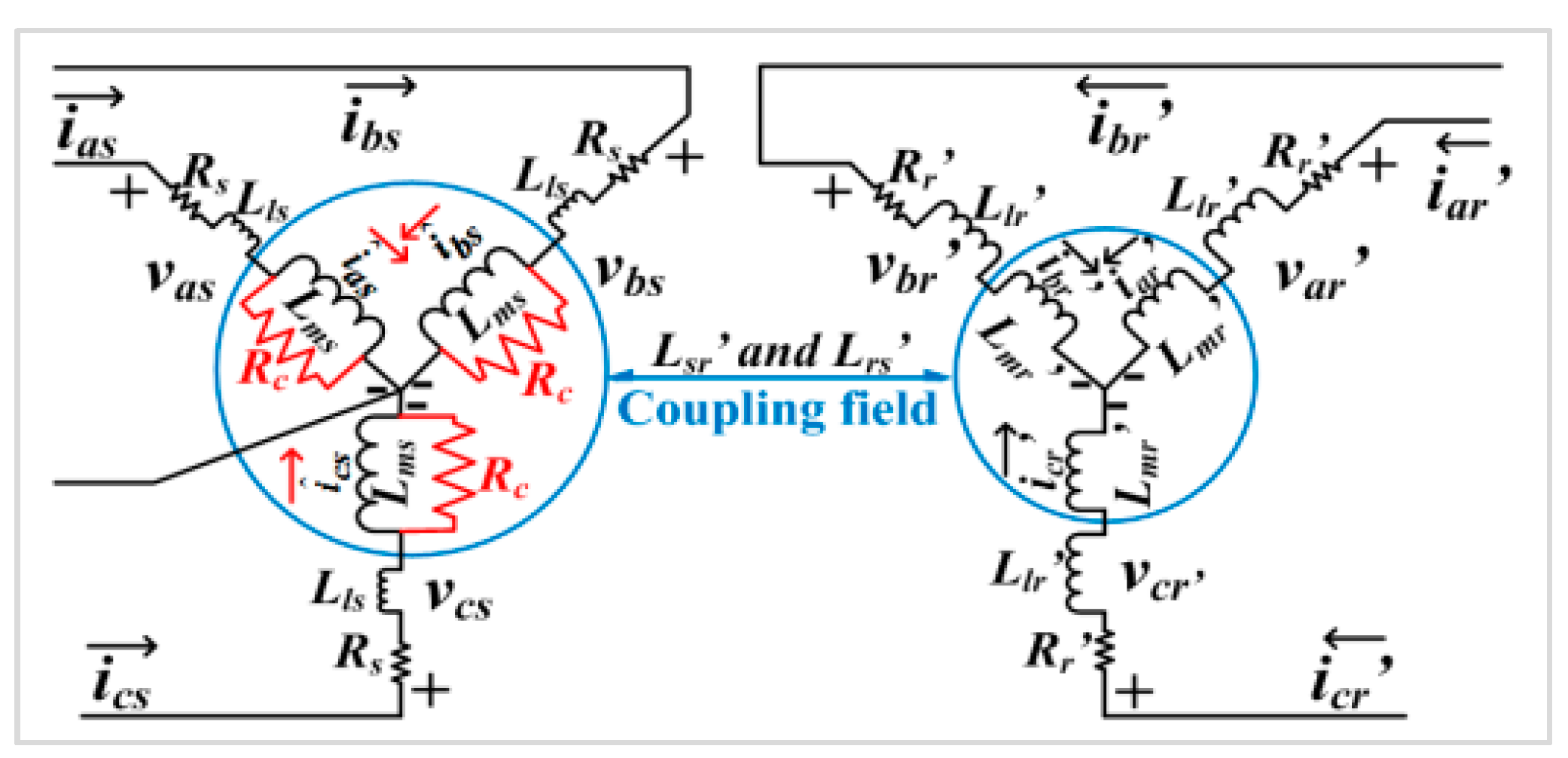
5.3. Loss Model
5.4. Simplified Model
5.5. Simplified d–q Design
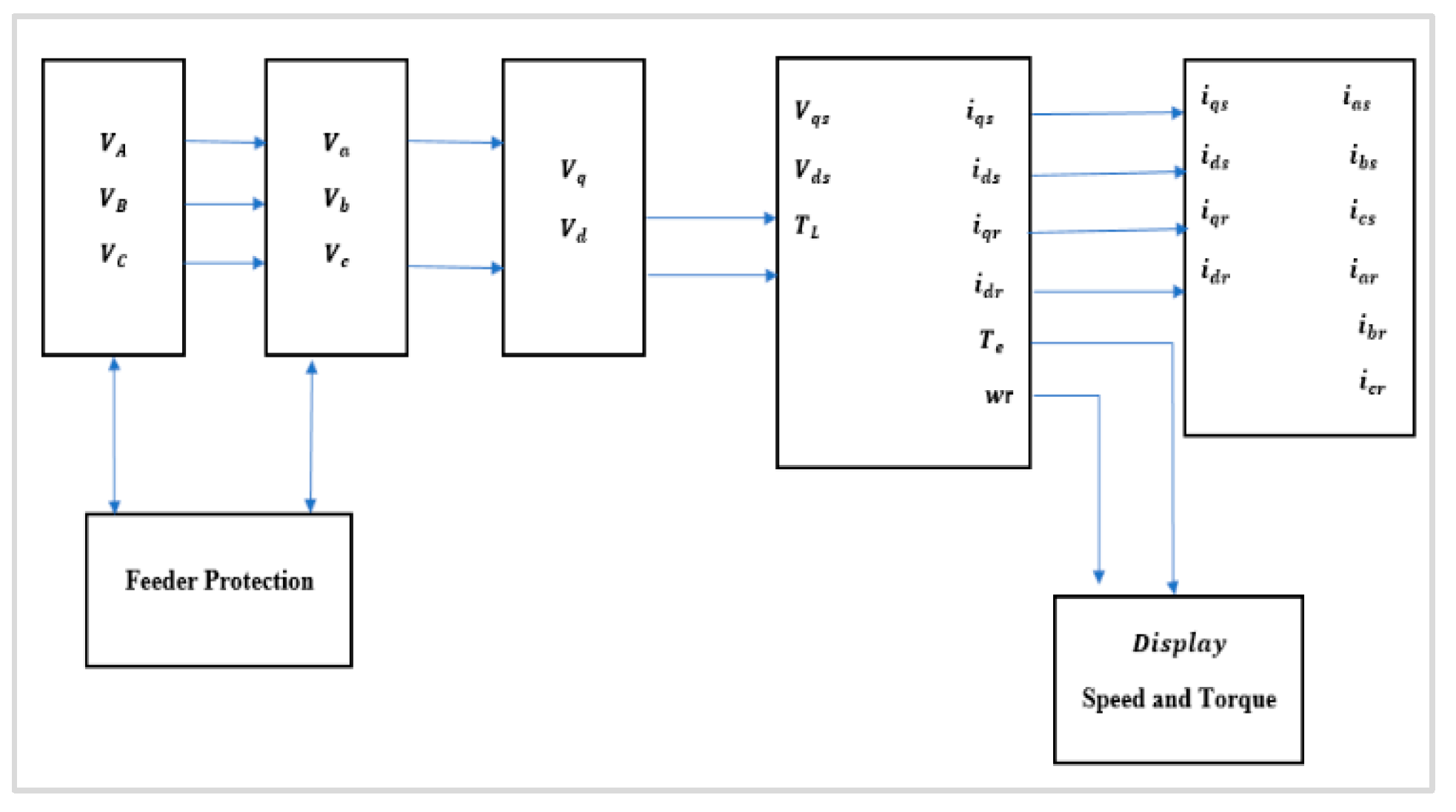
6. Proposed Design
7. Proposed Design
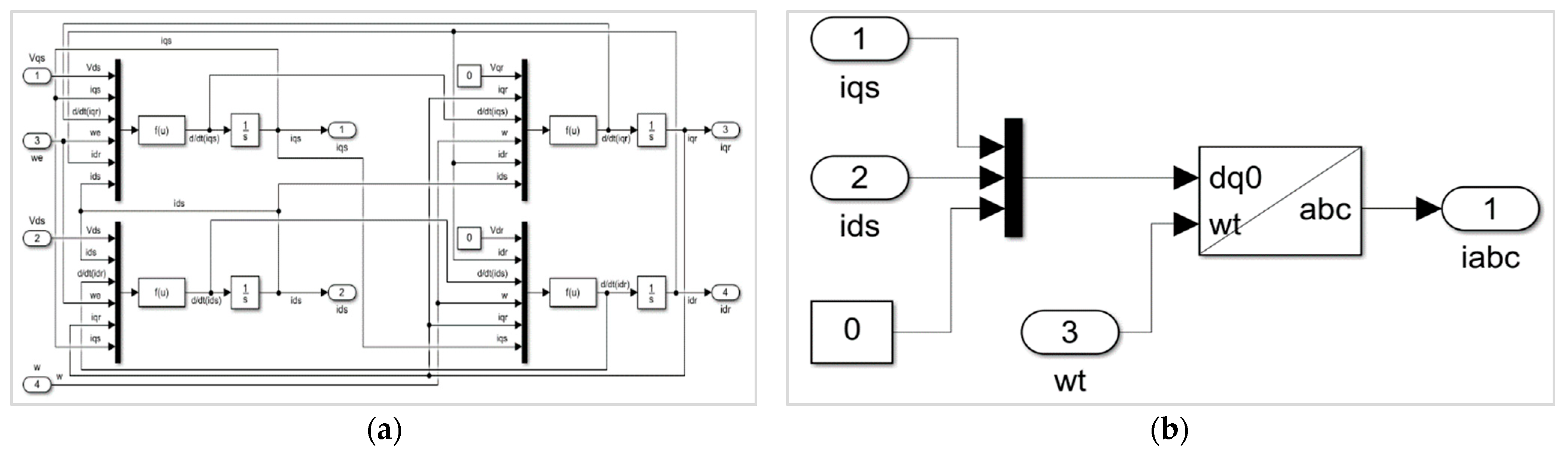
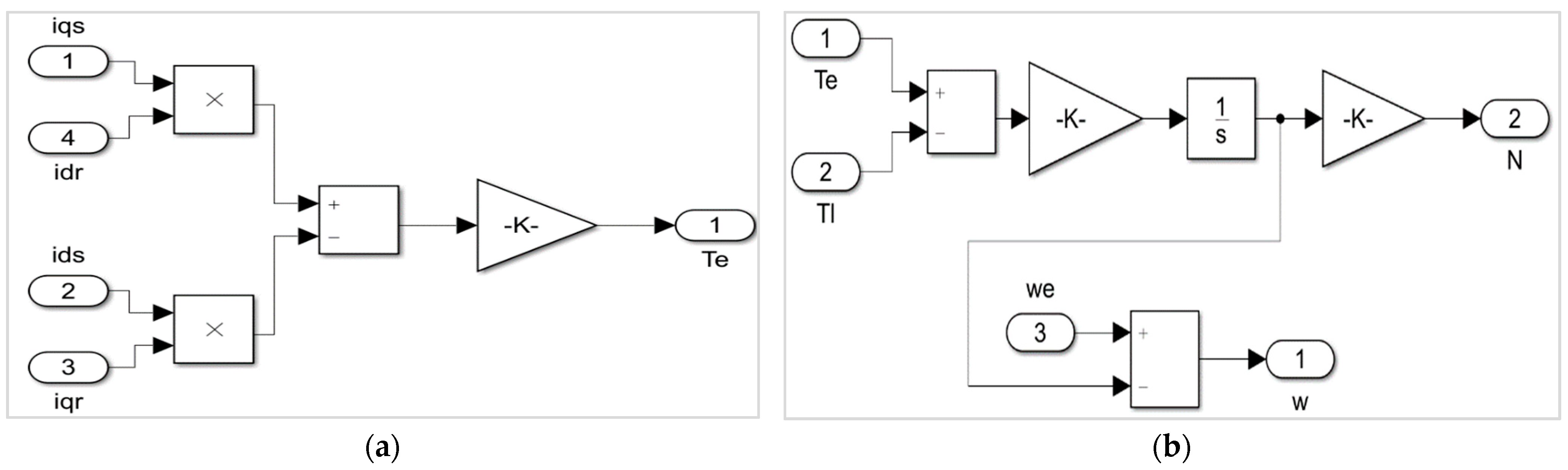
7.1. Dynamic Model
| axes of the stator voltage(s). | |
| axes of the rotor voltage(s). | |
| axes magnetising the flux linkages. | |
| is the stator resistance. | |
| is the rotor resistance. | |
| is the stator leakage reactance. | |
| is the rotor leakage reactance. | |
| is the number of poles. | |
| is the magnetic torque. |
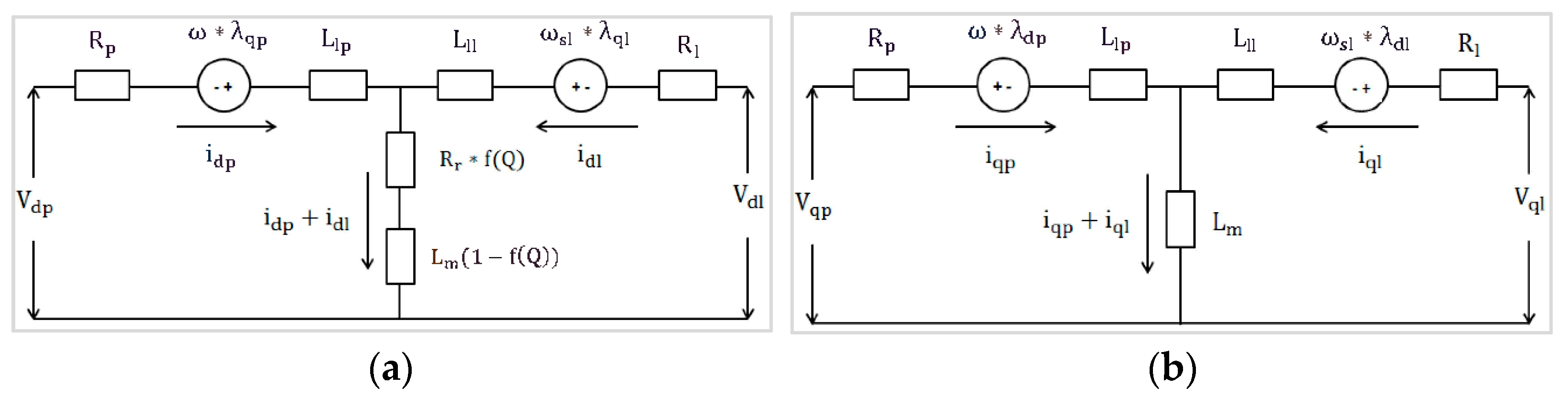
7.2. Static Model
8. Results
8.1. The Machine’s Steady-State Performance Behaviour When Loaded from 0 to 125% of the Rated Load, Shown in Both Tabular and Graphical Form with Current, Power Factor, Real Power, Reactive Power, Speed, Efficiency, and Power Factor versus the Percentage or Per-Unit Loading
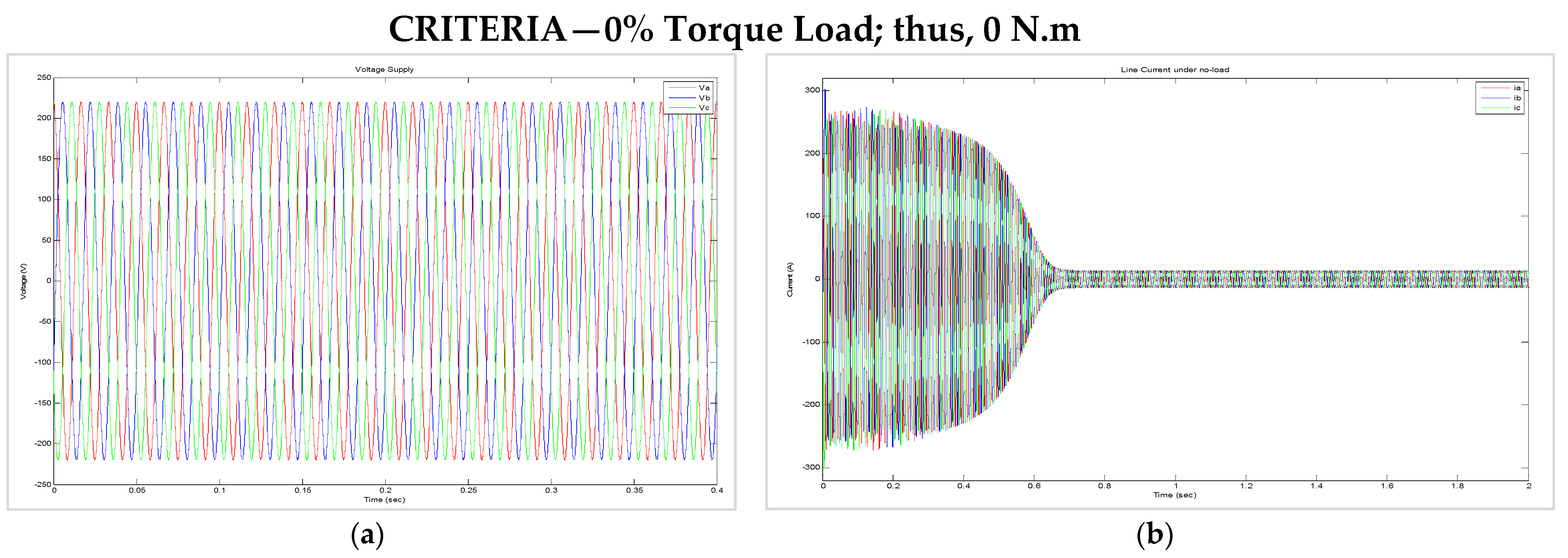
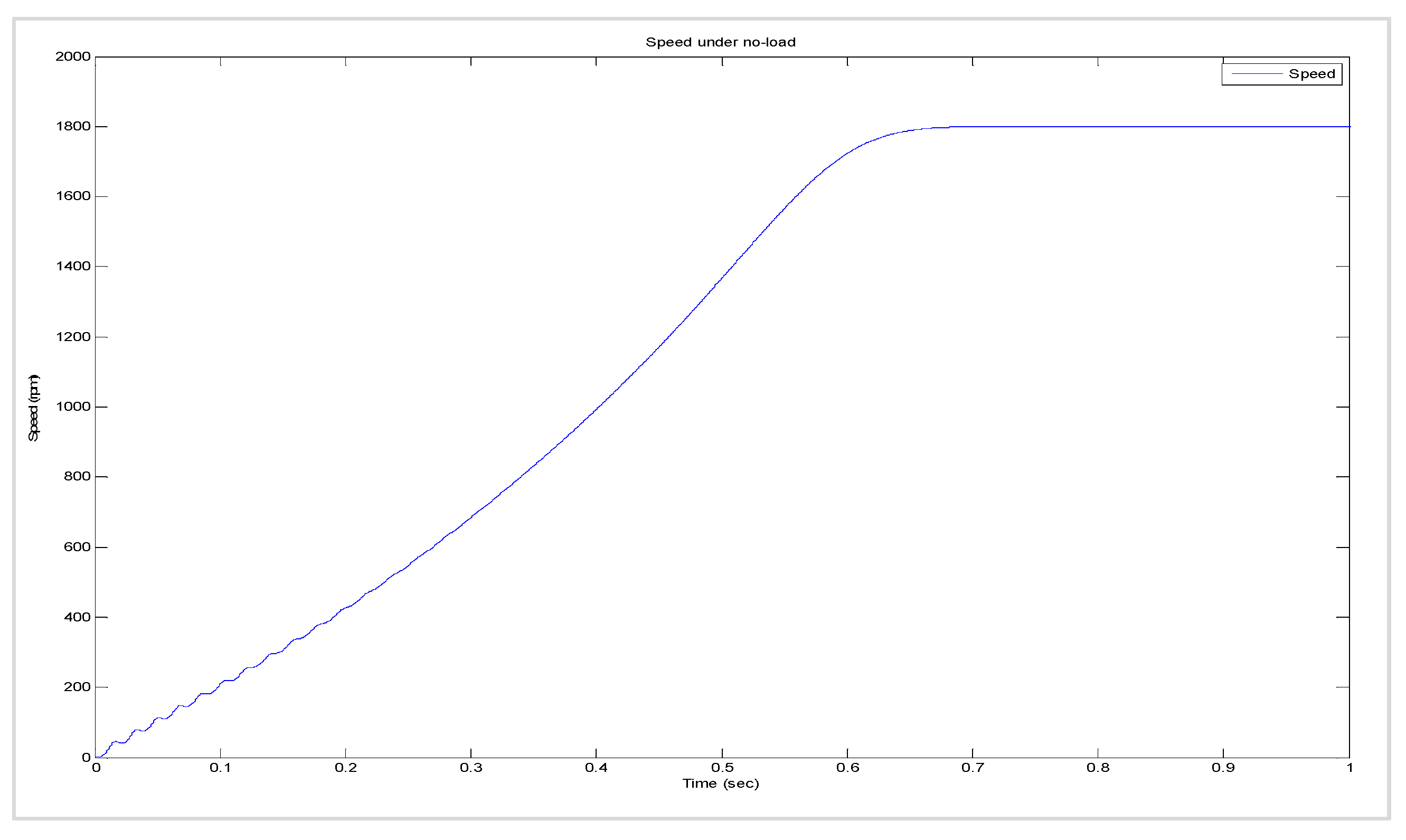
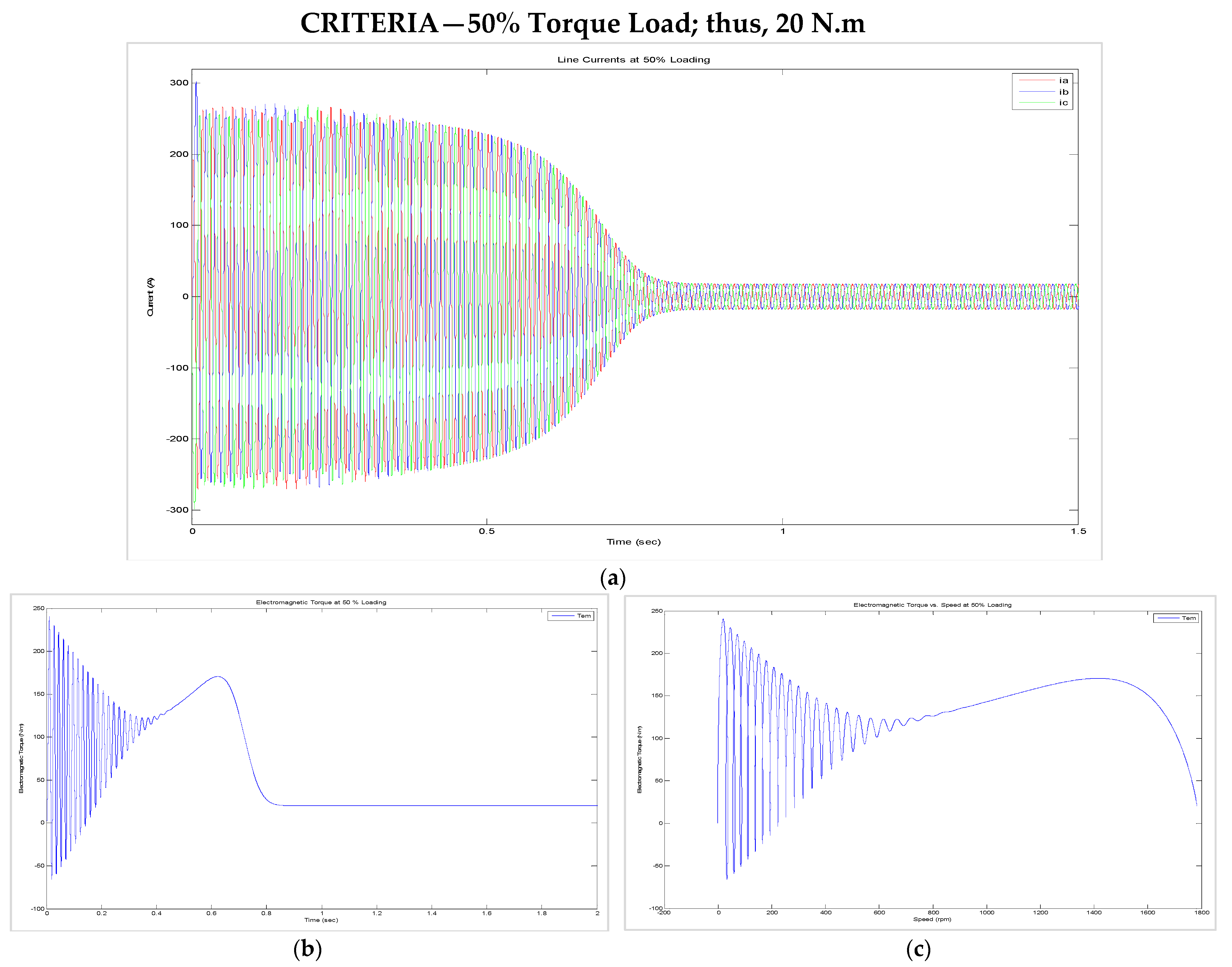
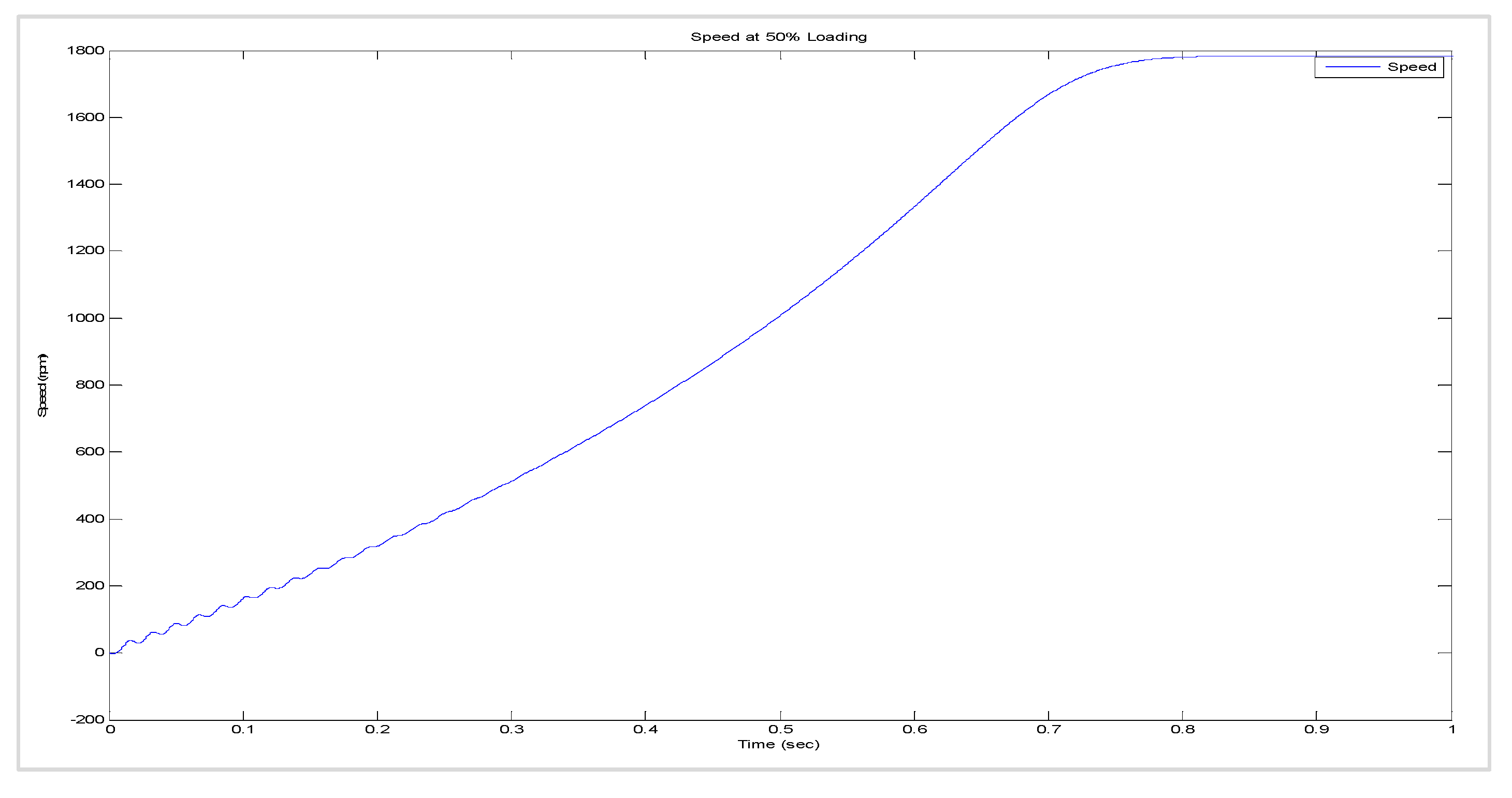
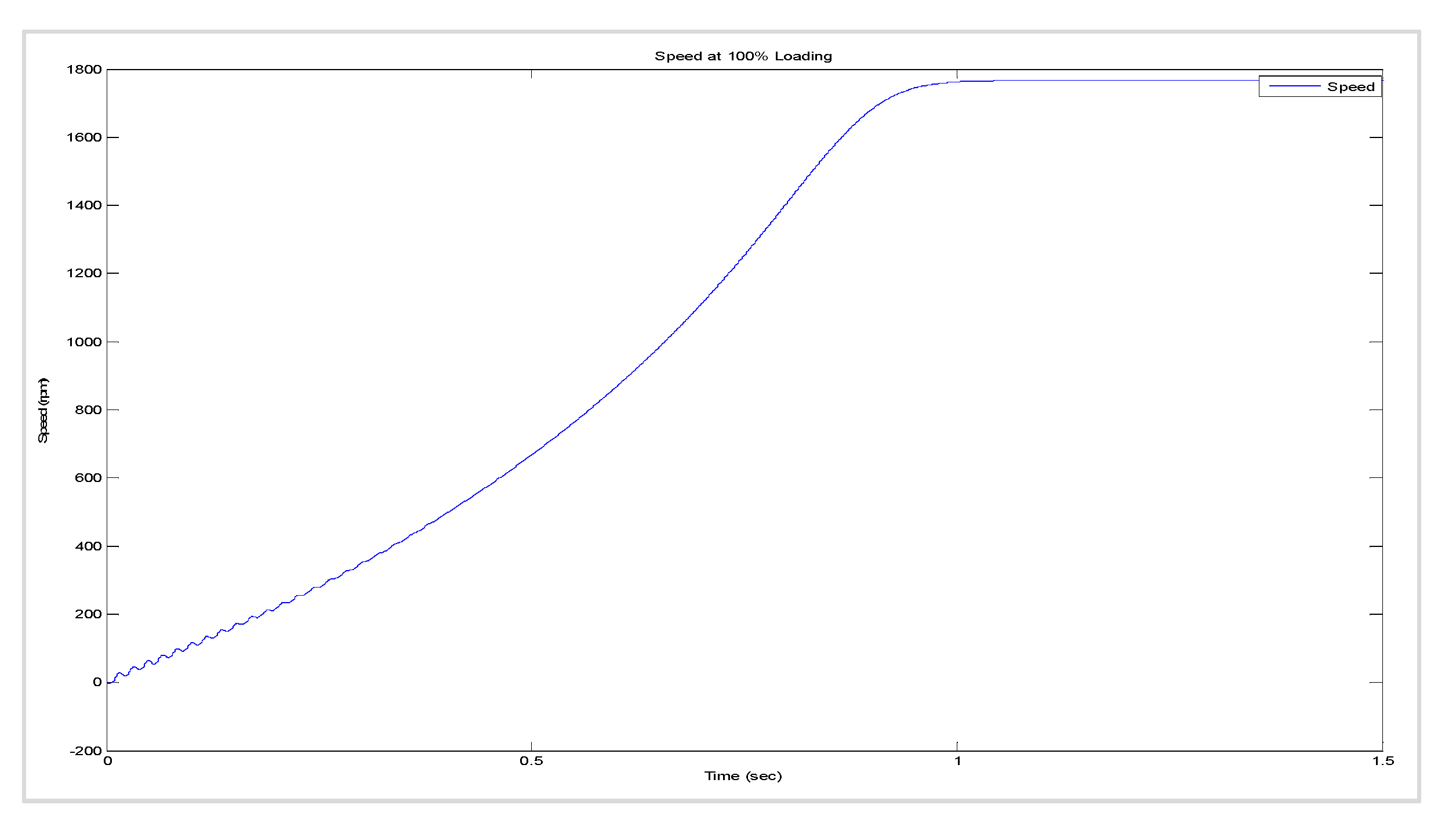
8.2. Transient Behaviour of the Current and Torque Versus Speed during Starting, Assuming That (i) the Machine Is Unloaded, (ii) the Machine Is 50% Loaded, and (iii) the Machine Is 100% Loaded
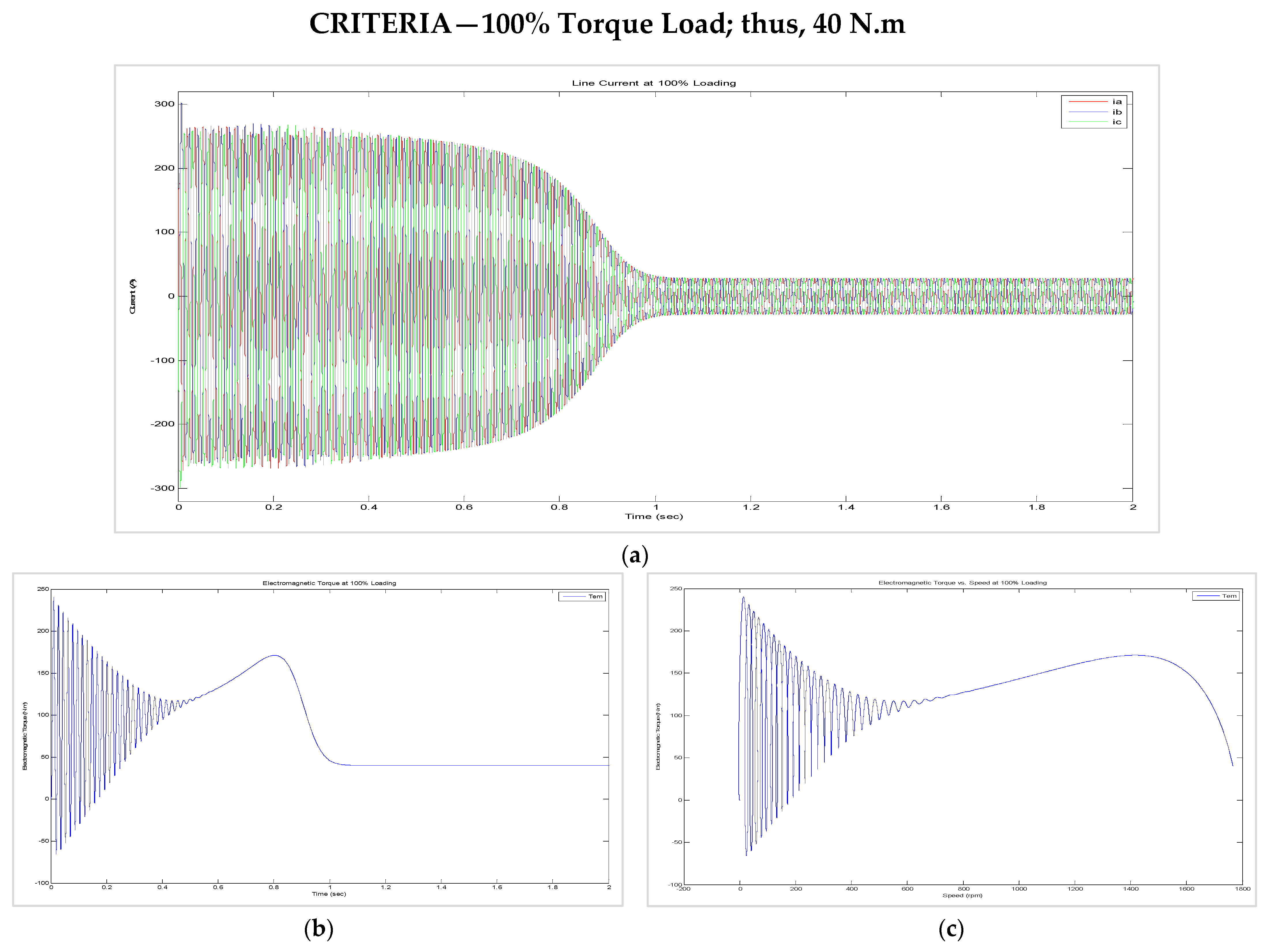
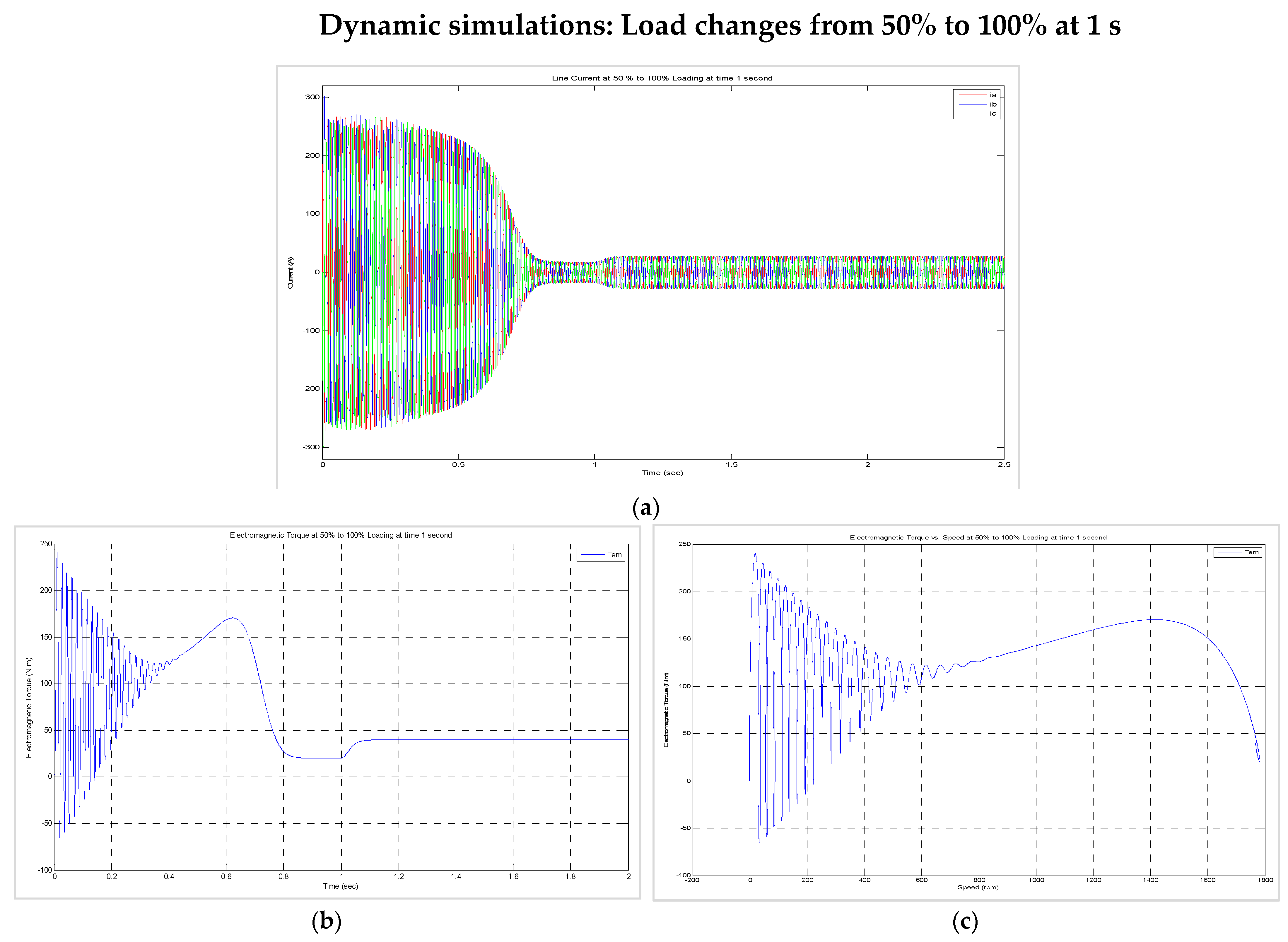
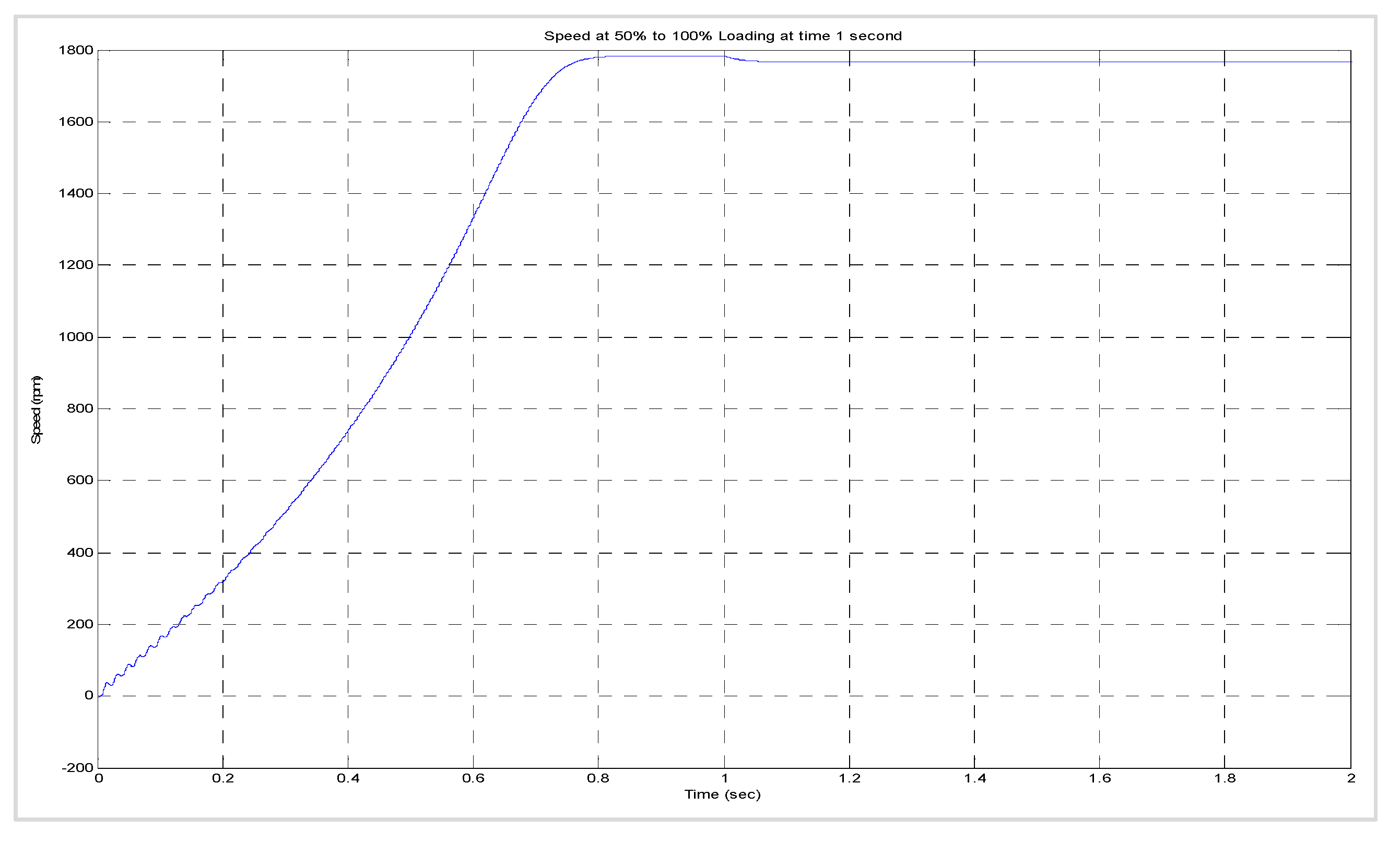
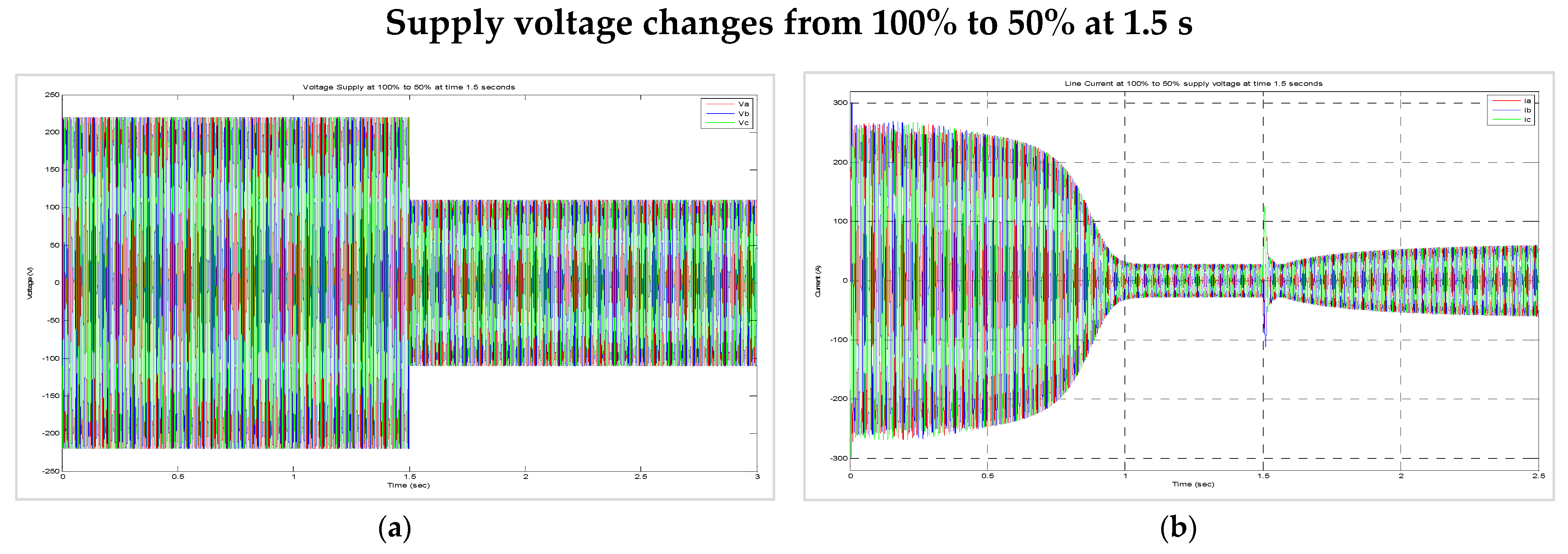
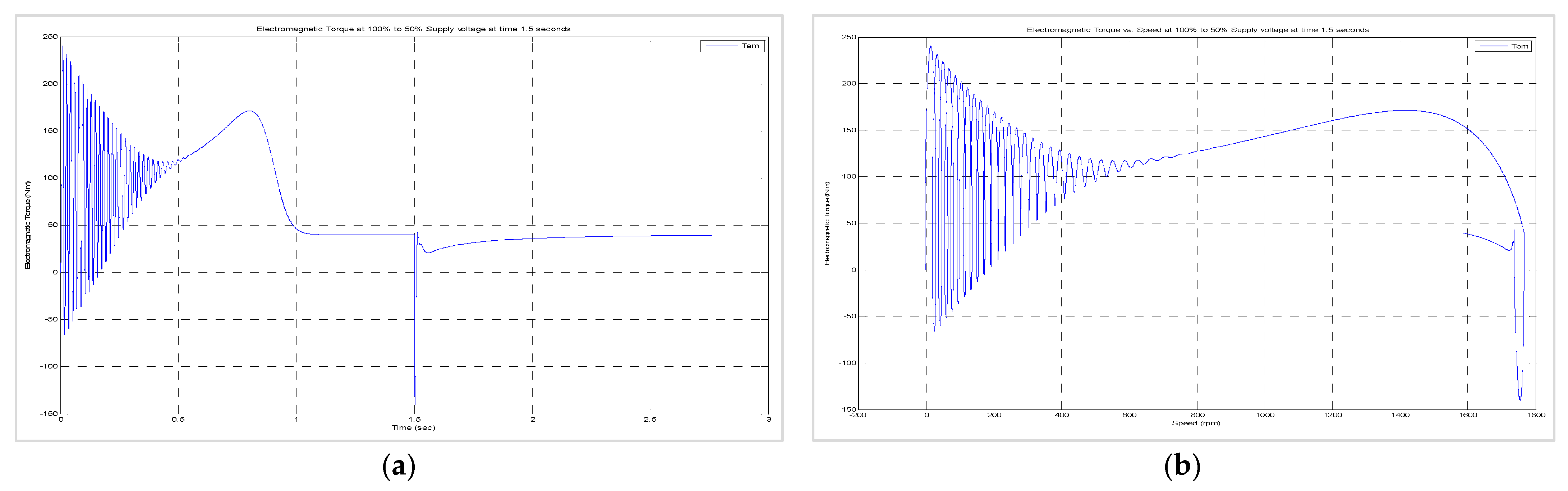
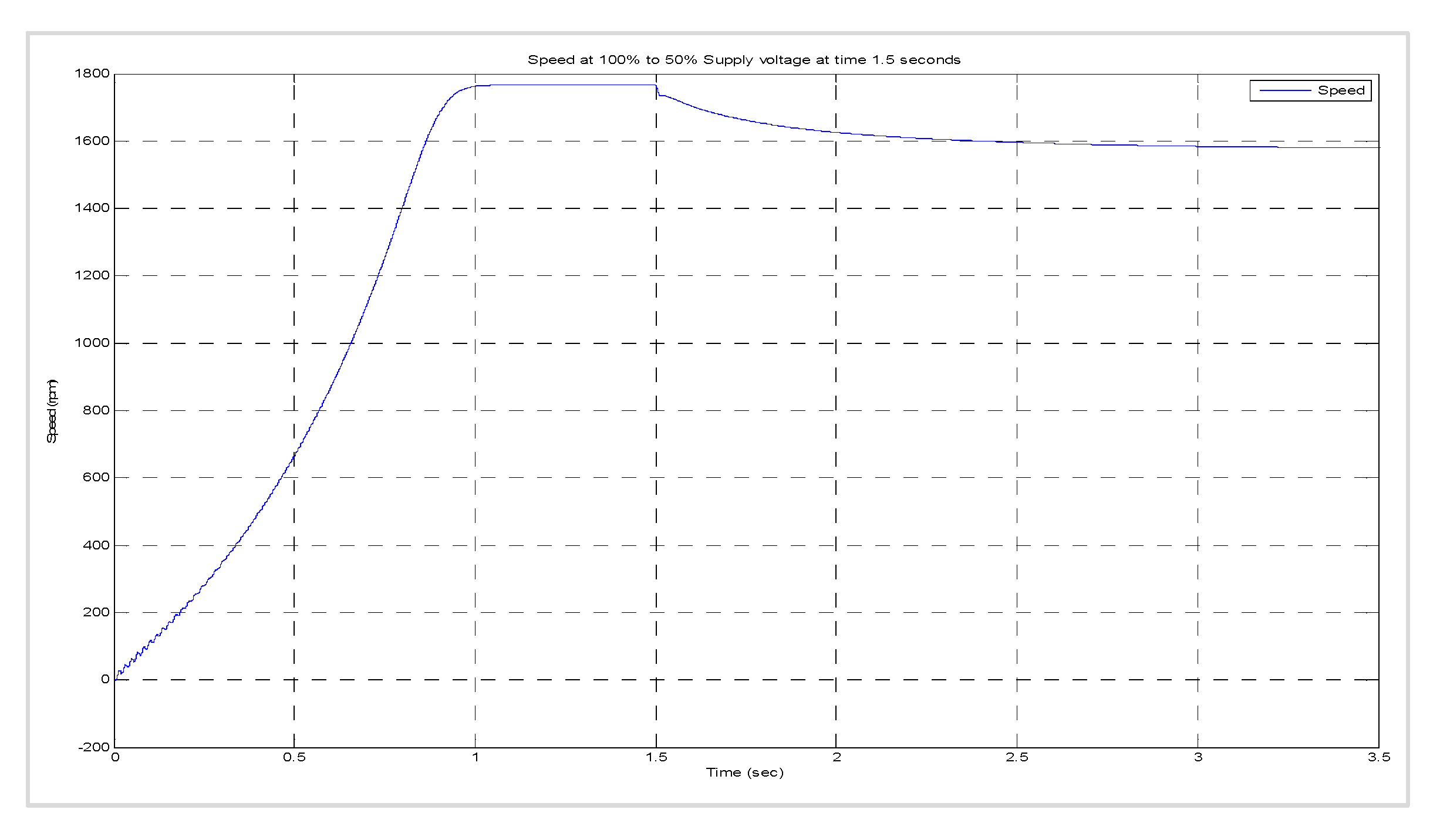
8.3. Dynamic Behaviour of the Machine When (i) the Load Was Suddenly Changed from 50% to 100% and (ii) the Supply Voltage (for the Motors) or the Torque Input (for the Generators) Was Suddenly Halved While the Load Was Maintained at 100%
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rajput, S.; Bender, E.; Averbukh, M. Simplified algorithm for assessment equivalent circuit parameters of induction motors. IET Electr. Power Appl. 2020, 14, 426–432. [Google Scholar] [CrossRef]
- Ahmed, M.; Vahidnia, A.; Datta, M.; Meegahapola, L. An adaptive power oscillation damping controller for a hybrid AC/DC microgrid. IEEE Access 2020, 8, 69482–69495. [Google Scholar] [CrossRef]
- Iegorov, O.; Iegorova, O.; Miroshnyk, O.; Savchenko, O. Improving the accuracy of determining the parameters of induction motors in transient starting modes. Energetika 2020, 66, 15–23. [Google Scholar] [CrossRef]
- Wang, H.; Chau, K.; Lee, C.H.; Cao, L.; Lam, W.H. Design, Analysis, and Implementation of Wireless Shaded-Pole Induction Motors. IEEE Trans. Ind. Electron. 2020, 68, 6493–6503. [Google Scholar] [CrossRef]
- Rahaman, N.; Govindraju, H. Modeling and Simulation of a Three-Phase Electric Traction Induction Motor Using MATLAB/Simulink. Int. J. Electr. Electron. Comput. Syst. 2014, 2, 5. [Google Scholar]
- Kozjaruk, A.E.; Vasilev, B.U.; Shtop, S.A.; Serdukov, N.A. Currents in bearings of induction motors of electric drives with semiconductor converter. In Proceedings of the 17th International Ural Conference on AC Electric Drives (ACED), Ekaterinburg, Russia, 26–30 March 2018; pp. 1–5. [Google Scholar]
- Maleki, M.G.; Chabanloo, R.M.; Farrokhifar, M. Accurate coordination method based on the dynamic model of overcurrent relay for industrial power networks taking contribution of induction motors into account. IET Gener. Transm. Distrib. 2019, 14, 645–655. [Google Scholar] [CrossRef]
- Abdelwanis, M.I.; Selim, F.; El-Sehiemy, R. An efficient sensorless slip dependent thermal motor protection schemes applied to submersible pumps. Int. J. Eng. Res. Afr. 2015, 14, 75–86. [Google Scholar] [CrossRef]
- Chitra, V.; Prabhakar, R. Induction motor speed control using fuzzy logic controller. World Acad. Sci. Eng. Technol. 2006, 23, 17–22. [Google Scholar]
- Elnaghi, B.E.; Mohammed, R.H.; Dessouky, S.S.; Shehata, M.K. Load test of induction motors based on PWM technique using genetic algorithm. Int. J. Eng. Manuf. 2019, 9, 1. [Google Scholar] [CrossRef]
- Sadasivan, J.; Mammen, O. Genetic algorithm based parameter identification of three phase induction motors. Int. J. Comput. Appl. 2011, 31, 51–56. [Google Scholar]
- Jirdehi, M.A.; Rezaei, A. Parameters estimation of squirrel-cage induction motors using ANN and ANFIS. Alex. Eng. J. 2016, 55, 357–368. [Google Scholar] [CrossRef] [Green Version]
- Keerthipala, W.; Duggal, B.; Chun, M.H. Torque and speed control of induction motors using ANN observers. Int. Conf. Power Electron. Drives Energy Syst. Ind. Growth Proc. 1998, 1, 282–288. [Google Scholar]
- Chen, J.; Severson, E.L. Design and modeling of the bearingless induction motor. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 343–350. [Google Scholar]
- Swami, H.; Jain, A.K. An Improved Scalar Controlled Drive Based on Steady State Model of Vector Controlled Drive for Squirrel Cage Induction Motor. In Proceedings of the IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–6. [Google Scholar]
- Levi, E.; Vukosavic, S.; Jones, M. Vector control schemes for series-connected six-phase two-motor drive systems. IEEE Proc.-Electr. Power Appl. 2005, 15, 226–238. [Google Scholar] [CrossRef] [Green Version]
- Goolak, S.; Gubarevych, O.; Yermolenko, E.; Slobodyanyuk, M.; Gorobchenko, O. Mathematical modeling of an induction motor for vehicles. East.-Eur. J. Enterp. Technol. 2020, 2, 104. [Google Scholar] [CrossRef]
- Prabakaran, S.; Venkatesan, S. Analysis of 3 phase Induction Motor Protection Using Numerical Relay. Int. J. Eng. Tech. 2018, 4, 513–519. [Google Scholar]
- Yildiz, R.; Barut, M.; Demir, R. Extended Kalman filter based estimations for improving speed-sensored control performance of induction motors. IET Electr. Power Appl. 2020, 14, 2471–2479. [Google Scholar] [CrossRef]
- Zhefeng, M.L.; Zhang, G.; Diao, L.; Liu, Z. Extended Kalman Filter based on inverse Γ model of induction motor. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–5. [Google Scholar]
- Khamehchi, S.; Mölsä, E.; Hinkkanen, M. Comparison of standstill parameter identification methods for induction motors. In Proceedings of the IEEE 9th International Symposium on Sensorless Control for Electrical Drives (SLED), Helsinki, Finland, 13–14 September 2018; pp. 156–161. [Google Scholar]
- Bimal, K. Modern Power Electronics and AC Drives; Prentice-Hall: Hoboken, NJ, USA, 2001. [Google Scholar]
- Tang, Y.; He, X.; Cao, J. Fast calculation method of transient temperature rise of motor for electro-mechanical braking. Sci. Prog. 2021, 104, 368504211024553. [Google Scholar] [CrossRef] [PubMed]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D.; Pekarek, S.D. Analysis of Electric Machinery and Drive Systems; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wang, L.; Aleksandrov, S.; Tang, Y.; Paulides, J.J.; Lomonova, E.A. Fault-tolerant electric drive and space-phasor modulation of flux-switching permanent magnet machine for aerospace application. IET Electr. Power Appl. 2017, 11, 1416–1423. [Google Scholar] [CrossRef]
- Duan, N.; Ma, X.; Lu, S.; Wang, S.; Wang, S. Simulation Calculation of Loss of Induction Traction Motor. In The Proceedings of the 9th Frontier Academic Forum of Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2021; pp. 599–606. [Google Scholar]
- Liu, Y.; Bazzi, A.M. A detailed induction machine core loss model in the arbitrary reference frame. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 2617–2622. [Google Scholar]
- Shepard, R.A. A Computational Investigation of Cathode Materials for Next-Generation Secondary Batteries. Ph.D. Thesis, State University of New York at Binghamton, Binghamton, NY, USA, 2021. [Google Scholar]
- Claassens, A.J. Transient Modelling of Induction Motors in a Petrochemical Plant Using Matlab. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2008. [Google Scholar]
- Smith, J.R.; Chen, M.J. Three-Phase Electrical Machine Systems: Computer Simulation; Research Studies Press Taunton: Taunton, UK, 1993. [Google Scholar]
- Pereira, L.; Kosterev, D.; Mackin, P.; Davies, D.; Undrill, J.; Zhu, W. An interim dynamic induction motor model for stability tudies in the WSCC. IEEE Trans. Power Syst. 2002, 17, 1108–1115. [Google Scholar] [CrossRef]
- Diaz, A.; Saltares, R.; Rodriguez, C.; Nunez, R.F.; Ortiz-Rivera, E.I.; Gonzalez-Llorente, J. Induction motor equivalent circuit for dynamic simulation. In Proceedings of the IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 858–863. [Google Scholar]
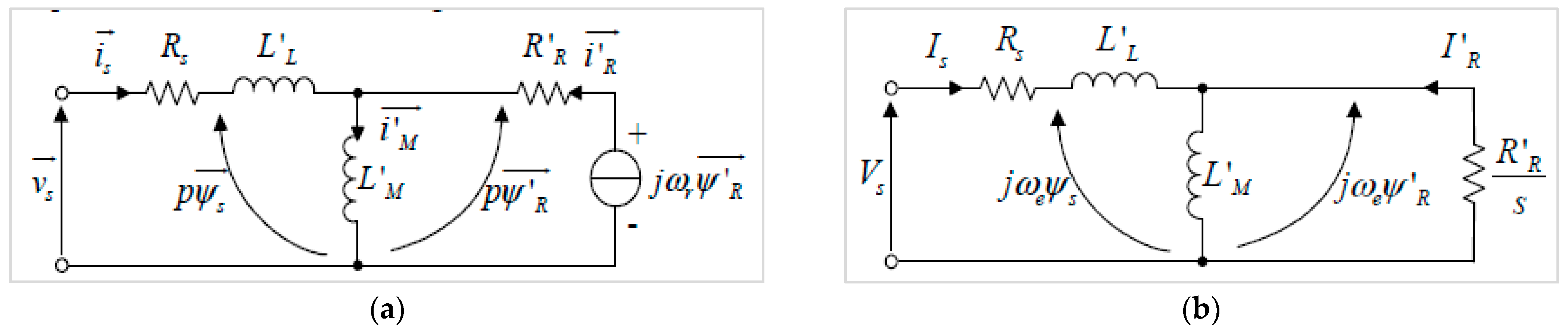



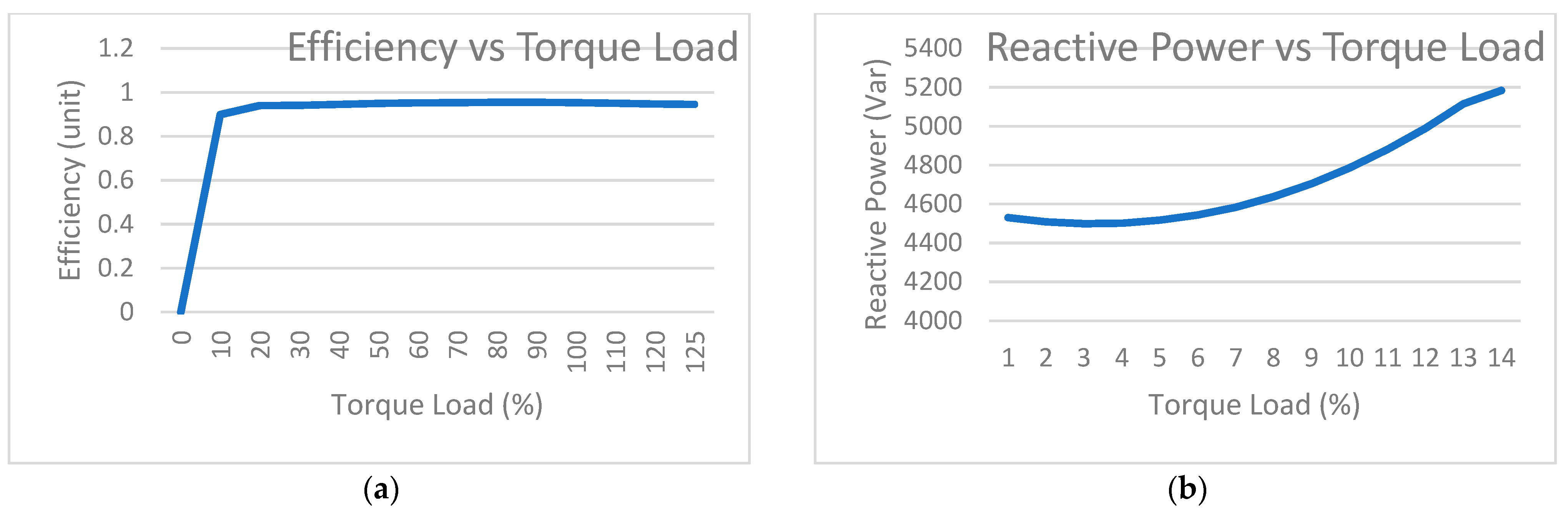


| Torque Load (%) | Current (A) | Pin | Pout | Efficiency (%) | Qin | Power Factor (PF) | Speed (rpm) | Tem (N.m) |
|---|---|---|---|---|---|---|---|---|
| (W) | (W) | (Var) | ||||||
| 0 | 9.708 | 81.42 | 1.14 × 10−7 | 1.40 × 10−9 | 4530 | 0.01797 | 1800 | 6.05 × 10−10 |
| 10 | 9.826 | 837.4 | 752.7 | 0.8988 | 4509 | 0.1826 | 1797 | 4 |
| 20 | 10.23 | 1598 | 1503 | 0.9401 | 4499 | 0.3348 | 1794 | 8 |
| 30 | 10.9 | 2365 | 2250 | 0.9411 | 4502 | 0.465 | 1790 | 12 |
| 40 | 11.78 | 3136 | 2994 | 0.9452 | 4517 | 0.5703 | 1787 | 16 |
| 50 | 12.85 | 3913 | 3736 | 0.9497 | 4544 | 0.6525 | 1784 | 20 |
| 60 | 14.06 | 4695 | 4475 | 0.9521 | 4584 | 0.7155 | 1780 | 24 |
| 70 | 15.39 | 5482 | 5210 | 0.9532 | 4638 | 0.7635 | 1777 | 28 |
| 80 | 16.81 | 6276 | 5943 | 0.9549 | 4705 | 0.8001 | 1773 | 32 |
| 90 | 18.3 | 7075 | 6672 | 0.9549 | 4786 | 0.8283 | 1770 | 36 |
| 100 | 19.86 | 7881 | 7399 | 0.9531 | 4881 | 0.8502 | 1766 | 40 |
| 110 | 21.48 | 8692 | 8122 | 0.9504 | 4990 | 0.8672 | 1763 | 44 |
| 120 | 23.14 | 9510 | 8841 | 0.9469 | 5115 | 0.8807 | 1759 | 48 |
| 125 | 23.99 | 9922 | 9199 | 0.9454 | 5184 | 0.8863 | 1757 | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Roux, P.F.; Ngwenyama, M.K. Static and Dynamic Simulation of an Induction Motor Using Matlab/Simulink. Energies 2022, 15, 3564. https://doi.org/10.3390/en15103564
Le Roux PF, Ngwenyama MK. Static and Dynamic Simulation of an Induction Motor Using Matlab/Simulink. Energies. 2022; 15(10):3564. https://doi.org/10.3390/en15103564
Chicago/Turabian StyleLe Roux, P. F., and M. K. Ngwenyama. 2022. "Static and Dynamic Simulation of an Induction Motor Using Matlab/Simulink" Energies 15, no. 10: 3564. https://doi.org/10.3390/en15103564
APA StyleLe Roux, P. F., & Ngwenyama, M. K. (2022). Static and Dynamic Simulation of an Induction Motor Using Matlab/Simulink. Energies, 15(10), 3564. https://doi.org/10.3390/en15103564






