Self-Supervised Railway Surface Defect Detection with Defect Removal Variational Autoencoders
Abstract
:1. Introduction
- We designed the RC-Net based on the feature complexity of railway inspection images, which greatly simplifies the model parameters, while ensuring rail surface detection accuracy.
- A self-supervised rail surface defect detection model based on DR-VAE is proposed with a structural similarity index measure (SSIM) [27] and introspective variational autoencoder structure, which avoids additional discriminators and simplifies the network structure, while improving the background reconstruction accuracy using adversarial training.
- A defect random mask (D-RM) module is applied to normal rail surfaces during the training process, which provides self-supervised data to improve the defect removal capability of the encoder when reconstructing the background.
- A distribution capacity attenuation factor is proposed in the testing phase to limit the sampling range of the decoder from the latent space, thus reducing the randomness of reconstruction during inferencing and suppressing the problem of excessive generalization of the autoencoder.
2. Materials and Methods
2.1. System Overview
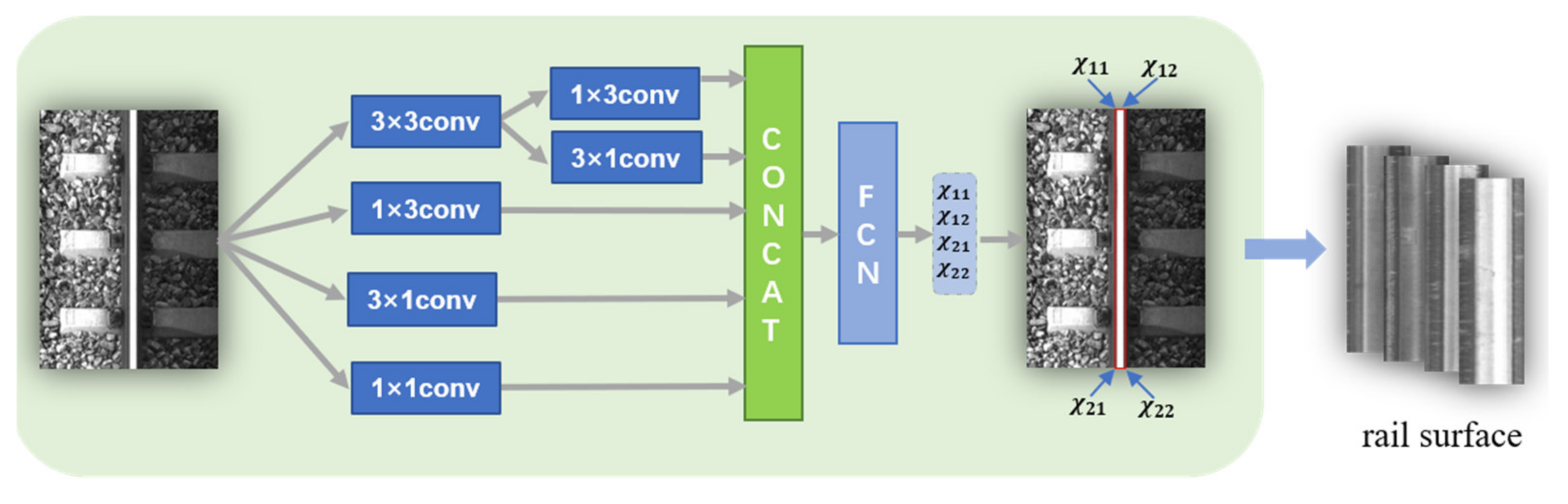
2.1.1. Rail Surface Detection
2.1.2. Defect Detection
2.2. Rail Surface Detection
2.3. Defect Detection
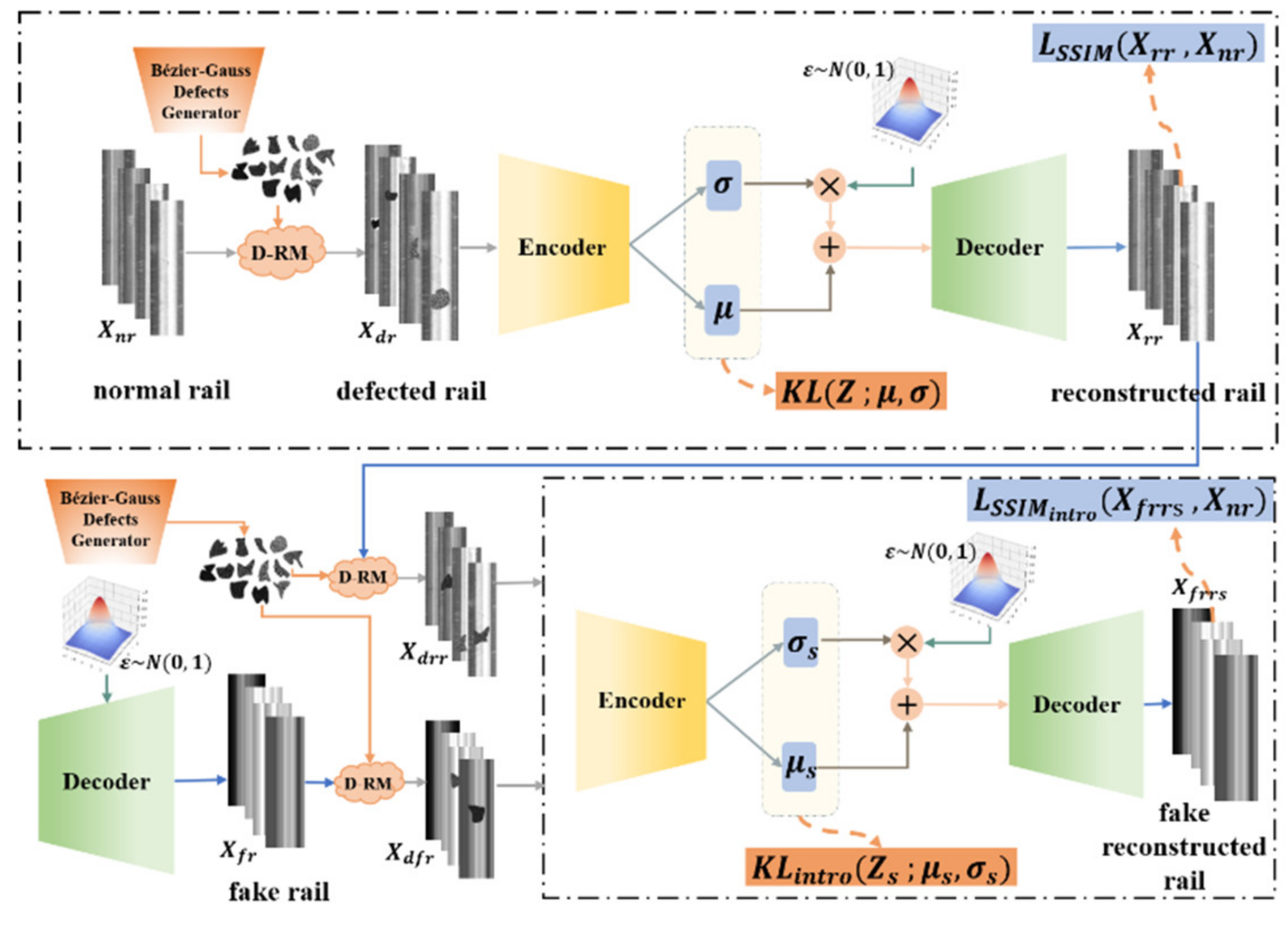
2.3.1. Defect Random Mask
2.3.2. Training Framework
| Algorithm 1 DR-VAE training pseudocode |
| Requireαkl, β, αneg, γ, ϕE, θD |
| while not converged do. |
| Xnr ← Get the normal rail surface data for a batch |
| Xdr ← D-RM(Xnr) generates pseudo-random defective rail surface data |
| μ,σ ← E(Xdr); z←μ + εσ;zf ← sampled from N(0,1) |
| Update Encoder E (ϕE).: |
| Xrr ← D(z); Xfr ← D(zf); Xdrr ←D-RM(Xrr); Xdfr ← D-RM(Xfr) |
| μs, σs ← E(Xddr, Xdfr); zs ← μs +εσs; Xfrrs ← D(zs) |
| KL← μ,σ; KLintro ←μs, σs |
| L ← XSSIMrr, Xnr; LSSIM(intro) ← Xffrs, Xn |
| L(ϕE) ← (αklKL + βLSSIM)/d − 0.5exp(−2(αnegKLintro + βLSSIM(intro)))/d |
| ϕE← ϕE − η∇L(ϕE) |
| end update |
| Update decoder D (θD): |
| Xrr ← D(z); Xfr ← D(zf); Xdrr ← D-RM(Xrr); Xdfr ← D-RM(Xfr) |
| μs, σs ← E(Xddr, Xdfr); zs ← μs + εσs; Xfrrs ← D(zs) |
| KLintro ← μs, σs; LSSIM ← Xrr, Xnr; LSSIM(intro) ← Xffrs, Xn |
| L(θD) ← βLSSIM/d + (αneg KLintro + γβLSSIM(intro))/d |
| θD← θD − η∇L(θD) |
| end update |
| end while |
2.3.3. Model Inference
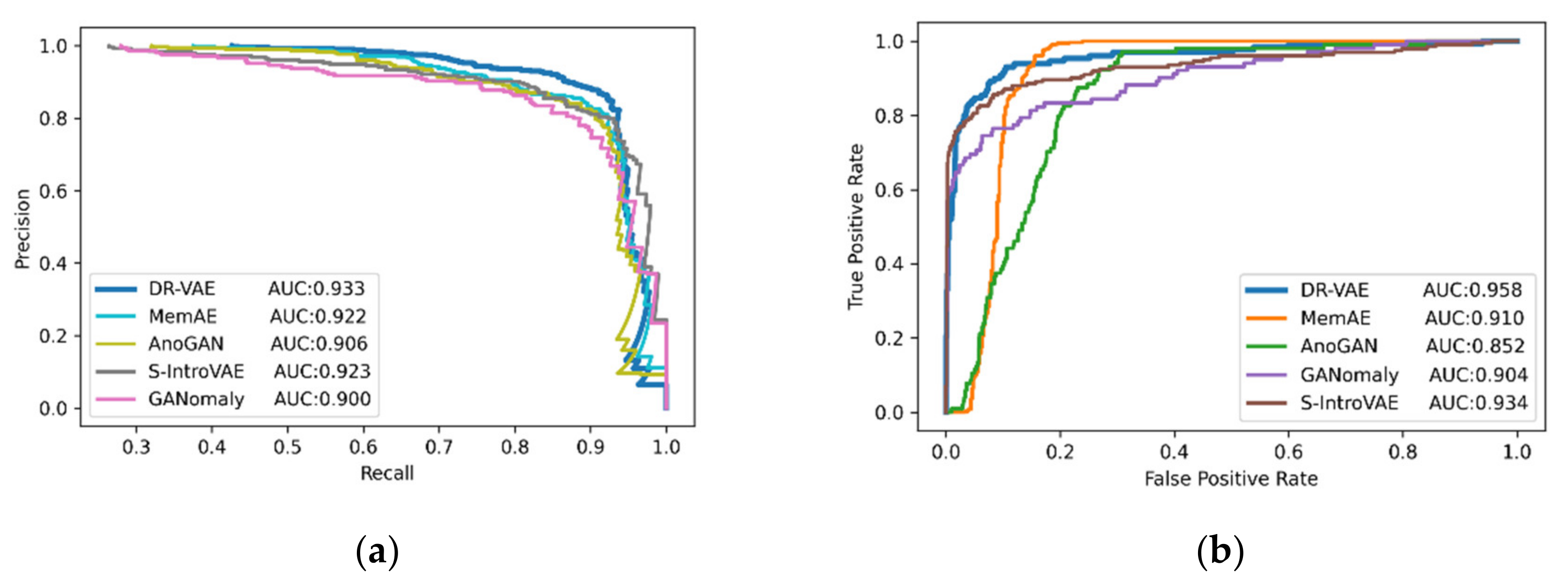
3. Results and Analysis
3.1. Rail Surface Detection
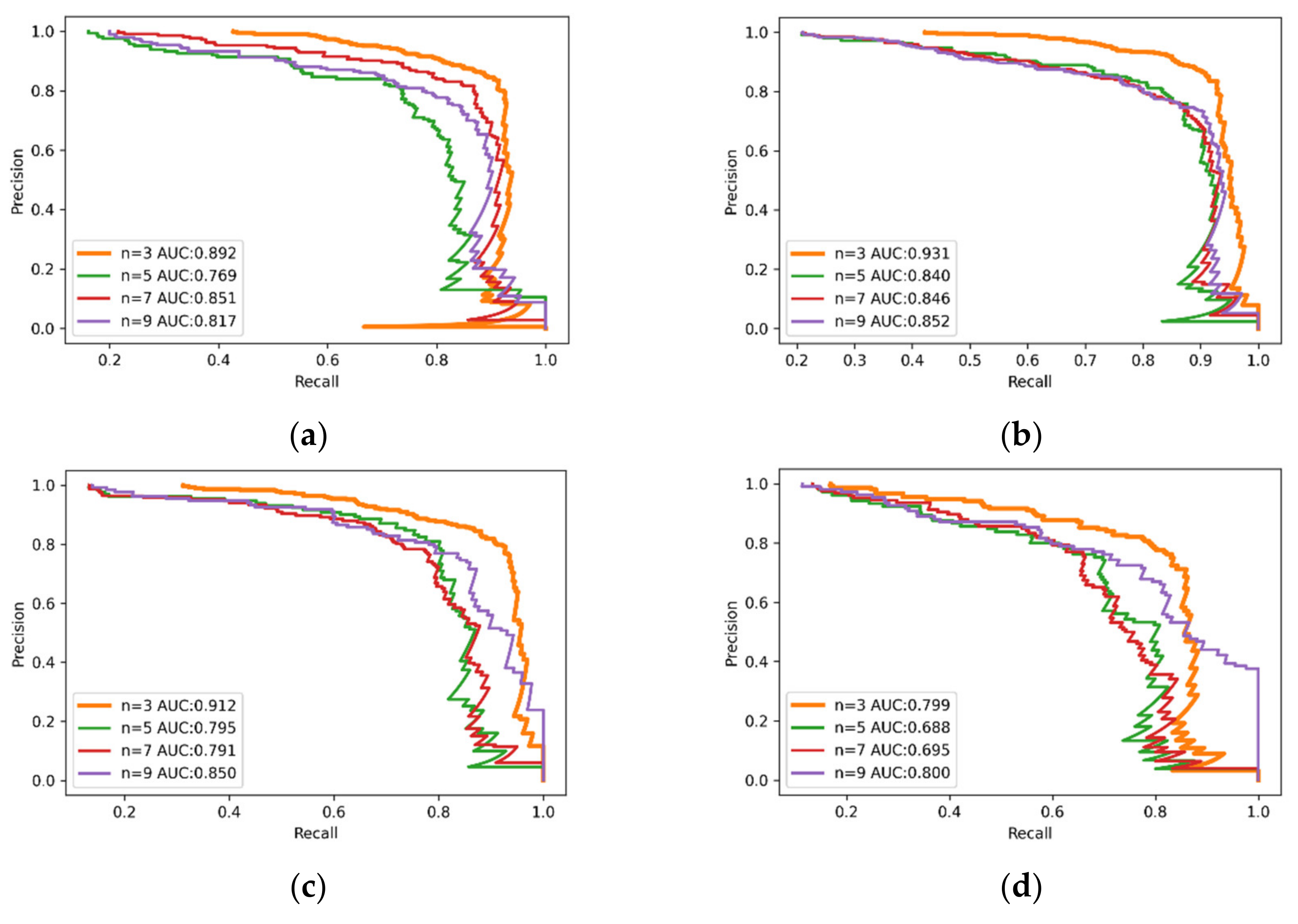
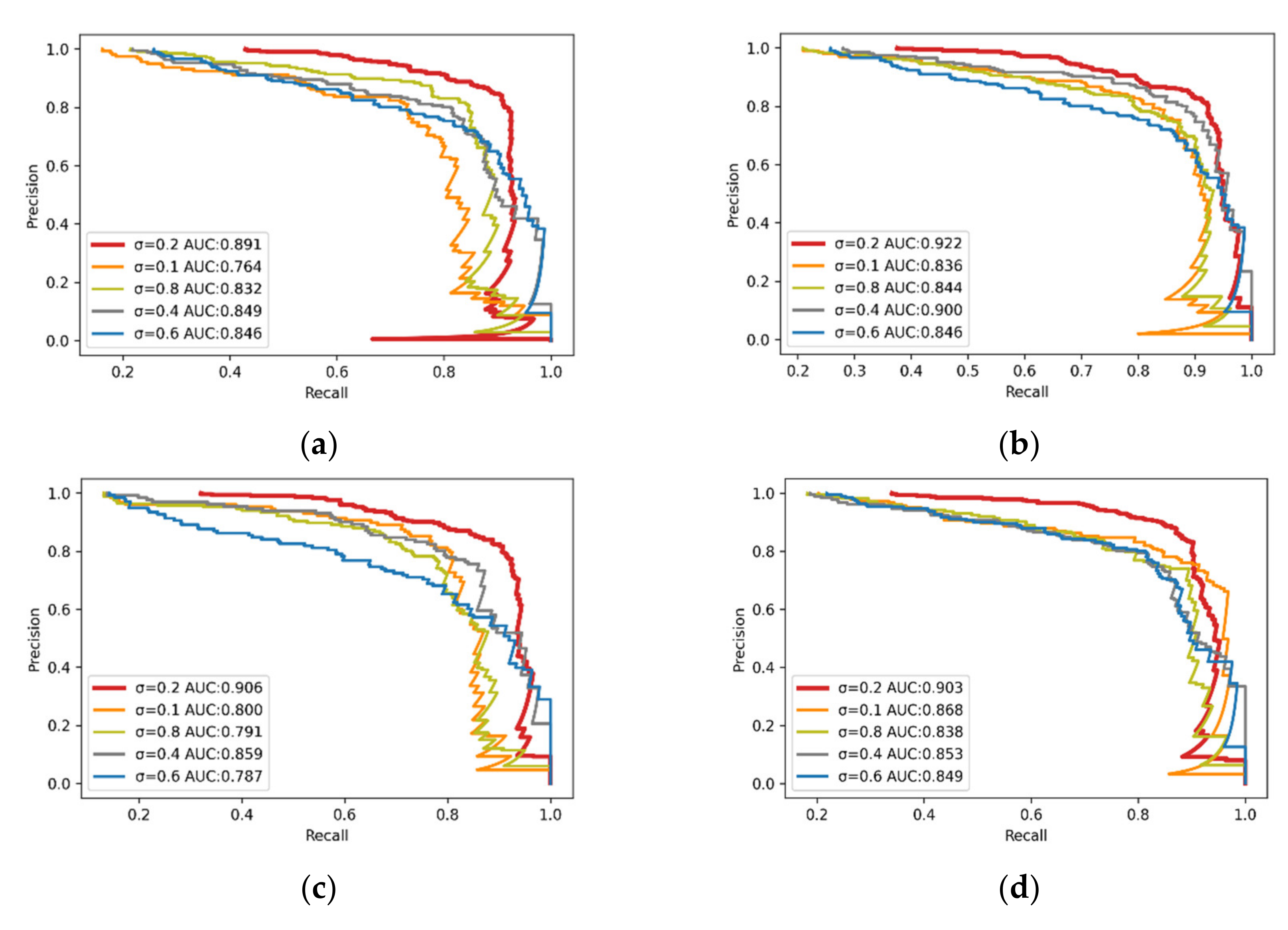
3.2. Rail Surface Defect Detection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, X.; Xie, W.; Ahmed, S.M.; Li, C.R. Defect Detection Method for Rail Surface Based on Line-Structured Light. Measurement 2020, 159, 107771. [Google Scholar] [CrossRef]
- Haomin, Y.; Li, Q.; Tan, Y.; Gan, J.; Wang, J.; Geng, Y.; Jia, L. A Coarse-to-Fine Model for Rail Surface Defect Detection. IEEE Trans. Instrum. Meas. 2019, 68, 656–666. [Google Scholar] [CrossRef]
- Gan, J.; Li, Q.; Wang, J.; Yu, H. A Hierarchical Extractor-Based Visual Rail Surface Inspection System. IEEE Sens. J. 2017, 17, 7935–7944. [Google Scholar] [CrossRef]
- Ni, X.; Ma, Z.; Liu, J.; Shi, B.; Liu, H. Attention Network for Rail Surface Defect Detection via Consistency of Intersection-over-Union(IoU)-Guided Center-Point Estimation. IEEE Trans. Ind. Inform. 2022, 18, 1694–1705. [Google Scholar] [CrossRef]
- Hajizadeh, S.; Núñez, A.; Tax, D.M.J. Semi-Supervised Rail Defect Detection from Imbalanced Image Data. IFAC-Pap. 2016, 49, 78–83. [Google Scholar] [CrossRef]
- Yaman, O.; Karakose, M.; Akin, E. A Vision Based Diagnosis Approach for Multi Rail Surface Faults Using Fuzzy Classificiation in Railways. In Proceedings of the 2017 International Conference on Computer Science and Engineering (UBMK), Antalya, Turkey, 5–8 October 2017; pp. 713–718. [Google Scholar]
- Yuan, H.; Chen, H.; Liu, S.; Lin, J.; Luo, X. A Deep Convolutional Neural Network for Detection of Rail Surface Defect. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; pp. 1–4. [Google Scholar]
- Jin, X.; Wang, Y.; Zhang, H.; Zhong, H.; Liu, L.; Wu, Q.M.J.; Yang, Y. DM-RIS: Deep Multimodel Rail Inspection System with Improved MRF-GMM and CNN. IEEE Trans. Instrum. Meas. 2020, 69, 1051–1065. [Google Scholar] [CrossRef]
- Sabokrou, M.; Khalooei, M.; Fathy, M.; Adeli, E. Adversarially Learned One-Class Classifier for Novelty Detection. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3379–3388. [Google Scholar]
- Nawaratne, R.; Alahakoon, D.; De Silva, D.; Yu, X. Spatiotemporal Anomaly Detection Using Deep Learning for Real-Time Video Surveillance. IEEE Trans. Ind. Inform. 2020, 16, 393–402. [Google Scholar] [CrossRef]
- He, Y.; Peng, Y.; Wang, S.; Liu, D. ADMOST: UAV Flight Data Anomaly Detection and Mitigation via Online Subspace Tracking. IEEE Trans. Instrum. Meas. 2019, 68, 1035–1044. [Google Scholar] [CrossRef]
- Castellani, A.; Schmitt, S.; Squartini, S. Real-World Anomaly Detection by Using Digital Twin Systems and Weakly Supervised Learning. IEEE Trans. Ind. Inform. 2021, 17, 4733–4742. [Google Scholar] [CrossRef]
- Luo, Q.; Fang, X.; Liu, L.; Yang, C.; Sun, Y. Automated Visual Defect Detection for Flat Steel Surface: A Survey. IEEE Trans. Instrum. Meas. 2020, 69, 626–644. [Google Scholar] [CrossRef] [Green Version]
- Xiong, L.; Póczos, B.; Schneider, J. Group Anomaly Detection Using Flexible Genre Models. In Advances in Neural Information Processing Systems; Shawe-Taylor, J., Zemel, R., Bartlett, P., Pereira, F., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2011; Volume 24. [Google Scholar]
- Zhuang, B.; Shen, C.; Tan, M.; Liu, L.; Reid, I. Structured Binary Neural Networks for Accurate Image Classification and Semantic Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 413–422. [Google Scholar]
- Zong, B.; Song, Q.; Min, M.R.; Cheng, W.; Lumezanu, C.; Cho, D.; Chen, H. Deep Autoencoding Gaussian Mixture Model for Unsupervised Anomaly Detection. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 15 February 2018; pp. 1–19. [Google Scholar]
- Hasan, M.; Choi, J.; Neumann, J.; Roy-Chowdhury, A.K.; Davis, L.S. Learning Temporal Regularity in Video Sequences. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 30 June 2016; pp. 733–742. [Google Scholar]
- Zhao, Y.; Deng, B.; Shen, C.; Liu, Y.; Lu, H.; Hua, X.-S. Spatio-Temporal AutoEncoder for Video Anomaly Detection. In Proceedings of the 25th ACM International Conference on Multimedia, New York, NY, USA, 23–27 October 2017; pp. 1933–1941. [Google Scholar]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. GANomaly: Semi-Supervised Anomaly Detection via Adversarial Training. In Proceedings of the Computer Vision–ACCV 2018, Perth, Australia, 2–6 December 2018; Jawahar, C.V., Li, H., Mori, G., Schindler, K., Eds.; Springer: Cham, Switzerland, 2019; pp. 622–637. [Google Scholar]
- Medel, J.R.; Savakis, A. Anomaly Detection in Video Using Predictive Convolutional Long Short-Term Memory Networks. arXiv 2016, arXiv:1612.00390. [Google Scholar]
- Perera, P.; Nallapati, R.; Xiang, B. OCGAN: One-Class Novelty Detection Using GANs with Constrained Latent Representations. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2893–2901. [Google Scholar]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery. In Proceedings of the Information Processing in Medical Imaging, Boone, NC, USA, 25–30 June 2017; Niethammer, M., Styner, M., Aylward, S., Zhu, H., Oguz, I., Yap, P.-T., Shen, D., Eds.; Springer: Cham, Switzerland, 2017; pp. 146–157. [Google Scholar]
- Zenati, H.; Romain, M.; Foo, C.-S.; Lecouat, B.; Chandrasekhar, V. Adversarially Learned Anomaly Detection. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 727–736. [Google Scholar]
- Gong, D.; Liu, L.; Le, V.; Saha, B.; Mansour, M.R.; Venkatesh, S.; Van Den Hengel, A. Memorizing Normality to Detect Anomaly: Memory-Augmented Deep Autoencoder for Unsupervised Anomaly Detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 1705–1714. [Google Scholar]
- Ye, F.; Huang, C.; Cao, J.; Li, M.; Zhang, Y.; Lu, C. Attribute Restoration Framework for Anomaly Detection. IEEE Trans. Multimed. 2022, 24, 116–127. [Google Scholar] [CrossRef]
- Daniel, T.; Tamar, A. Soft-IntroVAE: Analyzing and Improving the Introspective Variational Autoencoder. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19 June 2021; pp. 4389–4398. [Google Scholar]
- Bergmann, P.; Löwe, S.; Fauser, M.; Sattlegger, D.; Steger, C. Improving Unsupervised Defect Segmentation by Applying Structural Similarity to Autoencoders. arXiv 2018, arXiv:1807.02011. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. arXiv 2016, arXiv:1602.07261. [Google Scholar]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; MIT Press: Cambridge, MA, USA, 2015; Volume 1, pp. 91–99. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked Autoencoders Are Scalable Vision Learners. arXiv 2021, arXiv:2111.06377. [Google Scholar]
- Viquerat, J.; Hachem, E. A Supervised Neural Network for Drag Prediction of Arbitrary 2D Shapes in Laminar Flows at Low Reynolds Number. Comput. Fluids 2020, 210, 104645. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the Computer Vision–ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]






| Encoder | Parameters | Output | Decoders | Parameters | Output |
|---|---|---|---|---|---|
| Input | - | 64 × 64 × 1 | L-vector | - | 8 × 1 × 1 |
| Conv | 5 × 5, 8 | 64 × 64 × 8 | FC-16 | 16 | 16 × 1 × 1 |
| Avg pool | - | 32 × 32 × 8 | FC-1024 | 1024 | 1024 × 1 × 1 |
| Res-block | 1 × 1, 16 3 × 2, 16 3 × 3, 16 | Reshape | - | 4 × 4 × 64 | |
| 32 × 32 × 16 | Res-block | 3 × 3, 64 3 × 3, 64 | 4 × 4 × 64 | ||
| Avg pool | - | 16 × 16 × 16 | Up-sample | - | 8 × 8 × 64 |
| Res-block | 1 × 1, 32 3 × 3, 32 3 × 3, 32 | Res-block | 1 × 1, 32 3 × 3, 32 3 × 3, 32 | ||
| 16 × 16 × 32 | 8 × 8 × 32 | ||||
| Avg pool | - | 8 × 8 × 32 | Up-sample | - | 16 × 16 × 32 |
| Res-block | 1 × 1, 64 3 × 3, 64 3 × 3, 64 | Res-block | 3 × 3, 16 3 × 3, 16 | 16 × 16 × 16 | |
| 8 × 8 × 64 | |||||
| Up-sample | - | 32 × 32 × 16 | |||
| Avg pool | - | 4 × 4 × 64 | Res-block | 3 × 3, 8 3 × 3, 8 | 32 × 32 × 8 |
| Reshape | - | 1024 × 1 × 1 | |||
| FC-16 | 16 | 16 × 1 × 1 | Up-sample | - | 64 × 64 × 8 |
| Split | - | 8,8 | Conv | 5 × 5, 1 | 64 × 64 × 1 |
| Models | Precision | Recall | F1 Score |
|---|---|---|---|
| Faster R-CNN | 0.991 | 0.979 | 0.985 |
| YOLOv4 | 0.979 | 0.978 | 0.979 |
| SSD | 0.985 | 0.975 | 0.980 |
| RC-Net | 0.992 | 0.985 | 0.988 |
| Models | ACC | Precision | Recall | MCC | AUC | F1 |
|---|---|---|---|---|---|---|
| MemAE | 0.69 | 0.91 | 0.47 | 0.58 | 0.922 | 0.74 |
| Soft-IntroVAE | 0.68 | 0.93 | 0.46 | 0.57 | 0.923 | 0.78 |
| GANomaly | 0.68 | 0.92 | 0.46 | 0.57 | 0.900 | 0.73 |
| AnoGAN | 0.52 | 0.86 | 0.31 | 0.49 | 0.906 | 0.50 |
| DR-VAE | 0.71 | 0.95 | 0.48 | 0.59 | 0.933 | 0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, Y.; Li, Y. Self-Supervised Railway Surface Defect Detection with Defect Removal Variational Autoencoders. Energies 2022, 15, 3592. https://doi.org/10.3390/en15103592
Min Y, Li Y. Self-Supervised Railway Surface Defect Detection with Defect Removal Variational Autoencoders. Energies. 2022; 15(10):3592. https://doi.org/10.3390/en15103592
Chicago/Turabian StyleMin, Yongzhi, and Yaxing Li. 2022. "Self-Supervised Railway Surface Defect Detection with Defect Removal Variational Autoencoders" Energies 15, no. 10: 3592. https://doi.org/10.3390/en15103592
APA StyleMin, Y., & Li, Y. (2022). Self-Supervised Railway Surface Defect Detection with Defect Removal Variational Autoencoders. Energies, 15(10), 3592. https://doi.org/10.3390/en15103592






