Abstract
Dynamic adaptive streaming over HTTP (DASH) technique, the most popular streaming method, requires a large number of hard disk drives (HDDs) to store multiple bitrate versions of many videos, consuming significant energy. A solid-state drive (SSD) can be used to cache popular videos, thus reducing HDD energy consumption by allowing I/O requests to be handled by an SSD, but this requires effective HDD power management due to limited SSD bandwidth. We propose a new SSD cache management scheme to minimize the energy consumption of a video storage system with heterogeneous HDDs. We first present a technique that caches files with the aim of saving more HDD energy as a result of I/O processing on an SSD. Based on this, we propose a new HDD power management algorithm with the goal of increasing the number of HDDs operated in low-power mode while reflecting the heterogeneous HDD power characteristics. For this purpose, it assigns a separate parameter value to each I/O task based on the ratio of HDD energy to bandwidth and greedily selects the I/O tasks handled by the SSD within limits on its bandwidth. Simulation results show that our scheme consumes between 12% and 25% less power than alternative schemes under the same HDD configuration.
1. Introduction
Demand for video streaming applications such as YouTube, Netflix, and Twitch is growing rapidly. For example, in 2021, Netflix had 209 million subscribers worldwide [1], and YouTube viewers are expected to reach 210 million in the United States alone by 2022 [2]. Most of these streaming companies use a dynamic adaptive streaming over HTTP (DASH) technique, which splits each video into segments, each of which is then transcoded into multiple bitrate versions so that the most appropriate bitrate version can be streamed to support each request [3,4,5,6,7]. For example, YouTube recommends storing 11 bitrate versions between 500 and 35,000 kbps for each video segment [8]. This allows lower bitrate versions (e.g., 500 kbps) to be transmitted when network conditions are poor, enabling seamless streaming even under low network bandwidth.
DASH requires a lot of storage space to store multiple bitrate versions of each video [9,10]. In addition, redundancy techniques such as data replication are used to handle disk failures, significantly increasing storage space for video files. To support a large amount of storage space, video storage systems generally rely on cost-effective arrays of hard disk drives (HDDs) [9,10,11]. In addition, to support the increasing demand for video files, HDDs are gradually added, creating a storage array of heterogeneous HDDs [12,13].
Because of the large amount of storage space for storing video data, video storage systems inherently consume significant energy [14,15,16,17]. For example, recent studies have shown that the energy consumed by storage systems can account for 40% of the total data center energy [17]. Moreover, this high energy consumption negatively affects the reliability of the HDD array [10]. To address this, an HDD provides a standby mode in which the HDD completely stops spinning to reduce power consumption, and in this mode, it consumes much less power compared to other modes [11,18]. Therefore, in terms of energy saving, it is essential to extend the time the HDD stays in standby mode.
Solid-state-drives (SSDs) support lower power consumption, higher endurance, and lower I/O latency compared to HDDs [19,20,21]. Although the cost of SSDs is decreasing, they are still much more expensive than HDDs [10,19,20,21]. Since access patterns for video sets tend to be highly skewed, SSDs can be used as a cache of HDD arrays in video storage systems to store popular videos [22], but effective management of their bandwidth and storage space is essential.
Several studies have suggested techniques for improving performance and reducing power using SSDs in video servers. For example, Ryu et al. [22] introduced a caching method to improve the processing rate of the video server; Xie et al. [23] developed a technique to dynamically copy popular videos to an SSD; Song [10] presents an SSD bandwidth management technique to minimize power consumption in video servers using multi-speed disks. However, to the best of our knowledge, this paper is the first attempt to develop an SSD cache management scheme to minimize HDD energy consumption in video storage systems using heterogeneous HDDs while making use of redundant data for reducing energy consumption.
The major contributions of this paper are summarized as follows:
- We propose a new method of using an SSD cache to minimize overall HDD power consumption in video storage systems with heterogeneous HDDs by taking account of different HDD power characteristics.
- We propose an SSD storage management technique that allows files to be cached on an SSD with the aim of maximizing the sum of HDD energy saving as a result of I/O processing.
- We propose an SSD bandwidth management technique that allows the SSD to handle energy-intensive I/O tasks first, thereby saving more energy.
- We extensively evaluate the proposed scheme in terms of SSD size and bandwidth, popularity model, and number of HDDs.
The remainder of this paper is organized as follows: Section 2 reviews related works, and Section 3 provides a system model. Section 4 and Section 5 present SSD caching determination and bandwidth management algorithms, respectively. Section 6 evaluates the proposed scheme using simulations, and Section 7 finally concludes the paper.
2. Related Work
Storage energy-saving techniques, many of which use data placement and scheduling methods, have been extensively studied. For example, Machida et al. [24] formulated the file placement problem as a combinatorial optimization with capacity and performance constraints and presented a heuristic algorithm based on a stochastic process of disk state transitions to reduce HDD energy consumption. Karakoyunlu and Chandy [25] introduced several methods for energy-efficient storage node allocation by leveraging the metadata heterogeneity of cloud users and proposed an on-demand load balancing technique that allows inactive nodes to be transitioned into a low-power mode. Behzadnia et al. [26] presented a dynamic power management scheme that allows for disk-to-disk fragment migration to balance power consumption and query response time. Khatib and Bandic [27] presented a power-capping scheme that resizes I/O queues adaptively to improve throughput while reducing tail latency. Segu et al. [28] presented a data replication strategy that takes into account both energy consumption and expenditure of service providers in cloud storage systems.
Several techniques have been developed to conserve disk energy by turning off cold storage that stores rarely accessed data. Hu and Deng [29] presented a technique for aggregating and storing correlated cold data in the same cold node while mitigating the cost of power mode switching. Park et al. [30] introduced a cold-storage-based power management technique that can be progressively used for online services and presented the results of its implementation on a real distributed storage system. Lee et al. [31] introduced a tool for benchmarking a cold storage system, especially for mobile messenger applications and presented the results of constructing a cold storage test-bed based on it. However, none of these studies take into account the characteristics of the video data, so they cannot be used for video storage systems.
Some energy-saving techniques have been developed specifically for video storage systems. Han and Song [11] introduced a hot–cold data classification method, and presented storage and bandwidth management techniques with the aim of maximizing the quality of video files streamed to users. Yuan et al. [18] presented a prediction-based algorithm to formulate and solve optimization problems to determine the optimal choice of disk power mode for large-scale video sharing services. Chai et al. [32] presented a file migration scheme to construct energy-efficient data layouts without unnecessary data migrations for video storage systems. Song et al. [33] proposed a selective prefetching scheme to reduce power overhead and an interval-based caching method that maximizes the amount of energy saved. However, all of these schemes were developed for video storage systems with HDDs only.
SSDs can be effectively utilized to reduce power consumption in HDD-based disk arrays [15]. Salkhordeh et al. [34] presented a hybrid I/O caching architecture to improve energy efficiency under the same cost budget. For this purpose, it uses a three-level cache hierarchy based on DRAM, read-optimized SSD, and write-optimized SSD, addressing the trade-off between performance and durability and allowing for energy-efficient storage reconfiguration. Tomes and Altiparmak [35] examined the energy consumption characteristics of storage arrays with HDDs and SSDs and provided guidelines for building energy-efficient hybrid storage systems. Huang and Chang [36] presented a file system to manage three types of storage (NVRAM, flash memory, and magnetic disk) to improve energy efficiency by leveraging the parallelism between flash memory and disk during data distribution. Hui et al. [37] presented a new storage architecture that utilizes SSDs to get more opportunities to put underutilized HDDs into a low-power state. All of these studies were developed for general workloads, making them difficult to use for video servers
Ryu et al. [22] considered the use of SSDs, especially for DASH-based multi-tier video storage systems. They proposed a scheme that determines write granularity to overcome the write amplification effect of the SSDs. Manjunath and Xie [23] proposed a hybrid architecture in which video files are dynamically copied from an HDD to an SSD, reducing the load on the HDD to save energy consumption. Zhang et al. [38] presented an error tolerance technique to reduce the cost of an SSD-based video caching by using lower-cost flash memory chips for video storage systems. Song [10] presented an SSD management technique that minimizes the rotational speeds of HDDs, reducing their power consumption, specifically for a video storage system with multi-speed disks. However, none of these schemes take into account the issues of power and data redundancy characteristics of heterogeneous HDDs.
3. System Model
A video is divided into segments, each of which is transcoded into bitrate versions, where represents the jth bitrate version of segment i, (). Each bitrate version has a bitrate of where . Table 1 summarizes the notations used in this paper.

Table 1.
Notations.
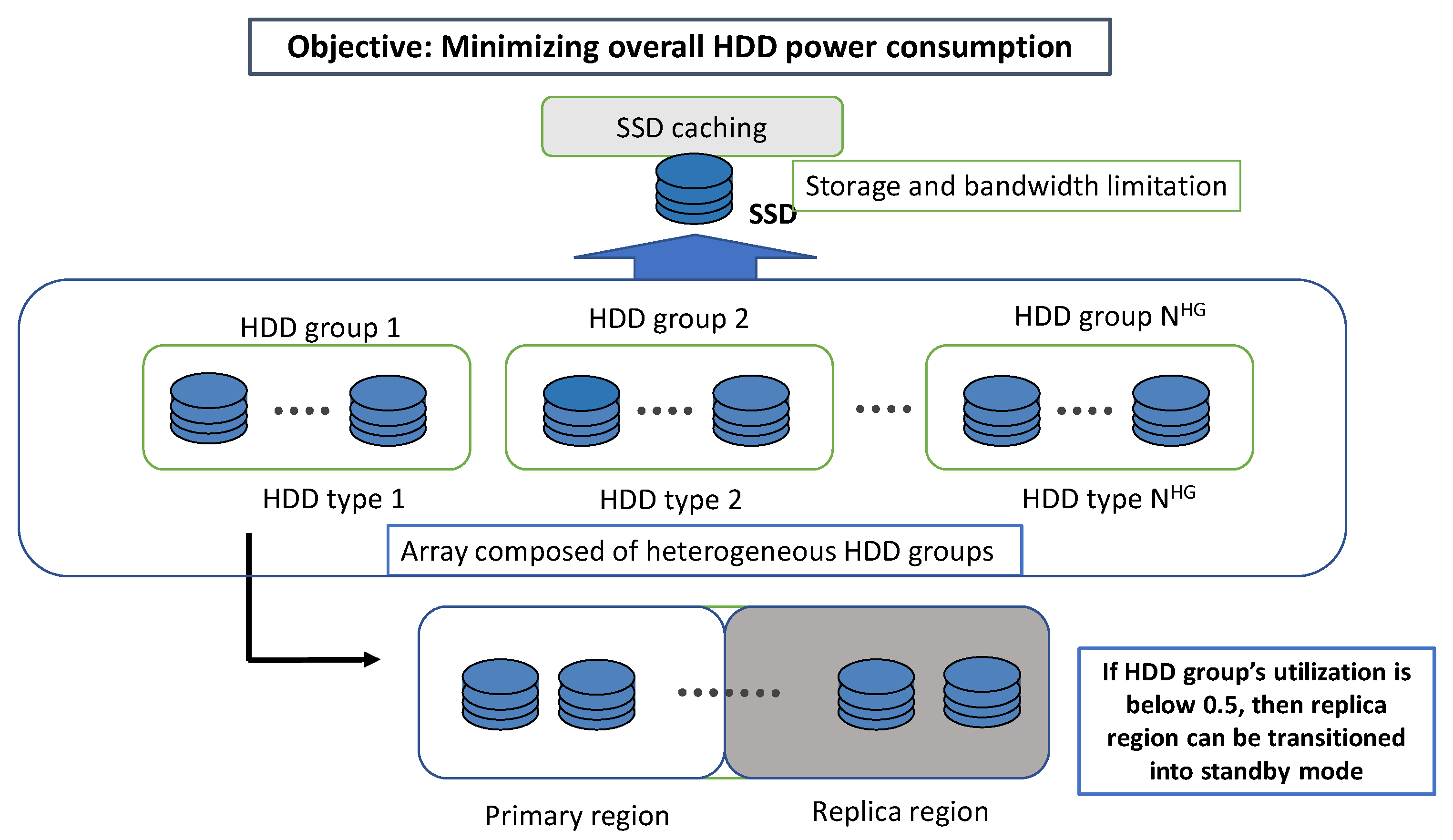
Figure 1 shows a video server architecture composed of an SSD and an array of heterogeneous HDDs with different power characteristics. The HDD array is divided into groups, each group consisting of HDDs of the same type. For ease of exposition, is assumed to be an even number.
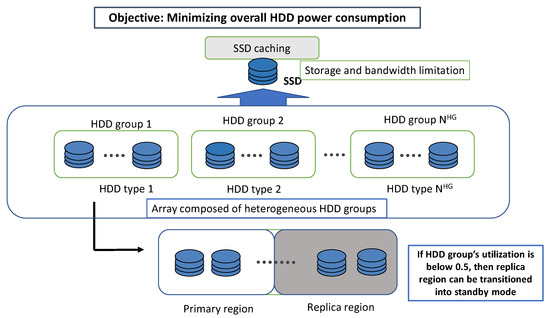
Figure 1.
System architecture.
Whenever the server receives a request, it first checks whether the requested bitrate version is stored and can be transmitted from the SSD; otherwise, these requests need to be handled from the HDD array. Although the requested version is stored on the SSD, it may not be handled from the SSD due to SSD bandwidth limitations.
Redundancy is essential in storage systems for fault tolerance and improved I/O throughput. In particular, data replication is widely used in video servers to support high I/O bandwidth requirements for video streaming [39]. Thus, we use RAID 1 for redundancy in which each HDD group is divided into primary and replica regions as shown in Figure 1.
All bitrate versions of the segments that make up a video are stored sequentially on successive HDDs in a single HDD group. Since a single video can be shared over all the HDDs in each HDD group, the workloads can be effectively balanced because each video can be handled over all the HDDs in each HDD group. Therefore, it is assumed that the I/O bandwidth over all HDDs in each HDD group is balanced.
To provide streaming for continuous video playback at clients’ devices, consecutive segments that make up each video must be read once every seconds, which is the length of the segment [33]. Then the server allocates I/O bandwidth to each request based on its bitrate for seconds. Thus, the amount of data that needs to be read for each bitrate version during a period of is to keep up with the playback rate. For example, to stream a 15.36 Mbps video clip with a segment length of 2 s, 30.72 Mbits of data must be read over the segment length.
HDDs provide four power phases: seek, active, idle, and standby. The head of the HDD is placed on the track where the data is stored during the seek phase. The HDD reads or writes data during the active phase, rotates without reading, writing, and seeking operations during the idle phase, and stops rotating completely during the standby phase [33]. The standby phase consumes much less power than the idle phase, so it is important to leave the HDD in the standby phase for a long time [33].
Let be the seek time of the HDD in group m. Let be the transfer rate of the HDD in group m. In a video storage system, each video segment can be large enough to span one or more complete HDD tracks, so the HDD head can start reading as soon as it reaches the track where the data is stored, allowing the entire track to be read [40]. Therefore, the rotational delay is assumed to be zero.
All bitrate versions for segment i are stored on the HDD group . Then the total time required to read bitrate version for seconds can be calculated as follows:
Since I/O time of is needed every seconds, I/O utilization for version , is calculated as follows:
Since it takes a few seconds to spin up the HDD, it is almost impossible to put the HDDs in standby on a video server that needs continuous reads unless replication is used. However, if the HDD bandwidth utilization over all the HDDs in each group is below 0.5 in an HDD array with replication in Figure 1, then the energy consumption may be greatly reduced by putting the HDDs in the replica area into standby phase because the actual I/O bandwidth provided by the HDDs in the primary group is sufficient to support all the requests.
4. SSD Caching Determination
4.1. Algorithm Concept
When I/O requests are handled by the SSD cache, the I/O bandwidth of each HDD is effectively reduced, which can reduce HDD energy consumption. However, due to SSD capacity limitations, effective SSD storage space management is essential. In particular, each HDD has different characteristics in terms of power consumption, so this should be taken into account when making SSD caching decisions.
For caching decisions, we introduce the concept of a popularity-weighted energy gain for each file that represents the amount of HDD energy saved when serving this file request from the SSD. Then the caching decision aims at maximizing popularity-weighted overall energy gain. Unlike other caching schemes that typically cache popular files first, our scheme considers different power characteristics of each HDD to minimize overall HDD power consumption.
Popular video files are cached on the SSD, so it is essential to effectively manage the limited SSD bandwidth to minimize HDD energy consumption. In particular, each group’s HDD bandwidth utilization is an important factor in determining the group’s energy consumption. Therefore, energy consumption can be effectively reduced by adjusting the HDD bandwidth utilization of each group, but this requires effective SSD bandwidth allocation. For this purpose, our scheme allocates SSD bandwidth with the aim of minimizing overall HDD energy consumption.
4.2. SSD Caching Determination
Let be the access probability of bitrate version j of video segment i, , . The popularity of segment i, is then calculated as: , and .
Let , and be the power required during the seek, active, and idle phases for HDD group m, respectively. Let be a parameter that indicates the popularity-weighted energy gain by serving from SSD, which can be expressed as:
A binary variable indicates whether version is cached or not. If , then version is cached on SSD. By contrast, if , is not cached. We aim to cache version files to maximize overall popularity-weighted energy gain, .
The total SSD storage requirement must not exceed ; thus, where is the size of version in MB. We can then formulate the SSD cache determination problem that finds the values of as follows:
This problem is the 0/1 knapsack problem [41], where each object has a weight and profit, and the problem involves selecting objects such that the total profit is maximized while satisfying the knapsack capacity constraint [41]. The problem above can correspond to the 0/1 knapsack problem by regarding the SSD as a knapsack and each video segment as an object.
The 0/1 knapsack problem is NP-hard [41]. The dynamic programming technique can be used to derive a solution, but this involves significant computational overhead to deal with very large numbers of segments [41]. We thus develop a greedy algorithm where the video segments with higher values are cached first while meeting SSD storage limit.
5. SSD Bandwidth Management
5.1. Problem Formulation
Among HDD power phases, the seek phase is known to consume the most energy, so it is important to reduce the number of seek operations [33]. To minimize the number of seek operations on the HDD, it is advantageous to serve the low bitrate requests from the SSD first [10]. For example, suppose three video segments at 2 Mbps, 4 Mbps, and 6 Mbps are cached on a SSD with a bandwidth limit of 6 Mbps, and each segment is stored contiguously on an HDD. Then, two segments (2 Mbps and 4 Mbps) or one 6 Mbps segment can be handled by the SSD at the same SSD bandwidth limit of 6 Mbps. In the former case, two seek operations, but in the latter case, one seek operation can be removed from the HDD. Therefore, requests for lower bitrate versions are given higher priority.
Let be the array of the indices for all requests that are directed to an HDD group m. Let be the array of request indices of which bitrate versions are cached on an SSD, sorted in non-descending order of bitrate of the requested version, where is the number of requests in . Obviously, is a subset of .
Let and be the video segment and version indices for request k, , where is the number of total requests. Among requests in , some requests may not be served by the SSD. To express this, we introduce a binary variable to indicate whether request k, can be served from the SSD. If so that request k is not cached, then .
is sorted in non-descending order of bitrate of the requested version, where represents the request index of the nth element in . Thus, . We derive the energy consumption for four power phases of seek (), active (), idle (), and standby () when requests from the first to nth elements of are served from the SSD for seconds as follows:
- Seek phase: The total seek time of the HDD group m, is calculated as follows:As a result, the energy required in the seek phase, , is calculated as:
- Active phase: The total time taken to read data for , is expressed as:Therefore, the active energy, , is calculated as:
- Idle phase: If no HDD activity is occurring, the HDD is rotating without reading or seeking, which requires the power of . We calculate the total idle time for seconds by subtracting the seek and read times from . However, if I/O utilization over all HDDs in the HDD group is less than or equal to 0.5, then half of HDDs can be put into standby mode, halving the idle time. Let be the I/O utilization for an HDD group m when requests from the first to nth elements of are served from the SSD. is then calculated as follows:Therefore, idle time, can be calculated as follows:Thus, the energy required in the idle phase, , can be calculated as:
- Standby phase: If , then half of HDDs can be put into standby mode. If is the standby power for an HDD group m, then can be calculated as follows:
Let be the selection parameter where requests between to are selected to be served by the SSD. It is noteworthy that ; otherwise, the I/O bandwidth will be exceeded, so some requests cannot be processed. To prevent this, we introduce a variable for each HDD group m that indicates the lowest value of n that satisfies the condition: . Thus, is calculated as follows:
Then the following inequality should hold: .
We determine the power consumed by an HDD k when requests between the first and nth elements of are processed, as:
If is the total bandwidth supported by the SSD in MB/s and is the SSD bandwidth in MB/s required to serve all of the requests from to , then is calculated as follows:
We can then formulate the SSD request selection (SRS) problem, which minimizes overall HDD power consumption, for determining , as follows:
5.2. SSD Request Selection (SRS) Algorithm
The SRS problem is a variant of the multiple-choice knapsack problem (MCKP), which is NP-hard [41]. In the MCKP, each object consists of a set of items, with each item having a weight and profit. Exactly one item from each object is then selected and put into the knapsack to maximize total profit without exceeding the knapsack weight limit [41]. Likewise, the SRS problem treats the SSD as a knapsack, and the value must be selected from each array to maximize the amount of power saved within the SSD bandwidth limits.
Because the SRS problem is NP-hard, we propose a heuristic solution called SSD request selection (SRS) algorithm that runs in polynomial time as shown in Algorithm 1. We use a greedy approach, which shows good performance with multiple-choice knapsack problems [41]. We thus define a series of parameters for each HDD group m, as follows:
where represents the ratio of increase in SSD bandwidth to decrease in total power consumption when is n compared to when .
The value of is initialized to (line 11). Then, without exceeding the SSD bandwidth limit, the value of is increased to reduce the increase in the amount of SSD bandwidth (denominator of ) while maximizing the decrease in the total power consumption (the numerator of ). Thus, the highest value of is selected from a set of values, for which and , and then the value of is increased to w. This step is repeated until , (lines 21–30). Based on the final results of , the values can be easily obtained, (lines 31–39).
Power consumption can vary depending on the fault-tolerance techniques used. Therefore, as long as the power values such as are modified according to various fault-tolerance methods, the SRS algorithm can be used without modification because it uses parameters based only on bandwidth and power consumption.
| Algorithm 1: SSD request selection(SRS) algorithm. |
 |
6. Experimental Results
6.1. Experimental Setup
We evaluate the effectiveness of our scheme through simulations. To configure the HDD array, the active power is set between 3.5 W and 9.2 W, and the idle power is set between 2.5 W and 8.0 W [42,43,44]. Standby power, seek time, and data transfer rate are set to 0.9 W, 9 ms, and 150 MB/s, respectively.
We compare our scheme with three other benchmark methods as follows:
- Lowest bitrate first selection (LS): To reduce the number of seek operations on the HDD, it is required to handle requests for the lowest bitrate possible on the SSD [10]. The LS scheme first selects the request with the lowest bitrate as long as it satisfies the SSD bandwidth limit.
- Random allocation (RA): This method randomly selects requests handled by the SSD subject to the SSD bandwidth limitation.
- Uniform allocation (UA): This method alternately selects the requests for the lowest bitrate version from each HDD group one by one subject to the SSD bandwidth limitation.
Video popularity follows a Zipf distribution with the measured parameter set to for real VoD applications [45]. The length of each video is selected randomly between 1 and 2 h. A server stores 2000 video content, each with 7 bitrate versions. Table 2 tabulates resolution and bitrate for each version, and the popularity of each version is modeled based on three types as follows:
- HVP: High-bitrate versions are popular, (, , , , , , , ).
- LVP: Low-bitrate versions are popular, (, , , , , , , ).
- MVP: Medium-bitrate versions are popular, (, , , , , , , ).

Table 2.
Resolution and bitrate for each version [11].
Table 2.
Resolution and bitrate for each version [11].
| Resolution | 1920 × 1080 | 1600 × 900 | 1280 × 720 | 1024 × 600 | 854 × 480 | 640 × 360 | 426 × 240 |
|---|---|---|---|---|---|---|---|
| Bitrate (Mbps) | 15.36 | 10.64 | 9.60 | 4.55 | 3.04 | 1.70 | 0.76 |
The arrival of client requests is modeled as a Poisson process [46,47] with an average arrival rate for requests of 1/s. Table 3 summarizes the parameters used for simulation, where default values are used unless otherwise stated. Power consumption is profiled over all the HDDs for 24 h.

Table 3.
Parameter settings for simulations.
6.2. HDD Power Consumption Comparison for Different SSD Sizes
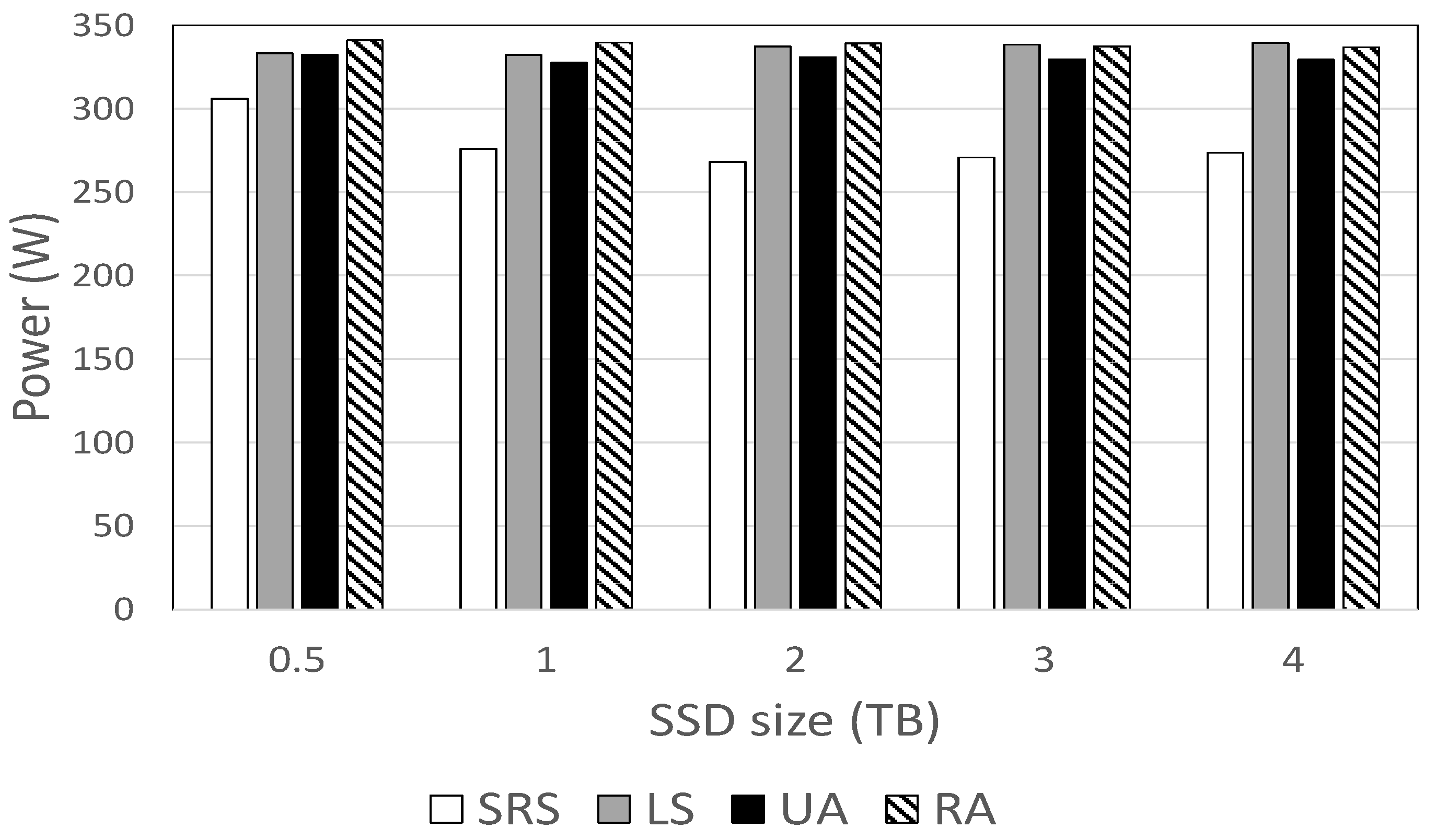
Figure 2 shows the effect of SSD size on HDD power consumption for each algorithm when GB/s. The SRS algorithm shows the best performance, consuming between 7.9% and 20.9% and on average 16.7% less power than other methods. This power difference is smallest when GB, but largest when TB. Among other benchmarks, the UA scheme consumes the smallest power. The power consumption decreases with the SSD size, but it gradually tails off.
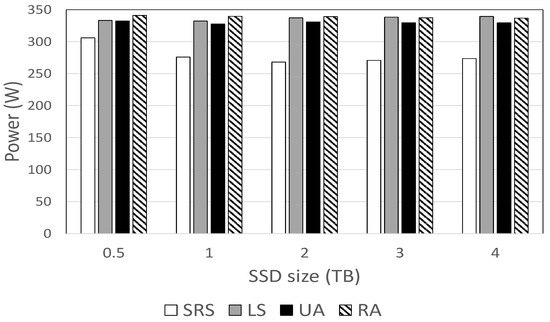
Figure 2.
HDD power consumption for different SSD sizes.
6.3. HDD Power Consumption Comparison for SSD Bandwidth
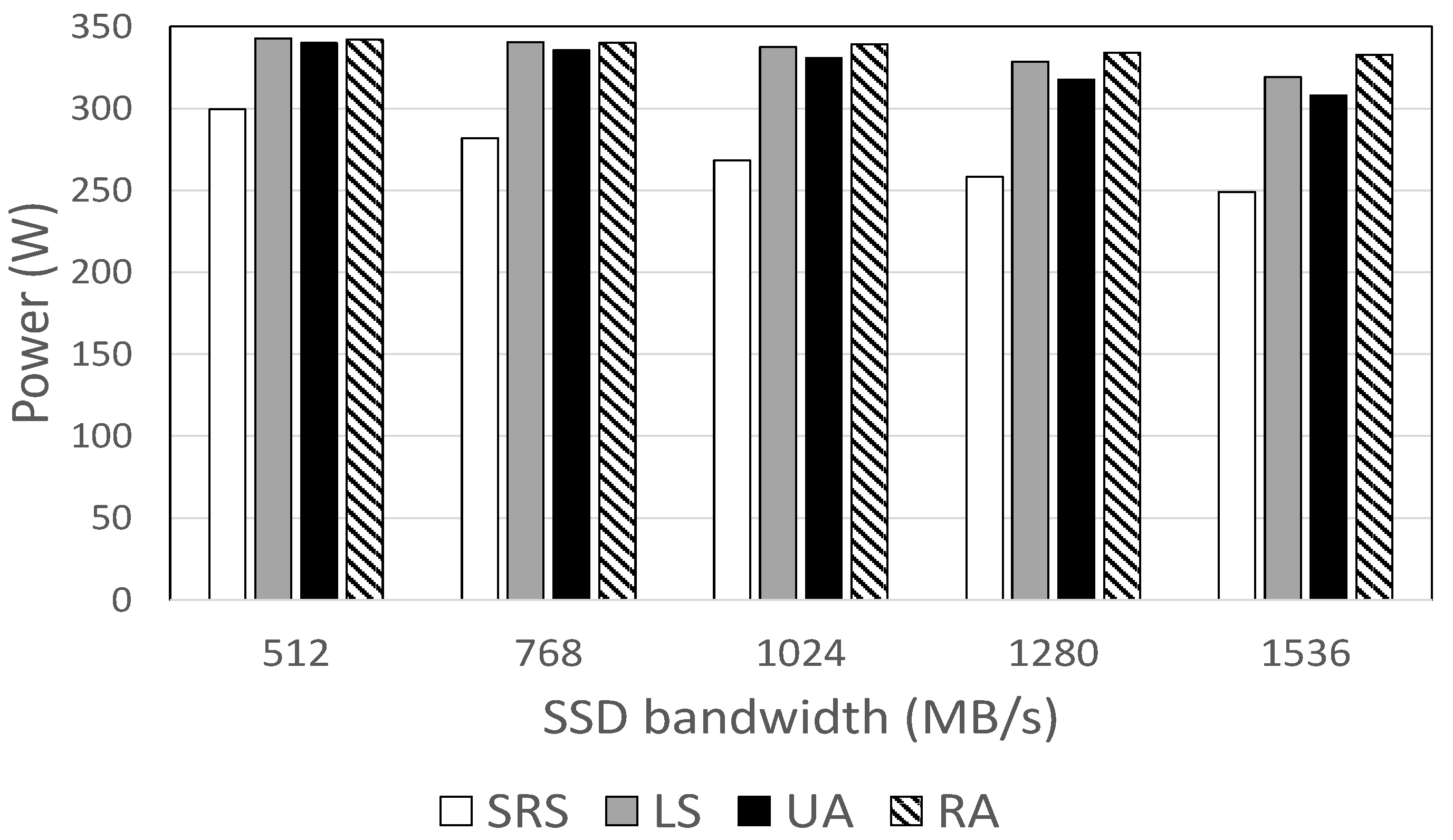
Figure 3 shows the effect of SSD bandwidth on HDD power consumption. Again, the SRS algorithm always exhibits the best performance, consuming 12% and 25.1% less power than other methods. The amount of power saved increases with SSD bandwidth for all methods, and these savings are more pronounced with the SRS algorithm, making a greater difference compared with other benchmarks when the SSD bandwidth is high.
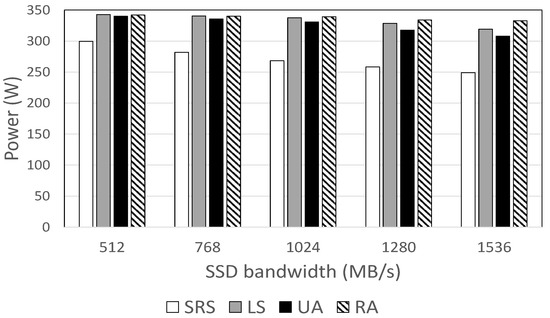
Figure 3.
HDD power consumption against SSD bandwidth.
6.4. Effect of the Number of HDD Groups
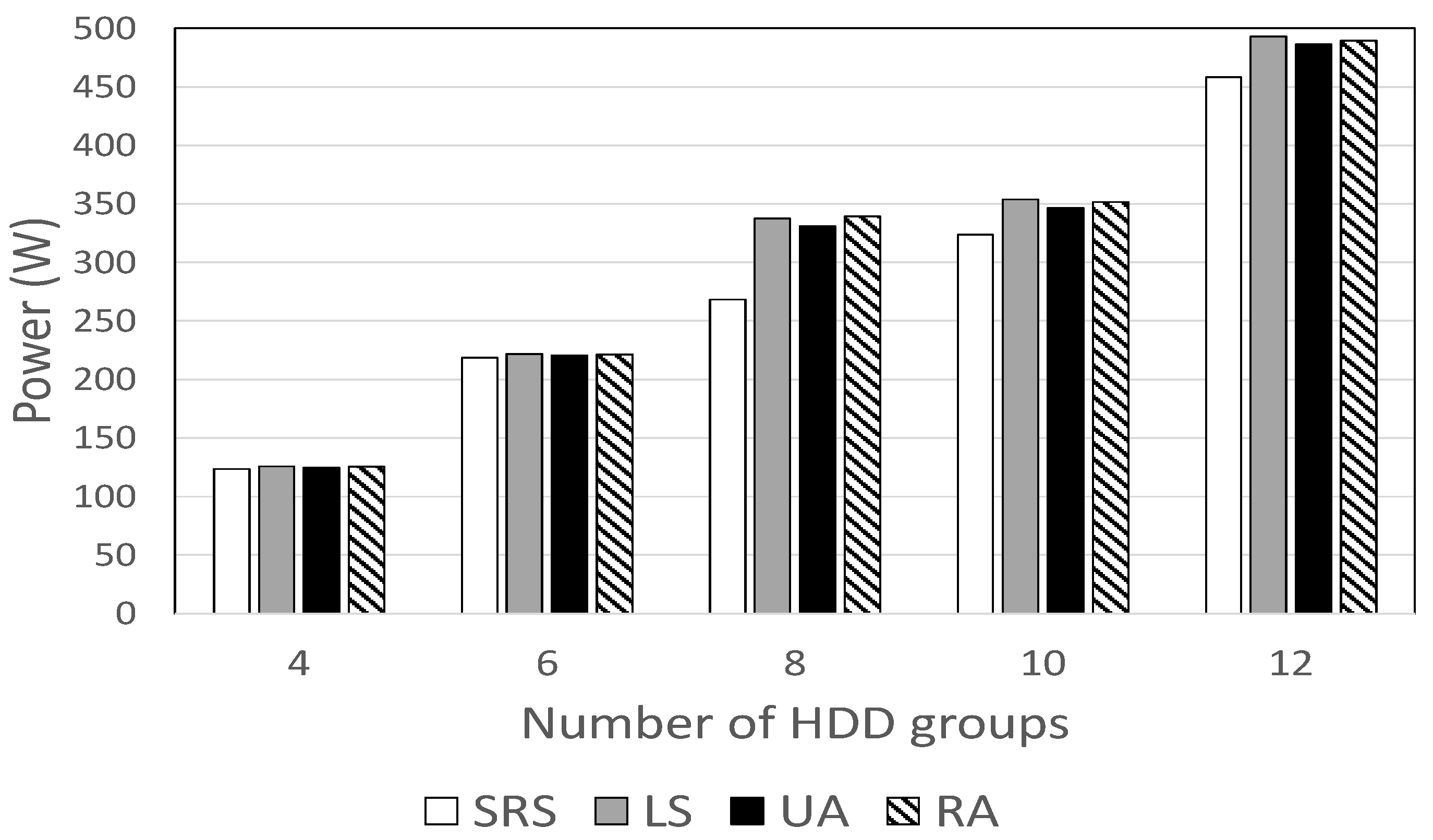
Figure 4 shows how HDD power consumption varies with the number of HDD groups. The SRS algorithm uses the smallest power, consuming between 1% and 29% less power than other schemes. When the number of HDD groups is at the median value (e.g., ), the power gap is the largest, but this gap decreases as the value of increases or decreases.
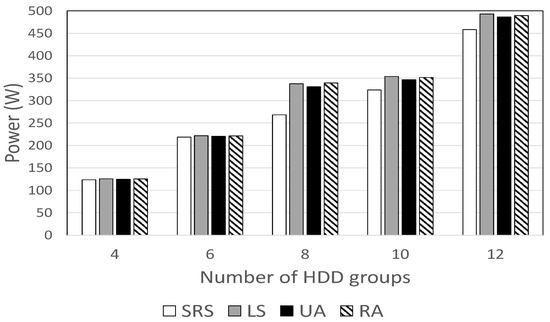
Figure 4.
HDD power consumption against the number of HDD groups.
6.5. Effect of Version Popularity
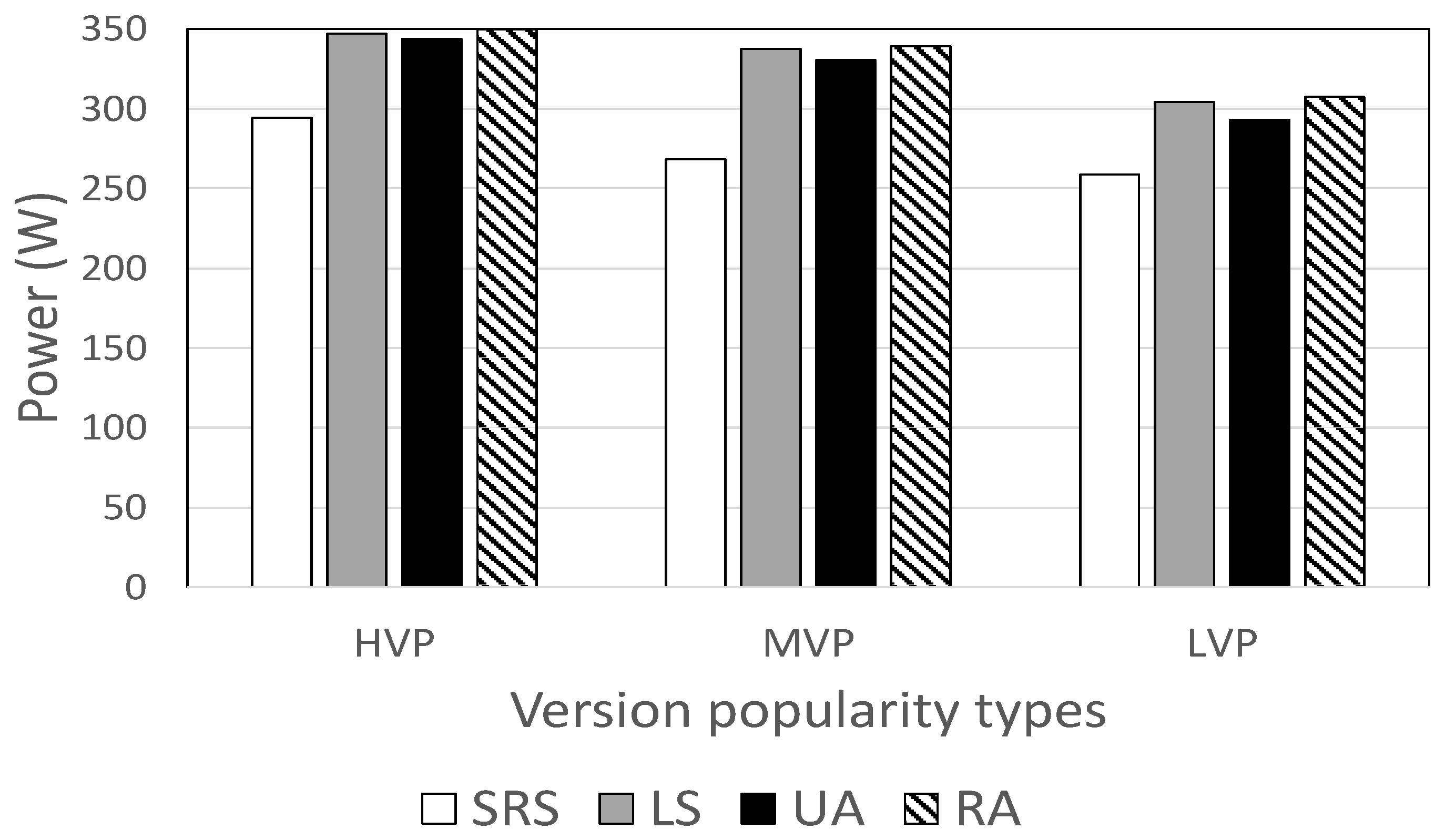
Figure 5 shows HDD power consumption against version popularity types. Again, the SRS algorithm consumes the least power, using 11.7% to 20.9% less than other methods. The power difference is greatest when the medium bitrate versions are popular, but smallest when the low bitrate versions are popular.
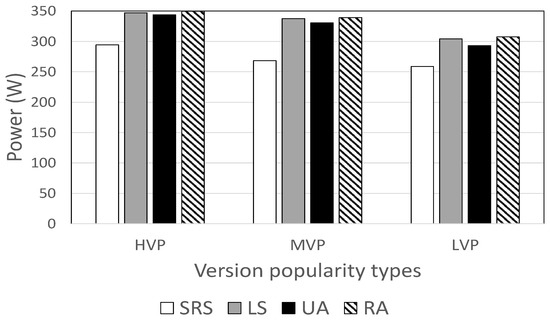
Figure 5.
HDD power consumption against version popularity types.
6.6. Effect of Zipf Parameters
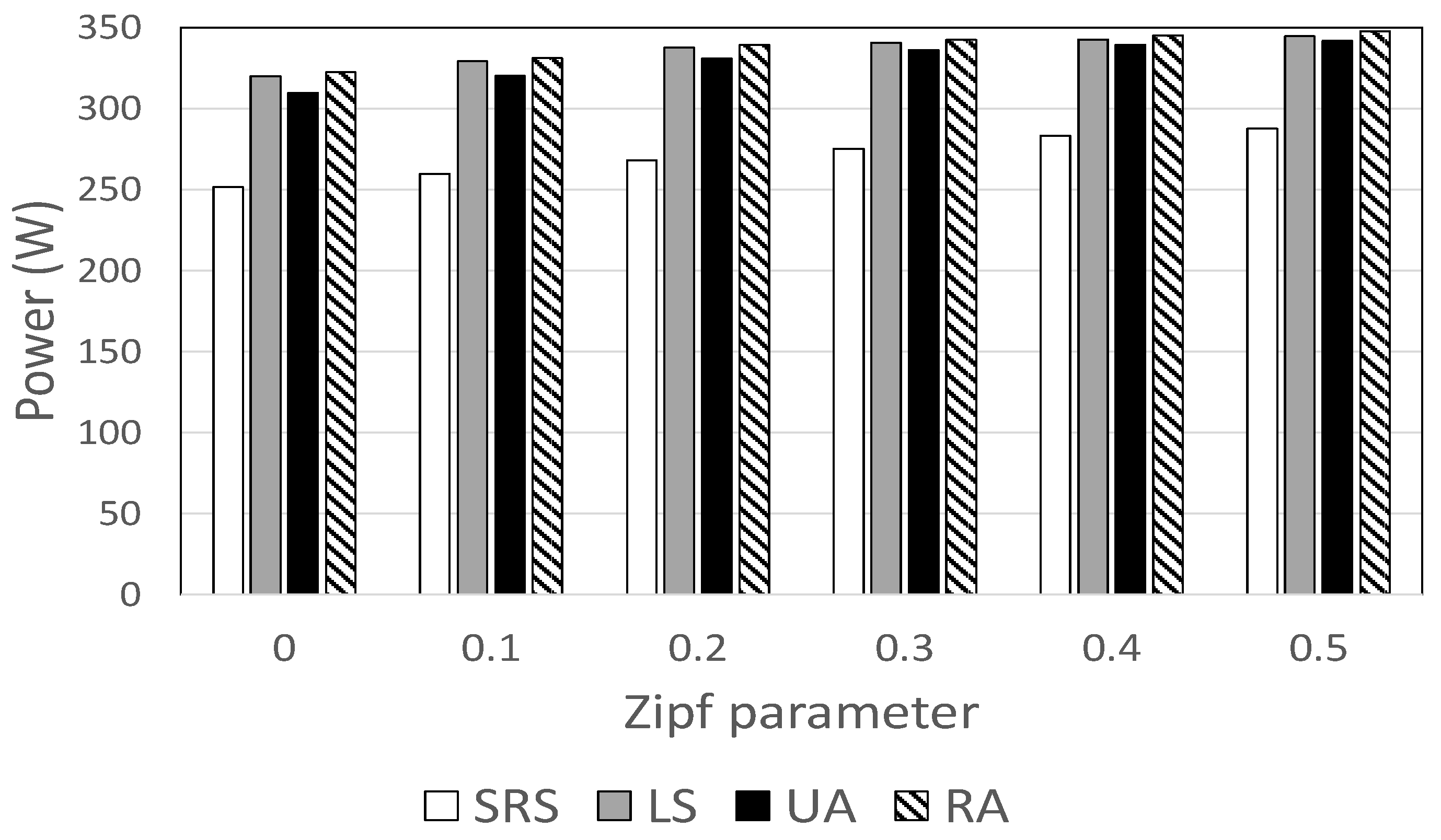
Figure 6 shows HDD power consumption for different values of . The SRS algorithm consumes between 16% and 22% less power than other methods. In the Zipf distribution, the popularity skewness decreases with the value of . In all schemes, the power savings decrease as the value of increases, because the caching effect becomes more pronounced when popularity is skewed. The power gap between SRS and other schemes is more pronounced when , indicating that the proposed technique is most effective when video popularity is highly skewed.
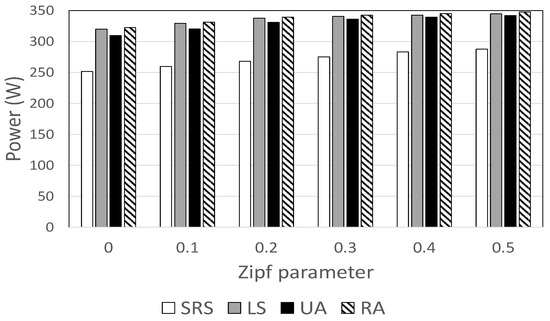
Figure 6.
HDD power consumption against Zipf parameters.
6.7. Comparison of Power Consumption in Gamma Popularity Distribution
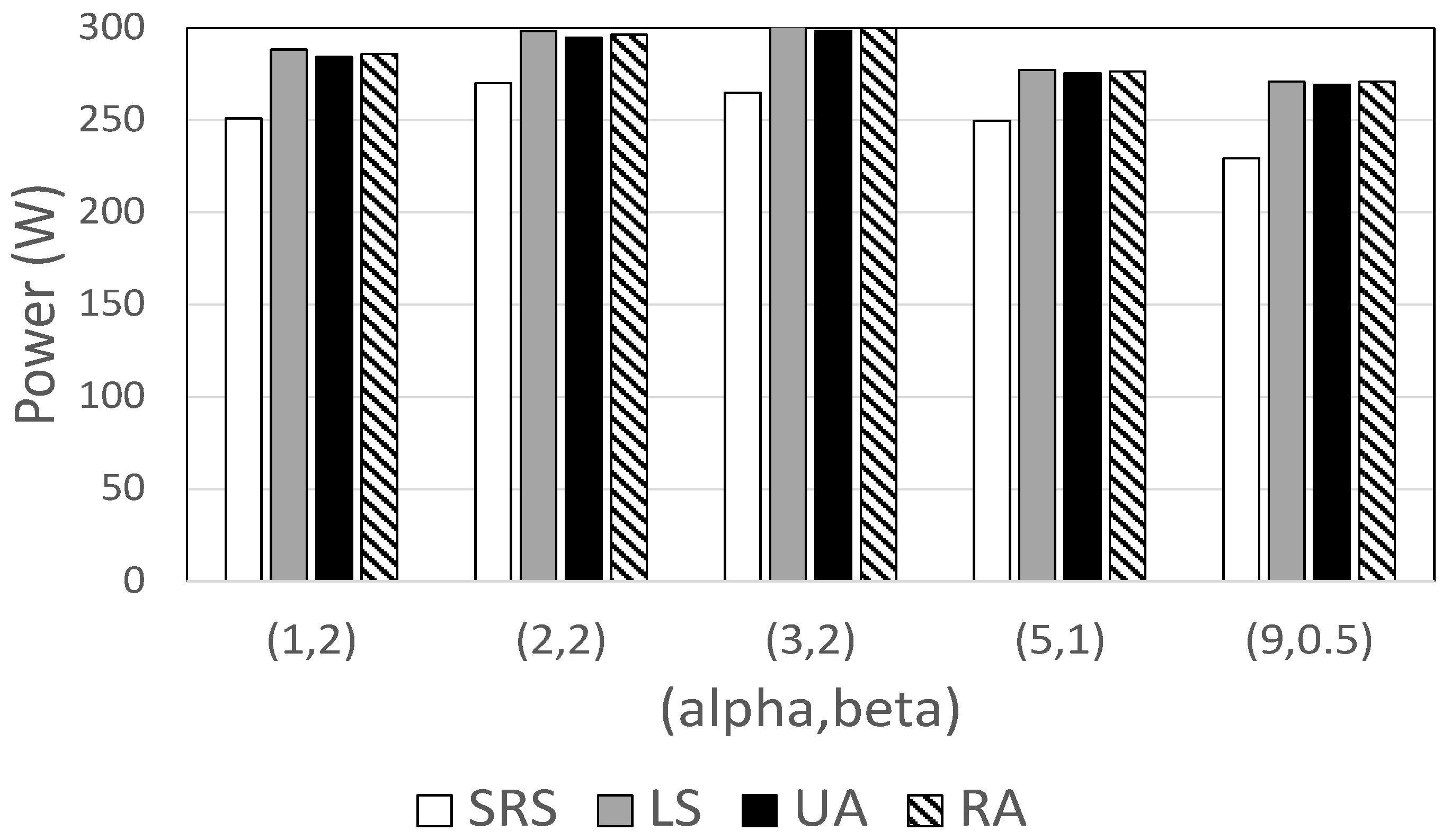
We also examine power consumption when video popularity follows a gamma distribution. Two parameters ( and ) are used to express the shape of the gamma distribution [48], so Figure 7 shows HDD power consumption for different pairs of and [48]. Again, the SRS algorithm always shows the best performance, consuming between 8% and 15% less power than other methods. This difference is greatest when the is the smallest (e.g., ).
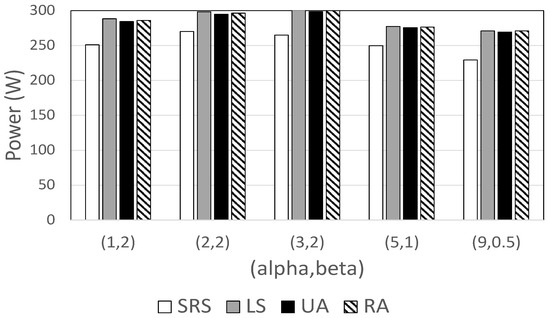
Figure 7.
HDD power consumption against and parameters of gamma distribution.
7. Conclusions
We presented a new power management technique for video storage servers consisting of an SSD cache and heterogeneous HDD arrays. We introduced the concept of popularity-weighted energy gain to express the amount of HDD power saved as a result of SSD caching and then proposed a new SSD caching decision algorithm that caches video files with high ratios of energy gain to their sizes. Based on a model for an array with heterogeneous HDDs, we proposed an algorithm that determines the I/O tasks handled by the SSD to allow more HDDs to enter low-power mode, thereby minimizing overall HDD power consumption. For this purpose, the I/O tasks with high ratios of HDD energy to bandwidth are greedily processed the first subject to the SSD bandwidth limit.
Experimental results show that our scheme reduces HDD power consumption between 12% and 25% compared with benchmark schemes. They also demonstrate that the proposed technique is more effective when the SSD capacity is moderate, the SSD bandwidth is high, the number of HDD groups is medium, the medium bitrate versions are popular, and the video popularity is highly skewed. These results provide useful guidelines for improving energy efficiency in video storage systems based on heterogeneous HDDs. With the advent of new SSDs such as a quad-level cell (QLC), the video storage cache tends to consist of heterogeneous SSDs. In future work, we plan to explore file caching and allocation techniques that minimize HDD power consumption in a video cache server composed of heterogeneous SSDs.
Author Contributions
Conceptualization, M.S.; methodology, M.S. and K.K.; software, K.K. and M.S.; supervision, M.S.; validation, M.S. and K.K.; writing—original draft, M.S. and K.K.; writing—review and editing, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by INHA UNIVERSITY Research Grant.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Available online: https://www.insiderintelligence.com/insights/netflix-subscribers/ (accessed on 12 May 2022).
- Available online: https://fortunelords.com/youtube-statistics/ (accessed on 12 May 2022).
- Krishnappa, D.; Zink, M.; Sitaraman, R. Optimizing the video transcoding workflow in content delivery networks. In Proceedings of the ACM Multimedia Systems Conference, Portland, OR, USA, 18–20 March 2015; pp. 37–48. [Google Scholar]
- Gao, G.; Wen, Y.; Westphal, C. Dynamic priority-based resource provisioning for video transcoding with heterogeneous QoS. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 1515–1529. [Google Scholar] [CrossRef]
- Mao, H.; Netravali, R.; Alizadeh, M. Neural adaptive video streaming with Pensieve. In Proceedings of the ACM Special Interest Group on Data Communication, New York, NY, USA, 19–23 August 2017; pp. 197–210. [Google Scholar]
- Spiteri, K.; Urgaonkar, R.; Sitaraman, R. BOLA: Near-optimal bitrate adaptation for online videos. In Proceedings of the IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Lee, D.; Song, M. Quality-aware transcoding task allocation under limited power in live-streaming system. IEEE Syst. J. 2021, 1–12. [Google Scholar] [CrossRef]
- Available online: https://support.google.com/youtube/answer/2853702 (accessed on 12 May 2022).
- Zhao, H.; Zheng, Q.; Zhang, W.; Du, B.; Li, H. A segment-based storage and transcoding trade-off strategy for multi-version VoD systems in the cloud. IEEE Trans. Multimed. 2017, 19, 149–159. [Google Scholar] [CrossRef]
- Song, M. Minimizing power consumption in video servers by the combined use of solid-state disks and multi-speed disks. IEEE Access 2018, 6, 25737–25746. [Google Scholar] [CrossRef]
- Han, H.; Song, M. QoE-aware video storage power management based on hot and cold data classification. In Proceedings of the ACM Workshop on Network and Operating Systems Support for Digital Audio and Video, Amsterdam, The Netherlands, 15 June 2018; pp. 7–12. [Google Scholar]
- Kadekodi, S.; Rashmi, K.; Ganger, G. Cluster storage systems gotta have HeART: Improving storage efficiency by exploiting disk-reliability heterogeneity. In Proceedings of the USENIX Conference on File and Storage Technologies, Boston, MA, USA, 25–28 February 2019; pp. 345–358. [Google Scholar]
- Kadekodi, S.; Maturana, F.; Subramanya, S.; Yang, J.; Rashmi, K.; Ganger, G. PACEMAKER: Avoiding HeART attacks in storage clusters with disk-adaptive redundancy. In Proceedings of the USENIX Symposium on Operating Systems Design and Implementation, Online, 4–6 November 2020; pp. 369–385. [Google Scholar]
- Matko, V.; Brezovec, B. Improved data center energy efficiency and availability with multilayer node event processing. Energies 2018, 11, 2478. [Google Scholar] [CrossRef] [Green Version]
- Bosten, T.; Mullender, S.; Berber, Y. Power-reduction techniques for data-center storage systems. ACM Comput. Surv. 2013, 45, 3. [Google Scholar] [CrossRef]
- Fernández-Cerero, D.; Fernández-Montes, A.; Velasco, F. Productive efficiency of energy-aware data centers. Energies 2018, 11, 2053. [Google Scholar] [CrossRef] [Green Version]
- Dayarathna, M.; Wen, Y.; Fan, R. Data center energy consumption modeling: A survey. IEEE Commun. Surv. Tutor. 2016, 18, 732–794. [Google Scholar] [CrossRef]
- Yuan, H.; Ahmad, I.; Kuo, C.J. Performance-constrained energy reduction in data centers for video-sharing services. J. Parallel Distrib. Comput. 2015, 75, 29–39. [Google Scholar] [CrossRef]
- Niu, J.; Xu, J.; Xie, L. Hybrid storage systems: A survey of architectures and algorithms. IEEE Access 2018, 6, 13385–13406. [Google Scholar] [CrossRef]
- Li, W.; Baptise, G.; Riveros, J.; Narasimhan, G.; Zhang, T.; Zhao, M. Cachededup: In-line deduplication for flash caching. In Proceedings of the USENIX Conference on File and Storage Technologies, Santa Clara, CA, USA, 27 February–2 March 2016; pp. 301–314. [Google Scholar]
- Arteaga, D.; Cabrera, J.; Xu, J.; Sundararaman, S.; Machines, P.; Zhao, M. Cloudcache: On-demand flash cache management for cloud computing. In Proceedings of the USENIX Conference on File and Storage Technologies, Santa Clara, CA, USA, 27 February–2 March 2016; pp. 355–369. [Google Scholar]
- Ryu, M.; Ramachandran, U. Flashstream: A multi-tiered storage architecture for adaptive HTTP streaming. In Proceedings of the ACM Multimedia Conference, New York, NY, USA, 21–25 October 2013; pp. 313–322. [Google Scholar]
- Manjunath, R.; Xie, T. Dynamic data replication on flash SSD assisted Video-on-Demand servers. In Proceedings of the IEEE International Conference on Computing, Networking and Communications, Maui, HI, USA, 30 January–2 February 2012; pp. 502–506. [Google Scholar]
- Machida, F.; Hasebe, K.; Abe, H.; Kato, K. Analysis of optimal file placement for energy-efficient file-sharing cloud storage system. IEEE Trans. Sustain. Comput. 2022, 7, 75–86. [Google Scholar] [CrossRef]
- Karakoyunlu, C.; Chandy, J. Exploiting user metadata for energy-aware node allocation in a cloud storage system. J. Comput. Syst. Sci. 2016, 82, 282–309. [Google Scholar] [CrossRef]
- Behzadnia, P.; Yuan, W.; Zeng, B.; Tu, Y.; Wang, X. Dynamic power-aware disk storage management in database servers. In Proceedings of the International Conference on Database and Expert Systems Applications, Porto, Portugal, 5–8 September 2016; pp. 315–325. [Google Scholar]
- Khatib, M.; Bandic, Z. PCAP: Performance-aware power capping for the disk drive in the cloud. In Proceedings of the USENIX USENIX Conference on File and Storage Technologies, Santa Clara, CA, USA, 22–25 February 2016; pp. 227–240. [Google Scholar]
- Segu, M.; Mokadem, R.; Pierson, J. Energy and expenditure aware data replication strategy. In Proceedings of the IEEE International Conference on Cloud Computing, Milan, Italy, 8–13 July 2019; pp. 421–426. [Google Scholar]
- Hu, C.; Deng, Y. Aggregating correlated cold data to minimize the performance degradation and power consumption of cold storage nodes. J. Supercomput. 2019, 75, 662–687. [Google Scholar] [CrossRef]
- Park, C.; Jo, Y.; Lee, D.; Kang, K. Change your cluster to cold: Gradually applicable and serviceable cold storage design. IEEE Access 2019, 7, 110216–110226. [Google Scholar] [CrossRef]
- Lee, J.; Song, C.; Kim, S.; Kang, K. Analyzing I/O request characteristics of a mobile messenger and benchmark framework for serviceable cold storage. IEEE Access 2017, 5, 9797–9811. [Google Scholar] [CrossRef]
- Chai, Y.; Du, Z.; Bader, D.; Qin, X. Efficient data migration to conserve energy in streaming media storage systems. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 2081–2093. [Google Scholar] [CrossRef] [Green Version]
- Song, M.; Lee, Y.; Kim, E. Saving disk energy in video servers by combining caching and prefetching. ACM Trans. Multimed. Comput. Commun. Appl. 2014, 10, 15. [Google Scholar] [CrossRef]
- Salkhordeh, R.; Hadizadeh, M.; Asadi, H. An efficient hybrid I/O caching architecture using heterogeneous SSDs. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 1238–1250. [Google Scholar] [CrossRef] [Green Version]
- Tomes, E.; Altiparmak, N. A comparative study of HDD and SSD RAIDs’ impact on server energy consumption. In Proceedings of the IEEE International Conference on Cluster Computing, Honolulu, HI, USA, 5–8 September 2017; pp. 625–626. [Google Scholar]
- Huang, T.; Chang, D. TridentFS: A hybrid file system for non-volatile RAM, flash memory and magnetic disk. Softw. Pract. Exp. 2016, 46, 291–318. [Google Scholar] [CrossRef]
- Hui, J.; Ge, X.; Huang, X.; Liu, Y.; Ran, Q. E-hash: An energy-efficient hybrid storage system composed of one SSD and multiple HDDs. Springer Lect. Notes Comput. Sci. 2012, 7332, 527–534. [Google Scholar]
- Chen, C.; Zhang, X.; Zhao, D.X.K.; Zhang, T. Realizing low-cost flash memory based video caching in content delivery systems. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 984–996. [Google Scholar]
- Zhang, Z.; Chan, S. An approximation algorithm to maximize user capacity for an auto-scaling VoD system. IEEE Trans. Multimed. 2021, 23, 3714–3725. [Google Scholar]
- Schindler, J.; Griffin, J.; Lumb, C.; Ganger, G. Track-aligned extents: Matching access patterns to disk drive characteristics. In Proceedings of the USENIX Conference on File and Storage Technologies, Monterey, CA, USA, 20–30 January 2002; pp. 175–186. [Google Scholar]
- Pisinger, D. Algorithms for Knapsack Problems. Ph.D. Thesis, University of Copenhagen, Copenhagen, Denmark, 1995. [Google Scholar]
- Available online: https://www.seagate.com/www-content/datasheets/pdfs/ironwolf-pro-14tb-DS1914-7-1807US-en_US.pdf (accessed on 12 May 2022).
- Available online: https://www.seagate.com/www-content/datasheets/pdfs/skyhawk-3-5-hddDS1902-7-1711US-en_US.pdf (accessed on 12 May 2022).
- Available online: https://www.westerndigital.com/ko-kr/products/internal-drives/wd-gold-sata-hdd#WD1005FBYZ (accessed on 12 May 2022).
- Dan, A.; Sitaram, D.; Shahabuddin, P. Dynamic batching policies for an on-demand video server. ACM/Springer Multimed. Syst. J. 1996, 4, 112–121. [Google Scholar] [CrossRef]
- Yu, H.; Zheng, D.; Zhao, B.Y.; Zheng, W. Understanding user behavior in large-scale Video-on-Demand systems. In Proceedings of the ACM European Conference on Computer Systems, New York, NY, USA, 18–21 April 2006; pp. 333–344. [Google Scholar]
- Zhou, Y.; Chen, L.; Yang, C.; Chiu, D. Video popularity dynamics and its implications for replication. IEEE Trans. Multimed. 2015, 17, 1273–1285. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Gamma_distribution (accessed on 12 May 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).