Capacity Sizing of Embedded Control Battery–Supercapacitor Hybrid Energy Storage System
Abstract
:1. Introduction
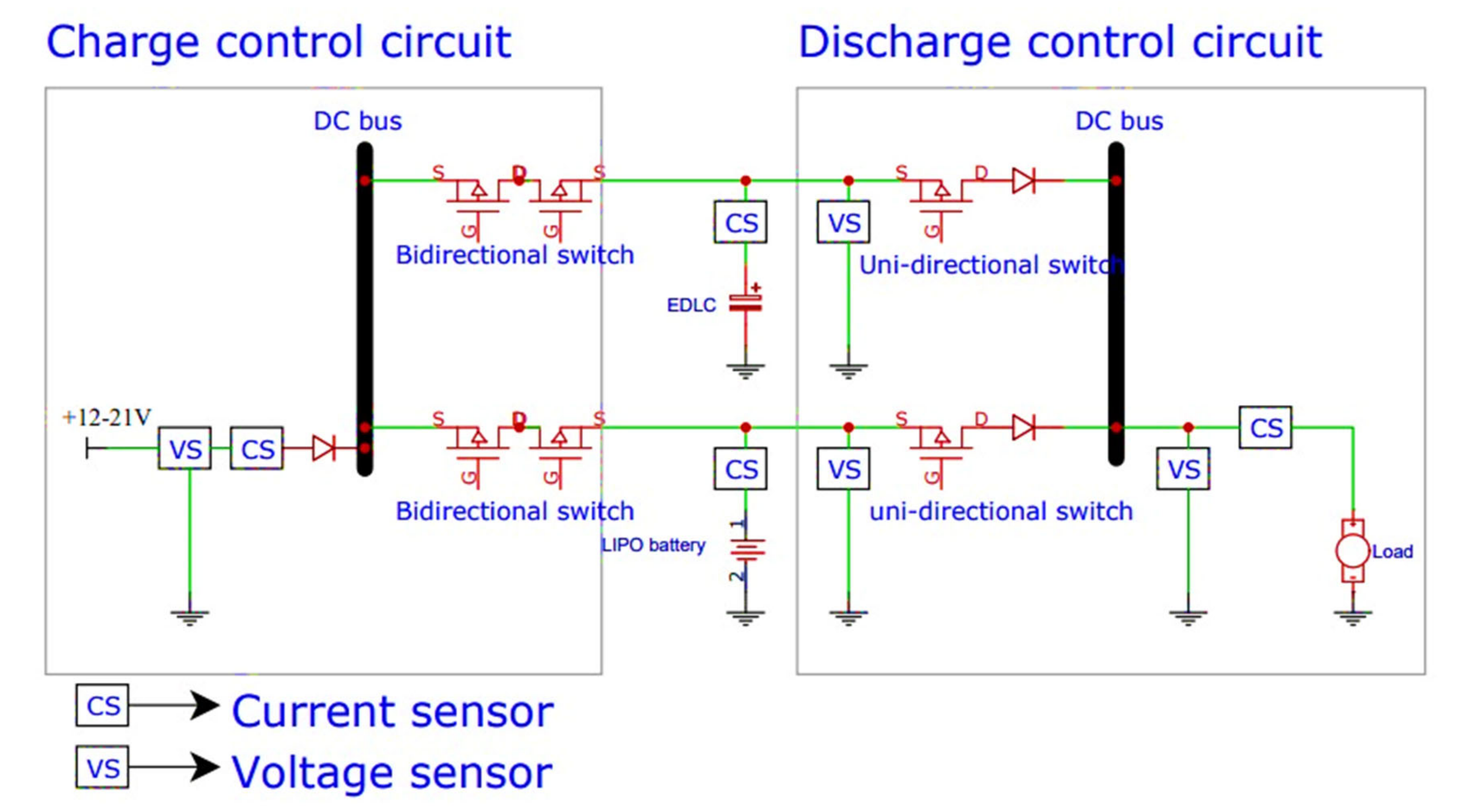
1.1. Battery–Supercapacitor HESS Topology
1.2. Sizing of Energy Storage
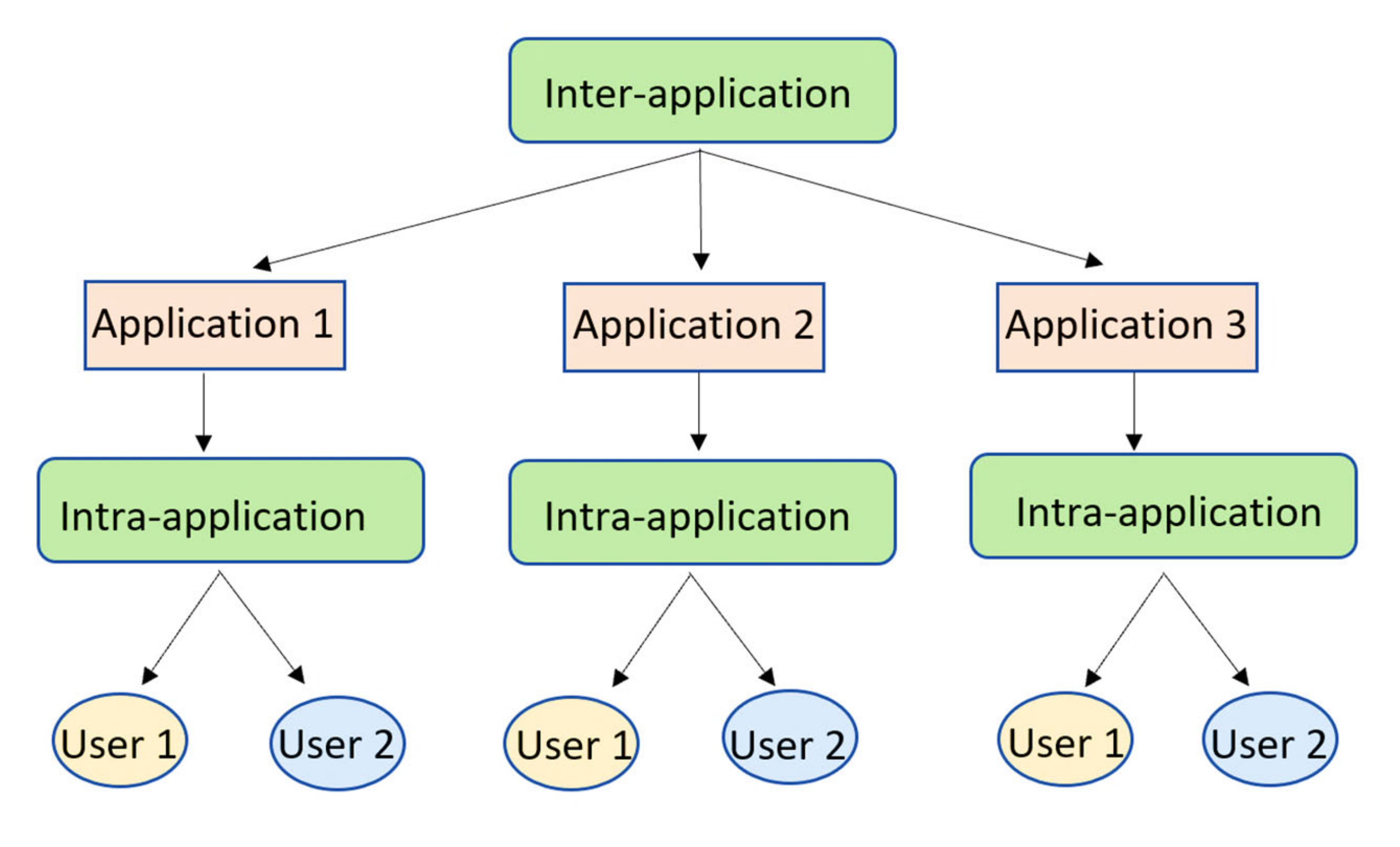
1.3. HESS Application
- Inter-application load demand difference,
- Intra-application load demand difference,
- Uncertain changes in future load demand.
2. Materials and Methods
2.1. Battery and Supercapacitor
2.2. Load Sharing Method of the Fully Active Battery–Supercapacitor HESS
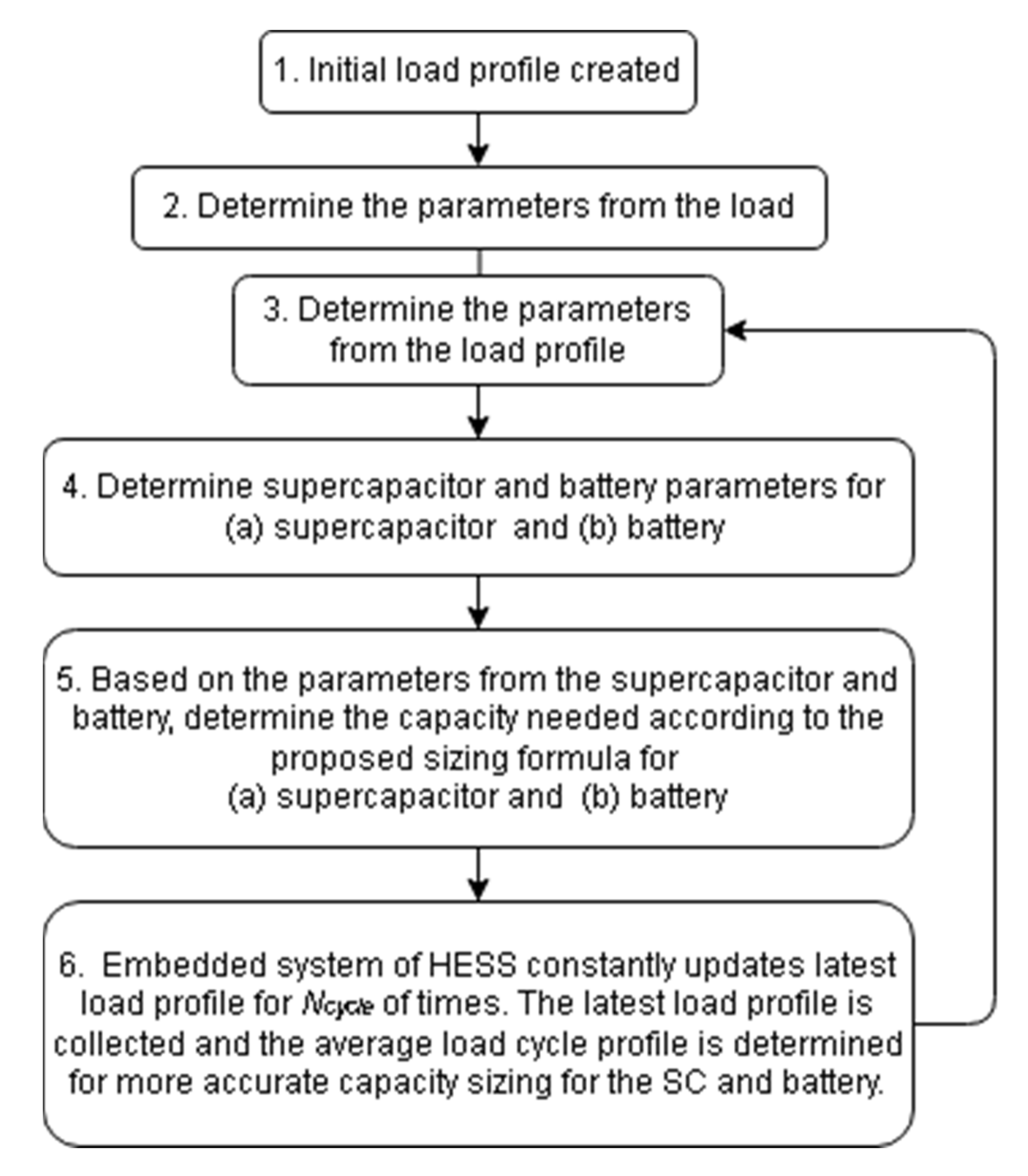
2.3. Sizing Strategy
- Step 1: Initial load profile
- Step 2: Parameters from the load
- -
- Rated load voltage, Vload (fixed value),
- -
- Rated load power, Pload (fixed value),
- -
- Max current, Imax (fixed value) is the maximum current drawn by the load Equation (1).
- -
- Threshold current, Ith (fixed value) is the battery maximum current rating.
- Step 3: Parameters from the load profile
- Step 4 (a) (supercapacitor): supercapacitor sizing parameter
- The capacity of a single supercapacitor cell/capacitance in Farad (F), CSCS.
- The voltage of a single supercapacitor cell, VSCS.
- Step 5 (a) (supercapacitor): supercapacitor sizing formula
- Step 4 (b) (battery): battery sizing parameter
- Capacity of single cell battery in Amp-hour (Ah), CBS.
- Voltage of single cell battery, VBS.
- Step 5 (b) (battery): Battery sizing formula
3. Results and Discussion
3.1. Battery and Supercapacitor Discharge Time
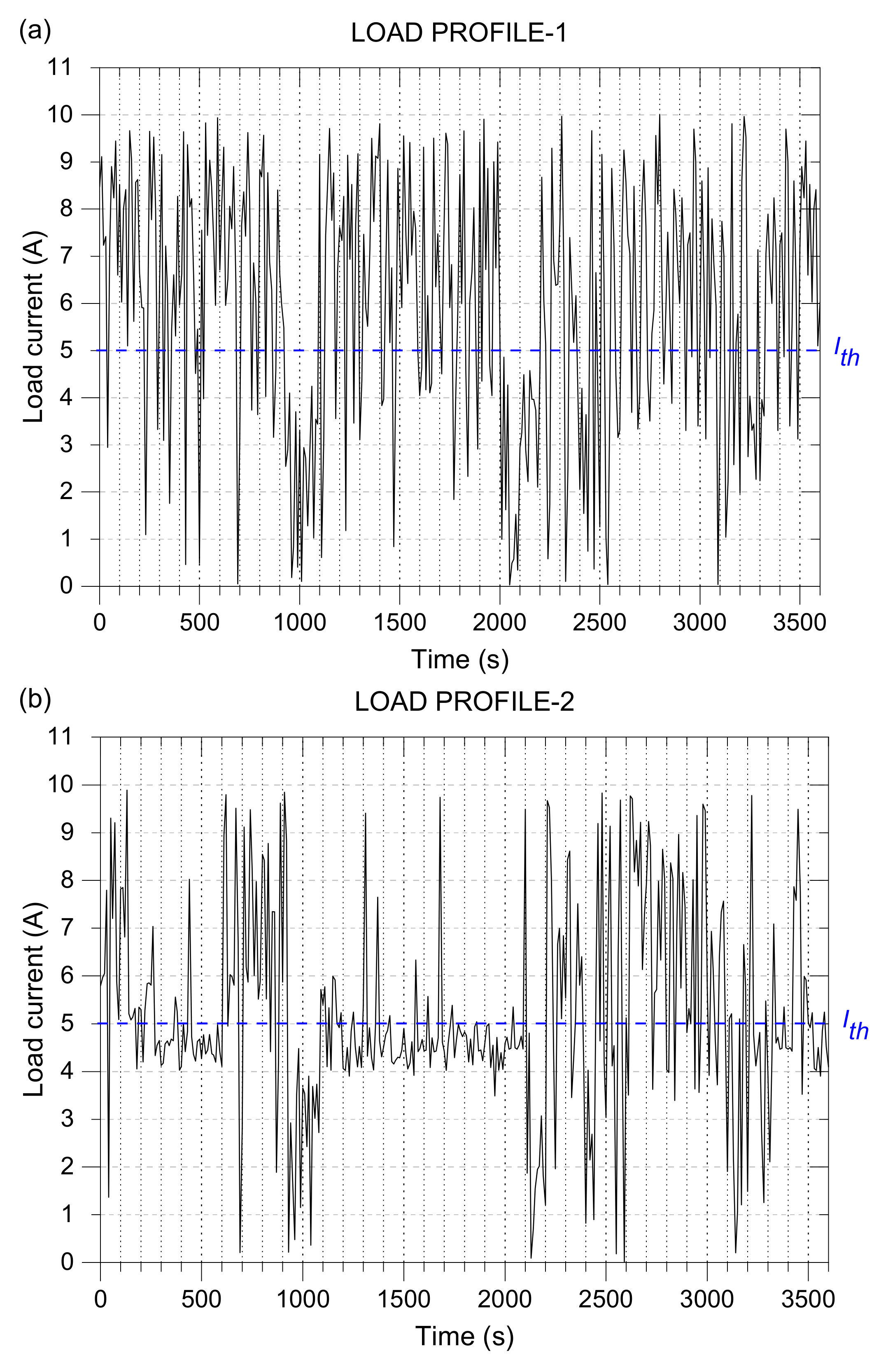
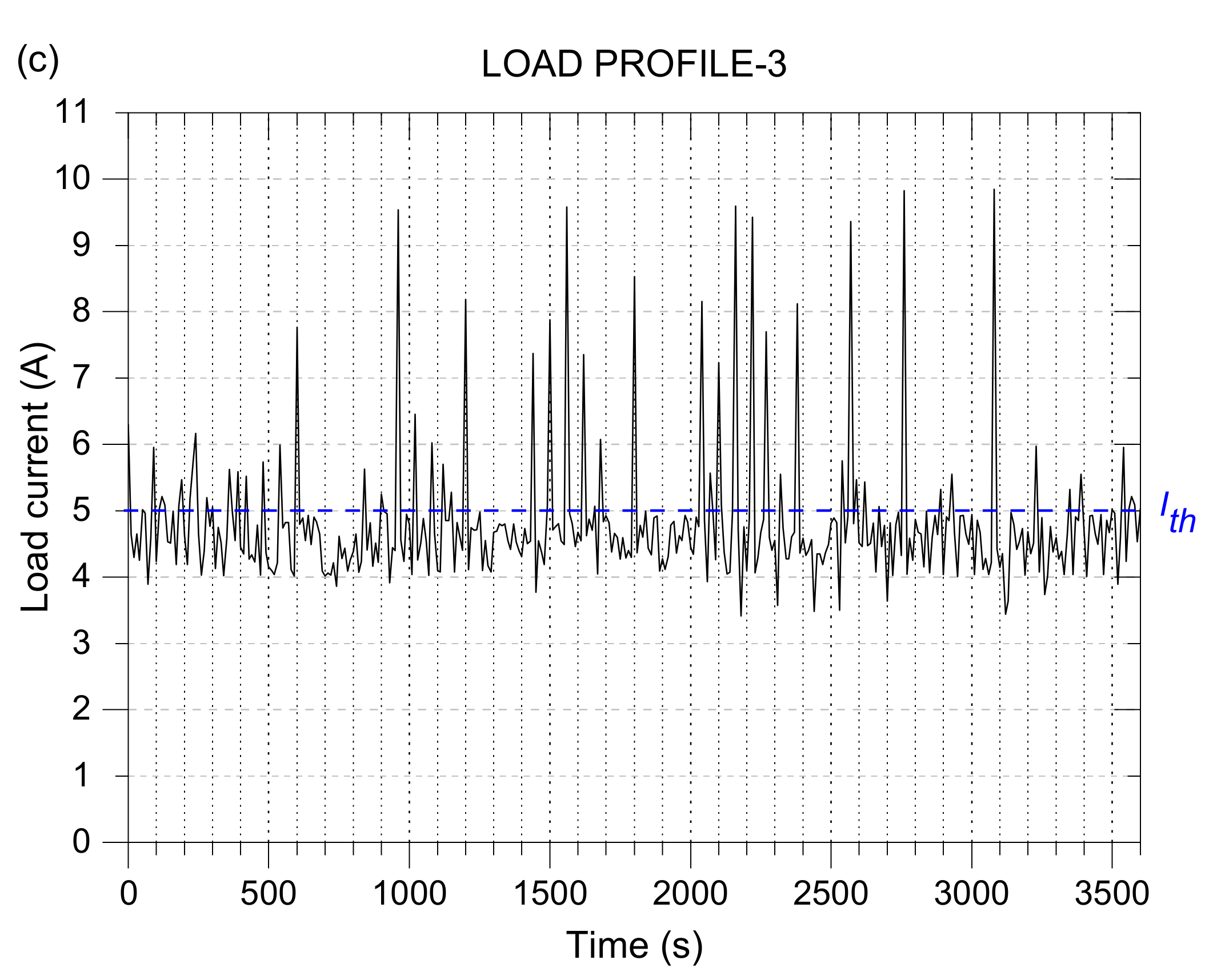
3.2. Load Profile from the Battery–Supercapacitor HESS Embedded Control System
3.3. Capacity Sizing Parameters for the Load Profiles
3.3.1. Parameters from the Load
3.3.2. Parameters from Supercapacitor and Battery
3.4. Capacity Sizing Result of Battery–Supercapacitors HESS
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jing, W.; Lai, C.H.; Wong, S.H.W.; Wong, M.L.D. Battery-supercapacitor hybrid energy storage system in standalone DC microgrids: A Review, IET Renew. Power Gener. 2017, 11, 461–469. [Google Scholar] [CrossRef]
- Babu, T.S.S.; Vasudevan, K.R.; Ramachandaramurthy, V.K.; Sani, S.B.; Chemud, S.; Lajim, R.M. A comprehensive review of hybrid energy storage systems: Converter topologies, control strategies and future prospects. IEEE Access 2020, 8, 148702–148721. [Google Scholar] [CrossRef]
- Cao, J.; Emadi, A. A new battery/ultra-capacitor hybrid energy storage system for electric, hybrid and plug-in hybrid electric vehicles. In Proceedings of the 5th IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 941–946. [Google Scholar] [CrossRef]
- Choi, M.E.; Kim, S.W.; Seo, S.W. Energy management optimization in a battery/supercapacitor hybrid energy storage system. IEEE Trans. Smart Grid. 2012, 3, 463–472. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Z.; Yu, X. Control strategies for battery/supercapacitor hybrid energy storage systems. In Proceedings of the 2008 IEEE Energy 2030 Energy Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 5–10. [Google Scholar] [CrossRef]
- Jing, W.; Lai, C.H.; Wong, W.S.H.; Wong, M.L.D. A comprehensive study of battery-supercapacitor hybrid energy storage system for standalone PV power system in rural electrification. Appl. Energy 2018, 224, 340–356. [Google Scholar] [CrossRef]
- Pay, S.; Baghzouz, Y. Effectiveness of battery-supercapacitor combination in electric vehicles. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; pp. 728–733. [Google Scholar] [CrossRef]
- Yee, Y.; Hong, L.; Shafiabady, N.; Isa, D.; Chia, Y.Y.; Lee, L.H.; Shafiabady, N.; Isa, D. A load predictive energy management system for supercapacitor-battery hybrid energy storage system in solar application using the Support Vector Machine. Appl. Energy 2015, 137, 588–602. [Google Scholar] [CrossRef]
- Chong, L.W.; Wong, Y.W.; Rajkumar, R.K.; Isa, D. An optimal control strategy for standalone PV system with Battery- Supercapacitor Hybrid Energy Storage System. J. Power Sources 2016, 331, 553–565. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, G. Experimental study on a semi-active battery-supercapacitor HESS. IEEE Trans. Power Electron. 2020, 35, 1014–1021. [Google Scholar] [CrossRef]
- Paul, T.T.; Mesbahi, T.; Durand, S.; Flieller, D.; Uhring, W. Study and influence of standardized driving cycles on the sizing of li-ion battery / supercapacitor hybrid energy storage. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Deng, J.; Dorrell, D.G.; Member, S.; Wang, Z.; Sun, F. Multiobjective optimal sizing of hybrid energy storage system for electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 1027–1035. [Google Scholar] [CrossRef]
- Sampietro, J.L.; Puig, V.; Costa-Castelló, R.; Sampietro, R.C.-C.J.; Puig, V. Optimal sizing of storage elements for a vehicle based on fuel cells, supercapacitors, and batteries. Energies 2019, 12, 925. [Google Scholar] [CrossRef] [Green Version]
- Afzal, A.; Mokashi, I.; Khan, S.A.; Abdullah, N.A.; Azami, M.H.B. Optimization and analysis of maximum temperature in a battery pack affected by low to high Prandtl number coolants using response surface methodology and particle swarm optimization algorithm. Numer. Heat Transf. Part A Appl. 2020, 79, 406–435. [Google Scholar] [CrossRef]
- Tie, S.F.; Tan, C.W. A review of energy sources and energy management system in electric vehicles. Renew. Sustain. Energy Rev. 2013, 20, 82–102. [Google Scholar] [CrossRef]
- Araújo, R.E.; de Castro, R.; Pinto, C.; Melo, P.; Freitas, D. Combined sizing and energy management in EVs with batteries and supercapacitors. IEEE Trans. Veh. Technol. 2014, 63, 3062–3076. [Google Scholar] [CrossRef] [Green Version]
- Jacob, A.S.; Banerjee, R.; Ghosh, P.C. Sizing of hybrid energy storage system for a PV based microgrid through design space approach. Appl. Energy 2018, 212, 640–653. [Google Scholar] [CrossRef]
- Paul, T.; Mesbahi, T.; Durand, S.; Flieller, D.; Uhring, W. Sizing of lithium-ion battery/supercapacitor hybrid energy storage system for forklift vehicle. Energies 2020, 13, 4518. [Google Scholar] [CrossRef]
- Zhang, L.; Ye, X.; Xia, X.; Barzegar, F. A real-time energy management and speed controller for an electric vehicle powered by a hybrid energy storage system. IEEE Trans. Ind. Inform. 2020, 16, 6272–6280. [Google Scholar] [CrossRef]
- Sadeq, T.; Wai, C.K.; Morris, E.; Tarboosh, Q.A.; Aydogdu, O. Optimal control strategy to maximize the performance of hybrid energy storage system for electric vehicle considering topography information. IEEE Access 2020, 8, 216994–217007. [Google Scholar] [CrossRef]
| Parameter | Specification |
|---|---|
| Maximum voltage | 4.2 V |
| Minimum voltage | 3.5 V |
| Capacity | 2.2 Ah |
| Maximum discharge current | 55 A |
| Maximum charging current | 1 A |
| Cycle life | 300–500 |
| Parameter | Specification |
|---|---|
| Voltage | 2.7 V |
| Capacitance | 500 F |
| Maximum continuous discharge current | 25 A (15 °C), 40 A (40 °C) |
| Maximum peak discharge current | 264.7 A |
| Cycle life | 500,000–1,000,000 |
| Discharge Current (A) | Total Discharge Time (s) | |||
|---|---|---|---|---|
| Battery | Supercapacitor | |||
| Calculated (Equation (10)) | Experimental | Calculated (Equation (18)) | Experimental | |
| 1.0 | 7920 | 13,200 | 950 | 913.8 |
| 0.7 | 15,840 | 17,400 | 1375 | 1299.0 |
| 0.3 | 39,600 | 33,600 | 3264 | 2866.8 |
| Profile | High Power Region | Nominal Power Region | Application |
|---|---|---|---|
| 1 | 64% | 36% | Urban electric bus |
| 2 | 43% | 57% | Urban electric bus |
| 3 | 16% | 84% | Mobile vaccination centre storage unit |
| Parameters | Value |
|---|---|
| Number of LiPo cell in series, NBS | 3 cells |
| Capacity of three cells in series | 2.2 Ah |
| Maximum voltage | 12.6 V |
| Minimum voltage | 10.5 V |
| Parameters | Value |
|---|---|
| Number of supercapacitor cell in series, Nscs | 6 cells |
| Capacity of six supercapacitor in series | 83.33 F |
| Maximum supercapacitor voltage, Vsc max | 16.2 V |
| Minimum supercapacitor voltage, Vsc max | 10.0 V |
| Discharge time of supercapacitor at max current, tsc | 208.2 s |
| Load Profile | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| Total time above threshold current (seconds) | 2317.8 | 1540.2 | 559.8 |
| Total time below threshold current (seconds) | 1282.2 | 2059.8 | 3040.2 |
| Total number of supercapacitor cells in parallel, NSCP (cells) | 13 | 9 | 4 |
| Total capacity of supercapacitor, CSCP (F) | 1083.29 | 749.97 | 777.47 |
| Number of battery cells in parallel, NBP (cells) | 2 | 3 | 3 |
| Total capacity of battery, CBP (Ah) | 4.4 | 6.6 | 6.6 |
| Load Profile | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| Maximum current of entire operation (A) | 10 | 10 | 10 |
| Total time of operation (seconds) | 3600 | 3600 | 3600 |
| No. of battery cells in parallel, NBP (cells) | 6 | 6 | 6 |
| Total capacity of battery, CBP (Ah) | 13.2 | 13.2 | 13.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, N.; Nee, C.H.; Yap, S.S.; Tham, K.K.; You, A.H.; Yap, S.L.; Mohd Arof, A.K.B. Capacity Sizing of Embedded Control Battery–Supercapacitor Hybrid Energy Storage System. Energies 2022, 15, 3783. https://doi.org/10.3390/en15103783
Lee N, Nee CH, Yap SS, Tham KK, You AH, Yap SL, Mohd Arof AKB. Capacity Sizing of Embedded Control Battery–Supercapacitor Hybrid Energy Storage System. Energies. 2022; 15(10):3783. https://doi.org/10.3390/en15103783
Chicago/Turabian StyleLee, Noah, Chen Hon Nee, Seong Shan Yap, Kwong Keong Tham, Ah Heng You, Seong Ling Yap, and Abdul Kariem Bin Mohd Arof. 2022. "Capacity Sizing of Embedded Control Battery–Supercapacitor Hybrid Energy Storage System" Energies 15, no. 10: 3783. https://doi.org/10.3390/en15103783
APA StyleLee, N., Nee, C. H., Yap, S. S., Tham, K. K., You, A. H., Yap, S. L., & Mohd Arof, A. K. B. (2022). Capacity Sizing of Embedded Control Battery–Supercapacitor Hybrid Energy Storage System. Energies, 15(10), 3783. https://doi.org/10.3390/en15103783






