Figure 1.
DSTATCOM induction motor starting.
Figure 1.
DSTATCOM induction motor starting.
Figure 2.
Equivalent circuits.
Figure 2.
Equivalent circuits.
Figure 3.
Possible filter arrangements—low pass filter most suitable in this application.
Figure 3.
Possible filter arrangements—low pass filter most suitable in this application.
Figure 4.
Failure of a capacitor in a star or delta connected bank.
Figure 4.
Failure of a capacitor in a star or delta connected bank.
Figure 5.
Complete system power circuit.
Figure 5.
Complete system power circuit.
Figure 6.
Power factor start for different motors.
Figure 6.
Power factor start for different motors.
Figure 7.
p.u. input resistances and reactances at start for different motors.
Figure 7.
p.u. input resistances and reactances at start for different motors.
Figure 8.
Variation of P. U. and for different motors.
Figure 8.
Variation of P. U. and for different motors.
Figure 9.
Motor No. 1: Comparison of 1.5 kW 220 V lab machine capacitor compensation starting.
Figure 9.
Motor No. 1: Comparison of 1.5 kW 220 V lab machine capacitor compensation starting.
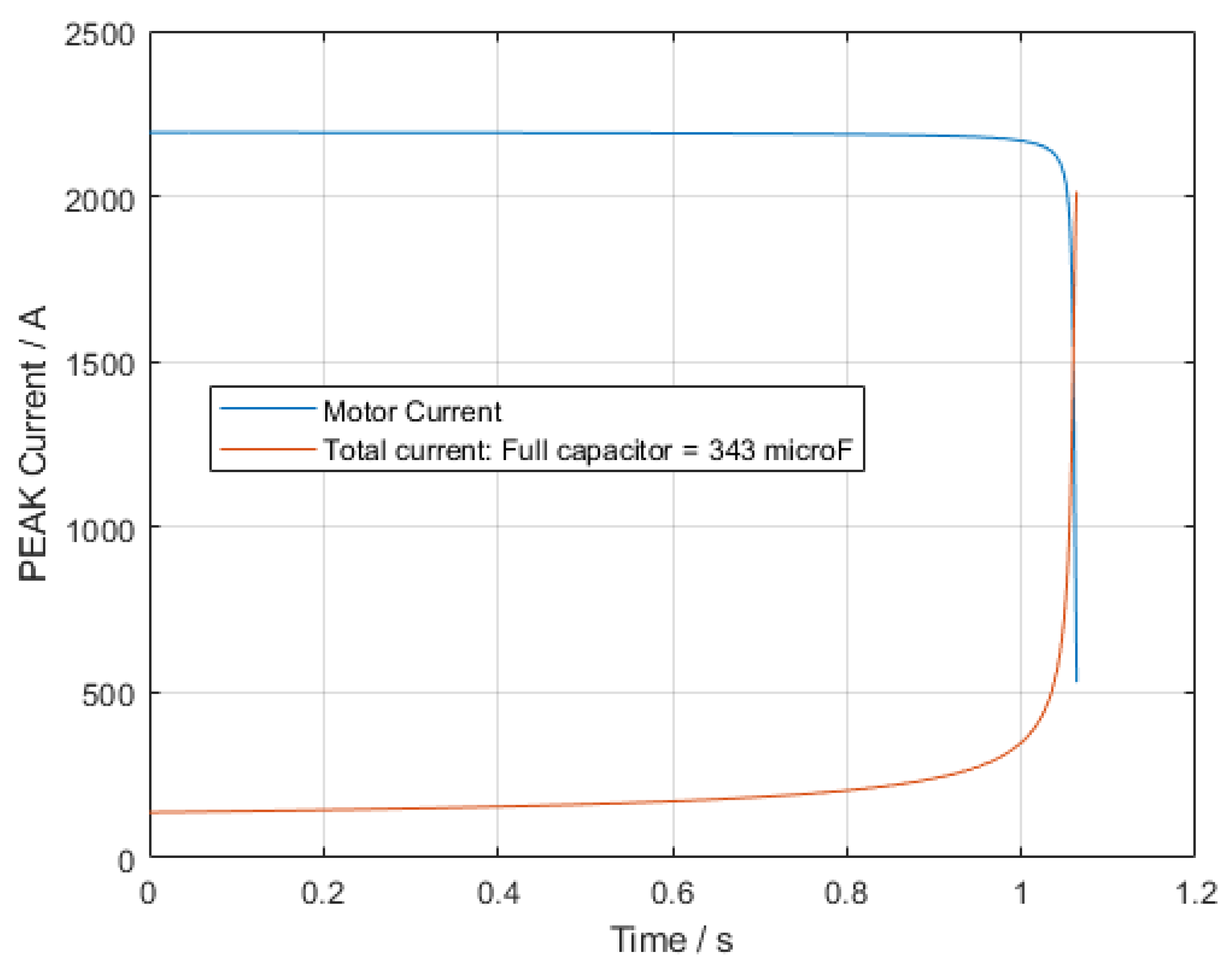
Figure 10.
Motor No. 1: Run-up time prediction for experimental machine at 100 V—currents with 50 µF and 90 µF.
Figure 10.
Motor No. 1: Run-up time prediction for experimental machine at 100 V—currents with 50 µF and 90 µF.
Figure 11.
Motor No. 2: Comparison of 1.5 kW 400 V Valiadas K90L-4 machine capacitor compensation starting.
Figure 11.
Motor No. 2: Comparison of 1.5 kW 400 V Valiadas K90L-4 machine capacitor compensation starting.
Figure 12.
Motor No. 3: Comparison of 3.75 kW 440 V Sen 5 HP machine capacitor compensation starting.
Figure 12.
Motor No. 3: Comparison of 3.75 kW 440 V Sen 5 HP machine capacitor compensation starting.
Figure 13.
Motor No. 4: Comparison of 45 kW 400 V Valiadis K200L-4 machine capacitor compensation starting.
Figure 13.
Motor No. 4: Comparison of 45 kW 400 V Valiadis K200L-4 machine capacitor compensation starting.
Figure 14.
Motor No. 4: Speed-torque curve of 45 kW 400 V Valiadis K200L-4 machine and load torque with . Blue line is motor torque, brown line is load torque.
Figure 14.
Motor No. 4: Speed-torque curve of 45 kW 400 V Valiadis K200L-4 machine and load torque with . Blue line is motor torque, brown line is load torque.
Figure 15.
Motor No. 4: Speed-time curve of 45 kW 400 V Valiadis K200L-4 machine with inertia of 0.492 kg m2 and speed-squared load torque function .
Figure 15.
Motor No. 4: Speed-time curve of 45 kW 400 V Valiadis K200L-4 machine with inertia of 0.492 kg m2 and speed-squared load torque function .
Figure 16.
Motor No. 4: Speed-time curve of 45 kW 400 V Valiadis K200L-4 machine with inertia of 0.492 kg m2 and no load.
Figure 16.
Motor No. 4: Speed-time curve of 45 kW 400 V Valiadis K200L-4 machine with inertia of 0.492 kg m2 and no load.
Figure 17.
Motor No. 5: Comparison of 200 kW 3300 V Valiadas KHV355-2 machine capacitor compensation starting.
Figure 17.
Motor No. 5: Comparison of 200 kW 3300 V Valiadas KHV355-2 machine capacitor compensation starting.
Figure 18.
Motor No. 6: Comparison of 1 MW 6000 V Valiadas TMKHV560-6 machine capacitor compensation starting.
Figure 18.
Motor No. 6: Comparison of 1 MW 6000 V Valiadas TMKHV560-6 machine capacitor compensation starting.
Figure 19.
Motor No. 6: Run-up time prediction for PEAK current for 1 MW machine at rated voltage and with load.
Figure 19.
Motor No. 6: Run-up time prediction for PEAK current for 1 MW machine at rated voltage and with load.
Figure 20.
Motor No. 6: Run-up time prediction for PEAK current for 1 MW machine at rated voltage and with no load.
Figure 20.
Motor No. 6: Run-up time prediction for PEAK current for 1 MW machine at rated voltage and with no load.
Figure 21.
Motor No. 7: Comparison of 3.75 MW 6900 V Sen 5000 HP machine capacitor compensation starting.
Figure 21.
Motor No. 7: Comparison of 3.75 MW 6900 V Sen 5000 HP machine capacitor compensation starting.
Figure 22.
Motor No. 7: Speed-torque curve of 3.75 MW 6900 V Sen 5000 HP machine and load torque with . Blue line is motor torque, brown line is load torque.
Figure 22.
Motor No. 7: Speed-torque curve of 3.75 MW 6900 V Sen 5000 HP machine and load torque with . Blue line is motor torque, brown line is load torque.
Figure 23.
Motor No. 7: Speed-time curve of 3.75 MW 6900 V Sen 5000 HP machine inertia of 290.84 kg m2 and no load.
Figure 23.
Motor No. 7: Speed-time curve of 3.75 MW 6900 V Sen 5000 HP machine inertia of 290.84 kg m2 and no load.
Figure 24.
Motor No. 1E steady-state simulation with 90 µF capacitors.
Figure 24.
Motor No. 1E steady-state simulation with 90 µF capacitors.
Figure 25.
Motor No. 1E steady-state simulation with 90 µF capacitors switching and 0.625 Nm of friction added.
Figure 25.
Motor No. 1E steady-state simulation with 90 µF capacitors switching and 0.625 Nm of friction added.
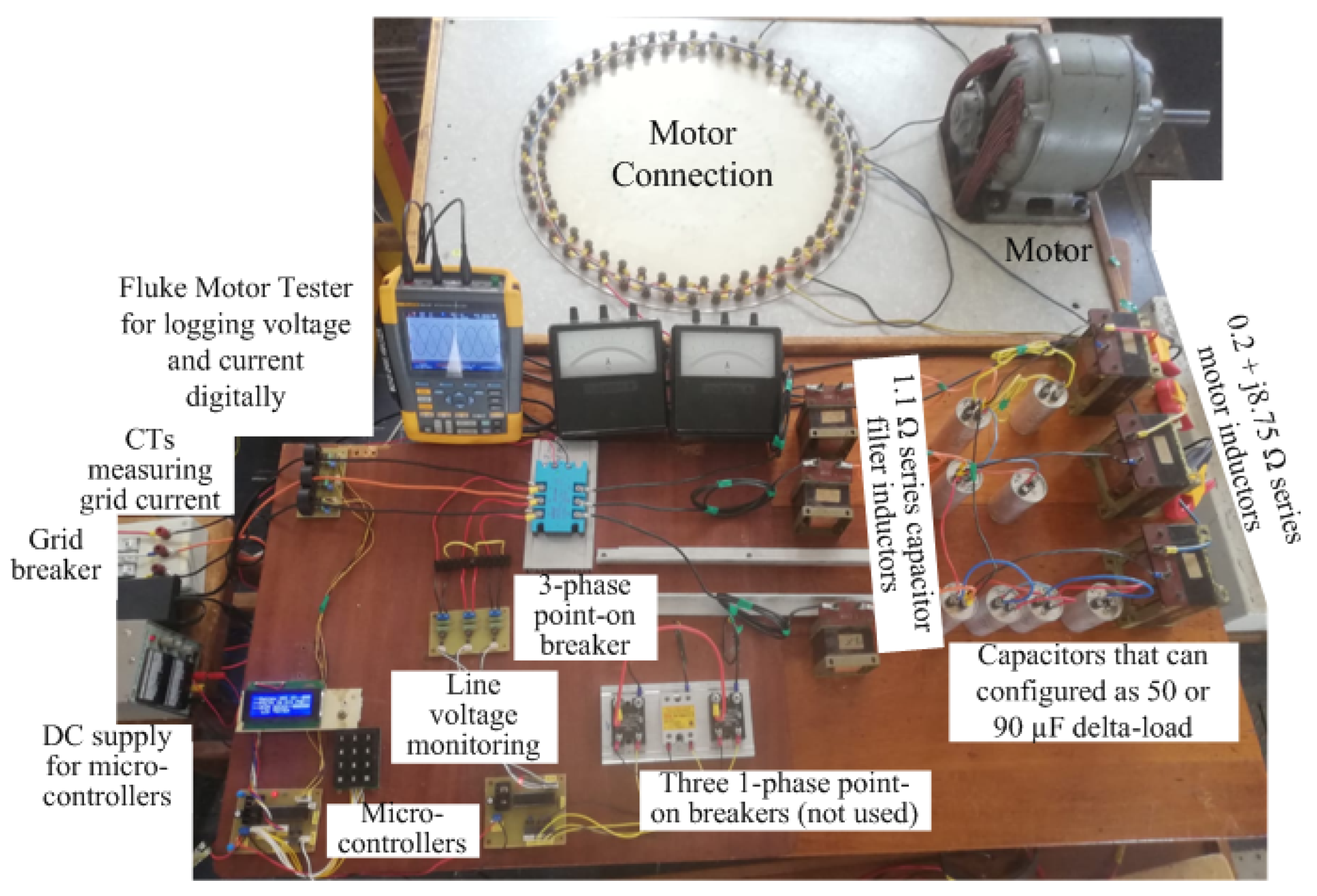
Figure 26.
Final layout of test rig.
Figure 26.
Final layout of test rig.
Figure 27.
Solid state breakers used.
Figure 27.
Solid state breakers used.
Figure 28.
Current waveforms for Motor No. 1 at 100 V—currents with and without and 90 µF—for locked-rotor testing, the motor current was high and this is a resistive motor circuit so the capacitor currents were not noticeable, but for running light, the current was much reduced and the motor was more inductive so that the capacitor current was now visible.
Figure 28.
Current waveforms for Motor No. 1 at 100 V—currents with and without and 90 µF—for locked-rotor testing, the motor current was high and this is a resistive motor circuit so the capacitor currents were not noticeable, but for running light, the current was much reduced and the motor was more inductive so that the capacitor current was now visible.
Figure 29.
Locked-rotor current waveform for Motor No. 1E at 100 V—currents with 90 µF capacitors—there is now substantial harmonic in the locked-rotor current.
Figure 29.
Locked-rotor current waveform for Motor No. 1E at 100 V—currents with 90 µF capacitors—there is now substantial harmonic in the locked-rotor current.
Figure 30.
Transient system voltage waveforms for Motor No. 1E at 100 V—the voltage waveform in (c) shows about 3% of the 7th harmonic; (a,b) have 100 V/div on the Y axis while (c) is in p.u.
Figure 30.
Transient system voltage waveforms for Motor No. 1E at 100 V—the voltage waveform in (c) shows about 3% of the 7th harmonic; (a,b) have 100 V/div on the Y axis while (c) is in p.u.
Figure 31.
Transient system current for Motor No. 1E at 100 V peak for the phase—with 90 µF compensation capacitors in parallel. The X-axis is 1 s/div and Y-axis is 5 A/div. This shows the initial capacitor turn-on current spikes, then a period of the motor and capacitor currents cancelled, and the capacitor current dominated at no load (they should be switched out before this point was reached).
Figure 31.
Transient system current for Motor No. 1E at 100 V peak for the phase—with 90 µF compensation capacitors in parallel. The X-axis is 1 s/div and Y-axis is 5 A/div. This shows the initial capacitor turn-on current spikes, then a period of the motor and capacitor currents cancelled, and the capacitor current dominated at no load (they should be switched out before this point was reached).
Figure 32.
Transient system current for Motor No. 1E at 100 V phase peak—with 90 µF parallel compensation capacitors, but with no capacitor filters. Y-scales: 5 A/division. A 7th harmonic would have a period of 2.86 ms, or 7 cycles every 20 ms—the waveforms all showed a harmonic of this order.
Figure 32.
Transient system current for Motor No. 1E at 100 V phase peak—with 90 µF parallel compensation capacitors, but with no capacitor filters. Y-scales: 5 A/division. A 7th harmonic would have a period of 2.86 ms, or 7 cycles every 20 ms—the waveforms all showed a harmonic of this order.
Figure 33.
Transient motor current for Motor No. 1E at 100 V phase peak—with 90 µF parallel compensation capacitors, but with no capacitor filters. Y-scales: 5 A/div. This illustrates that the harmonic currents in
Figure 32 were not due to the motor.
Figure 33.
Transient motor current for Motor No. 1E at 100 V phase peak—with 90 µF parallel compensation capacitors, but with no capacitor filters. Y-scales: 5 A/div. This illustrates that the harmonic currents in
Figure 32 were not due to the motor.
Figure 34.
Transient capacitor current for Motor No. 1E at 100 V phase peak—with 90 µF parallel compensation capacitors, but with no capacitor filters. Y-scales: 5 A/div. It can be seen that the capacitor currents were almost trapezoidal and generating the harmonic currents in
Figure 32. The total current in
Figure 32 was the currents in this figure added to the currents in
Figure 33.
Figure 34.
Transient capacitor current for Motor No. 1E at 100 V phase peak—with 90 µF parallel compensation capacitors, but with no capacitor filters. Y-scales: 5 A/div. It can be seen that the capacitor currents were almost trapezoidal and generating the harmonic currents in
Figure 32. The total current in
Figure 32 was the currents in this figure added to the currents in
Figure 33.
Figure 35.
Transient system current for Motor No. 1E at 100 V phase peak—with 90 µF capacitor and 1.1
series inductor filter. Y-scales: top—5 A/unit, rest—2 A/unit. This clearly shows the filter reducing the grid current harmonic when compared to
Figure 32.
Figure 35.
Transient system current for Motor No. 1E at 100 V phase peak—with 90 µF capacitor and 1.1
series inductor filter. Y-scales: top—5 A/unit, rest—2 A/unit. This clearly shows the filter reducing the grid current harmonic when compared to
Figure 32.
Figure 36.
Transient capacitor current for Motor No. 1E at 100 V phase peak—with 90 µF parallel compensation capacitors. Y-scales: top—5 A/unit, rest—2 A/unit. This shows a reduced harmonic content in the capacitor current when compared to
Figure 34.
Figure 36.
Transient capacitor current for Motor No. 1E at 100 V phase peak—with 90 µF parallel compensation capacitors. Y-scales: top—5 A/unit, rest—2 A/unit. This shows a reduced harmonic content in the capacitor current when compared to
Figure 34.
Figure 37.
Turn-on line voltages and currents for Motor No. 1 at 100 V line rms. Y-scales: top—50 V/div, bottom—5 A/div.
Figure 37.
Turn-on line voltages and currents for Motor No. 1 at 100 V line rms. Y-scales: top—50 V/div, bottom—5 A/div.
Figure 38.
Phasor diagram for turn-on sequence.
Figure 38.
Phasor diagram for turn-on sequence.
Figure 39.
Turn-on line voltages and currents for Motor No. 1E at 100 V line rms. Y-scales: top—50 V/div, bottom—5 A/div.
Figure 39.
Turn-on line voltages and currents for Motor No. 1E at 100 V line rms. Y-scales: top—50 V/div, bottom—5 A/div.
Figure 40.
Turn-on line voltages and currents for Motor No. 1 at 100 V line rms. Y-scales: top—50 V/div, middle—5 A/div and bottom—2 A/div.
Figure 40.
Turn-on line voltages and currents for Motor No. 1 at 100 V line rms. Y-scales: top—50 V/div, middle—5 A/div and bottom—2 A/div.
Table 1.
Motor parameters.
Table 1.
Motor parameters.
| No. | Machine | kW | [V] | [A] | Poles | [Hz] | rpm | J [kg·m2]
|
|---|
| 1 | Lab machine | 1.5 | 220 | 5.8 | 4 | 50 | 1425 | 0.012 |
| 2 | Valiadas K90L-4 | 1.5 | 400 | 3.3 | 4 | 50 | 1440 | — |
| 3 | Sen 5 HP | 3.75 | 440 | 3.73 | 4 | 60 | 1753 | 0.05 |
| 4 | Valiadis K200L-4 | 45 | 400 | 81.1 | 4 | 50 | 1480 | 0.246 |
| 5 | Valiadas KHV355-2 | 200 | 3300 | 44.4 | 2 | 50 | — | 2.6 |
| 6 | Valiadas TMKHV560-6 | 1000 | 6000 | 110 | 6 | 50 | 990 | 79 |
| 7 | Sen 5000 HP | 3730 | 6900 | 358 | 12 | 60 | 596 | 145.47 |
Table 2.
Motor equivalent circuit parameters (values in ).
Table 2.
Motor equivalent circuit parameters (values in ).
| No. | Machine | | | | | | X/R |
|---|
| 1 | Lab machine | 58 | 81 | 2.13 | 1.34 | 2.99 | 0.86 |
| 2 | Valiadas K90L-4 | 115.2 | 1568.2 | 1.325 | 3.87 | 8.44 | 1.62 |
| 3 | Sen 5 HP | 110 | 900 | 1.2 | 1.5 | 6.0 | 2.22 |
| 4 | Valiadis K200L-4 | 5.13 | 178.1 | 0.059 | 0.013 | 0.48 | 6.67 |
| 5 | Valiadas KHV355-2 | 118 | 1333 | 0.79 | 0.57 | 5.75 | 4.2 |
| 6 | Valiadas TMKHV560-6 | 102.5 | 900.0 | 0.97 | 0.24 | 4.78 | 3.97 |
| 7 | Sen 5000 HP | 46.0 | 600.0 | 0.083 | 0.080 | 2.60 | 15.95 |
Table 3.
Motor equivalent circuit parameters (values in p.u.).
Table 3.
Motor equivalent circuit parameters (values in p.u.).
| No. | Machine | | | | | | |
|---|
| 1 | Lab machine | 37.478 | 1.54 | 2.17 | 0.0568 | 0.0357 | 0.080 |
| 2 | Valiadas K90L-4 | 69.98 | 1.65 | 22.41 | 0.189 | 0.0554 | 0.121 |
| 3 | Sen 5 HP | 36.29 | 3.03 | 24.8 | 0.0331 | 0.0413 | 0.165 |
| 4 | Valiadis K200L-4 | 2.85 | 1.80 | 62.56 | 0.0207 | 0.0046 | 0.169 |
| 5 | Valiadas KHV355-2 | 42.91 | 2.75 | 31.08 | 0.0184 | 0.0314 | 0.134 |
| 6 | Valiadas TMKHV560-6 | 29.11 | 3.5 | 40.00 | 0.0332 | 0.0082 | 0.164 |
| 7 | Sen 5000 HP | 11.13 | 4.13 | 53.92 | 0.0075 | 0.0072 | 0.234 |
Table 4.
Motor No. 1 locked rotor test with and without 50 µF compensation capacitors—the peak measured current (peak) reduction was less than the simulated (peak) current reduction.
Table 4.
Motor No. 1 locked rotor test with and without 50 µF compensation capacitors—the peak measured current (peak) reduction was less than the simulated (peak) current reduction.
| 100 V Line 50 µF Caps. | Ia | Ib | Ic | Imeanrms | Imeanpeak | ISimpeak |
|---|
| Motor | 11.53 | 11.66 | 11.3 | 11.50 | 16.26 | 18.18 |
| Capacitors and motor | 11.22 | 11.39 | 10.96 | 11.19 | 15.83 | 15.93 |
Table 5.
Motor No. 1 locked rotor test with and without 90 µF compensation capacitors— peak reduction was less than peak current reduction.
Table 5.
Motor No. 1 locked rotor test with and without 90 µF compensation capacitors— peak reduction was less than peak current reduction.
| 100 V Line 90 µF Caps. | Ia | Ib | Ic | Imeanrms | Imeanpeak | ISimpeak |
|---|
| Motor | 11.18 | 11.3 | 11.09 | 11.19 | 15.83 | 18.18 |
| Capacitors and motor | 10.45 | 10.59 | 10.36 | 10.47 | 14.80 | 14.62 |
Table 6.
Motor No. 1 running light test with and without 50 µF compensation capacitors— peak reduction was less than peak current reduction.
Table 6.
Motor No. 1 running light test with and without 50 µF compensation capacitors— peak reduction was less than peak current reduction.
| 100 V Line 50 µF Caps. | Ia | Ib | Ic | Imeanrms | Imeanpeak | ISim peak |
|---|
| Motor | 0.95 | 1.07 | 0.79 | 0.94 | 1.32 | 1.75 |
| Capacitors and motor | 0.34 | 0.59 | 0.5 | 0.48 | 0.67 | 2.75 |
Table 7.
Motor No. 1 running light test with and without 90 µF compensation capacitors— peak reduction was less than peak current reduction.
Table 7.
Motor No. 1 running light test with and without 90 µF compensation capacitors— peak reduction was less than peak current reduction.
| 100 V Line 90 µF Caps. | Ia | Ib | Ic | Imean rms | Imeanpeak | ISim peak |
|---|
| Motor | 0.91 | 1.03 | 0.8 | 0.91 | 1.29 | 1.75 |
| Capacitors and motor | 0.86 | 0.95 | 1.04 | 0.95 | 1.34 | 5.75 |
Table 8.
Motor No. 1E locked rotor test with and without 50 µF compensation capacitors.
Table 8.
Motor No. 1E locked rotor test with and without 50 µF compensation capacitors.
| 100 V Line 50 µF Caps. | Ia | Ib | Ic | Imeanrms | Imeanpeak | ISimpeak |
|---|
| Motor | 5.34 | 5.41 | 5.45 | 5.4 | 7.64 | 7.02 |
| Capacitors and motor | 2.9 | 2.9 | 2.9 | 2.9 | 4.10 | |
Table 9.
Motor No. 1E locked rotor test with and without 90 µF compensation capacitors.
Table 9.
Motor No. 1E locked rotor test with and without 90 µF compensation capacitors.
| 100 V Line 90 µF Caps. | Ia | Ib | Ic | Imeanrms | Imeanpeak | ISimpeak |
|---|
| Motor | 5.45 | 5.65 | 5.61 | 5.57 | 7.88 | 7.02 |
| Capacitors and motor | 2 | 2.2 | 2.2 | 2.13 | 3.02 | 2.04 |
Table 10.
Motor No. 1E running light test with and without 50 µF parallel compensation capacitors.
Table 10.
Motor No. 1E running light test with and without 50 µF parallel compensation capacitors.
| 109 V Line 50 µF Caps. | Ia | Ib | Ic | Imeanrms | Imeanpeak | ISim peak |
|---|
| Motor | 0.98 | 1.12 | 0.83 | 0.98 | 1.38 | 1.6 |
| Capacitors and motor | 1.9 | 2 | 2.3 | 2.07 | 2.92 | |
Table 11.
Motor No. 1E running light test with and without 90 µF parallel compensation capacitors.
Table 11.
Motor No. 1E running light test with and without 90 µF parallel compensation capacitors.
| 109 V Line 90 µF Caps. | Ia | Ib | Ic | Imeanrms | Imeanpeak | ISim peak |
|---|
| Motor | 0.89 | 0.98 | 0.89 | 0.92 | 1.30 | 1.60 |
| Capacitors and motor | 4.2 | 4.8 | | 4.85 4.62 | 6.53 | 6.23 |