Investigation of Shock Wave Oscillation Suppression by Overflow in the Supersonic Inlet
Abstract
:1. Introduction
2. Methodology
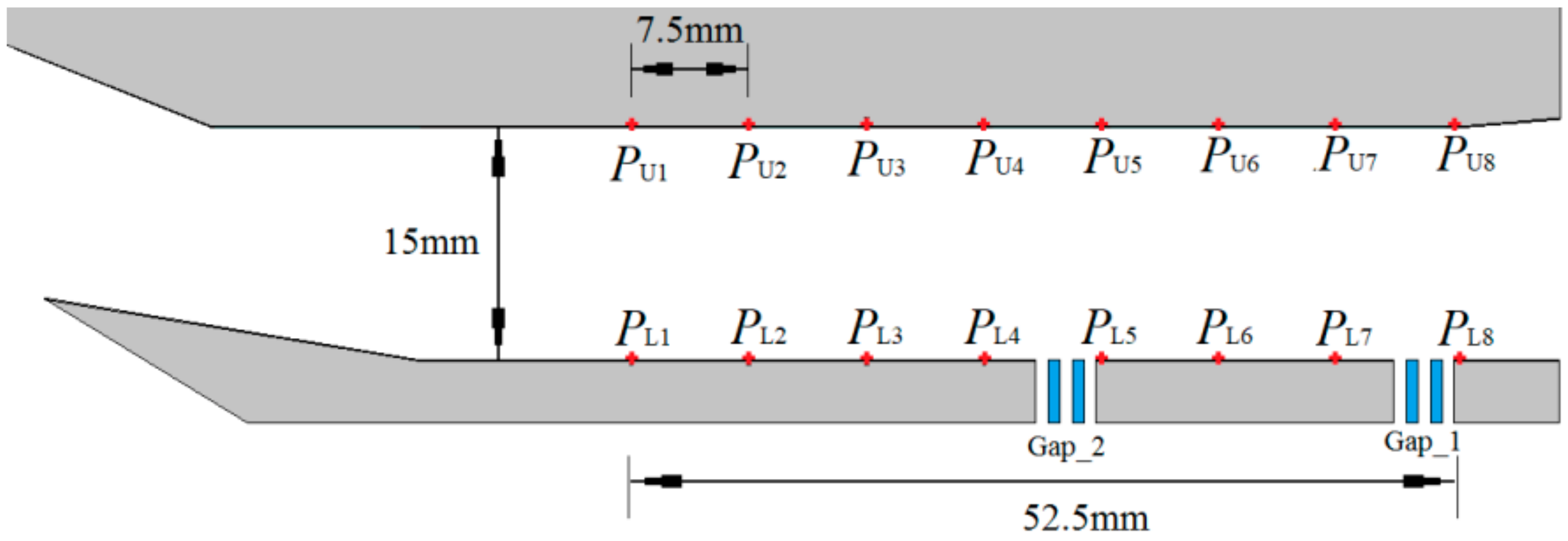
2.1. Geometric Model
2.2. Iso-Straight Channel Shock Dynamics Model
2.2.1. No Overflow Model
2.2.2. Overflow Model
2.2.3. Steady-State Parameter Verification
2.3. Numerical Modeling
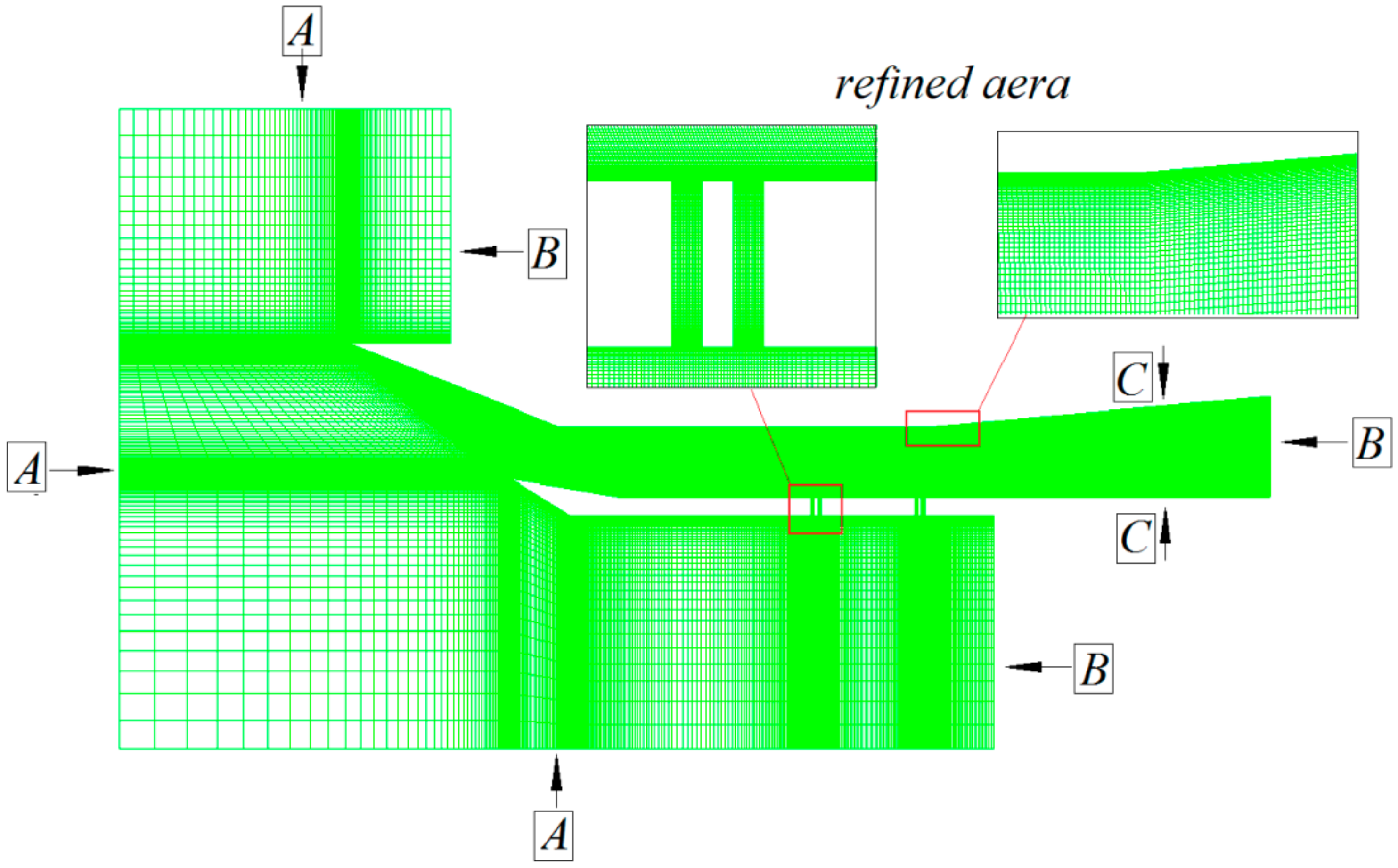
2.3.1. Numerical Method and Mesh
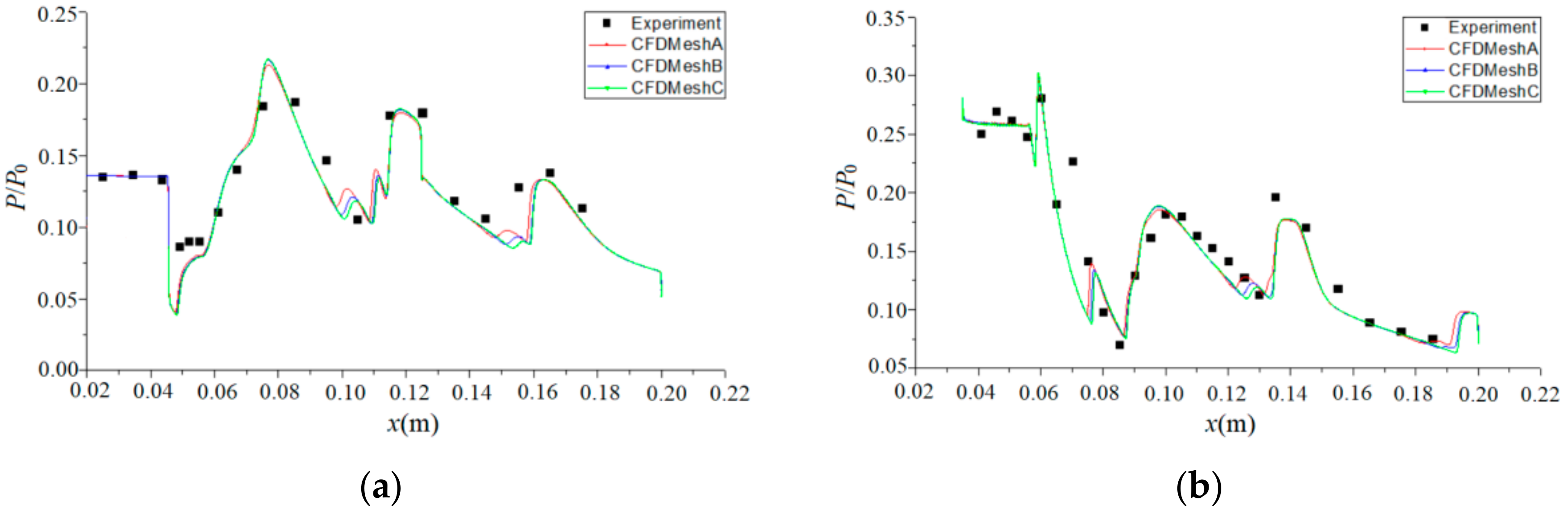
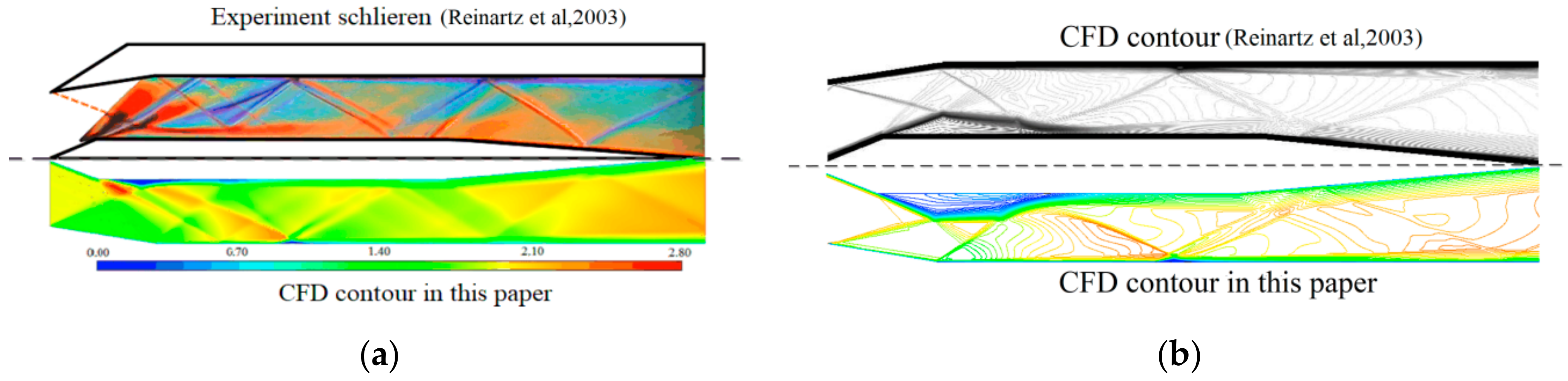
2.3.2. Numerical Model Verification
2.3.3. Computational Model and Time Step
3. Results and Discussion
3.1. Theoretical Analysis of Influence of Overflow Parameters on Shock Oscillation
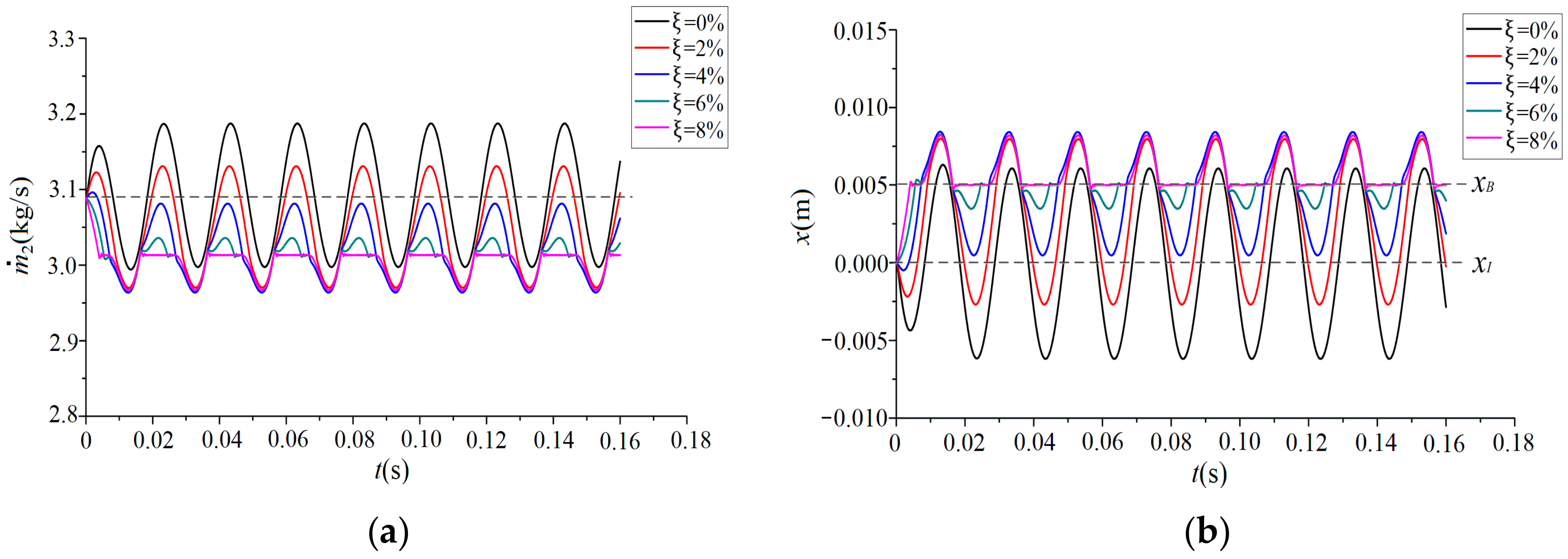
3.1.1. Influence of Overflow Gap Ratio
3.1.2. Influence of Overflow Position
3.2. Calculation and Analysis of Viscous Flow Field
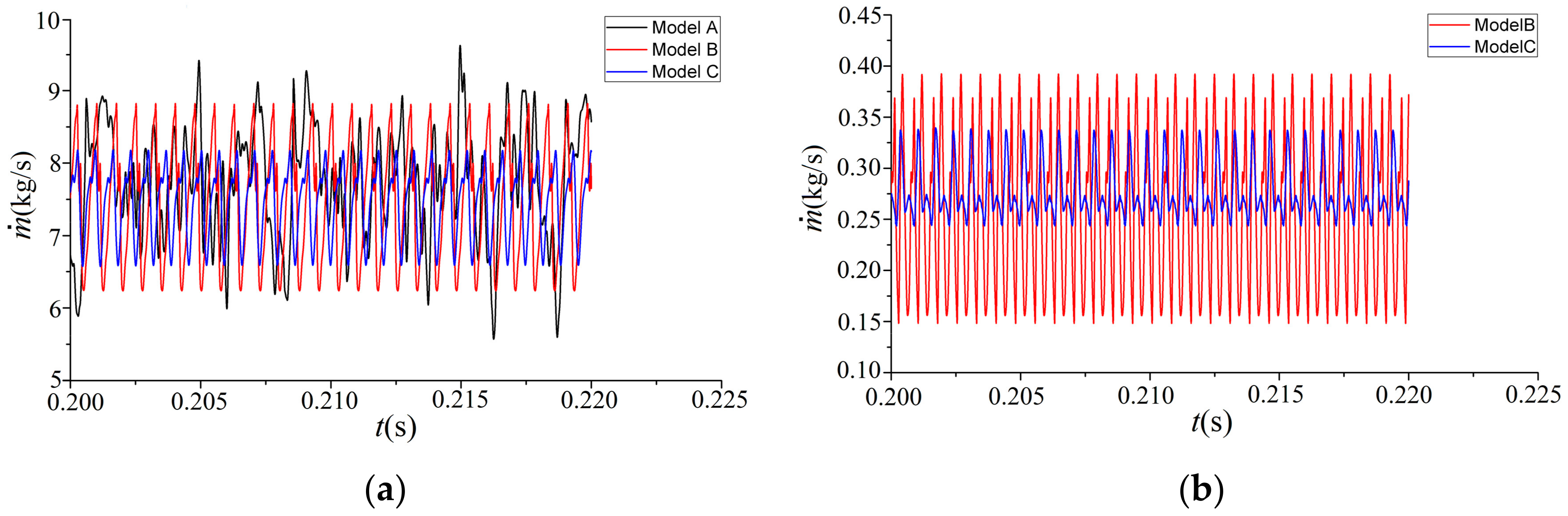
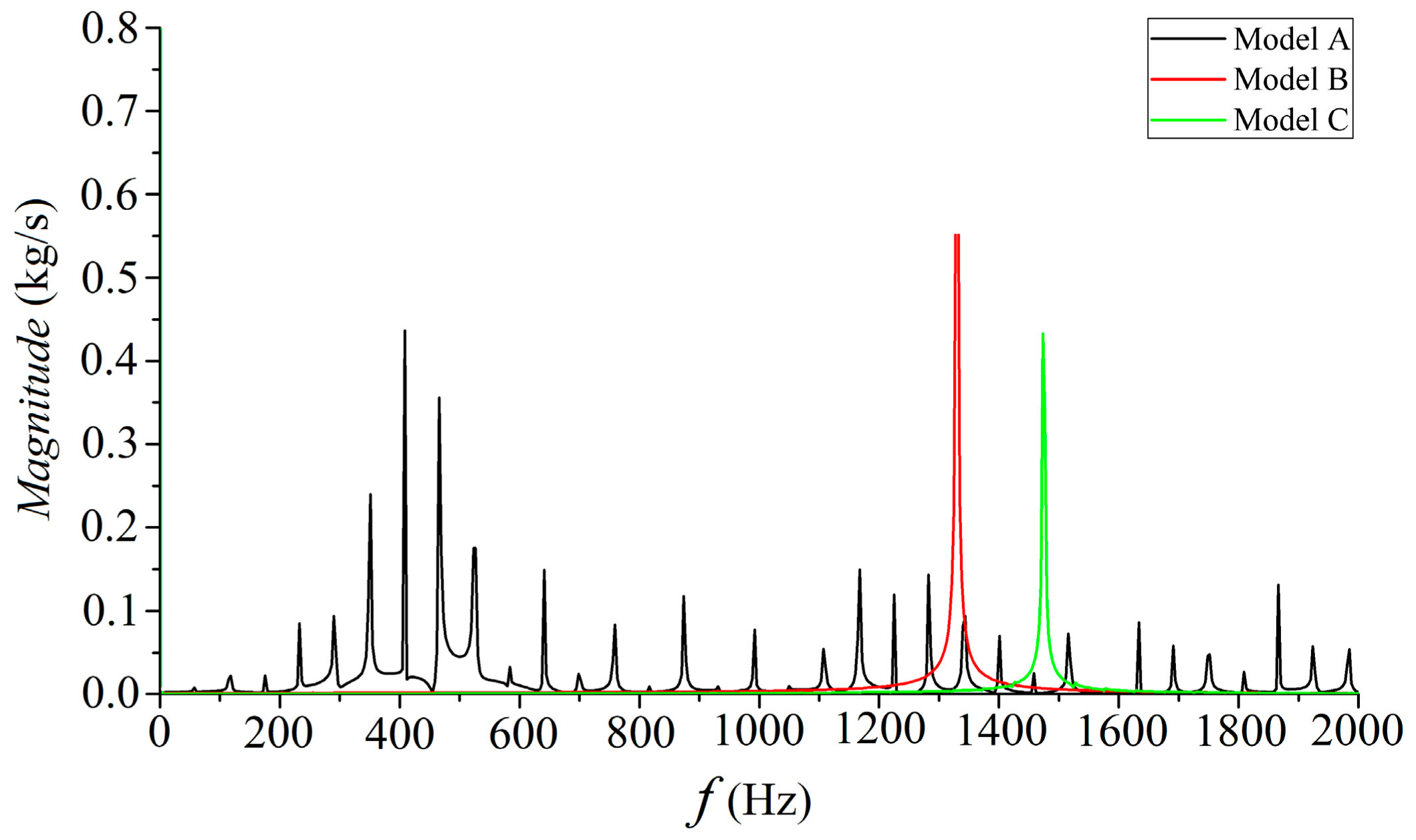
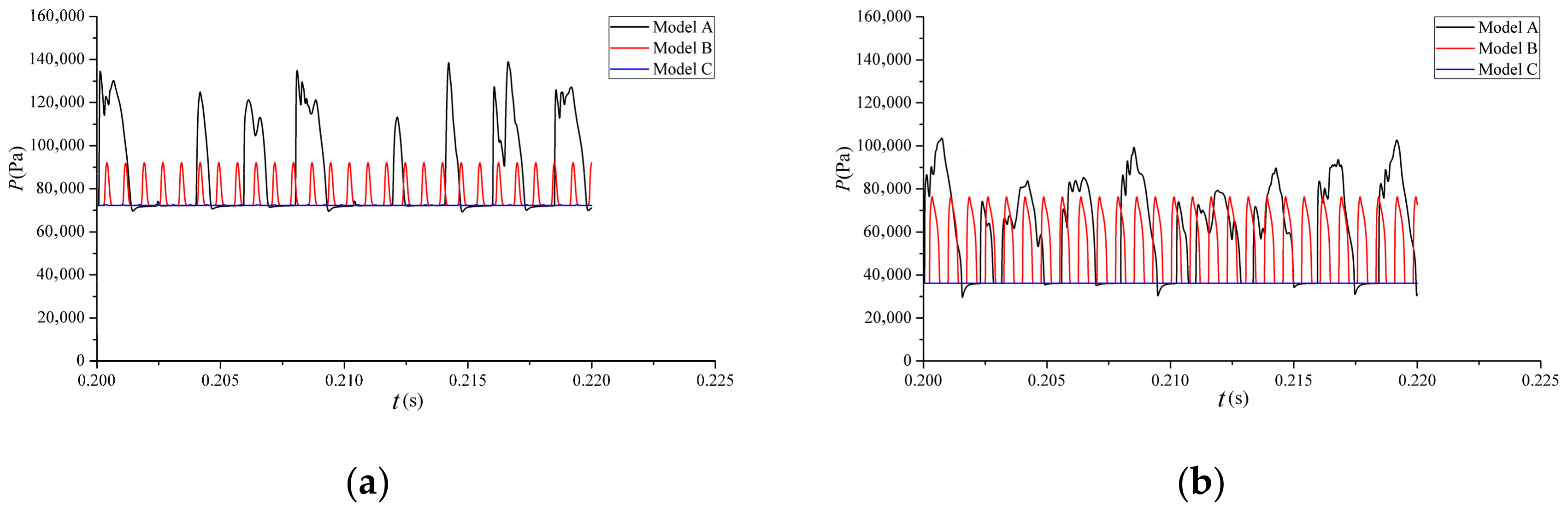
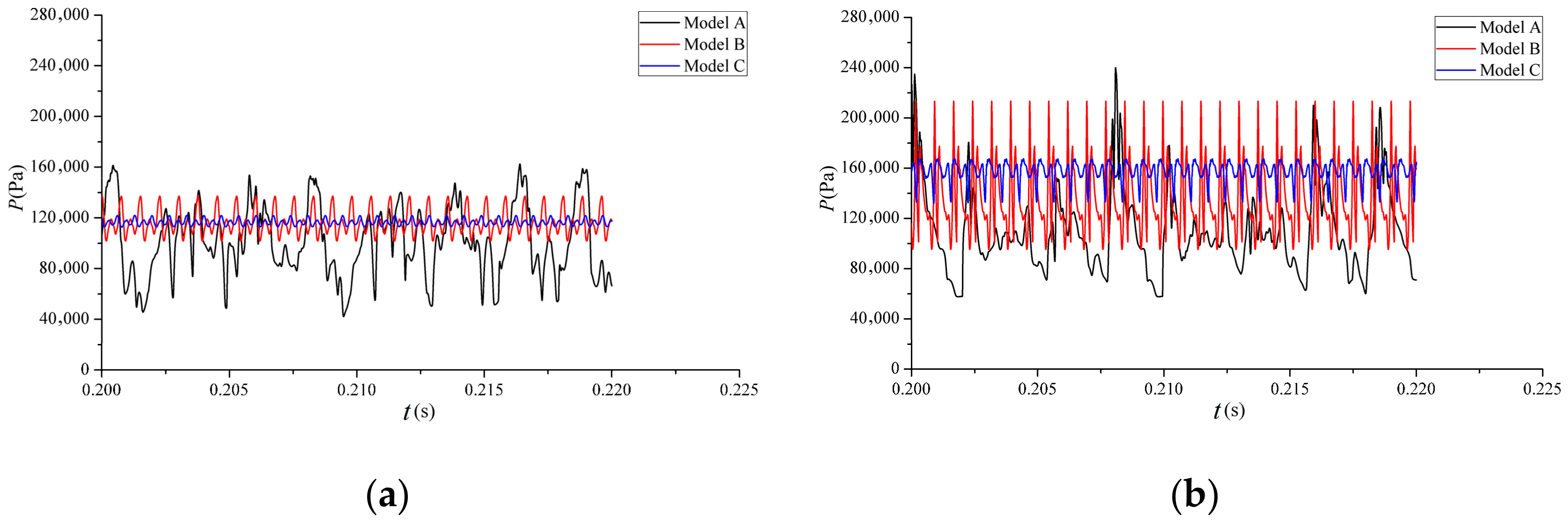
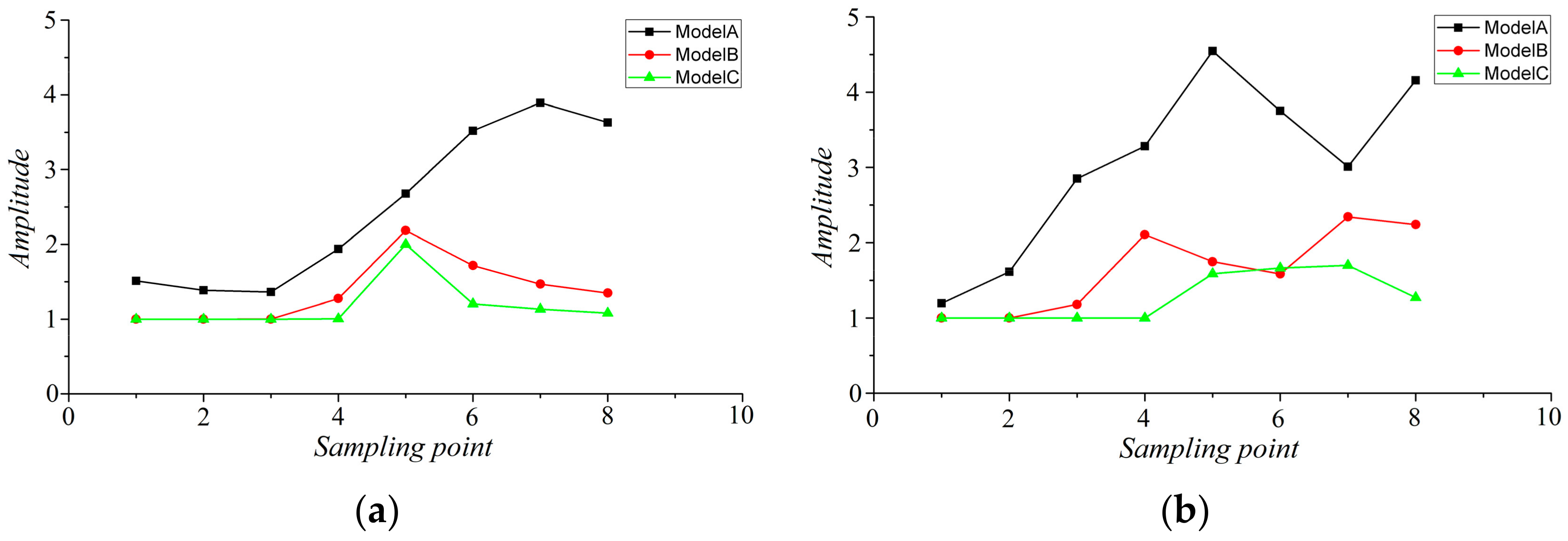
3.2.1. Calculation and Analysis of Flow Field Parameter Oscillation
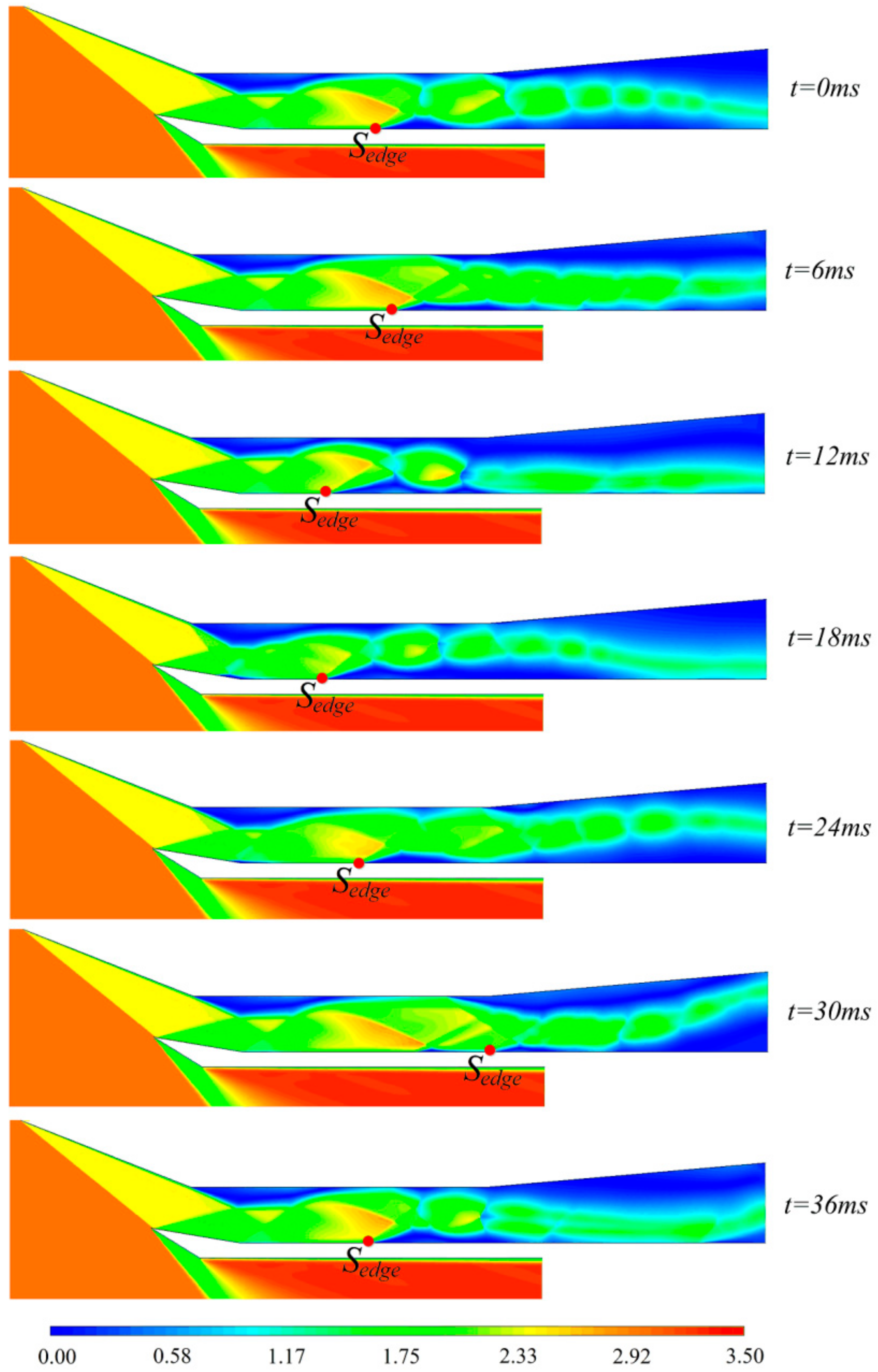
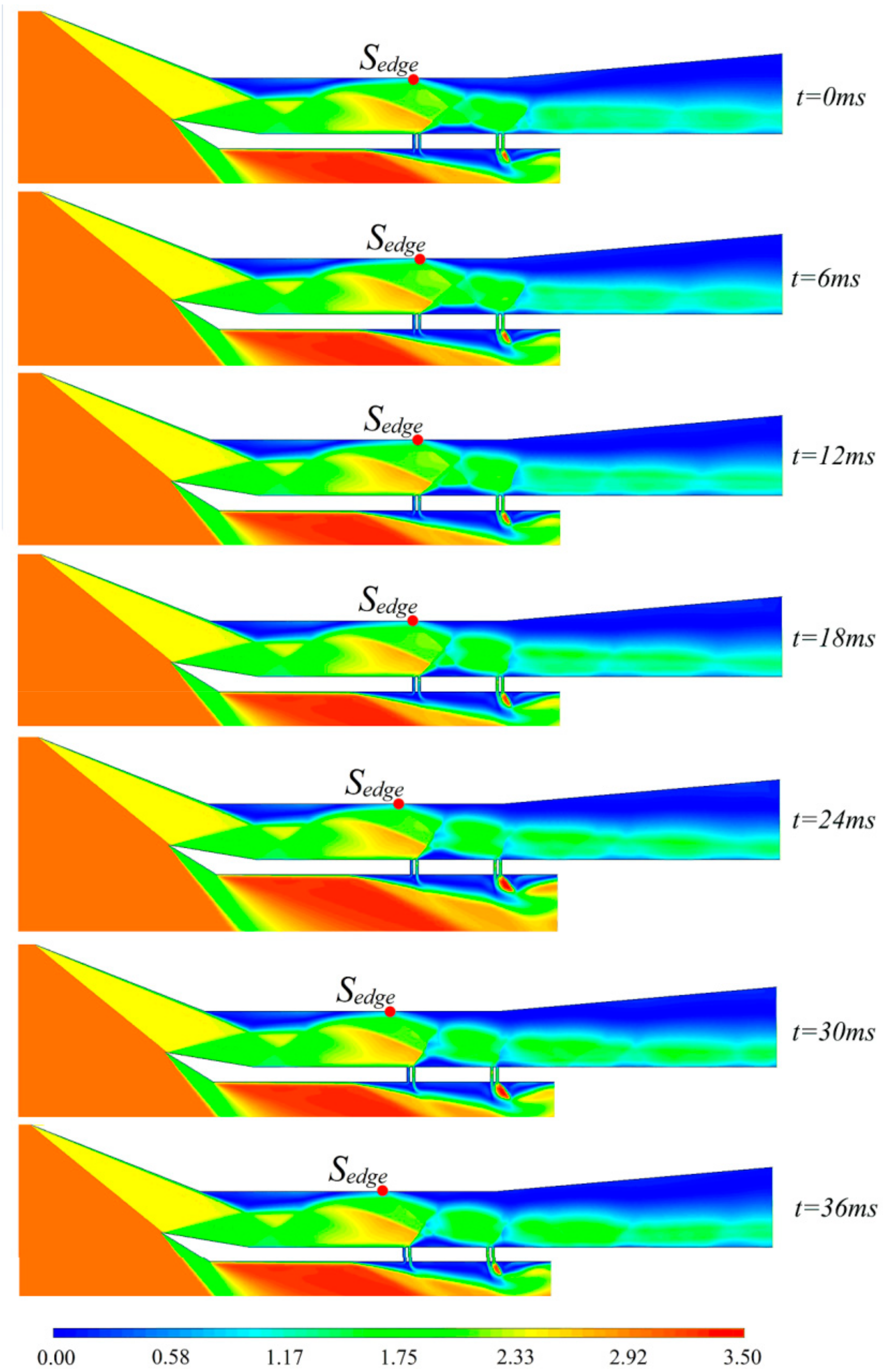
3.2.2. Analysis of Flow Field Characteristics and Flow Mechanism
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Matsuo, K.; Miyazato, Y.; Kim, H.D. Shock train and pseudo-shock phenomena in internal gas flows. Prog. Aerosp. Sci. 1999, 3, 33–100. [Google Scholar] [CrossRef]
- Shapiro, A. The Dynamics and Thermodynamics of Compressible Fluid Flow; Wiley: Hoboken, NJ, USA, 1953; Volume 1. [Google Scholar]
- Yu, J.; Li, J.; Wang, Q.; Zhang, X.; Zhang, S. Numerical and Experimental Study on the Duration of Nozzle Starting of the Reflected High-Enthalpy Shock Tunnel. Appl. Sci. 2022, 12, 2845. [Google Scholar] [CrossRef]
- Hadjadj, A.; Dussauge, J.P. Shock Wave Boundary Layer Interaction. Shock Waves 2009, 19, 449–452. [Google Scholar] [CrossRef]
- Humble, R.A.; Scarano, F.; Van Oudheusden, B.W. Unsteady aspects of an incident shock wave/turbulent boundary layer interaction. J. Fluid Mech. 2009, 635, 47–74. [Google Scholar] [CrossRef] [Green Version]
- Wang, B. The Investigation into the Shock Wave/Boundary-Layer Interaction Flow Field Organization; National University of Defense Technology: Changsha, China, 2015. [Google Scholar]
- Orton, G.F.; Scuderi, L.F.; Sanger, P.W.; Artus, J.; Laruelle, G.; Shkadov, L.H. Airbreathing hypersonic aircraft and transatmospheric vehicles. Prog. Astronaut. Aeronaut. 1997, 172, 297–372. [Google Scholar]
- Kejing, X.; Juntao, C.; Nan, L.; Wen, B.; Daren, Y. Recent research progress on motion characteristics and flow mechanism of shock train in an isolator with background wave. J. Exp. Fluid Mech. 2019, 33, 31–42. [Google Scholar]
- Meier, G.E.A.; Szumowski, A.P.; Selerowicz, W.C. Self-excited oscillations in internal transonic flows. Prog. Aerosp. Sci. 1990, 27, 145–200. [Google Scholar] [CrossRef]
- Bruce, P.J.; Babinsky, H. Unsteady shock wave dynamics. J. Fluid Mech. 2008, 603, 463–473. [Google Scholar] [CrossRef] [Green Version]
- Chakravarthy, R.V.K.; Nair, V.; Muruganandam, T.M.; Ghosh, S. Analytical and numerical study of normal shock response in a uniform duct. Phys. Fluids 2018, 30, 086–101. [Google Scholar] [CrossRef]
- Takefumi, I.; Kazuyasu, M. Oscillation phenomena of pseudo-shock waves. Bull. JSME 1974, 17, 1278–1285. [Google Scholar]
- Holger, B.; Harvey, J.K. Shock Wave Boundary-Layer Interactions; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Li, N.; Chang, J.; Yu, D.; Bao, W.; Song, Y. Mathematical model of shock-train path with complex background waves. J. Propuls. Power 2016, 33, 468–478. [Google Scholar] [CrossRef]
- Hankey, W.L.; Shang, J.S. Analysis of Self-Excited Oscillations in Fluid Flow; AIAA: Reston, VA, USA, 1980; p. 1346. [Google Scholar]
- Piponniau, S.; Dussauge, J.P.; Debieve, J.F.; Dupont, P. A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 2009, 629, 87–108. [Google Scholar] [CrossRef]
- Wagner, J.L.; Yuceil, K.B.; Valdivia, A.; Clemens, N.T.; Dolling, D.S. Experimental investigation of unstart in an inlet/isolator model in Mach 5 flow. AIAA J. 2009, 47, 1528–1542. [Google Scholar] [CrossRef]
- Tan, H.J.; Sun, S.; Huang, H.X. Behavior of shock trains in a hypersonic inlet/isolator model with complex background waves. Exp. Fluids 2012, 53, 1647–1661. [Google Scholar] [CrossRef]
- Tian, X.A.; Wang, C.P.; Cheng, K.M. Experimental investigation of dynamic characteristics of oblique shock train in Mach 5 flow. J. Propuls. Technol. 2014, 35, 1030–1039. [Google Scholar]
- Lu, L.; Wang, Y.; Fan, X.Q.; Yan, G.W.; Meng, Z.W. Investigation of Shock-Train Forward Movement in Mixer of RBCC. J. Propuls. Technol. 2019, 40, 69–75. [Google Scholar]
- Lv, H.; Wang, Z.; Chen, J.; Xu, L. The Influence of Boundary Layer Caused by Riblets on the Aircraft Surface. Appl. Sci. 2020, 10, 3686. [Google Scholar] [CrossRef]
- Kim, J.; Park, Y.M.; Lee, J.; Kim, T.; Kim, M.; Lim, J.; Jee, S. Numerical Investigation of Jet Angle Effect on Airfoil Stall Control. Appl. Sci. 2019, 9, 2960. [Google Scholar] [CrossRef] [Green Version]
- Weiss, A.; Olivier, H. Behaviour of a Shock Train under the Influence of Boundary-Layer Suction by a Normal Slot. Exp. Fluids 2012, 52, 273–287. [Google Scholar] [CrossRef]
- Harloff, G.J.; Smith, G.E. On Supersonic Inlet Boundary Layer Bleed Flow; AIAA: Reston, VA, USA, 1995; p. 0038. [Google Scholar]
- Soltani, M.R.; Daliri, A.; Younsi, J.S.; Farahani, M. Effects of bleed position on the stability of a supersonic inlet. J. Propuls. Power 2016, 32, 1153–1166. [Google Scholar] [CrossRef]
- Chang, J.T.; Bao, W.; Cui, T.; Yu, D.R. Effect of suctions on maximum backpressure ratios of hypersonic inlets. J. Aerosp. Power 2008, 23, 505–509. [Google Scholar]
- Ma, L.C. Study on the Effect of Suction Structure and Parameters on the Boundary Layer Oscillation Suction; Harbin Institute of Technology: Harbin, China, 2019. [Google Scholar]
- Cravero, C.; Leutcha, P.J.; Marsano, D. Simulation and Modeling of Ported Shroud Effects on Radial Compressor Stage Stability Limits. Energies 2022, 15, 2571. [Google Scholar] [CrossRef]
- Herrmann, D.; Siebe, F.; Gulhan, A. Pressure fluctuations (buzzing) and inlet performance of an airbreathing missile. J. Propuls. Power 2013, 29, 839–848. [Google Scholar] [CrossRef]
- Huang, R.; Li, Z.F.; Nie, B.P.; Hong, Y.T.; Yang, J.M.; Wu, Y.C. Shock train oscillations in a two-dimensional inlet/isolator with suction. J. Propuls. Technol. 2020, 41, 767–777. [Google Scholar]
- Reinartz, B.U.; Herrmann, C.D.; Ballmann, J.; Koschel, W.W. Aerodynamic performance analysis of a hypersonic inlet isolator using computation and experiment. J. Propuls. Power 2003, 19, 868–875. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, C.; Zhang, K.; Zhao, Z.; Xie, Z. Research on Computational Method of Supersonic Inlet/Isolator Internal Flow. Appl. Sci. 2021, 11, 9272. [Google Scholar] [CrossRef]
- Pan, J.S.; Shan, P. Fundamentals of Aerodynamics; National Defense Industry Press: Beijing, China, 2011. [Google Scholar]
- Zhao, R.; Yan, C. Evaluation of engineering turbulence models for complex supersonic flows. J. Beijing Univ. Aeronaut. Astronaut. 2011, 37, 202–205+215. [Google Scholar]
- Wong, H.Y.W. Theoretical prediction of resonance in nozzle flows. J. Propuls. Power 2015, 21, 300–313. [Google Scholar] [CrossRef]
- Xu, K.J.; Chang, J.T.; Zhou, W.X.; Yu, D. Mechanism and prediction for occurrence of shock-train sharp forward movement. AIAA J. 2016, 54, 1403–1412. [Google Scholar] [CrossRef]






| Theoretical Value | Dynamic Shock Model Values | |||
|---|---|---|---|---|
| △P0 (%) | --- | −10 | 10 | 15 |
| △P2 (%) | --- | 10 | −10 | 0 |
| P0 (Pa) | 26,465 | 26,465 | 26,465 | 26,465 |
| P2 (Pa) | 188,357 | 188,564 | 188,564 | 188,564 |
| Ma2 | 0.513 | 0.513 | 0.513 | 0.513 |
| P2* (Pa) | 225,943 | 225,645 | 225,645 | 225,645 |
| Model | Overflow Devices |
|---|---|
| A | / |
| B | Gap_1 |
| C | Gap_1, Gap_2 |
| ξ (%) | 0 | 2 | 4 | 6 | 8 |
|---|---|---|---|---|---|
| (kg/s) | 0.1898 | 0.1606 | 0.1176 | 0.0691 | 0.0506 |
| (m) | 0.01226 | 0.01066 | 0.00795 | 0.00473 | 0.00344 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, F.; Huang, G.; Liu, X. Investigation of Shock Wave Oscillation Suppression by Overflow in the Supersonic Inlet. Energies 2022, 15, 3879. https://doi.org/10.3390/en15113879
Cai F, Huang G, Liu X. Investigation of Shock Wave Oscillation Suppression by Overflow in the Supersonic Inlet. Energies. 2022; 15(11):3879. https://doi.org/10.3390/en15113879
Chicago/Turabian StyleCai, Feichao, Guanhong Huang, and Xiaowei Liu. 2022. "Investigation of Shock Wave Oscillation Suppression by Overflow in the Supersonic Inlet" Energies 15, no. 11: 3879. https://doi.org/10.3390/en15113879
APA StyleCai, F., Huang, G., & Liu, X. (2022). Investigation of Shock Wave Oscillation Suppression by Overflow in the Supersonic Inlet. Energies, 15(11), 3879. https://doi.org/10.3390/en15113879






