A Self-Tuning LCC/SP System for Electric Vehicle Wireless Charging against Large Self- and Mutual Inductance Variations
Abstract
:1. Introduction
| Topology | SS [5,6] | PP [7,8] | LCC/S [10,13] | LCC/LCC [9,17,18] | LCC/P [11,12] | LCC/SP [15,16] | LCL/N [14] | |
|---|---|---|---|---|---|---|---|---|
| Items | ||||||||
| Number of compensation elements on secondary side | 1 | 1 | 1 | 3 | 1 | 2 | 0 | |
| Cost and size | Low | Low | Medium | High | Medium | Medium | Low | |
| Degree of design freedom | 0 | 0 | 1 | 2 | 1 | 2 | 0 | |
| Harmonic suppression capability | Weak | Weak | Weak | Strong | Strong | Strong | / | |
| Output characteristic | CVO/CCO | CCO | CVO | CCO | CCO | CCO | / | |
| Anti-offset performance | Weak | Weak | Medium | Strong | Medium | Medium | Medium | |
- (1)
- A normalized detuned LCC/SP circuit model is proposed, which provides a theoretical basis for the self-tuning LCC/SP WPT system;
- (2)
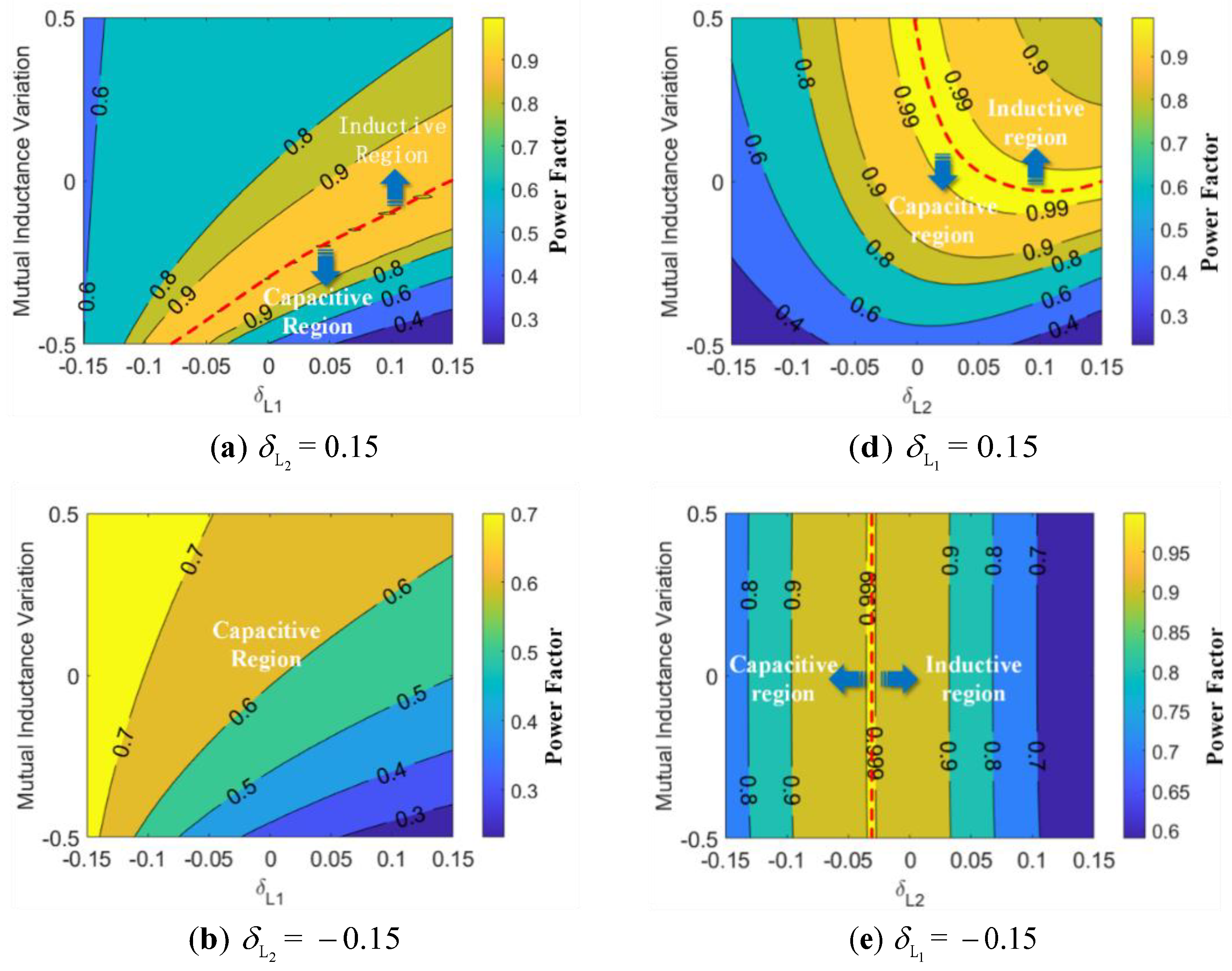
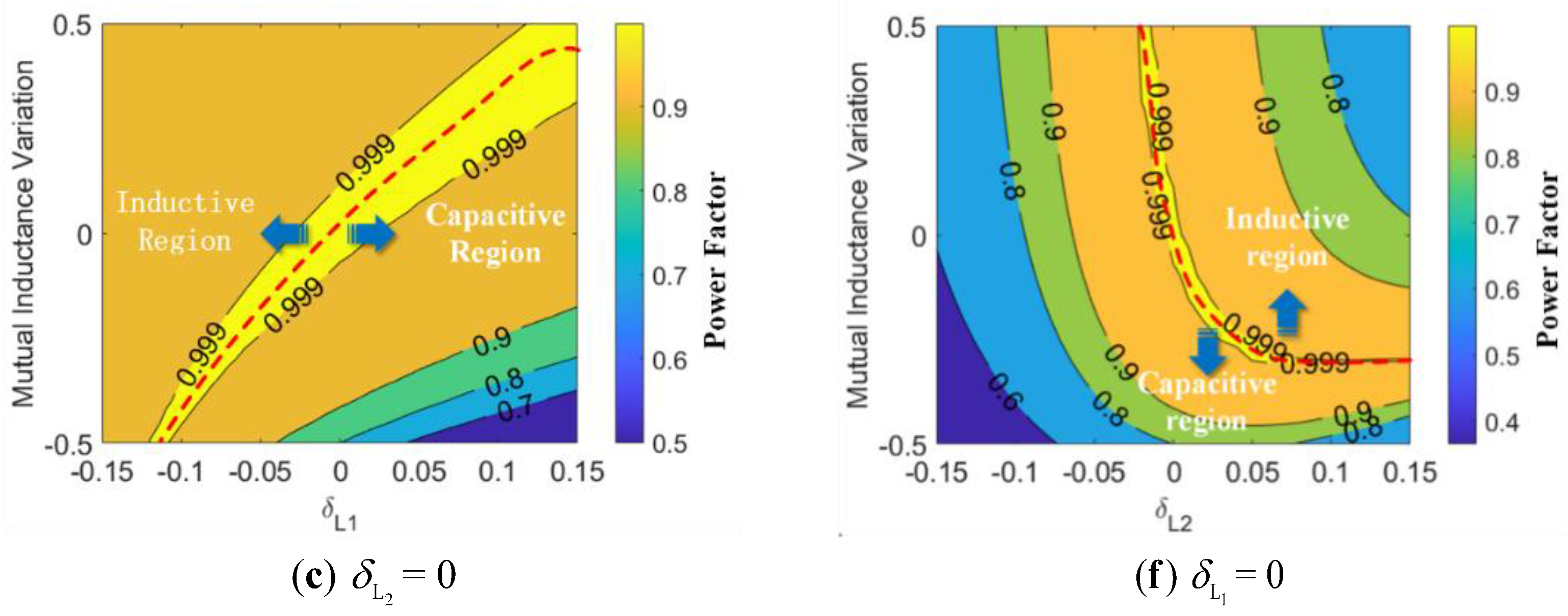
- The system can maintain a high power factor despite significant changes in self-inductance/mutual inductance, without additional parameter identification (the change in the value of mutual inductance was 47.7%, from 19.12 uH to 10 uH, and the change in self-inductance was 10%, from 54.10 uH to 48.5 uH). In addition, the loss of inverter can be effectively reduced when the system is consistently working at a high power factor (above 0.9). When it consistently works in a weak inductive range, ZVS can be achieved in the inverter, which reduces the voltage stress of the input DC bus.
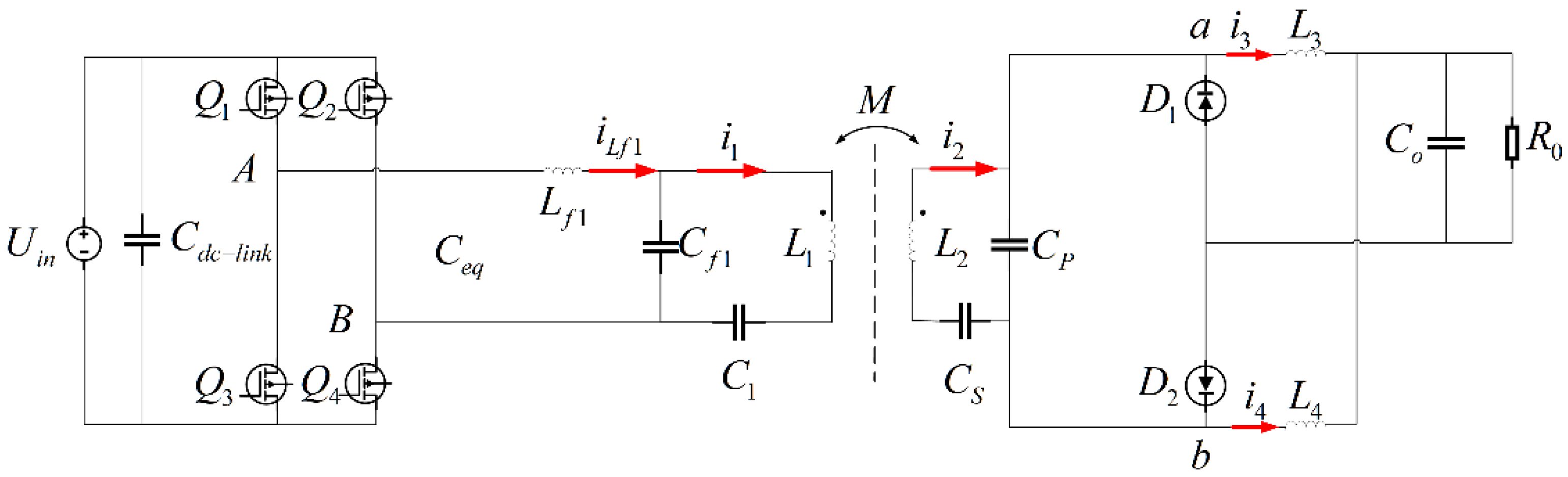
2. Characteristic Analysis of the LCC/SP Compensation Topology
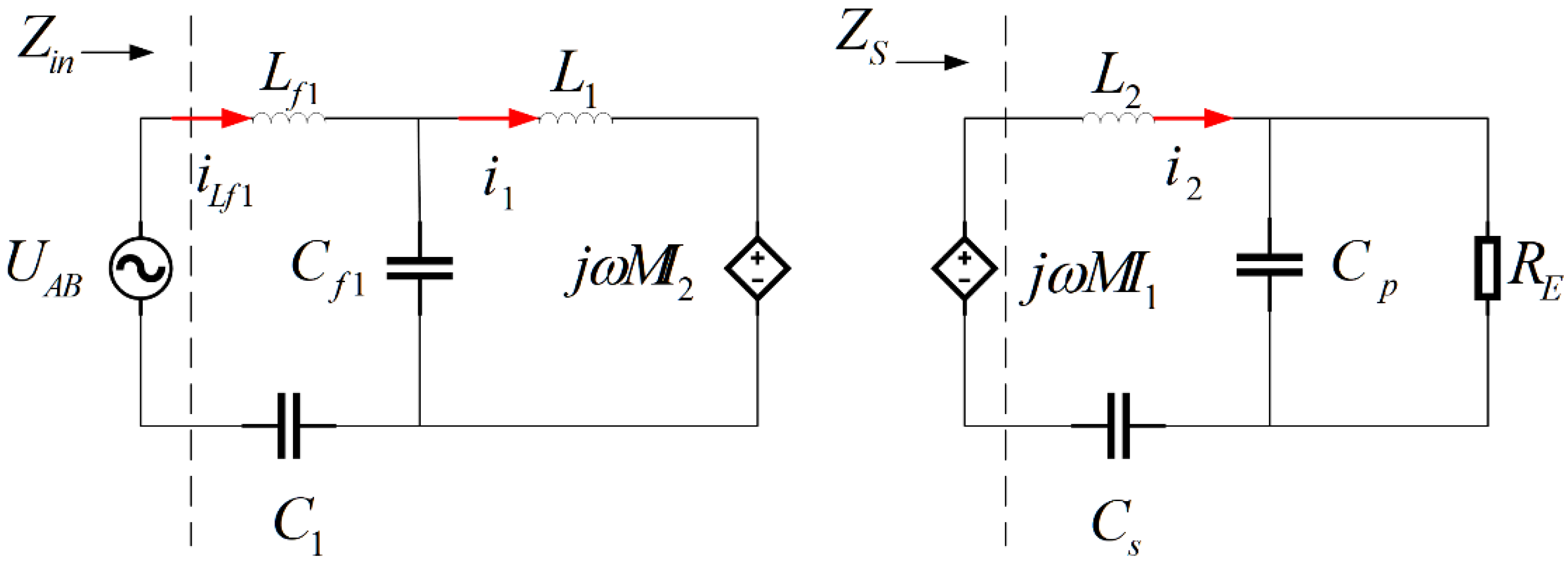
2.1. Basic Characteristics of the Well-Tuned LCC/SP Compensation Topology
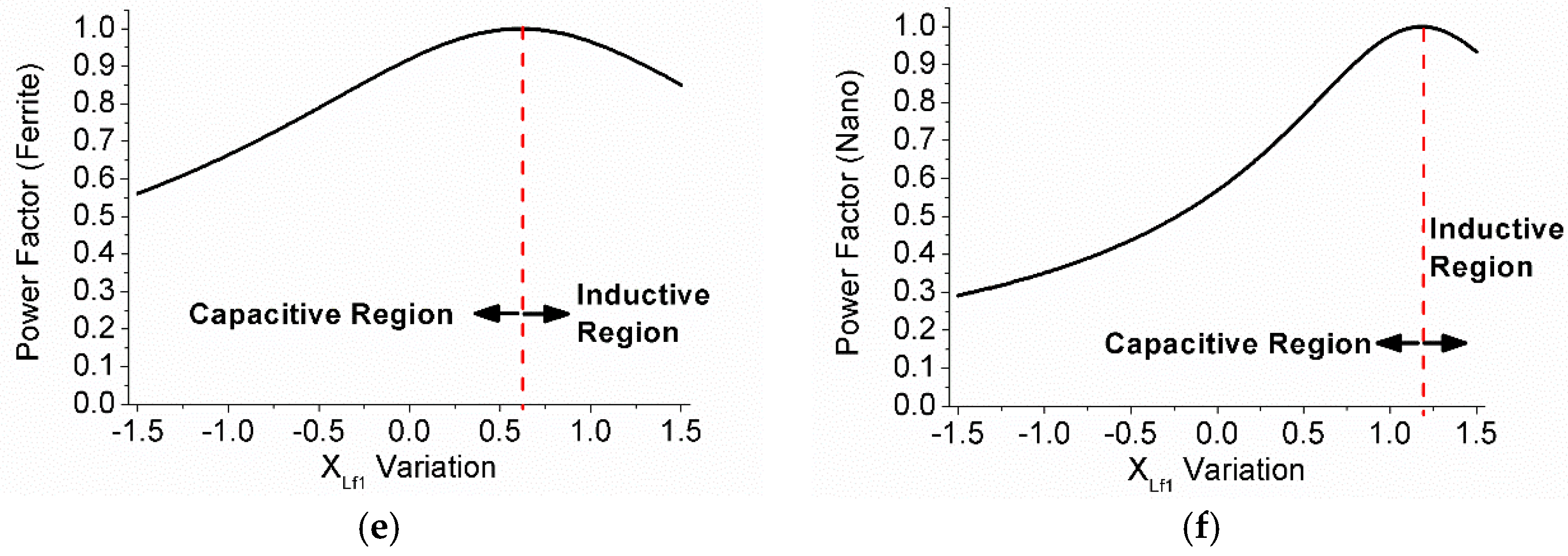
2.2. Basic Characteristics of the Mistuned LCC/SP Compensation Topology
3. Self-Tuning LCC/SP System Analysis and the Control Scheme
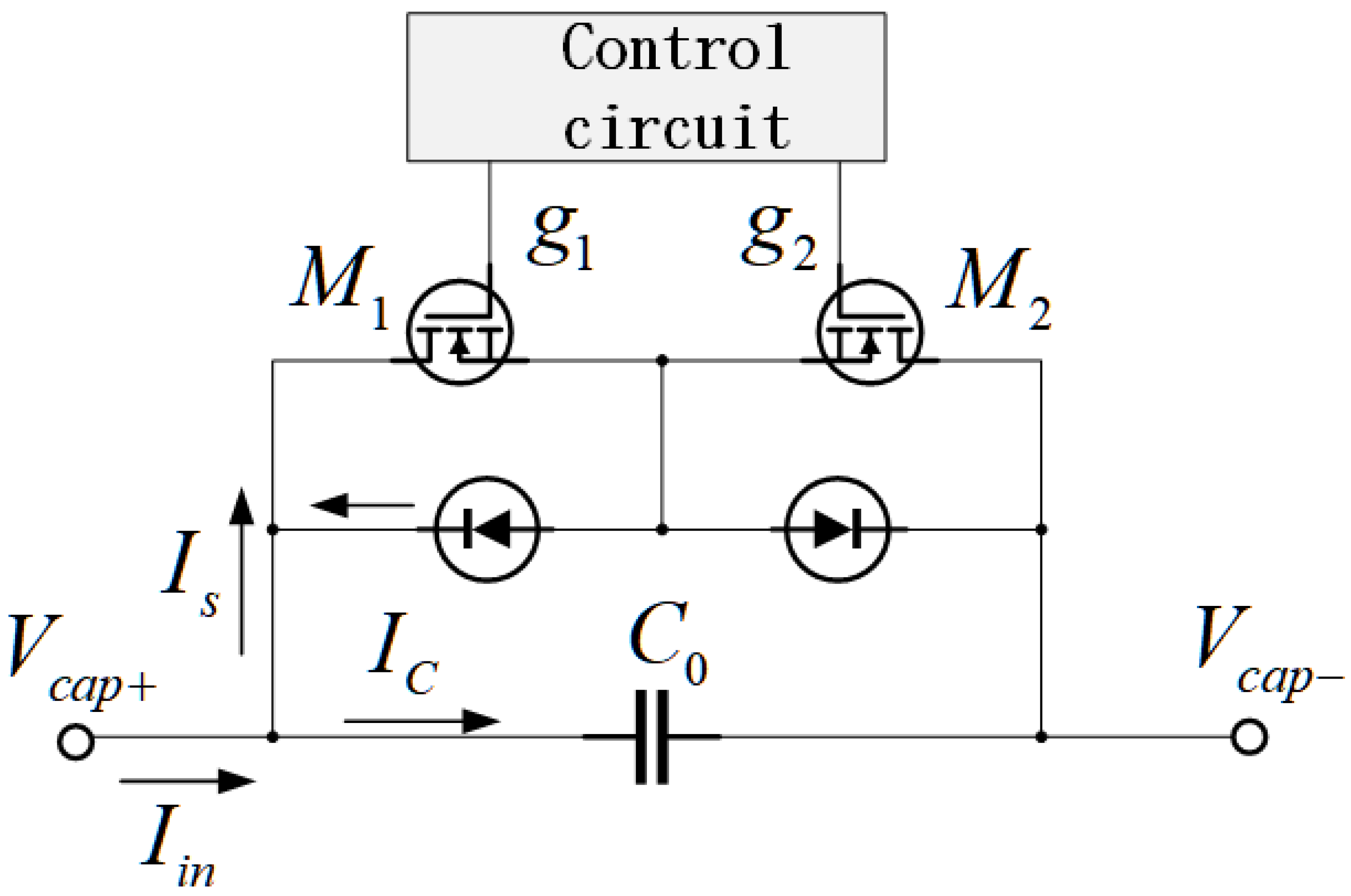
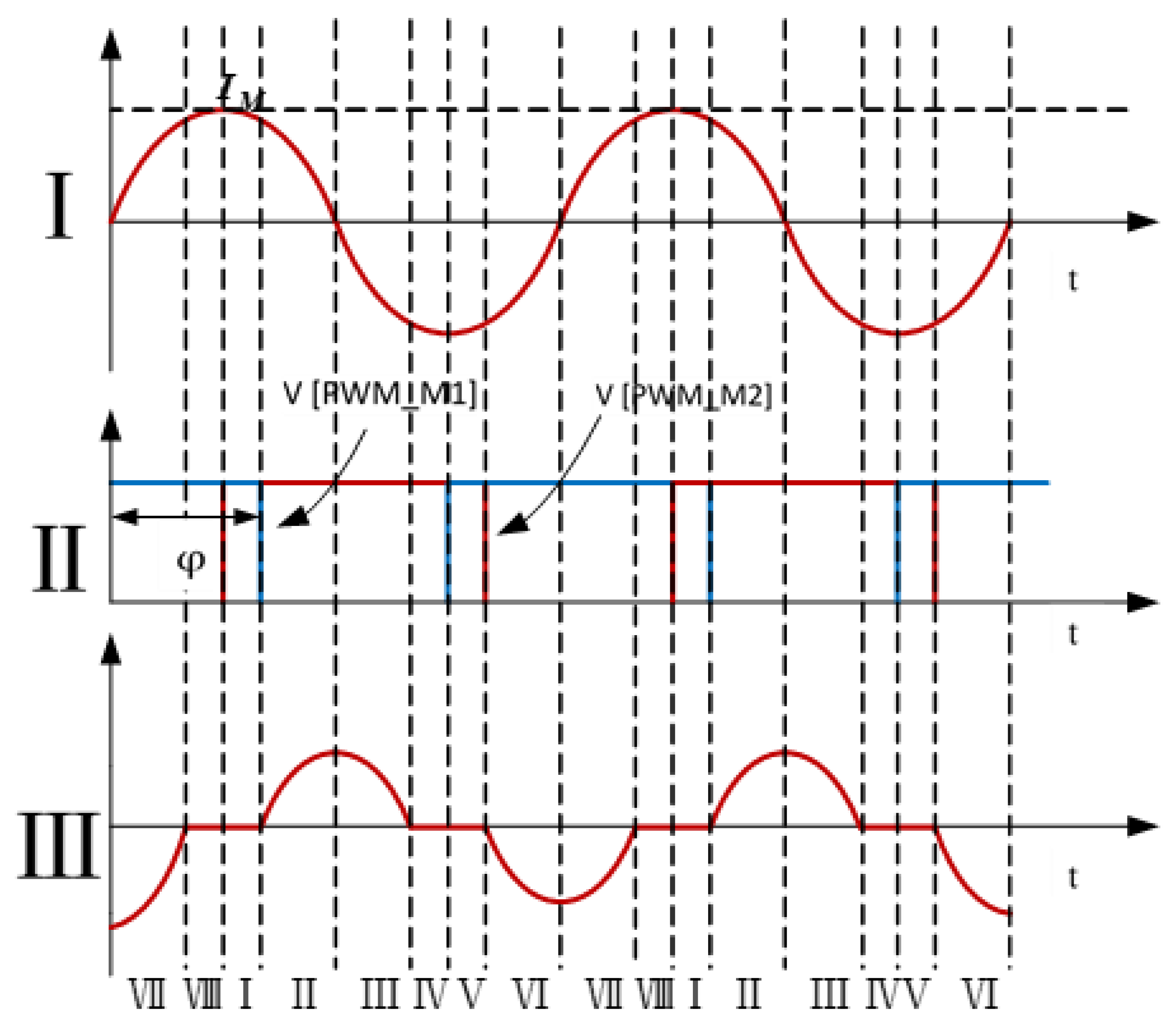
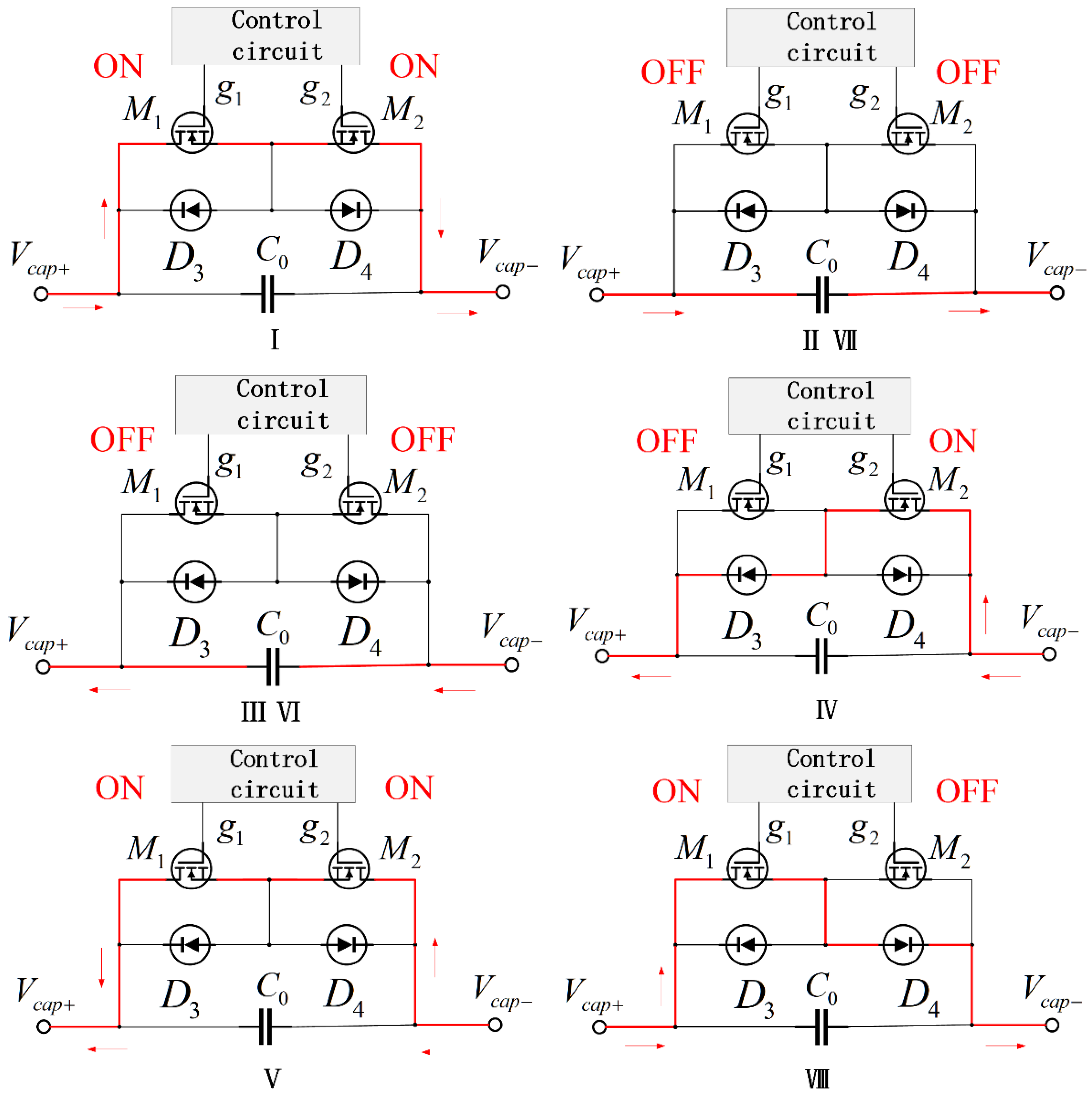
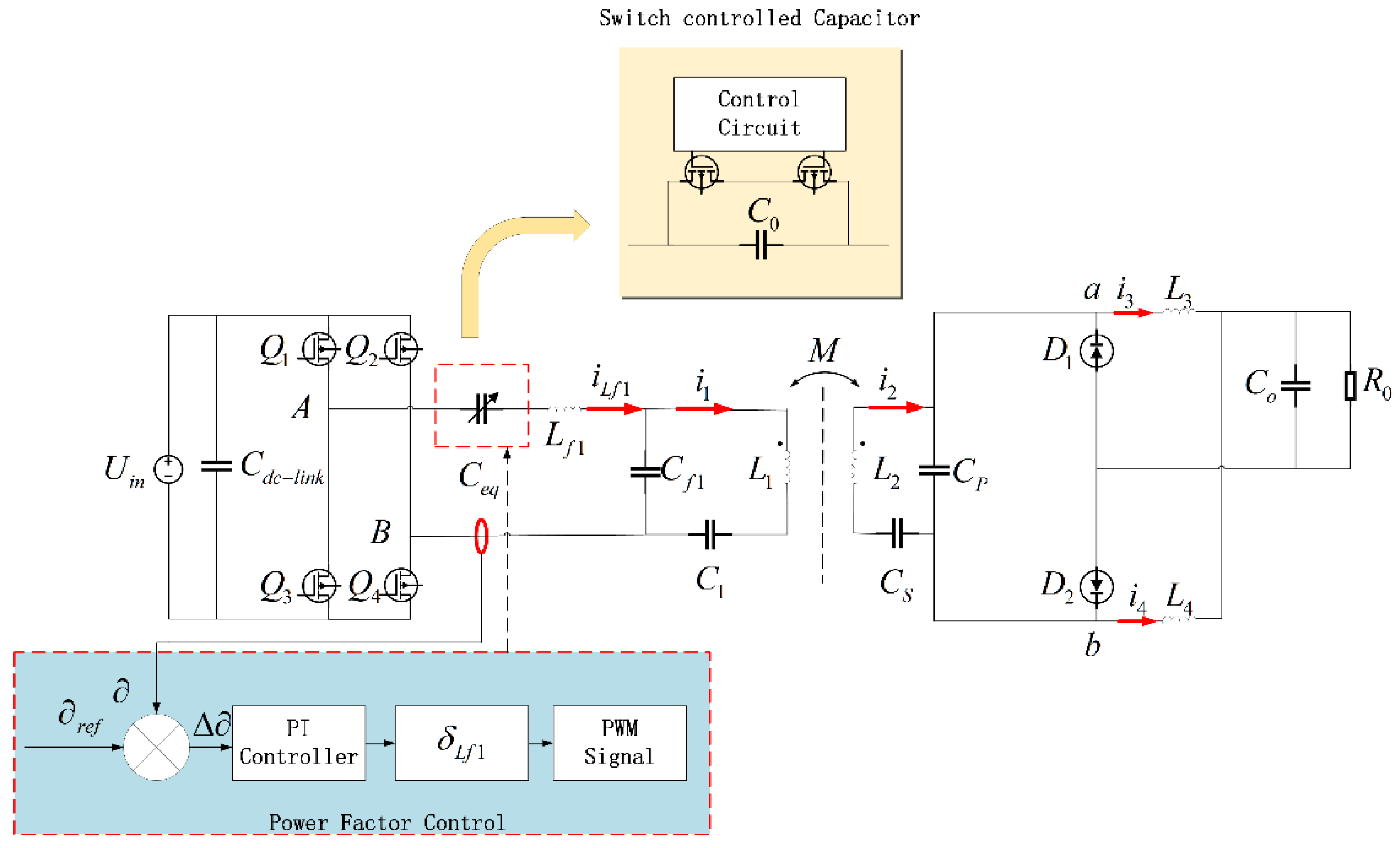
3.1. The Working Principle of the SCC
3.2. Comparison of Optimal Positions for SCCs
| Parameters | Value |
|---|---|
| Primary compensation inductance | 26.85 μH |
| Primary parallel compensation capacitor | 135.2 nF |
| Primary series compensation capacitor | 89.9 nF |
| Secondary side series compensation capacitor | 153.14 nF |
| Secondary side parallel compensation capacitor | 116.4 nF |
| Transmitting coil self-inductance | 78.33 μH |
| Receiving coil self-inductance | 53.21 μH |
| SCC initial value | 49 nF |
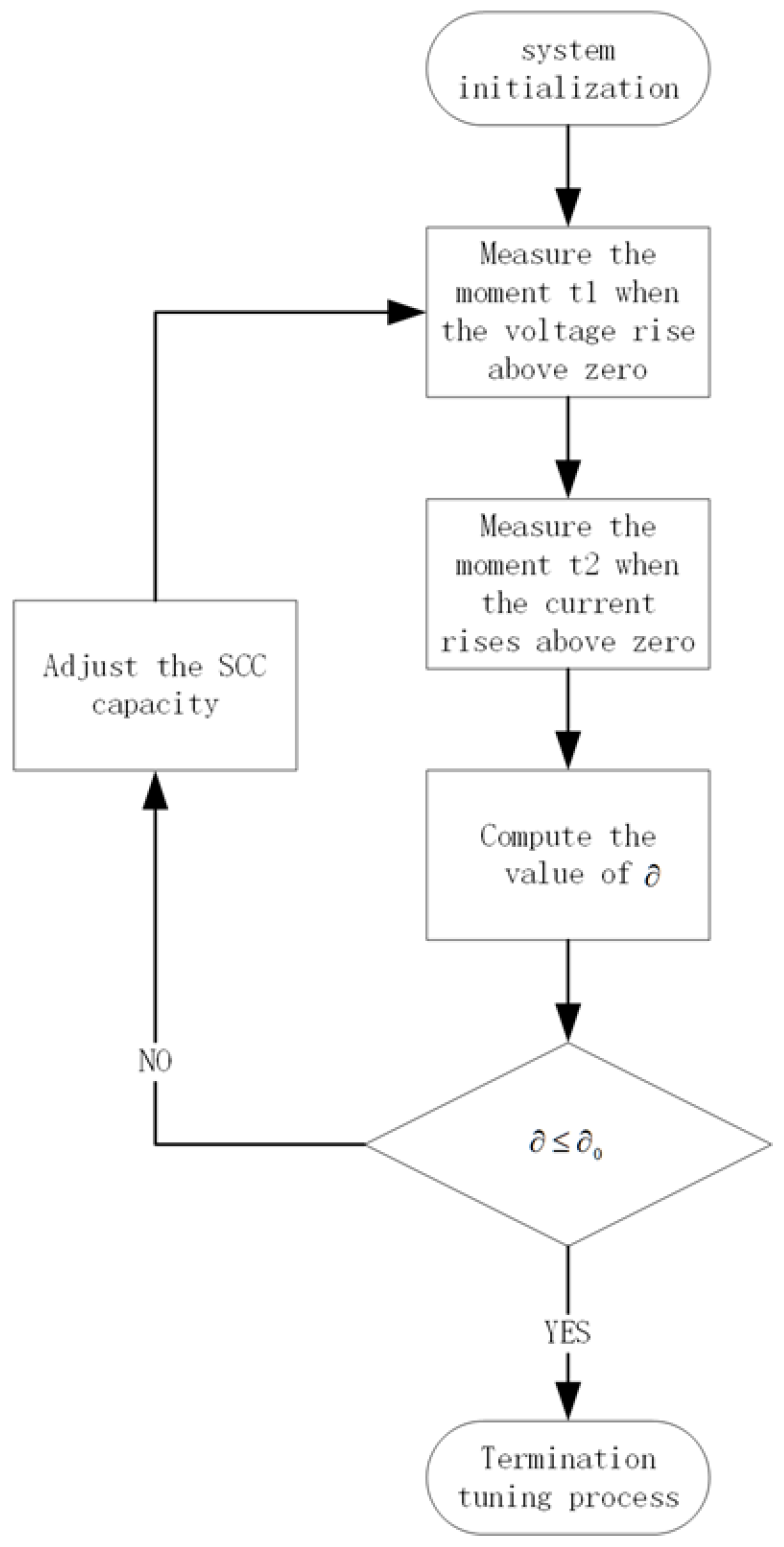
3.3. Self-Tuning LCC/SP System Control Method
4. Experimental Results and Discussion
4.1. Test Prototype Construction
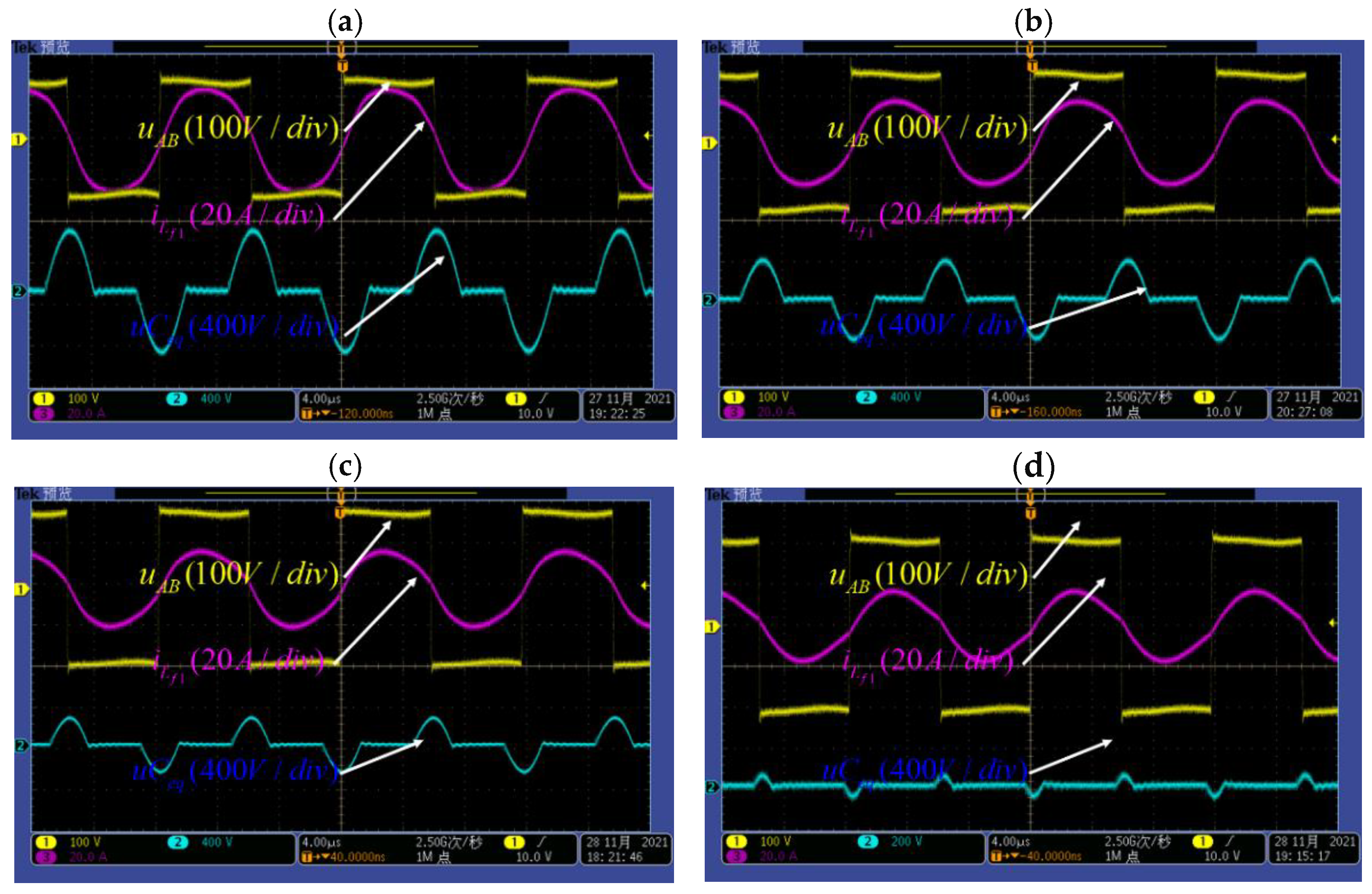
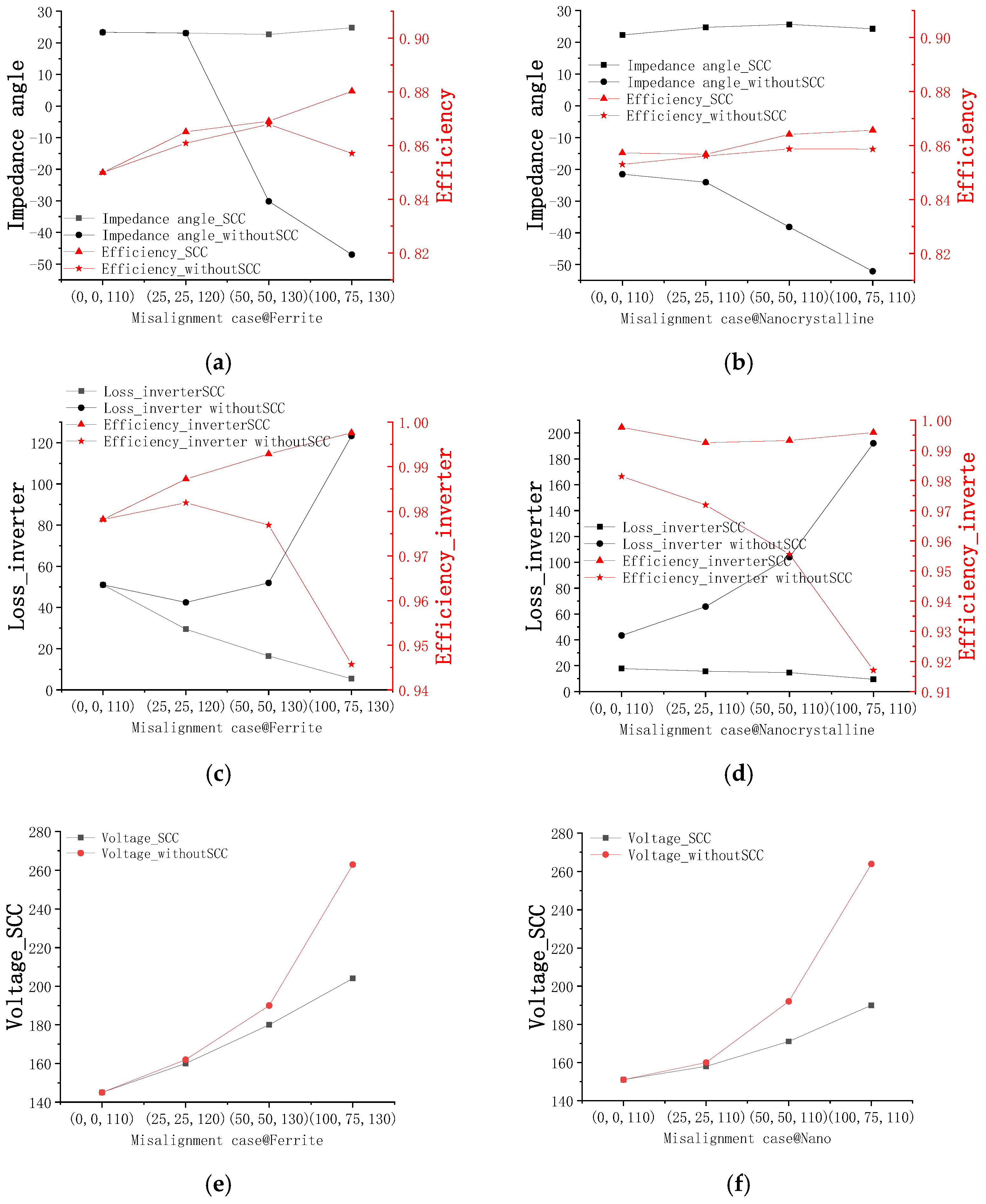
4.2. Performance Analysis of the System under Different Dislocation Conditions
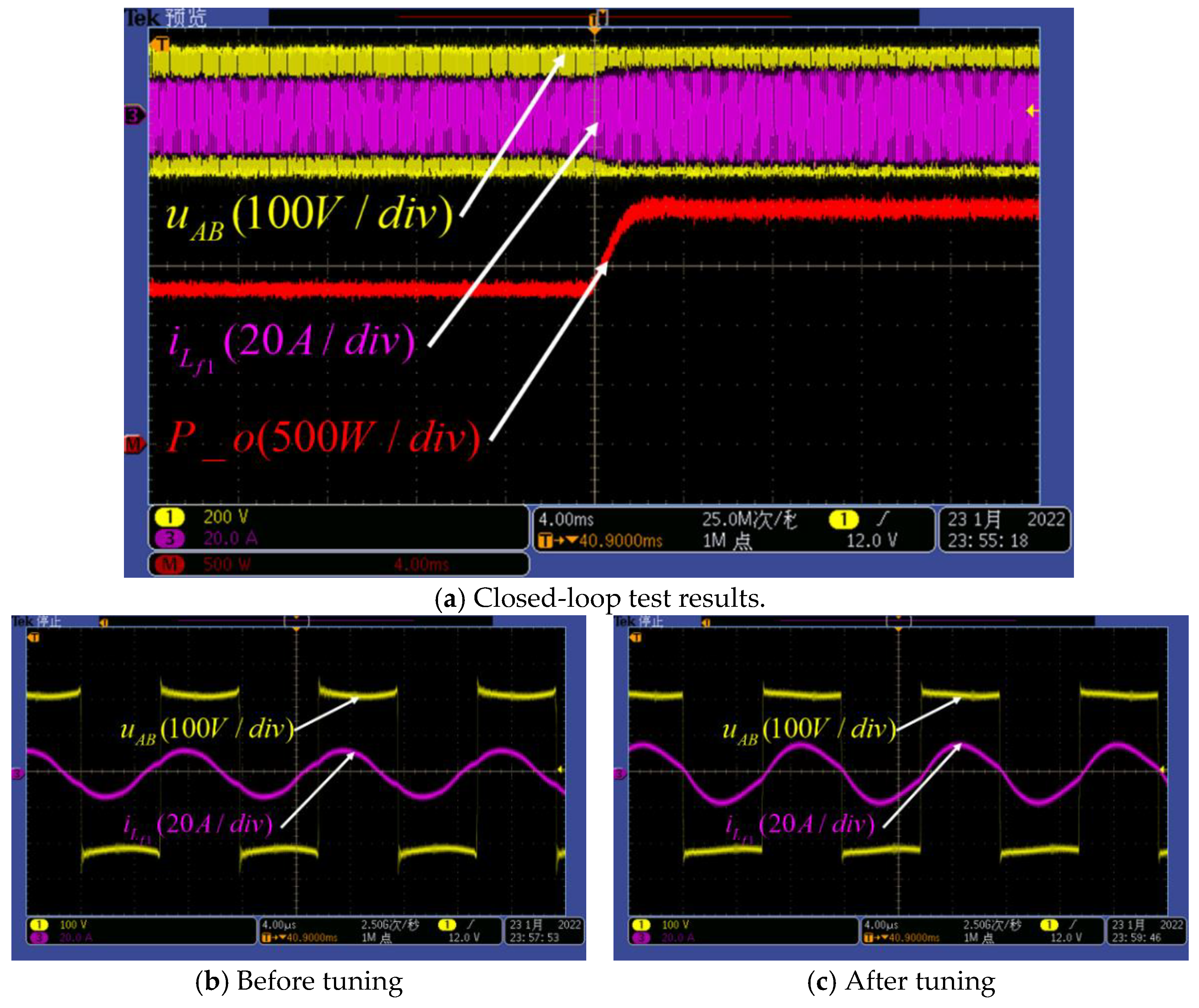
4.3. System Closed-Loop Performance Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclatures
| Symbol | Explanation |
| mutual inductance between the two coils | |
| the equivalent capacitance value of SCC | |
| thin film capacitors for SCC | |
| series compensation inductor of the primary side. | |
| series compensation capacitor of the primary side. | |
| parallel compensation capacitor of the secondary side. | |
| sine-wave output voltage of the secondary side before rectifier | |
| equivalent inductance of the primary side after partial compensation. | |
| operating frequency of the system | |
| the transmitter input impedance of a system operating at a resonant frequency | |
| the input impedance | |
| the real part of input impedance at the receiving end of the system | |
| active power coefficient | |
| power factor | |
| the actual value of after changing the resonance parameters of the system | |
| the difference between and | |
| the difference between and | |
| the ratio of the mutual inductance change to the initial value | |
| the equivalent impedance mode of the transmitting coil | |
| the ratio of the self-inductance of the secondary side to the primary coil | |
| the ratio of the secondary side’s equivalent series compensation inductance to the self-inductance of the same side coil | |
| the equivalent normalized receiver impedance | |
| the real part of the normalized input impedance (which takes into account the variation in coil parameters) | |
| equivalent normalized power factor (which takes into account the variation in coil parameters) | |
| nominal equivalent impedance of primary coil | |
| nominal impedance of primary side shunt compensation capacitor | |
| nominal impedance value of compensating inductance in series of primary side | |
| the relative change rates of | |
| the relative change rates of | |
| the difference between and | |
| normalized transmitter variable impedance operating at resonant frequency | |
| the imaginary part of the normalized transmitter variable impedance operating at resonant frequency | |
| phase difference between inverter voltage and current | |
| system input DC voltage. | |
| self-inductance of the primary coil. | |
| self-inductance of the secondary coil. | |
| parallel compensation capacitor of the primary side. | |
| series compensation capacitor of the secondary side. | |
| phasor of the input voltage | |
| simplified equivalent output resistance | |
| equivalent inductance of the secondary side after partial compensation | |
| the resonant operating frequency of the system | |
| input impedance of the system operating at resonant frequency | |
| transmitter input impedance | |
| the imaginary part of input impedance at the receiving end of the system | |
| reactive power coefficient | |
| the actual value of after changing the resonance parameters of the system | |
| the actual value of after changing the resonance parameters of the system | |
| the difference between and | |
| between the self-inductance change and the initial value | |
| the ratio of the operating frequency to the resonant frequency | |
| the ratio of the equivalent impedance mode of the transmitting coil to the equivalent load resistance | |
| the ratio of the primary series’ compensation inductance to the self-inductance of the same side coil | |
| the ratio of the self-inductance of the primary coil | |
| the equivalent normalized emitter impedance | |
| the imaginary part of the normalized input impedance (which takes into account the variation in coil parameters) | |
| Normalized transmitter adjustable impedance | |
| equivalent impedance of primary coil | |
| impedance of primary side shunt compensation capacitor | |
| impedance value of compensating inductance in series of primary side | |
| the relative change rates of | |
| after adjusting the actual value of the primary side series compensation inductance | |
| the relative change value of | |
| the real part of the normalized transmitter variable impedance operating at resonant frequency | |
| System cycle |
References
- Luo, Z.; Nie, S.; Pathmanathan, M.; Han, W.; Lehn, P.W. 3-D Analytical Model of Bipolar Coils with Multiple Finite Magnetic Shields for Wireless Electric Vehicle Charging Systems. IEEE Trans. Ind. Electron. 2022, 69, 8231–8242. [Google Scholar] [CrossRef]
- Lu, C.; Huang, X.; Liu, X.; Zeng, Y.; Liu, R.; Rong, C.; Liu, M. Design and Optimization of the Low-Frequency Metasurface Shield for Wireless Power Transfer System. IEEE Trans. Transp. Electrif. 2022, 8, 723–733. [Google Scholar] [CrossRef]
- Mi, C.C.; Buja, G.; Choi, S.Y.; Rim, C.T. Modern Advances in Wireless Power Transfer Systems for Roadway Powered Electric Vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6533–6545. [Google Scholar] [CrossRef]
- Shevchenko, V.; Husev, O.; Strzelecki, R.; Pakhaliuk, B.; Poliakov, N.; Strzelecka, N. Compensation Topologies in IPT Systems: Standards, Requirements, Classification, Analysis, Comparison and Application. IEEE Access 2019, 7, 120559–120580. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, W.; Xia, C.Y.; Liu, X. Maximum Efficiency Point Tracking Control Method for Series-Series Compensated Wireless Power Transfer System. IET Power Electron. 2018, 12, 2534–2542. [Google Scholar]
- Kamineni, A.; Covic, G.A.; Boys, J.T. Self-Tuning Power Supply for Inductive Charging. IEEE Trans. Power Electron. 2017, 32, 3467–3479. [Google Scholar] [CrossRef]
- Kamineni, A.; Neath, M.J.; Covic, G.A.; Boys, J.T. A Mistuning-Tolerant and Controllable Power Supply for Roadway Wireless Power Systems. IEEE Trans. Power Electron. 2017, 32, 6689–6699. [Google Scholar] [CrossRef]
- Joy, E.R.; Kushwaha, B.K.; Rituraj, G.; Kumar, P. Analysis and Comparison of Four Compensation Topologies of Contactless Power Transfer System. In Proceedings of the 4th International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 24–26 November 2015. [Google Scholar]
- Luo, Z.; Zhao, Y.; Xiong, M.; Wei, X.; Dai, H. A Self-Tuning LCC/LCC System Based on Switch-Controlled Capacitors for Constant-Power Wireless Electric Vehicle Charging. IEEE Trans. Ind. Electron. 2022. [Google Scholar] [CrossRef]
- Li, W.; Wei, G.; Cui, C.; Zhang, X.; Zhang, Q. A Double-Side Self-Tuning LCC/S System Using a Variable Switched Capacitor Based on Parameter Recognition. IEEE Trans. Ind. Electron. 2021, 68, 3069–3078. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, J.; Liang, Z.; Zhang, Z. Mutual-Inductance-Dynamic-Predicted Constant Current Control of LCC-P Compensation Network for Drone Wireless In-Flight Charging. IEEE Trans. Ind. Electron. 2022. [Google Scholar] [CrossRef]
- Mostafa, A.; Wang, Y.; Zhang, H.; Lu, F. A Z-Class LCC-P Compensated IPT System with a Reverse Coupled Compensation Inductor. In Proceedings of the 2021 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), San Diego, CA, USA, 1–4 June 2021; pp. 1–5. [Google Scholar]
- Chen, Y.; Zhang, H.; Shin, C.S.; Seo, K.H.; Kim, D.H. A Comparative Study of S-S and LCC-S Compensation Topology of Inductive Power Transfer Systems for EV Chargers. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019. [Google Scholar]
- Zhang, Y.; Yan, Z.; Liang, Z.; Li, S.; Mi, C.C. A High-Power Wireless Charging System Using LCL-N Topology to Achieve a Compact and Low-Cost Receiver. IEEE Trans. Power Electron. 2019, 35, 131–137. [Google Scholar] [CrossRef]
- Xiong, M.; Dai, H.; Li, Q.; Jiang, Z.; Luo, Z.; Wei, X. Design of the LCC-SP Topology With a Current Doubler for 11-kW Wireless Charging System of Electric Vehicles. IEEE Trans. Transp. Electrif. 2021, 7, 2128–2142. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, X.; Zhang, K.; Cui, X.; Yang, X. An LCC-SP Compensated Inductive Power Transfer System and Design Considerations for Enhancing Misalignment Tolerance. IEEE Access 2020, 8, 193285–193296. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, T.; Duan, S.; Feng, H.; Hu, H.; Niu, J.; Chen, C. A Control Strategy for Efficiency Optimization and Wide ZVS Operation Range in Bidirectional Inductive Power Transfer System. IEEE Trans. Ind. Electron. 2019, 66, 5958–5969. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Deng, J.; Nguyen, T.D.; Mi, C.C. A Double-Sided LCC Compensation Network and Its Tuning Method for Wireless Power Transfer. IEEE Trans. Veh. Technol. 2015, 64, 2261–2273. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.; Cui, C.; Wei, G. A Self-Tuning S/S Compensation WPT System Without Parameter Recognition. IEEE Trans. Ind. Electron. 2022, 69, 6741–6750. [Google Scholar] [CrossRef]
- Cota, K.A.; Gray, P.A.; Pathmanathan, M.; Lehn, P.W. An Approach for Selecting Compensation Capacitances in Resonance-Based EV Wireless Power Transfer Systems With Switched Capacitors. IEEE Trans. Transp. Electrif. 2019, 5, 1004–1014. [Google Scholar] [CrossRef]
- Hu, H.; Cai, T.; Duan, S.; Zhang, X.; Niu, J.; Feng, H. An Optimal Variable Frequency Phase Shift Control Strategy for ZVS Operation Within Wide Power Range in IPT Systems. IEEE Trans. Power Electron. 2020, 35, 5517–5530. [Google Scholar] [CrossRef]
- Luo, Z.; Wei, X.; Pearce, M.; Covic, G.A. Multi-objective Optimization of Inductive Power Transfer Double-D Pads for Electric Vehicles. IEEE Trans. Power Electron. 2020, 36, 5135–5146. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| 128 mΩ | |
| The number of turns of the transmitting coil | 8 |
| Transmitting size | 800 mm × 525 mm |
| 410 mΩ | |
| 19.6125 μH | |
| Receiving coil turns | 7 |
| Magnetic coupling gap | 110 mm |
| Receiving coil size | 340 mm × 260 mm |
| 13.3 Ω |
| Secondary Pad Position | L1 (μH) | L2 (μH) | M (μH) |
|---|---|---|---|
| (0, 0, 100) | 77.8 | 55 | 21 |
| (25, 25, 110) | 77.5 | 54.5 | 18.1 |
| (50, 50, 120) | 76.2 | 52.8 | 14.4 |
| (100, 75, 130) | 76.2 | 53.3 | 10.8 |
| Secondary Pad Position | L1 (μH) | L2 (μH) | M (μH) |
|---|---|---|---|
| (0, 0, 100) | 78 | 49.3 | 16.7 |
| (25, 25, 100) | 77.8 | 49.2 | 15.9 |
| (50, 50, 110) | 76.3 | 48.7 | 12.6 |
| (100, 75, 110) | 76.1 | 48.5 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wei, X.; Luo, Z.; Xiong, M.; Dai, H. A Self-Tuning LCC/SP System for Electric Vehicle Wireless Charging against Large Self- and Mutual Inductance Variations. Energies 2022, 15, 3980. https://doi.org/10.3390/en15113980
Zhao Y, Wei X, Luo Z, Xiong M, Dai H. A Self-Tuning LCC/SP System for Electric Vehicle Wireless Charging against Large Self- and Mutual Inductance Variations. Energies. 2022; 15(11):3980. https://doi.org/10.3390/en15113980
Chicago/Turabian StyleZhao, Yiyan, Xuezhe Wei, Zhichao Luo, Meng Xiong, and Haifeng Dai. 2022. "A Self-Tuning LCC/SP System for Electric Vehicle Wireless Charging against Large Self- and Mutual Inductance Variations" Energies 15, no. 11: 3980. https://doi.org/10.3390/en15113980
APA StyleZhao, Y., Wei, X., Luo, Z., Xiong, M., & Dai, H. (2022). A Self-Tuning LCC/SP System for Electric Vehicle Wireless Charging against Large Self- and Mutual Inductance Variations. Energies, 15(11), 3980. https://doi.org/10.3390/en15113980








