Impact of Separator Thickness on Temperature Distribution in Single Cell of Polymer Electrolyte Fuel Cell Operated at Higher Temperature of 90 °C and 100 °C
Abstract
1. Introduction
2. Heat-Transfer-Analysis Procedure of Single Cell of PEFC
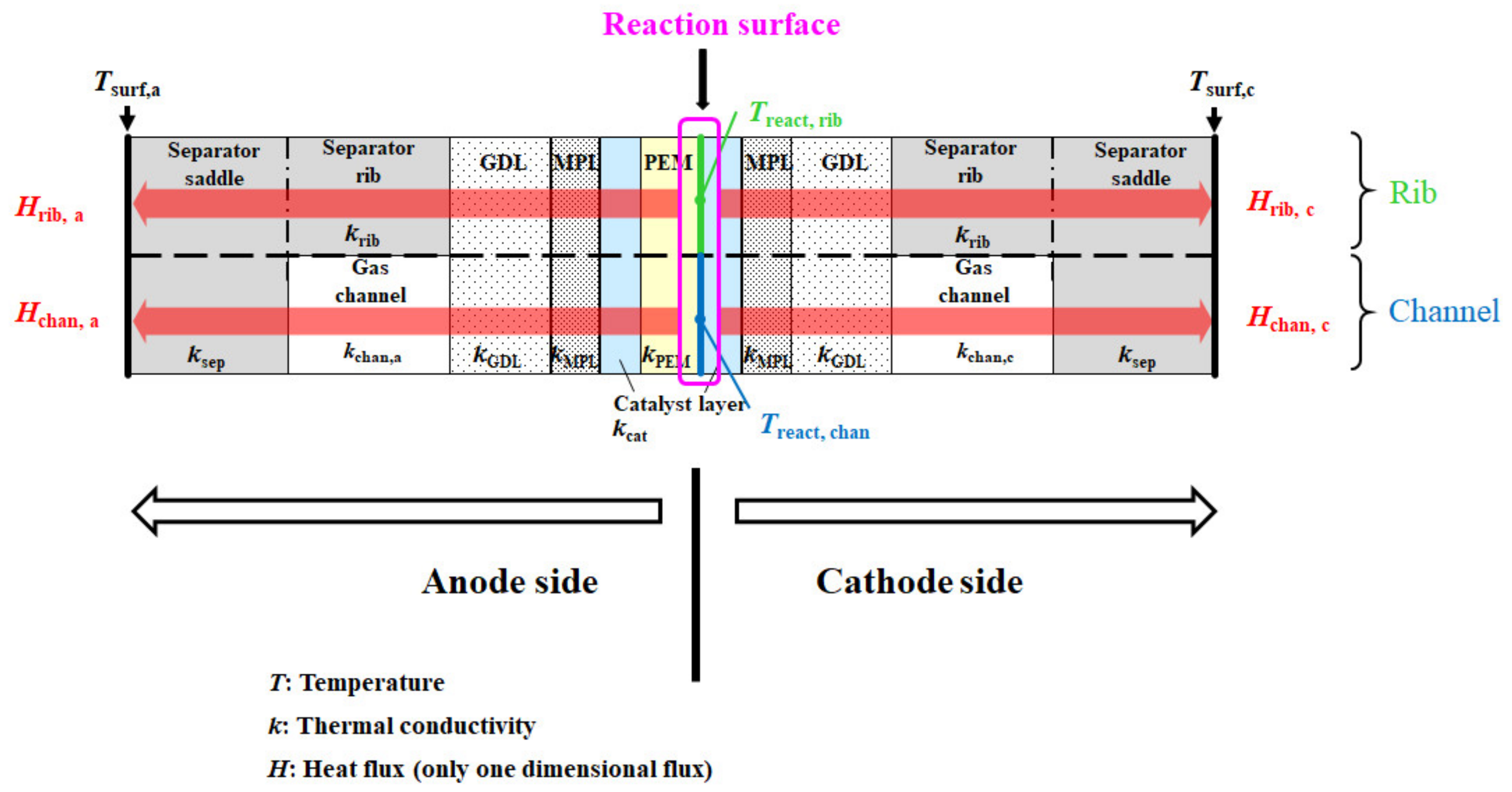
2.1. 1D Multi-Plate Heat-Transfer Model Developed by This Study
2.2. Heat-Generation Rate by Electrochemical Reaction in the Model Proposed by This Study
2.3. Heat-Balance Formulas to Calculate the Reaction Surface Temperature
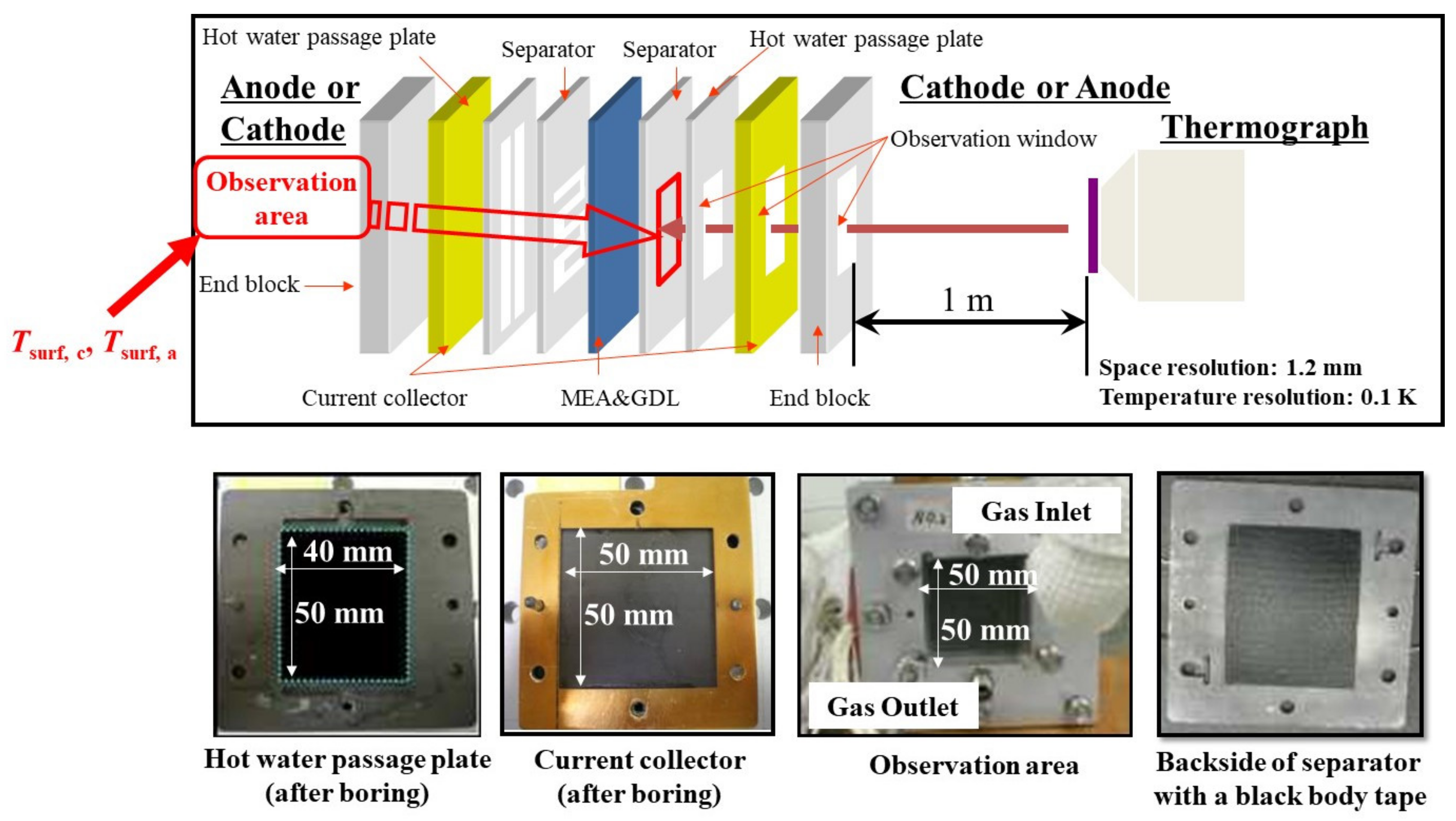
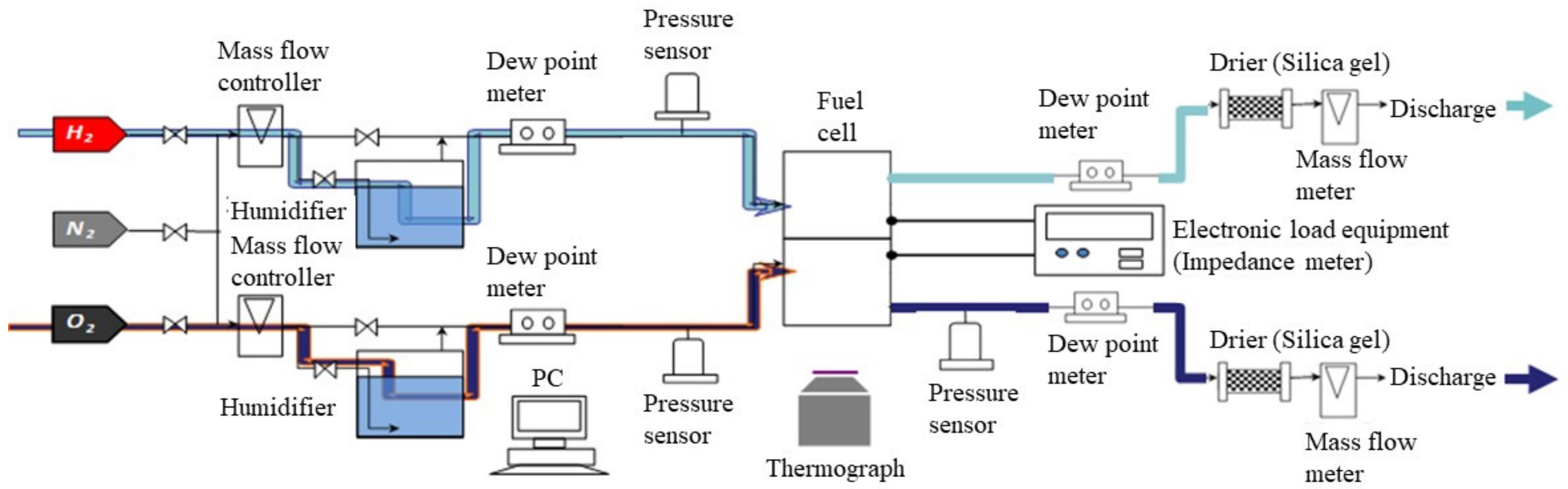
2.4. Validation
3. Results and Discussion
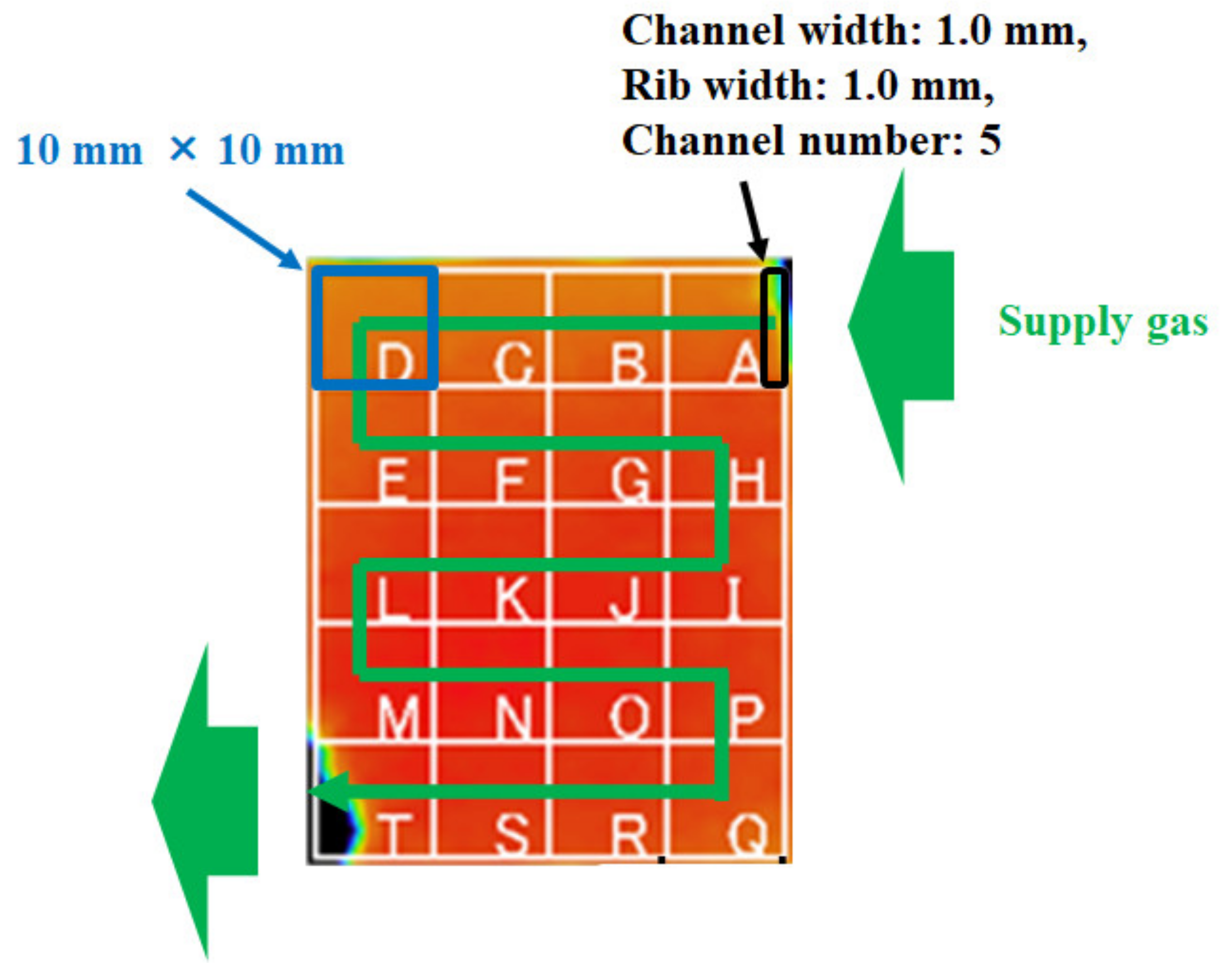
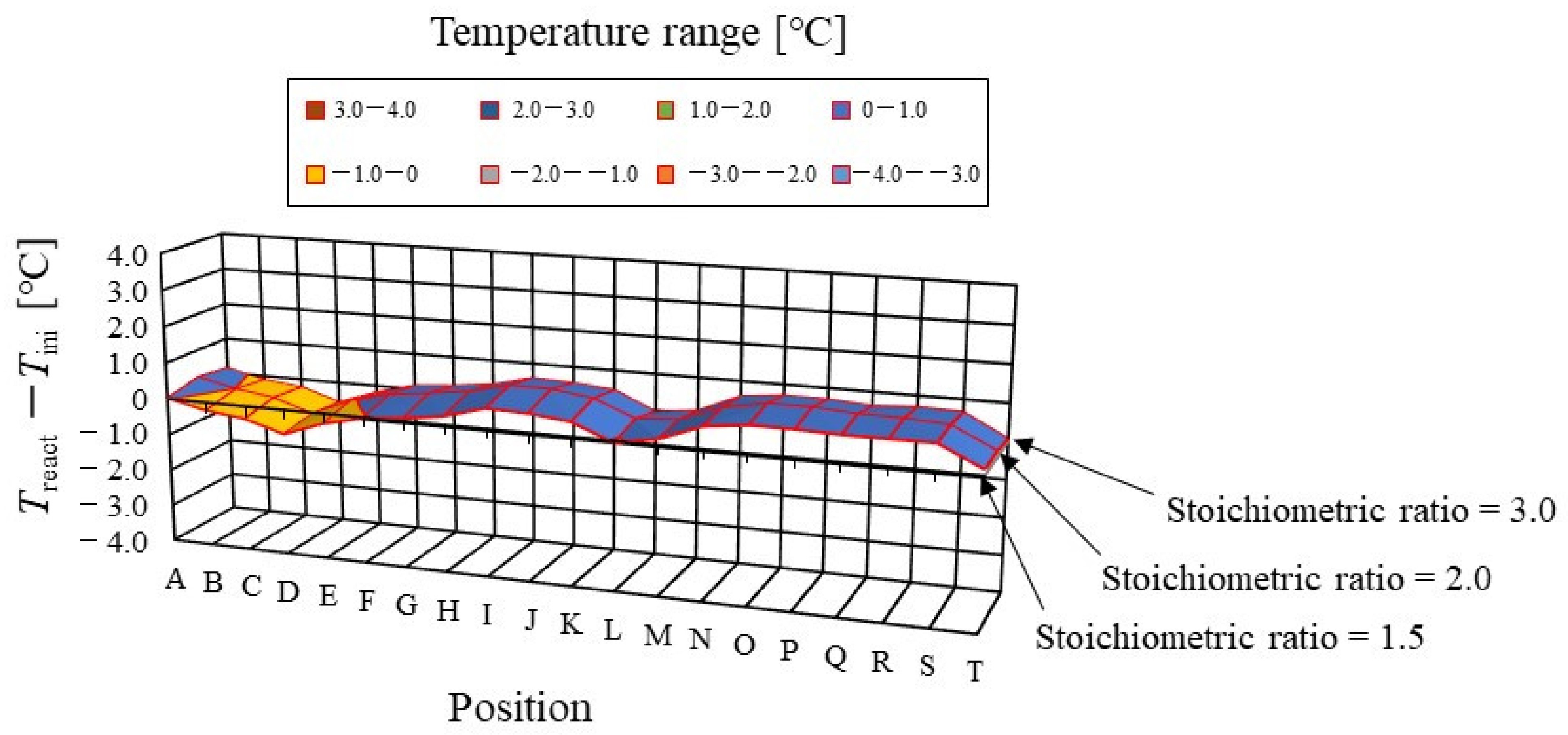
3.1. Effect of Flow Rate of Supply Gas on Distribution of Treact − Tini
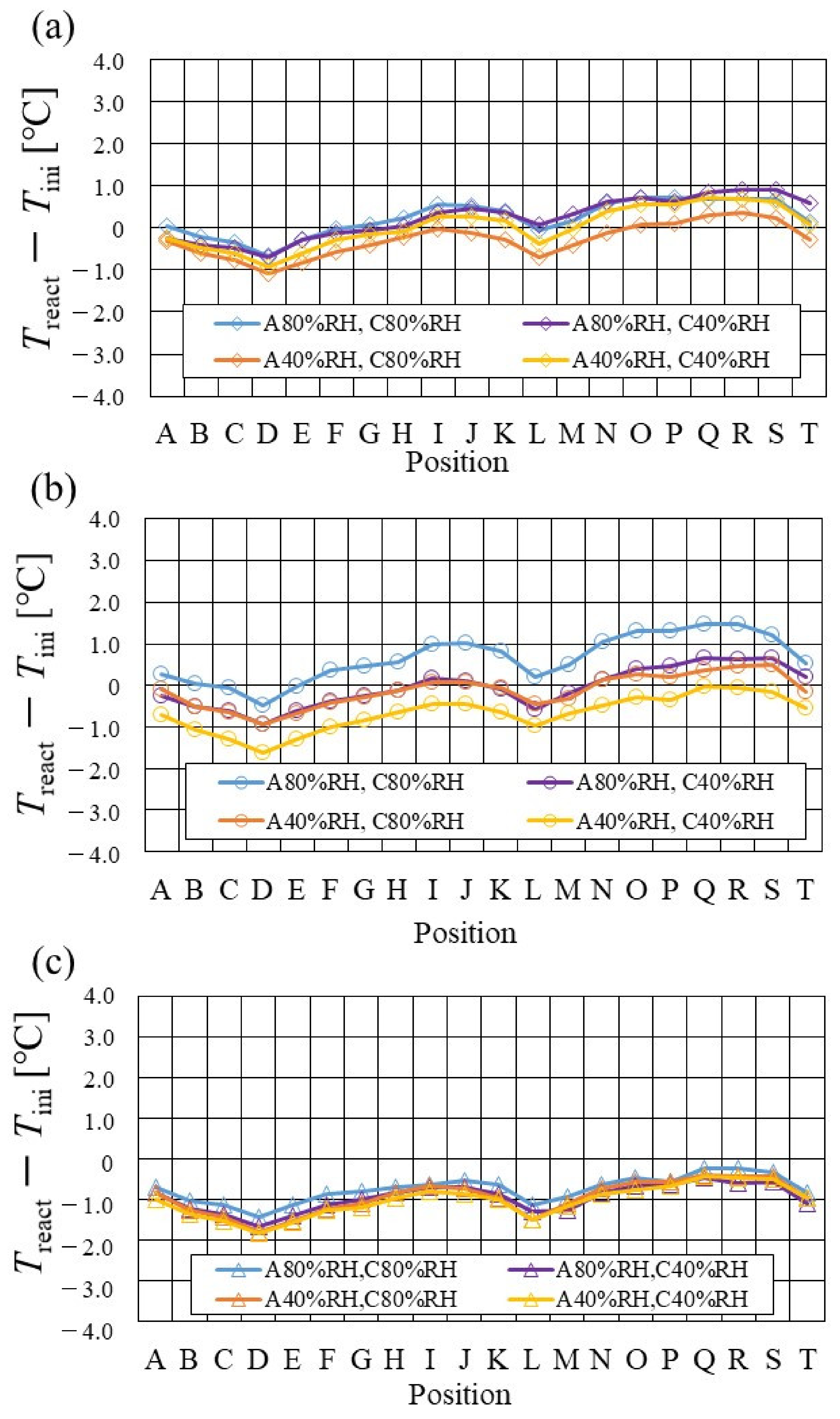
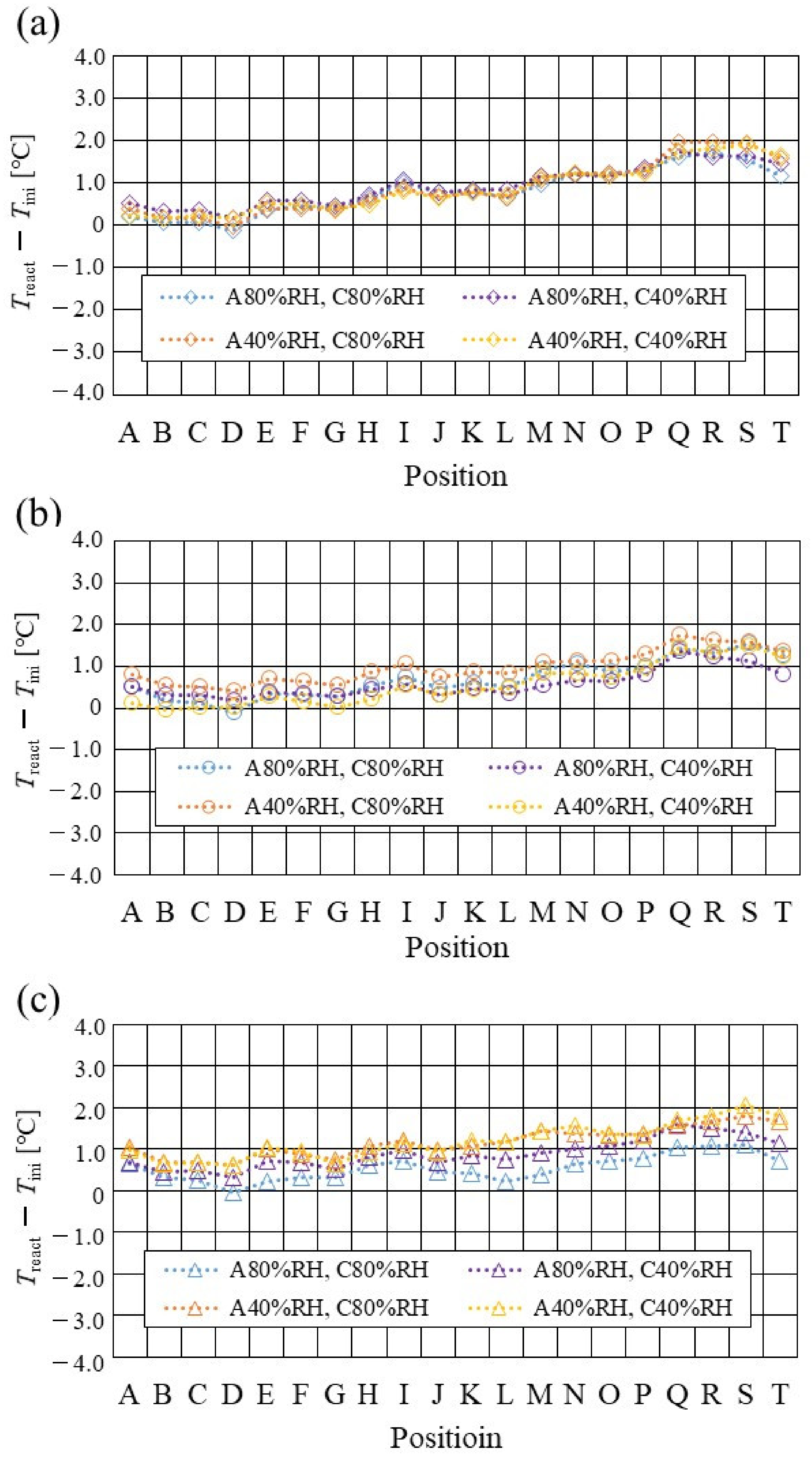
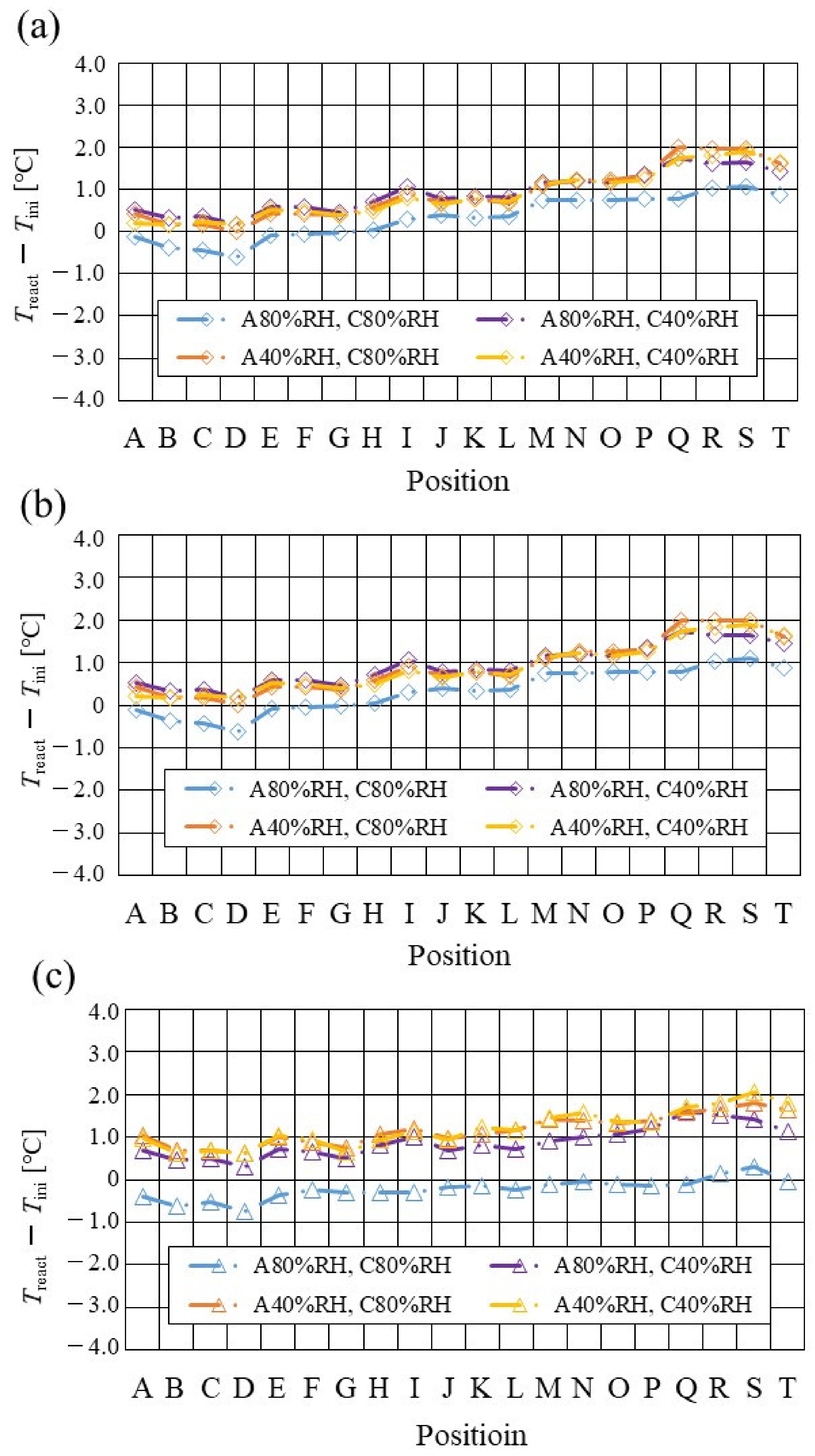
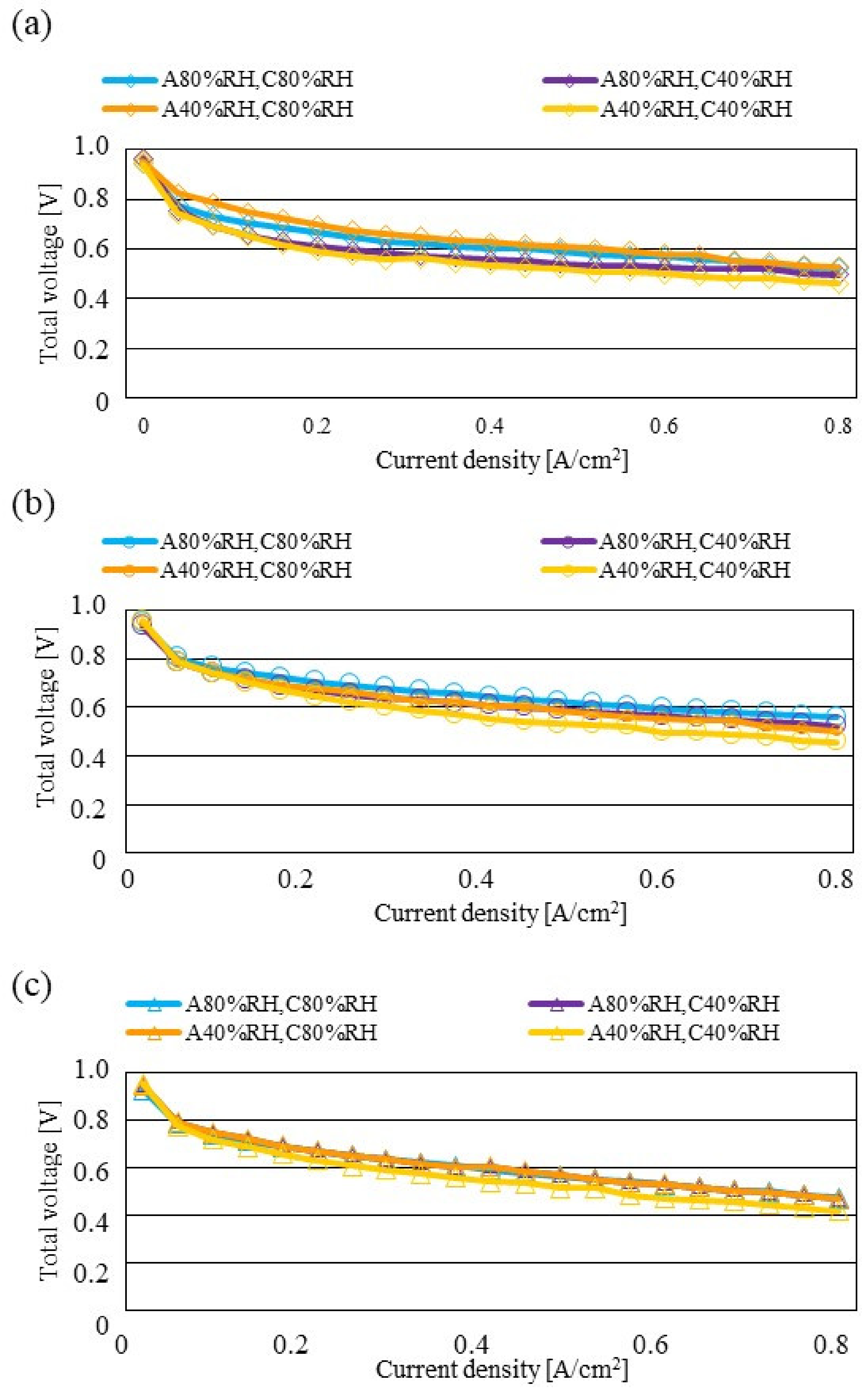
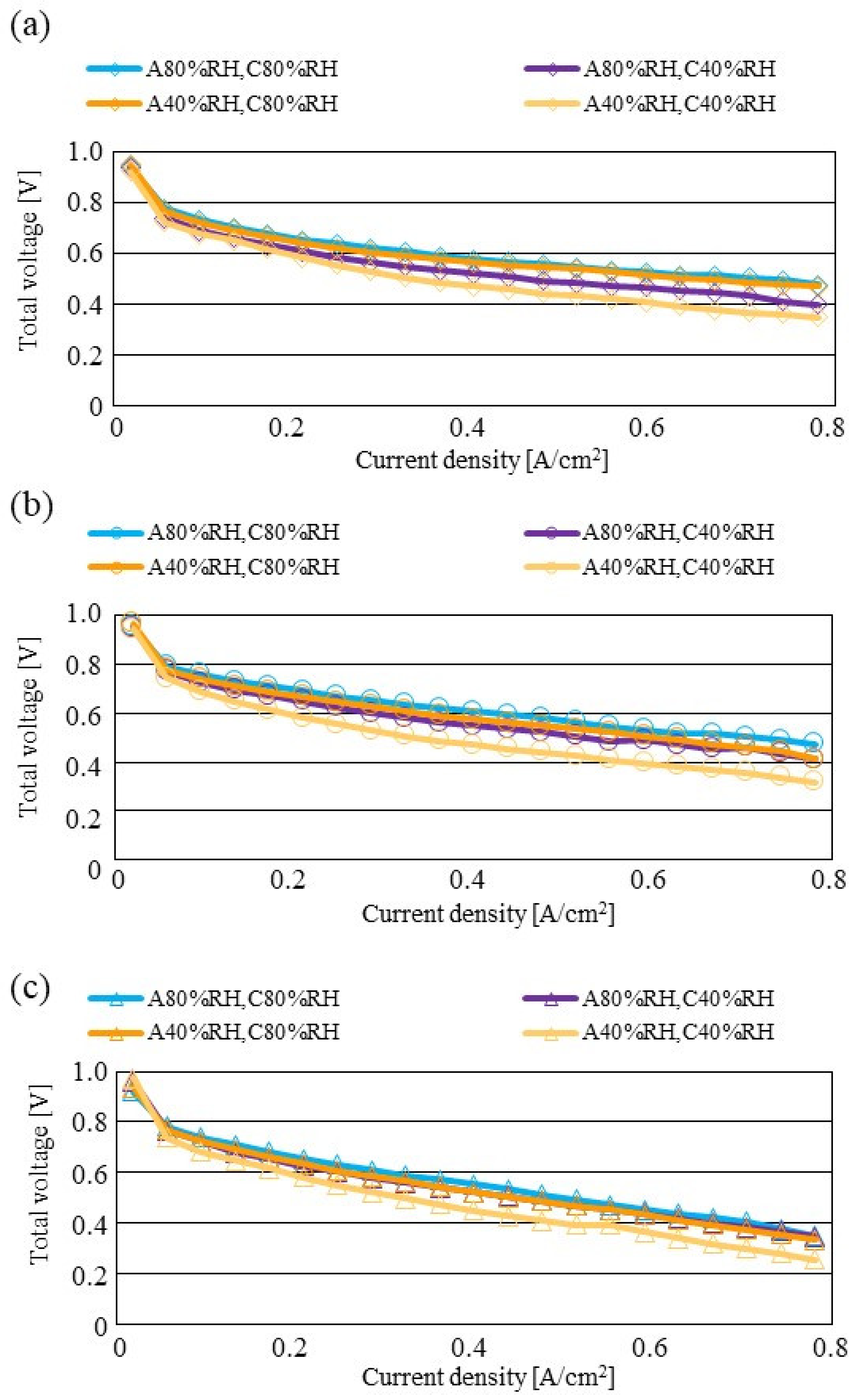
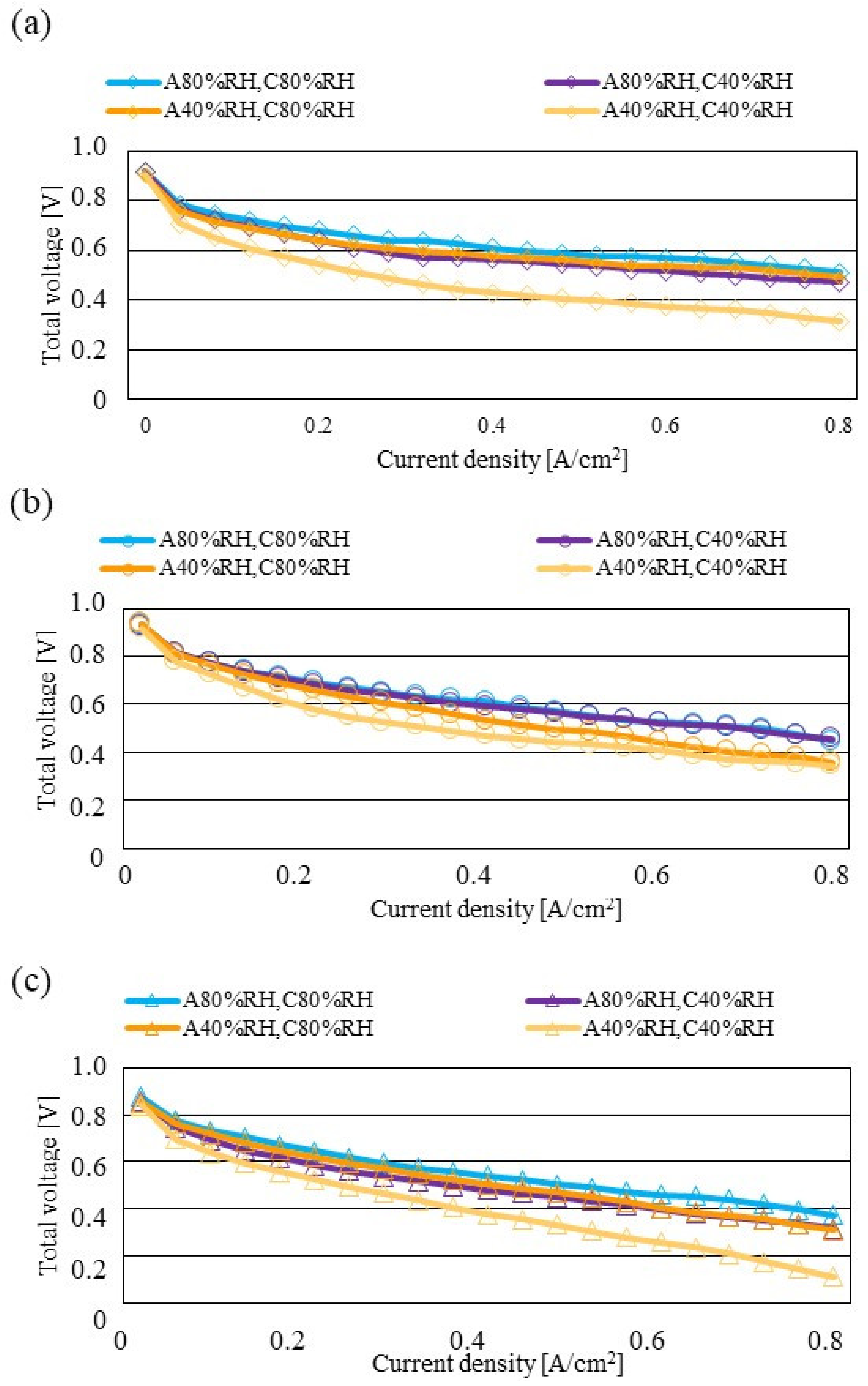
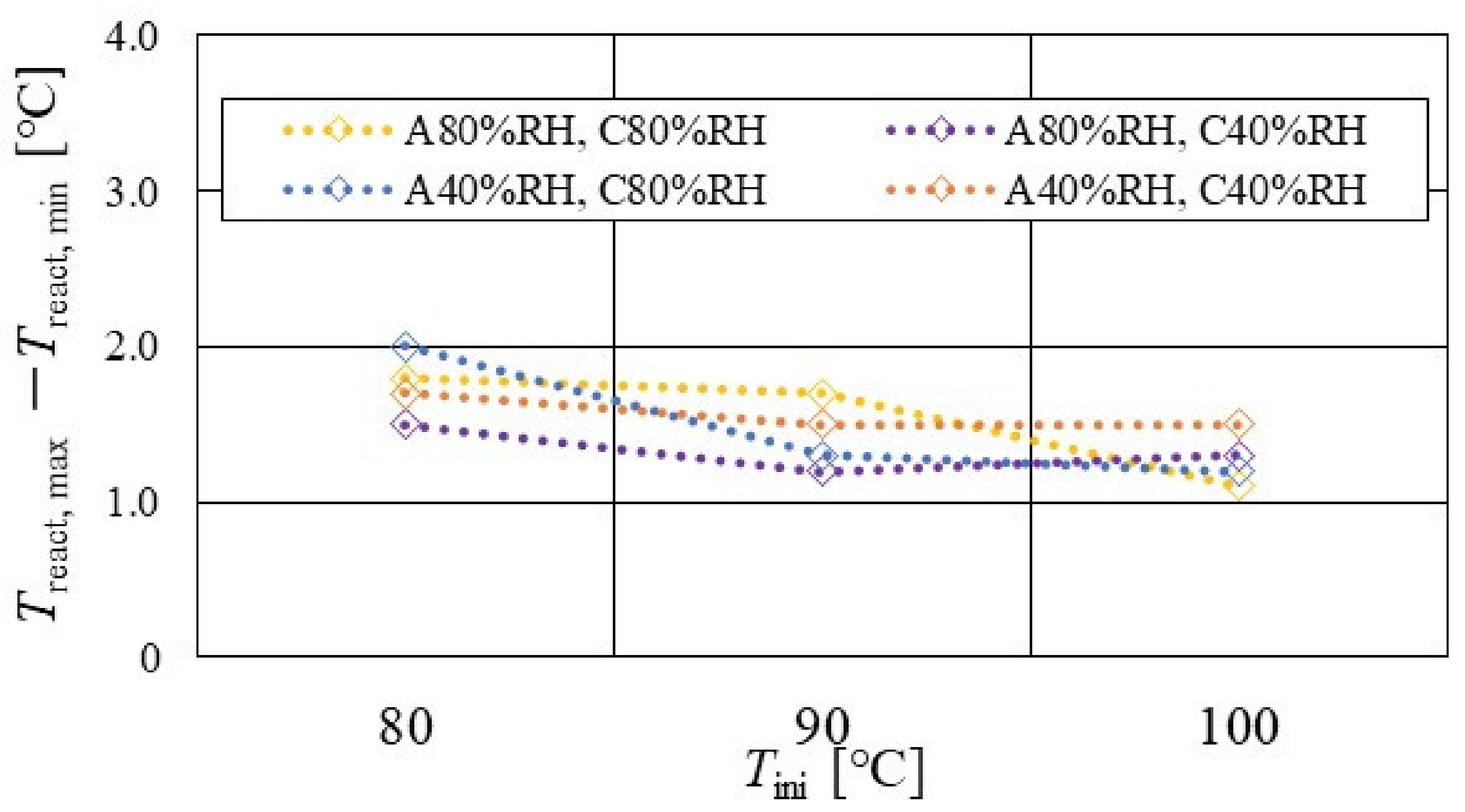
3.2. Impact of Separator Size with RH and Tini on Distribution of Treact − Tini
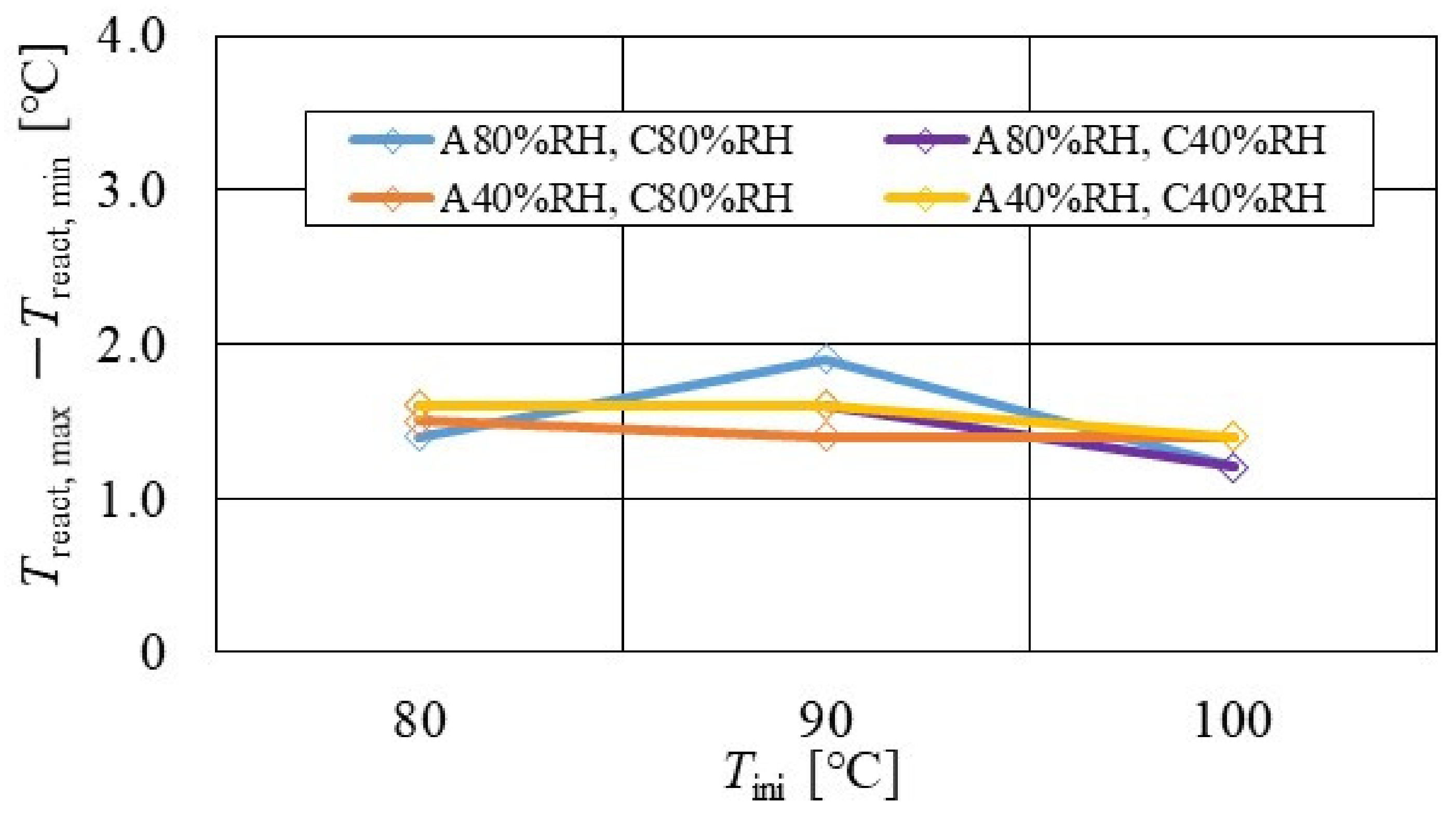
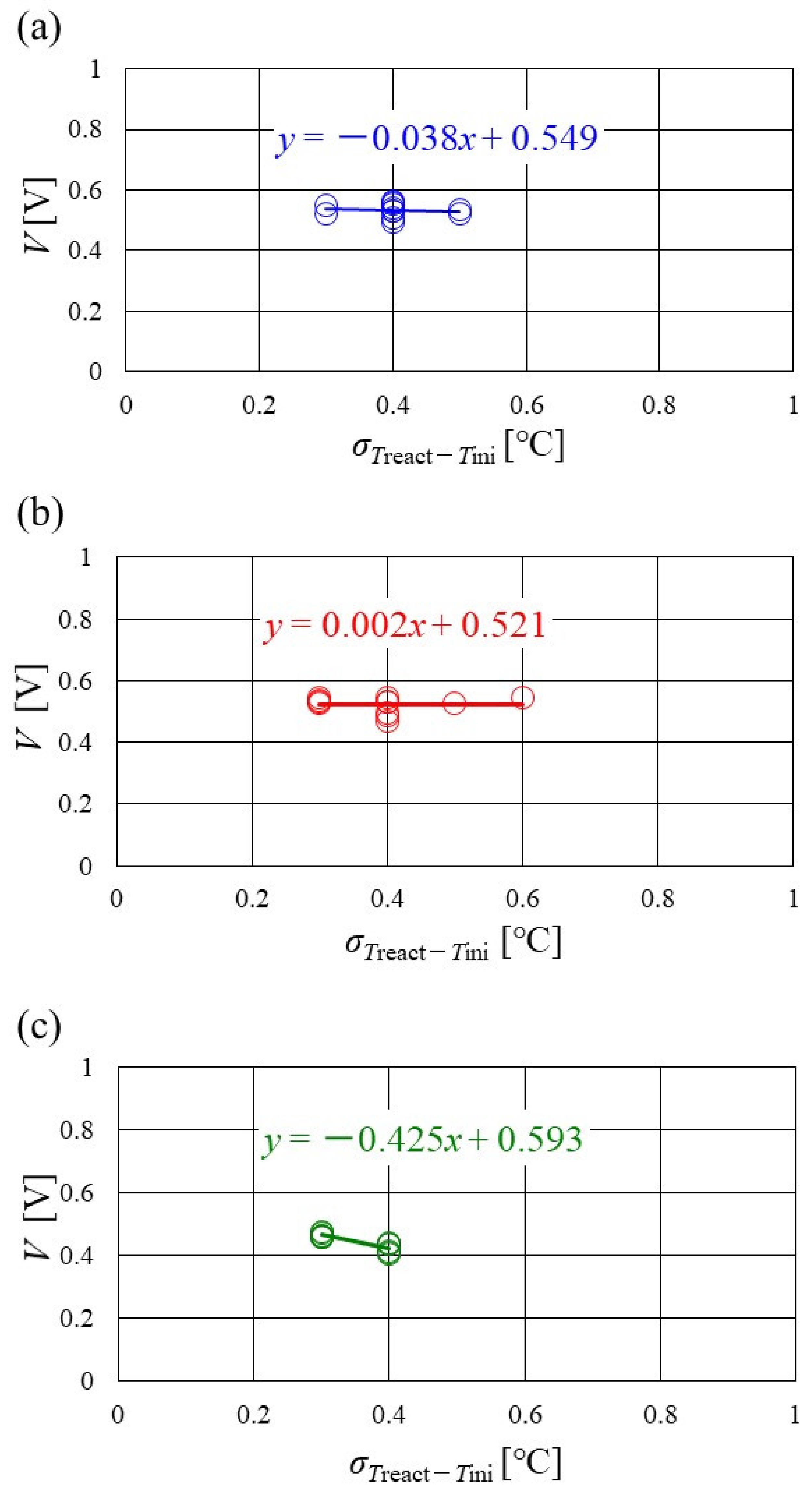
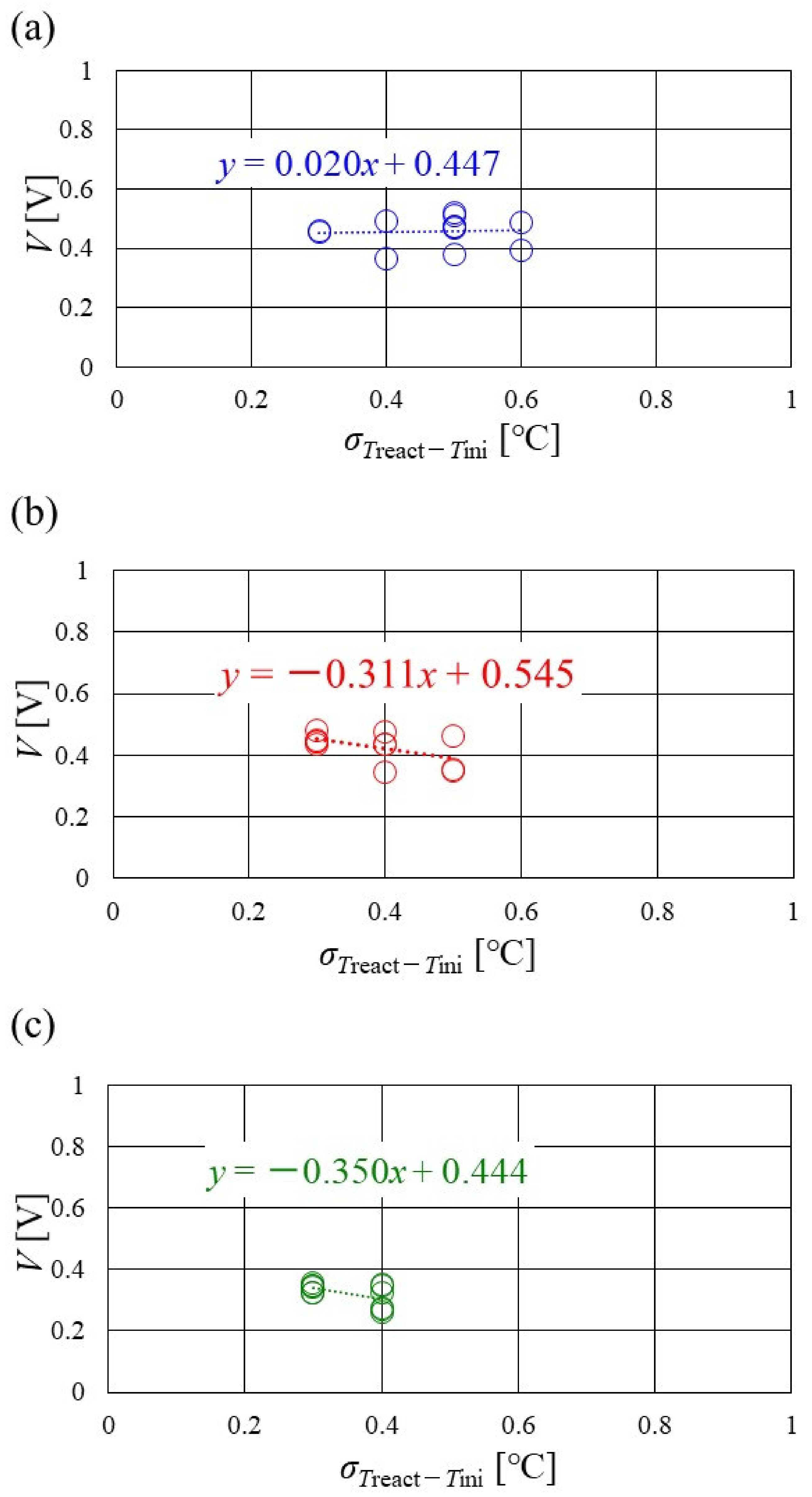
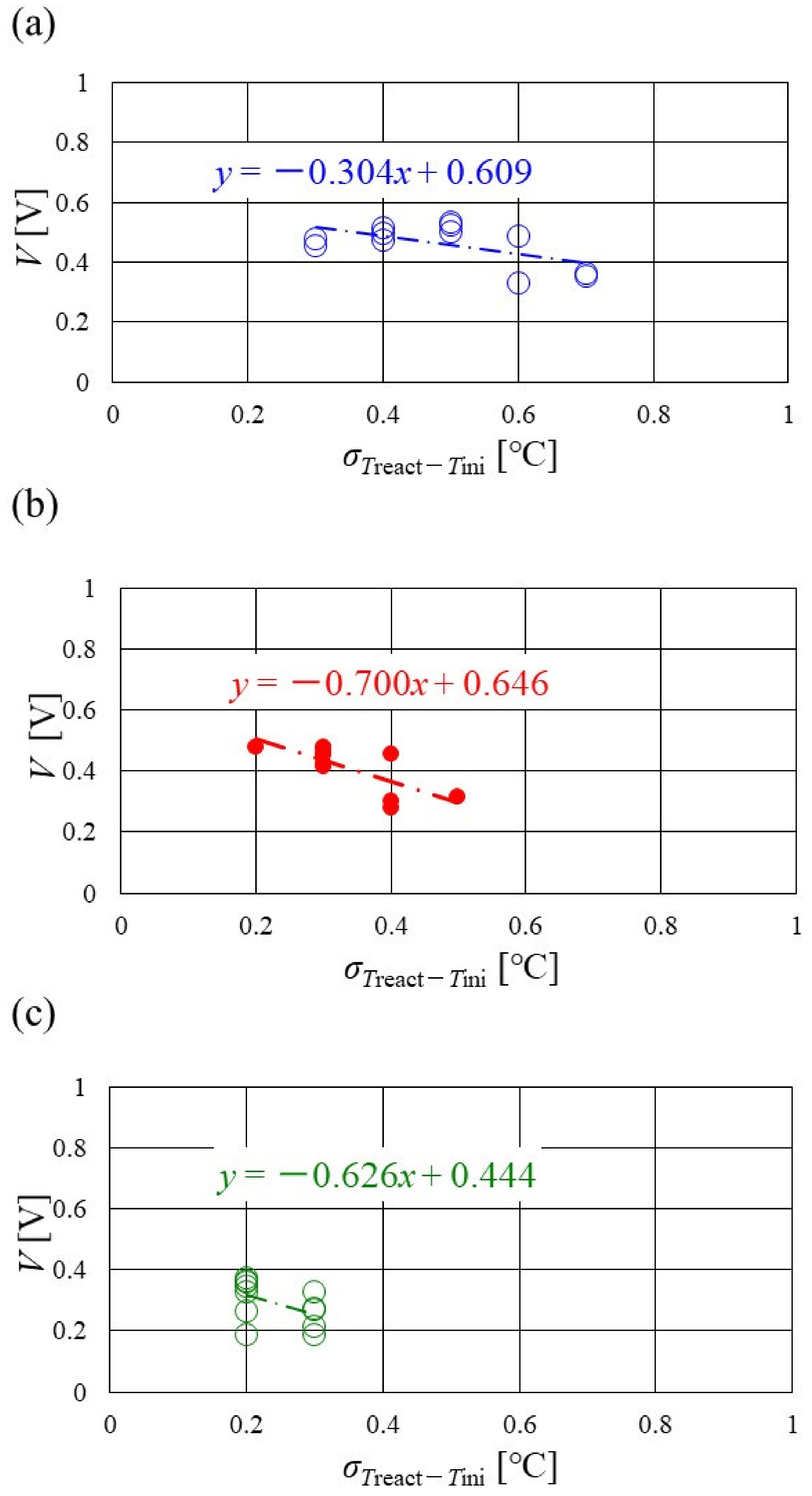
3.3. Evaluation on Temperature Difference and Standard Deviation of Distribution of Treact − Tini
4. Conclusions
- (i)
- The effect of the flow rate of the supply gases on the distribution of Treact − Tini is not significant, among the investigated conditions.
- (ii)
- The temperature declines at positions D, L, and T, in the case of a separator thickness of 2.0 mm, which is the thickest separator, though the temperature increases along with the gas flows through the gas channel, by approximately 2 °C, in the case of a thinner separator, compared to 2.0 mm.
- (iii)
- In the case of a separator thickness of 1.5 mm and 1.0 mm, the impact of the RH on the distributions of Treact − Tini is larger with the increase in Tini. Especially, this impact is larger at Tini = 100 °C, at a separator thickness of 1.0 mm. The heat capacity decreases with the decrease in separator thickness. Therefore, the whole cell temperature increases, resulting in it being easy to dehydrate the PEM and catalyst.
- (iv)
- Treact, max − Treact, min decreases with the increase in Tini, irrespective of the RH and separator thickness. However, in the case of A 80% RH and C 80% RH at a separator thickness of 2.0 mm, it has a different tendency.
- (v)
- It is revealed that the slope of the approximate line for the relation between the standard deviation of the distribution of Treact − Tini and the total voltage becomes negative and larger with the increase in Tini, irrespective of the separator’s thickness, indicating that a wider temperature distribution provides a reduction in power-generation performance. The distribution range regarding the standard deviation of the distribution of Treact − Tini, at Tini = 100 °C, is narrower than the other Tini. Since Tini = 100 °C is a higher temperature, it is difficult to manage the humidification of the PEM and catalyst, and the power-generation performance declines, even for a narrow temperature distribution. This study proposes that thin separators, such as a thickness of 1.5 mm and 1.0 mm, are not suitable for higher temperature operation than usual.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Heat-transfer area, which is the active area of MEA equal to the power-generation area | [m2] |
| Ei | Ideal energy generation rate from the water formation by H2 and O2, based on higher heating value | [W] |
| F | Faraday constant (= 96,500) | [C/mol] |
| Hchan, a | Heat flux through separator channel at anode | [W] |
| Hchan, c | Heat flux through separator channel at cathode | [W] |
| Hreact | Heat generation rate | [W] |
| Hrib, a | Heat flux through rib at anode | [W] |
| Hrib, c | Heat flux through rib at cathode | [W] |
| I | Load current | [A] |
| i | Segment | [-] |
| Kchan, a | Overall heat-transfer coefficient through separator channel at anode | [W/(m·K)] |
| Kchan, c | Overall heat-transfer coefficient through separator channel at cathode | [W/(m·K)] |
| Krib, a | Overall heat-transfer coefficient through rib at anode | [W/(m·K)] |
| Krib, c | Overall heat-transfer coefficient through rib at cathode | [W/(m·K)] |
| kcat | Thermal conductivity of catalyst layer | [W/(m·K)] |
| kchan, a | Thermal conductivity of mixture gas in separator channel at anode | [W/(m·K)] |
| kchan, c | Thermal conductivity of mixture gas in separator channel at cathode | [W/(m·K)] |
| kGDL | Thermal conductivity of GDL | [W/(m·K)] |
| kMPL | Thermal conductivity of MPL | [W/(m·K)] |
| kPEM | Thermal conductivity of PEM | [W/(m·K)] |
| krib, a | Thermal conductivity of separator rib at anode | [W/(m·K)] |
| krib, c | Thermal conductivity of separator rib at cathode | [W/(m·K)] |
| ksep | Thermal conductivity of separator except for rib | [W/(m·K)] |
| mH2 | Molar consumption rate of supplied H2 | [mol/s] |
| mO2 | Molar consumption rate of supplied O2 | [mol/s] |
| n | Valence ion (=2) | [-] |
| qHHV | Ideal energy generation rate on higher heating value | [kJ/mol] |
| qLHV | Ideal energy generation rate on lower heating value | [kJ/mol] |
| s.r. | Stoichiometric ratio | [-] |
| Tini | Initial operation temperature | [°C or K] |
| Treact | Reaction surface temperature | [°C or K] |
| Treact, chan | Temperature on reaction surface under separator channel | [°C or K] |
| Treact, rib | Temperature on reaction surface under separator rib | [°C or K] |
| Tsurf, a | Separator’s back surface temperature at anode | [°C or K] |
| Tsurf, c | Separator’s back surface temperature at cathode | [°C or K] |
| V | Voltage obtained by the experiment | [V] |
| WE | Electric power generated by PEFC | [W] |
| δcat | Thickness of catalyst layer | [m] |
| δchan | Thickness of separator channel | [m] |
| δGDL | Thickness of GDL | [m] |
| δMPL | Thickness of MPL | [m] |
| δPEM | Thickness of PEM | [m] |
| δsep | Thickness of separator except for rib | [m] |
References
- NEDO (New Energy and Industry Technology Development Organization). Available online: http://www.nedo.go.jp/cotent/100871973 (accessed on 18 April 2022). (In Japanese).
- Zhang, G.; Kandlikar, S.G.A. Critical Review of Cooling Technique in Proton Exchange Membrane Fuel Cell Stacks. Int. J. Hydrog. Energy 2012, 37, 2412–2429. [Google Scholar] [CrossRef]
- Agbossou, K.; Kolhe, M.; Hamelin, J.; Bose, T.K. Performance of a Stand-Alone Renewable Energy System Based on Energy Storage as Hydrogen. IEEE Trans. Energy Convers. 2004, 19, 633–640. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Hao, D.; Ni, M.; Huang, S.; Liu, D.; Zheng, Y. 3D Non-isothermal Dynamic Simulation of High Temperature Proton Exchange Membrane Fuel Cell in Start-up Process. Int. J. Hydrog. Energy 2021, 46, 2577–2593. [Google Scholar] [CrossRef]
- Li, Q.; He, R.; Jensen, J.O.; Bjerrum, N.J. Approaches and Recent Development Polymer Electrolyte Membrane for Fuel Cells Operating above 100 ℃. Chem. Mater. 2003, 15, 4896–4915. [Google Scholar] [CrossRef]
- Lee, C.Y.; Weng, F.; Kuo, Y.W.; Tsai, C.H.; Cheng, Y.T.; Cheng, C.K.; Lin, J.T. In-situ Measurement of High-temperature Proton Exchange Membrane Fuel Cell Stack Using Flexible Five-in-one Micro Sensor. Sensors 2016, 16, 1731. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Wang, T.; Che, X.; Dong, J.; Liu, R.; Yang, J. New High-performance Bulky N-heterocyclic Group Functionalized Poly (Terphenyl Piperidinium) Membrane for HT-PEMFC Applications. J. Mem. Sci. 2022, 641, 119884. [Google Scholar] [CrossRef]
- Budak, Y.; Devrim, Y. Micro-cogeneration Application of a High-temperature PEM Fuel Cell Stack Operated with Polybenzimidazole Based Membranes. Int. J. Hydrog. Energy 2020, 45, 35198–35207. [Google Scholar] [CrossRef]
- Kim, D.H.; Min, C.M.; Lee, E.; Lee, J.S.; Pak, C. Effect of Vinylphosphonic Acid and Polymer Binders with Phosphate Groups on Performance of High-temperature Polymer Electrolyte Membrane Fuel Cell. Catal. Today 2020, 358, 333–337. [Google Scholar] [CrossRef]
- Jia, T.; Shen, S.; Zhao, J.; Jin, J.; Pan, B.; Duan, X.; Meng, C.; Che, Q. Ultrathin Membranes Formation via the Layer Self-assembly of Carbon Nanotubes-based Inorganics as High Temperature Proton Exchange Membranes. Int. J. Hydrog. Energy 2020, 45, 14517–14527. [Google Scholar] [CrossRef]
- Wang, D.; Wang, S.; Tian, X.; Li, J.; Liu, F.; Wang, X.; Chen, H.; Mao, T.; Liu, G. Ethly Phosphoric Acid Grafted Amino-modified Polybenzimidazole with Improved Long-term Stability for High-temperature Proton Exchange Membrane Applications. Int. J. Hydrog. Energy 2020, 45, 3176–3185. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Li, W.; Zhang, J.; Lu, D.; Yan, W.; Xiang, Y.; Lu, S. Effect of Catalyst Layer Microstructures on Performance and Stability for High Temperature Polymer Electrolyte Membrane Fuel Cells. J. Power Sources 2021, 505, 230059. [Google Scholar] [CrossRef]
- Lee, W.J.; Lee, J.S.; Park, H.Y.; Park, H.S.; Lee, S.Y.; Song, K.H.; Kim, H.J. Improvement of Fuel Cell Performances through the Enhanced Dispersion of the PTFE Binder in Electrodes for Use in High Temperature Polymer Electrolyte Membrane Fuel Cells. Int. J. Hydrog. Energy 2020, 45, 32825–32833. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Zhu, Z.; Liu, P.; Cao, F.; Chen, J.; He, Q.; Dou, M.; Nan, S.; Lu, S. Usual Influence of Binder Composition and Phosphoric Acid Leaching on Oxygen Mass Transport in Catalyst Layers of High-temperature Proton Exchange Membrane Fuel Cells. J. Power Sources 2020, 473, 228616. [Google Scholar] [CrossRef]
- Kim, D.K.; Kim, H.; Park, H.; Oh, S.; Ahn, S.H.; Kim, H.J.; Kim, S.K. Performance Enhancement of High-temperature Electrolyte Membrane Fuel Cells Using Pt Pulse Electrodeposition. J. Power Sources 2019, 438, 227022. [Google Scholar] [CrossRef]
- Sasiwinmonrit, K.; Chang, W.C. To Improve the High Temperature Polymer Electrolyte Membrane Fuel Cells Performance by Alternating the Properties of Catalyst Layer. Int. J. Hydrog. Energy 2020, 45, 14491–14499. [Google Scholar] [CrossRef]
- Xu, Y.; Fan, R.; Chang, G.; Xu, S.; Cai, T. Investigating Temperature-driven Water Transport in Cathode Gas Diffusion Media of PEMFC with a Non-isothermal Two-phase Model. Energy Convers. Manag. 2021, 248, 114791. [Google Scholar] [CrossRef]
- Xia, L.; Ni, M.; Xu, Q.; Xu, H.; Zheng, K. Optimization of Catalyst Layer Thickness for Achieving High Performance and Low Cost of High Temperature Proton Exchange Membrane Fuel Cell. Appl. Energy 2021, 300, 117357. [Google Scholar] [CrossRef]
- Das, S.K.; Gibson, H.A. Three Dimensional Multi-physics Modeling and Simulation for Assessment of Mass Transport Impact on the Performance of a High Temperature Polymer Electrolyte Membrane Fuel Cell. J. Power Sources 2021, 499, 229844. [Google Scholar] [CrossRef]
- Xia, L.; Ni, M.; He, Q.; Cheng, C. Optimization of Gas Diffusion Layer in High Temperature PEMFC with the Focuses on Thickness and Porosity. Appl. Energy 2021, 300, 117357. [Google Scholar] [CrossRef]
- Huang, T.; Wang, W.; Yuan, Y.; Huang, J.; Chen, W.; Zhang, J.; Kong, X.; Zhang, Y.; Wan, Z. Optimization of High-temperature Proton Exchange Membrane Fuel Cell Flow Channel Based on Genertic Slgorithm. Energy Rep. 2021, 7, 1374–1384. [Google Scholar] [CrossRef]
- Chen, H.; Guo, H.; Ye, F.; Ma, C.F. A Numerical Study of Oriented-type Flow Channels with Porous-blocked Baffles of Proton Exchange Membrane Fuel Cells. Int. J. Hydrog. Energy 2021, 46, 29443–29458. [Google Scholar] [CrossRef]
- Zhang, T.; Li, J.; Li, Q.; Yu, M.; Sun, H. Combination Effects of Flow Filed Structure and Assembly Force on Performance of High Temperature Proton Exchange Membrane Fuel Cells. Int. J. Energy Res. 2021, 45, 7903–7917. [Google Scholar] [CrossRef]
- Xia, L.; Xu, Q.; He, Q.; Ni, M.; Seng, M. Numerical Study of High Temperature Proton Exchange Membrane Fuel Cell (HT-PEMFC) with a Focus on Rib Design. Int. J. Hydrog. Energy 2021, 46, 21098–21111. [Google Scholar] [CrossRef]
- Nanadegani, F.S.; Lay, E.N.; Sunden, B. Computational Analysis of the Impact of a Micro Porous Layer (MPL) on the Characteristics of a High Temperature PEMFC. Electrochim. Acta 2020, 333, 135552. [Google Scholar] [CrossRef]
- Nishimura, A.; Kono, N.; Toyod, K.; Kojima, Y.; Kolhe, M.L. Impact Analysis of MPL on a PEFC Cell’s Temperature Distribution with Thin PEM and GDL for Operating at Higher Temperature than Usual. J. Energy Power Eng. 2021, 15, 39–51. [Google Scholar] [CrossRef]
- Nishimura, A.; Yamamoto, K.; Okado, T.; Kojima, Y.; Hirota, M.; Kolhe, M. Impact of Analysis of MPL and PEM Thickness on Temperature Distribution within PEFC Operating at Relatively Higher Temperature. Energy 2020, 205, 117875. [Google Scholar] [CrossRef]
- Nishimura, A.; Sato, Y.; Kamiya, S.; Okado, T.; Yamamoto, K.; Hirota, M.; Hu, E. Impact of Thickness of Polymer Electrolyte Membrane and Gas Diffusion Layer on Temperature Distribution in Polymer Electrolyte Fuel Cell Operated at Temperature around 90 ℃. J. Power Eng. 2019, 13, 97–115. [Google Scholar] [CrossRef]
- Nishimura, A.; Sato, Y.; Yoshimura, M.; Kamiya, S.; Hirota, M. Impact of Thickness of Polymer Electrolyte Membrane on Temperature Distribution in Single Cell of Polymer Electrolyte Fuel Cell Operated at High Temperature. J. Energy Power Eng. 2018, 12, 80–92. [Google Scholar] [CrossRef][Green Version]
- Nishimura, A.; Shibuya, K.; Morimoto, A.; Tanaka, S.; Hirota, M.; Nakamura, M.; Kojima, Y.; Narita, M.; Hu, E. Dominant Factor and Mechanism of Coupling Phenomena in Single Cell of Polymer Electrolyte Fuel Cell. Appl. Energy 2012, 1, 73–79. [Google Scholar] [CrossRef]
- Nishimura, A.; Okado, T.; Kojima, Y.; Hirota, M.; Hu, E. Impact of MPL on Temperature Distribution in Single Polymer Electrolyte Fuel Cell with Various Thickness of Polymer Electrolyte Membrane. Energies 2020, 13, 2499. [Google Scholar] [CrossRef]
- Zamel, N.; Becker, J.; Wiegmann, A. Estimating the Thermal Conductivity and Diffusion Coefficient of the Microporous Layer of Polymer Electrolyte Membrane Fuel Cells. J. Power Sources 2012, 207, 70–80. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, G.; Guo, L.; Liu, H. Systematic Study on the Functions and Mechanisms of Micro Porous Layer on Water Transport in Proton Exchange Membrane Fuel Cells. Int. J. Hydrog. Energy 2016, 41, 5063–5073. [Google Scholar] [CrossRef]
- Nishimura, A.; Fukuoka, T.; Baba, M.; Hirota, M.; Hu, E. Clarification on Temperature Distribution in Single Cell of Polymer Electrolyte Fuel Cell under Different Operation Conditions by Means of 1D Multi-plate Heat-transfer Model. J. Chem. Eng. Jpn. 2015, 48, 862–871. [Google Scholar] [CrossRef]
- The Japan Society of Mechanical Engineers. JSME Heat Transfer Handbook, 1st ed.; The Japan Society of Mechanical Engineers; Maruzen: Tokyo, Japan, 1993; p. 387. [Google Scholar]
- Khandelwal, M.; Mench, M.M. Direct Measurement of Through-plane Thermal Conductivity and Contact Resistance in Fuel Cell Materials. J. Power Sources 2006, 161, 1106–1115. [Google Scholar] [CrossRef]
- Kawase, M.; Inagaki, T.; Kawashima, S.; Miura, K. Effective Thermal Conductivity of Gas Diffusion Layer in Through-plane Direction. ECS Trans. 2009, 25, 1529–1537. [Google Scholar] [CrossRef]
- Jung, C.Y.; Shim, H.S.; Koo, S.M.; Lee, S.H.; Yi, S.C. Investigation of the Temperature Distribution in Proton Exchange Membrane Fuel Cell. Appl. Energy 2012, 93, 733–741. [Google Scholar] [CrossRef]
- Nishimura, A.; Iio, K.; Baba, M.; Yamauchi, T.; Hirota, M.; Hu, E. Modeling of Heat Transfer in Single Cell of Polymer Electrolyte Fuel Cell by Means of Temperature Data Measured by Thermograph. J. Chem. Eng. Jpn. 2014, 47, 521–529. [Google Scholar] [CrossRef]
- Nishimura, A.; Zamami, K.P.; Yoshimoto, M.; Hirota, M.; Kolhe, M.L. Numerical Analysis of Temperature Distributions in Single Cell of Polymer Electrolyte Fuel Cell when Operated in Elevated Temperature Range. J. Energy Power Eng. 2017, 11, 193–408. [Google Scholar] [CrossRef][Green Version]
- Nishimura, A.; Osada, K.; Tsunoda, T.; Yoshimura, M.; Hirota, M.; Hu, E. Analysis on Temperature Distributions in Single Cell of Polymer Electrolyte Fuel Cell when Operated in High Temperature Range. J. Energy Power Eng. 2016, 10, 453–464. [Google Scholar] [CrossRef][Green Version]
- Nishimura, A.; Kojima, Y.; Ito, S.; Hu, E. Impacts of Separator Thickness on Temperature Distributions and Power Generation Characteristics of a Single PEMFC Operated at Higher Temperature of 363 and 373 K. Energies 2022, 15, 1558. [Google Scholar] [CrossRef]
- Akitomo, F.; Sasabe, T.; Yoshida, T.; Naito, H.; Kawamura, K.; Hirai, S. Investigation of Effects of High Temperature and Pressure on a Polymer Electrolyte Fuel Cell with Polarization Analysis and X-ray Imaging of Liquid Water. J. Power Sources 2019, 431, 205–209. [Google Scholar] [CrossRef]
- Mariani, M.; Latorrata, S.; Patrigani, S.; Stampino, P.G.; Dotelli, G. Characterization of Novel Graphene-based Microporous Layers for Polymer Electrolyte Membrane Fuel Cells Operating under Low Humidity and High Temperature. Int. J. Hydrog. Energy 2020, 45, 7046–7058. [Google Scholar] [CrossRef]
- Nishimura, A.; Mahadi, A.H.; Oasada, K.; Baba, M.; Hirota, M. Heat and Mass Transfer Characteristics on Single-cell of Polymer Electrolyte Fuel Cell Operated at Higher Temperature than Usual. Kagaku Kogaku Ronbunshu 2015, 41, 397–405. [Google Scholar] [CrossRef]
- Xu, Z.; Qiu, D.; Yi, P.; Peng, L.; Lai, X. Towards Mass Application: A Review on the Challenges and Developments in Metallic Bipolar Plates for PEMFC. Prog. Nat. Sci. Mater. Int. 2020, 46, 8672–8701. [Google Scholar] [CrossRef]
- Wu, S.; Yang, W.; Yan, H.; Zuo, X.; Cao, Z.; Li, H.; Shi, M.; Chen, H. A Review of Modified Metal Bipolar Plates for Proton Exchange Membrane Fuel Cells. Int. J. Hydrog. Energy 2021, 46, 8672–8701. [Google Scholar] [CrossRef]
- Saadat, N.; Dhakal, H.N.; Tjong, J.; Jaffer, S.; Yang, W.; Sain, M. Recent Advances and Future Perspectives of Carbon Materials for Fuel Cell. Renew. Sustain. Energy Rev. 2021, 138, 110535. [Google Scholar] [CrossRef]


| Components | Dimension | Characteristics | Porosity [-] | Effective Thermal Conductivity [W/(m·K)] |
|---|---|---|---|---|
| Polymer electrolyte membrane (PEM) | 50.0 mm × 50.0 mm × 0.025 mm | NRE-211 (produced by Du Pont Corp.) | 0.28 | 0.195 |
| Catalyst layer | 50.0 mm × 50.0 mm × 0.01 mm | Pt/C (20 wt% Pt loading) | 0.78 | 0.27 |
| Micro-porous layer (MPL) | 50.0 mm × 50.0 mm × 0.003 mm (attached with PEM) | Carbon black + PTFE | 0.60 | 1.0 |
| Gas-diffusion layer (GDL) | 50.0 mm × 50.0 mm × 0.11 mm | Carbon paper (TGP-H-030 produced by Toray Corp.) | 0.78 | 1.7 |
| Separator | 75.4 mm × 75.4 mm × 2.0 mm or 1.5 mm or 1.0 mm (2.0 mm = saddle thickness of 1.0 mm and channel height of 1.0 mm; 1.5 mm = saddle thickness of 0.5 mm and channel height of 1.0 mm; 1.0 mm = saddle thickness of 0.5 mm and channel height of 0.5 mm) (gas supply area: 50.0 mm × 50.0 mm) | Carbon graphite, serpentine | 0.15 | 25 |
| Initial temperature of cell (Tini) [°C] | 80, 90, 100 | |
| Load current [A] (current density [A/cm2]) | 20 (0.80) | |
| Condition of supply gas | ||
| Anode | Cathode | |
| Gas type | H2 | O2 |
| Temperature of supply gas at inelt [°C] | 80, 90, 100 | 80, 90, 100 |
| Relative humidity of supply gas [% RH] | 40, 80 | 40, 80 |
| Pressure of supply gas at inlet (absolute) [MPa] | 0.4 | 0.4 |
| Flow rate of supply gas at inlet [NL/min] (Stoichiometric ratio [-]) | 0.210 (1.5), 0.280 (2.0), 0.420 (3.0) | 0.105 (1.5), 0.140 (2.0), 0.210 (3.0) |
| Separator thickness: 2.0 mm | |||
| Tini = 80 °C | |||
| A 80% RH, C 80% RH | A 80% RH, C 40% RH | A 40% RH, C 80% RH | A 40% RH, C 40% RH |
| 0.565 V | 0.535 V | 0.540 V | 0.520 V |
| Tini = 90 °C | |||
| A 80% RH, C 80% RH | A 80% RH, C 40% RH | A 40% RH, C 80% RH | A 40% RH, C 40% RH |
| 0.545 V | 0.525 V | 0.530 V | 0.495 V |
| Tini = 100 °C | |||
| A 80% RH, C 80% RH | A 80% RH, C 40% RH | A 40% RH, C 80% RH | A 40% RH, C 40% RH |
| 0.465 V | 0.460 V | 0.435 V | 0.415 V |
| Separator thickness: 1.5 mm | |||
| Tini = 80 °C | |||
| A 80% RH, C 80% RH | A 80% RH, C 40% RH | A 40% RH, C 80% RH | A 40% RH, C 40% RH |
| 0.520 V | 0.475 V | 0.485 V | 0.395 V |
| Tini = 90 °C | |||
| A 80% RH, C 80% RH | A 80% RH, C 40% RH | A 40% RH, C 80% RH | A 40% RH, C 40% RH |
| 0.460 V | 0.450 V | 0.435 V | 0.355 V |
| Tini = 100 °C | |||
| A 80% RH, C 80% RH | A 80% RH, C 40% RH | A 40% RH, C 80% RH | A 40% RH, C 40% RH |
| 0.345 V | 0.340 V | 0.325 V | 0.275 V |
| Separator thickness: 1.0 mm | |||
| Tini = 80 °C | |||
| A 80% RH, C 80% RH | A 80% RH, C 40% RH | A 40% RH, C 80% RH | A 40% RH, C 40% RH |
| 0.535 V | 0.500 V | 0.490 V | 0.365 V |
| Tini = 90 °C | |||
| A 80% RH, C 80% RH | A 80% RH, C 40% RH | A 40% RH, C 80% RH | A 40% RH, C 40% RH |
| 0.475 V | 0.455 V | 0.425 V | 0.315 V |
| Tini = 100 °C | |||
| A 80% RH, C 80% RH | A 80% RH, C 40% RH | A 40% RH, C 80% RH | A 40% RH, C 40% RH |
| 0.365 V | 0.330 V | 0.275 V | 0.215 V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishimura, A.; Kono, N.; Toyoda, K.; Mishima, D.; Kolhe, M.L. Impact of Separator Thickness on Temperature Distribution in Single Cell of Polymer Electrolyte Fuel Cell Operated at Higher Temperature of 90 °C and 100 °C. Energies 2022, 15, 4203. https://doi.org/10.3390/en15124203
Nishimura A, Kono N, Toyoda K, Mishima D, Kolhe ML. Impact of Separator Thickness on Temperature Distribution in Single Cell of Polymer Electrolyte Fuel Cell Operated at Higher Temperature of 90 °C and 100 °C. Energies. 2022; 15(12):4203. https://doi.org/10.3390/en15124203
Chicago/Turabian StyleNishimura, Akira, Nozomu Kono, Kyohei Toyoda, Daiki Mishima, and Mohan Lal Kolhe. 2022. "Impact of Separator Thickness on Temperature Distribution in Single Cell of Polymer Electrolyte Fuel Cell Operated at Higher Temperature of 90 °C and 100 °C" Energies 15, no. 12: 4203. https://doi.org/10.3390/en15124203
APA StyleNishimura, A., Kono, N., Toyoda, K., Mishima, D., & Kolhe, M. L. (2022). Impact of Separator Thickness on Temperature Distribution in Single Cell of Polymer Electrolyte Fuel Cell Operated at Higher Temperature of 90 °C and 100 °C. Energies, 15(12), 4203. https://doi.org/10.3390/en15124203








