Review on Spatio-Temporal Solar Forecasting Methods Driven by In Situ Measurements or Their Combination with Satellite and Numerical Weather Prediction (NWP) Estimates
Abstract
:1. Introduction
- To provide, to the best of the authors’ knowledge, the first review on spatio-temporal solar forecasting, namely on GHI and PV generation, using in situ ground measurements or their combination with satellite or NWP estimates.
- Comprehensive overview of recent advances using such approaches. The goal here is to categorize and provide statistics and temporal patterns regarding the different models used, the different types of data exploited, and the various forecasting horizons addressed.
2. Remarks on Spatio-Temporal Solar Forecasting Found in Previous Relevant Review Works
3. Spatio-Temporal Approaches
3.1. Traditional Statistical Methods
| Reference | Year | Model | Location | Data Source | Time Resolution | Forecast Horizon | Area |
|---|---|---|---|---|---|---|---|
| [83] | 2011 | Analog | N.D. | PV | 10 min 1 h | 10–30 min 1–3 h | N.D. |
| [59] | 2013 | Kriging | Singapore | GHI (in situ) | 1 h | 1–3 h | 30 × 20 km2 |
| [82] | 2014 | Kriging, VARX, LASSO | Singapore | GHI (in situ) | 5 min | 5 min | 30 × 20 km2 |
| [71] | 2014 | ARX | Australia | PV | 1 h 24 h | 1–24 h | 0.25 × 0.4 km2 |
| [70] | 2014 | ARX | France | GHI (in situ) GHI (satellite) | 15 min | 15 min–2 h | N.D. |
| [74] | 2015 | VARX | Portugal | PV | 1 h | 1–6 h | 40 × 45 km2 |
| [14] | 2015 | LASSO | USA | GHI (in situ) | 10 s | 10 s–5 min | 1 × 1 km2 |
| [75] | 2015 | Kriging | USA | GHI (in situ) | 10 s | 10 s–5 min | 1 × 1 km2 |
| [72] | 2015 | ARX | France | PV | 15 min | 15 min–6 h | N.D. |
| [61] | 2015 | ARX | Guadalupe Island | GHI (in situ) | 10 min 1 h | 10 min–1 h | N.D. |
| [39] | 2015 | AR, ARX | USA | GHI (in situ) | 1 min 1 h | 1–120 min | 51.471 km2 |
| [40] | 2016 | VAR | Guadalupe Island | GHI (in situ) | 1 s | 10 min–1 h | N.D. |
| [85] | 2016 | Linear regression | generated data | PV | 10 min | 5–60 min | N.D. |
| [86] | 2016 | LVARr | USA | GHI (in situ) | 1 min | 5 min | N.D. |
| [87] | 2016 | ARIMAX | Singapore | GHI (in situ), PV | 15 min 30 min | 15–30 min | 30 × 20 km2 |
| [88] | 2016 | CSTF | Italy | GHI (in situ), PV | 10 min | 10 min | 113 × 77 km2 |
| [76] | 2017 | Kriging (SP, IST, AST) | USA | PV | 1 min 5 min 15 min | 1–15 min | N.D. |
| [84] | 2017 | P2P method | The Netherlands | GHI (in situ) | 60 s | 1–60 min | 1400 km2 |
| [57] | 2018 | ARX | USA UK | GHI (in situ), PV | 10 s 30 min | 10 s–2 h | N.D. |
| [17] | 2018 | LASSO ultra-fast pre-selection algorithm | USA | GHI (in situ) | 10 s 1 min | 10 s–1 min | N.D. |
| [89] | 2018 | ST model | France | PV | 15 min | 1–6 h | 230 km2 |
| [90] | 2018 | OLS, LAD, LASSO, Avg, VAR | USA Brazil Singapore | GHI (in situ) | 30 min 1 h 24 h | 30–60 min 24 h | N.D. |
| [30] | 2019 | QR-LASSO | France | NWP, PV | 15 min | 1–6 h | 191 × 130 km2 |
| [80] | 2019 | ARX | USA | GHI (in situ) | 10 s | 10 s | N.D. |
| [31] | 2019 | ARX | USA | GHI (in situ), NWP | 10 s | 10 s | N.D. |
| [77] | 2019 | co-Kriging | USA | GHI (in situ) | 1 h | 6 h | N.D. |
| [91] | 2019 | SRP-Enet | N.D. | PV | 10 s | 10 s | N.D. |
| [79] | 2019 | LASSO | USA | GHI (in situ), GHI (satellite) | 30 min | 30–120 min | 30 km2 |
| [33] | 2020 | ARIMAX | South Korea | GHI (satellite) PV, NWP | 1 h | 1 h | N.D. |
| [92] | 2020 | ST-AR | Switzerland | GHI (in situ), PV, NWP | 15 min | 6 h | N.D. |
| [73] | 2020 | ARX | Spain | GHI (in situ) | 30 min | 0.5–4 h | 94,226 km2 |
| [78] | 2021 | LASSO | France | GHI (satellite) PV, NWP | 15 min | 1–6 h | 191 × 130 km2 |
| [93] | 2021 | e-MVFTS | USA | GHI (in situ) | 15 min | 30–60 min | N.D. |
3.2. Machine Learning Methods
3.2.1. Traditional Machine Learning and Multilayer Perceptrons
| Reference | Year | Model | Location | Data Source | Time Resolution | Forecast Horizon | Area |
|---|---|---|---|---|---|---|---|
| [94] | 2013 | ANN | USA | GHI (in situ), GHI (satellite) | 30 min | 30 min–2 h | N.D. |
| [95] | 2014 | ANN | France | GHI (in situ), GHI (satellite) | 3 h | 3 h | N.D. |
| [97] | 2015 | ANN | Spain | GHI (in situ), GHI (satellite) | 1 h | 1–6 h | N.D. |
| [101] | 2015 | k-NN, SVR | Italy | GHI (in situ) | 1 h | 1 h | 9 × 6 km2 |
| [62] | 2015 | AANN | France | GHI (in situ), GHI (satellite) | 15 min | 15–60 min | 123 × 123 km2 |
| [11] | 2016 | ANN | Spain | GHI (in situ), GHI (satellite), NWP | 1 h | 1–6 h | 183 × 165 km2 |
| [98] | 2016 | ANN | N.D. | GHI (in situ) | 5 min | 60 min | N.D. |
| [102] | 2016 | GCRF | USA | GHI (in situ) | 1 h | 2–10 h | N.D. |
| [103] | 2016 | ANN | Spain | GHI (in situ) | 15 min | 1–6 h | 9503 km2 |
| [104] | 2016 | WNN | Singapore | GHI (in situ) | 1 h | 15–60 min | N.D. |
| [18] | 2016 | ANN | The Netherlands | PV | 15 min | 15 min 1 months | 11 × 11 km2 |
| [29] | 2017 | GBT | Portugal | PV, NWP | 1 h | 1–24 h 24–48 h 48–72 h | 2400 km2 |
| [41] | 2017 | Linear regression RF | Australia | GHI (in situ) | 5 min | 5 min–3 h | N.D. |
| [100] | 2017 | GBT | Japan | PV, NWP | 1 h | 1–6 h | 5 × 5 km2 |
| [99] | 2017 | RF, GBT | USA | NWP GHI (in situ) | 1 h | 24 h | N.D. |
| [65] | 2018 | ensemble (ridge regression GBM, SVM GP, NN, RF, BAG) | USA | GHI (in situ), NWP | N.D. | 24 h | N.D. |
| [79] | 2019 | SVM BRT MLP | USA | GHI (in situ), GHI (satellite) | 30 min | 30–120 min | 30 km2 |
| [22] | 2020 | MGGP, MLP | USA, Italy, Brazil | GHI (in situ) | 60 s | 15–120 min | N.D. |
| [21] | 2020 | CCN | USA | GHI (in situ) | 1 min | 5–15 min | N.D. |
| [20] | 2020 | CESN | USA | GHI (in situ) | 1 h | 1 h | N.D. |
| [73] | 2020 | ANN RF RT | Spain | GHI (in situ) | 30 min | 0.5–4 h | 94,226 km2 |
| [105] | 2021 | SVM, GBDT | China | PV | 15 min | 15 min 1–4 h | N.D. |
| [19] | 2018 | BPNN | China | GHI (in situ) | 1 h | 1 h | N.D. |
| [33] | 2020 | SVR ANN DNN | South Korea | GHI (satellite), PV, NWP | 1 h | 1 h | N.D. |
3.2.2. Advanced Deep Learning Methods
| Reference | Year | Model | Location | Data Source | Time Resolution | Forecast Horizon | Area |
|---|---|---|---|---|---|---|---|
| [24] | 2018 | DNN | The Netherlands | GHI (in situ), GHI (satellite), NWP | N.D. | 1–6 h | 41,543 km2 |
| [107] | 2019 | STCNN | USA | PV | 1 h | 1–6 h | N.D. |
| [32] | 2020 | LRCN | Germany | PV, NWP | 3 h | 24 h | 357,386 km2 |
| [108] | 2020 | CGAE | USA | GHI (in situ) | 30 min | 1–6 h | N.D. |
| [106] | 2020 | LSTM, GRU, CNN, Bidir-LSTM, Attention-LSTM | India | GHI (in situ), GHI (satellite) | 24 h | 1–10 days | 4.5 × 4.5 degrees |
| [26] | 2020 | LSTM | Morocco | GHI (in situ), GHI (satellite) | 1 h | 1 h | 40 × 40 km2 |
| [63] | 2020 | ConvLSTM | USA | PV | 5 min | 15–60 min | N.D. |
| [110] | 2020 | LSTM | N.D. | PV | 15 min | 20–80 min | 8 × 8 km2 |
| [111] | 2020 | ResNet-LSTM | USA | GHI (in situ) | 30 min | 1–12 h | N.D. |
| [34] | 2021 | GCLSTM, GCTrafo | Switzerland | GHI (in situ), PV, NWP | 15 min | 6 h | N.D. |
| [42] | 2021 | Conv-LSTM | USA | GHI (in situ) | 1 min | 1–61 min | 1 × 1 km2 |
| [23] | 2021 | ST-GNN | USA | PV | 5 min | 15–120 min | N.D. |
| [112] | 2021 | GSINN | USA | GHI (in situ) | 1 s | 10–40 s | N.D. |
| [113] | 2021 | DeepSTGDL | USA | PV | 15 min | 1–24 h | N.D. |
| [114] | 2021 | CGRVAE | USA | PV | 5 min | 10–30 min 1–6 h | N.D. |
| [115] | 2021 | STGANet | China | PV, GHI (in situ) | 1 h | 24 h | N.D. |
3.3. Physical Methods
| Reference | Year | Model | Location | Data Source | Time Resolution | Forecast Horizon | Area |
|---|---|---|---|---|---|---|---|
| [15] | 2013 | Advective | USA | PV | 15 min | 15–90 min | 50 × 50 km2 |
| [43] | 2014 | Advective | USA | GHI (in situ), PV | 5 min | 5–30 min | 37 × 44 km2 |
| [119] | 2015 | Advective | USA | GHI (in situ), PV | 1 min | 1 s–30 min | 40 × 30 km2 |
| [118] | 2015 | Advective | USA | PV | 1 s | 1–150 min | 1.8 × 0.5 km2 |
| [123] | 2017 | Coupled stochastic differential equations | USA | PV | 1 s | 5–120 s | N.D. |
| [122] | 2017 | Advective | Japan | PV | 1 s | 1 s | 6 × 6 m2 |
| [120] | 2017 | Advective | Japan | GHI (in situ), PV | 5 s 150 s | 10 min 50 s | 1.2 × 1.1 km2 160 × 40 km2 |
| [44] | 2019 | Advective | The Netherlands | GHI (in situ) | 15 min | 0–4 h | 6 × 4 km2 |
| [121] | 2019 | Advective | Japan | GHI (in situ) | 10–60 min | 10–60 min | 170 × 60 km2 |
3.4. Hybrid Methods
| Reference | Year | Model | Location | Data Source | Time Resolution | Forecast Horizon | Area |
|---|---|---|---|---|---|---|---|
| [124] | 2018 | Naïve Bayes Classifier, Kriging | South Korea | GHI (in situ), PV | 1 h | 24 h | N.D. |
| [125] | 2019 | Naïve Bayes Classifier, Kriging | South Korea | GHI (in situ), PV | 1 h | 24 h | N.D. |
| [126] | 2021 | Ensemble variations (GBM + GPR + RF + BAG) | South Korea | GHI (in situ), PV, NWP | 1 h | 12–52 h | N.D. |
| [28] | 2021 | SARIMAX-LSTM | South Korea | GHI (in situ), GHI (satellite), PV, NWP | 1 h | 3 h | N.D. |
4. Discussion
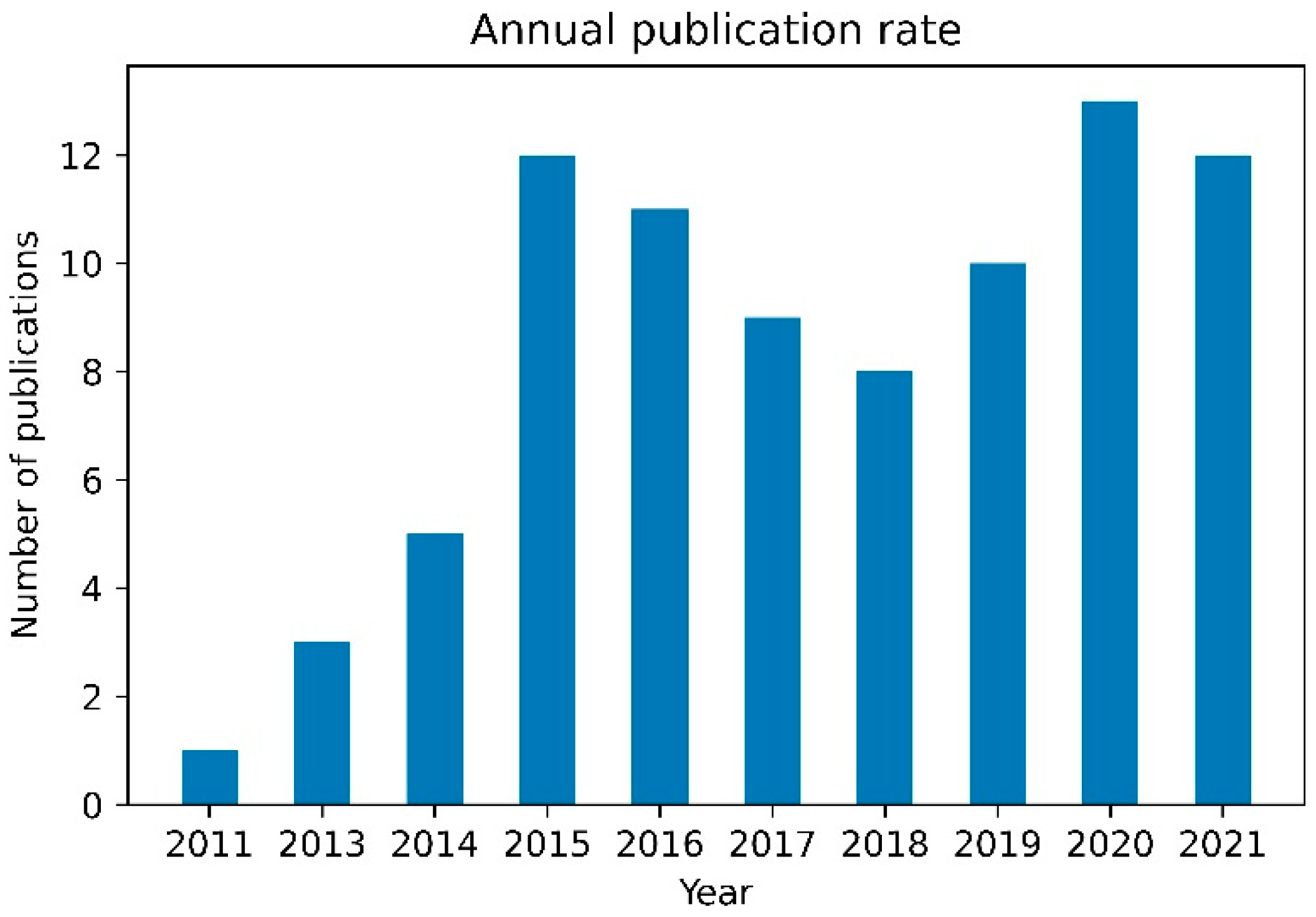
4.1. Number of Publications
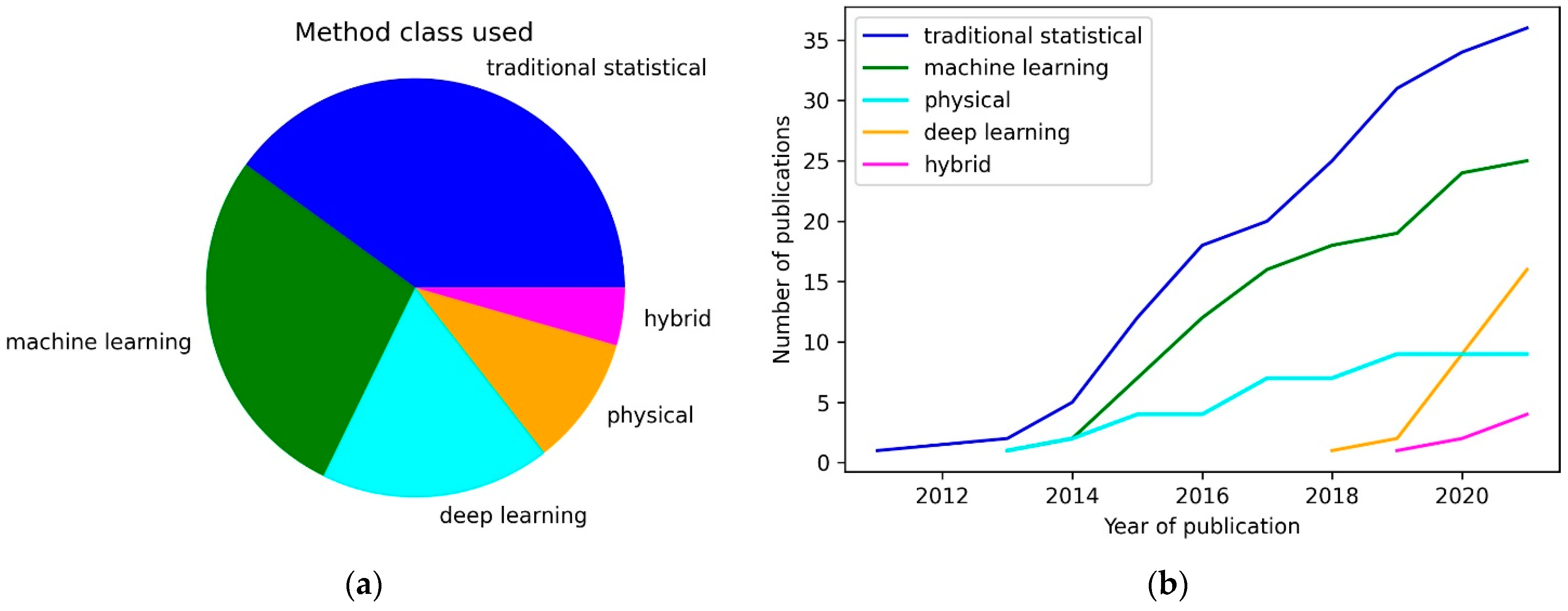
4.2. Data Sources
4.3. Methods
4.4. Forecasting Horizon
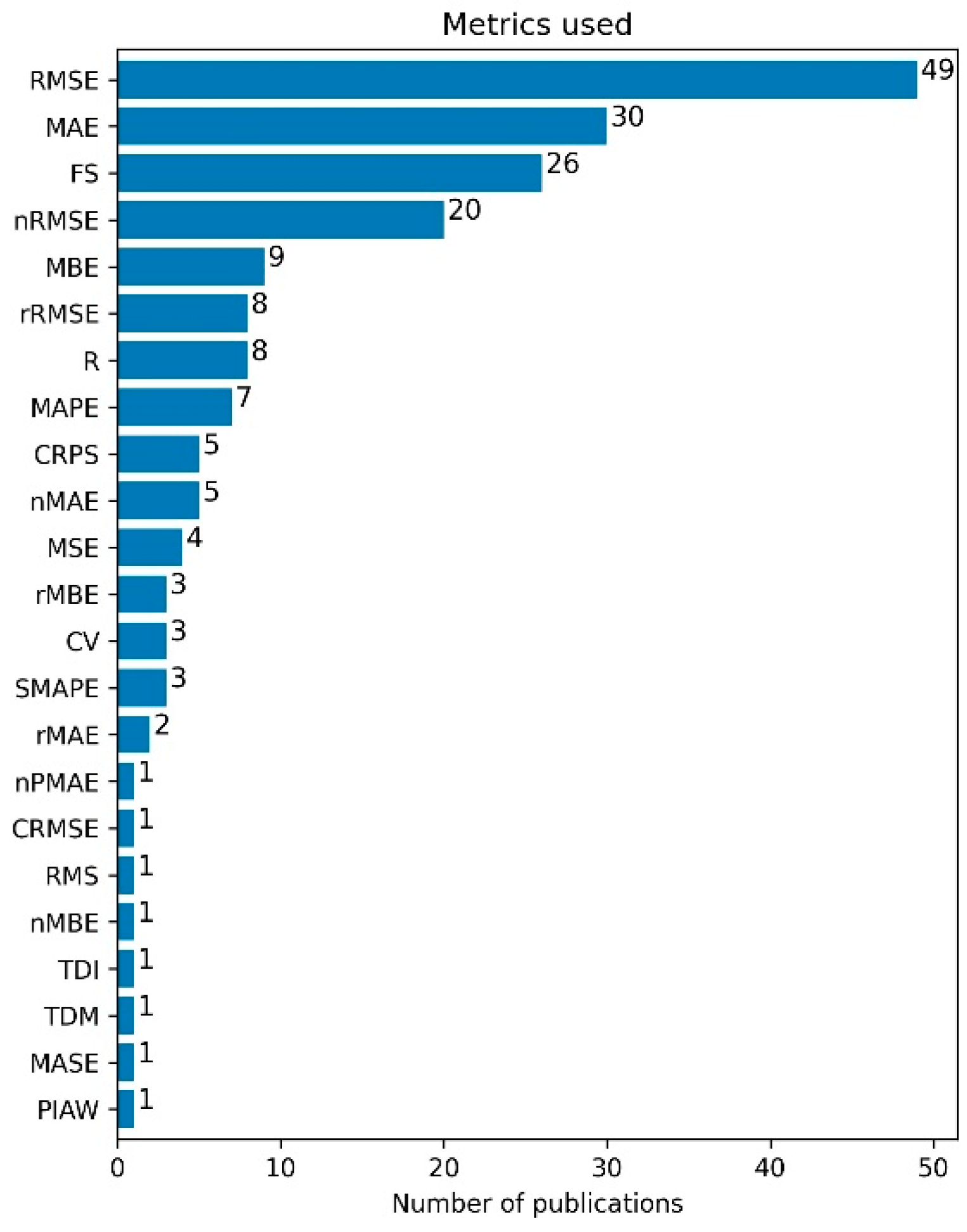
4.5. Evaluation Metrics
4.6. Considered Baseline
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hong, T.; Pinson, P.; Wang, Y.; Weron, R.; Yang, D.; Zareipour, H. Energy Forecasting: A Review and Outlook. IEEE Open Access J. Power Energy 2020, 7, 376–388. [Google Scholar] [CrossRef]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.C.; Coimbra, C.F.M. History and trends in solar irradiance and PV power forecasting: A preliminary assessment and review using text mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Perez, R.; David, M.; Hoff, T.E.; Jamaly, M.; Kivalov, S.; Kleissl, J.; Lauret, P.; Perez, M. Spatial and Temporal Variability of Solar Energy. Found. Trends Renew. Energy 2016, 1, 1–44. [Google Scholar] [CrossRef] [Green Version]
- Amaro e Silva, R. Spatio-Temporal Solar Forecasting. Ph.D. Thesis, Universidade de Lisboa, Lisboa, Portugal, 2019. [Google Scholar]
- Jimenez, P.A.; Hacker, J.P.; Dudhia, J.; Haupt, S.E.; Ruiz-Arias, J.A.; Gueymard, C.A.; Thompson, G.; Eidhammer, T.; Deng, A. WRF-SOLAR: Description and clear-sky assessment of an augmented NWP model for solar power prediction. Bull. Am. Meteorol. Soc. 2016, 97, 1249–1264. [Google Scholar] [CrossRef]
- Arbizu-Barrena, C.; Ruiz-Arias, J.A.; Rodríguez-Benítez, F.J.; Pozo-Vázquez, D.; Tovar-Pescador, J. Short-term solar radiation forecasting by advecting and diffusing MSG cloud index. Sol. Energy 2017, 155, 1092–1103. [Google Scholar] [CrossRef]
- Oh, M.; Kim, C.K.; Kim, B.; Yun, C.; Kang, Y.H.; Kim, H.G. Spatiotemporal optimization for short-term solar forecasting based on satellite imagery. Energies 2021, 14, 2216. [Google Scholar] [CrossRef]
- Chow, C.W.; Urquhart, B.; Lave, M.; Dominguez, A.; Kleissl, J.; Shields, J.; Washom, B. Intra-hour forecasting with a total sky imager at the UC San Diego solar energy testbed. Sol. Energy 2011, 85, 2881–2893. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, T.; Kalisch, J.; Lorenz, E.; Heinemann, D. Evaluating the spatio-temporal performance of sky-imager-based solar irradiance analysis and forecasts. Atmos. Chem. Phys. 2016, 16, 3399–3412. [Google Scholar] [CrossRef] [Green Version]
- Barbieri, F.; Rajakaruna, S.; Ghosh, A. Very short-term photovoltaic power forecasting with cloud modeling: A review. Renew. Sustain. Energy Rev. 2017, 75, 242–263. [Google Scholar] [CrossRef] [Green Version]
- Aguiar, L.M.; Pereira, B.; Lauret, P.; Díaz, F.; David, M. Combining solar irradiance measurements, satellite-derived data and a numerical weather prediction model to improve intra-day solar forecasting. Renew. Energy 2016, 97, 599–610. [Google Scholar] [CrossRef] [Green Version]
- Pedro, H.T.C.; Coimbra, C.F.M. Assessment of forecasting techniques for solar power production with no exogenous inputs. Sol. Energy 2012, 86, 2017–2028. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Abdel Aleem, S.H.E.; Omar, N.; Ahmadi, A.; Alenezi, F.Q. Short-term solar power forecasting considering cloud coverage and ambient temperature variation effects. Renew. Energy 2018, 123, 793–805. [Google Scholar] [CrossRef]
- Yang, D.; Ye, Z.; Lim, L.H.I.; Dong, Z. Very short term irradiance forecasting using the lasso. Sol. Energy 2015, 114, 314–326. [Google Scholar] [CrossRef] [Green Version]
- Lonij, V.P.A.; Brooks, A.E.; Cronin, A.D.; Leuthold, M.; Koch, K. Intra-hour forecasts of solar power production using measurements from a network of irradiance sensors. Sol. Energy 2013, 97, 58–66. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef] [Green Version]
- Yang, D. Ultra-fast preselection in lasso-type spatio-temporal solar forecasting problems. Sol. Energy 2018, 176, 788–796. [Google Scholar] [CrossRef]
- Vaz, A.G.R.; Elsinga, B.; van Sark, W.G.J.H.M.; Brito, M.C. An artificial neural network to assess the impact of neighbouring photovoltaic systems in power forecasting in Utrecht, The Netherlands. Renew. Energy 2016, 85, 631–641. [Google Scholar] [CrossRef] [Green Version]
- Lan, H.; Yin, H.; Hong, Y.Y.; Wen, S.; Yu, D.C.; Cheng, P. Day-ahead spatio-temporal forecasting of solar irradiation along a navigation route. Appl. Energy 2018, 211, 15–27. [Google Scholar] [CrossRef]
- Li, Q.; Wu, Z.; Zhang, H. Spatio-temporal modeling with enhanced flexibility and robustness of solar irradiance prediction: A chain-structure echo state network approach. J. Clean. Prod. 2020, 261, 121151. [Google Scholar] [CrossRef]
- Pathiravasam, C.; Arunagirinathan, P.; Jayawardene, I.; Venayagamoorthy, G.K.; Wang, Y. Spatio-Temporal Distributed Solar Irradiance and Temperature Forecasting. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020. [Google Scholar] [CrossRef]
- De Paiva, G.M.; Pimentel, S.P.; Alvarenga, B.P.; Marra, E.G.; Mussetta, M.; Leva, S. Multiple site intraday solar irradiance forecasting by machine learning algorithms: MGGP and MLP neural networks. Energies 2020, 13, 3005. [Google Scholar] [CrossRef]
- Karimi, A.M.; Wu, Y.; Koyuturk, M.; French, R.H. Spatiotemporal Graph Neural Network for Performance Prediction of Photovoltaic Power Systems. In Proceedings of the AAAI Conference on Artificial Intelligence, Palo Alto, CA, USA, 2–9 February 2021; Volume 35, pp. 15323–15330. [Google Scholar]
- Lago, J.; De Brabandere, K.; De Ridder, F.; De Schutter, B. Short-term forecasting of solar irradiance without local telemetry: A generalized model using satellite data. Sol. Energy 2018, 173, 566–577. [Google Scholar] [CrossRef] [Green Version]
- André, M.; Perez, R.; Soubdhan, T.; Schlemmer, J.; Calif, R.; Monjoly, S. Preliminary assessment of two spatio-temporal forecasting technics for hourly satellite-derived irradiance in a complex meteorological context. Sol. Energy 2019, 177, 703–712. [Google Scholar] [CrossRef]
- Benamrou, B.; Ouardouz, M.; Allaouzi, I.; Ahmed, M. Ben A proposed model to forecast hourly global solar irradiation based on satellite derived data, deep learning and machine learning approaches. J. Ecol. Eng. 2020, 21, 26–38. [Google Scholar] [CrossRef]
- Liu, G.; Qin, H.; Shen, Q.; Lyv, H.; Qu, Y.; Fu, J.; Liu, Y.; Zhou, J. Probabilistic spatiotemporal solar irradiation forecasting using deep ensembles convolutional shared weight long short-term memory network. Appl. Energy 2021, 300, 117379. [Google Scholar] [CrossRef]
- Kim, B.; Suh, D.; Otto, M.O.; Huh, J.S. A novel hybrid spatio-temporal forecasting of multisite solar photovoltaic generation. Remote Sens. 2021, 13, 2605. [Google Scholar] [CrossRef]
- Andrade, J.R.; Bessa, R.J. Improving Renewable Energy Forecasting with a Grid of Numerical Weather Predictions. IEEE Trans. Sustain. Energy 2017, 8, 1571–1580. [Google Scholar] [CrossRef] [Green Version]
- Agoua, X.G.; Girard, R.; Kariniotakis, G. Probabilistic Models for Spatio-Temporal Photovoltaic Power Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 780–789. [Google Scholar] [CrossRef] [Green Version]
- Amaro e Silva, R.; Brito, M.C. Spatio-temporal PV forecasting sensitivity to modules’ tilt and orientation. Appl. Energy 2019, 255, 113807. [Google Scholar] [CrossRef]
- Mathe, J.; Miolane, N.; Sebastien, N.; Lequeux, J. PVNet: A LRCN Architecture for Spatio-Temporal Photovoltaic PowerForecasting from Numerical Weather Prediction. arXiv 2019, arXiv:1902.01453. [Google Scholar]
- Kim, B.; Suh, D. A hybrid spatio-temporal prediction model for solar photovoltaic generation using numerical weather data and satellite images. Remote Sens. 2020, 12, 3706. [Google Scholar] [CrossRef]
- Simeunović, J.; Schubnel, B.; Alet, P.-J.; Carrillo, R.E. Spatio-temporal graph neural networks for multi-site PV power forecasting. IEEE Trans. Sustain. Energy 2021, 13, 1210–1220. [Google Scholar] [CrossRef]
- Inman, R.H.; Pedro, H.T.C.; Coimbra, C.F.M. Solar forecasting methods for renewable energy integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Singla, P.; Duhan, M.; Saroha, S. Acomprehensive review and analysis of solar forecasting techniques. Front. Energy 2021, 1–37. [Google Scholar] [CrossRef]
- Sperati, S.; Alessandrini, S.; Delle Monache, L. An application of the ECMWF Ensemble Prediction System for short-term solar power forecasting. Sol. Energy 2016, 133, 437–450. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Shimada, S.; Yoshino, J.; Kobayashi, T.; Miwa, Y.; Furuta, K. Ensemble forecasting of solar irradiance by applying a mesoscale meteorological model. Sol. Energy 2016, 136, 597–605. [Google Scholar] [CrossRef]
- Chen, Y.; Thatte, A.A.; Le, X. Multitime-scale data-driven spatio-temporal forecast of photovoltaic generation. IEEE Trans. Sustain. Energy 2015, 6, 104–112. [Google Scholar]
- André, M.; Dabo-Niang, S.; Soubdhan, T.; Ould-Baba, H. Predictive spatio-temporal model for spatially sparse global solar radiation data. Energy 2016, 111, 599–608. [Google Scholar] [CrossRef]
- Chen, Z.; Troccoli, A. Urban solar irradiance and power prediction from nearby stations. Meteorol. Z. 2017, 26, 277–290. [Google Scholar] [CrossRef]
- Prado-Rujas, I.I.; Garcia-Dopico, A.; Serrano, E.; Perez, M.S. A flexible and robust deep learning-based system for solar irradiance forecasting. IEEE Access 2021, 9, 12348–12361. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Holmgren, W.F.; Leuthold, M.; Kim, C.K.; Cronin, A.D.; Betterton, E.A. Short-term PV power forecasts based on a real-time irradiance monitoring network. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC 2014), Denver, CO, USA, 8–13 June 2014; pp. 75–79. [Google Scholar] [CrossRef]
- Wang, P.; van Westrhenen, R.; Meirink, J.F.; van der Veen, S.; Knap, W. Surface solar radiation forecasts by advecting cloud physical properties derived from Meteosat Second Generation observations. Sol. Energy 2019, 177, 47–58. [Google Scholar] [CrossRef]
- Amaro e Silva, R.C.; Brito, M. Understanding spatio-temporal solar forecasting. In Proceedings of the 7th Solar Integration Workshop, Berlin, Germany, 24–25 October 2017; pp. 1–9. [Google Scholar]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Deep learning models for solar irradiance forecasting: A comprehensive review. J. Clean. Prod. 2021, 318, 128566. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Wang, D.; Liu, X.; Wang, Y. A review on global solar radiation prediction with machine learning models in a comprehensive perspective. Energy Convers. Manag. 2021, 235, 113960. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Ogliari, E.; Leva, S.; Lughi, V. Advanced methods for photovoltaic output power forecasting: A review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, T.; Zhang, H.; Yan, B. A review on renewable energy and electricity requirement forecasting models for smart grid and buildings. Sustain. Cities Soc. 2020, 55, 102052. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.A.; Lee, H.J. A review on deep learning models for forecasting time series data of solar irradiance and photovoltaic power. Energie 2020, 13, 6623. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, H.; Zhang, Z.; Pei, S.; Wang, C.; Yu, X.; Jiang, Z.; Zhou, J. Ensemble spatiotemporal forecasting of solar irradiation using variational Bayesian convolutional gate recurrent unit network. Appl. Energy 2019, 253, 113596. [Google Scholar] [CrossRef]
- Amaro e Silva, R.C.; Brito, M. Impact of network layout and time resolution on spatio-temporal solar forecasting. Sol. Energy 2018, 163, 329–337. [Google Scholar] [CrossRef]
- Tascikaraoglu, A. Evaluation of spatio-temporal forecasting methods in various smart city applications. Renew. Sustain. Energy Rev. 2018, 82, 424–435. [Google Scholar] [CrossRef]
- Yang, D.; Gu, C.; Dong, Z.; Jirutitijaroen, P.; Chen, N.; Walsh, W.M. Solar irradiance forecasting using spatial-temporal covariance structures and time-forward kriging. Renew. Energy 2013, 60, 235–245. [Google Scholar] [CrossRef]
- Zhang, B.; Dehghanian, P.; Kezunovic, M. Spatial-temporal solar power forecast through use of Gaussian Conditional Random Fields. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016; pp. 16–20. [Google Scholar] [CrossRef]
- Boland, J. Spatial-temporal forecasting of solar radiation. Renew. Energy 2015, 75, 607–616. [Google Scholar] [CrossRef]
- Licciardi, G.A.; Dambreville, R.; Chanussot, J.; Dubost, S. Spatiotemporal pattern recognition and nonlinear PCA for global horizontal irradiance forecasting. IEEE Geosci. Remote Sens. Lett. 2015, 12, 284–288. [Google Scholar] [CrossRef]
- Chai, S.; Xu, Z.; Jia, Y.; Wong, W.K. A Robust Spatiotemporal Forecasting Framework for Photovoltaic Generation. IEEE Trans. Smart Grid 2020, 11, 5370–5382. [Google Scholar] [CrossRef]
- Lan, H.; Zhang, C.; Hong, Y.Y.; He, Y.; Wen, S. Day-ahead spatiotemporal solar irradiation forecasting using frequency-based hybrid principal component analysis and neural network. Appl. Energy 2019, 247, 389–402. [Google Scholar] [CrossRef]
- Baek, M.; Lee, D. Spatial and Temporal Day-Ahead Total Daily Solar Irradiation Forecasting: Ensemble Forecasting Based on the Empirical Biasing. Energies 2018, 11, 70. [Google Scholar] [CrossRef] [Green Version]
- Alqudah, M.; Djokic, T.; Kezunovic, M.; Obradovic, Z. Prediction of Solar Radiation Based on Spatial and Temporal Embeddings for Solar Generation Forecast. In Proceedings of the 53rd Hawaii International Conference on System Sciences, Grand Wailea, HI, USA, 7–10 January 2020; Volume 3, pp. 2971–2980. [Google Scholar] [CrossRef] [Green Version]
- van der Meer, D.W.; Widén, J.; Munkhammar, J. Review on probabilistic forecasting of photovoltaic power production and electricity consumption. Renew. Sustain. Energy Rev. 2018, 81, 1484–1512. [Google Scholar] [CrossRef]
- Yang, B.; Zhu, T.; Cao, P.; Guo, Z.; Zeng, C.; Li, D.; Chen, Y.; Ye, H.; Shao, R.; Shu, H. Classification and summarization of solar irradiance and power forecasting methods: A thorough review. CSEE J. Power Energy Syst. 2021, 1–19. [Google Scholar] [CrossRef]
- Wilbert, S.; Kraas, B.; Gueymard, C.; Services, S.C. Expert quality control of solar radiation ground data sets. In Proceedings of the ISES Solar World Congress, Online Event, 25–29 October 2021; Available online: https://www.swc2021.org/about-swc-2021/organisers (accessed on 6 June 2022).
- Dambreville, R.; Blanc, P.; Chanussot, J.; Boldo, D. Very short term forecasting of the global horizontal irradiance using a spatio-temporal autoregressive model. Renew. Energy 2014, 72, 291–300. [Google Scholar] [CrossRef]
- Basha, E.; Jurdak, R.; Rus, D. In-network distributed solar current prediction. ACM Trans. Sens. Netw. 2015, 11, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Agoua, X.G.; Girard, R.; Kariniotakis, G. Spatio-temporal models for photovoltaic power short-term forecasting. In Proceedings of the 5th Solar Integration Workshop, Brussels, Belgium, 19–20 October 2015; Volume 16, pp. 999–1012. [Google Scholar]
- Eschenbach, A.; Yepes, G.; Tenllado, C.; Gomez-Perez, J.I.; Pinuel, L.; Zarzalejo, L.F.; Wilbert, S. Spatio-Temporal Resolution of Irradiance Samples in Machine Learning Approaches for Irradiance Forecasting. IEEE Access 2020, 8, 51518–51531. [Google Scholar] [CrossRef]
- Bessa, R.J.; Trindade, A.; Silva, C.S.P.; Miranda, V. Probabilistic solar power forecasting in smart grids using distributed information. Int. J. Electr. Power Energy Syst. 2015, 72, 16–23. [Google Scholar] [CrossRef] [Green Version]
- Aryaputera, A.W.; Yang, D.; Zhao, L.; Walsh, W.M. Very short-term irradiance forecasting at unobserved locations using spatio-temporal kriging. Sol. Energy 2015, 122, 1266–1278. [Google Scholar] [CrossRef]
- Jamaly, M.; Kleissl, J. Spatiotemporal interpolation and forecast of irradiance data using Kriging. Sol. Energy 2017, 158, 407–423. [Google Scholar] [CrossRef]
- Heidari Kapourchali, M.; Sepehry, M.; Aravinthan, V. Multivariate Spatio-temporal Solar Generation Forecasting: A Unified Approach to Deal with Communication Failure and Invisible Sites. IEEE Syst. J. 2019, 13, 1804–1812. [Google Scholar] [CrossRef]
- Agoua, X.G.; Girard, R.; Kariniotakis, G. Photovoltaic Power Forecasting: Assessment of the Impact of Multiple Sources of Spatio-Temporal Data on Forecast Accuracy. Energies 2021, 14, 1432. [Google Scholar] [CrossRef]
- Huang, C.; Wang, L.; Lai, L.L. Data-Driven Short-Term Solar Irradiance Forecasting Based on Information of Neighboring Sites. IEEE Trans. Ind. Electron. 2019, 66, 9918–9927. [Google Scholar] [CrossRef]
- Amaro, E.; Silva, R.; Haupt, S.E.; Brito, M.C. A regime-based approach for integrating wind information in spatiooral solar forecasting models. J. Renew. Sustain. Energy 2019, 11, 056102. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Yang, D.; Dong, Z.; Reindl, T.; Jirutitijaroen, P.; Walsh, W.M. Solar irradiance forecasting using spatio-temporal empirical kriging and vector autoregressive models with parameter shrinkage. Sol. Energy 2014, 103, 550–562. [Google Scholar] [CrossRef]
- Berdugo, V.; Chaussin, C.; Dubus, L.; Hebrail, G.; Leboucher, V. Analog Method for Collaborative Very-Short-Term Forecasting of Power Generation from Photovoltaic Systems. In Proceedings of the Next Generation Data Mining Summit (NGDM-11), Athens, Greece, 4 September 2011. [Google Scholar]
- Elsinga, B.; van Sark, W.G.J.H.M. Short-term peer-to-peer solar forecasting in a network of photovoltaic systems. Appl. Energy 2017, 206, 1464–1483. [Google Scholar] [CrossRef]
- Domke, J.; Engerer, N.; Menon, A.; Webers, C. Distributed solar prediction with wind velocity. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Portland, OR, USA, 5–10 June 2016; pp. 1218–1223. [Google Scholar] [CrossRef]
- Xu, J.; Yoo, S.; Heiser, J.; Kalb, P. Sensor network based solar forecasting using a local vector autoregressive ridge framework. In Proceedings of the ACM Symposium on Applied Computing, Pisa, Italy, 4–8 April 2016; pp. 2113–2118. [Google Scholar] [CrossRef]
- Nobre, A.M.; Severiano, C.A.; Karthik, S.; Kubis, M.; Zhao, L.; Martins, F.R.; Pereira, E.B.; Rüther, R.; Reindl, T. PV power conversion and short-term forecasting in a tropical, densely-built environment in Singapore. Renew. Energy 2016, 94, 496–509. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Sanandaji, B.M.; Chicco, G.; Cocina, V.; Spertino, F.; Erdinc, O.; Paterakis, N.G.; Catalao, J.P.S. Compressive Spatio-Temporal Forecasting of Meteorological Quantities and Photovoltaic Power. IEEE Trans. Sustain. Energy 2016, 7, 1295–1305. [Google Scholar] [CrossRef]
- Agoua, X.G.; Girard, R.; Kariniotakis, G. Short-Term Spatio-Temporal Forecasting of Photovoltaic Power Production. IEEE Trans. Sustain. Energy 2018, 9, 538–546. [Google Scholar] [CrossRef] [Green Version]
- Yang, D. Spatial prediction using kriging ensemble. Sol. Energy 2018, 171, 977–982. [Google Scholar] [CrossRef]
- Chen, X.; Du, Y.; Lim, E.; Wen, H.; Jiang, L. Sensor network based PV power nowcasting with spatio-temporal preselection for grid-friendly control. Appl. Energy 2019, 255, 113760. [Google Scholar] [CrossRef]
- Carrillo, R.E.; Leblanc, M.; Schubnel, B.; Langou, R.; Topfel, C.; Alet, P.J. High-resolution pv forecasting from imperfect data: A graph-based solution. Energies 2020, 13, 5763. [Google Scholar] [CrossRef]
- Severiano, C.A.; Silva, P.C.; Weiss Cohen, M.; Guimarães, F.G. Evolving fuzzy time series for spatio-temporal forecasting in renewable energy systems. Renew. Energy 2021, 171, 764–783. [Google Scholar] [CrossRef]
- Marquez, R.; Pedro, H.T.C.; Coimbra, C.F.M. Hybrid solar forecasting method uses satellite imaging and ground telemetry as inputs to ANNs. Sol. Energy 2013, 92, 176–188. [Google Scholar] [CrossRef]
- Amrouche, B.; Le Pivert, X. Artificial neural network based daily local forecasting for global solar radiation. Appl. Energy 2014, 130, 333–341. [Google Scholar] [CrossRef]
- Kashyap, Y.; Bansal, A.; Sao, A.K. Spatial Approach of Artificial Neural Network for Solar Radiation Forecasting: Modeling Issues. J. Sol. Energy 2015, 2015, 410684. [Google Scholar] [CrossRef] [Green Version]
- Mazorra Aguiar, L.; Pereira, B.; David, M.; Díaz, F.; Lauret, P. Use of satellite data to improve solar radiation forecasting with Bayesian Artificial Neural Networks. Sol. Energy 2015, 122, 1309–1324. [Google Scholar] [CrossRef]
- Chen, C.R.; Kartini, U.T. Artificial Neural Networks Model for Short Term Forecasting Global Irradiation at Center Station in the Nine Station Photovoltaic. In Proceedings of the AMS 2015: Asia Modelling Symposium 2015—Asia 9th International Conference on Mathematical Modelling and Computer Simulation, Kuala Lumpur, Malaysia, 7–9 September 2016; pp. 3–8. [Google Scholar] [CrossRef]
- Gagne, D.J.; McGovern, A.; Haupt, S.E.; Williams, J.K. Evaluation of statistical learning configurations for gridded solar irradiance forecasting. Sol. Energy 2017, 150, 383–393. [Google Scholar] [CrossRef]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Lazzaroni, M.; Ferrari, S.; Piuri, V.; Salman, A.; Cristaldi, L.; Faifer, M. Models for solar radiation prediction based on different measurement sites. Meas. J. Int. Meas. Confed. 2015, 63, 346–363. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, H.; Zhao, X.; Liu, T.; Zhang, K. A Gaussian process regression based hybrid approach for short-term wind speed prediction. Energy Convers. Manag. 2016, 126, 1084–1092. [Google Scholar] [CrossRef]
- Gutierrez-Corea, F.V.; Manso-Callejo, M.A.; Moreno-Regidor, M.P.; Manrique-Sancho, M.T. Forecasting short-term solar irradiance based on artificial neural networks and data from neighboring meteorological stations. Sol. Energy 2016, 134, 119–131. [Google Scholar] [CrossRef]
- Sharma, V.; Yang, D.; Walsh, W.; Reindl, T. Short term solar irradiance forecasting using a mixed wavelet neural network. Renew. Energy 2016, 90, 481–492. [Google Scholar] [CrossRef]
- Wang, F.; Lu, X.; Mei, S.; Su, Y.; Zhen, Z.; Zou, Z.; Zhang, X.; Yin, R.; Duić, N.; Shafie-khah, M.; et al. A Satellite Image Data based Ultra-short-term Solar PV Power Forecasting Method Considering Cloud Information from Neighboring Plant. Energy 2021, 238, 121946. [Google Scholar] [CrossRef]
- Brahma, B.; Wadhvani, R. Solar irradiance forecasting based on deep learning methodologies and multi-site data. Symmetry 2020, 12, 1830. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, H. Multi-site photovoltaic forecasting exploiting space-time convolutional neural network. Energies 2019, 12, 4490. [Google Scholar] [CrossRef] [Green Version]
- Khodayar, M.; Mohammadi, S.; Khodayar, M.E.; Wang, J.; Liu, G. Convolutional graph autoencoder: A generative deep neural network for probabilistic spatio-temporal solar irradiance forecasting. IEEE Trans. Sustain. Energy 2020, 11, 571–583. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- De Jongh, S.; Riedel, T.; Mueller, F.; Yacoub, A.E.; Suriyah, M.; Leibfried, T. Spatio-Temporal Short Term Photovoltaic Generation Forecasting with Uncertainty Estimates using Machine Learning Methods. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Turin, Italy, 1–4 September 2020. [Google Scholar] [CrossRef]
- Ziyabari, S.; Du, L.; Biswas, S. A Spatio-temporal Hybrid Deep Learning Architecture for Short-term Solar Irradiance Forecasting. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, AB, Canada, 15 June–21 August 2020; pp. 0833–0838. [Google Scholar] [CrossRef]
- Jiao, X.; Li, X.; Lin, D.; Xiao, W. A Graph Neural Network based Deep Learning Predictor for Spatio-Temporal Group Solar Irradiance Forecasting. IEEE Trans. Ind. Inform. 2021, 3203, 1–9. [Google Scholar] [CrossRef]
- Khodayar, M.; Liu, G.; Wang, J.; Kaynak, O.; Khodayar, M.E. Spatiotemporal Behind-the-Meter Load and PV Power Forecasting via Deep Graph Dictionary Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4713–4727. [Google Scholar] [CrossRef]
- Saffari, M.; Khodayar, M.; Jalali, S.M.J.; Shafie-Khah, M.; Catalao, J.P.S. Deep convolutional graph rough variational auto-encoder for short-term photovoltaic power forecasting. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Fan, T.; Sun, T.; Liu, H.; Xie, X.; Na, Z. Spatial-Temporal Genetic-Based Attention Networks for Short-Term Photovoltaic Power Forecasting. IEEE Access 2021, 9, 138762–138774. [Google Scholar] [CrossRef]
- Bosch, J.L.; Kleissl, J. Cloud motion vectors from a network of ground sensors in a solar power plant. Sol. Energy 2013, 95, 13–20. [Google Scholar] [CrossRef]
- Bosch, J.L.; Zheng, Y.; Kleissl, J. Deriving cloud velocity from an array of solar radiation measurements. Sol. Energy 2013, 87, 196–203. [Google Scholar] [CrossRef] [Green Version]
- Lipperheide, M.; Bosch, J.L.; Kleissl, J. Embedded nowcasting method using cloud speed persistence for a photovoltaic power plant. Sol. Energy 2015, 112, 232–238. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Holmgren, W.F.; Cronin, A.D. Irradiance forecasts based on an irradiance monitoring network, cloud motion, and spatial averaging. Sol. Energy 2015, 122, 1158–1169. [Google Scholar] [CrossRef] [Green Version]
- Inage, S. Development of an advection model for solar forecasting based on ground data first report: Development and verification of a fundamental model. Sol. Energy 2017, 153, 414–434. [Google Scholar] [CrossRef]
- Inage, S.-I. Development of an advection model for solar forecasting based on ground data. Part II: Verification of the forecasting model over a wide geographical area. Sol. Energy 2019, 180, 257–276. [Google Scholar] [CrossRef]
- Nomura, R.; Harigai, T.; Suda, Y.; Takikawa, H. Second by second prediction of solar power generation based on cloud shadow behavior estimation near a power station. In Proceedings of the AIP Conference Proceedings 2017, Tokyo, Japan, 1–2 November 2016; Volume 1807. [Google Scholar] [CrossRef] [Green Version]
- Iversen, E.B.; Juhl, R.; Møller, J.K.; Kleissl, J.; Madsen, H.; Morales, J.M. Spatio-Temporal Forecasting by Coupled Stochastic Differential Equations: Applications to Solar Power. arXiv 2017, arXiv:1706.04394. [Google Scholar]
- Nam, S.; Hur, J. Probabilistic Forecasting Model of Solar Power Outputs Based on the Naive Bayes Classifier and Kriging Models. Energies 2018, 11, 2982. [Google Scholar] [CrossRef] [Green Version]
- Nam, S.; Hur, J. A hybrid spatio-temporal forecasting of solar generating resources for grid integration. Energy 2019, 177, 503–510. [Google Scholar] [CrossRef]
- Kim, H.; Lee, D. Probabilistic Solar Power Forecasting Based on Bivariate Conditional Solar Irradiation Distributions. IEEE Trans. Sustain. Energy 2021, 12, 2031–2041. [Google Scholar] [CrossRef]
- Wang, C.; Wu, J.; Wang, J.; Hu, Z. Short-term wind speed forecasting using the data processing approach and the support vector machine model optimized by the improved cuckoo search parameter estimation algorithm. Math. Probl. Eng. 2016, 2016, 4896854. [Google Scholar] [CrossRef]
- Haupt, S.E.; Kosović, B. Variable Generation Power Forecasting as a Big Data Problem. IEEE Trans. Sustain. Energy 2017, 8, 725–732. [Google Scholar] [CrossRef]
- Yang, D. Solar Irradiance Modeling and Forecasting Using Novel Statistical Techniques. Ph.D. Thesis, National University of Singapore, Singapore, 2014. [Google Scholar] [CrossRef]
- Zhang, J.; Florita, A.; Hodge, B.M.; Lu, S.; Hamann, H.F.; Banunarayanan, V.; Brockway, A.M. A suite of metrics for assessing the performance of solar power forecasting. Sol. Energy 2015, 111, 157–175. [Google Scholar] [CrossRef] [Green Version]
- Kostylev, V.; Pavlovski, A. Solar Power Forecasting Performance—Towards Industry Standards 2011. Available online: https://kipdf.com/solar-power-forecasting-performance-towards-industry-standards_5ab3c2db1723dd329c63dbf6.html (accessed on 6 June 2022).
- Zamo, M.; Mestre, O.; Arbogast, P.; Pannekoucke, O. A benchmark of statistical regression methods for short-term forecasting of photovoltaic electricity production. Part II: Probabilistic forecast of daily production. Sol. Energy 2014, 105, 804–816. [Google Scholar] [CrossRef]
- Pedro, H.T.C.; Coimbra, C.F.M.; David, M.; Lauret, P. Assessment of machine learning techniques for deterministic and probabilistic intra-hour solar forecasts. Renew. Energy 2018, 123, 191–203. [Google Scholar] [CrossRef]

| Forecast Horizon Class | Range |
|---|---|
| Intra-hour | A few seconds to 1 h ahead |
| Intra-day | 1 to 6 h ahead |
| Six hours to one day ahead | 6 to 48 h ahead |
| Two days ahead or longer | 48 h ahead |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benavides Cesar, L.; Amaro e Silva, R.; Manso Callejo, M.Á.; Cira, C.-I. Review on Spatio-Temporal Solar Forecasting Methods Driven by In Situ Measurements or Their Combination with Satellite and Numerical Weather Prediction (NWP) Estimates. Energies 2022, 15, 4341. https://doi.org/10.3390/en15124341
Benavides Cesar L, Amaro e Silva R, Manso Callejo MÁ, Cira C-I. Review on Spatio-Temporal Solar Forecasting Methods Driven by In Situ Measurements or Their Combination with Satellite and Numerical Weather Prediction (NWP) Estimates. Energies. 2022; 15(12):4341. https://doi.org/10.3390/en15124341
Chicago/Turabian StyleBenavides Cesar, Llinet, Rodrigo Amaro e Silva, Miguel Ángel Manso Callejo, and Calimanut-Ionut Cira. 2022. "Review on Spatio-Temporal Solar Forecasting Methods Driven by In Situ Measurements or Their Combination with Satellite and Numerical Weather Prediction (NWP) Estimates" Energies 15, no. 12: 4341. https://doi.org/10.3390/en15124341
APA StyleBenavides Cesar, L., Amaro e Silva, R., Manso Callejo, M. Á., & Cira, C.-I. (2022). Review on Spatio-Temporal Solar Forecasting Methods Driven by In Situ Measurements or Their Combination with Satellite and Numerical Weather Prediction (NWP) Estimates. Energies, 15(12), 4341. https://doi.org/10.3390/en15124341







