1. Introduction
Nanofluids are a new category of nanotechnology-based thermal transfer liquids that are created by dissolving and suspending nanosized particles with distinctive diameters on the order of 10 nanometers. Base liquids often include water, motor oil, organic liquids, and other basic liquids. Choi [
1] hypothesized about the possession of thermal conductivity and thermal transfer using nanofluids in 1995. A nanofluid is a developing liquid that has resulted in a number of scientific achievements in the nano industry. Choi, in his survey, discovered that a nanofluid is more efficient than any other fluid. The majority of nanofluid articles focus on understanding their behavior so that they may be used in situations where direct heat transfer improvement is critical, such as in many industrial applications, nuclear reactors, transportation, electronics, medicine, and food. Recently, in the context of a Casson nanofluid, Abu et al. [
2] conducted a theoretical examination of a single vapor bubble in power-law fluid impacted by varying surface tension over Al
2O
3/H
2O nanofluids. Prasannakumara [
3] used NaAlg-Cu nanofluid to conduct a quantitative investigation of the local thermal non-equilibrium conditions for a nano liquid (NaAlg-Cu) passing over a porous medium. Khan et al. [
4] investigated the Cattaneo–Christov thermal flow model and the OHAM approach across three distinct fluids. The study demonstrated that a progressive increase in thermal relaxation parameters results in fluid temperature exhaustion and an increased heat transfer rate. Alzahrani et al. [
5] explored the influence of thermal radiation with suction and slip conditions in the presence of a Casson nanofluid over a plane wall jet. Morad et al. [
6] examined the thermophysical bubble movements in an N-dimensional Al
2O
3/H
2O nano liquid under two-phase turbulent flow. Bhowmik et al. [
7] conducted a rod bundle thermal–hydraulic investigation with water and a water-based Al
2O
3 nanofluid for a tiny compact reactor. Computational assessment of the thermo-hydraulic performance of an Al
2O
3–water-based nanofluid in a hexagonal rod-bundle sub-channel was explored by Ahmed et al. [
8].
When a group of nanoparticles stick together, they combine to form nanoparticle aggregation (N-Ag). The decrease in the contact surface of the fluid–solid interfaces results in a drop in the potential energy of the fluid system. Viscosity and thermal conductivity directly impact N-Ag. The aggregated nanoparticles tend to build flowing networks and continuous links to create a reduced thermal pathway. As a result, heat may be conveyed rather rapidly across the groupings, which, when combined with the augmented aggregation volume compared to nanoparticles, can increase the thermal capacity of the nanofluid. Thermal conductivity enhancement by the aggregation of nanoparticles with the occurrence of metal oxides and nanoparticles was studied by Wensel et al. [
9]. Based on the nanolayer and nanoparticle aggregation, Xie et al. [
10] determined the effective thermal conductivity of nanofluids. Swain and Mahanthesh et al. [
11] investigated the N-Ag and Joule heating effect in a radiating magneto nano liquid flow over an exponential area. Rana et al. [
12] inspected the Cattaneo–Christov (C-C) model and heat flux effects on a spinning disk with the Hall current effect in the presence of N-Ag. With sensitivity analysis, Sabu et al. [
13] studied N-Ag dynamics on the quadratic convective magnetohydrodynamic flow of a nanomaterial across a slanted flat plate. Regarding the flow of a micropolar nanofluid across a stretching surface, Yu et al. [
14] explored N-Ag and the thermophoretic particle deposition process. Radiative heat transmission and unsteady movement in an uneven channel with the aggregation kinematics of a nanofluid were explored by Jestine and Mahanthesh [
15]. The aspects of a uniform horizontal magnetic field and N-Ag in the flow of a nanofluid with melting heat transfer were explored by Wang et al. [
16].
When particles in a gas move from hot to cold zones as a result of a temperature profile, this is known as thermophoretic particle deposition (T-P-D). Settlement on cold surfaces, such as heat exchanger walls, might be aided by this movement. It is vital to understand the transport mechanisms at work in systems such as exhaust systems and thermal precipitators, and optical waveguide production procedures are critical. The practical application of the present concept was explained by Green and Lane [
17] and Fuchs [
18]. T-P-D was first studied by Goren [
19]. Recently, Madhukesh et al. [
20] inspected the mass and thermal transfer during the occurrence of a Casson fluid containing hybrid nanoparticles over a Riga surface in the context of the T-P-D effect. Waini et al. [
21] investigated T-P-D and viscous dissipation effects in a micropolar hybrid nanofluid over a flat surface. Shankaralingappa et al. [
22] investigated the T-P-D on a three-dimensional flow of Casson nano liquid containing sodium alginate across a stretched surface. Chen et al. [
23] investigated T-P-D in the flow of a dual-layer Casson liquid with a magnetic dipole and extended Fourier’s and Fick’s equations. Madhukesh et al. [
24] considered the thermophoretic impact and convective thermal conditions on the flow of a hybrid nanofluid over a moving thin needle. Gowda et al. [
25] explored thermal transport in ferromagnetic liquid dynamics across a stretched sheet with the combined effects of T-P-D and a magnetic dipole.
Because all fluid flow and solid structure relationships are linked to stagnation point flow performance, stagnation point flow is a significant phenomenon. In engineering applications, the rate of fluctuation of the physical limitations around the flow is critical. The pressure and largest thermal exchange, as well as a reduction in velocity, occur near the flow’s environments in stagnation point motion. Electronic, hydrodynamic, and aerodynamic fields all play essential roles in flow at the stagnation point. The phenomenon of flow at the stagnation point has several applications in fluid flow and thermal transmission in a number of industries and technical domains. Zaib et al. [
26] explored the creation of entropy and the dual branch solution in a mixed convection stagnation point flow over a Riga surface in the context of a micropolar nanofluid flow. Khan et al. [
27] scrutinized the flow at the stagnation point in the presence of a hybrid nano liquid along a non-isothermal shrinking/stretching sheet with inertial and microstructure features. Gul et al. [
28] explored the stagnation point flow of a blood-based hybrid nanofluid under mixed convection around a revolving sphere. Ghasemi and Hatami [
29] investigated how solar radiation affects MHD stagnation point flow and heat conduction in a nanofluid over a stretched sheet.
The rotational flows and heat transfer properties of a driven flow stream over stationary spinning bodies of revolution are essential in a number of engineering applications, such as ballistic re-entry, fiber coatings, projectile motion, and rotational equipment design. The heat distribution between a fluid flow and a revolving sphere has several applications in technology, such as overcoming freezing system difficulties. Malvandi [
30] examined the time-dependent flow of an unsteady spinning sphere’s stagnation point zone. Entropy analysis and unsteady MHD mixed convection stagnation point flow of a Casson nanofluid around a spinning sphere were examined by Madhy et al. [
31]. Ahmed and Rashed [
32] examined unsteady MHD mixed convection flow with the slip effect in a nanofluid in the stagnation region of an impulsively rotating sphere with the effects of thermal radiation and convective boundary conditions.
The present study was conducted to explore the behavior of nanoparticle aggregation and stagnation point flow over a rotating sphere in the presence of thermophoretic particle deposition.
The current study seeks to answer the following questions:
What is the impact of the nanoparticle aggregation effect on the acceleration parameter in velocity, thermal, and concentration profiles?
What is the thermal performance in the presence/absence of nanoparticle aggregation?
What is the impact of the thermophoretic effect on the concentration profile in the presence/absence of nanoparticle aggregation?
The present manuscript is divided into five sections. The context of the study and implementation is discussed in the
Section 1.
Section 2 expands on the modeling and formulation of the problem.
Section 3 describes the numerical technique and validation of the code.
Section 4 delineates the results and physical perspectives of the problem.
Section 5 summarizes the outcomes of the study.
2. Materials and Methods
Consider the incompressible boundary layer unsteady movement of nanoparticles towards the forward stagnation point section at a persistent temperature on a rotating sphere, as in
Figure 1. The
coordinate is represented on the surface, and the direction normal to the sphere is denoted by
. The sphere is rotating with angular velocity (time-dependent)
,
. The temperature near the wall is assumed to be constant. Furthermore, the terms for viscous dissipation are negligible and the free stream and angular velocities vary with time in the aspect of
,
. The nanoparticle is in the thermal equilibrium state. The temperature at the wall and ambient temperature of the sphere are denoted by
. Similarly, for concentration, the terms are
. The mathematical model that represents the problem based on the assumptions stated above is as follows (see [
24,
28,
30,
31]).
These are subjected to the initial and boundary conditions (see [
30,
31]):
where
denote coordinates measured from the forward stagnation point and normal to the surface, respectively, and
denotes the axis in the rotational direction.
is the radial distance between a symmetry axis and the surface element (
in proximity to the point of stagnation,
and
are the velocity apparatuses along the
and
coordinates,
signifies time, the subscript
signifies the initial condition, thermal conductivity is
, heat capacitance is denoted by
,
denotes the Brownian diffusion coefficient, specific heat at constant temperature is
and
is the temperature.
The below similarity parameters are introduced (see [
30]):
The thermophoretic velocity is represented as
(see [
24]), where
and
are the thermophoretic constant and reference temperature, respectively.
According to experimental and empirical investigations (see [
30,
31,
32]), in the kinematics and thermal propagation of nanofluid movements, the nanoparticle aggregation factor is critical. The nanomaterial measurement findings agreed exactly when the aggregate component was considered. The nanoparticle volume fraction is determined by the aggregation kinetic factor, and it is given as
As shown in
Table 1 (see [
33]), the thermal conductivity is determined by mixing the modified Maxwell and Bruggeman models. Suitable expressions are given below (see [
34,
35,
36]).
From the above-stated expressions, the subscripts and signify aggregates and nanoparticles, denotes particles that are spherical in shape, fractional index denotes the ratio of radii of aggregates to radii of nanoparticles and are the commonly accepted values.
By using Equation (8), the system of Equations (1)–(5) reduces and boundary conditions are transformed into:
and
The above Equations (10)–(14) comprised different controlling parameters which are defined namely and mathematically in
Table 2.
The important engineering coefficients
,
,
and
which are defined and simplified in
Table 3. (see [
30,
31,
32]).
4. Results and Discussion
The effect of different dimensionless restrictions that control the flow, temperature and concentration characteristics across a spinning sphere in the presence of a
-based nanofluid is discussed in this section. For all limitations, the investigation is performed in the presence/absence of nanoparticle aggregation. The numerical results are graphically illustrated to demonstrate how the individual dimensionless parameters (
,
,
and
) vary on the primary velocity, secondary velocity, temperature and concentration profiles.
Table 1 shows the thermophysical characteristics of the nanomaterials.
Table 2 displays the flow controlling parameters. The important engineering coefficients and its reduced form are tabulated in
Table 3. The thermophysical characteristics of the base liquid and nanoparticles are shown in
Table 4. The acquired numerical findings are compared to previously published literature (see
Table 5,
Table 6 and
Table 7). The important engineering factors, such as
,
,
and
, are calculated for various constraints in the presence and absence of the nanoparticle aggregation, as shown in
Table 8 and
Table 9.
Figure 2,
Figure 3,
Figure 4 and
Figure 5 display the influence of the acceleration parameter
on the primary velocity profile
, secondary velocity profile
, temperature profile
and concentration profile
.
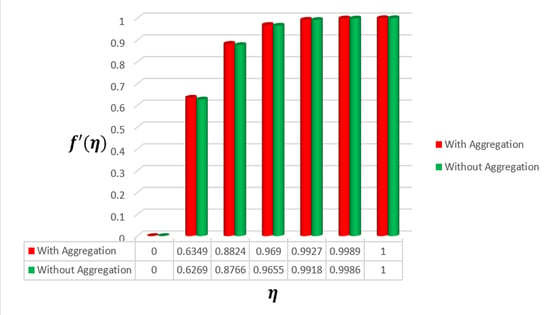
Figure 2 shows that an inclination in the values of
will increase the primary velocity
. The reverse trend is observed in the secondary velocity profile
(see
Figure 3). With the rise in the value of
, the
also rises, which reduces the thickness of the boundary layer and increases the velocity in the lateral axis within the boundary layer. As a consequence, thermal distribution is decreased with a rise in
(see
Figure 4). An increase in the values of
will diminish the thermal distribution due to a decrease in the thickness of the boundary layer. Similar behavior is exhibited by the concentration profile (see
Figure 5). The velocity of the nanofluid with aggregation is lower when compared to nanoparticles without aggregation in the primary and secondary velocity profiles. Thermal dispersal is greater in the case of nanoparticles without aggregation than nanoparticles with aggregation. A similar trend is detected in the concentration profile.
The variation in the rotational parameter
on the primary velocity
profile is shown in
Figure 6. The increase in
will accelerate the primary velocity
. This is due to the rise in the
, which includes additional momentum to the boundary layer, which results in a decline in the thickness of the boundary layer, causing the fluid to accelerate. It is also observed that nanoparticles without aggregation have lower velocity than nanoparticles with aggregation.
The impact of the Schmidt number
and thermophoretic parameter
on the concentration profile
is illustrated in
Figure 7 and
Figure 8. In the fluid flow, the ratio between mass and momentum diffusivity is called the Schmidt number. As the values of
decrease, the molecular diffusion results in a decrease in the concentration profile. A similar observation is noted in the case of
(see
Figure 8). As
increases, it results in an increase in the temperature gradient, which leads to the motion of the nanoparticles from the hot to cold region. The nanoparticles without aggregation show greater concentration than nanoparticles with aggregation.
Figure 9 and
Figure 10 show the influence of
on
and
for a variation in
. From the figure, it is observed that the surface drag force is enhanced with an improvement in the values of
and
. A rise in the values of
and
will decrease the thickness of the boundary layer, resulting in a high surface drag force. Surface drag force is greater in nanoparticles with aggregation than nanoparticles without aggregation in the
case but the reverse trend is seen in the
case.
Figure 11 shows the variation in
on
for numerous values of
. The rate of thermal distribution enhances with inclined values of
. As the values of the rotational parameter and solid volume fraction rise, the
decreases; this is due to a decrease in the thickness due to the presence of
. It is clearly seen from the plot that nanoparticles without aggregation exhibit a higher rate of heat transfer than nanoparticles with aggregation. The rate of mass transfer on
for numerous values of
is illustrated in
Figure 12. The growth in the values of
and
will increase the rate of mass transfer. The rate of mass transfer is greater in the case of nanoparticles without aggregation than nanoparticles with aggregation.