WOA (Whale Optimization Algorithm) Optimizes Elman Neural Network Model to Predict Porosity Value in Well Logging Curve
Abstract
:1. Introduction
2. Methodology
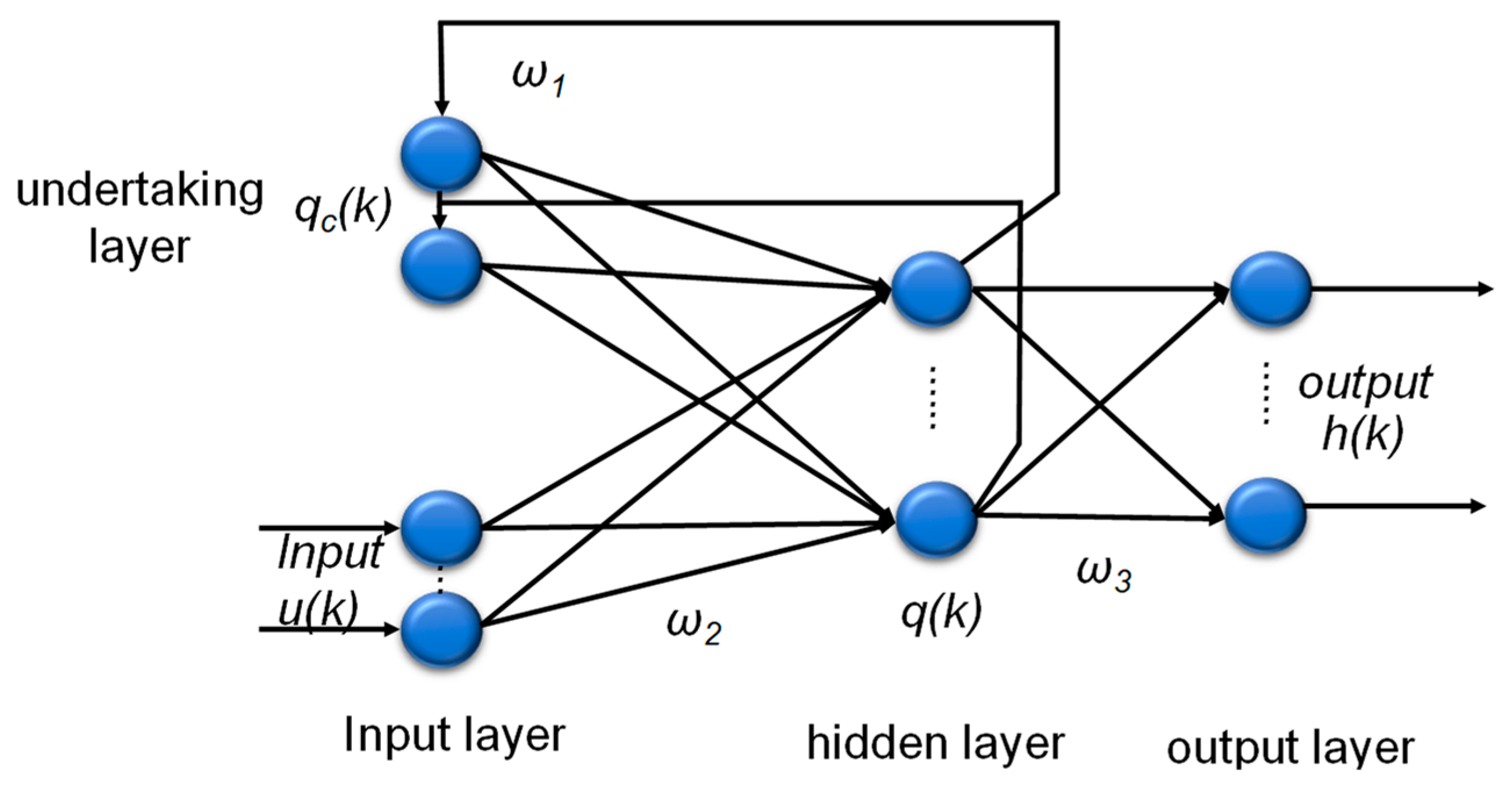
2.1. Elman
2.2. WOA
3. Dataset Preparation
4. Model Inspection and Evaluation
5. Analysis of Prediction Results
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Keelan, D.K. A critical review of core analysis techniques. J. Can. Pet. Technol. 1972, 11, 2. [Google Scholar] [CrossRef]
- Arora, A.; Bihani, A.D.; Padalkar, C.M.; Punase, A.D.; Patwardhan, S.D. Sidewall Coring: Advanced In-situ Freeze-Core Technique. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 15–17 November 2011. [Google Scholar]
- Permata, I.; Khakimov, S.; Kenzhekhanov, S.; Toktarov, M.; Clippinger, K. High resolution cuttings analysis for well placement in the Uinta Basin. In Proceedings of the Unconventional Resources Technology Conference, Online, 20–22 July 2020; pp. 1018–1037. [Google Scholar]
- Doyen, P.M. Porosity from seismic data: A geostatistical approach. Geophysics 1988, 53, 1263–1275. [Google Scholar] [CrossRef]
- Babadagli, T.; Al-Salmi, S. A review of permeability-prediction methods for carbonate reservoirs using well-log data. SPE Reserv. Eng. 2004, 7, 75–88. [Google Scholar] [CrossRef]
- Tao, G.; King, M.S. Porosity and pore structure from acoustic well logging data 1. Geophys. Prospect. 1993, 41, 435–451. [Google Scholar] [CrossRef]
- Marica, F.; Chen, Q.; Hamilton, A.; Hall, C.; Al, T.; Balcom, B.J. Spatially resolved measurement of rock core porosity. J. Magn. Reson. 2006, 178, 136–141. [Google Scholar] [CrossRef]
- Roksandić, M.M. Seismic facies analysis concepts. Geophys. Prospect. 1978, 26, 383–398. [Google Scholar] [CrossRef]
- Bloch, S. Empirical Prediction of Porosity and Permeability in Sandstones. Am. Assoc. Pet. Geol. Bull. 1991, 75, 1145–1160. [Google Scholar]
- Bryant, S.; Cade, C.; Mellor, D. Permeability Prediction from Geologic Models. Am. Assoc. Pet. Geol. Bull. 1993, 77, 1338–1350. [Google Scholar]
- Lander, R.H.; Walderhaug, O. Predicting Porosity through Simulating Sandstone Compaction and Quartz Cementation. Am. Assoc. Pet. Geol. Bull. 1999, 83, 433–449. [Google Scholar]
- Rogers, S.J.; Chen, H.C.; Kopaska-Merkel, D.C.; Fang, J.H. Predicting Permeability from Porosity using Artificial Neural Networks. Am. Assoc. Pet. Geol. Bull. 1995, 79, 1786–1797. [Google Scholar]
- Wong, P.M.; Gedeon, T.D.; Taggart, I.J. An improved technique in porosity prediction: A neural network approach. IEEE Trans. Geosci. Remote Sens. 1995, 33, 971–980. [Google Scholar] [CrossRef]
- Wong, P.M.; Jian, F.X.; Taggart, I.J. A critical comparison of neural networks and discriminant analysis in lithofacies, porosity and permeability predictions. J. Pet. Geol. 1995, 18, 191–206. [Google Scholar] [CrossRef]
- Al-Anazi, A.F.; Gates, I.D. Support vector regression for porosity prediction in a heterogeneous reservoir: A comparative study. Comput. Geosci. 2010, 36, 1494–1503. [Google Scholar] [CrossRef]
- El-Shahat, W.; Afify, W.; Hassan, A. Permeability and porosity prediction from wireline logs using Neuro-Fuzzy technique. Ozean J. Appl. Sci. 2010, 3, 157–175. [Google Scholar]
- Mohebbi, A.; Kamalpour, R.; Keyvanloo, K.; Sarrafi, A. The prediction of permeability from well logging data based on reservoir zoning, using artificial neural networks in one of an Iranian heterogeneous oil reservoir. Pet. Sci. Technol. 2012, 30, 1998–2007. [Google Scholar] [CrossRef]
- Al-Anazi, A.F.; Gates, I.D. Support vector regression to predict porosity and permeability: Effect of sample size. Comput. Geosci. 2012, 39, 64–76. [Google Scholar] [CrossRef]
- Shujath Ali, S.; Hossain, M.E.; Hassan, M.; Abdulraheem, A. Hydraulic Unit Estimation from Predicted Permeability and Porosity using Artificial Intelligence Techniques. OnePetro North Africa Technical Conference and Exhibition, Cairo, Egypt, 15–17 April 2013. [Google Scholar]
- Zerrouki, A.A.; Aifa, T.; Baddari, K. Prediction of natural fracture porosity from well log data by means of fuzzy ranking and an artificial neural network in Hassi Messaoud oil field, Algeria. J. Pet. Sci. Eng. 2014, 115, 78–89. [Google Scholar] [CrossRef]
- Aïfa, T.; Baouche, R.; Baddari, K. Neuro-fuzzy system to predict permeability and porosity from well log data: A case study of Hassi R׳ Mel gas field, Algeria. J. Pet. Sci. Eng. 2014, 123, 217–229. [Google Scholar] [CrossRef]
- Konate, A.A.; Pan, H.; Khan, N.; Yang, J.H. Generalized regression and feed-forward back propagation neural networks in modelling porosity from geophysical well logs. J. Pet. Explor. Prod. Technol. 2015, 5, 157–166. [Google Scholar] [CrossRef] [Green Version]
- Saputro, O.D.; Maulana, Z.L.; Latief, F.D.E. Porosity Log Prediction Using Artificial Neural Network. J. Phys. Conf. Ser. 2016, 739, 012092. [Google Scholar] [CrossRef] [Green Version]
- Rafik, B.; Kamel, B. Prediction of permeability and porosity from well log data using the nonparametric regression with multivariate analysis and neural network, Hassi R’Mel Field, Algeria. Egypt. J. Pet. 2017, 26, 763–778. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Bao, Z.; Cui, G. Permeability prediction using hybrid techniques of continuous restricted Boltzmann machine, particle swarm optimization and support vector regression. J. Nat. Gas Sci. Eng. 2018, 59, 97–115. [Google Scholar] [CrossRef]
- Elkatatny, S. A self-adaptive artificial neural network technique to predict total organic carbon (TOC) based on well logs. Arab. J. Sci. Eng. 2019, 44, 6127–6137. [Google Scholar] [CrossRef]
- Khan, N.; Rehman, K. Application of fuzzy logic and neural networks for porosity analysis using well log data: An example from the Chanda Oil Field, Northwest Pakistan. Earth Sci. Inform. 2021, 14, 2183–2199. [Google Scholar] [CrossRef]
- Lee, J.; Kwon, M.; Hong, Y. Predicting Porosity and Water Saturation from Well-Log Data Using Probabilistic Multi-Task Neural Network with Normalizing Flows. In Proceedings of the OnePetro Offshore Technology Conference, Virtual and Houston, TX, USA, 16–19 August 2021. [Google Scholar]
- Mulashani, A.K.; Shen, C.; Nkurlu, B.M.; Mkono, C.N.; Kawamala, M. Enhanced group method of data handling (GMDH) for permeability prediction based on the modified Levenberg Marquardt technique from well log data. Energy 2022, 239, 121915. [Google Scholar] [CrossRef]
- Koskela, T.; Lehtokangas, M.; Saarinen, J.; Kaski, K. Time series prediction with multilayer perceptron, FIR and Elman neural networks. In Proceedings of the World Congress on Neural Networks, San Diego, CA, USA, 15–18 September 1996; INNS Press: San Diego, CA, USA, 1996; pp. 491–496. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Jamshidian, M.; Hadian, M.; Zadeh, M.M.; Kazempoor, Z.; Bazargan, P.; Salehi, H. Prediction of Free-flowing Porosity and Permeability based on Conventional Well Logging Data using Artificial Neural Networks Optimized by Imperialist Competitive Algorithm–A Case Study in the South Pars Gas Field. J. Nat. Gas Sci. Eng. 2015, 24, 89–98. [Google Scholar] [CrossRef]
- An, P.; Yang, X.; Zhang, M. Porosity Prediction and Application with Multiwell-logging Curves based on Deep Neural Network. In SEG Technical Program Expanded Abstracts 2018; Society of Exploration Geophysicists: Houston, TX, USA, 2018; pp. 819–823. [Google Scholar]









| Abbreviation | Full Name |
|---|---|
| PE | Photoelectric absorption cross section index |
| DEN | Density |
| M2R1 | High resolution array induced resistivity |
| AC | Acoustic |
| GR | Gamma ray |
| R25 | 2.5 m bottom gradient resistivity |
| R4 | 4 m bottom gradient resistivity |
| CNL | Neutron |
| POR | Porosity |
| WOA | Whale optimization algorithm |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| BP | back propagation |
| Parameter | Min | Max | Median | Std | Average | Skew |
|---|---|---|---|---|---|---|
| PE | 3.042 | 6.46 | 4.602 | 0.7273 | 4.582238 | 0.144289 |
| DEN | 2.519 | 2.625 | 2.58 | 0.019115 | 2.579354 | −0.25568 |
| M2R1 | 143 | 705 | 382.5 | 117.3329 | 390.5579 | 0.374388 |
| AC | 55 | 63 | 57 | 1.425923 | 57.625 | 0.713462 |
| GR | 39 | 68 | 47 | 5.906085 | 48.8811 | 0.87834 |
| R25 | 111 | 143 | 126 | 6.855572 | 125.2835 | 0.126538 |
| R4 | 237 | 301 | 256 | 15.22972 | 257.6128 | 0.62556 |
| CNL | 5 | 12 | 8 | 1.549364 | 8.009146 | 0.123645 |
| POR | 1.272 | 6.182 | 2.9075 | 1.039905 | 3.161107 | 0.595966 |
| R2 | RMSE | MAE | VAF | |
|---|---|---|---|---|
| Elman | 0.8749 | 0.3066 | 0.2545 | 87.50 |
| WOA–Elman | 0.9696 | 0.1457 | 0.1182 | 97.01 |
| BP | 0.8608 | 0.7438 | 0.5265 | 86.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, J.; Yu, Z.; Liu, Z.; Yin, P. WOA (Whale Optimization Algorithm) Optimizes Elman Neural Network Model to Predict Porosity Value in Well Logging Curve. Energies 2022, 15, 4456. https://doi.org/10.3390/en15124456
Sun Y, Zhang J, Yu Z, Liu Z, Yin P. WOA (Whale Optimization Algorithm) Optimizes Elman Neural Network Model to Predict Porosity Value in Well Logging Curve. Energies. 2022; 15(12):4456. https://doi.org/10.3390/en15124456
Chicago/Turabian StyleSun, Youzhuang, Junhua Zhang, Zhengjun Yu, Zhen Liu, and Pengbo Yin. 2022. "WOA (Whale Optimization Algorithm) Optimizes Elman Neural Network Model to Predict Porosity Value in Well Logging Curve" Energies 15, no. 12: 4456. https://doi.org/10.3390/en15124456
APA StyleSun, Y., Zhang, J., Yu, Z., Liu, Z., & Yin, P. (2022). WOA (Whale Optimization Algorithm) Optimizes Elman Neural Network Model to Predict Porosity Value in Well Logging Curve. Energies, 15(12), 4456. https://doi.org/10.3390/en15124456





