Analysis of the Heat Transfer Coefficient, Thermal Effusivity and Mathematical Modelling of Drying Kinetics of a Partitioned Single Pass Low-Cost Solar Drying of Cocoyam Chips with Economic Assessments
Abstract
:1. Introduction
2. Material and Methods
2.1. Description of Solar Dryer Used
Novelty of Design
2.2. Drying Procedure and Instrumentation
2.3. Experimental Uncertainties
2.4. Performance Evaluation
2.5. Mathematical Modelling of the Drying Curve
2.6. Thermal Analysis
2.6.1. Effective Moisture Diffusivity
2.6.2. Heat and Mass Transfer Coefficient
2.6.3. Variation in Thermal Properties of Cocoyam
2.7. Cost Analysis of the Solar Dryers
2.7.1. Cost Saving
2.7.2. Payback Period
2.8. CO2 Emission Reduction Analysis
3. Results and Discussion
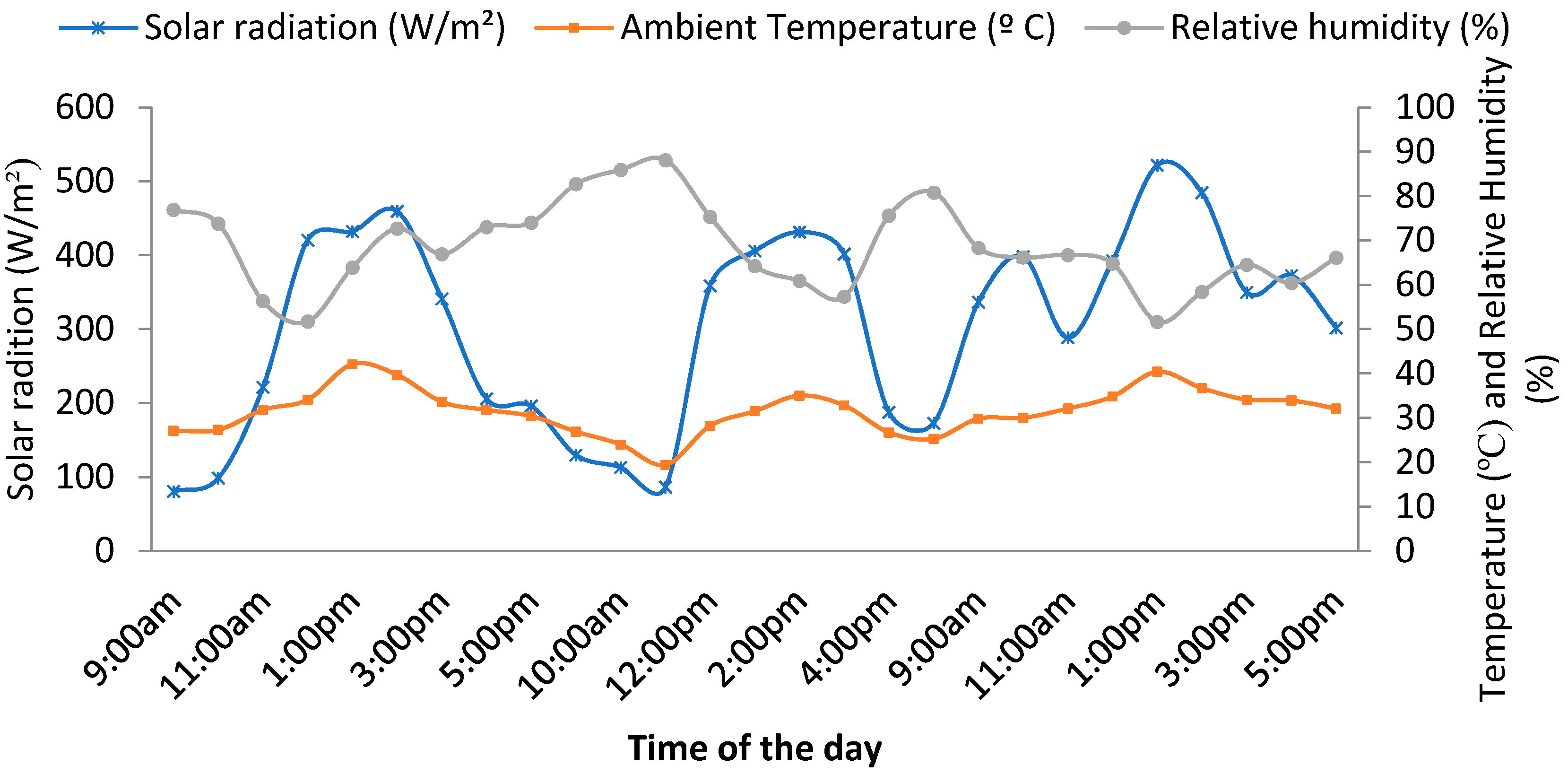
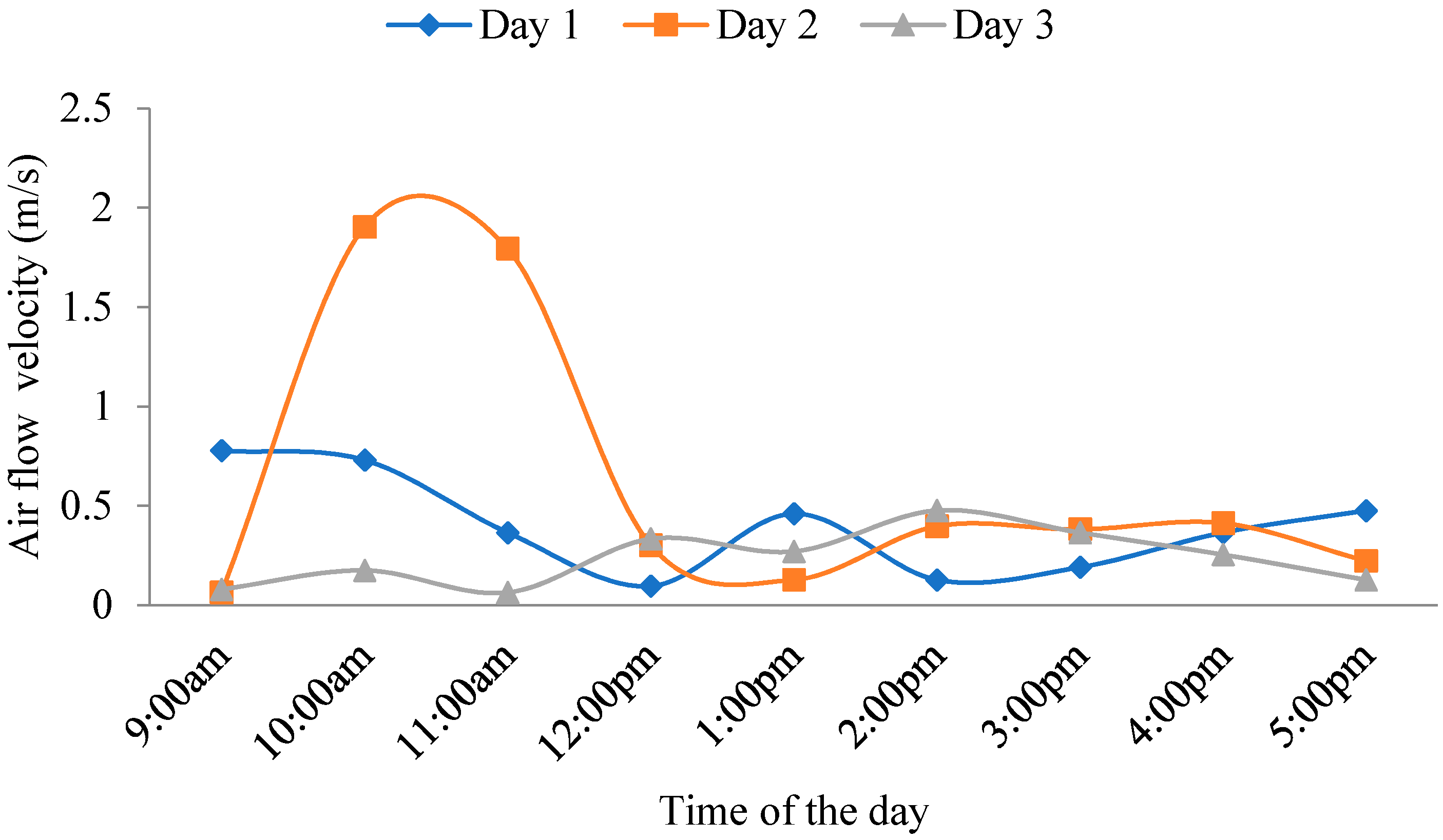
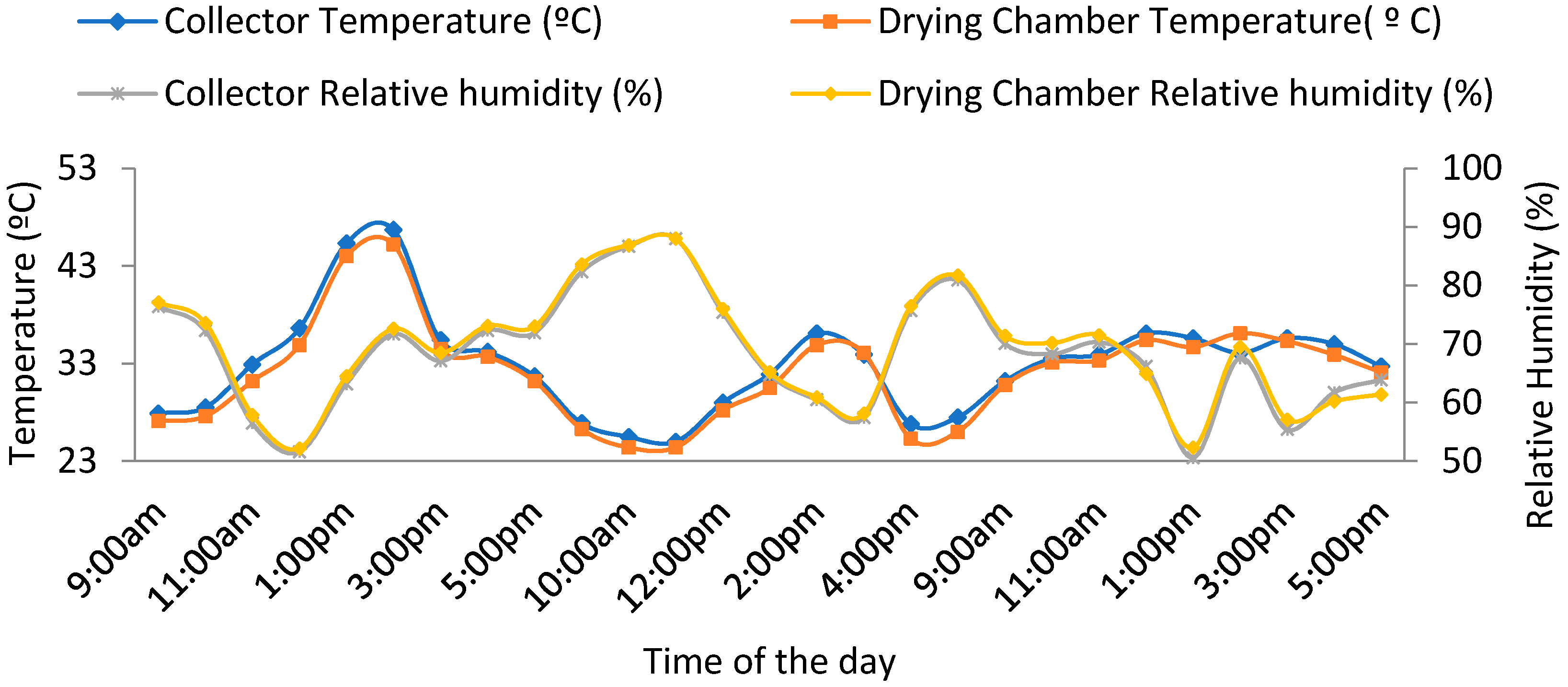
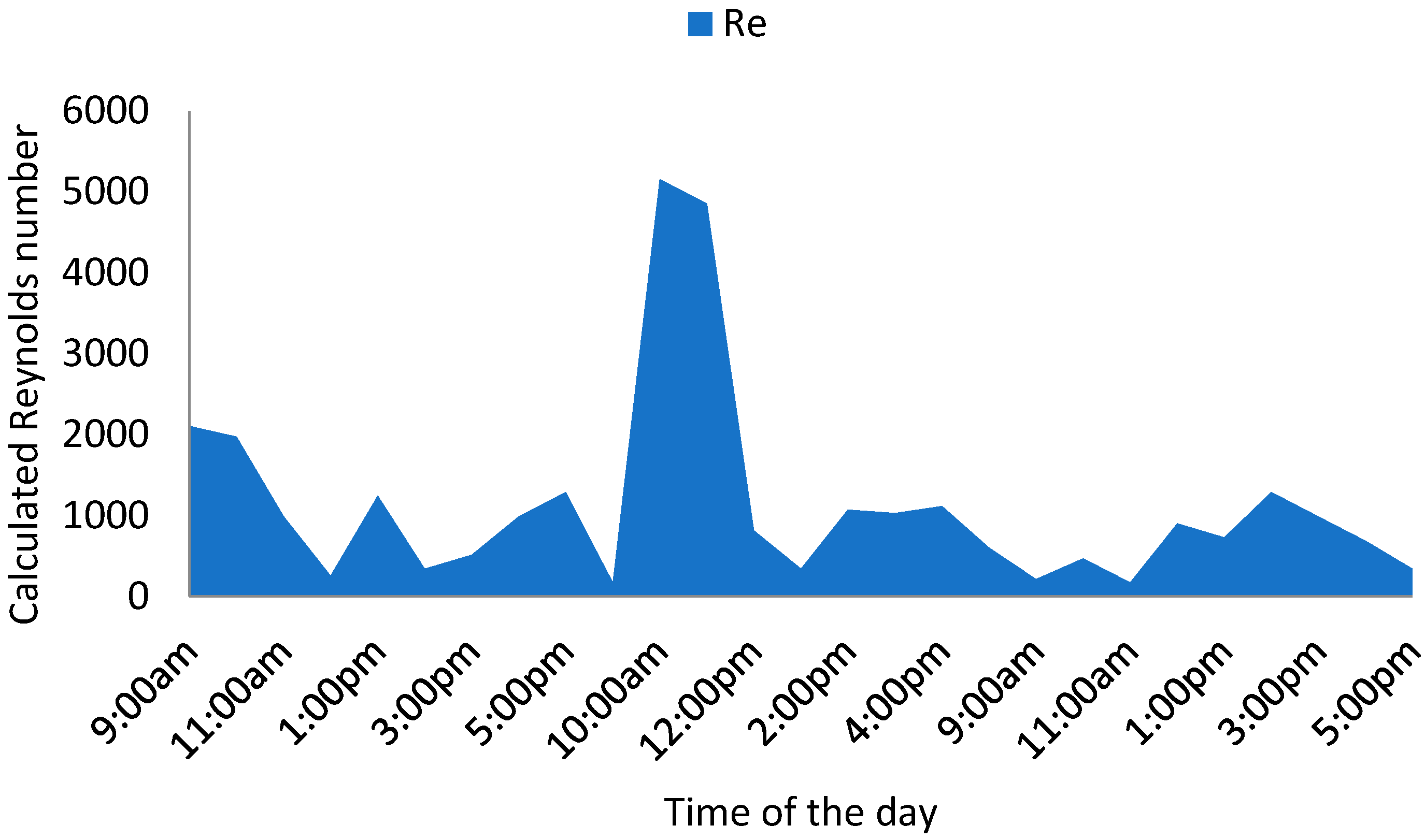
3.1. Dryer Performance
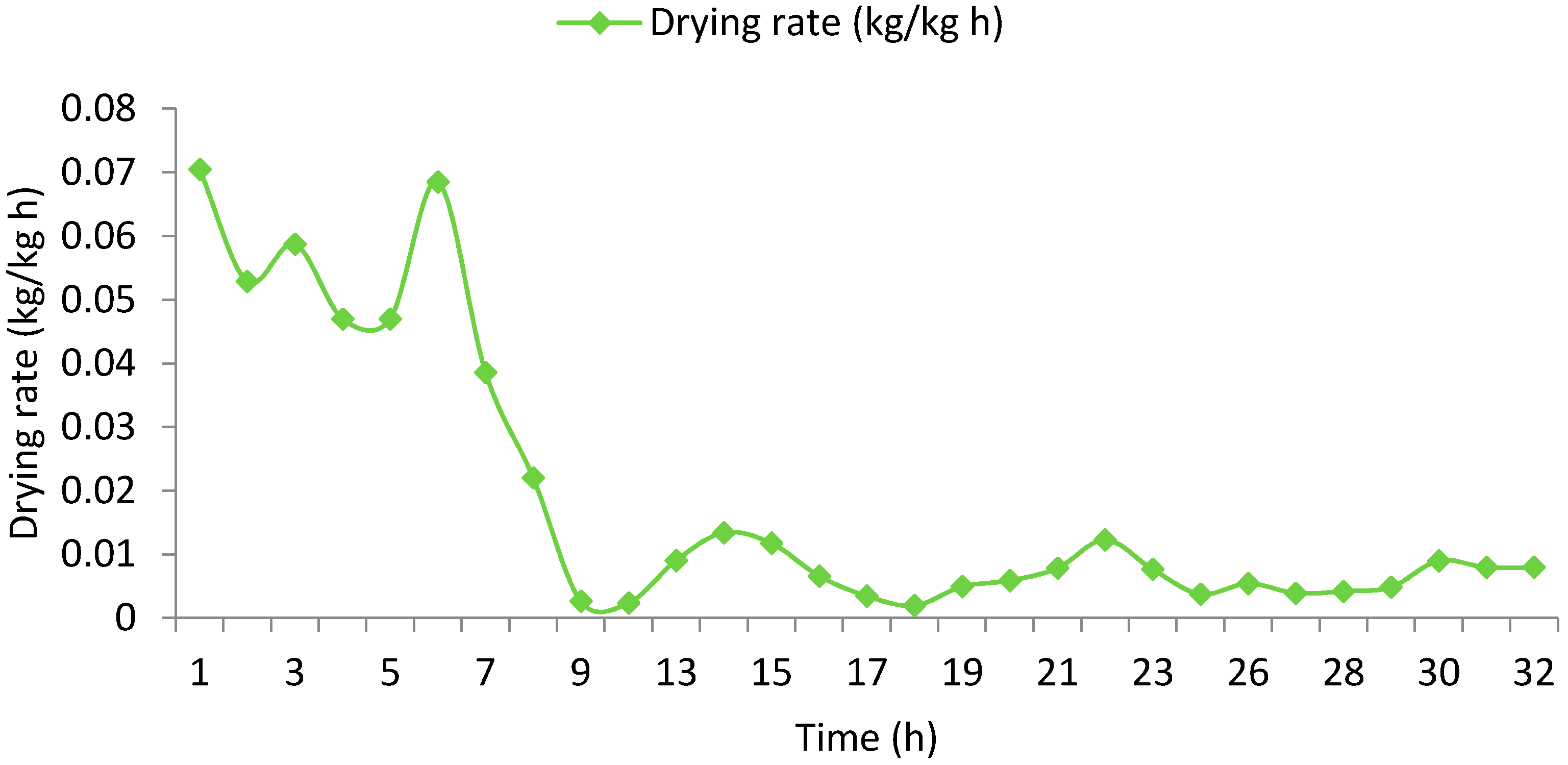
3.2. Drying Kinetics and Mathematical Modelling
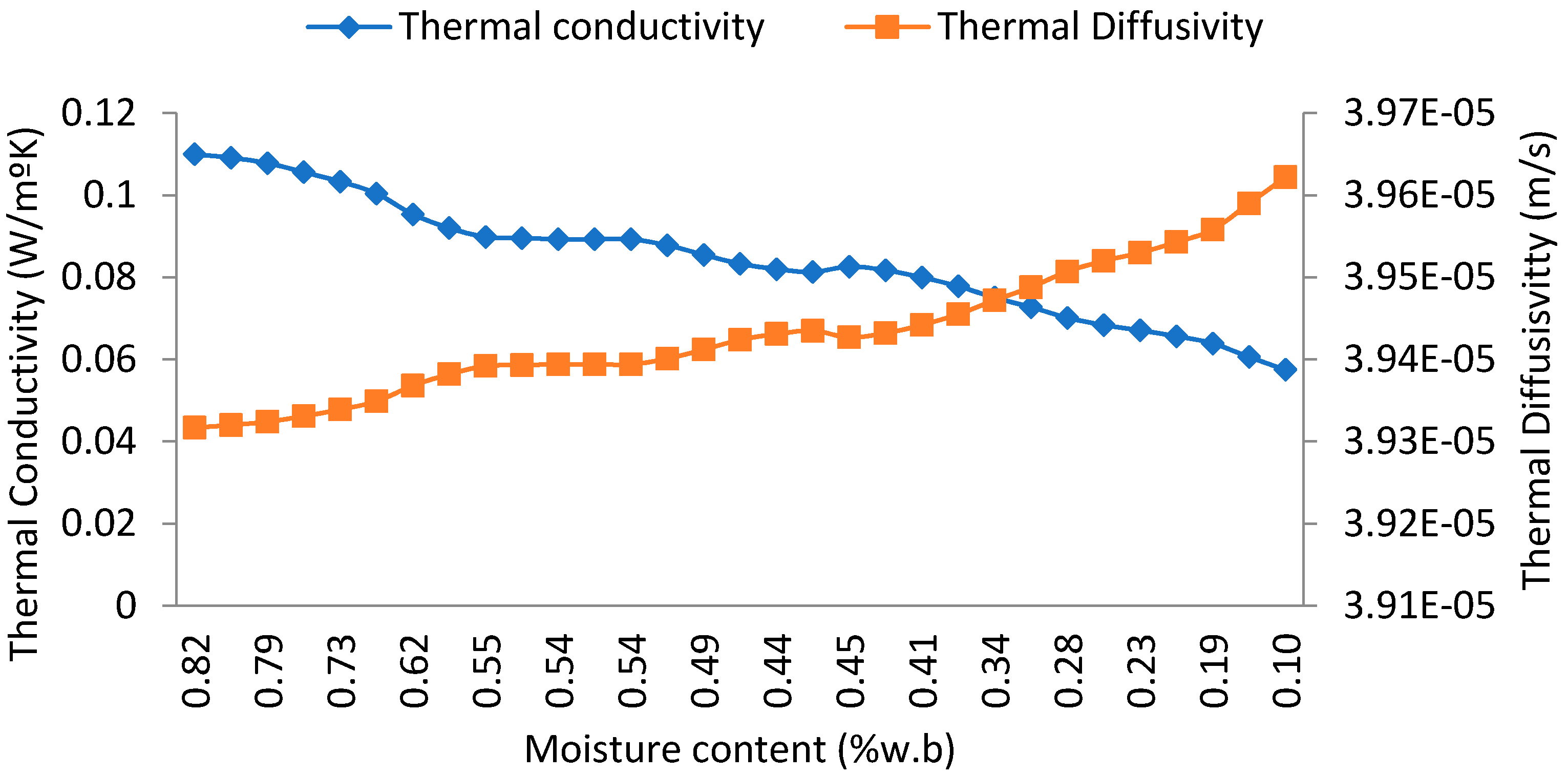
3.3. Evolution of the Thermal Properties
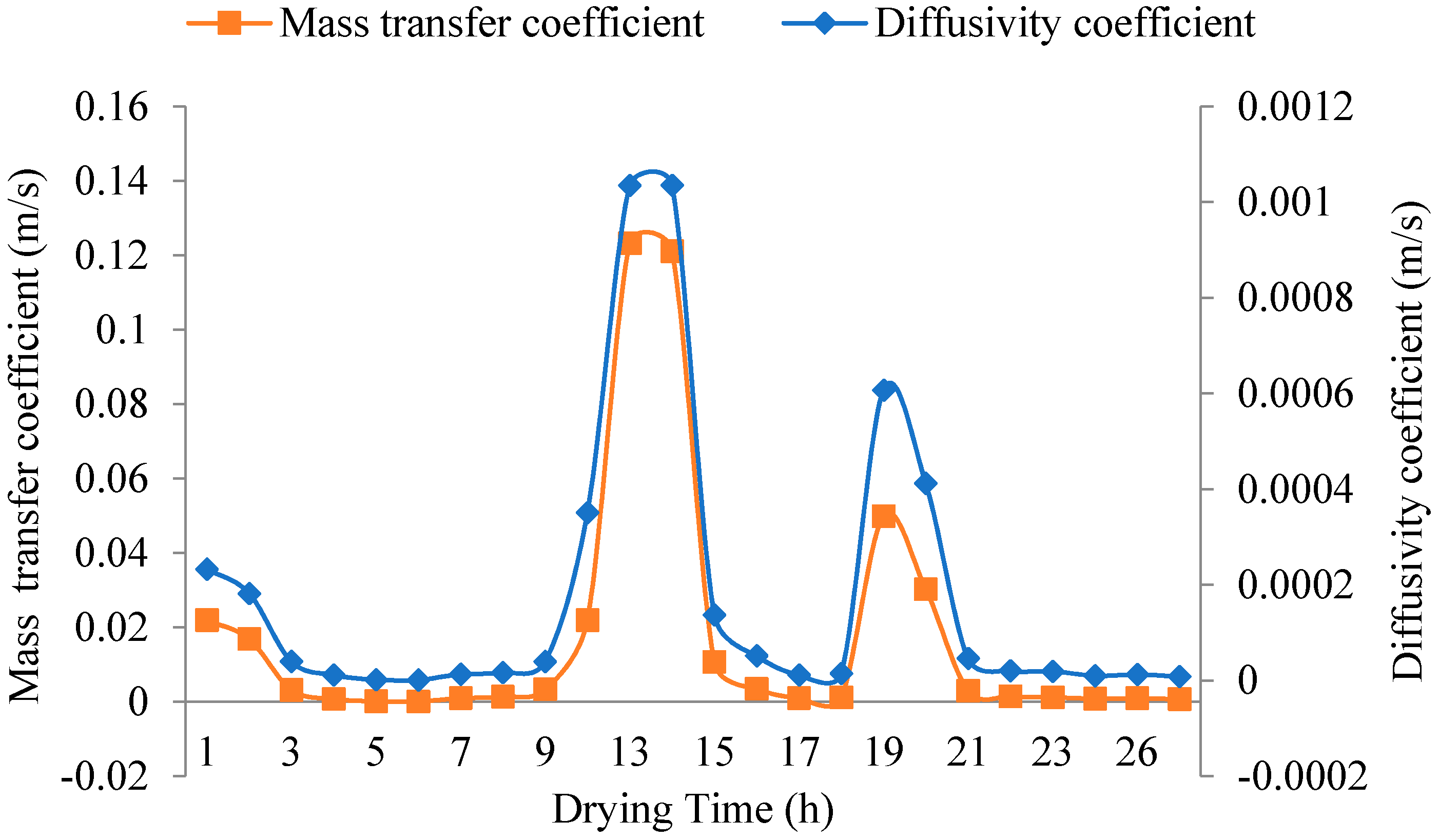
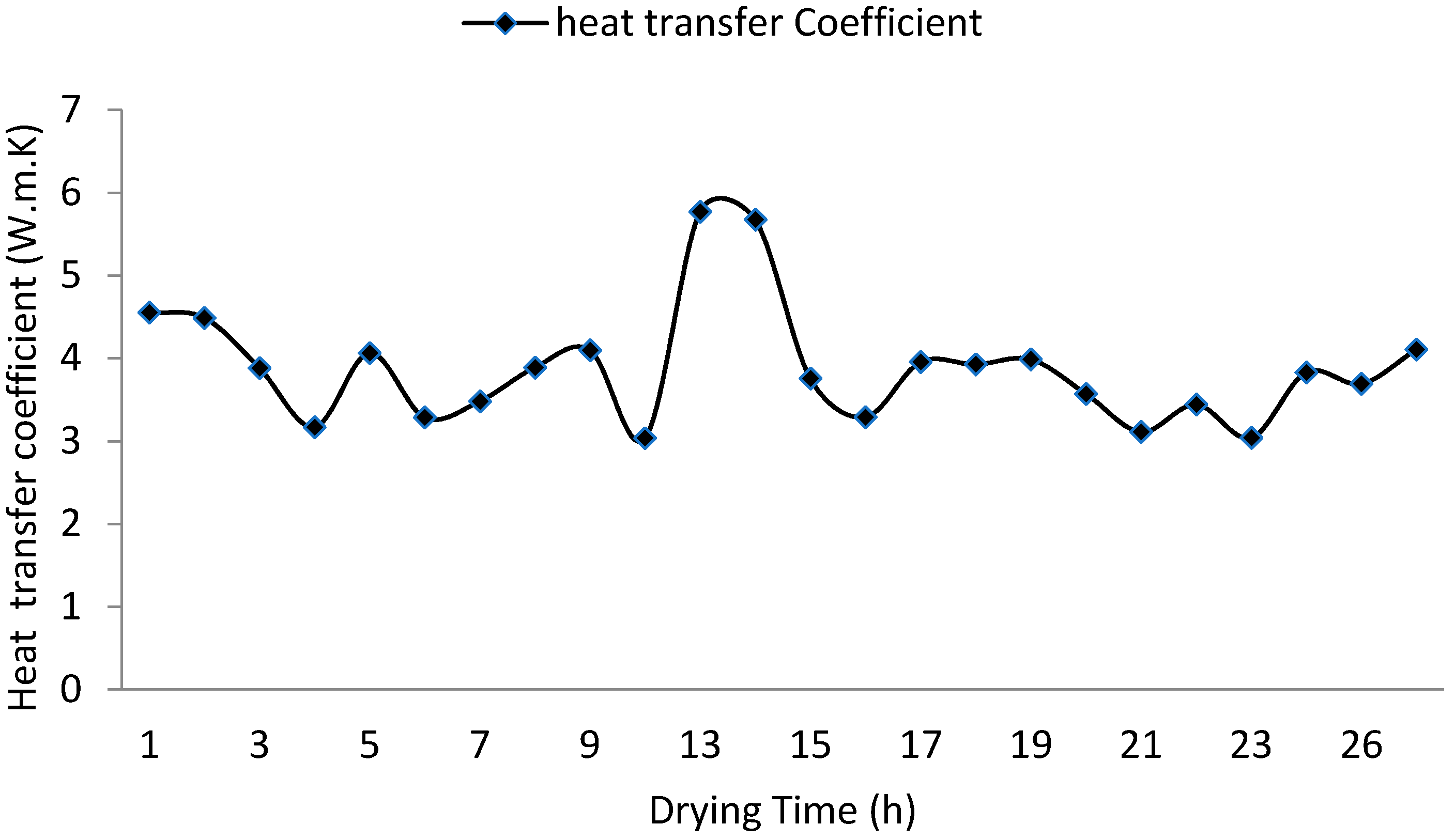
3.4. Variation in Heat and Mass Transfer Coefficient
3.5. Economic Assessment
3.6. Environmental Impact Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UNICEF. In Brief to the State of Food Security and Nutrition in the World 2021; FAO: Rome, Italy, 2021. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Diemuodeke, E.O.; Abam, F.I.; Abada, U.C.; Eke-emezie, N.; Simo-Tagne, M. Development and modelling of heat and mass transfer analysis of a low-cost solar dryer integrated with biomass heater: Application for West African Region. Sci. Afr. 2020, 10, e00615. [Google Scholar] [CrossRef]
- Gupta, A.; Das, B.; Biswas, A.; Mondol, J.D. An environmental and economic evaluation of solar photovoltaic thermal dryer. Int. J. Environ. Sci. Technol. 2021, 1–20. [Google Scholar] [CrossRef]
- Catorze, C.; Tavares, A.P.; Cardão, P.; Castro, A.; Silva, M.E.; Ferreira, D.W.; Lopes, S.; Brás, I. Study of a solar energy drying system—Energy savings and effect in dried food quality. Energy Rep. 2022, 8, 392–398. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Ndukwu, M.C.; Zoulalian, A.; Bennamoun, L.; Kifani-Sahban, F.; Rogaume, Y. Numerical analysis and validation of a natural convection mix-mode solar dryer for drying red chilli under variable conditions. Renew. Energy 2020, 151, 659–673. [Google Scholar] [CrossRef]
- Wang, W.; Li, M.; Hassanien, R.H.E.; Wang, Y.; Yang, L. Thermal performance of indirect forced convection solar dryer and kinetics analysis of mango. Appl. Therm. Eng. 2018, 134, 310–321. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Tamkam Etala, H.D.; Tagne Tagne, A.; Ndukwu, M.C.; El Marouani, M. Energy, environmental and economic analyses of an indirect cocoa bean solar dryer: A comparison between natural and forced convections. Renew. Energy 2022, 187, 1154–1172. [Google Scholar] [CrossRef]
- Fudholi, A.; Othman, M.Y.; Ruslan, M.H.; Yahya, M.; Zaharim, A.; Sopian, K. Design and testing of solar dryer for drying kinetics of seaweed in Malaysia. In Proceedings of the 4th World Scientific and Engineering Academy and Society( WSEAS) International Conference on Energy and Development-Environment-Biomedicine, Corfu Island, Greece, 14–16 July 2011; pp. 119–124. [Google Scholar]
- Nnamchi, O.A.; Ndukwu, M.C.; Nnamchi, S.N. Modelling and simulation of multi-coupled heat and mass transfer processes: A case study of solar biomass dryer. Therm. Sci. Eng. Prog. 2021, 25, 101007. [Google Scholar] [CrossRef]
- Goud, M.; Reddy, M.V.V.; Chandramohan, V.P.; Suresh, S. A novel indirect solar dryer with inlet fans powered by solar PV panels: Drying kinetics of Capsicum Annum and Abelmoschus esculentus with dryer performance. Sol. Energy 2019, 194, 871–885. [Google Scholar] [CrossRef]
- Gupta, A.; Das, B.; Biswas, A. Performance analysis of stand-alone solar photovoltaic thermal dryer for drying of green chili in hot-humid weather conditions of North-East India. J. Food Process Eng. 2021, 44, e13701. [Google Scholar] [CrossRef]
- Lingayat, A.; Chandramohan, V.P.; Raju, V.R.K.; Kumar, A. Development of indirect type solar dryer and experiments for estimation of drying parameters of apple and watermelon: Indirect type solar dryer for drying apple and watermelon. Therm. Sci. Eng. Prog. 2020, 16, 100477. [Google Scholar] [CrossRef]
- Gupta, A.; Biswas, A.; Das, B.; Reddy, B.V. Development and testing of novel photovoltaic-thermal collector-based solar dryer for green tea drying application. Sol. Energy 2022, 231, 1072–1091. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Onyenwigwe, D.; Abam, F.I.; Eke, A.B.; Dirioha, C. Development of a low-cost wind-powered active solar dryer integrated with glycerol as thermal storage. Renew. Energy 2020, 154, 553–568. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Bennamoun, L.; Abam, F.I. Experience of Solar Drying in Africa: Presentation of Designs, Operations, and Models. Food Eng. Rev. 2018, 10, 211–244. [Google Scholar] [CrossRef]
- Youcef-Ali, S. Study and optimization of the thermal performances of the offset rectangular plate fin absorber plates, with various glazing. Renew. Energy 2005, 30, 271–280. [Google Scholar] [CrossRef]
- Yassien, H.N.S.; Alomar, O.R.; Salih, M.M.M. Performance analysis of triple-pass solar air heater system: Effects of adding a net of tubes below absorber surface. Sol. Energy 2020, 207, 813–824. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Simo-Tagne, M.; Bennamoun, L. Solar drying research of medicinal and aromatic plants: An African experience with assessment of the economic and environmental impact. Afr. J. Sci. Technol. Innov. Dev. 2021, 13, 247–260. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Bennamoun, L. Potential of integrating Na2SO4 10H2O pellets in solar drying system. Dry. Technol. 2018, 36, 1017–1030. [Google Scholar] [CrossRef]
- Dai, H.; Dai, H.; Zhu, H.; Zhang, B.; He, S.; Wang, Z. Combustion characteristics of a low calorific gas burner with ceramic foam enclosed by alumina pellets. Heat Mass Transf. 2022, 58, 221–231. [Google Scholar] [CrossRef]
- Jayalakshmy, M.S.; Philip, J. Thermophysical properties of plant leaves and their influence on the environment temperature. Int. J. Thermophys. 2010, 31, 2295–2304. [Google Scholar] [CrossRef]
- Blaine, R.L. In search of thermal effusivity reference materials. J. Therm. Anal. Calorim. 2018, 132, 1419–1422. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Dirioha, C.; Abam, F.I.; Ihediwa, V.E. Heat and mass transfer parameters in the drying of cocoyam slice. Case Stud. Therm. Eng. 2017, 9, 62–71. [Google Scholar] [CrossRef]
- Tunde-Akintunde, T.Y.; Ogunlakin, G.O. Influence of drying conditions on the effective moisture diffusivity and energy requirements during the drying of pretreated and untreated pumpkin. Energy Convers. Manag. 2011, 52, 1107–1113. [Google Scholar] [CrossRef]
- Argo, B.D.; Ubaidillah, U. Thin-layer drying of cassava chips in multipurpose convective tray dryer: Energy and exergy analyses. J. Mech. Sci. Technol. 2020, 34, 435–442. [Google Scholar] [CrossRef]
- Gupta, A.; Das, B.; Mondol, J.D. Experimental and theoretical performance analysis of a hybrid photovoltaic-thermal (PVT) solar air dryer for green chillies. Int. J. Ambient. Energy 2020, 43, 2423–2431. [Google Scholar] [CrossRef]
- Dhanushkodi, S.; Wilson, V.H.; Sudhakar, K. Thermal Performance evaluation of Indirect forced cabinet solar dryer for cashew drying. Am. J. Agric. Environ. Sci. 2014, 14, 1248–1254. [Google Scholar]
- Gupta, A.; Das, B.; Biswas, A.; Mondol, J.D. Sustainability and 4E analysis of novel solar photovoltaic-thermal solar dryer under forced and natural convection drying. Renew. Energy 2022, 188, 1008–1021. [Google Scholar] [CrossRef]
- Hawa, L.C.; Ubaidillah, U.; Mardiyani, S.A.; Laily, A.N.; Yosika, N.I.W.; Afifah, F.N. Drying kinetics of cabya (Piper retrofractum Vahl) fruit as affected by hot water blanching under indirect forced convection solar dryer. Sol. Energy 2021, 214, 588–598. [Google Scholar] [CrossRef]
- Darvishi, H.; Khoshtaghaza, M.H.; Minaei, S. Fluidized bed drying characteristics of soybeans. J. Agric. Sci. Technol. 2014, 16, 1017–1031. [Google Scholar]
- Herez, A.; Khaled, M.; Murr, R.; Haddad, A.; Elhage, H.; Ramadan, M. Using Geothermal Energy for cooling—Parametric study. Energy Procedia 2017, 119, 783–791. [Google Scholar] [CrossRef]
- GPP. Nigeria Electricity Prices. Global Petrol Prices. 2021, pp. 1–5. Available online: www.globalpetrolprices.com/Nigeria/electricity_prices/ (accessed on 15 May 2022).
- Kirian, D.R. Principles of Economics and Management for Manufacturing Engineering; Elsevier Inc.: Amsterdam, The Netherlands, 2022. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Manuwa, S.I. A techno-economic assessment for viability of some waste as cooling pads in evaporative cooling system. Int. J. Agric. Biol. Eng. 2015, 8, 151–158. [Google Scholar] [CrossRef]
- Bennamoun, L.; Belhamri, A. Design and simulation of a solar dryer for agriculture products. J. Food Eng. 2003, 59, 259–266. [Google Scholar] [CrossRef]
- Ndukwu, M.C.; Bennamoun, L.; Abam, F.I.; Eke, A.B.; Ukoha, D. Energy and exergy analysis of a solar dryer integrated with sodium sulfate decahydrate and sodium chloride as thermal storage medium. Renew. Energy 2017, 113, 1182–1192. [Google Scholar] [CrossRef]
- Sagar, V.R.; Suresh Kumar, P. Recent advances in drying and dehydration of fruits and vegetables: A review. J. Food Sci. Technol. 2010, 47, 15–26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doymaz, I. Evaluation of some thin-layer drying models of persimmon slices (Diospyros kaki L.). Energy Convers. Manag. 2012, 56, 199–205. [Google Scholar] [CrossRef]
- Raigar, R.K.; Mishra, H.N. Effects of Temperature on Thermo-Physical Properties of Roasted Peanut Paste (Arachis hypogaea L.) Blended with Soybean Oil. J. Food Qual. 2016, 39, 323–330. [Google Scholar] [CrossRef] [Green Version]
- Oladunjoye, M.; Sanuade, O. Thermal Diffusivity, Thermal Effusivity and Specific Heat of Soils in Olorunsogo Powerplant, Southwestern Nigeria. Int. J. Res. Rev. Appl. Sci. 2012, 13, 502–521. [Google Scholar]
- Dimitrios, A.T.; Vouros, A.P.; Bardakas, A.V.; Filios, A.E.; Margaris, D.P. Case studies on the effect of the air drying conditions on the convective drying of quinces. Case Stud. Therm. Eng. 2014, 3, 79–85. [Google Scholar]
- Oyedepo, S.O. Towards achieving energy for sustainable development in Nigeria. Renew. Sustain. Energy Rev. 2014, 34, 255–272. [Google Scholar] [CrossRef] [Green Version]
- Oseni, M.O. Improving households’ access to electricity and energy consumption pattern in Nigeria: Renewable energy alternative. Renew. Sustain. Energy Rev. 2012, 16, 3967–3974. [Google Scholar] [CrossRef]
- Chavan, A.; Thorat, B. Techno-economic comparison of selected solar dryers: A case study. Dry. Technol. 2021, 1–11. [Google Scholar] [CrossRef]
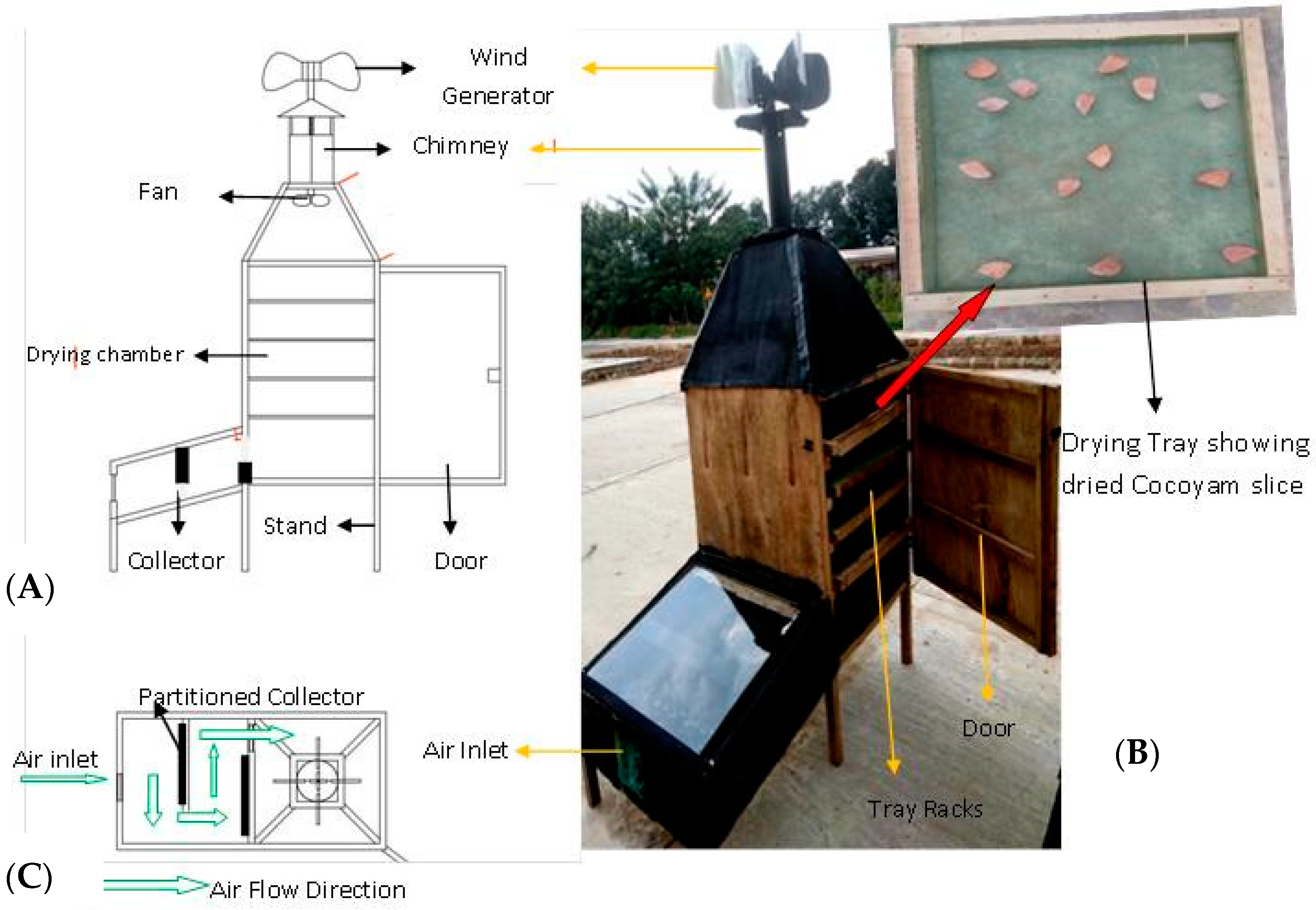



| Units | Specifications | Source |
|---|---|---|
| Solar collector | Hard wood (2 × 2 inch), tilted 15 °N, 0.6 m × 0.6 m × 0. 59 m | Custom design |
| Absorber | Black painted aluminum sheet, 0.6 × 0.6 m × 0.001 m | Custom design |
| Glazing | Transparent glass, 0.57 m × 0.6 m, 0.004 m | Perspex |
| Drying Chamber | Plywood (lined with black painted aluminum inside), 0.6 × 0.6 × 1 m, 45° tapering at 0.3 m height at 0.7 m from the base | Custom design |
| Drying trays | Hardwood (2 × 2 inches) skeleton, plastic wire mesh, 0.57 m × 0.57 m, 4 trays at 0.15 m gap | Custom design |
| Chimney | Hollow galvanized steel, pipe; ϕ 0.12 m and 0.3 m high | Custom design |
| Wind generator and fan | ϕ 0.05 m hollow pipe, 0.15 m−0.10 m, 3 curved aluminum arms, 0.156 m axial fan blade, frictionless bearings | Custom design |
| S/N | Materials | Specification | Quantity | Cost (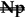 ) ) |
|---|---|---|---|---|
| 1 | Planks | 2 inches × 2 inches | 8 pieces | 2700 |
| 2 | Glass | 4mm thick (57 cm × 60 cm) | 1sheets | 2250 |
| 3 | Screw | 2 inches | 1 pack | 900 |
| 4 | Board | 4 feet × 8 feet | 2 | 8000 |
| 5 | Nail | 3inches and 1 inch | 1.5 pounds weight | 1200 |
| 6 | Door hinge | Medium size | 2 pieces | 400 |
| 7 | Paint | Black oil paint | 4 litters | 4500 |
| 8 | Painting brush | Big size | 1 piece | 350 |
| 9 | Aluminum sheet | 3.5 inches × 8 inches, black | 1 sheet | 4000 |
| 10 | Top bond gum | Medium size | 1 can | 1000 |
| 11 | Baton | Flat size | 2 pieces | 300 |
| 12 | Net | Green colour | 1.5 yards | 1050 |
| 13 | Suction fan blade | Steel type | 1 piece | 350 |
| 14 | Steel pipe | Cylindrical, 4 mm thick | 1 piece, 35 cm long | 800 |
| 15 | Bearing | 6mm diameter ring | 2 pieces | 500 |
| Variable Cost | ||||
| 16 | Labour | 18,000 | ||
| 17 | Transportation | 3000 | ||
| 18 | Miscellaneous | 2000 | ||
| 19 | Total Cost | 50,950 ($122.714 as of 3 May 2022) | ||
| Months | Rainfall (mm) | Temperature (°C) | Evaporation (mm) | Relative Humidity (%) | Sunshine (h) | |||
|---|---|---|---|---|---|---|---|---|
| amount | day | max | min | ---- | ----- | ------- | --- | |
| Jan | 0.0 | 0 | 32 | 23 | 0.22 | 72 | 45 | 6.4 |
| Feb | 88.2 | 7 | 35 | 22 | 0.46 | 73 | 50 | 6.3 |
| Mar | 57.0 | 3 | 35 | 23 | 0.50 | 77 | 53 | 3.9 |
| April | 142.0 | 17 | 33 | 24 | 0.82 | 76 | 59 | 6.1 |
| May | 233.7 | 16 | 32 | 24 | 4.70 | 84 | 70 | 5.0 |
| Jun | 213.0 | 14 | 31 | 23 | 9.25 | 87 | 77 | 3.2 |
| July | 362.0 | 24 | 30 | 23 | 10.55 | 86 | 75 | 3.4 |
| Aug | 161.8 | 19 | 30 | 24 | 6.10 | 88 | 78 | 2.2 |
| Sept | 349.0 | 25 | 30 | 24 | 8.80 | 59 | 75 | 2.9 |
| Oct | 244.6 | 16 | 31 | 24 | 4.80 | 86 | 78 | 2.9 |
| Nov | 58.5 | 6 | 33 | 25 | 0.31 | 97 | 70 | 4.1 |
| Dec | 0.0 | 0 | 32 | 21 | 0.20 | 75 | 49 | 4.9 |
| Instruments | Specifications | Sensitivity |
|---|---|---|
| Temperature | Thermocouple (TM-902C, −50 °C to 750 °C), type K thermocouple-China) | ±0.1 °C |
| Solar Radiation | Pynarometer (Lutron SPM-1116SD) | |
| Air Velocity | Anemometer (CR2032, 3 Volts Lithium Cell) | ±0.1 m/s |
| Relative Humidity | Humidity/Baro/Tempt Data recorder (Lutron MHB-382-Taiwan) | ±0.1 |
| Mass | Electronic Weighing Scale (KERRO SF-400-China) | 1000 g × 1 g; 353 oz × 0.1 oz |
| Model Name | Model | Reference |
|---|---|---|
| Lewis | [29] | |
| Henderson and Pabis’s | [29] | |
| Logarithmic model | [29] | |
| Wang and Singh | [29] | |
| Two term | [29] | |
| Vermer et al. | [29] | |
| Two Term Exponential | [29] |
| Parameters | Unite | Values |
|---|---|---|
| Average solar collector temperature | (°C) | 34.1 |
| Average solar drying chamber temperature | (°C) | 33.1 |
| Average relative humidity of the solar collector | (%) | 66.9 |
| Average relative humidity of the drying chamber | (%) | 67.4 |
| Average solar radiation | (W/m2) | 303.27 |
| Average ambient temperature | (°C) | 31.10 |
| Average flow rate | (kg/s) | 0.12 |
| Initial moisture content on a wet basis | (%) | 82.9 |
| Final moisture content on a wet basis | (%) | 10.32 |
| Final mass | (g) | 138 |
| Average drying rate | (kg/kg h) | 0.018686 |
| Energy consumed | (MJ) | 3.970 (1.103 kWh) |
| Solar collector efficiency | (%) | 13.47 |
| Overall solar drying efficiency | (%) | 7.59 |
| Drying time | (h) | 25 |
| CO2 mitigated per year | tons | 317.11 |
| Model | Constants | R2 | RMSE | χ2 |
|---|---|---|---|---|
| Lewis | k = 0.03157 | 0.9569 | 0.0347 | 0.001165 |
| Two Term | a = 0.16656 ko = 0.22505 b = 0.8701 k1 = 0.02673 | 0.9666 | 0.02923 | 0.00145 |
| Two term exponential | a = 0.17564 k = 0.14164 | 0.96648 | 0.03179 | 0.00145 |
| Henderson and Pabis | a = 0.98466 k = 0.03351 | 0.95837 | 0.03772 | 0.00171 |
| Logarithmic | a = 11.11849 k = 0.00376 c= −10.0901 | 0.96172 | 0.0745 | 0.00191 |
| Wang and Singh | a = −0.036 b = 0.000556 | 0.95821 | 0.03784 | 0.00172 |
| Modified page | k = 0.03202 n = 0.88042 | 0.96427 | 0.03341 | 0.00152 |
| Vermer et al. | a =1150.18 k = 0.03668 g = 0.03668 | 0.95421 | 0.03891 | 0.00185 |
| Thermal Property | Average Value | Standard Deviation |
|---|---|---|
| Specific heat capacity (J/kg K) | 1866.154 | 249.4573 |
| Thermal conductivity (W/m K) | 0.090049 | 0.011914 |
| Thermal diffusivity (m/s) | 3.93965 × 10−5 | 5.62695 × 10−8 |
| Effective moisture diffusivity (m/s) | 3.21462 × 10−10 | - |
| Thermal effusivity (S1/2 m−2 K−1) | 35.30598 | 7.690472 |
| Heat transfer coefficient (W/m K) | 3.85 | 0.67931 |
| Mass transfer coefficient (m/s) | 0.01757 | 0.034469 |
| Diffusivity coefficient(m2/s) | 0.000179 | 0.000306 |
| Equations | Regression Coefficients | R2 | Standard Error |
|---|---|---|---|
| 1026 | 0.99 | 0.0004041 | |
| = 1.2696 | |||
| 1256 | |||
| = 0.9334 | |||
| 0.99 | 0.0000608731 | ||
| −12.883 | |||
| 0.99 | 0.000003156964 | ||
| 0.98 | 0.00000000830198 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ndukwu, M.C.; Ibeh, M.; Ekop, I.; Abada, U.; Etim, P.; Bennamoun, L.; Abam, F.; Simo-Tagne, M.; Gupta, A. Analysis of the Heat Transfer Coefficient, Thermal Effusivity and Mathematical Modelling of Drying Kinetics of a Partitioned Single Pass Low-Cost Solar Drying of Cocoyam Chips with Economic Assessments. Energies 2022, 15, 4457. https://doi.org/10.3390/en15124457
Ndukwu MC, Ibeh M, Ekop I, Abada U, Etim P, Bennamoun L, Abam F, Simo-Tagne M, Gupta A. Analysis of the Heat Transfer Coefficient, Thermal Effusivity and Mathematical Modelling of Drying Kinetics of a Partitioned Single Pass Low-Cost Solar Drying of Cocoyam Chips with Economic Assessments. Energies. 2022; 15(12):4457. https://doi.org/10.3390/en15124457
Chicago/Turabian StyleNdukwu, Macmanus C., Mathew Ibeh, Inemesit Ekop, Ugochukwu Abada, Promise Etim, Lyes Bennamoun, Fidelis Abam, Merlin Simo-Tagne, and Ankur Gupta. 2022. "Analysis of the Heat Transfer Coefficient, Thermal Effusivity and Mathematical Modelling of Drying Kinetics of a Partitioned Single Pass Low-Cost Solar Drying of Cocoyam Chips with Economic Assessments" Energies 15, no. 12: 4457. https://doi.org/10.3390/en15124457










