Modelling Study of Cycle-To-Cycle Variations (CCV) in Spark Ignition (SI)-Controlled Auto-Ignition (CAI) Hybrid Combustion Engine by Using Reynolds-Averaged Navier–Stokes (RANS) and Large Eddy Simulation (LES)
Abstract
:1. Introduction
2. Methodology
2.1. Engine Experiments
2.2. RANS Modelling
2.3. LES Modelling
2.4. Simulation Conditions
2.5. Engine Mesh and Numerical Methods
3. Results and Discussions
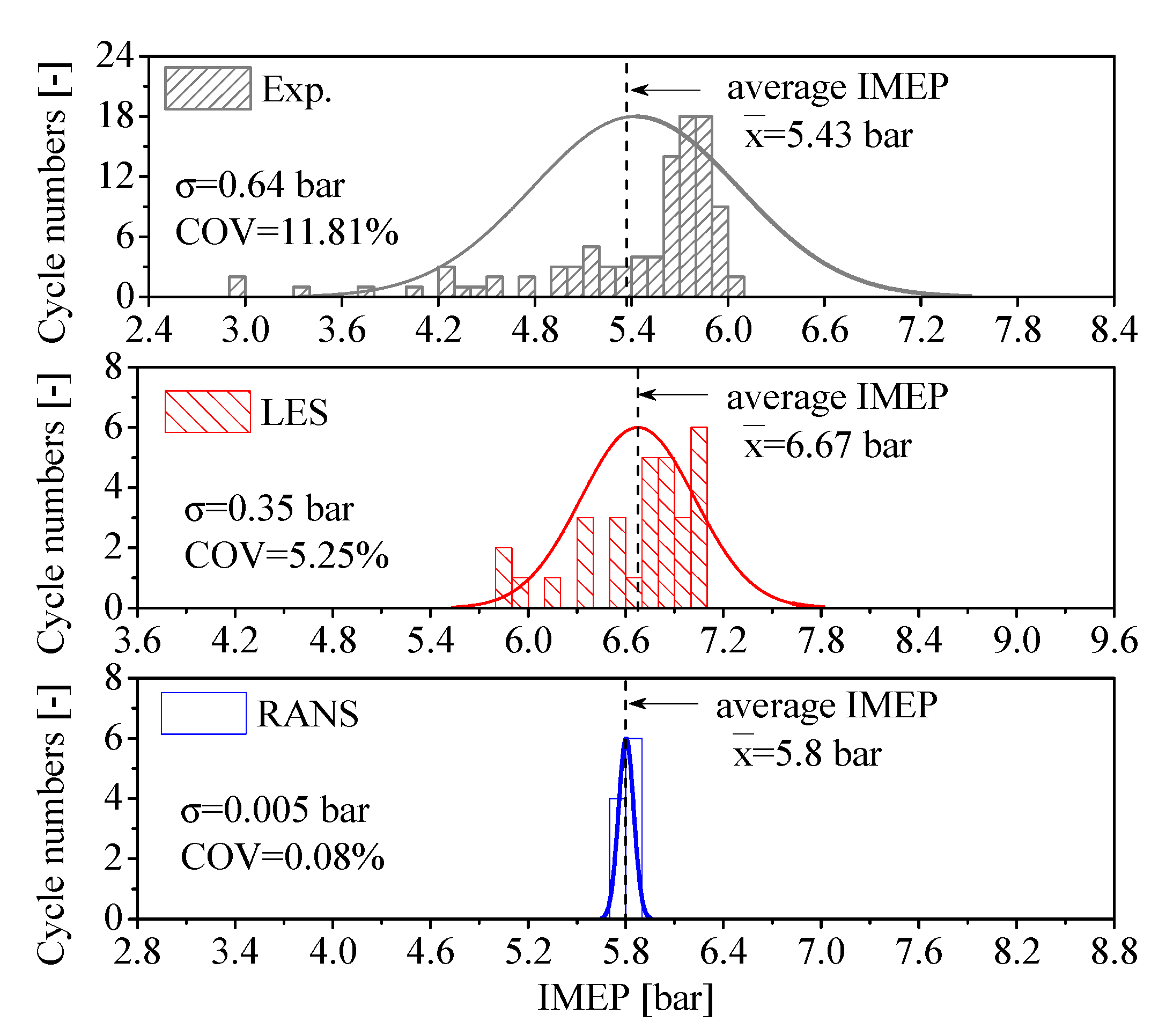
3.1. Validations of RANS and LES Results with Experimental Measurements
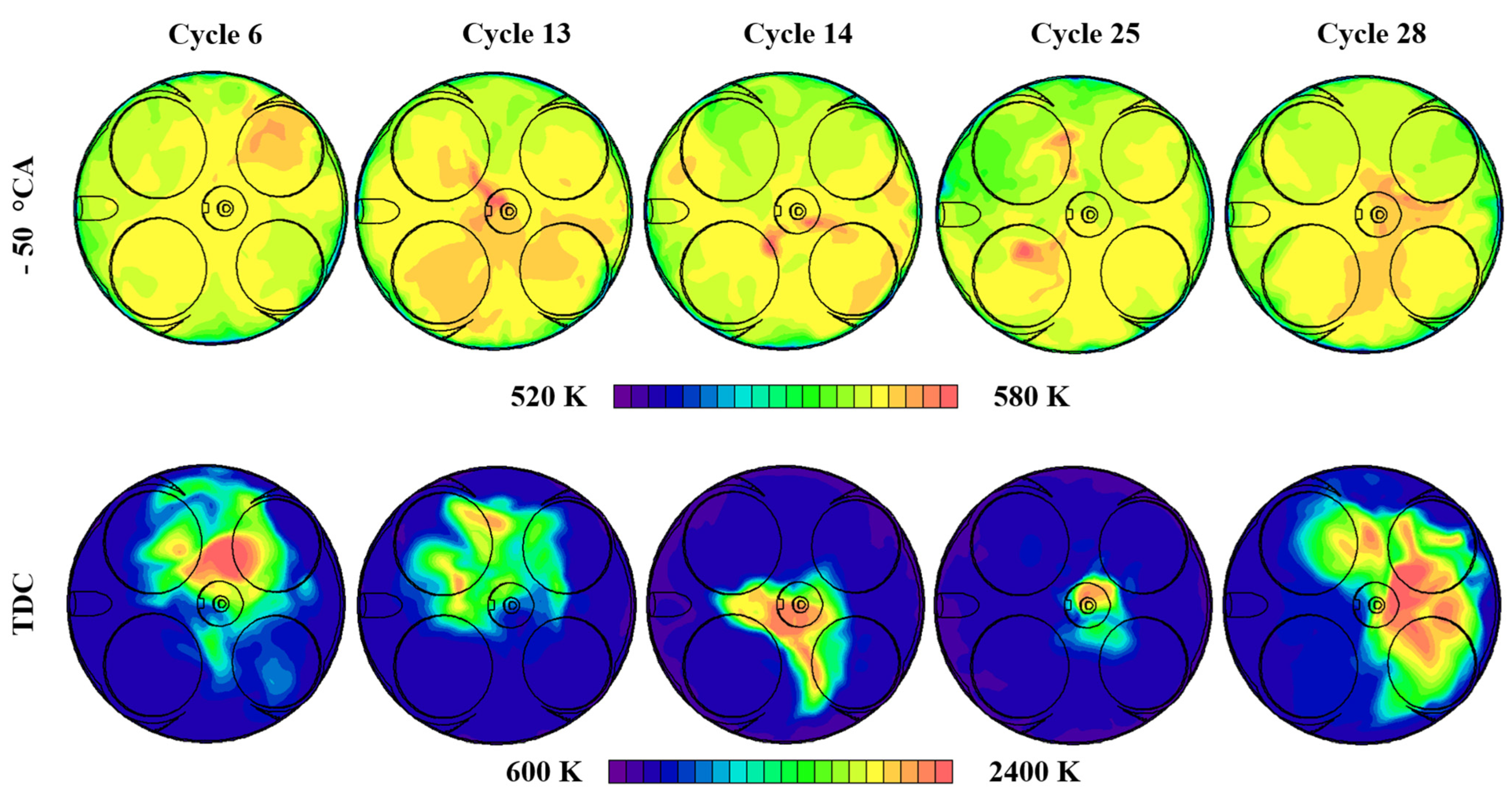
3.2. Analysis of the Cyclic Phenomenon of Hybrid Combustion
4. Conclusions
- (1)
- The adopted LES simulation is capable of predicting the cyclic variations in hybrid combustion observed in the experiments, with strong CCVs of IMEP and very similar histogram distribution patterns. However, RANS simulations fail to reproduce the cyclic characteristics of the hybrid combustion at the chosen engine operating conditions.
- (2)
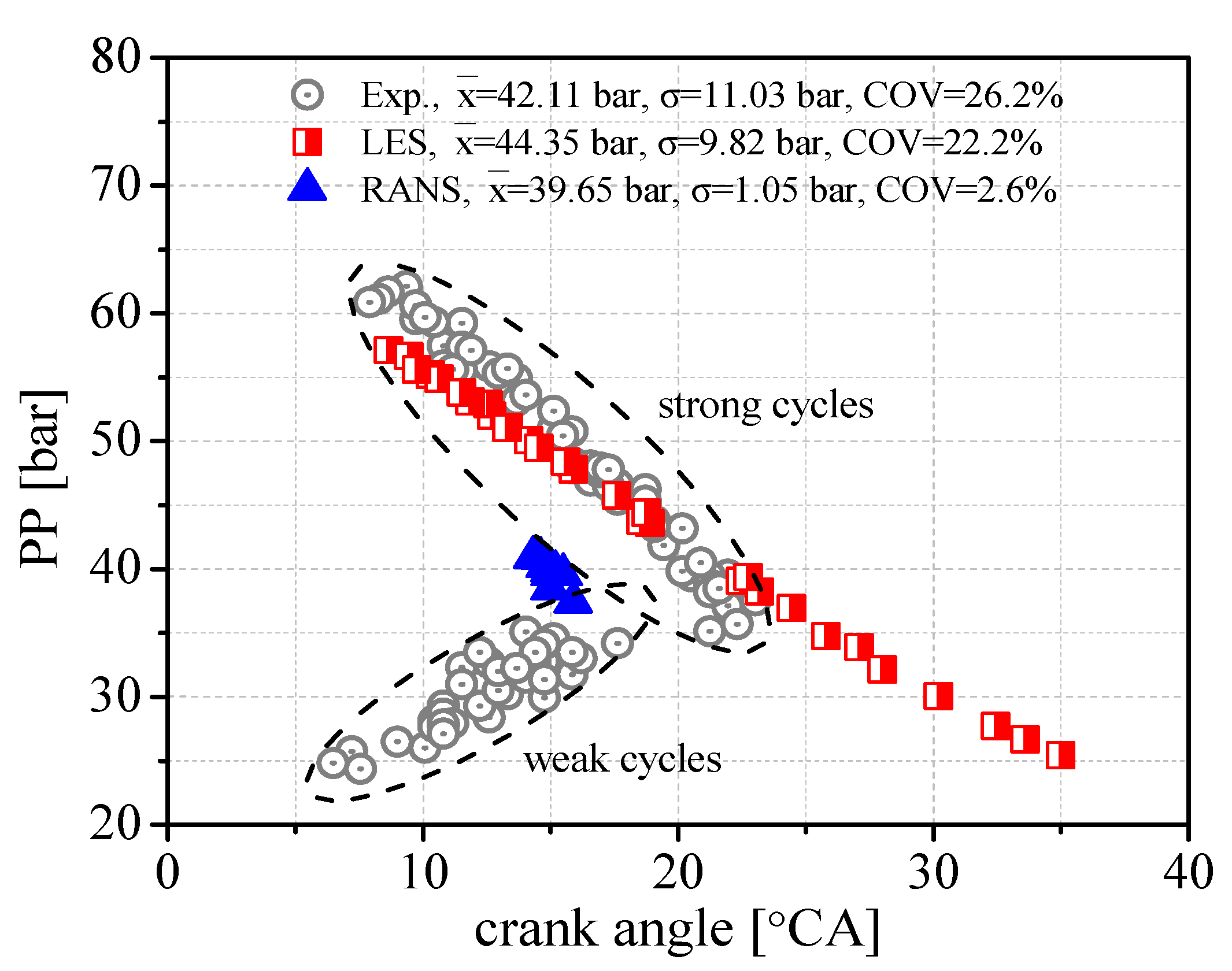
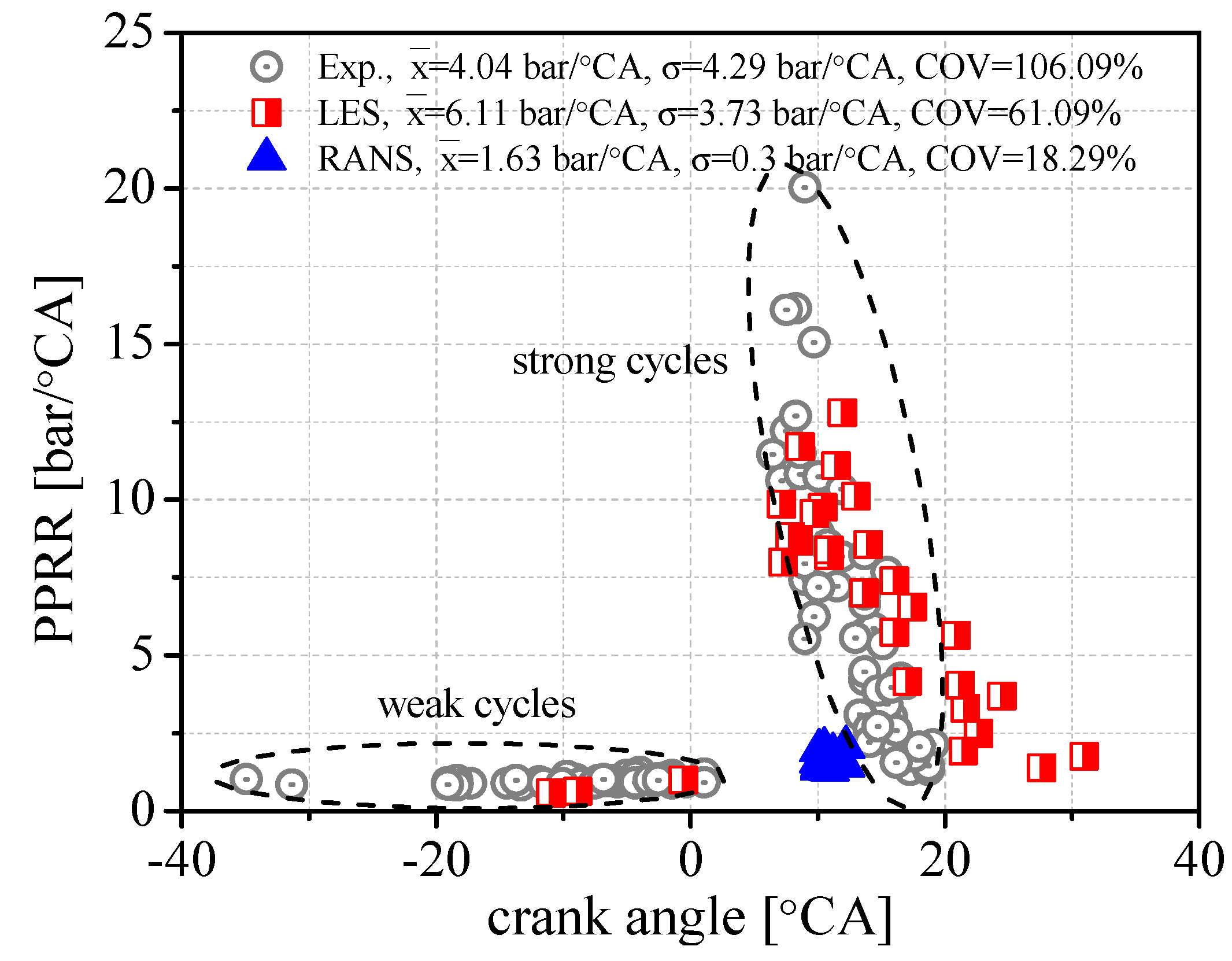
- The analysis shows the nonlinear relationship of PP/PPRR against the corresponding crank angles in the experimental results and the presence of two distinct combustion types (strong/weak cycles). The measured cyclic variation is gradually enlarged as the combustion process proceeds from CA10 to CA90.
- (3)
- The LES simulations are able to produce an excellent agreement between the predicted average PP (44.35 bar) and the COV (22.2%) and experimental observations (42.11 bar and 26.2%, respectively). The LES simulations are also able to predict the two distinct combustion types and CCVs in the PPRR-crank angle plot, and the enlarged cyclic variations from CA10 to CA90.
- (4)
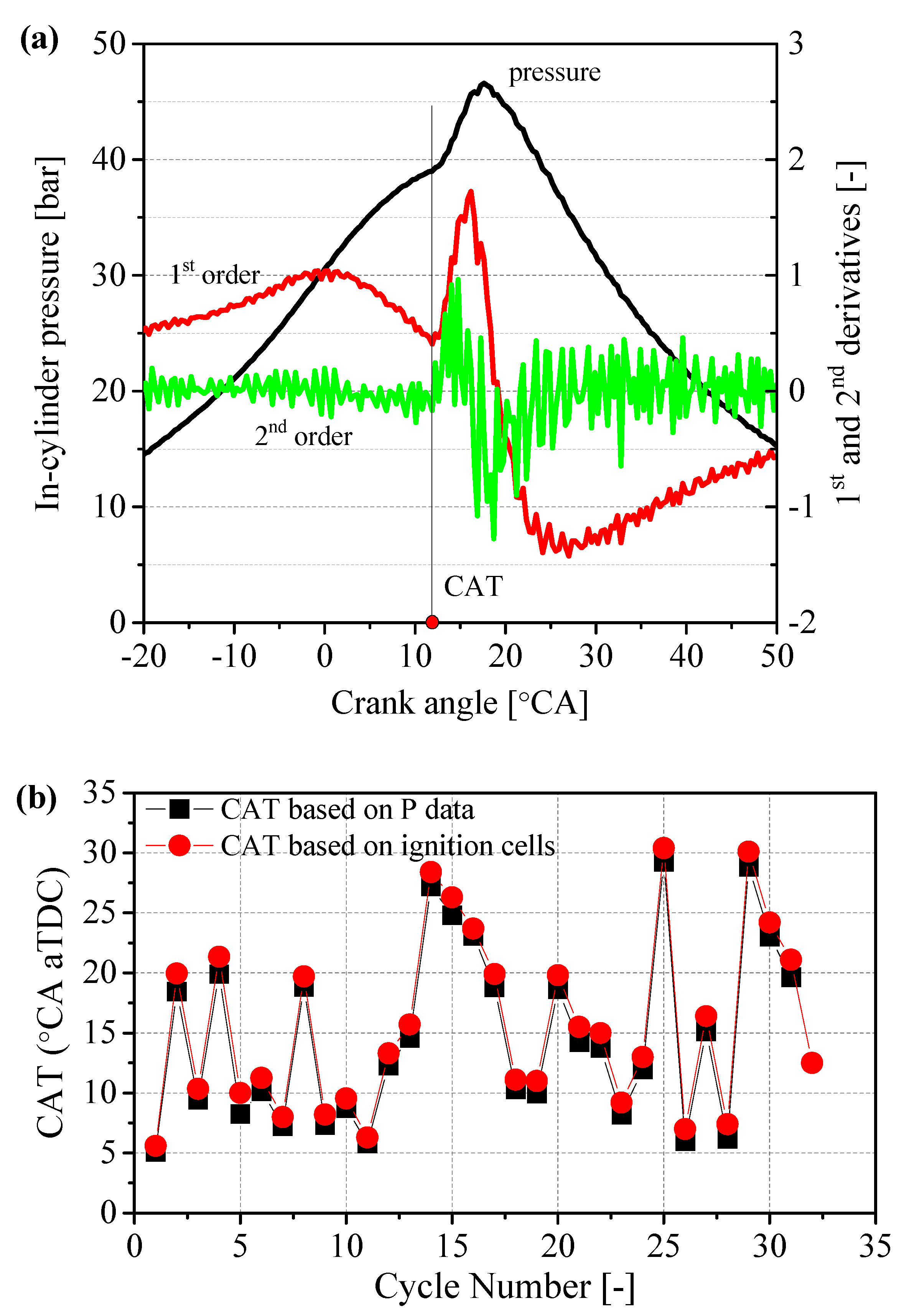
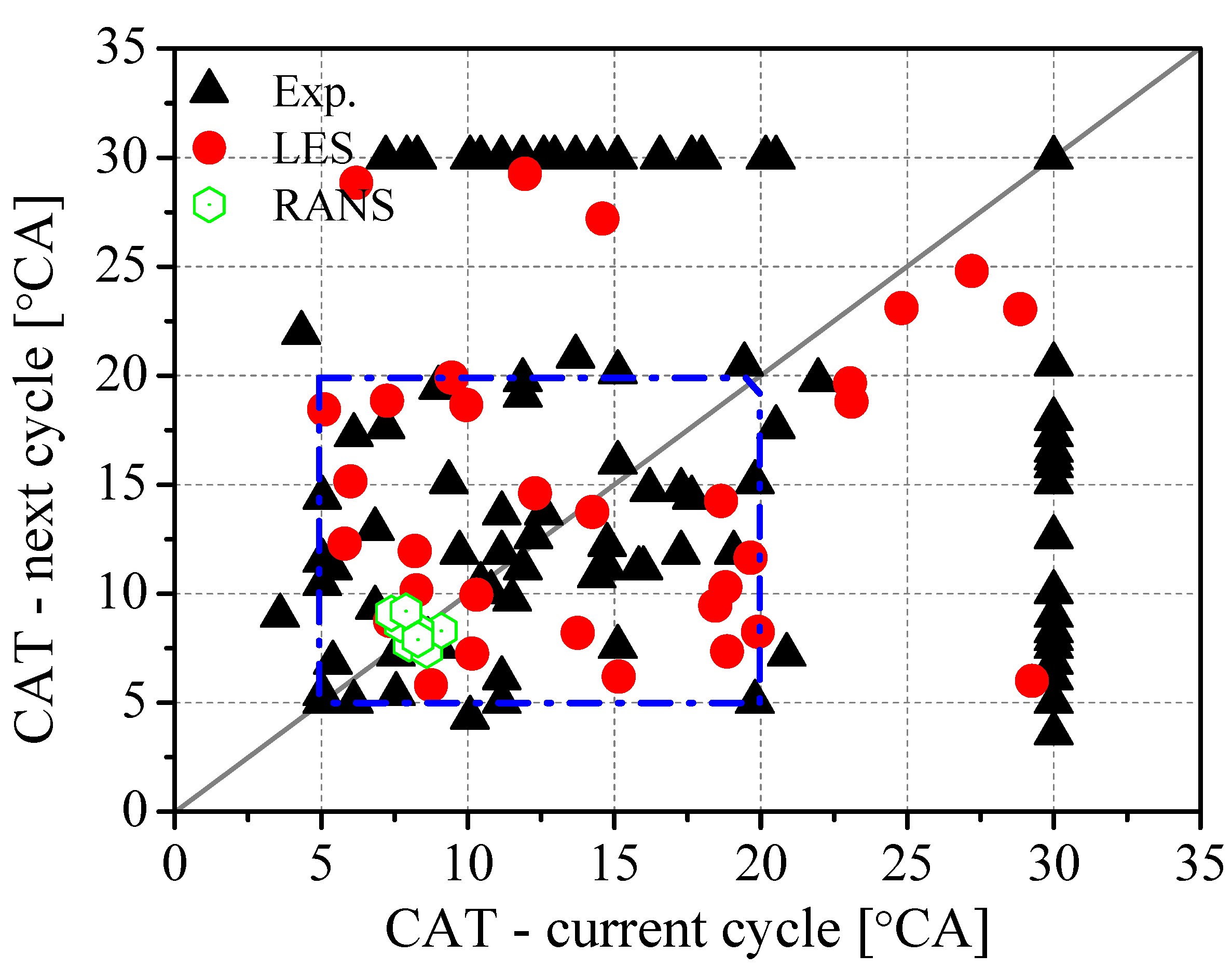
- The CAT pressure, defined as the transition point where the local first order derivative of the pressure trace is at the minimum, while the second order derivative just exceeds 0.1, shows very similar results of the crank angle with 1% cells auto-ignited (CAT ignition) in LES based on autoignition cells. The distribution of CATs of the current cycle and next cycle in LES shows a very good agreement with experimental results, indicating excellent capture of the combustion mode transitioning with the LES.
- (5)
- However, the detailed comparison between the LES and experimental data also highlights the challenges of modelling the nonlinear phenomenon of SI–CAI hybrid combustion. For example, the weak cycles are not well captured with the existing LES modelling, which produce late CAT, higher average IMEP and lower COV compared to the experiments. The reasons could be the overestimation of the flame propagation speed and auto-ignition combustion speed at extreme conditions near the experimental lower limit.
- (6)
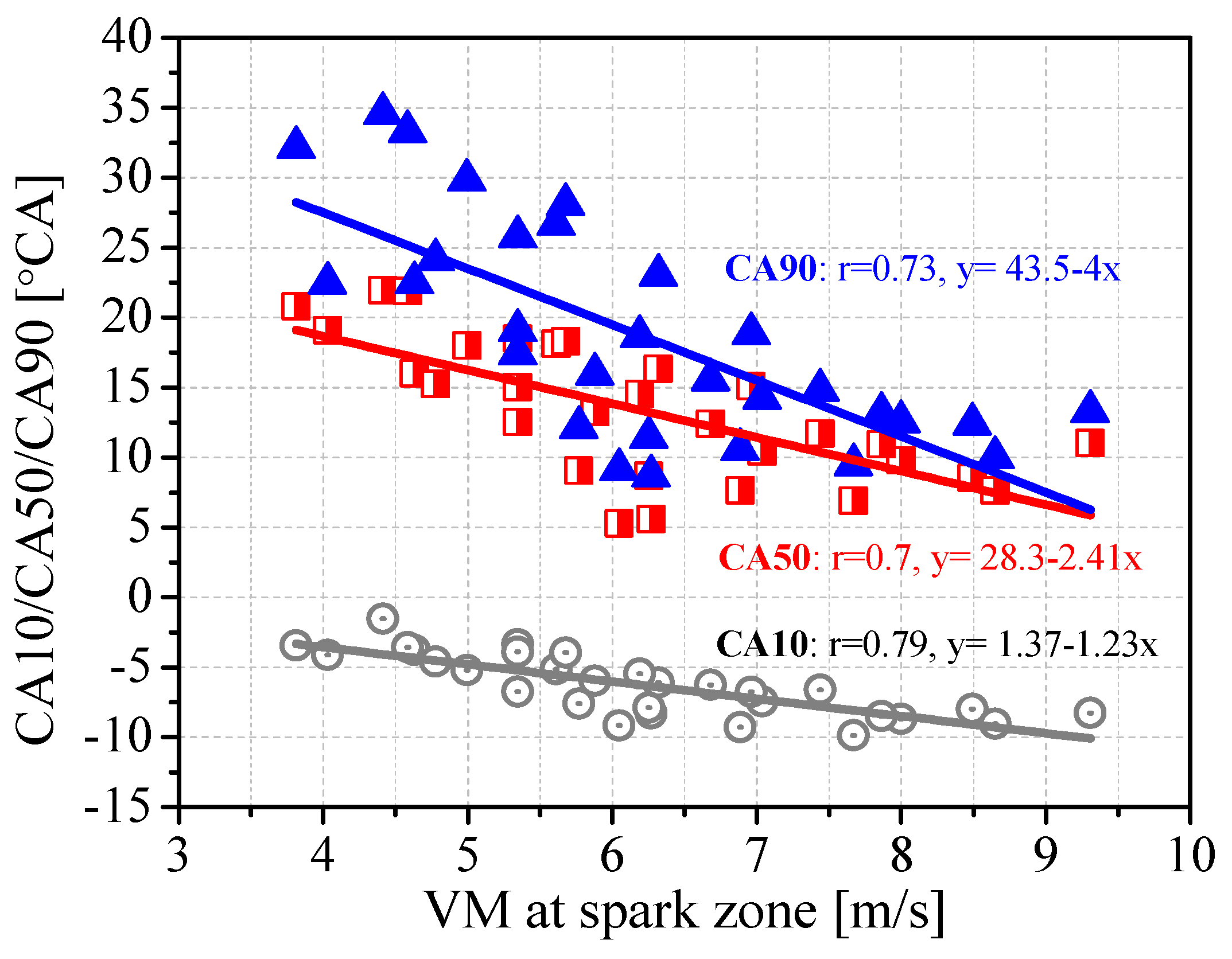
- The correlation study reveals that the local velocity magnitude (VM) around the spark plug before spark ignition timing has a large effect on the early flame propagation and CA10, while the induced thermal conditions by early flame propagation dominates the subsequent auto-ignition combustion in the late stage, as evidenced by the strong correlation between the temperatures at TDC and CA50, CA90 and CAT.
- (7)
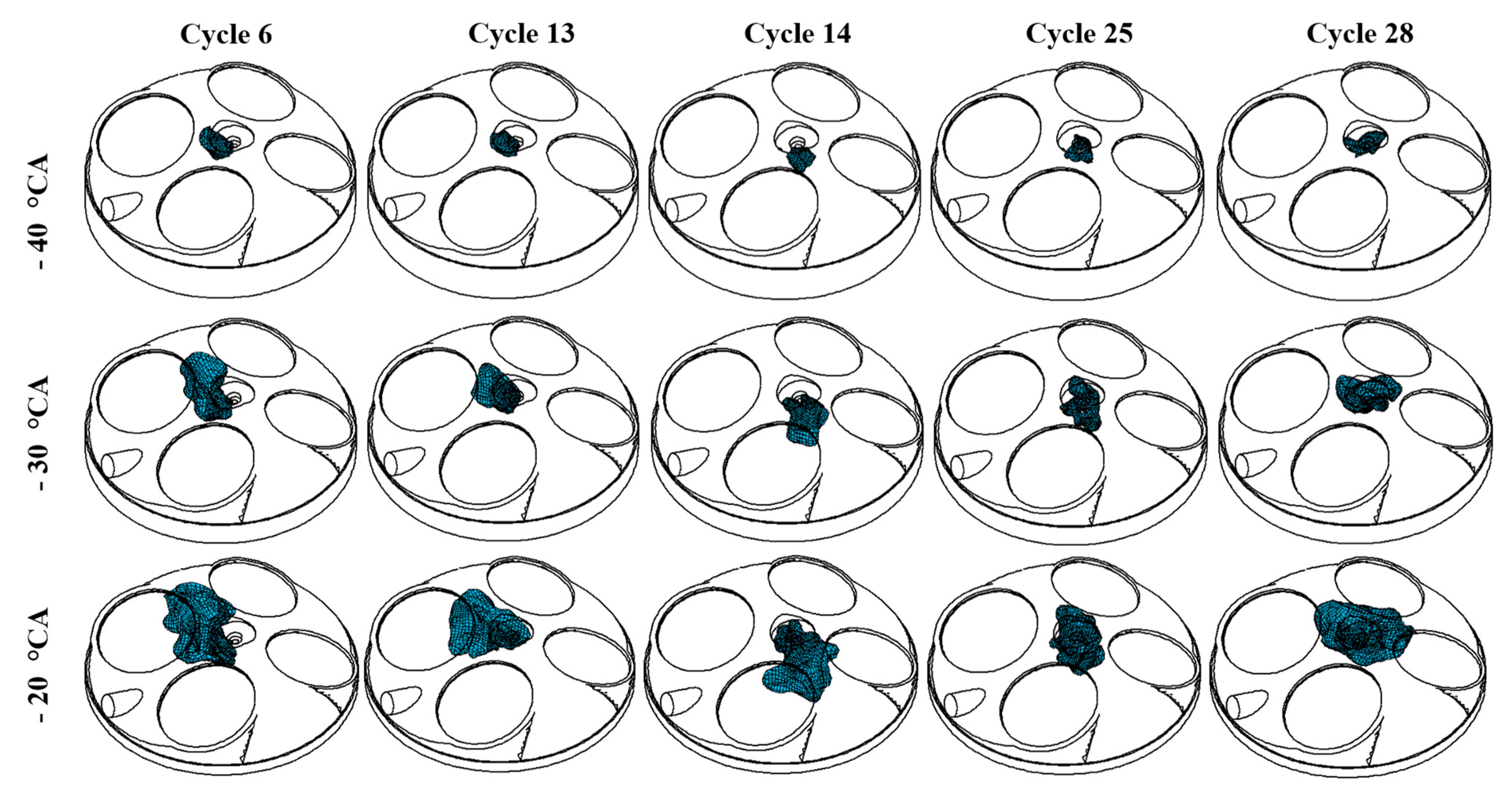
- Visualization of the in-cylinder flow motions, flame front and auto-ignition sites in selected cycles confirms the importance of flow fields around the spark plug for determining flame kernel formation and flame development. Strong and coordinated flow fields that cross the spark plug region are found to promote the flame propagation process. Auto-ignition sites are located very close to the flame front and are dominated by the local thermal conditions.
- (8)
- The correlations and visualizations indicate that the cyclic variations in the local velocity around the spark plug lead to the variations in the early flame propagation, which in turn produces temperature fluctuations among the cycles and resulted in greater variations in the subsequent auto-ignition combustion events.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CCV | Cycle-to-cycle variations |
| SI | Spark ignition |
| CAI | Controlled auto-ignition |
| RANS | Reynolds-averaged Navier–Stokes |
| LES | Large eddy simulation |
| IMEP | Indicated mean effective pressure |
| PP | Peak pressure |
| PPRR | Peak pressure rise rate |
| SACI | Spark assisted compression ignition |
| CFD | Computational fluid dynamics |
| CA10 | Crank angle with fuel mass fraction burned at 10% |
| CA50 | Crank angle with fuel mass fraction burned at 50% |
| CA90 | Crank angle with fuel mass fraction burned at 90% |
| CAT | Crank angle with fuel mass fraction burned at mode transition |
| EGR | Exhaust gas recirculation |
| NVO | Negative valve overlapping |
| COV | Coefficient of variation |
| RGF | Residual gas fraction |
| TDC | Top dead center |
| T TDC | Average temperature at TDC |
| VM | Velocity magnitude |
References
- Robertson, D.; Prucka, R. A Review of Spark-Assisted Compression Ignition (SACI) Research in the Context of Realizing Production Control Strategies. In Proceedings of the 14th International Conference on Engines & Vehicles, Napoli, Italy, 15–19 September 2019. SAE Technical Paper 2019-24-0027. [Google Scholar]
- Wang, Z.; Wang, J.-X.; Shuai, S.-J.; Ma, Q.-J. Effects of Spark Ignition and Stratified Charge on Gasoline HCCI Combustion with Direct Injection. In Proceedings of the SAE 2005 World Congress & Exhibition, Detroit, MI, USA, 11–14 April 2005. SAE Technical Paper 2005-01-0137. [Google Scholar]
- Milovanovic, N.; Blundell, D.; Gedge, S.; Turner, J. SI-HCCI-SI Mode Transition at Different Engine Operating Conditions. In Proceedings of the SAE 2005 World Congress & Exhibition, Detroit, MI, USA, 11–14 April 2005. SAE Technical Paper 2005-01-0156. [Google Scholar]
- Santoso, H.; Matthews, J.; Cheng, W.K. Managing SI/HCCI Dual-Mode Engine Operation. In Proceedings of the SAE 2005 World Congress & Exhibition, Detroit, MI, USA, 11–14 April 2005. SAE Technical Paper 2005-01-0162. [Google Scholar]
- Manofsky, L.; Vavra, J.; Assanis, D.N.; Babajimopoulos, A. Bridging the Gap between HCCI and SI: Spark—Assisted Compression Ignition. In Proceedings of the SAE 2011 World Congress & Exhibition, Detroit, MI, USA, 12–14 April 2011. Technical Paper 2011-01-1179. [Google Scholar]
- Zhou, L.; Song, Y.; Hua, J.; Liu, F.; Wei, H. Effects of miller cycle strategies on combustion characteristics and knock resistance in a spark assisted compression ignition (SACI) engine. Energy 2020, 206, 118119. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, Y.; Pei, Y.; Zhang, A.; Traver, M.; Ameen, M. Numerical Evaluation of Spark Assisted Cold Idle Operation in a Heavy-Duty Gasoline Compression Ignition Engine. In Proceedings of the SAE WCX Digital Summit, Detroit, MI, USA, 5–7 April 2021. SAE Technical Paper 2021-01-0410. [Google Scholar]
- Ortiz-Soto, E.A.; Lavoie, G.A.; Wooldridge, M.S.; Assanis, D.N. Thermodynamic efficiency assessment of gasoline spark ignition and compression ignition operating strategies using a new multi-mode combustion model for engine system simulations. Int. J. Engine Res. 2019, 20, 304–326. [Google Scholar] [CrossRef]
- Robertson, D.; Prucka, R. Evaluation of control-oriented flame propagation models for production control of a spark-assisted compression ignition engine. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 236, 334–342. [Google Scholar] [CrossRef]
- Adcock, I. Mazda’s Skyactiv-X beats the big guys to market with a promising new production engine that marries Otto and Diesel attributes. Automot. Eng. Int. 2017, 24–26. [Google Scholar]
- Mazda Skyactiv-X Technology. Available online: https://www.mazda.com/en/innovation/technology/skyactiv (accessed on 24 February 2022).
- Sen, A.; Litak, G.; Edwards, K.; Finney, C.; Daw, C.; Wagner, R. Characteristics of cyclic heat release variability in the transition from spark ignition to HCCI in a gasoline engine. Appl. Energy 2012, 88, 1649–1655. [Google Scholar] [CrossRef]
- Temel, V.K.; Sterniak, J. Characterization of SACI Combustion for Use in Model Based Controls. In Proceedings of the SAE 2014 World Congress & Exhibition, Detroit, MI, USA, 8–10 April 2014. SAE Technical Paper 2014-01-1289. [Google Scholar]
- Havstad, M.A.; Aceves, S.; McNenly, M.J.; Piggott, W.T.; Edwards, K.D.; Wagner, R.; Daw, C.S.; Finney, C.E.A. Detailed Chemical Kinetic Modeling of Iso-octane SI-HCCI Transition. In Proceedings of the Society of Automotive Engineers 2010 World Conference, Detroit, MI, USA, 13–15 April 2010. SAE Technical Paper 2010-01-1087. [Google Scholar]
- Larimore, J.; Hellström, E.; Sterniak, J.; Jiang, L.; Stefanopoulou, A.G. Experiments and Analysis of High Cyclic Variability at the Operational Limits of Spark-Assisted HCCI Combustion. In American Control Conference (ACC) 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2072–2077. [Google Scholar]
- Wagner, R.; Edwards, K.D.; Daw, C.S.; Green, J.B.; Bunting, B.G. On the Nature of Cyclic Dispersion in Spark Assisted HCCI Combustion. In Proceedings of the 2006 SAE World Congress, Detroit, MI, USA, 3–6 April 2006. SAE Technical Paper 2006-01-0418. [Google Scholar]
- Daw, C.S.; Wagner, R.M.; Edwards, K.D.; Green, J.B. Understanding the transition between conventional spark-ignited combustion and HCCI in a gasoline engine. Proc. Combust. Inst. 2007, 31, 2887–2894. [Google Scholar]
- Hunicz, J. Cycle-by-cycle variations in autonomous and spark assisted homogeneous charge compression ignition combustion of stoichiometric air–fuel mixture. Int. J. Spray Combust. Dyn. 2018, 10, 231–243. [Google Scholar] [CrossRef]
- Hunicz, J.; Mikulski, M.; Koszałka, G.; Ignaciuk, P. Detailed analysis of combustion stability in a spark-assisted compression ignition engine under nearly stoichiometric and heavy EGR conditions. Appl. Energy 2020, 280, 115955. [Google Scholar] [CrossRef]
- Triantopoulos, V.; Bohac, S.V.; Sterniak, J.; Lavoie, G.; Boehman, A.L.; Assanis, D.N.; Martz, J.B. Cycle-to-cycle variability in spark-assisted compression ignition engines near optimal mean combustion phasing. Int. J. Engine Res. 2021, 14680874211053061. [Google Scholar] [CrossRef]
- Chen, T.; Xie, H.; Li, L.; Yu, W.; Li, Z.; Zhao, H. Continuous Load Adjustment Strategy of a Gasoline HCCI-SI Engine Fully Controlled by Exhaust Gas. In Proceedings of the SAE 2011 World Congress & Exhibition, Detroit, MI, USA, 12–14 April 2011. SAE Technical Paper 2011-01-1408. [Google Scholar]
- Joelsson, T.; Yu, R.; Bai, X.S. Large eddy simulation of turbulent combustion in a spark-assisted homogenous charge compression ignition engine. Combust. Sci. Technol. 2012, 184, 1051–1065. [Google Scholar] [CrossRef] [Green Version]
- Yoo, C.S.; Luo, Z.; Lu, T.; Kim, H.-J.; Chen, J.H. A DNS study of ignition characteristics of a lean iso-octane/air mixture under HCCI and SACI conditions. Proc. Combust. Inst. 2013, 34, 2985–2993. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Zhao, H. Computational study of the influence of in-cylinder flow on spark ignition–controlled auto-ignition hybrid combustion in a gasoline engine. Int. J. Engine Res. 2015, 16, 795–809. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, H.; Xie, H. Effect of dilution strategies and direct injection ratios on Stratified Flame Ignition (SFI) hybrid combustion in a PFI/DI gasoline engine. Appl. Energy 2016, 165, 801–814. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Li, L.; Xie, L.; Chen, T.; Zhao, H. Effect of the thermal stratification on SI-CAI hybrid combustion in a gasoline engine. Appl. Therm. Eng. 2013, 61, 451–460. [Google Scholar] [CrossRef]
- Wang, X.; Xie, H.; Xie, L.; Zhang, L.; Li, L.; Chen, T.; Zhao, H. Numerical simulation and validation of SI-CAI hybrid combustion in a CAI/HCCI gasoline engine. Combust. Theory Model. 2013, 17, 142–166. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, H. Multi-cycle large eddy simulation (LES) of the cycle-to-cycle variation (CCV) of spark ignition (SI) - controlled auto-ignition (CAI) hybrid combustion in a gasoline engine. In Proceedings of the International Powertrains, Fuels & Lubricants Meeting, Beijing, China, 16–19 October 2017. SAE Technical Paper 2017-01-2261. [Google Scholar]
- Han, Z.; Reitz, R.D. Turbulence Modeling of Internal Combustion Engines Using RNG κ-ε Models. Combust. Sci. Technol. 1995, 106, 267–295. [Google Scholar] [CrossRef]
- Colin, O.; Benkenida, A. The 3-zones extended coherent flame model (ECFM3Z) for computing premixed/diffusion combustion. Oil Gas Sci. Technol. 2004, 59, 593–609. [Google Scholar] [CrossRef]
- CRUZ, A.P.D. Three-dimensional modeling of self-ignition in HCCI and conventional diesel engines. Combust. Sci. Technol. 2004, 176, 867–887. [Google Scholar] [CrossRef]
- Mehl, M.; Chen, J.Y.; Pitz, W.J.; Sarathy, S.M.; Westbrook, C.K. An approach for formulating surrogates for gasoline with application towards a reduced surrogate mechanism for CFD engine modeling. Energy Fuels 2011, 25, 5215–5223. [Google Scholar] [CrossRef]
- CD-Adapco. STAR Methodology; STAR-CD VERSION 4.22; CD-Adapco: Melville, NY, USA, 2014. [Google Scholar]
- Speziale, C.G. Analytical methods for the development of Reynolds-stress closures in turbulence. Annu. Rev. Fluid Mech. 1991, 23, 107–157. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Wang, T.; Jia, M.; Che, Z.; Liu, D. Investigation of the effect of the in-cylinder tumble motion on cycle-to-cycle variations in a direct injection spark ignition (DISI) engine using large eddy simulation (LES). Flow Turbul. Combust. 2016, 98, 1–31. [Google Scholar] [CrossRef]
- Kaario, O.T.; Vuorinen, V.; Kahila, H.; Im, H.G.; Larmi, M. The effect of fuel on high velocity evaporating fuel sprays: Large-Eddy simulation of Spray A with various fuels. Int. J. Engine Res. 2020, 21, 26–42. [Google Scholar] [CrossRef] [Green Version]
- Koch, J.; Schürch, C.; Wright, Y.M.; Boulouchos, K. Reactive computational fluid dynamics modelling methane–hydrogen admixtures in internal combustion engines part II: Large eddy simulation. Int. J. Engine Res. 2020, 22, 146808742091034. [Google Scholar] [CrossRef]
- Vermorel, O.; Richard, S.; Colin, O.; Angelberger, C.; Benkenida, A.; Veynante, D. Towards the understanding of cyclic variability in a spark ignited engine using multi-cycle LES. Combust. Flame 2009, 156, 1525–1541. [Google Scholar] [CrossRef]
- Colin, O.; Ducros, F.; Veynante, D.; Poinsot, T. A thickened flame model for large eddy simulations of turbulent premixed combustion. Phys. Fluids 2000, 12, 1843–1863. [Google Scholar] [CrossRef]
- Richard, S.; Colin, O.; Vermorel, O.; Benkenida, A.; Angelberger, C.; Veynante, D. Towards large eddy simulation of combustion in spark ignition engines. Proc. Combust. Inst. 2007, 31, 3059–3066. [Google Scholar] [CrossRef]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Zhao, H.; Xie, H.; He, B. Analysis of cyclic variations during mode switching between spark ignition and controlled auto-ignition combustion operations. Int. J. Engine Res. 2015, 16, 356–365. [Google Scholar] [CrossRef]
- Duan, X.; Liu, J.; Yuan, Z.; Guo, G.; Liu, Q.; Tang, Q.; Deng, B.; Guan, J. Experimental investigation of the effects of injection strategies on cycle-to-cycle variations of a DISI engine fueled with ethanol and gasoline blend. Energy 2018, 165, 455–470. [Google Scholar] [CrossRef]
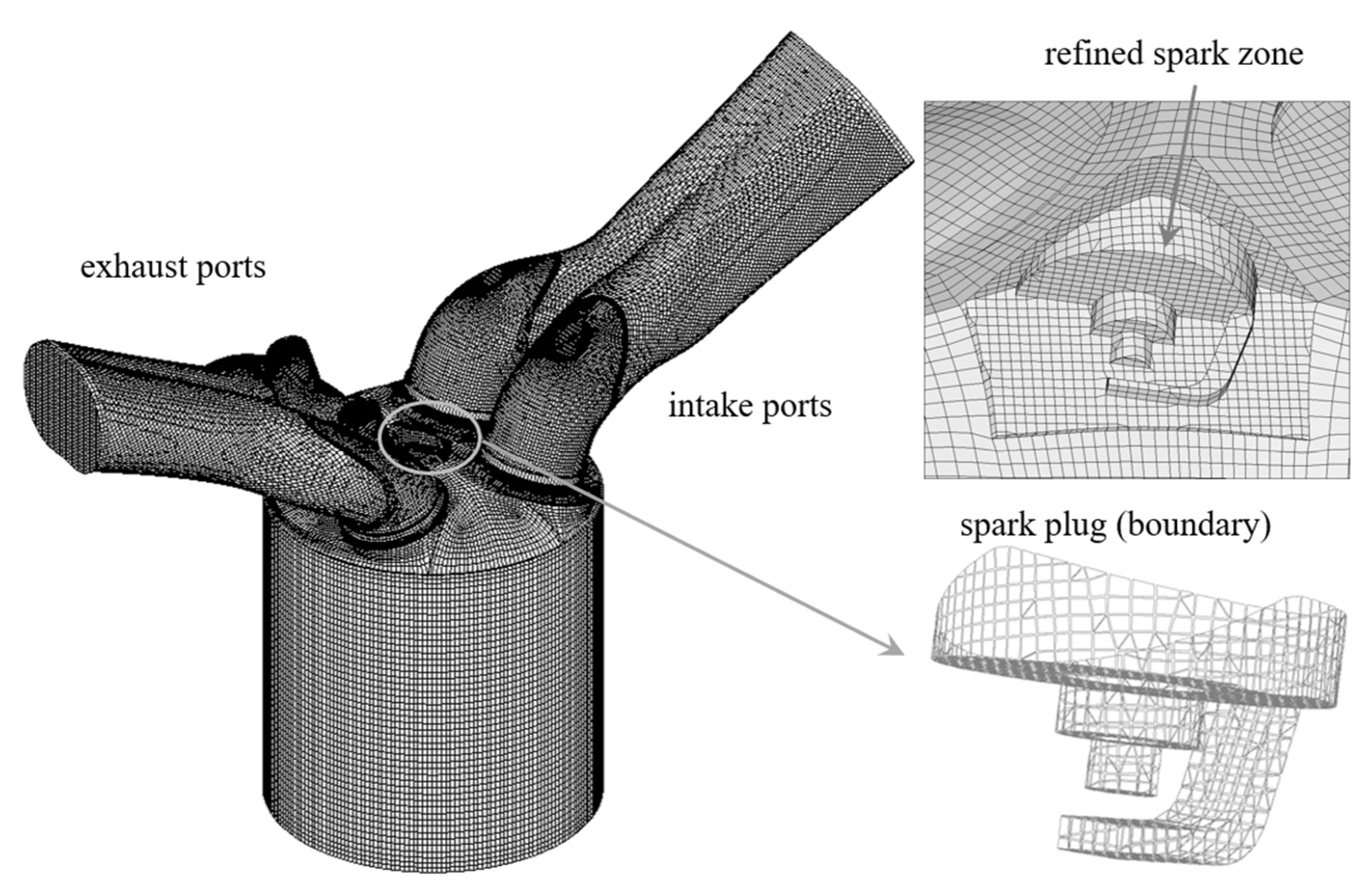






| Bore/stroke | 86/86 mm |
| Displacement | 0.5 L |
| Geometric compression ratio | 10.66:1 |
| Combustion chamber | Pent roof/4 valves |
| Fuel injection | Port fuel injection |
| Fuel | Gasoline 93 RON |
| Intake pressure | Naturally aspirated |
| EVO/EVC (°CA) | 167/383 |
| EL (mm) | 2.3 |
| IVO/IVC (°CA) | 411/593 |
| IL (mm) | 2.7 |
| Spark timing (°CA) | −49 |
| Fuel/air equivalence ratio (-) | 1 |
| Coolant temperature (°C) | 85 |
| Oil temperature (°C) | 55 |
| Fueling rate (mg/cycle) | 22.4 |
| Initial Conditions @ 400 °CA ATDC for 1st Cycle | |
|---|---|
| Cylinder temperature/pressure | 664 K/0.4 bar |
| Intake temperature/pressure | 320 K/0.985 bar |
| Exhaust temperature/pressure | 865 K/1.02 bar |
| Boundary Conditions | |
| Intake temperature/pressure | 320 K/0.95 bar |
| Exhaust temperature/pressure | 913 K/1.03 bar |
| Cylinder head temperature | 420 K |
| Spark plug temperature | 800 K |
| Piston top temperature | 482 K |
| Cylinder liner temperature | 377 K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhao, H. Modelling Study of Cycle-To-Cycle Variations (CCV) in Spark Ignition (SI)-Controlled Auto-Ignition (CAI) Hybrid Combustion Engine by Using Reynolds-Averaged Navier–Stokes (RANS) and Large Eddy Simulation (LES). Energies 2022, 15, 4478. https://doi.org/10.3390/en15124478
Wang X, Zhao H. Modelling Study of Cycle-To-Cycle Variations (CCV) in Spark Ignition (SI)-Controlled Auto-Ignition (CAI) Hybrid Combustion Engine by Using Reynolds-Averaged Navier–Stokes (RANS) and Large Eddy Simulation (LES). Energies. 2022; 15(12):4478. https://doi.org/10.3390/en15124478
Chicago/Turabian StyleWang, Xinyan, and Hua Zhao. 2022. "Modelling Study of Cycle-To-Cycle Variations (CCV) in Spark Ignition (SI)-Controlled Auto-Ignition (CAI) Hybrid Combustion Engine by Using Reynolds-Averaged Navier–Stokes (RANS) and Large Eddy Simulation (LES)" Energies 15, no. 12: 4478. https://doi.org/10.3390/en15124478
APA StyleWang, X., & Zhao, H. (2022). Modelling Study of Cycle-To-Cycle Variations (CCV) in Spark Ignition (SI)-Controlled Auto-Ignition (CAI) Hybrid Combustion Engine by Using Reynolds-Averaged Navier–Stokes (RANS) and Large Eddy Simulation (LES). Energies, 15(12), 4478. https://doi.org/10.3390/en15124478






