A Multistage Current Charging Method for Energy Storage Device of Microgrid Considering Energy Consumption and Capacity of Lithium Battery

Abstract

Modular multilevel converter battery energy storage systems (MMC-BESSs) have become an important device for the energy storage of grid-connected microgrids. The efficiency of the power transmission of MMC-BESSs has become a new research hotspot. This paper outlines a multi-stage charging method to minimize energy consumption and maximize the capacity of MMC-BESSs. Firstly, based on condition monitoring and data collection, the functional relationship between the internal resistance/capacity and other states of lithium batteries is established. Since the energy consumption of the battery is related to internal resistance, current, and time, the energy consumption calculation expression of the battery pack is established, and the objective function is designed to optimize energy consumption and capacity in order to determine the charging current curve of each stage. Compared with the constant current charging method, the proposed multistage current charging method for an MMC-BESS decreases energy consumption by 4.3% and increases the capacity of 5 SOC intervals by 1.56%.

1. Introduction

The wide applications of electric vehicles (EV) cause the problem of retired batteries. However, retired power batteries remain at 70–80% capacity and can be used for wind or solar energy storage, power grid peak cutting, and valley filling [1,2,3]. Therefore, battery energy storage systems (BESSs) have been grown in microgrid applications. Additionally, with the expansion of the scale of microgrids, the requirements for the capacity of BESSs are gradually increasing. Because of their diversified topology, BESSs are widely used. Under the constraints of power device performance and battery characteristics, the range of BESSs capacity that can be achieved by different topologies varies from kW to tens of MW.

When reusing retired batteries, it is important to know their state of health (SOH), so that batteries of similar SOH can be reassembled together, allowing the states of each battery in a BESS to be fully utilized, as the internal resistance and capacity of each battery various with its SOH. However, it is not possible to employ all retired batteries with a similar SOH in implementation because of the accuracy of existing SOH measurement methods and the state variability of retired batteries. There are many sources of health state uncertainty, including model parameter uncertainty, model structure uncertainty, degradation state uncertainty, and sensor measurement data uncertainty [4,5]. Some parameters can be directly measured and acquired that reflect the SOH of the target system, while some parameters cannot be directly reflected, so data are at the core of SOH monitoring [6]. Despite this, large-scale battery packs in a BESS with a serious SOH deviation during high-frequency and high-intensity operation under general charging/discharging control methods can be explained by the deformation (volume change) and fracture/crack of electrode materials caused by diffusion-induced stresses during cycling, which can result in short circuits that render electrode active materials incapable of storing Li-ions [7,8,9,10,11,12].

In practical applications, the energy consumption of battery packs has a close relationship with internal resistance, current, and operational temperature, but large-scale BESSs such as modular multilevel converter battery energy storage systems (MMC-BESSs) with high modularization and serviceability can offer a flexible power management capability and generally have sufficient space and low-cost measurements to effectively manage thermal behavior [13,14]. Therefore, the battery current will dominate energy consumption under the charge and discharge process. Efficient battery management systems include lithium-ion battery health management and life prediction, such as information perception, condition monitoring, and data collection. Among them, an accurate SOC estimation can balance the differences between single cells, optimize the charging and discharging strategy, prevent overheating, and prevent overcharge and overdischarge [15]. In [16,17,18,19], the authors used an MMC-BESS alternative to the classical grid battery storage system.

When managing batteries, stage-of-charge (SOC) should be fully considered [20,21,22]. Regulating SOC prevents the overcharge/over-discharge of battery packs. In practical applications, a balanced SOC in MMC-BESSs regulates circulating current [23]. However, it is clear that the SOC balancing of various SOH causes additional energy consumption. In order to minimize energy consumption, and consider the influence of current combinations on energy consumption during the charging/discharging in [24], a genetic algorithm is used to realize the multi-stage constant current charging method. In [25], H. Gui proposed a minimized energy consumption technique, which comprehensively considers the coupling relationship between initial/final current and temperature, SOH, and reactant concentration of a battery. Eventually, the minimized loss target of charging is achieved under variable-weight multi-stage constant current charging technology. The optimization of power consumption in [26] is based on the efficiency curve of a single device under various input variables. The optimization equation of the system consumption is established with all loads as constraints, and the power distribution with a minimized energy consumption is accurately calculated by the Lagrangian method. In the hardware structure, T. Vo proposed a balanced circuit structure with the highest energy utilization efficiency considering SOC balance in battery pack designed by the depth-first search algorithm [27].

In order to limit the charging time, traditional constant current fast-charging methods are widely used in lithium batteries, which have a lot of adverse effects on lithium batteries, such as large energy consumption, large temperature rise, high terminal voltage, and short life [28]. The multi-stage constant current charging method is considered to be a reasonable charging method that improves the capacity and service life of lithium batteries in engineering applications. Its advantages include long battery life, high battery charging/discharging efficiency, and short charging time [29,30].

To summarize, the existing charging methods have deficiencies in considering the capacity of lithium batteries and the flexibility of MMC-BESSs. To solve these problems, this paper proposes a multi-stage charging method for MMC-BESSs that comprehensively considers the energy consumption and capacity of lithium batteries. At first, the definition of SOH based on capacity and internal resistance is presented. Then, the internal resistance and other state variables of lithium batteries are analyzed according to experimental data. Based on this theory, the energy consumption and capacity of a lithium battery can be optimized by adjusting the charging current, thereby increasing the efficiency and capacity of the battery pack. A corresponding optimization method is proposed in this paper to solve the excessive energy consumption and capacity squeeze of the lithium battery pack. MATLAB/Simulink simulation results validate the proposed method.

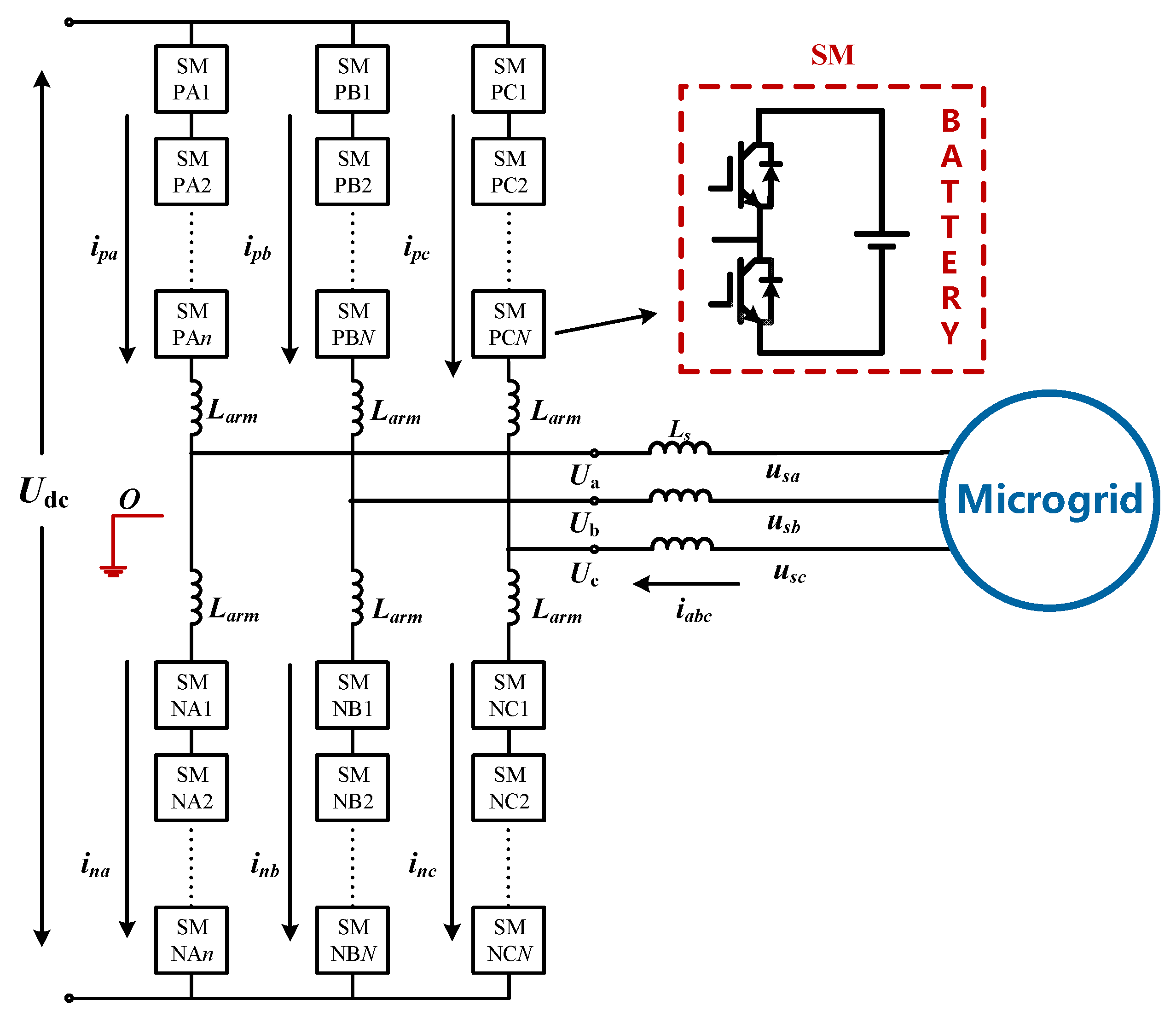
2. Working Principle of MMC-BESS

2.1. MMC-BESS

Unlike traditional MMC, energy storage batteries in MMC-BESSs are distributed by integrating SMs, which are inserted or bypassed by controlling SM.

The topology of an MMC-BESS is shown in Figure 1, where several SMs and one filter inductor are series-connected. Batteries are distributed into SMs as DC power sources.

The power of an MMC-BESS is flexibly adjusted by inserting or bypassing the number of SMs, which can be in both discharging and charging states. The switch status is shown in

Table 1. Switch status of MMC-BESS.

State	S1	S2	iSM	uSM	State
1	1	0	>0	VSM	charging
2	1	0	<0	VSM	discharging
3	0	1	>0	0	/
4	0	1	<0	0	/
5	0	0	/	0	bypassing

. Each phase leg has N SMs in the inserting state at any time for stable operation of the system.

The voltage of the upper and lower legs of each phase is as shown in Equation (1), assuming that all battery voltages are fixed [31]:

$$\left\{\begin{array}{l}{u}_{\mathrm{pk}}={\displaystyle \sum _{j=1}^{\mathrm{N}}{\mathrm{d}}_{\mathrm{pkj}}{u}_{\mathrm{pkj}}=\frac{u_{\mathrm{dck}}}{2}}-u_{\mathrm{k}}+L_{\mathrm{arm}}\frac{\mathrm{d}{i}_{\mathrm{pk}}}{\mathrm{d}t}\\ u_{\mathrm{nk}}={\displaystyle \sum _{j=1}^{\mathrm{N}}{\mathrm{d}}_{\mathrm{nkj}}{u}_{\mathrm{nkj}}=\frac{u_{\mathrm{dck}}}{2}}+u_{\mathrm{k}}+L_{\mathrm{arm}}\frac{\mathrm{d}{i}_{\mathrm{nk}}}{\mathrm{d}t}\end{array}\right.$$

(1)

where d_pkj and d_nkj are the duty cycle of jth SM of the upper and lower legs of k-phase, u_pkj and u_nkj are the battery voltage of jth SM of the upper and lower legs of k-phase, u_dck is the DC voltage of k-phase, u_k is the AC voltage of k-phase, L_arm is the inductance of the MMC-BESS legs. The current of the upper and lower legs of the k-phase are:

$$\left\{\begin{array}{l}{i}_{\mathrm{pk}}=i_{\mathrm{diffk}}-i_{\mathrm{k}}\\ i_{\mathrm{nk}}=i_{\mathrm{diffk}}+i_{\mathrm{k}}\end{array}\right.$$

(2)

where i_k is the grid-side current of k-phase, and i_diffk is the differential current of k-phase. Integrating Equations (1) and (2) provides the dynamic equation of an MMC-BESS:

$$\left\{\begin{array}{l}2L_{\mathrm{arm}}\frac{\mathrm{d}{i}_{\mathrm{diffk}}}{\mathrm{d}t}=u_{dc}-u_{\mathrm{dck}}\\ u_{\mathrm{oo}’}=u_{\mathrm{sk}}-u_{\mathrm{k}}-(\frac{L_{\mathrm{arm}}}{2}+L_{\mathrm{s}})\frac{\mathrm{d}{i}_{\mathrm{k}}}{\mathrm{d}t}\end{array}\right.$$

(3)

where u_oo’ is the voltage between the virtual midpoint of the DC side of an MMC-BESS and the neutral of the power grid. It follows that the DC power is controlled by differential current. The control strategy of an MMC-BESS is shown in Figure 2, where, i_d* and i_q* are the q-axis and d-axis current references for MMC-BESS respectively, u_a*, u_b*, and u_c* are the voltage reference for the NLM strategy.

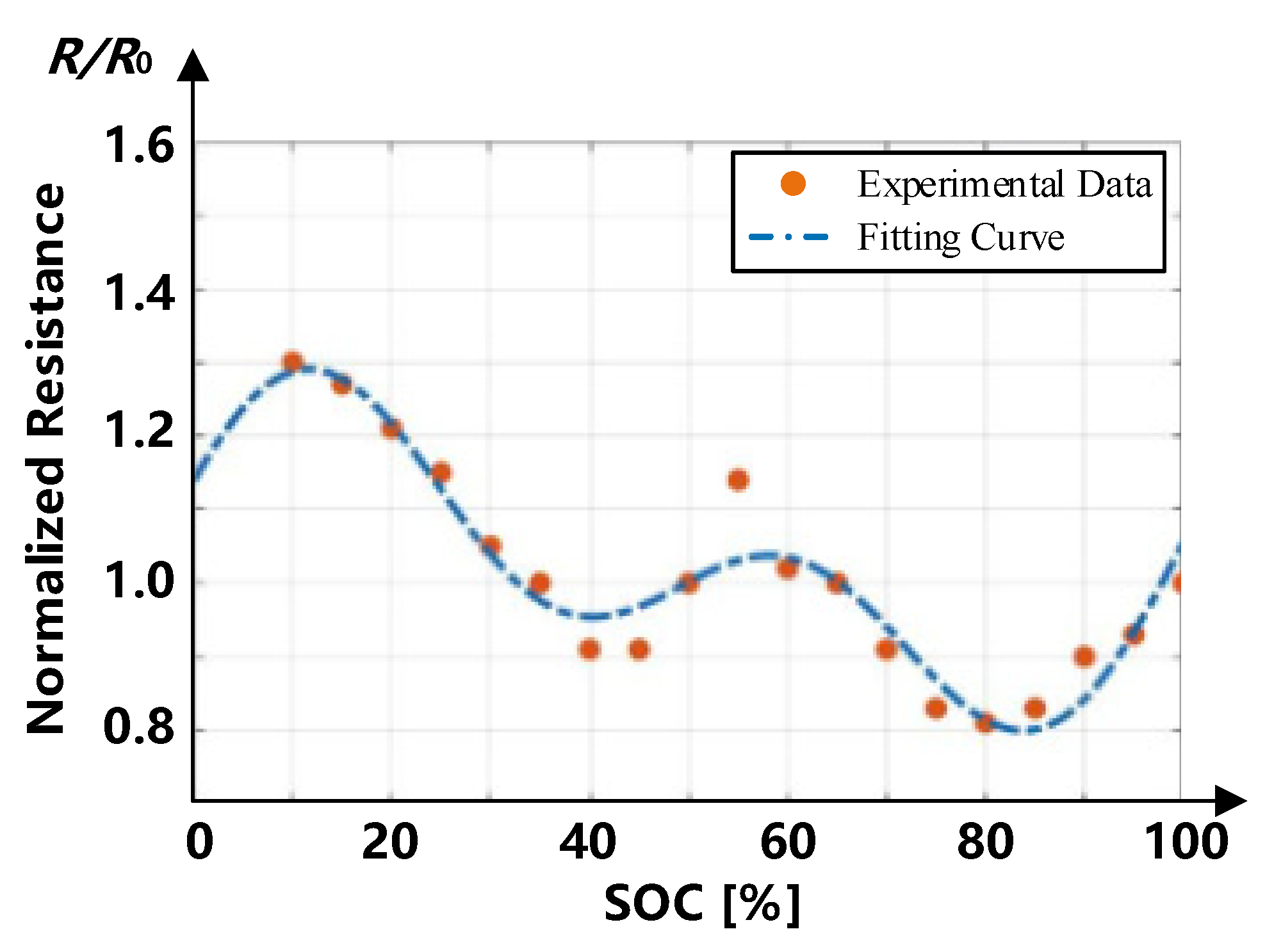
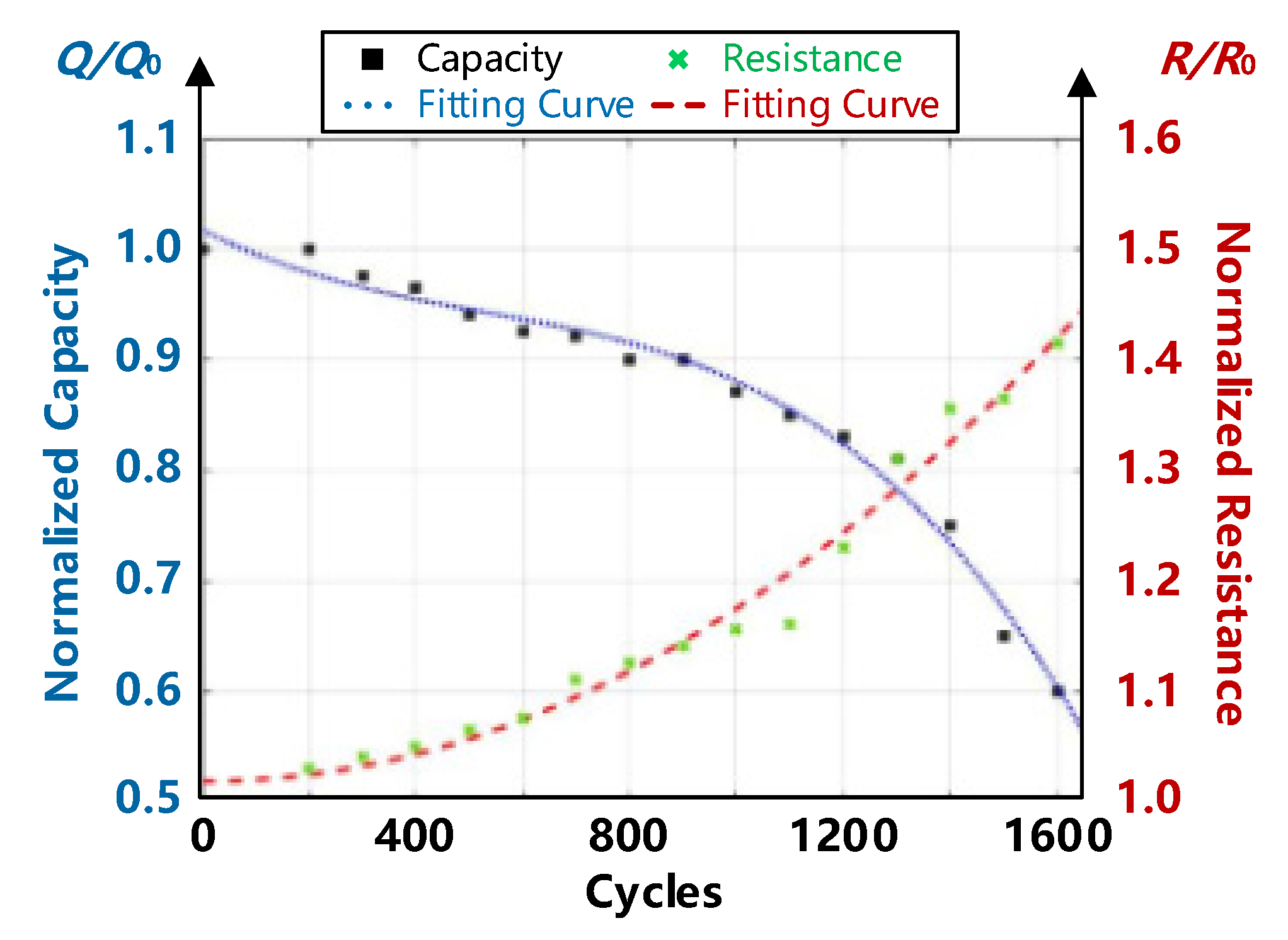
2.2. States of Lithium Battery

The second-order RC ladder model shown in Figure 3 is selected for the battery equivalent circuit model due to its high precision and relatively low computation [32].

The SOC is estimated by calculating the accumulated power of the battery during the charging and discharging period, called the ampere-hour integral method, which is commonly used for the SOC estimation [3]:

$${\mathrm{SOC}}_{\mathrm{t}}{=\mathrm{SOC}}_0-\frac{{\displaystyle {\int }_0^{t}i(t)\mathrm{d}t}}{Q_{\max }}$$

(4)

where Q_max is the maximum capacity of the battery. The SOH of the battery refers to the ratio of the maximum capacity to the rated capacity of the battery [3]. Generally, the maximum capacity slowly decreases with the cycles of the battery:

$${\mathrm{SOH}}_{\mathrm{Q}}=\frac{Q_{\mathrm{t}}}{Q_0}\times 100\%$$

(5)

where Q_t is the t moment capacity of the battery, and Q₀ is the rated capacity of the battery. Battery aging not only causes a decrease in capacity but also the ohmic resistance of the battery monotonically increases, so the SOH can also be estimated by its internal resistance [3]:

$${\mathrm{SOH}}_{\mathrm{R}}=\frac{R_0(end)-R_0(t)}{R_0(end)-R_0(0)}\times 100\%$$

(6)

where R₀(end) is the life termination resistance of the battery, R_t is the t moment resistance of the battery, and R₀ is the initial resistance of the battery. Equations (4)–(6) are used to evaluate the battery performance, and then select the internal resistance and capacity of the battery according to the experimental results in Figure 4, Figure 5 and Figure 6.

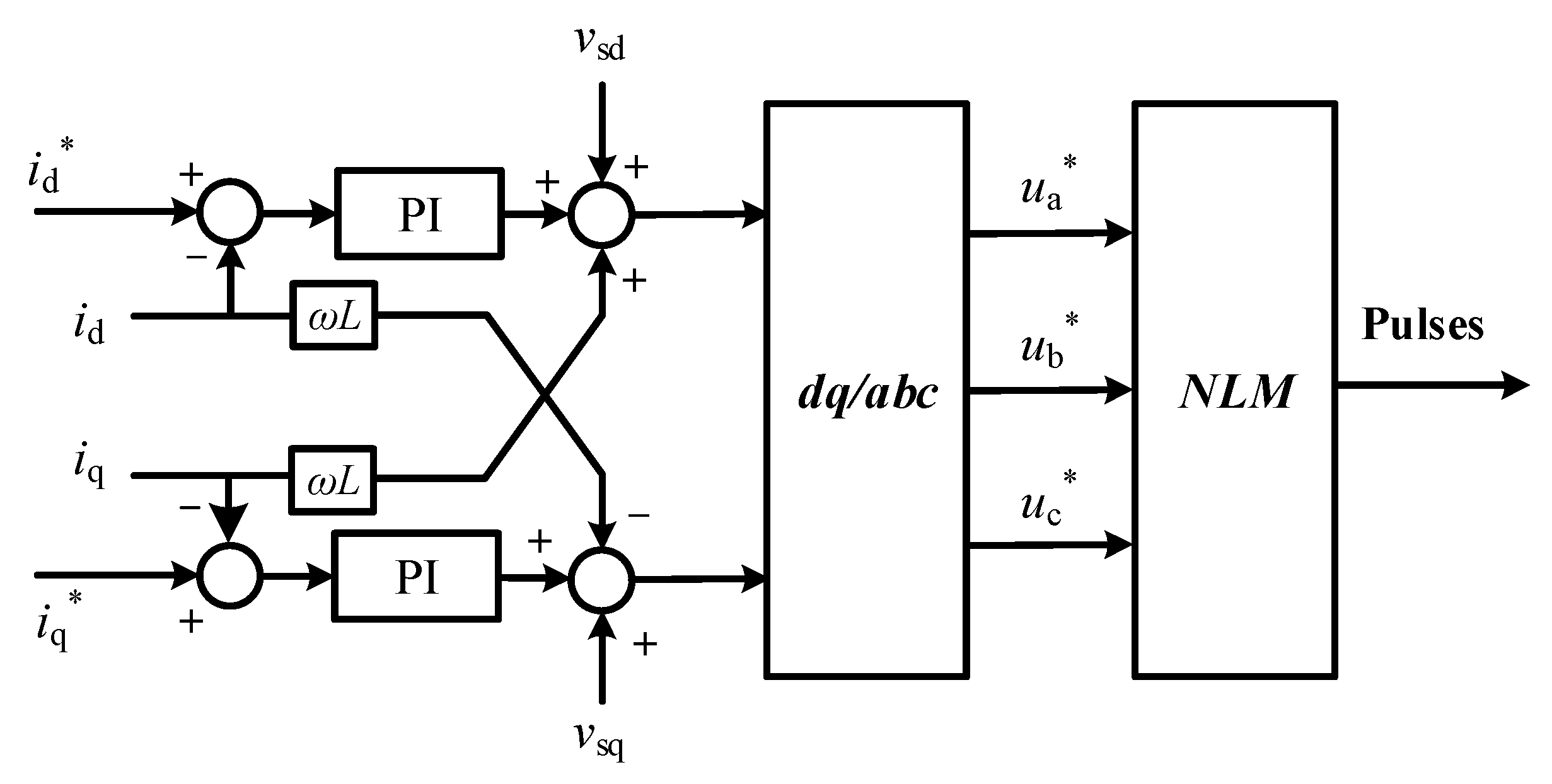
3. Energy Efficiency Optimization Method

The energy consumption of an MMC-BESS comprises battery consumption and converter consumption. The converter consumption keeps constant when an MMC-BESS is under stable operation and each SM is inserted or bypassed only once in a current cycle. However, the switching sequence of batteries in various conditions causes a huge variation in energy consumption, so the optimization strategy in this paper only considers the energy consumption of batteries.

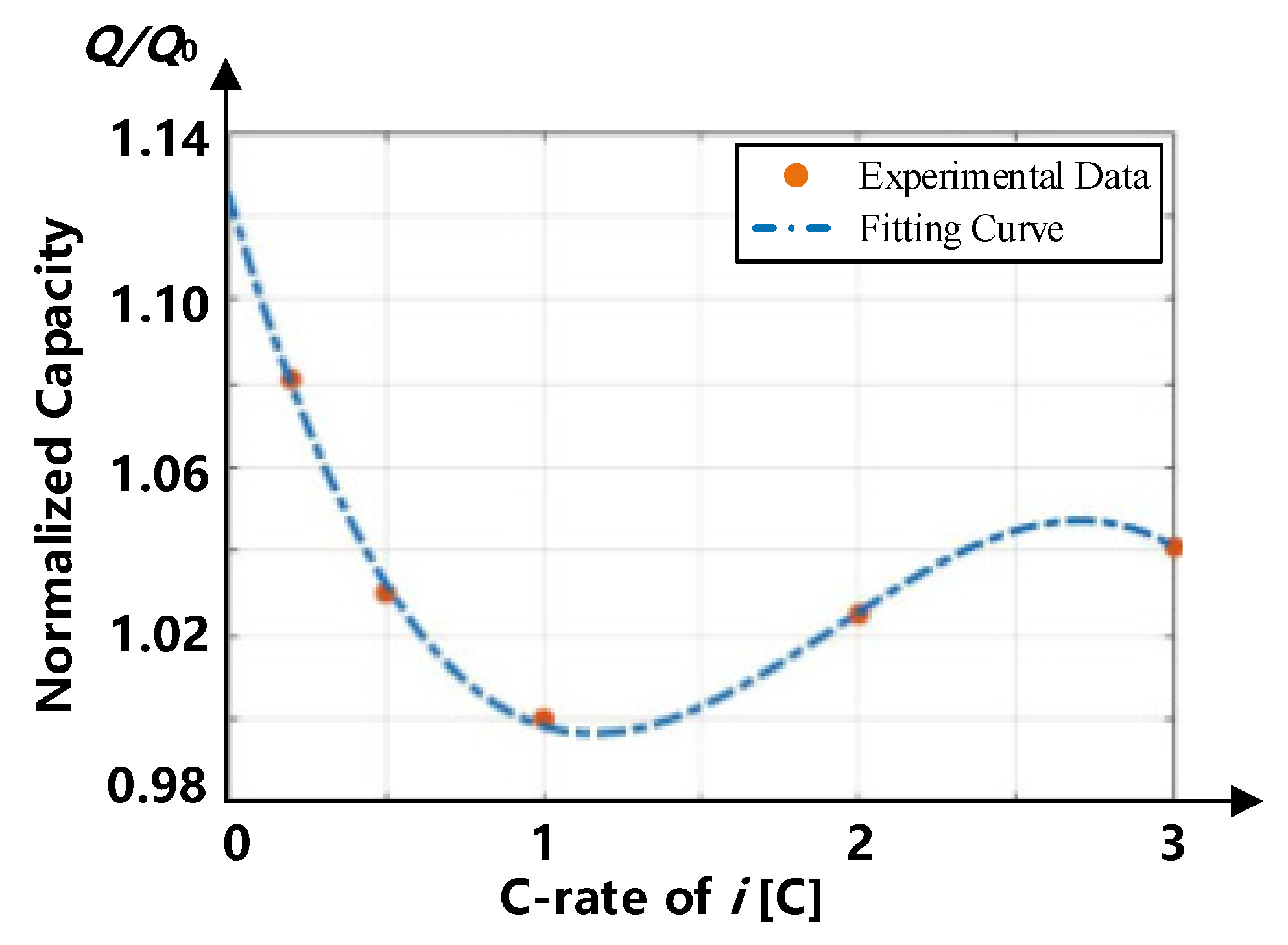
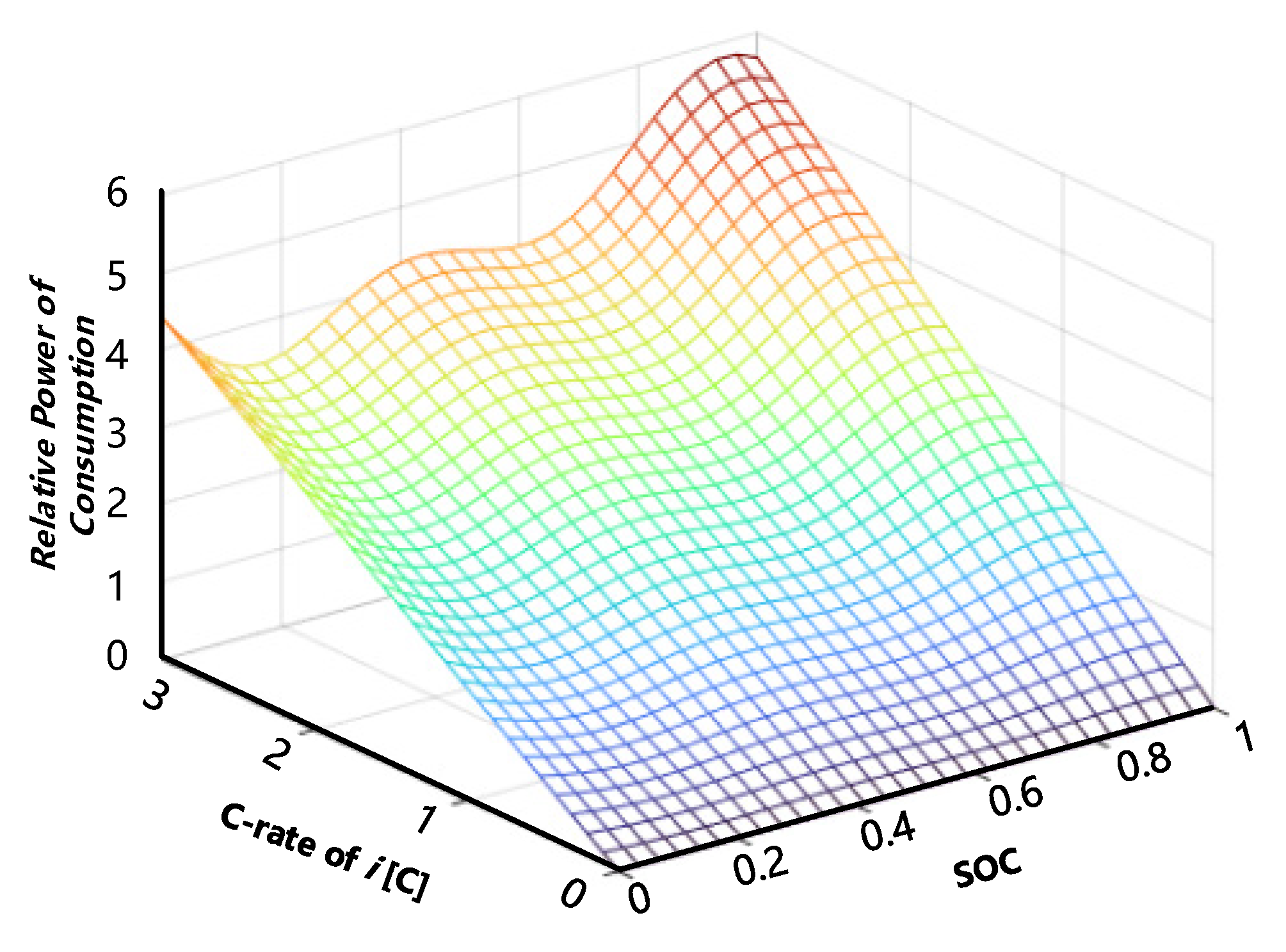
3.1. Energy Consumption of Lithium Battery

In the application of grid-connected energy storage systems with recycled batteries, the capacities of lithium batteries are usually higher than 55%. In this region, it is assumed that the internal resistance of the battery aligns with its SOC and there is a coupling relationship between capacity and internal resistance; its capacity is also related to the charging/discharging current. The internal resistance, cycles, SOC, and capacity results are summarized in Figure 4, Figure 5 and Figure 6, where the internal resistance of the battery is defined as the sum of Rs, R₁, and R₂. It appears that internal resistance varies depending on the SOC, tending to increase at a high SOC [2,8,29,33,34,35,36].

With the cyclic charging and discharging of batteries, the capacity of the battery will decrease, and the internal resistance will increase. The function of the resistance and capacity of the calculated results for lithium batteries in Figure 4, Figure 5 and Figure 6 are shown in Equations (7)–(9) [2,8,29,33,34,35,36]:

$$R^{\ast }{}_{\mathrm{SOC}}=1.06+0.16\cos (5.5\mathrm{soc})+0.12\sin (5.5\mathrm{soc})+0.13\cos \left(11\mathrm{soc}\right)+0.05\sin \left(11\mathrm{soc}\right)$$

(7)

$$\left\{\begin{array}{l}{R}^{\ast }{}_{\mathrm{SOH}}=-1.97L^3+3.1L^2-2.5\times {10}^{-4}L+1.017\\ {\mathrm{Q}}^{\ast }{}_{\mathrm{SOH}}=7.04\times {10}^{-11}{L}^3-1.3\times {10}^{-8}{L}^2+1.06\times {10}^{-4}L+1.005\end{array}\right.$$

(8)

$${\mathrm{Q}}^{\ast }{}_{\mathrm{I}}=-0.028I_{\mathrm{bat}}{}^3+0.16I^2{}_{\mathrm{bat}}-0.26I_{\mathrm{bat}}+1.126$$

(9)

where R_SOC is the internal resistance varying with the SOC, R_SOH is the internal resistance varying with the number of cycles of the battery, R₀ is the initial resistance, and L is the cycles [37].

Generally, according to Ohm’s law and the electric power calculation formula, the power of energy consumption during the charging process is:

$$P=I^{2}R$$

(10)

where R_SOC is the internal resistance that varies with the SOC, and I_bat is the battery current. Thus, from Equations (7)–(9), the capacity can be inferred from the internal resistance and current:

$$\left\{\begin{array}{l}{R}_{\mathrm{SOH}}=R^{\ast }{}_{\mathrm{SOH}}·R_0\\ R_{\mathrm{SOC}}=R^{\ast }{}_{\mathrm{SOC}}·R_{\mathrm{SOH}}\end{array}\right.\begin{array}{cc}& \end{array}\left\{\begin{array}{l}{\mathrm{Q}}_{\mathrm{SOH}}=Q^{\ast }{}_{\mathrm{SOH}}·Q_0\\ {\mathrm{Q}}_{\mathrm{I}}=Q^{\ast }{}_{\mathrm{I}}·Q_{\mathrm{SOH}}\end{array}\right.$$

(11)

$$\begin{array}{ll}{R}_{\mathrm{SOC}}=& R_0(-1.97L^3+3.1L^2-2.5\times {10}^{-4}L+1.017)\\ & \times (1.06+0.16\cos (5.5\mathrm{soc})+0.12\sin (5.5\mathrm{soc})+0.13\cos \left(11\mathrm{soc}\right)+0.05\sin \left(11\mathrm{soc}\right))\end{array}$$

(12)

$$\left\{\begin{array}{l}L=\frac{0.275}{\sqrt[3]{H}}+\sqrt[3]{H}+0.525\\ H=\sqrt{\left({\left(0.254R_{\mathrm{SOC}}-0.405\right)}^2-0.0208\right)}-0.254R_{\mathrm{SOC}}+0.402\end{array}\right.$$

(13)

$$Q_{I_{\mathrm{bat}}}=Q_0(7.04\times {10}^{-11}{N}^3-1.3\times {10}^{-8}{N}^2+1.06\times {10}^{-4}N+1.005)\times (-0.028I_{\mathrm{bat}}{}^3+0.16I^2{}_{\mathrm{bat}}-0.26I_{\mathrm{bat}}+1.126)$$

(14)

So, the capacity can be calculated from Equation (14), and the energy consumption of a single battery can be calculated from Equation (15), where t₁ is a function of the SOC and current. The battery is charged with 0–3 C current, and the power of consumption with various SOC is shown in Figure 7:

$$\left\{\begin{array}{l}{P}_{\mathrm{bat}\_\mathrm{loss}}=I_{\mathrm{bat}}^2{R}_{\mathrm{SOC}}\\ W_{\mathrm{Bat}\_\mathrm{loss}}={\displaystyle {\int }_{t_0}^{t_1}{P}_{\mathrm{bat}\_\mathrm{loss}}\mathrm{d}t}\end{array}\right.$$

(15)

Evidently, the current is positively related to the power of consumption, but the charging time is inevitably considered in practical engineering applications. Therefore, according to Figure 7, the charging current path with a minimized energy consumption can be found with time as a constraint.

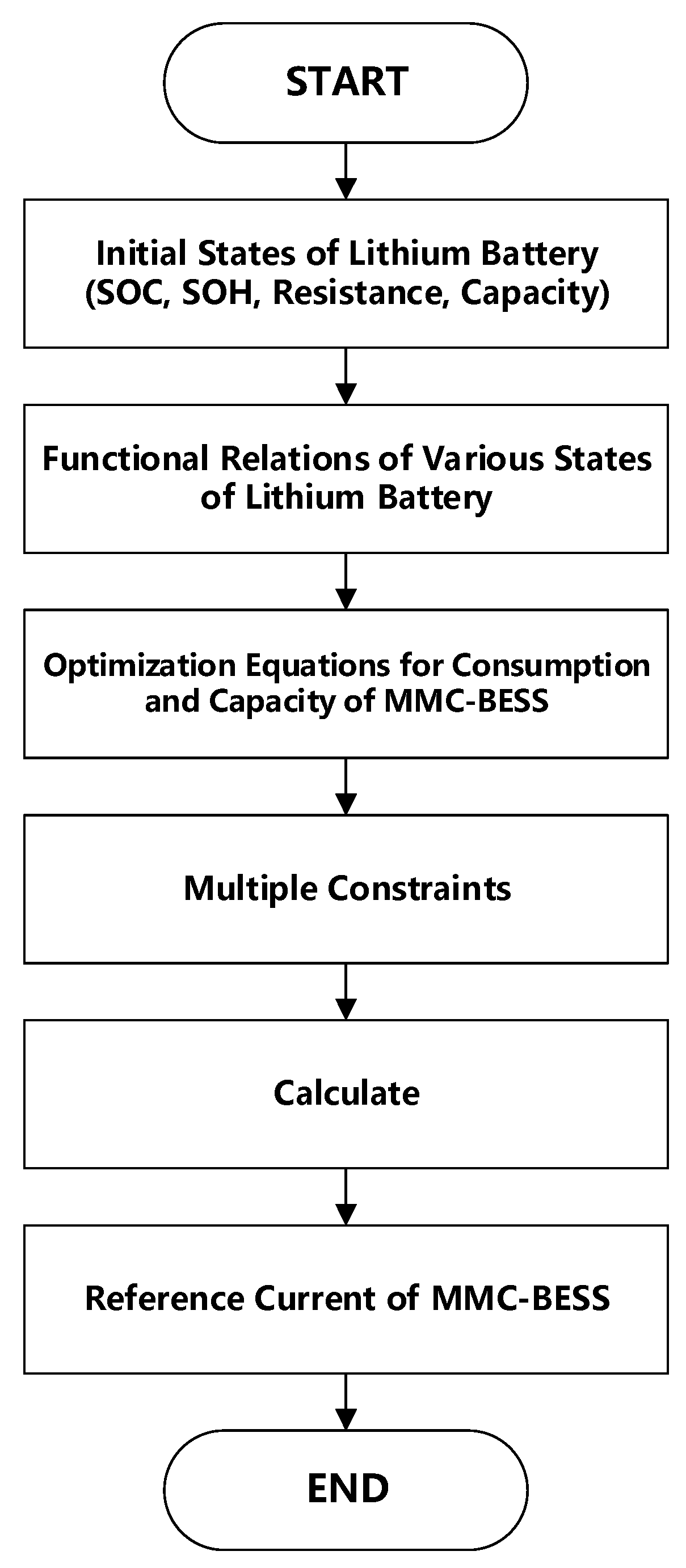
3.2. Principle of Proposed Optimization Method

The charging consumption and capacity of the battery can be calculated as the sum of each SOC interval:

$$\left\{\begin{array}{l}{W}_{{}_{\mathrm{loss}}}^{\mathrm{bat}}={\displaystyle \sum _{c=0}^{\mathrm{M}}{W}_{{}_{\mathrm{loss}}}^{\mathrm{c}}}={\displaystyle \sum _{c=0}^{\mathrm{M}}{i}_{\mathrm{c}}{}^2{R}_{\mathrm{SOC}}{t}_{\mathrm{c}}}\\ Q_{\mathrm{bat}}={\mathrm{SOC}}_0+{\displaystyle \sum _{c=0}^{\mathrm{M}}{Q}_{{}_{\mathrm{bat}}}^{\mathrm{c}}}={\mathrm{SOC}}_0+{\displaystyle \sum _{c=0}^{\mathrm{M}}{i}_{\mathrm{c}}{t}_{\mathrm{c}}}\end{array}\right.$$

(16)

where M is the number of discretized SOC intervals; i_c and t_c are the current and charging time of discretized SOC intervals, respectively; $W_{{}_{loss}}^c$ and $Q_{{}_{bat}}^c$ are the charging consumption and capacity of the battery in the cth interval, respectively. The charging strategy satisfies the constraint:

$$t={\displaystyle \sum _c^{\mathrm{M}}{t}_{\mathrm{c}}}={\displaystyle \sum _c^{\mathrm{M}}\frac{Q_{\mathrm{bat}}}{M}·\frac{1}{i_{\mathrm{c}}}}$$

(17)

where t is the charging time, and Q_bat is the capacity of the battery. The effect of the charging method is theoretically verified as supported by the simplified example (M = 2) shown in Figure 8. Once the value of the SOC interval is determined, the amplitude of i is determined by Equation (17). As shown in Figure 8b,c, the energy consumption of a battery of the proposed multistage current charging method is reduced by 1.3% compared with that of the constant current charging method. Moreover, the charging capacity for the proposed multistage current charging method is increased by 0.9% compared with that of the constant current charging method, and the total charging time for both methods is the same.

From the above analysis, it was found that current affects the energy consumption of a battery during charging, which is closely related to the duty cycle and switching sequence of the SM. So, the efficiency of an MMC-BESS can be optimized by adjusting SMs. The energy consumption and capacity of an MMC-BESS expressed as the sum of each SM is:

$$\left\{\begin{array}{l}{W}_{{}_{\mathrm{loss}}}^{\mathrm{tot}}={\displaystyle \sum _{i=1}^{\mathrm{N}}{W}_{\mathrm{loss}\_\mathrm{i}}}={\displaystyle \sum _{i=1}^{\mathrm{N}}g(I_i,{\mathrm{SOC}}_i,t_i)}\\ Q_{\mathrm{bat}}={\displaystyle \sum _{i=1}^{\mathrm{N}}{Q}_{\mathrm{bat}\_\mathrm{i}}}={\displaystyle \sum _{i=1}^{\mathrm{N}}f(I_i,t_i)}\end{array}\right.$$

(18)

where W_{loss_i} is the energy consumption of the ith battery, and N is the number of SMs. Therefore, an optimization function Equation (18) is established to calculate the energy consumption of the system, which takes the minimized energy consumption of the system and the corresponding power distribution as the result, with charging time as the constraint. The flow charts to calculate the reference current of an MMC-BESS and the control strategy of an MMC-BESS are shown in Figure 9 and Figure 10, respectively:

$$\begin{array}{ll}\min & W_{\mathrm{loss}}={\displaystyle \sum _{i=1}^{\mathrm{N}}g(I_i,{\mathrm{SOC}}_i,t_i)}\\ \max & Q_{\mathrm{bat}}={\displaystyle \sum _{i=1}^{N}f(I_i,t_i)}\\ subjectto& t_1\le t,t_2\le t,\cdots ,t_{\mathrm{N}}\le t\end{array}$$

(19)

where t is the maximum charging time. If the battery packs are still charging when they are already fully charged, this will cause serious security risks. Therefore, the SOC constraints are added to Equation (19), which is expressed as Equation (20). Therefore, the minimized energy consumption is an optimization of nonlinear equations under multiple constraints. Generally, the number of discretized SOC intervals is between 4 and 10. According to the computational complexity and optimization results, the number of discretized SOC intervals is five, and the ΔSOC of each interval is 20%.

$$\begin{array}{ll}\min & W_{\mathrm{loss}}={\displaystyle \sum _{i=1}^{\mathrm{N}}g(I_i,{\mathrm{SOC}}_i,t_i)}\\ \max & Q_{\mathrm{bat}}={\displaystyle \sum _{i=1}^{\mathrm{N}}f(I_i,t_i)}\\ subjectto& t_1\le t,t_2\le t,\cdots ,t_N\le t\\ & {\mathrm{SOC}}_1+\frac{{\displaystyle {\int }_0^{t_1}{I}_{1}dt}}{Q_1}={\mathrm{SOC}}_2+\frac{{\displaystyle {\int }_0^{t_2}{I}_{2}dt}}{Q_2}\cdots ={\mathrm{SOC}}_{\mathrm{N}}+\frac{{\displaystyle {\int }_0^{t_N}{I}_{\mathrm{N}}dt}}{Q_{\mathrm{N}}}=100\%\end{array}$$

(20)

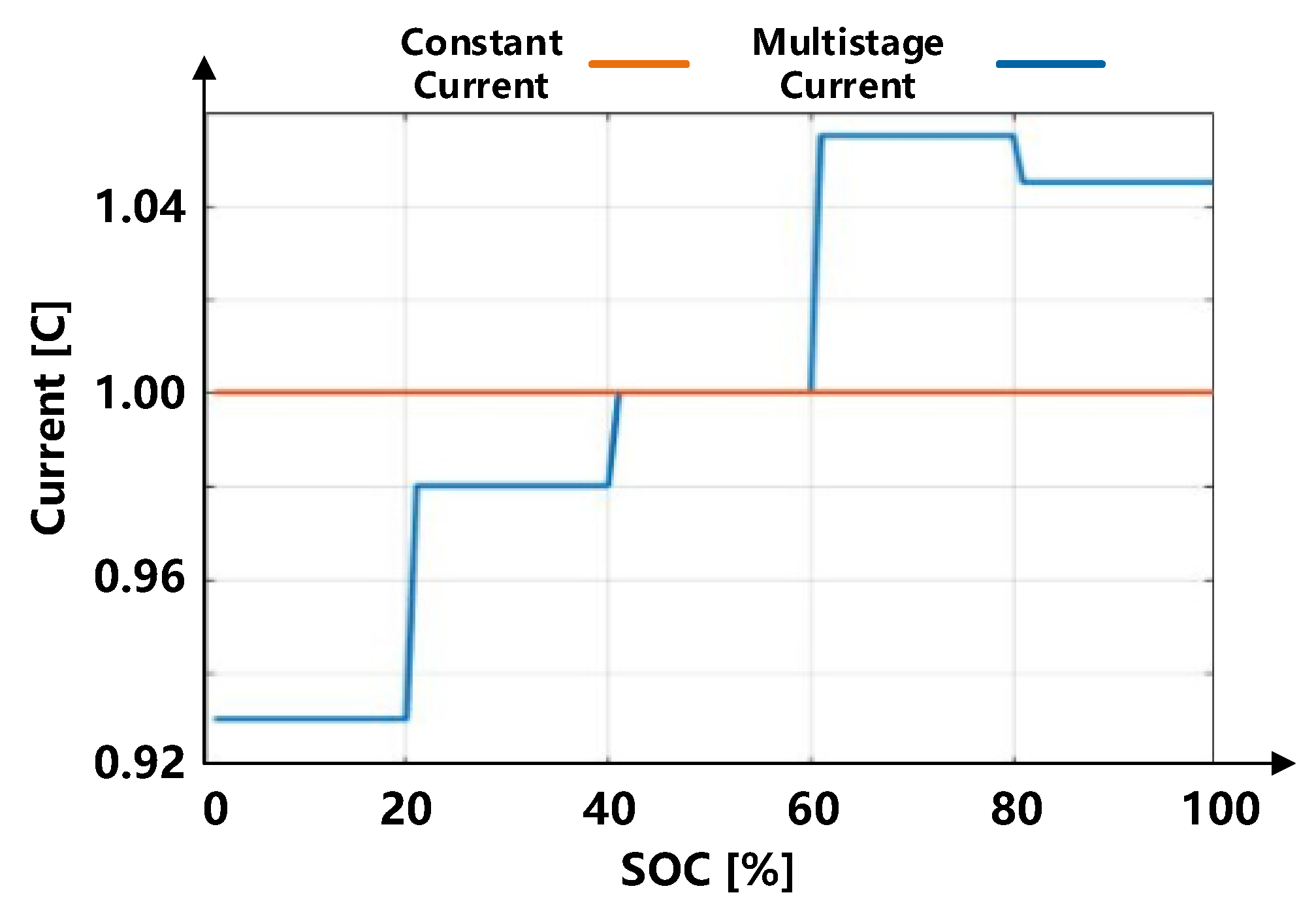
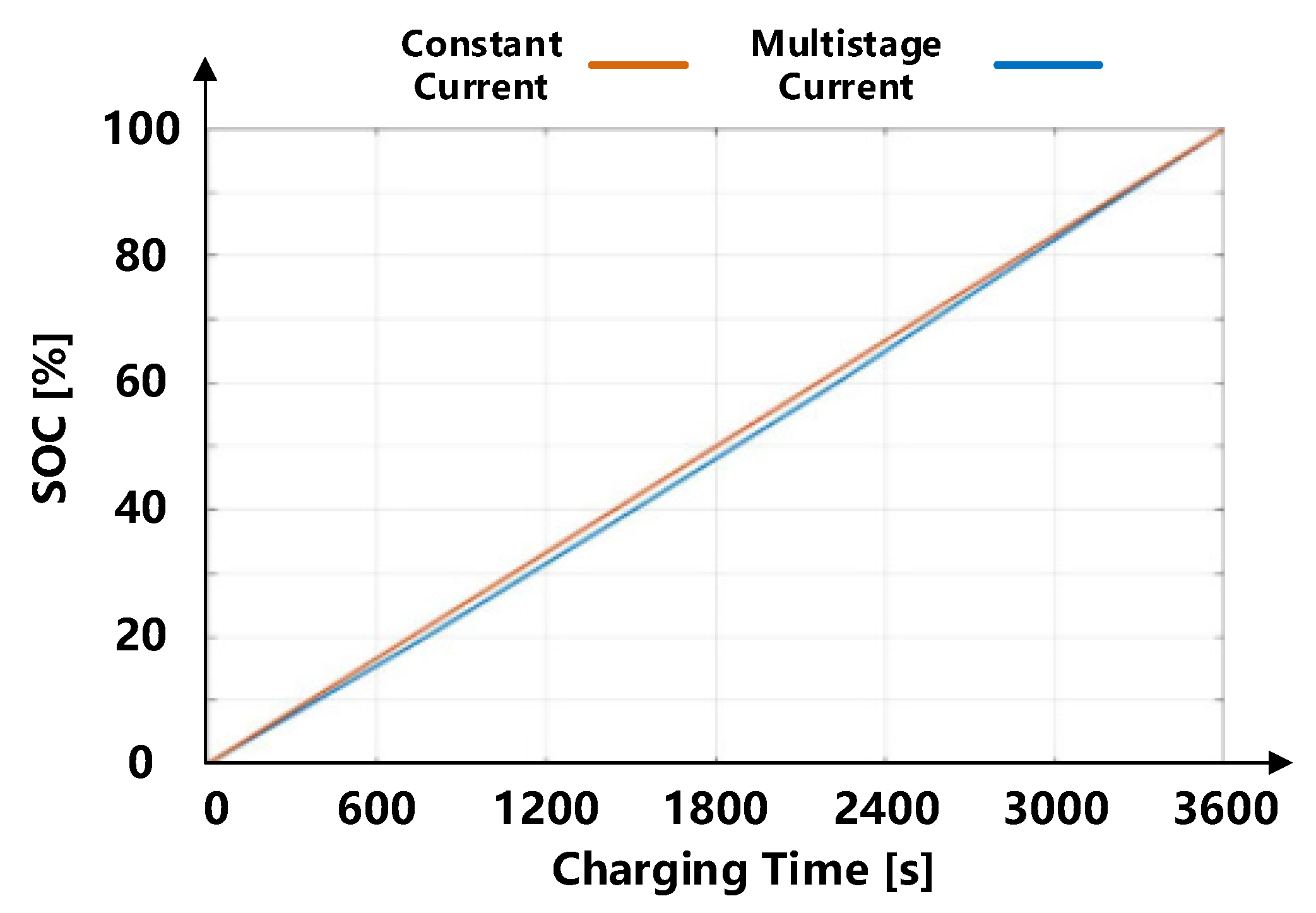
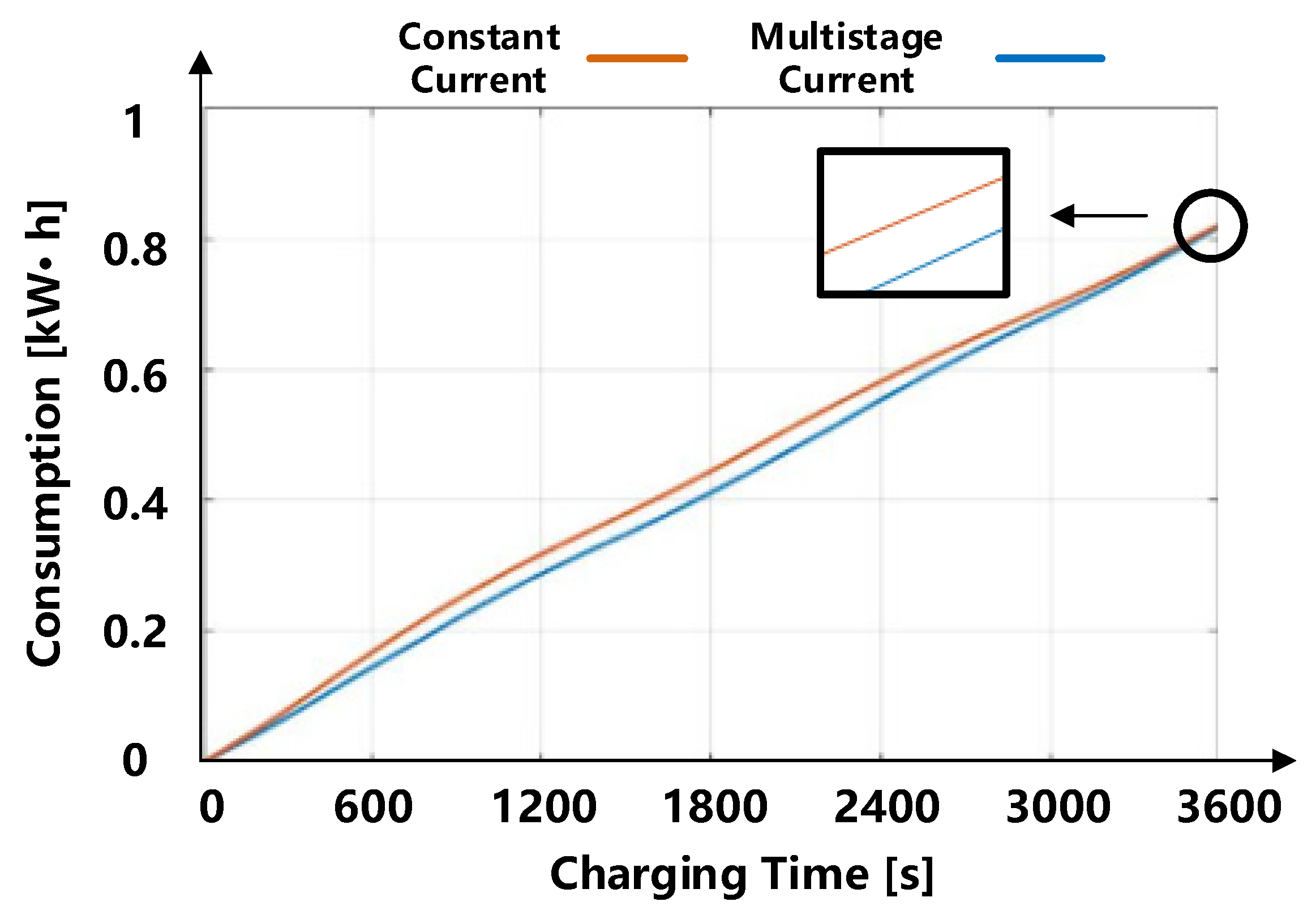
4. Validation of Results

The verification process of this paper is shown in Figure 10. The energy consumption optimization equation of charging, Equation (18), can be calculated by the initial conditions of the battery pack. Additionally, the calculated current preset value is used as the MMC input to verify the superiority of the multistage current charging method in an MMC-BESS with 8 sub-modules per phase. All of the batteries being fully charged indicates the end of the MMC-BESS charging, and the initial parameters of the battery pack in each SM (phase A) are shown in

Table 2. Upper leg battery parameters of phase A.

	Bata1	Bata2	Bata3	Bata4	Bata5	Bata6	Bata7	Bata8
SOC0	0%	0%	0%	0%	0%	0%	0%	0%
Qbat(Ah)	81.02	92.59	121.53	97.22	108.02	86.81	114.38	92.59
Vbat	1400	1400	1400	1400	1400	1400	1400	1400

.

Figure 11, Figure 12, Figure 13 and Figure 14 show the variables of one battery in the sub-module of phase A until fully charged, including the current of each interval, SOC of the battery, power of energy consumption, energy consumption, and battery capacity. The comparison of energy consumption and capacity of an MMC-BESS with a constant current and multistage current is shown in Figure 15.

In this paper, the intervals of the multistage current charging method are divided into five categories by SOC, which means that the current is switched for every 20% of the SOC; the constant charging method keeps the current at 1 C, as shown in Figure 11.

Since the currents of two methods in various SOC are different, the charging rate of the multistage current charging method is lower than that of the constant current charging method until the current exceeds the constant current, according to Equation (4). Eventually, the battery is fully charged at the same time.

According to Equation (4), within the same ΔSOC, the charging time is inversely proportional to the current. Additionally, it is shown from Equation (15) that the energy consumption of the battery is related to charging current, internal resistance, and charging time. So, the power of energy consumption is not divided into five equal intervals like SOC, as shown in Figure 13. The multistage current switches for the first time at 774 s, which is 54 s longer than the average 720 s. The delay in the switching time of the current is because the multistage current is less than the constant current in the first ΔSOC, which can infer the switching time of the subsequent current in each ΔSOC.

The formula expression of SOC is similar to the energy consumption, as shown in Equations (4) and (15). The trend of energy consumption is consistent with SOC, but the energy consumption and capacity are different, representing the differences between the variables of internal resistance and capacity, according to Equations (7)–(14). Therefore, the energy consumption of the multistage current charging method decreases, but the capacity increases when the battery is fully charged.

Figure 15 shows the comparison results of the energy consumption and capacity of an MMC-BESS under the constant current charging method and multistage current charging method, in which energy consumption is decreased by 0.92 kW∙h, and the capacity is increased by 0.05 MWh.

5. Conclusions

This paper proposes a multistage current charging method for an MMC-BESS considering the energy consumption and capacity of lithium batteries. The detailed conclusions are summarized as follows by specific case studies:

(1)

According to the theoretical analysis and the existing experimental results, the internal resistance of a lithium battery is related to its SOC, and increases with the cycles. The capacity of a lithium battery not only decreases with the increase in cycles, but is directly related to the charging/discharging current. Therefore, the energy consumption and capacity of a lithium battery can be optimized by adjusting the charging current.

(2)

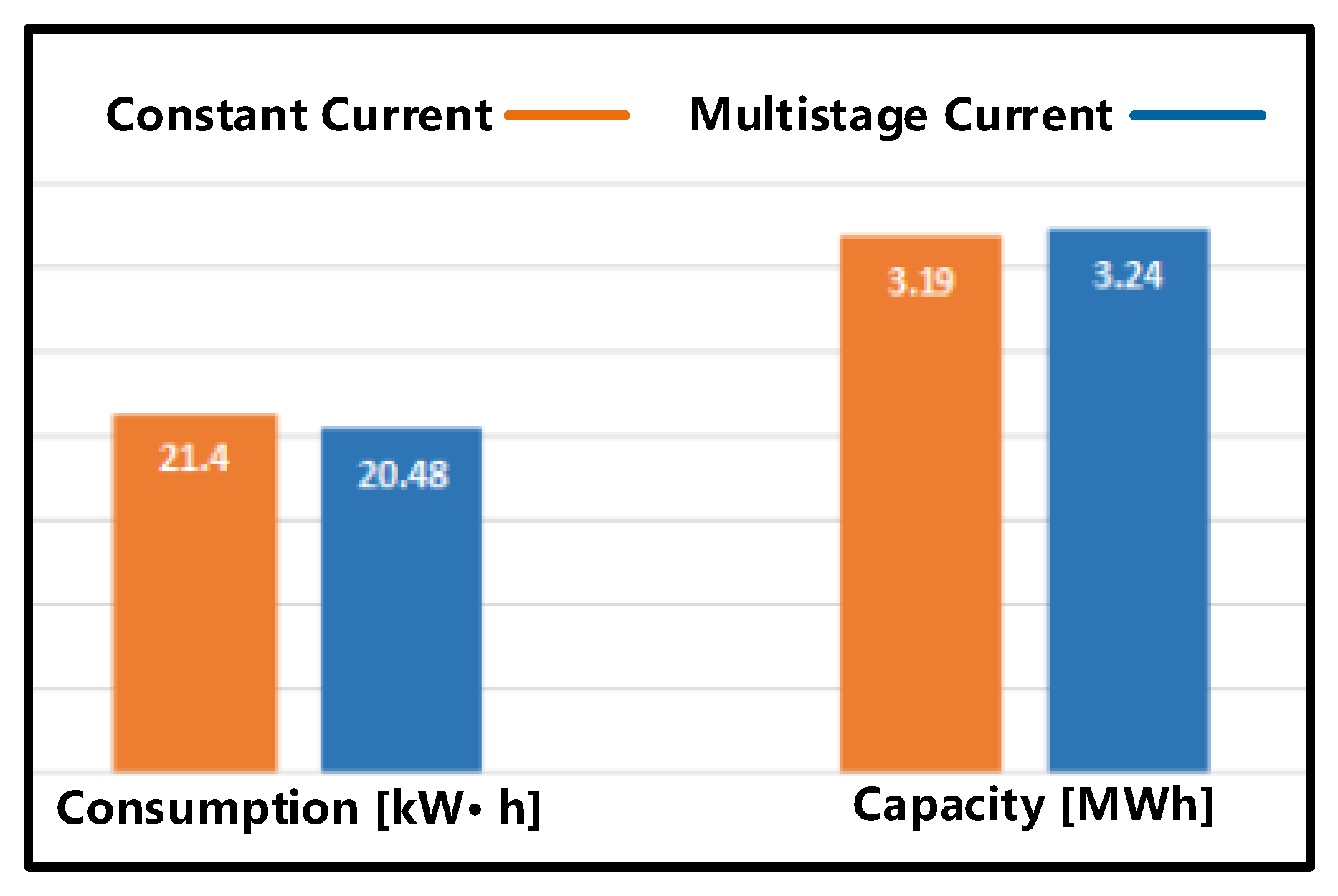
As a large-scale energy storage equipment, an MMC-BESS undertakes heavy power transmission tasks. The energy consumption optimization model proposed in this paper considers the states of the battery pack, including resistance, capacity, SOC, current, charging time, etc., which are superior in the large-scale battery packs. The simulation results demonstrate that the proposed multistage current charging method decreased the energy consumption of an MMC-BESS by 4.3% and increased the capacity of an MMC-BESS by 1.56% for five SOC intervals.

From the above analysis, it can be seen that the optimization results of the energy consumption and capacity of batteries are related to the resistance, SOC, SOH, and intervals of the multistage current charging method. The status of the battery should be monitored in real-time, and the intervals should be set to infinite to minimize the energy consumption and maximize capacity. Therefore, this is a research direction for accurately measuring the status of the battery in real-time and reducing the calculation time, while increasing the intervals.