Theoretical Analysis of Active Flow Ripple Control in Positive Displacement Pumps
Abstract
:1. Introduction
2. Description of the Active Methods
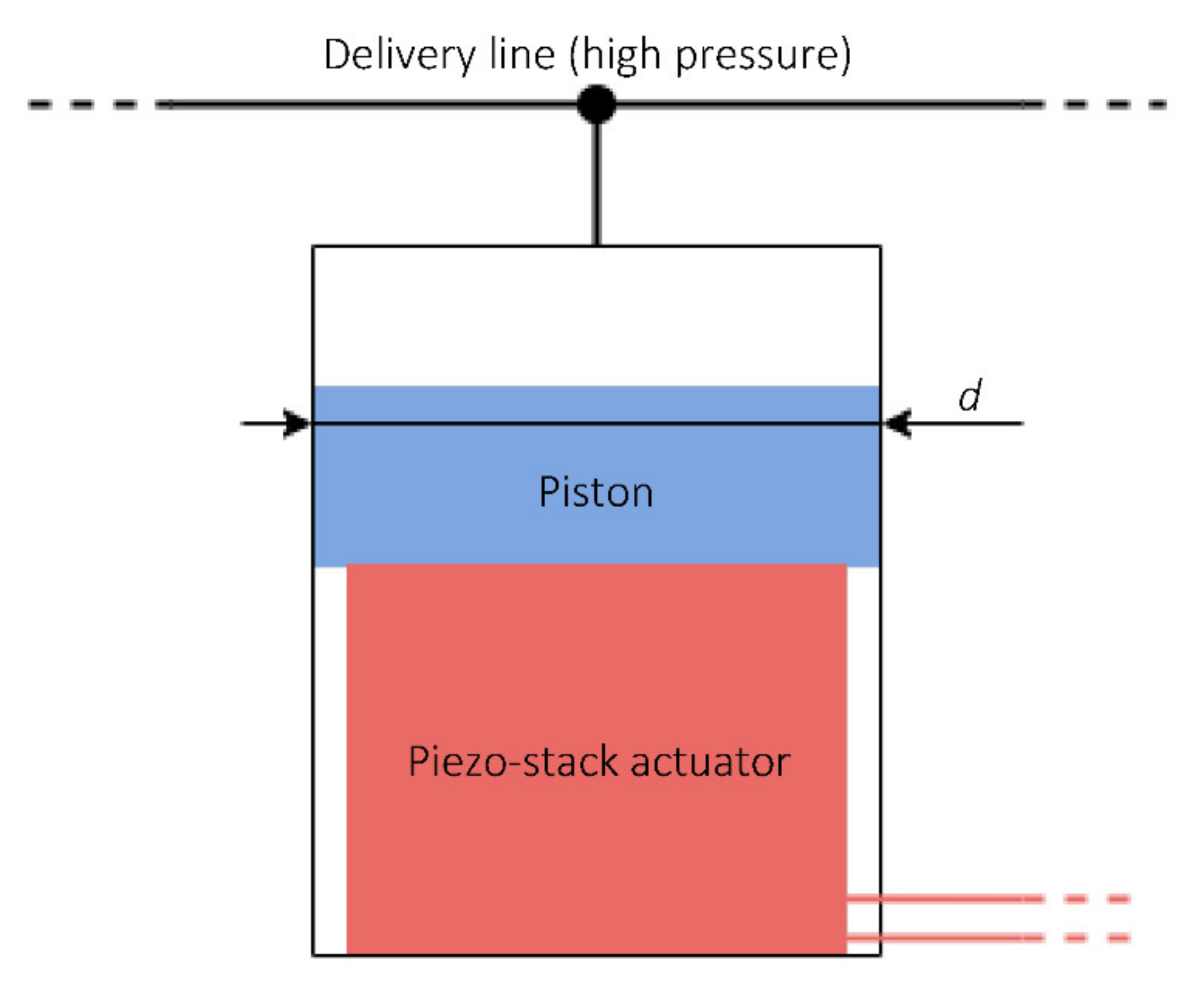
2.1. Piston Actuated by Piezo-Stack Actuator (1st Solution)
2.2. Hydraulically Actuated Piston (2nd Solution)
3. Sizing and Definition of Active System Operating Parameters
3.1. Piston Actuated by Piezo-Actuator (1st Solution)
3.2. Hydraulically Actuated Piston
4. Mathematical Model
4.1. Fluid Model
4.2. Pump Model
4.3. Piezo-Stack Actuator Model
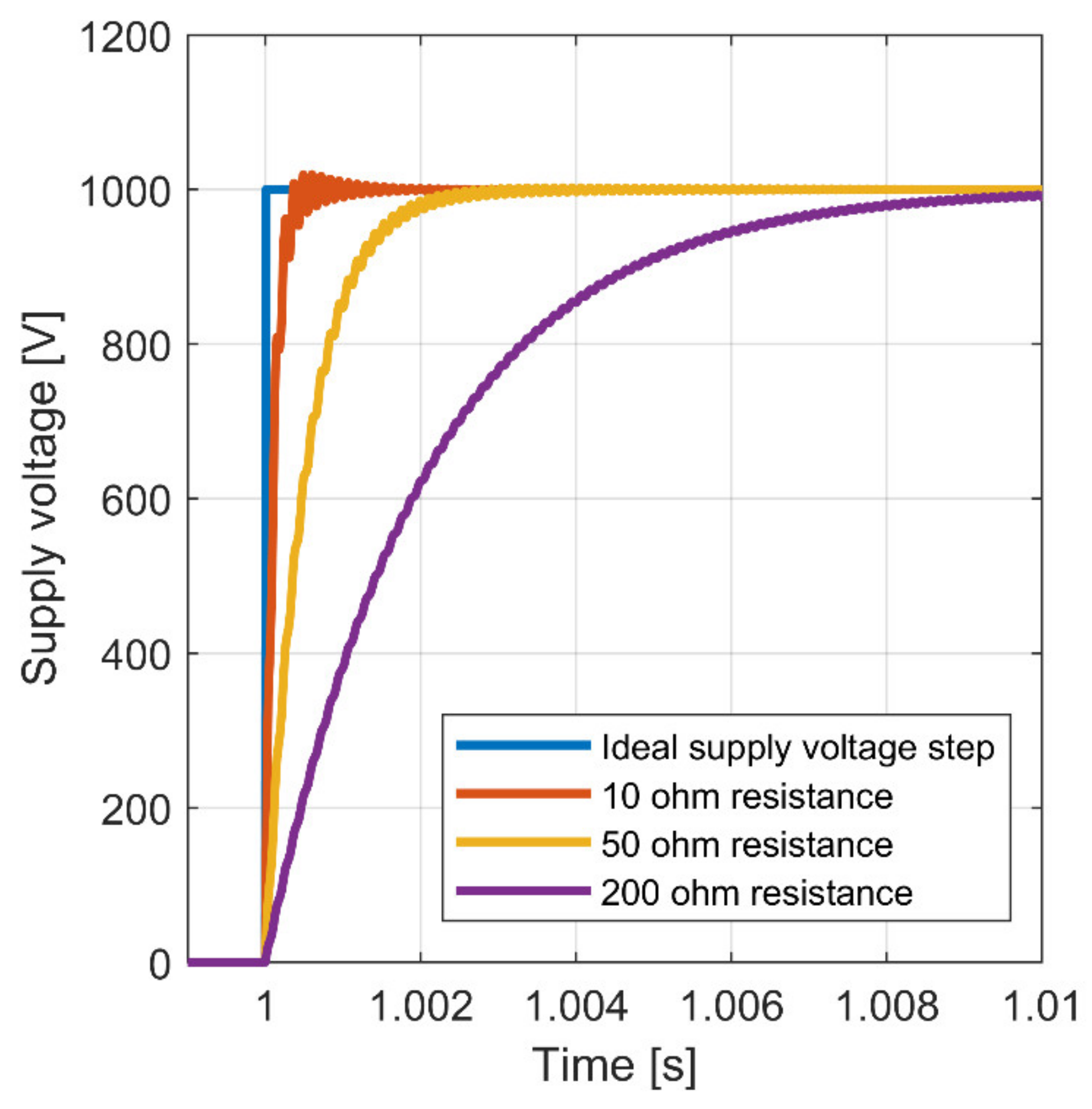
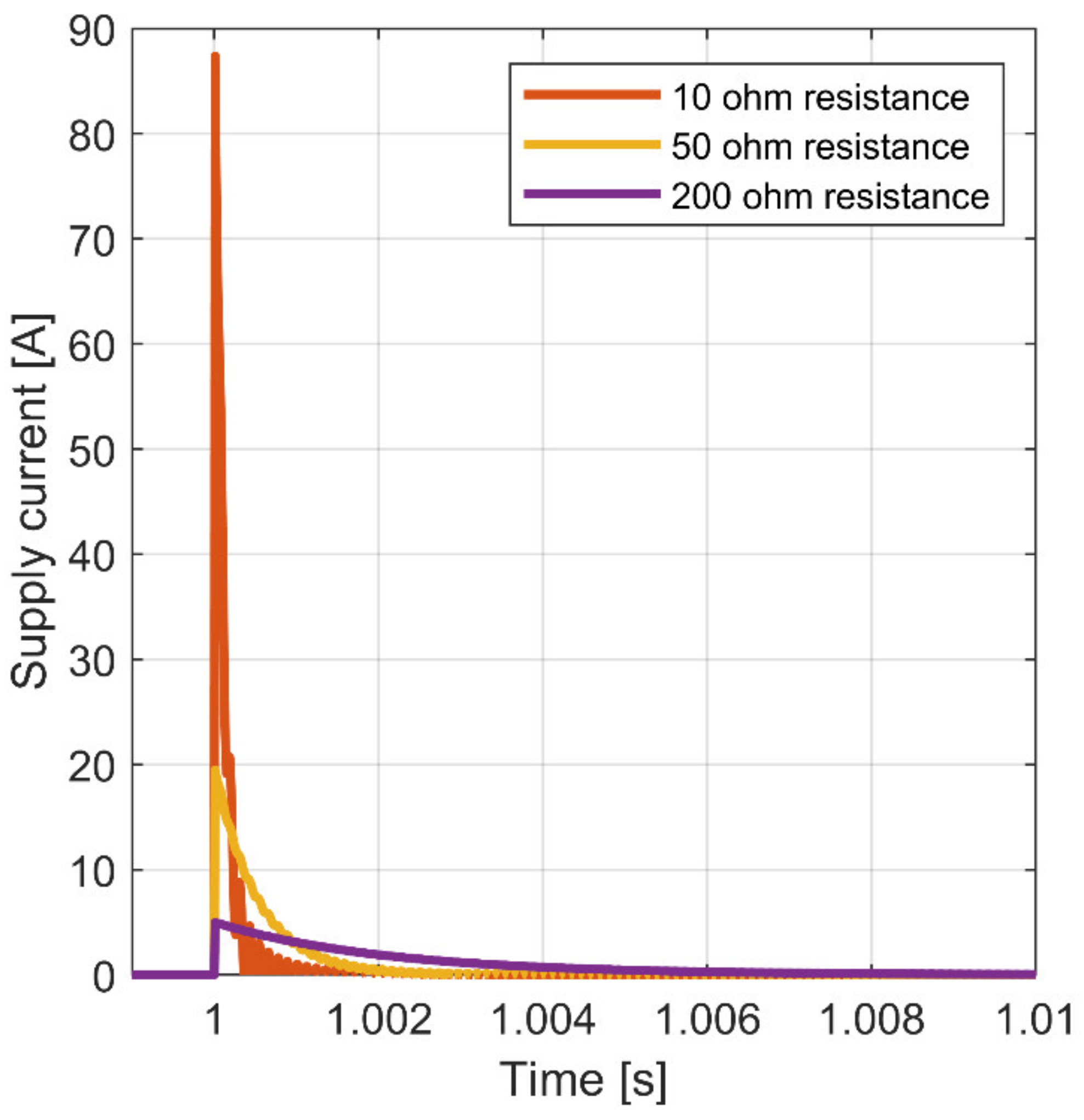
4.4. Piezo-Stack Actuator Power Supply
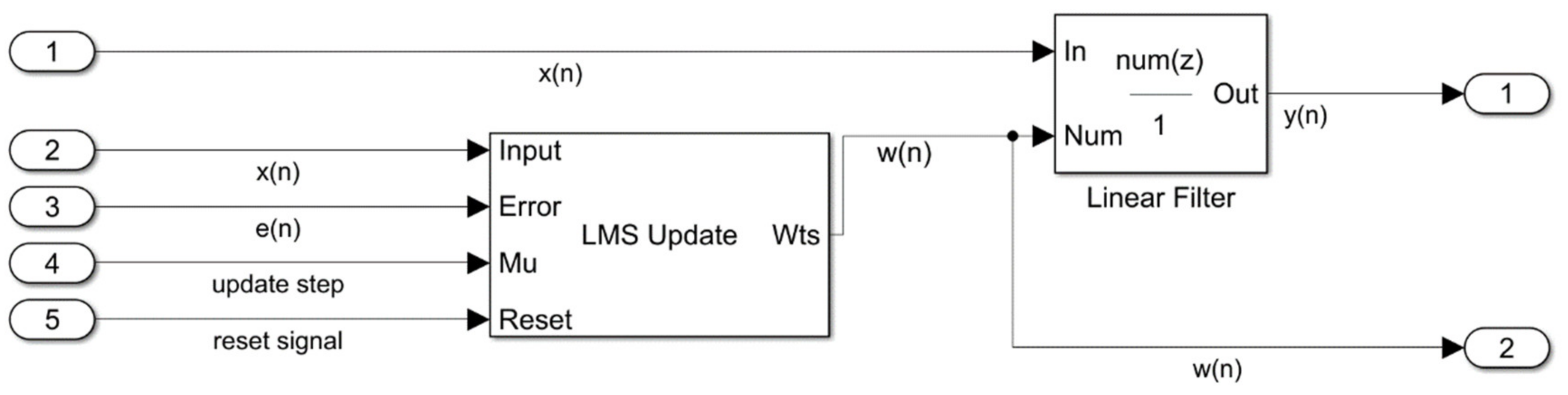
5. Control Algorithm Model
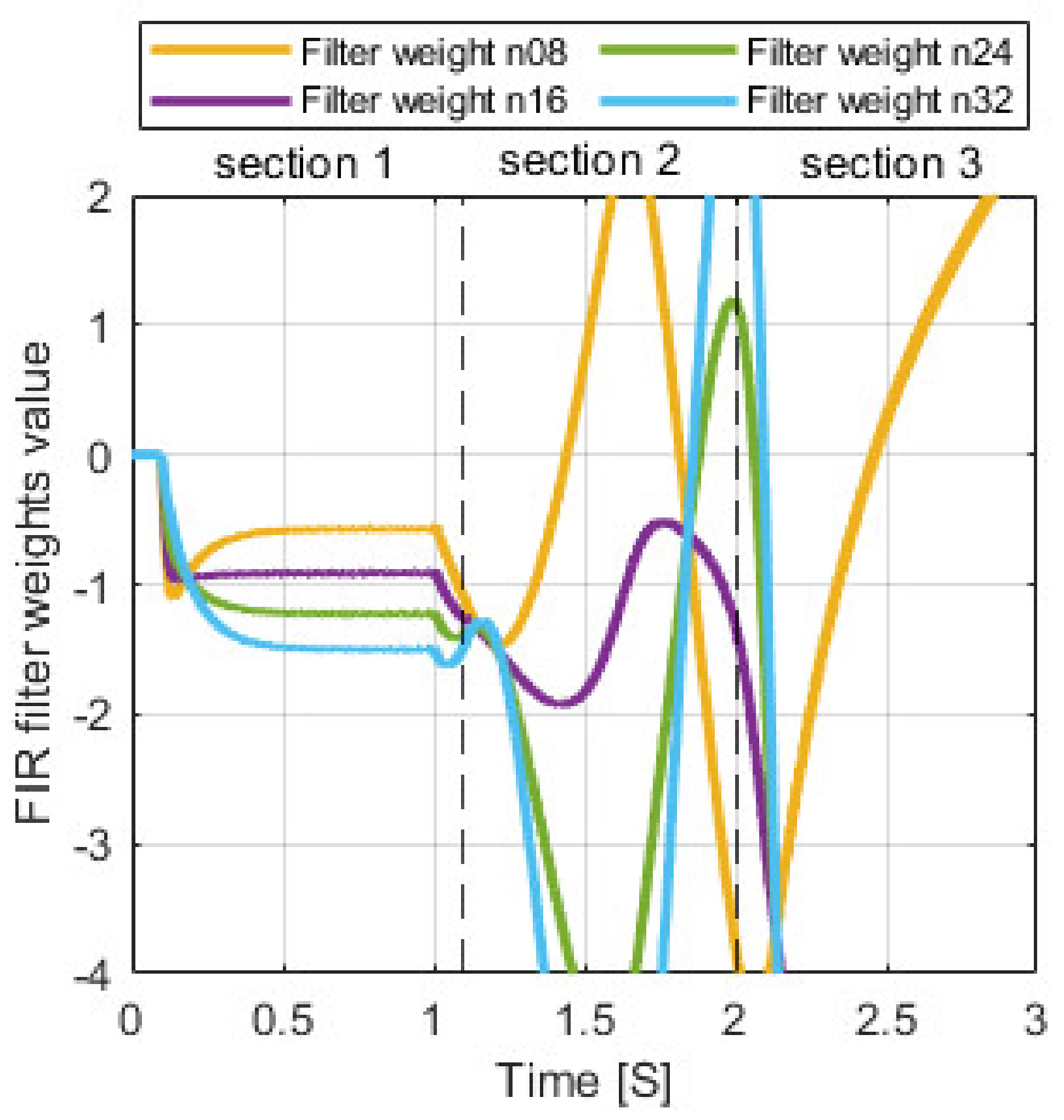
6. Simulations Results
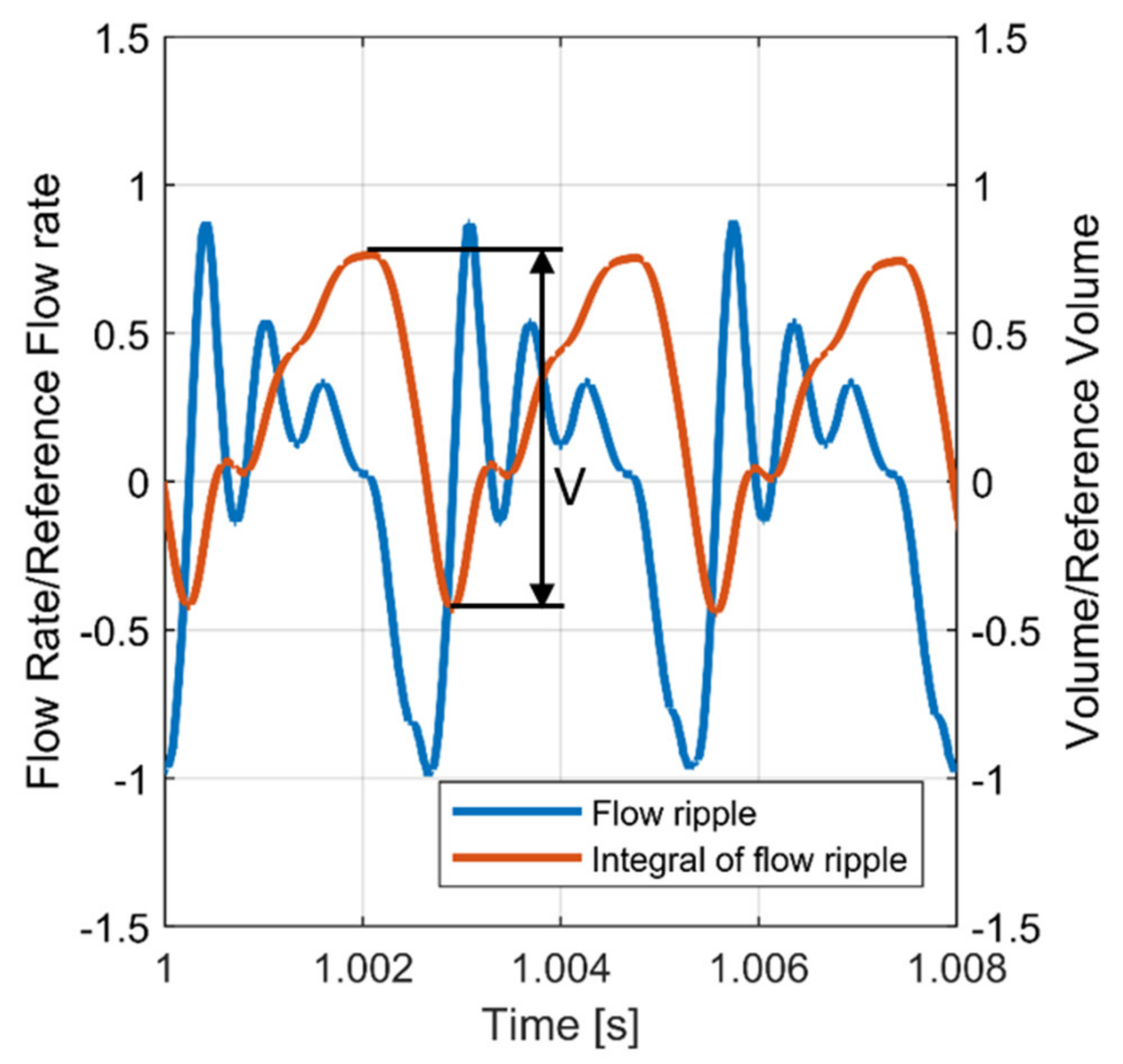
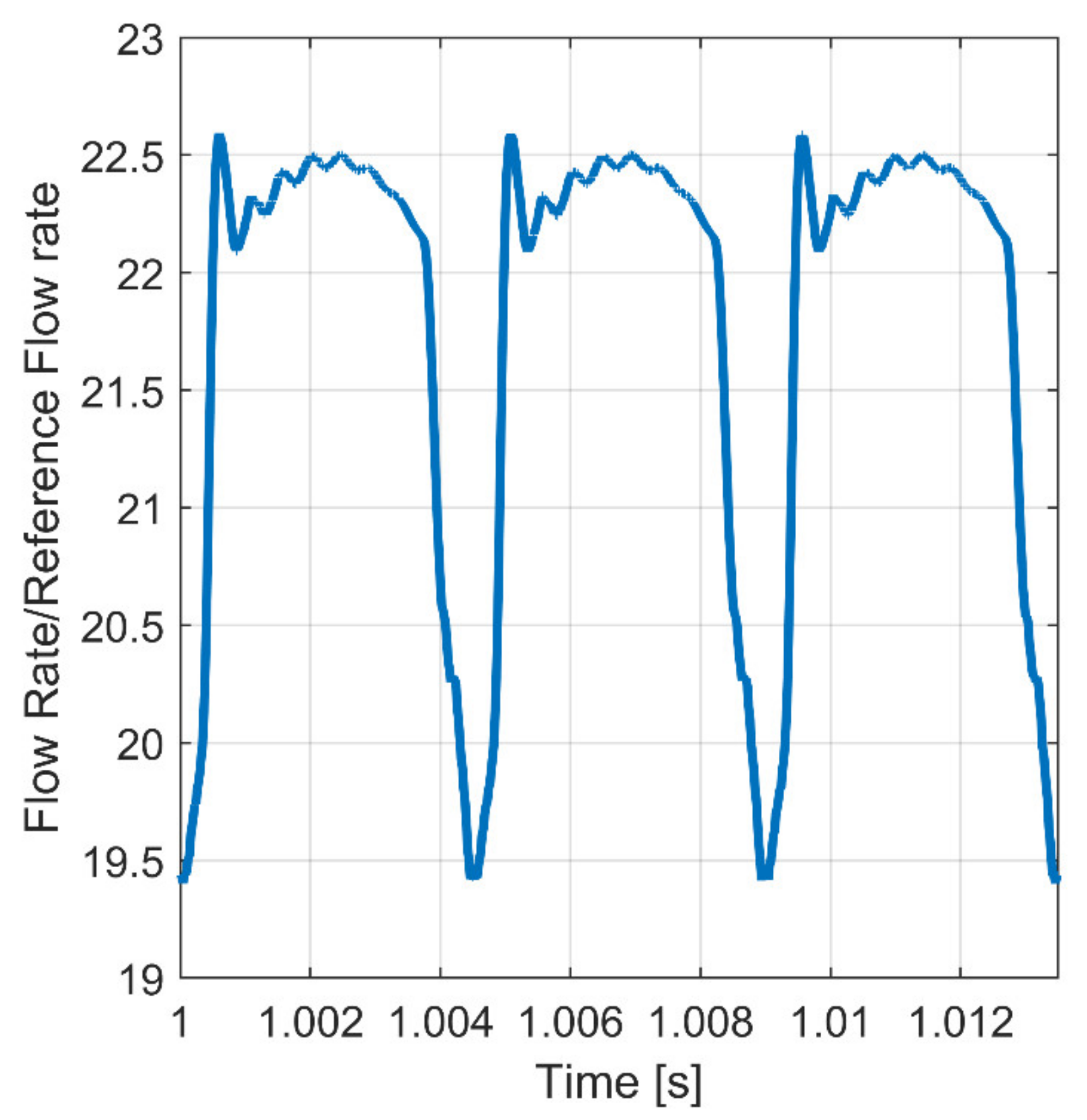
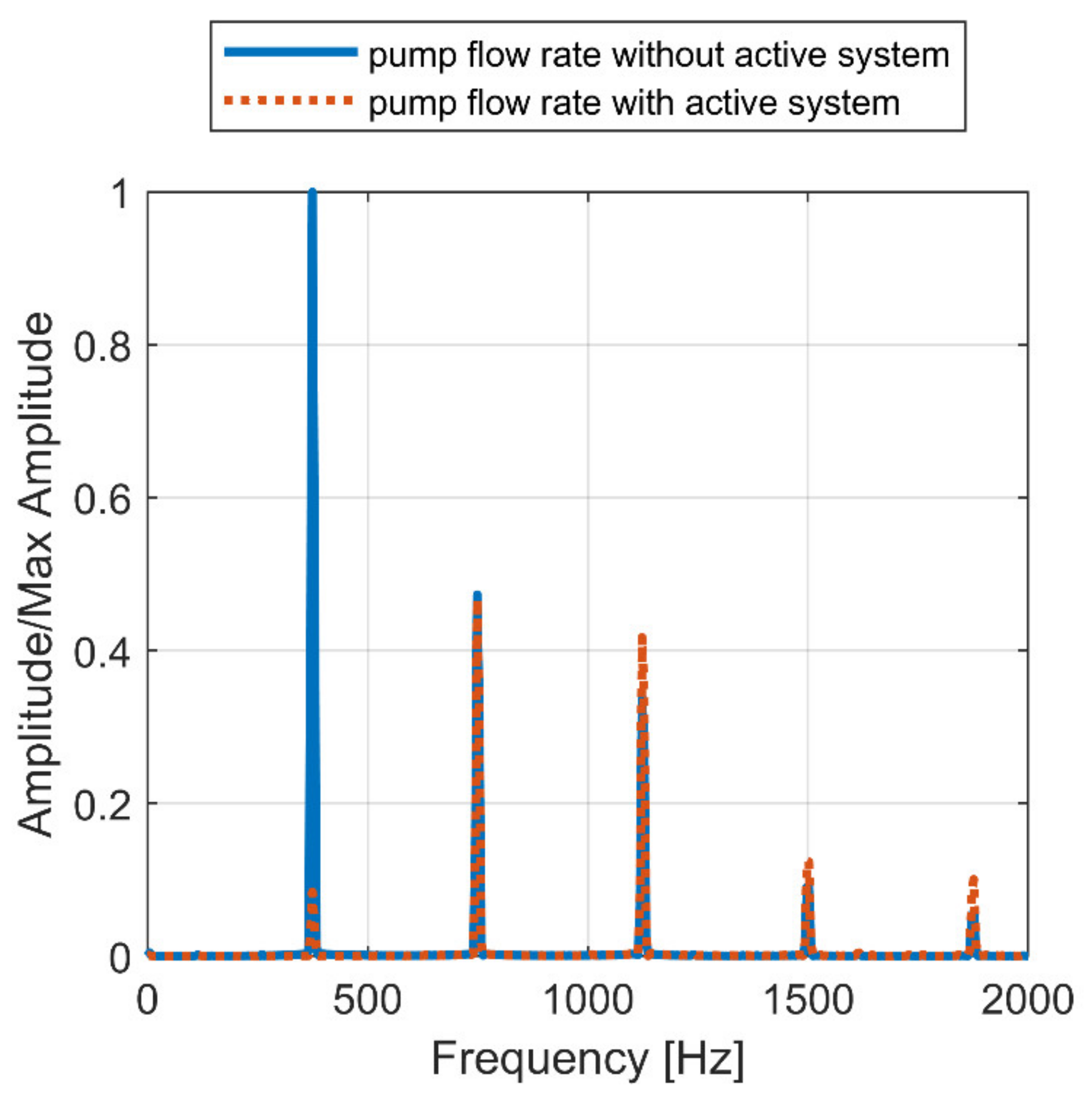
6.1. Piston Actuated by Piezo-Actuator (1st Solution)
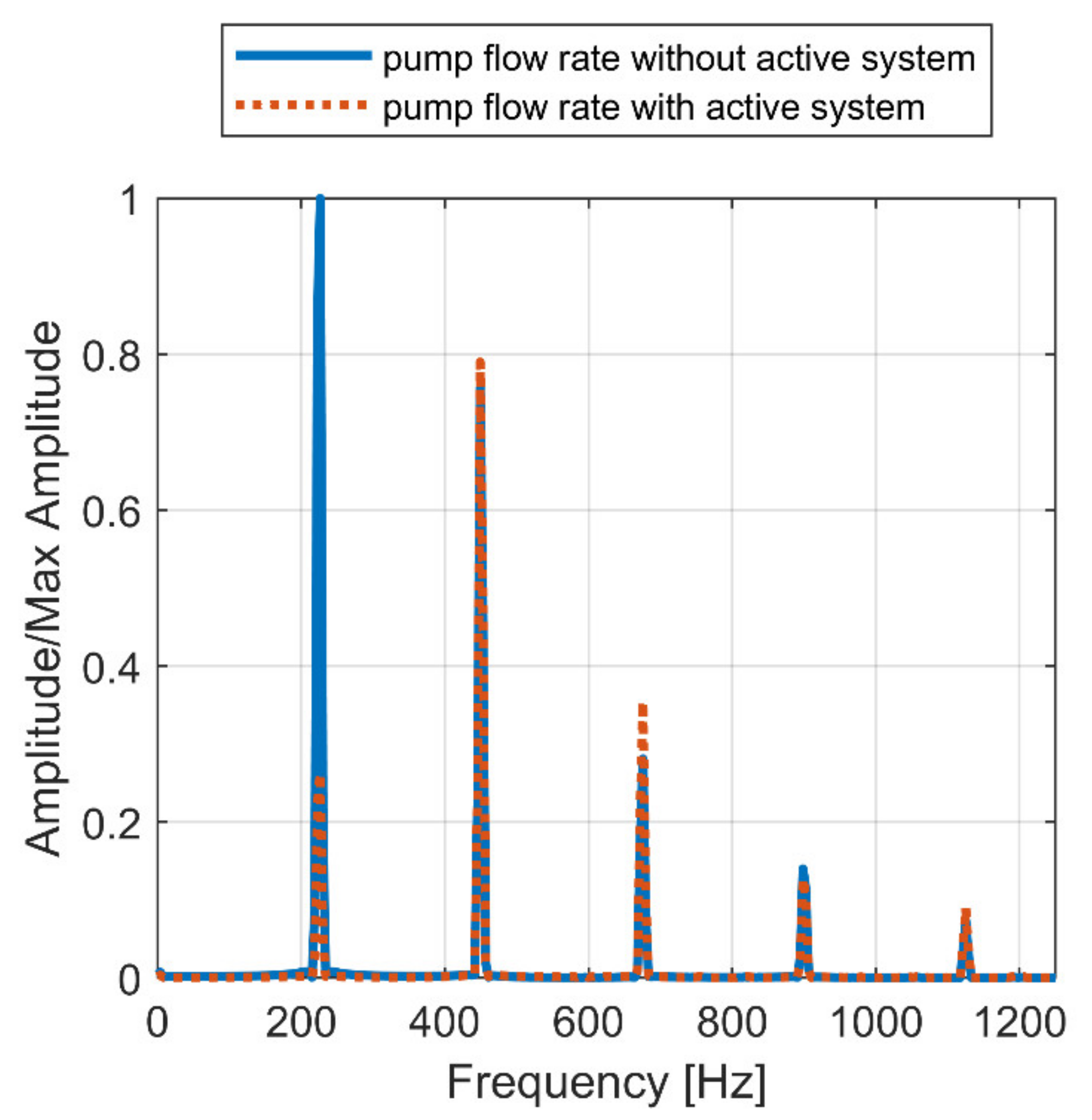
6.2. Piston Actuated Hydraulically via Piezo-Valve (2nd Solution)
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karpenko, M.; Prentkovskis, O.; Šukevičius, Š. Research on high-pressure hose with repairing fitting and influence on energy parameter of the hydraulic drive. In Eksploatacja i Niezawodnosc—Maintenance and Reliability; Polish Maintenance Society: Lublin, Poland, 2022; Volume 24, pp. 25–32. ISSN 1507-2711. [Google Scholar]
- Stosiak, M. The impact of hydraulic systems on the human being and the environment. J. Theor. Appl. Mech. 2015, 53, 409–420. [Google Scholar] [CrossRef] [Green Version]
- Ye, S.; Zhang, J.; Xu, B. Noise Reduction of an Axial Piston Pump by Valve Plate Optimization. Chin. J. Mech. Eng. 2018, 31, 57. [Google Scholar] [CrossRef] [Green Version]
- Johansson, A.; Olvander, J.; Palmberg, J.-O. Experimental verification of cross-angle for noise reduction in hydraulic piston pumps. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2007, 221, 321. [Google Scholar] [CrossRef]
- Harrison, A.M.; Edge, K. Reduction of axial piston pump pressure ripple. Proc. Inst. Mech. Eng. 2000, 214, 53–64. [Google Scholar]
- Borghi, M.; Zardin, B. Axial Balance of External Gear Pumps and Motors: Modelling and Discussing the Influence of Elastohydrodynamic Lubrication in the Axial Gap. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Vacca, A. Theoretical investigation into the ripple source of external gear pumps. Energies 2019, 12, 535. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Vacca, A. Numerical analysis of theoretical flow in external gear machines. Mech. Mach. Theory 2017, 108, 41–56. [Google Scholar] [CrossRef]
- Zhou, J.; Vacca, A.; Casoli, P. A Novel Approach for Predicting the Operation of External Gear Pumps Under Cavitating Conditions. Simul. Model. Pract. Theory 2014, 45, 35–49. [Google Scholar] [CrossRef]
- Rundo, M.; Altare, G.; Casoli, P. Simulation of the filling capability in vane pumps. Energies 2019, 12, 283. [Google Scholar] [CrossRef] [Green Version]
- Corvaglia, A.; Ferrari, A.; Rundo, M.; Vento, O. Three-dimensional model of an external gear pump with an experimental evaluation of the flow ripple. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1097–1105. [Google Scholar] [CrossRef]
- Pan, M.; Ding, B.; Yuan, C.; Zou, J.; Yang, H. Novel Integrated Control of Fluid-Borne Noise in Hydraulic Systems. In Proceedings of the BATH/ASME 2018 Symposium on Fluid Power and Motion Control FPMC 2018, Bath, UK, 12–14 September 2018. [Google Scholar]
- Shang, Y.; Tang, H.; Sun, H.; Guan, C.; Wu, S.; Xu, Y.; Jiao, Z. A novel hydraulic pulsation reduction component based on discharge and suction self-oscillation: Principle, design and experiment. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 433–445. [Google Scholar] [CrossRef]
- Pan, M.; Johnston, N.; Plummer, A. Hybrid Fluid-borne Noise Control in Fluid-filled Pipelines. J. Phys. Conf. Ser. 2016, 744, 012016. [Google Scholar] [CrossRef] [Green Version]
- Waitschat, A.; Thielecke, F.; Behr, R.M.; Heise, U. Active Fluid Borne Noise Reduction for Aviation Hydraulic Pumps. In Proceedings of the 10th International Fluid Power Conference, Dresden, Germany, 8–10 March 2016. [Google Scholar]
- Kim, T.; Ivantysynova, M. Active Vibration/Noise Control of Axial Piston Machine Using Swash Plate Control. In Proceedings of the ASME/BATH 2017 Symposium on Fluid Power and Motion Control, Sarasota, FL, USA, 16–19 October 2017; Paper No. FPMC2017-4304. p. V001T01A053. [Google Scholar] [CrossRef]
- Casoli, P.; Pastori, M.; Scolari, F.; Rundo, M. Active pressure ripple control in axial piston pumps through high-frequency swash plate oscillations—A theoretical analysis. Energies 2019, 12, 1377. [Google Scholar] [CrossRef] [Green Version]
- Casoli, P.; Pastori, M.; Scolari, F. Swash plate design for pressure ripple reduction—A theoretical analysis. In Proceedings of the AIP Conference, Modena, Italy, 11 September 2019. [Google Scholar] [CrossRef]
- Hagstrom, N.; Harens, M.; Chatterjee, A.; Creswick, M. Piezoelectric actuation to reduce pump flow ripple. In Proceedings of the ASME/BATH 2019 Symposium on Fluid Power and Motion Control 2019 FPMC, Sarasota, FL, USA, 7–9 October 2019. [Google Scholar]








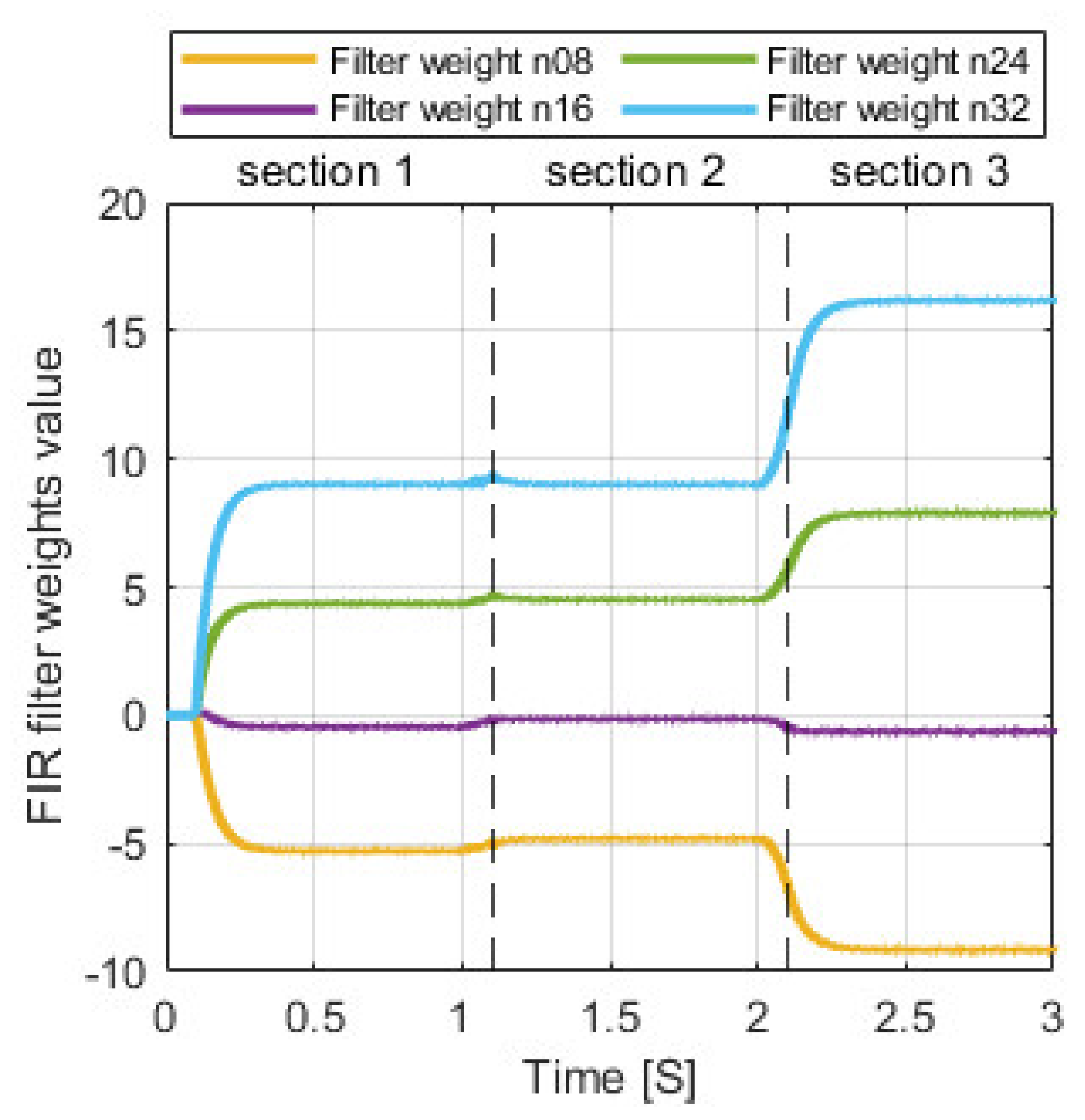
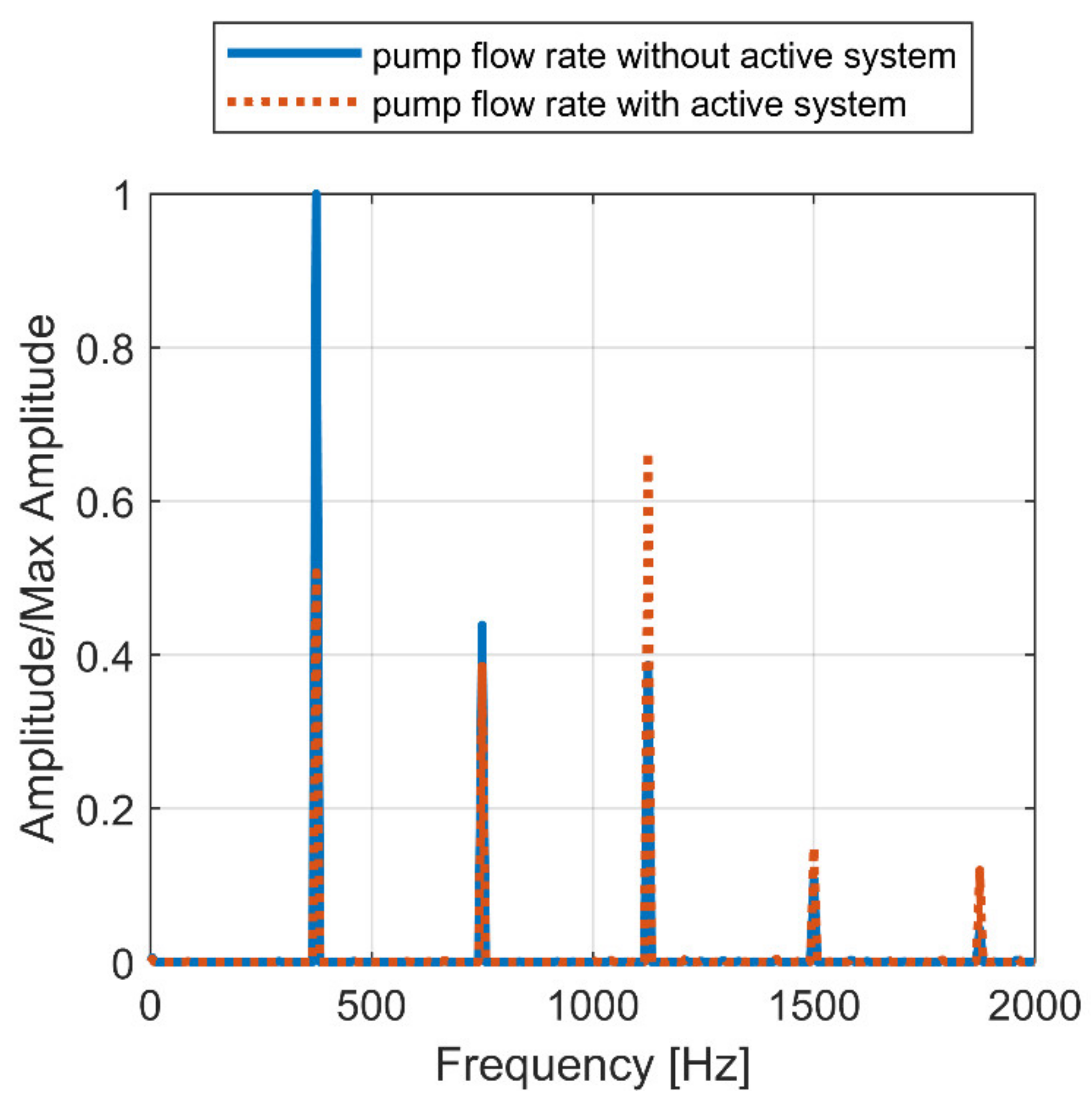
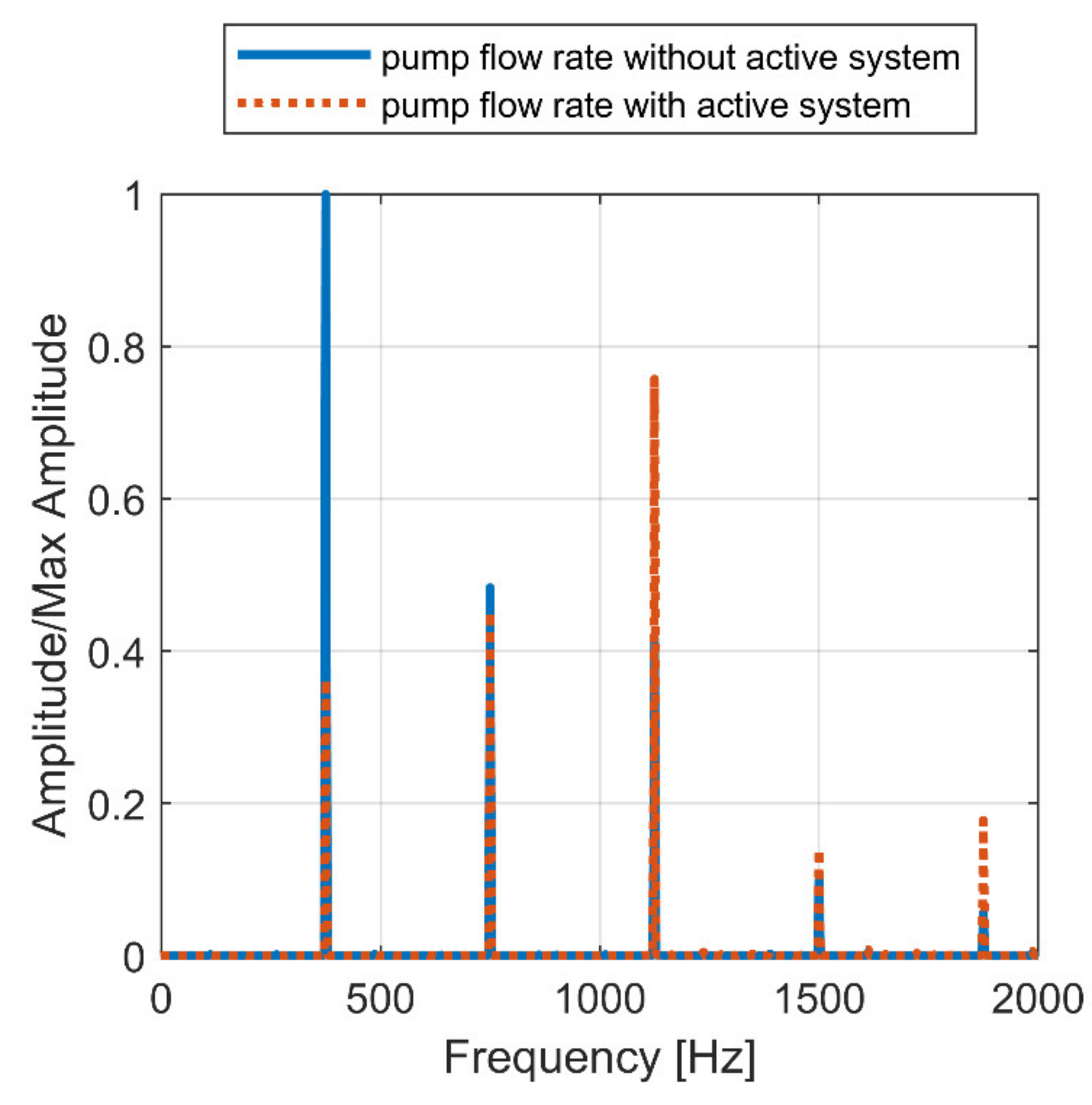
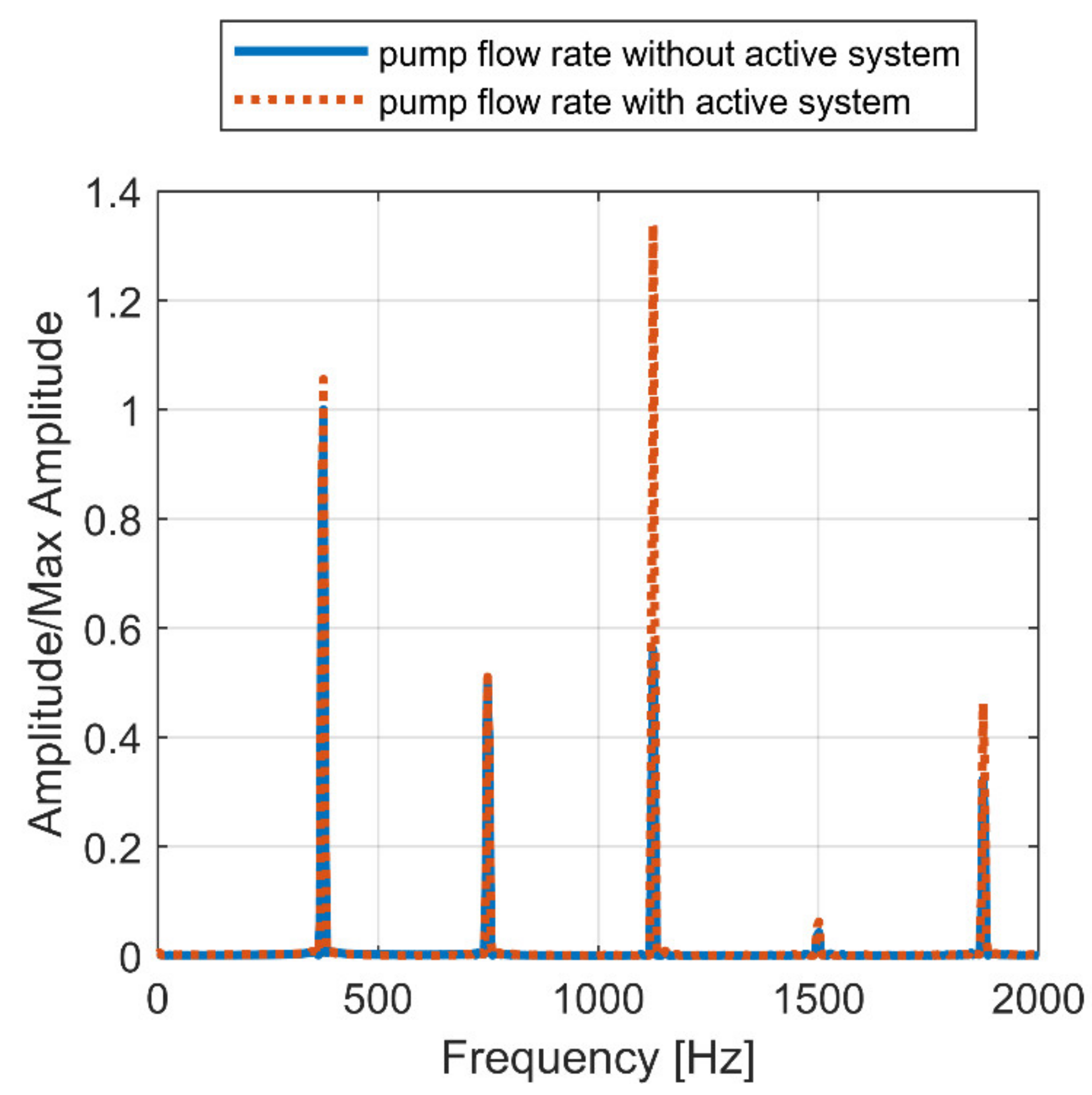
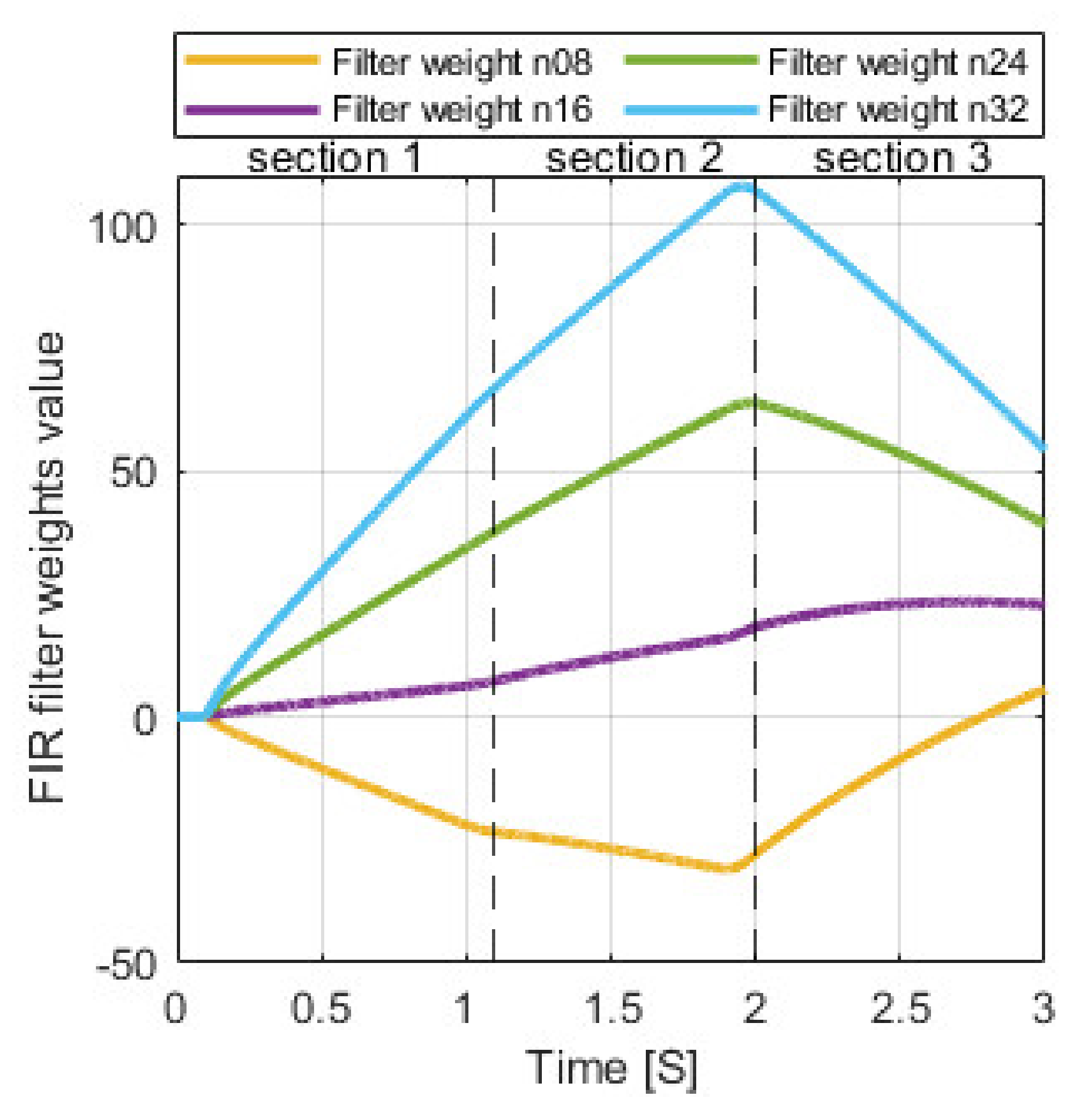


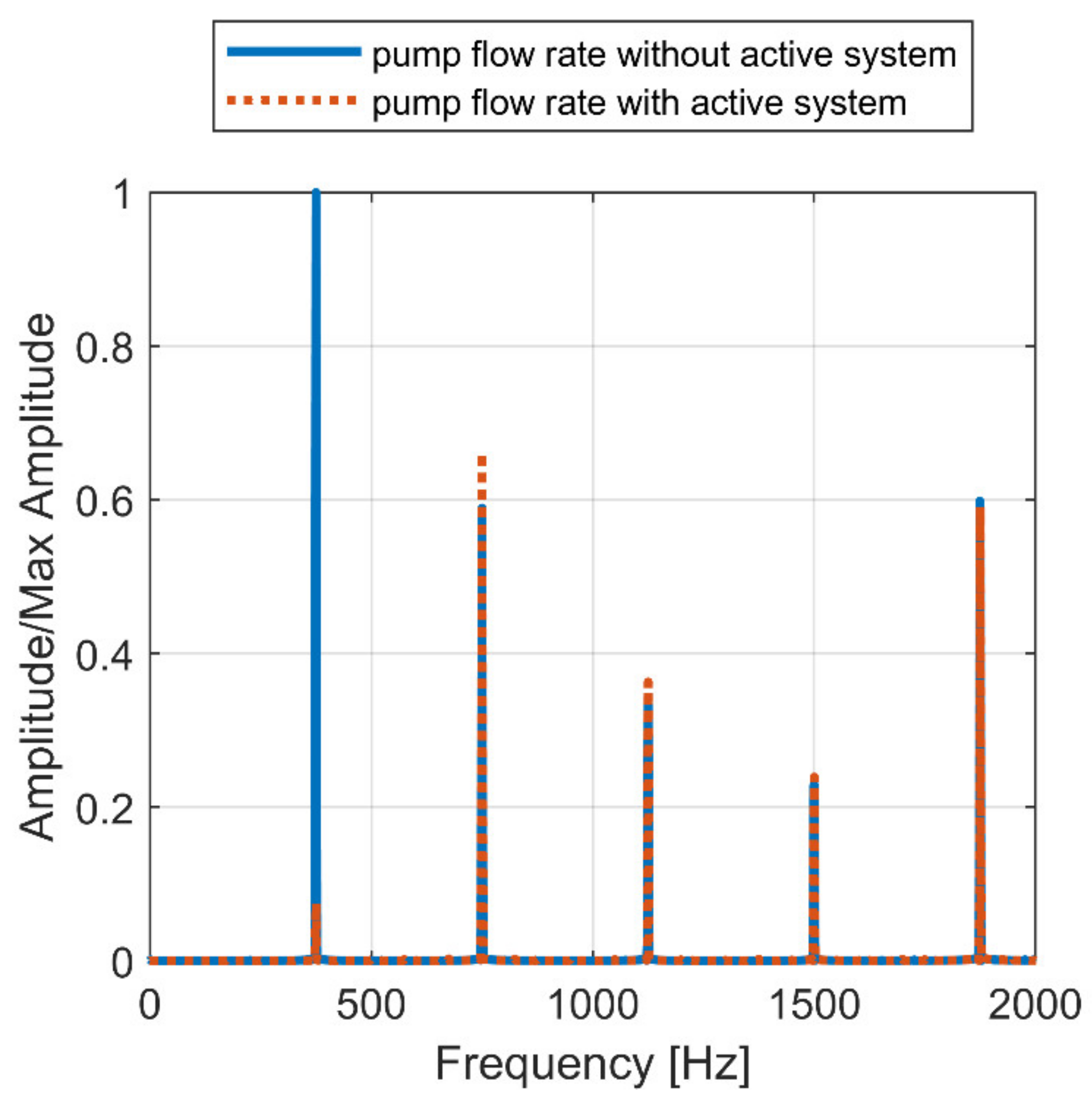
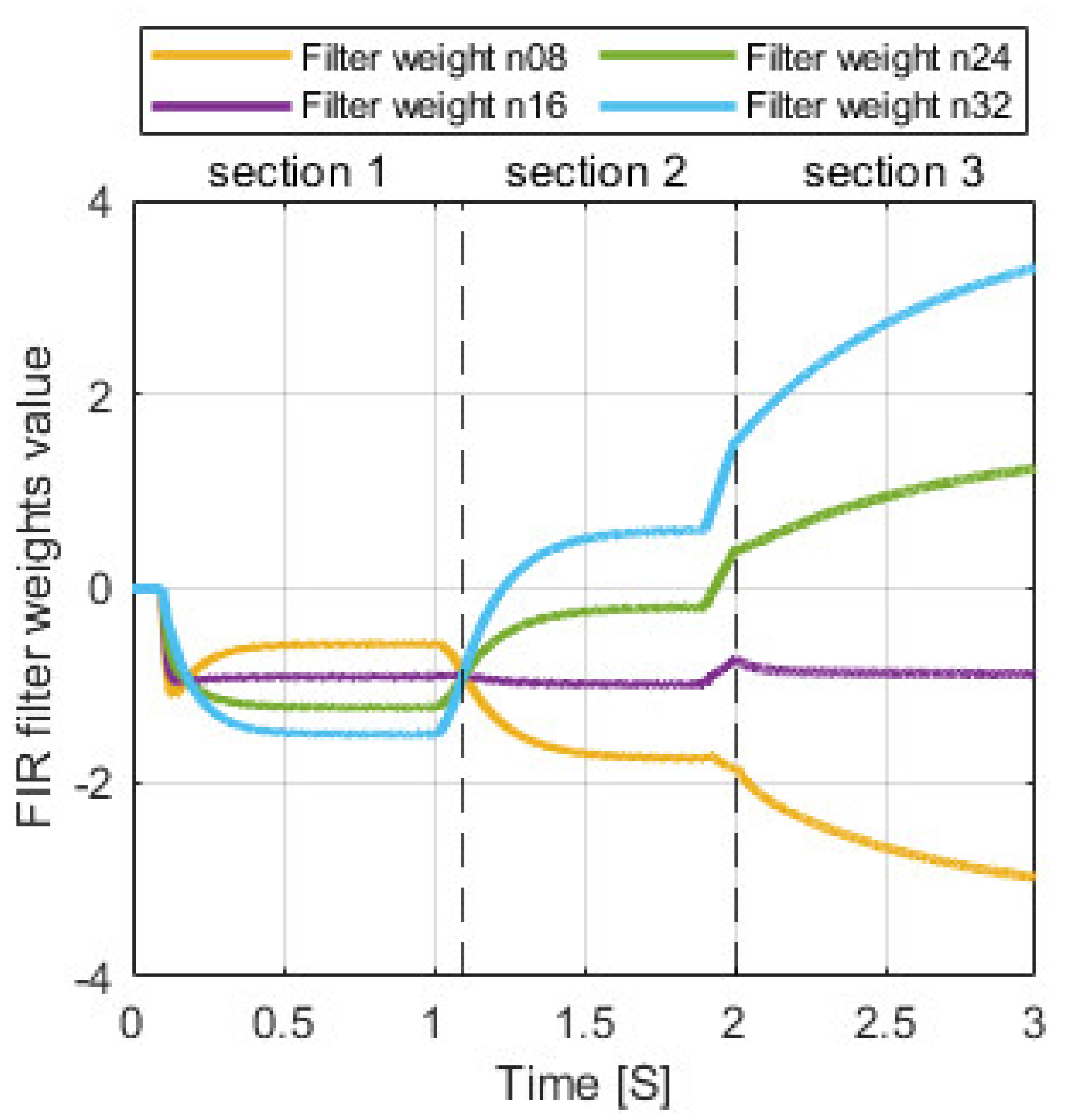

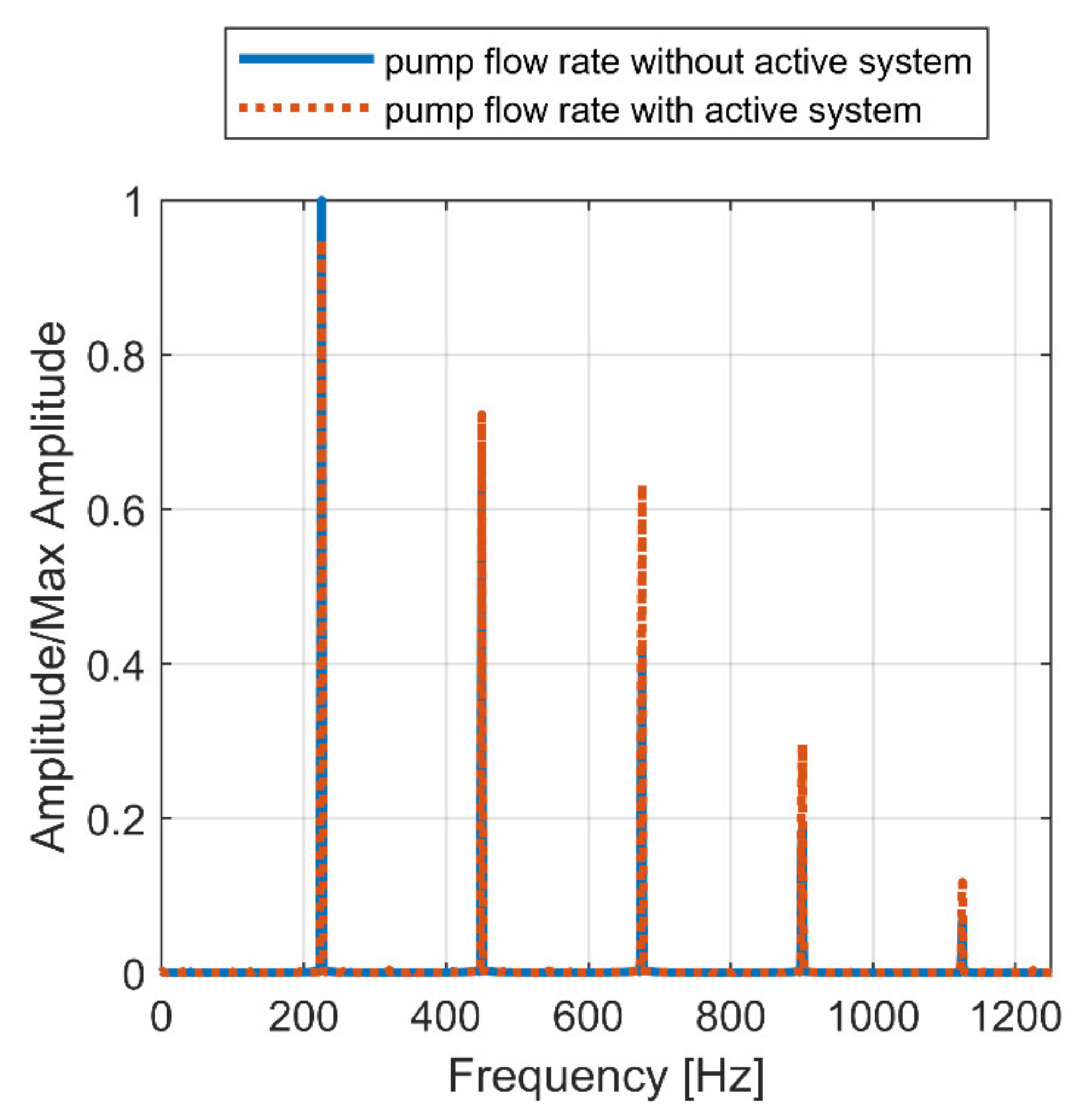
| Cycle Section | 1 | 2 | 3 |
|---|---|---|---|
| Average delivery pressure [bar] | 250 | 135 | 30 |
| Pump rotation speed [rpm] | 2500 | 2500 | 2500 |
| Swash plate angle/max. angle [%] | 100 | 100 | 50 |
| Average flow rate [L/min] | 200 | 200 | 100 |
| Cycle Section | 1 | 2 | 3 |
|---|---|---|---|
| Average delivery pressure [bar] | 250 | 90 | 220 |
| Pump rotation speed [rpm] | 2500 | 1500 | 1500 |
| Swash plate angle/max. angle [%] | 100 | 100 | 100 |
| Average flow rate [L/min] | 200 | 120 | 120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casoli, P.; Vescovini, C.M.; Scolari, F.; Rundo, M. Theoretical Analysis of Active Flow Ripple Control in Positive Displacement Pumps. Energies 2022, 15, 4703. https://doi.org/10.3390/en15134703
Casoli P, Vescovini CM, Scolari F, Rundo M. Theoretical Analysis of Active Flow Ripple Control in Positive Displacement Pumps. Energies. 2022; 15(13):4703. https://doi.org/10.3390/en15134703
Chicago/Turabian StyleCasoli, Paolo, Carlo Maria Vescovini, Fabio Scolari, and Massimo Rundo. 2022. "Theoretical Analysis of Active Flow Ripple Control in Positive Displacement Pumps" Energies 15, no. 13: 4703. https://doi.org/10.3390/en15134703






