Common Transmission Point (CTP) Gathers: A New Domain for Amplitude Variation with Offset
Abstract
:1. Introduction
2. Methodology
3. Common Transmission Point (CTP) Gather
- Use Equations (12)–(14) as well as the trace headers (i.e., survey geometry information) to calculate X2, 1, 2, and for every trace.
- Group traces based on their X2 value lying within a length on the interface equal to one half of the shot spacing. Each of these groups constitutes one CTP gather.
- Use Equation (15) to calculate the critical angle (c) value for models where < .
- Sort the traces in every CTP gather according to their value in increasing order from the trace with the minimum value available in that gather until the trace with value is less than or equal to (0.9 × c). If no critical angle exists, then, all traces of that gather are used.
- Pick the times and amplitudes of the direct (down going) PP (i.e., TPP) and PS (i.e., TPS) waves on each trace of the CTP gather.
- For every trace of the CTP gather, plot the picked TPP values versus their corresponding values.
- Fit a line to the (, TPP) data set. The intercept and gradient of this best-fit line are equal to A and B, respectively.
- Use Equations (8) and (9) to calculate the rock properties and at the position of this CTP gather.
- For every trace of the CTP gather, calculate .
- For a one-term approximation of the TPS, fit a line with zero intercept (i.e., f(x) = a1 x) to the (, TPS) data set. The slope of this line is equal to C (i.e., C = a1)
- For a two-term approximation of the TPS, fit a polynomial of the form f(x) = a2 x + b2 x3 to the (, TPS) data set. Then, C = a2 and D = b2.
- For a three-term approximation of the TPS, fit a polynomial of the form f(x) = a3 x + b3 x3 + c3 x5 to the (, TPS) data set. Then, C = a3 and D = b3.
- Use Equations (10) and (11) to calculate the rock properties and at the position of this CTP gather.
4. Results and Discussion
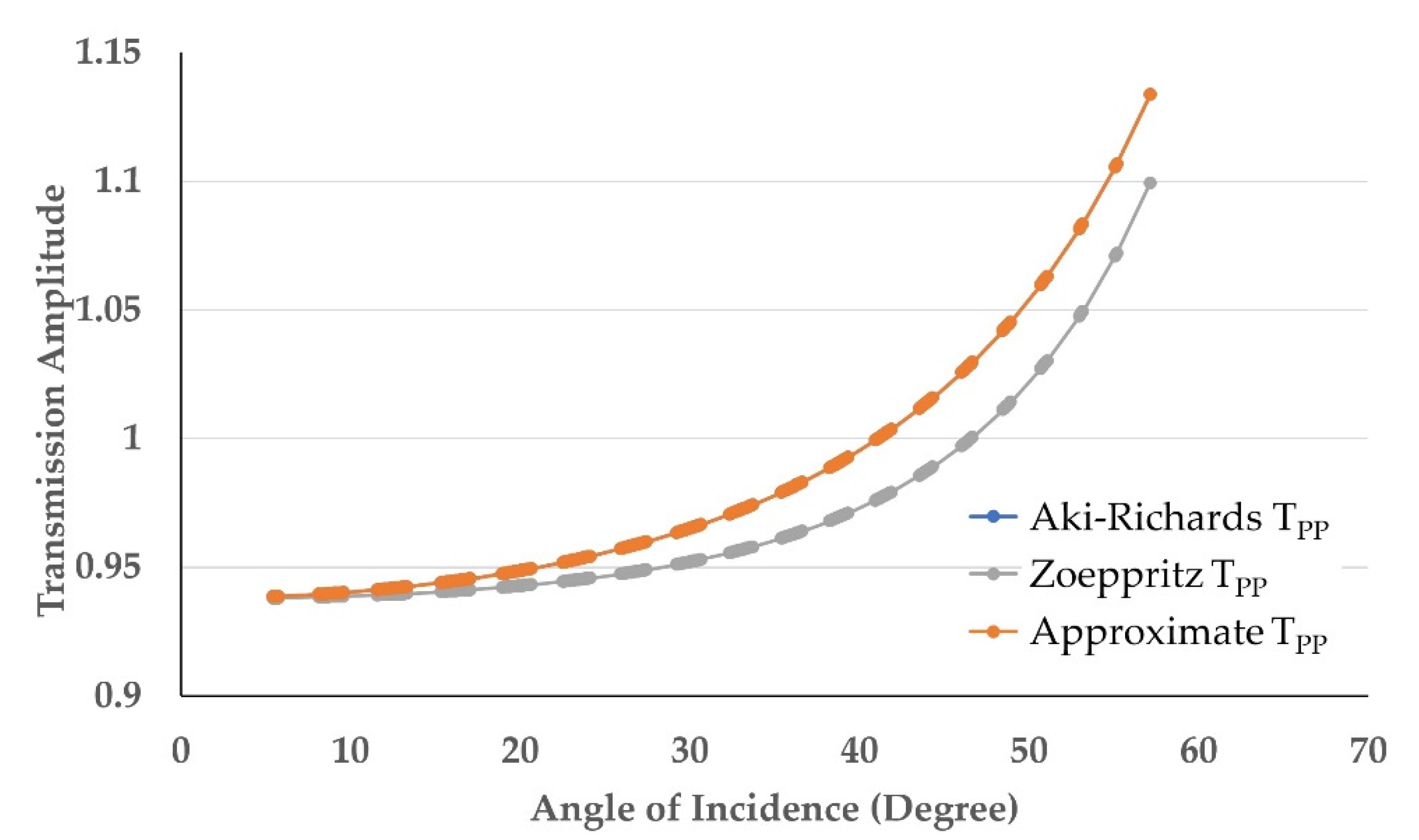
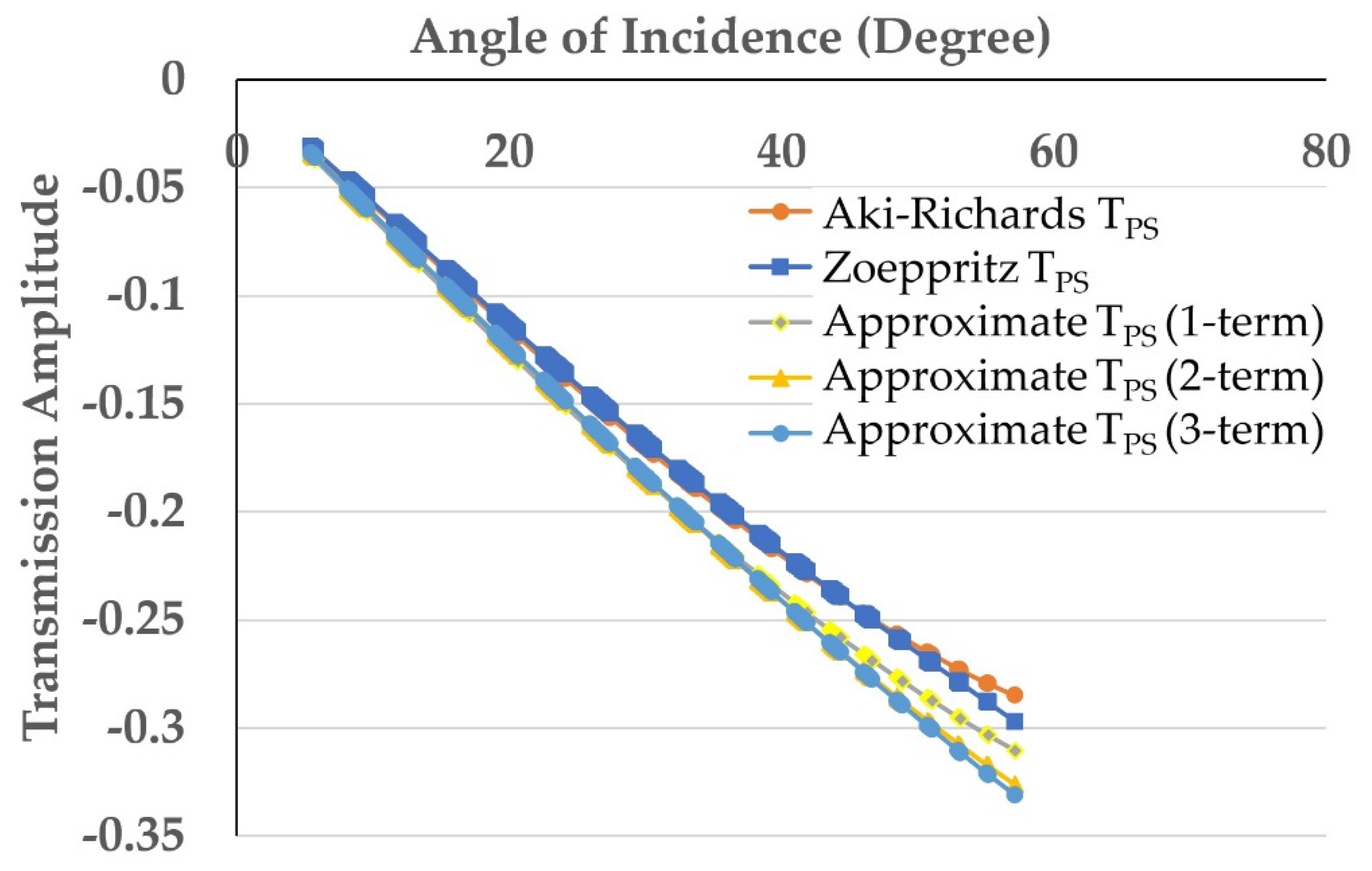
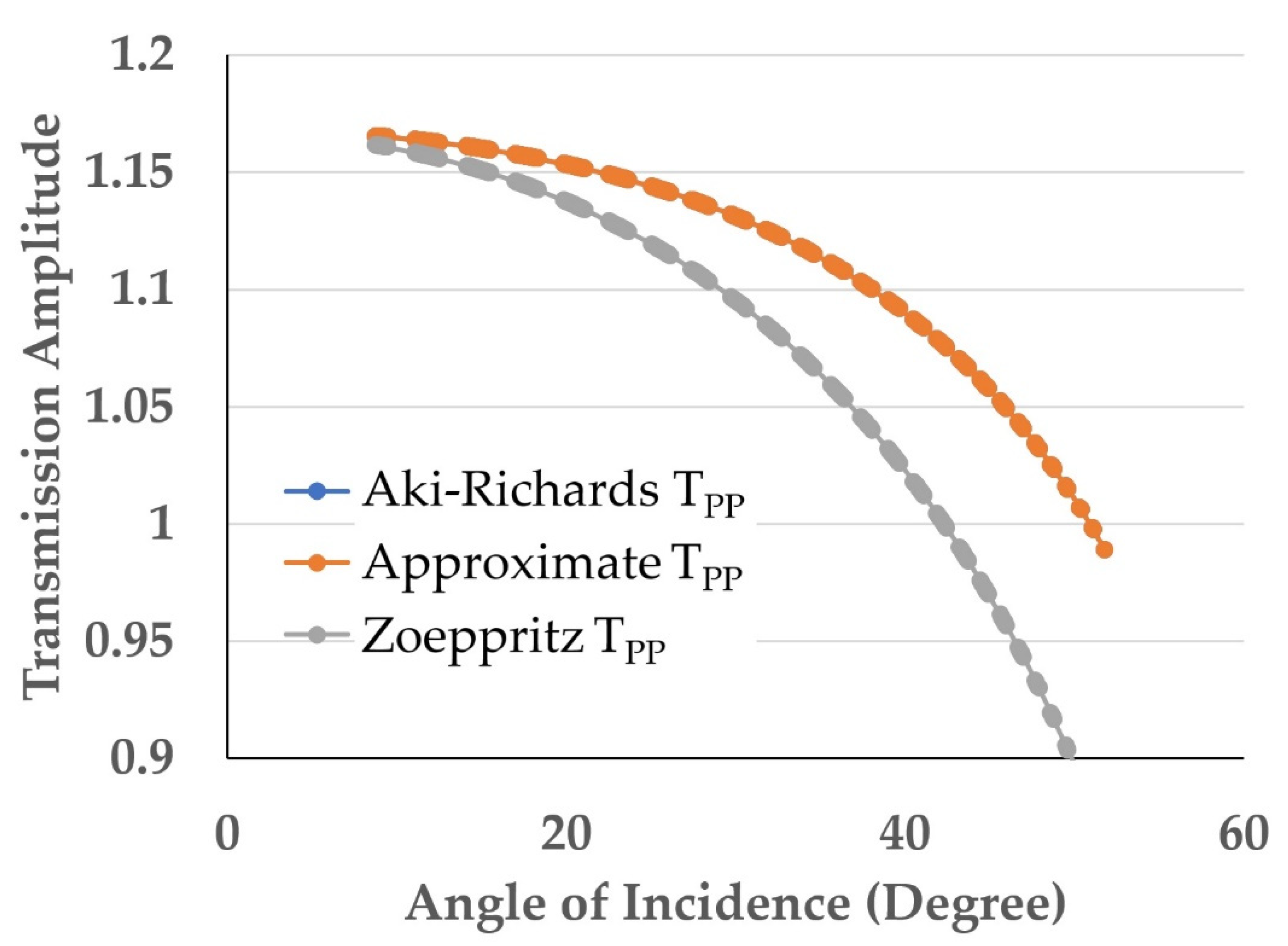
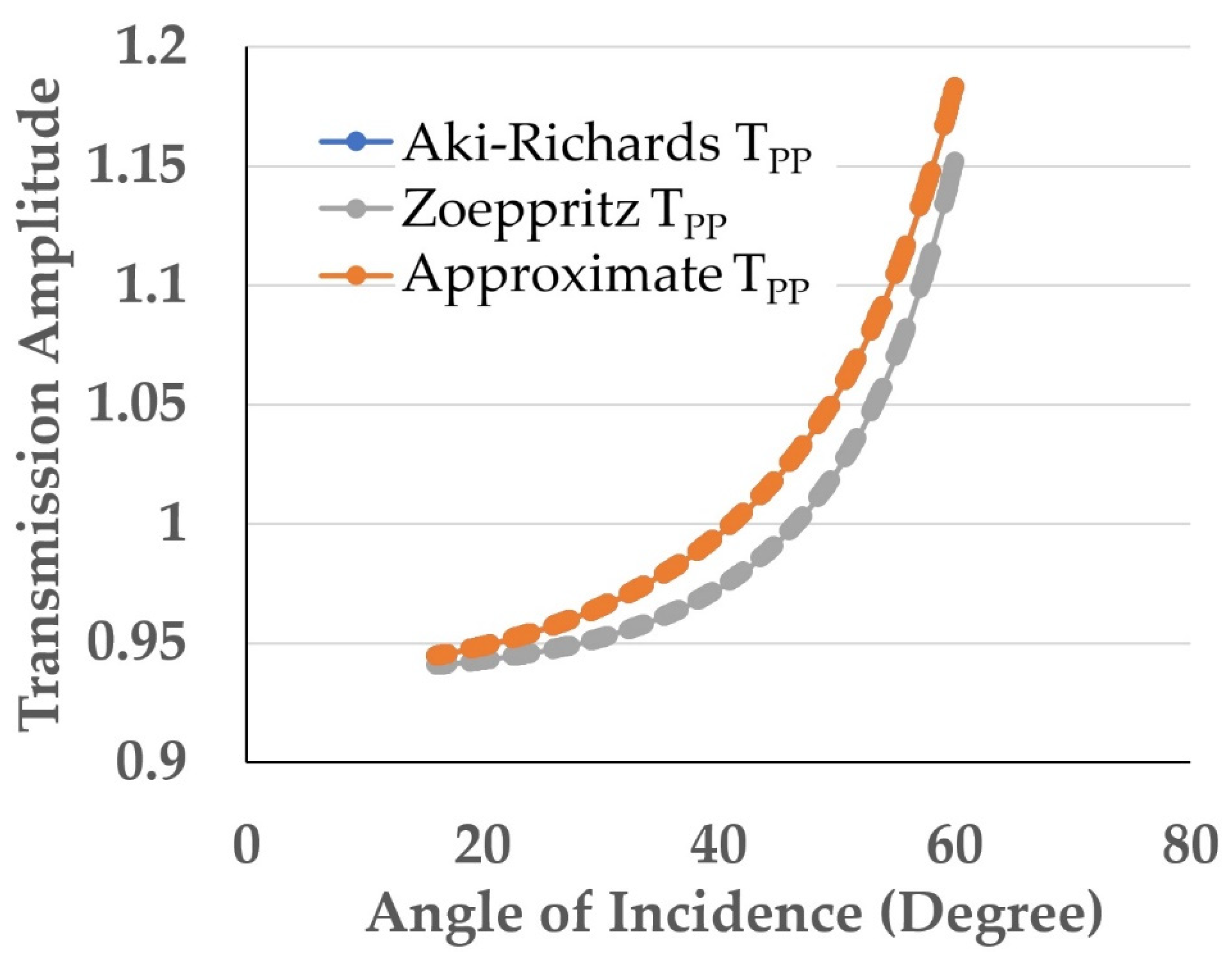
4.1. CTP Gather 26–50 m (CTP 38)
4.2. CTP Gather 51–75 m (CTP 63)
4.3. CTP Gather 76–100 m (CTP 88)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| P-Wave average velocity | |
| S-Wave average velocity | |
| S-Wave velocity contrast | |
| P-Wave velocity contrast | |
| Density contrast | |
| Average density | |
| Average incidence angle | |
| RPP | PP-reflection coefficient |
| RPS | PS-reflection coefficient |
| TPS | PS-transmission coefficient |
| TPP | PP-transmission coefficient |
| CRG | Common receiver gather |
| VSP | Vertical seismic profiling |
| TAVO | Transmission AVO |
Appendix A. Mathematica and Phyton Codes to Obtain the Common Transmission Points
- In [294]: = sxmin = 0.; (*min. offset of source*)
- ns = 61; (*no. sources*)
- dsx = 50.; (*increment of offset of source*)
- rzmin = 1000.; (*min. depth of receivers*)
- n = 101; (*no. receivers*)
- drz = 10.; (*increment of depth of receivers*)
- h = 800.; (*layer thickness*)
- a1 = 3170.; (*P-wave velocity in layer 1*)
- a2 = 3734.; (*P-wave velocity in layer 2*)
- In [303]: = theta =
- 0.0122695*. x - 6.73194 × 10^(-7) * x^2 (*x-theta relation - theta in degrees*)
- Out [303] = 0.0122695x - 6.73194 × 10^(-7) x^2
- In [305]: = txr = Pi/180.* theta (*theta in radians*)
- Out [305] = 0.0174533 (0.0122695 x - 6.73194 × 10^-7 x^2)
- In [307]: = xtpx = (z – h) * ((a2)/a1) * Sin[txr])/ Sqrt [1 – ((a2/a1) * Sin[txr])^2]
- Out [307] =
- 1.17792(-800.+. z) Sin[0.0174533 (0.0122695 x - 6.73194 × 10^−7 x^2)]/
- Sqrt(1 - 1.38749 Sin[0.0174533(0.0122695 x - 6.73194 × 10^−7 x^2)]^2)
- In [312]: = xzxtp = Flatten[Table[{(j − 1) * dsx + sxmin, (i − 1) * drz + rzmin,
- xtpx/. {x -> (j − 1) * dsx + sxmin, z → (i − 1) * drz + rzmin}}, {j, 61}, {i, 101}],
- 1](*. All possible transmission points*)
- Out [312] =
- {0., 1000., 0.}, {0., 1010., 0.}, {0., 1020., 0.}, {0., 1030., 0.},
- {0., 1040., 0.}, {0., 1050., 0.}, {0., 1060., 0.}, {0., 1070., 0.},
- {0., 1080., 0.}, {0., 1090., 0.}, {0., 1100., 0.}, {0., 1110., 0.},
- ⋯6138⋯, {3000., 1900., 829.864}, {3000., 1910., 837.409},
- {3000., 1920., 844.953}, {3000., 1930., 852.497}, {3000., 1940., 860.041},
- {3000., 1950., 867.586}, {3000., 1960., 875.13}, {3000., 1970., 882.674},
- {3000., 1980., 890.218}, {3000., 1990., 897.762}, {3000., 2000., 905.307}
- large output show less show more show all set size limit...
- In [313]: = Export[“xzxtp.xlsx”, xzxtp]
- Out [313] = xzxtp.xlsx
- import pandas as pd
- #import itertools
- df = pd.read_excel(‘xzxtp.xlsx’)
- X2_sorted = df.sort_values([“X2”, “Z”], ascending = True)
- df1 = X2_sorted[(X2_sorted[‘X2’] >= 0) & (X2_sorted[‘X2’] <= 26)]
- df2 = X2_sorted[(X2_sorted[‘X2’] >= 26) & (X2_sorted[‘X2’] <= 50)] -*CTP 38*-
- df3 = X2_sorted[(X2_sorted[‘X2’] >= 51) & (X2_sorted[‘X2’] <= 75)] -*CTP 63*-
- df4 = X2_sorted[(X2_sorted[‘X2’] >= 76) & (X2_sorted[‘X2’] <= 100)] -*CTP 88*-
- df5 = X2_sorted[(X2_sorted[‘X2’] >= 101) & (X2_sorted[‘X2’] <= 125)]
- df6 = X2_sorted[(X2_sorted[‘X2’] >= 126) & (X2_sorted[‘X2’] <= 150)]
- df7 = X2_sorted[(X2_sorted[‘X2’] >= 151) & (X2_sorted[‘X2’] <= 175)]
- df8 = X2_sorted[(X2_sorted[‘X2’] >= 176) & (X2_sorted[‘X2’] <= 200)]
- df9 = X2_sorted[(X2_sorted[‘X2’] >= 200) & (X2_sorted[‘X2’] <= 225)]
- df10 = X2_sorted[(X2_sorted[‘X2’] >= 226) & (X2_sorted[‘X2’] <= 250)]
- df11 = X2_sorted[(X2_sorted[‘X2’] >= 251) & (X2_sorted[‘X2’] <= 275)]
- df12 = X2_sorted[(X2_sorted[‘X2’] >= 276) & (X2_sorted[‘X2’] <= 300)]
- df13 = X2_sorted[(X2_sorted[‘X2’] >= 301) & (X2_sorted[‘X2’] <= 325)]
- df14 = X2_sorted[(X2_sorted[‘X2’] >= 326) & (X2_sorted[‘X2’] <= 350)]
- df15 = X2_sorted[(X2_sorted[‘X2’] >= 351) & (X2_sorted[‘X2’] <= 375)]
- df16 = X2_sorted[(X2_sorted[‘X2’] >= 376) & (X2_sorted[‘X2’] <= 400)]
- df17 = X2_sorted[(X2_sorted[‘X2’] >= 401) & (X2_sorted[‘X2’] <= 425)]
- df18 = X2_sorted[(X2_sorted[‘X2’] >= 426) & (X2_sorted[‘X2’] <= 450)]
- df19 = X2_sorted[(X2_sorted[‘X2’] >= 451) & (X2_sorted[‘X2’] <= 475)]
- df20 = X2_sorted[(X2_sorted[‘X2’] >= 476) & (X2_sorted[‘X2’] <= 500)]
- df21 = X2_sorted[(X2_sorted[‘X2’] >= 501) & (X2_sorted[‘X2’] <= 525)]
- df22 = X2_sorted[(X2_sorted[‘X2’] >= 526) & (X2_sorted[‘X2’] <= 550)]
- df23 = X2_sorted[(X2_sorted[‘X2’] >= 551) & (X2_sorted[‘X2’] <= 575)]
- df24 = X2_sorted[(X2_sorted[‘X2’] >= 576) & (X2_sorted[‘X2’] <= 600)]
- df25 = X2_sorted[(X2_sorted[‘X2’] >= 601) & (X2_sorted[‘X2’] <= 625)]
- df26 = X2_sorted[(X2_sorted[‘X2’] >= 626) & (X2_sorted[‘X2’] <= 650)]
- df27 = X2_sorted[(X2_sorted[‘X2’] >= 651) & (X2_sorted[‘X2’] <= 675)]
- df28 = X2_sorted[(X2_sorted[‘X2’] >= 676) & (X2_sorted[‘X2’] <= 700)]
- df29 = X2_sorted[(X2_sorted[‘X2’] >= 701) & (X2_sorted[‘X2’] <= 725)]
- df30 = X2_sorted[(X2_sorted[‘X2’] >= 726) & (X2_sorted[‘X2’] <= 750)]
- df31 = X2_sorted[(X2_sorted[‘X2’] >= 751) & (X2_sorted[‘X2’] <= 775)]
- df32 = X2_sorted[(X2_sorted[‘X2’] >= 776) & (X2_sorted[‘X2’] <= 800)]
- df33 = X2_sorted[(X2_sorted[‘X2’] >= 801) & (X2_sorted[‘X2’] <= 825)]
- df34 = X2_sorted[(X2_sorted[‘X2’] >= 826) & (X2_sorted[‘X2’] <= 850)]
- df35 = X2_sorted[(X2_sorted[‘X2’] >= 851) & (X2_sorted[‘X2’] <= 875)]
- df36 = X2_sorted[(X2_sorted[‘X2’] >= 876) & (X2_sorted[‘X2’] <= 900)]
- df37 = pd.concat([d.reset_index(drop = True) for d in [df1, df2,df3,df4,df5,df6,df7,df8,df9,df10,df11,df12,df13,df14,df15,df16,df17,df18,df19,df20,df21,df22,df23,df24,df25,df26,df27,df28,df29,df30,df31,df32,df33,df34,df35,df36]], axis = 1)
- df37.to_excel(‘xtpGrouping.xlsx’,index = False)
References
- Green, G. On the Laws of the Reflexion and Refraction of Light at the Common Surface of Two Noncrystallized Media; GeoScienceWorld: McLean, VA, USA, 2007. [Google Scholar]
- Knott, C.G., III. Reflexion and Refraction of Elastic Waves, with Seismological Applications. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1899, 48, 64–97. [Google Scholar] [CrossRef] [Green Version]
- Foster, D.J.; Keys, R.G.; Lane, F.D. Interpretation of AVO Anomalies. Geophysics 2010, 75, 75A3–75A13. [Google Scholar] [CrossRef]
- Gregory, A.R. Fluid Saturation Effects on Dynamic Elastic Properties of Sedimentary Rocks. Geophysics 1976, 41, 895–921. [Google Scholar] [CrossRef]
- Domenico, S.N. Elastic Properties of Unconsolidated Porous Sand Reservoirs. Geophysics 1977, 42, 1339–1368. [Google Scholar] [CrossRef]
- Ostrander, W.J.T. Plane-Wave Reflection Coefficients for Gas Sands at Nonnormal Angles of Incidence. Geophysics 1984, 49, 1637–1648. [Google Scholar] [CrossRef]
- Goodway, B.; Perez, M.; Varsek, J.; Abaco, C. Seismic Petrophysics and Isotropic-Anisotropic AVO Methods for Unconventional Gas Exploration. Lead Edge 2010, 29, 1500–1508. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Ma, J.; Li, L.; Wang, Y.; Tan, M.; Zhang, Y.; Cui, S.; Qu, Z. Effective Pressure Prediction from 4D Seismic AVO Data during CO2-EOR and Storage. Int. J. Greenh. Gas Control 2022, 113, 103525. [Google Scholar] [CrossRef]
- Zong, Z.; Yin, X.; Wu, G. Geofluid Discrimination Incorporating Poroelasticity and Seismic Reflection Inversion. Surv. Geophys. 2015, 36, 659–681. [Google Scholar] [CrossRef]
- Caldwell, J. Marine Multicomponent Seismology. Lead Edge 1999, 18, 1274–1282. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Thomsen, L. Converted-Wave Reflection Seismology over Inhomogeneous, Anisotropic Media. Geophysics 1999, 64, 678–690. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Innanen, K. A Review of Converted Wave AVO Analysis. CREWES Res. Rep. 2014, 26, 1–13. [Google Scholar]
- JafarGandomi, A.; Bukola, O.; Refaat, R.; Hoeber, H. Specular Imaging of Converted Wave Data and Its AVO Impact. In Proceedings of the 81st EAGE Conference and Exhibition 2019, London, UK, 3–6 June 2019; European Association of Geoscientists & Engineers: Bunnik, The Netherlands, 2019; Volume 2019, pp. 1–5. [Google Scholar]
- Innanen, K.A. Anelastic P-Wave, S-Wave and Converted-Wave AVO Approximations. In Proceedings of the 74th EAGE Conference and Exhibition Incorporating EUROPEC 2012, Copenhagen, Denmark, 4–7 June 2012; European Association of Geoscientists & Engineers: Bunnik, The Netherlands, 2012; p. cp-293-00569. [Google Scholar]
- Gal’perin, E.I.; White, J.E. Vertical Seismic Profiling; Society of Exploration Geophysicists: Houston, TX, USA, 2000. [Google Scholar]
- Donati, M.; Martin, N.W. A Comparison of Approximations for the Converted-Wave Reflection. Techn. Rep. CREWES Res. Rep. 1998, 10, 16. [Google Scholar]
- Popoola, A.K.; Al-Shuhail, A.A.; Sanuade, O.A. Transmission Amplitude Variation with Offset (TAVO). J. Seism. Explor. 2019, 28, 413–424. [Google Scholar]
- Ursin, B.; Favretto-Cristini, N.; Cristini, P. Amplitude and Phase Changes for Reflected and Transmitted Waves from a Curved Interface in Anisotropic Media. Geophys. J. Int. 2021, 224, 719–737. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology; University Science Books: Herndon, VA, USA, 2002. [Google Scholar]
- Al-Shuhail, A.A.; Popoola, A.K. Transmission Amplitude Variation with Offset (TAVO). In Proceedings of the Second EAGE Workshop on Borehole Geophysics, St. Julian’s, Malta, 21–24 April 2013; European Association of Geoscientists & Engineers: Bunnik, The Netherlands, 2013; p. cp-343-00042. [Google Scholar]




| First Layer | Second Layer | |||||
|---|---|---|---|---|---|---|
| Model | (m/s) | (m/s) | (kg/m3) | (m/s) | (m/s) | (kg/m3) |
| Oil reservoir | 3170 | 1698 | 2360 | 3734 | 2279 | 2270 |
| Gas channel | 3048 | 1245 | 2400 | 2439 | 1630 | 2140 |
| Parameter | Value |
|---|---|
| Top of reservoir (H) | 800 m |
| The first shot location (x,z) | (0,0) |
| Shot spacing Δx | 50 m |
| Receiver depth | 1000–2000 m |
| Number of sources | 61 |
| Maximum offset | 3000 m |
| Receiver spacing Δz | 10 m |
| Fitting Parameter | Value |
|---|---|
| A | 0.937746672 |
| B | 0.081691773 |
| C | −0.356696 |
| D | −0.0446039 |
| Subsurface Parameter | True Values | Estimated Values | Absolute Error (%) |
|---|---|---|---|
| 0.163383546 | 0.163383546 | 0 | |
| −0.03887689 | −0.03887689 | 0 | |
| 0.292609351 | 0.290922794 | 0.58 | |
| 0.57618771 | 0.621136276 | 7.8 |
| Fitting Parameter | Value |
|---|---|
| A | 1.168071277 |
| B | −0.110802555 |
| C | −0.275596 |
| D | −0.0127772 |
| Subsurface Parameter | True Values | Estimated Values | Absolute Error (%) |
|---|---|---|---|
| −0.22160511 | −0.22160511 | 0 | |
| −0.114537445 | −0.114537445 | 0 | |
| 0.267783314 | 0.266117906 | 0.62 | |
| 0.523910025 | 0.522691241 | 0.23 |
| Fitting Parameter | Value |
|---|---|
| A | 0.937746672 |
| B | 0.081691773 |
| C | −0.353375 |
| D | −0.0561697 |
| Subsurface Parameter | True Values | Estimated Values | Absolute Error (%) |
|---|---|---|---|
| 0.163383546 | 0.163383546 | 0 | |
| −0.03887689 | −0.03887689 | 0 | |
| 0.292609351 | 0.27408299 | 6.33 | |
| 0.57618771 | 0.655691553 | 13.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Surachman, L.M.; Al-Shuhail, A. Common Transmission Point (CTP) Gathers: A New Domain for Amplitude Variation with Offset. Energies 2022, 15, 4825. https://doi.org/10.3390/en15134825
Surachman LM, Al-Shuhail A. Common Transmission Point (CTP) Gathers: A New Domain for Amplitude Variation with Offset. Energies. 2022; 15(13):4825. https://doi.org/10.3390/en15134825
Chicago/Turabian StyleSurachman, Lutfi Mulyadi, and Abdullatif Al-Shuhail. 2022. "Common Transmission Point (CTP) Gathers: A New Domain for Amplitude Variation with Offset" Energies 15, no. 13: 4825. https://doi.org/10.3390/en15134825
APA StyleSurachman, L. M., & Al-Shuhail, A. (2022). Common Transmission Point (CTP) Gathers: A New Domain for Amplitude Variation with Offset. Energies, 15(13), 4825. https://doi.org/10.3390/en15134825






