A Fuzzy-PSO-PID with UPFC-RFB Solution for an LFC of an Interlinked Hydro Power System

Abstract

An LFC plays a vital part in passing on quality electric energy to energy consumers. Furthermore, with cutting-edge designs to move to modern and pollution-free energy generation, it may be conceivable to have a major hydropower in the future. Hydro plants are not suitable for continuous load alteration due to the large response time of hydroturbines. Hence, this paper shows a novel control design for an LFC of a hydro-hydro interlinked system based on joint actions of fuzzy logic with PID effectively optimized through particle swarm optimization (PSO) resulting in a Fuzzy-PSO-PID. The outcome of Fuzzy-PSO-PID is evaluated for step load variation in one of the regions of hydropower, and the outcomes of Fuzzy-PSO-PID are compared with a recently published LFC with respect to integral time absolute error (ITAE) value, values of PID, and graphical outcomes to show the impact of the proposed LFC action. The numerical results show that the ITAE value (0.002725) obtained through the proposed design is minimum in comparison to error values achieved through other LFC actions, and the pickup values obtained on these error values are considered to achieve the desired LFC. However, there is still scope for LFC enhancement as responses of hydropower are sluggish with higher oscillations; hence the UPFC and RFB are integrated into the interlinked hydro-hydro system, and the application outcomes are evaluated again considering the non-linearity, standard load alteration, random load pattern, and in view of parametric alterations. It is seen that the ITAE value reduces to 0.002471 from 0.002725 when UPFC is connected to the tie-line, and it further reduces to 0.001103 when a UPFC-RFB combination is used with Fuzzy-PSO-PID for a hydro leading system. The positive impact of the UPFC-RFB for hydropower is also seen from the application results.

1. Introduction

The electrical time and demand network is currently developing, giving cost-effective power generation with superior electrical energy delivery to the demand system despite the diverse working constraints of the network. To make this network more reliable, secure, and economical, the electrical system operates in an interconnected model. This illustrates that tie-lines connect power generation zones. By extension, these control ranges have power interchange as characterized by the transmission network operator. As a result, every control zone can meet its own load demand to maintain the fixed power interchange via the AC tie-line. The mismatch between electrical energy generation and demand causes the framework frequency and the AC tie-line power to deviate from the predefined system value, affecting power delivery to various customers. The LFC strategy controls this change in frequency and tie-power. The adjustment of the indirect structure of these amounts is well-defined as the Area Control Error (ACE) in LFC [1,2]. The LFC controllers’ role is to connect electrical power generated with electrical energy consumption to maintain or specific ACE deviations to zero. A primary action during this part would be to set up an LFC described as a conventional control hypothesis [3,4,5]. In either circumstance, the gain of a standard LFC controller’s action is limited for a specific situation and incapable of supplying the desired control movement under arranged working circumstances. Subsequently, the investigators and researchers are working hard and exploring the various controller design and plans such as optimal control, control based on few states, variable structure control, decentralized control, etc. to ensure a productive LFC for the electrical generation system [6,7,8,9,10]. In [6], the authors have shown the design of a variable structure LFC for an interlinked hydrothermal with a variable structure LFC for a multi-area system in [7]. A Dual mode controller with the impact of non-linearity was well covered in [8]. In [9,10], the impact of merging wind turbines and their assessments for LFC using all states and few states for the LFC were shown. The artificial-intelligence-based LFC [11] designs, especially artificial neural networks and fuzzy logic, are increasing day by day to solve the LFC problem in a two-area or multi-area power system considering various types of power generation in view of the regulated or deregulated power system. From the above two techniques, the fuzzy logic technique is much more popular these days due to its better capability to deal with differing types of instabilities and system non-linearities and hence may prove to be beneficial concerning variable loading conditions of power systems [12,13,14,15,16]. The LFC technique based on hybrid evolutionary fuzzy PI is discussed in [12]. The effective Takagi–Sugeno base controller for LFC is demonstrated in [13] such that, the created fuzzy framework runs perfectly for non-linearity as well as parametric changes. The fuzzy methodology for interconnected an LFC is presented in [14]. The type-2 fuzzy-based research considering GRC non-linearity is demonstrated in [15]. In [16], a fuzzy gain scheduling control for an LFC using a genetic algorithm (GA) has already been presented. Some limitations in GA, such as convergence issues and trapping in local minima while finding optimal results of the problem, have been observed by researchers. The change in the optimization method, namely PSO, has significantly reduced the issues associated with the application of GA. PSO has fewer chances of becoming trapped in local minima for the same degree of execution, and it also takes very little calculation time [17]. Furthermore, the majority of control methodologies are based on thermal–thermal control models or hydrothermal LFC models. Hydroturbines have a much longer response time than thermal turbines; the LFC composition lacks an appropriate and guide control arrangement for hydropower systems. As a result, the LFC yield of the hydro-overseeing framework is slow and has persistent motions [18,19,20]. Furthermore, modern and developing society is approaching cleaner and renewable energy sources; hence hydropower may generate bulk electrical power or limited power, i.e., micro-hydro. As a result, the interconnected power framework may become more complex, with hydro-leading control regions included.

The cutting-edge and rapid advancement of power electronics industries has prompted the advancement of the Flexible Alternating Current Transmission System (FACTS) to provide a solution to various technical limitations of the power system. FACTS has the ability to regulate (i.e., active and reactive) power and hence can improve the output of the power system such as frequency and tie-line responses to a great extent. A redox flow battery (RFB) is additionally within the framework of FACTS and may well be a fast-acting useful capacity mechanism that can give the capacity in development to the dynamic essentialness of generator rotors. This can effectively dampen the electromechanical oscillations of the system by sharing the unexpected changes within the power demand [21,22]. At any point, there is a sudden rise within the control area (i.e, area-1). The power in an RFB is immediately discharged via the control conversion mechanism which consists of an inverter/rectifier. Basically, it adapts to the system through the quick delivery of loads. But it is not conceivable to put an RFB in each area or region of interlinked regions due to financial reasons, and subsequently unified power flow control (UPFC) may prove to be a viable solution. It is very cheap and can be presented in a course of action with a tie-line in position to progress the execution of the electrical system [23,24]. In this way, the simulated performance of an RFB and UPFC is used to improve the output of an LFC for hydro-leading system in a more cost-effective and quicker manner. Given the above discussion, the current research work is set to;

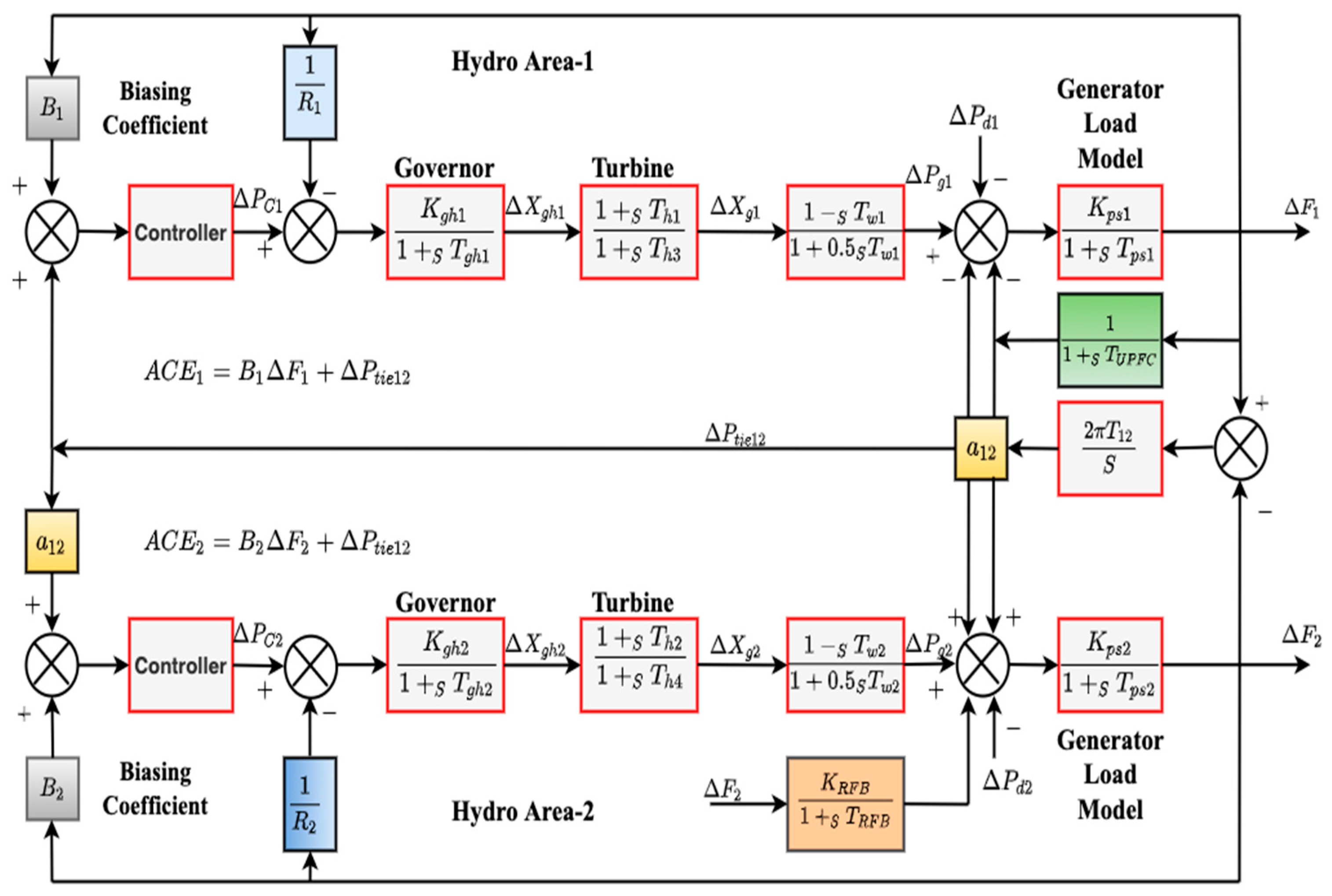
• Create a linear design of the hydro-leading system using an interconnected approach for LFC studies. The hydro framework is divided into hydro zones and connected via an AC tie-line.
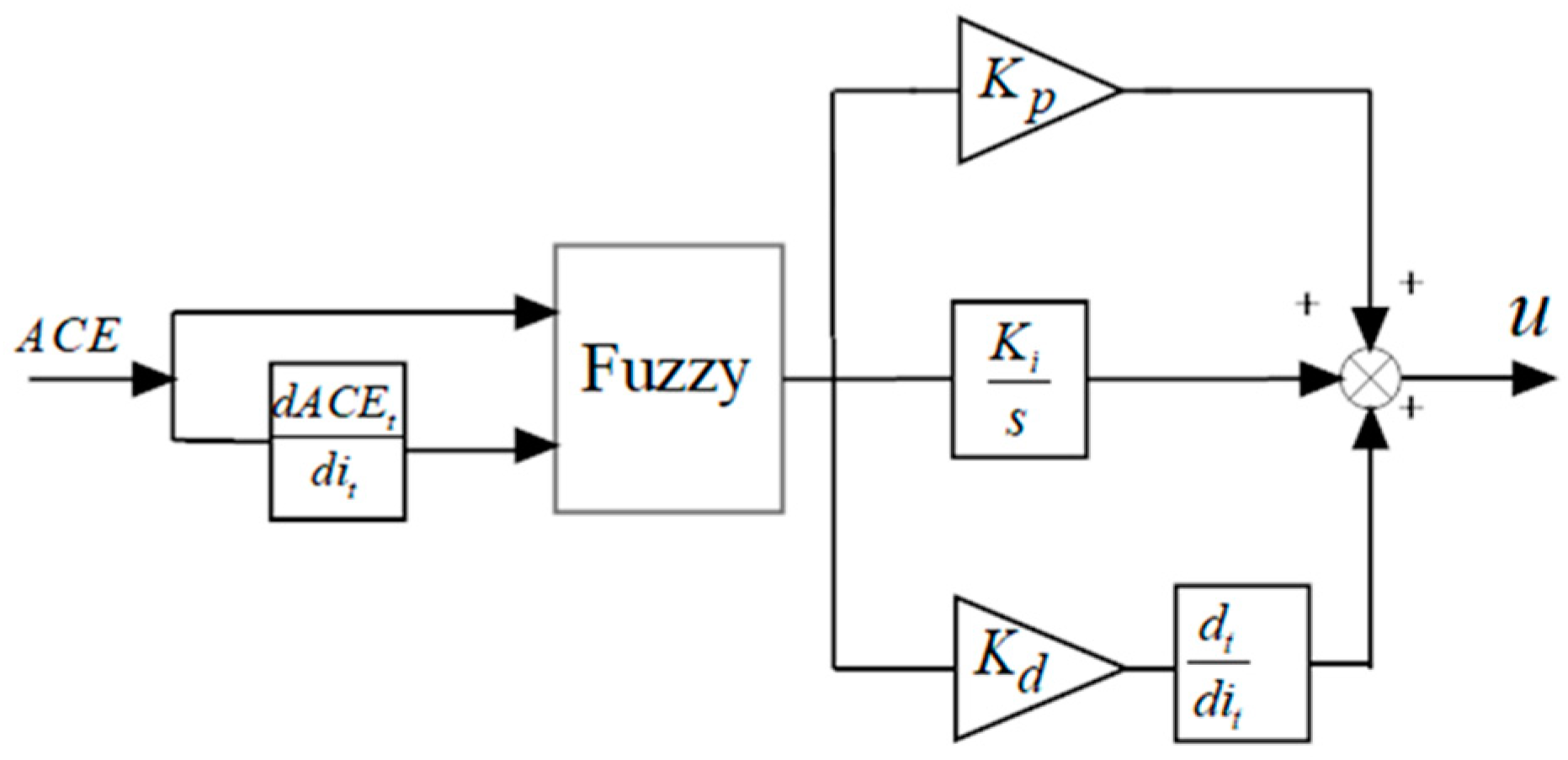
• Develop a fuzzy logic control with two inputs for a hydro-leading system and then use the fuzzy outputs as PID inputs.
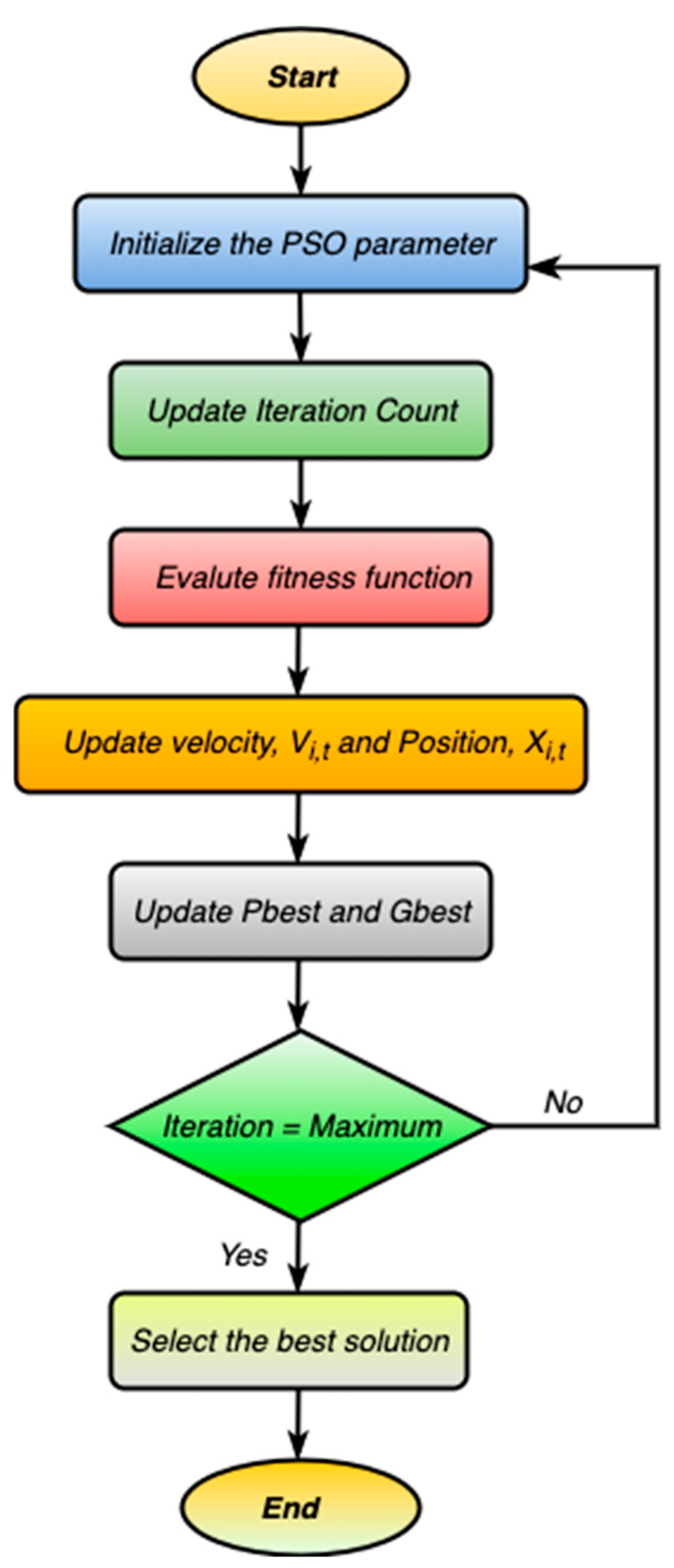
• Determine the PID gains using PSO by selecting the appropriate error definition, i.e., Integral Time Multiplied Absolute Error (ITAE). The performance of the PSO is evaluated by performing it for 100 iterations and using the outcome of the 100th iteration to obtain the final control action, which is Fuzzy-PSO-PID.
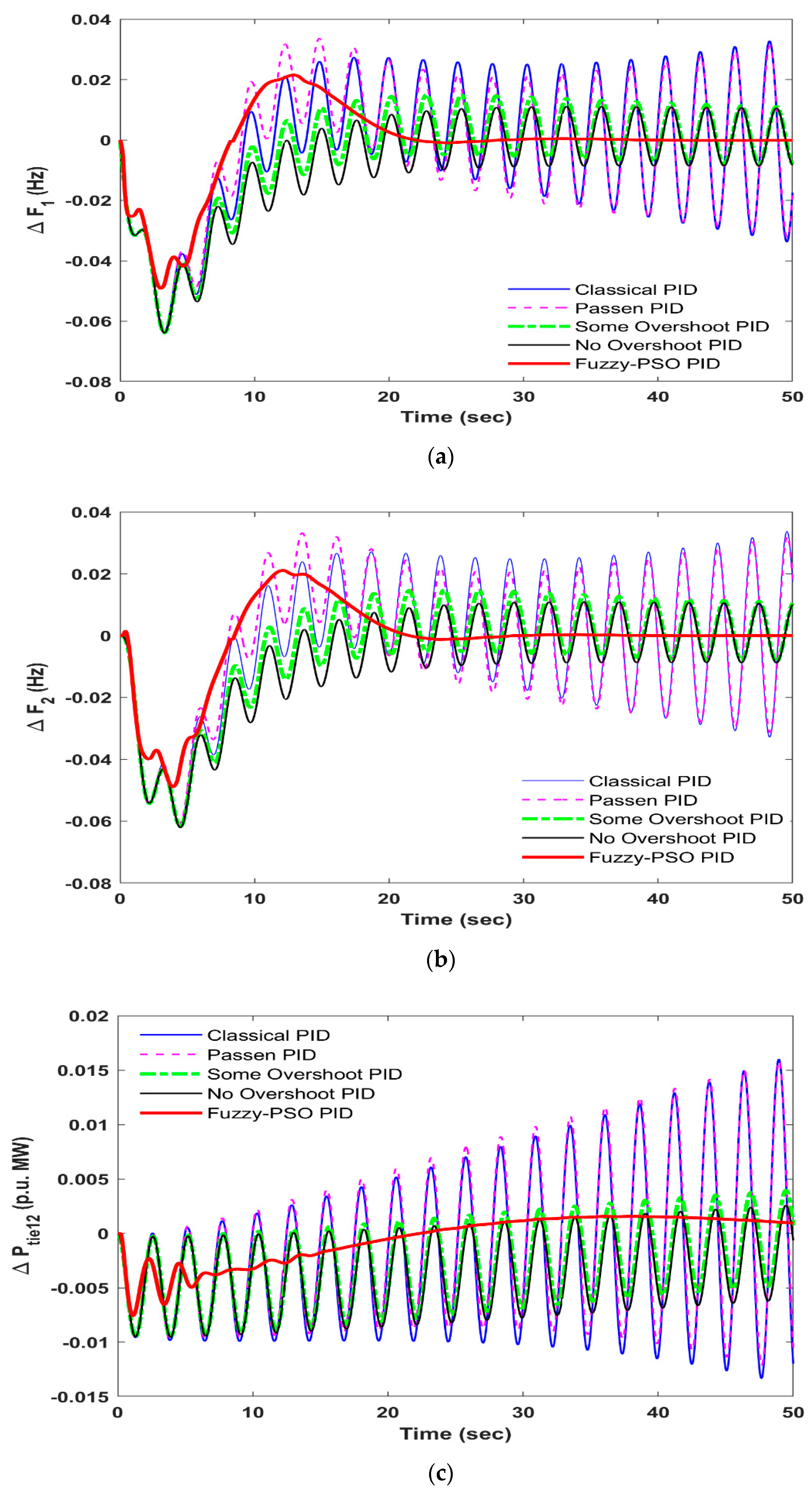
• Validate the Fuzzy-PSO-PID result for regular load variation from one of the control zones, and the result is compared with a recently published LFC to pick up the value of PID, ITAE, and through a graphical LFC.
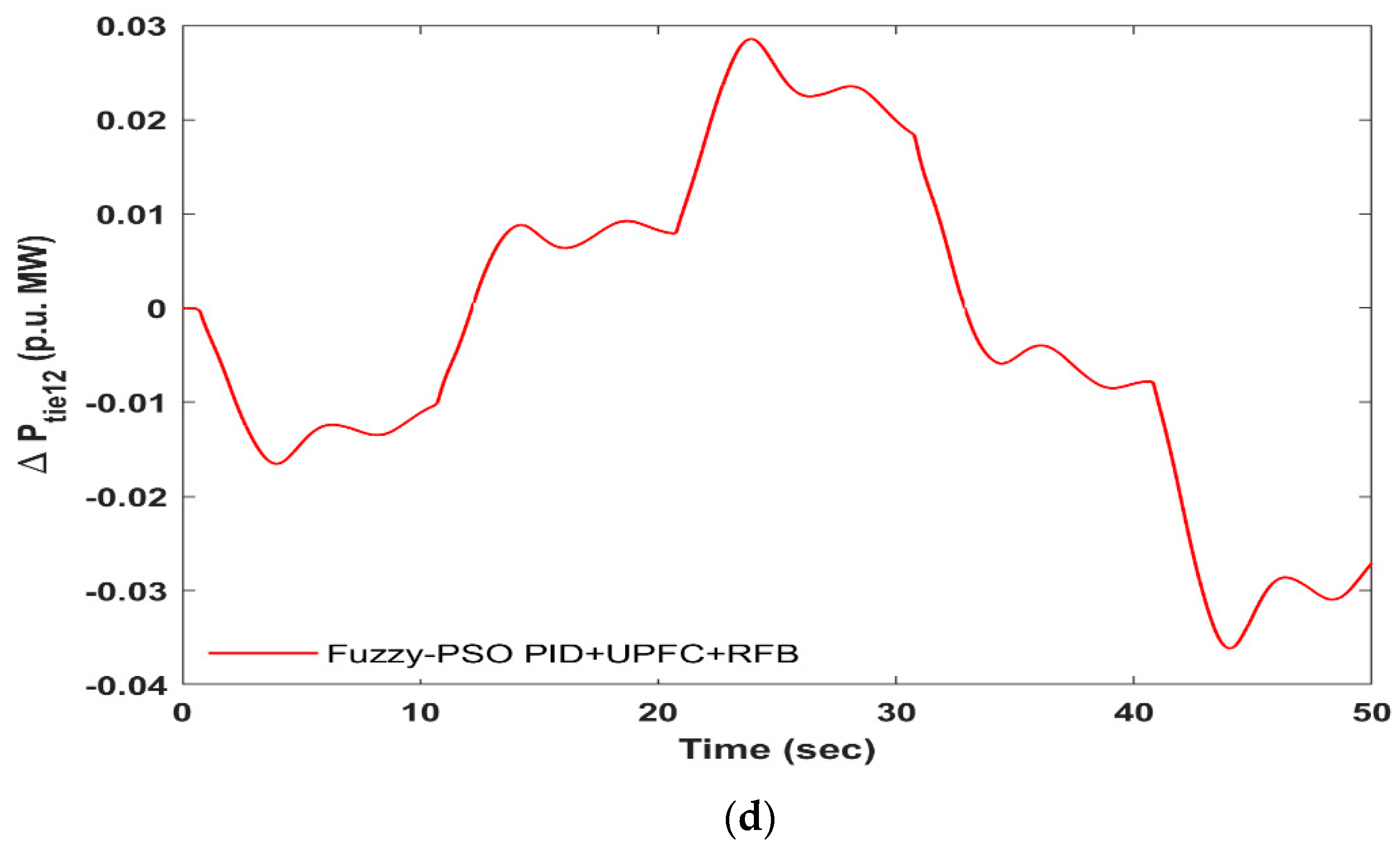
• The results of Fuzzy-PSO-PID are good with regard to earlier published LFC outcomes. However, it still needs enhancement; hence the UPFC and the RFB are added to the hydro model, and the output is observed again considering load alteration, random load pattern, and parametric alterations from the original values.
• At last, all results are concluded to show the benefits of Fuzzy-PSO-PID, UPFC and RFB integration with regard to the present research work.

2. Model Details of the Hydro System

This is an interlinked system that uses hydroturbines in each area or region linked through an AC tie-line. Figure 1 shows the model of a hydro-hydro system. In Appendix A, all necessary system values are listed. For workspace programmers using SIMULINK modeling, MATLAB software edition (R2022a) was utilized to study the output of an LFC for the considered system. Two hydro plants with mechanical governors are utilized to increase or decrease the power generation as per the requirement of each area. To make frequency domain calculations easier, each element is represented using transfer function blocks. The next sections discuss the transfer functions of each region for a two-area hydro-hydro system. Figure 2 shows the transfer function model used for simulation and investigations for an LFC.

3. Modelling of Fuzzy-PSO-PID

The design and implementation of advanced control activity is a fuzzy sequence including PID. In addition, the pickup of PID is determined with results of an optimization technique identified as Particle Swarm Optimization (PSO) resulting in a Fuzzy-PSO-PID. The performance of the Fuzzy-PSO-PID depends on the value of K_P, K_I, and K_D. Hence, in arranging an absolute LFC activity, K_P, K_I, and K_D pickup must be taken suitably to attain extra beneficial active performance for the framework of the closed-loop. In this investigation, a new tuning methodology called PSO is used to actuate the foremost promising result of screen pickups to remove better dynamic accomplishment of the Fuzzy-PSO-PID screen LFC. The numerical description of PID is:

$$K\left(s\right)=K_P+\frac{K_I}{s}+K_D$$

(1)

where K_P = proportional gain, K_I = integral gain, and K_D = derivative gain.

K_P, K_I, and K_D are the pickups of the control activity, and the LFC output exceedingly depends upon this amount. These amounts are chosen for the PSO optimization handle detailed in this article. On the other hand, the FLC is composed of four leading components: the fuzzification, the fuzzy acceptance model, the run showing up the range, and the defuzzification. The Fuzzy-PSO-PID has two input signals, an area control error (ACE) and a derivative of (ACE), and one output signal. The developed structure of the Fuzzy-PSO-PID is given in Figure 3.

3.1. Fuzzification

Fuzzification is the component by which a crisp value of the results changes over transform fuzzy value by utilizing points of interest within the information base. Different sorts of bends are present in various broadly utilized regions within the fuzzification strategy within the history as Gaussian, triangle, and trapezoidal membership functions (MFs). In any case, in the present investigation, triangle MFs are preferred due to effortlessness and balance. The Fuzzy-PSO-PID maintains two information signals namely, (1) area control error (ACE) and (2) derivative of (ACE), and one creation yield. Each information and output becomes five contributions (every one MF is triangular). The step middle way of MFs is likely applied, i.e., [–1 to 1].

3.2. Fuzzy Inference System

The input MFs, the fuzzy in the case of next etymological laws, and the output MF are formed of the fuzzy inference design (fis). The fis regulation is completed in four stages. A fundamental level is now to fuzzify the appropriate data crisp factors that further are in here as ACE as well as a subsidiary of ACE. It defines the degree to which that necessary information can reach the specific basic fuzzy locations by MFs. The specific action is how the evaluation or inference is displayed. The fuzzified information data are achieved on the heralds of the fuzzy laws. The fuzzy law includes the formation of a rule base to achieve the desired output. The rules are formed on an IF-THEN condition to reach a decision on the basis of the level of inputs with expert knowledge. The decision is taken on the basis of the min–max concept in the inference engine, and finally, the output need to be converted back to real values before applying to the plant from crisp values. A fourth stage is the defuzzification of the accumulated individual fuzzy location, which is performed with the help of the center of gravity method.

3.3. Allocation of Region of Inputs

The feature of the control laws might be a little more challenging than MFs, based upon the responsibility and approaching the required action. The laws are included for them to be used in the composition of K_P, K_I, and K_D. Shifting inputs and outputs individually has 5 MFs and 25 rules to obtain a fuzzy output. If-then laws are used in the following way: If ACE is NB-1 and a dACE is NB-1, the output is NB-1.

Table 1. Rule structure for the Fuzzy-PSO PID.

	dACE	NB−1	NS−1	Z0	PS1	PB1
ACE
NB−1		NB−1	NB−1	NS−1	NS−1	Z0
NS−1		NB−1	NS−1	NS−1	Z0	PS1
Z0		NB−1	NS−1	Z0	PS1	PB1
PS1		NS−1	Z0	PS1	PS1	PB1
PB1		Z0	PS1	PS1	PB1	PB1

contains the entire rule framework.

3.4. Defuzzfying the Output Value

The crisp amount is defuzzified by the well-popular technique called the centroid.

3.5. Objective Function

The proper selection of the objective function within the technique of a modern heuristic optimization technique-based controller plays a significant role in achieving the required target with the minimum of effort. The error definitions available and well tested in the history of LFC are Integral of Absolute Error (IAE), Integral of Squared Error (ISE), Integral of Time Absolute Error (ITAE) and Integral of Time multiplied Squared Error (ITSE). The ITAE degree decreases the settling duration, which IAE and ISE-based tuning do not achieve. The ITAE type also reduces the maximum overshoot. ITSE-based control provides a sweeping control product for an instantaneous variation into state problem which is not useful in case the control determines the condition of seeing. It necessitates that ITAE may perform a major supportive accurate work in an LFC point by point. Concurrently, ITAE is used as an error definition in this work to optimize the measured value and calculate the pickups of Fuzzy-PSO-PID [19]. Expression for the ITAE objective work is depicted in Equation (2).

$$J=ITAE=\underset{0}{\overset{t_{sim}}{{\displaystyle \int }}}\left(\left|\Delta F_1\right|\right)+\left(\left|\Delta F_2\right|\right)+\left(\left|\Delta P_{tie12}\right|\right)·tdt$$

(2)

where ΔF₁ and ΔF₂ = the framework frequencies of region 1 and region 2, ΔP_tie12 = the incremental alteration in tie-line power regions 1 and 2, and t_sim = the simulation period.

The issue objectives continue these PID component boundaries. In this system, the organized problem is capable to be established such as catching subsequent optimization problems. Depending upon the performance record, the J optimization problem can be signified as: Reduction J restrained to:

$$K_P^{min}\le K_P\le K_P^{max }$$

(3)

$$K_I^{min}\le K_I\le K_I^{max }$$

(4)

$$K_D^{min}\le K_D\le K_D^{max }$$

(5)

where $K_P^{min} \mathrm{and} K_P^{max}$ = proportional gain with minimum and maximum limit, $K_I^{min} \mathrm{and} K_I^{max}$ = integral gain with minimum and maximum limit, and $K_D^{min}\mathrm{and} K_D^{max}$ = derivative gain with minimum and maximum limit.

3.6. PSO Algorithm

This advanced approach highlights various goals of interest; it is fundamental, quick, and can be coded in a few lines. Other than that, this research has several advantages over human evolution and genetic algorithms. Each particle recalls its best course of action (adjacent best) as well as the bunch’s best organization (around the world best). Some other benefit of PSO is that the beginning population of a PSO is kept up; there is no need for utilizing supervisors toward the state, and it is a time and memory-storage-consuming designation. In extension, PSO is based upon “helpful cooperation” connecting particles, differentiating from the genetic algorithms, which are based on ‘‘the survival of the fittest”.

PSO begins with a population of self-assertive organizations referred to as “particles” in a D-dimensional interior. The ith particle is described by Xi = (xi₁, xi₂, …, xi_D). Various particles maintain a record of their hyperspace organization, which also is related to the most appropriate organization they have obtained so distantly. The standard of eligibility for particles (pbest) is also saved as Pi = (pi₁, pi₂,…,pi_D). PSO keeps a record of the common best standard (gbest), and its region, received in this way distant by any particle inside the populace. PSO covers for every step by varying the speed with which every particle approaches its pbest and gbest. The speed of particles is talked to as Vi = (vi₁, vi₂, …, vi_D). Ramping up is weighted by such a variable term, and confined subjective numbers are generated for increasing speed forward into pbest and gbest. The balanced speed and place of every particle can really be calculated using the actual speed as well as separations from pbest_j,g to gbest_g as shown in the following conditions [17]:

$$v_{j,g}^{\left(t+1\right)}=w\times v_{j,g}^{(t)}+c_1\times r_1()\times (pbes{t}_{j,g}-x_{j,g}^{(t)})+c_2\times r_2()\times (gbes{t}_g-x_{j,g}^{(t)})$$

(6)

$$x_{j,g}^{\left(t+1\right)}=X_{j,g }^{\left(t\right)}+v_{j,g}^{\left(t+1\right)}$$

(7)

As for j = 1, 2, …, n and g = 1, 2, …, m. Where n = value of particles inside the swarm, m = number of elements for the vectors v_j and x_j, t = value of times (generations), $v_{j,g}^{(t)}$ = the gth element of the velocity of particle j at iteration t, $v_g^{\min }\le v_{j,g}^{(t)}\le v_g^{\max }$, w = inertia weight calculate, c₁; c₂ = cognitive and communicative speeding up factors independently, r₁; r₂ = irregular values reliably passed on inside the run (0, 1), $x_{j,g}^{(t)}$ = the gth component of the position of particle j at cycle t, pbest_j = pbest of particle j, and gbest = gbest of the particle.

The execution steps of PSO are given in Figure 4.

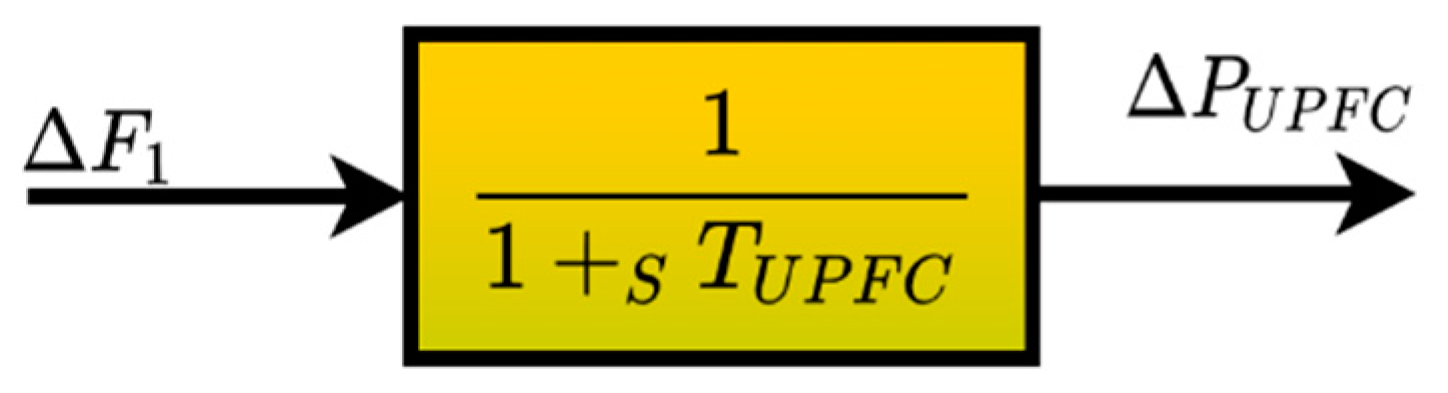
3.7. UPFC Modeling

The settling time of the LFC system responses for hydropower is longer than 20 s. This is because hydroturbines have a faster response time, and as a result, UPFC is set up in series with the tie-line. Figure 2 depicts a point-by-point design of UPFC interconnected between two interconnected hydro regions, with a schematic model of UPFC in Figure 5 and its corresponding linear transfer function block in Figure 6.

In [21], the numerical calculations of UPFC are developed, and the combined power (i.e., complex power) at the receiving end of the line is calculated as:

$$P_{real}-j{Q}_{reactive}=\overline{V_r^{*}}{I}_{line}=\overline{V_r^{*}}\left\{\left(\overline{V_s}+{\overline{V}}_{se}-{\overline{V}}_r\right)/j(X)\right\}$$

(8)

and,

$${\overline{V}}_{se}=\left|V_{se}\right|\angle ({\delta }_s-{\varphi }_{se})$$

(9)

In the equation, the Vse implies the voltage magnitude in series, and ${\varphi }_{se}$ is the series phase angle. By assembling Equation (8), the real value can be written as:

$$\begin{gathered} P_{real}=\frac{\left|V_s\right|\left|V_r\right|}{X}\sin \delta +\frac{\left|V_s\right|\left|V_{se}\right|}{X}\sin (\delta -{\varphi }_{se}) \\ =P_0(\delta )+P_{se}(\delta , {\varphi }_{se}) \end{gathered}$$

(10)

In the above equation, in case V_se = 0, it means that real power is uncompensated, and the UPFC series voltage can regulate between 0 and V_se to its maximum value. Finally, the phase angle can be varied from 0° to 360°. In an LFC, the UPFC operation can be written in the form of single order gain and time constant with frequency deviation of area-1 as input and altered power from the UPFC as [21];

$$\Delta P_{UPFC}(s)=\left\{\frac{1}{1+s{T}_{UPFC}}\right\}\Delta F_1(s)$$

(11)

T_UPFC = UPFC time constant.

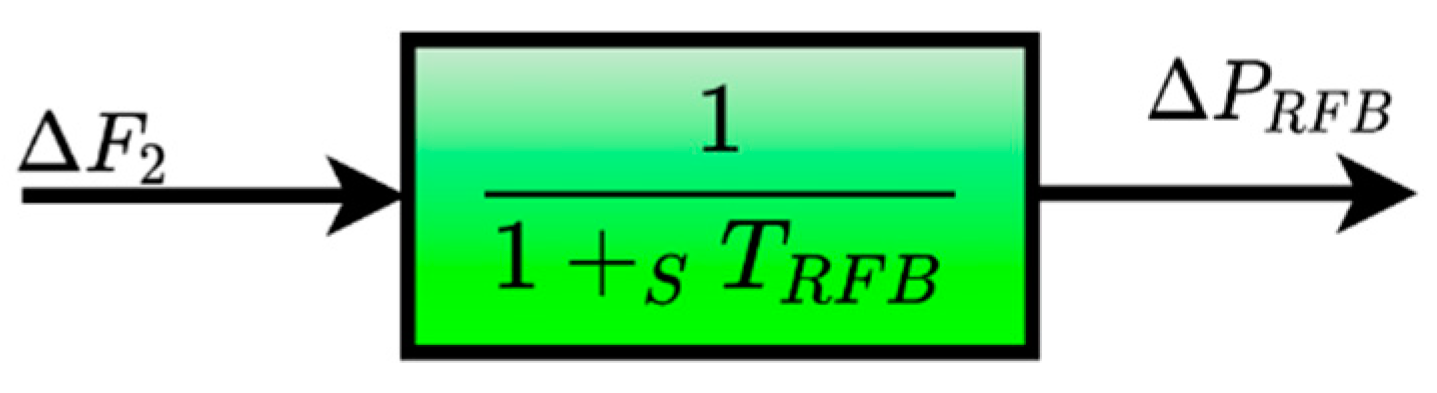
3.8. RFB Modeling

The RFB is a rechargeable battery whose life is not affected if it is charged more than once or released frequently, and it has a quick response time for unexpected load variations. When it comes to load leveling, the RFB is more valuable for the performance of the LFC, and it also helps to maintain power quality. The RFB operation time is fast enough to be considered zero secs through LFC research. The model of the RFB for an LFC is as taken after [22] and given by Figure 7:

$$\Delta P_{RFB}(s)=\left\{\frac{K_{RBF}}{1+s{T}_{RFB}}\right\}\Delta F_2(s)$$

(12)

4. Simulation of Fuzzy-PSO-PID and Its Analysis

The present work is set to study and investigate the two-area interlinked power system with hydroturbines in each area or region and interlinked via an AC tie-line. The idea is to analyze the performance for such a type of power system to illustrate and propose a convincing arrangement of Fuzzy-PSO-PID to determine the execution of control for an LFC under different system working conditions. Researchers are avoiding the hydro-leading system model as the time taken by hydroturbines to reply for load alteration is significantly higher than other types of turbines and hence affect the frequency and power deviations with higher overshoot, more settling time, and a larger steady state error.

The Fuzzy-PSO-PID controller is presented in each area or region, and the obtained output (u) is fed to each area or region so that power can be up or down per its requirement and hence achieve the required LFC. Furthermore, GRC non-linearity is also considered in each area to see the impact of this non-linearity on LFC output as it it is seen in the past literature that LFC output is limited by considering the GRC non-linearity. At first, the fuzzy logic action is designed for the hydro system, and the ACE and the rate of change of ACE are taken as input to the fuzzy logic system. The two inputs of the fuzzy system are scaled with the help of the membership function to convert original values into crisp values. The rule base of the fuzzy logic system for two input and one control output, i.e., ‘u’ having a total of 25 rules, is given in Table 1. The output is defuzzified to get back the original value from the crisp value and fed as input to PID. The best pickup value of PID is obtained by running the PSO technique. The ITAE is selected to achieve the best pickup value for PID, and these values are selected by achieving the ITAE minimum value. The pickup values of PID are selected through the PSO concerning minimum and maximum constraints as set in the optimization technique. The PSO technique is executed for 100 iterations and the best solution achieved after 100 iterations concerning the minimum value of ITAE and corresponding pickup values of PID are mentioned in

Table 2. Numerical outcomes of the Fuzzy-PSO PID.

Methods	KP	KI	KD	ITAE
Classical PID [19]	−0.12	−0.091603	0.0393	41.1935015
Pessen PID [19]	−0.14	−0.050381	0.05502	46.5603916
Some overshoot PID [19]	−0.066	0.050381	0.05764	38.0953828
No overshoot PID [19]	−0.04	−0.030533	0.034933	31.388228
Fuzzy-PSO-PID	−1.0684	−0.0591	−0.1305	0.002725

and used to check LFC standards. The Fuzzy-PSO-PID result is evaluated for standard load deviation (0.01 p.u.) in area-1, and the application outcomes are compared with recent LFC studies [19].

From Table 2 results, it is observed that ITAE is reduced to the best value, i.e., 0.002725, which shows the financial aspects of the LFC strategy implementation. It is also observed that the value of ITAE is quite less in comparison to Classical PID (41.1935015), Pessen PID (46.5603916), Some overshoot PID (38.0953828), and No overshoot PID (31.388228). The graphical LFC outcomes are given in Figure 8a–c, and it is shown that frequency and tie-power deviations have a minimum value of the first peak and settle back to the original value very quickly after load alteration. The same outcome or near to Fuzzy-PSO-PID outcomes for an LFC are not achieved through other LFC techniques which are Classical PID, Pessen PID, Some overshoot PID, and No overshoot PID. It is also discovered that LFC outcomes are completely free of oscillations, which is not conceivable with the other LFC behavior for the hydro-leading system.

Still, there is a scope for further enhancement, particularly UPFC links with a tie-line in series connection and an RFB connected in region-2. Now the studies are extended to see the impact of these FACTS in an LFC for the hydro-hydro system. The pickup value of the Fuzzy-PSO-PID and the value of the ITAE are matched with the Fuzzy-PSO-PID with the UPFC and the Fuzzy-PSO-PID with the UPFC-RFB. These results are tabulated in

Table 3. Numerical outcomes of Fuzzy-PSO PID+UPFC+RFB.

Models	KP	KI	KD	ITAE
Fuzzy-PSO PID	−1.0684	−0.0591	−0.1305	0.002725
Fuzzy-PSO PID+UPFC	−1.0684	−0.0591	−0.1305	0.002471
Fuzzy-PSO PID+UPFC+RFB	−1.0684	−0.0591	−0.1305	0.001103

. It is seen that UPFC integration has resulted in a reduction of ITAE (i.e., 0.002471) and further reduction seen with joint efforts from UPFC-RFB (i.e., 0.001103). Figure 9a–c shows the LFC results when UPFC only as well as UPFC with an RFB is connected in the hydropower sytem at suitable location and the performance of the Fuzzy-PSO-PID is evaluated again for load change in region-1, and it is observed that combination of the Fuzzy-PSO-PID with the UPFC and an RFB outperforms other LFC results in view of reduced overshoot, better settling time, and oscillation free system results. LFC results are also matched by considering the overshoot, undershoot, and settling time for frequency deviations of each area and for tie-power deviations. Numerical results are listed in

Table 4. Comparison performance overshoot, undershoot, and settling time shown in Figure 8a–c.

	Overshoot (Hz)			Undershoot (Hz)			Settling Time (S)
	ΔF1	ΔF2	Ptie12	ΔF1	ΔF2	Ptie12	ΔF1	ΔF2	Ptie12
Fuzzy PSO	0.02136	0.02293	0.00343	−0.04975	−0.0498	−0.00992	33.10	34.48	49.99
Fuzzy-PSO-PID+UPFC	0.02345	0.02395	0.001803	−0.04748	−0.0457	−0.00754	32.42	33.90	49.55
Fuzzy-PSO-PID+UC+RFB	0.009904	0.009585	0.001562	−0.02248	−0.01495	−0.00450	30.91	25.99	49.24

, and it is seen that results obtained via the Fuzzy-PSO-PID with UPFC-RFB is best when compared with other investigated LFC results.

The random load pattern is applied to hydro power system for 50 s, and the LFC results are revealed in Figure 10a–d. It is realized that the Fuzzy-PSO-PID with UPFC and an RFB culminates in taking after the random load pattern continuously and reducing the frequency and tie-power deviations successfully to zero value continuously over the period of 50 s.

In addition, the affectability examination of the Fuzzy-PSO PID with UPFC and an RFB control surveyed by changing the original parameters (i.e., T₁₂ coefficient of tie-line synchronizing), and T_g (governor’s response time) over the extensive run from standard parameters, and the results are shown in Figure 11a–c. From the results of Figure 11a–c, it is clearly seen that the changing system parameters from standard parameters. whether positive or negative change from the original value, hardly affect the system output. and all LFC results are reaching back to nominal value after load alteration. Hence, it can be said that the Fuzzy-PSO-PID with UPFC and an RFB combination is robust and promising in reaching the LFC standards for a hydro-leading power system.

5. Conclusions

This research paper proposes a novel strategy of linking the fuzzy logic technique with PID, effectively evaluated through PSO resulting in an advanced and robust design known as the Fuzzy-PSO-PID for an LFC of the hydro-leading system. The proposed Fuzzy-PSO-PID arrangement is attempted for standard load variation in one of the regions of the hydro-leading system, and the positive outcomes are shown over other LFC actions. The following conclusions are drawn from the research work carried out:

• Fuzzy-PSO-PID is agreeably sufficient to meet the LFC guidelines of hydropower systems with regards to ITAE value, pickups of PID, and LFC responses in comparison to other LFC actions. Still, it needs change and enhancement to have superior LFC designs for such systems.
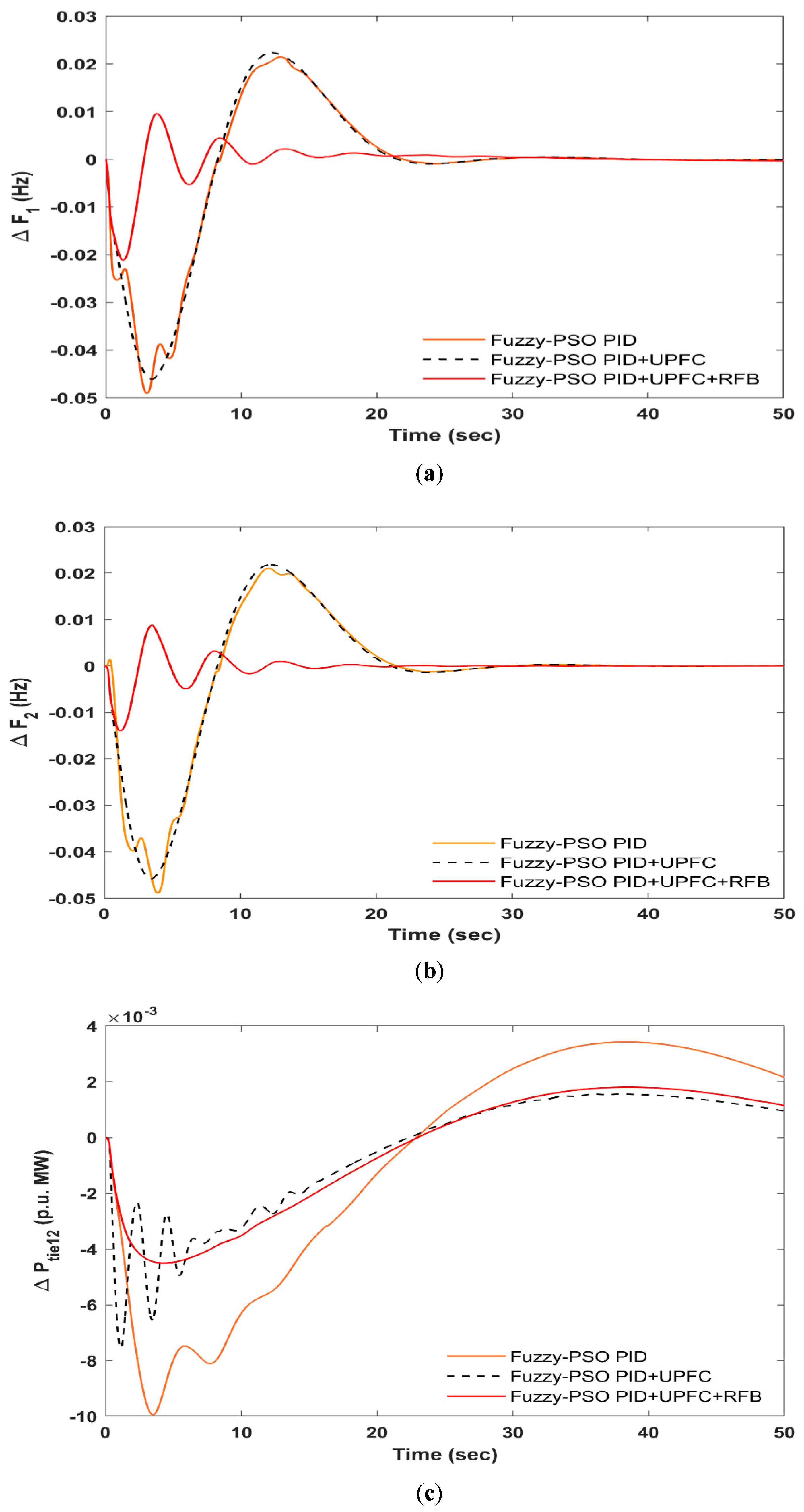
• The synchronization of UPFC with an AC tie-line as well as an RFB in region-2 of a hydro-leading system with the Fuzzy-PSO-PID has very well covered the frequency and tie-line power variations of the hydro system to an extraordinary degree also in the presence of non-linearity.
• The reduction in ITAE achieved via the Fuzzy-PSO-PID with UPFC and an RFB demonstrates the importance and regulates the reasonability of the current research work.
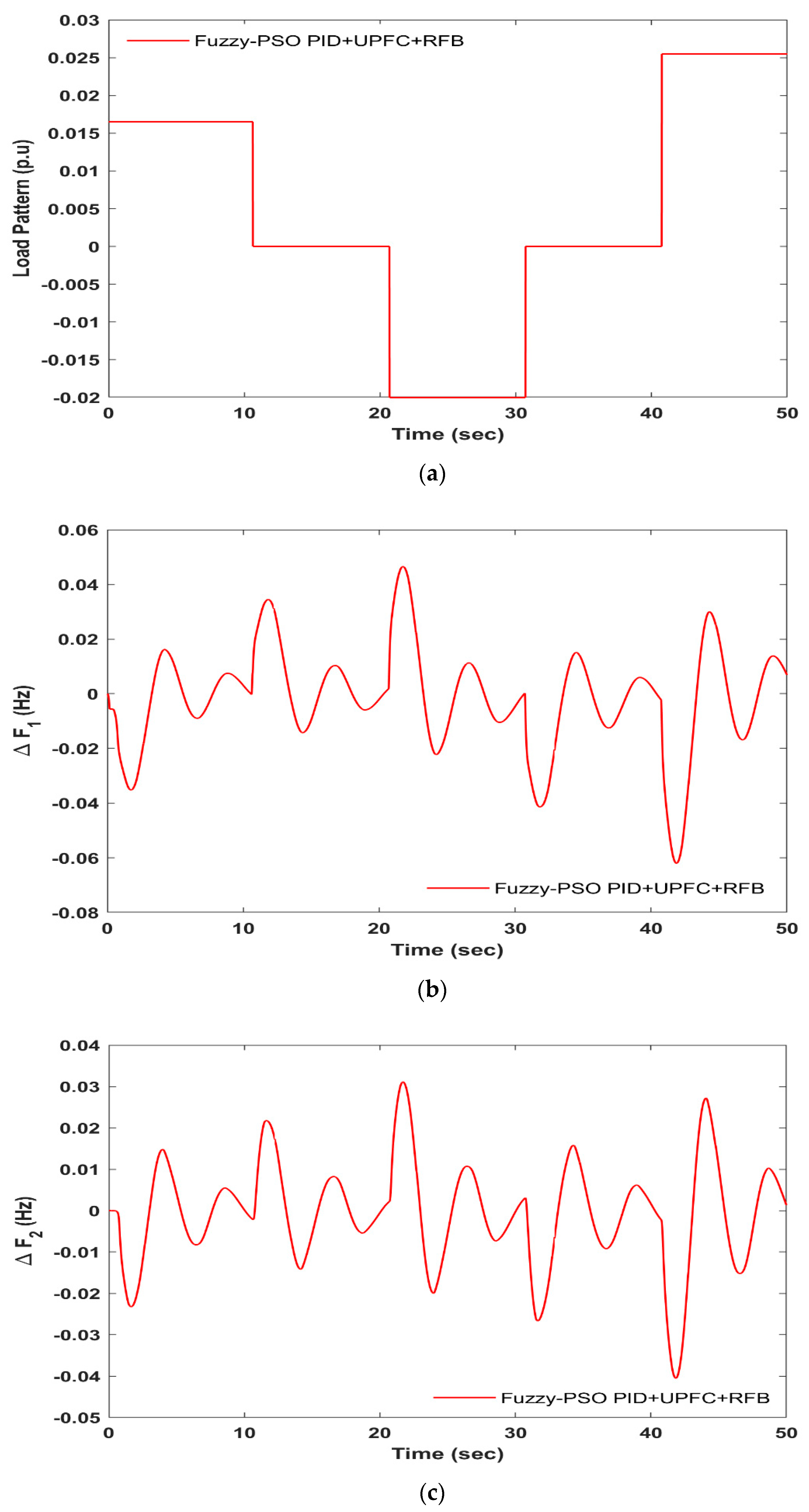
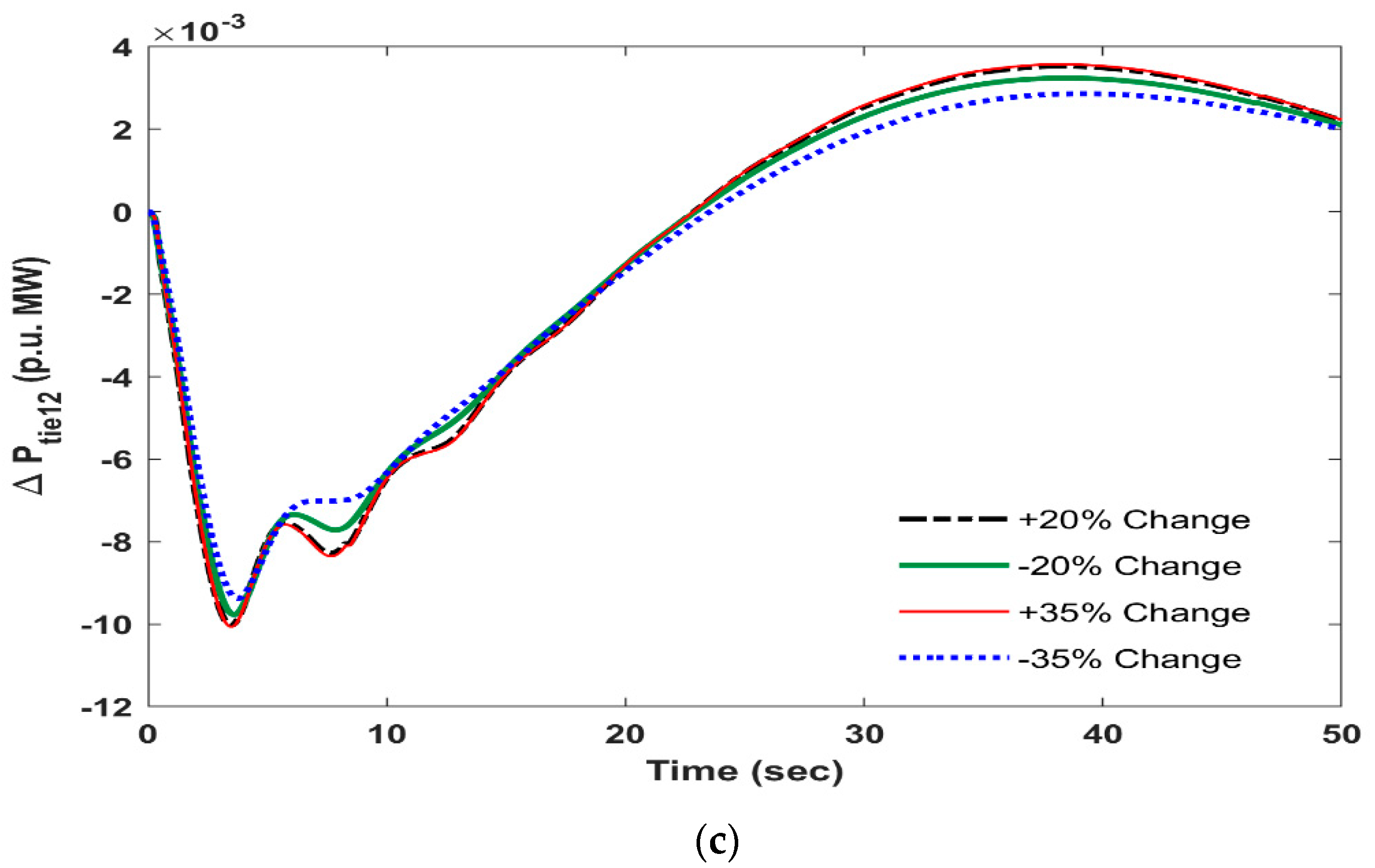
• The sensitivity analysis and random load pattern for the Fuzzy-PSO-PID with UPFC-RFB shows that the Fuzzy-PSO-PID design is reasonably good, clear, and capable of supporting the LFC output of a hydro-leading system.
• In the present research work, triangular MFs are used for FL. However, diverse MFs can affect the LFC output, and it needs to be explored further. The Type-2 FL can be a better solution for an LFC of a hydro-leading system.
• The research work can be extended to multi-areas with a hydro-leading system in a regulated and deregulated environment. Furthermore, the design of a proposed LFC can further improve by using other and advanced optimization techniques.
• The energy storage devices will play a major role in improving the LFC action further.
• The output of the Fuzzy-PSO-PID can be evaluated again using OPAL-RT and other real-time software in comparison to standard MATLAB software.