Modelling and Control Development of a Cascaded NPC-Based MVDC Converter for Harmonic Analysis Studies in Power Distribution Networks †
Abstract
:1. Introduction
1.1. Background
- Connectivity between AC networks irrespective of line voltage amplitude, phase angle, phase sequence, or operational frequency synchronisation requirements;
- Flexible controllability of active power flow between linked networks, allowing more renewables systems to be hosted;
- Control of reactive power at each AC terminal independently, allowing for dynamic voltage regulation. Additionally, the MVDC system may accomplish Static Synchronous Compensator (STATCOM) functions;
- The inclusion of advanced control systems can help isolate faults, improve the power quality, and enable ancillary services capabilities.
1.2. Literature Survey
1.3. Aim and Contributions
1.4. Paper Organization
2. Different Structures of MVDC Systems
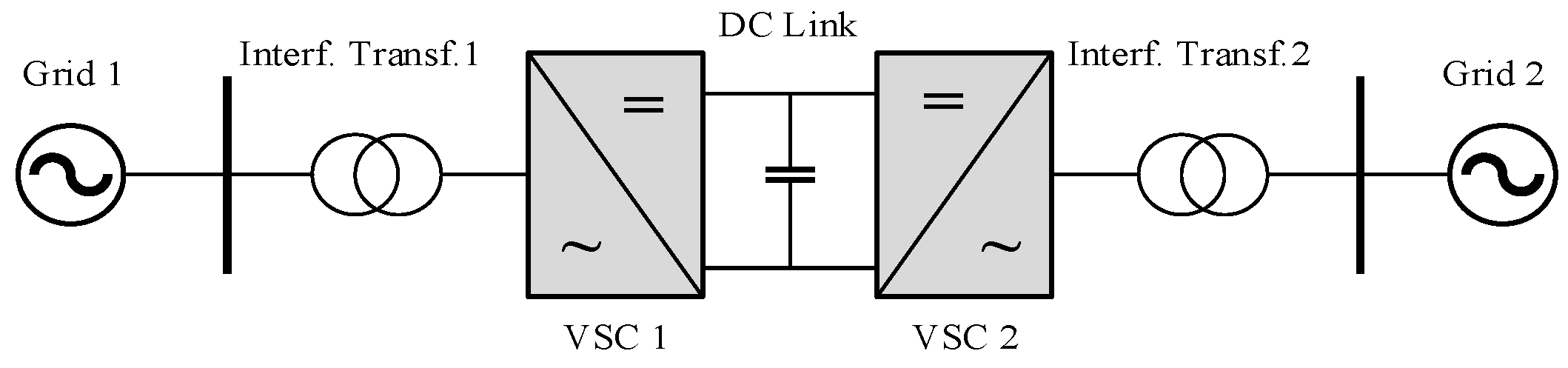
2.1. Back-to-Back MVDC System Topology
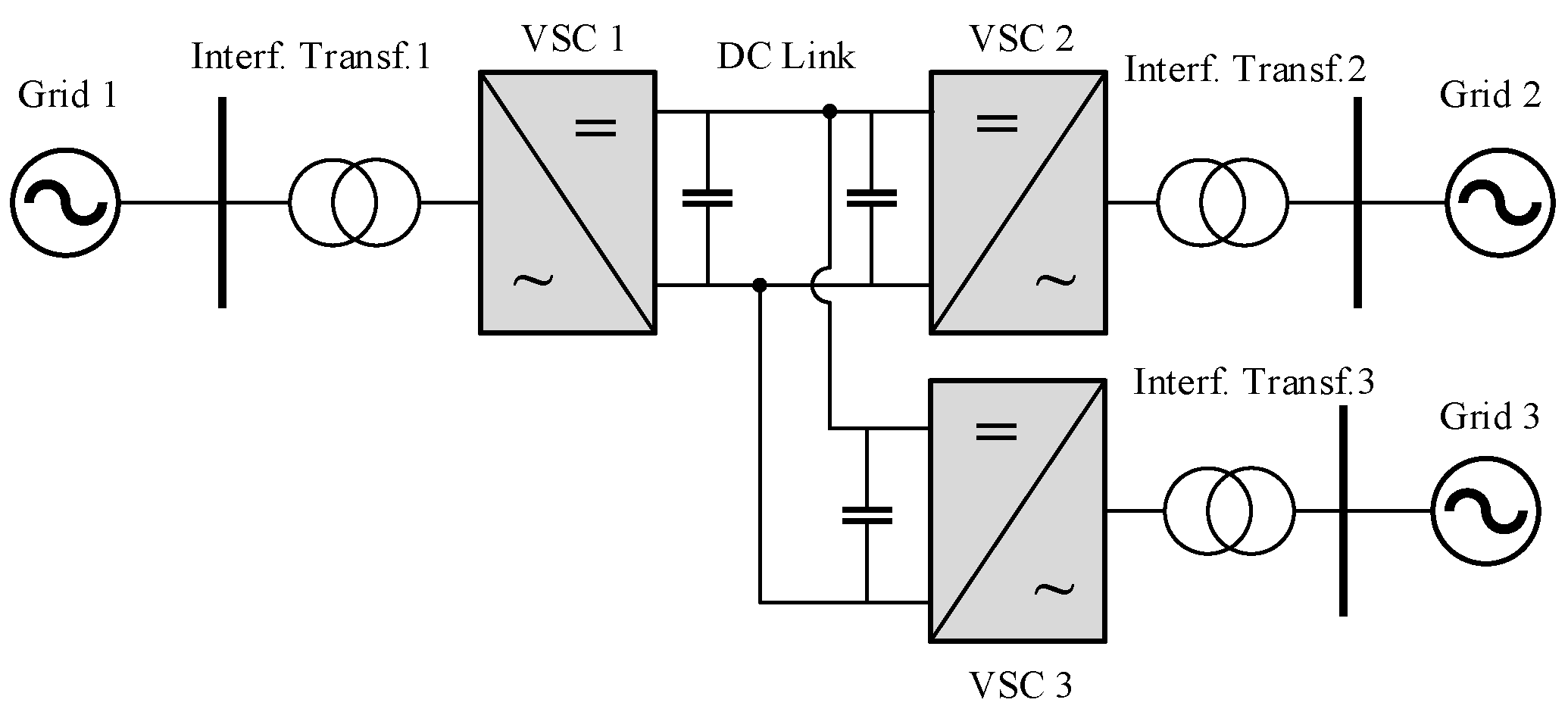
2.2. Multi-Terminal MVDC System Topology
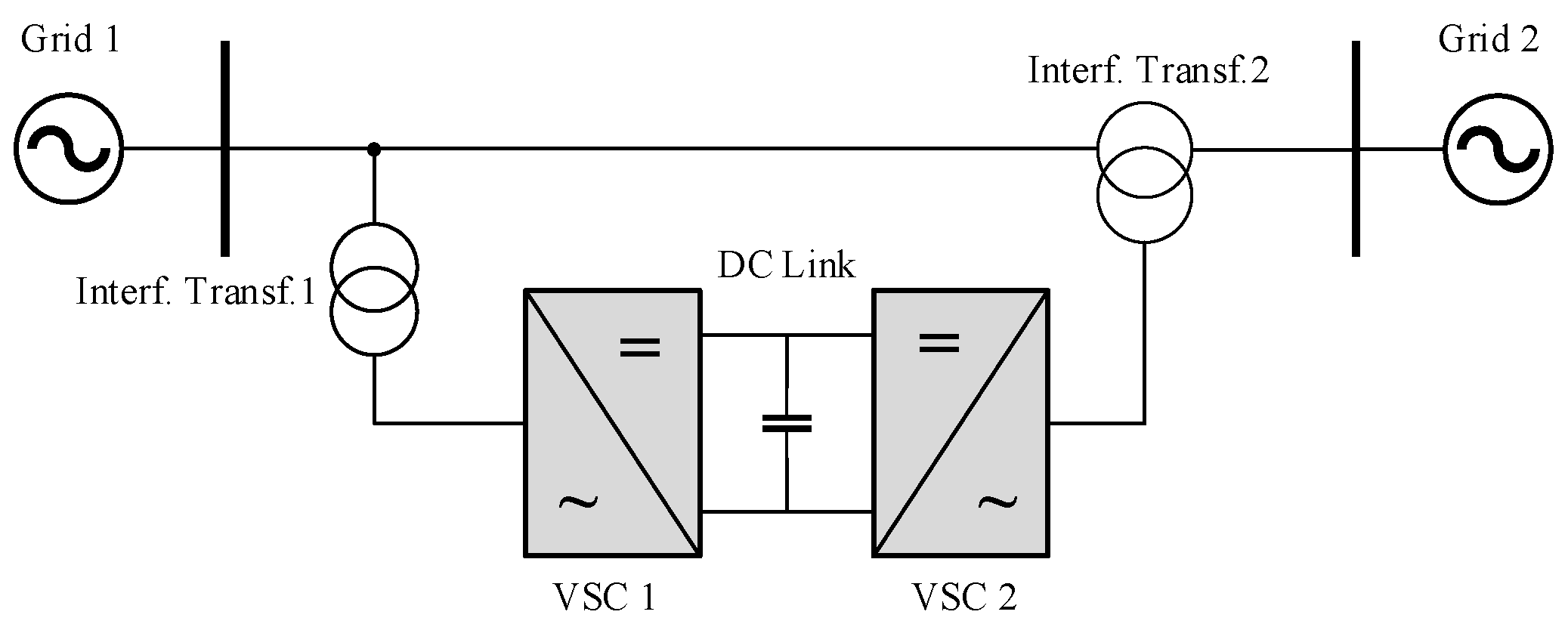
2.3. Unified Power Flow Control System Topology
3. Multilevel Power Converter Topologies
- The output voltage and current of a multilevel converter have reduced distortions in comparison to a two-level converter;
- Because multilevel converters have several output voltages levels, the dv/dt stress is decreased, which in turn lessens the Electromagnetic Compatibility (EMC) problems;
- The switches of multilevel converters can be operated using PWM of the fundamental frequency or higher switching frequencies. However, high switching frequency causes higher switching losses, which decrease the overall efficiency of the conversion system;
- The multilevel converter makes better utilisation of the DC-link voltage when compared to the two-level converter.
3.1. Cascaded H-Bridge (CHB) Multilevel Converter
- ○
- The levels of the AC output voltage are more than the number of H-bridge units used;
- ○
- With a high number of H-bridge units, an AC output with very low harmonic distortions can be achieved even with a lower switching frequency;
- ○
- System modification simplicity due to the series H-bridges modularity.
- ○
- The main constraint of the CHB converter is that independent DC capacitors (or sources) are essential for each H-bridge unit that consequently restricting its application;
- ○
- Due to harmonic distortion reductions requirements, a high number of H-bridges is used for a high number of AC output levels, which means more DC capacitors and thus a bulky and costly system;
- ○
- The complexity of the control system to operate the CHB converter for maintaining equal voltages across the DC capacitors when controlling output active and reactive power components.
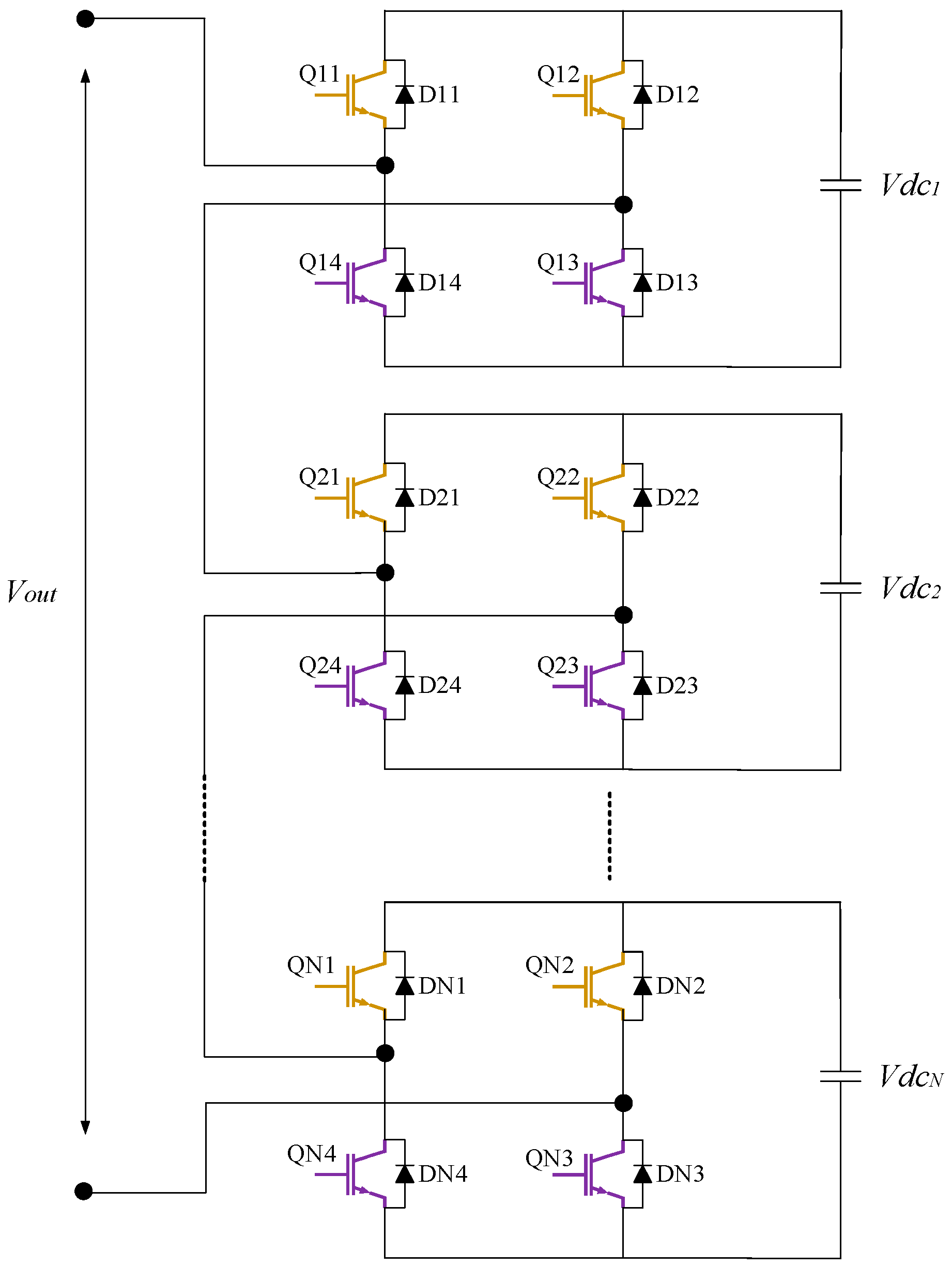
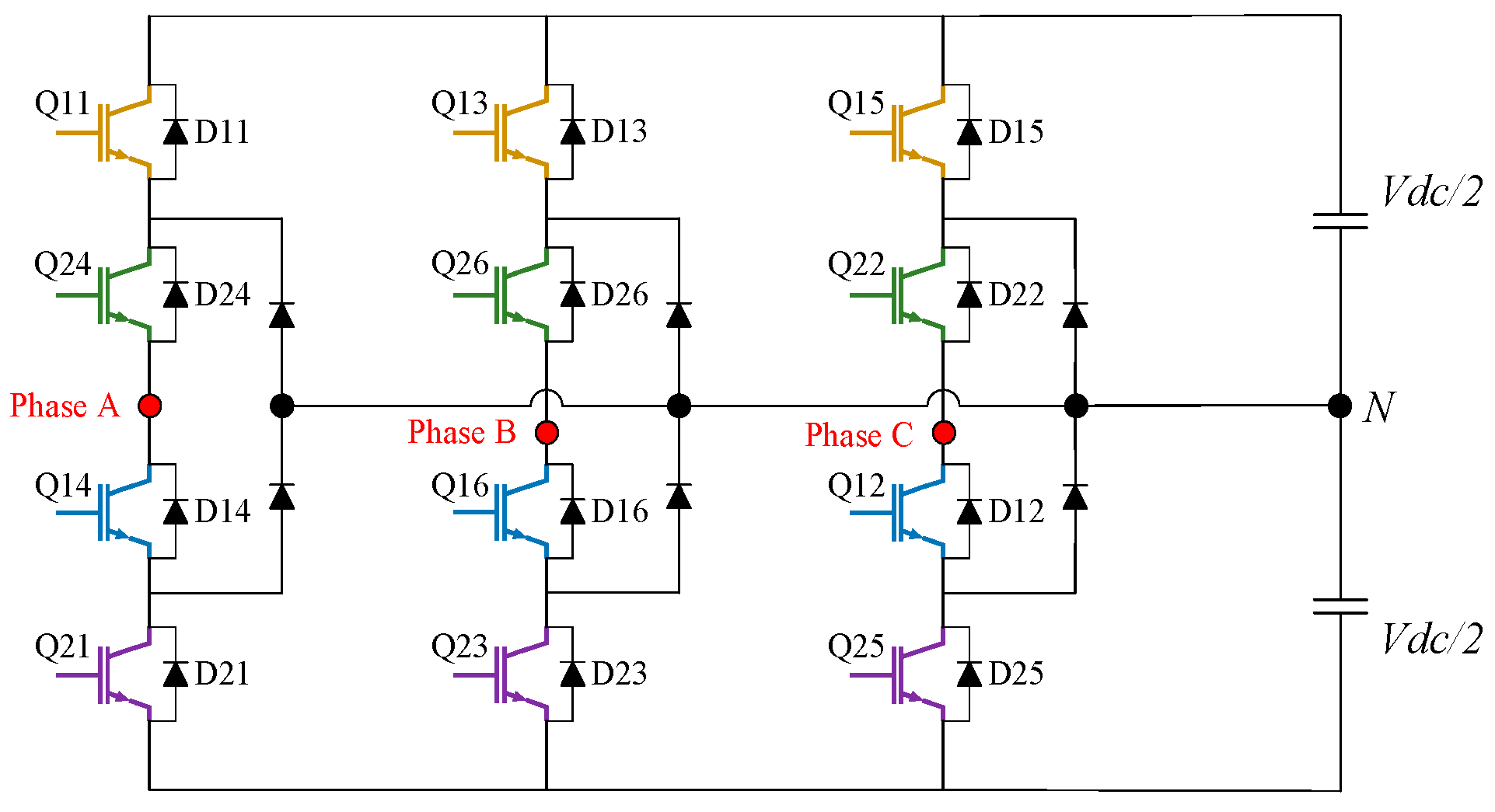
3.2. Neutral Point-Clamped (NPC) Multilevel Converter
- ○
- A common DC-link is shared by the three-phase terminals, minimising the number of DC capacitors required, and system size and cost;
- ○
- Since the DC-link voltage is divided through the midpoint, lower voltage rating switches can be utilised, and voltage stress issues can be minimized;
- ○
- Lower output harmonic distortions and high efficiency with a lower switching frequency;
- ○
- The pre-charging of the DC capacitors as a group is possible, thus improving system dynamics.
- ○
- Increase in the number of diodes required for clamping;
- ○
- Voltages across the DC capacitors must be balanced for all operating conditions, thus requiring an effective control system.
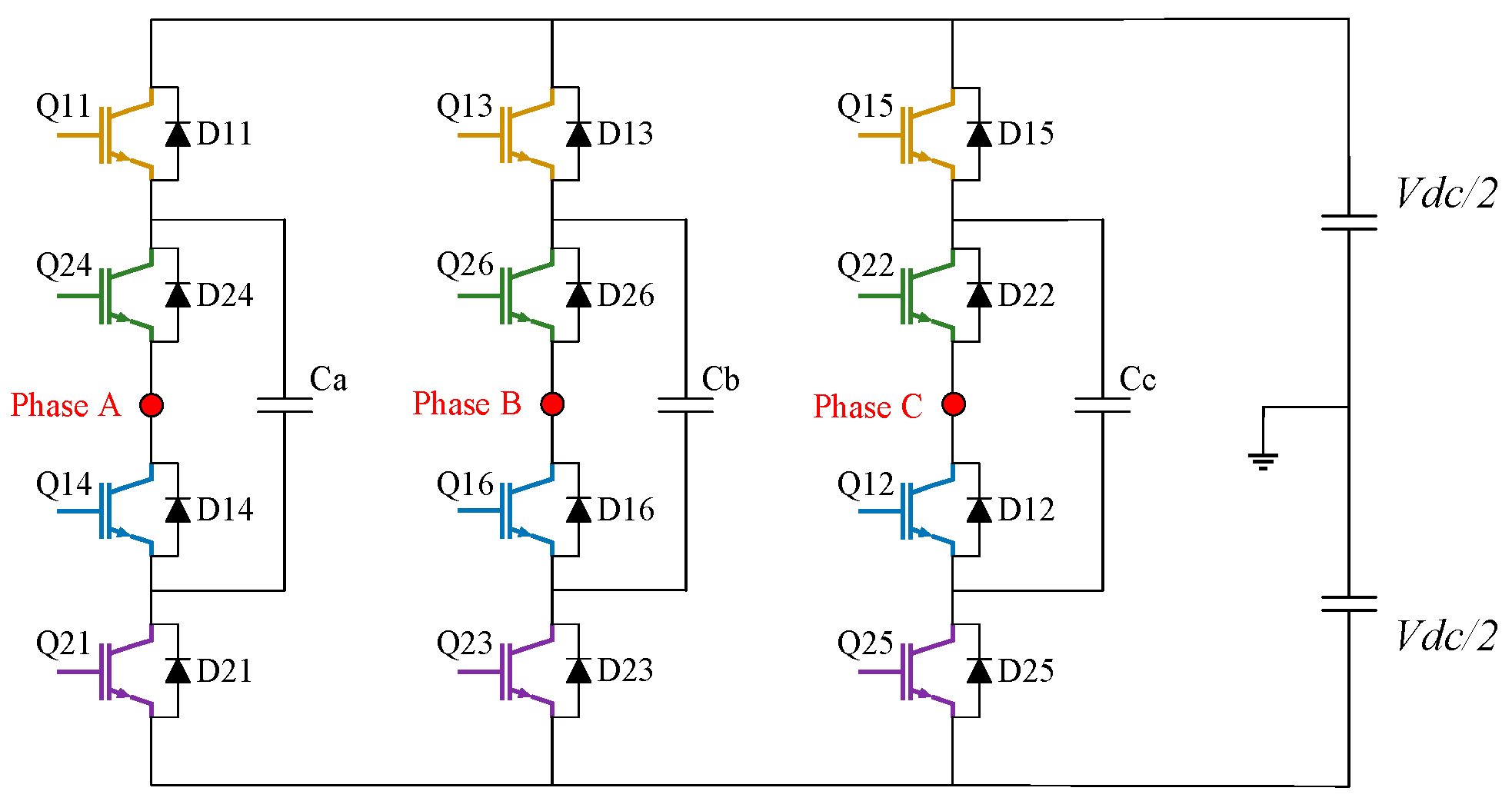
3.3. Flying Capacitor Clamped (FCC) Multilevel Converter
- ○
- The voltage across capacitors can be balanced by the redundant switching states available;
- ○
- Short duration outages ride through capability due to the increased number of capacitors.
- ○
- The high cost and the bulky size of the system due to many capacitors in comparison to the NPC topology;
- ○
- Requirement of a separate pre-charge circuit and complicated control system for voltage balancing of clamping and DC link capacitors.
4. Modelling and Control Development of an MVDC Converter
4.1. Topology and Specifications
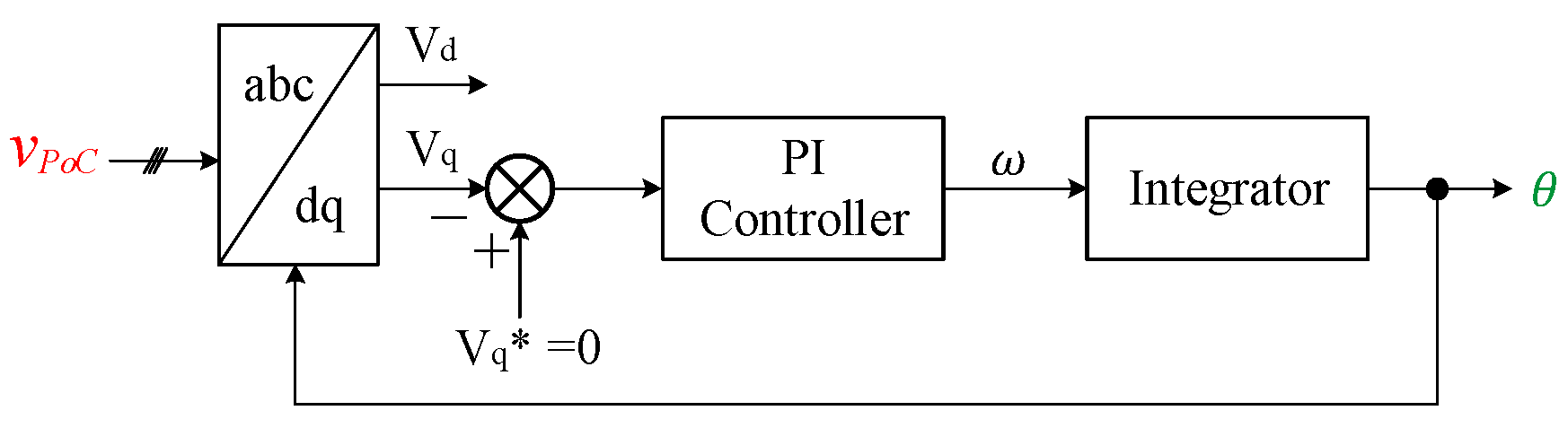
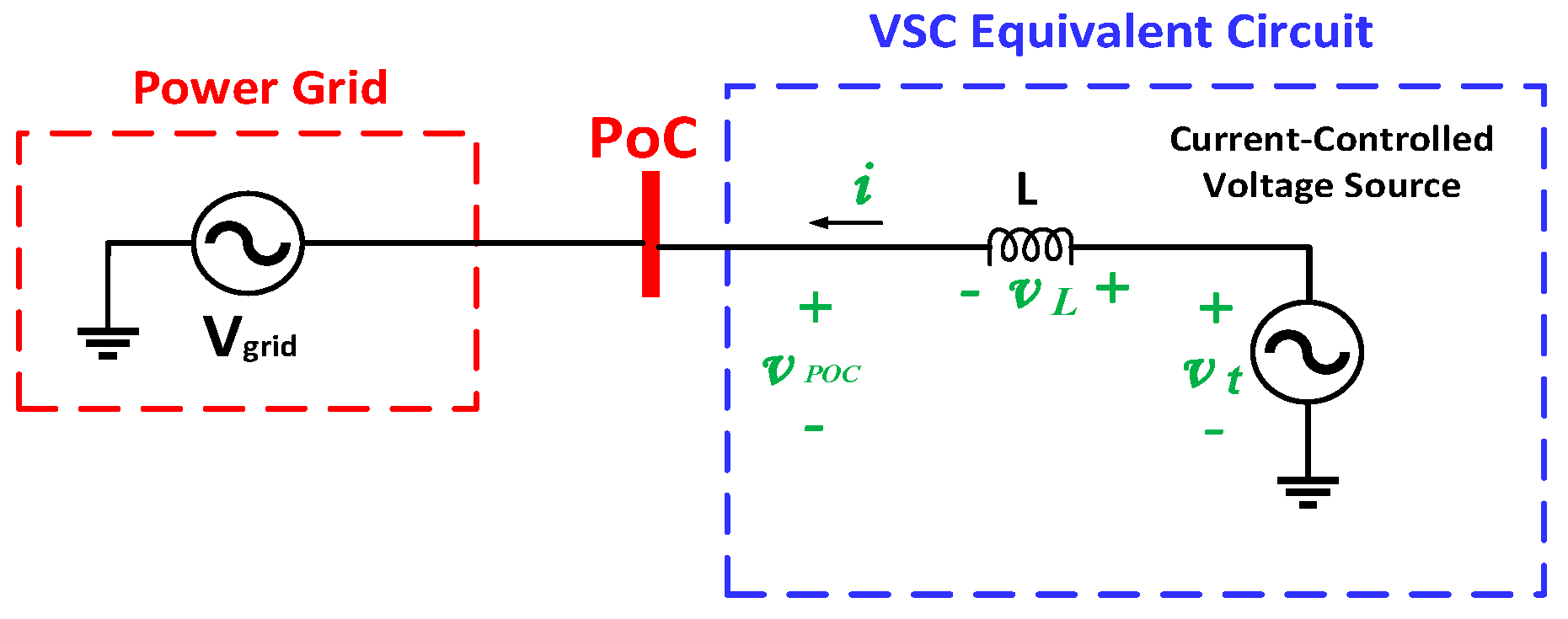
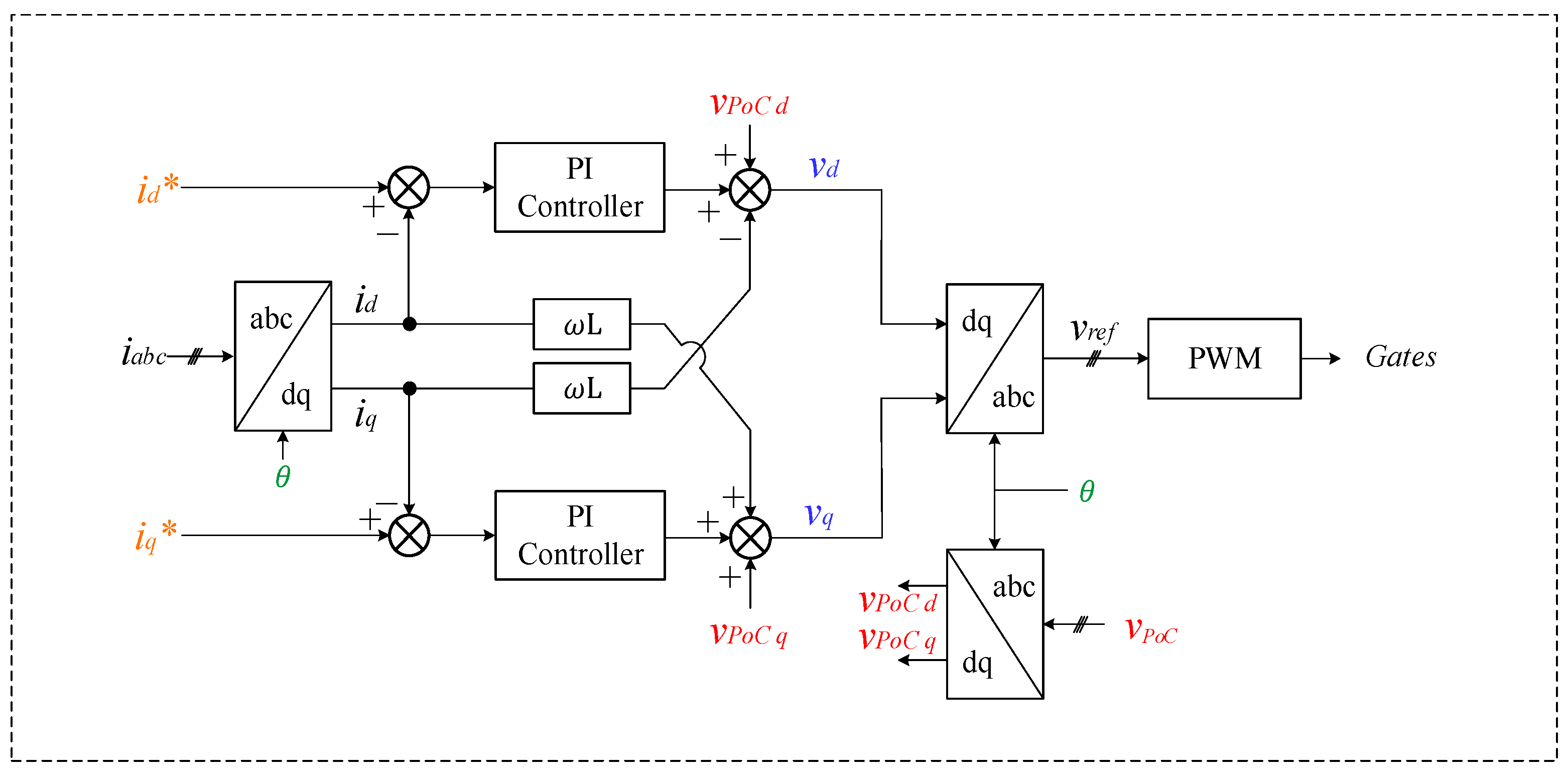
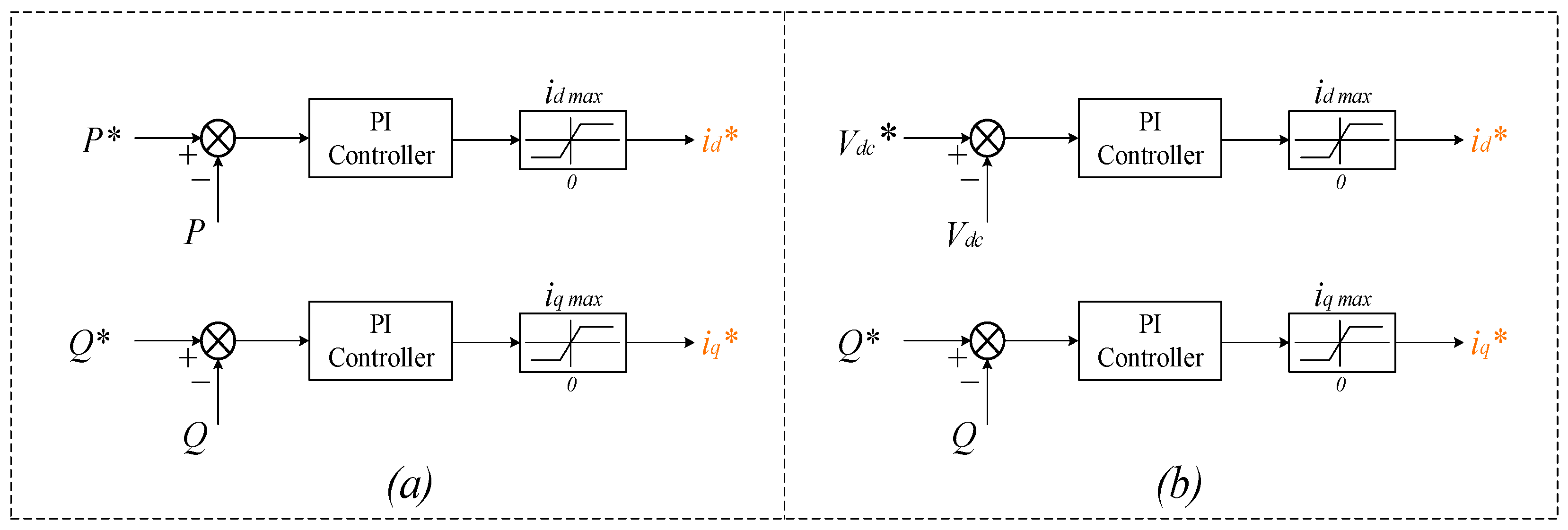
4.2. MVDC Converter Control System
- Inner Control Loop
- Outer Control Loop
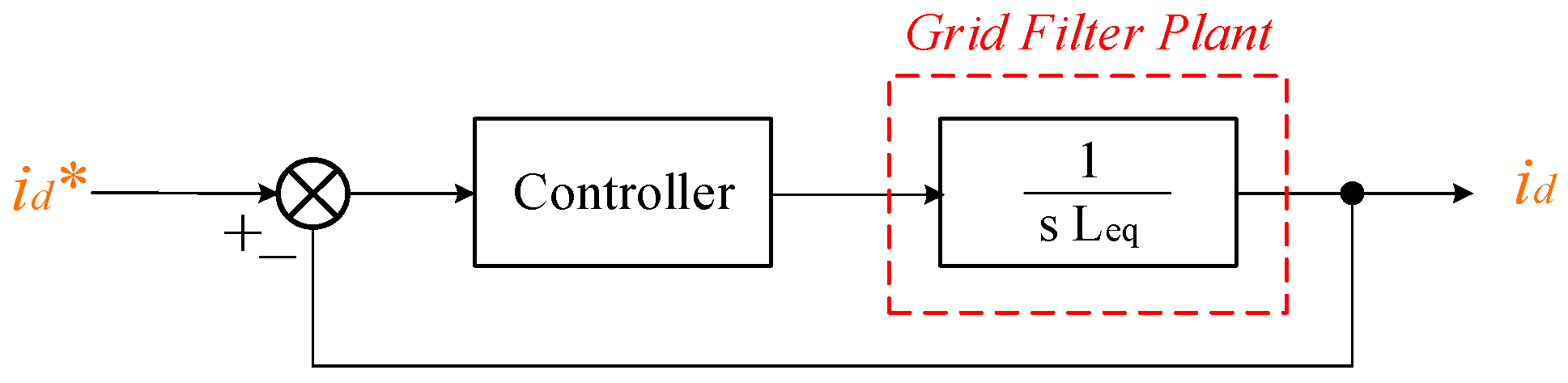
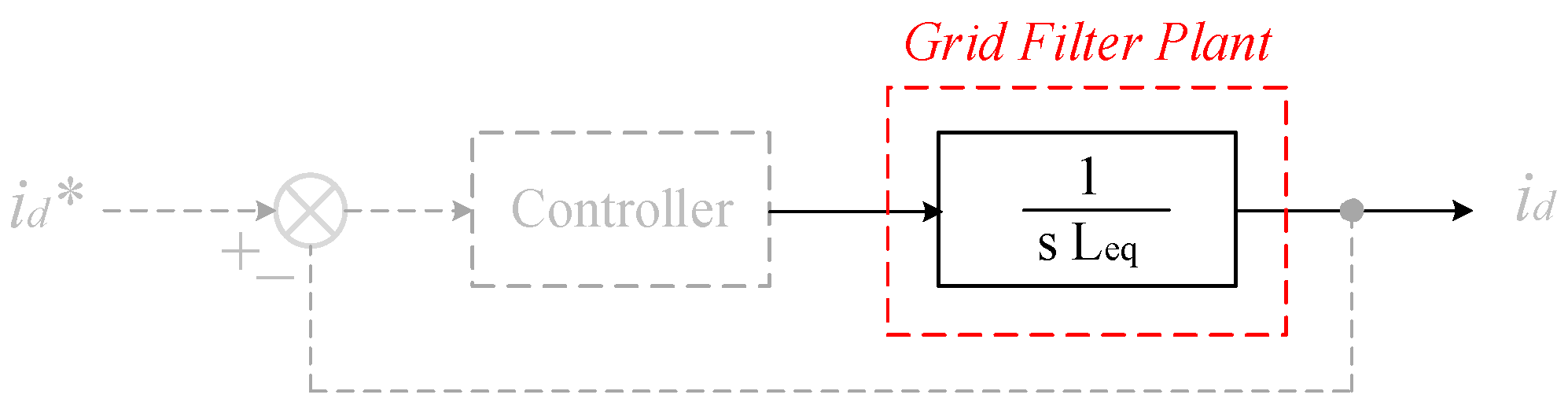
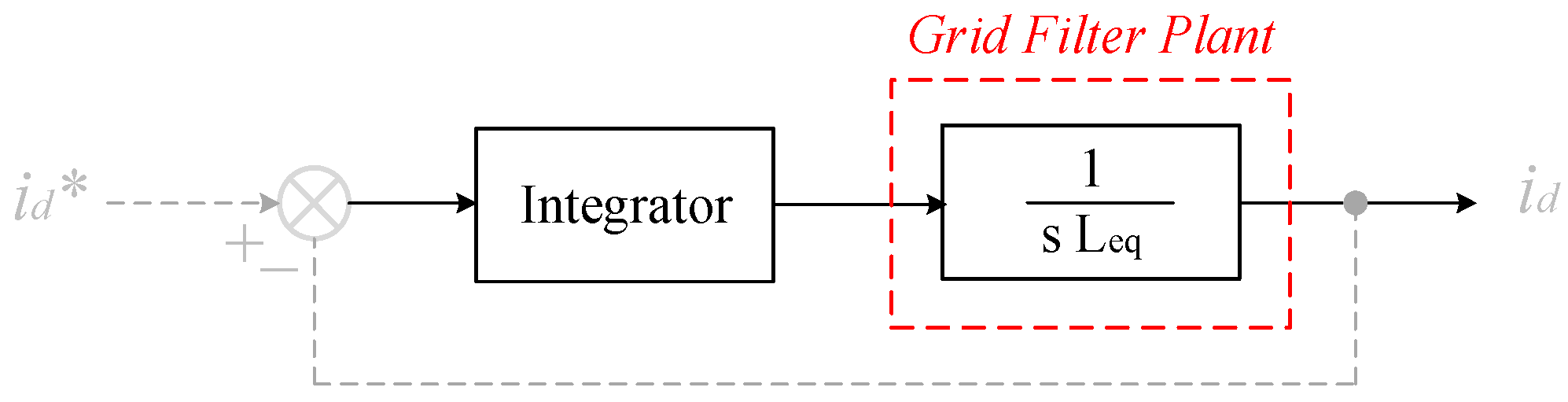
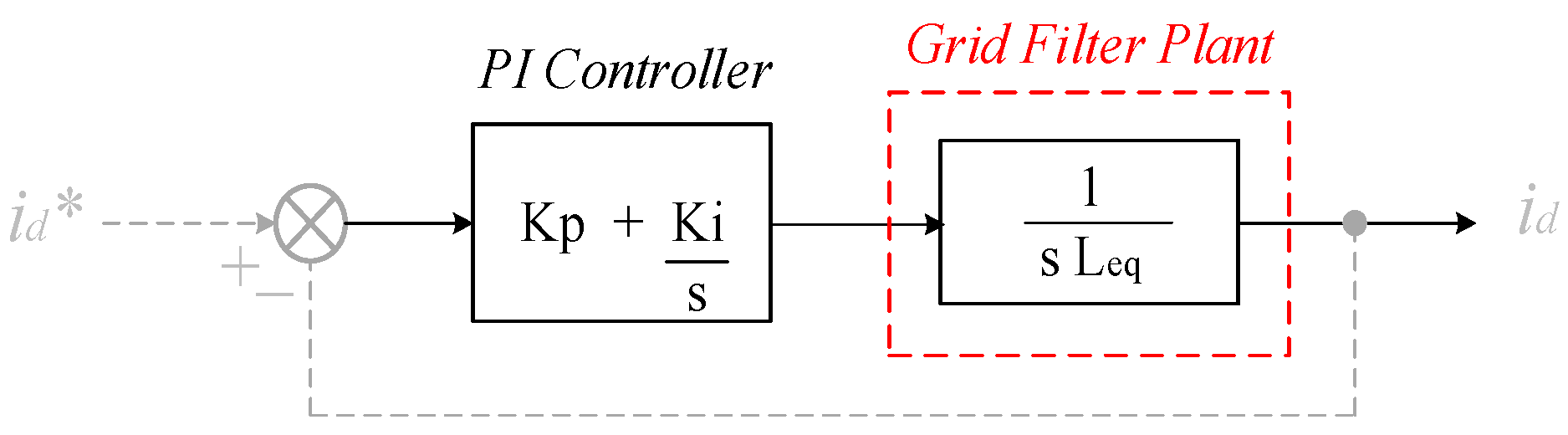
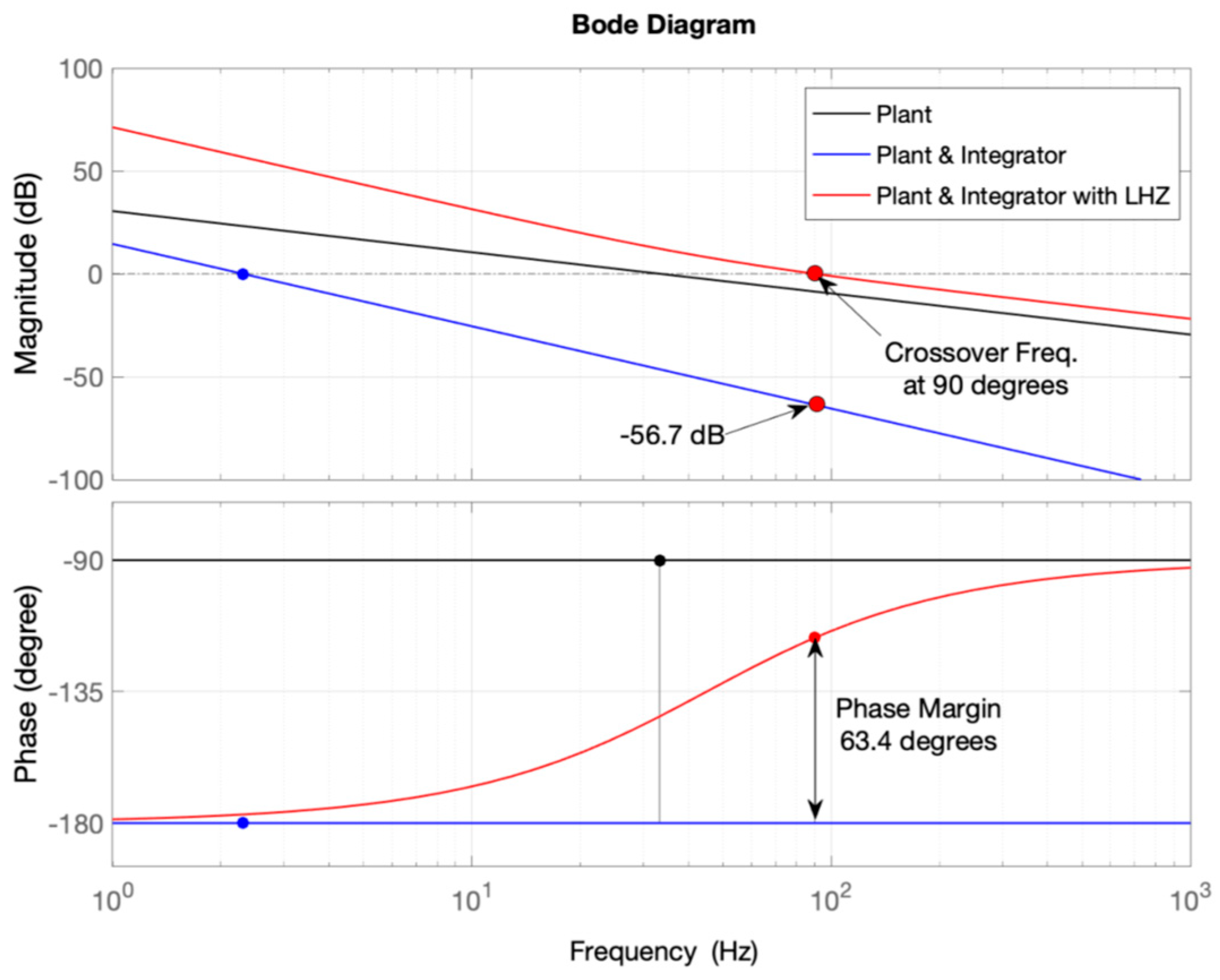
5. PI Controller Parameters Design
6. Pulse Width Modulation Techniques
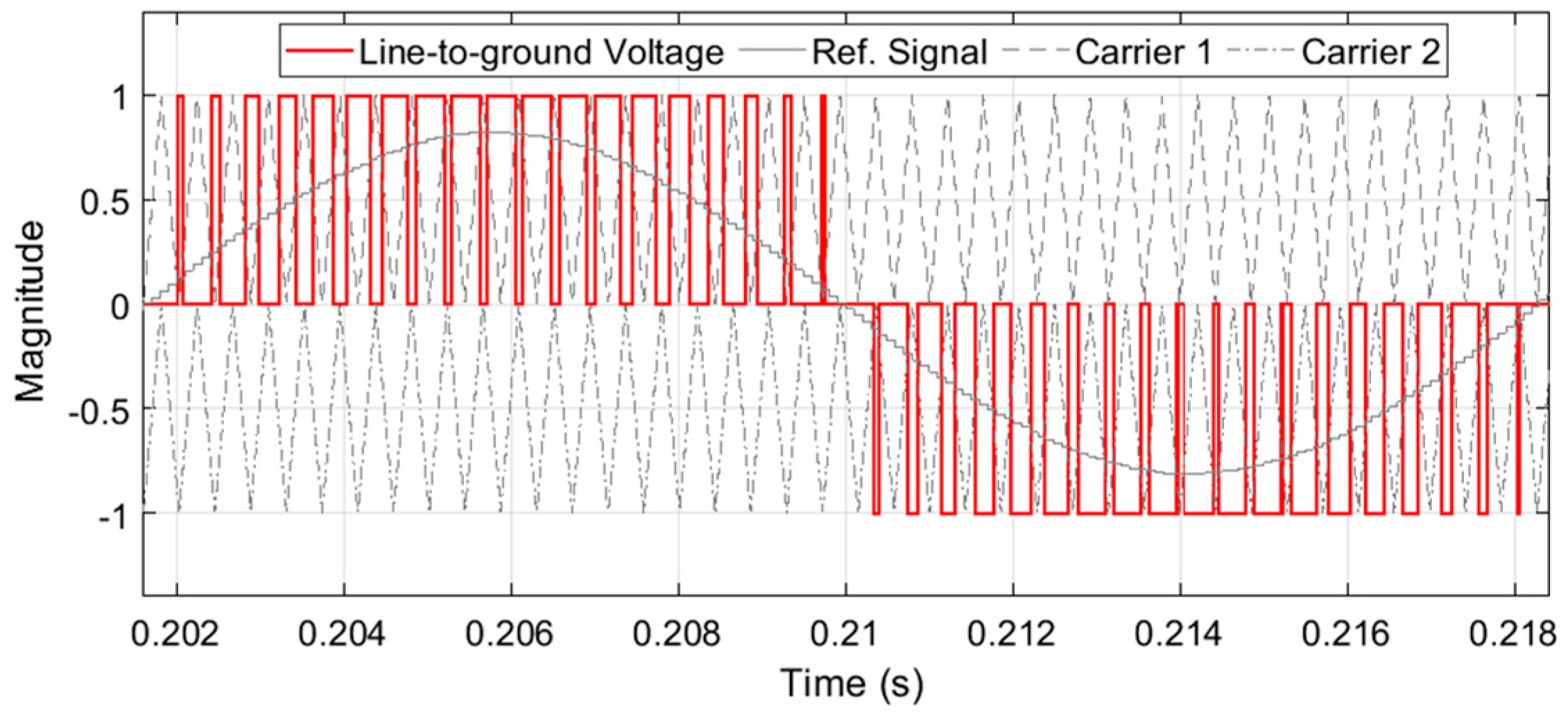
6.1. Interleaved SPWM Technique
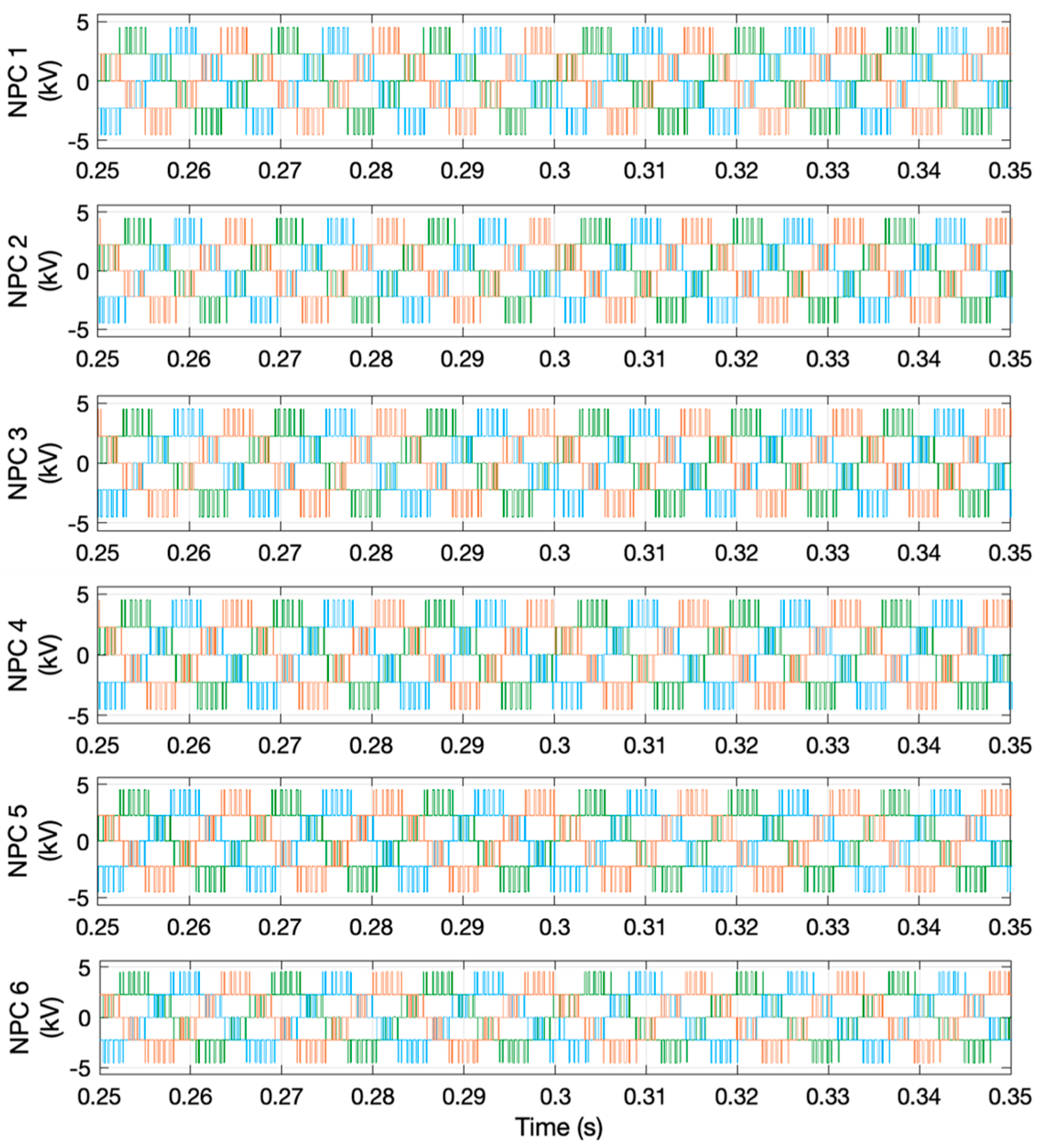
6.2. Interleaved SPWM Application in the MVDC Converter
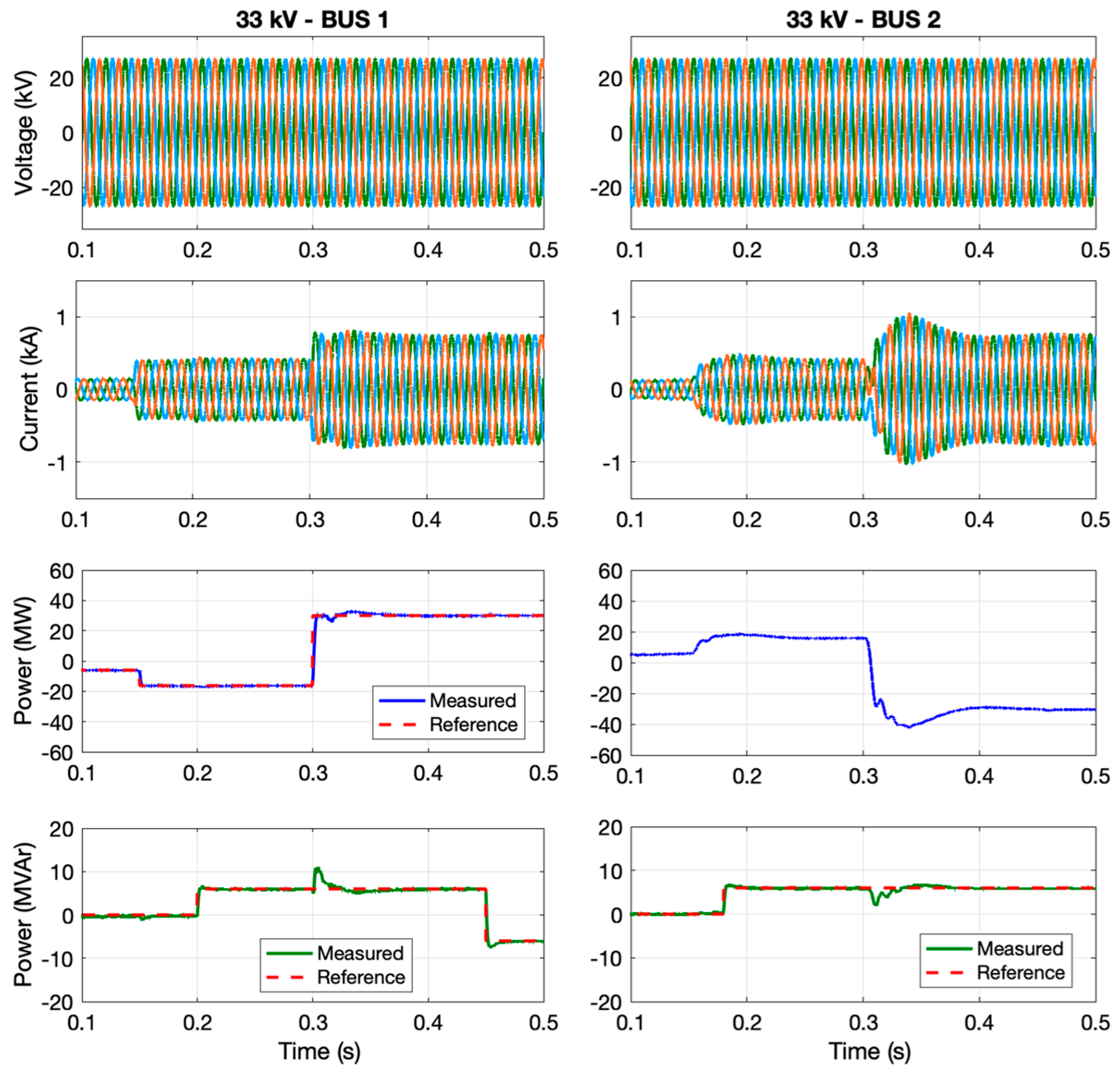
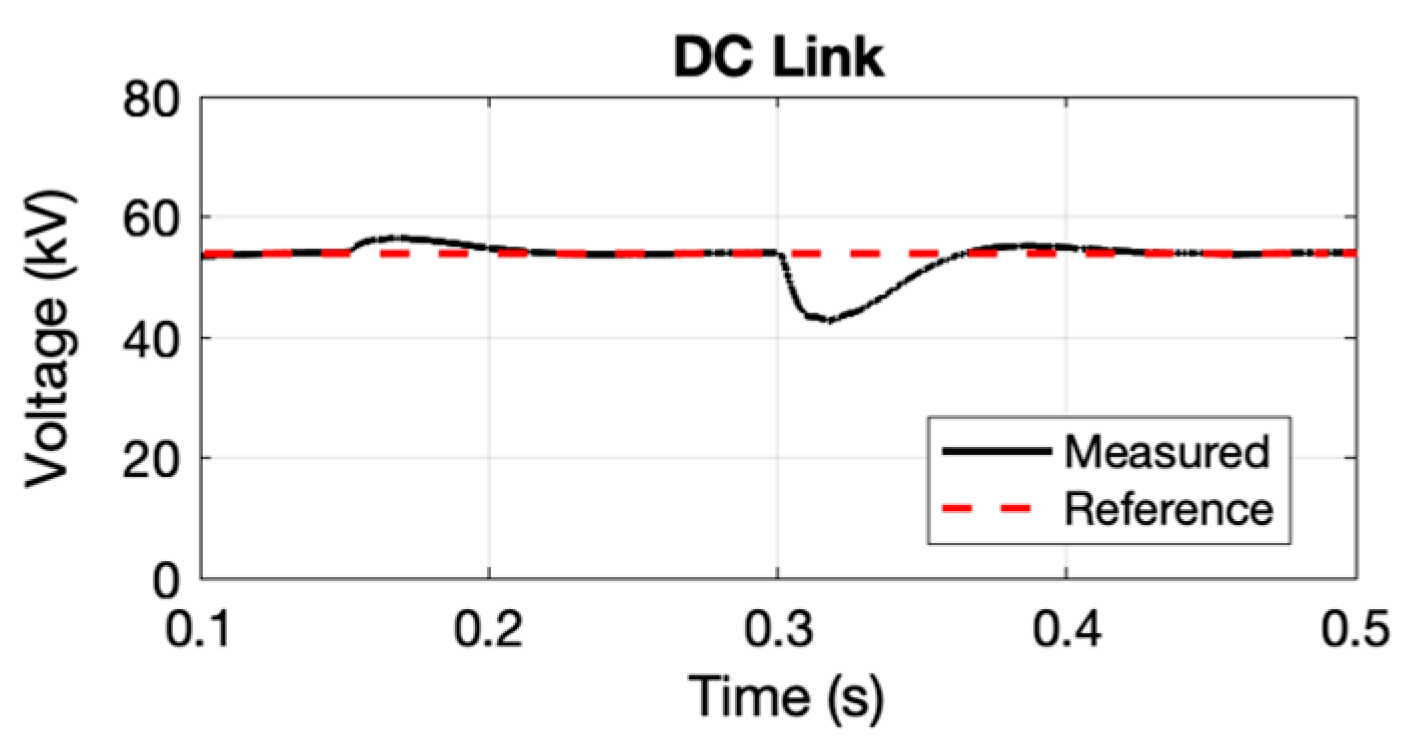
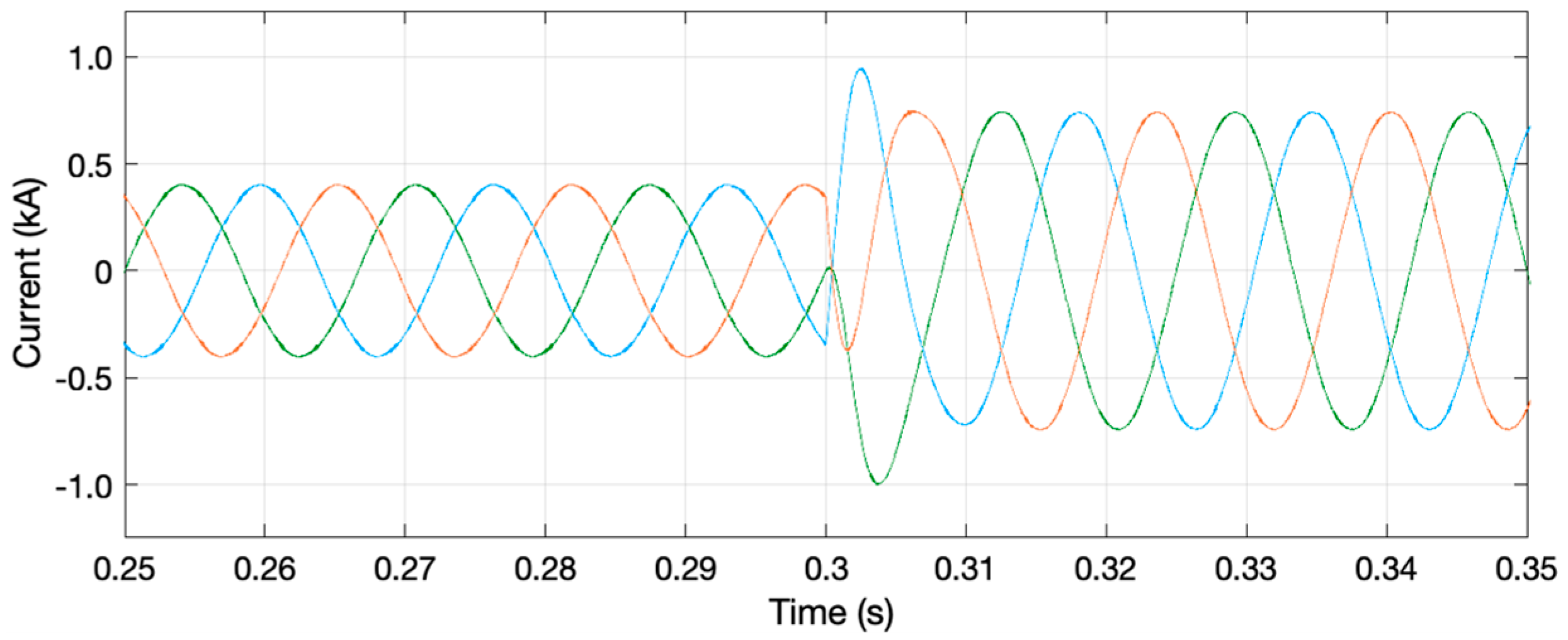
7. MVDC System Performance Analysis
7.1. The Fundamental Frequency Performance of the MVDC Converter
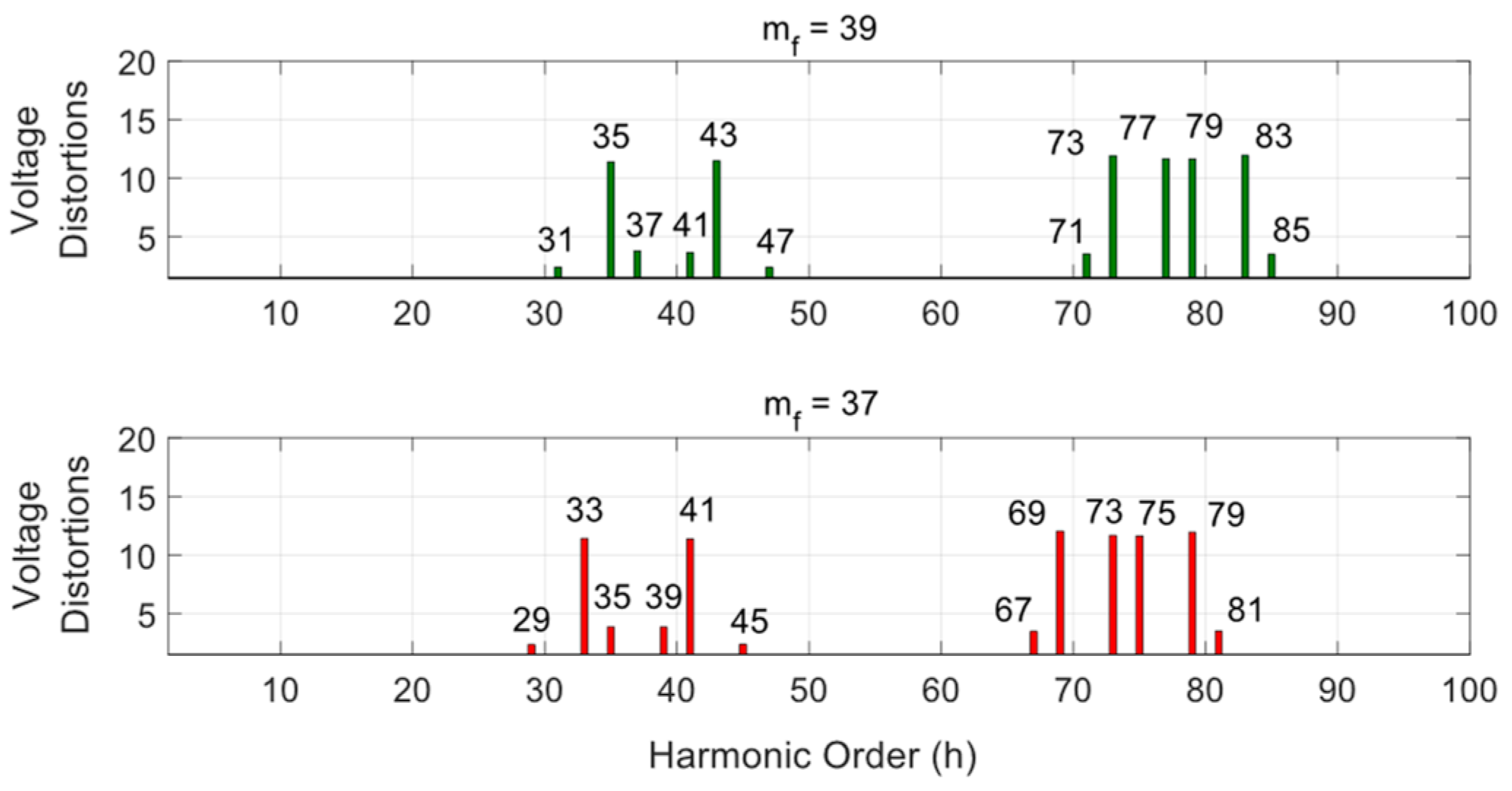
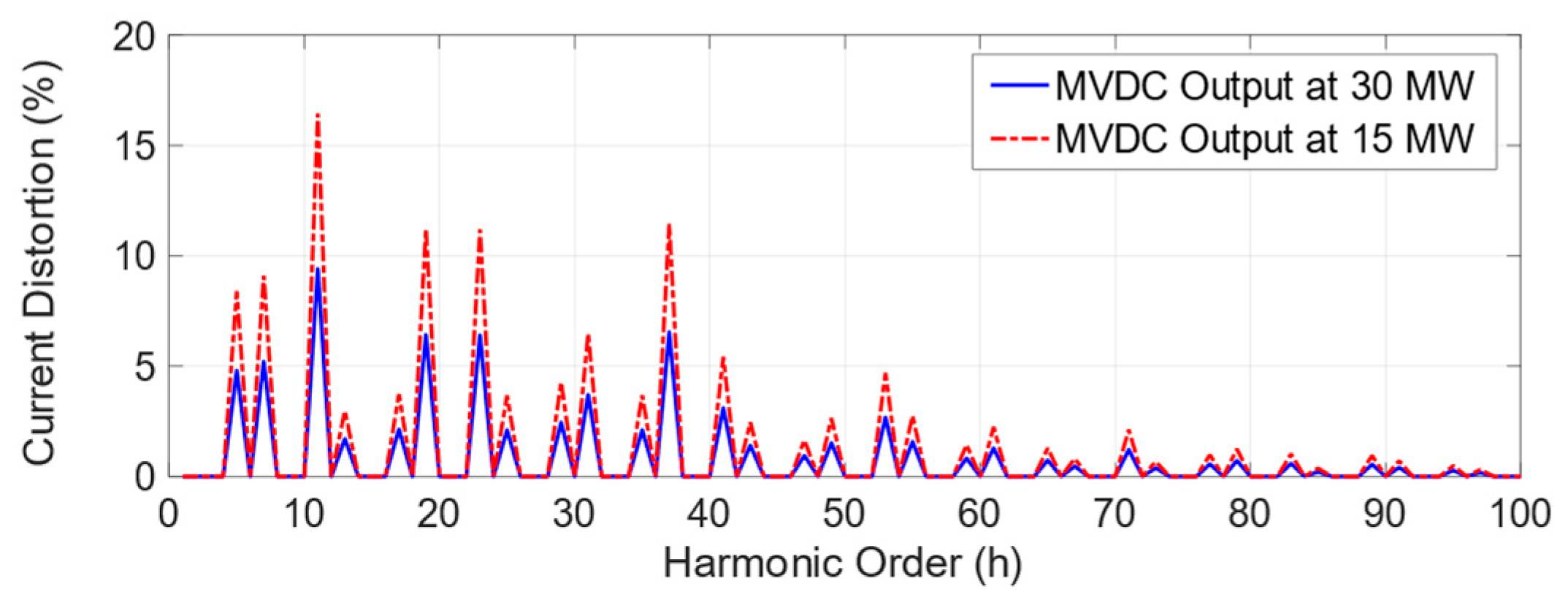
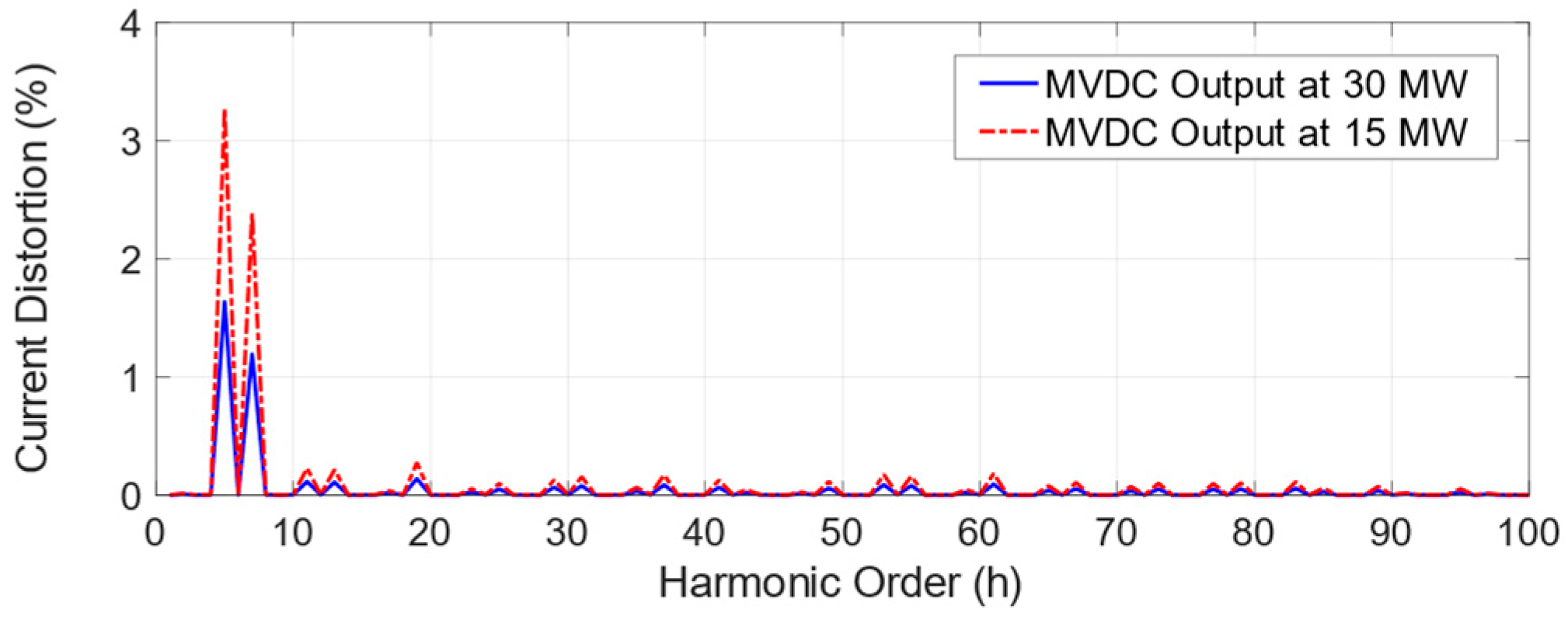
7.2. The Harmonic Performance of the MVDC Converter
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| AC | Alternating Current |
| CHB | Cascaded H-Bridge |
| DC | Direct Current |
| DER | Distributed Energy Resources |
| DG | Distributed Generation |
| dq | Direct-Quadrature |
| EMC | Electromagnetic Compatibility |
| FCC | Flying Capacitor-Clamped |
| FFT | Fast Fourier Transform |
| LHZ | Left-Hand Zero |
| MVDC | Medium Voltage Direct Current |
| NPC | Neutral Point-Clamped |
| p.u. | per unit |
| PE | Power Electronics |
| PI | Proportional Integral |
| PLL | Phase-Locked Loop |
| PoC | Point of Connection |
| SPWM | Sinusoidal Pulse-Width Modulation |
| STATCOM | Static Synchronous Compensator |
| THD | Total Harmonic Distortions |
| VSC | Voltage Source Converter |
| Transformer Inductance Voltage | |
| Power Converter Terminal Voltage | |
| PoC Voltage | |
| Integral Controller Gain | |
| LHZ Frequency | |
| PI Proportional Gain | |
| PI Integral Gain | |
| mf | Frequency Modulation Index |
References
- Rezkallah, M.; Chandra, A.; Hamadi, A.; Ibrahim, H.; Ghandour, M. Power quality in smart grids. In Pathways to a Smarter Power System; Elsevier: London, UK, 2019. [Google Scholar]
- Bloemink, J.M.; Green, T.C. Benefits of Distribution-Level Power Electronics for Supporting Distributed Generation Growth. IEEE Trans. Power Deliv. 2013, 28, 911–919. [Google Scholar] [CrossRef] [Green Version]
- Networks, S.E. 2015 ANGLE-DC Electricity Network Innovation Competition; Ofgem: London, UK, 2015; pp. 1–101. [Google Scholar]
- Alghamdi, T.A.H.; Anayi, F.J. Modelling and control development of an MVDC converter implemented for Albaha power network. In Proceedings of the 5th International Conference on Power and Energy Engineering (ICPEE), Xiamen, China, 2–4 December 2021. [Google Scholar]
- Alghamdi, T.A.H.; Anayi, F.; Packianather, M. Optimal Design of Passive Power Filters Using the MRFO Algorithm and a Practical Harmonic Analysis Approach including Uncertainties in Distribution Networks. Energies 2022, 15, 2566. [Google Scholar] [CrossRef]
- Tang, C.-Y.; Chen, Y.-F.; Chen, Y.-M.; Chang, Y.-R. DC-Link Voltage Control Strategy for Three-Phase Back-to-Back Active Power Conditioners. IEEE Trans. Ind. Electron. 2015, 62, 6306–6316. [Google Scholar] [CrossRef]
- Romero-Ramos, E.; Gómez-Expósito, A.; Marano-Marcolini, A.; Maza-Ortega, J.; Martinez-Ramos, J. Assessing the loadability of active distribution networks in the presence of DC controllable links. IET Gener. Transm. Distrib. 2011, 5, 1105–1113. [Google Scholar] [CrossRef]
- Maza-Ortega, J.; Barragán-Villarejo, M.; Romero-Ramos, E.; Marano-Marcolini, A.; Gómez-Expósito, A. Voltage source converter-based topologies to further integrate renewable energy sources in distribution systems. IET Renew. Power Gener. 2012, 6, 435–445. [Google Scholar] [CrossRef]
- Bloemink, J.M.; Green, T.C. Increasing distributed generation penetration using soft normally-open points. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Cao, W.; Wu, J.; Jenkins, N.; Wang, C.; Green, T. Operating principle of Soft Open Points for electrical distribution network operation. Appl. Energy 2016, 164, 245–257. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Zhang, Y.; Gao, Z.; Cao, C.; Wang, Z.; Xu, F. Research on Topology and Control Technology of Soft Multi-State Open Point with Fault Isolation Capability. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1467–1473. [Google Scholar]
- Aithal, A.; Wu, J. Operation and performance of a medium-voltage DC link. CIRED Open Access Proc. J. 2017, 2017, 1355–1358. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Ming, W.; Ugalde-Loo, C.E.; Wang, S.; Jenkins, N. Analysis and Mitigation of DC Voltage Imbalance for Medi-um-Voltage Cascaded Three-Level Neutral-Point-Clamped Converters. IEEE Trans. Power Electron. 2022, 37, 4320–4336. [Google Scholar] [CrossRef]
- Graaff, R.A.A.; Myrzik, J.M.; Kling, W.L.; Enslin, J.H.R. Series Controllers in Distribution Systems—Facilitating Increased Loading and Higher DG Penetration. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1926–1930. [Google Scholar]
- Thomas, L.J.; Burchill, A.; Rogers, D.J.; Guest, M.; Jenkins, N. Assessing Distribution Network Hosting Capacity with the Addition of Soft Open Points. In Proceedings of the 5th IET International Conference on Renewable Power Generation (RPG) 2016, London, UK, 21–23 September 2016; Institution of Engineering and Technology: London, UK, 2016; pp. 1–6. [Google Scholar]
- de Graaff, R.A.A.; Myrzik, J.M.A.; Kling, W.L.; Enslin, J.H.R. Intelligent Nodes in Distribution Systems—Optimizing Steady State Settings. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 391–395. [Google Scholar]
- Li, P.; Song, G.; Ji, H.; Zhao, J.; Wang, C.; Wu, J. A Supply Restoration Method of Distribution System Based on Soft Open Point. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 535–539. [Google Scholar]
- Joseph, T.; Liang, J.; Li, G.; Moon, A.; Smith, K.; Yu, J. Dynamic control of MVDC link embedded in distribution network-Case study on ANGLE-DC. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Joseph, T.; Balasubramaniam, S.; Li, G.; Liang, J.; Ming, W.; Moon, A.; Smith, K.; Yu, J. Dynamic Average Converter Model for MVDC Link Harmonic Analysis. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Joseph, T.; Wenlong, M.; Gen, L.; Jun, L.; Moon, A.; Smith, K.; Yu, J. Analysis of Harmonic Transfer through an MVDC Link. In Proceedings of the 15th IET International Conference on AC and DC Power Transmission (ACDC 2019), Coventry, UK, 5–7 February 2019; Institution of Engineering and Technology: London, UK, 2019; pp. 1–6. [Google Scholar]
- Abdelrahman, M.A.; Long, C.; Wu, J.; Jenkins, N. Optimal Operation of Multi-Terminal Soft Open Point to Increase Hosting Capacity of Distributed Generation in Medium Voltage Networks. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Andersen, B.R.; Nilsson, S.L. Flexible AC Transmission Systems, 1st ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Kabalci, E. Multilevel Inverters: Introduction and Emergent Topologies; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Gonzalez, S.A.; Verne, S.A.; Valla, M.I. Multilevel Converters for Industrial Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Marchesoni, M.; Mazzucchelli, M.; Tenconi, S. A Non-Conventional Power Converter for Plasma Stabilization. IEEE Trans. Power Electron. 1990, 5, 212–219. [Google Scholar] [CrossRef]
- Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, IA-17, 518–523. [Google Scholar] [CrossRef]
- Meynard, T.A.; Foch, H. Multi-Level Choppers for High Voltage Applications. EPE J. 1992, 2, 45–50. [Google Scholar] [CrossRef]
- Poorfakhraei, A.; Narimani, M.; Emadi, A. A Review of Multilevel Inverter Topologies in Electric Vehicles: Current Status and Future Trends. IEEE Open J. Power Electron. 2021, 2, 155–170. [Google Scholar] [CrossRef]
- Renken, F. Analytic Calculation of the DC-Link Capacitor Current for Pulsed Three-Phase Inverters. In Proceedings of the 11th International Conference on Power Electronics Motion Control, Riga, Latvia, 2–4 September 2004; pp. 1–9. [Google Scholar]
- Sharkh, S.M.; Abusara, M.A.; Orfanoudakis, G.I.; Hussain, B. Loss Comparison of Two- and Three-Level Inverter Topologies. In Power Electronic Converters for Microgrids; John Wiley & Sons: Singapore, 2014. [Google Scholar]
- Adam, G.P. Voltage Source Converter: Modulation, Control and Applications in Power Systems; CreateSpace Independent Pub.: Scotts Valley, CA, USA, 2013. [Google Scholar]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Zhou, D.; Song, Y.; Blaabjerg, F. Modeling and Control of Three-Phase AC/DC Converter Including Phase-Locked Loop. In Control of Power Electronic Converters and Systems; Blaabjerg, F., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 117–151. [Google Scholar]
- Suntio, T.; Messo, T.; Puukko, J. Power Electronic Converters: Dynamics and Control in Conventional and Renewable Energy Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Adam, G.P.; Anaya-Lara, O.; Burt, G.; Finney, S.J.; Williams, B.W. Comparison between Two VSC-HVDC Transmission Technologies: Modular and Neutral Point Clamped Multilevel Converter. In Proceedings of the 35th Annual Conference of the IEEE Industrial Electronics Society (IECON 2009), Porto, Portugal, 3–5 November 2009; pp. 1–6. [Google Scholar]
- Hart, D.W. Power Electronics; Tata McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
- Dubey, G.K. Fundamentals of Electrical Drives; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Abu Sharkh, S.M.; Abu-Sara, M.A. Current Control of Utility-Connected Two-Level and Three-Level Pwm Inverters. EPE J. 2004, 14, 13–18. [Google Scholar] [CrossRef]
- Jung, H.-S. Interleaved Pulse Width Modulation Based on Modified Carrier in Parallel Operation. IEEE Access 2021, 9, 109775–109784. [Google Scholar] [CrossRef]
- Tamyurek, B.; Torrey, D.A. A Three-Phase Unity Power Factor Single-Stage AC–DC Converter Based on an Interleaved Flyback Topology. IEEE Trans. Power Electron. 2010, 26, 308–318. [Google Scholar] [CrossRef]

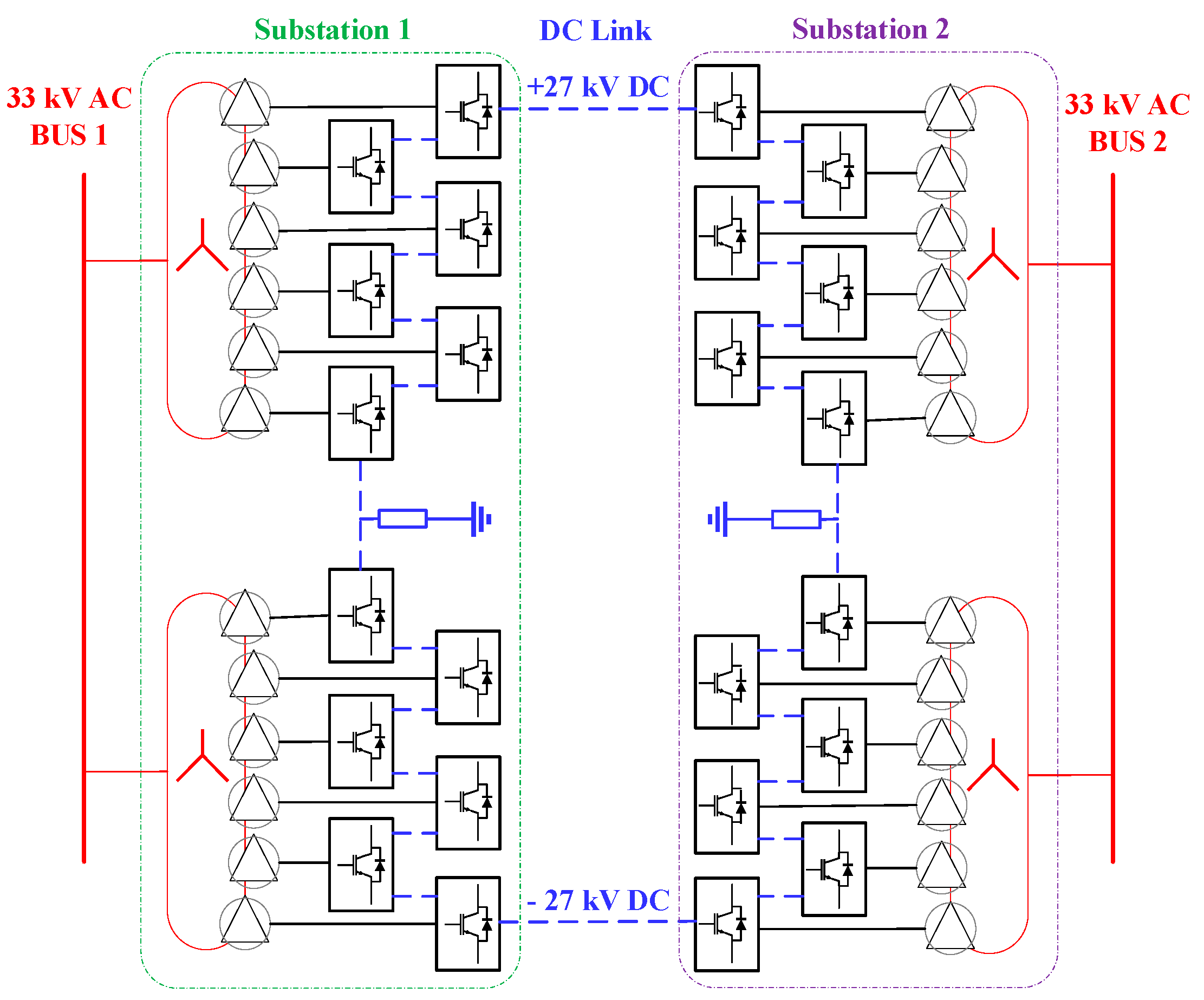






| Parameter | Value |
|---|---|
| MVDC Capacity | 30 MW |
| Line Voltage | 33 kV–60 Hz |
| DC Voltage | ±27 kV |
| Transformer Rating (each) | 17 MVA |
| Transformer Reactance (each) | 0.2 p.u. |
| Switching Frequency () | 900 Hz |
| DC Reactor | 6 mH |
| Grounding Resistor | 10 Ω |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, T.A.H.; Anayi, F.; Packianather, M. Modelling and Control Development of a Cascaded NPC-Based MVDC Converter for Harmonic Analysis Studies in Power Distribution Networks. Energies 2022, 15, 4867. https://doi.org/10.3390/en15134867
Alghamdi TAH, Anayi F, Packianather M. Modelling and Control Development of a Cascaded NPC-Based MVDC Converter for Harmonic Analysis Studies in Power Distribution Networks. Energies. 2022; 15(13):4867. https://doi.org/10.3390/en15134867
Chicago/Turabian StyleAlghamdi, Thamer A. H., Fatih Anayi, and Michael Packianather. 2022. "Modelling and Control Development of a Cascaded NPC-Based MVDC Converter for Harmonic Analysis Studies in Power Distribution Networks" Energies 15, no. 13: 4867. https://doi.org/10.3390/en15134867
APA StyleAlghamdi, T. A. H., Anayi, F., & Packianather, M. (2022). Modelling and Control Development of a Cascaded NPC-Based MVDC Converter for Harmonic Analysis Studies in Power Distribution Networks. Energies, 15(13), 4867. https://doi.org/10.3390/en15134867






