Seepage Law of Nearly Flat Coal Seam Based on Three-Dimensional Structure of Borehole and the Deep Soft Rock Roadway Intersection
Abstract
:1. Introduction
2. Materials and Methods
2.1. Gas–Solid Coupling Physical Model of the Gas-Bearing Coalbed
2.2. Principle of Effective Stress of the Gas-Bearing Coal Body
2.3. Dynamic Evolution Equations of Coal Porosity and Permeability
2.4. Diffusion Equation of Gas in Coal
2.5. Gas Seepage Equation
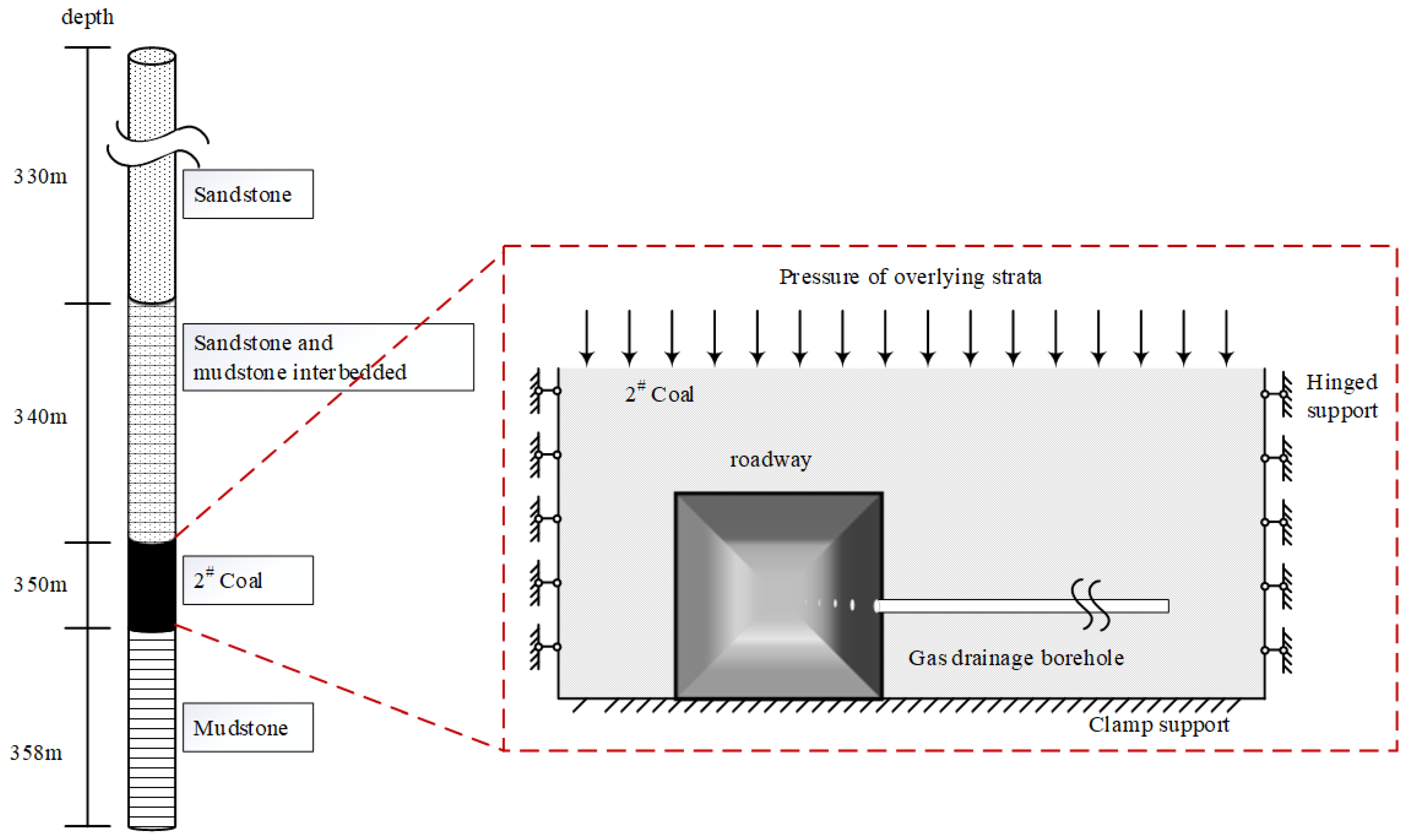
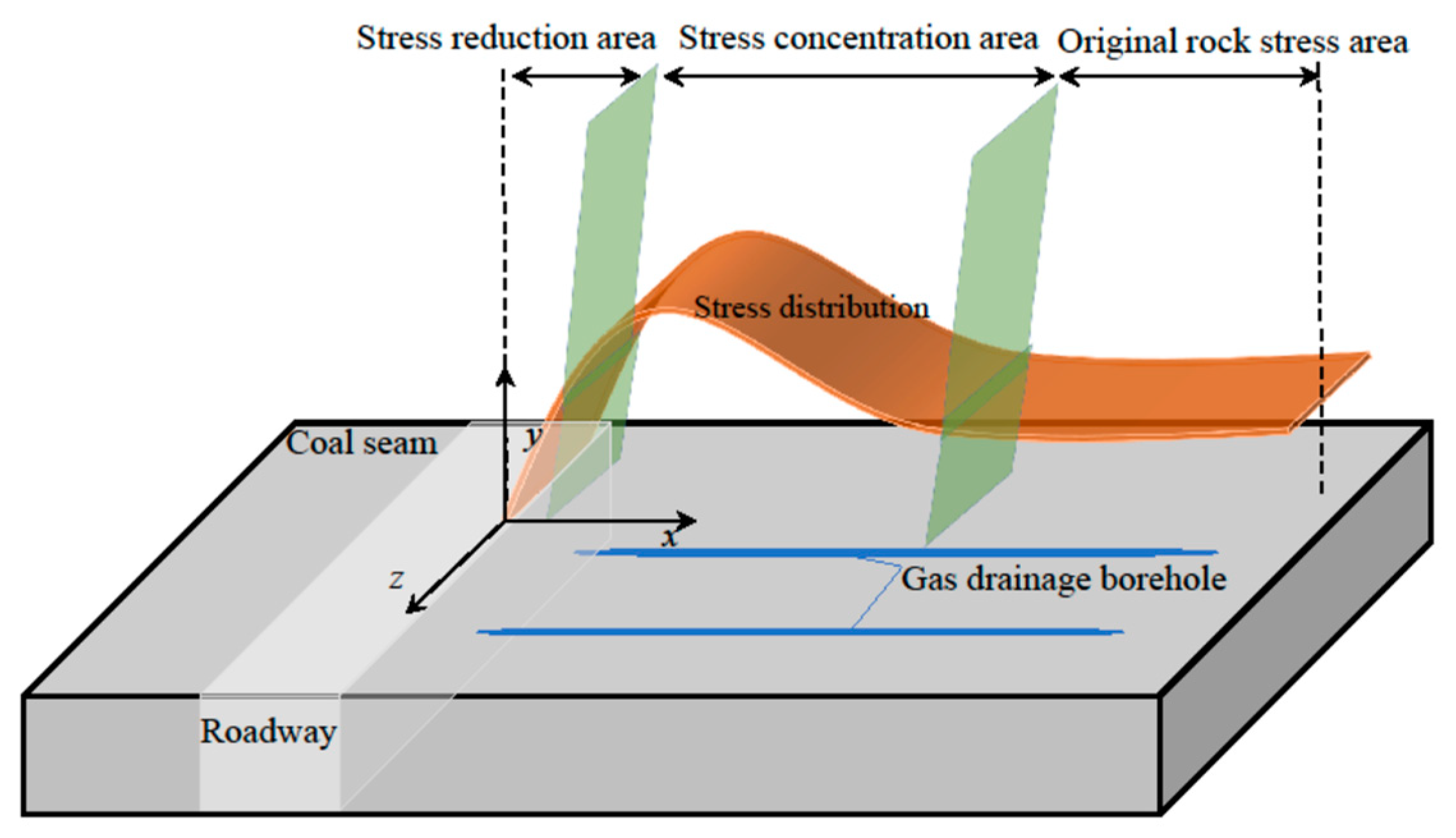
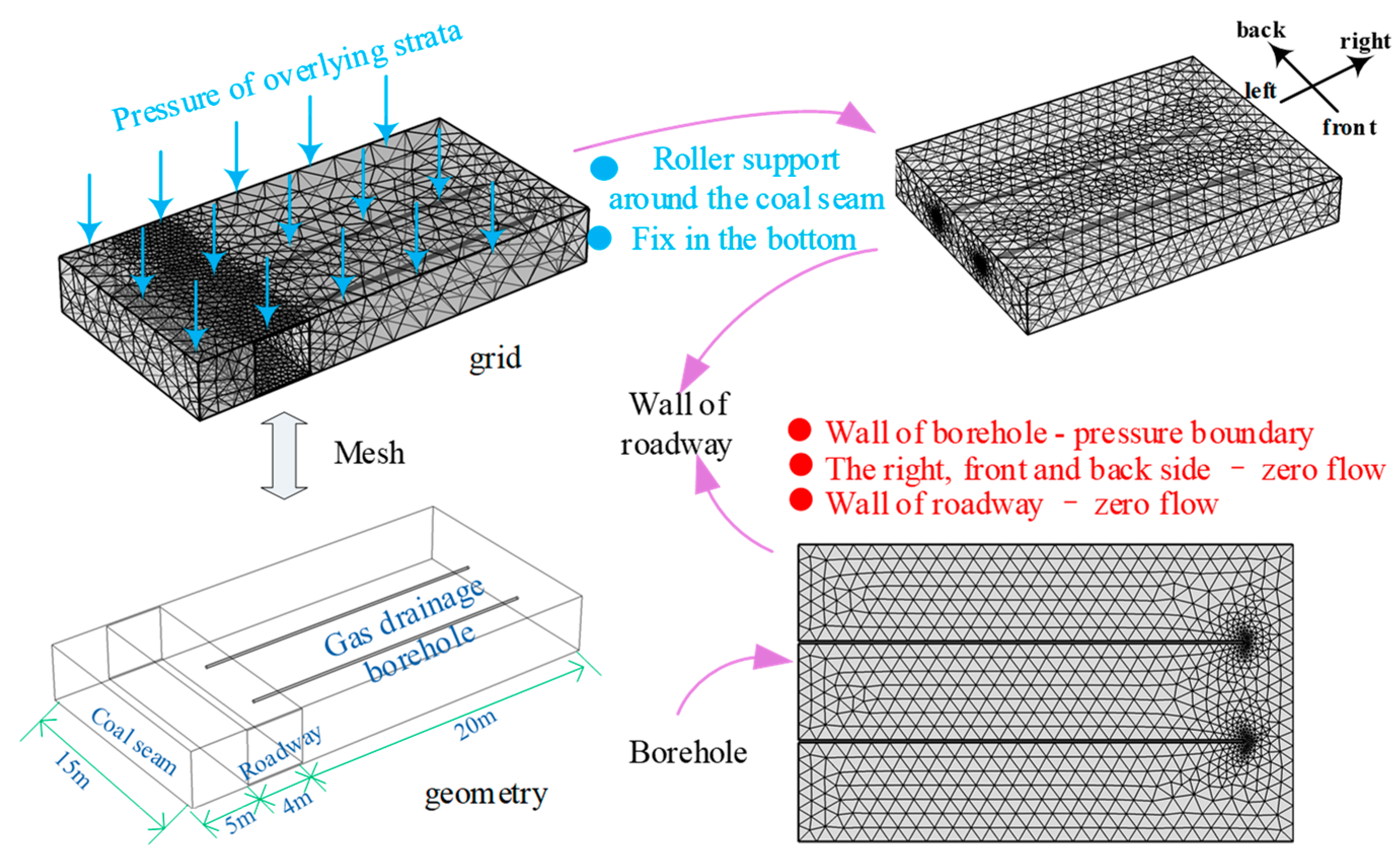
2.6. Model Settings
3. Results and Discussion
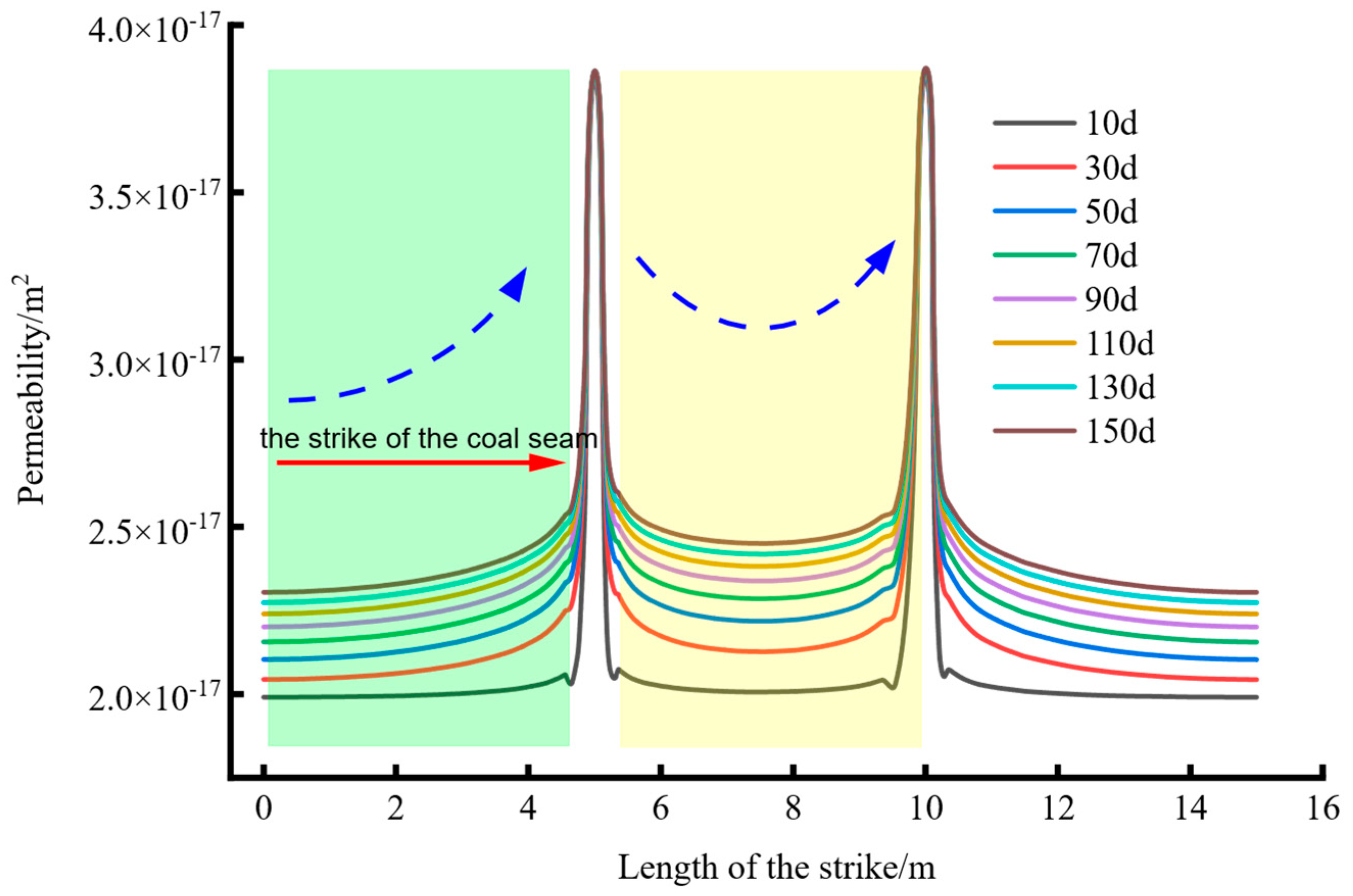
3.1. Characteristics of the Spatiotemporal Evolution of Coal Seam Permeability
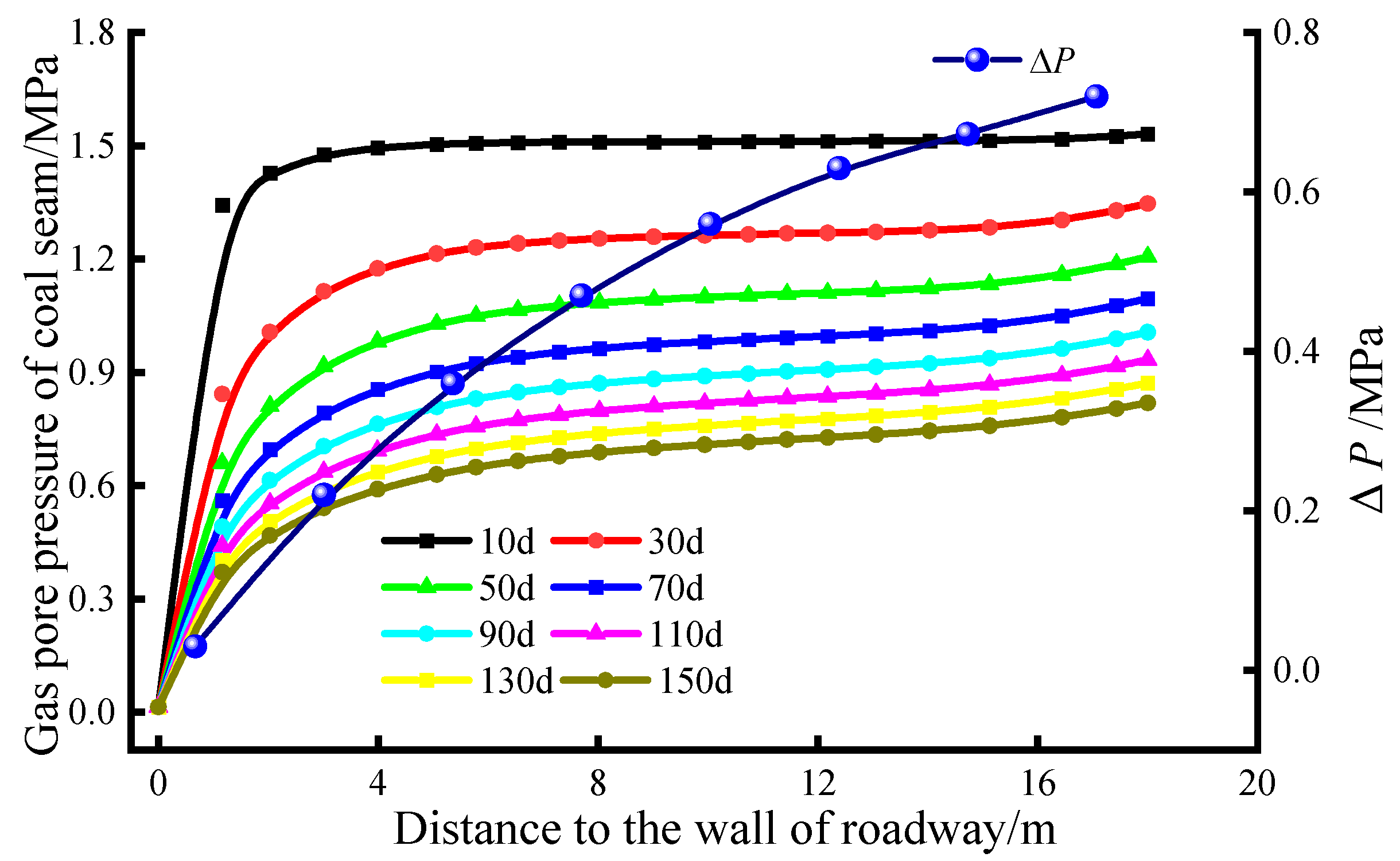
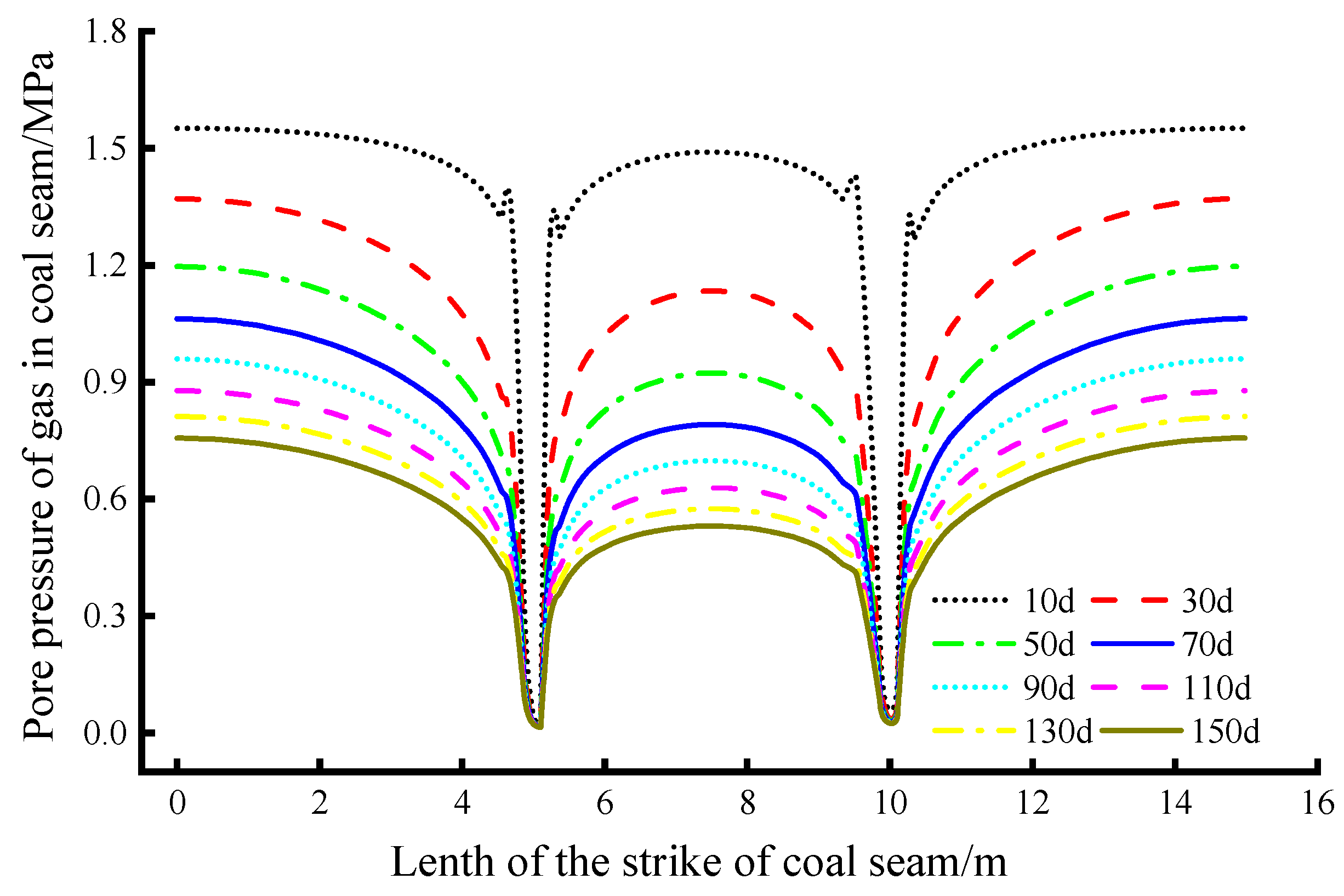
3.2. Time and Space Evolution of Coal Seam Gas Pressure
3.3. Field Test and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, L. Theory and practice of integrated coal production and gas extraction. Int. J. Coal Sci. Technol. 2015, 2, 3–11. [Google Scholar] [CrossRef]
- Pang, M.; Zhang, T.; Meng, Y.; Ling, Z. Experimental study on the permeability of crushed coal medium based on the ergun equation. Sci. Rep. 2021, 11, 23030. [Google Scholar] [CrossRef] [PubMed]
- Xia, T.; Zhou, F.; Liu, J.; Hu, S.; Liu, Y. A fully coupled coal deformation and compositional flow model for the control of the pre-mining coal seam gas extraction. Int. J. Rock Mech. Min. Sci. 2014, 72, 138–148. [Google Scholar] [CrossRef]
- Frank, H.; Ting, R.; Naj, A. Evolution and application of in-seam drilling for gas drainage. Int. J. Min. Sci. Technol. 2013, 23, 543–553. [Google Scholar] [CrossRef]
- Zhang, T.; Jing, C.; Zhang, L.; Ji, X.; Pan, H. Strain localization characteristics of perforation failure of perforated specimens. Meitan Xuebao/J. China Coal Soc. 2020, 45, 4087–4094. [Google Scholar]
- Zhang, T.; Zhang, L.; Li, S.; Liu, J.; Pan, H.; Song, S. Stress inversion of coal with a gas drilling borehole and the law of crack propagation. Energies 2017, 10, 1743. [Google Scholar] [CrossRef] [Green Version]
- Hu, G.Z.; Wang, H.T.; Tan, H.X.; Fan, X.G.; Yuan, Z.G. Gas seepage equation of deep mined coal seams and its application. J. China Univ. Min. Technol. 2008, 18, 483–487. [Google Scholar] [CrossRef]
- Lin, B.; Song, H.; Zhao, Y.; Liu, T.; Kong, J.; Huang, Z. Significance of gas flow in anisotropic coal seams to underground gas drainage. J. Pet. Sci. Eng. 2019, 180, 808–819. [Google Scholar] [CrossRef]
- Junxiang, Z.; Bo, L.; Yuning, S. Dynamic leakage mechanism of gas drainage borehole and engineering application. Int. J. Min. Sci. Technol. 2018, 28, 505–512. [Google Scholar] [CrossRef]
- Connell, L.D. Coupled flow and geomechanical processes during gas production from coal seams. Int. J. Coal Geol. 2009, 79, 18–28. [Google Scholar] [CrossRef]
- Connell, L.D.; Sander, R.; Camilleri, M.; Heryanto, D.; Pan, Z.; Lupton, N. Nitrogen enhanced drainage of co 2 rich coal seams for mining. Int. J. Min. Sci. Technol. 2017, 27, 755–761. [Google Scholar] [CrossRef]
- Celik, E.; Hoang, L. Maximum estimates for generalized forchheimer flows in heterogeneous porous media. J. Differ. Equ. 2017, 262, 2158–2195. [Google Scholar] [CrossRef] [Green Version]
- Bukowski, P. Water hazard assessment in active shafts in upper silesian coal basin mines. Mine Water Environ. 2011, 30, 302–311. [Google Scholar] [CrossRef] [Green Version]
- Davarpanah, A.; Mirshekari, B. Experimental investigation and mathematical modeling of gas diffusivity by carbon dioxide and methane kinetic adsorption. Ind. Eng. Chem. Res. 2019, 58, 12392–12400. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, Y.; Wang, H.; Zhou, H.; Liang, W.; Wei, L.; Liu, H. Numerical assessment of the effect of equilibration time on coal permeability evolution characteristics. Fuel 2015, 140, 81–89. [Google Scholar] [CrossRef]
- Wei, X.; Wang, G.G.X.; Massarotto, P.; Golding, S.D.; Rudolph, V. A review on recent advances in the numerical simulation for coalbed-methane-recovery process. SPE Reserv. Eval. Eng. 2007, 10, 657–666. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Chen, Z.; Elsworth, D.; Miao, X.; Mao, X. Evaluation of stress-controlled coal swelling processes. Int. J. Coal Geol. 2010, 83, 446–455. [Google Scholar] [CrossRef]
- Seomoon, H.; Lee, M.; Sung, W. Analysis of sorption-induced permeability reduction considering gas diffusion phenomenon in coal seam reservoir. Transport. Porous Media 2015, 108, 713–729. [Google Scholar] [CrossRef]
- Zhu, W.C.; Liu, J.; Sheng, J.C.; Elsworth, D. Analysis of coupled gas flow and deformation process with desorption and klinkenberg effects in coal seams. Int. J. Rock Mech. Min. Sci. 2007, 44, 971–980. [Google Scholar] [CrossRef]
- Wang, S.; Elsworth, D.; Liu, J. Permeability evolution during progressive deformation of intact coal and implications for instability in underground coal seams. Int. J. Rock Mech. Min. Sci. 2013, 58, 34–45. [Google Scholar] [CrossRef]
- Xue, Y.; Gao, F.; Gao, Y.; Cheng, H.; Liu, Y.; Hou, P.; Teng, T. Quantitative evaluation of stress-relief and permeability-increasing effects of overlying coal seams for coal mine methane drainage in wulan coal mine. J. Nat. Gas Sci. Eng. 2016, 32, 122–137. [Google Scholar] [CrossRef]
- Cheng, Y.; Huo, A.; Zhang, J.; Lu, Y. Early warning of meteorological geohazard in the loess plateau: A study in huangling county of shaanxi province in china. Environ. Earth Sci. 2015, 73, 1057–1065. [Google Scholar] [CrossRef]
- Tang, W.; Zhai, C.; Yu, X.; Xu, J.; Sun, Y.; Cong, Y.; Zheng, Y.; Li, Y. Numerical study on the effect of sudden change in coal property on coal and gas outburst during roadway excavation. Environ. Earth Sci. 2022, 81, 328. [Google Scholar] [CrossRef]
- Durucan, S.; Edwards, J.S. Effects of stress and fracturing on permeability of coal. Min. Sci. Technol. 1986, 3, 205–216. [Google Scholar] [CrossRef]
- Ma, Y.-K.; Nie, B.-S.; He, X.-Q.; Li, X.-C.; Meng, J.-Q.; Song, D.-Z. Mechanism investigation on coal and gas outburst: An overview. Int. J. Miner. Metall. Mater. 2020, 27, 872–887. [Google Scholar] [CrossRef]
- Guo, P.; Cao, S.-G.; Zhang, Z.-G.; Luo, F.; Liu, Y. Theoretical study of deformation model of coal swelling induced by gas adsorption. Yantu Lixue/Rock Soil Mech. 2014, 35, 3467–3472. [Google Scholar]
- Palmer, I.; Mansoori, J. How permeability depends on stress and pore pressure in coalbeds: A new model. SPE Reserv. Eng. 1998, 1, 539–543. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, Y.; Zhao, B.; Yang, D. Nonlinear coupled mathematical model for solid deformation and gas seepage in fractured media. Transp. Porous Media 2004, 55, 119–136. [Google Scholar] [CrossRef]
- Wu, Y.-S.; Pruess, K.; Persoff, P. Gas flow in porous media with klinkenberg effects. Transp. Porous Media 1998, 32, 117–137. [Google Scholar] [CrossRef]
- Mora, C.A.; Wattenbarger, R.A. Analyst and Verification of Dual Porosity and CBM Shape Factors. In Proceedings of the Canadian International Petroleum Conference, CIPC 2006, Calgary, AB, Canada, 13–15 June 2006. [Google Scholar]
- Haifeng, W.; Yuanping, C.; Lei, W. Regional gas drainage techniques in Chinese coal mines. Int. J. Min. Sci. Technol. 2012, 22, 873–878. [Google Scholar] [CrossRef]
- Zhang, T.-J.; Pang, M.-K.; Jiang, X.-K.; Peng, W.-Q.; Ji, X. Influence of negative pressure on gas percolation characteristics of coal body in perforated drilling hole. Yantu Lixue/Rock Soil Mech. 2019, 40, 2517–2524. [Google Scholar]
- Brown, E.T.; Hoek, E. Trends in relationships between measured in-situ stresses and depth. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 211–215. [Google Scholar] [CrossRef]
- Xia, T.; Zhou, F.; Liu, J.; Gao, F. Evaluation of the pre-drained coal seam gas quality. Fuel 2014, 130, 296–305. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, Y.; Li, W.; Jin, K.; He, T.; Zhao, W. Mathematical model of coupled gas flow and coal deformation process in low-permeability and first mined coal seam. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2015, 34, 2749–2758. [Google Scholar]
- Liu, T.; Lin, B. Time-dependent dynamic diffusion processes in coal: Model development and analysis. Int. J. Heat Mass Transf. 2019, 134, 1–9. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Initial permeability of coal/mD | 0.02 | Coal seam initial temperature/K | 293.14 |
| Initial porosity of coal matrix | 0.06 | Limiting Adsorption Swell Variable A | 0.004 |
| Initial gas pressure of coal fractures/MPa | 1.56 | Limiting Adsorption Swell Variable B | 0.008 |
| Initial gas pressure of coal matrix/MPa | 1.56 | Elastic modulus of coal/MPa | 2713 |
| Initial coal gas diffusion coefficient/m2·s−1 | 3.48 × 10−11 | Coal Matrix Elastic Modulus/MPa | 8139 |
| Coal apparent density/kg·m3 | 1300 | Klinkenberg coefficient/kPa | 10 |
| Gas dynamic viscosity/Pa·s | 1.84 × 10−5 | The amount of gas adsorbed per unit mass of coal, a/m3·kg−1 | 0.015 |
| Coal Poisson’s ratio | 0.35 | Adsorption constant of coalb/MPa−1 | 6.11 |
| Time of gas drainage (day) | 10 | 30 | 50 | 70 | 90 | 110 | 130 | 150 |
| Max difference of pressure (MPa) | 0.0612 | 0.2307 | 0.2740 | 0.2618 | 0.2615 | 0.2493 | 0.2371 | 0.2258 |
| The ratio of improvement (%) | 3.94% | 15.19% | 17.56% | 16.78% | 16.76% | 15.98% | 15.20% | 14.48% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Jing, C.; Li, S.; Bao, R.; Zhang, T. Seepage Law of Nearly Flat Coal Seam Based on Three-Dimensional Structure of Borehole and the Deep Soft Rock Roadway Intersection. Energies 2022, 15, 5012. https://doi.org/10.3390/en15145012
Zhang L, Jing C, Li S, Bao R, Zhang T. Seepage Law of Nearly Flat Coal Seam Based on Three-Dimensional Structure of Borehole and the Deep Soft Rock Roadway Intersection. Energies. 2022; 15(14):5012. https://doi.org/10.3390/en15145012
Chicago/Turabian StyleZhang, Lei, Chen Jing, Shugang Li, Ruoyu Bao, and Tianjun Zhang. 2022. "Seepage Law of Nearly Flat Coal Seam Based on Three-Dimensional Structure of Borehole and the Deep Soft Rock Roadway Intersection" Energies 15, no. 14: 5012. https://doi.org/10.3390/en15145012






