Application of Selected Machine Learning Techniques for Identification of Basic Classes of Partial Discharges Occurring in Paper-Oil Insulation Measured by Acoustic Emission Technique
Abstract
:1. Introduction
- Class 1—partial discharges in the needle–needle system. These discharges may correspond to the PD caused by failure to the insulation of two adjacent turns of the transformer windings.
- Class 2—partial discharges in the needle–needle system accompanied by freely displaced gas bubbles. Such PD can occur in the oil-paper insulation of the adjacent transformer windings and resulst from the fault or deterioration of the insulation system in oil with high gas mass ratio (due to the developed aging process of dielectrics).
- Class 3—discharges in the plate–needle system. These discharges may correspond to PD occurring between the faulty part of the transformer winding insulation and grounded flat parts, such as core, yoke, tank or magnetic screens.
- Class 4—discharges in the surface system of two flat and curved electrodes comprising a paper-oil insulation. PD modeling discharges occurring in the so-called triple point, i.e., at the interface of the live conductors of the transformer winding and the paper dielectric impregnated with electro-insulating oil, one in which the core has a smooth and even surface. This is the most common type of PD.
- Class 5—discharges in a surface system with one flat electrode, the other multi-needle electrode, between which there is a paper-oil insulation. Discharges that may represent PDs develop at the interface of copper conductors and the paper-oil insulation system (the so-called triple point), in the case where an irregularity occurs in the winding surface (places where a joint occurs between individual winding elements, e.g., in wire splices).
- Class 6—discharges in the multi-needle–plate in oil system. Discharges that may correspond to PDA occurring between the multi-point insulation failure of the transformer winding and grounded flat parts such as core, yoke, tank or magnetic screens.
- Class 7—discharges in the multi-needle–plate in oil system with freely displaced gas bubbles. The PD modeling discharges between the fragment of the transformer winding comprises faults as a result of the degradation of the layers of impregnated cable paper (instead of one PD generation point, there may be several or a dozen of them within a small distance), and the grounded elements such as core, yoke, tank or magnetic screens.
- Class 8—discharges in a multi-needle–plate system with freely displaced solid particles with non-specific potential. Such discharges can represent PDs that occur in transformers with a long service life, during which aging processes of paper insulation take place, combined with the separation of cellulose fibers [4,7,8,10].
2. Characteristics of Selected Machine Learning Methods
- supervised learning
- unsupervised learning
- reinforcement learning
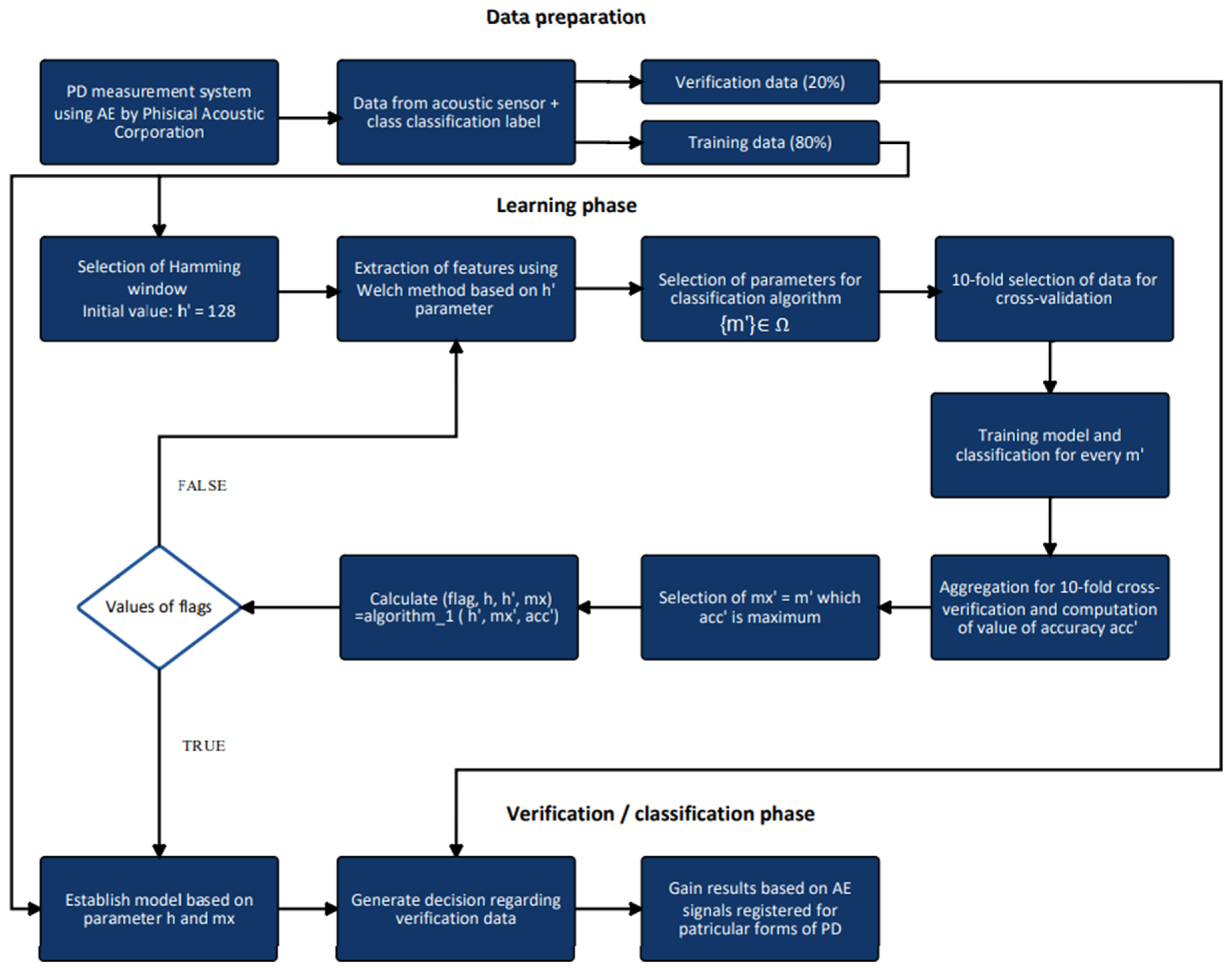
3. Methodology
| Algorithm 1 |
| 1. Get current values of acc′, mx′, h′. 2. IF first algorithm iteration: a. direction = 1; step = 0; op = 0 b. acc = acc′, mx = mx′, h = h′, h′ = h′*2; c. IF acc == 100 THEN direction = 3 and goto 5. d. flag = FALSE and goto point 6. 3. IF direction == 1 THEN a. IF acc′ > acc THEN FLAG = FALSE, step = 0, h = h′, h′ = h′*2, acc = acc′, mx = mx′, op = 1 b. IF acc′ == acc THEN FLAG = FALSE , step++, h′ = h′*2, c. IF acc′ < acc THEN FLAG = FALSE and direction = 3, d. IF step == 2 THEN direction = 3, 4. IF direction == 2 THEN a. IF acc′ >= acc THEN FLAG = FALSE, h = h′, h′ = h′/2, acc = acc′, mx = mx′, b. ELSE FLAG = TRUE 5. IF direction == 3 THEN a. IF op ==1 THEN FLAG = TRUE and goto point 6 b. ELSE h′ = h/2, direction = 2; 6. Return flag and h′. |
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Mirzaei, H.; Akbari, A.; Gockenbach, E.; Miralikhani, K. Advancing new techniques for UHF PD detection and localization in the power transformers in the factory tests. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 448–455. [Google Scholar]
- Murugan, R.; Ramasamy, R. Failure analysis of power transformer for effective maintenance planning in electric utilities. Eng. Fail. Anal. 2015, 55, 182–192. [Google Scholar] [CrossRef]
- Takahashi, R.H.C.; Diniz, H.E.P.; Carrano, E.G.; Campelo, F.; Batista, L.S. Multicriteria transformer asset management with maintenance and planning perspectives. IET Gener. Transm. Distrib. 2016, 10, 2087–2097. [Google Scholar]
- Boczar, T.; Cichon, A.; Borucki, S. Diagnostic expert system of transformer insulation systems using the acoustic emission method. IEEE Trans. Dielectr. Electr. Insul. 2015, 21, 854–865. [Google Scholar] [CrossRef]
- Fuhr, J. Procedure for identification and localization of dangerous partial discharges sources in power transformers. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 1005–1014. [Google Scholar] [CrossRef]
- Rubio-Serrano, J.; Rojas-Moreno, M.V.; Posada, J.; Martienez-Tarifa, J.M.; Robles, G.; Garcia-Souto, J.A. Electro-acoustic detection, identification and location of PD sources in oil-paper insulation systems. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1569–1578. [Google Scholar] [CrossRef]
- Boczar, T. Identification of a specific type of PD form acoustics emission frequency spectra. IEEE Trans. Dielectr. Electr. Insul. 2001, 8, 598–606. [Google Scholar] [CrossRef]
- Borucki, S.; Łuczak, J.; Zmarzły, D. Using Clustering Methods for the Identification of Acoustic Emission Signals Generated by the Selected Form of Partial Discharge in Oil-Papier Insulation. Arch. Acoust. 2018, 43, 207–215. [Google Scholar]
- Castro Heredia, L.C.; Rodrigo Mor, A. Density-based clustering methods for unsupervised separation of partial discharge sources. Int. J. Electr. Power Energy Syst. 2019, 107, 224–230. [Google Scholar]
- Boczar, T.; Borucki, S.; Cichoń, A.; Zmarzły, D. Application Possibilities of Artificial Neural Networks for Recognizing Partial Discharges Measured by the Acoustic Emission Method. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 214–223. [Google Scholar] [CrossRef]
- Boczar, T.; Borucki, S.; Cichoń, A.; Lorenc, M. Recognizing partial discharge forms measured by the acoustic emission method using the spectrum power density as a parameter of the artificial neuron network. Mol. Quantum Acoust. Annu. J. 2005, 26, 35–44. [Google Scholar]
- Kurtasz, P.; Boczar, T. The application of the optimized multicomparative algorithm for classifying acoustic signals, generated by partial discharges, cataloged in the modified database. Meas. Autom. Robot. 2010, 12, 73–79. [Google Scholar]
- Barber Bayesian, D. Reasoning and Machine Learning; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Mahdavinejad, M.S.; Rezvan, M.; Barekatain, M.; Adibi, P.; Barnaghi, P.; Sheth, A.P. Machine learning for internet of things data analysis: A survey. Digit. Commun. Netw. 2018, 4, 161–175. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Cunningham, P.; Delany, S.J. K-nearest neighbour classifiers. Mult. Classif. Syst. 2007, 34, 1–17. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Eberhart, R.C. Neural Network PC Tools: A Practical Guide; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the 13th International Conference Artificial Intelligence and Statistics (AISTATS), Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Ziółkowski, J.; Oszczypała, M.; Małachowski, J.; Szkutnik-Rogoż, J. Use of Artificial Neural Networks to Predict Fuel Consumption on the Basis of Technical Parameters of Vehicles. Energies 2021, 14, 2639. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Bro, R.; Smilde, A.K. Principal component analysis. Anal. Methods 2014, 6, 2812–2831. [Google Scholar] [CrossRef] [Green Version]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Jollie, I. Principal Component Analysis; Wiley Online Library: Hoboken, NJ, USA, 2002. [Google Scholar]
- Bach, F.R.; Jordan, M.I. Kernel independent component analysis. J. Mach. Learn. Res. 2002, 3, 1–48. [Google Scholar]
- Hotelling, H. Relations between two sets of variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Keerthi, S.S.; Shevade, S.K.; Bhattacharyya, C.; Murthy, K.R.K. Improvements to Platt’s SMO Algorithm for SVM Classifier Design. Neural Comput. 2001, 13, 637–649. [Google Scholar] [CrossRef]
- Platt, C. Sequential Minimal Optimization: A Fast Algorithm for Training Suppor Vector Machines. In Advances in Kernel Methods-Support Vector Learning; MIT Press: Cambridge, MA, USA, 1999; pp. 185–208. [Google Scholar]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef] [Green Version]
- De Lautour, O.R.; Omenzetter, P. Damage classification and estimation in experimental structures using time series analysis and pattern recognition. Mech. Syst. Signal Process. 2010, 24, 1556–1569. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H. The optimality of naive bayes. AA 2004, 1, 3. [Google Scholar]
- Rabiner, L.R. A tutorial on hidden markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef] [Green Version]
- Sejnowski, T.J.; Rosenberg, C.R. Parallel networks that learn to pronounce english text. Complex Syst. 1987, 1, 145–168. [Google Scholar]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar]
- Laerty, J.; McCallum, A.; Pereira, F. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In Proceedings of the Eighteenth International Conference on Machine Learning, ICML, Williamstown, MA, USA, 28 June–1 July 2001; Volume 1, pp. 282–289. [Google Scholar]
- Williams, R.J.; Zipser, D. A learning algorithm for continually running fully recurrent neural networks. Neural Comput. 1989, 1, 270–280. [Google Scholar] [CrossRef]
- Baltrušaitis, T.; Ahuja, C.; Morency, L. Multimodal Machine Learning: A Survey and Taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 423–443. [Google Scholar] [CrossRef] [Green Version]
- McCallum, A.; Freitag, D.; Pereira, F. Maximum Entropy Markov Models for Information Extraction and Segmentation. In Proceedings of the 17th International Conference on Machine Learning, ICML, Stanford, CA, USA, 29 June–2 July 2000; Volume 17, pp. 591–598. [Google Scholar]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electr. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Jancarczyk, D.; Bernaś, M.; Boczar, T. Classification of Low Frequency Signals Emitted by Power Transformers Using Sensors and Machine Learning Methods. Sensors 2019, 19, 4909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jancarczyk, D.; Bernaś, M.; Boczar, T. Distribution Transformer Parameters Detection Based on Low-Frequency Noise, Machine Learning Methods, and Evolutionary Algorithm. Sensors 2020, 20, 4332. [Google Scholar] [CrossRef]
- Berthold, M.R.; Cebron, N.; Dill, F.; Gabriel, T.R.; Tobias, K.; Meinl, T.; Ohl, P.; Sieb, C.; Thiel, K.; Wiswedel, B. KNIME: The Konstanz Information Miner. In Data Analysis, Machine Learning and Applications. Studies in Classification, Data Analysis, and Knowledge Organization; Preisach, C., Burkhardt, H., Schmidt-Thieme, L., Decker, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Selman, B.; Gomes, C.P. Hill-climbing search. In Encyclopedia of Cognitive Science; John Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Raymond, W.J.K.; Illias, H.A.; Bakar, A.H.A.; Mokhlis, H. Partial discharge classifications: Review of recent progress. Measurement 2015, 68, 164–181. [Google Scholar] [CrossRef] [Green Version]
- Barrios, S.; Buldain, D.; Comech, M.P.; Gilbert, I.; Orue, I. Partial Discharge Classification Using Deep Learning Methods—Survey of Recent Progress. Energies 2019, 12, 2485. [Google Scholar] [CrossRef] [Green Version]


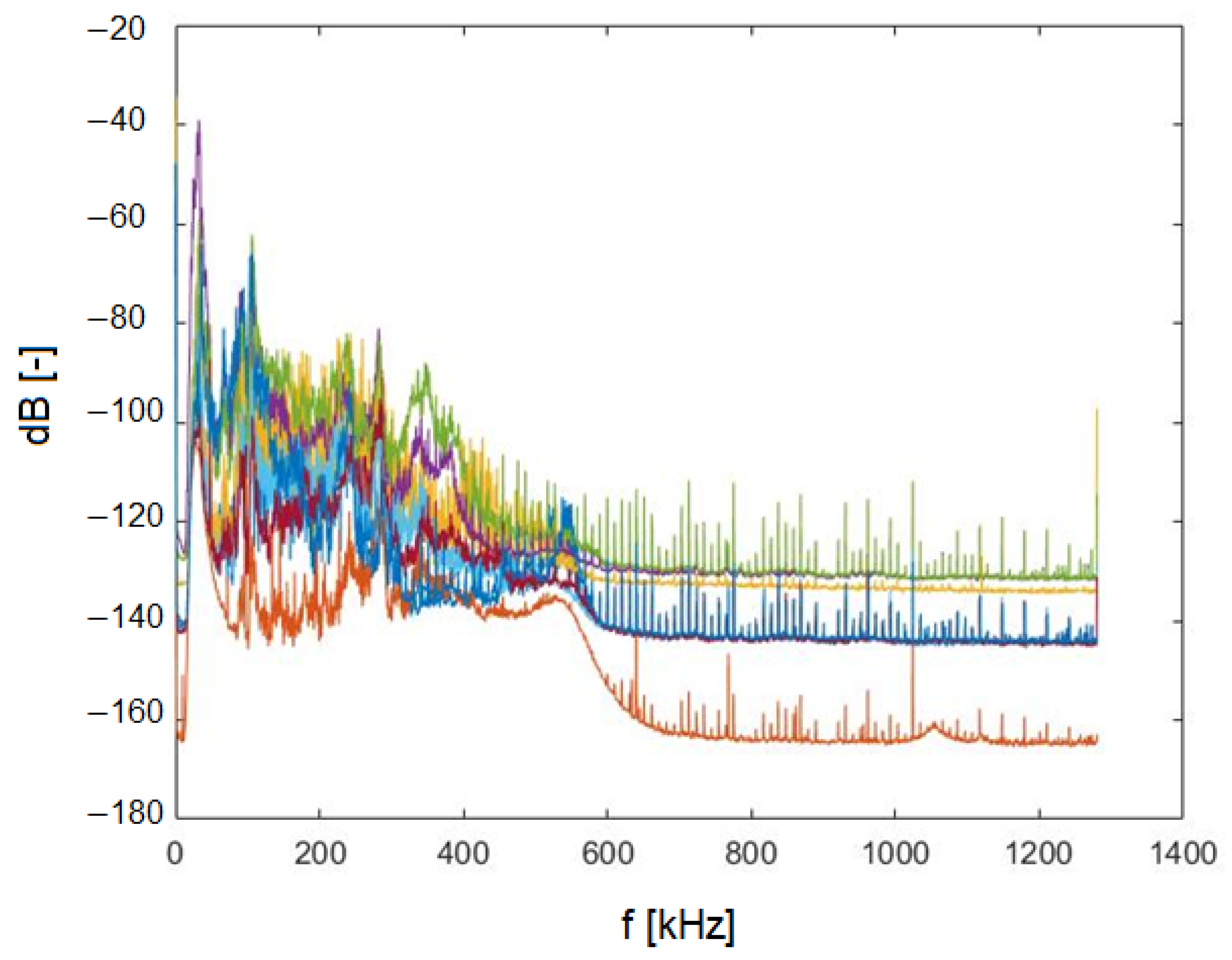
| Accuracy [%] | |||||
|---|---|---|---|---|---|
| Hamming Window | KNN | SVM | Random Trees | Bayes | PNN |
| 8192 | 99.3 | 99.9 | 97.3 | 98.2 | 91.4 |
| 4096 | 99.3 | 99.9 | 97.7 | 98.1 | 91.5 |
| 2048 | 99.2 | 99.9 | 98.6 | 98.2 | 91.3 |
| 1024 | 99.1 | 99.9 | 98.9 | 98.2 | 91.4 |
| 512 | 99.1 | 99.9 | 97.4 | 97.8 | 91.4 |
| 256 | 98.9 | 99.9 | 98.7 | 97.7 | 91.8 |
| 128 | 98.8 | 100 | 98.3 | 97.7 | 89.7 |
| 64 | 98.4 | 99.9 | 97.2 | 96 | 87.9 |
| 32 | 97.6 | 99.8 | 97.4 | 94.8 | 84.4 |
| 16 | 96.1 | 98 | 96.6 | 93.8 | 79 |
| 8 | 91.1 | 90.2 | 93 | 89.8 | 72 |
| 4 | 90.4 | 79.3 | 90.1 | 87.3 | 63.3 |
| 2 | 88.7 | 60.5 | 87.9 | 86.4 | 59.8 |
| 1 | 70.2 | 30.9 | 64.3 | 70.2 | 67.3 |
| k (Accuracy) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| It. | h′ | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 128 | 99.2 | 99.3 | 99 | 98.9 | 98.5 | 98.5 | 97.3 | 98.3 | 97.9 | 97.6 |
| 2 | 256 | 99 | 99 | 99.2 | 99 | 99.2 | 98.3 | 98.5 | 98.3 | 98.3 | 98.2 |
| 3 | 512 | 99.6 | 99.4 | 99.3 | 99 | 99.2 | 98.3 | 98.2 | 98.3 | 98.3 | 98.1 |
| 4 | 1024 | 99 | 99.2 | 98.9 | 98.9 | 98.6 | 98.9 | 98.9 | 98.6 | 98.6 | 98.6 |
| 5 | 2048 | 99.4 | 99.5 | 99.3 | 99.2 | 98.7 | 98.9 | 98.8 | 98.8 | 98.5 | 98.5 |
| SVM | |||||
|---|---|---|---|---|---|
| It. | h′ | P | B | g | Acc |
| 1a | 128 | 1.2 | 0.6 | 0.6 | 100 |
| 1b | 128 | 1 | 1.4 | 0.6 | 100 |
| 2a | 64 | 0.6 | 0.6 | 0.6 | 99.9 |
| 2b | 64 | 0.6 | 1 | 0.6 | 99.9 |
| 2c | 64 | 1 | 0.6 | 0.8 | 99.9 |
| ML Method | ML Method Parameters | Training | Accuracy | Cohen Cappa |
|---|---|---|---|---|
| kNN | h = 512, k = 3 | 99.7% | 100% | 100% |
| naive Bayes | h = 1024 | 98.2% | 97.8% | 97.5% |
| MLP | h = 256, tm = 0.2, tp = 0.4 | 91.4% | 92.2% | 91.1% |
| RF | h = 128, t = 12 | 98.4% | 97.2% | 96.8% |
| SVM | h = 128, p = 1.2, b = 0.6, g = 0.6 | 100% | 100% | 100% |
| Class | True Positive | False Positive | True Negative | False Negative | Recall | Accuracy | Sensitivity | Specificity | f-Measure |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 22 | 0 | 157 | 1 | 96% | 100% | 96% | 100% | 98% |
| 2 | 23 | 0 | 157 | 0 | 100% | 100% | 100% | 100% | 100% |
| 3 | 23 | 0 | 157 | 0 | 100% | 100% | 100% | 100% | 100% |
| 4 | 21 | 1 | 157 | 1 | 95% | 95% | 95% | 99% | 95% |
| 5 | 20 | 2 | 157 | 1 | 95% | 91% | 95% | 99% | 93% |
| 6 | 18 | 2 | 158 | 2 | 90% | 90% | 90% | 99% | 90% |
| 7 | 22 | 3 | 153 | 2 | 92% | 88% | 92% | 98% | 90% |
| 8 | 23 | 0 | 156 | 1 | 96% | 100% | 96% | 100% | 98% |
| Class | True Positive | False Positive | True Negative | False Negative | Recall | Accuracy | Sensitivity | Specificity | f-Measure |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 22 | 0 | 157 | 1 | 96% | 100% | 96% | 100% | 98% |
| 2 | 23 | 0 | 157 | 0 | 100% | 100% | 100% | 100% | 100% |
| 3 | 23 | 0 | 157 | 0 | 100% | 100% | 100% | 100% | 100% |
| 4 | 22 | 2 | 156 | 0 | 100% | 92% | 100% | 99% | 96% |
| 5 | 19 | 0 | 159 | 2 | 90% | 100% | 90% | 100% | 95% |
| 6 | 19 | 0 | 160 | 1 | 95% | 100% | 95% | 100% | 97% |
| 7 | 24 | 2 | 154 | 0 | 100% | 92% | 100% | 99% | 96% |
| 8 | 24 | 0 | 156 | 0 | 100% | 100% | 100% | 100% | 100% |
| Class | True Positive | False Positive | True Negative | False Negative | Recall | Accuracy | Sensitivity | Specificity | f-Measure |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 22 | 1 | 156 | 1 | 96% | 96% | 96% | 99% | 96% |
| 2 | 23 | 9 | 148 | 0 | 100% | 72% | 100% | 94% | 84% |
| 3 | 23 | 1 | 156 | 0 | 100% | 96% | 100% | 99% | 98% |
| 4 | 21 | 1 | 157 | 1 | 95% | 95% | 95% | 99% | 95% |
| 5 | 20 | 1 | 158 | 1 | 95% | 95% | 95% | 99% | 95% |
| 6 | 18 | 1 | 159 | 2 | 90% | 95% | 90% | 99% | 92% |
| 7 | 15 | 0 | 156 | 9 | 63% | 100% | 63% | 100% | 77% |
| 8 | 24 | 0 | 156 | 0 | 100% | 100% | 100% | 100% | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boczar, T.; Borucki, S.; Jancarczyk, D.; Bernas, M.; Kurtasz, P. Application of Selected Machine Learning Techniques for Identification of Basic Classes of Partial Discharges Occurring in Paper-Oil Insulation Measured by Acoustic Emission Technique. Energies 2022, 15, 5013. https://doi.org/10.3390/en15145013
Boczar T, Borucki S, Jancarczyk D, Bernas M, Kurtasz P. Application of Selected Machine Learning Techniques for Identification of Basic Classes of Partial Discharges Occurring in Paper-Oil Insulation Measured by Acoustic Emission Technique. Energies. 2022; 15(14):5013. https://doi.org/10.3390/en15145013
Chicago/Turabian StyleBoczar, Tomasz, Sebastian Borucki, Daniel Jancarczyk, Marcin Bernas, and Pawel Kurtasz. 2022. "Application of Selected Machine Learning Techniques for Identification of Basic Classes of Partial Discharges Occurring in Paper-Oil Insulation Measured by Acoustic Emission Technique" Energies 15, no. 14: 5013. https://doi.org/10.3390/en15145013
APA StyleBoczar, T., Borucki, S., Jancarczyk, D., Bernas, M., & Kurtasz, P. (2022). Application of Selected Machine Learning Techniques for Identification of Basic Classes of Partial Discharges Occurring in Paper-Oil Insulation Measured by Acoustic Emission Technique. Energies, 15(14), 5013. https://doi.org/10.3390/en15145013









