Combining Deep Learning and the Heat Flux Method for In-Situ Thermal-Transmittance Measurement Improvement
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical U-Value
2.2. Heat-Flux Method
- The heat transfer coefficients and thermal properties of the materials are constant under actual ambient conditions during the test.
- The heat storage effect is negligible. This usually results in long measurement periods.
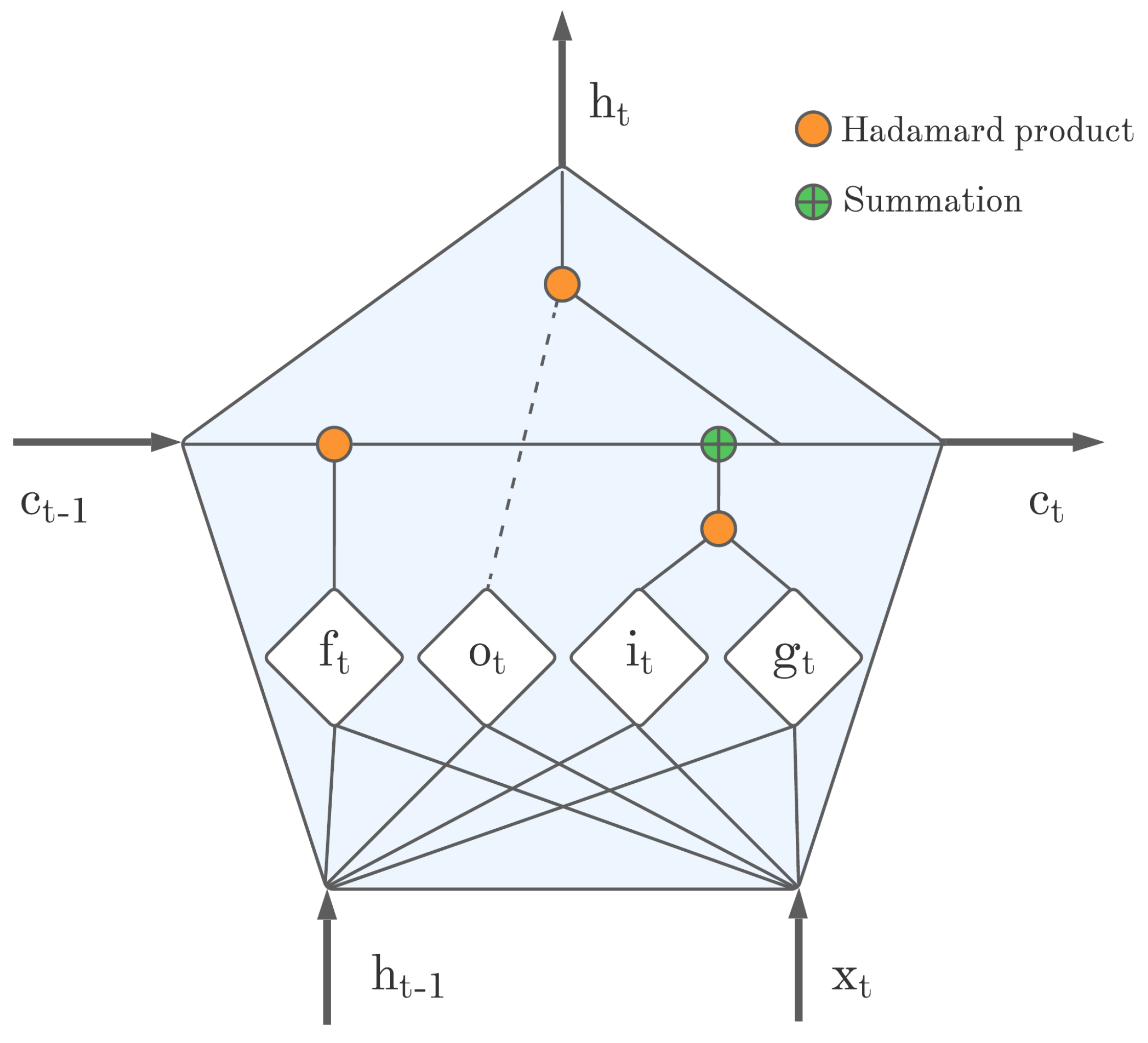
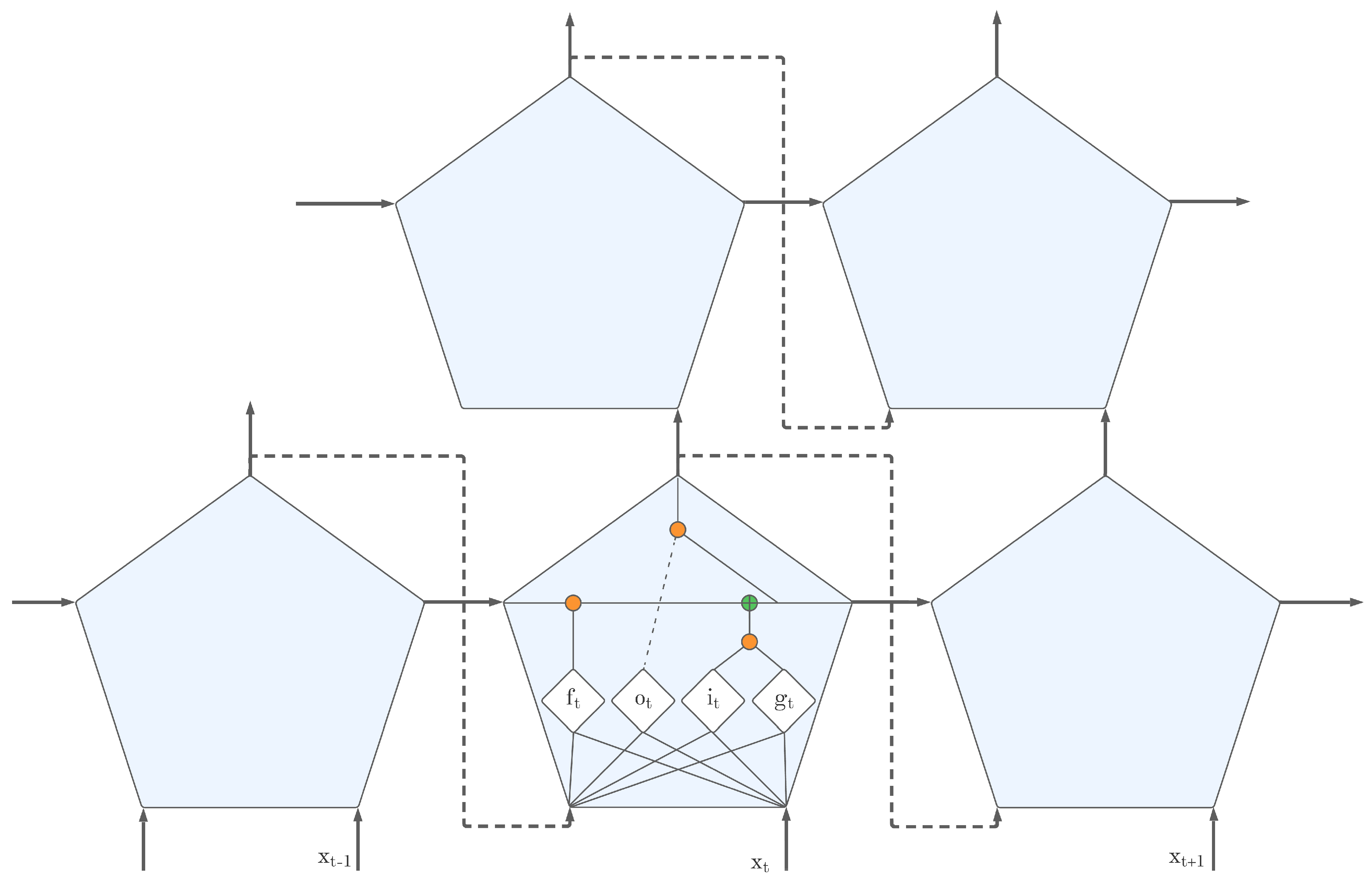
2.3. Long Short-Term Memory Units Deep-Learning Model
2.4. Experimental Setup and Research Design
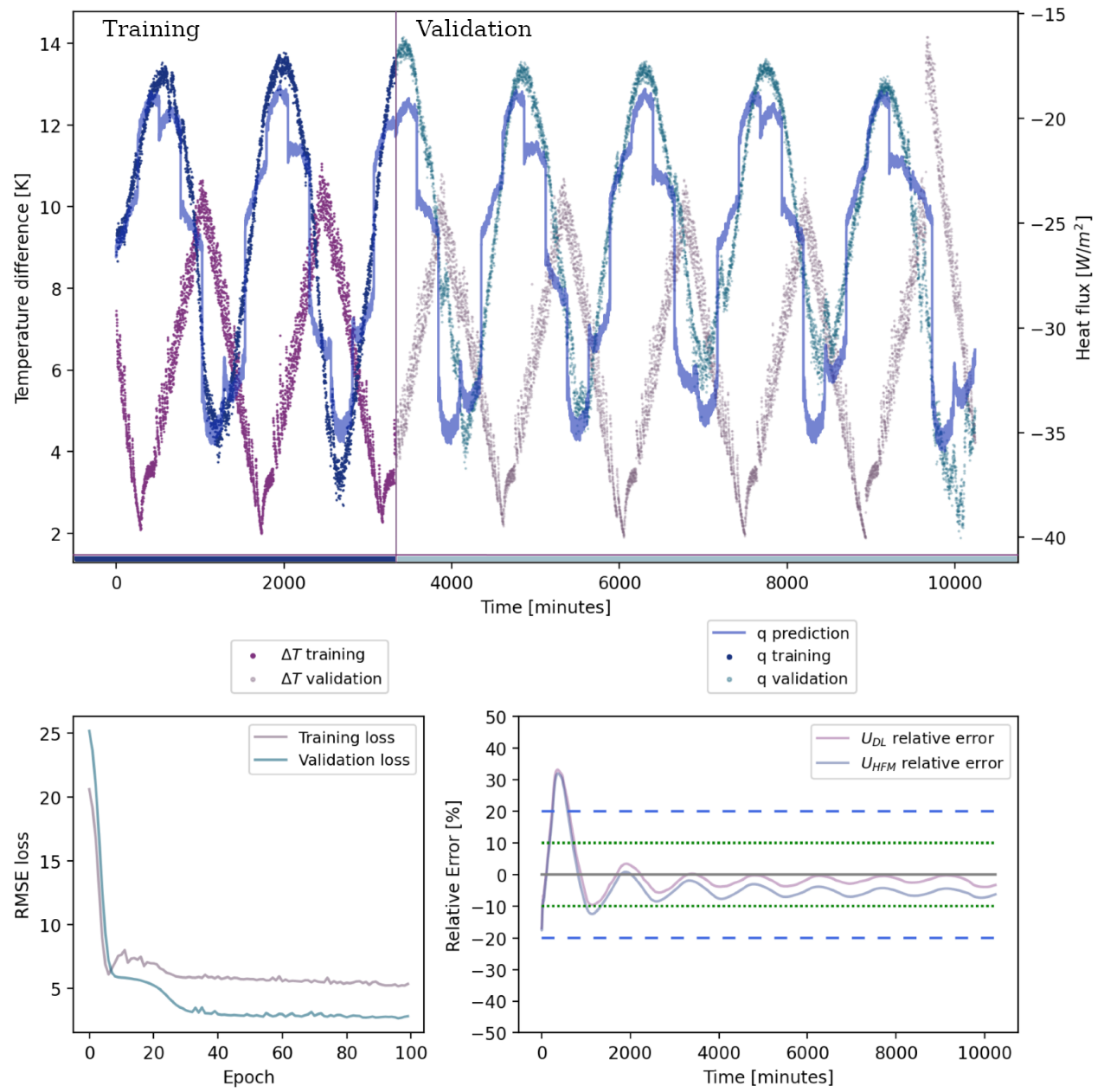
3. Results
Pilot In-Situ Measurement
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Commission, E. A Clean Planet for All—A European Strategic Long-Term Vision for A Prosperous, Modern, Competitive and Climate Neutral Economy; (COM (2018) 773 Final); European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Buildings Performance Institute Europe (BPIE). State of the Building Stock Briefing; BPIE: Brussels, Belgium, 2017. [Google Scholar]
- Jensen, P.A.; Maslesa, E.; Berg, J.B.; Thuesen, C. 10 questions concerning sustainable building renovation. Build. Environ. 2018, 143, 130–137. [Google Scholar] [CrossRef]
- Laaroussi, Y.; Bahrar, M.; Zavrl, E.; Mankibi, M.E.; Stritih, U. New qualitative approach based on data analysis of European building stock and retrofit market. Sustain. Cities Soc. 2020, 63, 102452. [Google Scholar] [CrossRef]
- Kavgic, M.; Mavrogianni, A.; Mumovic, D.; Summerfield, A.; Stevanovic, Z.; Djurovic-Petrovic, M. A review of bottom-up building stock models for energy consumption in the residential sector. Build. Environ. 2010, 45, 1683–1697. [Google Scholar] [CrossRef]
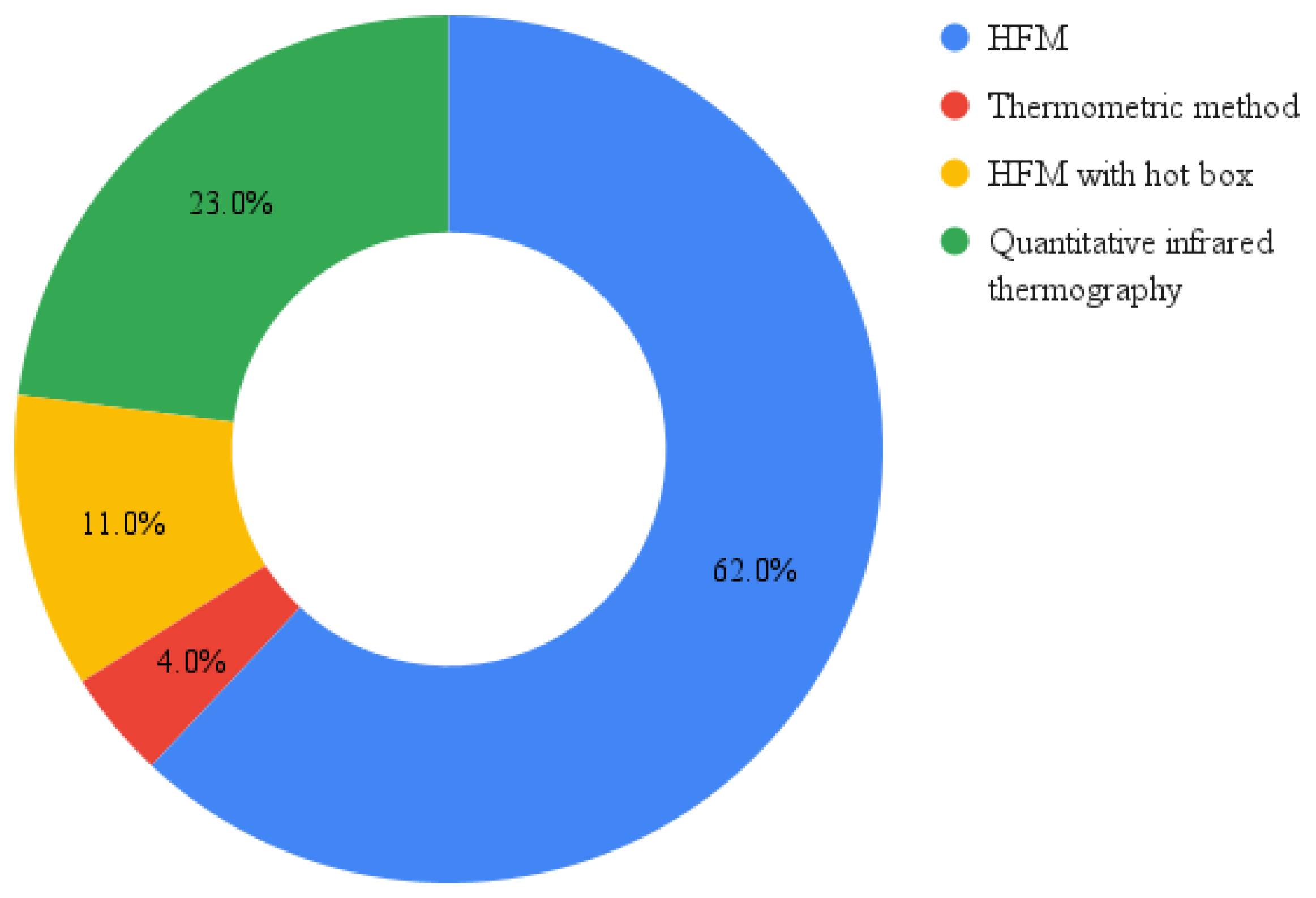
- Nardi, I.; Lucchi, E.; de Rubeis, T.; Ambrosini, D. Quantification of heat energy losses through the building envelope: A state-of-the-art analysis with critical and comprehensive review on infrared thermography. Build. Environ. 2018, 146, 190–205. [Google Scholar] [CrossRef] [Green Version]
- Bazazzadeh, H.; Pilechiha, P.; Nadolny, A.; Mahdavinejad, M.; sara Hashemi safaei, S. The Impact Assessment of Climate Change on Building Energy Consumption in Poland. Energies 2021, 14, 4084. [Google Scholar] [CrossRef]
- Ji, Q.; Bi, Y.; Makvandi, M.; Deng, Q.; Zhou, X.; Li, C. Modelling Building Stock Energy Consumption at the Urban Level from an Empirical Study. Buildings 2022, 12, 385. [Google Scholar] [CrossRef]
- Yadav, M.; Agarwal, M. Biobased building materials for sustainable future: An overview. Mater. Today Proc. 2021, 43, 2895–2902. [Google Scholar] [CrossRef]
- Shawa, B.A. The ability of Building Stock Energy Models (BSEMs) to facilitate the sector’s climate change target in the face of socioeconomic uncertainties: A review. Energy Build. 2022, 254, 111634. [Google Scholar] [CrossRef]
- Li, X.; Yao, R. Modelling heating and cooling energy demand for building stock using a hybrid approach. Energy Build. 2021, 235, 110740. [Google Scholar] [CrossRef]
- Martín-Garín, A.; Millán-García, J.A.; Terés-Zubiaga, J.; Oregi, X.; Rodríguez-Vidal, I.; Baïri, A. Improving Energy Performance of Historic Buildings through Hygrothermal Assessment of the Envelope. Buildings 2021, 11, 410. [Google Scholar] [CrossRef]
- Buda, A.; de Place Hansen, E.J.; Rieser, A.; Giancola, E.; Pracchi, V.N.; Mauri, S.; Marincioni, V.; Gori, V.; Fouseki, K.; López, C.S.P.; et al. Conservation-Compatible Retrofit Solutions in Historic Buildings: An Integrated Approach. Sustainability 2021, 13, 2927. [Google Scholar] [CrossRef]
- Lizarraga, J.M.P.S.; Picallo-Perez, A. Design and optimization of the envelope and thermal installations of buildings. In Exergy Analysis and Thermoeconomics of Buildings; Elsevier: Amsterdam, The Netherlands, 2020; pp. 911–1005. [Google Scholar] [CrossRef]
- Thani, S.K.S.O.; Mohamad, N.H.N.; Idilfitri, S. Modification of Urban Temperature in Hot-Humid Climate Through Landscape Design Approach: A Review. Procedia-Soc. Behav. Sci. 2012, 68, 439–450. [Google Scholar] [CrossRef] [Green Version]
- Milovanović, B.; Bagarić, M. How to achieve Nearly zero-energy buildings standard. J. Croat. Assoc. Civ. Eng. 2020, 72, 703–720. [Google Scholar] [CrossRef]
- Gaši, M.; Milovanović, B.; Gumbarević, S. Comparison of Infrared Thermography and Heat Flux Method for Dynamic Thermal Transmittance Determination. Buildings 2019, 9, 132. [Google Scholar] [CrossRef] [Green Version]
- Gomes, M.G.; Flores-Colen, I.; Manga, L.; Soares, A.; de Brito, J. The influence of moisture content on the thermal conductivity of external thermal mortars. Constr. Build. Mater. 2017, 135, 279–286. [Google Scholar] [CrossRef]
- Lucchi, E. Thermal transmittance of historical brick masonries: A comparison among standard data, analytical calculation procedures, and in situ heat flow meter measurements. Energy Build. 2017, 134, 171–184. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Moyano, J.; Marín, D.; Fresco-Contreras, R. Review of in situ methods for assessing the thermal transmittance of walls. Renew. Sustain. Energy Rev. 2019, 102, 356–371. [Google Scholar] [CrossRef]
- Martin, M.; Chong, A.; Biljecki, F.; Miller, C. Infrared thermography in the built environment: A multi-scale review. Renew. Sustain. Energy Rev. 2022, 165, 112540. [Google Scholar] [CrossRef]
- ISO 9869-1:2014; Thermal Insulation—Building Elements—In-Situ Measurement of Thermal Resistance and Thermal Transmittance—Part 1: Heat Flow Meter Method. International Organization for Standardization (ISO): Geneva, Switzerland, 2014.
- Evangelisti, L.; Scorza, A.; Vollaro, R.D.L.; Sciuto, S.A. Comparison between Heat Flow Meter (HFM) and Thermometric (THM) Method for Building Wall Thermal Characterization: Latest Advances and Critical Review. Sustainability 2022, 14, 693. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D. Assessing the Environmental Impact of Thermal Transmittance Tests Performed in Façades of Existing Buildings: The Case of Spain. Sustainability 2020, 12, 6247. [Google Scholar] [CrossRef]
- Tejedor, B.; Gaspar, K.; Casals, M.; Gangolells, M. Analysis of the Applicability of Non-Destructive Techniques to Determine In Situ Thermal Transmittance in Passive House Façades. Appl. Sci. 2020, 10, 8337. [Google Scholar] [CrossRef]
- Trabelsi, A.; Belarbi, R.; Abahri, K.; Qin, M. Assessment of temperature gradient effects on moisture transfer through thermogradient coefficient. Build. Simul. 2012, 5, 107–115. [Google Scholar] [CrossRef]
- Nardi, I.; Ambrosini, D.; de Rubeis, T.; Sfarra, S.; Perilli, S.; Pasqualoni, G. A comparison between thermographic and flow-meter methods for the evaluation of thermal transmittance of different wall constructions. J. Phys. Conf. Ser. 2015, 655, 012007. [Google Scholar] [CrossRef] [Green Version]
- Evangelisti, L.; Guattari, C.; Asdrubali, F. Comparison between heat-flow meter and Air-Surface Temperature Ratio techniques for assembled panels thermal characterization. Energy Build. 2019, 203, 109441. [Google Scholar] [CrossRef]
- Rezvani, F.; Bribián, I.Z. Evaluating in-situ thermal transmittance measurement to analyze devia-tions between actual house thermal performance and modelled one by means of energy simulation software. Rev. Constr. 2019, 18, 311–322. [Google Scholar] [CrossRef]
- ISO 6946:2017; Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods. International Organization for Standardization (ISO): Geneva, Switzerland, 2017.
- Roque, E.; Vicente, R.; Almeida, R.M.; da Silva, J.M.; Ferreira, A.V. Thermal characterisation of traditional wall solution of built heritage using the simple hot box-heat flow meter method: In situ measurements and numerical simulation. Appl. Therm. Eng. 2020, 169, 114935. [Google Scholar] [CrossRef]
- Meng, X.; Luo, T.; Gao, Y.; Zhang, L.; Shen, Q.; Long, E. A new simple method to measure wall thermal transmittance in situ and its adaptability analysis. Appl. Therm. Eng. 2017, 122, 747–757. [Google Scholar] [CrossRef]
- Gaspar, K.; Casals, M.; Gangolells, M. In situ measurement of façades with a low U-value: Avoiding deviations. Energy Build. 2018, 170, 61–73. [Google Scholar] [CrossRef]
- Marquez, J.M.A.; Bohorquez, M.A.M.M.S.G. A New Metre for Cheap, Quick, Reliable and Simple Thermal Transmittance (U-Value) Measurements in Buildings. Sensors 2017, 17, 2017. [Google Scholar] [CrossRef] [Green Version]
- Bienvenido-Huertas, D.; Moyano, J.; Rodríguez-Jiménez, C.E.; Marín, D. Applying an artificial neural network to assess thermal transmittance in walls by means of the thermometric method. Appl. Energy 2019, 233–234, 1–14. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Rubio-Bellido, C.; Pérez-Ordóñez, J.L.; Moyano, J. Optimizing the evaluation of thermal transmittance with the thermometric method using multilayer perceptrons. Energy Build. 2019, 198, 395–411. [Google Scholar] [CrossRef]
- Gumbarević, S.; Milovanović, B.; Gaši, M.; Bagarić, M. Application of Multilayer Perceptron Method on Heat Flow Meter Results for Reducing the Measurement Time. Eng. Proc. 2020, 2, 29. [Google Scholar] [CrossRef]
- Gumbarević, S.; Milovanović, B.; Gaši, M.; Bagarić, M. Thermal transmittance prediction based on the application of artificial neural networks on heat flux method results. J. Phys. Conf. Ser. 2021, 2069, 012152. [Google Scholar] [CrossRef]
- Chen, L.; Zhan, C.; Li, G.; Zhang, A. An artificial neural network identification method for thermal resistance of exterior walls of buildings based on numerical experiments. Build. Simul. 2019, 12, 425–440. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A Review of Machine Learning Interpretability Methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef] [PubMed]
- Namuduri, S.; Narayanan, B.N.; Davuluru, V.S.P.; Burton, L.; Bhansali, S. Review—Deep Learning Methods for Sensor Based Predictive Maintenance and Future Perspectives for Electrochemical Sensors. J. Electrochem. Soc. 2020, 167, 037552. [Google Scholar] [CrossRef]
- Thomas, L.; Marino, B.; Muñoz, N. Steady-state and time-dependent heat fluxes through building envelope walls: A quantitative analysis to determine their relative significance all year round. J. Build. Eng. 2020, 29, 101122. [Google Scholar] [CrossRef]
- Gumbarević, S.; Dunović, I.B.; Milovanović, B.; Gaši, M. Method for Building Information Modeling Supported Project Control of Nearly Zero-Energy Building Delivery. Energies 2020, 13, 5519. [Google Scholar] [CrossRef]
- Gaspar, K.; Casals, M.; Gangolells, M. Influence of HFM Thermal Contact on the Accuracy of In Situ Measurements of Façades’ U-Value in Operational Stage. Appl. Sci. 2021, 11, 979. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Rubio-Bellido, C.; Pérez-Ordóñez, J.L.; Oliveira, M.J. Automation and optimization of in-situ assessment of wall thermal transmittance using a Random Forest algorithm. Build. Environ. 2020, 168, 106479. [Google Scholar] [CrossRef]
- Asdrubali, F.; D’Alessandro, F.; Baldinelli, G.; Bianchi, F. Evaluating in situ thermal transmittance of green buildings masonries—A case study. Case Stud. Constr. Mater. 2014, 1, 53–59. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sak, H.; Senior, A.; Beaufays, F. Long Short-Term Memory Based Recurrent Neural Network Architectures for Large Vocabulary Speech Recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Zia, T.; Zahid, U. Long short-term memory recurrent neural network architectures for Urdu acoustic modeling. Int. J. Speech Technol. 2018, 22, 21–30. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutnik, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [Green Version]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Smith, S.L.; Kindermans, P.J.; Le, Q.V. Don’t Decay the Learning Rate, Increase the Batch Size. arXiv 2017, arXiv:1711.00489. [Google Scholar]
- Hoffer, E.; Hubara, I.; Soudry, D. Train Longer, Generalize Better: Closing the Generalization Gap in Large Batch Training of Neural Networks. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017. NIPS’17. pp. 1729–1739. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Alizadeh, S.; Fazel, A. Convolutional Neural Networks for Facial Expression Recognition. arXiv 2017, arXiv:cs.CV/1704.06756. [Google Scholar]
- Zeng, S.; Zhang, B.; Zhang, Y.; Gou, J. Collaboratively Weighting Deep and Classic Representation via l2 Regularization for Image Classification. In Proceedings of the 10th Asian Conference on Machine Learning, Beijing, China, 14–16 November 2018; Volume 95, pp. 502–517. [Google Scholar]
- Cobbe, K.; Klimov, O.; Hesse, C.; Kim, T.; Schulman, J. Quantifying Generalization in Reinforcement Learning. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; Volume 97, pp. 1282–1289. [Google Scholar]
- Republic of Croatia Ministry of Construction and Physical Planning. Technical Regulation on Rational Use of Energy and Heat Retention in Buildings; Republic of Croatia Ministry of Construction and Physical Planning: Zagreb, Croatia, 2015.
- Gumbarević, S. 2022. Available online: https://github.com/sanjin94/HFMpred (accessed on 10 May 2022).
- Chattopadhyay, A.; Hassanzadeh, P.; Subramanian, D. Data-driven prediction of a multi-scale Lorenz 96 chaotic system using deep learning methods: Reservoir computing, ANN, and RNN-LSTM. Nonlin. Processes Geophys. 2020, 27, 373–389. [Google Scholar] [CrossRef]
- Martinuzzi, F.; Rackauckas, C.; Abdelrehim, A.; Mahecha, M.D.; Mora, K. ReservoirComputing.jl: An Efficient and Modular Library for Reservoir Computing Models. arXiv 2022, arXiv:2204.05117. [Google Scholar]




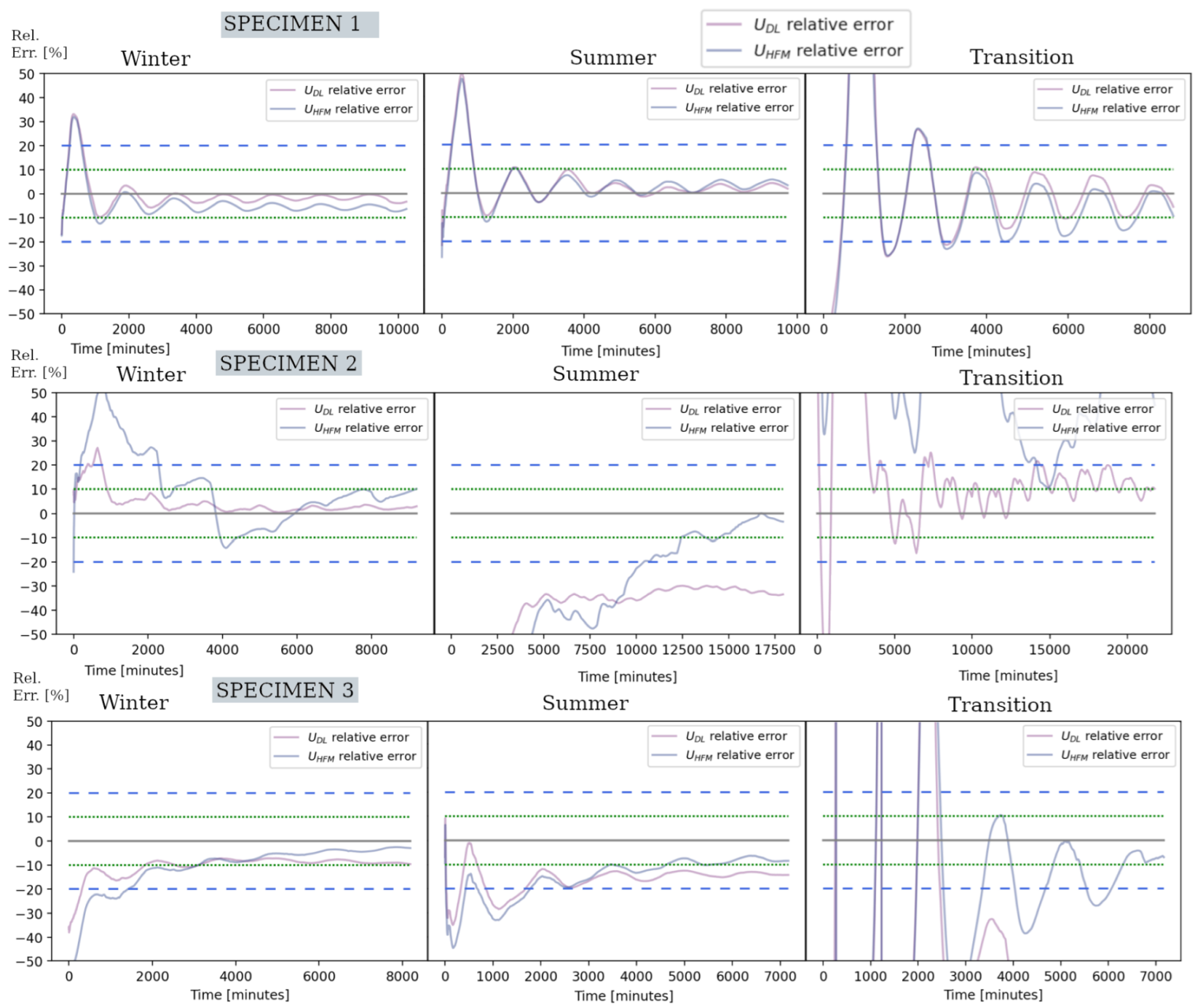
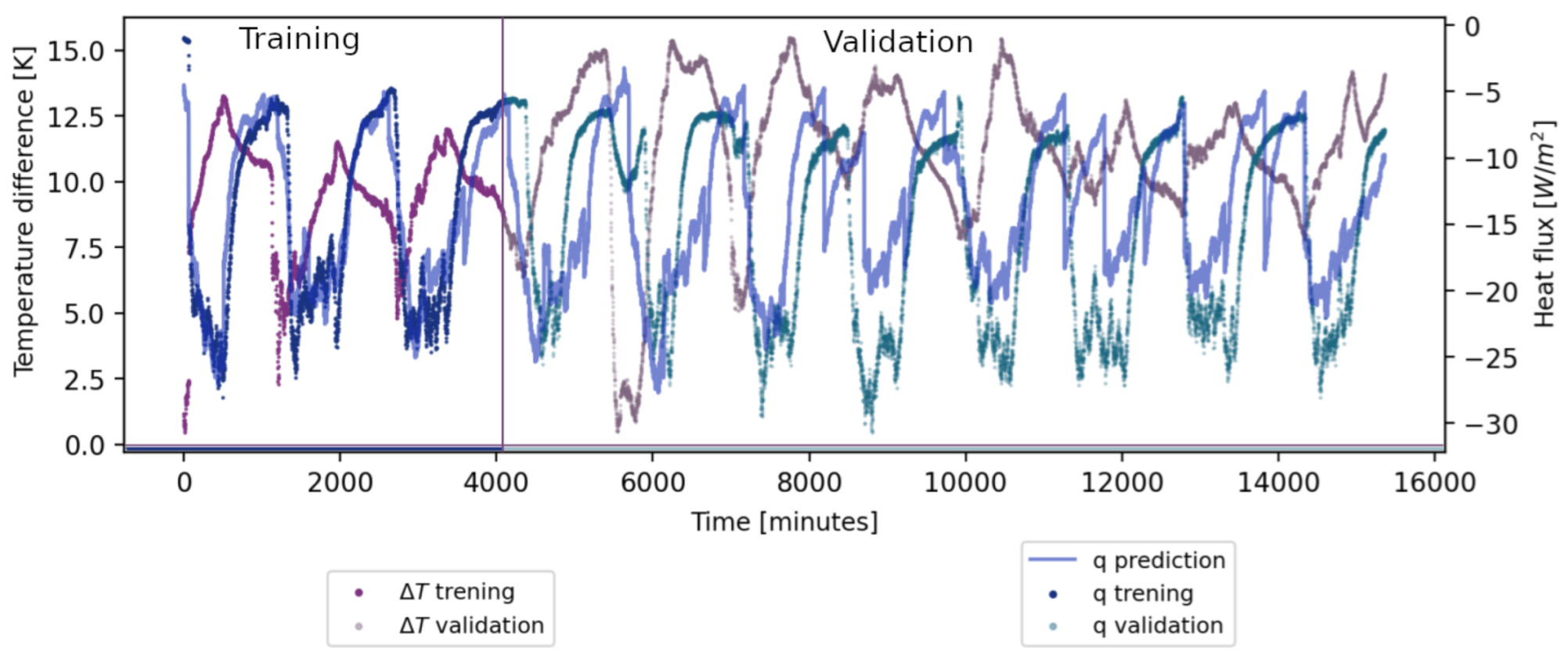
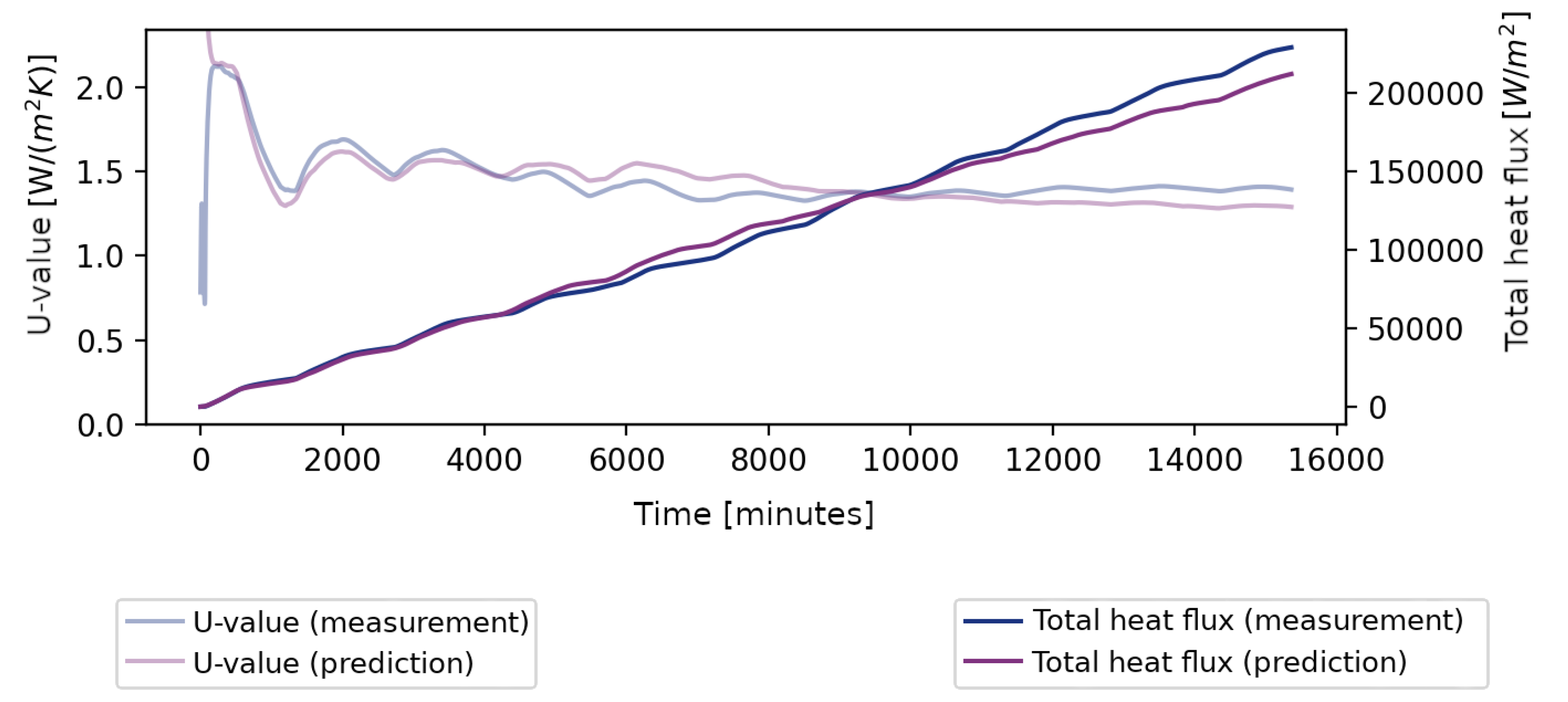
| Test Duration | End vs. (End—24 h) | First 2/3 vs. Last 2/3 |
|---|---|---|
| min 72 h | ≤5% | ≤5% |
| Specimen | Layer | Layers Thickness [m] | [W/(m K)] [61] | [m2 K/W] [30] | U [W/(m2 K)] [30] |
|---|---|---|---|---|---|
| S1 | concrete | 0.135 | 2.0 | 0.25 | 4.30 |
| concrete | 0.135 | 2.0 | |||
| S2 | mineral wool | 0.16 | 0.035 | 4.82 | 0.21 |
| EPS | 0.16 | 0.035 | |||
| S3 | concrete | 0.135 | 2.0 | 4.82 | 0.21 |
| Model | Number of Layers | Batch Size | Dropout Probability | L2 Regularization Parameter | Number of Epochs |
|---|---|---|---|---|---|
| S1 winter | 16 | 256 | 0.5 | 0.05 | 100 |
| S1 summer | 4 | 512 | 0.05 | 0.01 | 200 |
| S1 transition | 4 | 128 | 0 | 0.1 | 80 |
| S2 winter | 16 | 128 | 0.5 | 0.01 | 100 |
| S2 summer | 16 | 512 | 0.5 | 0.008 | 60 |
| S2 transition | 16 | 128 | 0.5 | 0.1 | 150 |
| S3 winter | 8 | 256 | 0.1 | 0.02 | 300 |
| S3 summer | 8 | 512 | 0.5 | 0.02 | 200 |
| S3 transition | 8 | 256 | 0 | 0.005 | 100 |
| Specimen | [W/(m2K)] | [W/(m2K)] | [W/(m2K)] | [%] | [%] |
|---|---|---|---|---|---|
| S1 winter | 4.30 | 4.06 | 4.16 | −3.26 | |
| S1 summer | 4.64 | 4.18 | 7.91 | −2.79 | |
| S1 transition | 3.88 | 3.76 | −9.77 | −12.56 | |
| S2 winter | 0.21 | 0.17 | 0.22 | −19.05 | 4.76 |
| S2 summer | 0.28 | 0.15 | 33.33 | ||
| S2 transition | 0.41 | 0.33 (0.24) 1 | 95.23 | 57.14 (14.29) | |
| S3 winter | 0.21 | 0.21 | 0.20 | 0.00 | −4.76 |
| S3 summer | 0.20 | 0.18 | −4.76 | −14.29 | |
| S3 transition | 0.19 | 0.08 | −9.52 | −61.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gumbarević, S.; Milovanović, B.; Dalbelo Bašić, B.; Gaši, M. Combining Deep Learning and the Heat Flux Method for In-Situ Thermal-Transmittance Measurement Improvement. Energies 2022, 15, 5029. https://doi.org/10.3390/en15145029
Gumbarević S, Milovanović B, Dalbelo Bašić B, Gaši M. Combining Deep Learning and the Heat Flux Method for In-Situ Thermal-Transmittance Measurement Improvement. Energies. 2022; 15(14):5029. https://doi.org/10.3390/en15145029
Chicago/Turabian StyleGumbarević, Sanjin, Bojan Milovanović, Bojana Dalbelo Bašić, and Mergim Gaši. 2022. "Combining Deep Learning and the Heat Flux Method for In-Situ Thermal-Transmittance Measurement Improvement" Energies 15, no. 14: 5029. https://doi.org/10.3390/en15145029
APA StyleGumbarević, S., Milovanović, B., Dalbelo Bašić, B., & Gaši, M. (2022). Combining Deep Learning and the Heat Flux Method for In-Situ Thermal-Transmittance Measurement Improvement. Energies, 15(14), 5029. https://doi.org/10.3390/en15145029







