Modelling and Design of a Coils Structure for 100 kW Three-Phase Inductive Power Transfer System
Abstract
:1. Introduction
2. System Modelling & Problem Definition
3. Numerical Pre-Design
3.1. Mutual Inductance: Calculation
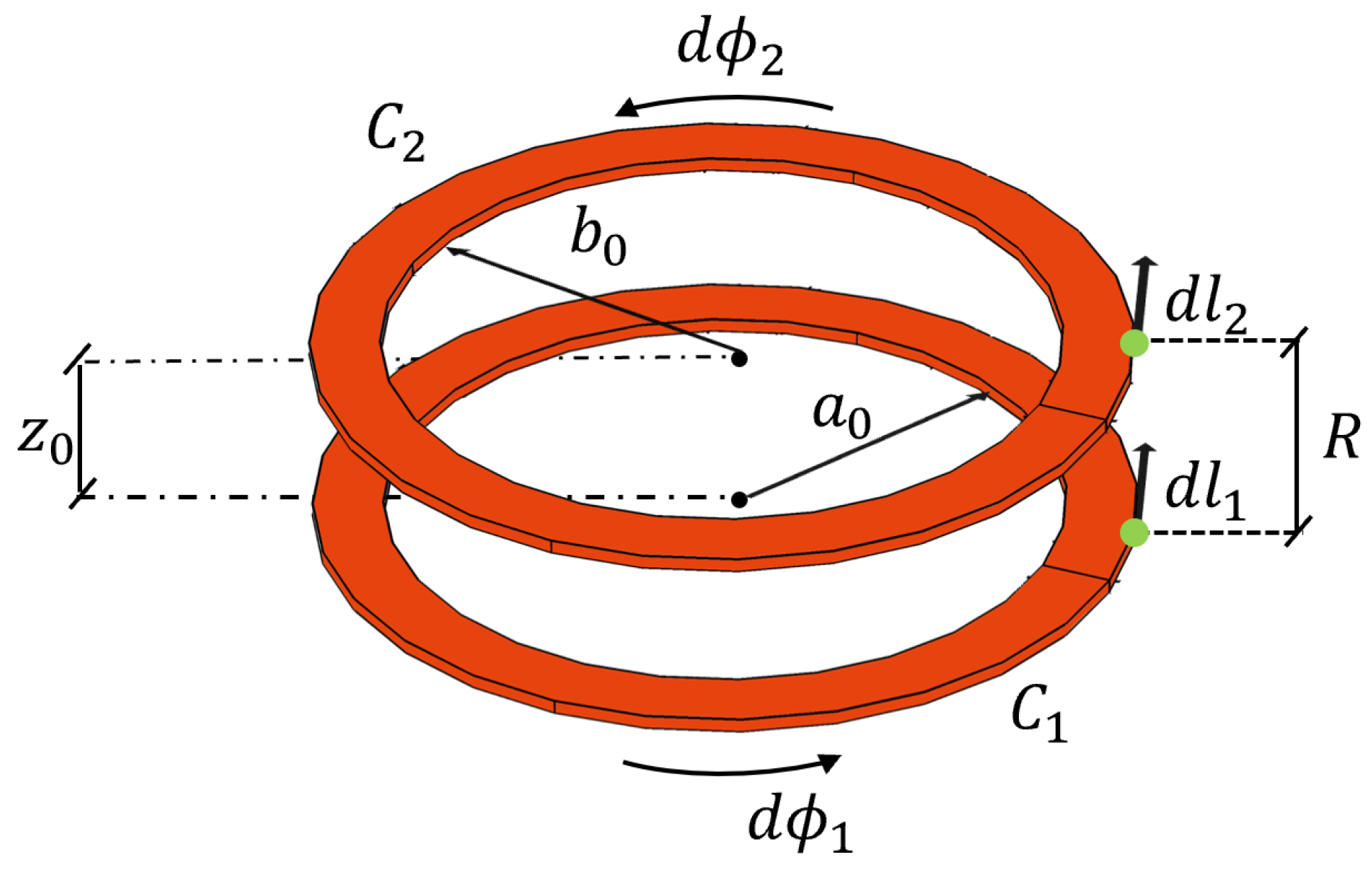
3.2. Concentric Coils Mutual Inductance
3.3. Non-Concentric Coils Mutual Inductance
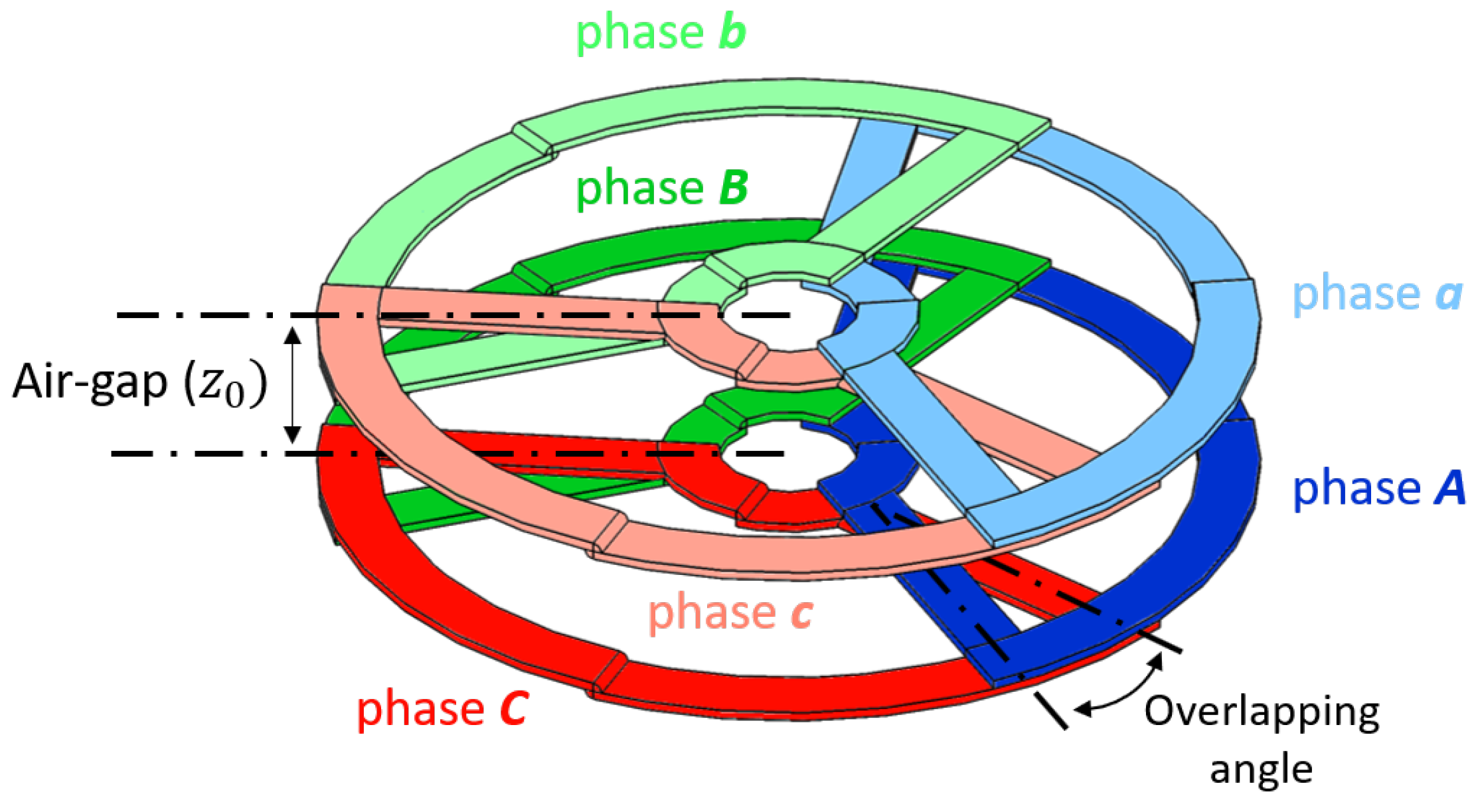
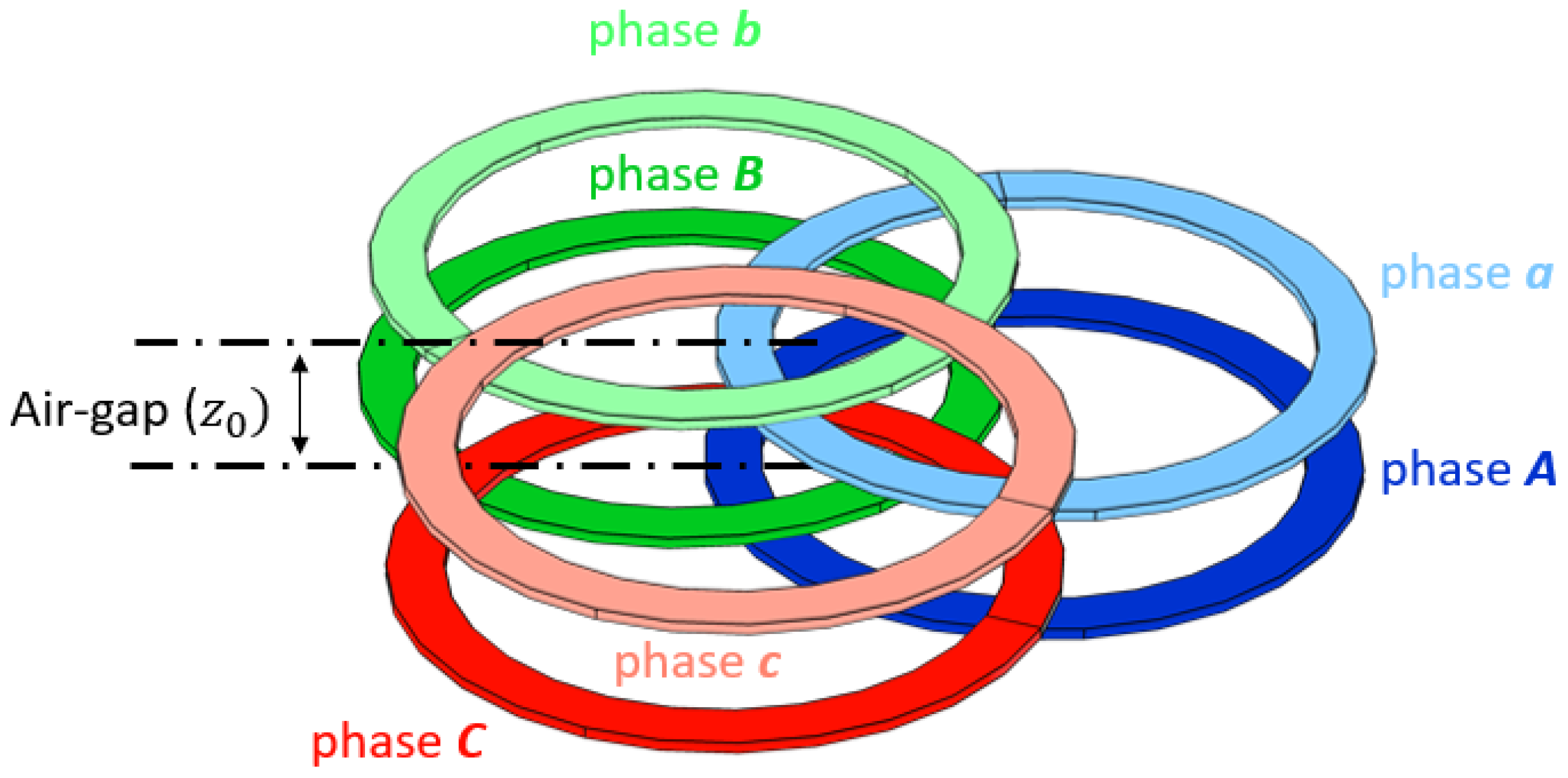
3.4. Three-Phase Structure Non-Concentric Coil Mutual Inductance
- is the total surface of the coil considering the overlapping and then function of the total opening angle of: .
- is the surface of the coil not considering the overlapping, with an opening angle of .
- is the outer radius of the sector-coil net of the turns cross section area.
- is the inner radius of the sector-coil net of the turns cross section area.
- is the overlapping angle of two adjacent coils.
3.5. Objective and Pre-Design Comparison
3.6. Resonance Topology
3.7. Pre-Design Conclusions
4. FEA Electromagnetic Design
- represents the minimum inner space left at the center of the three-phase structure to guarantee enough room for cables to connect the compensation tank to every single coil.
- is the overlapping angle for the simulation. Differently to the numerical solution, the FEA study has been split in two different simulation. These simulation indeed have been done for the intervals: and the second to reduce the total computational weight for the single simulation.
- is the distance between two adjacent turns of a single coil and it is placed theoretically to zero.
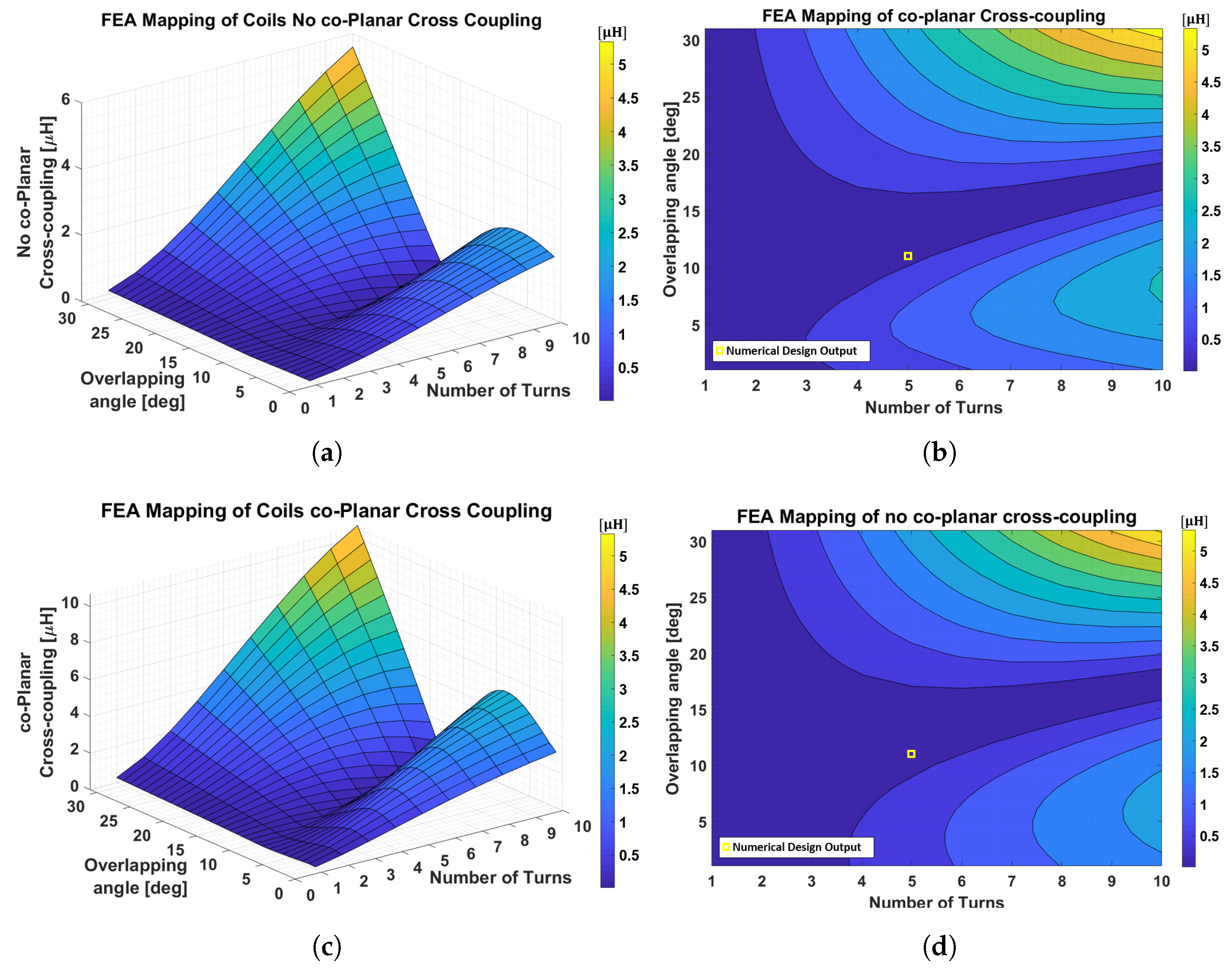
4.1. Comparison of 3D-FEA and Numerical Results
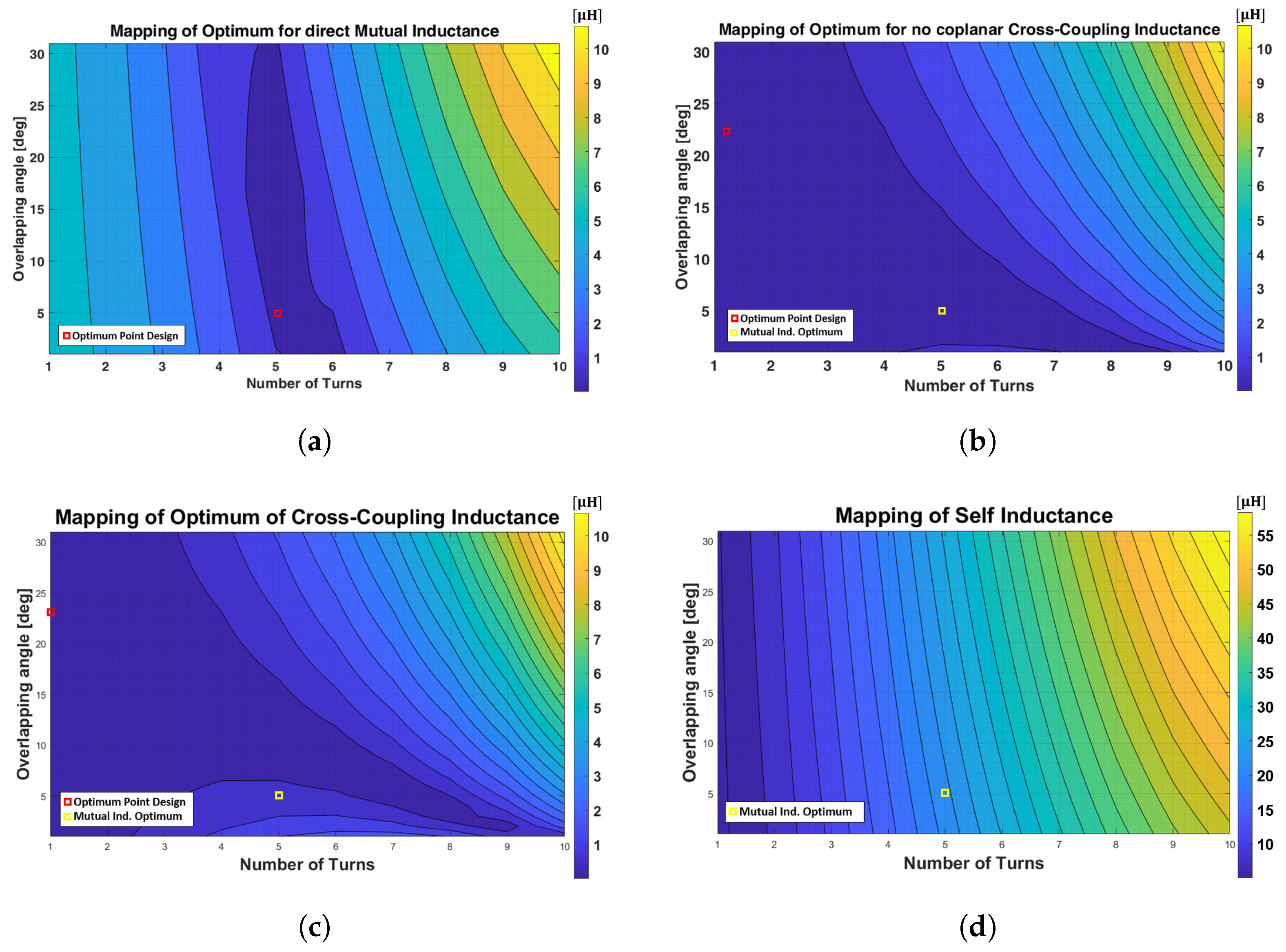
- The general behavior of the mapping pictures is similar, but the geometry and the overlapping angle have a strong impact in terms of inductance value. This implies a differences between the numerical and the 3D-FEA analysis, especially for a high number of turns.
- Finally, considering the area of minimum values, it can be observed that there are several values of overlapping angle and number of turns that verify this criterium, as it happened, in a similar way, of the numerical study. Although, for a high number of turns, this area modifies its shape due to, as already mentioned, the difference in geometry.
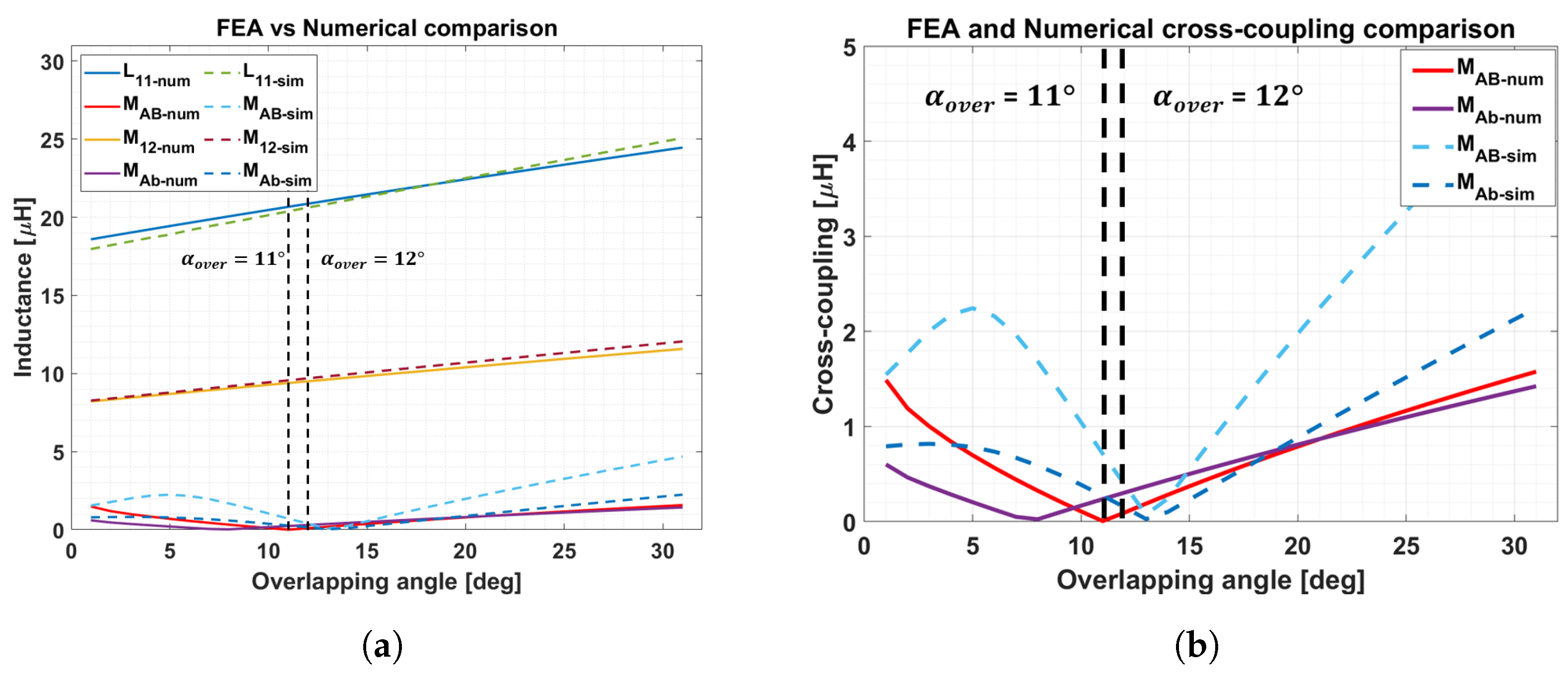
- In Figure 8a, a comprehensive overview of the numerical and 3D-FEA results is provided to underline the small contribution of the cross-coupling effects compared to the direct mutual inductance.
- Looking at Figure 8b, at the operating point chosen in the numerical design of , the FEA output for co-planar cross-coupling results higher compared with the homologous from numerical design. Thus, a little variation in terms of the overlapping angle must be taken into consideration.
- The error for the co-planar cross coupling at , referring again to Figure 8b becomes as difference of the two studies: nH.
- The error for the non co-planar cross coupling at becomes in terms of difference between numerical and 3D-FEA approach: nH.
- The complete numerical analysis, for all the combinations of the number of turns and overlapping angle values, takes an approximative time of s.
- The complete finite-element design, running on the same machine of the previous study, takes an approximative time of h.
- The single FEA investigation, for a single value of the number of turns and overlapping angle, takes an approximative time of s.
4.2. Real Case Study and Final Design
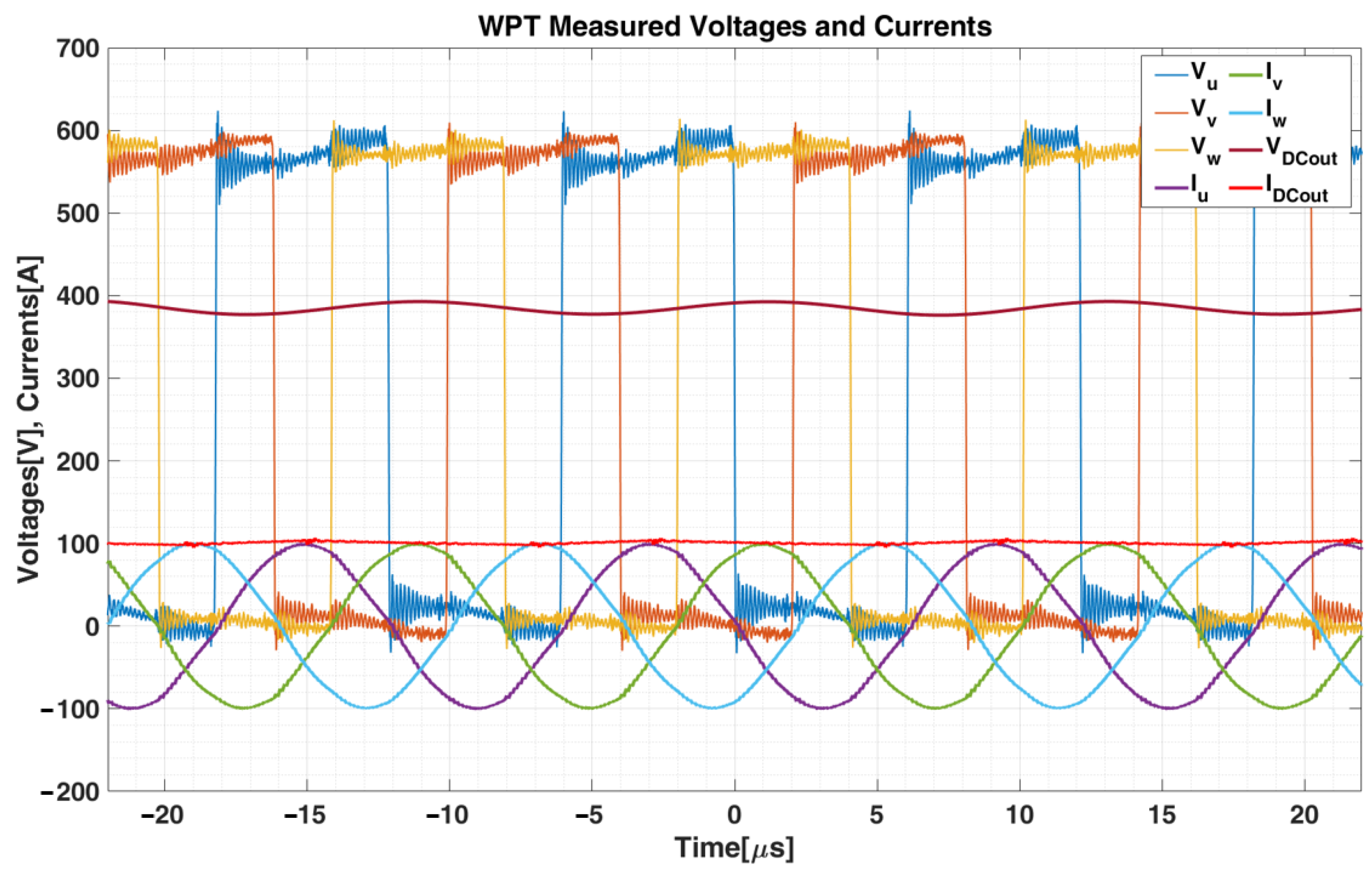
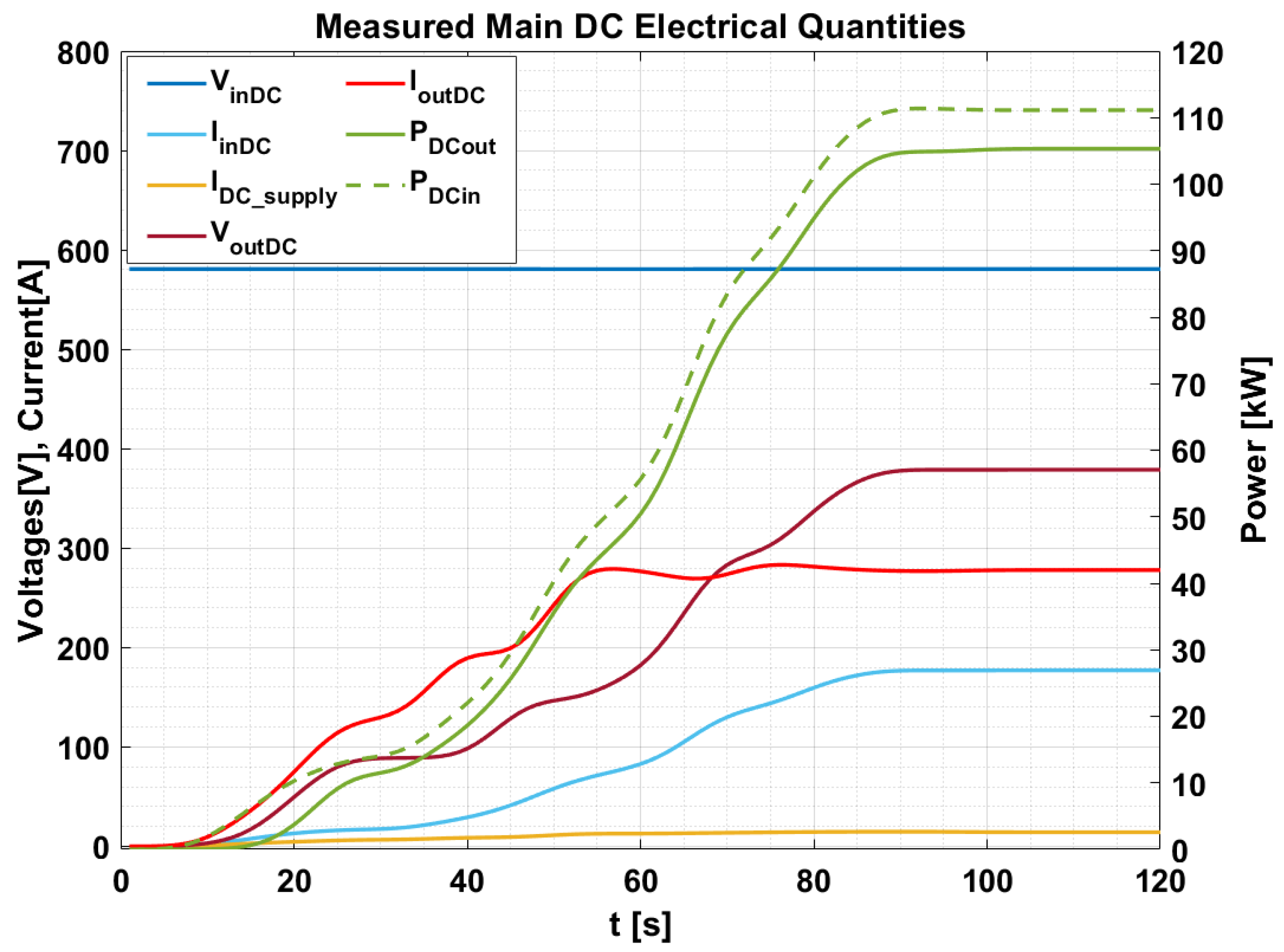
5. Experimental Validation
5.1. Experimental Setup
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Yilmaz, M.; Krein, P.T. Review of Battery Charger Topologies, Charging Power Levels, and Infrastructure for Plug-In Electric and Hybrid Vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Mohammed, S.A.Q.; Jung, J.W. A Comprehensive State-of-the-Art Review of Wired/Wireless Charging Technologies for Battery Electric Vehicles: Classification/Common Topologies/Future Research Issues. IEEE Access 2021, 9, 19572–19585. [Google Scholar] [CrossRef]
- Aggeler, D.; Canales, F.; Zelaya-De La Parra, H.; Coccia, A.; Butcher, N.; Apeldoorn, O. Ultra-fast DC-charge infrastructures for EV-mobility and future smart grids. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, Sweden, 11–13 October 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Du, Y.; Lukic, S.; Jacobson, B.; Huang, A. Review of high power isolated bi-directional DC-DC converters for PHEV/EV DC charging infrastructure. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 553–560. [Google Scholar] [CrossRef]
- Mahesh, A.; Chokkalingam, B.; Mihet-Popa, L. Inductive Wireless Power Transfer Charging for Electric Vehicles—A Review. IEEE Access 2021, 9, 137667–137713. [Google Scholar] [CrossRef]
- Ahmad, A.; Alam, M.S.; Chabaan, R. A Comprehensive Review of Wireless Charging Technologies for Electric Vehicles. IEEE Trans. Transp. Electrif. 2018, 4, 38–63. [Google Scholar] [CrossRef]
- Sanz, J.F.; Villa, J.L.; Sallán, J.; Perié, J.M.; Duarte, L.G. UNPLUGGED project: Development of a 50 kW inductive electric vehicle battery charge system. In Proceedings of the 2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Bagchi, A.C.; Kamineni, A.; Zane, R.A.; Carlson, R. Review and Comparative Analysis of Topologies and Control Methods in Dynamic Wireless Charging of Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4947–4962. [Google Scholar] [CrossRef]
- Zaheer, A.; Neath, M.; Beh, H.Z.Z.; Covic, G.A. A Dynamic EV Charging System for Slow Moving Traffic Applications. IEEE Trans. Transp. Electrif. 2017, 3, 354–369. [Google Scholar] [CrossRef]
- Chen, Z.; Jing, W.; Huang, X.; Tan, L.; Chen, C.; Wang, W. A Promoted Design for Primary Coil in Roadway-Powered System. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Thai, V.X.; Choi, S.Y.; Choi, B.H.; Kim, J.H.; Rim, C.T. Coreless power supply rails compatible with both stationary and dynamic charging of electric vehicles. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Sallan, J.; Villa, J.L.; Llombart, A.; Sanz, J.F. Optimal Design of ICPT Systems Applied to Electric Vehicle Battery Charge. IEEE Trans. Ind. Electron. 2009, 56, 2140–2149. [Google Scholar] [CrossRef]
- Luo, Z.; Wei, X. Analysis of Square and Circular Planar Spiral Coils in Wireless Power Transfer System for Electric Vehicles. IEEE Trans. Ind. Electron. 2018, 65, 331–341. [Google Scholar] [CrossRef]
- Ridge, A.; Ahamad, K.K.; McMahon, R.; Miles, J. Development of a 50 kW Wireless Power Transfer System. In Proceedings of the 2019 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), London, UK, 18–21 June 2019; pp. 406–409. [Google Scholar] [CrossRef]
- Yang, Y.; Cui, J.; Cui, X. Design and Analysis of Magnetic Coils for Optimizing the Coupling Coefficient in an Electric Vehicle Wireless Power Transfer System. Energies 2020, 13, 4143. [Google Scholar] [CrossRef]
- Liu, X.; Hui, S.Y. Optimal Design of a Hybrid Winding Structure for Planar Contactless Battery Charging Platform. IEEE Trans. Power Electron. 2008, 23, 455–463. [Google Scholar] [CrossRef]
- Pries, J.; Galigekere, V.P.N.; Onar, O.C.; Su, G. A 50-kW Three-Phase Wireless Power Transfer System Using Bipolar Windings and Series Resonant Networks for Rotating Magnetic Fields. IEEE Trans. Power Electron. 2020, 35, 4500–4517. [Google Scholar] [CrossRef]
- Song, Y.; Madawala, U.K.; Duleepa, J.T.; Hu, A.P. Cross coupling effects of poly-phase bi-directional inductive power transfer systems used for EV charging. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Song, C.; Kim, H.; Jung, D.H.; Yoon, K.; Cho, Y.; Kong, S.; Kwack, Y.; Kim, J. Three-phase magnetic field design for low EMI and EMF automated resonant wireless power transfer charger for UAV. In Proceedings of the 2015 IEEE Wireless Power Transfer Conference (WPTC), Boulder, CO, USA, 13–15 May 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Cirimele, V.; Colussi, J.; Villa, J.L.; Ganga, A.L.; Guglielmi, P. Modelling of a 100 kW-85 kHz Three-Phase System for Static Wireless Charging and Comparison with a Classical Single-Phase System. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Thrimawithana, D.J.; Madawala, U.K.; Francis, A.; Neath, M. Magnetic modeling of a high-power three phase bi-directional IPT system. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 1414–1419. [Google Scholar] [CrossRef]
- Kim, S.; Covic, G.A.; Boys, J.T. Tripolar Pad for Inductive Power Transfer Systems for EV Charging. IEEE Trans. Power Electron. 2017, 32, 5045–5057. [Google Scholar] [CrossRef]
- Colussi, J.; La Ganga, A.; Re, R.; Guglielmi, P.; Armando, E. 100 kW Three-Phase Wireless Charger for EV: Experimental Validation Adopting Opposition Method. Energies 2021, 14, 2113. [Google Scholar] [CrossRef]
- Ruffo, R.; Khalilian, M.; Cirimele, V.; Guglielmi, P.; Cesano, M. Theoretical and experimental comparison of two interoperable dynamic wireless power transfer systems for electric vehicles. In Proceedings of the 2017 IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics. Converters, Applications and Design, 3rd ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kassakian, J.; Schlecht, M.; Verghese, G. Principles of Power Electronics; Addison-Wesley Series in Electrical Engineering; Addison-Wesley: Boston, MA, USA, 1991. [Google Scholar]
- Fang, C.; Song, J.; Lin, L.; Wang, Y. Practical considerations of series-series and series-parallel compensation topologies in wireless power transfer system application. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 20–22 May 2017; pp. 255–259. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Yu, S.D.; Yim, S.W.; Park, K. Optimizing compensation topologies for inductive power transfer at different mutual inductances. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 20–22 May 2017; pp. 153–156. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Lei, Y. Analysis on wireless charging circuit characteristic under the hybrid compensation topology. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 2450–2454. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Y.; Liu, X.; Xu, D.; Cai, L. An LC/S Compensation Topology and Coil Design Technique for Wireless Power Transfer. IEEE Trans. Power Electron. 2018, 33, 2007–2025. [Google Scholar] [CrossRef]
- Esteban, B.; Stojakovic, N.; Sid-Ahmed, M.; Kar, N.C. Development of mutual inductance formula for misaligned planar circular spiral coils. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 1306–1313. [Google Scholar] [CrossRef]
- Kishan, D.; Vinod, M. Analysis of Mutual Inductance between Asymmetrical Spiral Circular Coils of WIPTS for EV Battery Charging. In Proceedings of the 2020 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 2–4 July 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, S.; Su, J.; Lai, J. Accurate Expressions of Mutual Inductance and Their Calculation of Archimedean Spiral Coils. Energies 2019, 12, 2017. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Mi, C.C. Compensation Topologies of High-Power Wireless Power Transfer Systems. IEEE Trans. Veh. Technol. 2016, 65, 4768–4778. [Google Scholar] [CrossRef]
- Kuperman, A. Additional Two-Capacitor Basic Compensation Topologies for Resonant Inductive WPT Links. IEEE Trans. Power Deliv. 2020, 35, 2568–2570. [Google Scholar] [CrossRef]
- Mude, K.N.; Aditya, K. Comprehensive review and analysis of two-element resonant compensation topologies for wireless inductive power transfer systems. Chin. J. Electr. Eng. 2019, 5, 14–31. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Park, S.J.; Kim, D.H. A Switching Hybrid LCC-S Compensation Topology for Constant Current/Voltage EV Wireless Charging. IEEE Access 2019, 7, 133924–133935. [Google Scholar] [CrossRef]
- Chang, R.; Quan, L.; Zhu, X.; Zong, Z.; Zhou, H. Design of a wireless power transfer system for EV application based on finite element analysis and MATLAB simulation. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Rezmerita, G.; Bobaru, L.; Stanculescu, M.; Iordache, M.; Niculae, D. A self and mutual inductance calculation resonators with finite element analysis. In Proceedings of the 2017 International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 6–9 June 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Lu, X.; Chen, K.; Wang, L.; Wang, X.; Liu, Q.H. Wideband Low-Frequency Design of Inductors and Wireless Power Transfer Coils Using the Mixed Finite-Element Time-Domain Method. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 709–712. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Y.; Ho, S.L.; Fu, W.N. Analysis of Wireless Power Transfer System Based on 3-D Finite-Element Method Including Displacement Current. IEEE Trans. Magn. 2012, 48, 3692–3695. [Google Scholar] [CrossRef]
- Kushwaha, B.K.; Rituraj, G.; Kumar, P. 3-D Analytical Model for Computation of Mutual Inductance for Different Misalignments With Shielding in Wireless Power Transfer System. IEEE Trans. Transp. Electrif. 2017, 3, 332–342. [Google Scholar] [CrossRef]
- Desmoort, A.; De Gréve, Z.; Dular, P.; Geuzaine, C.; Deblecker, O. Surface Impedance Boundary Condition With Circuit Coupling for the 3-D Finite-Element Modeling of Wireless Power Transfer. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]



| Three-Phase Problem Input Parameters | ||
|---|---|---|
| Parameter | Variable | Value |
| Working frequency | 85 kHz | |
| DC input voltage | 580 V | |
| DC output max voltage | 380 V | |
| Rated power transferred | 100 kW | |
| Coils max external diameter | 710 mm | |
| Transmitter-receiver air-gap | 50 mm | |
| Inductances Pre-Design Comparison at | |||
|---|---|---|---|
| Parameter | Variable | ||
| Self inductance | 19.43 H | 20.66 H | |
| Mutual inductance | 8.689 H | 9.4 H | |
| Coplanar cross-coupling inductance | 697 nH | 5.1 nH | |
| No coplanar cross-coupling inductance | 203 nH | 236 nH | |
| Parameter | Variable | Values |
|---|---|---|
| Frequency | f | 85 kHz |
| Number of turns | 5 | |
| Overlapping angle | ||
| Mutual inductance | 9.4 H | |
| Self inductance | 20.66 H | |
| Coplanar cross-coupling inductance | 5.1 nH | |
| No-coplanar cross-coupling inductance | 236 nH | |
| Capacitors (SS compensation ) | 170 nF |
| Parameter | Variable | Value |
|---|---|---|
| Simulation frequency | 85 kHz | |
| Coils max external diameter | 710 mm | |
| Transmitter-receiver air-gap | 50 mm | |
| Coils internal diameter | 50 mm | |
| Wire cross section | 56 mm2 | |
| Overlapping angle simulation | ||
| Number of turns per coil simulation | ||
| Coil’s turns pitch | 0 mm |
| Parameter | Variable | Numerical Design | 3D-FEA Design | Error Numerical Design |
|---|---|---|---|---|
| Direct mutual inductance | H | H | ||
| Self inductance | H | H | ||
| Coplanar cross-coupling inductance | 98 nH | 350 nH | 252 nF | |
| Weight of coplanar cross-coupling on direct mutual inductance | ||||
| No-coplanar cross-coupling inductance | 304 nH | 157 nH | 147 nF | |
| Weight of no-coplanar cross-coupling on direct mutual inductance | ||||
| Capacitors (SS compensation) | 168 nF | 170 nF |
| Parameter | Variable | No Ferrite | No Ferrite | Ferrite |
|---|---|---|---|---|
| Mutual inductance | 5 H | H | H | |
| Self inductance | H | H | H | |
| Coplanar cross-coupling inductance | 219 nH | 484 nH | 393 nH | |
| No-coplanar cross-coupling inductance | 237 nH | 295 nH | 160 nH | |
| Capacitors (SS compensation) | 252 nF | 193 nF | 147 nF |
| Measures Single Frequency Spot: kHz | |||
|---|---|---|---|
| Parameter | Variable | Ferrite | Error 3D-FEA |
| Mutual inductance (per each phase) | H H H | ≈10% ≈7% ≈12% | |
| Self inductance (maximum error) | H | ||
| Coplanar cross-coupling inductance (maximum error) | 205 nH | ||
| No-coplanar cross-coupling inductance (maximum error) | 183 nH | ||
| Parameter | Variable | Value |
|---|---|---|
| Supply voltage | 580.49 V | |
| Supply current | 14.83 A | |
| Supply Power | 8.61 kW | |
| WPT Input DC current | 192.12 A | |
| WPT Input Power | 111.52 kW | |
| WPT Output DC voltage | 378.87 V | |
| WPT Output DC current | 277.97 A | |
| WPT Output DC Power | 105.31 kW | |
| WPT overall DC-DC efficiency | 94.43% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colussi, J.; Re, R.; Guglielmi, P. Modelling and Design of a Coils Structure for 100 kW Three-Phase Inductive Power Transfer System. Energies 2022, 15, 5079. https://doi.org/10.3390/en15145079
Colussi J, Re R, Guglielmi P. Modelling and Design of a Coils Structure for 100 kW Three-Phase Inductive Power Transfer System. Energies. 2022; 15(14):5079. https://doi.org/10.3390/en15145079
Chicago/Turabian StyleColussi, Jacopo, Roberto Re, and Paolo Guglielmi. 2022. "Modelling and Design of a Coils Structure for 100 kW Three-Phase Inductive Power Transfer System" Energies 15, no. 14: 5079. https://doi.org/10.3390/en15145079
APA StyleColussi, J., Re, R., & Guglielmi, P. (2022). Modelling and Design of a Coils Structure for 100 kW Three-Phase Inductive Power Transfer System. Energies, 15(14), 5079. https://doi.org/10.3390/en15145079






