Direct Model Reference Adaptive Control of a Boost Converter for Voltage Regulation in Microgrids

Abstract

In this study, we present a Direct Model Reference Adaptive Control (DMRAC) algorithm in a boost converter used in islanded microgrids (MG) with a solar photovoltaic (PV) system. Islanded types of microgrids have very sensitive voltage and frequency variability; therefore, a robust and adaptive controller is always desired to control such variations within the MG. A DC–DC boost converter with a modified MIT rule controller is proposed in this paper, which stabilizes output voltage variations in islanded MG. Since the boost converter is a non-minimum phase, the controller design that relies only on output voltage feedback becomes challenging. Even though output voltage control can be achieved using inductor current control, such current mode controllers may also require prior knowledge of the load resistance and more states, such as output and inductor currents in feedback. Here, two control loops are used to achieve a stable output voltage; a PID controller can regulate the output voltage at a fixed level, and the outer loop is designed to implement the MIT rule for a DMRAC. To ensure that the actual system is following the desired reference model, using only an output voltage feedback sensor, a DMRAC is devised to update the PID controller parameters in real-time. Compared to a DC–DC boost converter connected to the MG, a controller, such as the one introduced in this paper, is more successful in dealing with unknown parameter fluctuations and disturbance changes. The MATLAB/SIMULINK is used to design and simulate the controller with different load disturbances and input voltage variances. The hardware validation is also carried out to show the performance of the proposed controller. Our results suggest that the DMRAC provides robust regulation against parameter variations.

1. Introduction

Microgrids (MG) are small-scale energy grids supplying energy to loads at the distribution level. Besides the traditional AC power grids, DC microgrids are emerging as efficient alternatives. In general, the small grids have control capabilities and can be categorized into grid-connected and islanded or isolated grids [1]. Grid-connected MGs are governed by the main power network, and their voltage and frequency are defined by it. However, for the islanded MG, due to the low system inertia and fast changes in the output power of wind and solar power sources, the frequency and voltage can experience large excursions and thus easily deviate from nominal operating conditions. Multi nanogrids can also be connected to power a local network. There are few works [2,3] considering power sharing among multiple nanogrids by using power management system.

When we have a DC MG, the DC–DC converters are the most significant part of the system. Many DC–DC converter topologies [4,5], such as the boost topology, the buck topology, buck-boost converters, and single-ended primary inductor converter (SEPIC) topology [5], have been discussed in the literature. DC–DC boost converters are the simplest converters for effective reproduction of output amplification for a given input voltage. Many applications have been undertaken by it, including those related to the automotive industry, power amplifications, adaptive control applications, battery power systems, robotics, wind power, and photovoltaic (PV) systems (e.g., DC MG) [6].

Many studies compare different types of converters’ performances. In [7], research has been conducted over step-up DC–DC converters in various configurations. In [8], the authors analyzed boost and SEPIC converters, considering output voltage ripple, total harmonic distortion, power factor for both converters, and boost converters produced better results. Besides mentioned features, boost converters are easier to use. So, the boost-type converter is frequently used because of its superior performance. As illustrated in Figure 1, the main elements of a boost converter are the inductor, diode, capacitor, and switch. In this research, we use MOSFET as a switch that can consistently turn ON and OFF based on the generated duty cycle.

Because these converters display poor voltage regulation and inadequate dynamic response when run in an open loop, they are often equipped with closed-loop control for output voltage regulation [9]. Due to the nonlinear dynamics of boost converters and non-minimum phase (NMP) behavior, controller design for boost converters is more complex and challenging than for buck converters.

Many control techniques have been presented to regulate the switch ON/OFF (duty cycle) to achieve the required output voltage. The most common controllers are linear PID controllers. The PID control design is based on linear control theory, such as the Ziegler–Nichols method [10], the root locus approach [11], the circle-based criterion [12], and the hysteresis method [13], the bode plot, and so on. These control methods perform well around the linearized model’s operating points. The small-signal model of a boost converter, on the other hand, changes when the operating point changes. It is important to mention here that the duty cycle determines the poles and a right-half-plane zero and the amplitude of the frequency response. As a result, PID controllers have a hard time respecting changes in operating points, and they function poorly when the system is subjected to substantial load fluctuations.

Despite the necessity of changes in input, the Ziegler–Nichols technique for PID tuning is an experimental one that is extensively utilized. One downside of this technique is that it necessitates a prior understanding of plant models. A decent but not optimal system response is achieved when the controller is adjusted using the Ziegler–Nichols technique. If the dynamics of the plant change, the transient reaction might be considerably worse. It should be noted that many plants have time-varying dynamics due to external/environmental factors, such as temperature and pressure. The controller must respond to changes in the dynamics of the plant features to provide a robust system. Nonlinear control techniques [14,15,16,17], such as fuzzy logic and sliding mode control, have recently offered good static and dynamic responsiveness. The disadvantage of the fuzzy logic technique is that all available data are needed, and the algorithm has to be trained before use. The sliding mode controller is suffering from a chattering issue.

This paper considers a microgrid that is isolated and is displayed in Figure 2. DC–DC converters are used to connect a PV system and batteries to a DC bus, with the converter output controlled by a controller. The proposed DMRAC controller essentially contains two loops of voltage control rather than some previous works that just contained the adaptive loop [18,19]. The inner loop of the controller regulates the output voltage at a fixed level, which is vital for correct power injection to the MG. The outer loop implements the MIT rule for a model reference adaptive control. In other word, a specially developed controller that corrects for NMP dynamics is employed in this study by utilizing both PID control and reference model adaptive control. Additionally, the PID controller parameters are updated in real-time to ensure that the actual system is following the desired reference model even if there are uncertainties in system model parameters and load. In this way, the output voltage behavior is similar to the model, and the characteristics of the output, such as settling time, overshoot, and rising time, are manageable. Moreover, the controller does not require any current sensor feedback. All the symbols used in this work are listed in

Table 1. Nomenclature.

Symbol	Meaning
$v_{in}$	Input voltage
$v_c$	Capacitor voltage
$i_l$	Inductor current
$d$	Duty cycle
$y_m$	The output of the reference model
$y$	Plant output
$u_c$	Plant input
$G\left(s\right)$	Second-order transfer function
$K$	Known parameter
$K_o$	Unknown parameter
$\gamma$	Adaptation gain

. The significant contributions of the proposed work are summarized as follows:

• An adaptive controller is designed to regulate the output voltage of the DC–DC converters in an isolated MG system.
• This paper proposes a DMRAC that can adjust the parameters of the PID controller in real-time to ensure that the actual system is following the desired reference model.
• The PID controller regulates the output voltage at a fixed level, essential for correct power injection when the DC–DC boost converter is connected to the MG. The outer loop implements the MIT rule for a model reference adaptive control. Besides, no training or database is needed in this method.
• The proposed controller does not require using any current sensor, and the control scheme is only obtained using the voltage feedback of the boost converter. So, the proposed design is cost-effective.
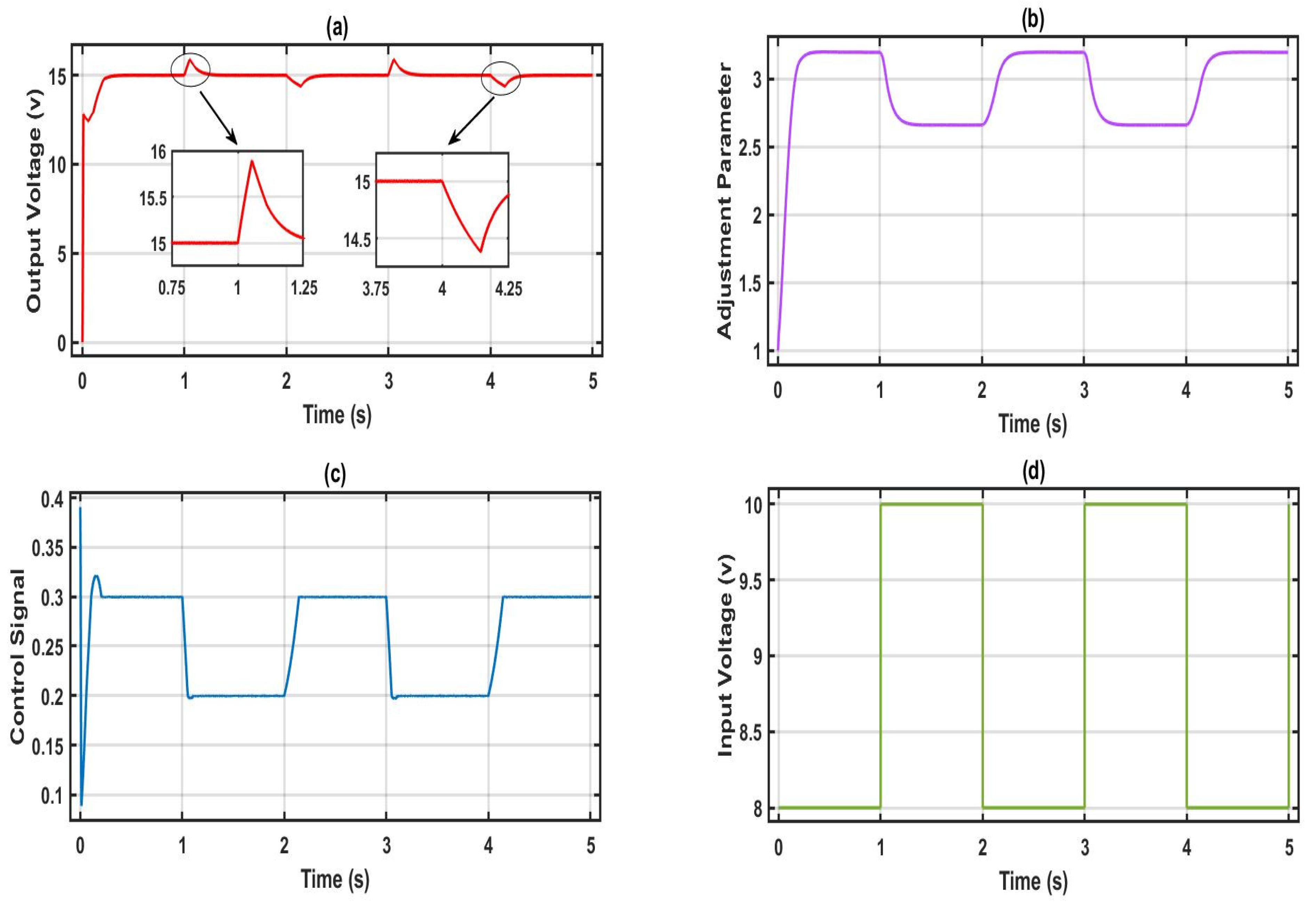
• The proposed controller’s effectiveness and robustness are validated through simulation and hardware implementation when subjected to load variations, input voltage changes, and reference voltage changes.

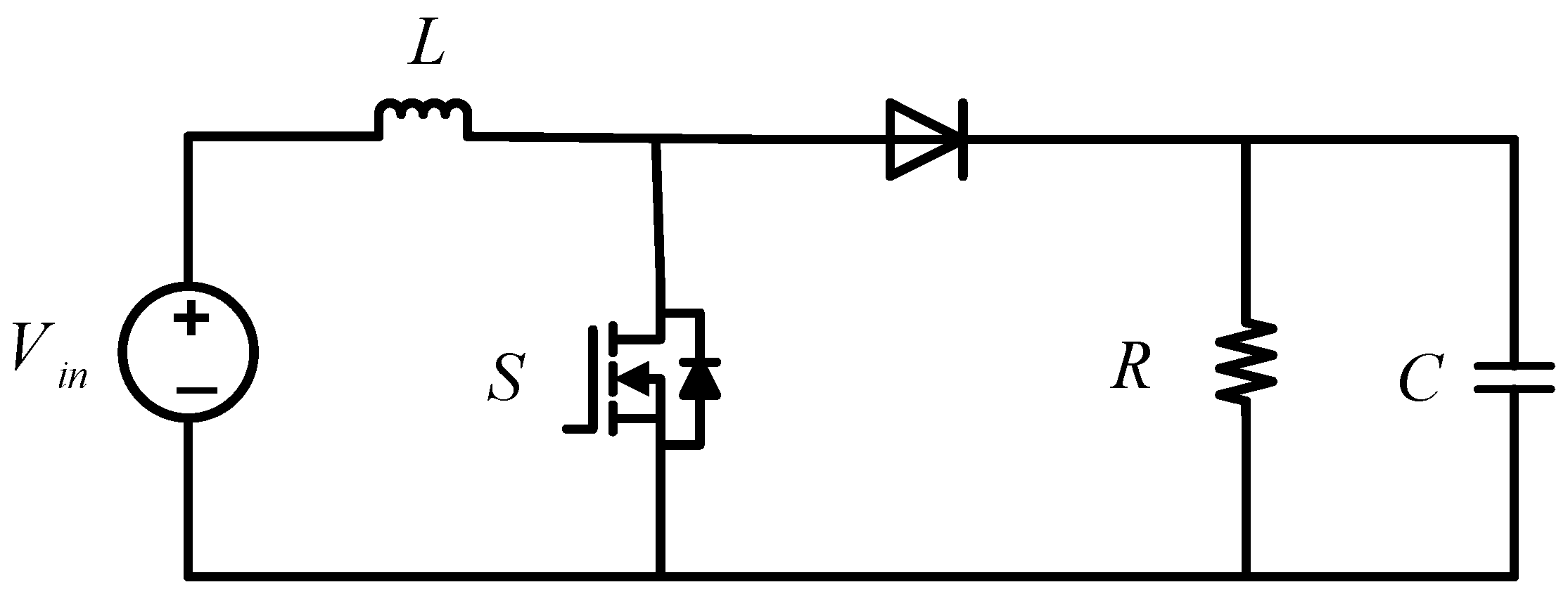
2. DC–DC Converter Dynamic Modelling

2.1. Ideal Dynamic Model

The controller’s performance depends upon the accurate modeling of the DC–DC converter. A well-established average modeling technique [17] is used to design the controller. The boost converter consists of a DC input voltage source, an inductor L, a controlled switch S, a diode, a filter capacitor C, and a load resistance R. The current in the inductor grows linearly when the switch is turned on, but the diode remains off. When the switch is turned off, the energy stored in the inductor is released to the load. As the converter’s name implies, the output voltage is always greater than the input voltage. The DC–DC boost converters operate in three different modes: Continuous Conduction Mode (CCM), Discontinuous Conduction Mode (DCM), and Critical Conduction Mode (CrCM). The CCM operating mode-based DC–DC converter is considered in this research.

T is the switching period, and the switch is closed for time $DT$ and open for $\left(1-D\right)T$, where D is the steady-state duty cycle. When the switch is on, there are two loops, one for inductor current and the other for the capacitor current. Using the KVL for the mentioned loops, the following equations can be obtained.

Defining the state vector as $x={\left[i_l v_c\right]}^T$ and the output voltage $v_o=v_c$, the state space form during the “ON” mode can be written as follows:

$$\left[\begin{array}{c}\frac{d{i}_l}{dt}\\ \frac{d{v}_c}{dt}\end{array}\right]=\left[\begin{array}{cc}0& 0\\ 0& -\frac{1}{RC}\end{array}\right]\left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]v_{in}$$

(1)

$$v_o=\left[0 1\right] \left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]$$

(2)

During the “OFF” mode state, the energy stored in the inductor is released to the output RC circuit through the diode.

We can derive the following state equations for the OFF mode by using KVL and KCL equations for the boost converter circuit in Figure 1, when the switch is off:

$$\left[\begin{array}{c}\frac{d{i}_l}{dt}\\ \frac{d{v}_c}{dt}\end{array}\right]=\left[\begin{array}{cc}0& -\frac{1}{L}\\ \frac{1}{C}& -\frac{1}{RC}\end{array}\right]\left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]v_{in}$$

(3)

$$v_o=\left[0 1\right]\left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]i_l-\frac{V_c}{R}-C\frac{d{v}_c}{dt}=0$$

(4)

A state-space averaging approach is utilized to obtain a converter model across one switching period. In other words, the state-space descriptions of the two modes must be replaced with a single state-space description that approximates the behavior of the circuit across the whole time T. By using the state-space averaging technique, the averaged modified model is given by:

$$A=A_{1}d+A_2\left(1-d\right)$$

(5)

$$B=B_{1}d+B_2\left(1-d\right)$$

(6)

where $A_1$, $A_2$, $B_1$ and $B_2$ are given below, and $d$ is changes in the duty cycle:

$$A_1=\left[\begin{array}{cc}0& 0\\ 0& -\frac{1}{RC}\end{array}\right], A_2=\left[\begin{array}{cc}0& -\frac{1}{L}\\ \frac{1}{C}& -\frac{1}{RC}\end{array}\right]$$

$$B_1=\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right],B_2=\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]$$

Using Equations (5) and (6), we obtain the following:

$$\left[\begin{array}{c}\frac{d{i}_l}{dt}\\ \frac{d{v}_c}{dt}\end{array}\right]=\left[\begin{array}{cc}0& -\frac{\left(1-d\right)}{L}\\ \frac{1-d}{C}& -\frac{1}{RC}\end{array}\right]\left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]v_{in}$$

(7)

$$v_o=\left[0 1\right] \left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]$$

The boost converter’s steady-state model may be calculated from Equation (7) by letting:

$$\left[\begin{array}{c}\frac{d{i}_l}{dt}\\ \frac{d{v}_c}{dt}\end{array}\right]=0 \mathrm{and} d=D$$

In this case, Equation (7) becomes:

$$\left[\begin{array}{c}0\\ 0\end{array}\right]=\left[\begin{array}{cc}0& -\frac{\left(1-D\right)}{L}\\ \frac{1-D}{C}& -\frac{1}{RC}\end{array}\right]\left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]v_{in}$$

(8)

$$v_o=\left[0 1\right] \left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]$$

The steady-state relationship between $v_o$ and $v_{in}$ may be expressed as using Equation (8):

$$\frac{V_o}{V_{in}}=\frac{1}{1-D}$$

(9)

To obtain the boost converter’s transfer function, the model given by Equation (8) must first be linearized around a particular operating point. To this end, we assume that the inductor’s current $I_l$, capacitor voltage $V_c$, duty cycle $D$, and input voltage $V_{in}$determine the steady-state operating point. Now, by considering small perturbations of the operating point, the variables associated with the average model can be written as:

$$i_l=I_l+\widetilde{i_l}$$

$$v_c=V_c+\widetilde{v_c}$$

$$v_{in}=V_{in}+\widetilde{v_{in}}$$

$$d=D+\tilde{d}$$

where the $\widetilde{i_l}$, $\widetilde{v_c}$ and $\widetilde{v_{in}}$ are the small perturbations of the inductor current, capacitor voltage, and input voltage, respectively. Therefore, Equation (7) becomes:

$$\frac{d}{dt}\left[\begin{array}{c}{I}_l+\widetilde{i_l}\\ V_c+\widetilde{v_c}\end{array}\right]=\left[\begin{array}{cc}0& -\frac{\left(1-D\right)}{L}\\ \frac{1-D}{C}& -\frac{1}{RC}\end{array}\right]\left[\begin{array}{c}{I}_l\\ V_c\end{array}\right]+\left[\begin{array}{cc}0& -\frac{\left(1-D\right)}{L}\\ \frac{1-D}{C}& -\frac{1}{RC}\end{array}\right]\left[\begin{array}{c}\widetilde{i_l}\\ \widetilde{v_c}\end{array}\right]+\left[\begin{array}{cc}0& \frac{\tilde{d}}{L}\\ -\frac{\tilde{d}}{C}& 0\end{array}\right]\left[\begin{array}{c}{I}_l\\ V_c\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]\left[V_{in}+\widetilde{v_{in}}\right]$$

(10)

It is worth noting that the steady-state portion of Equation (10) is given by:

$$\left[\begin{array}{cc}0& -\frac{\left(1-D\right)}{L}\\ \frac{1-D}{C}& -\frac{1}{RC}\end{array}\right]\left[\begin{array}{c}{I}_l\\ V_c\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]\left[V_{in}\right]=0$$

and:

$$\left[\begin{array}{cc}0& \frac{\tilde{d}}{L}\\ -\frac{\tilde{d}}{C}& 0\end{array}\right]\left[\begin{array}{c}{I}_l\\ V_c\end{array}\right]=\left[\begin{array}{c}\frac{V_c}{L}\\ -\frac{I_l}{C}\end{array}\right]\left[\begin{array}{c}\tilde{d}\end{array}\right]$$

(11)

Hence, Equation (10) is reduced to:

$$\frac{d}{dt}\left[\begin{array}{c}\widetilde{i_l}\\ \widetilde{v_c}\end{array}\right]=\left[\begin{array}{cc}0& -\frac{\left(1-D\right)}{L}\\ \frac{1-D}{C}& -\frac{1}{RC}\end{array}\right]\left[\begin{array}{c}\widetilde{i_l}\\ \widetilde{v_c}\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L}& \frac{V_c}{L}\\ 0& -\frac{I_l}{C}\end{array}\right]\left[\begin{array}{c}\widetilde{v_{in}}\\ \tilde{d}\end{array}\right]$$

(12)

Finally, the output voltage perturbation may be expressed directly as:

$$\widetilde{v_o}=\left[0 1\right] \left[\begin{array}{c}\widetilde{i_l}\\ \widetilde{v_c}\end{array}\right]$$

(13)

The state-space model of Equations (12) and (13) are given by:

$$\dot{x}=Ax+Bu$$

$$y=Cx$$

$$A=\left[\begin{array}{cc}0& -\frac{\left(1-D\right)}{L}\\ \frac{1-D}{C}& -\frac{1}{RC}\end{array}\right]$$

$$B=\left[\begin{array}{cc}\frac{1}{L}& \frac{V_c}{L}\\ 0& -\frac{I_l}{C}\end{array}\right]$$

$$C=\left[0 1\right]$$

In this research, we design a controller to generate duty cycle correction $\tilde{d}$ in such a way that the output voltage remains constant. In this regard, we consider the transfer function given in Equation (14) using the state transition matrix, which may be expressed as follows in terms of the converter’s parameters:

$$\frac{\widetilde{v_o}\left(s\right)}{\tilde{d}\left(s\right)}=\frac{\left(1-D\right)V_o-\left(L{I}_l\right)s}{\left(LC\right)s^2+\frac{L}{R}s+{\left(1-D\right)}^2}$$

(14)

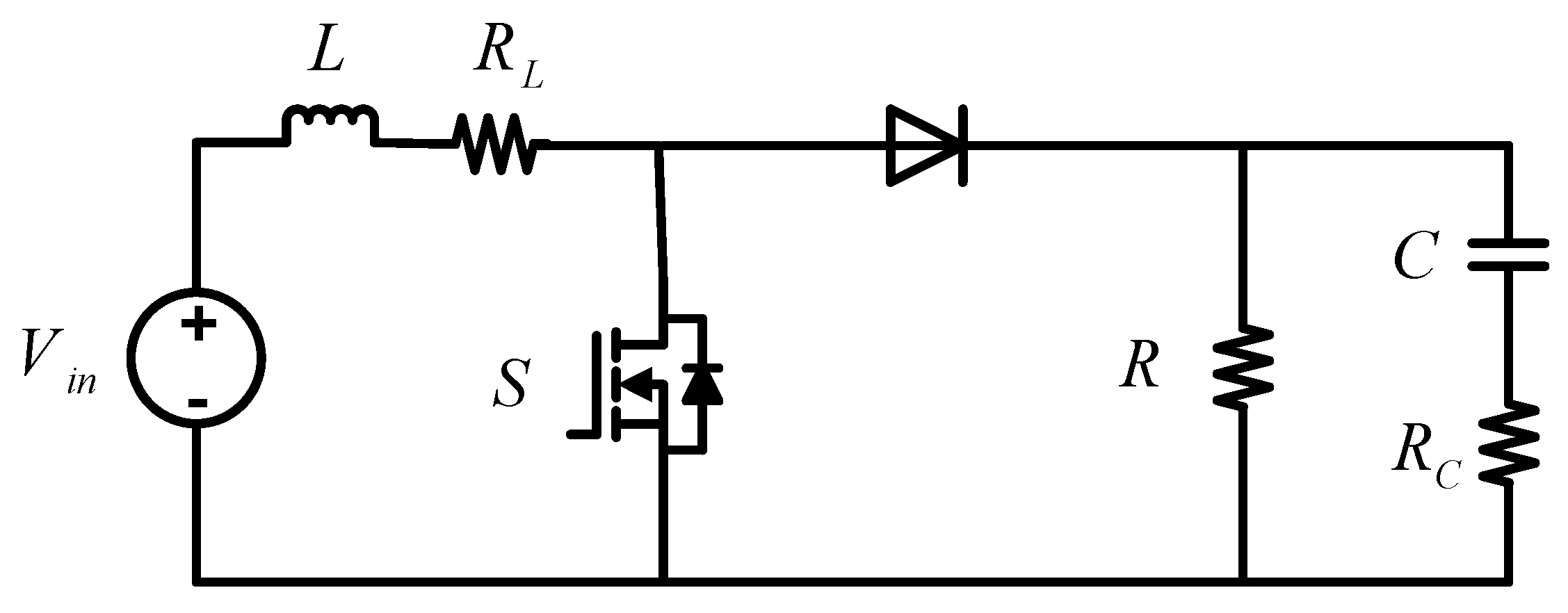
2.2. Parasitic Realisation in Boost Converter Dynamic Model

The goal of analyzing ideal/lossless components and leaving parasitic elements out, as we have before, is to simplify model development and to figure out the fundamental features of the switching system. Nevertheless, parasitic elements and losses need to be considered for improving model accuracy, analyzing system efficiency, and studying dynamic behavior. As a result of including the parasitic elements, nonlinear current and voltage waveforms are generated, and this complicates the process of developing a model. The schematic in Figure 3 shows a simplified equivalent circuit for the DC–DC boost converter with parasitic elements. A capacitance $C$ and inductor $L$ can be considered as an output filter. An analysis of capacitor equivalent series resistance (ESR), $R_C$, and inductor DC resistance, $R_L$, is performed.

Per switching cycle, the boost converter has two modes in CCM. Again, the switch is closed for time $DT$ and open for $\left(1-D\right)T$, where D is the steady-state duty cycle. Defining the state vector as $x={\left[i_l v_c\right]}^T$ and the output voltage $v_o=v_c$, and writing the KVL and KCL for loops in Figure 3, we can obtain the state space (ss) form for “ON” and “OFF” modes of the converter. During the “ON” mode state, the ss form will be:

$$\left[\begin{array}{c}\frac{d{i}_l}{dt}\\ \frac{d{v}_c}{dt}\end{array}\right]=\left[\begin{array}{cc}-\frac{R_L}{L}& 0\\ 0& -\frac{1}{\left(R_C+R\right)C}\end{array}\right]\left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]v_{in}$$

(15)

$$v_o=[0 \frac{R}{R+R_C}] \left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]$$

During the “OFF” mode state, ss form is:

$$\left[\begin{array}{c}\frac{d{i}_l}{dt}\\ \frac{d{v}_c}{dt}\end{array}\right]=\left[\begin{array}{cc}(-\frac{R_L}{L})-\frac{R{R}_C}{L\left(R+R_C\right)}& -\frac{R}{L\left(R+R_C\right)}\\ \frac{R}{\left(R_C+R\right)C}& -\frac{1}{\left(R_C+R\right)C}\end{array}\right]\left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]v_{in}$$

(16)

$$v_o=\left[\frac{R{R}_C}{\left(R+R_C\right)} \frac{1}{R+R_C}\right] \left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]$$

Using Equations (5) and (6), we obtain the following:

$$\left[\begin{array}{c}\frac{d{i}_l}{dt}\\ \frac{d{v}_c}{dt}\end{array}\right]=\left[\begin{array}{cc}(-\frac{R_L}{L})-\frac{{(1-d)}^{2}R{R}_C}{L\left(R+R_C\right)}& -\frac{\left(1-d\right)R}{L\left(R+R_C\right)}\\ \frac{R}{\left(R_C+R\right)C}& -\frac{1}{\left(R_C+R\right)C}\end{array}\right]\left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]v_{in}$$

(17)

$$v_o=\left[\frac{\left(1-d\right)R{R}_C}{\left(R+R_C\right)} \frac{1}{R+R_C}\right] \left[\begin{array}{c}{i}_l\\ v_c\end{array}\right]$$

Now, applying perturbation, this will result in the small signal model as:

$$\frac{d}{dt}\left[\begin{array}{c}\widetilde{i_l}\\ \widetilde{v_c}\end{array}\right]=\left[\begin{array}{cc}(-\frac{R_L}{L})-\frac{{(1-d)}^{2}R{R}_C}{L\left(R+R_C\right)}& -\frac{\left(1-D\right)R}{L\left(R+R_C\right)}\\ \frac{\left(1-D\right)R}{\left(R_C+R\right)C}& -\frac{1}{\left(R_C+R\right)C}\end{array}\right]\left[\begin{array}{c}\widetilde{i_l}\\ \widetilde{v_c}\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L}& \frac{v_o}{L}+\frac{\left(1-DR{R}_C{I}_L\right)}{L\left(R+R_C\right)}\\ 0& -\frac{R{I}_L}{C\left(R+R_C\right)}\end{array}\right]\left[\begin{array}{c}\widetilde{v_{in}}\\ \tilde{d}\end{array}\right]$$

(18)

$$v_o=\left[\frac{\left(1-D\right)R{R}_C}{\left(R+R_C\right)} \frac{C}{R+R_C}\right]\left[\begin{array}{c}\widetilde{i_l}\\ \widetilde{v_c}\end{array}\right]+\left[0-\frac{R{R}_C{I}_L}{R+R_C}\right]\left[\begin{array}{c}\widetilde{v_{in}}\\ \tilde{d}\end{array}\right]$$

$$\frac{\widetilde{v_o}\left(s\right)}{\tilde{d}\left(s\right)}=\frac{s\left[\left(\frac{\left(1-D\right)R{R}_C}{\left(R+R_C\right)}\right)\left(\frac{v_o}{L}+\frac{\left(1-D)R{R}_C{I}_L\right)}{L\left(R+R_C\right)}\right)-\frac{R^2{I}_L}{C{\left(R+R_C\right)}^2}\right]+\left(\frac{v_o}{L}+\frac{\left(1-D)R{R}_C{I}_L\right)}{L\left(R+R_C\right)}\right)\left[\left(\frac{\left(1-D\right)R{R}_C}{C{\left(R+R_C\right)}^2}\right)+\left(\frac{R^2\left(1-D\right)}{C{\left(R+R_C\right)}^2}\right)\right]-\frac{R^2{I}_L}{C{\left(R+R_C\right)}^2}\left(\frac{R_L}{L}+\left(\frac{{\left(1-D\right)}^{2}R{R}_C}{L\left(R+R_C\right)}\right)\right)+\frac{\left(1-D{)}^2{R}^3{R}_C{I}_L\right)}{LC{\left(R+R_C\right)}^3}}{s^2+s\left[\left(\frac{R_L}{L}\right)+\frac{{(1-d)}^{2}R{R}_C}{L\left(R+R_C\right)}+\frac{1}{\left(R_C+R\right)C}\right]+\left[\frac{R_L}{L}+\left(\frac{{\left(1-D\right)}^{2}R{R}_C}{L\left(R+R_C\right)}\right)\right]\left[\frac{1}{\left(R_C+R\right)C}\right]+\frac{{\left(1-D\right)}^2{R}^2}{CL{\left(R+R_C\right)}^2}}$$

(19)

3. Controller Design and Simulation

3.1. Model Reference Adaptive Controller

Adaptive control is a popular control strategy for developing sophisticated control systems with higher performance and accuracy [20]. The DMRAC is a direct adaptive method with adjustable controller settings and an adjusting mechanism. Adaptive controllers are far more successful at dealing with unknown parameter fluctuations and environmental changes than the well-known and easily structured fixed gain PID controllers. The outer loop, or regular feedback loop, and the inner loop, or parameter adjustment loop, make up an adaptive controller. This work designs the adaptive controller with a DMRAC scheme using the MIT rule to control a DC–DC boost converter.

The MRAC is designed using an adaptive control approach that adjusts the controller settings such that the output of the real plant follows the output of a reference model with the same reference input.

The reference model is used to simulate the adaptive control system’s ideal response to the reference input. A controller is generally characterized by various parameters that may be changed. Only one parameter is utilized to define the control law in this article. The amount of adaption gain mostly determines the value. The adjustment mechanism component is used to change the controller’s settings so that the real plant can follow the reference model. The adjusting mechanism can be developed using mathematical techniques, such as the MIT rule, Lyapunov theory, and the theory of augmented error. However, our work focuses on the MIT rule.

Figure 4 depicts the DMRAC system’s fundamental block diagram. As indicated in the diagram, $y_m$ represents the output of the reference model, whereas y is the output of the real plant, with $e$ denoting the difference between them.

$$\epsilon \left(t\right)=y\left(t\right)-y_m\left(t\right)$$

(20)

The MIT rule was initially created in 1960 by Massachusetts Institute of Technology (MIT) academics and was used to construct aviation autopilot systems. For every system, the MIT rule may be used to build a controller with the DMRAC scheme.

A cost function is defined as follows in this rule:

$$J\left(\theta \right)={\epsilon }^2/2$$

(21)

where $\epsilon$ is the difference between the plant’s outputs and the model’s outputs, and $\theta$ is the variable parameter.

The parameter is changed in such a way that the cost function may be reduced to zero. As a result, the change in the $\theta$ parameter is maintained in the direction of $J$’s negative gradient, i.e.,:

$$\frac{d\theta }{dt}=-\gamma \frac{\partial J}{\partial \theta }$$

(22)

From Equation (21):

$$\frac{d\theta }{dt}=-\gamma e\frac{\partial \epsilon }{\partial \theta }$$

(23)

The partial derivative phrase $\frac{\partial \epsilon }{\partial \theta }$is referred to as the system’s sensitivity derivative. This phrase describes how the error changes as a function of the parameter $\theta$. Equation (22) shows how the parameter changes over time, allowing the cost function $J\left(\theta \right)$to be lowered to zero.

Here $\gamma$is a positive number that represents the controller’s adaptation gain.

Assume the process is linear, with the transfer function $KG\left(s\right)$, where $K$ is an unknown parameter and $G\left(s\right)$ is a known second-order transfer function. Our objective is to create a controller that will allow our process to monitor the reference model using the transfer function $G_m$(s) = $K_{o}G\left(s\right)$, where $K_o$ is a known parameter.

From Equation (20):

$$\epsilon \left(s\right)=KG\left(s\right)U\left(s\right)-K_{o}G\left(s\right)U_c\left(s\right)$$

(24)

Furthermore, Equation (14) can be written as follows:

$$\widetilde{v_o}\left(s\right)=R\frac{\left(1-D\right)V_o-\left(L{I}_l\right)s}{\left(RLC\right)s^2+Ls-R{\left(1-D\right)}^2}\tilde{d}\left(s\right)$$

(25)

where $R$ in (25) can be considered as $K$ in (24) and $\tilde{d}\left(s\right)$ is the $U\left(s\right)$. Moreover, $R$ can be considered a system uncertainty.

Defining a PID control law, $=k_p,$ $k_i, k_d$. Therefore $u\left(t\right)$ is as follows:

$$u\left(t\right)=k_{p}e\left(t\right)+k_i\int e\left(t\right)dt+k_d\dot{e\left(t\right)}$$

(26)

where: $k_p$ is the proportional gain; $k_i$ is the integral gain; $k_d$ is the derivative gain; 𝑦 is the plant output; and $e\left(t\right)=r\left(t\right)-y\left(t\right)$, with $r\left(t\right)$as the input of the reference model.

The representation of the PID controller in Laplace domain is:

$$U\left(s\right)=k_{p}E\left(s\right)+\frac{1}{s}{k}_{i}E\left(s\right)+s{k}_{d}E\left(s\right)$$

(27)

Therefore, the Laplace domain of the system output will be as follows:

$$Y\left(s\right)=G\left(s\right)U\left(s\right)=G\left(s\right)[k_{p}E\left(s\right)+\frac{1}{s}{k}_{i}E\left(s\right)+s{k}_{d}E\left(s\right)]$$

(28)

As $e\left(t\right)=r\left(t\right)-y\left(t\right),$ it is clear that:

$$Y\left(s\right)=G\left(s\right)\left[R\left(s\right)-Y\left(s\right)\right][k_p+\frac{1}{s}{k}_i+s{k}_d]$$

(29)

Then we can obtain:

$$Y\left(s\right)[1+G\left(s\right)[k_p+\frac{1}{s}{k}_i+s{k}_d]]=G\left(s\right)R\left(s\right)[k_p+\frac{1}{s}{k}_i+s{k}_d]$$

(30)

$$Y\left(s\right)=\frac{G\left(s\right)R\left(s\right)\left[k_p+\frac{1}{s}{k}_i+s{k}_d\right]}{\left[1+G\left(s\right)\right[k_p+\frac{1}{s}{k}_i+s{k}_d]]}$$

(31)

Now the time domain of the system output can be written as:

$$y\left(t\right)=\frac{g\left(t\right)r\left(t\right)\left[p{k}_p+k_i+p^2{k}_d\right]}{\left[1+g\left(t\right)\right[p{k}_p+k_i+p^2{k}_d]]}$$

(32)

According to Equation (20):

$$\epsilon \left(t\right)=\frac{g\left(t\right)r\left(t\right)\left[p{k}_p+k_i+p^2{k}_d\right]}{\left[1+g\left(t\right)\left[p{k}_p+k_i+p^2{k}_d\right]\right]}-\frac{{\omega }_n{}^2}{p^2+2\xi {\omega }_{n}p+{\omega }_n{}^2}r\left(t\right)$$

(33)

Derivative of Equation (33) over PID parameters, is as follows:

$$\frac{\partial \epsilon \left(t\right)}{\partial k_p}=\frac{g\left(t\right)ep}{\left[1+g\left(t\right)\left[p{k}_p+k_i+p^2{k}_d\right]\right]}$$

$$\frac{\partial \epsilon \left(t\right)}{\partial k_i}=\frac{g\left(t\right)e}{\left[1+g\left(t\right)\left[p{k}_p+k_i+p^2{k}_d\right]\right]}$$

$$\frac{\partial \epsilon \left(t\right)}{\partial k_d}=\frac{g\left(t\right)e{p}^2}{\left[1+g\left(t\right)\left[p{k}_p+k_i+p^2{k}_d\right]\right]}$$

(34)

For the sake of ensuring that the tracking error is perfect, we will assume the time behavior of this close loop process is equal to the time behavior of the close loop reference model, as follows:

$$\frac{g\left(t\right)}{\left[1+g\left(t\right)\left[p{k}_p+k_i+p^2{k}_d\right]\right]}=\frac{{\omega }_n{}^2}{p^2+2\xi {\omega }_{n}p+{\omega }_n{}^2}$$

(35)

Now the gradient method described in Equation (23) is applied to find the expressions of the control parameters:

$$\frac{d{k}_p}{dt}=-{\gamma }_p\epsilon \left(t\right)\frac{p{\omega }_n{}^2}{p^2+2\xi {\omega }_{n}p+{\omega }_n{}^2}e\left(t\right)$$

$$\frac{d{k}_i}{dt}=-{\gamma }_i\epsilon \left(t\right)\frac{{\omega }_n{}^2}{p^2+2\xi {\omega }_{n}p+{\omega }_n{}^2}e\left(t\right)$$

$$\frac{d{k}_d}{dt}=-{\gamma }_d\epsilon \left(t\right)\frac{p^2{\omega }_n{}^2}{p^2+2\xi {\omega }_{n}p+{\omega }_n{}^2}e\left(t\right)$$

(36)

3.2. Stability and Robustness Analysis

Lyapunov stability theory was introduced in [21]. Lyapunov proposed two methods of demonstrating stability in his original work of 1892. The first method developed the solution into a sequence, which then proved to be convergent within parameters. Another approach, known as the Lyapunov stability criterion or direct method, uses an analogy of the potential function of classical dynamics with the Lyapunov function $V\left(x\right)$. For a system as $\dot{x}=f\left(x\right)$, if the Lyapunov function has three following conditions:

$$V\left(x\right)=0 \mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}x=0$$

$$V\left(x\right)>0 \mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}x\ne 0$$

$$\dot{V}\left(x\right)<0$$

The system is stable in the sense of Lyapunov. By considering (21) as the Lyapunov function, the mentioned equation can be rewritten as:

$$V\left(\theta \right)={\epsilon }^2/2$$

(37)

where $e$ is the error equation in Equation (20), the second term of the error equation is the output of the model reference, and the first term is the output of the DC–DC boost converter, which can be obtained from Equation (14).

Now the derivative of the Lyapunov equation is:

$$\dot{V}\left(\theta \right)=\epsilon \dot{\epsilon }$$

(38)

By considering the derivative of error term in Equation (38), we reach the following equation:

$$\dot{V}\left(\theta \right)=\left(\epsilon \right)\frac{d\epsilon }{d\theta }\frac{d\theta }{dt}$$

(39)

Therefore, by substituting Equations (34) and (36):

$$\dot{V}\left(k_p\right)=\left(\epsilon \right)\left(y_{m}ep\right)\left(-{\gamma }_p\epsilon y_{m}ep\right)=-{\gamma }_p{\epsilon }^2{y}_m{}^2{e}^2{p}^2$$

$$\dot{V}\left(k_i\right)=\left(\epsilon \right)\left(y_{m}e\right)\left(-{\gamma }_i\epsilon y_{m}e\right)=-{\gamma }_i{\epsilon }^2{y}_m{}^2{e}^2$$

$$\dot{V}\left(k_d\right)=\left(\epsilon \right)\left(y_{m}e{p}^2\right)\left(-{\gamma }_d\epsilon y_{m}e{p}^2\right)=-{\gamma }_d{\epsilon }^2{y}_m{}^2{e}^2{p}^4$$

(40)

From Equation (40), it is easy to claim that the derivative of the Lyapunov equation is negative in Equation (38), which is the third condition of Lyapunov stability.

3.3. Simulation Results

Simulink is an extension to MATLAB that allows you to create dynamic models in Windows. The benefit is that models are inserted as block diagrams once the target system’s matching mathematical equations are established. To simulate an electrical system, such as a DC–DC converter, one must enter equations for various blocks in the system and use icons in Simulink to create an analogous block diagram. Individual icon settings can be defined for the process. Finally, an equation solver and simulation duration are selected. A Simulink model can readily be constructed, as shown in the flowchart in Figure 5, referring to the model reference adaptive controller block diagram in Figure 4.

In this simulation, the inductor is $L=1.3\times {10}^{-3} \mathrm{H}$, the capacitor is$C=6.5\times {10}^{-3} \mathrm{F}$, the resistor is $R=100 \mathsf{\Omega },$ and the input voltage source is considered to be $V_{in}=5 \mathrm{V}$. Therefore, the transfer function of the boost converter, which gives the output voltages in terms of duty ratio, is:

$$\frac{\widetilde{v_o}\left(s\right)}{\tilde{d}\left(s\right)}=\frac{\left(1-0.5\right)15-\left(1.3\times {10}^{-3}\right)\left(45\right)s}{\left(1.3\times {10}^{-3}\right)\left(6.5\times {10}^{-3}\right)s^2+\frac{1.3\times {10}^{-3}}{100}s-{\left(0.5\right)}^2}$$

(41)

where the reference input is $15\mathrm{V}$, and the model reference block of the adaptive method is a first order transfer function with a pole far enough from the origin. The mentioned block is shown in the following Figure 6.

The model is a first-order system with a pole lying on the left-hand side of the complex plane. Figure 7 below shows the model reference block step response.

The adjustment mechanism block, illustrated in Figure 8 below, has two inputs: the error and the output of the model reference block, and only has one output, $\mathsf{\theta },$ which multiplies the PID parameters to adjust the controller.

The controller block is a PID controller tuned using automated tuning of Simulink to figure out the initial condition of PID parameters. Figure 9 below shows some more details of the controller block, where the $Y_p$ stands for the capacitor voltage $V_c$.

Finally, a PWM generator is used to produce pulses based on the controller output. The pulses are vital as an input of the switching component.

Simulations were carried out to verify the controller’s capabilities for DC–DC converters that achieve voltage regulation. The switching frequency is considered 2 kHz. As load variation is expected in a typical MG, the proposed controller’s effectiveness and robustness are validated through load variations. The transient response of the step-up converter is illustrated in Figure 10a when the reference voltage is V = 15 V. The output signal reaches the reference value set at $~$0.04 s. The overshoot is $~0.03 \mathrm{V}$ which is negligible. In the case of the change in load (from $R$ = 100 Ω to $R$ = 150 Ω), the worst-case settling time shown in Figure 10a (in the right figure magnifier) was obtained as $~$0.1 s with a maximum overshoot of $~$0.5 V. The adjustment parameter is being adapted by the load changes in Figure 10b, and the control signal is changed as a consequence of adjustment parameter changes in Figure 10c.

The control signal generates the desired value of the duty cycle, which is updated by the MIT rule to obtain the desired voltage and connect it to the Pulse Width Modulator (PWM). This duty cycle change changes the output voltage to reduce the error signal to zero.

In the other case, as the output of the PV system that is connected to a DC–DC converter in the considered MG is not stable, the input voltage of the DC–DC converter is changed, and the results are shown in Figure 11. The input voltage is changed by 2 V from 8 V to 10 V (and vice-versa), and the worst overshoot response is less than $~$1 V. It means that the maximum overshoot in the effect of input voltage changing is less than $~$6.6%.

As is shown in [22], the lowest overshoot in 15 V setpoint, among three different PID tuning methods, namely the Ziegler–Nichols frequency-domain method, damped oscillation method, and Good Gain method, is 34%, and the fastest rise time is 1.5 ms. Therefore, it is evident from the simulation results that the proposed algorithm has better performance in dealing with the maximum overshoot issues. Moreover, comparing the proposed method with nonlinear methods, such as the improved sliding mode controller presented in [23], shows that the output’s overshoot of DMRAC is still negligible.

The bode plot of the DMRAC is presented in Figure 12, where the model reference is as shown in Figure 7 and the adjustment parameters shown in Figure 11d. The following figure shows the gain margin is 8.44 dB and the phase margin is 65.3 deg.

3.4. Experimental Results

A hardware implementation is conducted to evaluate the controller’s performance in the real world. The Arduino Uno is used to interface Simulink’s DMRAC controller and the DC–DC boost converter circuit to implement hardware in the loop. It is worth mentioning that the analog input pins of Arduino Uno are limited to 5 V, so a voltage divider circuit is used to reduce the feedback output voltage. Therefore, it is inevitable to revise the feedback voltage in Simulink. Figure 13 shows the designed Simulink to create an embedded system on Arduino Uno. Figure 14a illustrates the setup connectivity between Simulink and the DC–DC boost converter. The components used to implement the experimental test are shown in Figure 14b. The components used to build the circuit are listed in

Table 2. Hardware description.

Device/Component	Model/Value
Arduino	Uno
Capacitor	$330\mathsf{\mu }\mathrm{F}$
Inductor	$250 \mathsf{\mu }\mathrm{H}$
Load resistor	$330 \Omega$
Voltage divider resistors	$100 \Omega , 220 \Omega$
Mosfet	IRLZ44 N
Diode	In4004

.

Figure 15a shows the transient output response of the boost converter for the reference voltage of 15 V. The effect of input voltage changes from 8 V to 10 V (and vice-versa) is shown in Figure 15b. In Figure 15c, we can see how the output voltage changes with the presence of a change in voltage reference from 15 V to 10 V (and vice-versa). In all cases, the settling time is about 0.2 s. Moreover, it is evident in Figure 15a,c that the system is tracking the reference voltage with almost no overshoot.

4. Conclusions

This work presents an adaptive controller to regulate the output voltage of the DC–DC converters that exist in an isolated MG. Since the converter system is a non-minimum phase, the controller design that relies only on output voltage feedback becomes challenging. Even though output voltage control can be achieved using inductor current control, such current mode controllers may also require prior knowledge of the load resistance and more states, such as output and inductor currents in feedback. In this work, the output voltage is stabilized by two control loops. A PID controller regulates the output voltage at a fixed level, and the outer loop implements the MIT rule for DMRAC. The DMRAC updates the PID controller parameters in real-time to ensure that the existing system tracks the desired reference model, using only an output voltage feedback sensor.

The proposed controller and the model are tested in MATLAB/SIMULINK for load disturbances. The load was changed by ~50% of its original value, and the worst-case settling time and maximum overshoot were less than ~0.1 s and 0.5 V, respectively, as compared to well-tuned PID controllers. The hardware validation is also carried out to show the performance of the proposed controller. Our results suggest that the DMRAC provides robust regulation against parameter variations. Therefore, it is suitable to use in any isolated MG.

The control scheme is implemented with a single output voltage feedback sensor, so no additional sensing circuitry was required.

The limitation of the proposed design is that the time delay effect on stability was not studied. Additionally, the simulation parameters were ideal. In future research work, the mentioned limitations will be addressed.