Powers and Power Factor in Non-Sinusoidal and Non-Symmetrical Regimes in Three-Phase Systems
Abstract
:1. Introduction
2. Theories of Powers in Three-Phase Systems Operating in Non-Sinusoidal and Non-Symmetrical Regimes
2.1. The Theory Relying on Powers Decomposition into Active, Reactive, Distorting, and Apparent Components
2.1.1. Relations Used for the Definitions of Active, Reactive and Distorting Powers in a Balanced Three-Phase System Operating in a Distorting Regime
- -
- for voltages:
- -
- for currents:where: Uj and Ij (j = l, 2, 3)—represent the vectors (first order tensors) of the phase voltage and current in the vectorial space E,represent the projections of the vectors Uj along the axis Kx of a subspace E1 of odd functions (similar equations can be written for currents [14]);represent the projections of the vectors Uj along the axis Ky of a subspace E2 of odd functions (similar equations can be written for currents [14]).
2.1.1.1. Active Powers of Phases and Total Active Power for Phases without Magnetic Couplings
2.1.1.2. Reactive Powers of Phases and Total Reactive Power
2.1.1.3. Distorting Powers and Their Vectorial Features of Distorting Powers. Total Distorting Power of a Balanced Three-Phase Network in Distorting Regimes
- (a)
- One can define in this theory (“Antoniu–Gafencu” theory) the (re)active, distorting and apparent powers by using the separation of power components according to Budeanu’s theory for single-phase systems.
- (b)
- Despite Equation (20), one can evaluate the total distorting power as the sum of phase distorting powers. The experience proved that the results yielded by Equations (19) and (20) are close to the sum . As a consequence, one can determine the total apparent power with and evaluate the power factor with (24).
- (c)
- The results yielded by Equations (7), (11), (15) and (20) provide modalities for measuring, charging, compensation and correct definition of some PQ indices before and after compensation, from both technical and economic points of view.
- (d)
- Distorting powers diminishing actually assumes the diminishing of harmonic power components from voltages and currents with different harmonic orders. This process is followed by a diminishing of high harmonic components from the spectrum of (re)active powers.
2.1.2. Defining the Active, Reactive and Distorting Powers in a Non-Symmetrical Three-Phase System Considering the Symmetrical Voltage and Current Components
- -
- for corresponding voltages:
- -
- for the corresponding currents:
2.1.2.1. Expression of Active Power with Respect to the Symmetrical Components of Voltage and Current
2.1.2.2. Expression of Reactive Power with Respect to the Symmetrical Components of Voltage and Current
2.1.2.3. Expression of Distorting Power with Respect to the Symmetrical Components of Voltage and Current. Vectorial Feature of the Distorting Power in Non-Symmetrical Three-Phase Networks
- (a)
- make possible both the apparent powers and power factor measurement, allowing for the accomplishment of a full load compensation, which involves the following steps: (a1) removing the high order harmonics from the currents and voltages non-sinusoidal waveforms; (a2) symmetrisation of consumers by using symmetrisation schematics on the fundamental harmonic (e.g., Steinmetz connection); (a3) improving the power factor for the fundamental harmonic.
- (b)
- make possible the issuing of definitions for (b1) certain parameters to be used for the quantification of the full load compensation effect; (b2) indices related to the economic effects and the ROI associated with the equipment used during the compensation process.
2.2. Powers Definition Addressed by the IEEE Standard 1459-2010
- -
- a term corresponding to fundamental equivalent voltage and superior harmonics of currents:
- -
- a term corresponding to fundamental equivalent current and superior harmonics of voltages:
- -
- a term corresponding to the superior harmonics of equivalent voltages and currents:
- -
- Equivalent harmonic distortion of the three-phase voltages:
- -
- Equivalent harmonic distortion of three-phase currents:
2.3. Powers Definition Based on the Decomposition with Wavelet Transforms
2.3.1. Power Components Definitions for Single-Phase Waveforms, Based on DWT
2.3.1.1. Power Components Definitions When DWT Is Used, Single Phase
- Calculation of RMS
- 2.
- Total harmonic distortion
- 3.
- Active power
- 4.
- Apparent power
- 5.
- Power Factor
- 6.
- Details pollution
2.3.1.2. Power Components Definitions When DWT Is Used, Three-Phase Systems
- Calculation of Root Mean Square (RMS) values
- 2.
- Active power
- 3.
- Apparent power
- 4.
- Power Factor
- 5.
- Details Pollution
- 6.
- Load Unbalance
2.4. Theory Relying on the Powers’ Definition Using the Real and Imaginary Powers Definition
- -
- For the reactive power:
- -
- The active power can be computed with the formula from Equation (10).
3. Results
3.1. Study of Waveforms Acquired from the Secondary Winding of a Transformer Used to Supply the Excitation of a Power Group
3.1.1. Operational Context
3.1.2. Data Processing and Powers Computation by Using Fast Fourier Transform
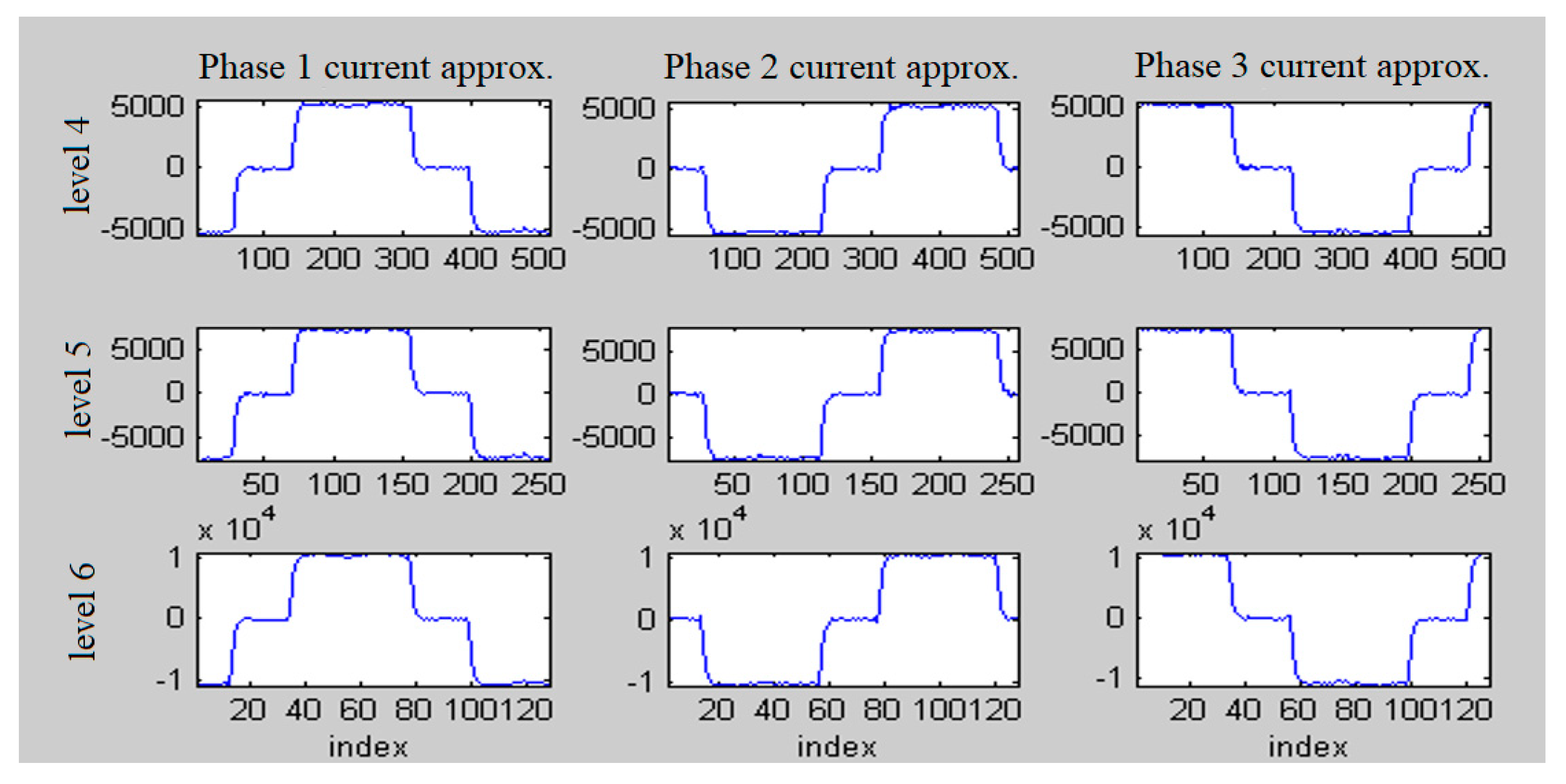
3.1.3. Data Processing and Powers Computation by Using Discrete Wavelet Transform
3.2. Study of Waveforms Acquired from the Primary Winding of a Transformer Used to Supply the Excitation of a Power Group
3.2.1. Data Processing and Powers Computation by Using Fast Fourier Transform
3.2.2. Data Processing and Powers Computation by Using Discrete Wavelet Transform
3.3. Study of Waveforms Acquired from the Terminals of the Main Generator from a Power Group
3.3.1. Data Processing and Powers Computation by Using Fast Fourier Transform
3.3.2. Data Processing and Powers Computation by Using Discrete Wavelet Transform
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| instantaneous three-phase voltages | |
| the voltage RMS value for the k’th order harmonic | |
| initial phase for the k-th order harmonic voltage | |
| instantaneous three-phase currents | |
| the current RMS value for the k’th order harmonic | |
| initial phase for the k-th order harmonic current | |
| the vectors (first-order tensors) of the phase voltages in the vectorial space E, in Antoniu–Gafencu Theory | |
| I1, I2, I3 | the vectors (first-order tensors) of the phase currents in the vectorial space E, in Antoniu–Gafencu Theory |
| , , | the projections of the vectors U1, U2, U3 along the axis Kx of a subspace E1 of odd functions (similar equations can be written for currents); |
| , , | the projections of the vectors along the axis Ky of a subspace E2 of odd functions (similar equations can be written for currents). |
| phase-shift between the voltage and the current corresponding to the harmonic order k, in the Antoniu–Gafencu Theory | |
| phase-shift between the voltage and the current corresponding to the harmonic order l, in the Antoniu–Gafencu Theory | |
| total active power of the (un)balanced three-phase network operating in a distorting regime | |
| active powers for each of the three phases in the Antoniu–Gafencu Theory | |
| rotation operator with | |
| rotation operator with | |
| total reactive power, in the Antoniu–Gafencu Theory | |
| total distorting power in the Antoniu–Gafencu Theory | |
| distorting power for each phase in the Antoniu–Gafencu Theory | |
| zero-sequence, positive-sequence, negative-sequence components of phase voltages | |
| positive sequence voltage for the kth harmonic order in the Antoniu–Gafencu Theory | |
| negative sequence voltage for the kth harmonic order | |
| zero sequence voltage for the kth harmonic order | |
| , , | positive sequence current components of phases in the Antoniu–Gafencu Theory |
| positive sequence current for the kth harmonic order | |
| , , | negative sequence current components of phases in the Antoniu–Gafencu Theory |
| negative sequence current for the kth harmonic order in the Antoniu–Gafencu Theory | |
| zero sequence current components of phases in the Antoniu–Gafencu Theory | |
| zero sequence current for the kth harmonic order in the Antoniu–Gafencu Theory | |
| total Root Mean Square (RMS) current in IEEE 1459 Std. | |
| RMS current of the fundamental harmonic in IEEE 1459 Std. | |
| equivalent RMS harmonic current in IEEE 1459 Std. | |
| total Root Mean Square (RMS) voltage in IEEE 1459 Std. | |
| RMS voltage of the fundamental harmonic in IEEE 1459 Std. | |
| equivalent RMS harmonic voltage in IEEE 1459 Std. | |
| total effective apparent power in IEEE 1459 Std. | |
| fundamental effective apparent power in IEEE 1459 Std. | |
| non-symmetrical apparent power in IEEE 1459 Std. | |
| fundamental positive-sequence apparent power in IEEE 1459 Std. | |
| nonfundamental effective apparent power in IEEE 1459 Std. | |
| current distortion power in IEEE 1459 Std. | |
| voltage distortion power in IEEE 1459 Std. | |
| harmonic apparent power for superior harmonics in IEEE 1459 Std. | |
| harmonic active power for superior harmonics in IEEE 1459 Std. | |
| harmonic distortion power for superior harmonics in IEEE 1459 Std. | |
| equivalent total voltage harmonic distortion in IEEE 1459 Std. | |
| equivalent total current harmonic distortion in IEEE 1459 Std. | |
| fundamental positive-sequence active power in IEEE 1459 Std. | |
| fundamental positive-sequence reactive power in IEEE 1459 Std. | |
| fundamental positive-sequence power factor in IEEE 1459 Std. | |
| equivalent power factor in IEEE 1459 Std. | |
| fundamental positive-sequence power factor in IEEE 1459 Std. | |
| discrete wavelet coefficient corresponding to the voltage for the level | |
| , | discrete Wavelet coefficients for the levels , sample k |
| RMS voltage value for the level with the lowest frequency j0 (“approximation” voltage) | |
| RMS voltage for higher frequency bands (“details” voltage) | |
| discrete Wavelet coefficient corresponding to the current for the level | |
| RMS current value for the level with the lowest frequency j0 (“approximation” current) | |
| RMS current for higher frequency bands (“details” current) | |
| Wavelet function | |
| single-phase approximation active power in the Morsi theory | |
| single-phase details active power in the Morsi theory | |
| single-phase active power for higher frequency bands (“details” active power) | |
| single-phase non-active power in the Morsi theory | |
| single-phase approximate apparent power in the Morsi theory | |
| single-phase RMS voltage for higher frequency bands (“details” voltage) | |
| single-phase RMS current for higher frequency bands (“details” current) | |
| single-phase “non-approximation” apparent power | |
| single-phase displacement power factor (dPF) | |
| single-phase total power factor | |
| single-phase oscillating power factor | |
| single-phase details pollution | |
| “approximation” effective RMS values for three-phase voltages and currents in the Morsi theory | |
| “details” effective RMS values for three-phase voltages and currents in the Morsi theory | |
| , | three-phase effective RMS values of voltage and current in the Morsi theory |
| three-phase positive sequence active power in the Morsi theory | |
| total active power in the Morsi theory | |
| Seapp | three-phase “approximation” effective apparent power in the Morsi theory |
| SUapp | three-phase “approximation” unbalanced power in the Morsi theory |
| three-phase positive sequence apparent approximation power in the Morsi theory | |
| , | positive sequence effective RMS approximation voltage, current in the three-phase case in the Morsi theory |
| three-phase “non-approximation” effective apparent power in the Morsi theory | |
| three-phase details apparent power in the Morsi theory | |
| three-phase “approximation” positive sequence power factor in the Morsi theory | |
| load unbalance in the Morsi theory | |
| instantaneous power in the Akagi theory | |
| the stationary reference frame used in the Akagi theory for the Clarke transformation | |
| phase voltages of a three-phase load in the Akagi theory | |
| phase currents of a three-phase load in the Akagi theory | |
| modified α, β, 0 voltage components supplying the load in the Akagi theory | |
| modified α, β, 0 current components supplying the load in the Akagi theory | |
| phase active powers | |
| the instantaneous real power without zero-components in the Akagi theory | |
| total instantaneous real power without zero-components in the Akagi theory | |
| the instantaneous zero power in the Akagi theory | |
| instantaneous imaginary (reactive) power in the Akagi theory | |
| average and fluctuating components of the instantaneous real power | |
| average and fluctuating components of the instantaneous reactive power |
References
- Budeanu, C. Puissances Reactives and Fictives; Institut National Roumaine–pour l’etude de l’amenagement et de l’utilisation des Sources de l’energie: Bucharest, Romania, 1927. [Google Scholar]
- Fryze, S. Wirk-, Blind- und Scheinleistung in Electrisken Stromkreisen mit nichtsinusoidalen, Verlauf von Strom und Spannung. ETZ 1931, 25, 33. [Google Scholar]
- Depenbrock, M. Wirk-und Blindleistung; ETG-Fachtagung “Blindleistung”: Aachen, Germany, 1979. [Google Scholar]
- Kusters, N.L.; Moore, W.J.M. On the definition of reactive power under nonsinusoidal conditions. IEEE Trans. Power Appl. Syst. 1980, PAS-99, 1845–1854. [Google Scholar] [CrossRef]
- Czarnesky, L.S. Powers in nonsinusoidal networks, interpretation and measurement. IEEE Trans. Instrum. Meas. 1990, 39, 340–345. [Google Scholar] [CrossRef]
- Depenbrock, M. The FDB-method a generalized applicable tool for analyzing power relations. IEEE Trans. Power Deliv. 1993, 8, 381–387. [Google Scholar] [CrossRef]
- European Standard EN 50160; Voltage Characteristics of Electricity Supplied by Public Distribution Systems. CENELEC: Brussels, Belgium, 1999.
- IEEE Standard 519-2014; IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2014.
- Czarnesky, L.S. Currents’ Physical Components (CPC) concept: A fundamental of power theory. In Proceedings of the 2008 International School on Nonsinusoidal Currents and Compensation (ISNCC), Zielona Gora, Poland, 10–13 June 2008; pp. 727–732. [Google Scholar] [CrossRef]
- Czarnecki, L.S.; Haley, P. Reactive compensation in three-phase four-wire systems at sinusoidal voltages and currents. In Proceedings of the International School on Nonsinusoidal Currents and Compensation 2013 (ISNCC 2013), Zielona Gora, Poland, 17–20 June 2012; pp. 727–732. [Google Scholar] [CrossRef]
- Akagi, H.; Kanazawa, Y.; Nabae, A. Generalized theory of the instantaneous reactive power in three-phase circuits. In Proceedings of the International Power Electronics Conference—IPEC’83, Tokyo, Japan, 27–31 March 1983; pp. 1375–1386. [Google Scholar]
- Akagi, H.; Ogasawara, S.; Kim, H. The theory of instantaneous power in three-phase four-wire systems: A comprehensive approach. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference, Thirty-Forth IAS Annual Meeting (Cat. No. 99CH36370), Phoenix, AZ, USA, 3–7 October 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 1, pp. 431–439. [Google Scholar] [CrossRef] [Green Version]
- Akagi, H.; Kanazawa, Y.; Nabae, A. Instantaneous Reactive Power compensators comprising switching devices without energy storage components. IEEE Trans. Ind. Appl. 1984, IA-20, 625–630. [Google Scholar] [CrossRef]
- Antoniu, I.S.; Gafencu, M. Les puissances dans une systeme triphase fonctionnant en regime deformant. Rev. Roum. Des Sci. Tech. (RRST) Electroteh. Energetique 1976, 21, 519–530. [Google Scholar]
- Antoniu, I.S.; Gafencu, M. L’expresion des puissance dans une systeme triphase desequilibre et deformant en fonction des composantes symetrique. Rev. Roum. Des Sci. Tech. (RRST) Electroteh. Energetique 1977, 22, 3–10. [Google Scholar]
- IEEE 1459-2010; Definitions for the Measurement of Electric Power Quantities under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions Unbalanced and Nonlinear Systems. IEEE: Piscataway, NJ, USA, 2010.
- Nicolae, P.M. Considerations on instantaneous components of powers based on the decomposition of voltages and currents in instantaneous symmetrical components. In Proceedings of the 3rd National Seminar for theoretical Electrotechnics, Al Treilea Seminar National de Electrotehnica Teoretica; Politechnica University Bucuresti: Bucharest, Romania, 1997; pp. 1–12. [Google Scholar]
- Morsi, W.G.; El-Hawary, M.E. Reformulating Power Components Definitions Contained in the IEEE Standard 1459-2000 Using Discrete Wavelet Transform. IEEE Trans. Power Deliv. 2007, 22, 1910–1916. [Google Scholar] [CrossRef]
- Morsi, W.G.; El-Hawary, M.E. Reformulating Three-Phase Power Components Definitions Contained in the IEEE Standard 1459-2000 Using Discrete Wavelet Transform. IEEE Trans. Power Deliv. 2007, 22, 1917–1923. [Google Scholar] [CrossRef]
- Nicolae, I.D.; Nicolae, P.M. Using Wavelet Transform for the Evaluation of Power Quality in Distorting Regimes. Acta Electroteh. 2011, 52, 445–448. [Google Scholar]
- Nicolae, I.D.; Nicolae, P.M.; Purcaru, D.M. Computational Issues Related to the Discrete Wavelet Analysis of Power. Ann. Univ. Craiova Autom. Comput. Electron. Mechatron. Ser. 2011, 8, 25–30. [Google Scholar]
- Nicolae, I.D.; Nicolae, P.M. Using Discrete Wavelet Transform to evaluate power quality at highly distorted three-phase systems. In Proceedings of the 11th International Conference on Electrical Power Quality and Utilisation, Lisbon, Portugal, 17–19 October 2011. [Google Scholar] [CrossRef]
- Nicolae, P.M. On Real and Imaginary Instantaneous Powers Theory in Three-Phase Networks. Rev. Roum. Des Sci. Tech. (RRST) Ser. Electroteh. Energetique (EEA) 1995, 40, 215–226. [Google Scholar]
- Nicolae, P.M. Instantaneous Real and Imaginary Powers at Three-Phase Networks with Balanced Loads that Function Under Distorting Regime. Rev. Roum. Des Sci. Tech. (RRST) Ser. Electroteh. Energetique (EEA) 1995, 40, 311–319. [Google Scholar]
- Bojoi, R.I.; Griva, G.; Bostan, V.; Guerriero, M.; Farina, F.; Profumo, F. Current control strategy for power conditioners using sinusoidal signal integrators in synchronous reference frame. IEEE Trans. Power Electron. 2005, 20, 1402–1412. [Google Scholar] [CrossRef]
- Nicolae, P.M.; Vladut, G.C.; Constantinescu, M.C.; Nicolae, I.D.; Nicolae, M.S.; Constantinescu, I.I. System and Method for Determining Simultaneous of Electrical Measurement from Stations, Substations and Transformer Stations. Patent 127575, 30 December 2016. Awarded with Gold Medal at Geneva International Exhibition of Inventions, 2016. [Google Scholar]
- Pigazo, A.; Moreno, V.M. Accurate and computationally efficient implementation of the IEEE 1459-2000 standard in three-phase three-wire power systems. IEEE Trans. Power Deliv. 2007, 22, 752–757. [Google Scholar] [CrossRef]
- Zheng, T.; Makram, E.B.; Girgis, A.A. Evaluating power system unbalance in the presence of harmonic distortion. IEEE Trans. Power Deliv. 2003, 18, 393–397. [Google Scholar] [CrossRef]
- Ferrero, A. Definitions of Electrical Quantities Commonly Used in Non- Sinusoidal Conditions. Eur. Trans. Electr. Power Eng. (ETEP) 1998, 4, 235–240. [Google Scholar] [CrossRef]
- Tenti, P.; Matavelli, P. A Time-Domain Approach to Power Term Definitions under Non-Sinusoidal Conditions. In Proceedings of the Sixth International Workshop on Power Definitions and Measurements under Non-Sinusoidal Conditions, Milano, Italy, 13–15 October 2003; pp. 1–10. [Google Scholar]
- Willems, L. Reflections on apparent power and power factor in non-sinusoidal and poly-phase situations. IEEE Trans. Power Deliv. 2004, 19, 835–840. [Google Scholar] [CrossRef]
- Tugulea, A. Criteria for the Definitions of the Electric Power Quality and its Measurement Systems. Eur. Trans. Electr. Power Eng. (ETEP) 1996, 6, 357–363. [Google Scholar] [CrossRef]
- Morsi, W.G.; El-Hawary, M.E. Wavelet Packet Transform-Based Power Quality Indices for Balanced ad Unbalanced Three-Phase Systems under Stationary and Non-stationary Operating Conditions. IEEE Trans. Power Deliv. 2009, 24, 2300–2310. [Google Scholar] [CrossRef]
- Czarnecki, L. Instantaneous Reactive Power p-q Theory and Power Properties of Three-Phase Systems. IEEE Trans. Power Deliv. 2006, 21, 362–367. [Google Scholar] [CrossRef]
- Akagi, H. Modern active filters and traditional passive filters. Bull. Pol. Acad. Sci. Tech. Ser. 2006, 54, 255–268. [Google Scholar]
- Kulvitit, Y. DC analysis of converters using rectifier control cell. In Proceedings of the IEEE International Conference on Industrial Technology—ICIT 2002, Bankok, Thailand, 11–14 December 2002; Volume 2, pp. 774–779. [Google Scholar] [CrossRef]
- Stankovic, A.V.; Chen, K. A New Control Method for Input-Output Harmonic Elimination of the PWM Boost-Type Rectifier under Extreme Unbalanced Operating Conditions. IEEE Trans. Ind. Electron. 2009, 56, 2420–2430. [Google Scholar] [CrossRef]


























| Index | Units | Phase Number | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Total RMS of currents | A | 1048.85 | 1053.77 | 1067.91 |
| RMS of currents for the fundamental harmonic | A | 1011.46 | 1017.03 | 1029.31 |
| Distorting residue of currents | A | 227.47 | 275.76 | 283.96 |
| Total harmonic distortion of currents | % | 26.46 | 26.17 | 26.59 |
| Total RMS of voltages | V | 337.55 | 336.77 | 333.81 |
| RMS of voltages for the fundamental harmonic | V | 336.88 | 336.18 | 333.06 |
| Distorting residue of voltages | V | 21.27 | 20.07 | 22.21 |
| Total harmonic distortion of voltages | % | 6.3 | 5.96 | 6.65 |
| Phase active powers | kW | 96.51 | 100.28 | 103.09 |
| Total active power | kW | 299.88 | ||
| Phase active powers for the fundamental harmonic | kW | 98.67 | 102.62 | 105.97 |
| Total active power for the fundamental harmonic | kW | 307.26 | ||
| Phase reactive powers | kVAr | 321.59 | 321.91 | 321.52 |
| Phase reactive powers on the fundamental harmonic | kVAr | 326.14 | 326.14 | 326.03 |
| Total reactive power | kVAr | 978.36 | ||
| Phase distorting powers | kVAd | 112.29 | 110.74 | 114.32 |
| Total distorting power | kVAd | 337.35 | ||
| Phase apparent powers | kVA | 354.04 | 354.88 | 356.76 |
| Phase apparent powers on the fundamental harmonic | kVA | 340.74 | 341.9 | 342.82 |
| Total apparent power | kVA | 1065.4 | ||
| Power factor on the fundamental harmonic | 0.299 (inductive character) | |||
| Power factor | 0.281 (inductive character) | |||
| Parameters | Units | Phase Number | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Total RMS of currents | A | 1048.01 | 1054.76 | 1067.36 |
| RMS of currents for the fundamental harmonic | A | 1014.63 | 1021.28 | 1030.5 |
| Distorting residues of currents | A | 262.42 | 263.66 | 278.07 |
| Total harmonic distortions of currents | % | 26.04 | 25.49 | 26.05 |
| Node zero voltages | V | 337.87 | 336.55 | 333.59 |
| RMS of voltages for the fundamental harmonic | V | 337.2 | 335.99 | 332.79 |
| Distorting residues of voltages | V | 21.2 | 19.32 | 23.09 |
| Total harmonic distortions of voltages | % | 6.28 | 5.74 | 6.92 |
| Active powers of approximations, Papp | kW | 99.09 | 102.55 | 104.92 |
| Active power of details, Pdet | kW | −2.38 | −1.91 | −2.72 |
| Phase active powers | kW | 96.7 | 100.51 | 102.2 |
| Total active power of approximations | kW | 300.76 | ||
| Total active power of details | kW | −7.15 | ||
| Total active power | kW | 292.98 | ||
| Reactive powers of approximations, Qapp | kVAr | 327.47 | 327.5 | 326.51 |
| Reactive powers of details, Qdet | kVAr | 5.03 | 4.72 | 5.82 |
| Total reactive power of approximation | kVAr | 985.33 | ||
| Distorting powers of currents | kVAd | 88.49 | 88.58 | 92.54 |
| Distorting powers of voltages | kVAd | 21.51 | 19.73 | 23.79 |
| Distorting powers of details, Ddet | kVAd | 6.06 | 5.44 | 6.97 |
| Non-active powers, N | kVAd | 367.06 | 368.94 | 370.45 |
| Effective apparent power of approximations Sapp | kVA | 342.14 | 343.14 | 342.95 |
| Effective apparent power of details Sdet | kVA | 5.56 | 5.09 | 6.42 |
| “Non-approximation” effective apparent power SeN | kVA | 91.24 | 90.9 | 95.77 |
| Apparent powers | kVA | 354.09 | 354.98 | 356.07 |
| Effective apparent powers of approximation, Seapp | kVA | 1028.31 | ||
| Unbalanced power of approximations SUapp | kVAd | 58.84 | ||
| Effective apparent powers of details, Sedet | kVAd | 17.1 | ||
| Total distorting power of current, DeI | kVA | 269.76 | ||
| Total distorting power of voltage DeV | kVA | 65.19 | ||
| “Non-approximation” effective apparent power SeN | kVA | 278.05 | ||
| Total non-active power, N | kVA | 1024.15 | ||
| Effective apparent powers | kVA | 1065.23 | ||
| Power factor of approximations on positive sequence | 0.291 (inductive character) | |||
| Total power factor | 0.275 (with inductive character) | |||
| Parameter | Phase Number | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Total RMS for currents | 0.08 | −0.09 | 0.05 |
| RMS for currents (fundamental harmonic) | −0.31 | −0.42 | −0.12 |
| Total harmonic distortions of currents | 1.58 | 2.59 | 2.03 |
| Total RMS for voltages | 0.09 | 0.06 | 0.06 |
| RMS for voltages (fundamental harmonic) | −0.09 | 0.05 | 0.08 |
| Distorting residue of voltages | 0.33 | 3.73 | 3.96 |
| Total harmonic distortion of voltages | 0.32 | 3.69 | 4.06 |
| Active powers | 0.19 | 0.23 | 0.86 |
| Total active power | 2.3 | ||
| Apparent powers | −0.01 | −0.26 | 0.19 |
| Total apparent power | 0.02 | ||
| Power factor | 2.14 | ||
| Parameters | Units | Phase Number | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Total RMS of currents | A | 27.92 | 29.15 | 29.62 |
| RMS of currents on the fundamental harmonic | A | 26.94 | 28.15 | 27.65 |
| Distorting residues of currents | A | 7.34 | 7.56 | 7.40 |
| Total harmonic distortions of currents | % | 26.28 | 25.95 | 25.86 |
| Total RMS of voltages | kV | 13.532 | 13.535 | 13.556 |
| RMS of voltages on the fundamental harmonic | kV | 13.526 | 13.529 | 13.552 |
| Distorting residues of voltages | V | 369.46 | 371.44 | 327.05 |
| Total harmonic distortion of voltages | % | 2.73 | 2.74 | 2.41 |
| Active powers | kW | 112.97 | 123.33 | 114.23 |
| Total active power | kW | 350.53 | ||
| Active powers on the fundamental harmonic | kW | 113.10 | 123.73 | 114.42 |
| Total active power on the fundamental harmonic | kW | 351.25 | ||
| Reactive powers | kVAr | 346.73 | 360.65 | 357.07 |
| Reactive powers on the fundamental harmonic | kVAr | 346.40 | 360.25 | 356.75 |
| Total reactive power | kVAr | 1064.45 | ||
| Distorting powers | kVAd | 99.02 | 101.98 | 99.92 |
| Total distorting power | kVAd | 300.92 | ||
| Apparent powers of phases | kVA | 377.88 | 394.56 | 387.99 |
| Apparent powers on the fundamental harmonic | kVA | 364.40 | 380.90 | 374.64 |
| Total apparent power | kVA | 1119.94 | ||
| Power factor on the fundamental harmonic | 0.314 (with inductive character) | |||
| Power factor | 0.302 (with inductive character) | |||
| Parameters | Units | Phase Number | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Total RMS of currents | A | 27.90 | 29.17 | 28.63 |
| RMS of currents on the fundamental harmonic | A | 26.95 | 28.23 | 27.74 |
| Distorting residues of currents | A | 7.19 | 7.33 | 7.07 |
| Total harmonic distortions of currents | % | 26.95 | 26.63 | 26.34 |
| Node zero voltage | kV | 13.54 | ||
| Total RMS of voltages | kV | 13.545 | 13.527 | 13.551 |
| RMS of voltages on the fundamental harmonic | kV | 13.542 | 13.52 | 13.548 |
| Distorting residue of voltages | V | 206.34 | 285.26 | 235.66 |
| Total harmonic distortion of voltages | % | 1.52 | 2.11 | 1.74 |
| Active powers of approximations, Papp | kW | 112.73 | 125.36 | 113.84 |
| Active powers of details, Pdet | W | 448.20 | −1153.99 | −60.60 |
| Active powers | kW | 113.18 | 124.21 | 113.77 |
| Total active power of approximation | kW | 350.67 | ||
| Total active power of details | W | −766.39 | ||
| Total active power | kW | 349.90 | ||
| Reactive powers of approximations, Qapp | kVAr | 347.18 | 360.57 | 358.25 |
| Active powers of details, Qdet | kVAr | 1.414 | 1.745 | 1.665 |
| Total reactive power of approximation | MVAr | 1.065 | ||
| Current distorting powers | kVAd | 97.37 | 99.19 | 95.80 |
| Voltage distorting powers | kVAd | 5.561 | 8.052 | 6.538 |
| Distorting powers of details, Ddet | kVAd | 1.549 | 2.389 | 1.667 |
| Non-active powers, N | kVAd | 394.42 | 413.60 | 404.31 |
| Apparent powers of approximations, Sapp | kVA | 365.02 | 381.74 | 375.90 |
| Apparent powers of details, Sdet | kVA | 1.483 | 2.092 | 1.666 |
| “Non-approximation” apparent power, SN | kVA | 97.54 | 99.54 | 96.04 |
| Apparent powers | kVA | 377.83 | 394.50 | 387.98 |
| Effective apparent powers of approximation, Seapp | MVA | 1.123 | ||
| Unbalanced power of approximations, SUapp | kVAd | 67.123 | ||
| Effective apparent powers of details, Sedet | kVAd | 5.283 | ||
| Total distorting power of current, DeI | kVA | 292.396 | ||
| Total distorting power of voltage, DeV | kVA | 20.287 | ||
| “Non-approximation” effective apparent power SeN | kVA | 293.146 | ||
| Total non-active power, N | MVA | 1.107 | ||
| Total effective apparent powers | MVA | 1.161 | ||
| Power factor of approximations on positive sequence | 0.313 (with inductive character) | |||
| Total power factor | 0.302 (with inductive character) | |||
| Parameters | Phase Number | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Total RMS of currents | 0.071 | 0.069 | 3.342 |
| RMS on the fundamental harmonic of currents | 0.037 | 0.284 | 0.325 |
| Distorting residue of currents | 2.043 | 3.042 | 4.459 |
| Total harmonic distortion of currents | 2.48 | 2.55 | 1.82 |
| Total RMS of voltages | 0.092 | 0.062 | 0.042 |
| Active powers | 0.186 | 0.714 | 0.402 |
| Total active power | 0.180 | ||
| Apparent powers | 0.014 | 0.015 | 0.193 |
| Power factor | 0.188 | ||
| Parameters | Units | Phase Number | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Total RMS of currents | A | 4125.69 | 4275.78 | 4233.23 |
| RMS current of the fundamental harmonic | A | 4124.82 | 4274.77 | 4232.20 |
| Distorting residue of currents | A | 74.38 | 87.83 | 93.11 |
| Total harmonic distortion of currents | % | 1.80 | 2.05 | 2.20 |
| Total RMS of voltages | V | 13,613.39 | 13,591.04 | 13,539.51 |
| RMS voltage of the fundamental harmonic | V | 13,609.05 | 13,585.98 | 13,534.1981 |
| Distorting residue of voltages | V | 341.64 | 369.66 | 375.26 |
| Total harmonic distortion of voltages | % | 2.51 | 2.72 | 2.77 |
| Active powers | MW | 56.10 | 58.05 | 57.19 |
| Total active power | MW | 171.34 | ||
| Active powers on the fundamental harmonic | MW | 56.11 | 58.05 | 57.19 |
| Total active power on the fundamental harmonic | MW | 171.35 | ||
| Reactive powers | MVAr | 16.62 | 184.47 | 319.01 |
| Reactive powers on the fundamental harmonic | MVAr | 16.60 | 18.44 | 31.82 |
| Total reactive power | MVAr | 66.96 | ||
| Distorting powers | MVAd | 2.05 | 1.87 | 2.13 |
| Total distorting power | MVAd | 6.05 | ||
| Apparent powers | MVA | 56.08 | 57.86 | 56.53 |
| Apparent powers on the fundamental harmonic | MVA | 56.16 | 58.11 | 57.32 |
| Total apparent powers | MVA | 171.59 | ||
| Power factor on the fundamental harmonic | 0.999 (inductive character) | |||
| Power factor | 0.998 (inductive character) | |||
| Parameters | Units | Phase Number | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Total RMS of currents | A | 4127.10 | 4280.16 | 4267.74 |
| RMS of currents for the fundamental harmonic | A | 4126.13 | 4279.42 | 4266.13 |
| Distorting residue of currents | A | 89.26 | 79.50 | 117.10 |
| Total harmonic distortion of currents | % | 2.16 | 1.86 | 2.74 |
| Node zero voltage | kV | 13.621 | ||
| Total RMS of voltages | kV | 13.617 | 13,620 | 13,636 |
| RMS of voltages for the fundamental harmonic | kV | 13,614 | 13.618 | 13.631 |
| Distorting residue of voltages | V | 270.73 | 213.37 | 377.76 |
| Total harmonic distortion of voltages | % | 1.99 | 1.57 | 2.77 |
| Active power of approximations, Papp | MW | 56.13 | 58.24 | 58.04 |
| Active power of details, Pdet | MW | 12.719 | 14.36 | 22.652 |
| Phase active powers | MW | 56.17 | 58.28 | 58.07 |
| Total active power of approximations | kW | 171,800 | ||
| Total active power of details | kW | 36.81 | ||
| Total active power | kW | 171,837 | ||
| Reactive power of approximations, Qapp | MVAr | 2.37 | 2.26 | 3.55 |
| Reactive power of details, Qdet | kVAr | 20.55 | 16.9 | 37.99 |
| Total reactive power of approximation | kVAr | 16,912 | ||
| Distorting powers of currents | MVAd | 1.22 | 1.08 | 1.59 |
| Distorting powers of voltages | MVAd | 1.12 | 0.91 | 1.61 |
| Distorting powers of details Ddet | kVAd | 27.31 | 17.02 | 49,69 |
| Non-active powers, N | MVAd | 79.44 | 82.4 | 82.21 |
| Apparent power of approximations Sapp | MVA | 56.17 | 58.28 | 58.15 |
| Apparent power of details Sdet | kVA | 24.16 | 16.96 | 44.24 |
| “Non-approximation” apparent power SeN | MVA | 1.65 | 1.42 | 2.27 |
| Apparent powers | MVA | 56.20 | 58.30 | 58.20 |
| Effective apparent powers of approximation, Seapp | MVA | 172.63 | ||
| Unbalanced power of approximation SUapp | MVAd | 20.15 | ||
| Effective apparent powers of details, Sedet | kVAd | 85.57 | ||
| Total current distorting power, DeI | MVA | 3.95 | ||
| Total voltage distorting power DeV | MVA | 3.74 | ||
| Effective apparent power | MVA | 172.71 | ||
| Power factor of approximations on positive sequence | 0.9952 (inductive character) | |||
| Total power factor | 0.9949 (inductive character) | |||
| Parameters | Calculation Method | Phase Number | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Total RMS of currents [A] | FFT | 4125.69 | 4275.78 | 4233.23 |
| DWT | 4127.10 | 4280.16 | 4267.74 | |
| Total harmonic distortion of currents [%] | FFT | 1.80 | 2.05 | 2.20 |
| DWT | 2.16 | 1.86 | 2.74 | |
| Total RMS of voltages [V] | FFT | 13,613.39 | 13,591.04 | 13,539.51 |
| DWT | 13,617 | 13,620 | 13,636 | |
| Total harmonic distortion of voltages [%] | FFT | 2.51 | 2.72 | 2.77 |
| DWT | 1.99 | 1.57 | 2.77 | |
| Total phase active powers {MW] | FFT | 56.10 | 58.05 | 57.19 |
| DWT | 56.17 | 58.28 | 58.07 | |
| Total active power [MW] | FFT | 171.34 | ||
| DWT | 171.84 | |||
| Total apparent power [MVA] | FFT | 171.59 | ||
| DWT | 172.71 | |||
| Total power factor | FFT | 0.9854 | ||
| DWT | 0.9949 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolae, P.-M.; Nicolae, I.-D.; Nicolae, M.-Ş. Powers and Power Factor in Non-Sinusoidal and Non-Symmetrical Regimes in Three-Phase Systems. Energies 2022, 15, 5130. https://doi.org/10.3390/en15145130
Nicolae P-M, Nicolae I-D, Nicolae M-Ş. Powers and Power Factor in Non-Sinusoidal and Non-Symmetrical Regimes in Three-Phase Systems. Energies. 2022; 15(14):5130. https://doi.org/10.3390/en15145130
Chicago/Turabian StyleNicolae, Petre-Marian, Ileana-Diana Nicolae, and Marian-Ştefan Nicolae. 2022. "Powers and Power Factor in Non-Sinusoidal and Non-Symmetrical Regimes in Three-Phase Systems" Energies 15, no. 14: 5130. https://doi.org/10.3390/en15145130






