A Method of Determining Optimal Parameters for the Secondary Energy Source of a Multisource Hydrostatic Drive System in Machines Working in Closed Spaces
Abstract
:1. Introduction
- Is the expansion of a single-source drive system to a multisource drive system justified for the given drive system?
- If so, what benefits can be gained from the drive system expansion?
- What benefits can we obtain from using the appropriate parameters for the secondary energy source (volume and initial gas pressure ) for a given cycle of operation of a machine operating in closed rooms, from the point of view of energy and environmental efficiency?
2. State of Knowledge
- Increasing the efficiency of drive system components;
- Appropriately matching the operating areas of the drive system’s highly efficient components;
- Using a multisource (hybrid) drive system to restrict the primary energy source performance characteristic to the most advantageous areas and to recover some of the kinetic or potential energy that is usually lost.
- Knowledge of the load characteristics constituting the basis for a system energy analysis. The characteristics, comprising intensity variables (linear and angular velocities, flow rates) and strain variables (forces, torques, pressures), can be represented by a duty point, load curves, an operating area, an operation cyclogram or a representative operation cycle. Sometimes a load spectrum (a more general form) is used.
- Knowledge of the energy characteristics (efficiency or loss of energy) in the whole operating area of every energy transformation, transmission, distribution, recuperation and accumulation component.
- The possibility of quantitatively assessing the energy efficiency of different drive system variants operating under the same load conditions.
- The solution of the problems connected with the choice of a structure and components for the drive system.
- The solution of the problems relating to control, and especially to the synthesis of control systems.
- Increasing the efficiency of the classic drive system through the use of more efficient components and their more advantageous matching;
- Optimizing the control of energy transformation processes in classic drive systems;
- Building drive systems with a multisource structure to optimize the machine’s energy balance by stabilizing the operation of the primary energy source and/or recuperating energy.
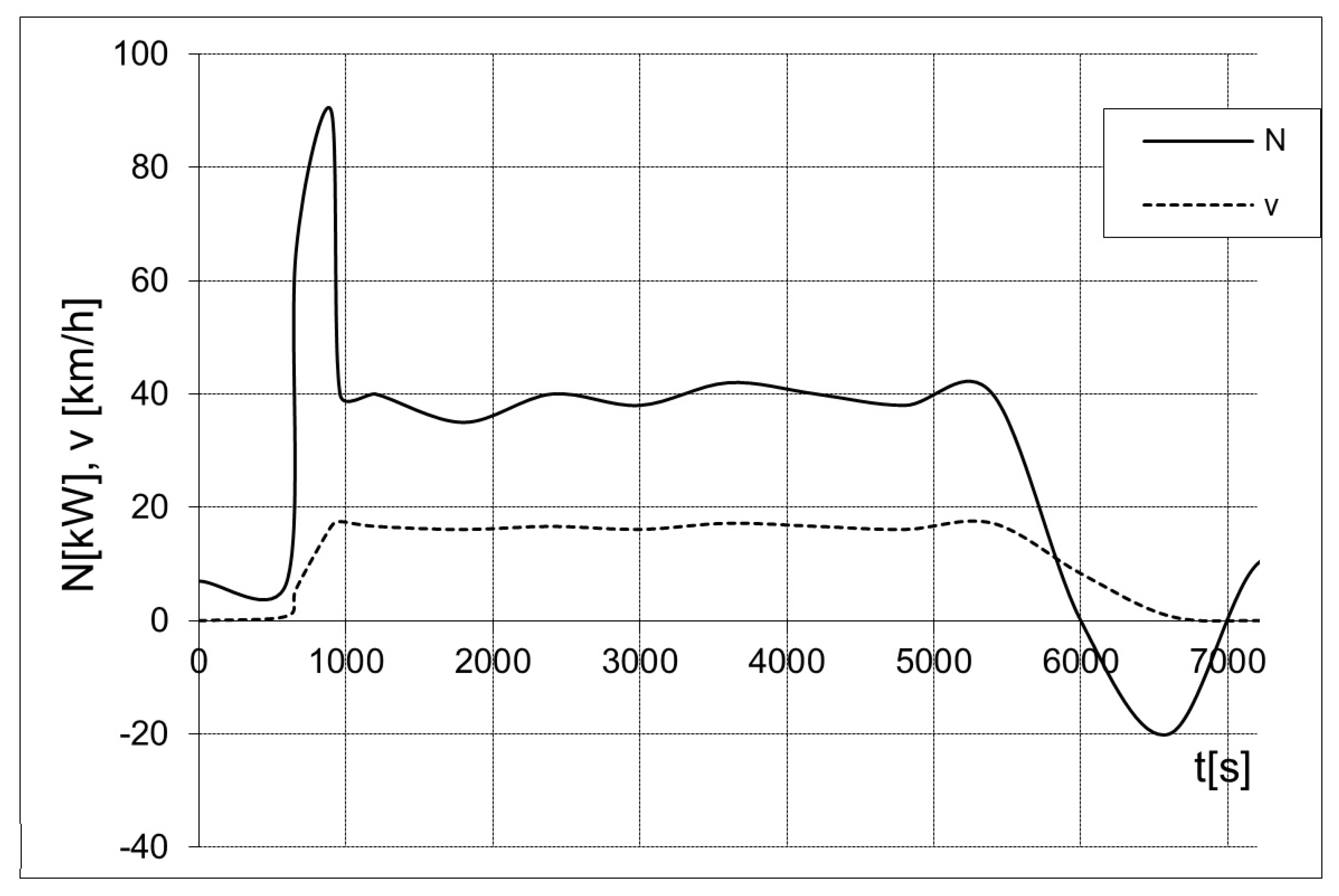
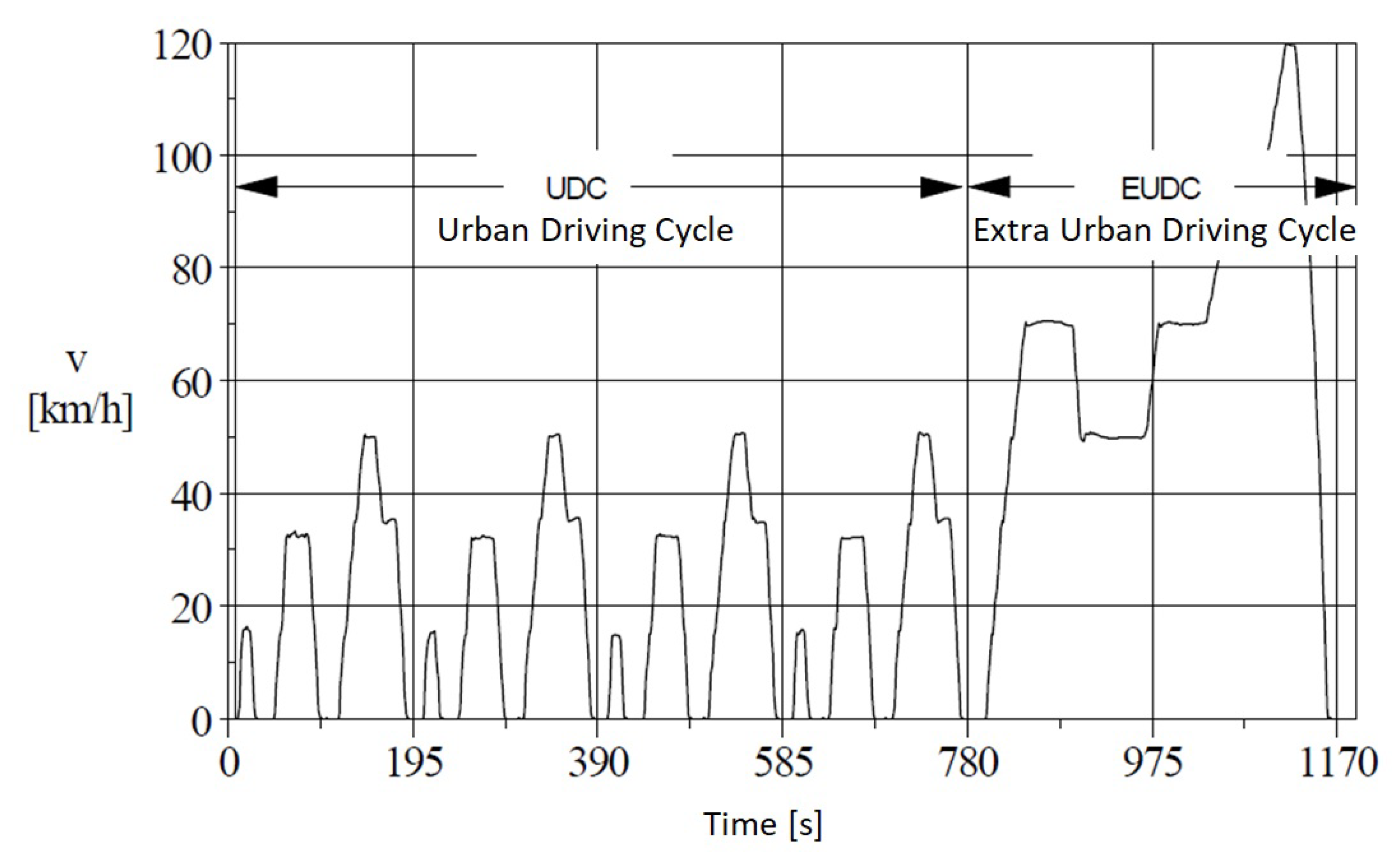
2.1. Machine Operation Cycles
2.2. Primary Energy Sources and Stipulations Regarding Characteristics of Primary Energy Sources
- ;
- ;
- for ;
- ;
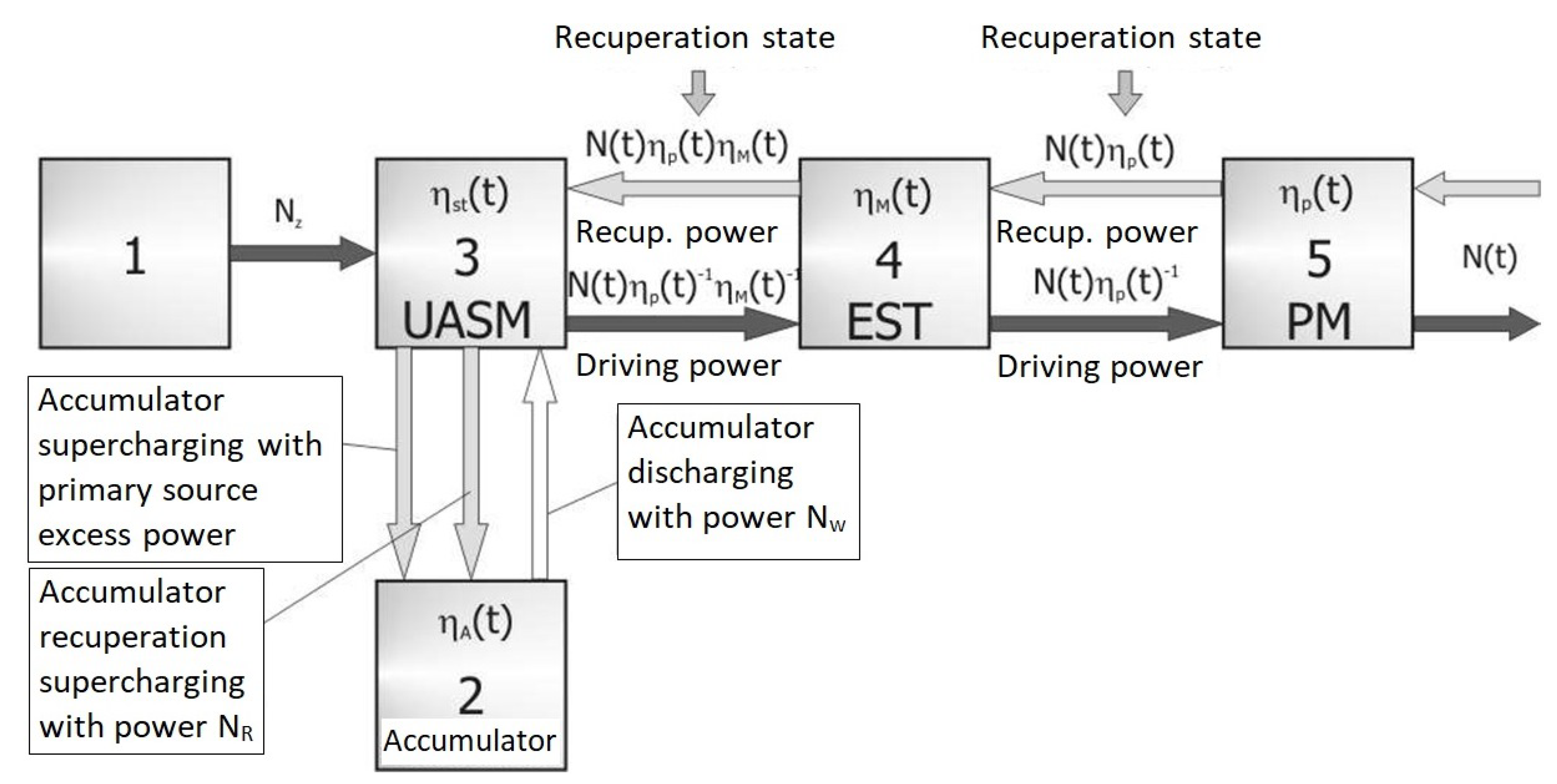
2.3. Secondary Energy Sources—General Characterization
- A high-energy-flow instantaneous power with a high energy efficiency at the source input;
- The smallest possible internal losses in the secondary energy source during energy storage for a suitably long time;
- A high-energy-flow instantaneous power with a high energy efficiency at the source output;
- A high specific power ;
- A high specific energy .
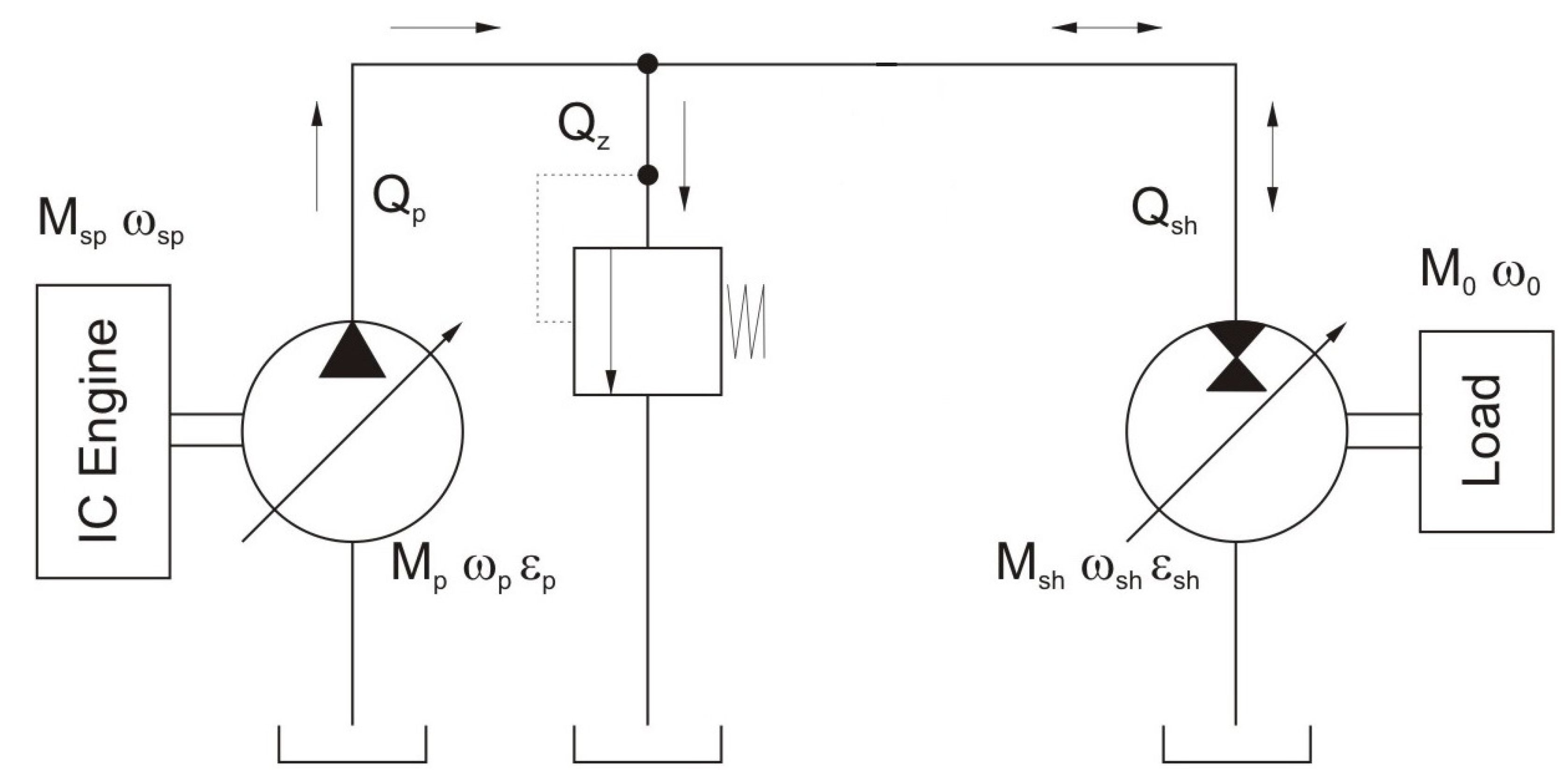
2.4. Hydrostatic Transmission—Exemplary Performer of Energy Transformation and Transmission Functions in Hybrid Drive Systems
2.5. Determination of Energy Parameters of Primary and Secondary Energy Source
- Proper interaction between the primary energy source and the secondary energy source;
- The choice of a proper operating range for each of the sources;
- Matching the accumulator’s energy capacity.
2.6. Control of Multisource Systems
2.7. Drive System Performance Measures
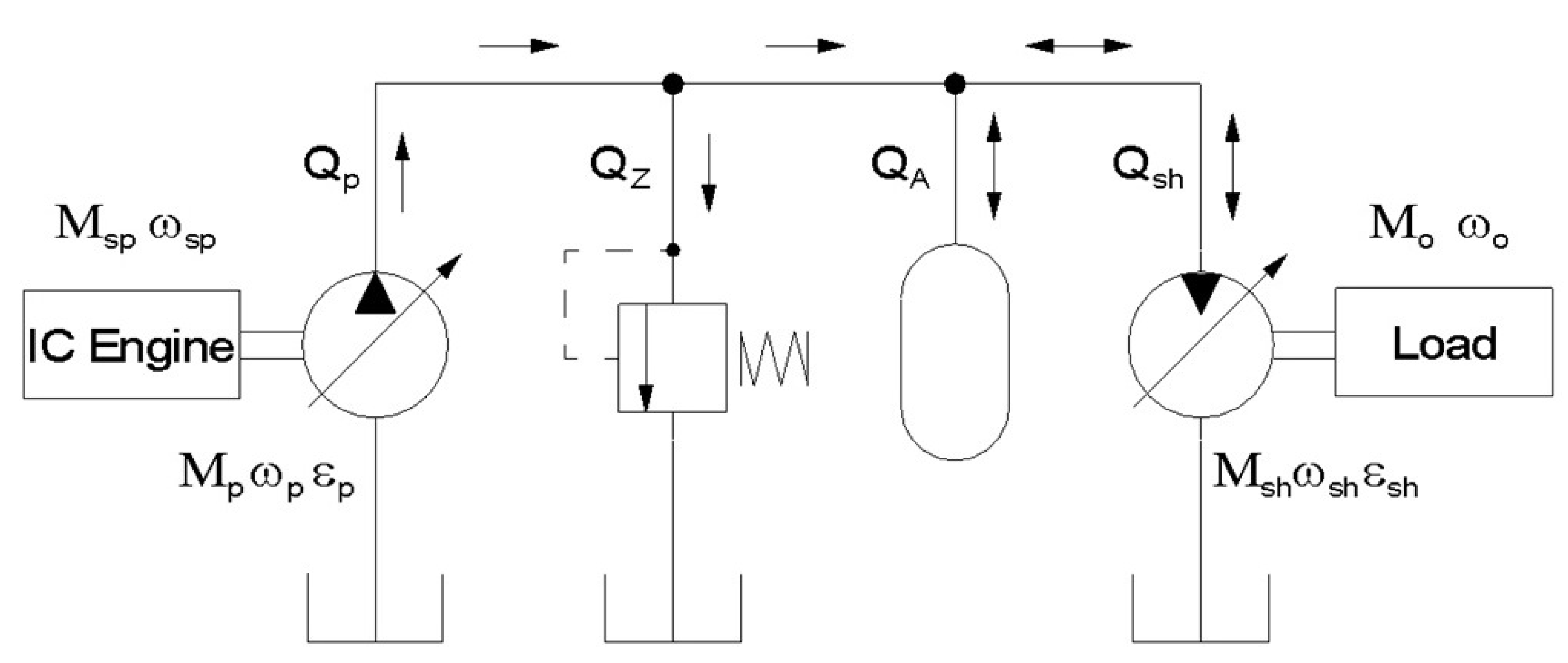
3. Kinetostatic Method of Selecting Work Parameters for Multisource Hydrostatic Drive System
- The optimal duty point of the primary energy source;
- The initial parameters of the secondary energy source;
- The control paths for the other components of the drive system.
- The primary energy source operated at one duty point throughout the system work cycle;
- The charge levels of the secondary energy source at the beginning and end of the work cycle were the same.
3.1. Computer Program for Determining Operating Parameters of Multisource Hydrostatic Drive System
3.1.1. Input Data and Results
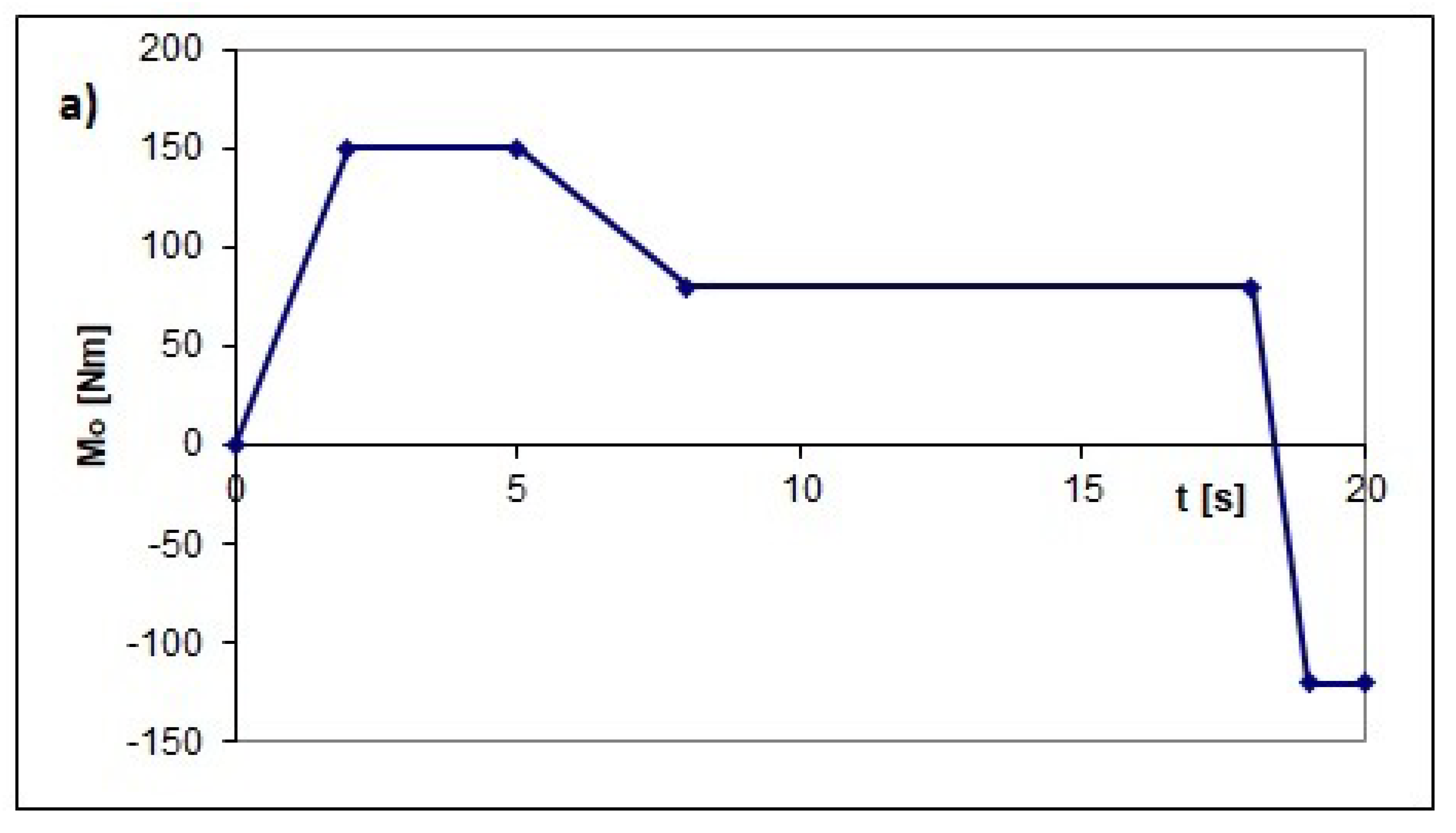
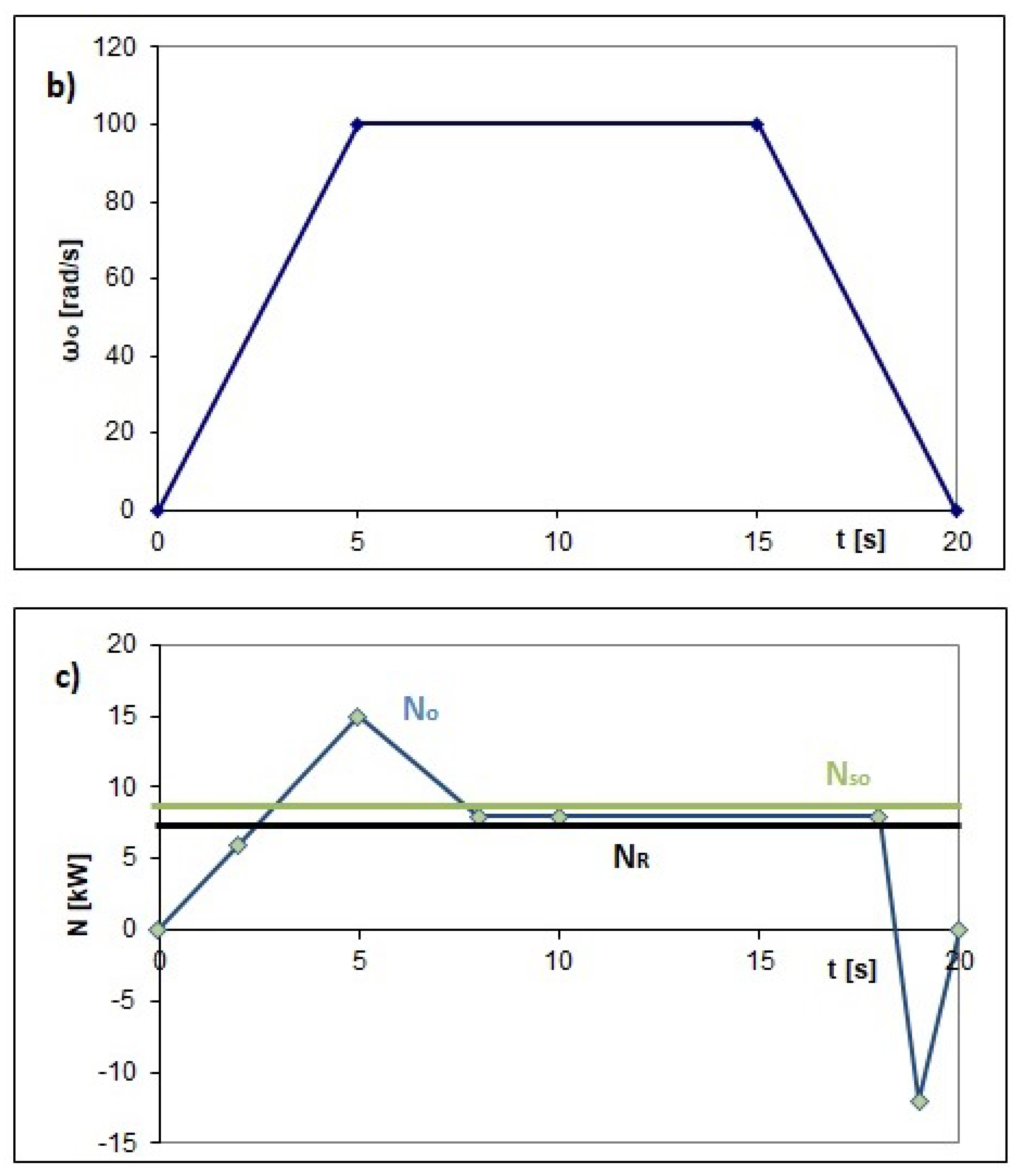
- Load characteristics in the form of cyclograms of:
- Angular velocity ;
- Torque in the form of BRUTTO [Nm].
- Universal combustion engine characteristics concerning:
- Fuel consumption in the work cycle ;
- The carbon oxide content in the exhaust gas [ppm];
- The nitrogen oxides content in the exhaust gas [ppm];
- The exhaust gas opacity [CD BOSCH].
- The characteristics of the hydrostatic units:
- Torque , [Nm];
- Angular velocity , ;
- Capacity or displacement , .
- The specifications of the hydraulic accumulator:
- Total accumulator capacity .
- Losses in the hydraulic system.
- The duty points , of a combustion engine selected with regard to the optimization criterion, e.g., minimal fuel consumption at point , minimal nitrogen oxides in the exhaust gas, etc.;
- Cycle control paths and for hydrostatic units;
- Initial accumulator pressure [Pa];
- The accumulator pre-charge pressure [Pa] (gas pressure in the accumulator not connected to the hydraulic system) [80].
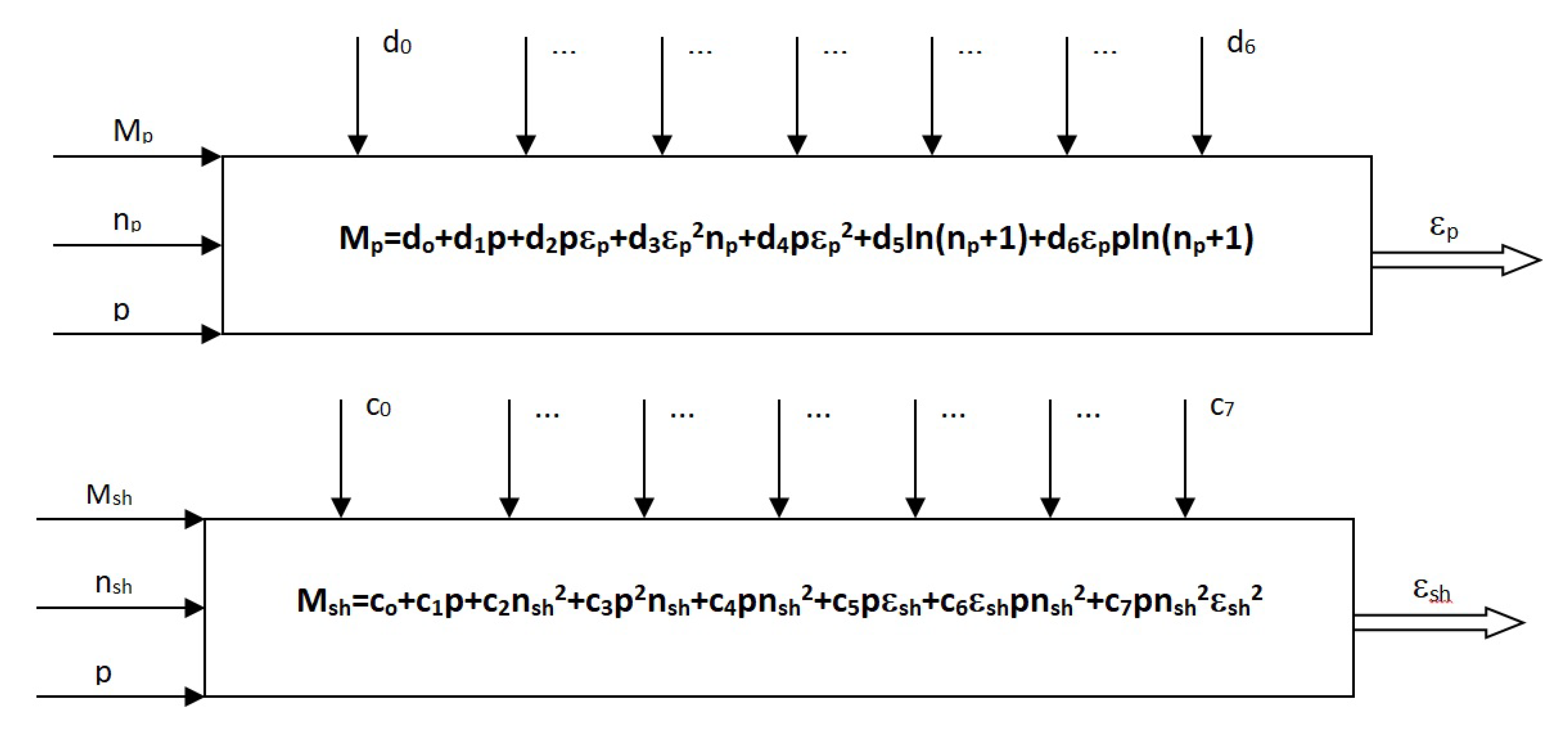
3.1.2. Mathematical Models Used in Kinetostatic Method Algorithm
3.2. Description of Program Operation
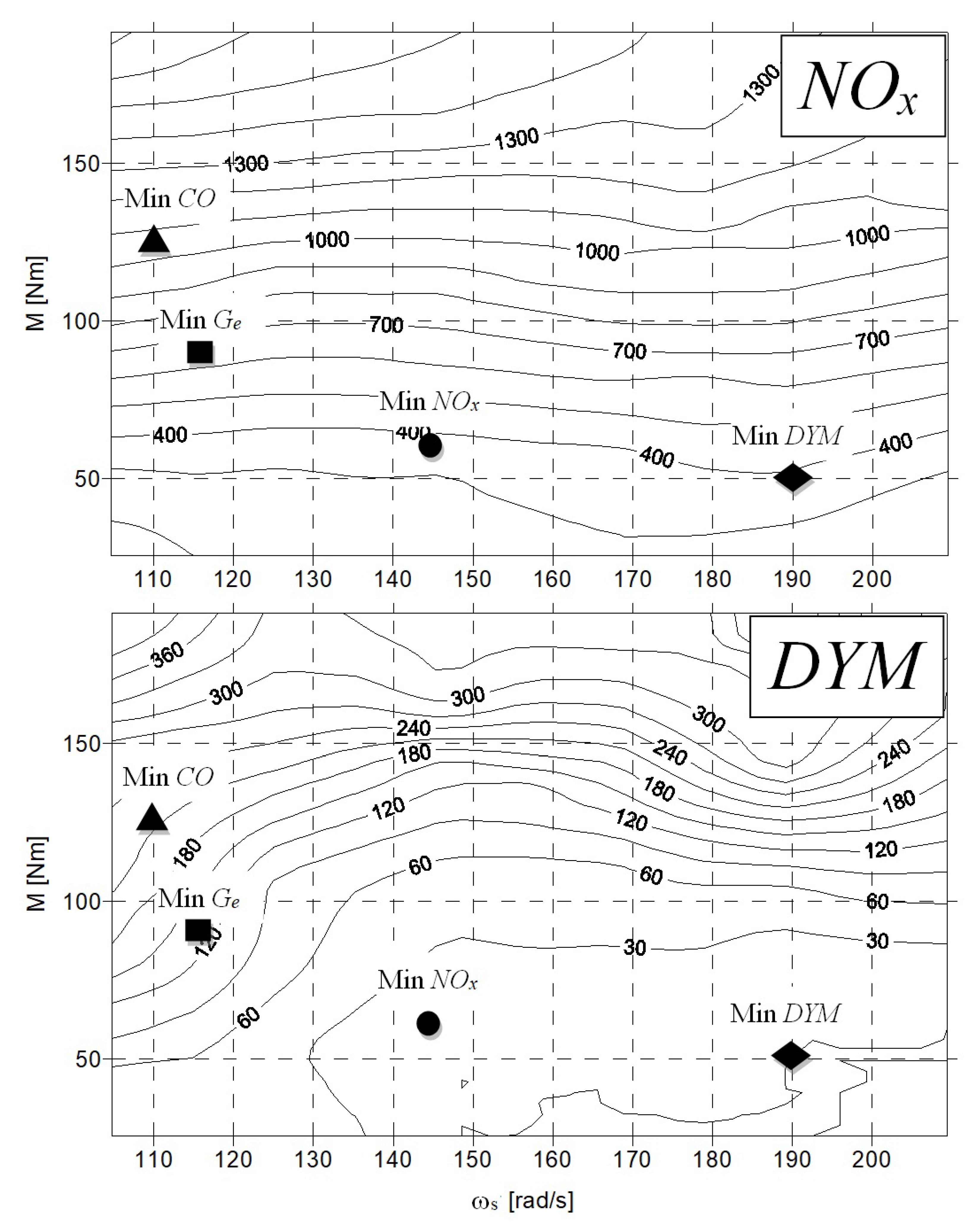
3.3. Results Yielded by Kinetostatic Method
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stosiak, M. The impact of hydraulic systems on the human being and the environment. J. Theor. Appl. Mech. 2015, 53, 409–420. [Google Scholar] [CrossRef] [Green Version]
- Kędzia, K. An algorithm for the determination of the control parameters of a multisource drive system. Tech. Trans. 2017, 3, 173–182. [Google Scholar]
- Karpenko, M.; Bogdevičius, M. Review of energy-saving technologies in modern hydraulic drives. Moksl.-Liet. Ateitis: Statyb. Transp. Aviac. Technol. 2017, 9, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Albright, H.D.; Rollins, W.R. Hybrid Power System for Driving a Motor Vehicle. U.S. Patent 4588040, 13 May 1986. [Google Scholar]
- Chrostowski, H. Modelowanie rozpływu mocy w hydrostatycznych wieloźródłowych układach napędowych. In Prace Naukowe Centralnego Programu Badan Podstawowych 02.05; Chrostowski, H., Ed.; Politechnika Wrocławska: Wrocław, Poland, 1990; pp. 32–58. [Google Scholar]
- Lewandowski, W.M. Proekologiczne Odnawialne Zródła Energii; WNT: Warszawa, Poland, 2007. [Google Scholar]
- Ocioszyński, J. Elektroenergetyka Hybrydowych Elektromechanicznych Układów Napędowych Pojazdów; Wydawnictwa Politechniki Warszawskiej: Warszawa, Poland, 1981. [Google Scholar]
- Pawelski, Z. Modelowanie i Obliczanie Napędu Hydrobusu; Monografie Politechniki Łódzkiej: Łódź, Poland, 2000. [Google Scholar]
- Chrostowski, H. Podstawy Budowy Mechano-Hydraulicznych Układów Napędowych z Akumulacją Energii- Sprawozdanie Merytoryczne z Projektu Badawczego KBN nr 1309/P4/92/02; Politechnika Wrocławska: Wrocław, Poland, 1998. [Google Scholar]
- Klop, R.; Ivantysynova, M. Investigation of Noise Sources on a Series Hybrid Transmission. Int. J. Fluid Power 2011, 12, 17–30. [Google Scholar] [CrossRef]
- Ocioszyński, J. Metody Energetyczne Określania Parametrów Hybrydowego Układu Napędowego Pojazdów i Maszyn Roboczych; I Konferencja Naukowa Mechanizacji Budownictwa: Warszawa, Poland, 1981. [Google Scholar]
- Sradomski, W. Metoda Oceny Charakterystyk Energetycznych i Ekologicznych Układu Silnik Spalinowy—Przekładnia Hydrostatyczna dla Widmowej Postaci Obciążeń; Praca doktorska: Wrocław, Poland, 2002. [Google Scholar]
- Szumanowski, A. (Ed.) Układy Napędowe z Akumulacją Energii; PWN: Warszawa, Poland, 1990. [Google Scholar]
- Malinowski, J. (Ed.) Analiza Widm Obciążeń Osprzętów Koparek; Wydawnictwa Politechniki Warszawskiej: Warszawa, Poland, 1990. [Google Scholar]
- Szumanowski, A. Czas Energii; WKiŁ: Warszawa, Poland, 1988. [Google Scholar]
- Andersson, J.D.; Jemma, C.A.; Bosteels, D.; Searles, R.A. Particle Emissions From a EU3 Heavy-duty Diesel Engine with Catalyst-based Diesel Particle Filter and Selective Catalytic Reduction System: Size, Number, Mass und Chemistry, 11. In Proceedings of the Aachener Kolloquium Fahrzeug und Motorentechnik, Aachen, Germany, 7–9 October 2002. [Google Scholar]
- Fice, M. Zarządzanie Rozpływem Energii w Napędzie Hybrydowym; Praca doktorska: Gliwice, Poland, 2010. [Google Scholar]
- Fice, M.; Setlak, R. Analiza energetyczna rzeczywistych cykli jazdy. Zesz. Probl. 2011, 90, 99–103. [Google Scholar]
- Siłka, W. Energochłonność Ruchu Samochodu; WNT: Warszawa, Poland, 1997. [Google Scholar]
- Szumanowski, A. Akumulacja Energii w Pojazdach; WKiŁ: Warszawa, Poland, 1984. [Google Scholar]
- Siłka, W. Teoria Ruchu Samochodu; WNT: Warszawa, Poland, 2002. [Google Scholar]
- Żółtowski, A. Pomiar emisji w warunkach nieustalonych. J. Kones Intern. Combust. Engines 2003, 10, 3–4. [Google Scholar]
- Kędzia, K.; Chrostowski, H. Optimization of work parameters of hydrostatic multisources power systems in term of selected criteria. In Proceedings of the Riadenie Tekutinovych Systemov, V. Vedecka a Odborna Konferencia, Terchova-Biely Potok, Slovensko, 25–27 October 2000; pp. 19–23. [Google Scholar]
- Kędzia, K.; Chrostowski, H. Control of hydrostatic multisources power systems in term of selected criteria. In Proceedings of the International Carpathian Control Conference, ICCC 2001, Krynica, Poland, 22–25 May 2001; pp. 609–614. [Google Scholar]
- Stryczek, S. Napęd Hydrostatyczny tom I i II; WNT: Warszawa, Poland, 1995. [Google Scholar]
- Van de Ven, J.D.; Olson, M.W.; Li, P.Y. Development of a hydro-mechanical hydraulic hybrid drive train with independent wheel torque control for an urban passenger vehicle. In Proceedings of the International Fluid Power Exposition, Las Vegas, NV, USA, 14–18 March 2008. [Google Scholar]
- Kucybała, P. Akumulator Hydropneumatyczny Jako Wtórne Zródło Energii w Przkładni Hydrostatycznej, Praca Doktorska; Politechnika Krakowska: Kraków, Poland, 2011. [Google Scholar]
- Rannow, M.; Li, P.; Chase, T.; Tu, H.; Wang, M. Optimal design of a high-speed on/off valve for a hydraulic hybrid vehicle application. In Proceedings of the 7th International Fluid Power Conference, Aachen, Germany, 22–24 March 2010. [Google Scholar]
- Sim, T.P.; Li, P.Y. Analysis and Control Design of a Hydro-Mechanical Hydraulic Hybrid Passenger Vehicle. In Proceedings of the ASME 2009 Dynamic Systems and Control Conference No. 2763, Hollywood, CA, USA, 12–14 October 2009. [Google Scholar]
- Balawender, A. Analiza Energetyczna i Metodyka Badań Silników Hydraulicznych Wolnoobrotowych, Zeszyty Naukowe Politechniki Gdańskiej nr 422; Mechanika nr LIV: Gdańsk, Poland, 1988. [Google Scholar]
- Cheong, K.L.; Li, P.Y.; Chase, T.R. Optimal Design of Power-Split Transmission for Hydraulic Hybrid Passenger Vehicles. In Proceedings of the American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011. [Google Scholar]
- Cheong, K.L.; Li, P.Y.; Chase, T.R. Comparison between input coupled and output coupled power-split configurations in hybrid vehicles. In Proceedings of the 2011 International Fluid Power Exhibition (IFPE), Paper number:10.2, Las Vegas, NV, USA, 14–18 March 2011. [Google Scholar]
- Dindorf, R. Napędy Płynowe Hydrostatyczne i Pneumatyczne. Podstawy Teoretyczne i Metody Obliczania; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2009. [Google Scholar]
- Grandall, D.R. Performance and Efficiency of Hydraulic Pumps and Motors. Master’s Thesis, Department of Mechanical Engineering, University of Minnesota, Saint Paul, MN, USA, 2010. [Google Scholar]
- Paszota, Z. Uściślenie Teoretyczne Związane z Wyznaczaniem Strat i Sprawności dla Przekładni Hydrostatycznych, W: A. Garbacik (red.) W: Kierunki Rozwoju Napędów Hydraulicznych i Konstrukcji Maszyn Roboczych; Fluid Power Net Publication: Kraków, Poland, 1999. [Google Scholar]
- Triet, H.H.; Ahn, K.K. Comparison and assessment of hydraulic energy-saving system for hydrostatic drives. Proc. Inst. Mech. Eng. Part J. Syst. Control. Eng. 2011, 225, 21–34. [Google Scholar] [CrossRef]
- Dietrich, M. (Ed.) Podstawy Konstrukcji Maszyn, Part 2; WNT: Warszawa, Poland, 1999. [Google Scholar]
- Moszyński, W. Wykład Elementów Maszyn, cz. III, Napędy; Państwowe Wydawnictwa Techniczne: Warszawa, Poland, 1965. [Google Scholar]
- Śliwiński, P. The methodology of design of axial clearances compensation unit in hydraulic satellite displacement machine and their experimental verification. Arch. Civ. Mech. Eng. 2019, 19, 1163–1182. [Google Scholar] [CrossRef]
- Kędzia, K.; Chrostowski, H. Self-Locking Phenomenon in Hydrostatic Motor Working as Reversible Unit in Multisources Hydrostatic Driving System; Hydraulika a Pneumatika: Žilina, Slovakia, 2006. [Google Scholar]
- Kornberger, Z. Przekładnie Slimakowe, Konstrukcja, Wykonanie, Sprawdzanie; WNT: Warszawa, Poland, 1971. [Google Scholar]
- Łaguna, J.; Łypacewicz, K. Połączenia Srubowe i Nitowe; Arkady: Warszawa, Poland, 1986. [Google Scholar]
- Orlik, Z.; Surowiak, W. Części Maszyn, cz. 1; Wydawnictwa Szkolne i Pedagogiczne: Warszawa, Poland, 1976. [Google Scholar]
- Osiński, Z.; Bajon, W.; Szucki, T. Podstawy Konstrukcji Maszyn; Państwowe Wydawnictwa Naukowe: Warszawa, Poland, 1978. [Google Scholar]
- Szydelski, Z. Hydrauliczna Akumulacja Energii w Napędach Pojazdów, Auto Technika Motoryzacyjna. 1984.
- Szumanowski, A. Opracowanie Metody Właściwego Doboru Układu Elektromaszynowego do Napędu Pojazdów Samochodowych. Praca Doktorska; Politechnika Warszawska: Warszawa, Poland, 1978. [Google Scholar]
- Grabowiecki, K. (Ed.) Symulacja Procesów Energetycznych w Napędach Wieloźródłowych; Wydawnictwa Politechniki Warszawskiej: Warszawa, Poland, 1990. [Google Scholar]
- Grzegorek, W. Przekładnie o ciąGłej Zmianie Przełożenia (CTV) w Układach Napędowych Pojazdów; Wydawnictwo PK: Kraków, Poland, 2011. [Google Scholar]
- Guzowski, A.; Sobczyk, A. Modernizacja Hydrostatycznego Układu Napędowego Jazdy Pod Katem Poprawy Jakości Sterowania, Inżynieria Maszyn, nr 2012 nr 4; Wydawnictwo Wrocławskiej Rady FSNT NOT: Wrocław, Poland, 2012; p. 14. ISSN 1426-708X. [Google Scholar]
- Herzog, S.; Zink, M.; Michael, P. Hydraulic Fluid Viscosity Selection for Improved Fuel Economy. SAE J. Commer. Veh. 2009, 2, 61–65. [Google Scholar] [CrossRef]
- Hippalgaonkar, R.; Ivantysynova, M.; Zimmerman, J. Fuel Savings of a Mini-Excavator through a hydraulic hybrid displacement controlled system. In Proceedings of the 8th IFK International Conference on Fluid Power, Dresden, Germany, 8–10 March 2012; Volume 2, pp. 139–154. [Google Scholar]
- Hippalgaonkar, R.; Ivantysynova, M. A Series-Parallel Hydraulic Hybrid Mini-Excavator with Displacement Controlled Actuators. In Proceedings of the 13th Scandinavian International Conference on Fluid Power (SICFP2013), Linkoping, Sweden, 3–5 January 2013. [Google Scholar]
- Hoffmann, W.; Hesse, K. Digitale Simulation des Dynamischen Verhaltens Hydraulischer Gerate. Oelhydraul. Pneumat 1980, 24, 159–166. [Google Scholar]
- Zimmerman, J.; Hippalgaonkar, R.; Ivantysynova, M. Optimal Control for the Series-Parallel Displacement Controlled Hydraulic Hybrid Excavator. In Proceedings of the 2011 ASME Dynamic Systems and Control Conference and Bath/ASME Symposium on Fluid Power and Motion Control, Arlington, VA, USA, 31 October–2 November 2011. [Google Scholar]
- Kędzia, K. Development of kinetostatic method algorithm of control system of multisource driving system. Hidraulica 2009, 3/4, 39–45. [Google Scholar]
- Kędzia, K.; Chrostowski, H. Modelling of an energy-saving hybrid hydrostatic driving system. In Proceedings of the Hydraulics and Pneumatics 98, the 16th International Conference, Czech Machinery Association, Czech Association for Hydraulics and Pneumatics, Brno, Czech Republic, 30 Septermber–2 October 1998; pp. 158–164. [Google Scholar]
- Kędzia, K.; Chrostowski, H. Modelowanie energooszczędnego hybrydowego hydrostatycznego układu napędowego. In Proceedings of the Symulacja Procesów Dynamicznych, SPD-10, Prace X sympozjum. PTETiS Oddział Warszawski, Wydział Elektryczny PWarsz, Kościelisko, Poland, 15–19 June 1998; pp. 67–72. [Google Scholar]
- Kędzia, K.; Chrostowski, H. Modelowanie energooszczędnych hydrostatycznych wieloźródłowych układów napędowych. In Proceedings of the Napędy i Sterowania Hydrauliczne’99, Konferencja Naukowo-Techniczna, Ośrodek Doskonalenia Kadr SIMP, Wrocław-Polanica Zdrój, Poland, 18–20 May 1999; pp. 226–236. [Google Scholar]
- Kędzia, K.; Chrostowski, H. Optymalizacja parametrów pracy hydrostatycznego wieloźródłowego układu napędowego ze względu na wybrane kryteria. In Proceedings of the Problemy Rozwoju Maszyn Roboczych, XIV Konferencja Naukowa, Zakopane, Poland, 22–25 January 2001; pp. 73–80. [Google Scholar]
- Kombinat PZL HYDRAL we Wrocławiu: Dokumentacja modelowo obliczeniowa możliwości zastosowania zmodernizowanego wzmacniacza AW10 do jednostki tłokowo osiowej IT3-32.
- Kollek, W.; Osiński, P. Modeling and Design of Gear Pumps, Oficyna Wyd; Politechniki Wrocławskiej: Wrocław, Poland, 2009. [Google Scholar]
- Meyer, J.J.; Stelson, K.A.; Hencey, B.; Alleyne, A.G. Power management strategy for a hydraulic hybrid passenger vehicle using stochastic dynamic programming. In Proceedings of the 7th International Fluid Power Conference, Aachen, Germany, 1 March 2010. [Google Scholar]
- Sobczyk, A. Improvement of Hydraulic System Efficiency by Means of Energy Recuperation; Wydawnictwa Politechniki Krakowskiej: Kraków, Poland, 2011. [Google Scholar]
- Sobczyk, A.; Pobędzia, J.; Kucybała, P. Badania symulacyjne hydraulicznego układu odzysku energii w pojazdach i maszynach roboczych. In Proceedings of the XII Warsztaty Naukowe Polskiego Towarzystwa Symulacji Komputerowej, Sarbinowo, Poland, 15–19 September 2005. [Google Scholar]
- Sprengel, M.; Ivantysynova, M. Investigation and Energetic Analysis of a Novel Hydraulic Hybrid Architecture for On-Road Vehicles. In Proceedings of the 13th Scandinavian International Conference on Fluid Power (SICFP2013), Linkoping, Sweden, 3–5 January 2013. [Google Scholar]
- Kucybała, P.; Pobędzia, J.; Sobczyk, A. Określenie sprawności hydraulicznego układu odzysku energii w mechanizmie jazdy. In Proceedings of the Problemy Rozwoju Maszyn Roboczych, Zakopane, Poland, 27–31 January 2006. [Google Scholar]
- Kumar, R.; Ivantysynova, M. An Instantaneous Optimization Based Power Management Strategy to Reduce Fuel Consumption in Hydraulic Hybrids. Int. J. Fluid Power 2011, 12, 15–25. [Google Scholar] [CrossRef]
- Michael, P.; Wanke, T.; Devlin, M. An Investigation of Hydraulic Fluid Properties and Low-Speed Motor Efficiency. In Proceedings of the 7th International Fluid Power Conference, Aachen, Germany, 22–24 March 2010; Volume 3, pp. 341–353. [Google Scholar]
- Ostaszewicz, J. Energochłonność Transportu Miejskiego; WKiŁ: Warszawa, Poland, 1984. [Google Scholar]
- Paszota, Z. Podwyższenie sprawności energetycznej kierunkiem rozwoju napędu hydrostatycznego, Hydraulika i Pneumatyka 5/1998.
- Siłka, W. Analiza Wpływu Parametrów Cyklu Jezdnego na Energochłonność Ruchu Samochodu; Polska Akademia Nauk, Oddział w Krakowie: Kraków, Poland, 1998. [Google Scholar]
- Śliwiński, P. Methods of Determining Pressure Drop in Internal Channels of a Hydraulic Motor. Energies 2021, 14, 5669. [Google Scholar] [CrossRef]
- Cristescu, C. Recuperarea Energiei Cinetice la Franarea Autovehiculelor; Editura AGIR: Bucharest, Romania, 2008. [Google Scholar]
- Dindorf, R. Zmniejszenie Zużycia Energii w Systemach Sprężonego Powietrza. Pneumatyka 2011, nr2, 30–35. [Google Scholar]
- Du, Z.; Cheong, K.L.; Li, P.Y.; Chase, T.R. Fuel Economy Comparisons of Series, Parallel and HMT Hybrid Architectures. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Kędzia, K.; Chrostowski, H. Sterowanie hydrostatycznym hybrydowym układem napędowym. Hydraul. Pneumatyka 2006, nr2, 35–38. [Google Scholar]
- Kędzia, K.; Pyrc, M. Modelowanie wieloźródłowego układu napędowego z hydrostatycznym przetwarzaniem strumienia energii. In Proceedings of the 19. Międzynarodowe Sympozjum Naukowe Studentów i Młodych Pracowników Nauki, PZielonogórs, Zielona Góra, Poland, 28–29 March 1997; pp. 168–172. [Google Scholar]
- Kędzia, K.; Matus, M. Modelowanie i symulacja wieloźródłowego hydrostatycznego układu napędowego. In Proceedings of the 20. Międzynarodowe Sympozjum Naukowe Studentów i Młodych Pracowników Nauki, PZielonogórska, Zielona Góra, Poland, 13–14 May 1998; pp. 151–156. [Google Scholar]
- Śliwiński, P. Determination of the Theoretical and Actual Working Volume of a Hydraulic Motor. Energies 2020, 13, 5933. [Google Scholar] [CrossRef]
- Kędzia, K.; Chrostowski, H. The analysis of pneumo-hydraulic accumulator efficiency, applied as element of hybrid driving system. Sci. Pap. Univ. Pardubic. Ser. Jan Perner Transp. Fac. 2004, 10, 93–99. [Google Scholar]
- Kędzia, K.; Chrostowski, H. Electrohydraulic controller as a hydrotronic element of driving system. In Proceedings of the 4th FPNI—PhD Symposium, Sarasota, FL, USA, 13–17 June 2006; Volume 2, pp. 523–532. [Google Scholar]
- Osiński, P.; Chruścielski, G. Strength calculations of an element compensating circumferential backlash in the external gear pump. J. Theor. Appl. Mech. 2016, 54, 251–262. [Google Scholar] [CrossRef] [Green Version]

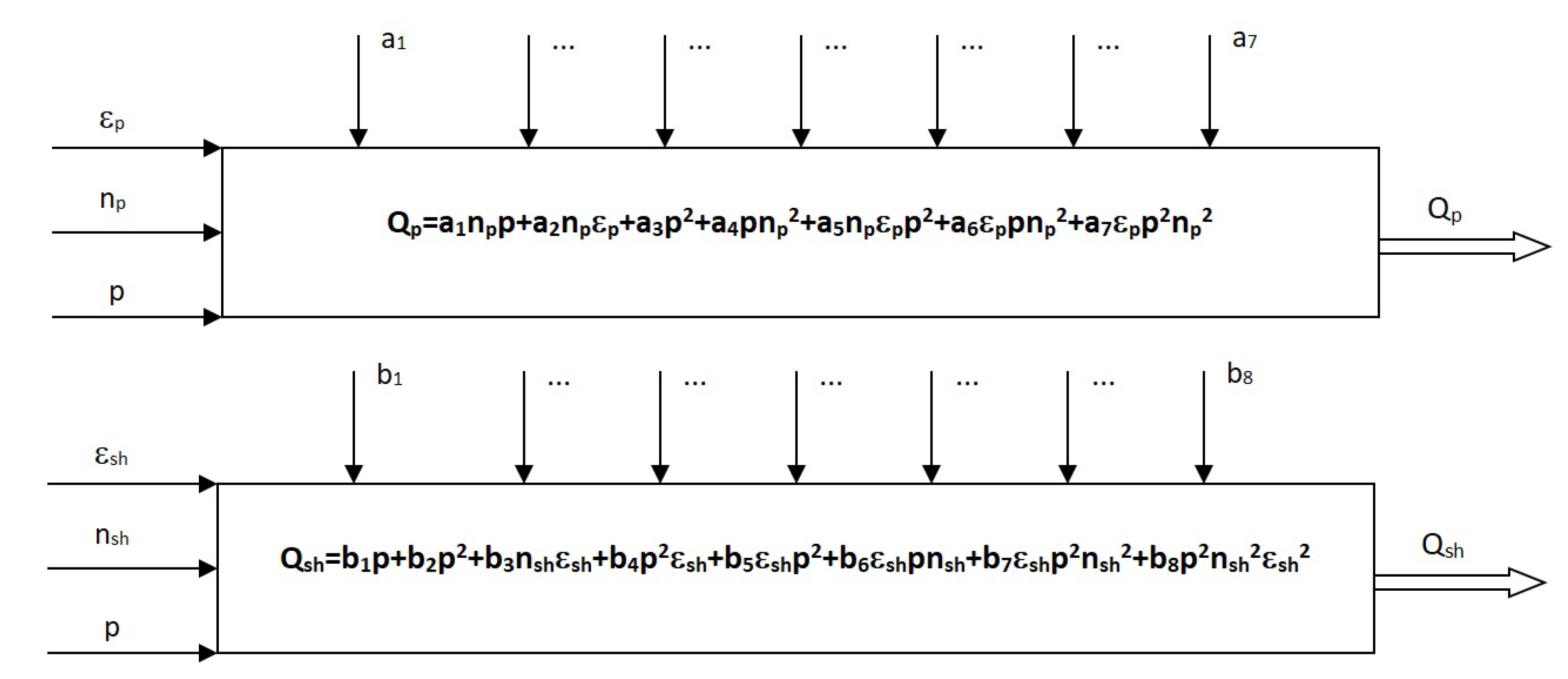

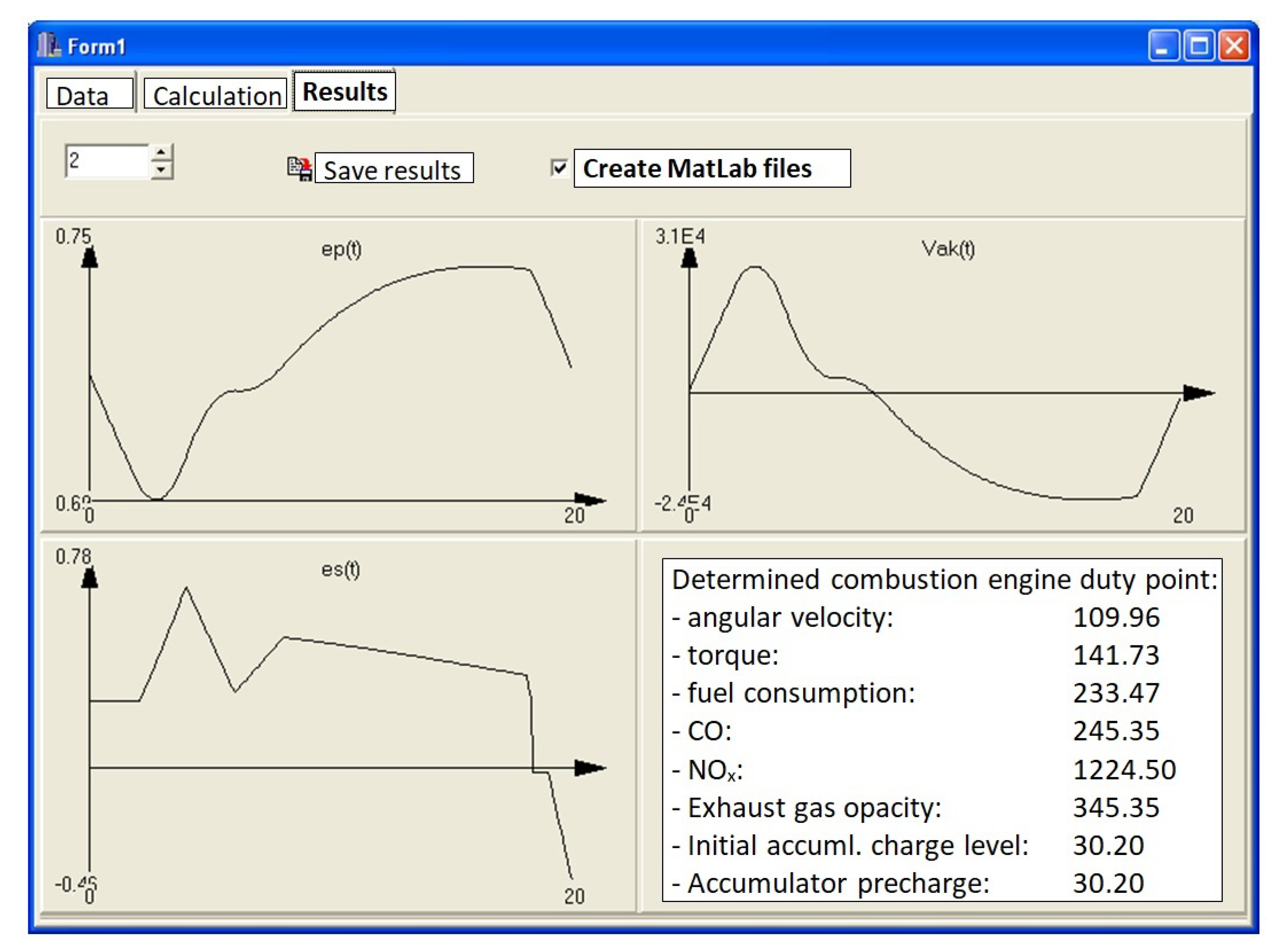

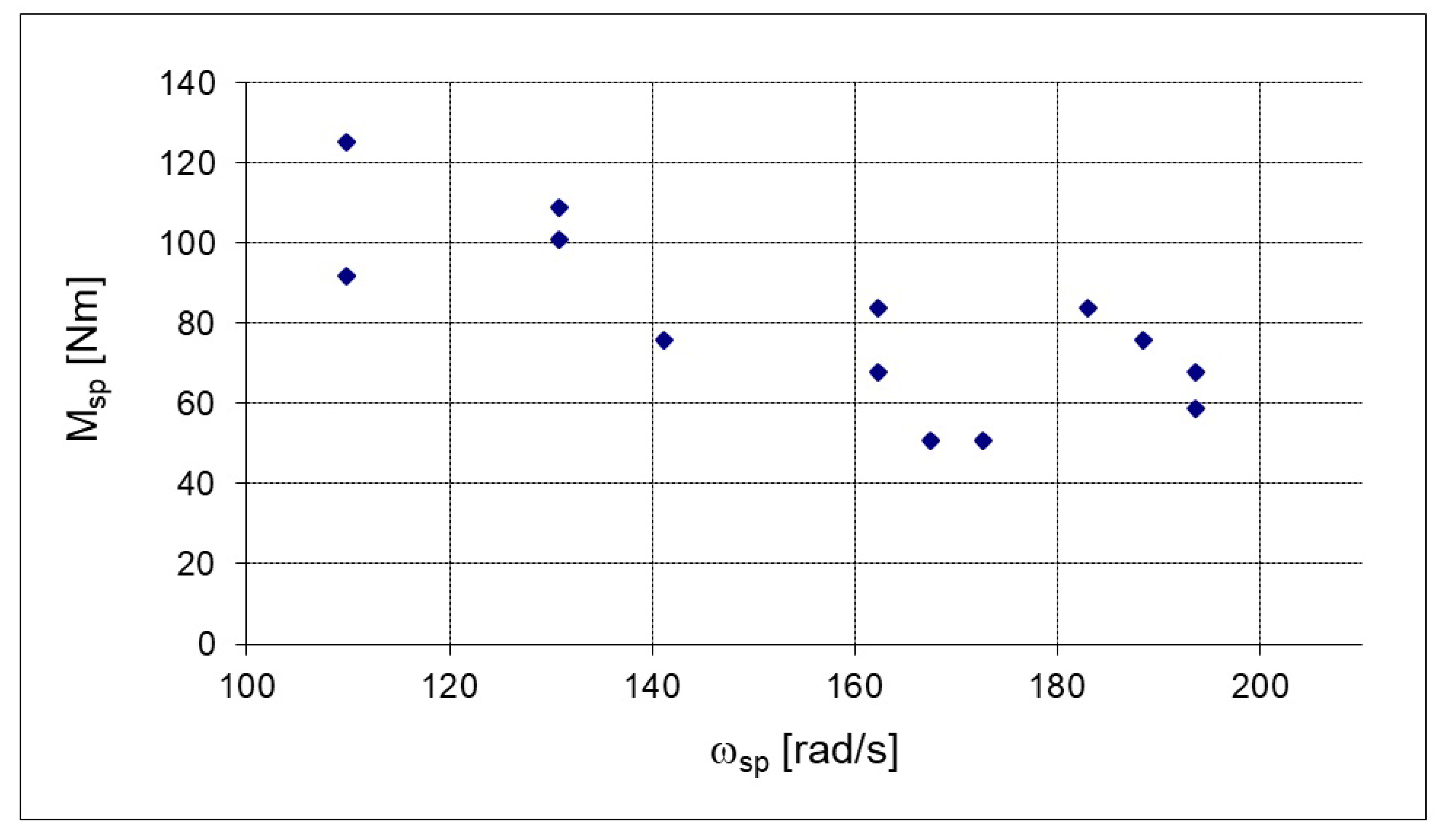

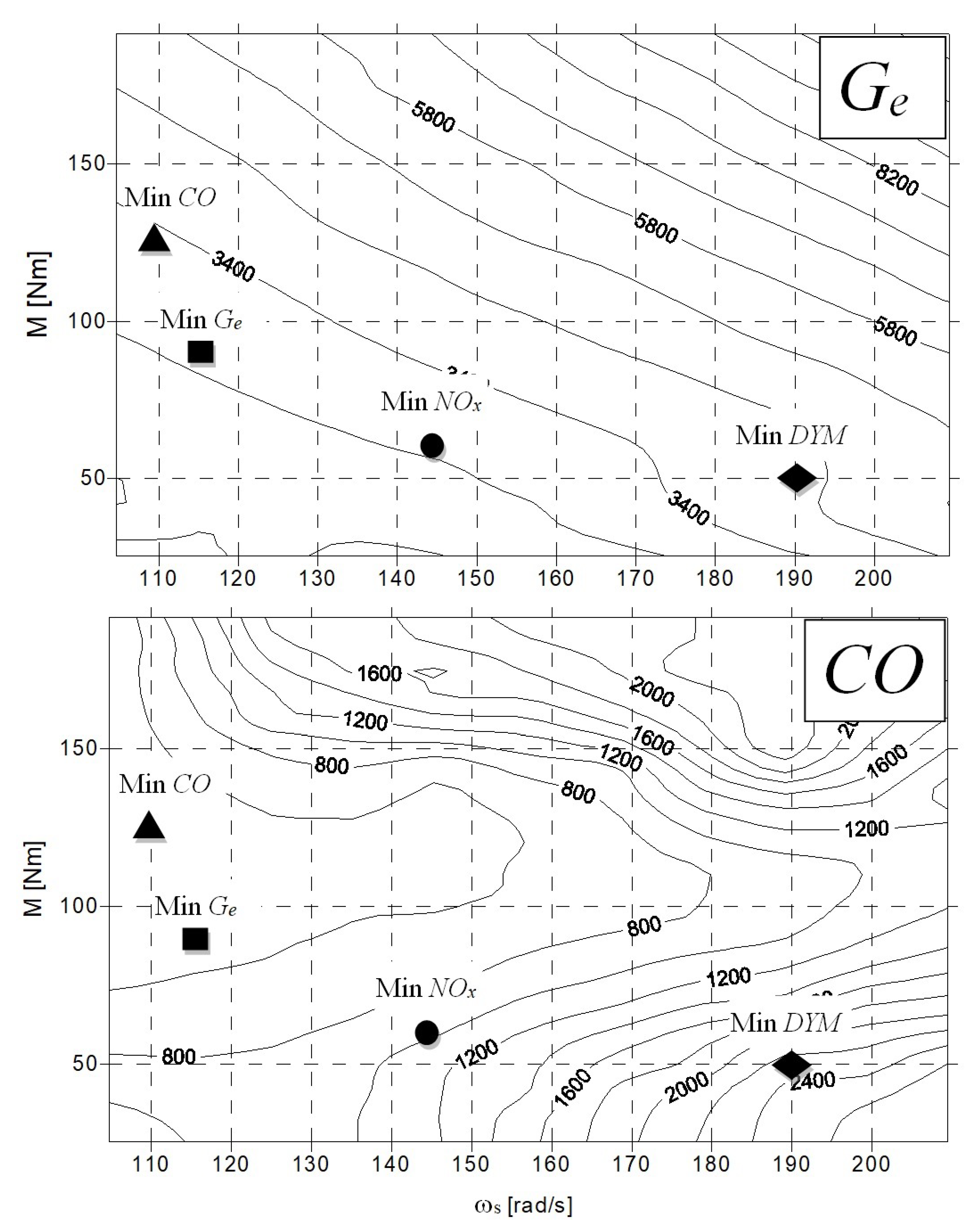
| No. | [Nm] | [ppm] | [ppm] | : | [MPa] | ||
|---|---|---|---|---|---|---|---|
| 1 | 110 | 92 | 14.70 | 526 | 696 | 163 | 14.63 |
| 2 | 141 | 75 | 16.93 | 749 | 496 | 29 | 14.63 |
| 3 | 168 | 50 | 17.18 | 1656 | 353 | 2 | 14.63 |
| 4 | 110 | 125 | 18.27 | 497 | 1061 | 214 | 10.98 |
| 5 | 162 | 67 | 18.64 | 1157 | 457 | 20 | 25.61 |
| 6 | 131 | 100 | 18.73 | 572 | 711 | 68 | 14.63 |
| 7 | 173 | 50 | 18.82 | 1742 | 369 | 5 | 21.95 |
| 8 | 131 | 109 | 19.75 | 558 | 797 | 79 | 10.98 |
| 9 | 162 | 84 | 21.15 | 871 | 616 | 29 | 25.61 |
| 10 | 194 | 59 | 23.50 | 2052 | 421 | 1 | 21.95 |
| 11 | 194 | 67 | 24.05 | 1710 | 480 | 4 | 14.63 |
| 12 | 188 | 75 | 24.18 | 1292 | 564 | 11 | 18.29 |
| 13 | 183 | 84 | 24.85 | 1074 | 628 | 25 | 21.95 |
| No. | [Nm] | [ppm] | [ppm] | [CD BOSCH] | IC Efficiency | Hyd. Trans. Efficiency | Total Efficiency | ||
|---|---|---|---|---|---|---|---|---|---|
| 111 | 92 | 14.70 | 526 | 696 | 163 | 0.353 | 0.835 | 0.294 | |
| 111 | 125 | 18.27 | 497 | 1061 | 214 | 0.386 | 0.613 | 0.237 | |
| 168 | 50 | 17.18 | 1656 | 353 | 1.65 | 0.253 | 0.908 | 0.252 | |
| 193 | 59 | 23.50 | 2052 | 421 | 0.30 | 0.248 | 0.741 | 0.184 |
| No. | [Nm] | [ppm] | [ppm] | : | [MPa] | ||
|---|---|---|---|---|---|---|---|
| 1 | 147 | 59 | 14.94 | 1016 | 346 | 8 | 12.94 |
| 2 | 115 | 92 | 15.39 | 549 | 672 | 136 | 12.94 |
| 3 | 147 | 75 | 17.62 | 776 | 501 | 23 | 17.26 |
| 4 | 131 | 92 | 17.69 | 596 | 630 | 63 | 17.26 |
| 5 | 136 | 100 | 19.93 | 585 | 710 | 56 | 21.57 |
| 6 | 183 | 50 | 20.69 | 2047 | 391 | 4 | 25.89 |
| 7 | 136 | 109 | 20.73 | 562 | 800 | 68 | 12.94 |
| 8 | 152 | 92 | 21.01 | 684 | 668 | 33 | 30.20 |
| 9 | 152 | 100 | 22.28 | 620 | 746 | 38 | 25.89 |
| 10 | 199 | 67 | 25.58 | 1855 | 465 | 5 | 30.20 |
| 11 | 204 | 59 | 26.54 | 2204 | 373 | 0.3 | 21.57 |
| 12 | 199 | 75 | 26.99 | 1576 | 531 | 14 | 17.26 |
| No. | [Nm] | [ppm] | [ppm] | [CD BOSCH] | IC Efficiency | Hyd. Trans. Efficiency | Total Efficiency | ||
|---|---|---|---|---|---|---|---|---|---|
| 126 | 84 | 15.92 | 603 | 561 | 74 | 0.339 | 0.803 | 0.272 | |
| 105 | 125 | 17.41 | 467 | 1078 | 235 | 0.386 | 0.644 | 0.249 | |
| 168 | 67 | 19.36 | 1230 | 467 | 21 | 0.298 | 0.751 | 0.224 | |
| 204 | 75 | 28.10 | 1636 | 507 | 10.30 | 0.281 | 0.549 | 0.154 |
| No. | [Nm] | [ppm] | [ppm] | : | [MPa] | ||
|---|---|---|---|---|---|---|---|
| 1 | 152 | 59 | 15.94 | 1132 | 360 | 10 | 12.94 |
| 2 | 105 | 125 | 17.41 | 476 | 1078 | 235 | 12.94 |
| 3 | 115 | 125 | 19.12 | 518 | 1044 | 193 | 25.89 |
| 4 | 168 | 67 | 19.36 | 1230 | 467 | 21 | 30.20 |
| 5 | 126 | 117 | 19.80 | 558 | 895 | 115 | 17.26 |
| 6 | 183 | 50 | 20.69 | 2047 | 391 | 4.3 | 30.20 |
| 7 | 173 | 92 | 24.59 | 835 | 721 | 34 | 12.94 |
| 8 | 204 | 75 | 28.10 | 1636 | 507 | 10.3 | 30.20 |
| No. | [Nm] | [ppm] | [ppm] | [CD BOSCH] | IC Efficiency | Hyd. Trans. Efficiency | Total Efficiency | ||
|---|---|---|---|---|---|---|---|---|---|
| 152 | 59 | 15.94 | 1132 | 360 | 9,9 | 0.287 | 0.946 | 0.272 | |
| 105 | 125 | 17.41 | 476 | 1078 | 235 | 0.386 | 0.644 | 0.249 | |
| 152 | 59 | 15.94 | 1132 | 360 | 9.9 | 0.287 | 0.946 | 0.272 | |
| 183 | 50 | 20.69 | 2047 | 391 | 4.30 | 0.229 | 0.912 | 0.209 |
| No. | [Nm] | [ppm] | [ppm] | : | [MPa] | ||
|---|---|---|---|---|---|---|---|
| 1 | 126 | 84 | 15.92 | 603 | 561 | 74 | 17.26 |
| 2 | 105 | 125 | 17.41 | 476 | 1078 | 235 | 17.26 |
| 3 | 168 | 67 | 19.36 | 1230 | 467 | 21 | 25.89 |
| 4 | 126 | 117 | 19.80 | 558 | 895 | 115 | 17.26 |
| 5 | 204 | 75 | 28.10 | 1636 | 507 | 10.30 | 30.20 |
| No. | [Nm] | [ppm] | [ppm] | [CD BOSCH] | IC Efficiency | Hyd. Trans. Efficiency | Total Efficiency | ||
|---|---|---|---|---|---|---|---|---|---|
| 126 | 84 | 15.92 | 603 | 561 | 74 | 0.339 | 0.803 | 0.272 | |
| 105 | 125 | 17.41 | 476 | 1078 | 235 | 0.386 | 0.644 | 0.249 | |
| 168 | 67 | 19.36 | 1230 | 467 | 21 | 0.298 | 0.751 | 0.224 | |
| 204 | 75 | 28.10 | 1636 | 507 | 10.30 | 0.281 | 0.548 | 0.154 |
| No. | [Nm] | [ppm] | [ppm] | : | [MPa] | ||
|---|---|---|---|---|---|---|---|
| 1 | 126 | 84 | 15.92 | 603 | 561 | 74 | 125 |
| 2 | 168 | 67 | 19.36 | 1230 | 467 | 21 | 168 |
| 3 | 204 | 75 | 28.10 | 1636 | 507 | 10.3 | 204 |
| No. | [Nm] | [ppm] | [ppm] | [CD BOSCH] | IC Efficiency | Hyd. Trans. Efficiency | Total Efficiency | ||
|---|---|---|---|---|---|---|---|---|---|
| 126 | 84 | 15.92 | 603 | 561 | 74 | 0.339 | 0.803 | 0.272 | |
| 126 | 84 | 15.92 | 603 | 561 | 74 | 0.339 | 0.803 | 0.272 | |
| 67 | 67 | 19.36 | 1230 | 467 | 21 | 0.298 | 0.751 | 0.224 | |
| 204 | 75 | 28.10 | 1636 | 507 | 10.30 | 0.281 | 0.548 | 0.154 |
| No. | [Nm] | [ppm] | [ppm] | : | [MPa] | ||
|---|---|---|---|---|---|---|---|
| 1 | 126 | 84 | 15.92 | 603 | 561 | 74 | 17.26 |
| 2 | 168 | 67 | 19.36 | 1230 | 467 | 21 | 17.26 |
| 3 | 183 | 50 | 20.69 | 2047 | 391 | 4.3 | 17.26 |
| 4 | 204 | 75 | 28.10 | 1636 | 507 | 10.3 | 12.94 |
| No. | [Nm] | [ppm] | [ppm] | [CD BOSCH] | IC Efficiency | Hyd. Trans. Efficiency | Total Efficiency | ||
|---|---|---|---|---|---|---|---|---|---|
| 126 | 84 | 15.92 | 603 | 561 | 74 | 0.339 | 0.803 | 0.272 | |
| 126 | 84 | 15.92 | 603 | 561 | 74 | 0.339 | 0.803 | 0.272 | |
| 183 | 50 | 20.69 | 2047 | 391 | 4.3 | 0.229 | 0.912 | 0.209 | |
| 183 | 50 | 20.69 | 2047 | 391 | 4.3 | 0.229 | 0.912 | 0.209 |
| No. | [Nm] | [ppm] | [ppm] | [CD BOSCH] | [MPa] | |||
|---|---|---|---|---|---|---|---|---|
| 110 | 92 | 14.70 | 526 | 696 | 163 | 0.005 | 14.63 | |
| 105 | 125,14 | 17.41 | 476 | 1078 | 235 | 0.03 | 17.26 | |
| 147 | 59 | 14.94 | 1016 | 346 | 8.4 | 0.01 | 12.94 | |
| 194 | 59 | 23.50 | 2052 | 241 | 0.3 | 0.005 | 21.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kędzia, K. A Method of Determining Optimal Parameters for the Secondary Energy Source of a Multisource Hydrostatic Drive System in Machines Working in Closed Spaces. Energies 2022, 15, 5132. https://doi.org/10.3390/en15145132
Kędzia K. A Method of Determining Optimal Parameters for the Secondary Energy Source of a Multisource Hydrostatic Drive System in Machines Working in Closed Spaces. Energies. 2022; 15(14):5132. https://doi.org/10.3390/en15145132
Chicago/Turabian StyleKędzia, Krzysztof. 2022. "A Method of Determining Optimal Parameters for the Secondary Energy Source of a Multisource Hydrostatic Drive System in Machines Working in Closed Spaces" Energies 15, no. 14: 5132. https://doi.org/10.3390/en15145132
APA StyleKędzia, K. (2022). A Method of Determining Optimal Parameters for the Secondary Energy Source of a Multisource Hydrostatic Drive System in Machines Working in Closed Spaces. Energies, 15(14), 5132. https://doi.org/10.3390/en15145132