Optimization of Power and Thermal Management System of Hypersonic Vehicle with Finite Heat Sink of Fuel
Abstract
:1. Introduction
2. Method
2.1. System Description
2.2. Two-Level Optimization Method
3. Simulation Model and Its Verification
3.1. Simulation Model
3.2. Model Validation
4. Results and Analysis
4.1. System-Level Optimization
- (1)
- Fuel weight penalty mainly depends on the weight of PCHE, compressor, and turbines. The weight of PCHE is much greater than that of other components. The initial PWR of PCHE is fixed at 10, so the weight of PCHE depends on the heat exchange capability. Therefore, in the direction shown by Trend 1 in Figure 10, the greater Qhs, the greater Mtotal.
- (2)
- For Pareto points of A~F in the direction shown by Trend 2, there is a conclusion opposite to Trend 1. When Qhs is the maximum value of 1251.6 kw, Mtotal is the minimum of 129.6 kg. When Qhs is the minimum value of 1243.6 kw, Mtotal is the maximum of 130.3 kg. This is because the weight of turbomachinery decreases significantly with the increase in Qhs. Qhs and Mtotal become two competitive optimization variables. When Qhs decreases, Mtotal increases accordingly, and vice versa. The Pareto points are located in the regions close to the coordinate axes.
- (3)
- The slope of the Pareto front changes significantly near point C (1244.6 kW, 130.0 kg). When Qhs is less than 1244.6 kW, Mtotal increases significantly with the decrease in Qhs. When Qhs is greater than 1244.6 kW, the change rate of Mtotal decreases with the increase in Qhs. Thus, point C can be considered as a compromise between Mtotal and Qhs.
- (1)
- On the whole, increasing πC or reducing P1 not only reduces Qhs, but also increases Mtotal. When ηhx is less than 91%, increasing ηhx can reduce Qhs and Mtotal at the same time. Pareto points of A~F have approximately the same ηhx.
- (2)
- Tc,n and ṁc are constants, so Qhs depends on Ph, Th,0, ṁh, and ηhx from Section 3. Among the above factors, only Ph and Th,0 change significantly, as shown in Table 6. However, Qhs decreases with the increase in Th and the decrease in Ph, which indicates that Ph is the main influencing factor of Qhs.
- (3)
- For Pareto points, Mtotal mainly depends on the weight of turbomachinery. Increasing πC or decreasing P1 leads to a decrease in Had, which in turn leads to an increase in the weight of the turbomachinery from Equations (10)–(14).
4.2. Component-Level Optimization
5. Conclusions
- (1)
- The system-level optimization can obtain the preliminary solution set. To ensure the feasibility of heat exchanger design, the SEG method is employed to analyze the detailed heat transfer process in PCHE. The minimum temperature difference of PCHE is limited to 10 °C, and the unfeasible solutions are removed. The minimum Th,0 is 770~800 °C, and the maximum ηhx is 90% in feasible solutions.
- (2)
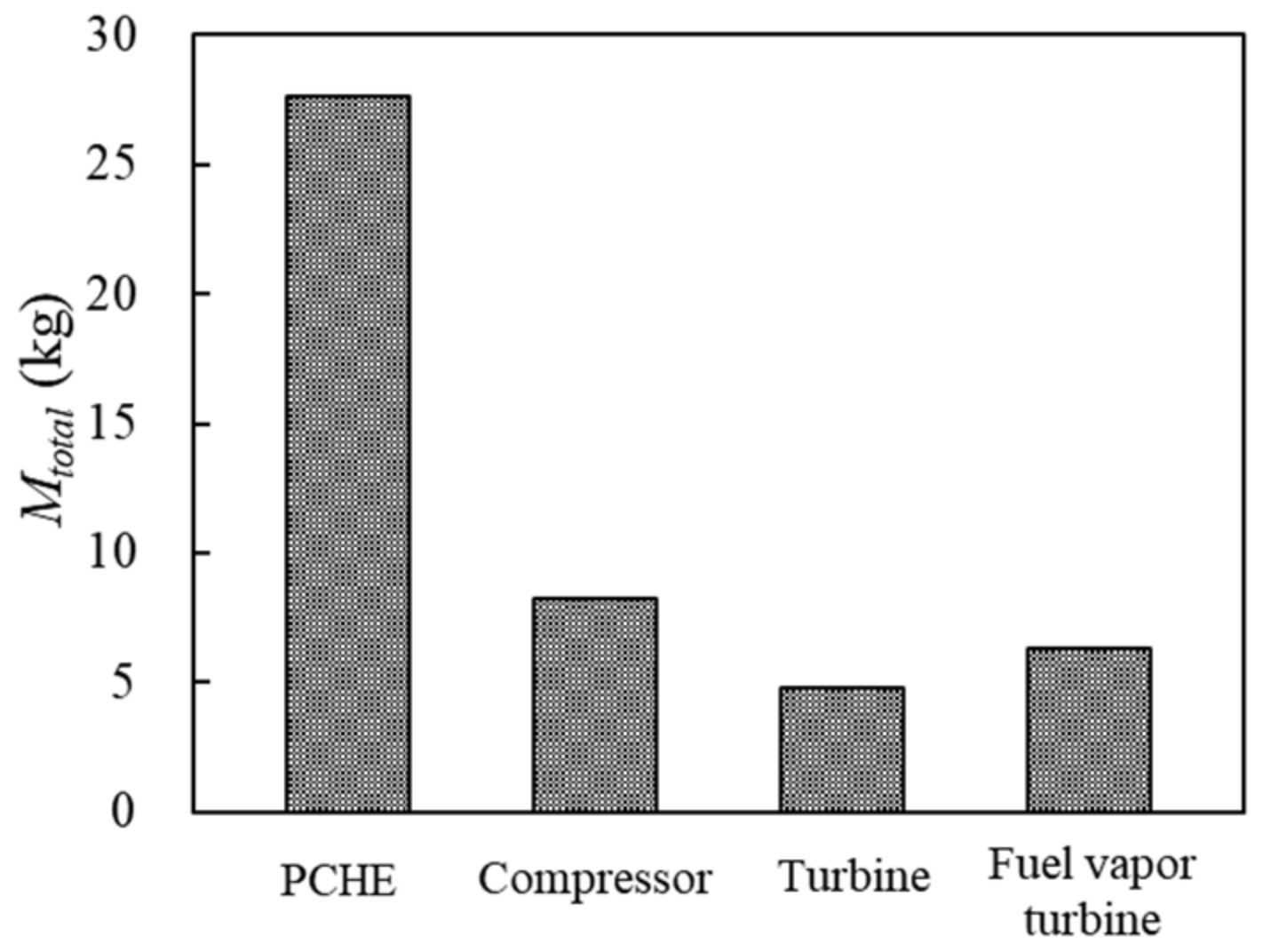
- The turbomachinery adopts compact components, and their optimal design parameters are given. The results of the component-level optimization show that the weight of PCHE is greater than the sum of other components, and the total fuel weight penalty mainly depends on the weight of PCHE.
- (3)
- The proposed two-level optimization method gives the optimal system parameters and the optimal size of key components. It can reduce the heat sink consumption of fuel by 20.2 kW and the fuel weight penalty by 85.2 kg compared to the reference system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Denotation |
| πC | Compressor pressure ratio |
| πfT | Pressure drop ratio of fuel vapor turbine |
| πT | Pressure drop ratio of turbine in SCO2 cycle |
| C | The efficiency of compressor, % |
| G | The efficiency of the generator, % |
| P | The efficiency of the fuel pump, % |
| S,T | The efficiency of turbine in SCO2 cycle, % |
| ηhx | Heat exchanger efficiency, % |
| ηfT | The efficiency of fuel vapor turbine, % |
| cc | Relative pressure loss coefficient in cooling channels, % |
| hx | Relative pressure loss coefficient of PCHE, % |
| hx,s | Relative pressure loss coefficient of PCHE in system-level optimization, % |
| ṁc | Fuel mass flow rate, kg/s |
| ṁh | SCO2 mass flow rate, kg/s |
| As | Cross area, m2 |
| Ce | The specific fuel consumption, kg/(N·s) |
| core | Heat exchanger core |
| dc | Channel depth, mm |
| dh | Hydraulic diameter, mm |
| G | Mass flow flux, kg/(m2·s) |
| hS,2 | Compressor outlet-specific enthalpy, kJ/kg |
| hS,3 | Turbine inlet-specific enthalpy, kJ/kg |
| hS,2s | Ideal outlet-specific enthalpy of the compressor, kJ/kg |
| hS,24 | Ideal outlet-specific enthalpy of the turbine, kJ/kg |
| H | Core height of PCHE, m |
| K | Lift–drag ratio |
| L | The channel length of PCHE, m |
| Li | The channel length of each subheat exchanger, m |
| M | Weight of PCHE, kg |
| Mtotal | Total fuel weight penalty, kg |
| Ns | Specific speed |
| P1 | Compressor inlet pressure |
| POF | Pareto front |
| Ph | Hot side inlet pressure of PCHE, MPa |
| Ploss | Pressure loss of PCHE, % |
| Pp,in | Inlet pressure of the fuel pump, MPa |
| Pp,out | Outlet pressure of the fuel pump, MPa |
| PS,1 | Compressor inlet pressure, MPa |
| PS,2 | Compressor outlet pressure, MPa |
| PS,3 | Cooling channel outlet pressure, MPa |
| PS,4 | Turbine outlet pressure, MPa |
| PWR | Power-to-Weight Ratio of PCHE |
| Qhs | Heat sink consumption of fuel, kW |
| Qtotal | Engine heat production, kW |
| Sg | Total entropy production, J/kg·K |
| SgP | Pressure entropy production, J/kg·K |
| SgT | Heat transfer entropy production, J/kg·K |
| tf | Fin thickness, mm |
| tp | Plate width, mm |
| tw | Wall thickness, mm; |
| Tc,0 | The outlet temperature of the cold side of PCHE, °C |
| Tc,n | The inlet temperature of the cold side of PCHE, °C |
| Th,0 | The hot side inlet temperature of the first sub-heat exchanger, °C |
| Tmax | The maximum temperature of the SCO2 cycle, °C |
| TS,1 | Compressor inlet temperature |
| TS,4 | Turbine outlet temperature |
| TSFC | Thrust-specific fuel consumption, s-1 |
| wc | Channel width, mm |
| W | Core width of PCHE, m |
| ΔTmin | Pinch temperature difference |
References
- Office of Space Systems Development. NASA Headquarters, Access to Space Study: Summary Report; NASA-TM-109693, 1994-01.1994; NASA: Washington, DC, USA, 1994. [Google Scholar]
- Wu, X.; Yang, J.; Zhang, H.; Shen, C. System design and analysis of hydrocarbon scramjet with regeneration cooling and expansion cycle. J. Therm. Sci. 2015, 24, 350–355. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, E.; You, Y.; Yin, C.; Wu, Z. Thermal protection system and thermal management for combined-cycle engine: Review and prospects. Energies 2019, 12, 240. [Google Scholar] [CrossRef] [Green Version]
- Helenbrook, R.G.; Anthony, F.M. Design of a Convective Cooling System for a Mach 6 Hypersonic Transport Airframe; NASA: Washington, DC, USA, 1971. [Google Scholar]
- Qin, J.; Zhou, W.; Bao, W.; Yu, D. Thermodynamic analysis and parametric study of a closed Brayton cycle thermal management system for scramjet. Int. J. Hydrogen Energy 2010, 35, 356–364. [Google Scholar] [CrossRef]
- Cheng, K.; Qin, J.; Sun, H.; Li, H.; He, S.; Zhang, S.; Bao, W. Power optimization and comparison between simple recuperated and recompressing supercritical carbon dioxide Closed-Brayton-Cycle with finite cold source on hypersonic vehicles. Energy 2019, 181, 1189–1201. [Google Scholar] [CrossRef]
- Hank, J.; Murphy, J.; Mutzman, R. The X-51A scramjet engine flight demonstration program. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008; p. 2540. [Google Scholar]
- Qin, J.; Zhang, S.; Bao, W.; Jia, Z.; Yu, B.; Zhou, W. Experimental study on the performance of recooling cycle of hydrocarbon fueled scramjet engine. Fuel 2013, 108, 334–340. [Google Scholar] [CrossRef]
- Powell, O.A.; Edwards, J.T.; Norris, R.B.; Numbers, K.E.; Pearce, J.A. Development of hydrocarbon-fueled scramjet engines: The hypersonic technology (HyTech) program. J. Propuls. Power 2001, 17, 1170–1176. [Google Scholar] [CrossRef]
- Zhang, D.; Qin, J.; Feng, Y.; Ren, F.; Bao, W. Performance evaluation of power generation system with fuel vapor turbine onboard hydrocarbon fueled scramjets. Energy 2014, 77, 732–741. [Google Scholar] [CrossRef]
- Bao, W.; Qin, J.; Zhou, W.; Zhang, D.; Yu, D. Power generation and heat sink improvement characteristics of recooling cycle for thermal cracked hydrocarbon fueled scramjet. Sci. China Technol. Sci. 2011, 54, 955–963. [Google Scholar] [CrossRef]
- Miao, H.; Wang, Z.; Niu, Y. Key issues and cooling performance comparison of different closed Brayton cycle based cooling systems for scramjet. Appl. Therm. Eng. 2020, 179, 115751. [Google Scholar] [CrossRef]
- Miao, H.; Wang, Z.; Niu, Y. Performance analysis of cooling system based on improved supercritical CO2 Brayton cycle for scramjet. Appl. Therm. Eng. 2020, 167, 114774. [Google Scholar] [CrossRef]
- Guo, L.; Pang, L.P.; Yang, X.D.; Jiao, C.; Cui, S.; Kong, Y.; Jiao, J.; Shen, X. Study on a Power and Thermal Management System for Long Endurance Hypersonic Vehicle. Chin. J. Aeronaut. 2017, 126, 78–93. [Google Scholar]
- Marchionni, M.; Bianchi, G.; Tassou, S.A. Techno-economic assessment of JouleBrayton cycle architectures for heat to power conversion from high-grade heat sources using CO2 in the supercritical state. Energy 2018, 148, 1140–1152. [Google Scholar] [CrossRef]
- Rong, A.; Pang, L.; Jiang, X.; Qi, B.; Shi, Y. Analysis and comparison of potential power and thermal management systems for high-speed aircraft with an optimization method. Energy Built Environ. 2021, 2, 13–20. [Google Scholar]
- Long, C.; Xingjuan, Z.; Chunxin, Y. A new concept environmental control system with energy recovery considerations for commercial aircraft. In Proceedings of the 44th International Conference on Environmental Systems, Tuscon, AZ, USA, 13–17 July 2014. [Google Scholar]
- SAE Aerospace Applied Thermodynamics ManualAircraft Fuel Weight Penalty Due to Air Conditioning; SAE International: Warrendale, PA, USA, 2004.
- Nikitin, K.; Kato, Y.; Ngo, L. Printed circuit heat exchanger thermal–hydraulic performance in supercritical CO2 experimental loop. Int. J. Refrig. 2006, 29, 807–814. [Google Scholar] [CrossRef]
- Marchionni, M.; Chai, L.; Bianchi, G.; Tassou, S.A. Numerical modelling and transient analysis of a printed circuit heat exchanger used as recuperator for supercritical CO2 heat to power conversion systems. Appl. Therm. Eng. 2019, 161, 114190. [Google Scholar] [CrossRef]
- Tsuzuki, N.; Kato, Y.; Ishiduka, T. High performance printed circuit heat exchanger. Appl. Therm. Eng. 2007, 27, 1702–1707. [Google Scholar] [CrossRef]
- Dostal, V. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors; MIT-ANP-TR-100; Massachusetts Institute of Technology: Cambridge, MA, USA, 2004. [Google Scholar]
- Tu, Y.; Zeng, Y. Numerical Study on Flow and Heat Transfer Characteristics of Supercritical CO2 in Zigzag Microchannels. Energies 2022, 15, 2099. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Zou, Z. Experimental study and performance analysis of high-performance micro-channel heat exchanger for hypersonic precooled aero-engine. Appl. Therm. Eng. 2021, 182, 116108. [Google Scholar] [CrossRef]
- Cavalcanti Alvarez, R.; Sarmiento, A.; Victor Colin Batista, J.; Mantelli, M.H. Entropy generation analysis applied to diffusion-bonded compact heat exchangers. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3467. [Google Scholar]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Guo, J.; Huai, X. Performance analysis of printed circuit heat exchanger for supercritical carbon dioxide. J. Heat Transf. 2017, 139, 061801. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Liping, P.; Guoxiang, L.; Hongquan, Q.; Yufeng, F. Flexible operation strategy for environment control system in abnormal supply power condition. Acta Astronaut. 2017, 133, 334–345. [Google Scholar] [CrossRef]
- Foli, K.; Okabe, T.; Olhofer, M.; Jin, Y.; Sendhoff, B. Optimization of micro heat exchanger: CFD, analytical approach and multi-objective evolutionary algorithms. Int. J. Heat Mass Transf. 2006, 49, 1090–1099. [Google Scholar] [CrossRef]
- Wang, S.; Xiao, J.; Wang, J.; Jian, G.; Wen, J.; Zhang, Z. Application of response surface method and multi-objective genetic algorithm to configuration optimization of Shell-and-tube heat exchanger with fold helical baffles. Appl. Therm. Eng. 2018, 129, 512–520. [Google Scholar] [CrossRef]
- Lander, H.; Nixon, A.C. Endothermic fuels for hypersonic vehicles. J. Aircr. 1971, 8, 200–207. [Google Scholar] [CrossRef]
- Fuller, R.L.; Batton, W. Practical considerations in scaling supercritical carbon dioxide closed Brayton cycle power systems. In Proceedings of the Supercritical CO2 Power Cycle Symposium, Troy, NY, USA, 29 April 2009; pp. 29–30. [Google Scholar]
- Fuller, R.; Preuss, J.; Noall, J. Turbomachinery for supercritical CO2 power cycles. Turbo Expo: Power for Land, Sea, and Air. Am. Soc. Mech. Eng. 2012, 44717, 961–966. [Google Scholar]
- Logan, E., Jr. Handbook of Turbomachinery; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Balje, O.E. Turbomachines: A Guide to Design, Selection, and Theory; Wiley-Interscience: New York, NY, USA, 1981; 521p. [Google Scholar]
- Holaind, N.; Bianchi, G.; De Miol, M.; Saravi, S.S.; Tassou, S.A.; Leroux, A.; Jouhara, H. Design of radial turbomachinery for supercritical CO2 systems using theoretical and numerical CFD methodologies. Energy Procedia 2017, 123, 313–320. [Google Scholar] [CrossRef]
- Balje, O.E. A study on design criteria and matching of turbomachines: Part a—similarity relations and design criteria of turbines. J. Eng. Power 1962, 84, 83–102. [Google Scholar] [CrossRef]
- Xu, C. Design experience and considerations for centrifugal compressor development. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2007, 221, 273–287. [Google Scholar] [CrossRef]
- Liang, Z.; Yu, M.; Gui, Y.; Zhao, Q. Corrosion behavior of heat-resistant materials in high-temperature carbon dioxide environment. JOM 2018, 70, 1464–1470. [Google Scholar] [CrossRef]
- NIST Standard Reference Data. The U.S. Secretary of Commerce on behalf of the United States of America. 2011. Available online: http://www.nist.gov/srd/ (accessed on 1 March 2022).
- Zhang, D.; Wang, Y.; Deng, X. Design and computational study of waverider configuration with high performance. J. Beijing Univ. Aeronaut. Astronaut. 2004, 30, 429–433. [Google Scholar]
- El-Sayed, A.F. Pulsejet, ramjet, and scramjet engines. In Fundamentals of Aircraft and Rocket Propulsion; Springer: London, UK, 2016; pp. 315–401. [Google Scholar]
- Zhang, Y.; Peng, M.; Xia, G.; Wang, G.; Zhou, C. Performance analysis of S-CO2 recompression Brayton cycle based on turbomachinery detailed design. Nucl. Eng. Technol. 2020, 52, 2107–2118. [Google Scholar] [CrossRef]
- Cho, J.; Shin, H.; Cho, J.; Baik, Y.-J.; Choi, B.; Roh, C.; Ra, H.-S.; Kang, Y.; Huh, J. Design, flow simulation, and performance test for a partial-admission axial turbine under supercritical CO2 condition. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Kim, S.; Cho, Y.; Kim, M.S.; Kim, M. Characteristics and optimization of supercritical CO2 recompression power cycle and the influence of pinch point temperature difference of recuperators. Energy 2018, 147, 1216–1226. [Google Scholar] [CrossRef]
- Marchionni, M.; Chai, L.; Bianchi, G.; Tassou, S.A. Numerical modelling and performance maps of a printed circuit heat exchanger for use as recuperator in supercritical CO2 power cycles. Energy Procedia 2019, 161, 472–479. [Google Scholar] [CrossRef]
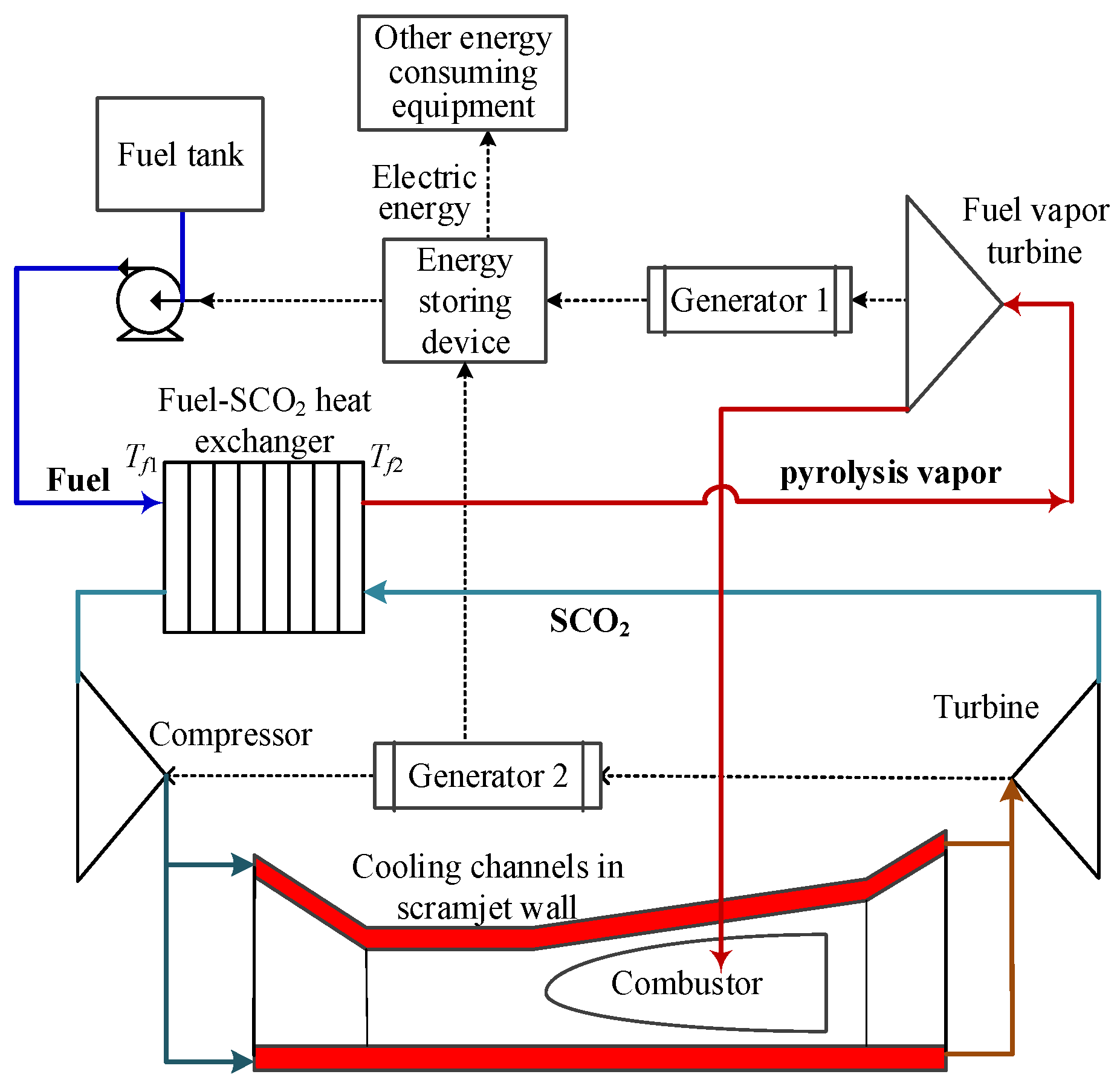



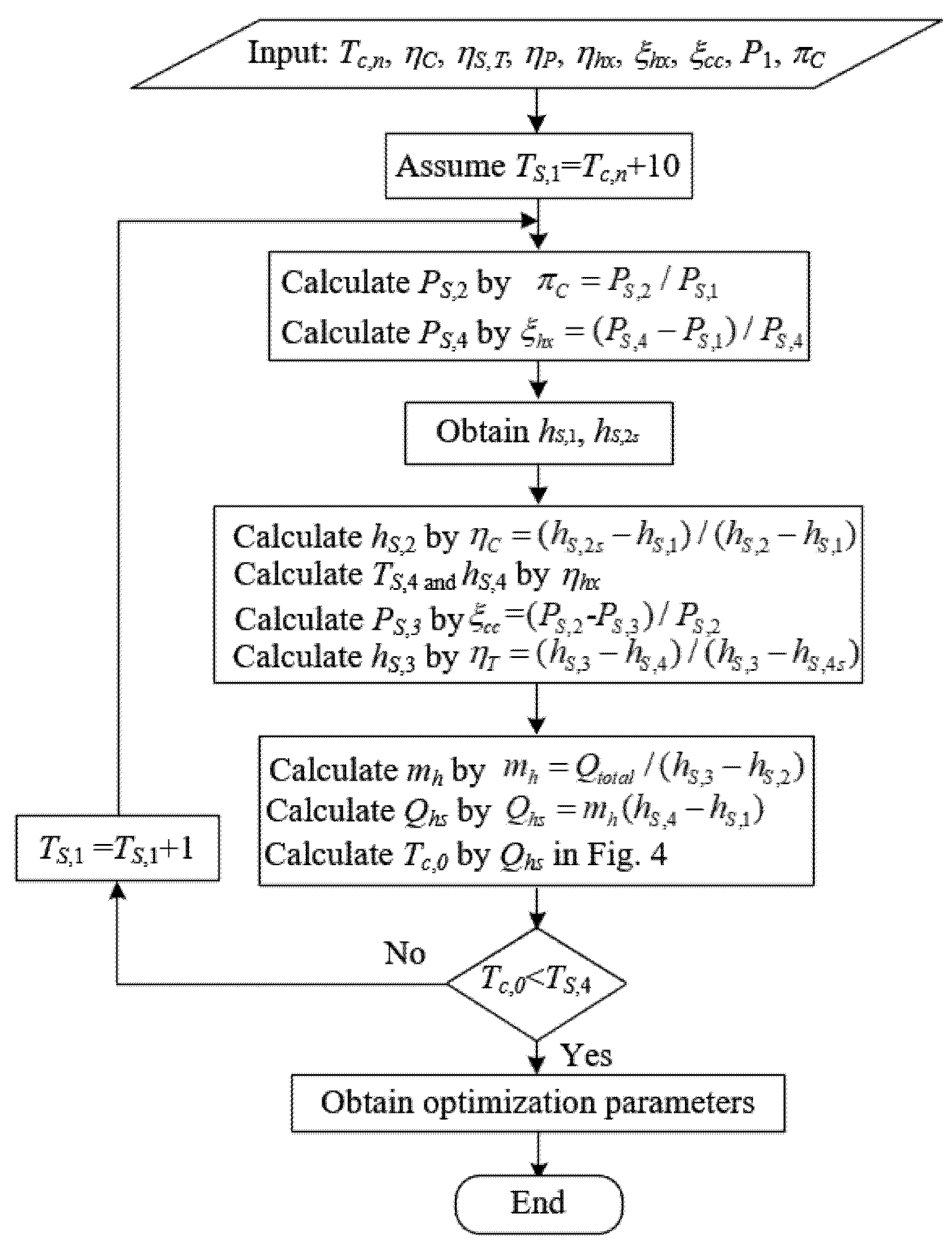
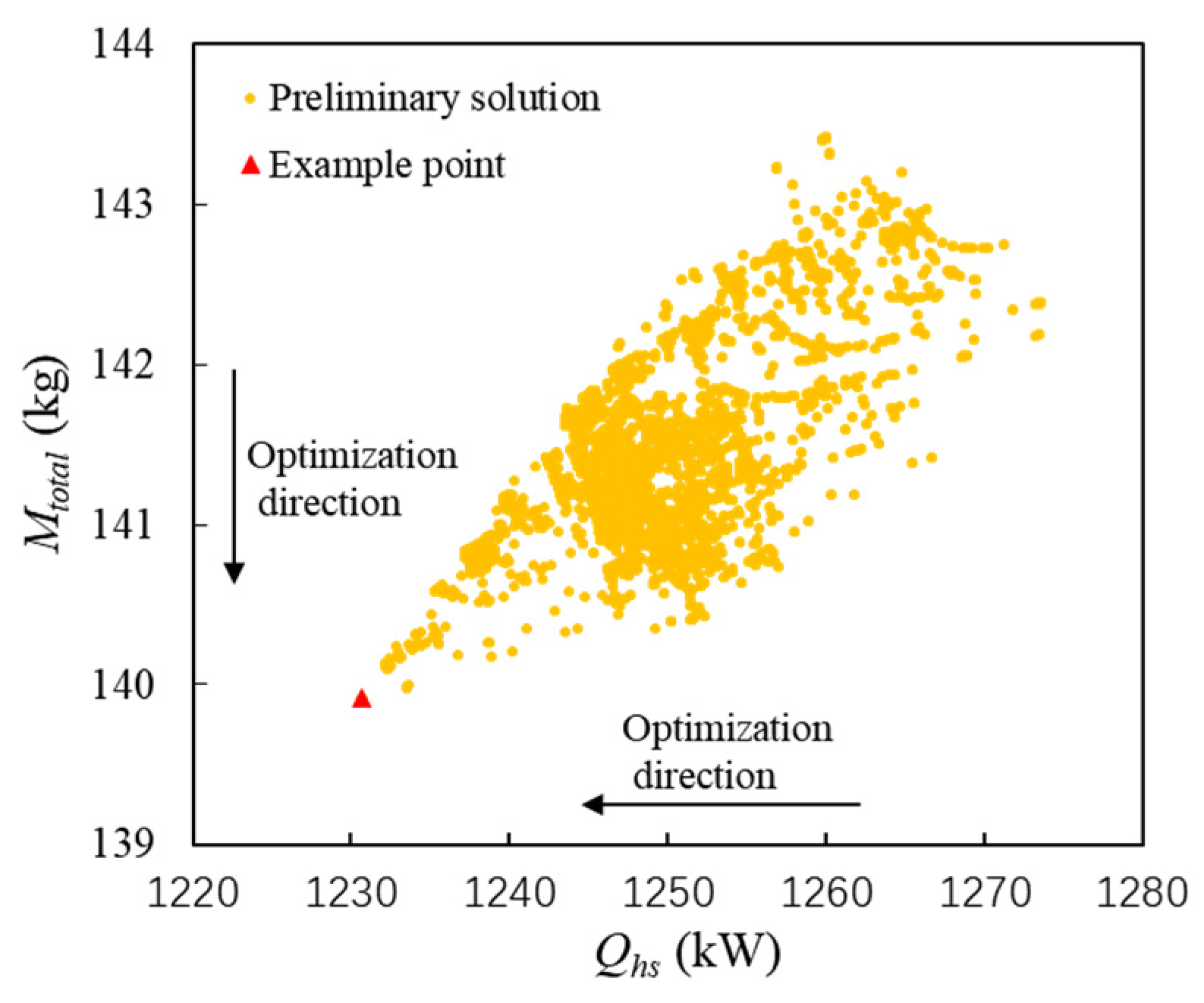
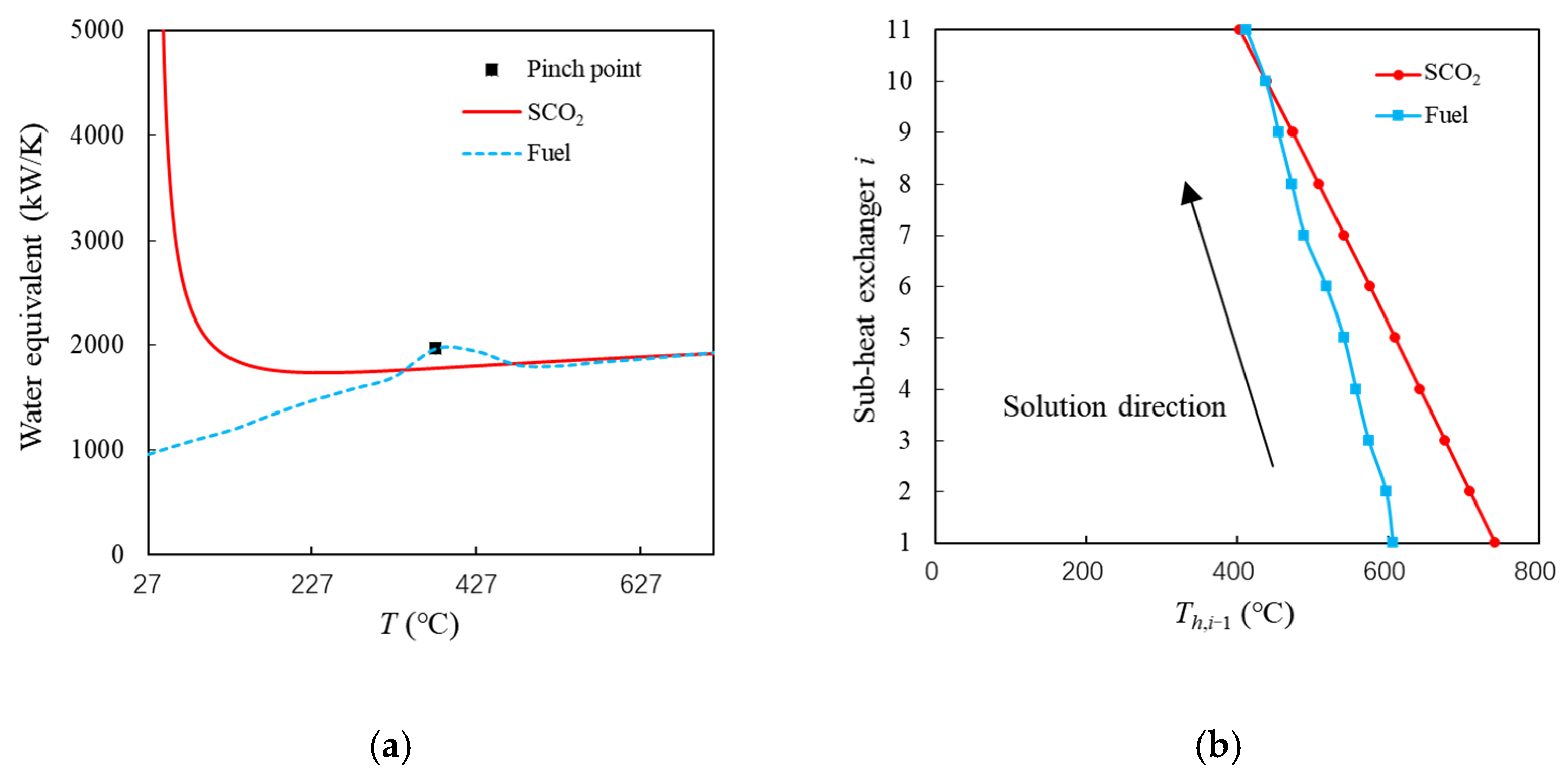








| Parameter | Value |
|---|---|
| Flight speed (Ma) | 6 |
| Flight height (H) | 22 km |
| Fuel mass flow rate for combustion (ṁc) | 0.5 kg/s |
| The inlet temperature of the cold side of PCHE (Tc,n) | 50 °C |
| The outlet temperature of the cold side of PCHE (Tc,0) | 500~680 °C |
| Specific speed of compressor and fuel vapor turbine (Ns) | 0.4 |
| The efficiency of the compressor (ηC) | 0.9 |
| The efficiency of fuel vapor turbine (ηfT) | 0.75 |
| The efficiency of the turbine in the SCO2 cycle (ηST) | 0.9 |
| The efficiency of the fuel pump (ηP) | 0.7 |
| The efficiency of the generator (ηG) | 0.9 |
| Pinch temperature difference (ΔTmin) | ≥10 °C |
| The initial power-to-weight ratio of PCHE (PWR) | 10 |
| Maximum temperature of SCO2 cycle (Tmax) | <1000 |
| Relative pressure loss coefficient of PCHE (ξhx,s) in system-level optimization | 2% |
| Maximum relative pressure loss coefficient of PCHE (ξhx) | 2% |
| Maximum relative pressure loss coefficient of cooling channels (ξcc) | 2% |
| Heat dissipated from the scramjet wall at Mach 6 (Qtotal) | 1350 kW |
| Lift–drag ratio | 2.95 |
| TSFC (s−1) | 0.001 |
| Inlet pressure of the cold side of PCHE (Pc,n) | 5 MPa |
| Inlet pressure of fuel pump (Pp,in) | 0.1 MPa |
| Flight duration | 1 h |
| Pressure drop ratio of fuel vapor turbine (πfT) | 3 |
| Compressor inlet pressure (PS1) | ≥7.4 MPa |
| Compressor pressure ratio (πC) | 2~5 |
| Step | Process |
|---|---|
| 1 | Initialize parameters |
| 2 | Let i = 1 and assume Pc,0 |
| 3 | Calculate the average temperature and pressure of the segment |
| 4 | Calculate the thermodynamic properties of SCO2 [41] and fuel [11] |
| 5 | Calculate Rei, fi, Nui, Li, Pc,i, Tc,i, Ph,i, and Th,i |
| 6 | Let i = i + 1. If i ≤ n, then return to Step 3, otherwise, proceed to the next step |
| 7 | Calculate Ploss. If Ploss ≥ 2%, then return to Step 2, otherwise proceed to the next step |
| 8 | Calculate Th,I, Tc,i, L, M, PWR, ηhx, Sg, and end the process |
| Component | Rotation Speed (rad/min) | ṁh (kg/s) | Inlet Temperature (K) | Inlet Pressure (MPa) | πC/πT | Impeller Diameter (mm) | ||
|---|---|---|---|---|---|---|---|---|
| Experiment | Simulation | Difference (%) | ||||||
| Compressor | 75,000 | 3.5 | 305 | 7.7 | 1.8 | 18.7 | 19.2 | 2.7 |
| Turbine | 45,000 | 8 | 392 | 13.5 | 1.8 | 73 | 69.6 | 4.7 |
| Parameter | L (mm) | wc (mm) | dc (mm) | tp (mm) | tf (mm) | Tc,n (K) | Pc,n (MPa) | Ph,0 (MPa) | mc/mh (kg/s) | Number of Channels, N |
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 150 | 0.4 | 0.225 | 0.48 | 0.2 | 295 | 3 | 2.6 | 0.01 | 2400 |
| Th,0 (K) | ηhx (%) | ||
|---|---|---|---|
| Experiment | Simulation | Difference (%) | |
| 400 | 88.2 | 86.7 | 1.7 |
| 412 | 89.4 | 88.0 | 1.6 |
| 432 | 90.0 | 87.6 | 2.7 |
| 452 | 90.0 | 89.2 | 0.9 |
| Pareto Point | ηhx (%) | P1 (MPa) | πC | (Kg/s) | Ph (MPa) | Th,0 (°C) | Tc,n (°C) | Qhs (kW) | Mtotal (kg) |
|---|---|---|---|---|---|---|---|---|---|
| A | 89.9 | 7.5 | 3.4 | 1.52 | 7.6 | 813.8 | 616.8 | 1243.6 | 130.3 |
| B | 90.0 | 7.6 | 3.3 | 1.53 | 7.7 | 812.5 | 616.9 | 1243.8 | 130.2 |
| C | 90.0 | 7.7 | 3.2 | 1.55 | 7.8 | 801.2 | 617.1 | 1244.6 | 130.0 |
| D | 90.0 | 8.0 | 3.2 | 1.56 | 8.1 | 797.3 | 617.3 | 1246.5 | 129.9 |
| E | 89.9 | 8.5 | 3.0 | 1.54 | 8.6 | 799.2 | 617.8 | 1249.8 | 129.7 |
| F | 89.9 | 8.8 | 2.9 | 1.54 | 8.9 | 801.3 | 618.0 | 1251.6 | 129.6 |
| Pareto Point | wc (mm) | W (m) | H (m) | L (m) | Weight (kg) | SgT (J/kg·K) | SgP (J/kg·K) | Sg (J/kg·K) | Ploss (%) | Efficiency (%) | PWR | Volume (cm3) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 1.1 | 0.15 | 0.27 | 0.72 | 57.2 | 46.1 | 0.2 | 46.3 | 0.05 | 89.83 | 21.8 | 28,458 |
| C2 | 1.0 | 0.21 | 0.16 | 0.70 | 44.7 | 46.1 | 0.4 | 46.4 | 0.08 | 89.83 | 27.9 | 22,214 |
| C3 | 1.0 | 0.10 | 0.25 | 0.73 | 38.1 | 45.9 | 0.7 | 46.6 | 0.14 | 89.83 | 32.7 | 18,925 |
| C4 | 1.0 | 0.26 | 0.07 | 0.95 | 32.7 | 45.5 | 1.7 | 47.2 | 0.36 | 89.84 | 38.0 | 16,285 |
| C5 | 1.0 | 0.07 | 0.20 | 1.02 | 30.9 | 45.2 | 2.3 | 47.6 | 0.49 | 89.85 | 40.3 | 15,354 |
| C6 | 1.0 | 0.08 | 0.14 | 1.27 | 29.6 | 44.3 | 4.5 | 48.8 | 0.95 | 89.87 | 42.1 | 14,711 |
| C7 | 1.1 | 0.08 | 0.12 | 1.43 | 26.9 | 43.8 | 6.1 | 49.8 | 1.24 | 89.88 | 46.3 | 13,371 |
| C8 | 1.0 | 0.10 | 0.09 | 1.28 | 22.2 | 43.3 | 7.1 | 50.4 | 1.46 | 89.89 | 56.2 | 11,025 |
| Parameter | Compressor | Turbine in SCO2 Cycle | Fuel Vapor Turbine |
|---|---|---|---|
| Ns | 0.4 | 0.51 | 0.4 |
| Rotation speed in optimal working condition (rad/min) | 10,778 | 10,778 | 5761 |
| Impeller diameter (mm) | 226 | 173 | 197 |
| Weight (kg) | 9.3 | 5.4 | 7.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Pang, L.; Zhao, J.; Yang, X. Optimization of Power and Thermal Management System of Hypersonic Vehicle with Finite Heat Sink of Fuel. Energies 2022, 15, 5332. https://doi.org/10.3390/en15155332
Guo L, Pang L, Zhao J, Yang X. Optimization of Power and Thermal Management System of Hypersonic Vehicle with Finite Heat Sink of Fuel. Energies. 2022; 15(15):5332. https://doi.org/10.3390/en15155332
Chicago/Turabian StyleGuo, Liang, Liping Pang, Jingquan Zhao, and Xiaodong Yang. 2022. "Optimization of Power and Thermal Management System of Hypersonic Vehicle with Finite Heat Sink of Fuel" Energies 15, no. 15: 5332. https://doi.org/10.3390/en15155332
APA StyleGuo, L., Pang, L., Zhao, J., & Yang, X. (2022). Optimization of Power and Thermal Management System of Hypersonic Vehicle with Finite Heat Sink of Fuel. Energies, 15(15), 5332. https://doi.org/10.3390/en15155332






