An Anomaly Detection Method of Time Series Data for Cyber-Physical Integrated Energy System Based on Time-Frequency Feature Prediction

Abstract

An integrated energy system (IES) is vulnerable to network attacks due to the coupling features of multi-energy systems, as well as the deep integration between a physical system and an information system. The anomaly detection of the time-series data in an IES is a key problem to defend against network attacks and ensure the cyber-physical security of IES. Aiming at false data injection attacks (FDIAs) on IES, this paper proposes an anomaly detection method for time-series data in a cyber-physical integrated energy system based on time-frequency feature prediction. The time-frequency features of the time-series data are extracted based on three time-frequency transform methods (DWT, EMD, and EWT). Then the extracted time-frequency features are input to the autoencoder (AE) to capture the hidden features and nonlinear structure of the original data in the frequency domain. The time-domain data within the detected time period are predicted by applying regression prediction on the top-layer features of AE. Considering the uncertainty of regression prediction, kernel density estimation (KDE) is used to estimate the probability density function of prediction error and the interval of the predicted data is estimated accordingly. The estimated lower boundary value of the predicted data is selected as the attack judgment threshold for anomaly detection. The results of the case study verify the advantages of the proposed method in reducing the false positive rate and improving the anomaly detection accuracy.

1. Introduction

In view of the shortage of energy supply and environmental problems caused by fossil fuels, the idea of an integrated energy system (IES) provides a feasible framework for future energy systems due to the complementarity, flexibility, and reciprocity among multiple energy forms [1]. Through the conversion between different energy forms, IES is able to adjust the energy flow in the links of production, transmission, distribution, and consumption. It is a complex cyber-physical system interconnected with the smart grid, the thermal system, the natural gas system, the transportation system, and other types of energy systems, in order to realize the coordinated operation of multiple energy subsystems [2]. However, in the links of energy supply, transmission, and consumption, a cyber-physical integrated energy system has the characteristics of strong coupling among different energy subsystems, as well as deep interaction between the physical system and the information system. With the increasing penetration of renewable energy and other newly appearing distributed sources and loads such as heat pumps and electric vehicles, the safety and reliability of IES are facing new challenges and requirements. As the physical systems of each energy forms, as well as the information system, are all interconnected in IES, and a fault in any single energy subsystem may affect the rest of the interconnected energy subsystems and the information system, resulting in the expansion of the fault range. Therefore, it is of great significance to study the cyber-physical security of IES under the new challenge of high randomness of system operation, high nonlinearity and complexity of system modelling, and interaction uncertainty between the physical system and information system.

Since the 21st century, a number of malicious network attacks on cyber-physical systems have occurred worldwide. Attacks on information systems of power systems have resulted in the loss of power supply capacity of the actual physical power grid, which eventually led to significant energy accidents and serious economic and social losses. In 2010, Stuxnet invaded the SIEMENS PCS7 control system used in Iran’s Natanz uranium enrichment base and the Bushehr nuclear power plant, resulting in the failure of a large number of uranium enrichment centrifuges and generator units in the Bushehr nuclear power plant, which delayed Iran’s nuclear program for at least two years. In 2015, the Ukrainian power grid suffered a malicious network attack in which the implantation of computer viruses made the control server fail to sense and control the physical equipment of the power grid, leading to a large-scale power outage. In March 2018, the U.S. Department of Homeland Security and the Federal Bureau of Investigation issued an alert that energy and other key systems had been subject to network attacks in which a number of confidential documents of the industrial control system workstation and the supervisory control and data acquisition (SCADA) system were stolen [3]. The above network security incidents demonstrate that network attacks to an IES information system can cause huge damage to the physical system, including core equipment failure, system instability, heavy load loss, and power failure. Current research mainly focuses on the simulation, operation optimization, and planning of IES, whereas research on the anomaly detection and defense of a cyber-physical integrated energy system under network attack is very little, which is an important gap that needs to be filled.

The main target of the network attack on an IES is to destroy the confidentiality, accuracy, and availability of the information in an IES. There are various forms of network attacks based on the different attack targets. At present, common attack forms include false data injection attacks (FDIAs), denial of service (DOS), and man-in-the-middle attacks (MTIM). An FDIA aims to destroy the data accuracy in an IES. Attackers invade remote measurement instruments and use carefully camouflaged and designed data to tamper with measurement data or cut off normal measurement data and upload erroneous camouflaged data during communication. The decision-making center obtains the wrong data after the attack and therefore the decision-making process is interrupted, threatening the stability of the whole system and causing great economic losses [4]. DOS aims at destroying the availability of information elements or centers in the system, and then hindering the information transmission and intervening in the normal communication of dispatching and operation commands in the system [5]. MITM aims at destroying the confidentiality of IES information, during which the attacker steals and monitors the communication channel to illegally obtain users’ private energy data [6]. Among them, an FDIA makes it easy to exert a significant impact on the economic and stable operation of the integrated energy system due to its high concealment and destructive attack characteristics [7,8,9]. This paper studies FDIAs as the main attack form.

Making defense against network attacks necessary is an important guarantee to maintain the safe and stable operation of an IES, and the first step in the defense is to detect the existence of a network attack, distinguish the mode of attack, and predict the attacker’s purpose and potential impact. The detection methods proposed for the above attacks can be divided into three categories. The first is the detection method based on trajectory prediction. Track analysis is carried out with historical data to predict the current state of the system and compared with the actual measurement to analyze the areas that may be attacked. Reference [10] proposed a multi-sensor track fusion-based prediction method to extract the initial correlation information about the attacked oscillation parameters, using a Kalman-like particle filter-based smoother at each monitoring node. The characteristics of moving horizon estimation are used to deal with the continuous load fluctuation and disturbance caused by data injection in the power grid. Reference [11] proposed a quick intrusion detection algorithm to detect FDIAs in smart grids, in which the statistical characteristics of dynamic gird states are analyzed and a time-varying dynamic model is established to accurately capture the dynamic state transition caused by the change in system configuration. The second category is the detection method based on state estimation, mainly including the residual detection method, the sudden variable detection measurement method, etc. Reference [12] proposed a new method for false data detection, in which equivalent measurement transformation is applied instead of traditional weighted least squares state estimation and the false data are distinguished by the residual researching method. Reference [13] proposed a method to screen and protect a specific subset of measurement devices, through which the data mutations in the selected subset of measurement devices can be quickly detected and significant security losses caused by attacks can be avoided as much as possible under limited protection resources. In recent years, the third kind of detection method based on artificial intelligence has been developing quickly. Reference [14] used the compressive sampling method in compressed sensing theory and SVM to develop an anomaly detection model, and SVM was adopted to classify the feature compression results. Reference [15] used statistical tools of binary logistic regression to detect attacks. Reference [16] proposed a decision tree algorithm based on relative decision entropy, which combined with rough set attribute reduction technology to delete redundant features and improve attack detection accuracy.

In current research, the selection of features in the anomaly detection process has not been extended to the time-frequency field. However, the operation data of each energy subsystem in an IES (power subsystem, heating subsystem, gas subsystem, etc.) are mostly time-series data. For time-series data, the time-frequency features have higher accuracy and effectiveness than time-domain features. The typical time-frequency transform methods include wavelet transform (WT), discrete wavelet transform (DWT), empirical mode decomposition (EMD), and empirical wavelet transform (EWT). These methods have already proven their excellent feature extraction ability for time-series data in current studies. In Reference [17], a wavelet representation method is proposed, in which the difference of information between the approximation of a signal at the resolutions can be extracted on the basis of WT. The application of this representation to data compression in image coding, texture discrimination, and fractal analysis is discussed. Reference [18] established a protection scheme for microgrids using DWT and a decision tree, in which the DWT method is applied to the time-series data for fault classification. Reference [19] verified the effectiveness of the EMD method for analyzing nonlinear and non-stationary data and interpreted the final presentation of the results as an energy–frequency–time distribution. Reference [20] explored the performance of EMD based on numerical experiments in cases with fractional Gaussian noise, and the results showed that EMD can act effectively as a dyadic filter bank in stochastic situations involving broadband noise. Reference [21] proposed a simple and logical definition of “trend” for nonlinear and nonstationary time-series data based on EMD. Climate data are used to illustrate how the intrinsic trend is determined and how the variability of the data on various time scales can be derived. Reference [22] explored power quality disturbances based on EWT and DWT and the results showed that the two methods had different performances in combination with different classification methods.

Though the above time-frequency transform methods have already been adopted in feature extraction of time-series data in some other fields, the methods have not been applied in the anomaly detection process of an IES. In this paper, three time-frequency transform methods (DWT, EMD, and EWT) are used to extract the time-frequency features of IES time-series data, and the extracted time-frequency features are used for prediction instead of the conventional time-domain prediction for anomaly detection.

Besides, previous studies seldom consider the uncertainty of prediction error, and often use the percentage of prediction error distribution as the judgment threshold. In this paper, kernel density estimation (KDE) is used to estimate the probability density function of prediction error. Based on this, the interval of the predicted data considering prediction error is estimated, and the lower estimated interval value is used as the attack judgment threshold.

In summary, this paper proposes an anomaly detection method of time-series data in a cyber-physical integrated energy system based on time-frequency feature prediction. The technical framework of this paper is shown in Figure 1. In Section 2, the time-frequency features are constructed on the basis of three time-frequency transform methods of DWT, EMD, and EWT. Then in Section 3, an anomaly detection method is proposed, in which the autoencoder (AE) and regression prediction are applied to the time-frequency features in order to predict the time-domain data within the detection period. Considering the prediction uncertainty, kernel density estimation (KDE) is used to estimate the interval of the time-domain prediction data. The attack judgment threshold is determined as the lower estimated bound of the predicted data. A case study is conducted for method validation, the data processing of which is interpreted in Section 4 and the results analysis is presented in Section 5. The results verify that the proposed method can significantly improve the anomaly detection accuracy on time-series data. Thus, the proposed model can effectively help resist network attacks and maintain the economic and stable operation of an IES.

2. Construction of the Time-Frequency Features

As the operation data of an IES are mostly time-series data with timing characteristics, research on anomaly detection of time-series data can effectively detect attack intrusion on an IES and ensure system safety and stability. The operation data of an IES usually undergo complex changes in a day without explicit seasonal or periodic patterns. When an FDIA occurs, the spatial and temporal correlation of the operation data in an IES may also differ from that in the normal state. Therefore, the feature extraction methods of time-frequency transform are adopted to analyze the implicit time-frequency characteristics of IES time-series data, such as discrete wavelet transform (DWT), empirical mode decomposition (EMD), and empirical wavelet transform (EWT). The excellent feature extraction ability of the above time-frequency feature extraction methods was verified in Refs. [17,18,19,20,21,22]. Based on the extracted time-frequency features, the autoencoder (AE) is further adopted in Section 3 to mine the nonlinear hidden structure inside the features, which together address the correlation inconsistency and improve the anomaly detection accuracy.

2.1. Time-Frequency Transform Methods

To extract comprehensive and sufficient time-frequency characteristics of IES time-series data, three typical time-frequency transform methods are employed. The methods of DWT, EMD, and EWT are briefly introduced in this section.

2.1.1. Discrete Wavelet Transform (DWT)

DWT is a time-frequency extraction method that can obtain the time position of the spectral component of non-stationary signal. For a given time-series datum f (t), the DWT of f (t) includes both scale transform and translation transform, which equals the convolution of f (t), as shown in Equation (1) [23].

$$d(m,n)={\displaystyle {\int }_{-\infty }^{\infty }f(t) \overline{{\psi }_{mn}(t)} dt}, \forall m,n\in \mathbb{Z}$$

(1)

where m and n are the scale and position parameters of the wavelet function, respectively. The wavelet function ψ_m,n (t) is shown in Equation (2).

$${\psi }_{mn}(t)=a_0^{\frac{m}{2}}\psi (a_0^{m}t-n{b}_0) , \forall m,n\in \mathbb{Z}$$

(2)

2.1.2. Empirical Mode Decomposition (EMD)

EMD decomposes time-series data according to the time-scale characteristics of the data themselves instead of preset basis functions. Therefore, EMD is suitable for analyzing nonlinear and nonstationary time-series data. It can decompose the complex signal into finite intrinsic mode functions (IMF), and each IMF component contains the local characteristic signals of different time scales of the original signal. Then the time-frequency spectrum can be obtained through a Hilbert transform of each IMF, where the frequency with physical significance is obtained. Compared with short-time Fourier transform, wavelet transform (WT), and other methods, EMD decomposes the data themselves to form the basis functions, which can preserve the local time-scale characteristics of the original data [19,20,21]. As a result, the time-frequency features obtained by EMD is an effective supplement to the features extracted by DWT.

The decomposition process of EMD is as follows [19].

For a given signal f (t), the upper and lower envelopes are determined from the local maximum and minimum values of cubic spline interpolation. m₁ represents the mean value of the upper and lower envelopes. h₁ is calculated as follows.

$$h_1=f(t)-m_1$$

(3)

In the second decomposition process, h₁ is the data to be decomposed, and m₁₁ is the mean value of upper and lower envelopes of h₁. h₁₁ is calculated as follows.

$$h_1=f(t)-m_1\hspace{1em}{h}_{11}=h_1-m_{11}$$

(4)

The decomposition process is repeated K times until h_1K is an eigenmode function. h_1K is calculated as follows.

$$h_{1K}=h_{1(K-1)}-m_{1K}$$

(5)

Then the first IMF component of f (t) is obtained as Equation (6), which contains the shortest periodic component.

$$c_1=h_{1K}$$

(6)

Then c₁ is separated from the rest of the data, as shown in Equation (7).

$$r_1=f(k)-c_1$$

(7)

Repeat the above process n times, as shown in Equation (8).

$$\begin{array}{l}{r}_2=r_1-c_2\\ \hspace{1em} ⋮\\ r_{\mathrm{n}}=r_{n-1}-c_n\end{array}$$

(8)

Through the process of EMD, f (t) is decomposed as the sum of a set of IMF functions c₁, …, c_n. n is decided by the features of f (t) itself.

2.1.3. Empirical Wavelet Transform (EWT)

Although EMD has the advantage of self-adaption and performs particularly well when dealing with nonlinear and non-stationary signals, problems such as over envelope, under envelope, endpoint effect, and mode aliasing still exist in varying degrees in the application process. Empirical wavelet transform (EWT) combines the self-adaptive decomposition concept of EMD and the compact support feature of WT, which provides a new idea of self-adaptive time-frequency analysis. Compared with EMD, the EWT method can adaptively select the frequency band and overcome the problem of modal aliasing caused by the discontinuity of the time-frequency scale. At the same time, it has a complete and reliable mathematical theoretical basis, low computational complexity, and can also overcome the problems of over envelope and under envelope [24]. Therefore, this paper selected EWT as one of the methods to extract the time-frequency features of time-series data so as to further enrich the time-frequency feature set.

In the computation process of EWT, the Fourier spectrum of the original signal is divided into continuous intervals. Then wavelet filter banks are constructed on each interval for filtering, and a group of AM and FM components is obtained at last through signal reconstruction. This method can identify the position of the signal’s feature information in the Fourier spectrum through the wavelet filter bank and adaptively extract the different frequency components of the signal. The design of the filter bank is based on the idea of constructing Littlewood Paley and Meyer wavelets. For n > 0, the empirical wavelet function ψ_n (ω) and empirical scaling function ϕ_n (ω) are shown in Equations (9) and (10) [22].

$${\psi }_n(\omega )=\{\begin{array}{c}1\hspace{1em} \mathrm{if} (1+\gamma ){\omega }_n\le \left|\omega \right|\le (1-\gamma ){\omega }_{n+1}\\ \cos \left[\frac{\pi }{2}\beta \left(\gamma ,{\omega }_{n+1}\right)\right]\hspace{1em} \mathrm{if} (1-\gamma ){\omega }_{n+1}\le \left|\omega \right|\le (1+\gamma ){\omega }_{n+1}\\ \sin \left[\frac{\pi }{2}\beta \left(\gamma ,{\omega }_n\right)\right]\hspace{1em} \mathrm{if} (1-\gamma ){\omega }_n\le \left|\omega \right|\le (1+\gamma ){\omega }_n\\ 0\hspace{1em} \mathrm{if} \mathrm{otherwise}\end{array}$$

(9)

$${\varphi }_n(\omega )=\{\begin{array}{c}1\hspace{1em} \mathrm{if} |\omega |\le (1-\gamma ){\omega }_n\\ \cos [\frac{\pi }{2}\beta (\frac{1}{2\gamma {\omega }_n}(|\omega |-(1-\gamma ){\omega }_n)]\hspace{1em} \mathrm{if} ((1-\gamma ){\omega }_n\le \left|\omega \right|\le (1+\gamma ){\omega }_n\\ 0\hspace{1em} \mathrm{if} \mathrm{otherwise} \end{array}$$

(10)

where γ is a parameter determining the spectrum interval width and γ∈ (0, 1). β (x) ∈C^k ([0, 1]) and satisfies the conditions in Equation (11).

$$\{\begin{array}{l}\beta (x)=0\hspace{1em} \mathrm{if} x\le 0\\ \beta (x)+\beta (1-x)=1\\ \beta (x)=1\hspace{1em} \mathrm{if} x\ge 1\end{array} \mathrm{if} \forall x\in [0,1]$$

(11)

The functions satisfying the conditions in Equation (11) are diverse, among which the most used one is shown in Equation (12).

$$\beta (x)=x^4\left(35-84x+70x^2-20x^3\right)$$

(12)

Referring to the idea of classical WT, the empirical wavelet coefficient constructed by Gilles is generated by the inner product, and the detail coefficient EWT (n,t)_d is generated by the inner product of empirical wavelet function ψ_n (ω) and signal f (t), as shown in Equation (13).

$$EWT{(n,t)}_d=<f(t),{\psi }_n(\omega )>=\mathrm{IFFT}\left(f(\omega )\times {\psi }_n(\omega )\right)$$

(13)

The approximate coefficient is determined by the inner product of the empirical scaling function ϕ_n (ω) and signal f (t), as shown in Equation (14).

$$EWT{(n,t)}_a=<f(t),{\varphi }_n(\omega )>=\mathrm{IFFT}\left(f(\omega )\times {\psi }_n(\omega )\right)$$

(14)

2.2. Modeling of FDIA

Due to the interconnection of the cyber-physical integrated energy system, even a small network attack may give rise to huge stability problems and economic losses. The detection and defense of network attacks is of huge significance for the safety and stability of an IES. Though the forms of attack are various, the core attack purpose is consistently to destroy the operation stability of the IES and obtain economic benefits from the intrusion. In the introduction section, three common forms of network attack against cyber-physical integrated energy systems were introduced, namely, false data injection attacks (FDIAs), denial of service (DOS), and man-in-the-middle attacks (MITM). Among the three attack forms, it is easier for FDIA to have a significant and profound impact on the economic and stable operation of an IES in view of its high concealment and strong destructiveness. Therefore, this paper selects FDIA as the main attack form.

Since the control center in an IES is directly connected with the network dispatching center, the measurement data of the energy supply is difficult to modify. By comparison, the measuring instruments at the load end are widely distributed, and the FDIA against the load end is easier to implement. Therefore, this paper uses the method in Ref. [25] to model and analyze the load redistribution (LR) attack, a specific type of FDIA. The attacker intends to threaten and affect the overall economy and stability of the system by modifying the measurement data at the partial load end of an IES. By modifying the measurement data at the load end, the dispatching system will receive the wrong load data and make wrong dispatching orders, resulting in the redistribution of the power flow in the whole network. The imbalance of the power flow distribution may cause further load loss at the load end, heavy load or overload of transmission lines, equipment damage, and even large-scale energy supply suspension accidents in the end. From an economic perspective, the attack may also raise the system operation cost and affect relevant economic transactions, which may eventually cause huge economic losses [26,27,28].

To further model the LR attack process, suppose that the load of node i in subsystem m is $D_{i,m}^{(0)}$ before being attacked, where $m\in \left\{e,h,g\right\}$ and e, h, and g are the subscripts of the power, heating, and gas subsystems, respectively. The attacker modifies the node load to make the original node load $D_{i,m}^{(0)}$ superimpose on an attack vector $\Delta D_{i,m}$, which causes the transmission power of each transmission line $P_{ij,m}^{(0)}$ superimposed on $\Delta P_{ij,m}$, influencing the energy flow distribution of the whole system.

In addition, if the sudden increase or decrease in node load or line transmission power is too much, the system detector can detect the change behavior through residual inspection and give an alarm. Therefore, assuming that the attacker has certain knowledge and experience of LR attacks in advance, the attacker limits the change in load and transmission power to within a range so as to bypass the residual inspection and avoid sounding an alarm. The limiting conditions are shown in Equations (15) and (16).

$${\alpha }_{i,m}^{\min }·D_{i,m}^{(0)}\le \Delta D_{i,m}\le {\alpha }_{i,m}^{\max }·D_{i,m}^{(0)}\hspace{1em}m\in \{e,h,g\}$$

(15)

$${\beta }_{ij,m}^{\min }·P_{ij,m}^{(0)}\le \Delta P_{ij,m}\le {\beta }_{ij,m}^{\max }·P_{ij,m}^{(0)}\hspace{1em}m\in \{e,h,g\}$$

(16)

where ${\alpha }_{i,m}^{\min }$ and ${\alpha }_{i,m}^{\max }$ represent the lower and upper limit factors of the load change range at node i of subsystem m, respectively. ${\beta }_{ij,m}^{\min }$ and ${\beta }_{ij,m}^{\max }$ represent the lower and upper limit factors of the transmission power range from node I to node j in subsystem m, respectively. $D_{i,m}^{(0)}$ indicates the initial load at node i of subsystem m before the attack and $\Delta D_{i,m}$ represents the attack vector at node i. $P_{ij,m}^{(0)}$ indicates the initial transmission power on the transmission line from node i to node j in subsystem m before the attack. $\Delta P_{ij,m}$ represents the corresponding power change caused by the attack on the line from node i to node j in subsystem m.

2.3. Time-Frequency Feature Analysis of IES Load Data under FDIA

To further explore the feature extraction potential based on the three time-frequency transform methods of DWT, EMD, and EWT, a case study was conducted on the time-series data of a power subsystem node under LR attack. The load data of 100 time points were selected, and three different types of FDIA (slope attack, incentive attack, and delay attack) were assumed to exert on this node. The time-frequency features were qualitatively analyzed after applying DWT, EMD, and EWT on the attacked data so as to lay a foundation for the subsequent selection and construction of time-frequency features.

Figure 2, Figure 3 and Figure 4 present the three attack modes of slope attack, incentive attack, and delay attack, respectively. Figure 2 shows the first attack mode—a slope attack. The attack vector is depicted by the orange line, which increases and decreases linearly. The red line indicates the normal state of the time-series load data, and the blue line presents the series data after the slope attack.

Figure 3 shows the second attack mode—an incentive attack. The attack vector is suddenly superimposed and lasts until the end of the attack.

Figure 4 presents the third attack mode—a delay attack. The attacked data repeat the signal value of the previous time period.

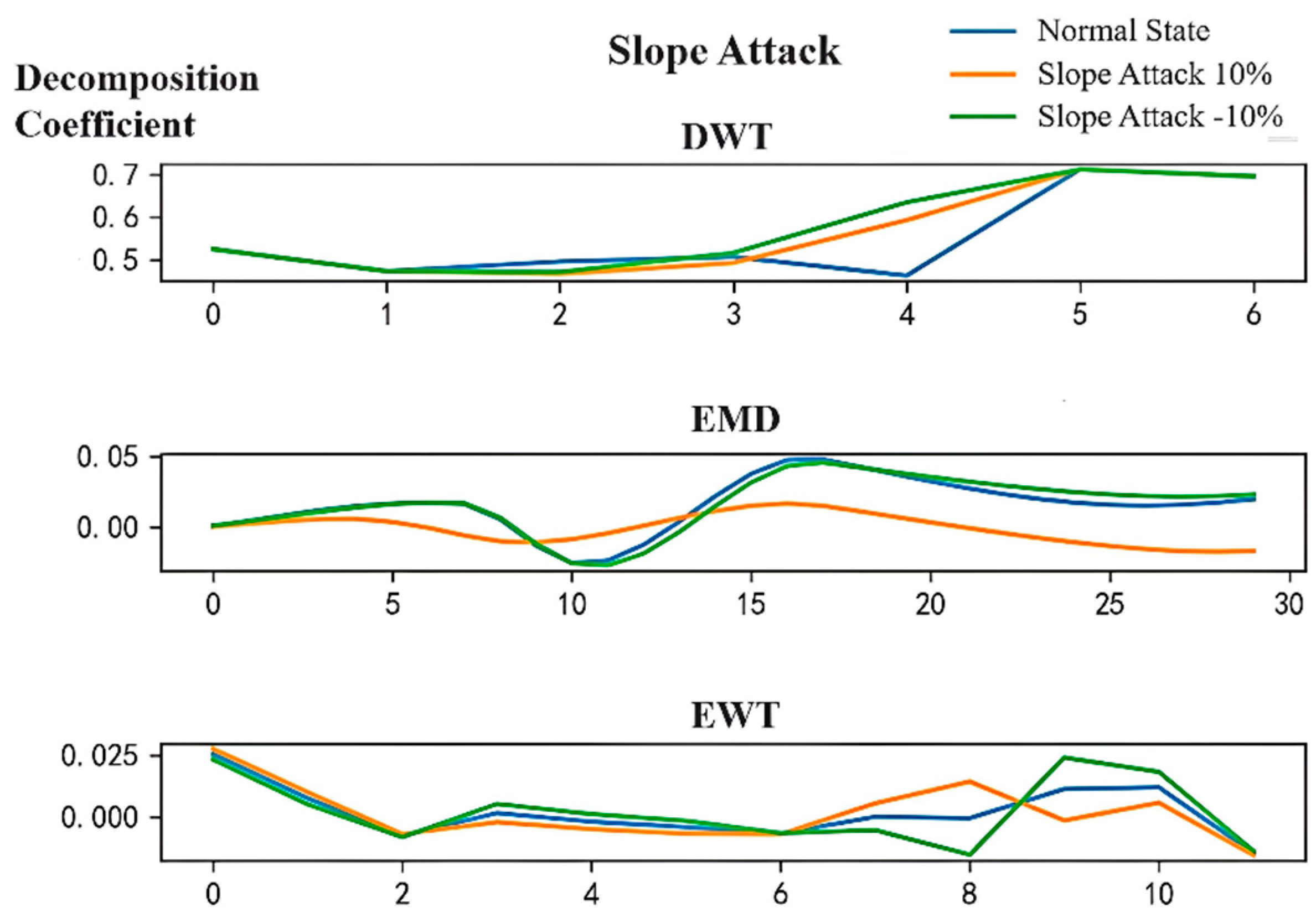
To observe the change in the time-frequency features under the three attack modes, the time-frequency transform methods of DWT, EMD, and EWT were applied to the case data. As for the setting of DWT, it can be seen from Equation (1) that the selection of wavelet functions ψ_m,n (k) and the decomposition level m can lead to different decomposition coefficients. These coefficients will further affect the feature extraction ability of a DWT-based feature extractor. Although the best setting of wavelet function and decomposition level m to achieve the best detection performance exists, it is impractical to test all types of wavelet functions. In this paper, the bior wavelet was chosen as the basis wavelet function in consideration of its biorthogonality and compact support by MATLAB. In addition, the mode components decomposed by EMD and EWT together form the original time-series data, and the coefficients of all mode function components are retained for feature extraction.

Figure 5, Figure 6 and Figure 7 present the decomposition coefficients of DWT, EMD, and EWT under the three attack modes, where the results of DWT only preserve the first-level detail coefficients. Under each attack mode, both the positive attack and the negative attack were studied.

As shown in Figure 5, different feature extraction methods had different sensitivity to different attack modes. For example, under the action of a positive slope attack, the decomposition coefficient of EMD was very different from that of the normal state, whereas there was almost no difference under a negative slope attack. The decomposition coefficients of DWT and EWT were quite different in both positive and negative attacks. As presented in Figure 6 and Figure 7, for incentive and delay attacks, the decomposition coefficients of EMD and EWT were very different from the normal state, whereas those of DWT were not obvious.

By globally observing the decomposition coefficient diagram from Figure 5, Figure 6 and Figure 7, it can be seen that DWT was more accurate at locating the time point of the abnormal value, and EMD and EWT had more advantages in judging the occurrence of the abnormal value. Therefore, the above three types of time-frequency transform methods, DWT, EMD, and EWT, can together provide good screening features for both judging whether an attack is occurring and locating the beginning and end time of the attack. The three methods complement each other and together form rich and diverse time-frequency features of the time-series data, which provides strong support for subsequent attack anomaly detection.

2.4. Composition of Time-Frequency Features

Based on the conclusions drawn in Section 2.3, the decomposition coefficients obtained by DWT, EMD, and EWT can help distinguish the attacked time-series data in an IES. References [29,30,31] proved that it is effective to analyze the statistical characteristics of decomposition coefficients obtained by time-frequency transform for time-series data. Therefore, to determine the time-frequency feature composition of IES time-series data, extracting the statistical features of the decomposition coefficients obtained by time-frequency transform is considered an important part. Based on the existing research, the statistical features are determined to be the variance and the distribution and the average of local maximum and local minimum of the time-frequency decomposition coefficients. To effectively reduce the feature dimension and avoid the “dimension disaster” in the subsequent application of the autoencoder, the vulnerability evaluation method proposed in Ref. [26] can be first adopted to determine the vulnerable nodes of the system, and then the time-frequency feature extraction can be conducted only on the selected vulnerable points. Figure 8 shows an overview of the time-frequency features and

Table 1. Composition of the time-frequency features.

Transform Method	Feature 1~m	Feature m + 1	Feature m + 2	Feature m + 3	Feature m + 4
DWT	Level 1 detail coefficients	Variance	Average of the local maximum	Average of the local minimum	Distribution mark sequence of local maximum and minimum
EMD	Coefficients of the IMF	Variance	Average of the local maximum	Average of the local minimum	Distribution mark sequence of local maximum and minimum
EWT	Coefficients of the mode components	Variance	Average of the local maximum	Average of the local minimum	Distribution mark sequence of local maximum and minimum

presents the detailed composition of the time-frequency features.

In Figure 8, n₁ represents the number of DWT-related features. n₂ represents the number of features related to EMD. n₃ represents the number of features related to EWT. Node 1~ Node K represents K nodes whose data are used for anomaly detection.

In Table 1, m represents the number of the first-level detail coefficients of DWT, the coefficient of the m-th IMF component of EMD, or the m-th mode component value in EWT. The distribution mark sequence of local maximum and minimum defines a sequence whose value is 1 for all the positions where the local maximum appears, and −1 for the positions where the local minimum appears, with the rest being zero.

3. Anomaly Detection Based on AE and KDE

3.1. Framework of Anomaly Detection Based on AE and KDE

When constructing an FDIA attack vector, existing research tends to focus on the spatial dependence among system variables, and the time dependence is usually ignored. However, as the operation data in an IES are mostly time-series data, the proposed detection mechanism was established based on both the time and space correlation of the time-series data. In Section 2, a time-frequency feature extraction method based on DWT, EMD, and EWT was proposed. In this section, to construct an anomaly detector based on time-frequency feature prediction, the time-frequency features are first inserted into the autoencoder (AE) to capture the hidden characteristics and non-linear structure of the data in the frequency domain. Then the predicted data in the time domain are obtained by using a regression predictor on the top-layer features. Considering the prediction uncertainty, the prediction error probability density function is obtained utilizing kernel density estimation (KDE). Based on the predicted data and the error probability density function, the estimated time-domain prediction interval within the detection period can be outlined and the lower boundary of such an estimated interval is used to determine whether a network attack is occurring. Figure 9 shows the schematic diagram of the proposed anomaly detector.

3.2. AE-Based Time-Frequency Feature Prediction

AE is a feed-forward and non-recursive neuronal network designed to reproduce its own input. In principle, AE can automatically extract certain hidden linear and non-linear structural relationships from the time-series data and learn the changing patterns of the data to implement data prediction. AE involves encoding and decoding steps where the encoding passes the input data to the hidden layer to generate latent mapping while decoding maps the latent mapping to the reconstructed output. The decoder in AE only uses the latent variables in the hidden layer to perfectly reconstruct the original input, meaning that the latent variables retain sufficient information for the input. Thus, the nonlinear transformation obtained via learning with the use of model parameters defined in the hidden layer can be regarded as an advanced feature extractor [32]. This means that the extractor can effectively retain the hidden abstract features and invariant structures in the data. Furthermore, a standard regression predictor is added to the top layer of the feature extractor so that the predicted load data in the frequency domain can be derived from the input frequency domain feature data.

The AE has an input layer with d visible inputs, a hidden cell layer h, a d-cell reconstruction layer, and an activation function, as shown in Figure 10.

During the training process, the input x ∈ R^d is mapped to the hidden layer to generate the potential mappings y ∈ R^h, and the corresponding network is depicted as the shaded green session in Figure 10, which is the encoder. Subsequently, the output layer is mapped by the decoder to the input layer with the same size, and this is the reconstruction step. The reconstructed value is expressed as z ∈ R^d. The aforementioned two steps can be expressed by Equation (17).

$$\{\begin{array}{l}y=f\left(W_{y}x+b_y\right)\hfill \\ z=f\left(W_{z}y+b_z\right)\hfill \end{array}$$

(17)

where W_y and W_z denote the weight of input to hidden and hidden to output, respectively. b_y and b_z are the deviation of the hidden units and output units, respectively. F (·) represents the activation function. The sigmoid function, hyperbolic tangent function, or rectified linear function are typically used as the activation function.

The constraint of W_y = W_z’ = W needs to be satisfied in order to halve the number of model parameters, and the learning shall be applied to the remaining three sets of parameters of the AE model with a single hidden layer, which are W, b_y, and b_z.

The objective of training is to minimize the error between the input and reconstruction, which can be illustrated by Equation (18).

$${\mathrm{argmin}}_{W,b_y,b_z}[c(x,z)]$$

(18)

In Equation (18), the value of z depends on the parameters W, b_y, and b_z. The input x is given. c (x,z) denotes the error between the input and the reconstruction and can be defined in any form. The updating rule of weight can be defined by Equation (19).

$$\{\begin{array}{l}W=W-\eta \frac{\partial \mathrm{cost}(x,z)}{\partial W}\hfill \\ b_y=b_y-\eta \frac{\partial \cos t(x,z)}{\partial b_y}\hfill \\ b_z=b_z-\eta \frac{\partial \cos t(x,z)}{\partial b_z}\hfill \end{array}$$

(19)

where η is the learning rate. After the training, the reconstruction layer and its parameters are removed and the obtained features are located in the hidden layer, and are subsequently used as the input to higher layers to produce deeper features.

The advantage of AE lies in the reconstruction-oriented training, which uses only the hidden-layer activity during reconstruction, and such information is encoded as features in the input. If the model can flawlessly recover the original input from y, it means sufficient input information is retained. Moreover, the learned non-linear transformations defined by the weights and errors can be considered as a good step for extracting features. The hidden time-frequency features extracted by AE are fed into the regression predictor to obtain time-domain predictions over the detection time.

Based on the case study in Section 2.2, the obtained time-frequency features are input into AE with three hidden layers to acquire the hidden time-frequency features. In the training process, the training set is divided into several mini-batches, with each containing 50 samples. The mean squared error (MSE) is selected to represent the loss function with the validation set division ratio configured as 0.1. The adaptive moment estimation optimization algorithm with 200 iterations is used, and this algorithm can adaptively adjust the optimization learning rate.

Figure 11 indicates the change in the loss function of the anomaly detector model for 200 training iterations. After 75 iterations, the loss function shows a negligible decrease and the difference between the validation error and the training error is small, suggesting that there is no overfitting.

Figure 12 plots the predicted time-series data generated from the training set and test set, as well as the actual time-series load data under normal circumstances. Figure 13 shows the error between the predicted time-series data and the actual time-series load data. According to results of Figure 12 and Figure 13, it can be seen that the proposed time-frequency feature prediction model is able to fit the load variation pattern when the prediction time interval is 2 min.

In practical application, the size of the time window may differ according to different demands for detection. From a theoretical point of view, the time window for training should contain at least two complete periods of the data. According to different detection objectives and demands, the length of the period may also vary. For short-time anomaly detection, the period may be selected as one day and the time resolution can be determined as more (such as 15 min). For rough detection with lower resolution (such as 1 h), the period can be selected as one month or even one year. When one year is chosen as the period, then the yearly variation of the data (such as the influence of the seasons) can be considered in the detection. When the length of the time window increases, the detection accuracy will apparently increase accordingly, but the computation speed will become slower. Therefore, a balance should be achieved between the computation accuracy and speed depending on the actual scenarios and demands.

3.3. Predicted Error Estimation Based on Kernel Density Estimation

Prediction uncertainty exists in the predicted data obtained from the AE-based time-frequency feature predictor described in Section 3.2. In this section, the prediction error is quantified and modelled. The KDE is adopted to learn the probability distribution of prediction error, and a fitted probability density function of the prediction error can be obtained. Based on the fitted error function, the interval of the predicted data considering prediction error can be estimated. If the estimated data fall outside the expected range, the data will be identified as abnormal data and an alarm will be raised.

KDE is a type of non-parametric test that does not rely on prior knowledge about the data distribution and does not apply any assumption to the data distribution. It is a method of studying the characteristics of the data distribution based on the data samples themselves and using a smoothed peak function to fit the observed data points, which models the true probability distribution function of the input sample data.

The input sample data are the prediction error, and the probability distribution of the prediction error calculated via KDE is expressed by Equation (20).

$$f_E(x)=\frac{1}{nh}{\displaystyle \sum _{i=1}^{n}K}\left(\frac{x-x_i}{h}\right)$$

(20)

where x indicates the prediction error and f_E (x) is the probability density function of the prediction error. K(·) is the kernel function with an infinite integral of 1 and a mean of 0. h denotes the smoothing parameter, which is also called the bandwidth or window (h > 0).

The time-series data at time t + 1 will fall into the prediction interval shown in Equation (21) with a probability of 1 − α.

$$\left[x_t-\overline{X_e\left(x,\frac{\alpha }{2}\right)},x_t+\underset{\_}{X_e\left(x,\frac{\alpha }{2}\right)}\right]$$

(21)

where x_t is the data at time t, $\overline{X_e\left(x,\frac{\alpha }{2}\right)}$ and $\underset{\_}{X_e\left(x,\frac{\alpha }{2}\right)}$ denote the value of x when the integral area value under the error probability function f_E (x) is α, and α is the confidence coefficient.

By feeding the prediction errors obtained in the case study in Section 3.2 (Figure 13) into the KDE, the fitted error probability density function can be obtained, as shown in Figure 14. The purple shaded area indicates the integral area below the probability density function, namely, the predicted error probability P (a ≤ X ≤ b) within the prediction range [a, b].

When α = 0.1, $\overline{X_e\left(x,\frac{\alpha }{2}\right)}=-\infty$, and $\underset{\_}{X_e\left(x,\frac{\alpha }{2}\right)}=0.1$, the predicted error probability $P\left(\overline{X_e\left(x,\frac{\alpha }{2}\right)}\le X\le \underset{\_}{X_e\left(x,\frac{\alpha }{2}\right)}\right)=0.9418$.

4. Data Processing of the Case Study

The studied case of an IES is derived from the UoM MED test case in Ref. [33], which comprises a 22-node power network, a 31-node heat network, and a 37-node gas network. The system is assumed to be fully observable, which means all loads, flow rate, pressure, and temperature, as well as other state variables on the transmission carriers, can be measured and monitored. The detailed structure of the studied IES case is presented in Figure 15.

In the studied case, there are three coupling devices in total, which involves eight nodes within the whole IES system. The coupling relationships are listed in

Table 2. Types and locations of the coupling devices.

Number	Device Type	Electric	Heat	Gas
1	CHP	1 (electric load)	2 (heat source)	12 (gas load)
2	CHP	9 (electric load)	1 (heat source)	1 (gas load)
3	Gas boiler	-	28 (heat source)	36 (gas load)

.

As shown in Table 2, the CHP unit is a power–heat–gas-coupling device, which acts as a load in the gas network and sources in the electric and heat network. The gas boiler couples with the heat and gas network, which behaves as a load in the gas network and a heat source in the heat network.

It is worth noting that the load data used in the UoM MED test case are not time-series data, and this study uses capacity-matched time-series load data obtained from multiple sources. More specifically, the power load data are from Belgian Grid’s 2020 annual report [34], with a sampling period of 15 min. As the data are on a yearly scale, a time resolution of 1 h was selected for broad detection in the case study, so the power load data were resampled to produce hourly data. The gas load data came from the third-party datasets of specific open-source projects [35]. The thermal load data were acquired from the building thermal simulation data offered by Transys, with a data granularity of 1 h. A total of 8760 data points exist for both electrical and thermal load for an entire year. With regard to the gas data, they were expanded through interpolation so that the size of the dataset could be upscaled to 8760 samples.

The data of the electric, gas, and heat system were adjusted to the same scale with a time resolution of 1 h so that their time-frequency features were also on the same scale. Then the time-frequency features of the electric, gas, and heat could together compose multi-dimensional time-frequency features. The multi-dimensional features were then input into the AE to dig out the hidden features within and between different nodes and subsystems.

The attacked samples were constructed based on the three attack modes described in Section 2.3. The time at which the attack started and the corresponding duration were randomly generated. The samples were split into a test set and a training set in the ratio of 7:3.

Due to improper collection, equipment failure, and other reasons, the raw data may be missing, repeated, abnormal, or redundant. The following preprocessing steps were carried out for data cleaning.

Step 1. Fill in missing values: For a single value that is missing, the method of interpolation is used to fill in the vacancy.

Step 2. Correct abnormal values: For data that are apparently out of the normal operation interval, the values should be modified. The method of interpolation is still adopted in this case.

Step 3. Eliminate redundant values: Data that are not consistent with the time resolution will be eliminated. When multiple values exist for the same time point, the average value will be retained as the only value.

Step 4. Normalize the data: Due to the significant difference in the magnitude of different types of load data, the samples are normalized to eliminate possible impact on the prediction results. The normalization process is implemented according to Equation (22).

$$x^{\prime }=\frac{x-\mu }{{\sigma }^2}$$

(22)

where x is the raw data before normalization, and x’ is the normalized data. μ and σ denote the mean and standard deviation of the raw data, respectively.

The normalized time-series sample dataset under normal state is depicted in Figure 16, illustrating the time-series sample load data at grid node 9, heat network node 20, and gas network node 12.

To simulate the scenario of being attacked, 100 incentive attacks with random start time and 20% attacking magnitude were imposed on the original data. A detailed diagram of the incentive attack process for certain load samples of the electric, heat, and gas network is shown in Figure 17.

5. Results and Analysis

The normalized samples in Section 4 were input to the proposed AE-based time-frequency feature predictor. More specifically, there were eight hidden layers and seven loss layers within the AE model to help extract the hidden time-frequency features. In the training process, the training set was divided into several mini-batches, with each containing 32 samples. The mean squared error (MSE) was selected to represent the loss function with the validation set division ratio configured as 0.1. The adaptive moment estimation (ADAM) optimization algorithm with 300 iterations was used—this algorithm can adaptively adjust the optimization learning rate. Figure 18 indicates the changes in the training loss function of the AE-based predictor.

According to Figure 18, the loss function of the training set converged at about 1.01 after 25 training iterations, and the loss function of the test set tended to converge at 0.99 after 27 training iterations. It should be noted that there was only a small difference between the test set error and the training set error, which indicates that no overfitting existed.

The mean square error between the predicted data and the real data was input to the KDE to obtain the fitted error probability density function, as plotted in Figure 19. The purple area indicates the integral area below the probability density function within the prediction range of (−∞, b]. When the confidence factor is 0.05, the value $\underset{\_}{X_e\left(x,\frac{\alpha }{2}\right)}$ is 0.167.

5.1. Comparison of Anomaly Detection Methods

To verify the higher accuracy of the proposed anomaly detection method, a comparison between different anomaly detection methods was carried out. In the comparison case study, 100 incentive attacks with an attack magnitude of 20% were randomly exerted, and the detection accuracy of each method was compared. Three methods were selected for comparison, including the proposed method based on AE and KDE, the method based on a support vector machine (SVM), and the method based on a multilayer perception classifier (MLPC). Comparison was also made between using time-domain features and using time-frequency features. The time-domain features used include mean, variance, root mean square, peak, local maximum, local minimum, and distribution of local maximum and minimum. The results are presented in Figure 20.

The detection accuracy in Figure 20 is calculated by Equation (23).

$$accuracy={\displaystyle \sum _t\frac{TP(t)+TN(t)}{all(t)}}$$

(23)

where TP (t) denotes the number of samples for which the detector correctly raised the alarm for an attack at moment t, and TN (t) is the number of samples for which the detector correctly showed no attack occurring at moment t. all (t) represents the total number of samples.

It can be observed from Figure 20 that the detection accuracy was better for all three types of detectors (i.e., AEDE, SVM, MLPC) when the time-frequency features were employed, with an average detection accuracy improvement of 0.65%, which indicates that the detection based on time-frequency features was more accurate for time-series data. Furthermore, the detection accuracy based on AE-KDE was higher than that of the conventional SVM method and MLPC method, with 1.54% more accuracy when only the time-domain features were used and 1.70% more accuracy when time-frequency features were used.

5.2. Comparison of Judgment Threshold Determination Method

In general, prediction-based detection methods usually use a certain percentile of the prediction error to determine the judgment threshold of whether an attack is occurring. More specifically, when the prediction error of the test data set is higher than 90% of the prediction error of the training data set, the system is identified as under attack, and vice versa. The proposed AE-KDE-based detector in this paper introduces a new judgement threshold determination method. As illustrated in Section 3.3, when the prediction error exceeds the lower boundary value of the interval under the confidence coefficient of 0.1, it is concluded that an attack exists, and vice versa.

In order to compare and analyze the impact of the two different judgement threshold determination methods on the detection accuracy, 200 attacks in three different attack modes (i.e., incentive attack, ramp attack, and delayed attack) were exerted randomly. The comparison results are shown in Figure 21.

As shown in Figure 21, for all three types of attack modes, the judgement threshold based on KDE always had higher detection accuracy than simply using the 90% percentile. The average detector accuracy improvement was 1.23%.

5.3. Comparison of Prediction Accuracy for Different Attack Modes

To compare the detection accuracy of the proposed anomaly detection method for different attack modes, a total of 200 attacks were exerted in three different attack modes of incentive attack, slope attack, and delay attack. The attack magnitudes of the incentive attack and slope ranged from −30% to 30% (the magnitude of the delay attack could not be changed). The comparison results are shown in Figure 22.

It can be observed from Figure 22 that differences existed for positive and negative attacks when the detector dealt with incentive attacks and slope attacks. For the incentive attack, the detection accuracy for the positive attack was significantly better than the negative attack, with an average difference of 3.19%. With respect to the slope attack, the average difference between the positive and negative detection accuracies was 1.05%. It is worth noting that the detection accuracy increased as the attack amplitude grew for the slope attack, whereas the detection accuracy did not show an obvious trend for the incentive attack. In addition, as the delay attack was not affected by the attack amplitude, the detection accuracy did not vary and stayed at 87.2%.

6. Conclusions

FDIA poses a serious threat to the security, stability, and economy of a cyber-physical integrated energy system. In order to effectively detect FDIAs, this paper proposed an anomaly detection method for time-series data in a cyber-physical integrated energy system on the basis of time-frequency feature prediction. The following conclusions can be drawn.

• Three time-frequency transform methods, including DWT, EMD, and EWT, were adopted in this paper to extract and construct the time-frequency features of IES time-series data. It was verified that all three time-frequency transform methods have their own advantages and can complement each other in terms of determining whether and when an attack is occurring. The constructed time-frequency features are adequate and diverse enough to support subsequent attack detection.
• An anomaly detection method based on AE and KDE was proposed. Firstly, an AE-based time-frequency feature predictor was constructed. AE was adopted to capture the hidden features and non-linear structure of the time-frequency features and regression prediction was applied on the top layer of the features to predict the data in the next time period. Then, a KDE-based prediction interval estimation method was proposed. Considering regression uncertainty, the prediction interval was estimated based on the prediction error probability density function obtained by KDE. The lower boundary value of the estimated interval was selected as the attack judgement threshold to determine whether an attack was occurring. The results of case study show that the proposed method is superior in improving the anomaly detection accuracy, which can effectively help resist network attacks and ensure the safe operation of an IES.

The proposed method Innovatively applies time-frequency feature extraction and prediction methods to the anomaly detection of a cyber-physical integrated energy system, which effectively improves the attack defense ability of an IES. However, with the increase utilization of renewable energy, the randomness and volatility of renewable energy also brings new challenges to the anomaly detection in an IES, which still deserves further exploration in future research.