Aerodynamic Performance Analysis of Adaptive Drag-Lift Hybrid Type Vertical Axis Wind Turbine
Abstract
:1. Introduction
2. Structural Design and Experimental Models
2.1. Structural Design
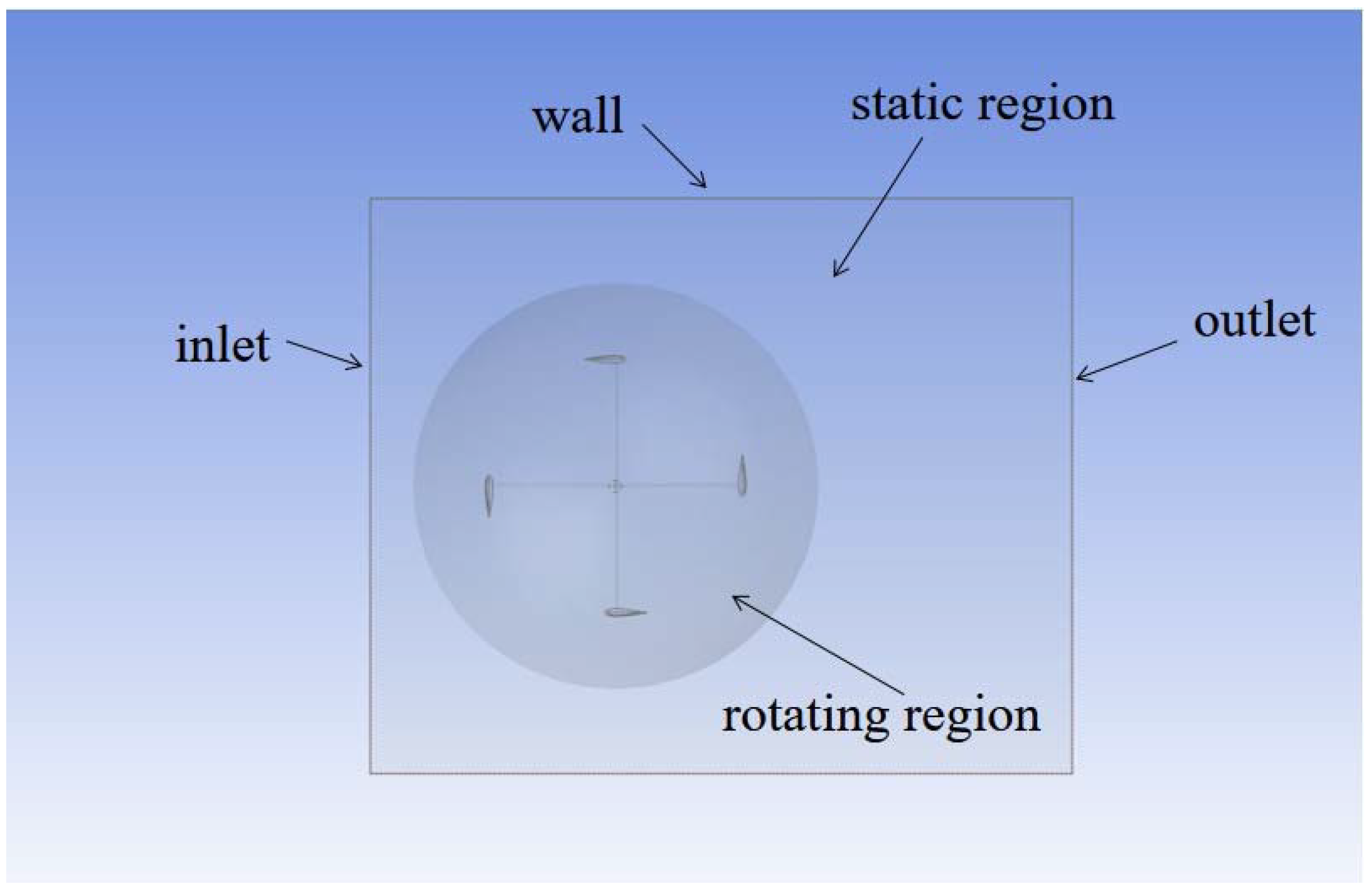
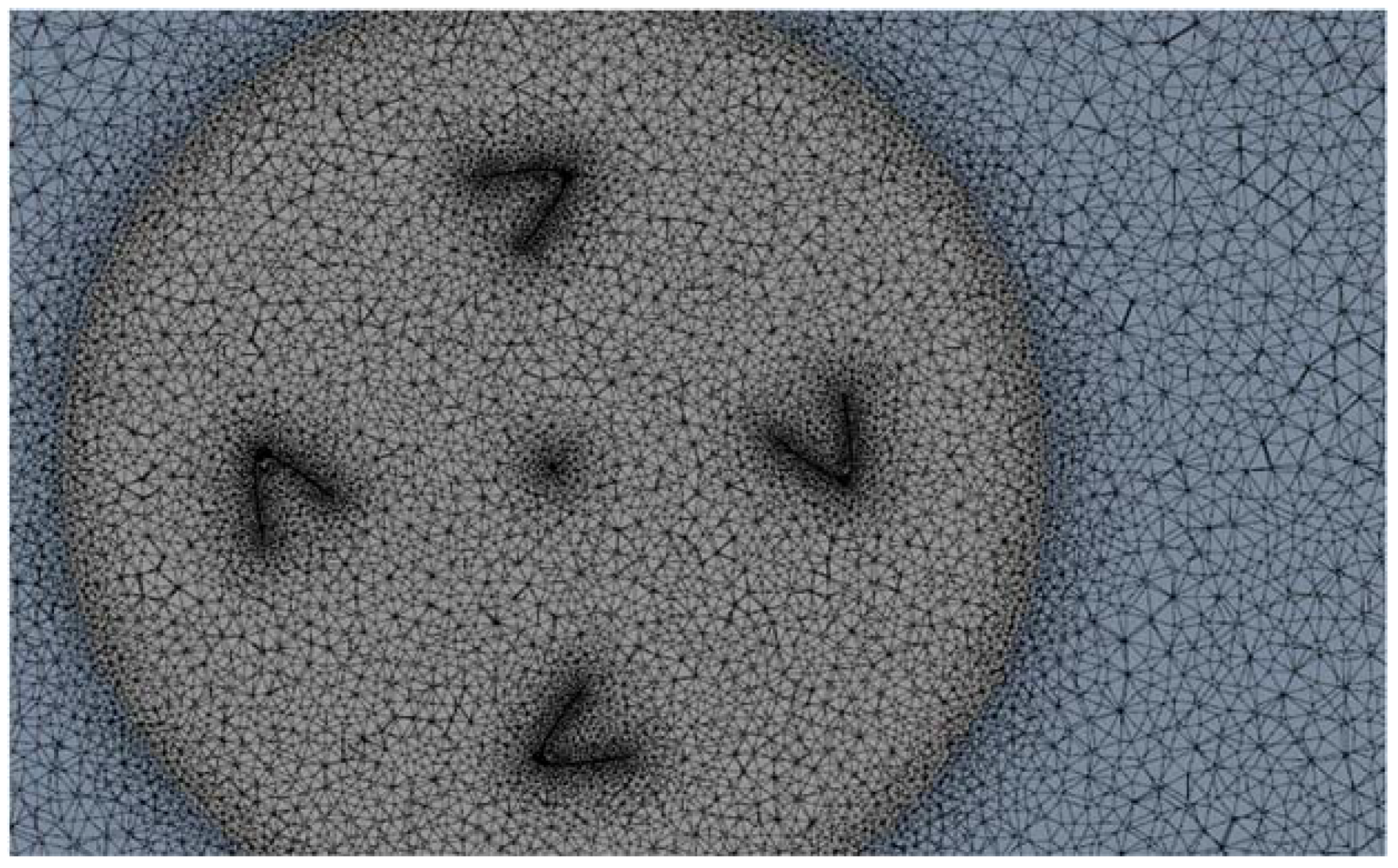
2.2. CFD Model
2.3. Data Processing
3. Experimental Results and Discussion
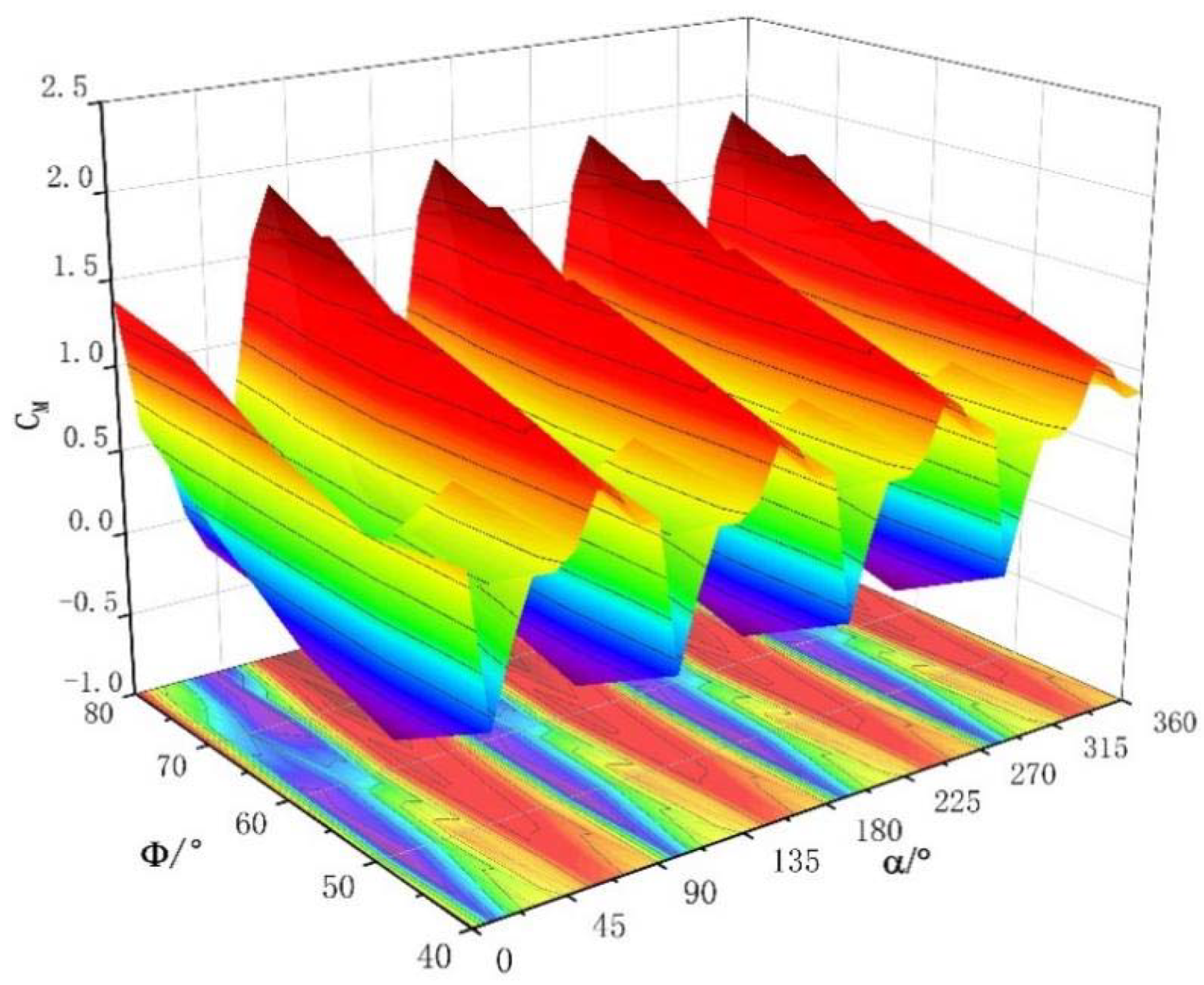
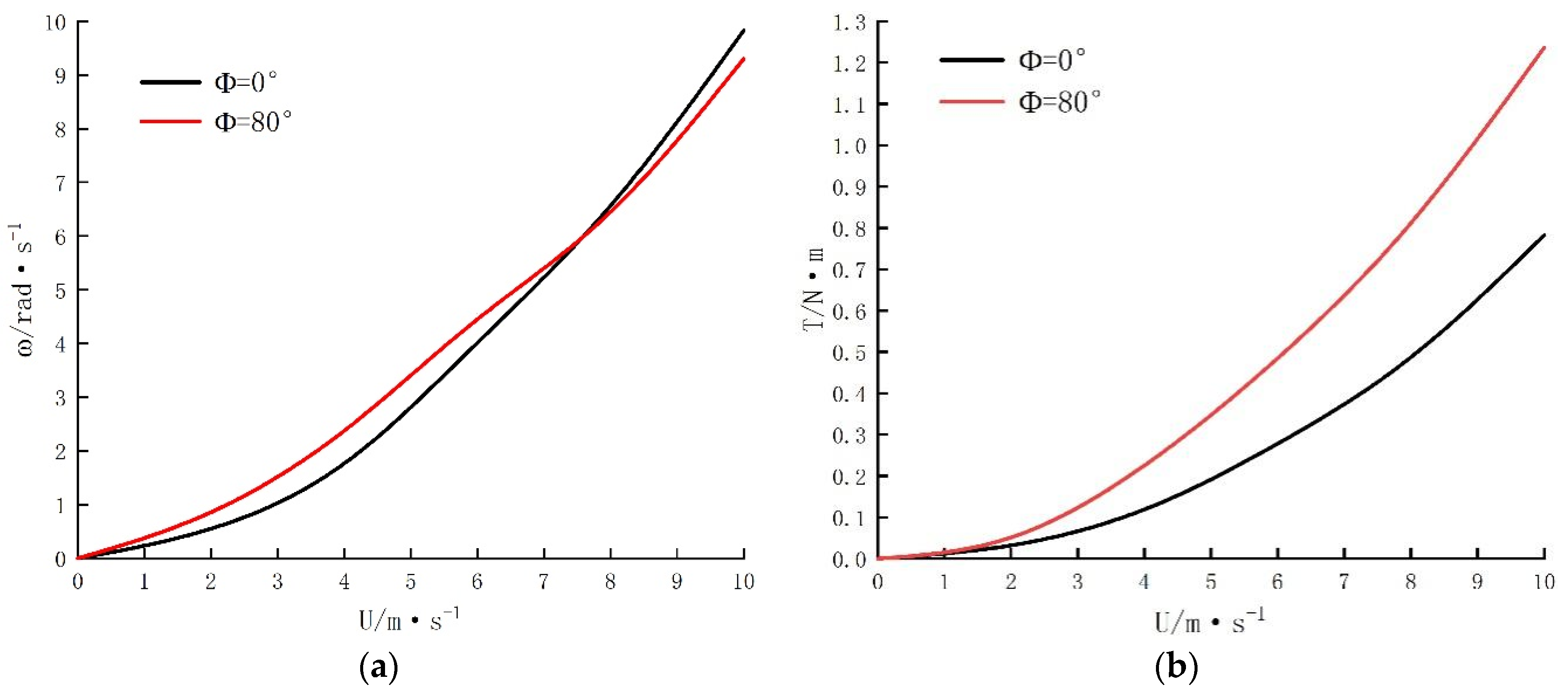
3.1. Analysis of Influence of Blade Opening Angle on Wind Turbine
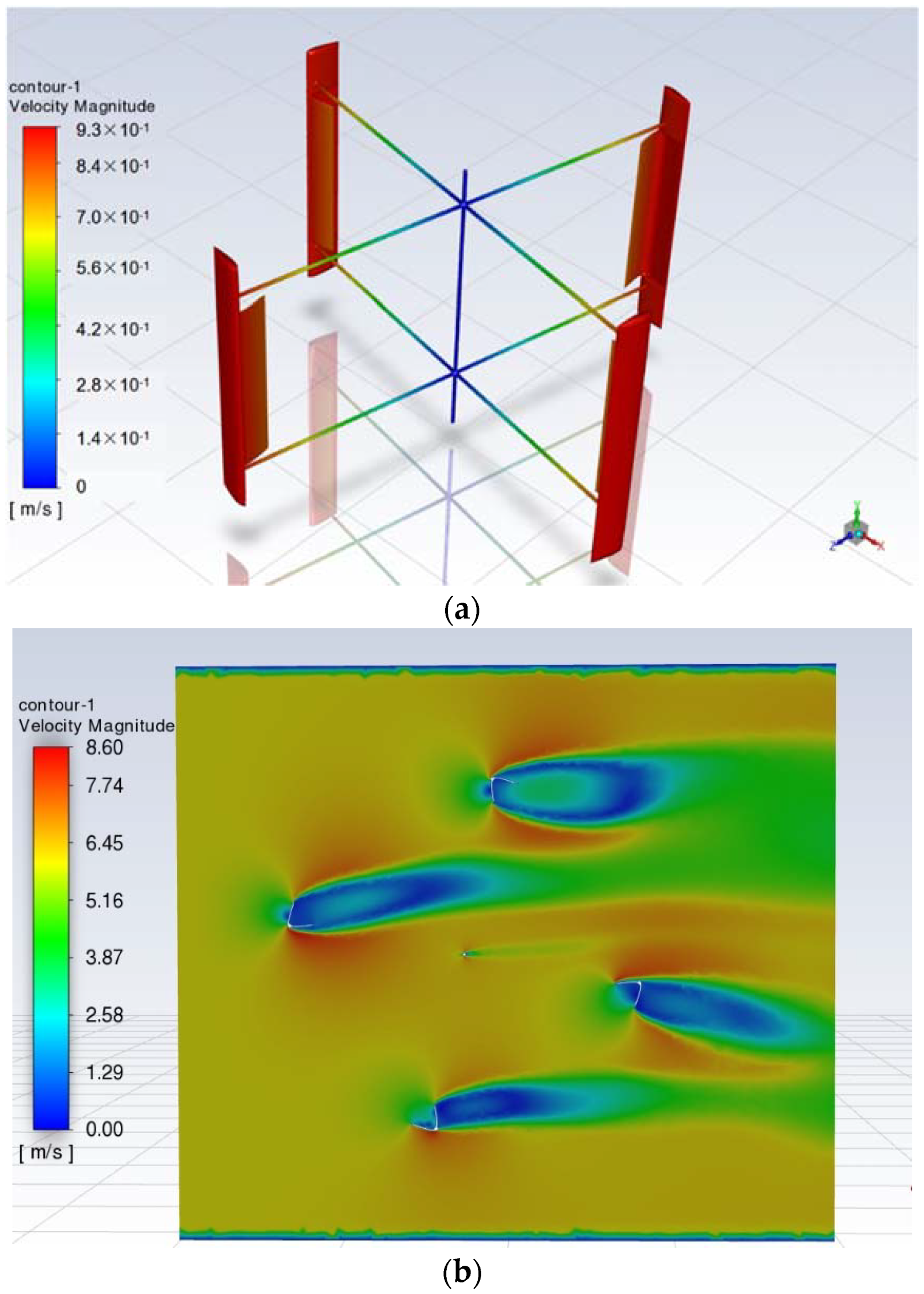
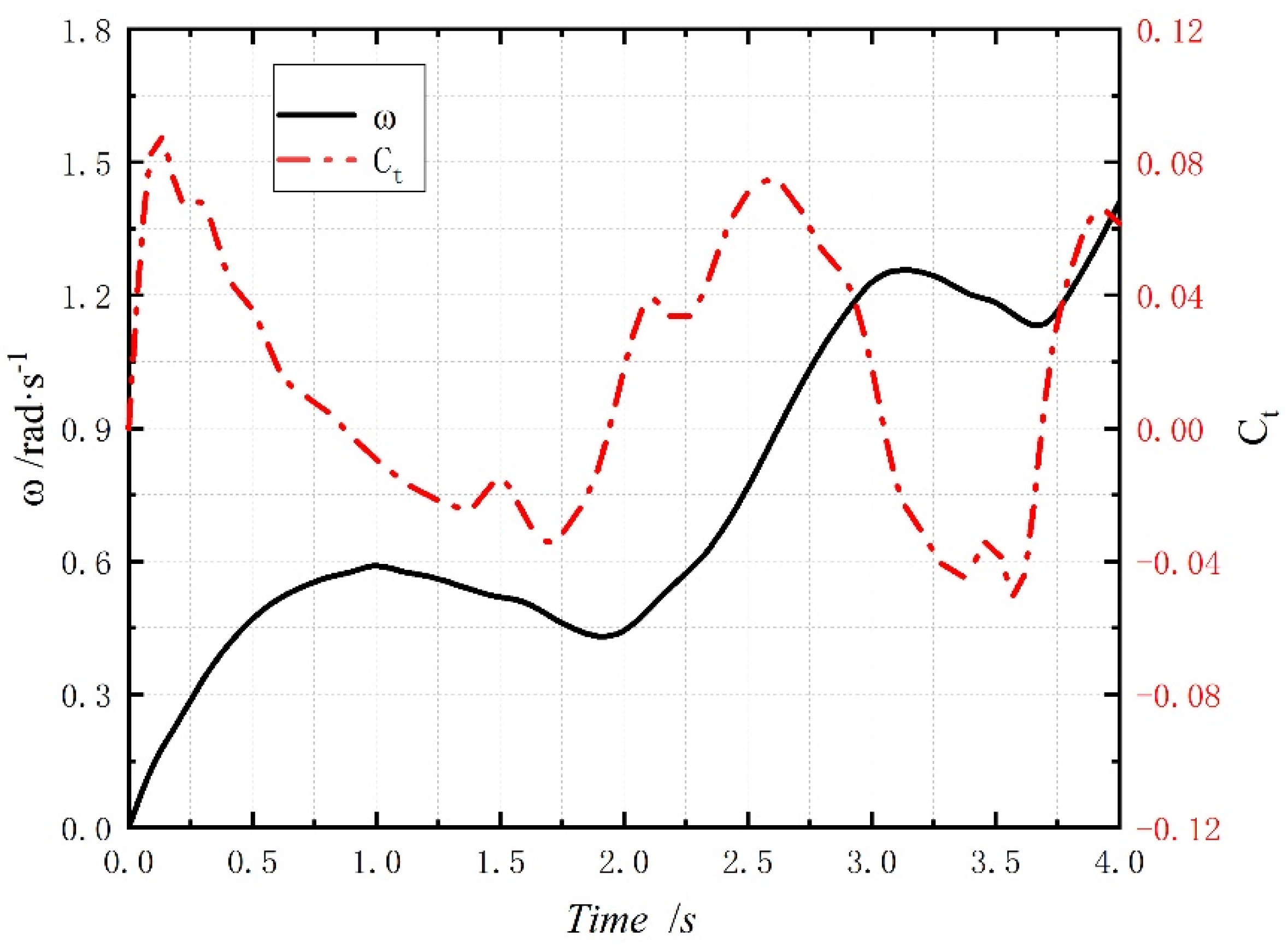
3.2. Impact Analysis of Wind Speed on Lift Drag Combined Wind Turbine
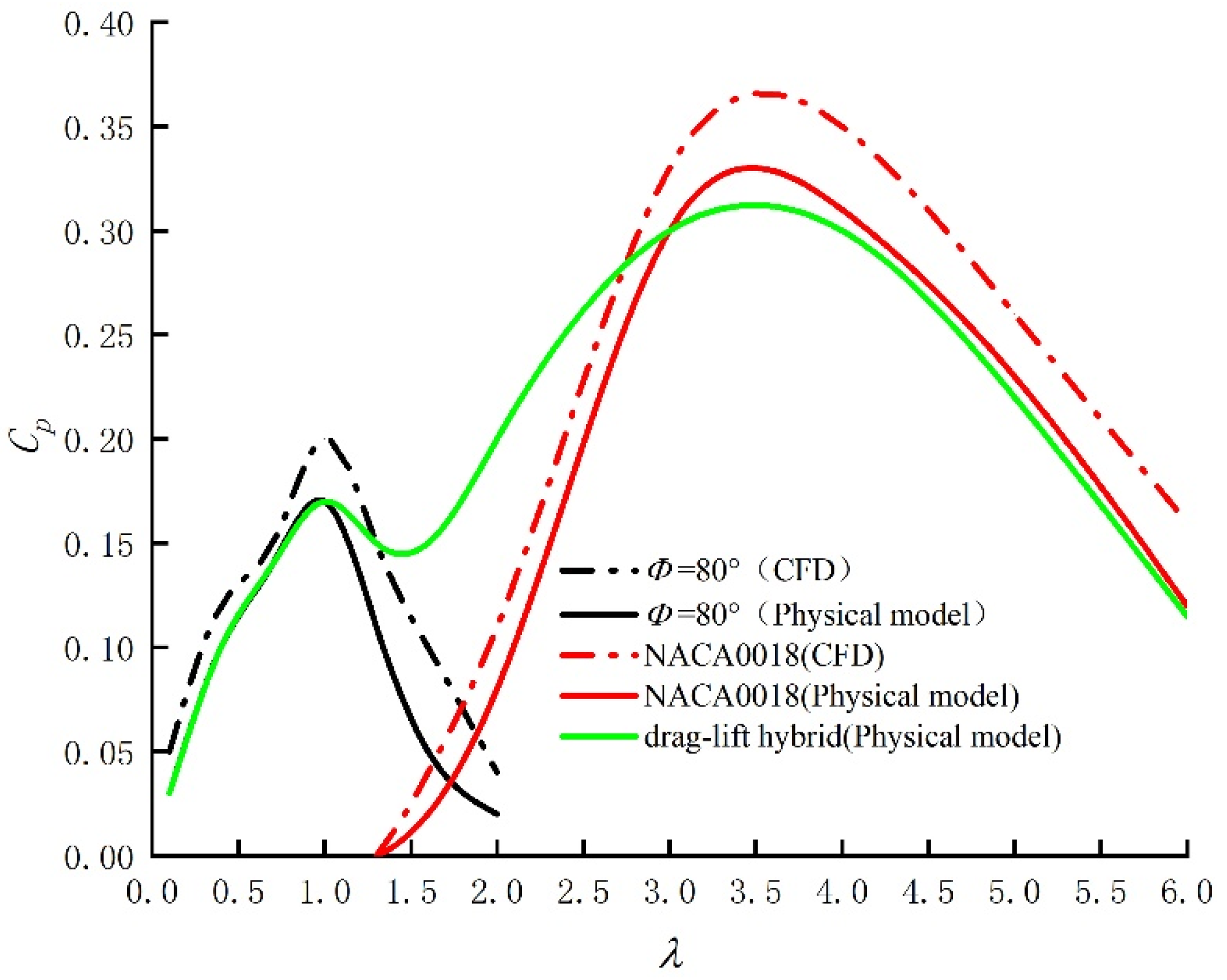
3.3. Effects of Different Tip Speed Ratios on the Performance of Wind Turbines with Drag Configuration
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karthikeyan, N.; Kalidasa Murugavel, K.; Arun Kumar, S.; Rajakumar, S. Review of aerodynamic developments on small horizontal axis wind turbine blade. Renew. Sustain. Energy Rev. 2015, 42, 801–822. [Google Scholar] [CrossRef]
- Almekhlafi, M.A.A.; Al-Wesabi, F.N.; Eltahir, M.M.; Mustafa Hilal, A.; El-Kustaban, A.M.; Motwakel, A.; Yaseen, I.; Ahmed Hamza, M. Analysis and Assessment of Wind Energy Potential of Almukalla in Yemen. Comput. Mater. Contin. 2022, 72, 3113–3129. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, H.; Shen, H. Self-starting aerodynamics analysis of vertical axis wind turbine. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef] [Green Version]
- Fang, F. Study on Aerodynamic Characteristics of Combined Vertical Axis Wind Turbine with Lift Drag Composite Starting Structure; Northeast Agricultural University: Harbin, China, 2018. [Google Scholar]
- Liu, Q.; Miao, W.; Ye, Q.; Li, C. Performance assessment of an innovative Gurney flap for straight-bladed vertical axis wind turbine. Renew. Energy 2022, 185, 1124–1138. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, S.; Qu, C.; Feng, F.; Kotaro, T. Effects of Offset Blade on Aerodynamic Characteristics of Small-Scale Vertical Axis Wind Turbine. J. Therm. Sci. 2019, 28, 326–339. [Google Scholar] [CrossRef]
- Wu, S.; Bao, D.; Liu, X. Structural design and performance analysis of a new variable pitch wind turbine. Res. Energy Resour. 2022, 40, 350–355. [Google Scholar]
- Aboujaoude, H.; Beaumont, F.; Murer, S.; Polidori, G.; Bogard, F. Aerodynamic performance enhancement of a Savonius wind turbine using an axisymmetric deflector. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104882. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, F.; Dreyer, M.; Farhat, M. Effect of trailing edge shape on hydrodynamic damping for a hydrofoil. J. Fluids Struct. 2014, 51, 189–198. [Google Scholar] [CrossRef] [Green Version]
- Ge, M.-W.; Ke, W.-M.; Chen, H.-X. Pitch control strategy before the rated power for variable speed wind turbines at high altitudes. J. Hydrodyn. 2018, 31, 379–388. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, Y.; Zhang, A.; Hu, C.; Liu, S.; Li, Z. Hydrodynamic performance of vertical axis hydrokinetic turbine based on Taguchi method. Renew. Energy 2022, 186, 573–584. [Google Scholar] [CrossRef]
- Celik, Y.; Ingham, D.; Ma, L.; Pourkashanian, M. Design and aerodynamic performance analyses of the self-starting H-type VAWT having J-shaped aerofoils considering various design parameters using CFD. Energy 2022, 251, 123881. [Google Scholar] [CrossRef]
- Yao, X.; Han, S.; Dewancker, B. Wind Environment Simulation Accuracy in Traditional Villages with Complex Layouts Based on CFD. Int. J. Environ. Res. Public Health 2021, 18, 8644. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, C.; Pan, C.; Opare, W. Numerical investigation of performance and flow patterns of a modified Savonius hydraulic rotor. IOP Conf. Ser.: Earth Environ. Sci. 2019, 240, 042009. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, X.; Dong, X.; Zhu, B.; Huang, D.; Zheng, Z. Numerical investigation on aerodynamic performance of a novel vertical axis wind turbine with adaptive blades. Energy Convers. Manag. 2016, 108, 275–286. [Google Scholar] [CrossRef]
- Zeng, Y.-S.; Yao, Z.-F.; Huang, B.; Wang, F.-J.; Wu, Q.; Xiao, R.-F.; Wang, G.-Y. Numerical studies of the hydrodynamic damping of a vibrating hydrofoil in torsional mode. J. Hydrodyn. 2021, 33, 347–360. [Google Scholar] [CrossRef]
- Li, Q.A.; Maeda, T.; Kamada, Y.; Murata, J.; Kawabata, T.; Furukawa, K. Analysis of aerodynamic load on straight-bladed vertical axis wind turbine. J. Therm. Sci. 2014, 23, 315–324. [Google Scholar] [CrossRef]
- Doerffer, P.; Doerffer, K.; Ochrymiuk, T.; Telega, J. Variable Size Twin-Rotor Wind Turbine. Energies 2019, 12, 2543. [Google Scholar] [CrossRef] [Green Version]
- Saad, A.S.; Elwardany, A.; El-Sharkawy, I.I.; Ookawara, S.; Ahmed, M. Performance evaluation of a novel vertical axis wind turbine using twisted blades in multi-stage Savonius rotors. Energy Convers. Manag. 2021, 235, 114013. [Google Scholar] [CrossRef]
- Maleki Dastjerdi, S.; Gharali, K.; Al-Haq, A.; Nathwani, J. Application of Simultaneous Symmetric and Cambered Airfoils in Novel Vertical Axis Wind Turbines. Appl. Sci. 2021, 11, 8011. [Google Scholar] [CrossRef]
- Ashok Gandhi, R.; Ravinthiran, A.; Palanikumar, K. Design and development of sail type wind turbine with solar panel. Mater. Today Proc. 2021, 46, 3989–3992. [Google Scholar] [CrossRef]
- Durkacz, J.; Islam, S.; Chan, R.; Fong, E.; Gillies, H.; Karnik, A.; Mullan, T. CFD modelling and prototype testing of a Vertical Axis Wind Turbines in planetary cluster formation. Energy Rep. 2021, 7, 119–126. [Google Scholar] [CrossRef]
- Müller, S.; Muhawenimana, V.; Wilson, C.A.M.E.; Ouro, P. Experimental investigation of the wake characteristics behind twin vertical axis turbines. Energy Convers. Manag. 2021, 247, 114768. [Google Scholar] [CrossRef]
- Sakamoto, L.; Fukui, T.; Morinishi, K. Blade Dimension Optimization and Performance Analysis of the 2-D Ugrinsky Wind Turbine. Energies 2022, 15, 2478. [Google Scholar] [CrossRef]
- Peng, H.Y.; Zhong, B.W.; Hu, G.; Liu, H.J. Optimization analysis of straight-bladed vertical axis wind turbines in turbulent environments by wind tunnel testing. Energy Convers. Manag. 2022, 257, 115411. [Google Scholar] [CrossRef]
- Sun, X.; Zhu, J.; Li, Z.; Sun, G. Rotation improvement of vertical axis wind turbine by offsetting pitching angles and changing blade numbers. Energy 2021, 215, 119177. [Google Scholar] [CrossRef]
- Divakaran, U.; Ramesh, A.; Mohammad, A.; Velamati, R.K. Effect of Helix Angle on the Performance of Helical Vertical Axis Wind Turbine. Energies 2021, 14, 393. [Google Scholar] [CrossRef]
- Eltayesh, A.; Castellani, F.; Burlando, M.; Bassily Hanna, M.; Huzayyin, A.S.; El-Batsh, H.M.; Becchetti, M. Experimental and numerical investigation of the effect of blade number on the aerodynamic performance of a small-scale horizontal axis wind turbine. Alex. Eng. J. 2021, 60, 3931–3944. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, C.; Li, L. Hydrodynamics and wake flow analysis of a Π-type vertical axis twin-rotor tidal current turbine in surge motion. Ocean Eng. 2021, 224, 108625. [Google Scholar] [CrossRef]
- Rosado-Hau, N.; Ma, L.; Ingham, D.; Pourkashanian, M. A procedure to predict the power coefficient of vertical axis wind turbines at low tip speed ratios. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; pp. 1–13. [Google Scholar] [CrossRef]
- Rosado Hau, N.; Ma, L.; Ingham, D.; Pourkashanian, M. A critical analysis of the stall onset in vertical axis wind turbines. J. Wind Eng. Ind. Aerodyn. 2020, 204, 104264. [Google Scholar] [CrossRef]






| Parameter Name/unit | Number | Parameter Name/Unit | Number |
|---|---|---|---|
| Blade height/mm | 730 | Blade offset angle/° | 0 |
| Blade chord length/mm | 100 | Installation angle of outer blade/° | 90 |
| Number of blades | 4 | Sliding block moving range S/m | 0.0648 |
| Blade sweep area A/m2 | 0.964 | Slider mass/kg | 0.3 |
| Radius R/mm | 660 | Blade opening angle range Φ/° | 0–80 |
| Scheme | Number of Grids | Node Number | CM |
|---|---|---|---|
| 1 | 3,225,714 | 722,858 | 1.4561 |
| 2 | 5,341,874 | 1,238,897 | 1.4302 |
| 3 | 7,512,853 | 1,598,226 | 1.3822 |
| 4 | 9,371,458 | 2,368,939 | 1.3835 |
| 5 | 10,252,393 | 2,592,826 | 1.3826 |
| Parameter Name/unit | Number | Parameter Name/unit | Number |
|---|---|---|---|
| Generator model | NE-100WS | Rated voltage/V | 12 |
| Starting torque/N·m | >0.15 | Mass/kg | 3 |
| Rated power/W | 100 | Rated speed/rpm | 750 |
| Working temperature rise/°C | <70 | Insulation class | H |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Lian, S.; Yan, H. Aerodynamic Performance Analysis of Adaptive Drag-Lift Hybrid Type Vertical Axis Wind Turbine. Energies 2022, 15, 5600. https://doi.org/10.3390/en15155600
Gao Q, Lian S, Yan H. Aerodynamic Performance Analysis of Adaptive Drag-Lift Hybrid Type Vertical Axis Wind Turbine. Energies. 2022; 15(15):5600. https://doi.org/10.3390/en15155600
Chicago/Turabian StyleGao, Qiang, Shuai Lian, and Hongwei Yan. 2022. "Aerodynamic Performance Analysis of Adaptive Drag-Lift Hybrid Type Vertical Axis Wind Turbine" Energies 15, no. 15: 5600. https://doi.org/10.3390/en15155600
APA StyleGao, Q., Lian, S., & Yan, H. (2022). Aerodynamic Performance Analysis of Adaptive Drag-Lift Hybrid Type Vertical Axis Wind Turbine. Energies, 15(15), 5600. https://doi.org/10.3390/en15155600





