Effect of In-Situ Stress on Hydraulic Fracturing of Tight Sandstone Based on Discrete Element Method
Abstract
1. Introduction
2. Sandstone Rock Mechanical Parameter Testing
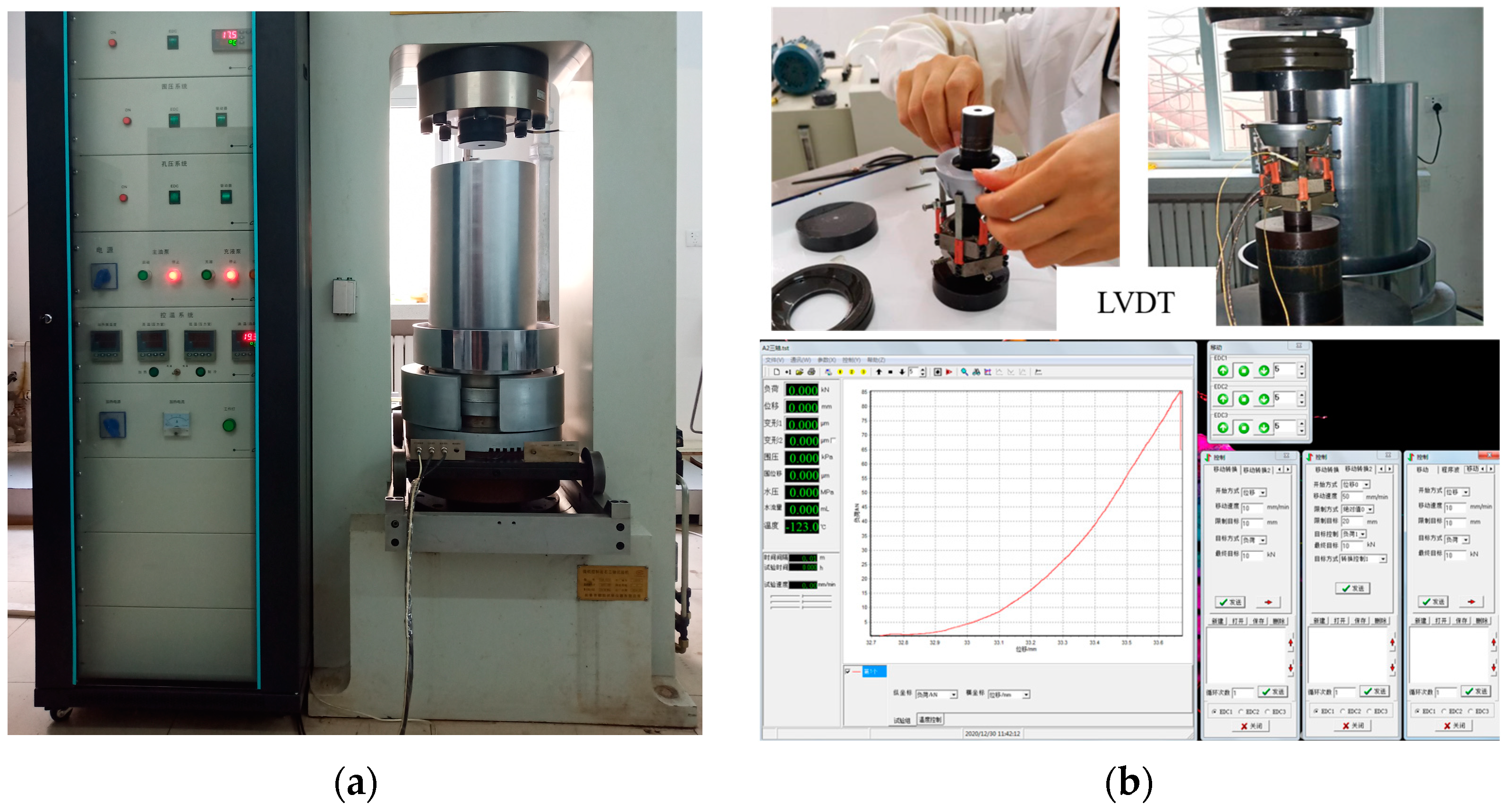
2.1. Experiment System
2.2. Experimental Scheme and Test Results
3. Numerical Analysis of Hydraulic Fracturing Based on Discrete Element Method
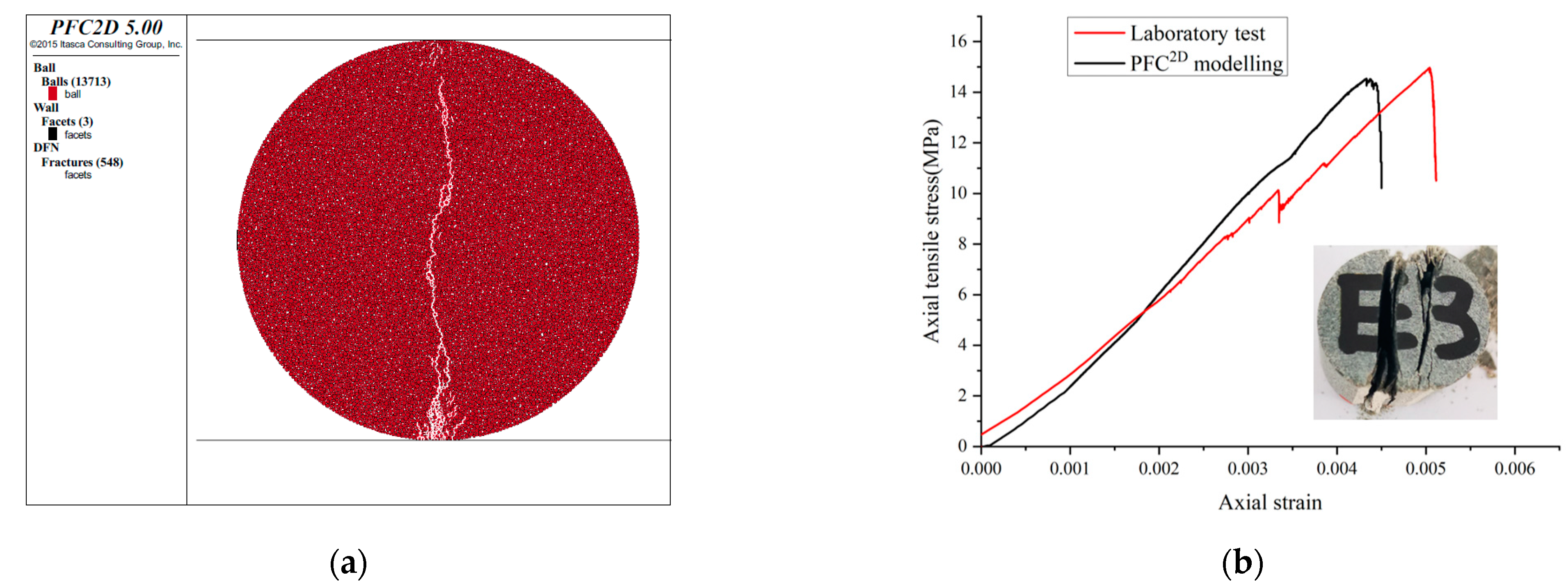
3.1. Microparameter Calibration
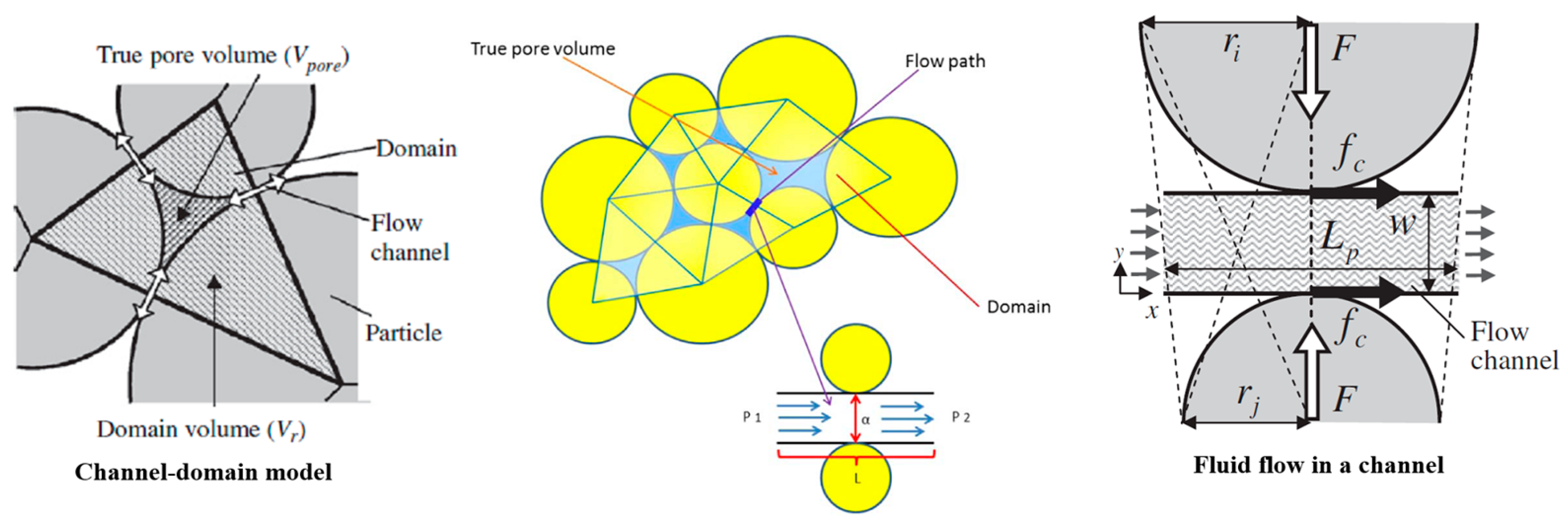
3.2. Fluid-Mechanical Coupling Theory of PFC2D
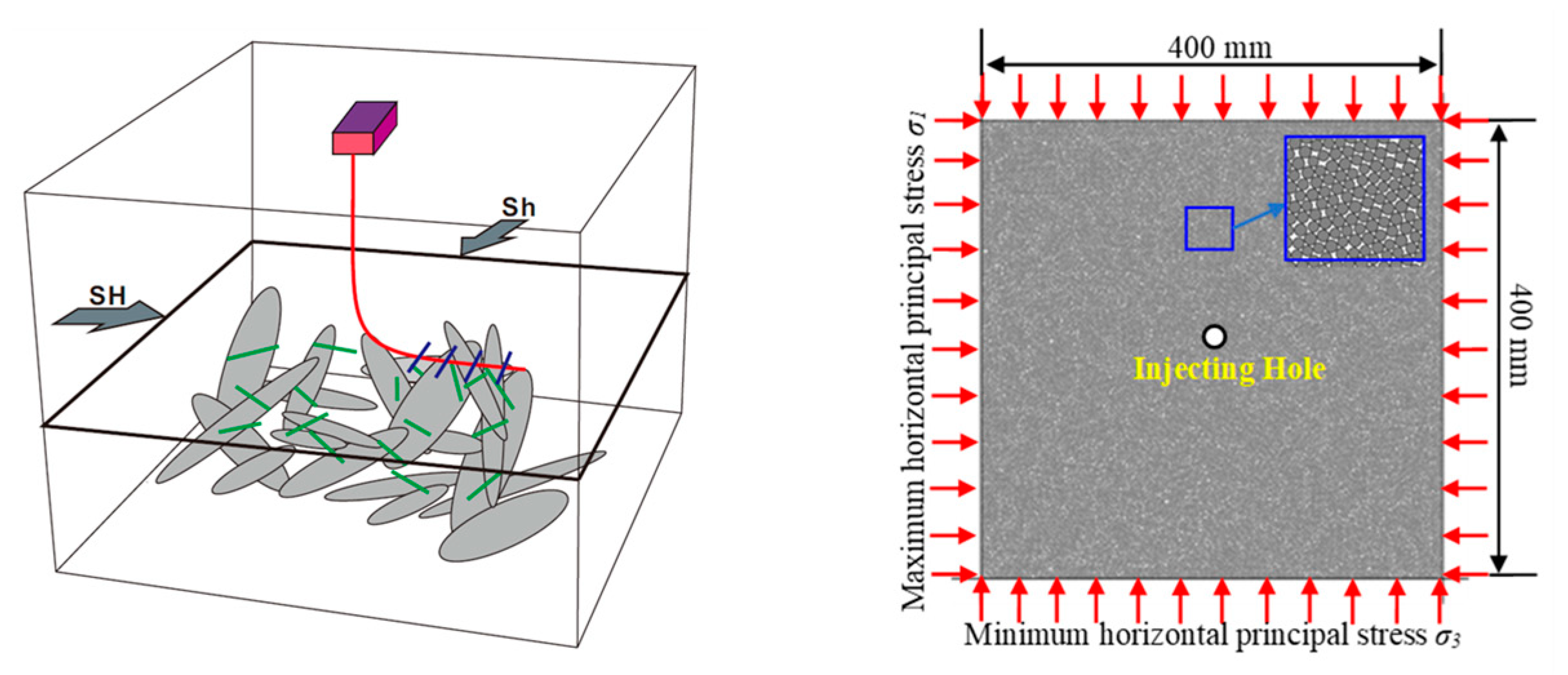
3.3. Sandstone Models for Hydraulic Fracturing
4. Influence of In-Situ Stress Difference Coefficient on Hydraulic Fracturing Effect
5. Discussion
6. Conclusions
- (1)
- The influence of in-situ stress on the direction, shape and quantity of fracture propagation is quite crucial, and the fractures generated by hydraulic fracturing are mainly tension fractures, accounting for more than 90% of total longitudinal fractures.
- (2)
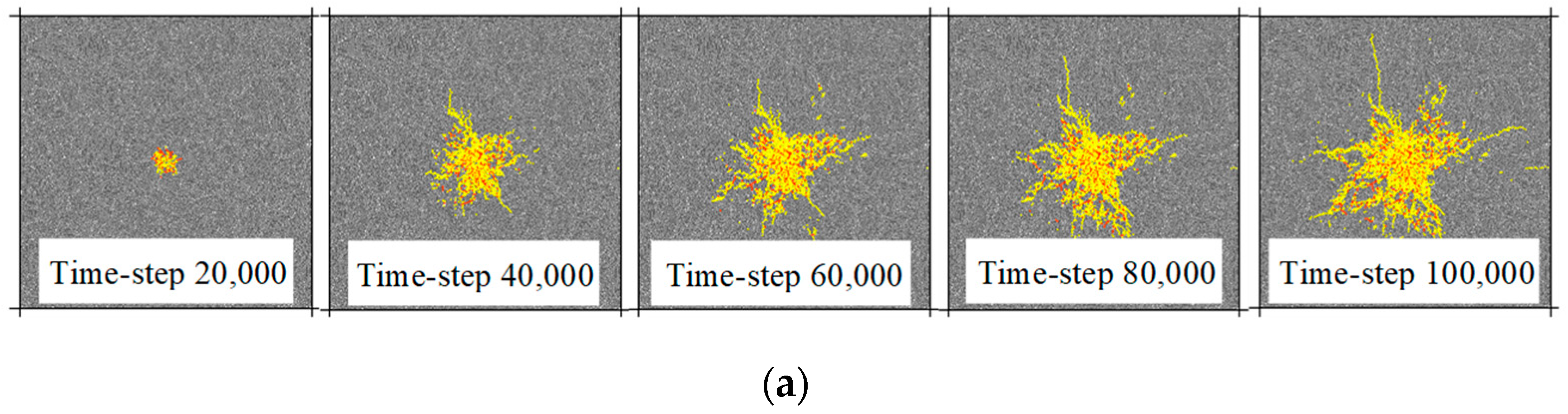
- When the in-situ stress difference coefficient is small, the fractures gradually extend and expand outwards after the initiation of fracturing around the wellbore. The largest number of fractures emerge in the initial stage of pumping the fracturing fluid, with a higher degree of fracture concentration. As the fracturing fluid is continuously pumped into the wellbore, the inefficiency of the hydraulic fracturing can be seen when generating the fractures, and the fractures expand from disorder to the extension of several main fractures.
- (3)
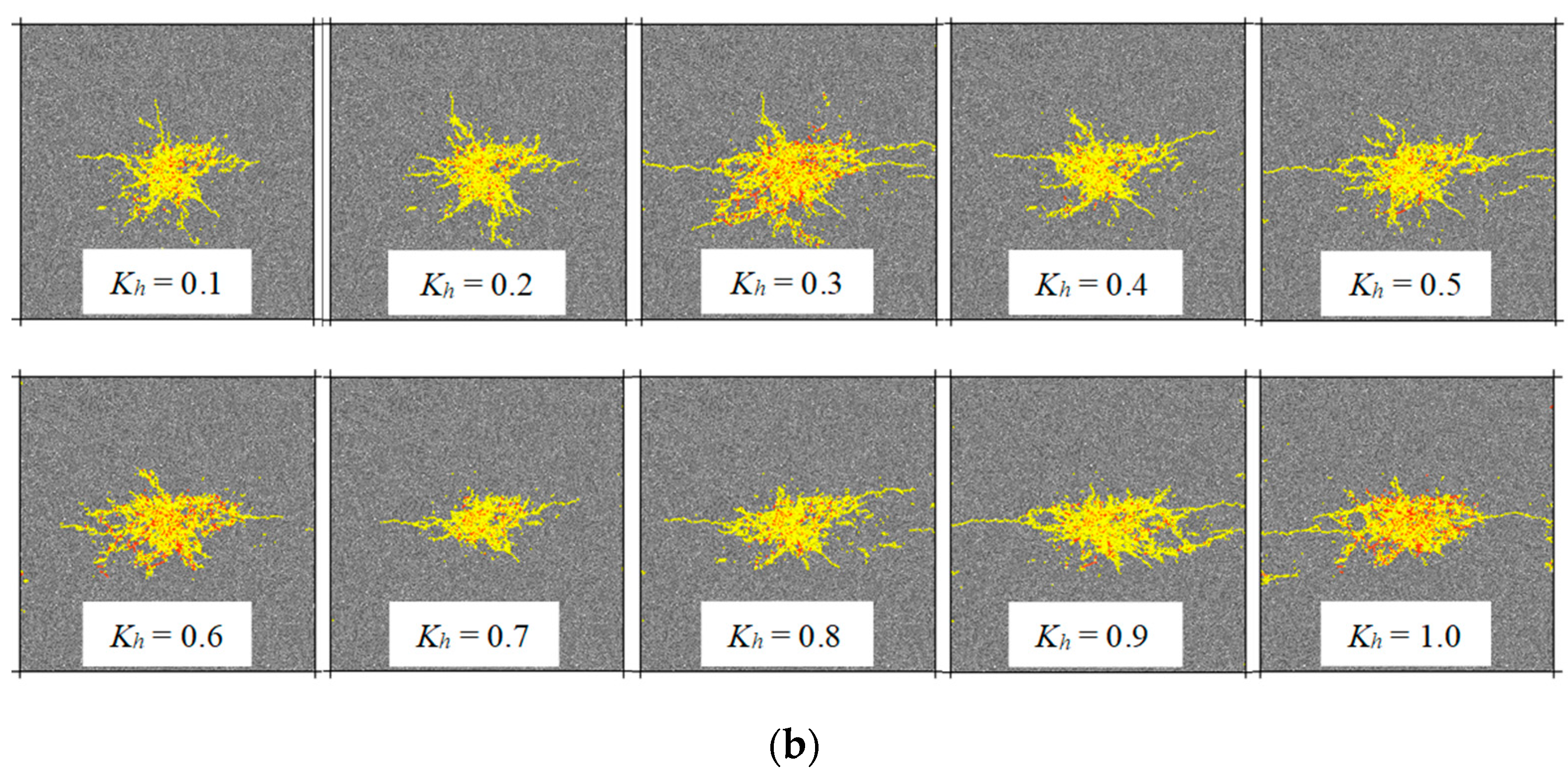
- When the horizontal in-situ stress difference coefficient Kh is between 0 and 0.2, the fractures formed by hydraulic fracturing randomly expand around the wellbore. When Kh is between 0.3 and 0.6, the fractures form by fracturing gradually and expanding along the main crack in the direction of the maximum principal stress. When the stress difference coefficient Kh is above 0.6, the development of hydraulic fractures is mainly controlled by the in-situ stress; the fractures expand along the minimum horizontal principal stress in the vertical direction, leading to a relatively singular fracture shape.
- (4)
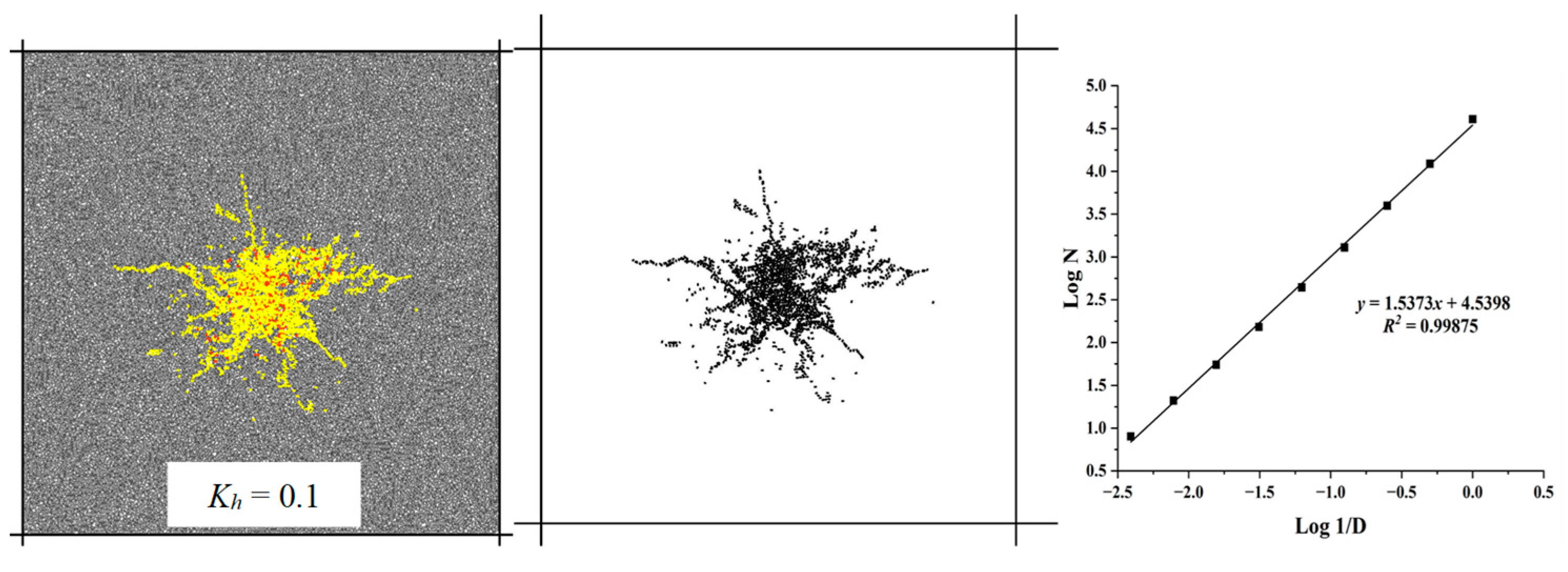
- As for the continental tight sandstone with good homogeneity, two aspects of construction cost and fracturing effect should be considered. When the local stress difference coefficient is 0.3, the maximum number of fractures generated by fracturing is 3121, and the main fractures along the direction of the maximum principal stress are generated, in relation to the development of secondary fractures. The fractal dimension D value of the fracture network complexity is 1.60 and the fracture pressure is 43.73 MPa; in this case, the fracturing shows the most effective result. The lower fracture pressure is more accessible for fracturing in large-scale volume to achieve economical and effective development.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zou, C.; Zhu, R.; Wu, S.; Yang, Z.; Tao, S.; Yuan, X.; Hou, L.; Yang, H.; Xu, C.; Li, D.; et al. Types, characteristics, genesis and prospects of conventional and unconventional hydrocarbon accumulations: Taking tight oil and tight gas in China as an instance. Acta Pet. Sin. 2012, 33, 173–187. [Google Scholar] [CrossRef]
- Holditch, S.A. Tight gas sands. J. Pet. Technol. 2006, 58, 86–93. [Google Scholar] [CrossRef]
- Matthews, H.L.; Schein, G.W.; Malone, M.R. Stimulation of gas shales: They’re all the same-right. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, College Station, TX, USA, 29–31 January 2007. [Google Scholar]
- Chong, K.K.; Grieser, B.; Jaripatke, O.; Passman, A. A completions roadmap to shale-play development: A review of successful approaches toward shale-play stimulation in the last two decades. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–20 June 2010. [Google Scholar]
- Mutalik, P.N.; Gibson, R.W. Case history of sequential and simultaneous fracturing of the Barnett Shale in parker county. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- White, J.; Read, R. The shale shaker. Oil Gas Investor 2007, 47, 2–9. [Google Scholar]
- Vassilellis, G.D.; LI, C.; Seager, R.; Moos, D. Investigating the expected long-term production performance of shale reservoirs. In Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010. [Google Scholar]
- Maxwell, S.C.; Urbancic, T.I.; Steinsberger, N.; Zinno, R. Microseismic imaging of hydraulic fracture complexity in the Barnett Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–1 October 2002. [Google Scholar]
- Kennedy, R.L.; Knecht, W.N.; Georgi, D.T. Comparisons and contrasts of shale gas and tight gas developments, North American experience and trends. In Proceedings of the SPE Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 8–11 April 2012. [Google Scholar]
- Zhao, Z.; Wang, H.; Cui, Z.; Zhao, F.; Tang, T.; Han, W.; Wang, X. Experimental study on Mode-I fracture toughness using Chevron Straight-notched Semi-circular Bend (CSNSCB) method. Theor. Appl. Fract. Mech. 2021, 116, 103093. [Google Scholar] [CrossRef]
- Perkins, T.K.; Kern, L.R. Widths of hydraulic fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Nordgren, R.P. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Khristianovic, S.; Zheltov, Y. Formation of vertical fractures by means of highly viscous liquid. In Proceedings of the 4th World Petroleum Congress, Rome, Italy, 6–15 June 1955; pp. 579–586. [Google Scholar]
- Geertsma, J.; Klerk, F.D. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 1969, 21, 1571–1581. [Google Scholar] [CrossRef]
- Ito, T.; Nagano, Y. Development of experimental apparatus for real-time observation of hydraulic fracture in unconsolidated sands by X-ray CT method. In Proceedings of the 49th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015; pp. 1595–1603. [Google Scholar]
- Chitrala, Y.; Moreno, C.; Sondergeld, C.; Rai, C. An experimental investigation into hydraulic fracture propagation under different applied stresses in tight sands using acoustic emissions. J. Pet. Sci. Eng. 2013, 108, 151–161. [Google Scholar] [CrossRef]
- He, J.; Lin, C.; Li, X.; Zhang, Y.; Chen, Y. Initiation, propagation, closure and morphology of hydraulic fractures in sandstone cores. Fuel 2017, 208, 65–70. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, F.; Huang, Z.; Yao, Y.; Yuan, G. Experimental study of mode-I fracture toughness for layered shale based on two ISRM-suggested methods. Rock Mech. Rock Eng. 2017, 50, 1933–1939. [Google Scholar] [CrossRef]
- Zhang, F.; Damjanac, B.; Maxwell, S. Investigating hydraulic fracturing complexity in naturally fractured rock masses using fully coupled multiscale numerical modeling. Rock Mech. Rock Eng. 2019, 52, 5137–5160. [Google Scholar] [CrossRef]
- Roche, V.; van Der Baan, M.; Preisig, G. A study of 3D modeling of hydraulic fracturing and stress perturbations during fluid injection. J. Pet. Sci. Eng. 2018, 170, 829–843. [Google Scholar] [CrossRef]
- Savitski, A.A.; Lin, M.; Riahi, A.; Damjanac, B.; Nagel, N.B. Explicit modeling of hydraulic fracture propagation in fractured shales. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2013. [Google Scholar]
- Damjanac, B.; Cundall, P. Application of distinct element methods to simulation of hydraulic fracturing in naturally fractured reservoirs. Comput. Geotech. 2016, 71, 283–294. [Google Scholar] [CrossRef]
- Hamidi, F.; Mortazavi, A. A new three dimensional approach to numerically model hydraulic fracturing process. J. Pet. Sci. Eng. 2014, 124, 451–467. [Google Scholar] [CrossRef]
- Bhide, R.J.; Zhao, N.; McLennan, J.D.; Deo, M.D. Modeling hydraulic fracture propagation in low permeability reservoirs. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012. [Google Scholar]
- McLennan, J.D.; Tran, D.T.; Zhao, N.; Thakur, S.V.; Deo, M.D.; Gil, I.; Damjanac, B. Modeling fluid invasion and hydraulic fracture propagation in naturally fractured formations: A three-dimensional approach. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 10–20 February 2010. [Google Scholar]
- Sarmadivaleh, M. Experimental and Numerical Study of Interaction of a Pre-Existing Natural Interface and an Induced Hydraulic Fracture. Ph.D. Thesis, Curtin University, Perth, Australia, 2012. [Google Scholar]
- Yoon, J.S.; Zimmermann, G.; Zang, A. Numerical investigation on stress shadowing in fluid injection-induced fracture propagation in naturally fractured geothermal reservoirs. Rock Mech. Rock Eng. 2015, 48, 1439–1454. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L.; Braun, A.; Han, Z. Investigation of processes of interaction between hydraulic and natural fractures by PFC modeling comparing against laboratory experiments and analytical models. Energies 2017, 10, 1001. [Google Scholar] [CrossRef]
- Nagaso, M.; Mikada, H.; Takekawa, J. The role of rock strength heterogeneities in complex hydraulic fracture formation–Numerical simulation approach for the comparison to the effects of brittleness. J. Pet. Sci. Eng. 2019, 172, 572–587. [Google Scholar] [CrossRef]
- PFC2D—Particle Flow Code in 2 Dimensions; Version 4.0; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2008.
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zang, A.; Stephansson, O. Numerical investigation on optimized stimulation of intact and naturally fractured deep geothermal reservoirs using hydro-mechanical coupled discrete particles joints model. Geothermics 2014, 52, 165–184. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, F.; Huang, Z.; Yu, H.; Niu, J.; Zhang, P. Study on acoustic emission characteristics of sandstone under different fracture modes. Arab. J. Geosci. 2018, 11, 772. [Google Scholar] [CrossRef]
- Wang, H.; Liu, D.; Cui, Z.; Cheng, C.; Jian, Z. Investigation of the fracture modes of red sandstone using XFEM and acoustic emissions. Theor. Appl. Fract. Mech. 2016, 85, 283–293. [Google Scholar] [CrossRef]
- Ivars, D.M.; Potyondy, D.O.; Pierce, M.; Cundall, P.A. The smooth-joint contact model. In Proceedings of the 8th World Congress on Computational Mechanics and 5th European Congress on Computational Methods in Applied Sciences and Engineering, Venice, Italy, 30 June–5 July 2008. [Google Scholar]
- Zhou, J.; Zhang, L.; Pan, Z.; Han, Z. Numerical investigation of fluid-driven near-borehole fracture propagation in laminated reservoir rock using PFC2D. J. Nat. Gas Sci. Eng. 2016, 36, 719–733. [Google Scholar] [CrossRef]
- Shimizu, H. Distinct Element Modeling for Fundamental Rock Fracturing and Application to Hydraulic Fracturing. Ph.D. Thesis, Kyoto University, Tokyo, Japan, 2010. [Google Scholar]
- Shimizu, H.; Murata, S.; Ishida, T. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. Int. J. Rock Mech. Min. Sci. 2011, 48, 712–727. [Google Scholar] [CrossRef]
- Wang, H.; Li, J.; Zhao, F.; Dong, J.; Cui, Y.; Gong, W. Experimental study of volumetric fracturing properties for shale under different stress states. Geofluids 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, J.; Peng, S.; Yan, F.; Yang, W.; Cheng, L.; Ni, G. Influence of geo-stress on dynamic response characteristics of coal and gas outburst. Rock Mech. Rock Eng. 2020, 53, 4819–4837. [Google Scholar] [CrossRef]
- Du, S.; Lin, H.; Yong, R.; Liu, G. Characterization of joint roughness heterogeneity and its application in representative sample investigations. Rock Mech. Rock Eng. 2022, 55, 3253–3277. [Google Scholar] [CrossRef]
- Meng, W.; He, C. Back analysis of the initial geo-stress field of rock masses in high geo-temperature and high geo-stress. Energies 2020, 13, 363. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Y.; Li, A.; Chen, Z.; Chen, Y.; Zou, Y. Experimental study on propagation mechanism of complex hydraulic fracture in coal-bed. J. China. Coal. Soc. 2012, 37, 73–77. [Google Scholar] [CrossRef][Green Version]
- Beugelsdijk, L.; Pater, C.; Sato, K. Experimental hydraulic fracture propagation in a multi-fractured medium. In Proceedings of the SPE Asia Pacific Conference on Integrated Modelling for Asset Management, Yokohama, Japan, 25–26 April 2000. [Google Scholar]
- Chen, M.; Zhou, J.; Jin, Y.; Zhang, G. Experimental study on fracturing features in naturally fractured reservoir. Acta Pet. Sin. 2008, 29, 431–434. [Google Scholar] [CrossRef]
- Du, C.M.; Zhang, X.; Zhan, L.; Gu, H.; Hay, B.; Tushingham, K.; Ma, Y.Z. Modeling Hydraulic Fracturing Induced Fracture Networks in Shale Gas Reservoirs as a Dual Porosity System. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010. [Google Scholar]


| Brazilian Splitting Test Results | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number | Depth /m | Diameter /mm | Height /mm | Failure Pressure /kN | Tensile Strength /MPa | Average Tensile Strength /MPa | |||
| E1 | 3408 | 24.32 | 23.99 | 17.03 | 18.583 | 16.76 | |||
| E2 | 3408 | 24.44 | 24.01 | 14.684 | 15.931 | ||||
| E3 | 3408 | 24.3 | 24.03 | 14.45 | 15.754 | ||||
| E4 | 3408 | 24.51 | 24.21 | 8.076 | 8.665 | - | |||
| Uniaxial/Triaxial Test Results | |||||||||
| Number | Depth /m | Confining Pressure /MPa | Diameter /mm | Height /mm | E /GPa | υ | σc /MPa | Cohesion /MPa | Internal Friction Angle /° |
| E1 | 3408 | 0 | 24.30 | 50.92 | 33.55 | 0.051 | 197.08 | 43.05 | 42.8 |
| E2 | 3408 | 5 | 24.25 | 51.70 | 34.63 | 0.088 | 233.85 | ||
| E3 | 3408 | 10 | 24.32 | 50.74 | 34.80 | 0.052 | 258.13 | ||
| E4 | 3408 | 20 | 24.49 | 50.97 | 35.81 | 0.098 | 301.88 | ||
| Parameters | Remarks and References | Value (Unit) |
|---|---|---|
| Particle density (kg/m3) | ρ | 2650 |
| Lower bound of particle radius (mm) | r | 2 |
| Ratio of particle radius | Rmax/Rmin | 1.66 |
| Young’s modulus of the particle (GPa) | E | 16 |
| Ratio of normal to shear stiffness of the particle | kn/ks | 3 |
| Friction coefficient of particle | μ | 0.577 |
| Young’s modulus of the parallel bond (GPa) | Epb | 16 |
| Tensile strength of the parallel particle (MPa) | σt | 15 |
| Shear strength of the parallel particle (MPa) | σs | 18 |
| Cohesion (MPa) | c | 35 |
| Normal stiffness of SJM (GPa) | [36] | 1300 |
| Shear stiffness of SJM (GPa) | [36] | 500 |
| Tensile strength of SJM (MPa) | [36] | 3.2 |
| Friction angle of SJM (°) | φ [27,36] | 30 |
| Cohesive of SJM (MPa) | [36] | 3.2 |
| Specimen Number | In-Situ Stress Difference Coefficient /% | Tension Crack | Shear Crack | Total Cracks | Fracture Stress /MPa | Fractal Dimension D | ||
|---|---|---|---|---|---|---|---|---|
| Amount | Proportion /% | Amount | Proportion /% | |||||
| 1 | 0 | 2155 | 91.1 | 211 | 8.9 | 2366 | 43.06 | 1.5654 |
| 2 | 10 | 1826 | 90.0 | 202 | 10.0 | 2028 | 43.06 | 1.5373 |
| 3 | 20 | 2079 | 90.8 | 211 | 9.2 | 2290 | 43.73 | 1.5604 |
| 4 | 30 | 2836 | 90.9 | 284 | 9.1 | 3120 | 44 | 1.6094 |
| 5 | 40 | 2093 | 91.0 | 206 | 9.0 | 2299 | 44.19 | 1.5667 |
| 6 | 50 | 2357 | 90.6 | 244 | 9.4 | 2601 | 45.72 | 1.5759 |
| 7 | 60 | 1782 | 89.5 | 209 | 11.5 | 1991 | 44.75 | 1.5989 |
| 8 | 70 | 1358 | 89.6 | 158 | 11.4 | 1516 | 44.91 | 1.5376 |
| 9 | 80 | 2019 | 90.1 | 221 | 9.9 | 2240 | 45.1 | 1.5543 |
| 10 | 90 | 2715 | 90.2 | 292 | 9.8 | 3007 | 44.31 | 1.6117 |
| 11 | 100 | 1938 | 89.8 | 220 | 11.2 | 2158 | 44.7 | 1.3924 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Gong, W.; Yuan, G.; Wang, X.; Zhao, J.; Su, Y.; Wang, Y. Effect of In-Situ Stress on Hydraulic Fracturing of Tight Sandstone Based on Discrete Element Method. Energies 2022, 15, 5620. https://doi.org/10.3390/en15155620
Wang H, Gong W, Yuan G, Wang X, Zhao J, Su Y, Wang Y. Effect of In-Situ Stress on Hydraulic Fracturing of Tight Sandstone Based on Discrete Element Method. Energies. 2022; 15(15):5620. https://doi.org/10.3390/en15155620
Chicago/Turabian StyleWang, Hongjian, Wanlin Gong, Guangxiang Yuan, Xiaodong Wang, Jitao Zhao, Yujie Su, and Yuchen Wang. 2022. "Effect of In-Situ Stress on Hydraulic Fracturing of Tight Sandstone Based on Discrete Element Method" Energies 15, no. 15: 5620. https://doi.org/10.3390/en15155620
APA StyleWang, H., Gong, W., Yuan, G., Wang, X., Zhao, J., Su, Y., & Wang, Y. (2022). Effect of In-Situ Stress on Hydraulic Fracturing of Tight Sandstone Based on Discrete Element Method. Energies, 15(15), 5620. https://doi.org/10.3390/en15155620





