Regenerative Braking Logic That Maximizes Energy Recovery Ensuring the Vehicle Stability
Abstract
:1. Introduction
- For gradual braking and emergency braking;
- With or without the estimation of the road surface friction coefficient;
- With fixed or allocated torque distribution;
- By tools used for simulation (MATLAB/Simulink®, AMESim®, CARSim®, or co-simulation);
- By the type of model validation (without validation, with physical imitators, or with real vehicles).
- Various vehicle, driveline, electric motor(s), and brake system data are considered;
- The model calculates the brake force request, starting from the brake demand i.e., from driver force acting on the brake pedal;
- The optimal braking distribution between front and rear axles is obtained considering the load transfer due to longitudinal acceleration/deceleration;
- The logic aims at maximizing energy recovery under braking considering various limitations that can come into play;
- The limitations related to tire grip are considered;
- Motor and battery limitations are also considered;
- Finally, traditional brakes integrate regenerative braking to ensure the braking torque request is met in all conditions while keeping the system closer to the optimal braking distribution.
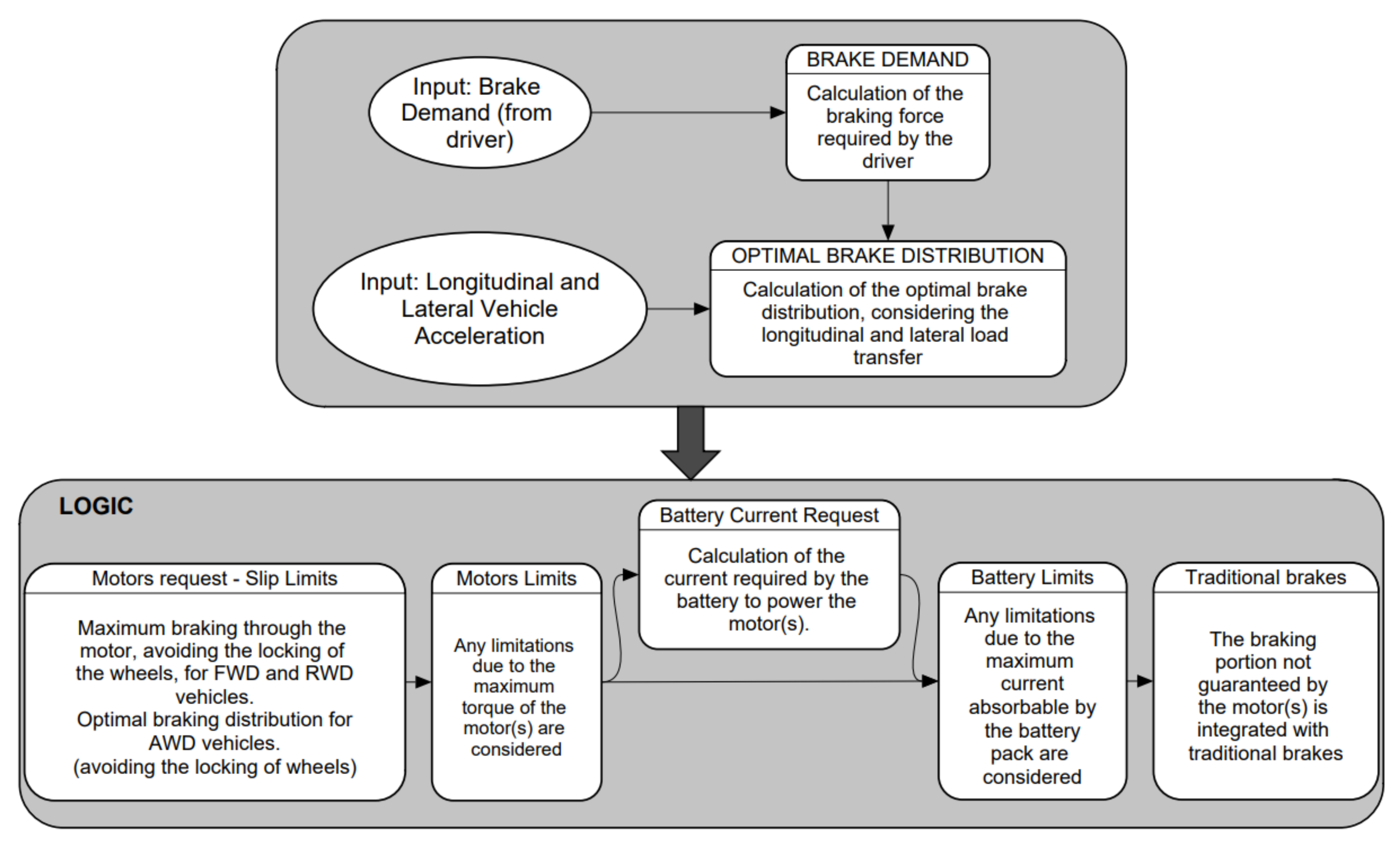
- In Section 2, the general layout of this logic is presented together with the related mathematical background. In particular, the logic is modular, and the details of each submodel are provided. This section begins with the definition of the model’s inputs and outputs, including an explanation of how the logic interprets the brake demand signal and a calculation of the optimal braking distribution. The calculation of the electric motor' torque requests, which also prevents wheel locking, is then shown. Subsequently, various situations are considered that may make it necessary to limit these motor torques, that is, the maximum braking torques available from the electric motor/s and the battery pack limitations. Finally, once these torques have been calculated, taking into account all the limitations, the logic will calculate pressures in the front and rear braking systems in order to guarantee the amount of braking required by the brake demand.
- In Section 3, the results achieved through this logic are presented. In particular, results based on standard driving cycles (to validate energy savings) and test outcomes (aimed at showing how the logic does not impair vehicle stability) are shown.
- In Section 4, the results obtained in Section 3 are discussed, some future developments for the logic object of this paper are presented, and some future fields of application are proposed (the context in which it is possible to know the road friction coefficient, for example, in the context of smart roads).
- Finally, Appendix A includes the nomenclature with all symbols and abbreviations used in this paper.
2. Materials and Methods
2.1. Model Inputs and Outputs
- Brake demand (): value from 0 to 1, proportional to the force imposed by the driver on the brake pedal.
- Longitudinal vehicle deceleration (): positive value for vehicle deceleration.
- Lateral vehicle acceleration (): absolute value.
- Vehicle speed ( ): longitudinal vehicle speed.
- Angular velocity of the front wheels (): average value between left and right front wheels.
- Angular velocity of the rear wheels (): average value between left and right front wheels.
- Angular velocity of the front electric motor (): if the front motor is present.
- Angular velocity of the rear electric motor (): if the rear motor is present.
- Battery voltage ().
- Maximum charging current of the battery pack (): maximum current that the battery is able to accept in input from the motors at the moment considered.
- Front brake pressure (): signal required for the control logic of the front braking system.
- Rear brake pressure (): signal required for the control logic of the rear braking system.
- Front motor torque (): output torque of the front electric motor.
- Rear motor torque (): output torque of the rear electric motor.
2.2. Brake Demand
2.3. Optimal Brake Distribution
2.4. Motors Request – Slip Limits
2.4.1. FWD
2.4.2. RWD
2.4.3. AWD
2.5. Motors Limits
2.6. Battery Current Request
2.7. Battery Limits
2.7.1. FWD
2.7.2. RWD
2.7.3. AWD
2.8. Traditional Brakes
3. Results
3.1. Reference Vehicles
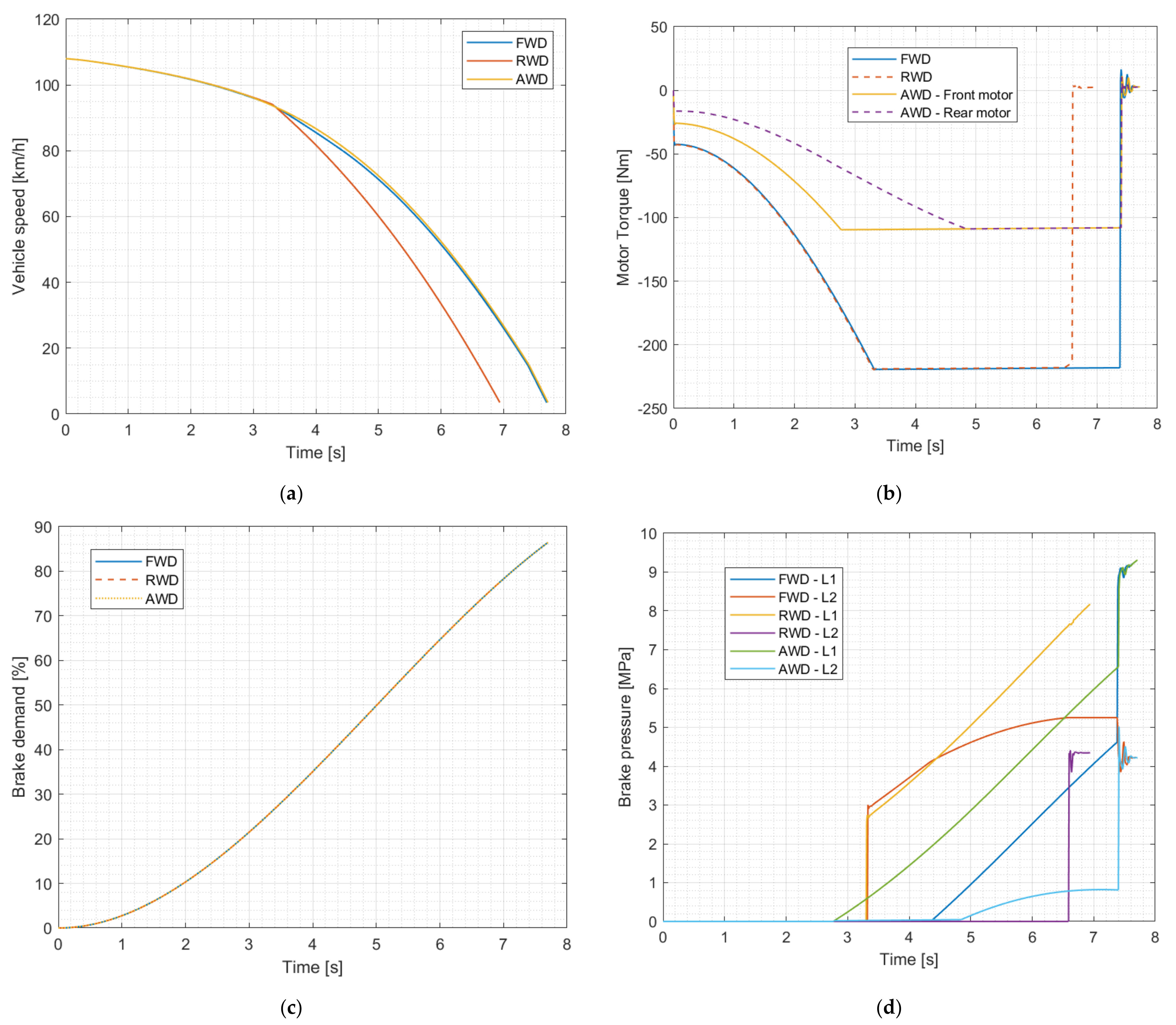
3.2. Test of the Regenerative Braking Logic
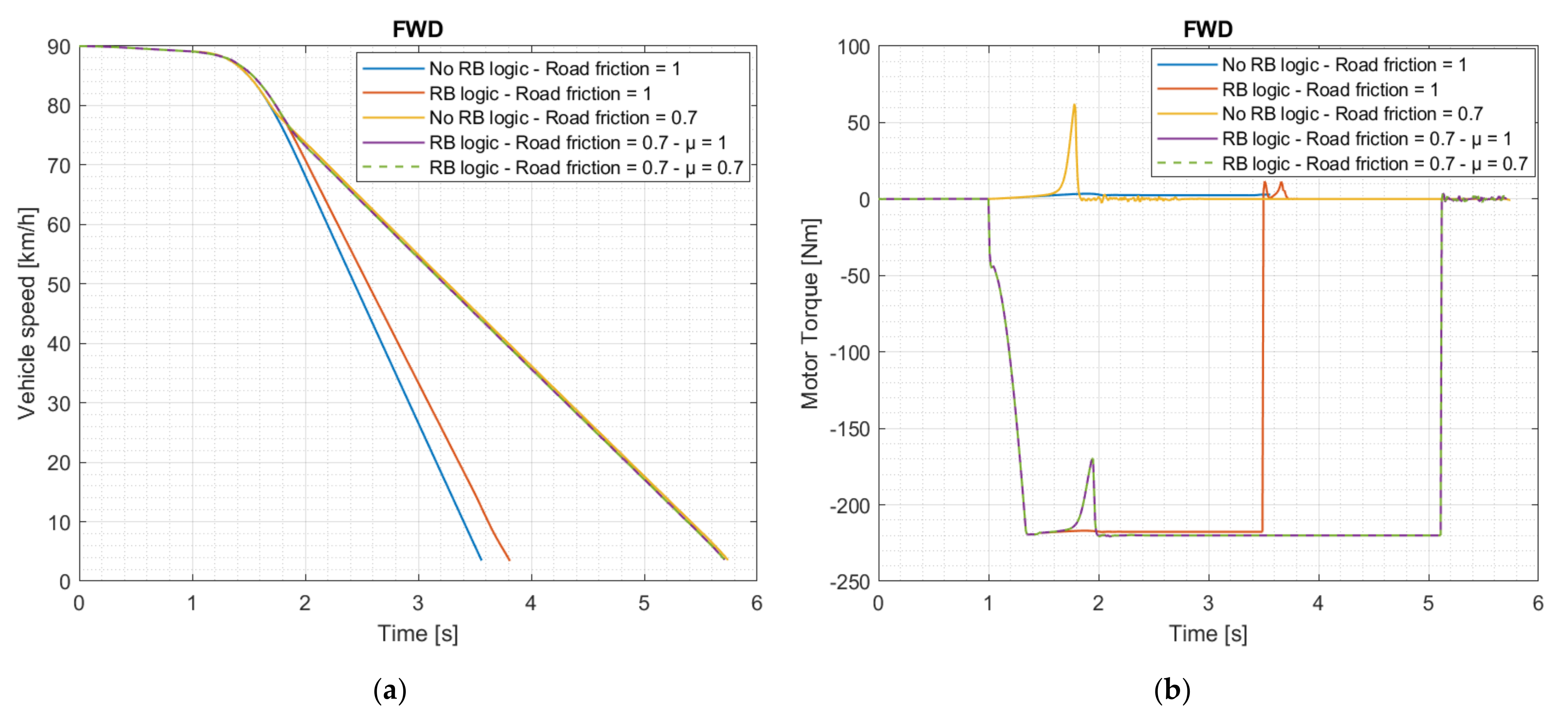
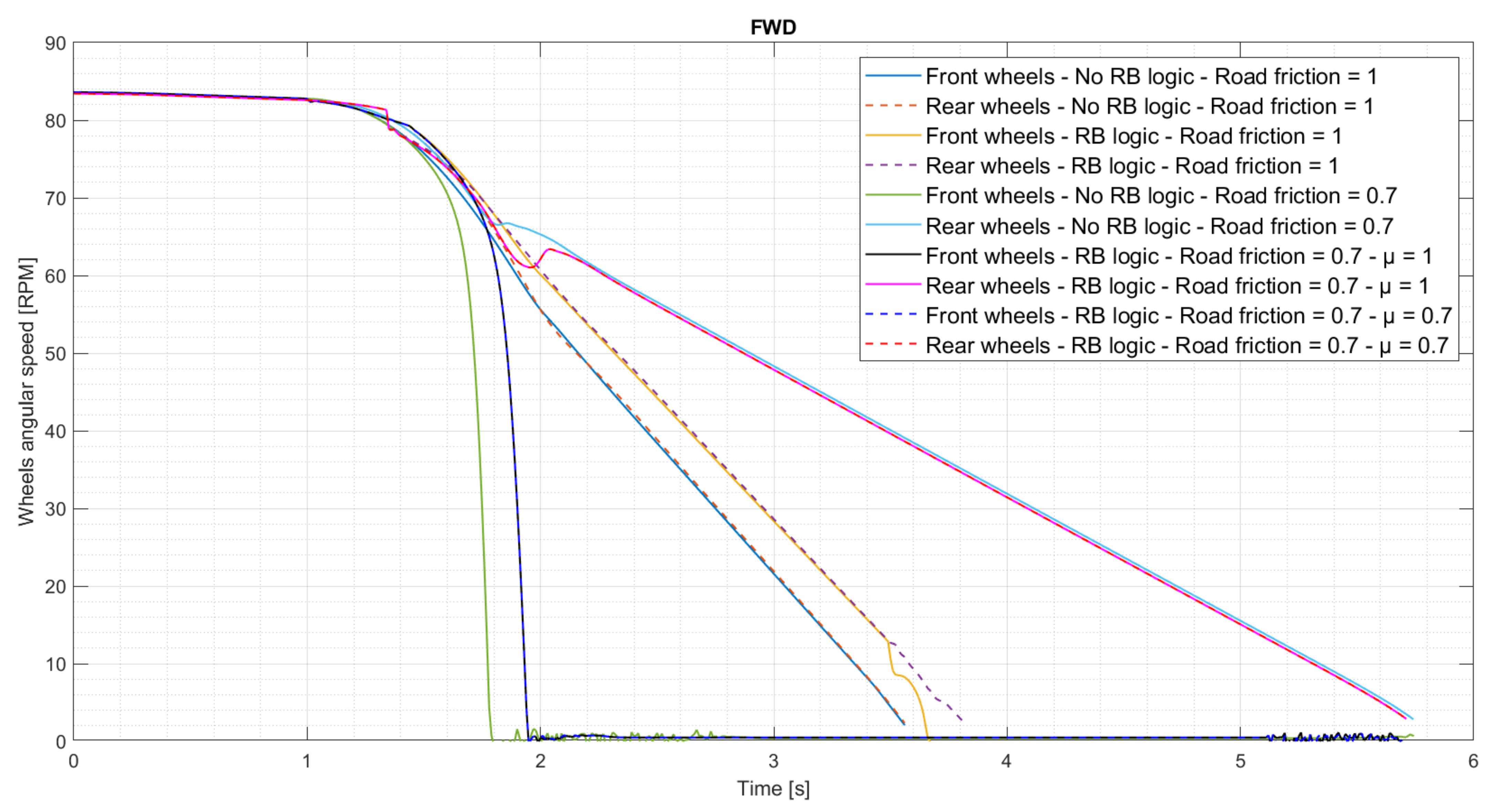
3.3. Braking Performance and Handling
3.3.1. Straightline Panic Brake
3.3.2. Braking in Turn
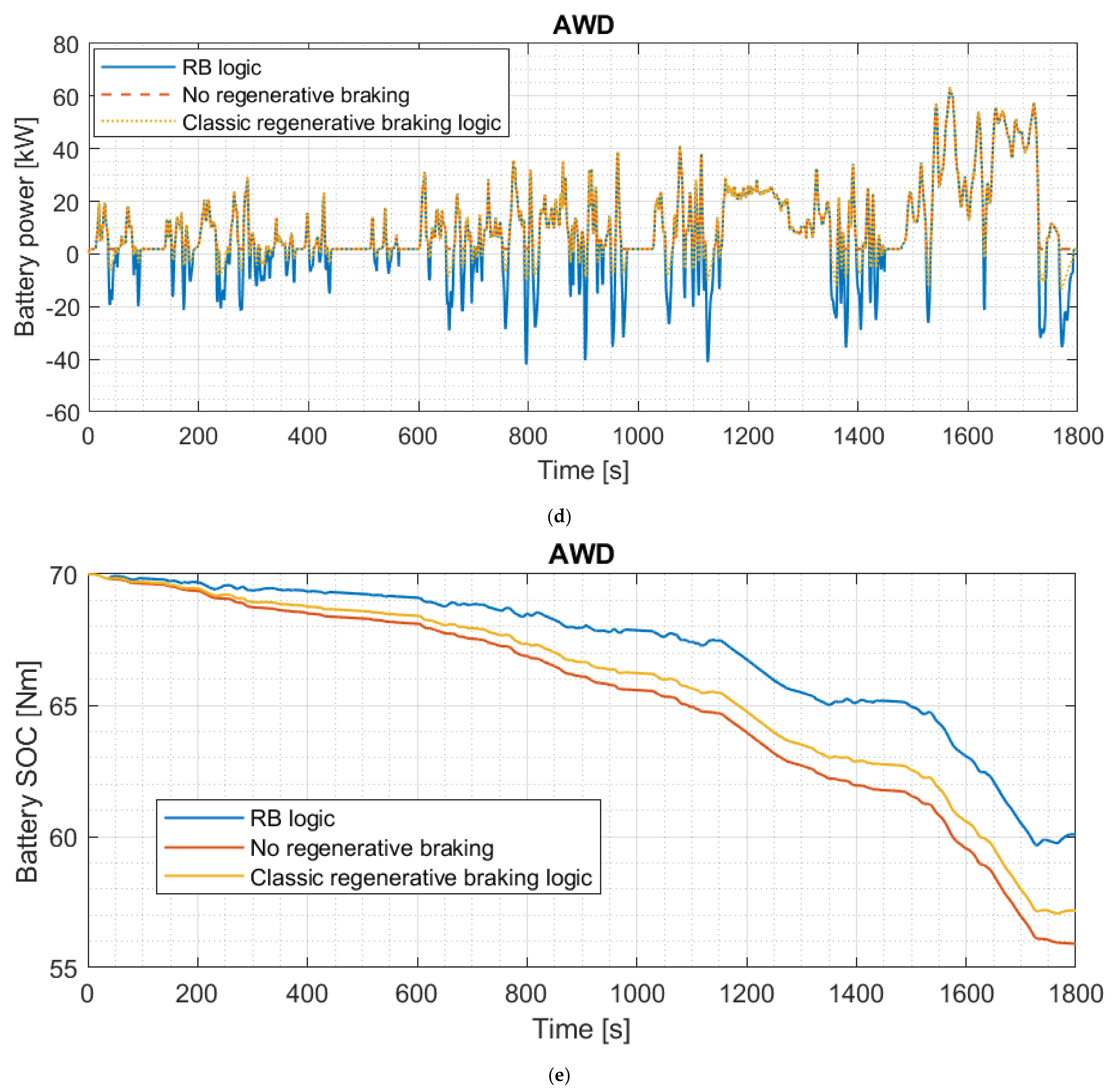
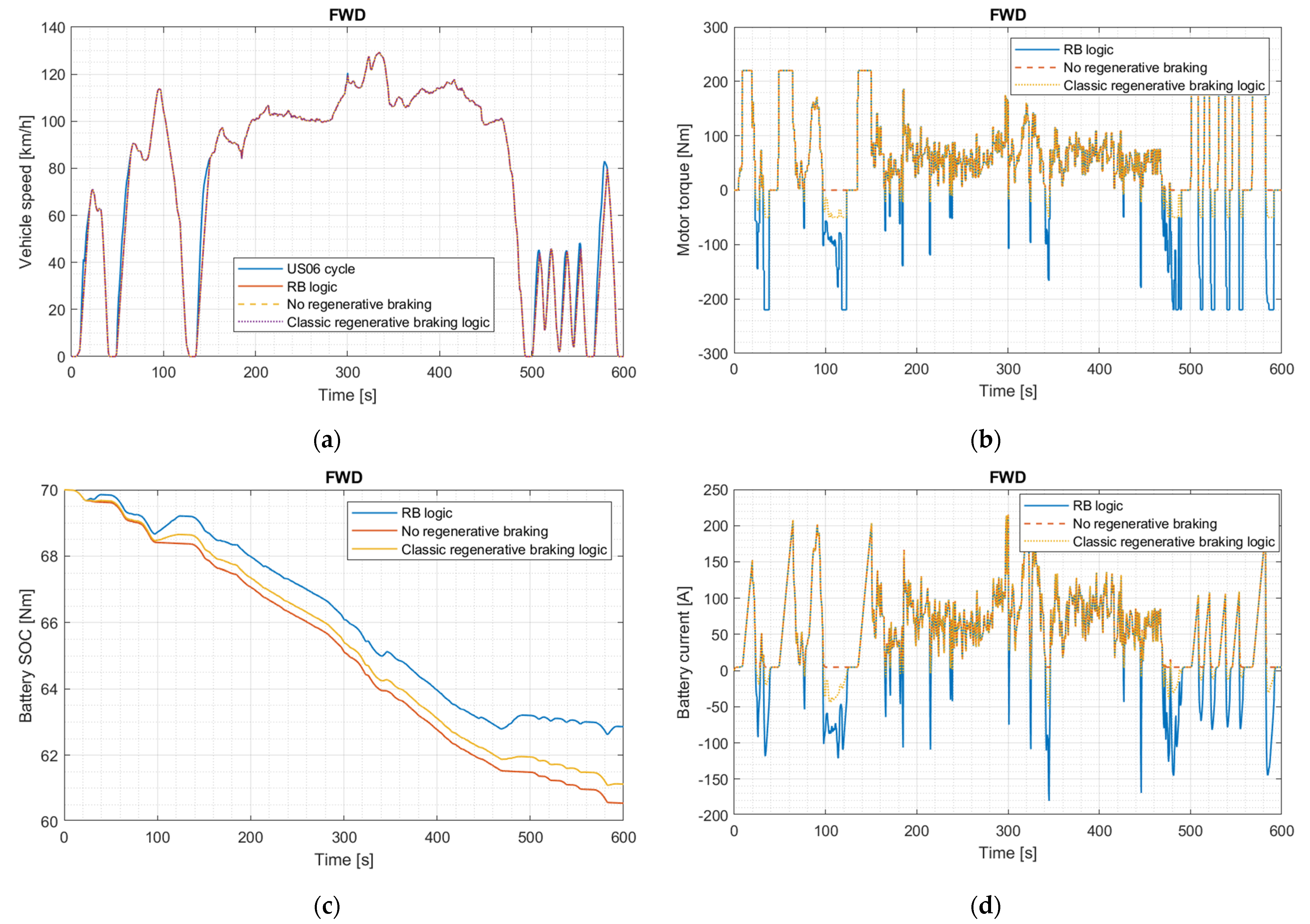
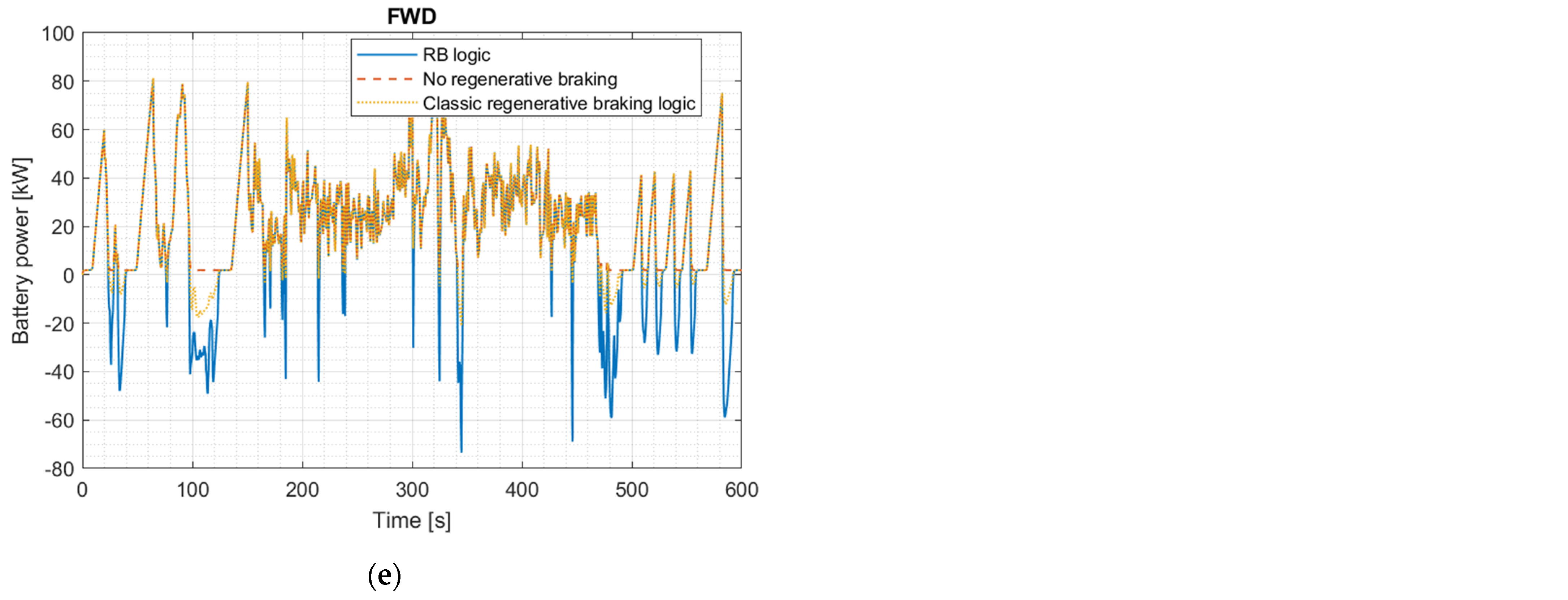
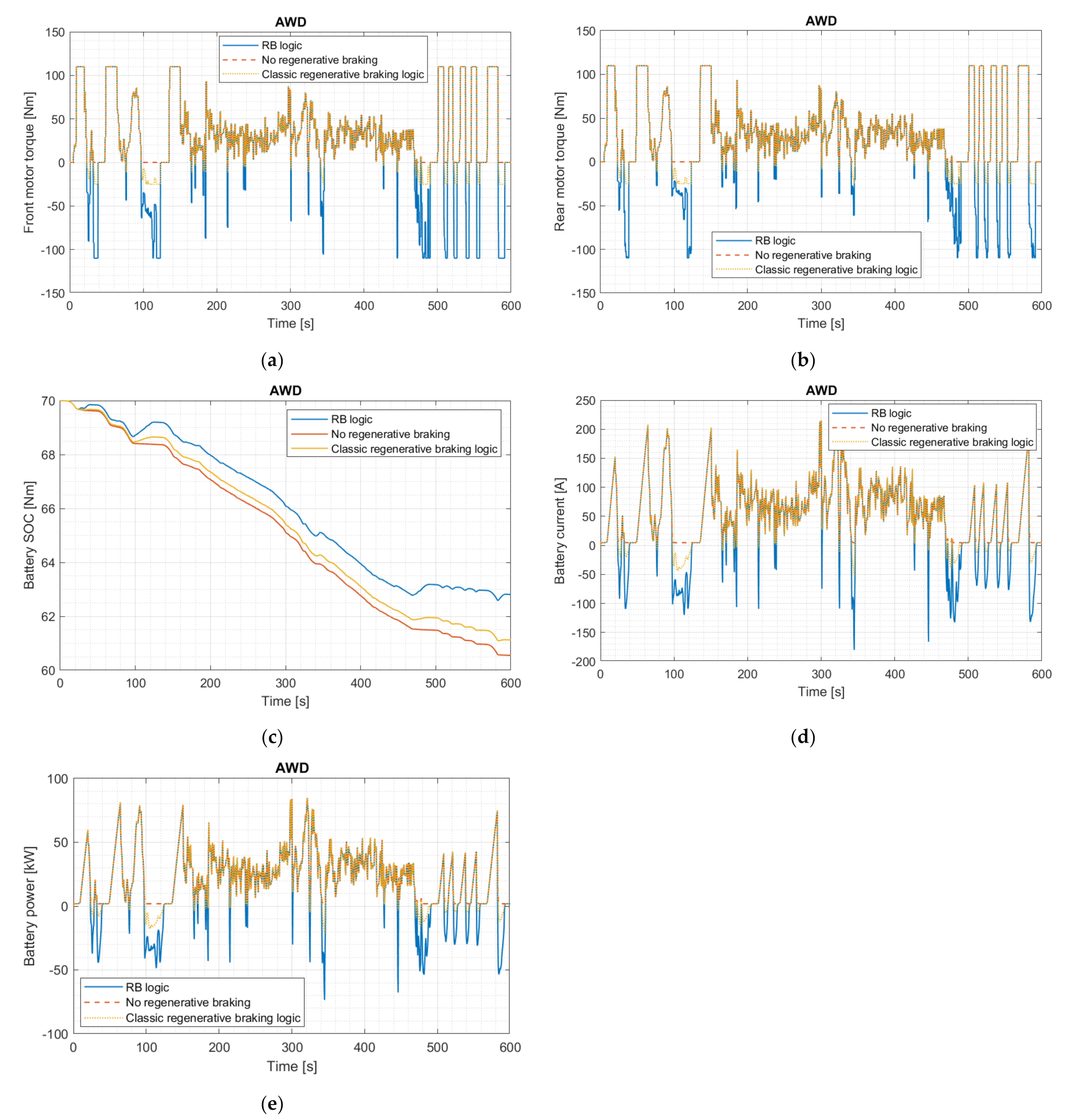
3.4. Energy Consumption and Recovery Estimation
3.4.1. Vehicle Models
3.4.2. WLTP Procedure
3.4.3. US06 Cycle
4. Discussion
- Offboard sensors (laser profilometer, camera, intelligent tire with accelerometer, ultrasonic transmitter, receiver, etc.);
- Onboard sensors and vehicle dynamics model (lateral, longitudinal, and coupled dynamics model);
- Data-driven (neural networks and so on).
- Integration of the logic with a model for the estimation of the tire–road friction coefficient, as stated above;
- Improvement of the tire simulation model—in particular, the tire–road interaction, for example, by implementing a fully nonlinear Pacejka Magic Equation;
- Integration of a specific ABS strategy also acting on the braking torques of the electric motors; see [9] for an example.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviation | Description |
|---|---|
| ABS | From the German: Antiblockiersystem. Anti-lock system. Avoid locking the vehicle’s wheels when braking. |
| Lateral vehicle acceleration (of the center of gravity), absolute value 3 | |
| Total area of the brake pistons, front calipers 1 | |
| Total area of the brake pistons, rear calipers 1 | |
| APU | Auxiliary power unit |
| AWD | All-wheel drive vehicle |
| Optimal braking distribution 4 | |
| Brake demand (from 0 to 1) 3 | |
| CG | Center of gravity |
| Maximum charging current of the battery pack 3 | |
| Charging current of the battery pack generated by the motor or motors 4 | |
| Current that the front motor sends to the battery pack when it produces a regenerative motor torque equal to Tref F 4 | |
| Current that the rear motor sends to the battery pack when it produces a regenerative motor torque equal to Tref F 4 | |
| Total charging current generated by the motor or motors | |
| Charging current generated by the front motor 4 | |
| Charging current generated by the rear motor 4 | |
| EPA | Environmental Protection Agency |
| Total braking force request 4 | |
| Front braking force associated with the driver demand 4 | |
| Rear braking force associated with the driver demand 4 | |
| FLC | Fuzzy logic controllers |
| Theoretical total maximum braking force that the front axle can unload on the ground 4 | |
| Theoretical total maximum braking force that the rear axle can unload on the ground 4 | |
| Maximum braking force that the traditional brakes can unload on the ground 4 | |
| Maximum braking force that the traditional front brakes can unload on the ground 4 | |
| Maximum braking force that the traditional rear brakes can unload on the ground 4 | |
| Braking force required from the front motor 4 | |
| Braking force required from the rear motor 4 | |
| FWD | Front-wheel drive vehicle |
| Acceleration of gravity 1 | |
| Height of the front roll center 1 | |
| Height of the rear roll center 1 | |
| Height of the center of gravity of the vehicle 1 | |
| Longitudinal vehicle deceleration (positive value) 3 | |
| Moment of inertia of the transmission after the front motor reducer 1 | |
| Moment of inertia of the transmission after the rear motor reducer 1 | |
| Moment of inertia of the front electric motor 1 | |
| Moment of inertia of the rear electric motor 1 | |
| Moment of inertia of the transmission before the front motor reducer 1 | |
| Moment of inertia of the transmission before the rear motor reducer 1 | |
| Moment of inertia of a single front wheel 1 | |
| Moment of inertia of a single rear wheel 1 | |
| Stiffness of the front anti-roll bar 1 | |
| Stiffness of the rear anti-roll bar 1 | |
| The roll stiffness of the front axle 1 | |
| The roll stiffness of the rear axle 1 | |
| Stiffness of the front suspension springs 1 | |
| Stiffness of the rear suspension springs 1 | |
| Wheelbase 1 | |
| Distance between the front axle and the center of gravity of the vehicle 1 | |
| Distance between the rear axle and the center of gravity of the vehicle 1 | |
| Total length of the connection cables of the front motor 1 | |
| Total length of the connection cables of the rear motor 1 | |
| Vehicle mass 1 | |
| Half the front unsprung mass of the vehicle 1 | |
| Half the rear unsprung mass of the vehicle 1 | |
| Front sprung mass of the vehicle 1 | |
| Rear sprung mass of the vehicle 1 | |
| MRC | Model reference controllers |
| NNC | Neutral networks controllers |
| Hypothetical power absorbed by the battery pack, coming from the front motor, in the case of an AWD vehicle, with battery limitations 4 | |
| Hypothetical charging power provided by the rear motor 4 | |
| Charging power provided by the front motor in case of approximation error in the calculation of TmotR, for AWD vehicles 4 | |
| Hypothetical power absorbed by the battery pack, coming from the rear motor, in the case of an AWD vehicle, with battery limitations 4 | |
| PIDC | Proportional-integral-differential controllers |
| Front master cylinder brake pressure 4 | |
| Rear master cylinder brake pressure 4 | |
| Maximum pressure that can be generated inside the master cylinder of the front brake system 1 | |
| Maximum pressure that can be generated inside the master cylinder of the rear brake system 1 | |
| RB | Regenerative Braking |
| Electric resistance of the front connection cables 2 | |
| Electric resistance of the rear connection cables 2 | |
| Average radius of application of the braking force on the front discs 1 | |
| Average radius of application of the braking force on the rear discs 1 | |
| RPM | Revolutions per minute |
| RWD | Rear-wheel drive vehicle |
| Nominal rolling radius of the front wheels 1 | |
| Nominal rolling radius of the rear wheels 1 | |
| Safety coefficient for the braking force guarantee by the front motor, for avoiding the locking of the front driving wheels 1 | |
| Safety coefficient for the braking force guarantee by the rear motor, for avoiding the locking of the rear driving wheels 1 | |
| SFTP | Supplemental Federal Test Procedure |
| SMC | Sliding-mode controllers |
| SOC | Battery State of Charge |
| Hypothetical front regenerative torque, minimum value between TAWD_MAXf and TrefF 4 | |
| Hypothetical rear regenerative torque, calculated starting from the power PAWD_HYPr 4 | |
| Maximum regenerative torque that can be obtained from the front motor, exploiting the absorbable power PAWDf by the battery pack 4 | |
| TC | Threshold controllers |
| TEST | Target-speed EV Simulation Tool |
| Regenerative torque of the front electric motor 4 | |
| Regenerative torque of the rear electric motor 4 | |
| Front track of the vehicle 1 | |
| Rear track of the vehicle 1 | |
| Regenerative torque required from the front electric motor (respecting the limitations of the motor) 4 | |
| Regenerative torque required from the rear electric motor (respecting the limitations of the motor) 4 | |
| Regenerative torque required from the front electric motor (not considering any limitations) 4 | |
| Regenerative torque required from the rear electric motor (not considering any limitations) 4 | |
| US06 | Normed driving cycle, SFTP-US06 |
| Longitudinal vehicle speed 3 | |
| VCU | Vehicle control unit |
| Battery pack voltage 3 | |
| Load on the front axle, considering only the static weight and the longitudinal load transfer 4 | |
| WLTC | Worldwide harmonized Light-duty vehicles Test Cycles |
| WLTP | Worldwide harmonized Light-Duty vehicles Test Procedure |
| Load on the rear axle, considering only the static weight and the longitudinal load transfer 4 | |
| Reference load on the front axle, used in the Simulink® model 4 | |
| Reference load on the rear axle, used in the Simulink® model 4 | |
| Front-load transfer due to lateral acceleration 4 | |
| Rear-load transfer due to lateral acceleration 4 | |
| Time derivative | |
| Electrical efficiency of the front motor at the operating point characterized by the parameters PAWD f and ωmotF 4 | |
| Electrical efficiency of the rear motor at the operating point characterized by the parameters PAWD_HYP r and ωmotR 4 | |
| Electrical efficiency of the front motor at the operating point characterized by the parameters PAWD_NEW f and ωmotF 4 | |
| Electrical efficiencies of the front motor (FWD vehicles) 4 | |
| Electrical efficiencies of the front motor (before considering possible battery limitations) 4 | |
| Electrical efficiencies of the rear motor (before considering possible battery limitations) 4 | |
| Electrical efficiency of the front motor at the operating point characterized by the parameters Tref F and ωmotF 4 | |
| Electrical efficiency of the rear motor at the operating point characterized by the parameters Tref F and ωmotR 4 | |
| Electrical efficiencies of the rear motor (RWD vehicles) 4 | |
| General efficiency of the entire front transmission 1 | |
| General efficiency of the entire rear transmission 1 | |
| Diameter of the front motor cables 1 | |
| Diameter of the rear motor cables 1 | |
| Road–tire friction coefficient 1 | |
| Dynamic coefficient of friction between front brake pads and brake calipers 1 | |
| Dynamic coefficient of friction between rear brake pads and brake calipers 1 | |
| Electric resistivity of copper (or in any case of the conductive material of the electric cables) 1 | |
| Roll angle of the vehicle 4 | |
| Reduction ratios of the front differential 1 | |
| Reduction ratios of the rear differential 1 | |
| Reduction ratios of the front motor reductor 1 | |
| Reduction ratios of the rear motor reductor 1 | |
| Angular velocity of the front electric motor 3 | |
| Angular velocity of the rear electric motor 3 | |
| Angular velocity of the front wheels 3 | |
| Angular velocity of the rear wheels 3 |
References
- Automotive World. An ICE-y Road to an Electric Future. Available online: https://www.automotiveworld.com/articles/anice-y-road-to-an-electric-future/ (accessed on 21 December 2021).
- Official Journal of the European Union. REGULATION (EU) 2021/1119 OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL of 30 June 2021. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32021R1119&from=EN (accessed on 21 December 2021).
- Ehsani, M.; Gao, Y.; Longo, S.; Ebrahimi, K. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles. In CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 2018; pp. 1–11. [Google Scholar]
- Zhang, Y.-J.; Yang, P.-P. Modeling and Simulation of Regenerative Braking System for Pure Electric Vehicle. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2010, 15, 90–94. [Google Scholar] [CrossRef]
- Biao, J.; Xiangwen, Z.; Yangxiong, W.; Wenchao, H. Regenerative Braking Control Strategy of Electric Vehicles Based on Braking Stability Requirements. Int. J. Automot. Technol. 2021, 22, 465–473. [Google Scholar] [CrossRef]
- Sandrini, G.; Có, B.; Tomasoni, G.; Gadola, M.; Chindamo, D. The Environmental Performance of Traction Batteries for Electric Vehicles from a Life Cycle Perspective. Environ. Clim. Technol. 2021, 25, 700–716. [Google Scholar] [CrossRef]
- Li, P.; Jin, D.F.; Luo, Y.G. Regenerative Braking Control Strategy for a Mild HEV. Automot. Eng. 2005, 27, 570–574. [Google Scholar] [CrossRef]
- Regulation No 13 of the Economic Commission for Europe of the United Nations (UN/ECE)—Uni-form Provisions Concerning the Approval of Vehicles of Categories M, N and O with Re-gard to Braking [2016/ 194]. 2016. Available online: https://op.europa.eu/en/publication-detail/-/publication/0a43f880-d612-11e5-a4b5-01aa75ed71a1/language-en (accessed on 8 August 2022).
- He, L.; Ye, W.; He, Z.; Song, K.; Shi, Q. A combining sliding mode control approach for electric motor anti-lock braking system of battery electric vehicle. Control Eng. Pract. 2020, 102, 104520. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Cao, B. Brake-Force Distribution Strategy for Electric Vehicle Based on Maximum Energy Recovery. Hsi-An Chiao Tung Ta Hsueh/J. Xi’an Jiaotong Univ. 2008, 42, 607–611. [Google Scholar]
- Li, Y.F.; Tian, Y.T.; Hu, L.L.; Yin, C. A Study on Control Algorithm of Regenerative Braking for EV/HEV. Automot. Eng. 2007, 29, 1059–1063. [Google Scholar]
- Kim, J.; Ko, S.; Lee, G.; Yeo, H.; Kim, P.; Kim, H. Development of co-operative control algorithm for parallel HEV with electric booster brake during regenerative braking. In Proceedings of the 2021 IEEE Vehicle Power and Propulsion Conference (VPPC); Chicago, IL, USA, 6–9 September 2011. [Google Scholar] [CrossRef]
- Ko, J.W.; Ko, S.Y.; Kim, I.S.; Hyun, D.Y.; Kim, H.S. Co-operative control for regenerative braking and friction braking to increase energy recovery without wheel lock. Int. J. Automot. Technol. 2014, 15, 253–262. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles. Appl. Energy 2012, 89, 413–420. [Google Scholar] [CrossRef]
- Tjonnas, J.; Johansen, T.A. Stabilization of Automotive Vehicles Using Active Steering and Adaptive Brake Control Allocation. IEEE Trans. Control. Syst. Technol. 2010, 18, 545–558. [Google Scholar] [CrossRef]
- Lian, Y.-F.; Tian, Y.-T.; Hu, L.-L.; Yin, C. A new braking force distribution strategy for electric vehicle based on regenerative braking strength continuity. J. Central South Univ. 2013, 20, 3481–3489. [Google Scholar] [CrossRef]
- Vodovozov, V.; Raud, Z.; Petlenkov, E. Review on Braking Energy Management in Electric Vehicles. Energies 2021, 14, 4477. [Google Scholar] [CrossRef]
- Vodovozov, V.; Raud, Z.; Aksjonov, A.; Petlenkov, E. Fuzzy Logic Control of Electric Vehicles in Changing Braking Conditions. In Proceedings of the 2020 XI International Conference on Electrical Power Drive Systems (ICEPDS), Saint Petersburg, Russia, 4–7 October 2020; pp. 1–6. [Google Scholar]
- Sandrini, G.; Gadola, M.; Chindamo, D. Longitudinal Dynamics Simulation Tool for Hybrid APU and Full Electric Vehicle. Energies 2021, 14, 1207. [Google Scholar] [CrossRef]
- Chindamo, D.; Gadola, M.; Romano, M. Simulation tool for optimization and performance prediction of a generic hybrid electric series powertrain. Int. J. Automot. Technol. 2014, 15, 135–144. [Google Scholar] [CrossRef]
- Chindamo, D.; Economou, J.T.; Gadola, M.; Knowles, K. A neurofuzzy-controlled power management strategy for a series hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D: J. Automob. Eng. 2014, 228, 1034–1050. [Google Scholar] [CrossRef]
- Chindamo, D.; Gadola, M. What is the Most Representative Standard Driving Cycle to Estimate Diesel Emissions of a Light Commercial Vehicle? IFAC-PapersOnLine 2018, 51, 73–78. [Google Scholar] [CrossRef]
- COMMISSION REGULATION (EU) 2017/1151. Available online: https://www.legislation.gov.uk/eur/2017/1151/contents (accessed on 8 August 2022).
- Acosta, M.; Kanarachos, S.; Blundell, M. Road Friction Virtual Sensing: A Review of Estimation Techniques with Emphasis on Low Excitation Approaches. Appl. Sci. 2017, 7, 1230. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J.; Wang, F.; Dong, H.; Yan, Y.; Ren, Y.; Zhou, C.; Yin, G. Tire Road Friction Coefficient Estima-tion: Review and Research Perspectives. Chin. J. Mech. Eng. 2022, 35, 6. [Google Scholar] [CrossRef]


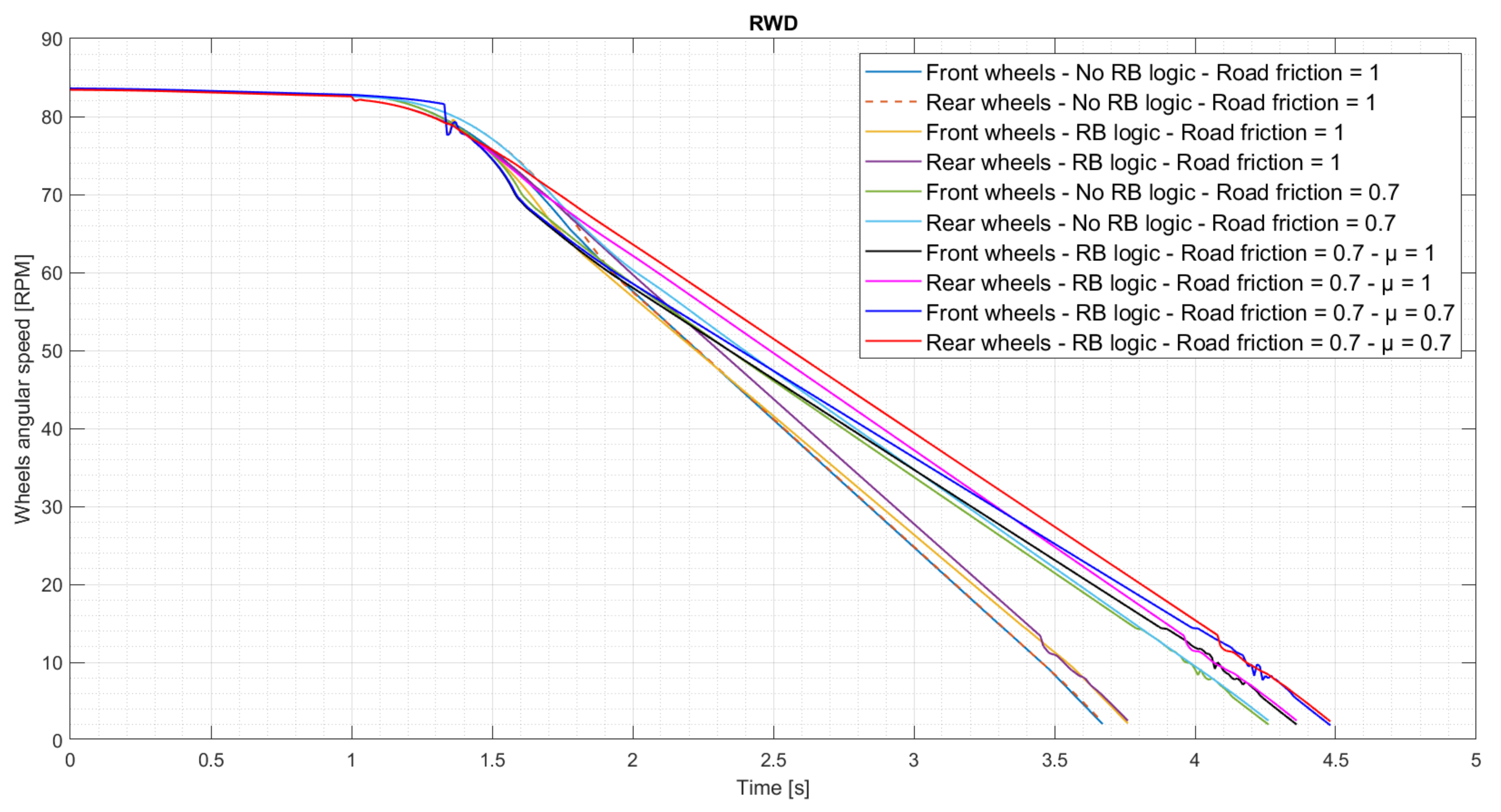
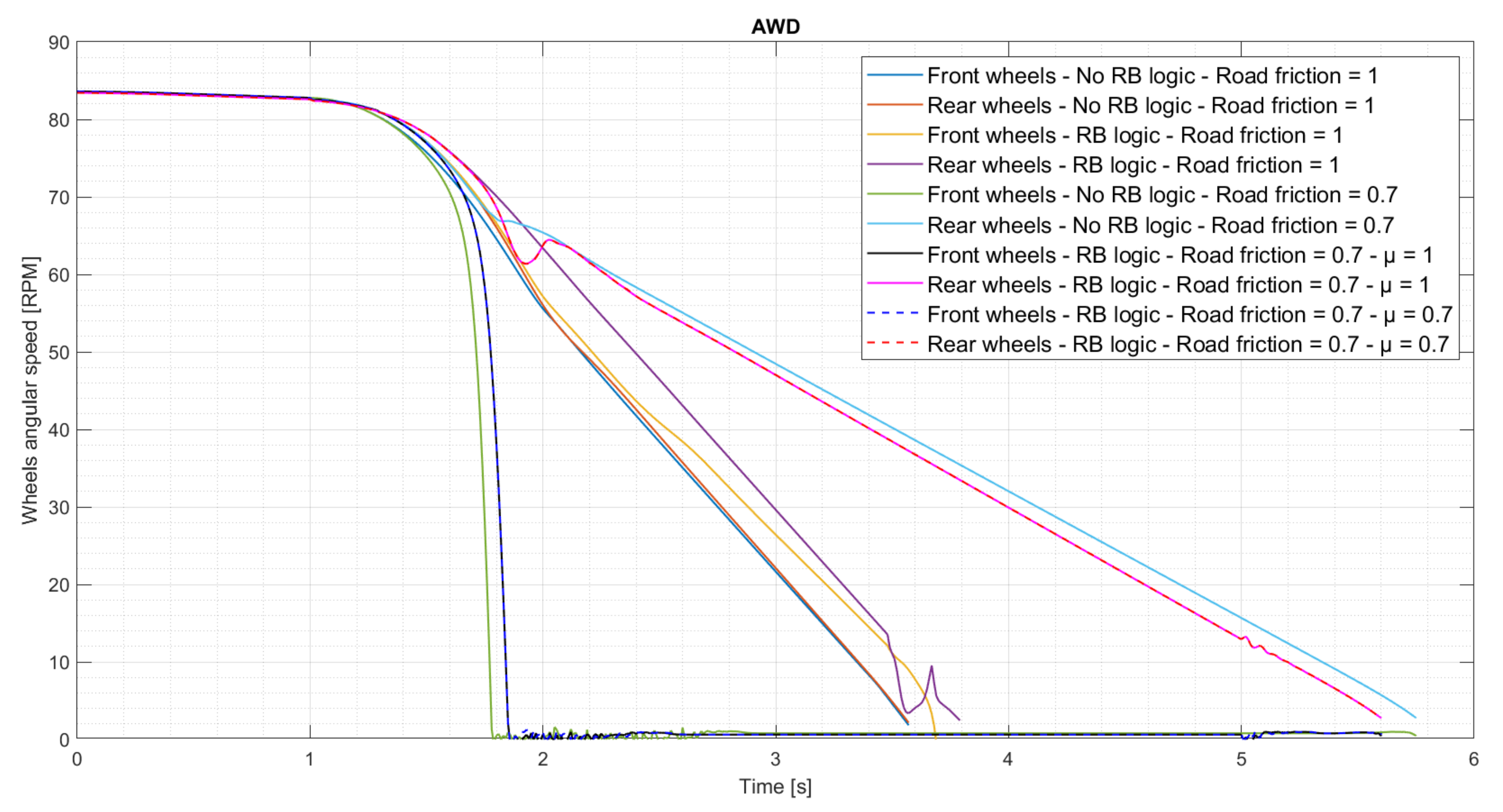
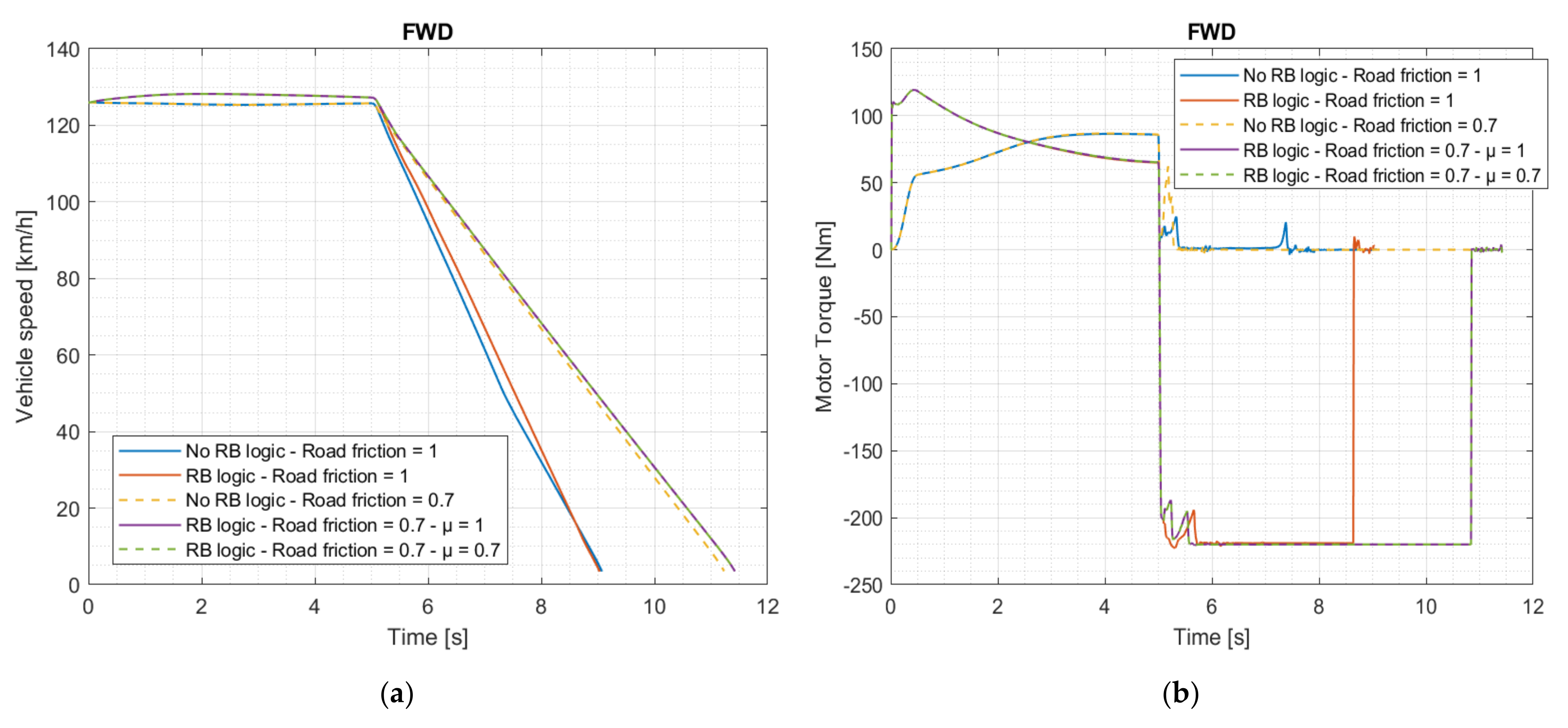
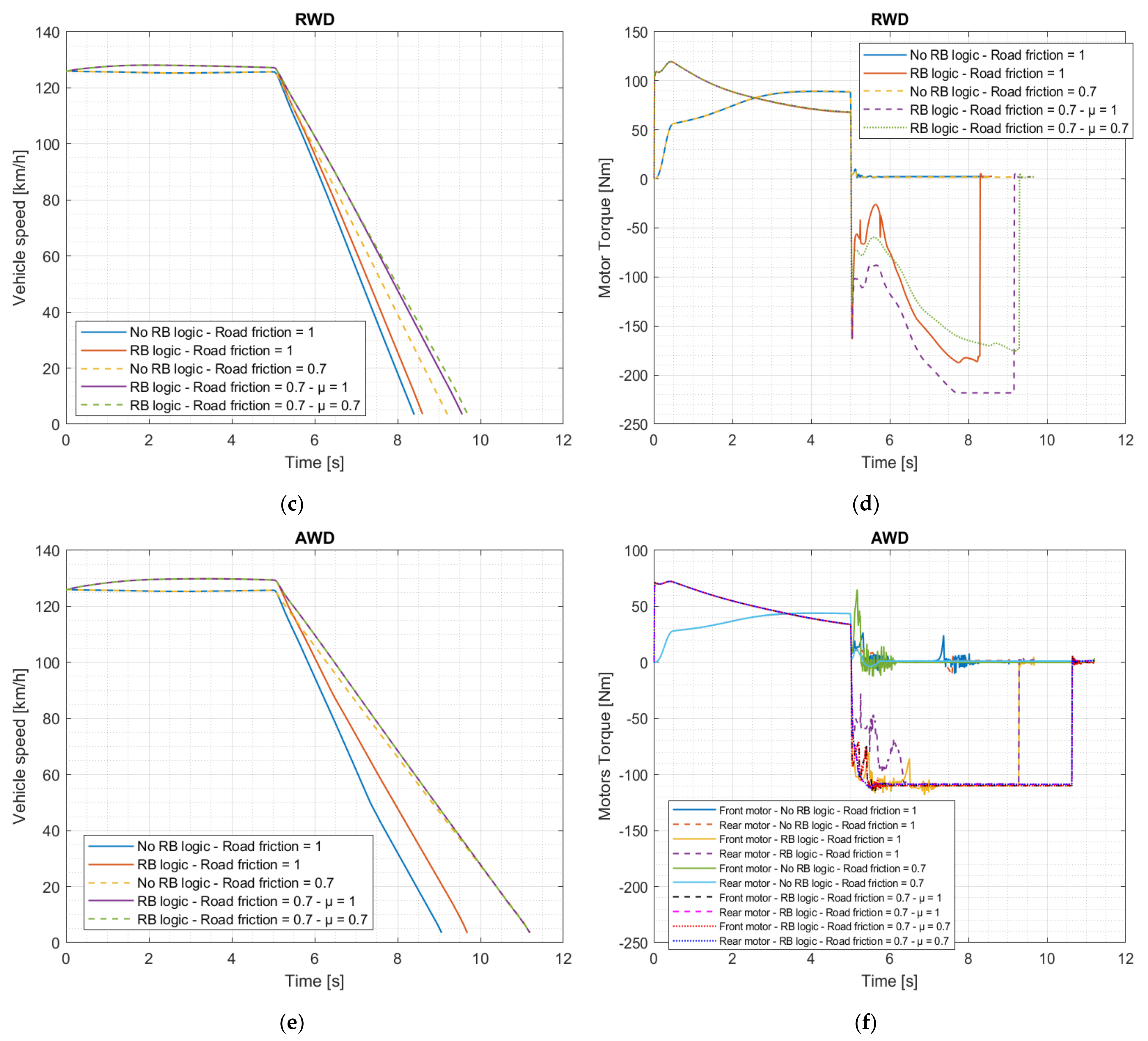

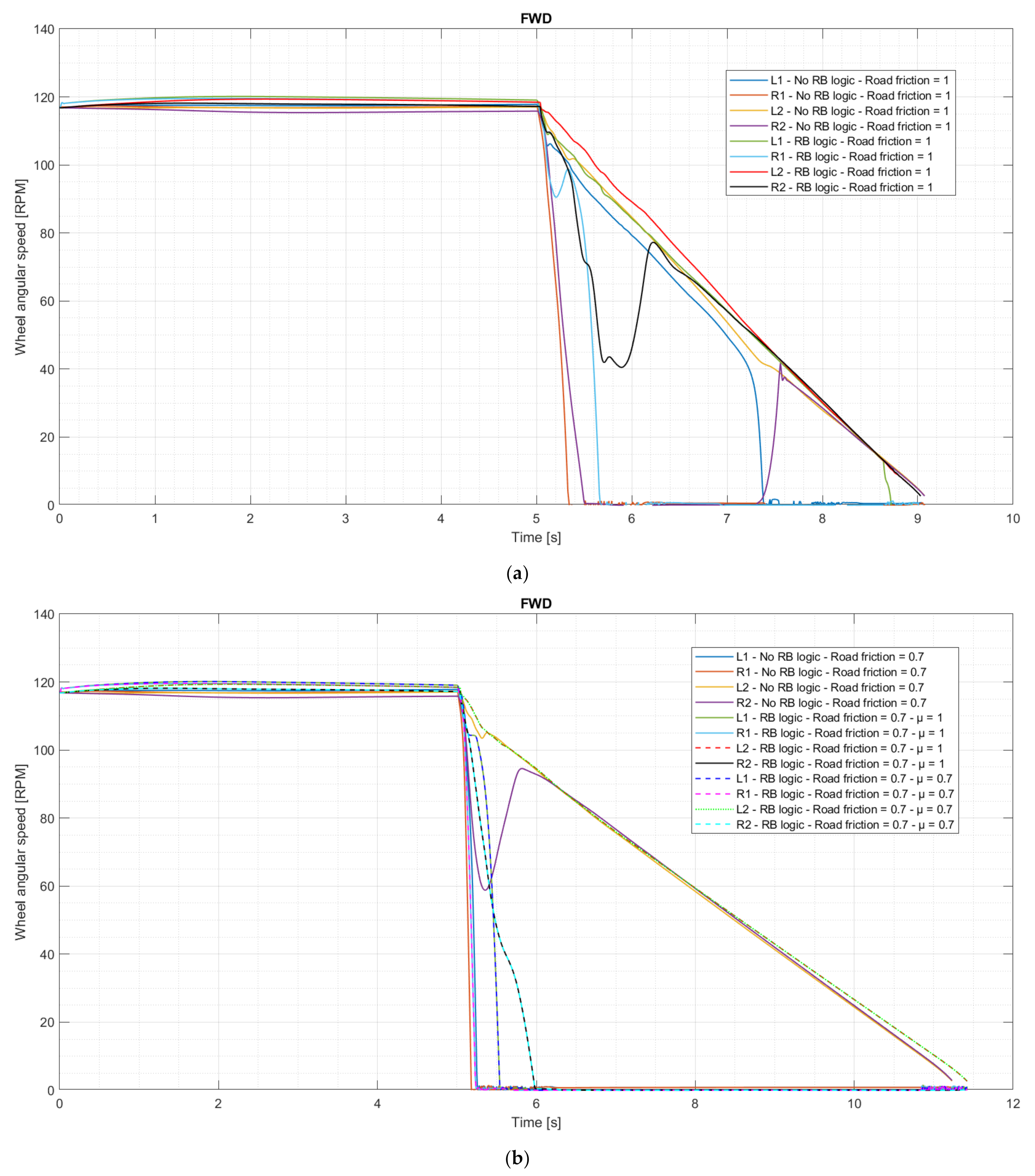
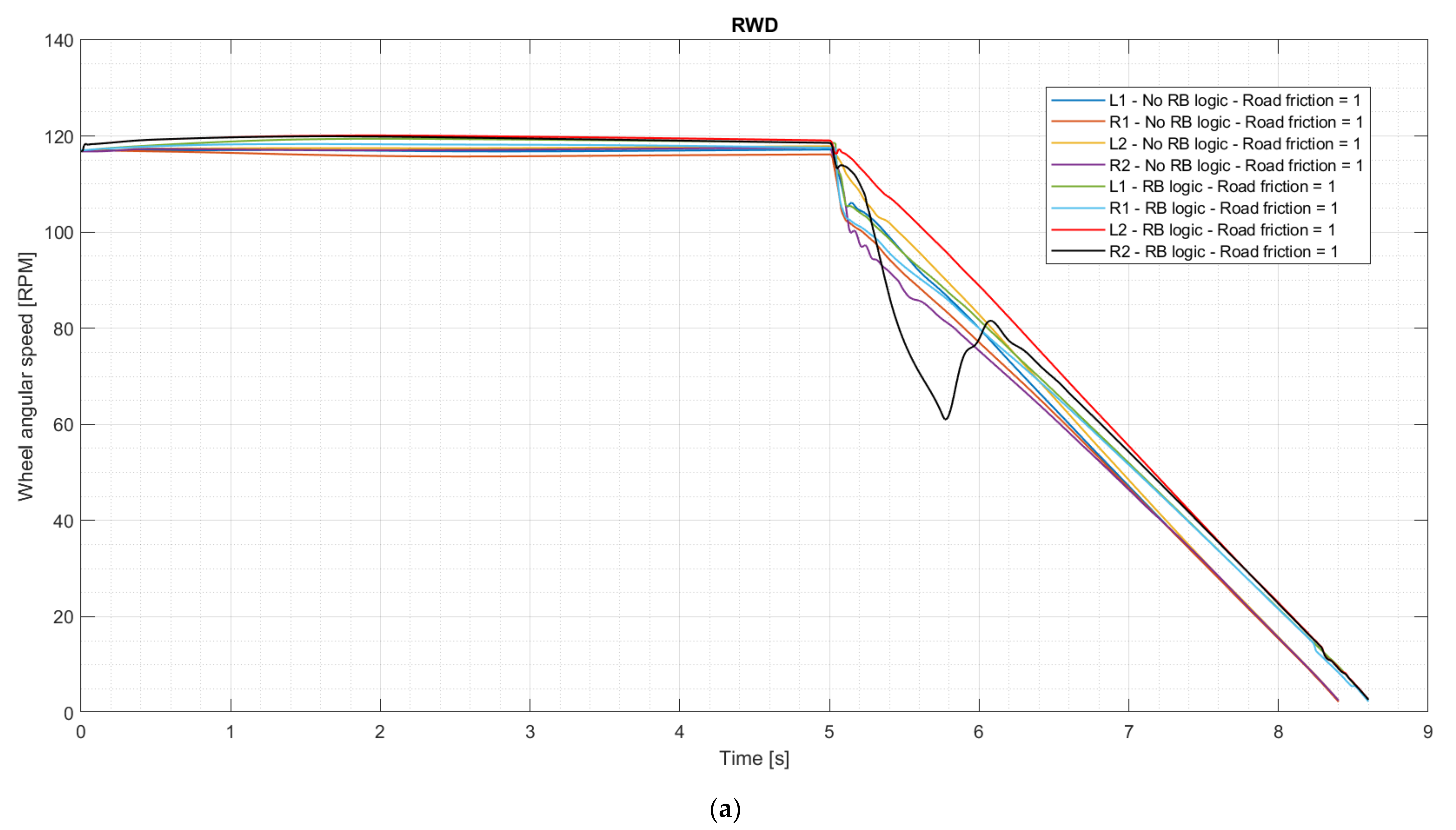



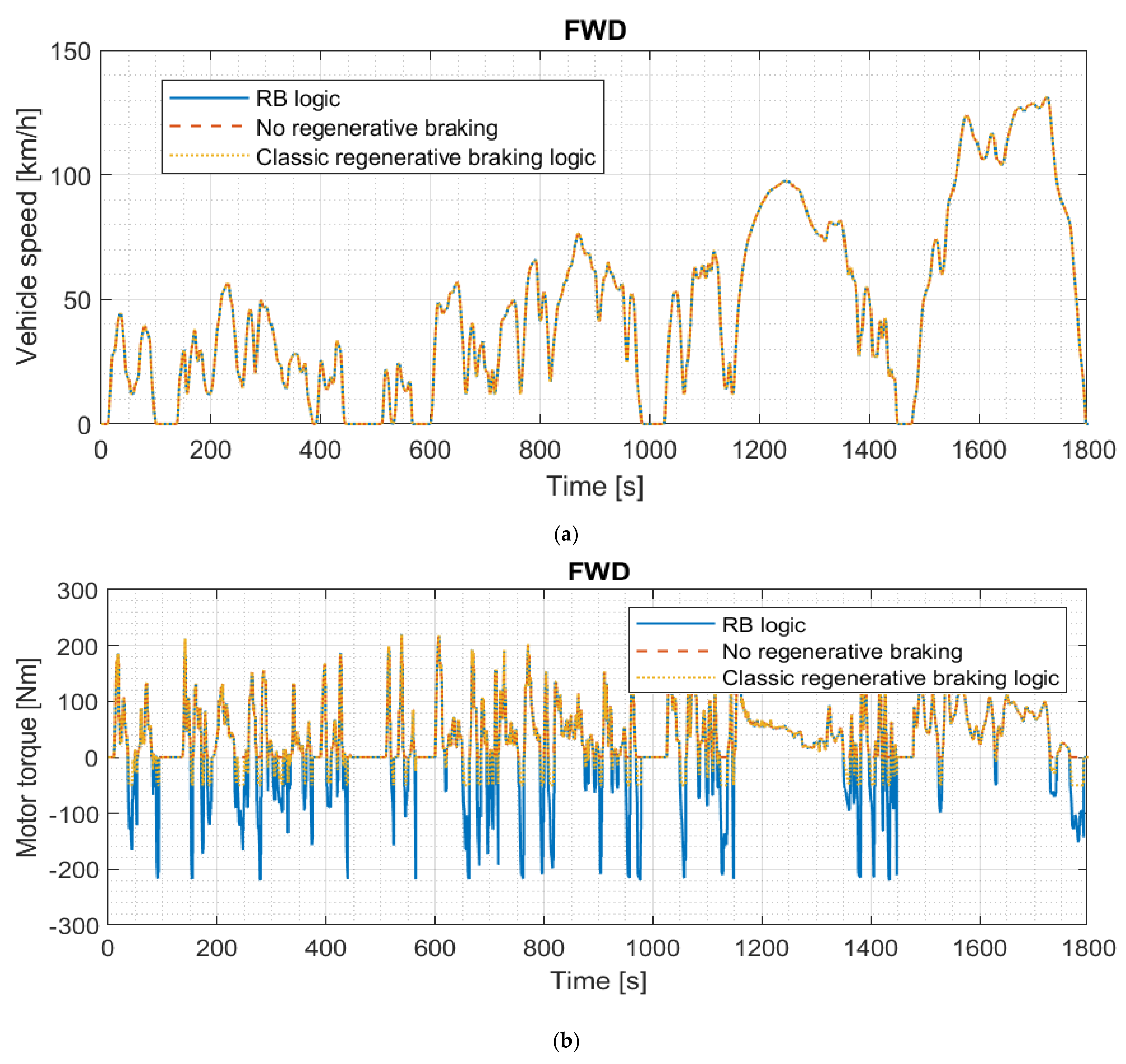
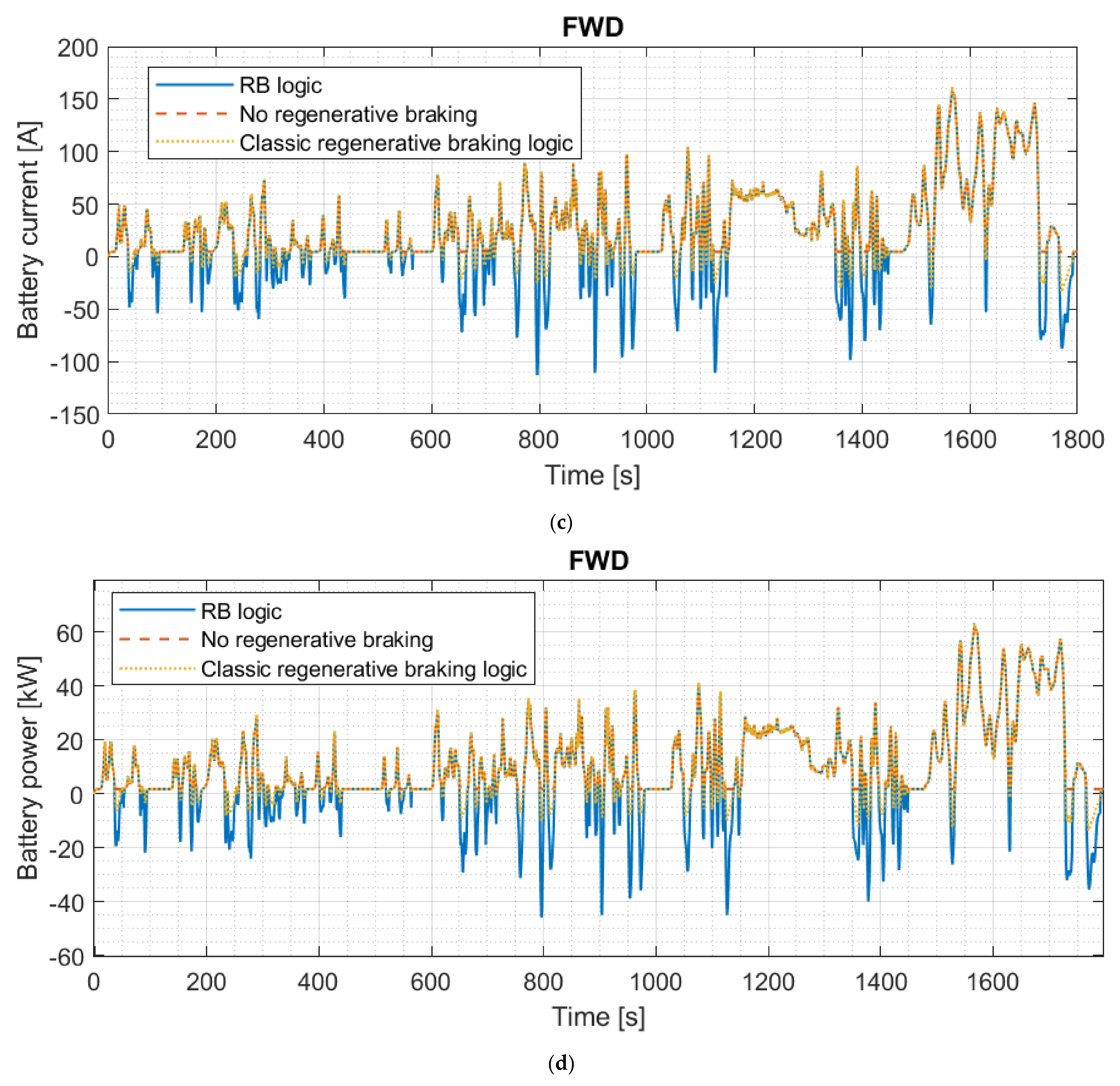

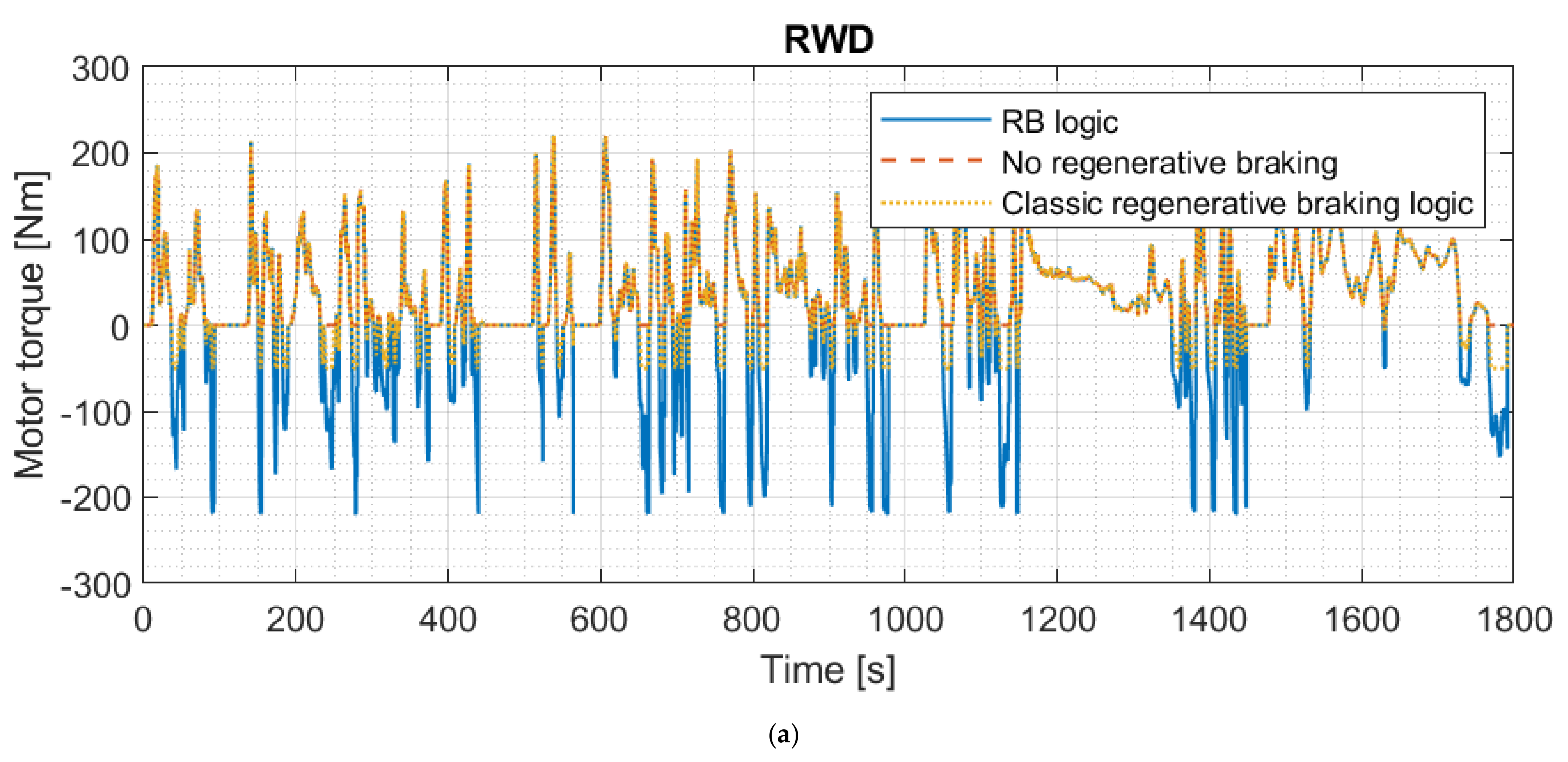

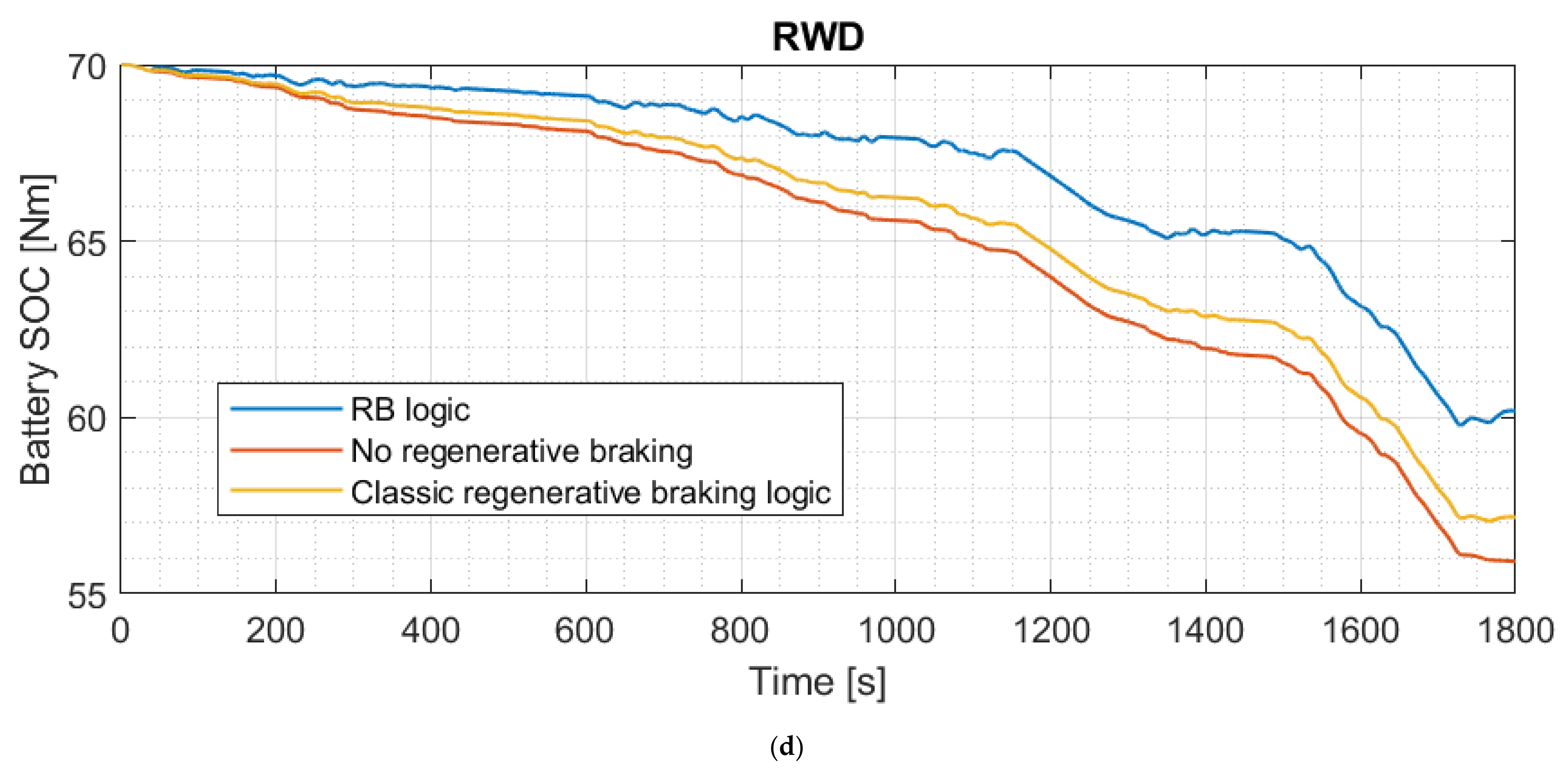
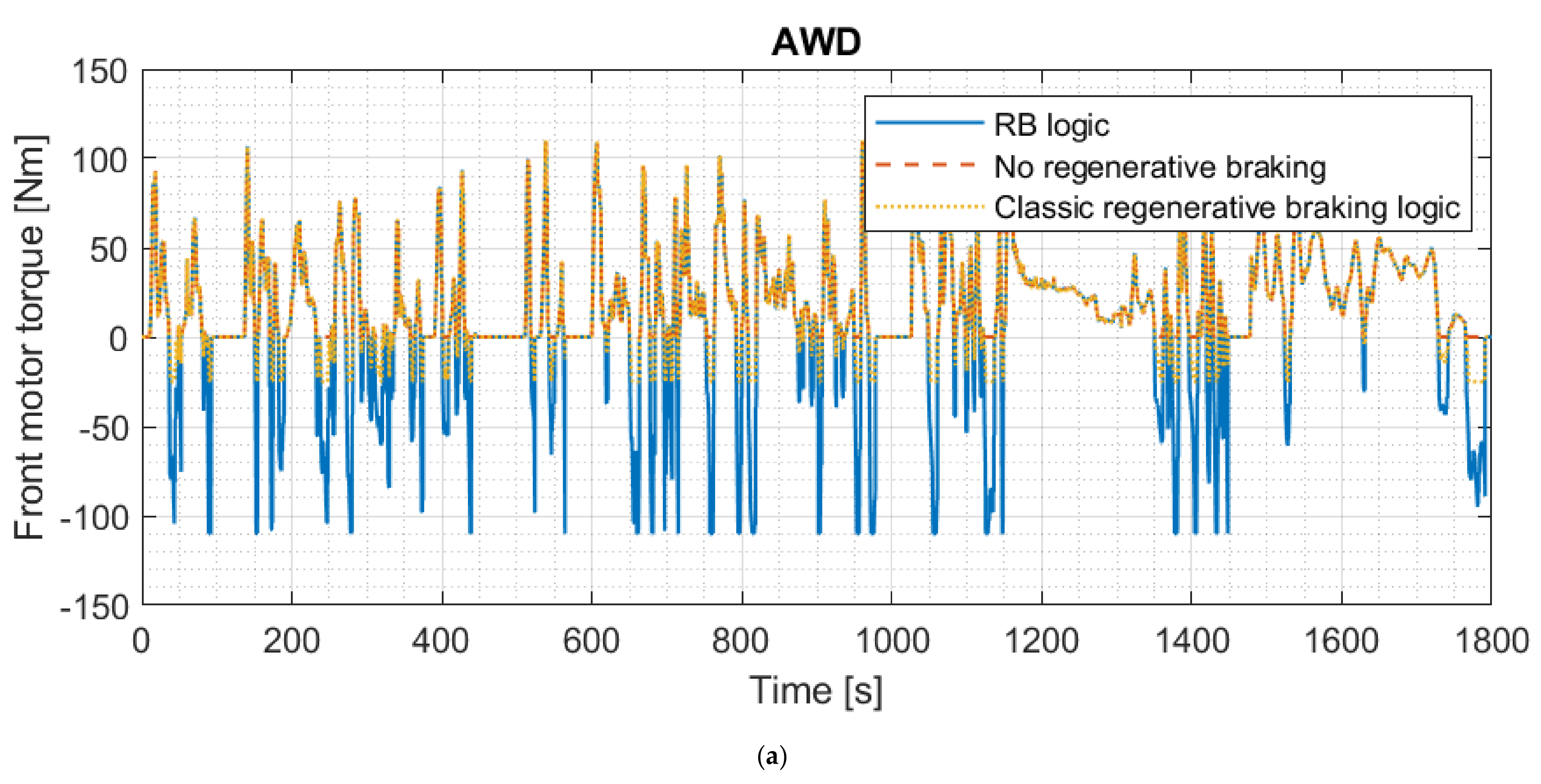
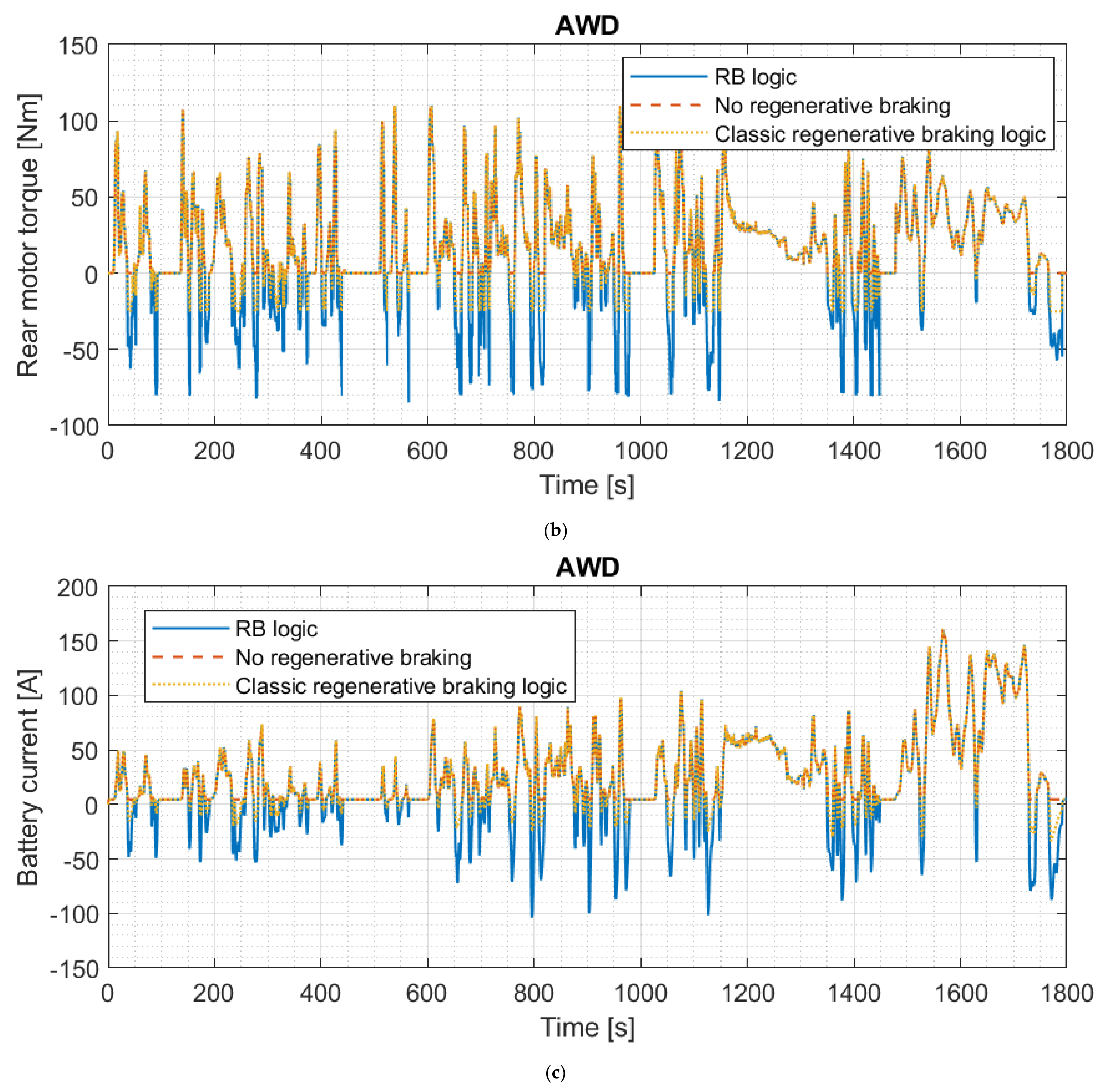

| Dimension | Unit | Value |
|---|---|---|
| Total weight | kg | 1548.38 |
| Front suspended mass | kg | 835.50 |
| Rear suspended mass | kg | 548.15 |
| Front unsprung mass (of a single wheel group) | kg | 44.21 |
| Rear unsprung mass (of a single wheel group) | kg | 38.15 |
| Wheelbase | mm | 2577.4 |
| Front track | mm | 1506.3 |
| Rear track | mm | 1476.9 |
| Center of gravity height | mm | 563.92 |
| CG longitudinal front wheel distance | mm | 1021.55 |
| Front area of the vehicle | m2 | 3.23 |
| Drag coefficient | - | 0.32 |
| Front rolling wheel radius | mm | 298.7 |
| Rear rolling wheel radius | mm | 300.5 |
| Rolling friction coefficient of the wheels | - | 0.01 |
| Transmission ratio | - | 1 |
| Drive ratio of differential 1 | - | 3.7 |
| Power absorbed by vehicle accessories | W | 1500 |
| Dimension | Unit | Value |
|---|---|---|
| Maximum front brake pressure | MPa | 9.75 |
| Maximum rear brake pressure | MPa | 5.25 |
| Front pistons area | mm2 | 2000 |
| Rear pistons area | mm2 | 1100 |
| Front effective piston radius | Mm | 134 |
| Rear effective piston radius | Mm | 104 |
| Dimension | Unit | Value |
|---|---|---|
| Front center roll height | Mm | 39.20 |
| Rear center roll height | Mm | 128.84 |
| Front spring stiffness | N/mm | 25 |
| Rear spring stiffness | N/mm | 27 |
| Dimension | Unit | Value |
|---|---|---|
| Number of cells in series | - | 96 |
| Number of cells in parallel | - | 2 |
| Nominal capacity of the pack | Ah | 105 |
| Nominal capacity of the pack | kWh | 42 |
| Available battery capacity | kWh | 37.5 |
| Operating temperature | °C | 23 |
| Maximum deliverable power in discharge | kW | 87 |
| Maximum absorbable power in charge | kW | 85 |
| Open circuit voltage of a single cell | V | 4.17 |
| Dimension | Unit | Value |
|---|---|---|
| Initial vehicle speed | km/h | 108 |
| Final vehicle speed | km/h | 0 |
| Start time | s | 0 |
| Ramp up time | s | 10 |
| Brake demand | - | 1 |
| Road friction coefficient | - | 1 |
| Dimension | Unit | Value |
|---|---|---|
| Initial vehicle speed | km/h | 90 |
| Final vehicle speed | km/h | 0 |
| Start time | s | 1 |
| Ramp up time | s | 1 |
| Brake demand | - | 1 |
| Dimension | Unit | Value |
|---|---|---|
| Initial vehicle speed | m/s | 35 |
| Final vehicle speed of the test | m/s | 0 |
| Constant deceleration in braking | m/s2 | 10 |
| Turn radius | m | 300 |
| Turn direction | - | right |
| Start time of the braking | s | 5 |
| Distance traveled before the start of the maneuver | m | 5 |
| Type of Vehicle | Regenerative Braking Logic | Final SOC (%) | SOC Consumption (%) | Energy Consumption (kWh) | Specific Energy Consumption (kWh/(100 km)) |
|---|---|---|---|---|---|
| FWD | RB logic | 60.18 | 9.82 | 4.12 | 17.73 |
| No brake recovery | 55.91 | 14.09 | 5.92 | 25.43 | |
| Classic logic | 57.17 | 12.83 | 5.39 | 23.16 | |
| RWD | RB logic | 60.19 | 9.81 | 4.12 | 17.72 |
| No brake recovery | 55.91 | 14.09 | 5.92 | 25.43 | |
| Classic logic | 57.17 | 12.83 | 5.39 | 23.16 | |
| AWD | RB logic | 60.07 | 9.93 | 4.17 | 17.92 |
| No brake recovery | 55.91 | 14.09 | 5.92 | 25.44 | |
| Classic logic | 57.17 | 12.83 | 5.39 | 23.17 |
| Type of Vehicle | Regenerative Braking Logic | Final SOC (%) | SOC Consumption (%) | Energy Consumption (kWh) | Specific Energy Consumption (kWh/(100 km)) |
|---|---|---|---|---|---|
| FWD | RB logic | 62.86 | 7.14 | 3.00 | 23.67 |
| No brake recovery | 60.55 | 9.45 | 3.97 | 31.33 | |
| Classic logic | 61.12 | 8.88 | 3.73 | 29.42 | |
| RWD | RB logic | 62.86 | 7.14 | 3.00 | 23.68 |
| No brake recovery | 60.55 | 9.45 | 3.97 | 31.32 | |
| Classic logic | 61.12 | 8.88 | 3.73 | 29.43 | |
| AWD | RB logic | 62.81 | 7.19 | 3.02 | 23.84 |
| No brake recovery | 60.55 | 9.45 | 3.97 | 31.34 | |
| Classic logic | 61.12 | 8.88 | 3.73 | 29.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandrini, G.; Chindamo, D.; Gadola, M. Regenerative Braking Logic That Maximizes Energy Recovery Ensuring the Vehicle Stability. Energies 2022, 15, 5846. https://doi.org/10.3390/en15165846
Sandrini G, Chindamo D, Gadola M. Regenerative Braking Logic That Maximizes Energy Recovery Ensuring the Vehicle Stability. Energies. 2022; 15(16):5846. https://doi.org/10.3390/en15165846
Chicago/Turabian StyleSandrini, Giulia, Daniel Chindamo, and Marco Gadola. 2022. "Regenerative Braking Logic That Maximizes Energy Recovery Ensuring the Vehicle Stability" Energies 15, no. 16: 5846. https://doi.org/10.3390/en15165846
APA StyleSandrini, G., Chindamo, D., & Gadola, M. (2022). Regenerative Braking Logic That Maximizes Energy Recovery Ensuring the Vehicle Stability. Energies, 15(16), 5846. https://doi.org/10.3390/en15165846








