An Exponential Solvent Chamber Geometry for Modeling the VAPEX Process
Abstract
:1. Introduction
2. Materials and Methods
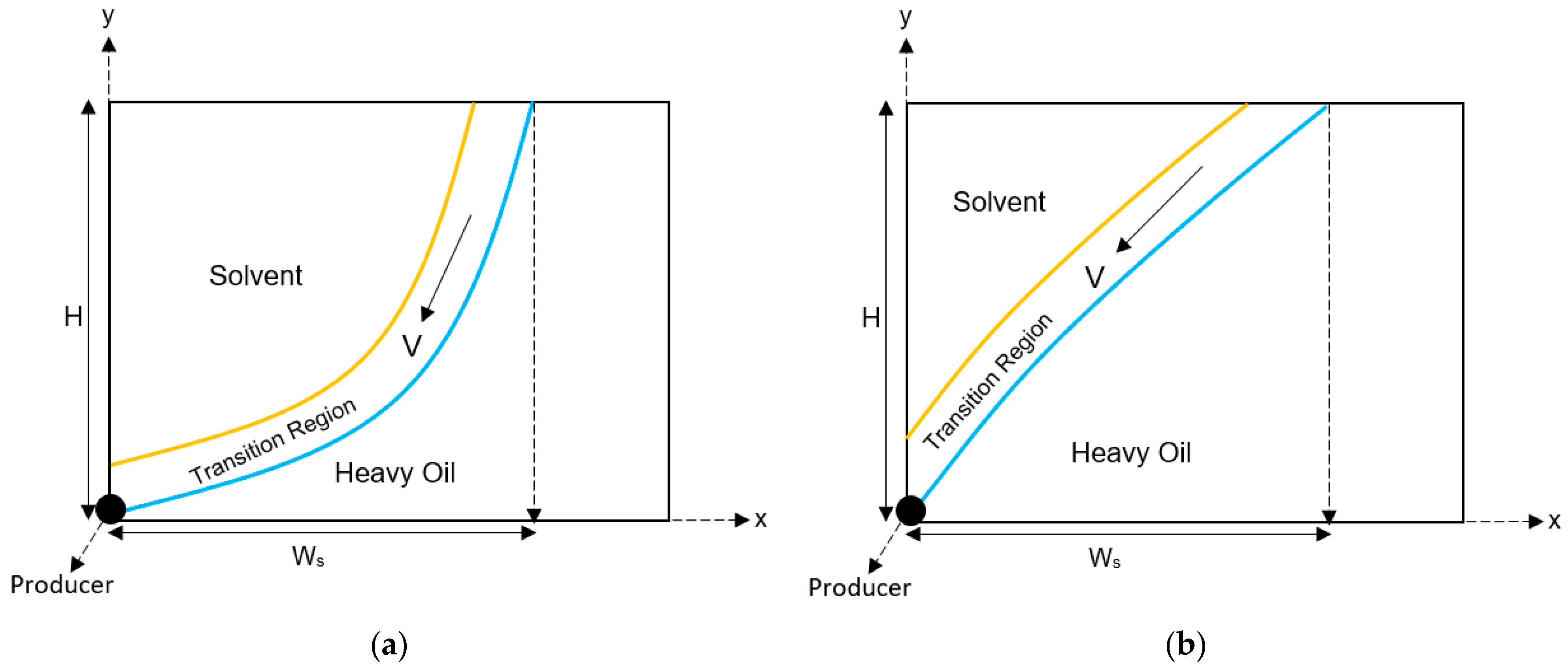
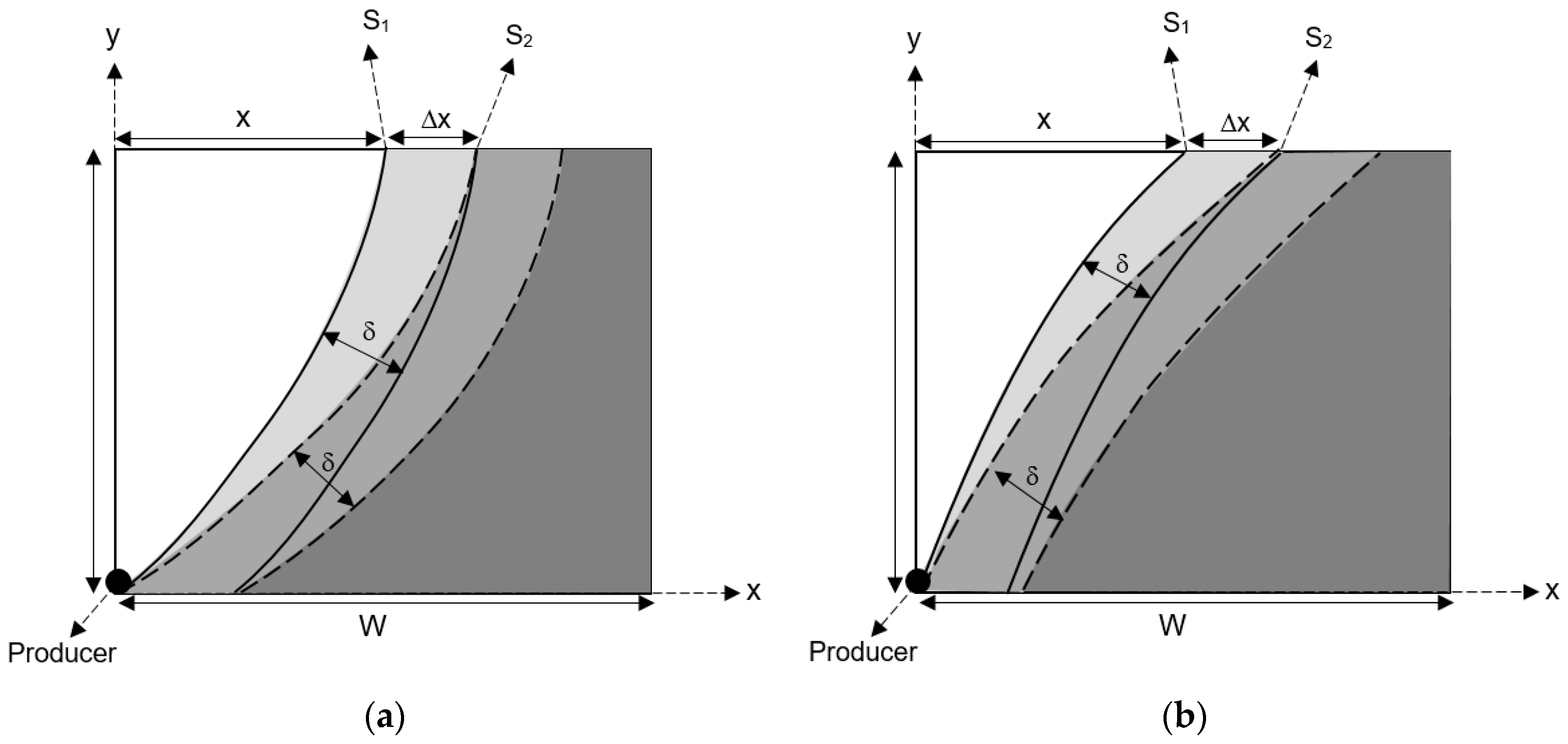
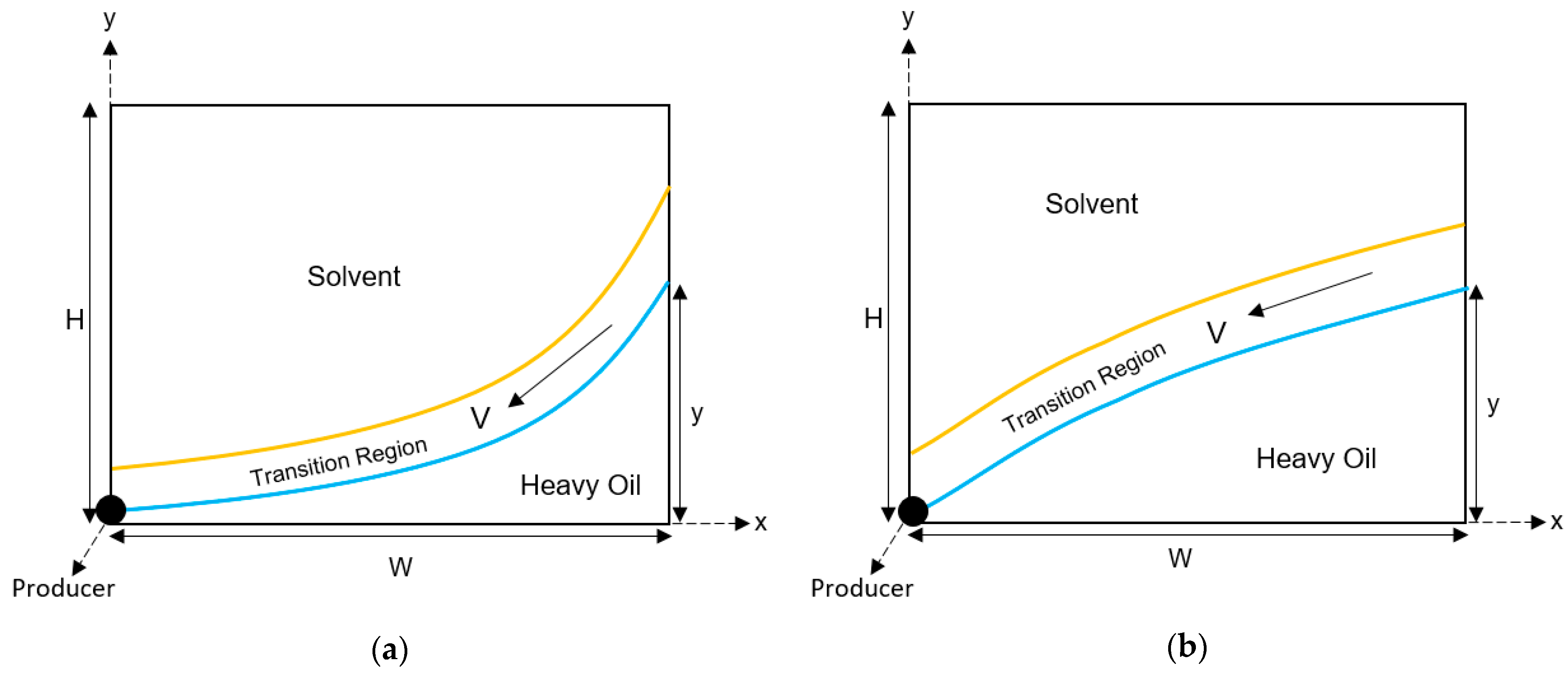
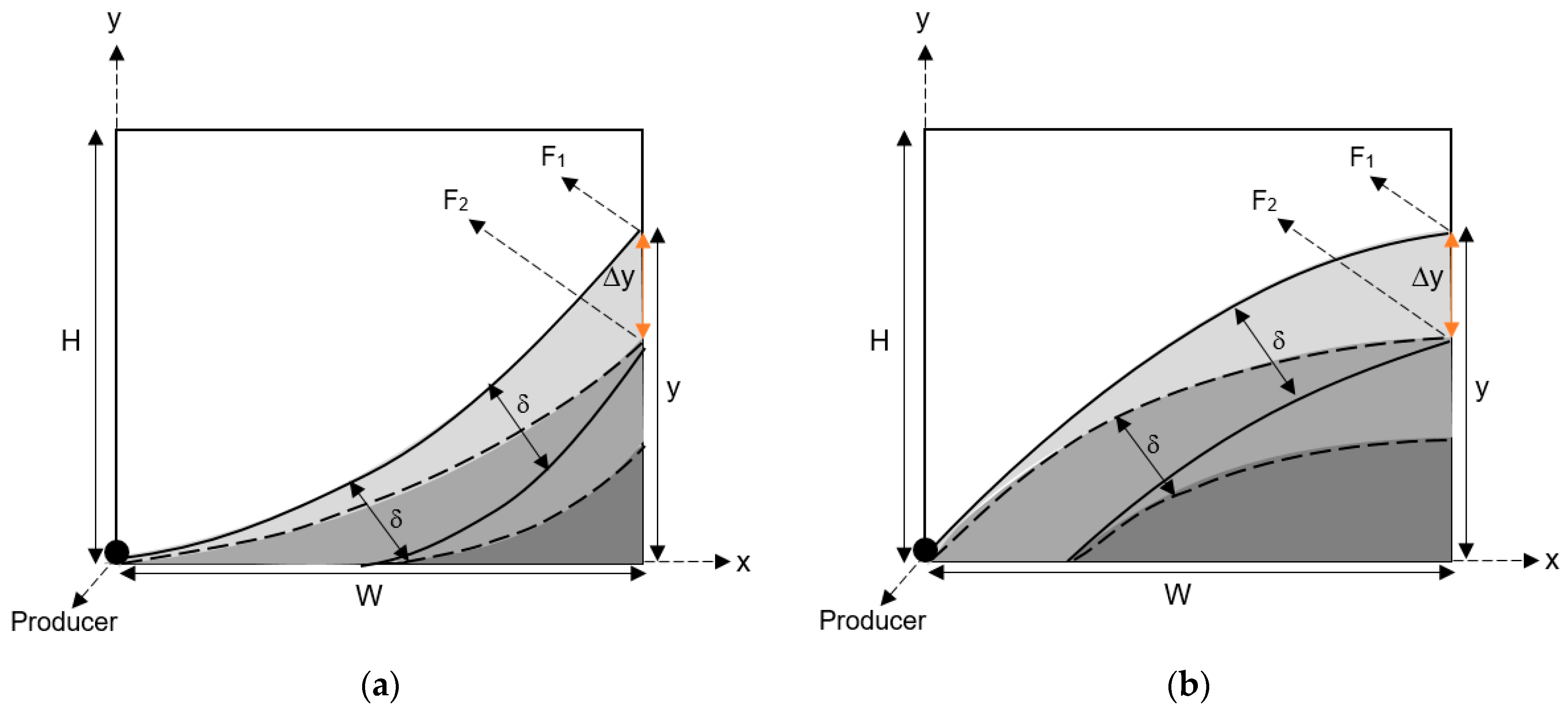
- The transition region is constant in thickness during the whole process.
- Oil saturation within the transition region rapidly falls to its minimum value of residual oil saturation.
- The physical model is homogenous and isotropic.
- The diluted heavy oil within the transition region moves at its maximum velocity.
- Temperature and pressure remain constant throughout the process.
- There is no driving force for moving oil inside the transition region other than the gravity drainage.
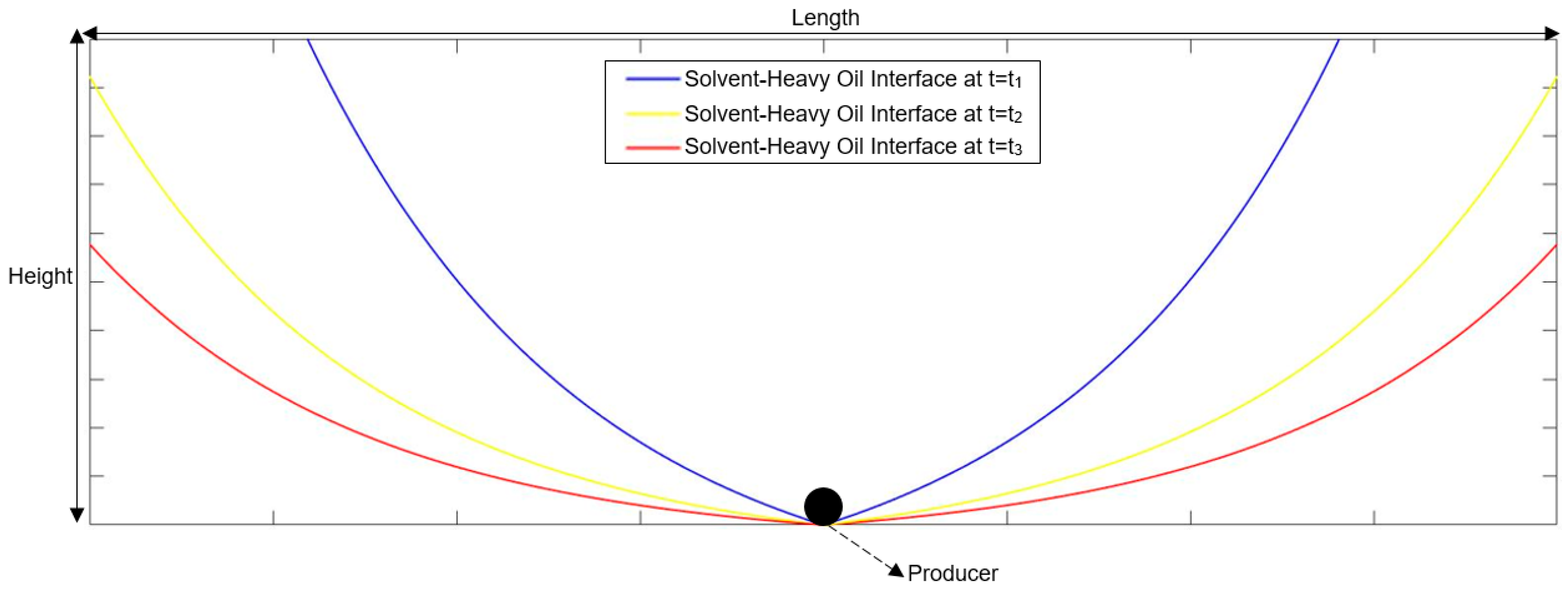
2.1. Mathematical Modeling of the Rising Stage
2.2. Mathematical Modeling of the Falling Stage
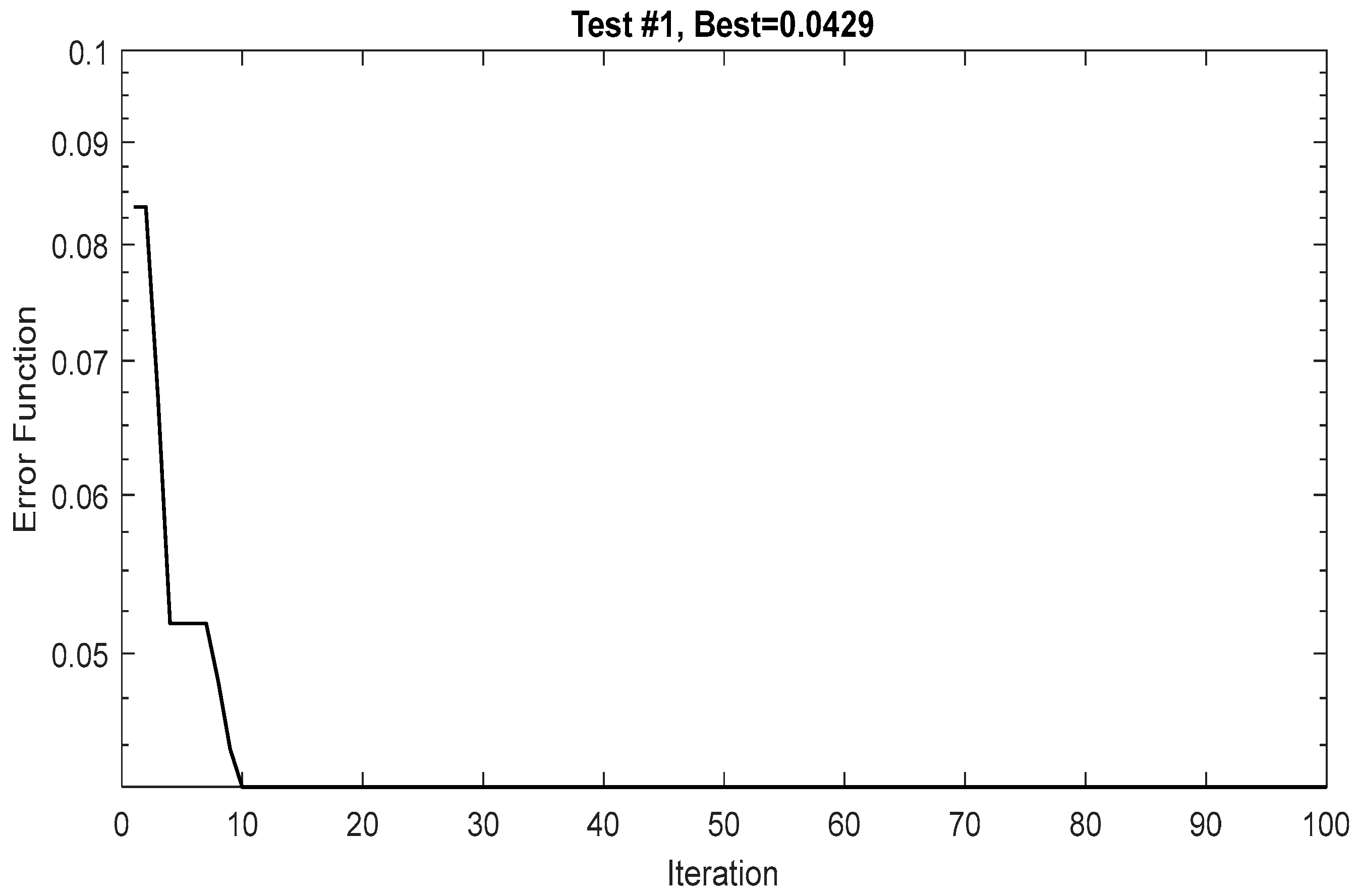
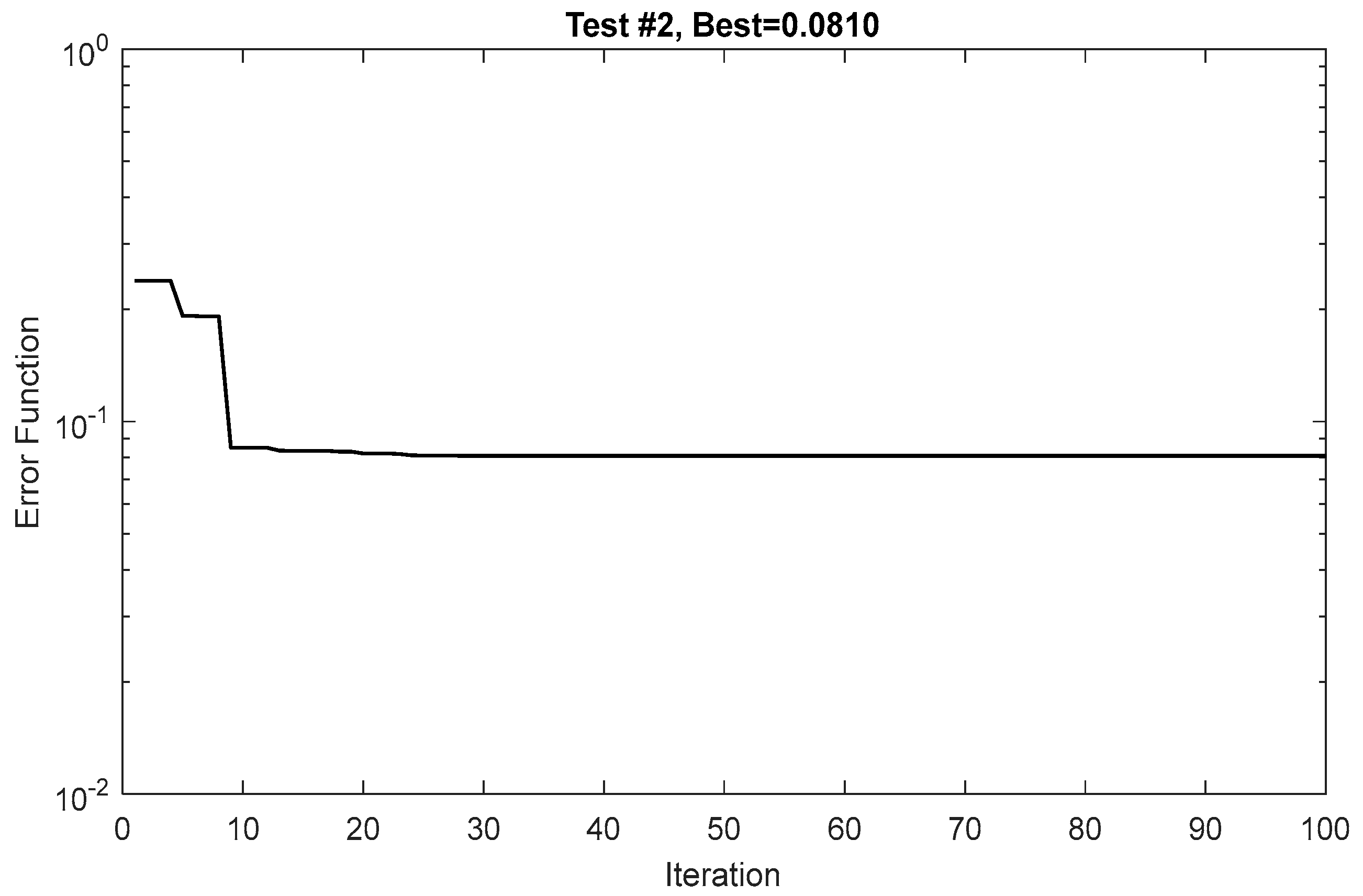
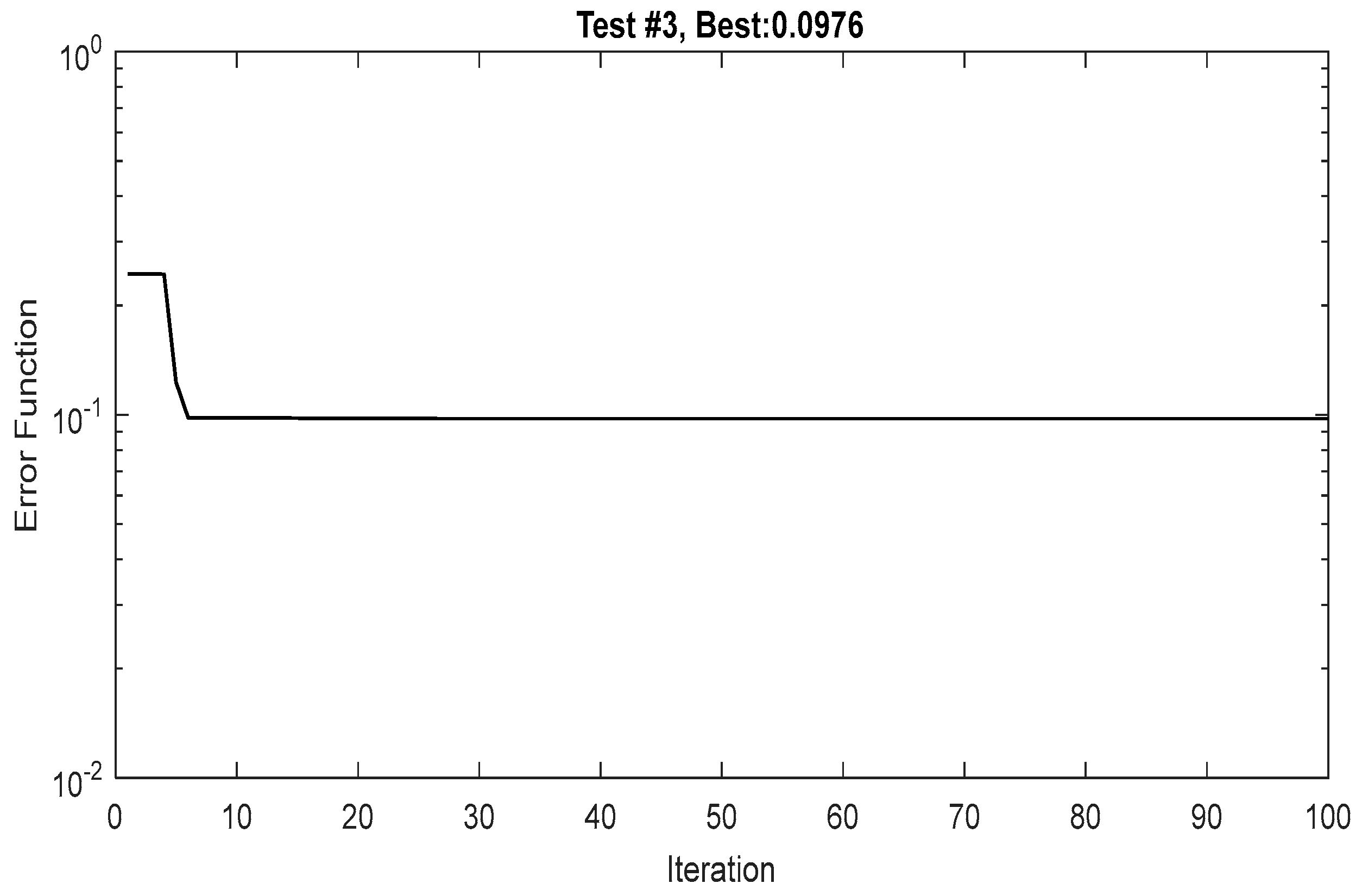
2.3. Problem Solving and Objective Function
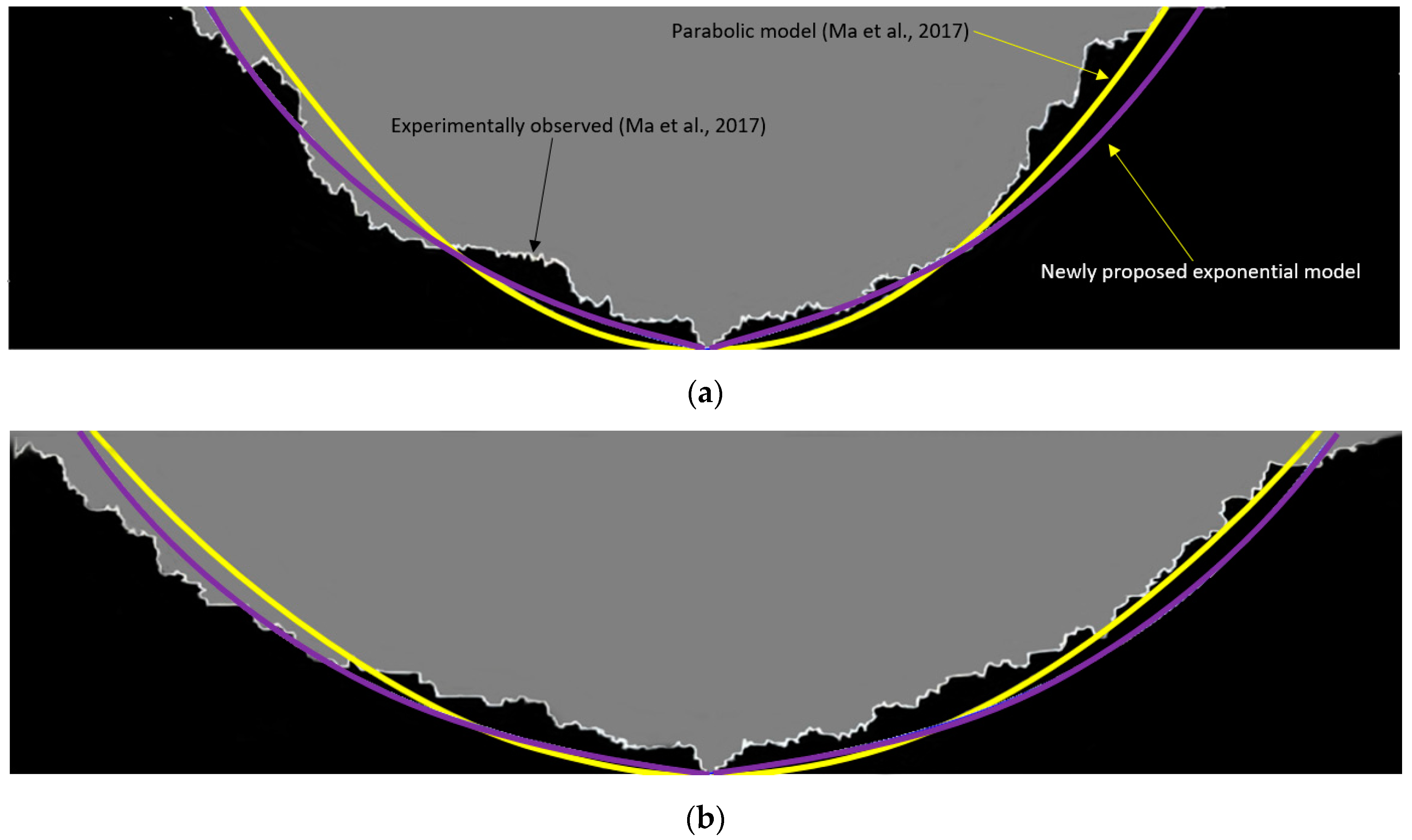
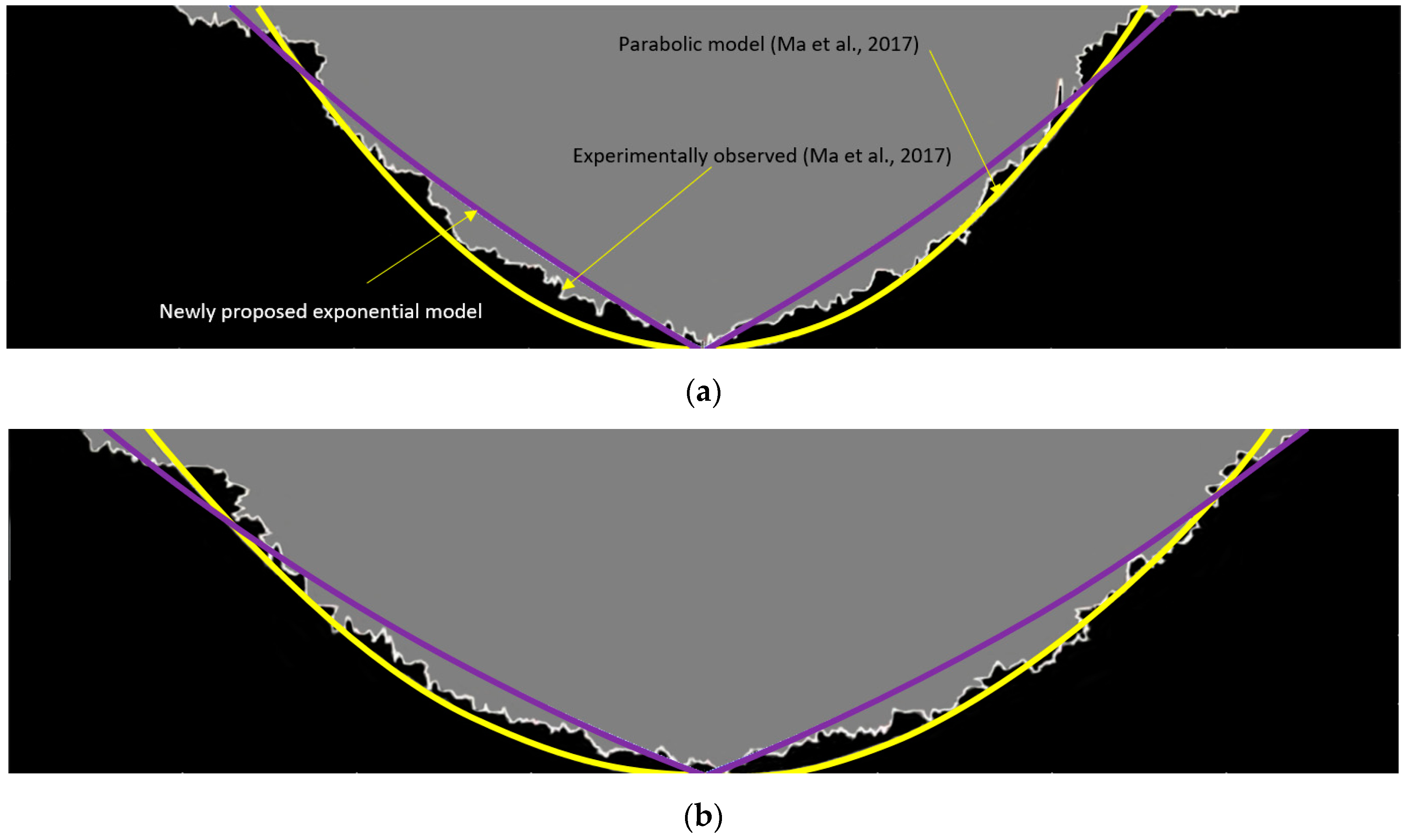
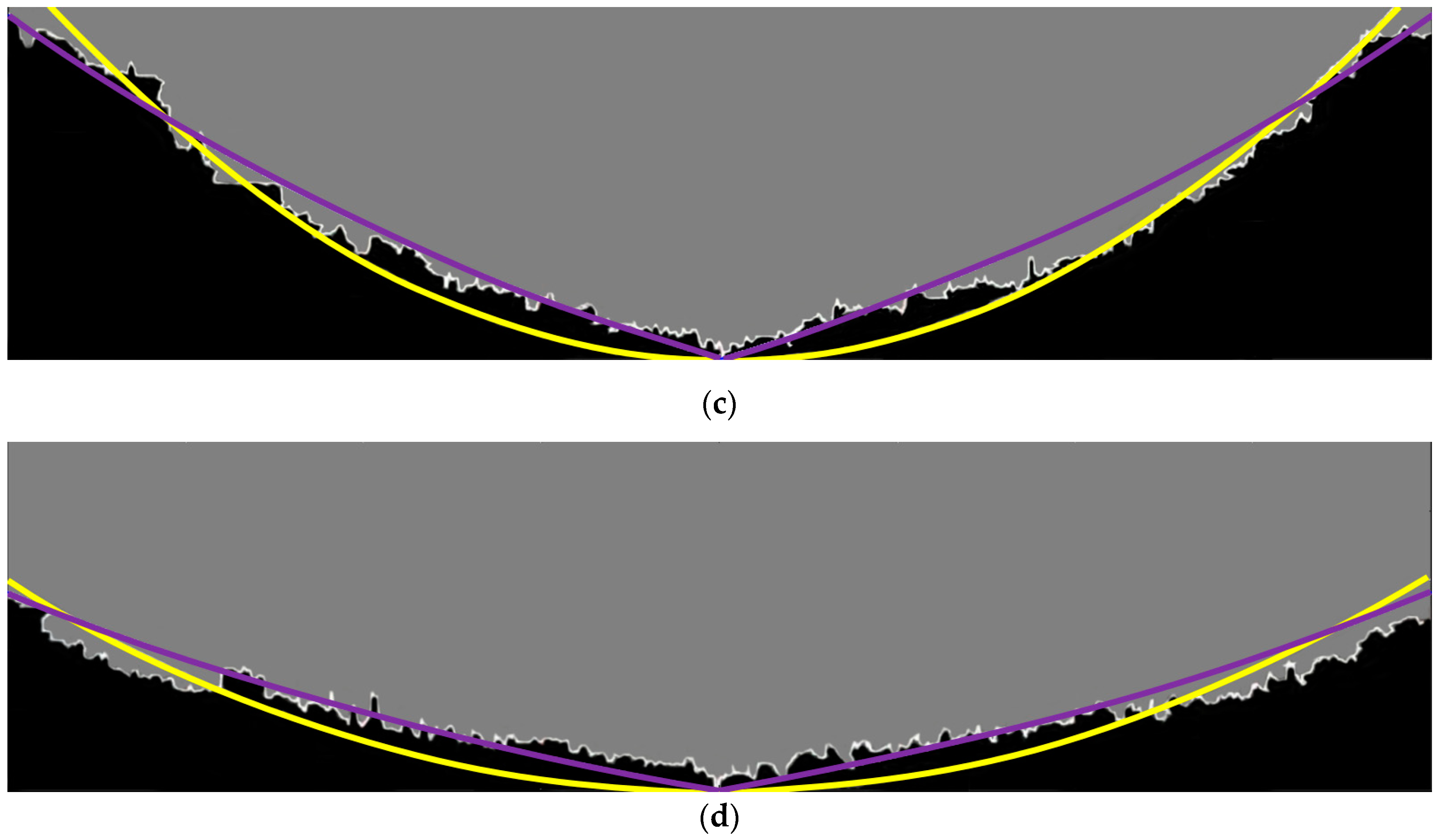
3. Results and Discussion
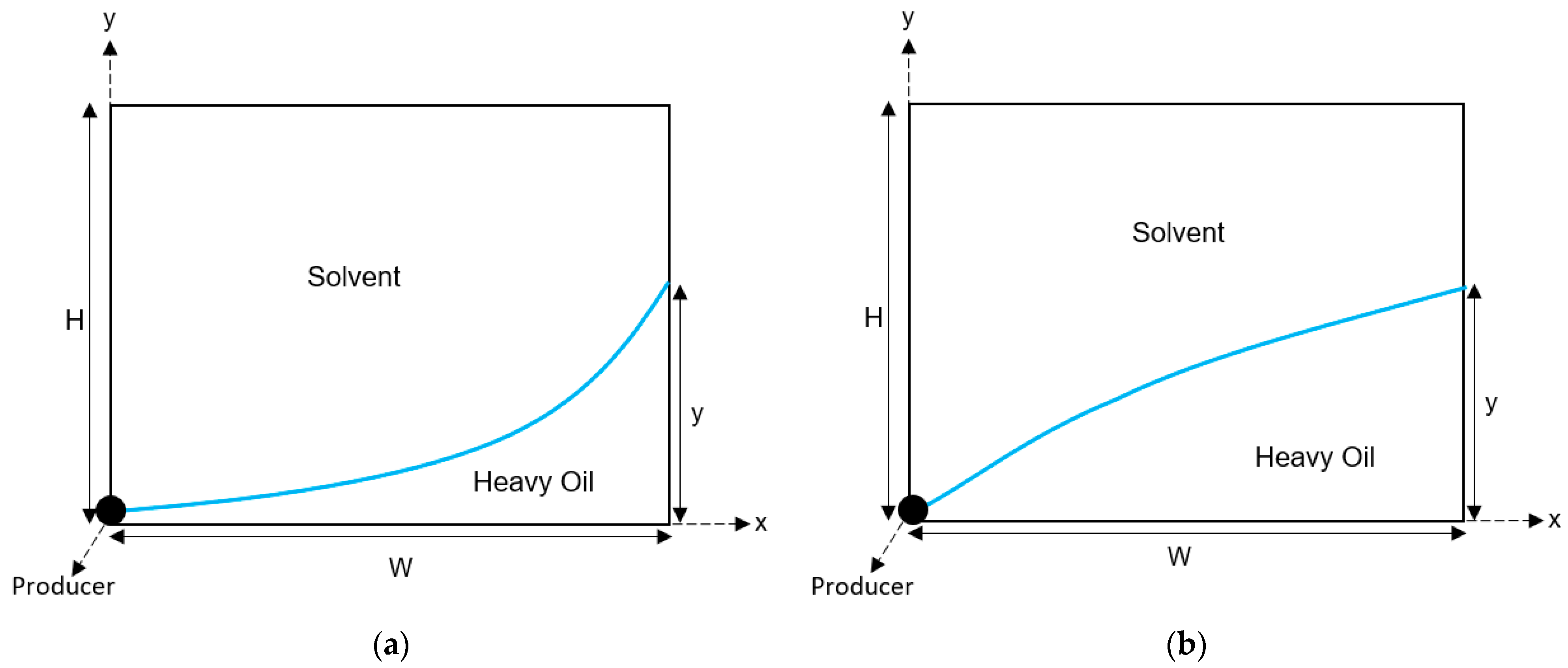
3.1. Solvent Chamber Propagation
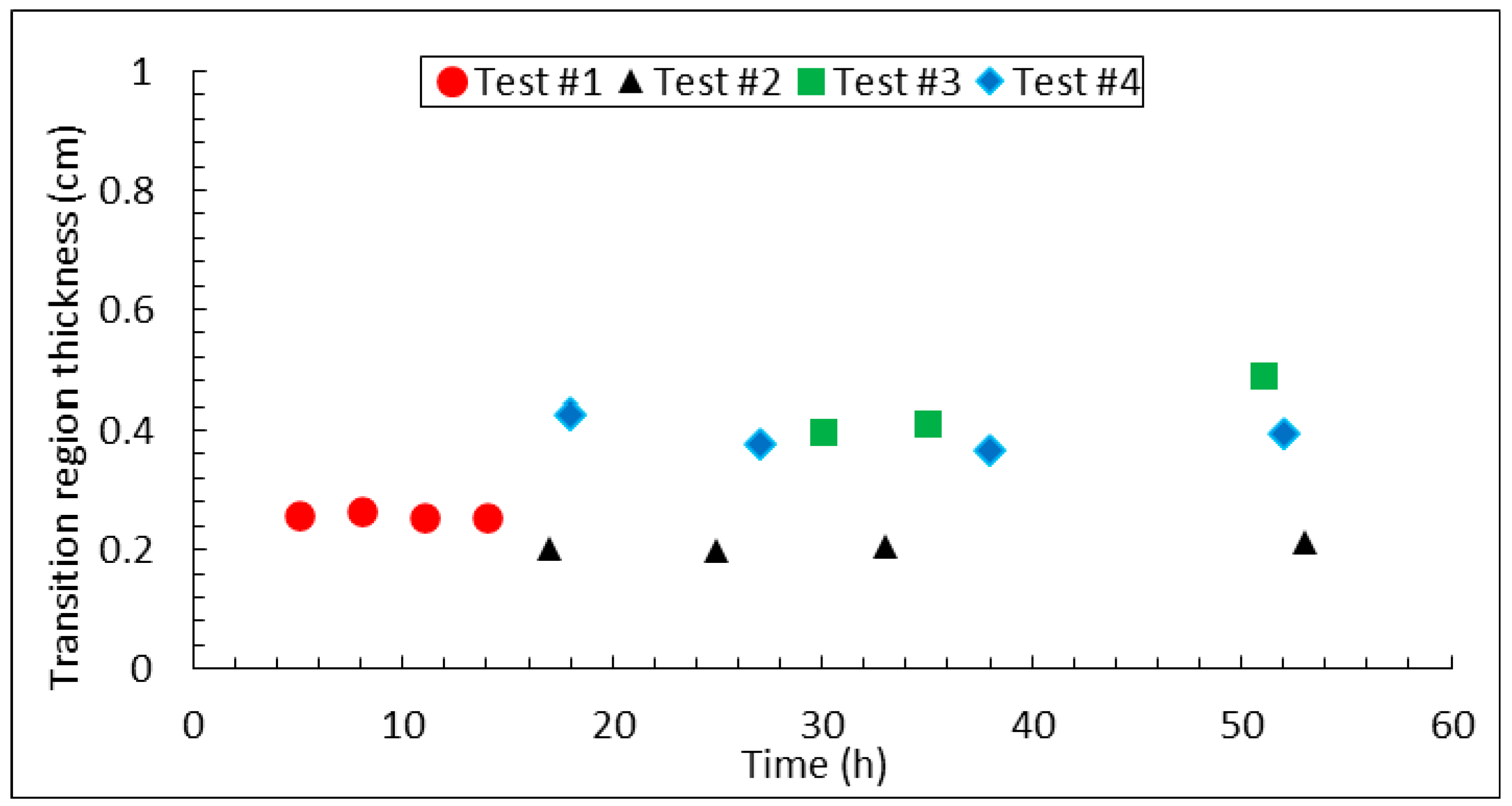
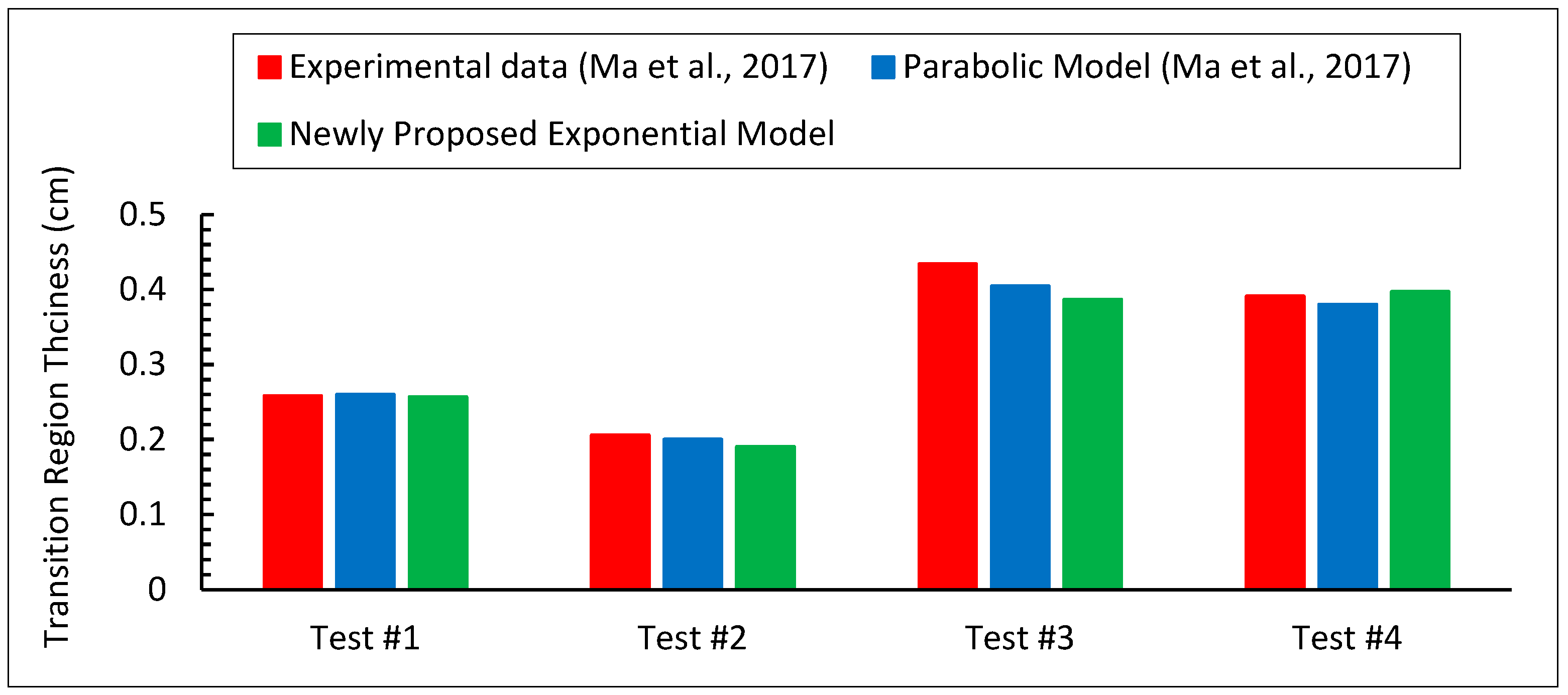
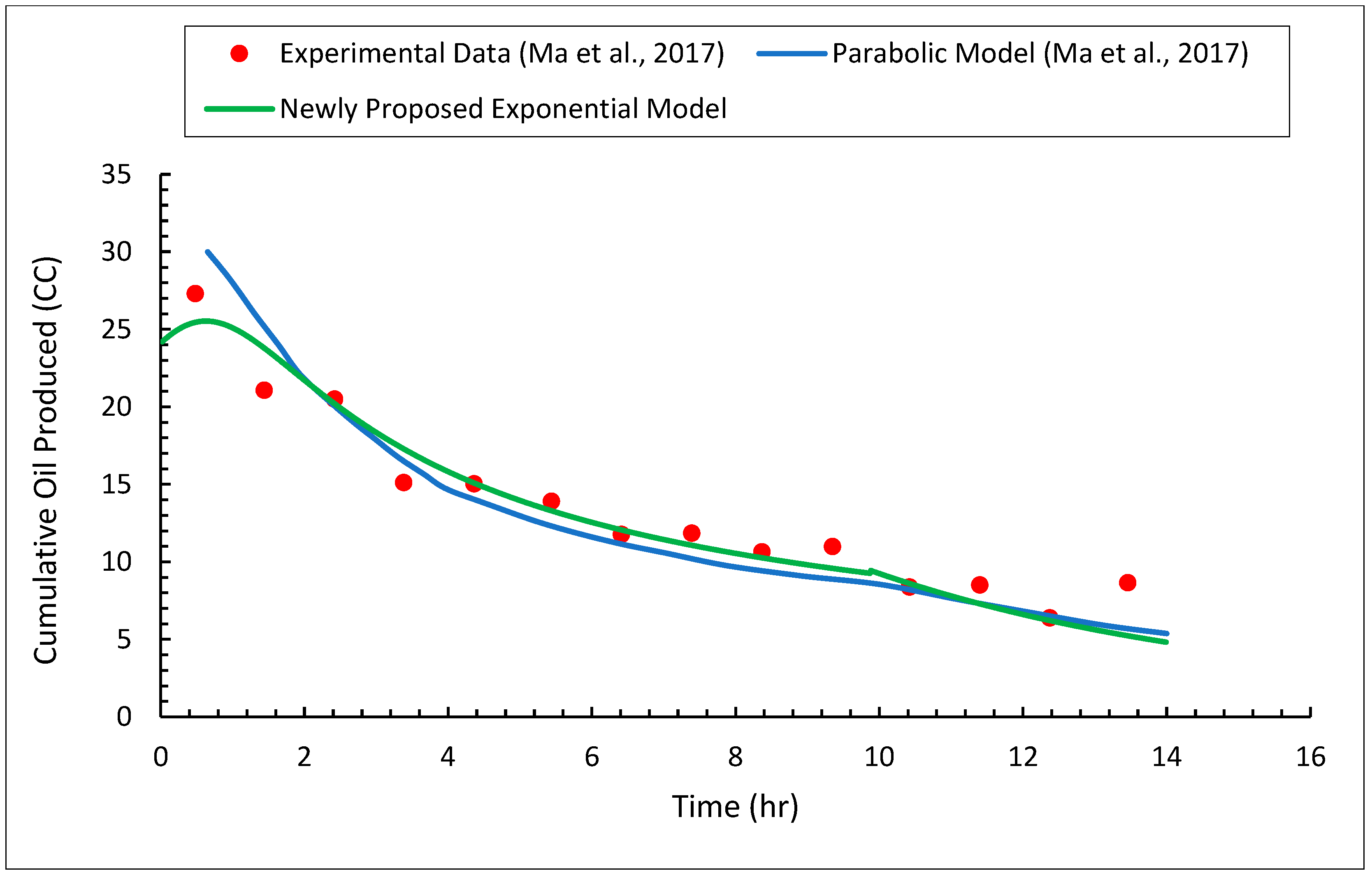
3.2. Transition Region Thickness
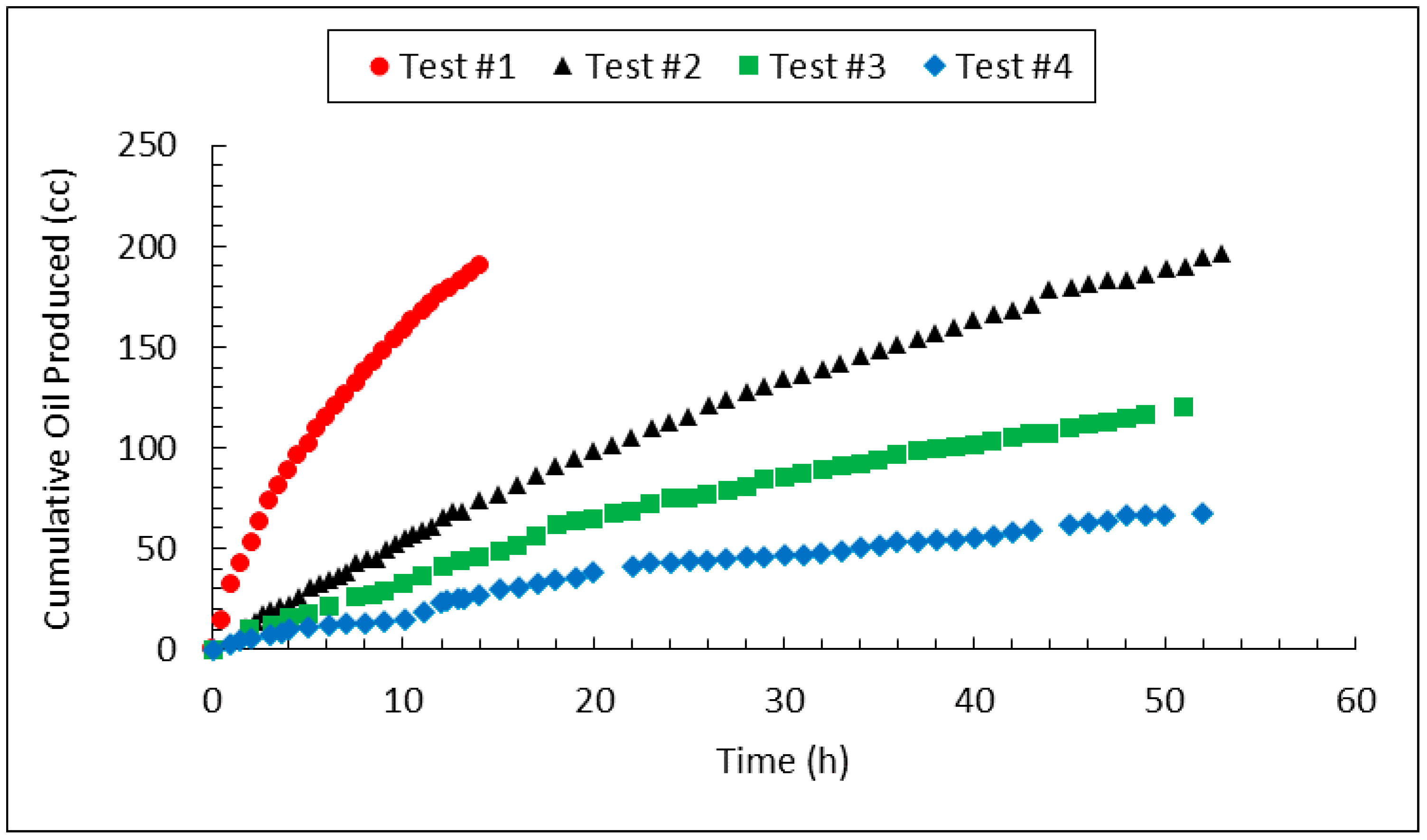
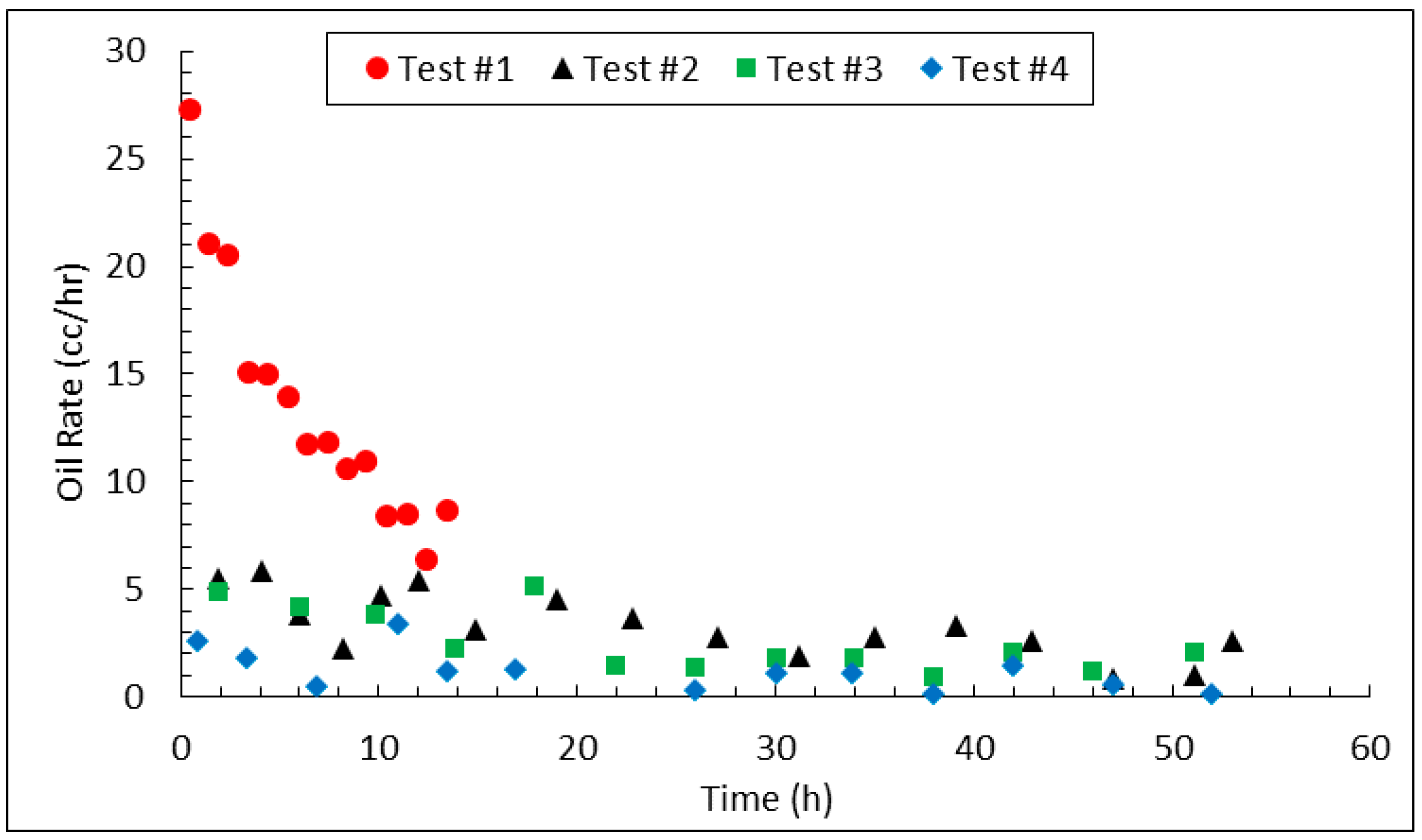
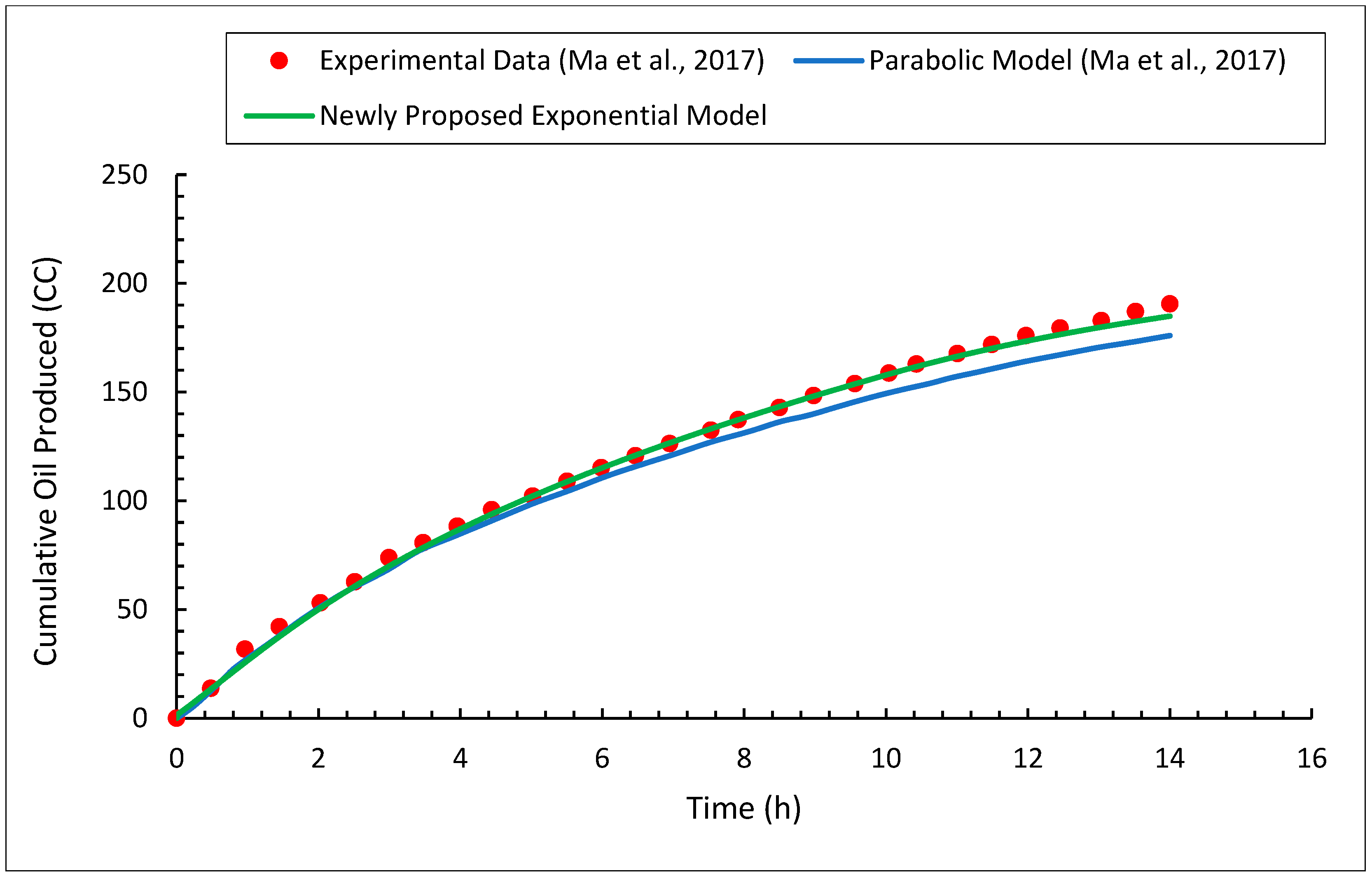
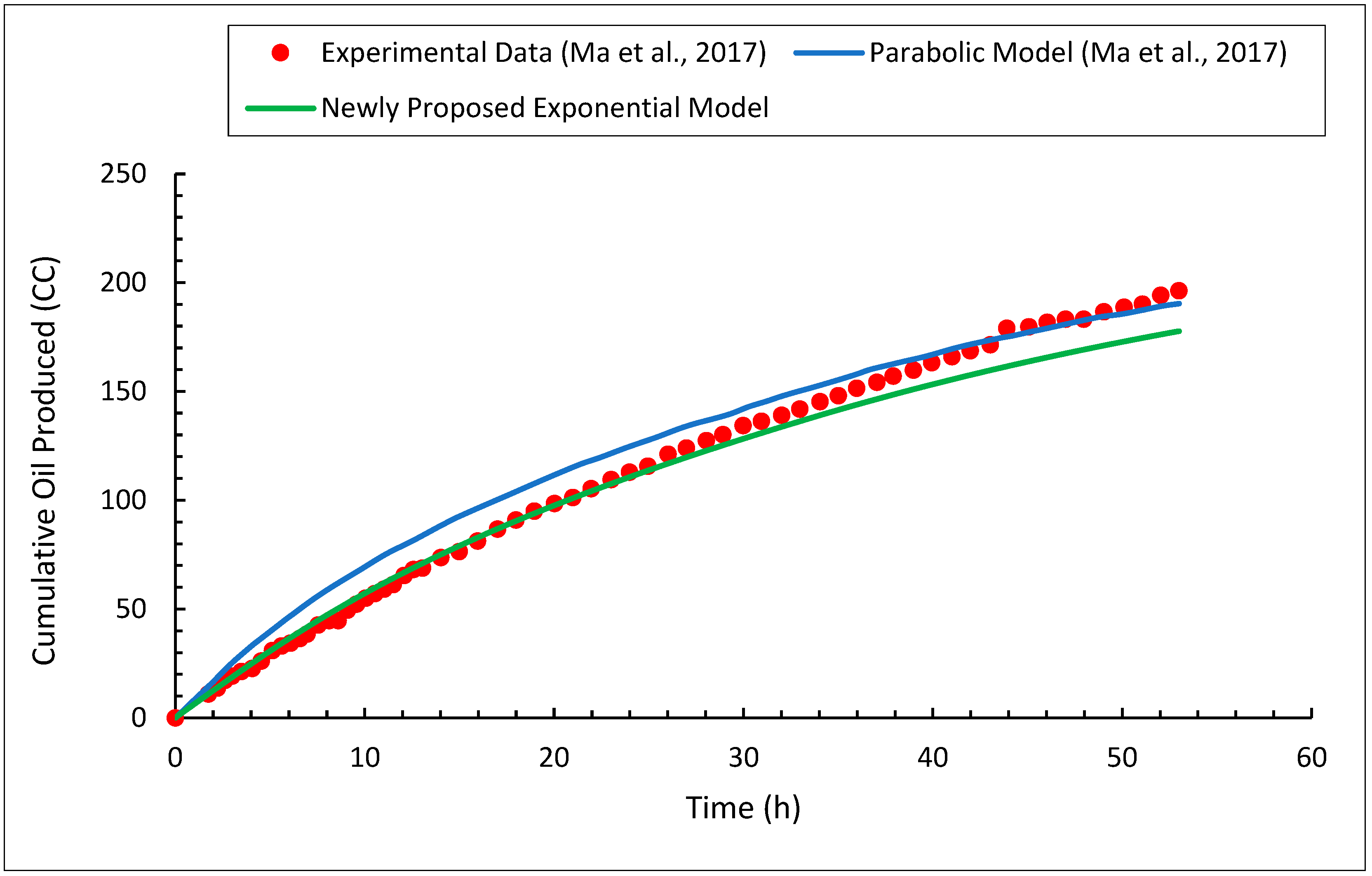
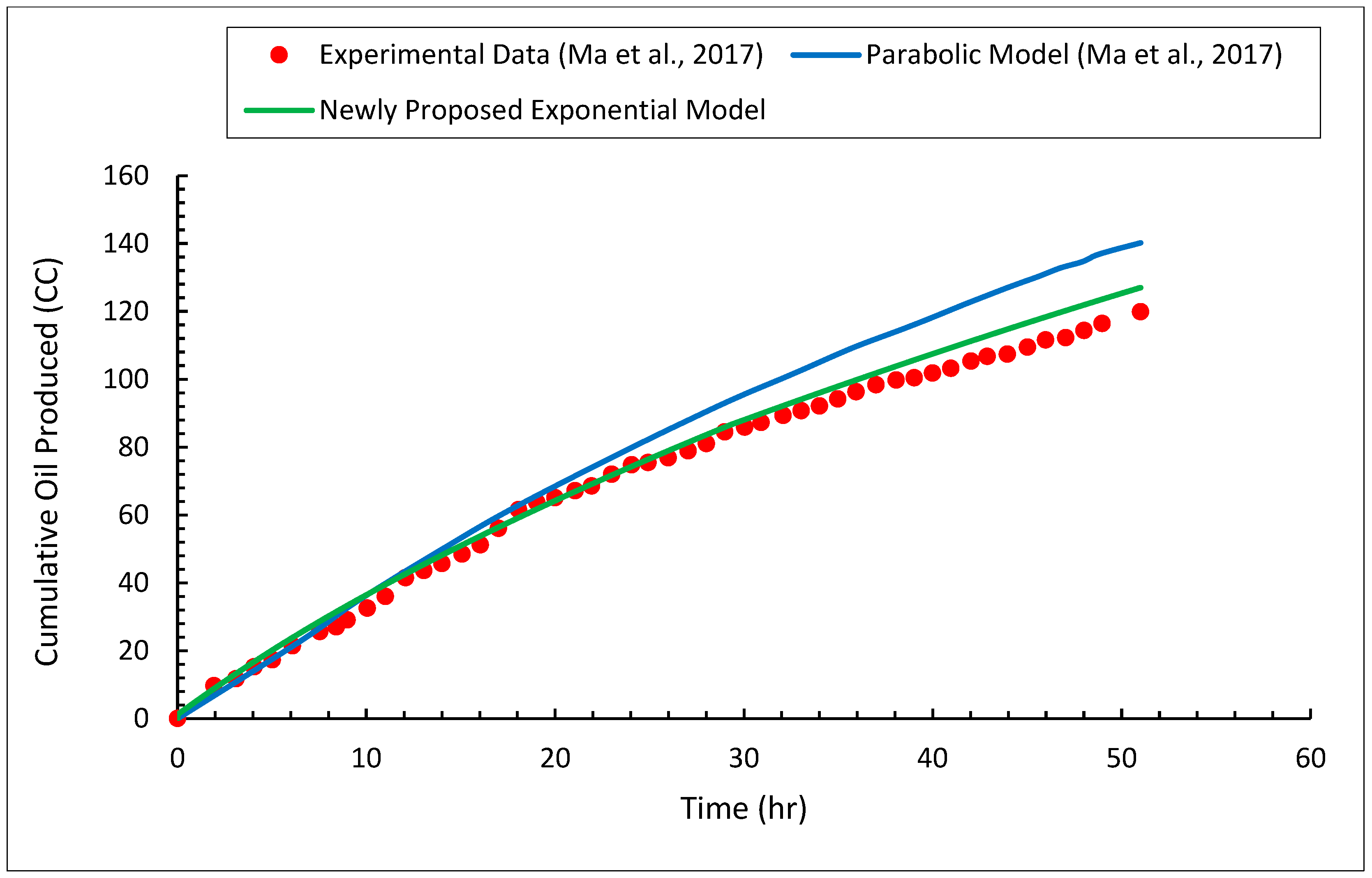
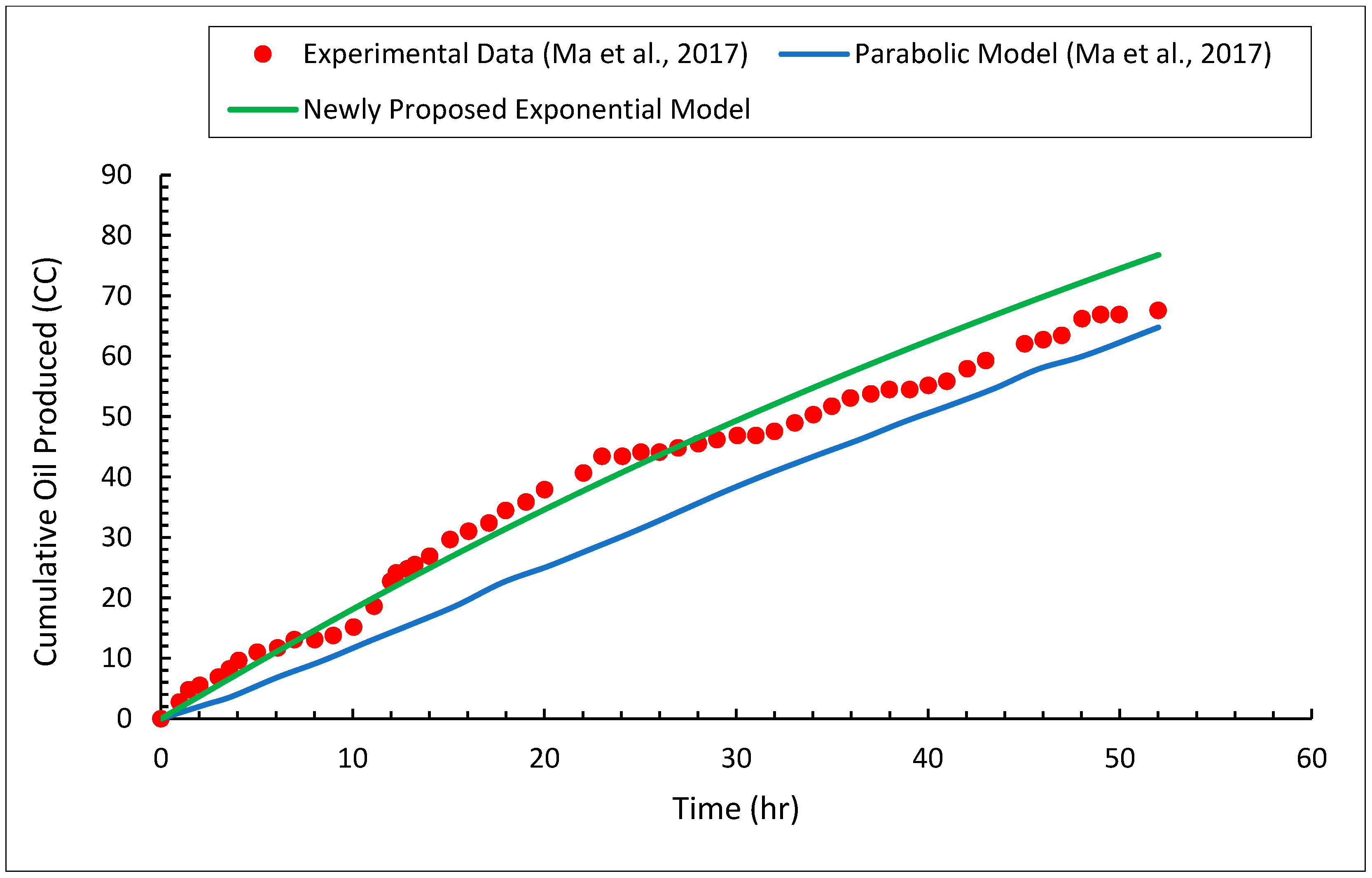
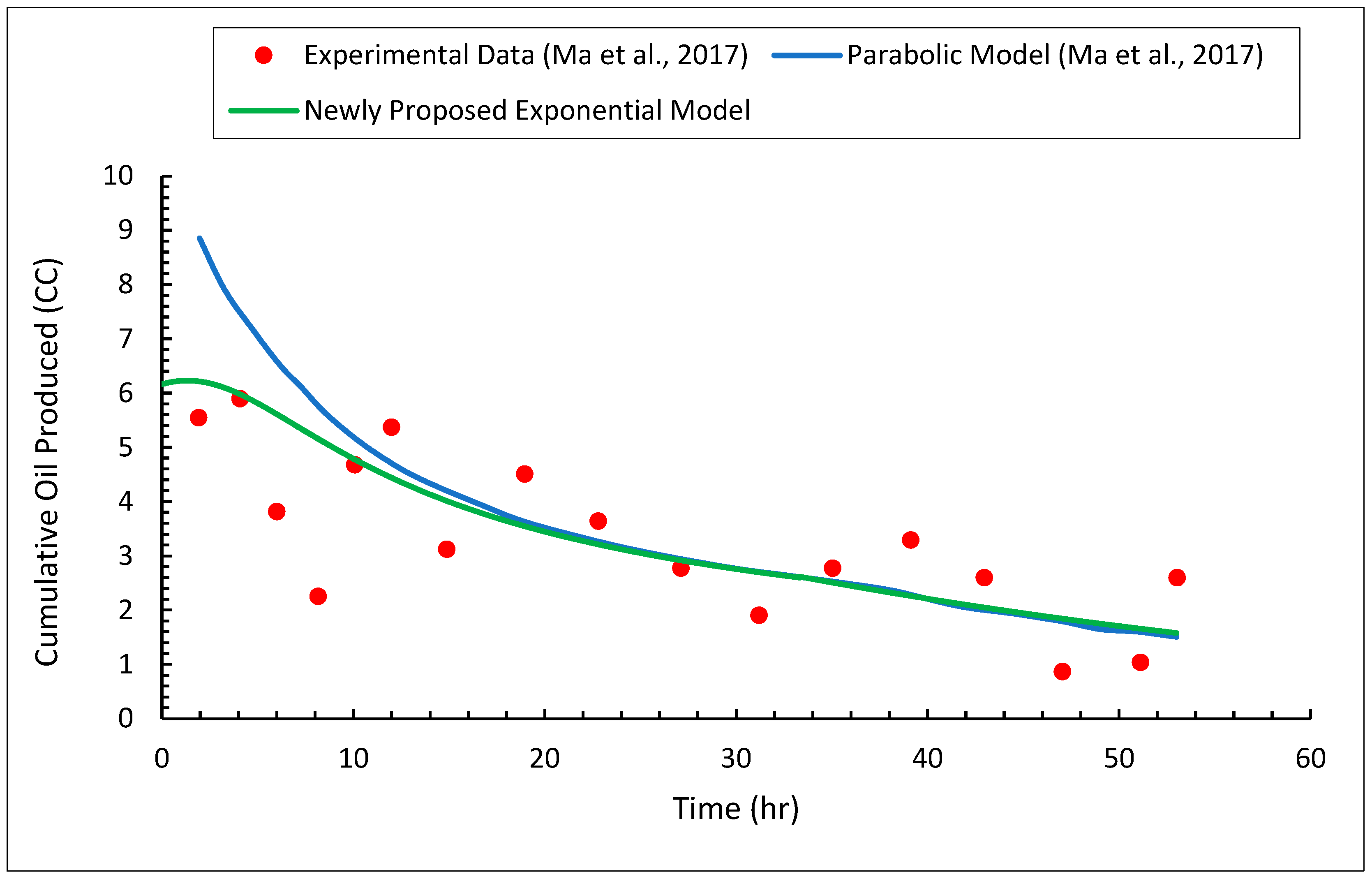
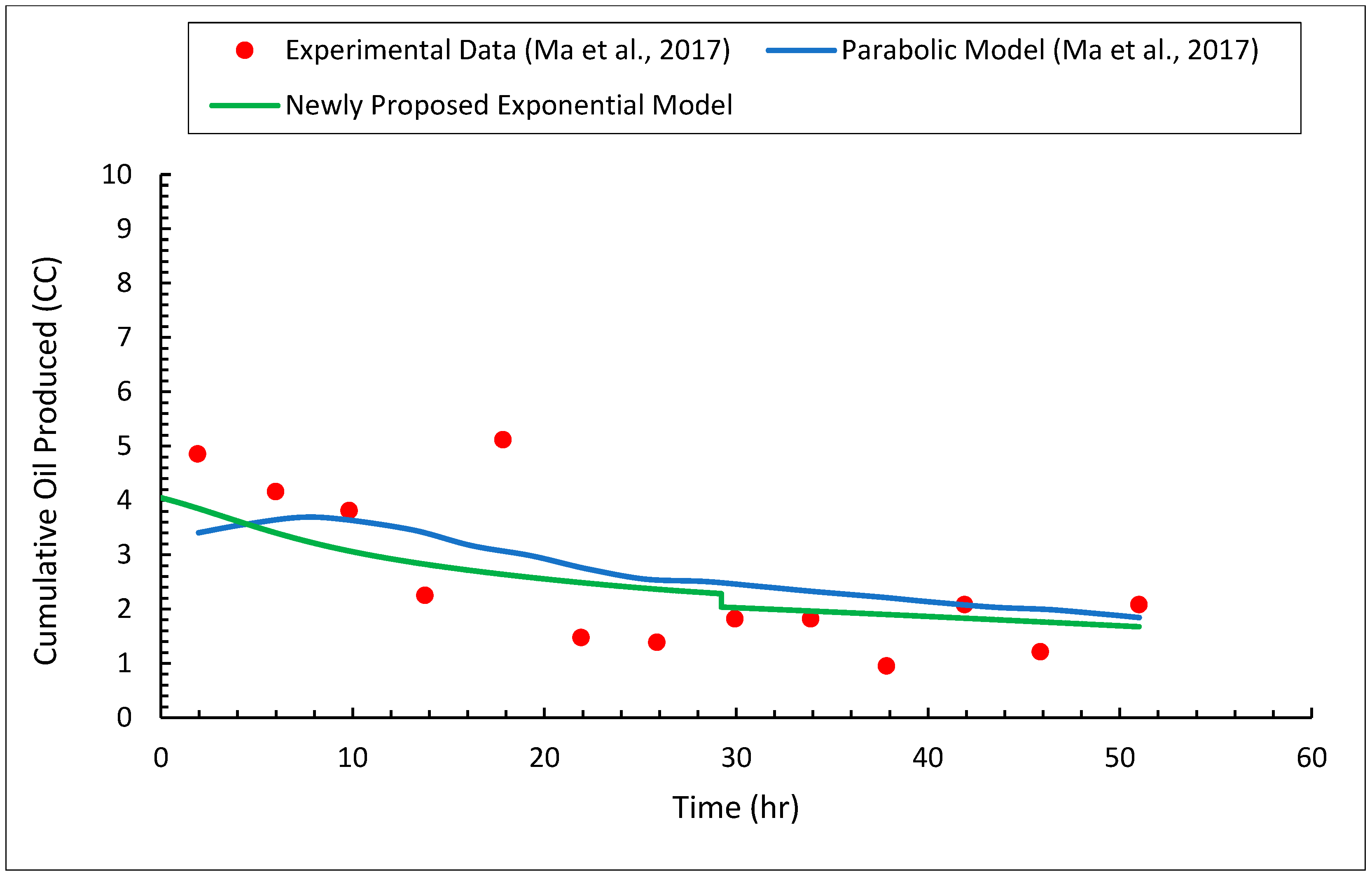
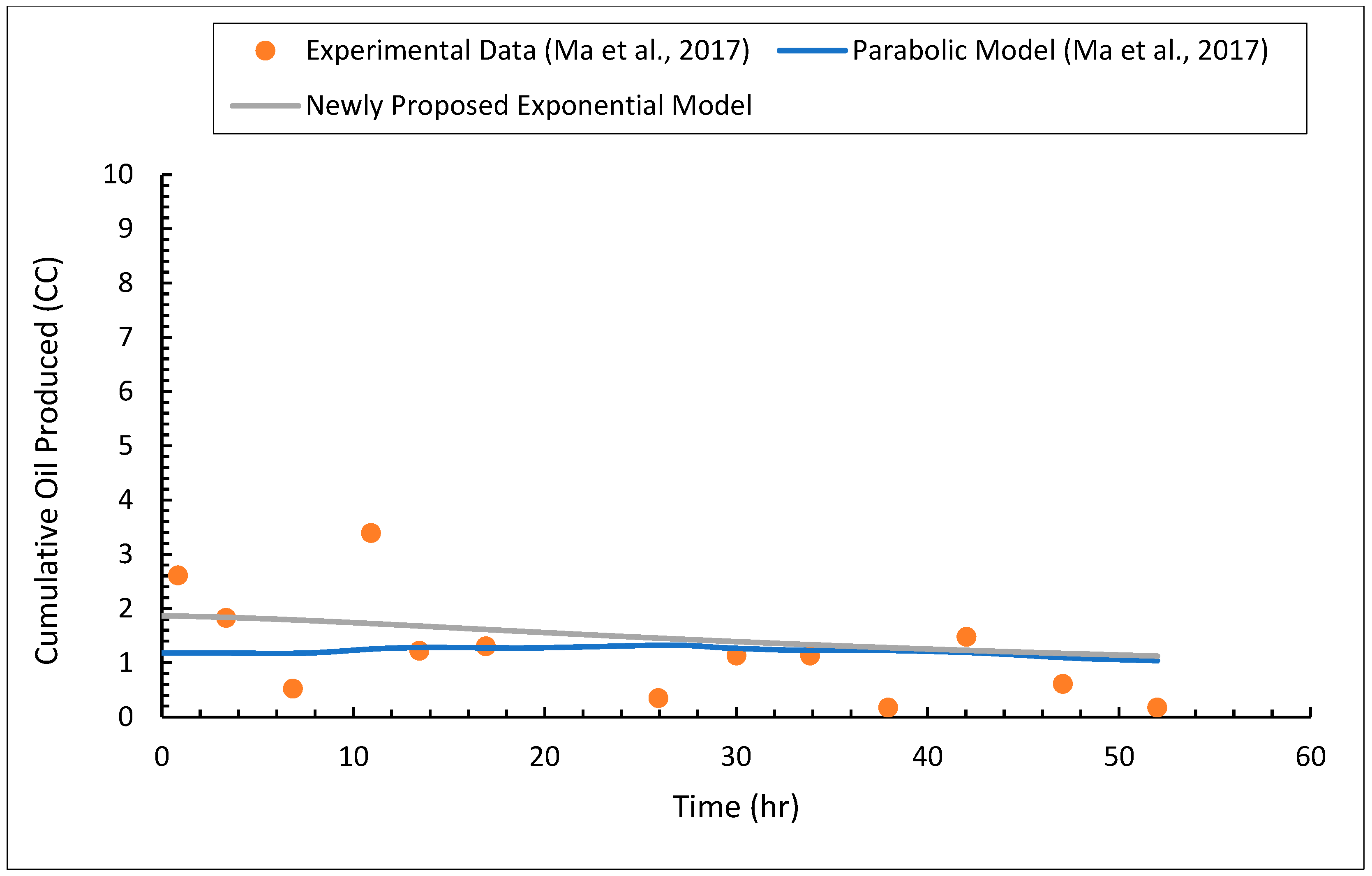
3.3. Heavy Oil Production
4. Conclusions
- Using the proposed exponential model, the solvent chamber, heavy oil production rate, and cumulative heavy oil production can be accurately predicted.
- With a relative error of less than 5.12%, the newly proposed model closely matches the measurements of transition region thickness.
- The exponential model can accurately predict the transition region thicknesses, with the average relative errors of all cases being around 7.73%.
- The assumption of constant transition region thickness reduces the complexity of the model and produces reliable results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Butler, R.M.; Mokrys, I.J. A new process (VAPEX) for recovering heavy oils using hot water and hydrocarbon vapour. J. Can. Pet. Technol. 1991, 30, PETSOC-91-01-09. [Google Scholar] [CrossRef]
- Das, S.K.; Butler, R.M. Mechanism of the vapor extraction process for heavy oil and bitumen. J. Pet. Sci. Eng. 1998, 21, 43–59. [Google Scholar] [CrossRef]
- Ma, H.; Yu, G.; She, Y.; Gu, Y. A parabolic solvent chamber model for simulating the solvent vapor extraction (VAPEX) heavy oil recovery process. J. Pet. Sci. Eng. 2017, 149, 465–475. [Google Scholar] [CrossRef]
- Karmaker, K.; Maini, B.B. Applicability of vapor extraction process to problematic viscous oil reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003; OnePetro: Richardson, TX, USA, 2003. [Google Scholar]
- Singhal, A.; Das, S.; Leggitt, S.; Kasraie, M.; Ito, Y. Screening of reservoirs for exploitation by application of steam assisted gravity drainage/vapex processes. In Proceedings of the International Conference on Horizontal Well Technology, Calgary, AB, Canada, 18–20 November 1996; OnePetro: Richardson, TX, USA, 1996. [Google Scholar]
- Luo, P.; Gu, Y. Effects of asphaltene content and solvent concentration on heavy oil viscosity. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium, Calgary, AB, Canada, 1–3 November 2005; OnePetro: Richardson, TX, USA, 2005. [Google Scholar]
- Qi, R. Simulation Study of Warm VAPEX Process Using Water-Soluble Solvent. Master’s Thesis, Schulich School of Engineering, Calgary, AB, Canada, 2020. [Google Scholar]
- Xu, J.; Chen, Z.; Dong, X.; Zhou, W. Effects of lean zones on steam-assisted gravity drainage performance. Energies 2017, 10, 471. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Z.; Cao, J.; Li, R. Numerical study of the effects of lean zones on SAGD performance in periodically heterogeneous media. In Proceedings of the SPE Heavy Oil Conference-Canada, Calgary, AB, Canada, 10–12 June 2014; OnePetro: Richardson, TX, USA, 2014. [Google Scholar]
- Butler, R.; Mokrys, I. Solvent Analog Model of Steam-Assisted Gravity Drainage. AOSTRA J. Res. 1989, 5, 17, (Reprint). [Google Scholar]
- Yazdani, A.; Maini, B.B. Modeling of the VAPEX process in a very large physical model. Energy Fuels 2008, 22, 535–544. [Google Scholar] [CrossRef]
- Wang, Q.; Jia, X.; Chen, Z. Mathematical modeling of the solvent chamber evolution in a vapor extraction heavy oil recovery process. Fuel 2016, 186, 339–349. [Google Scholar] [CrossRef]
- Moghadam, S.; Nobakht, M.; Gu, Y. Theoretical and physical modeling of a solvent vapour extraction (VAPEX) process for heavy oil recovery. J. Pet. Sci. Eng. 2009, 65, 93–104. [Google Scholar] [CrossRef]
- Lin, L.; Zeng, F.; Gu, Y. A circular solvent chamber model for simulating the VAPEX heavy oil recovery process. J. Pet. Sci. Eng. 2014, 118, 27–39. [Google Scholar] [CrossRef]
- Cuthiell, D.; McCarthy, C.; Frauenfeld, T.; Cameron, S.; Kissel, G. Investigation of the VAPEX process using CT scanning and numerical simulation. J. Can. Pet. Technol. 2003, 42, PETSOC-03-02-04. [Google Scholar] [CrossRef]
- Nghiem, L.; Kohse, B.; Sammon, P. Compositional simulation of the VAPEX process. J. Can. Pet. Technol. 2001, 40, PETSOC-01-08-05. [Google Scholar] [CrossRef]
- Nourozieh, H.; Kariznovi, M.; Abedi, J.; Chen, Z.J. A new approach to simulate the boundary layer in the vapour extraction process. J. Can. Pet. Technol. 2011, 50, 11–18. [Google Scholar] [CrossRef]
- Yazdani, A.; Maini, B.B. Pitfalls and solutions in numerical simulation of VAPEX experiments. Energy Fuels 2009, 23, 3981–3988. [Google Scholar] [CrossRef]
- Chapra, S.C. Applied Numerical Methods with MATLAB for Engineers and Scientists; McGraw-Hill Higher Education: New York, NY, USA, 2008. [Google Scholar]
- McCall, J. Genetic algorithms for modelling and optimisation. J. Comput. Appl. Math. 2005, 184, 205–222. [Google Scholar] [CrossRef]





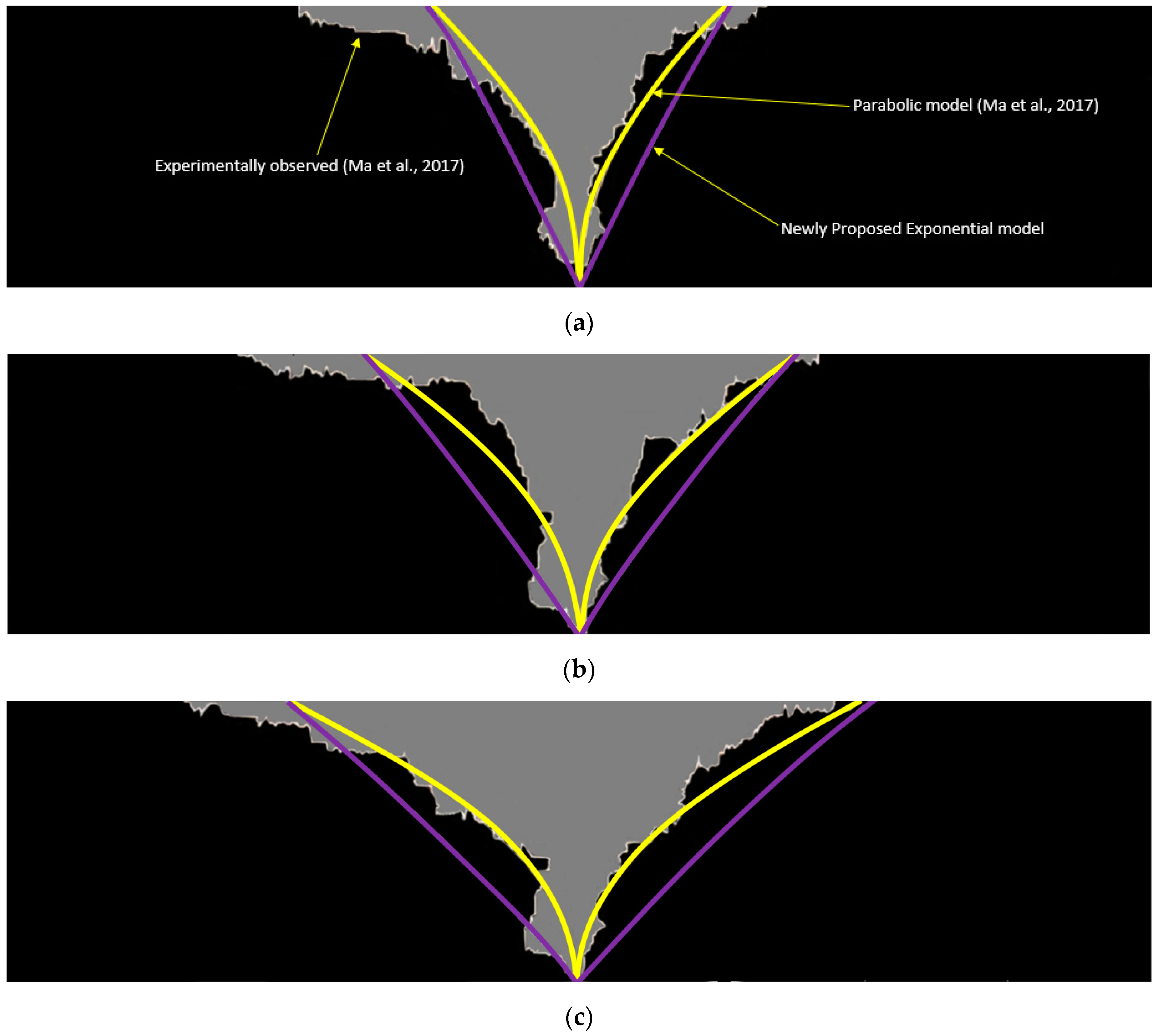
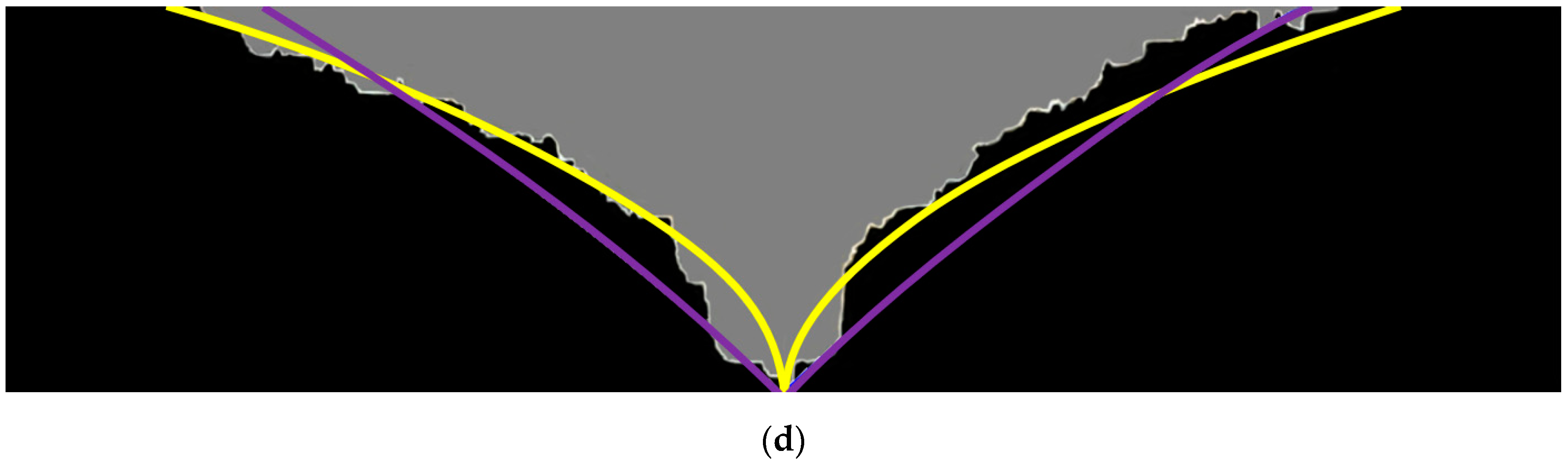
| Test No. | (%) | H (cm) | W (cm) | d (cm) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 31.4 | 152 | 0.828 | 8.51 | 10 | 20 | 2 | 0.975 | 0.085 |
| 2 | 32.9 | 52 | 0.828 | 8.51 | 10 | 20 | 2 | 0.977 | 0.071 |
| 3 | 35.7 | 18 | 0.828 | 8.51 | 10 | 20 | 2 | 0.962 | 0.109 |
| 4 | 36.3 | 8 | 0.828 | 8.51 | 10 | 20 | 2 | 0.962 | 0.106 |
| Test No. | Solvent Chamber Shape | n | (cm) |
|---|---|---|---|
| 1 | Concave | 0.1343 | 0.2567 |
| 2 | Concave | 0.0459 | 0.1905 |
| 3 | Convex | 0.0919 | 0.3867 |
| 4 | Convex | 0.0322 | 0.3972 |
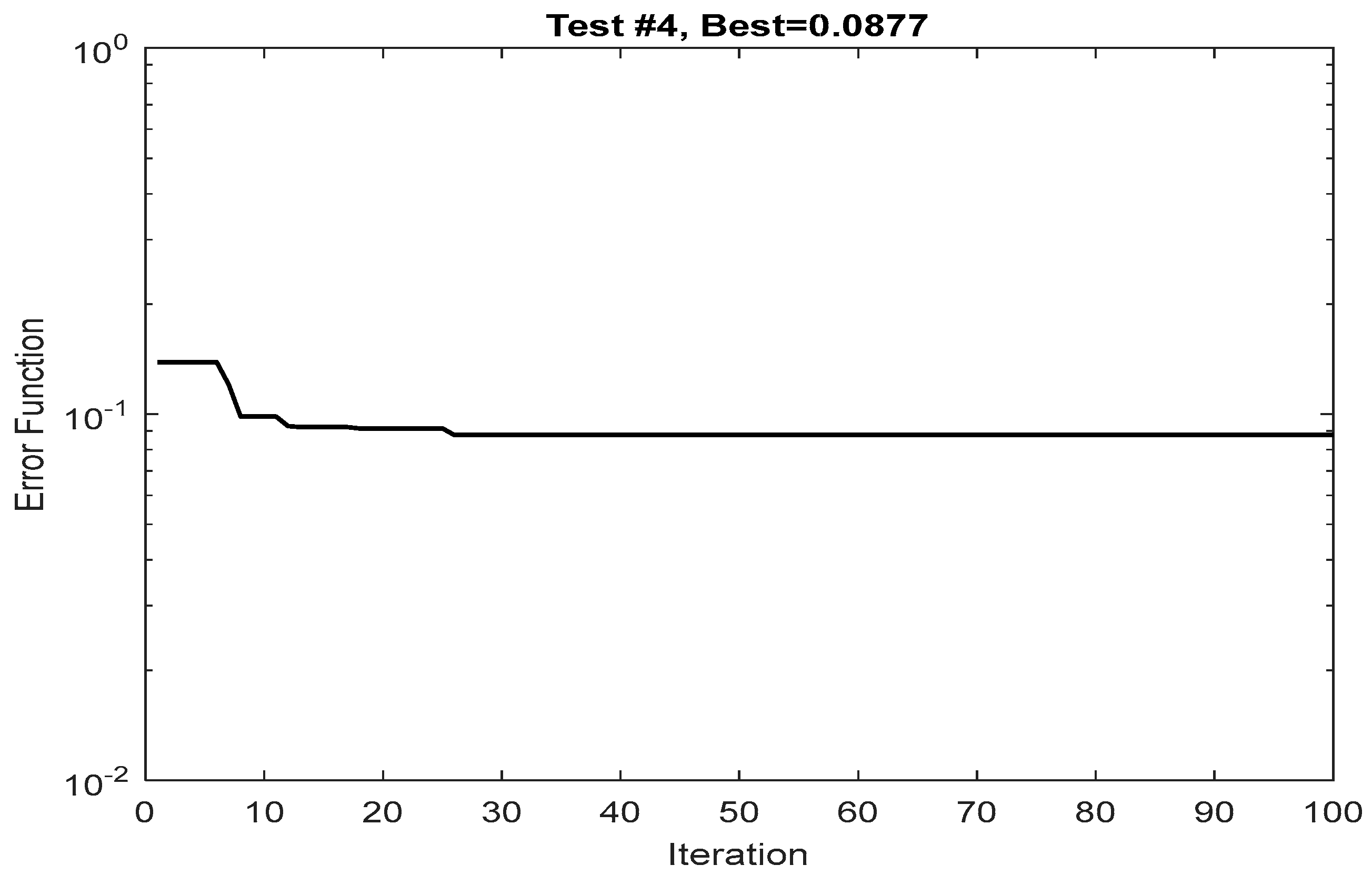
| Test No. | Minimum Value of Error Function |
|---|---|
| Test #1 | 0.0429 |
| Test #2 | 0.0810 |
| Test #3 | 0.0976 |
| Test #4 | 0.0877 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheperli, A.; Torabi, F.; Sabeti, M.; Rahimbakhsh, A. An Exponential Solvent Chamber Geometry for Modeling the VAPEX Process. Energies 2022, 15, 5874. https://doi.org/10.3390/en15165874
Cheperli A, Torabi F, Sabeti M, Rahimbakhsh A. An Exponential Solvent Chamber Geometry for Modeling the VAPEX Process. Energies. 2022; 15(16):5874. https://doi.org/10.3390/en15165874
Chicago/Turabian StyleCheperli, Ali, Farshid Torabi, Morteza Sabeti, and Aria Rahimbakhsh. 2022. "An Exponential Solvent Chamber Geometry for Modeling the VAPEX Process" Energies 15, no. 16: 5874. https://doi.org/10.3390/en15165874





