Control and Design of a Boost-Based Electrolytic Capacitor-Less Single-Phase-Input Drive
Abstract
:1. Introduction
2. Materials and Methods
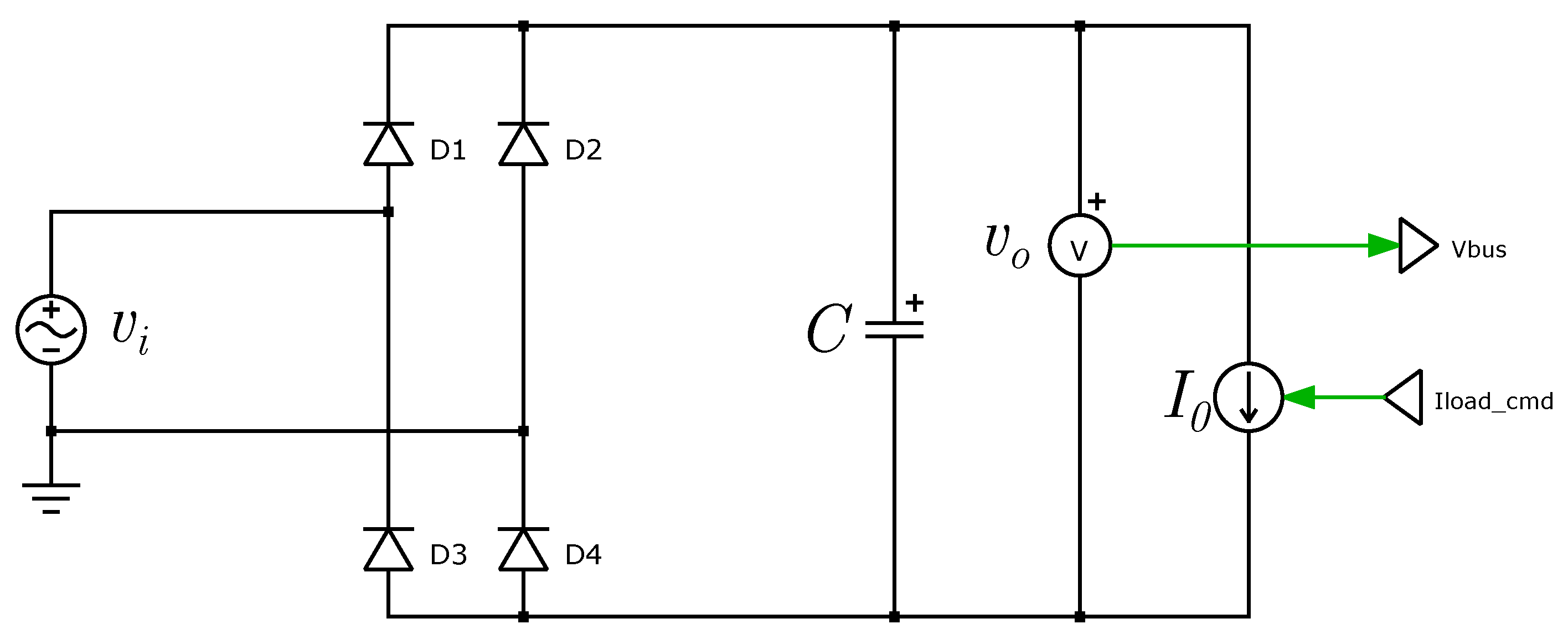
2.1. Uncontrolled Rectifier and Its Limitations
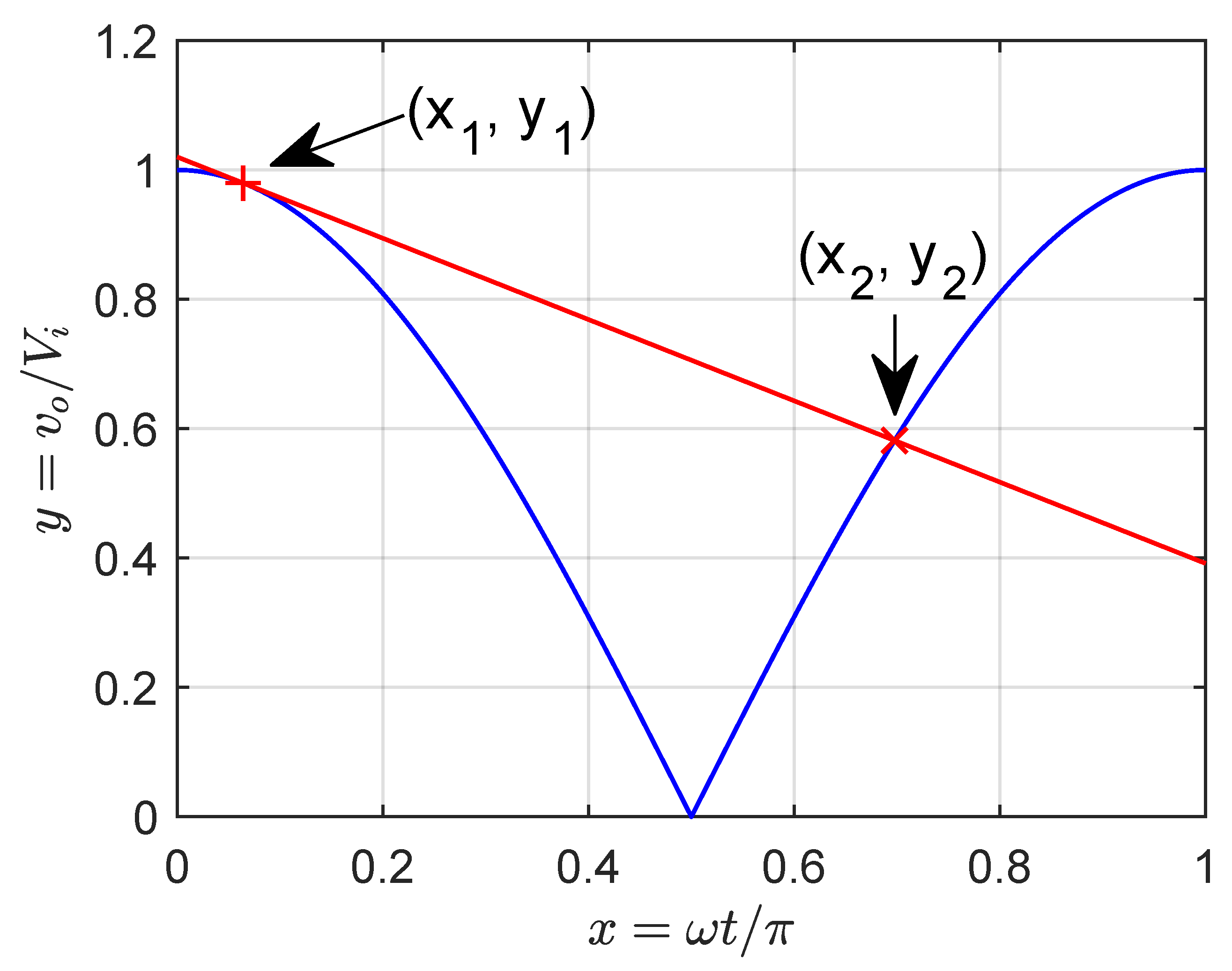
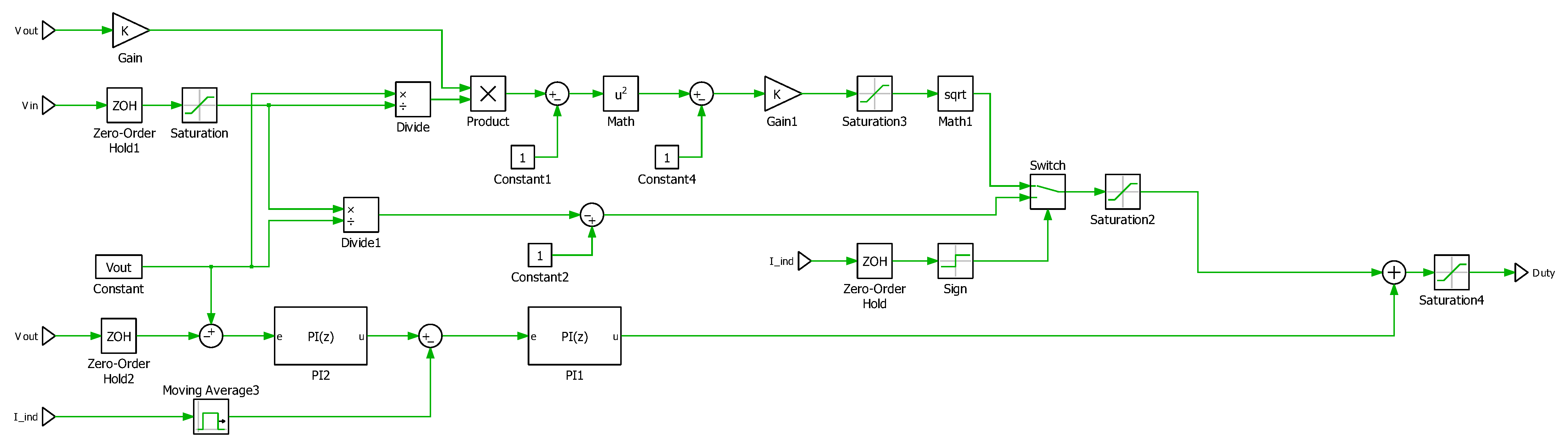
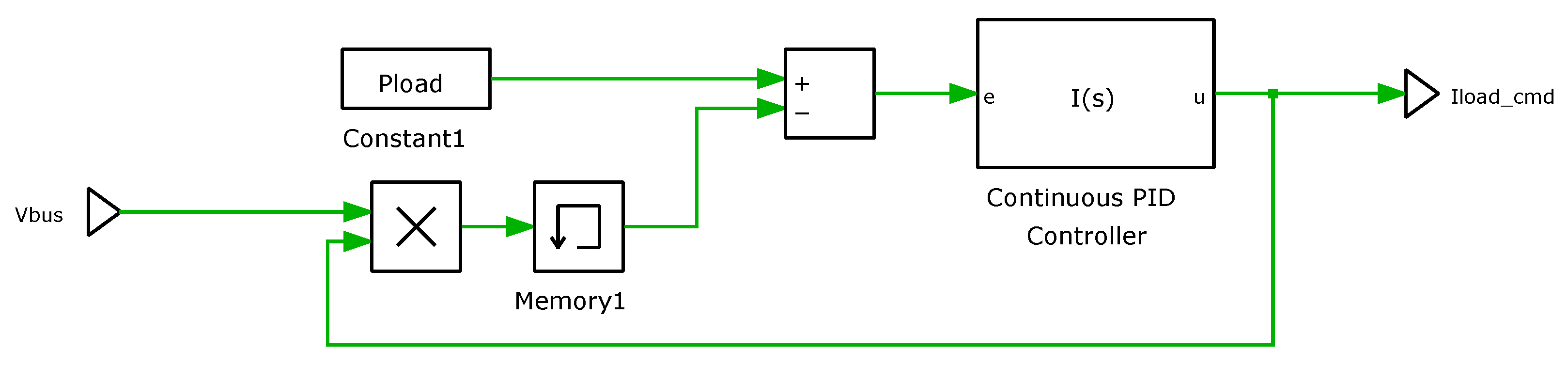
2.2. Proposed Control for DC Link Capacitance Reduction
- 1.
- Feed-forward control [24,25]: Boost converter can work in two distinct modes, continuous conduction mode (CCM) and discontinuous conduction mode (DCM), depending on whether the inductor current reaches zero during the switching period. The duty cycle definition is different in the two modes once input and output voltage are chosen:CCM control methods are more commonly used given their simplicity; however, in variable load applications, DCM may occur, changing the duty cycle relationship.
- 2.
- Feed-back control [26,27]: a dual nested loop linear feedback control is implemented for parameter adaptation and to improve load and line regulation. The inner current loop generates the duty cycle to control (and limit) the inductor current; the outer voltage loop generates a current setpoint to regulate the voltage of the DC link to the desired value, while minimizing the ripple.
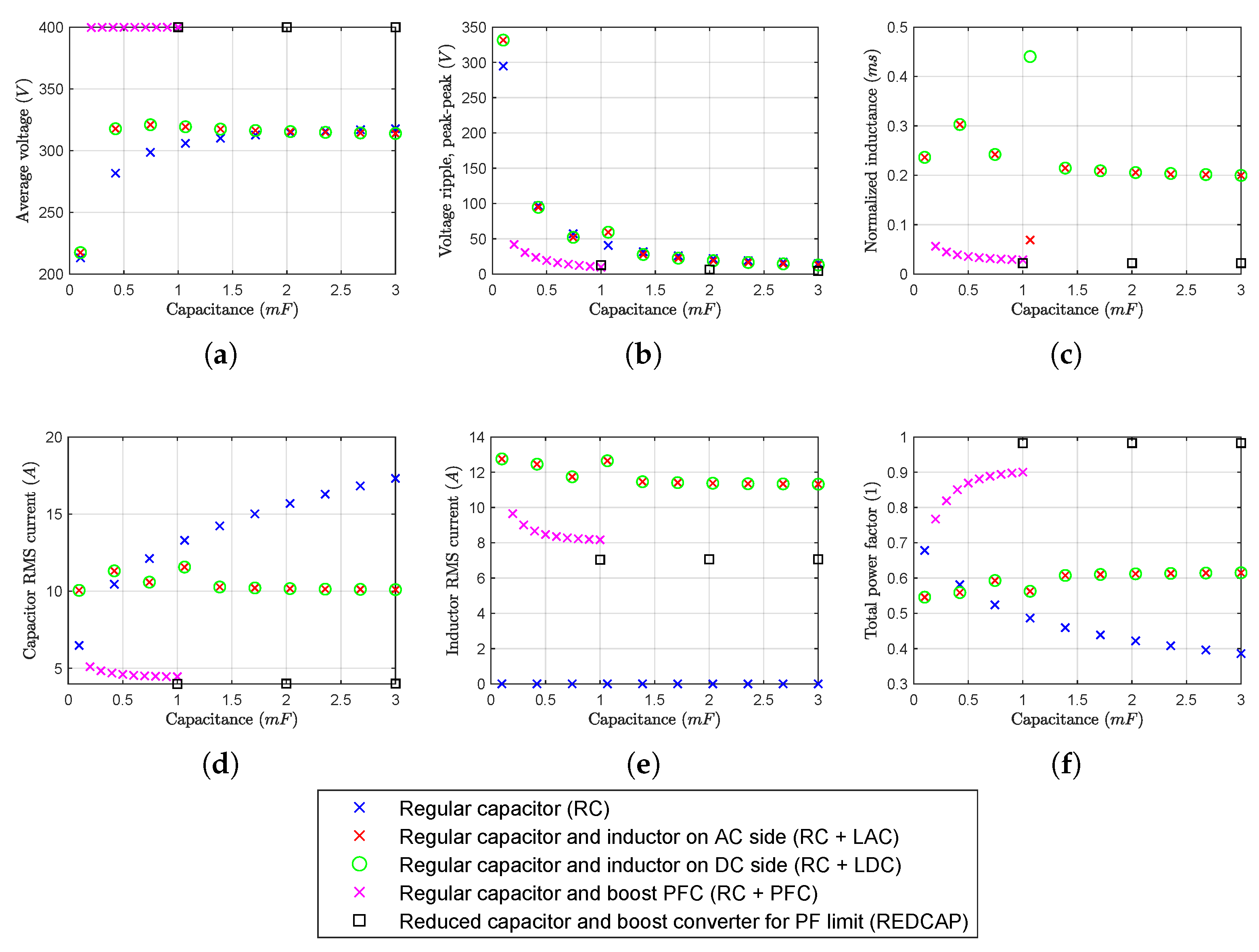
2.3. Comparison of Different Rectifier Topologies
- 1.
- Regular capacitor (RC);
- 2.
- Regular capacitor and inductor on DC side (RC + LDC);
- 3.
- Regular capacitor and inductor on AC side (RC + LAC);
- 4.
- Regular capacitor and boost PFC (RC + PFC);
- 5.
- Reduced capacitor and boost converter for PF limit (REDCAP).
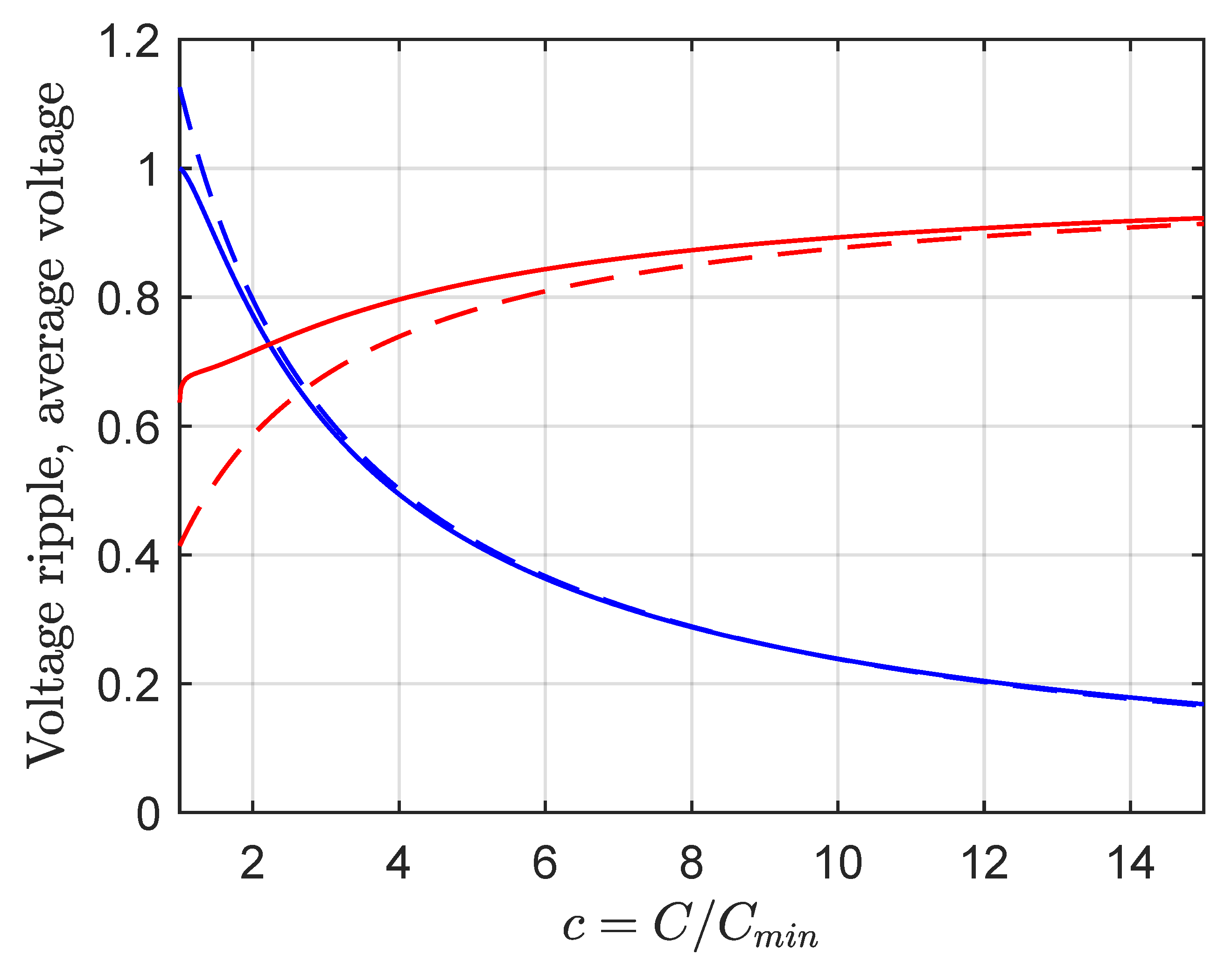
2.4. Control Design Tradeoff
3. Results
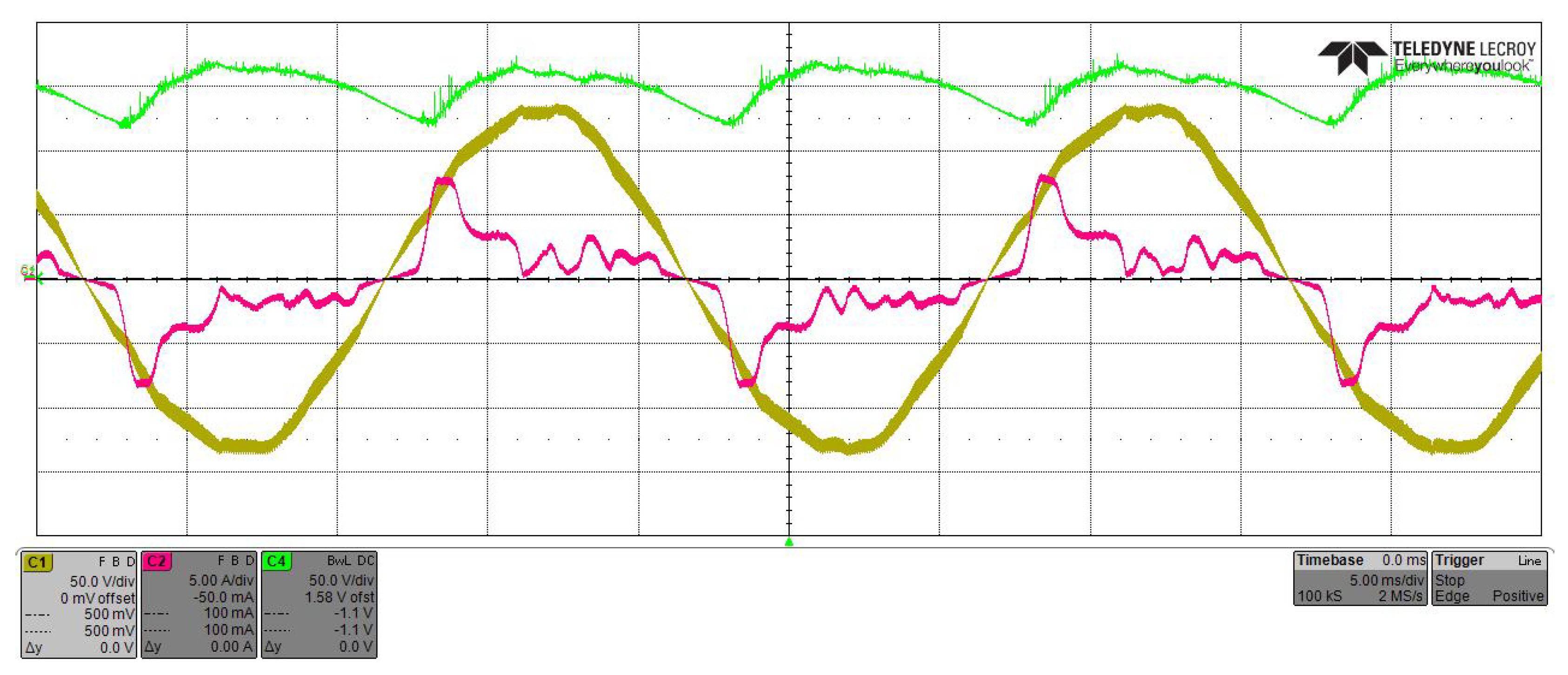
3.1. Boost Front-End with Film Capacitor
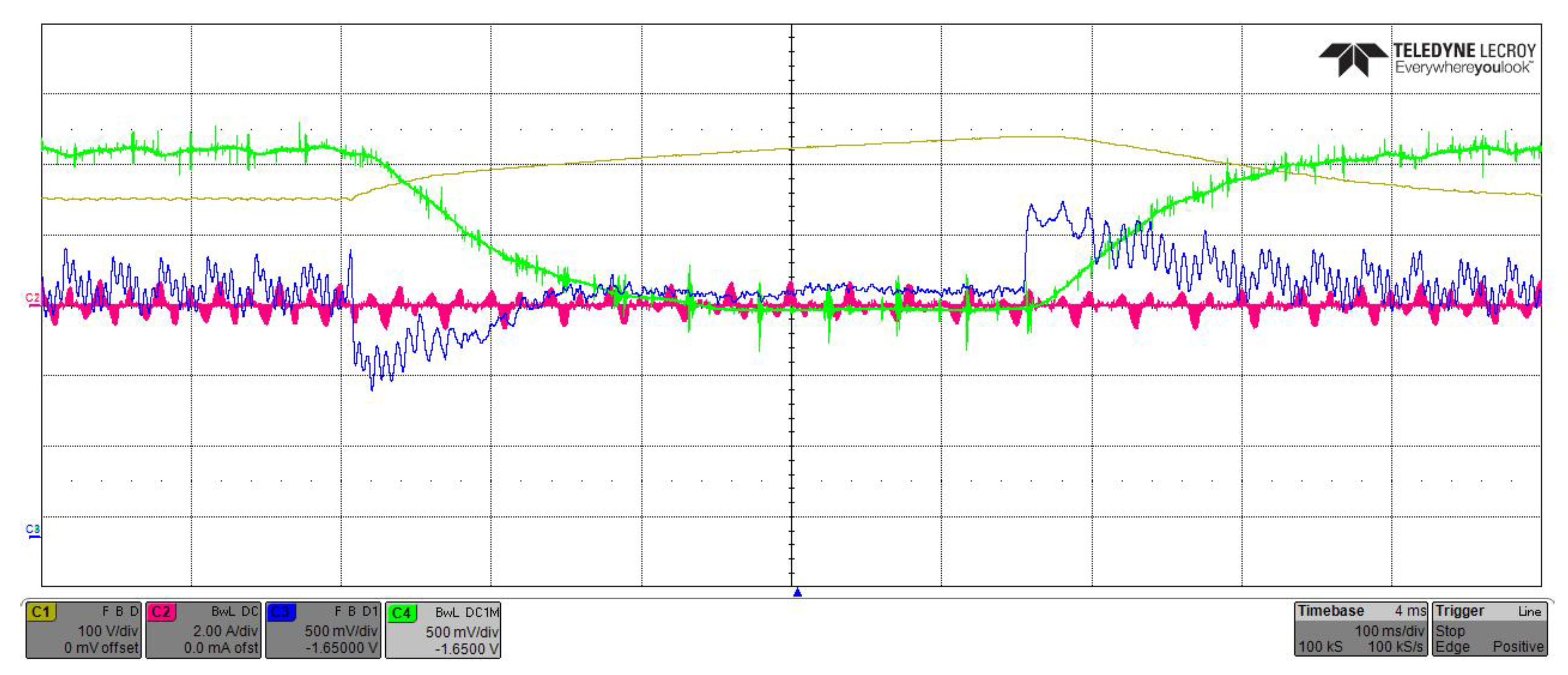
3.2. System Performance in Regenerative Conditions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCM | Continuous Conduction Mode |
| DCM | Discontinuous Conduction Mode |
| ESR | Equivalent Series Resistance |
| LL | Line-to-Line |
| PEC | Power Electronics Converter |
| PF | Power Factor |
| PFC | Power Factor Correction |
| RMS | Root Mean Square |
| THD | Total Harmonic Distortion |
References
- Åhag, P.; Hed, L.; Lundow, P.H.; Olsson, L. Are We Ready for the Agenda 2030 for Sustainable Development? In Proceedings of the 2019 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Macao, China, 15–18 December 2019; pp. 224–227. [Google Scholar] [CrossRef]
- United Nations General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015. Available online: https://unric.org/en/sdgs-in-your-language/ (accessed on 19 July 2022).
- Samad, H.A.; Zhang, F. Benefits of Electrification and the Role of Reliability: Evidence from India; Policy Research Working Paper Series 7889; The World Bank: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Hasanbeigi, A. Industrial Heating Profile and Electrification. 2021. Available online: https://www.globalefficiencyintel.com/new-blog/2021/3/22/industrial-heating-profile-and-electrification (accessed on 19 July 2022).
- Stoffel, B. Chapter 1—The Role of Pumps for Energy Consumption and Energy Saving. In Assessing the Energy Efficiency of Pumps and Pump Units; Stoffel, B., Ed.; Elsevier: Boston, MA, USA, 2015; pp. 1–24. [Google Scholar] [CrossRef]
- Hasanbeigi, A. Infographic: The Profile of Energy Use in Industrial Motor Systems. 2017. Available online: https://www.globalefficiencyintel.com/new-blog/2017/infographic-energy-industrial-motor-systems (accessed on 19 July 2022).
- Waide, P.; Brunner, C.U. Energy Efficiency Policy Opportunities for Electric Motor-Driven Systems; Technical report; International Energy Agency: Paris, France, 2011.
- Tanaka, T. Environment friendly revolution in home appliances. In Proceedings of the 13th International Symposium on Power Semiconductor Devices & ICs. IPSD ’01 (IEEE Cat. No.01CH37216), Osaka, Japan, 7 June 2001; pp. 91–95. [Google Scholar] [CrossRef]
- Williams, M. The Role of Power Semiconductors in Enhancing Home Appliance Efficiency. 2021. Available online: https://www.embedded.com/the-role-of-power-semiconductors-in-enhancing-home-appliance-efficiency/ (accessed on 19 July 2022).
- Xia, Y.; Fletcher, J.; Finney, S.; Ahmed, K.; Williams, B. Torque ripple analysis and reduction for wind energy conversion systems using uncontrolled rectifier and boost converter. IET Renew. Power Gener. 2011, 5, 377–386. [Google Scholar] [CrossRef]
- Kolli, N.; Pramod, P.; Bhattacharya, S. Analysis of Different Operating Modes of PMSM during Regeneration with Uncontrolled Rectifier. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 204–209. [Google Scholar] [CrossRef]
- Turchi, J.; Dalal, D.; Wang, P.; Jenck, L. Power Factor Correction (PFC) Handbook; HBD853/D; ON Semiconductor: Denver, CO, USA, 2014. [Google Scholar]
- Rossetto, L.; Spiazzi, G.; Tenti, P. Control Techniques for Power Factor Correction Converters. In Proceedings of the International Conference on Power Electronics and Motion Control, Warsaw, Poland, 20–22 September 1994; pp. 1310–1318. [Google Scholar]
- De Souza, A.F.; Pereira, D.C.; Tofoli, F.L. Comparison of control techniques used in power factor correction rectifiers. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, Brazil, 29 November–2 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Kim, J.; Choi, H.; Won, C.Y. New Modulated Carrier Controlled PFC Boost Converter. IEEE Trans. Power Electron. 2018, 33, 4772–4782. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, W.; Hong, F. Single-Phase Input Variable-Speed AC Motor System Based on an Electrolytic Capacitor-Less Single-Stage Boost Three-Phase Inverter. IEEE Trans. Power Electron. 2016, 31, 7043–7052. [Google Scholar] [CrossRef]
- Ramos-Paja, C.A.; Saavedra-Montes, A.J.; Bastidas-Rodriguez, J.D. Co-Design of the Control and Power Stages of a Boost-Based Rectifier with Power Factor Correction Depending on Performance Criteria. Computation 2022, 10, 61. [Google Scholar] [CrossRef]
- Rossetto, L.; Spiazzi, G.; Tenti, P. Boost PFC with 100 Hz switching frequency providing output voltage stabilization and compliance with EMC standards. In Proceedings of the Conference Record of 1998 IEEE Industry Applications Conference, Thirty-Third IAS Annual Meeting (Cat. No.98CH36242), St. Louis, MO, USA, 12–15 October 1998; Volume 2, pp. 1567–1573. [Google Scholar] [CrossRef]
- Albertsen, A. Electrolytic Capacitor Lifetime Estimation. Bodos Power Magazine, 1 April 2010. [Google Scholar]
- Reliability of Aluminum Electrolytic Capacitors. Technical Report; ELNA America Inc.: Marietta, GA, USA, 2022.
- Lifetime of Aluminum Electrolytic Capacitors. Available online: https://www.chemi-con.co.jp/en/faq/detail.php?id=29BDBH5 (accessed on 19 July 2022).
- Wang, H.; Blaabjerg, F. Power Electronics Reliability: State of the Art and Outlook. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6476–6493. [Google Scholar] [CrossRef]
- Manohar, S.S.; Sahoo, A.; Subramaniam, A.; Panda, S.K. Condition monitoring of power electronic converters in power plants—A review. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Wu, S.T.; Chen, F.Y.; Chien, M.C.; Wang, J.M.; Su, Y.Y. A Hybrid Control Scheme with Fast Transient and Low Harmonic for Boost PFC Converter. Electronics 2021, 10, 1848. [Google Scholar] [CrossRef]
- Chen, M.; Sun, J. Feedforward current control of boost single-phase PFC converters. IEEE Trans. Power Electron. 2006, 21, 338–345. [Google Scholar] [CrossRef]
- Gupta, A.; Panwar, A.; Sahoo, S.K.; Jacob Raglend, I. A CCM/DCM Hybrid Control Scheme for Single Channel Boost PFC Converter to Improve Power Quality. In Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 22–23 March 2019; Volume 1, pp. 1–5. [Google Scholar] [CrossRef]
- Moldaschl, J.; Broulím, J.; Paločko, L. Boost power factor correction topology with average current control. In Proceedings of the 2014 International Conference on Applied Electronics, Pilsen, Czech Republic, 9–10 September 2014; pp. 213–216. [Google Scholar] [CrossRef]
- Tripathi, P.R.; Thakura, P.; Keshri, R.K.; Ghosh, S.; Guerrero, J.M. Twenty-Five Years of Single-Stage Buck–Boost Inverters: Development and Challenges. IEEE Ind. Electron. Mag. 2022, 16, 4–10. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value |
|---|---|---|
| Input voltage (peak) | ||
| Input frequency | ||
| Switching frequency | ||
| Output voltage | ||
| Inductance | L | |
| Capacitance | C | |
| Resistive load |
| Parameter | Tuning 1 | Tuning 2 | Tuning 3 |
|---|---|---|---|
| P 1 | |||
| I 1 | 80 | 80 | 300 |
| P 2 | |||
| I 2 | 20 | 20 | 20 |
| Inductor current (RMS) | |||
| Output voltage ripple (peak-peak) | |||
| Total power factor |
| Parameter | Symbol | Value |
|---|---|---|
| Input voltage (peak) | ||
| Input frequency | ||
| Switching frequency | ||
| Output voltage | ||
| Inductance | L | |
| Capacitance | C | |
| Resistive load |
| Parameter | Symbol | Value |
|---|---|---|
| Motor rated torque | ||
| Motor rated speed | ||
| Motor rated power | ||
| Motor rated current (phase, RMS) | ||
| Motor rated voltage (LL, RMS) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musetti, A.; Sadegh Lafmejani, H.; Soldati, A. Control and Design of a Boost-Based Electrolytic Capacitor-Less Single-Phase-Input Drive. Energies 2022, 15, 5929. https://doi.org/10.3390/en15165929
Musetti A, Sadegh Lafmejani H, Soldati A. Control and Design of a Boost-Based Electrolytic Capacitor-Less Single-Phase-Input Drive. Energies. 2022; 15(16):5929. https://doi.org/10.3390/en15165929
Chicago/Turabian StyleMusetti, Alex, Hossein Sadegh Lafmejani, and Alessandro Soldati. 2022. "Control and Design of a Boost-Based Electrolytic Capacitor-Less Single-Phase-Input Drive" Energies 15, no. 16: 5929. https://doi.org/10.3390/en15165929
APA StyleMusetti, A., Sadegh Lafmejani, H., & Soldati, A. (2022). Control and Design of a Boost-Based Electrolytic Capacitor-Less Single-Phase-Input Drive. Energies, 15(16), 5929. https://doi.org/10.3390/en15165929








