The Effect of Bedding Plane Angle on Hydraulic Fracture Propagation in Mineral Heterogeneity Model
Abstract
:1. Introduction
2. Principle of Numerical Calculation
2.1. Constitutive Equation for the Cohesive Element
2.2. Stiffness-Setting Principle
2.3. Equation of the Fluid–Solid-Coupling
2.3.1. Equilibrium Equation
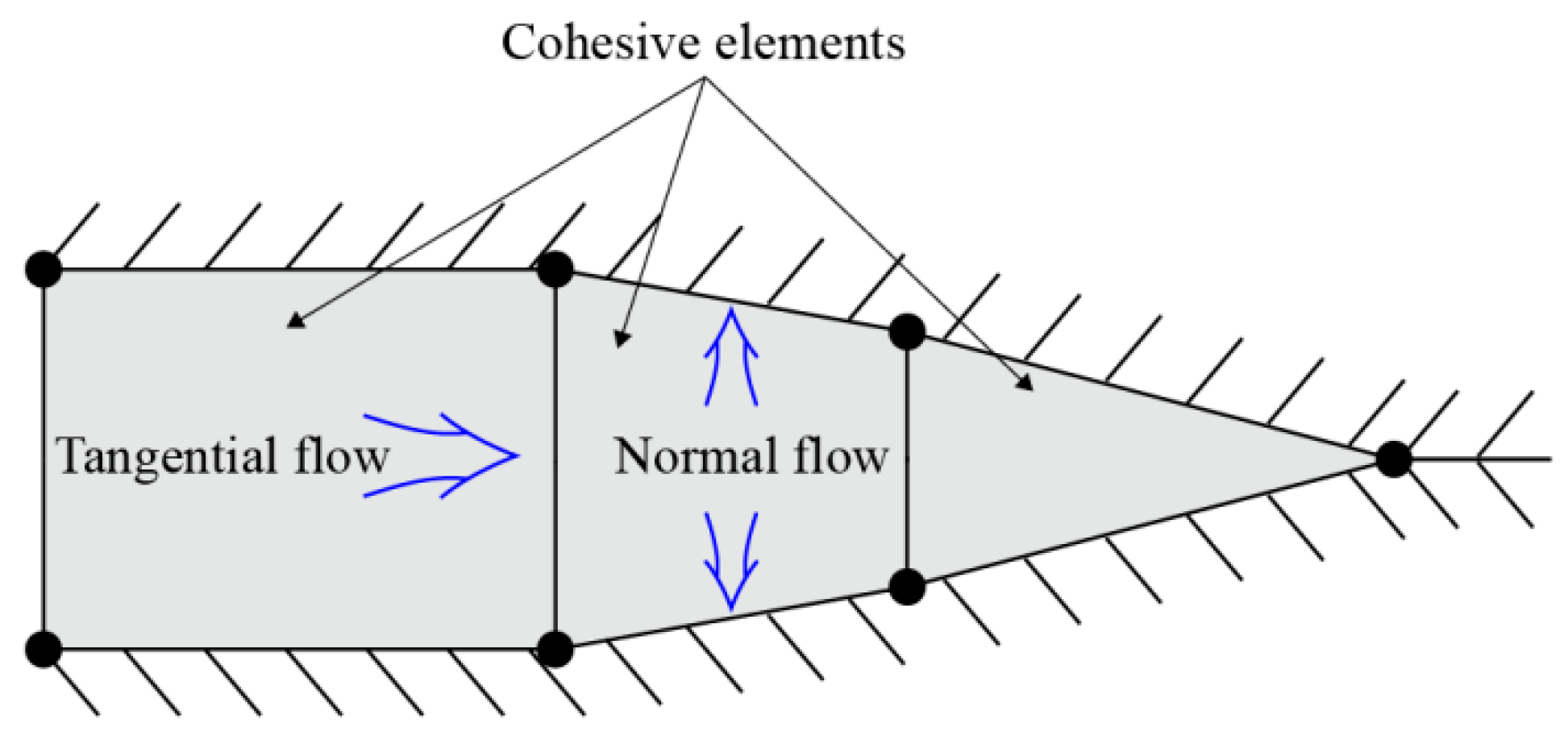
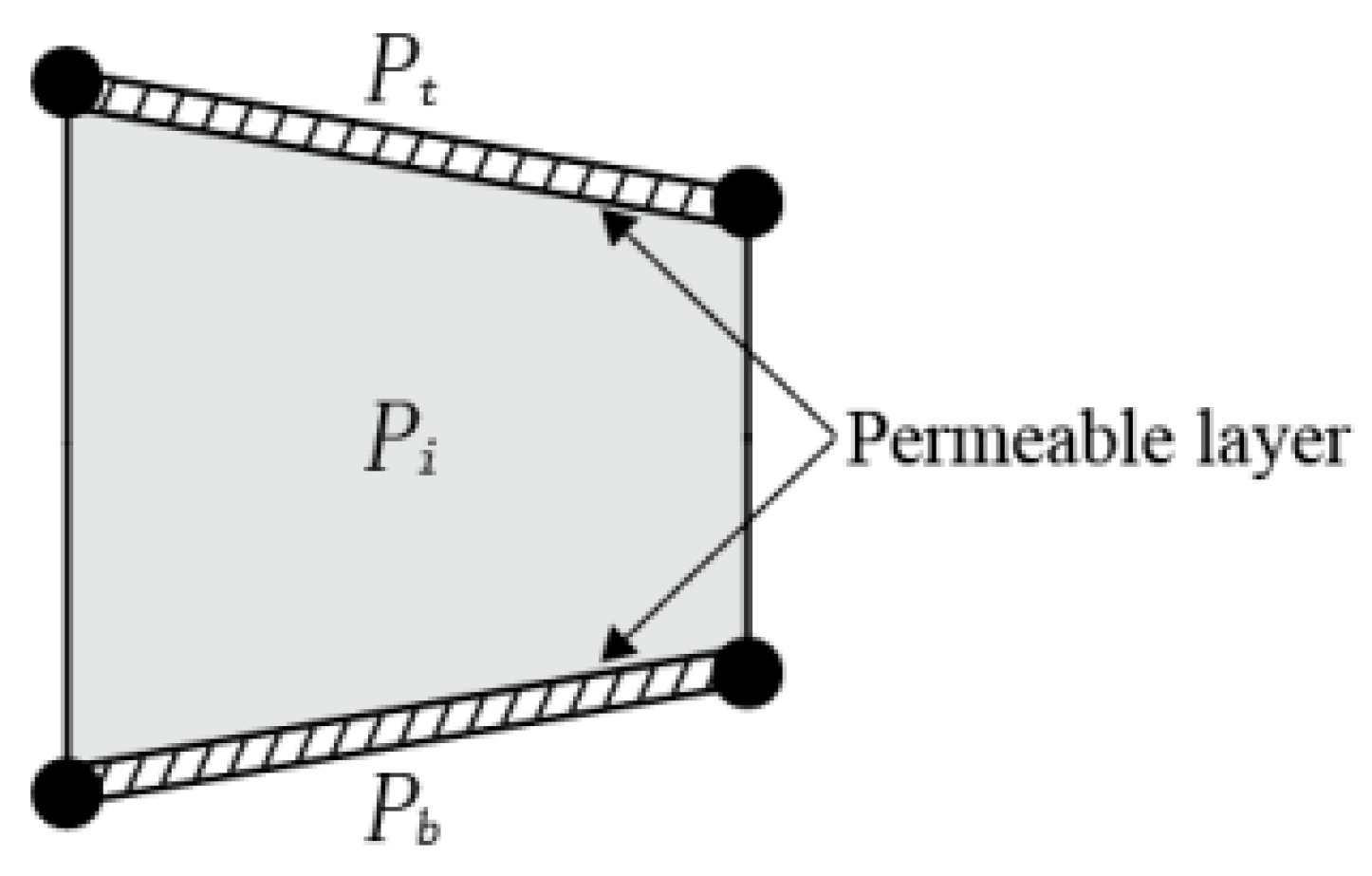
2.3.2. Fluid-Flow Model in Cohesive Elements
2.4. Fracture-Propagation Criterion
2.4.1. Damage Initiation
2.4.2. Damage Evolution Criterion
2.5. AE Based Numerical Simulation Method
3. Numerical Model
4. Simulation Results
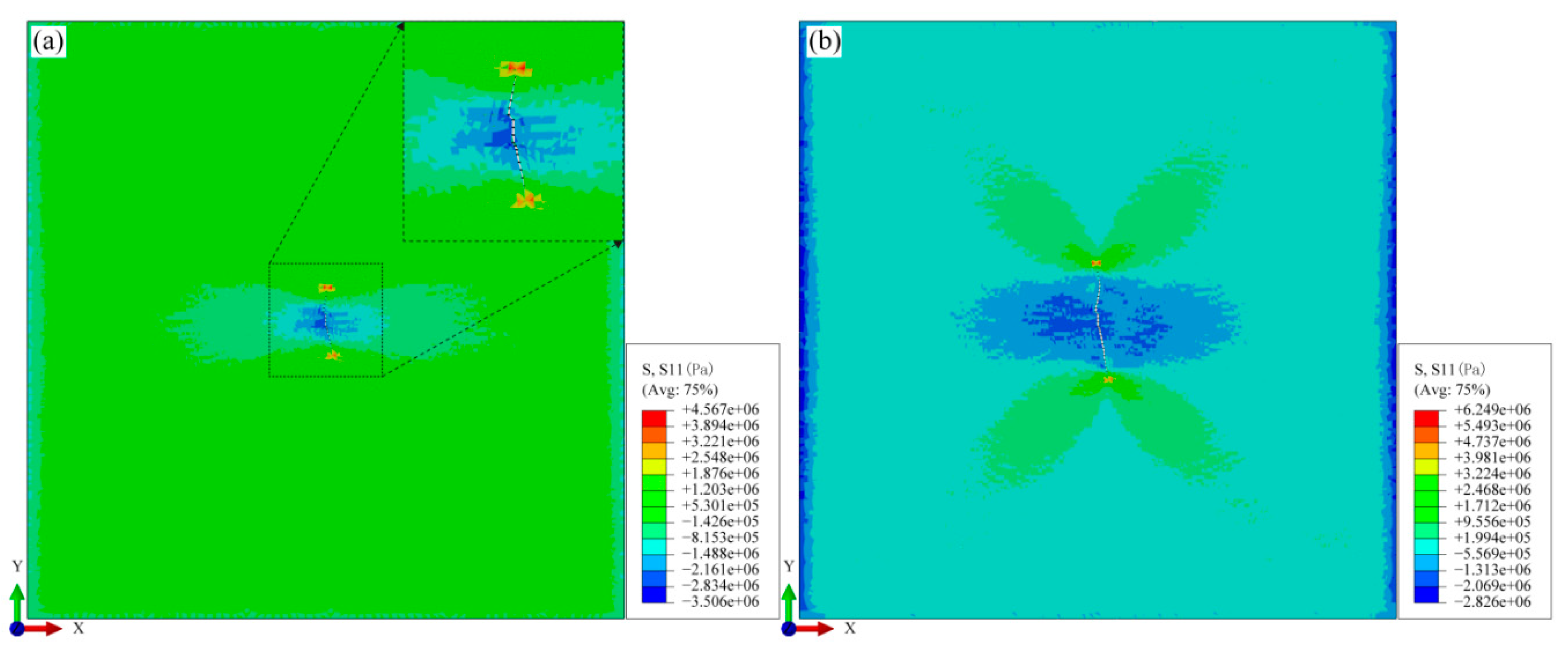
4.1. Fracture Path and AE-Location Map
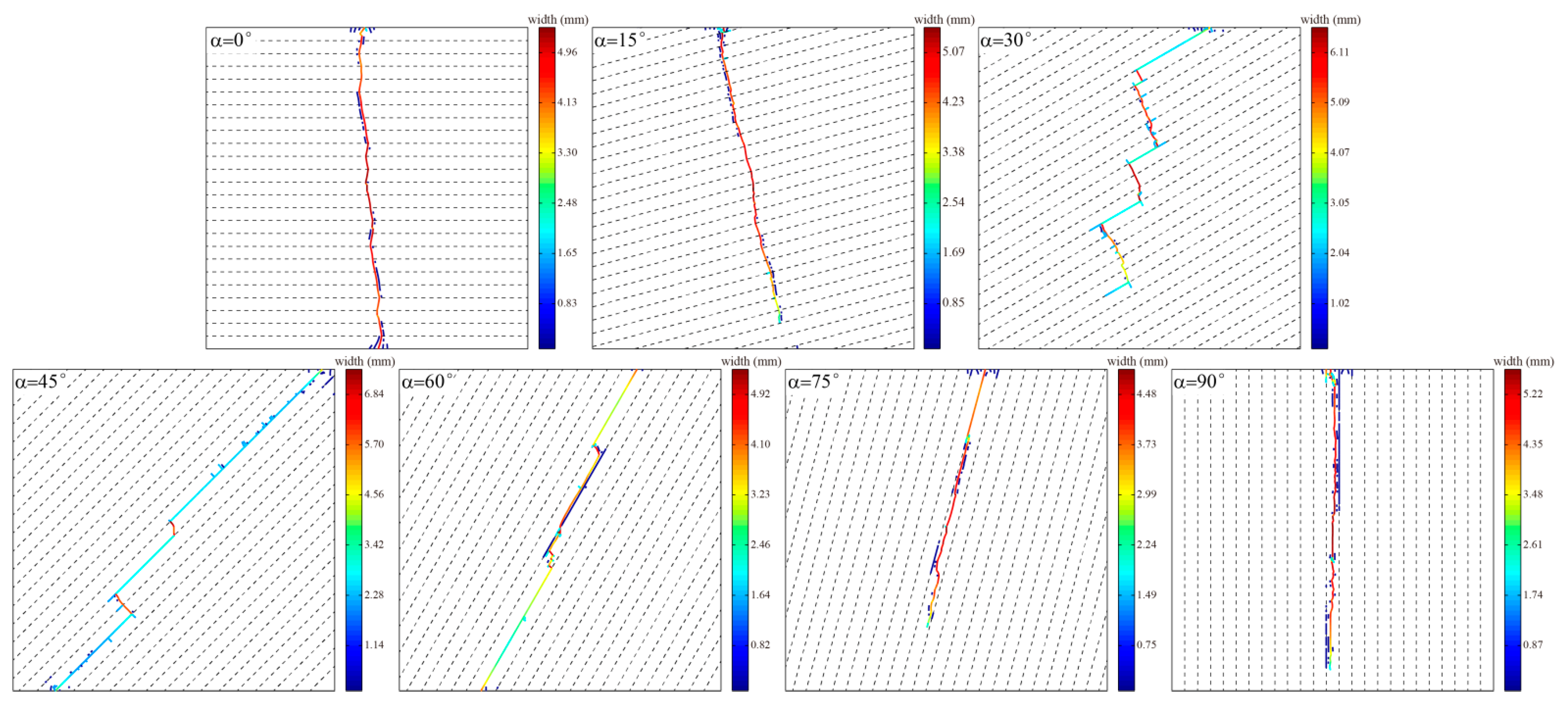
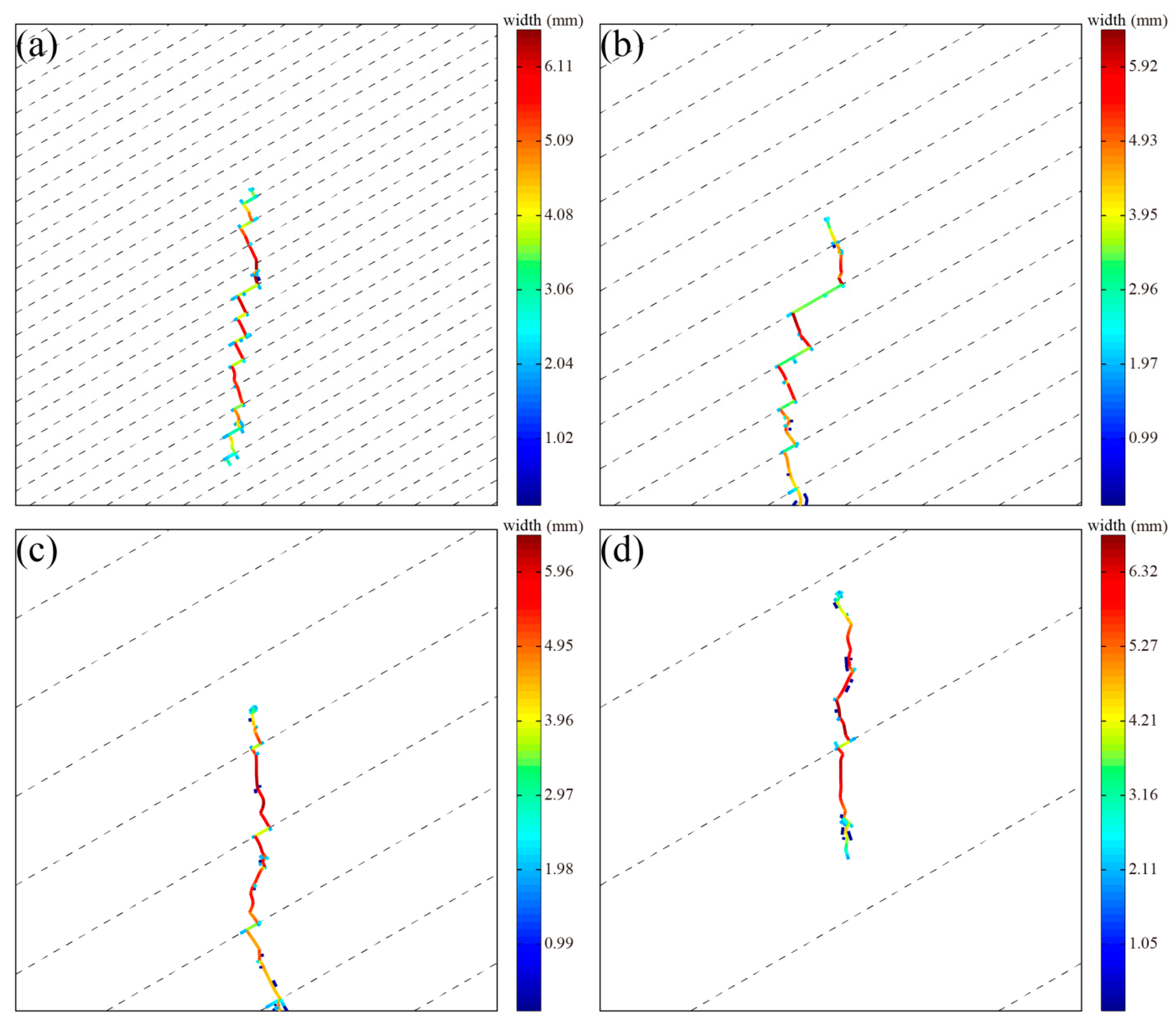
4.1.1. Fracture-Propagation Paths
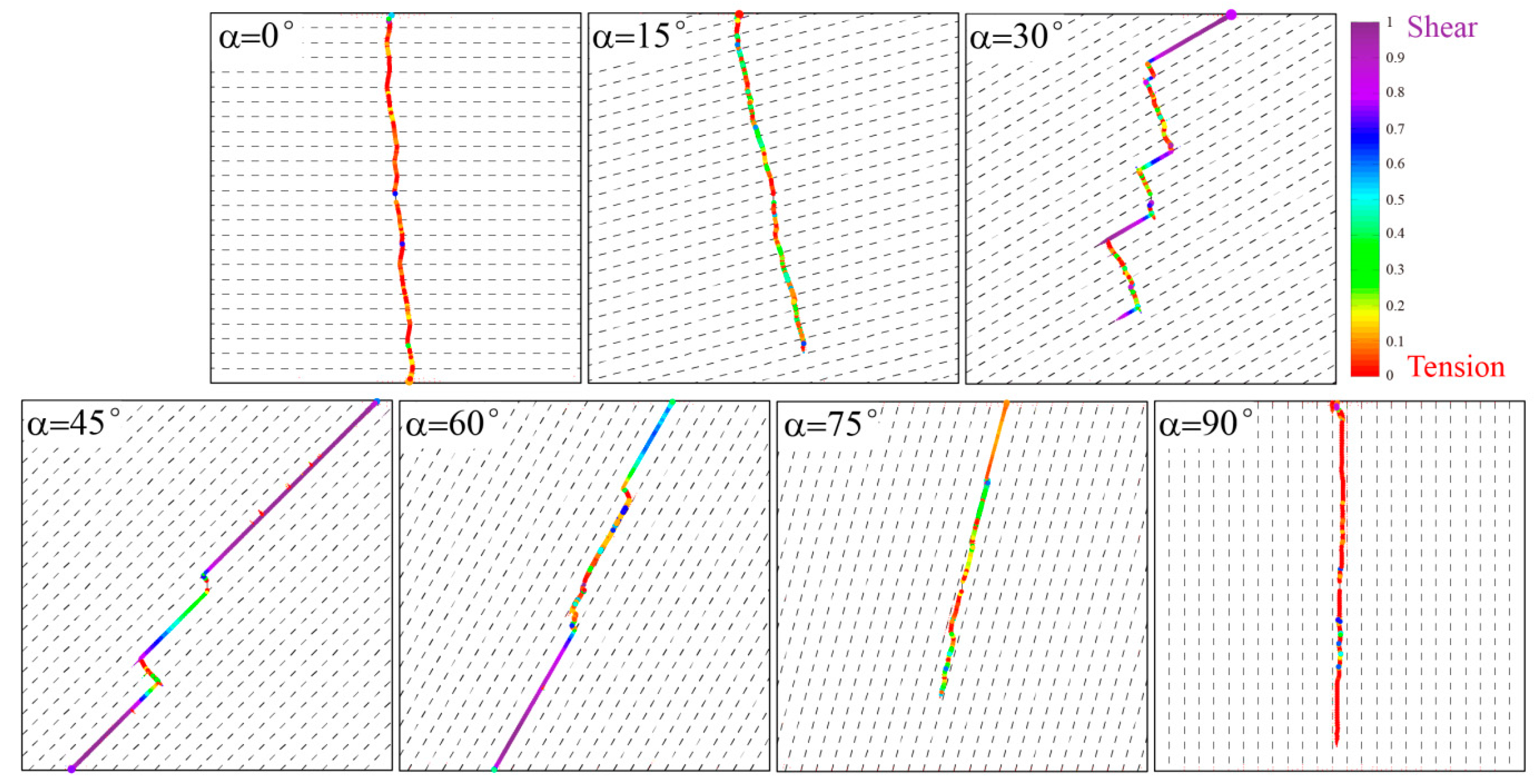
4.1.2. AE-Location Map
4.2. Fracture Lengths and Numbers of AE Events
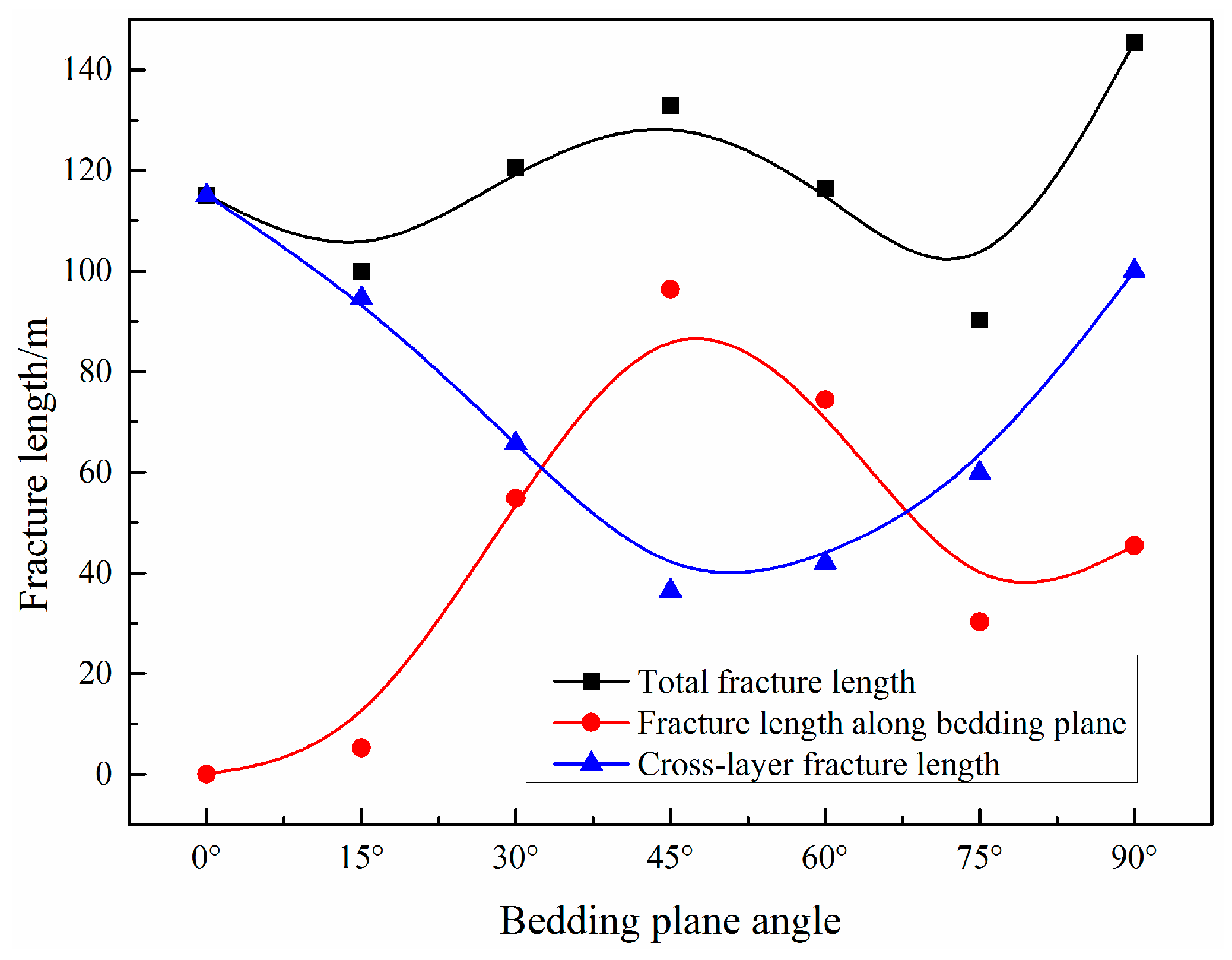
4.2.1. Fracture Length
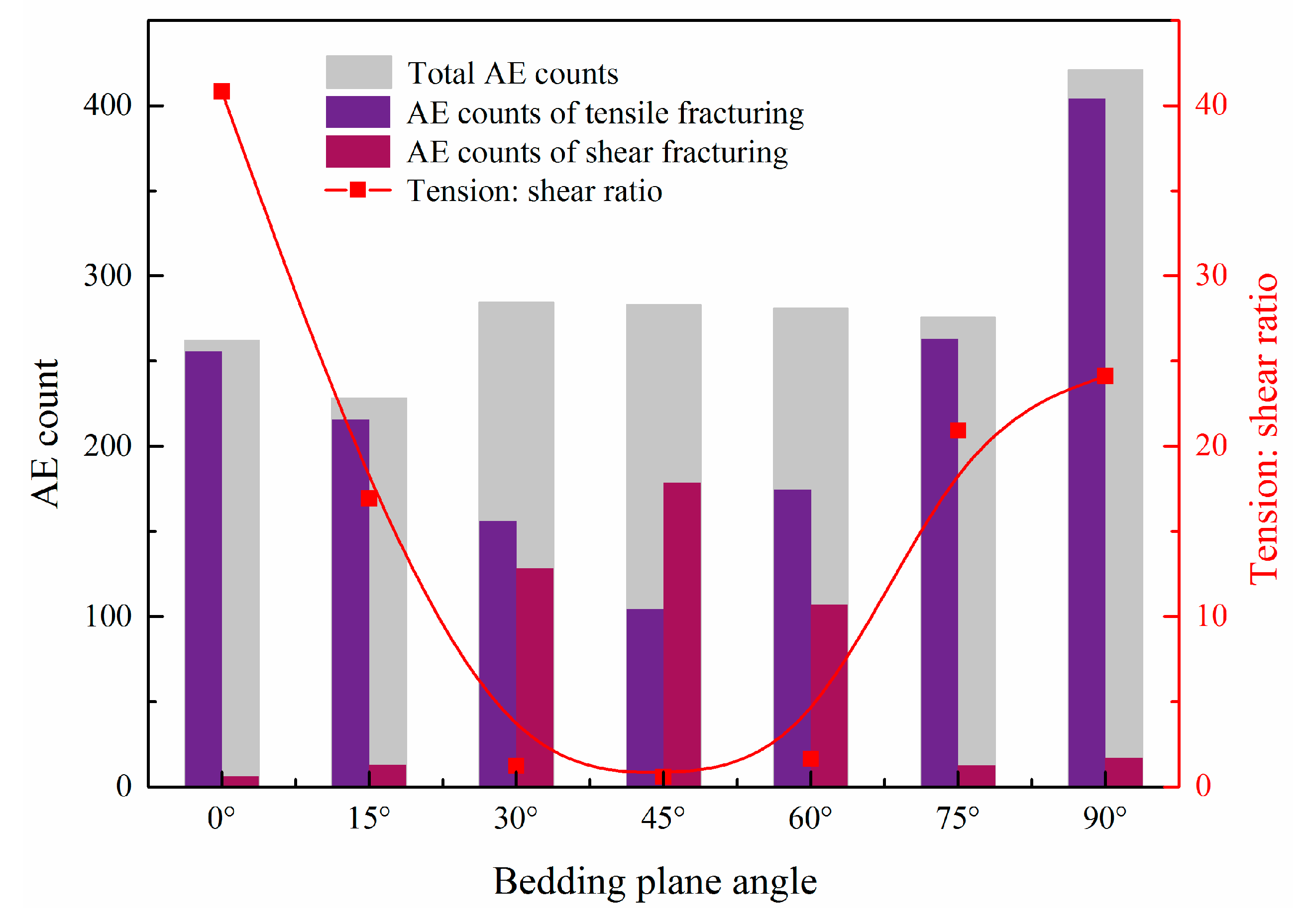
4.2.2. Number of AE Events
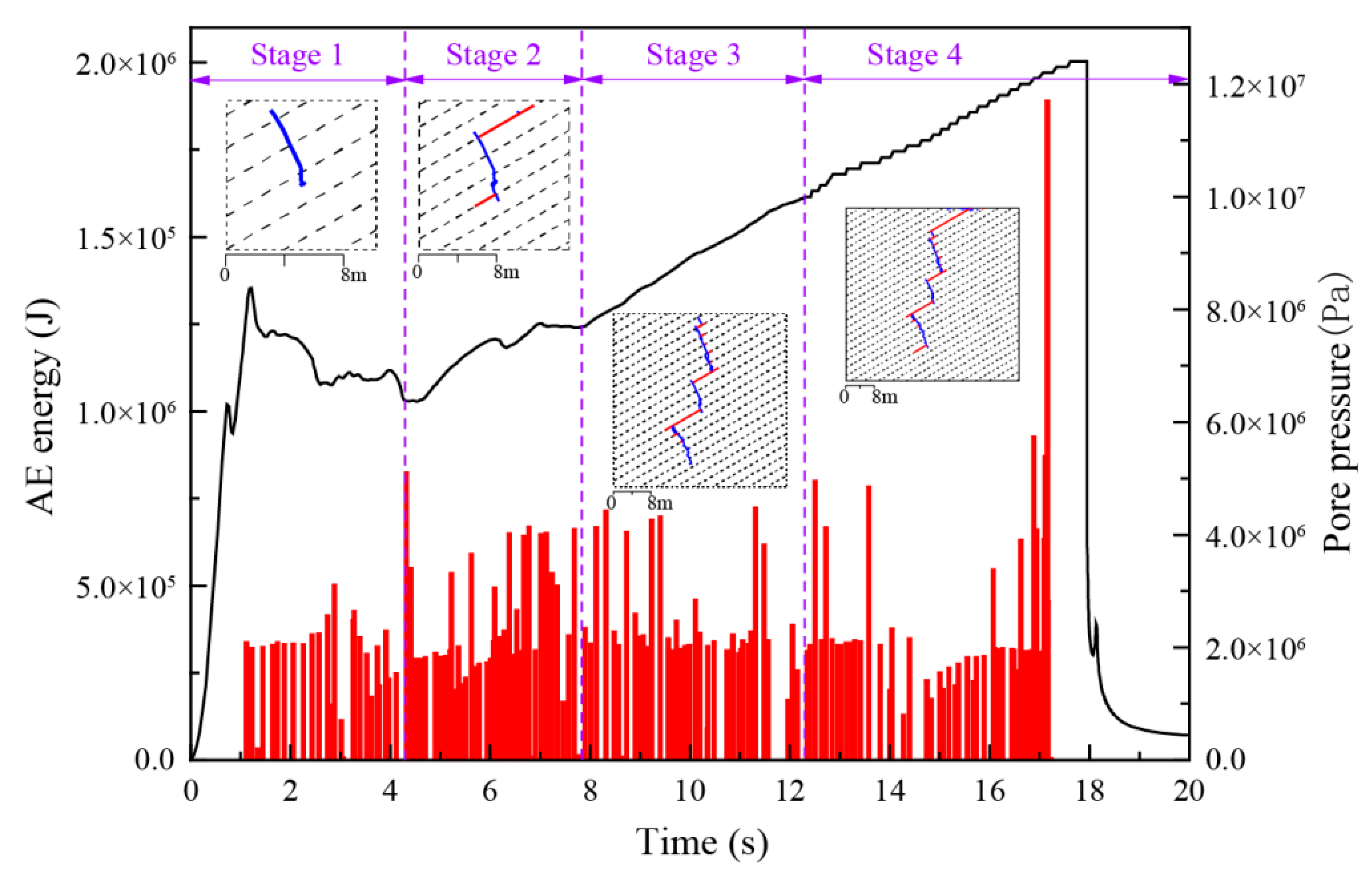
4.3. Pore-Water Pressure Curves and AE-Energy Distributions
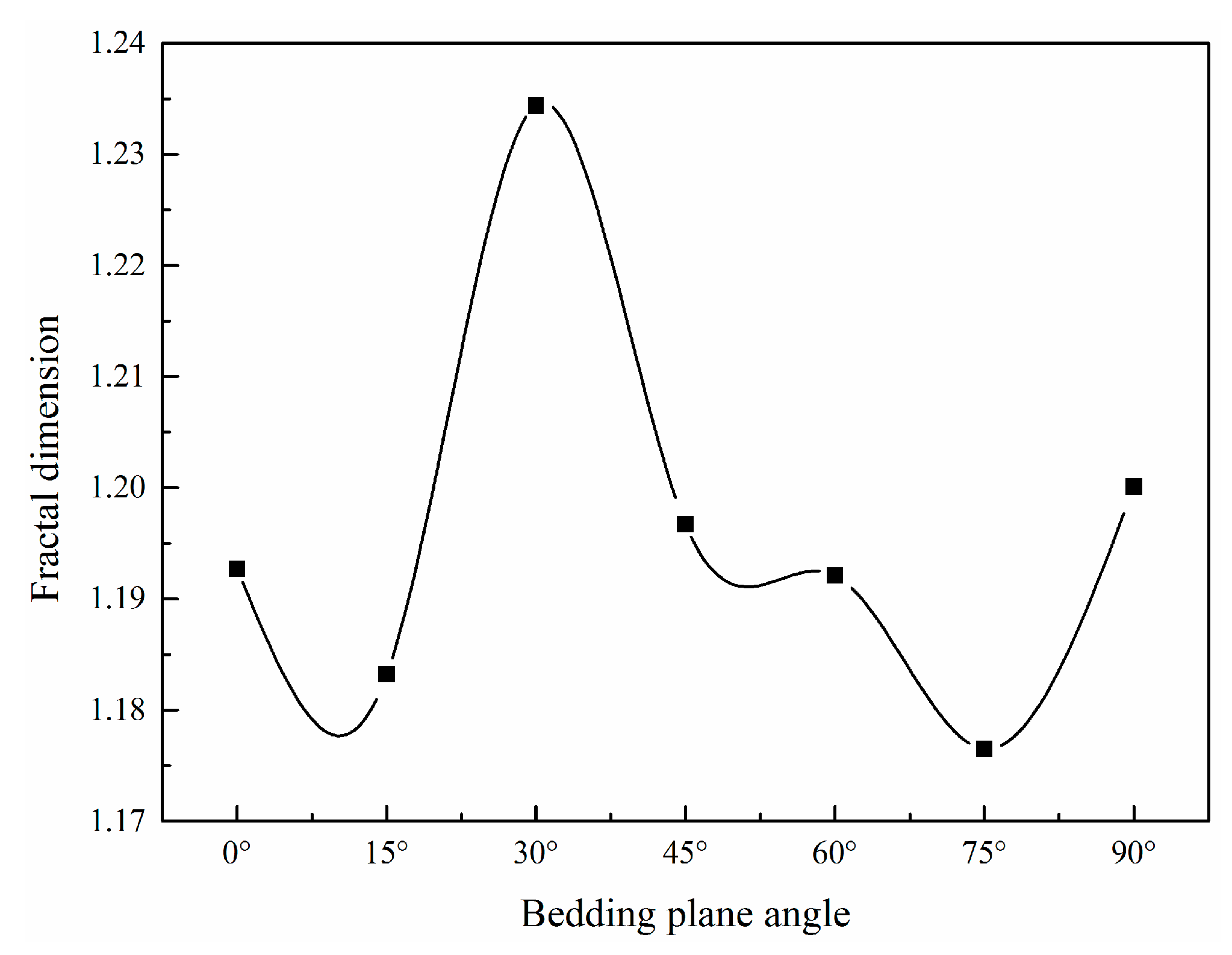
4.4. Fractal Dimensions (FDs)
5. Discussion
6. Conclusions
- (1)
- The maximum principal stress was always the main factor controlling the propagation of HFs, and the BPs captured HFs to inhibit their propagation along the direction of maximum principal stress. The larger the angle between the BP and the minimum principal stress, the stronger the capture ability. In addition, when a BP captured an HF, the phenomena of cross-layer and bedding slip fractures occurred alternately, showing characteristics of an intermittent dislocation fracture, which were most obvious when the BP angle was 30°. These results indicate that the final fracture path of the HF was determined by the maximum principal stress and BP.
- (2)
- The entire fracturing process was mainly dominated by cross-layer fractures, which are tensile fractures with a large fracture width, whereas bedding slip fractures are shear fractures with a small fracture width. A tensile fracture with a large fracture width is more effective for proppant migration and filling, whereas a shear fracture with a small fracture width is more effective for maintenance of the HF width.
- (3)
- Mineral heterogeneity directly affected the stress-contour distribution and indirectly affected the fracture-propagation direction and stress–shadow effect. Therefore, mineral heterogeneity plays an important role in multi-cluster and multi-batch fracturing.
- (4)
- When combining the fracture path, fracture length, AE-fracture type, and fractal dimension, the best fracturing effect was obtained when the BP angle was 30° with moderate interlayer spacing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| K | element stiffness |
| heff | element geometric thickness |
| V | integral space |
| S | surface of the integral space |
| δε | virtual strain field |
| δv | virtual-velocity field of the rock node |
| T | external surface force of the unit integral region |
| liquid density | |
| g | acceleration of gravity |
| Q | injection rate |
| kt | tangential permeability |
| ∇p | pressure gradient along the fracture surface |
| d | opening displacement of the fracture element |
| μ | viscosity of the fracturing fluid |
| q | volume-flow rate |
| c | filtration coefficient |
| p | pore pressure |
| D | damage variable |
| effective displacement when a failure occurs | |
| effective displacement of the damage initiation evolution | |
| maximum effective displacement | |
| effective traction force | |
| fracture energy | |
| number of grids containing cracks | |
| edge lengths of the grids | |
| A | initial value of the image distribution |
References
- Men, X.; Tang, C.a.; Wang, S.; Li, Y.; Yang, T.; Ma, T. Numerical simulation of hydraulic fracturing in heterogeneous rock: The effect of perforation angles and bedding plane on hydraulic fractures evolutions. In Proceedings of the SRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, QLD, Australia, 20–22 May 2013. [Google Scholar]
- Daneshy, A.A. Hydraulic fracture propagation in layered formations. Soc. Pet. Eng. J. 1978, 18, 33–41. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y.; Wang, C.; Liu, Q. Hydraulic fracturing characteristics and evaluation of fracturing effectiveness under different anisotropic angles and injection rates: An experimental investigation in absence of confining pressure. J. Nat. Gas Sci. Eng. 2022, 97, 104343. [Google Scholar] [CrossRef]
- Weng, X.; Chuprakov, D.; Kresse, O.; Prioul, R.; Wang, H. Hydraulic fracture-height containment by permeable weak bedding interfaces. Geophysics 2018, 83, MR137–MR152. [Google Scholar] [CrossRef]
- Li, J.; Zou, Y.; Shi, S.; Zhang, S.; Wang, J.; Ma, X.; Zhang, X. Experimental study on fracture propagation mechanism of shale oil reservoir of Lucaogou Formation in Jimusar. Geofluids 2022, 2022, 6598575. [Google Scholar] [CrossRef]
- Wu, S.; Ge, H.; Li, T.; Wang, X.; Li, N.; Zou, Y.; Gao, K. Characteristics of fractures stimulated by supercritical carbon dioxide fracturing in shale based on acoustic emission monitoring. Int. J. Rock Mech. Min. Sci. 2022, 152, 105065. [Google Scholar] [CrossRef]
- Huang, B.X.; Liu, J.W. Experimental Investigation of the Effect of Bedding Planes on Hydraulic Fracturing Under True Triaxial Stress. Rock Mech. Rock Eng. 2017, 50, 2627–2643. [Google Scholar] [CrossRef]
- Guo, Y.T.; Yang, C.H.; Wang, L.; Xu, F. Study on the Influence of Bedding Density on Hydraulic Fracturing in Shale. Arab. J. Sci. Eng. 2018, 43, 6493–6508. [Google Scholar] [CrossRef]
- Fu, W.; Savitski, A.A.; Damjanac, B.; Bunger, A.P. Three-dimensional lattice simulation of hydraulic fracture interaction with natural fractures. Comput. Geotech. 2019, 107, 214–234. [Google Scholar] [CrossRef]
- Zhang, F.; Dontsov, E.; Mack, M. Fully coupled simulation of a hydraulic fracture interacting with natural fractures with a hybrid discrete-continuum method. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1430–1452. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L.; Braun, A.; Han, Z. Investigation of processes of interaction between hydraulic and natural fractures by PFC modeling comparing against laboratory experiments and analytical models. Energies 2017, 10, 1001. [Google Scholar] [CrossRef] [Green Version]
- Cui, Z.; Han, W. In situ scanning electron microscope (SEM) observations of damage and crack growth of shale. Microsc. Microanal. 2018, 24, 107–115. [Google Scholar] [CrossRef] [PubMed]
- Abell, B.; Xing, P.; Bunger, A.; Dontsov, E.; Suarez-Rivera, R. Laboratory Investigation of Leak-Off During Hydraulic Fracturing into Bedding Interfaces. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar]
- Xie, J.; Tang, J.; Yong, R.; Fan, Y.; Zuo, L.; Chen, X.; Li, Y. A 3-D hydraulic fracture propagation model applied for shale gas reservoirs with multiple bedding planes. Eng. Fract. Mech. 2020, 228, 106872. [Google Scholar] [CrossRef]
- Zou, Y.; Ma, X.; Zhang, S.; Zhou, T.; Li, H. Numerical investigation into the influence of bedding plane on hydraulic fracture network propagation in shale formations. Rock Mech. Rock Eng. 2016, 49, 3597–3614. [Google Scholar]
- Tang, J.; Wu, K.; Li, Y.; Hu, X.; Liu, Q.; Ehlig-Economides, C. Numerical investigation of the interactions between hydraulic fracture and bedding planes with non-orthogonal approach angle. Eng. Fract. Mech. 2018, 200, 1–16. [Google Scholar] [CrossRef]
- Li, Y.; Hu, W.; Zhang, Z.; Zhang, Z.; Shang, Y.; Han, L.; Wei, S. Numerical simulation of hydraulic fracturing process in a naturally fractured reservoir based on a discrete fracture network model. J. Struct. Geol. 2021, 147, 104331. [Google Scholar] [CrossRef]
- Gong, T.; Xia, B.; Liu, L.; Peng, Z.; Gao, Y. Propagation of hydraulic fracture under the joint impact of bedding planes and natural fractures in shale reservoirs. Energy Sci. Eng. 2019, 7, 2690–2702. [Google Scholar] [CrossRef]
- Sun, C.; Zheng, H.; Liu, W.D.; Lu, W. Numerical simulation analysis of vertical propagation of hydraulic fracture in bedding plane. Eng. Fract. Mech. 2020, 232, 107056. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J. Numerical simulation of fracture network generation in naturally fractured reservoirs. J. Nat. Gas Sci. Eng. 2016, 30, 430–443. [Google Scholar] [CrossRef]
- Nagel, N.B.; Sanchez-Nagel, M.A.; Zhang, F.; Garcia, X.; Lee, B. Coupled Numerical Evaluations of the Geomechanical Interactions Between a Hydraulic Fracture Stimulation and a Natural Fracture System in Shale Formations. Rock Mech. Rock Eng. 2013, 46, 581–609. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Han, W.; Cui, Z.; Zhang, J. Fracture path interaction of two adjacent perforations subjected to different injection rate increments. Comput. Geotech. 2020, 122, 103500. [Google Scholar] [CrossRef]
- Camanho, P.P.; Dávila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials; Langley Research Center: Hampton, VA, USA, 2002.
- He, M.C.; Miao, J.L.; Feng, J.L. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions. Int. J. Rock Mech. Min. Sci. 2010, 47, 286–298. [Google Scholar] [CrossRef]
- Han, W.; Cui, Z.; Tang, T.; Zhang, J.; Wang, Y. Effects of different bedding plane strength on crack propagation process un-der three points bending. J. China Coal Soc. 2019, 44, 3022–3030. (In Chinese) [Google Scholar]
- Cui, Z.; Qi, S.; Han, W. The role of weak bedding planes in the cross-layer crack growth paths of layered rocks. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 22. [Google Scholar] [CrossRef]
- Han, W.; Cui, Z.; Zhu, Z. The Effect of Perforation Spacing on the Variation of Stress Shadow. Energies 2021, 14, 4040. [Google Scholar] [CrossRef]
- Li, J.; Du, Q.; Sun, C. An improved box-counting method for image fractal dimension estimation. Pattern Recognit. 2009, 42, 2460–2469. [Google Scholar] [CrossRef]



| Minerals (Shale) | Elastic Modulus (GPa) | Poisson’s Ratio | Percentage (%) |
|---|---|---|---|
| Quartz | 40 | 0.2 | 49 |
| Muscovite | 18 | 0.27 | 17 |
| Albite | 21 | 0.24 | 11 |
| Calcite | 27 | 0.23 | 6 |
| Dolomite | 21 | 0.23 | 5 |
| Microcline | 20 | 0.25 | 4 |
| Kaolinite | 22 | 0.23 | 4 |
| Pyrite | 35 | 0.22 | 4 |
| Simulation Parameter | Value | |
|---|---|---|
| Cohesive Elements in the BP | Cohesive Elements in the Matrix | |
| Knn | 15 | 17 |
| Kss | 15 | 17 |
| Ktt | 15 | 17 |
| Tensile strength (MPa) | 3 | 6 |
| Shear strength (MPa) | 6 | 12 |
| Horizontal maximum principal stress | 13 | |
| Horizontal minimum principal stress | 7 | |
| Permeability coefficient (m/s) | 1−7 | |
| Filtration coefficient (m/[Pa × s]) | 1−14 | |
| Fracturing fluid viscosity (Pa × S) | 0.001 | |
| Injection rate (m2/s) | 0.01 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Cui, Z.; Zhu, Z.; Han, X. The Effect of Bedding Plane Angle on Hydraulic Fracture Propagation in Mineral Heterogeneity Model. Energies 2022, 15, 6052. https://doi.org/10.3390/en15166052
Han W, Cui Z, Zhu Z, Han X. The Effect of Bedding Plane Angle on Hydraulic Fracture Propagation in Mineral Heterogeneity Model. Energies. 2022; 15(16):6052. https://doi.org/10.3390/en15166052
Chicago/Turabian StyleHan, Weige, Zhendong Cui, Zhengguo Zhu, and Xianmin Han. 2022. "The Effect of Bedding Plane Angle on Hydraulic Fracture Propagation in Mineral Heterogeneity Model" Energies 15, no. 16: 6052. https://doi.org/10.3390/en15166052
APA StyleHan, W., Cui, Z., Zhu, Z., & Han, X. (2022). The Effect of Bedding Plane Angle on Hydraulic Fracture Propagation in Mineral Heterogeneity Model. Energies, 15(16), 6052. https://doi.org/10.3390/en15166052






