A Review on Magnet Loss Analysis, Validation, Design Considerations, and Reduction Strategies in Permanent Magnet Synchronous Motors
Abstract
:1. Introduction
2. Loss Mechanism and Modeling Techniques
2.1. Hysteresis Loss
2.2. Eddy Current Loss
2.3. A Comparison Study
3. Material Properties
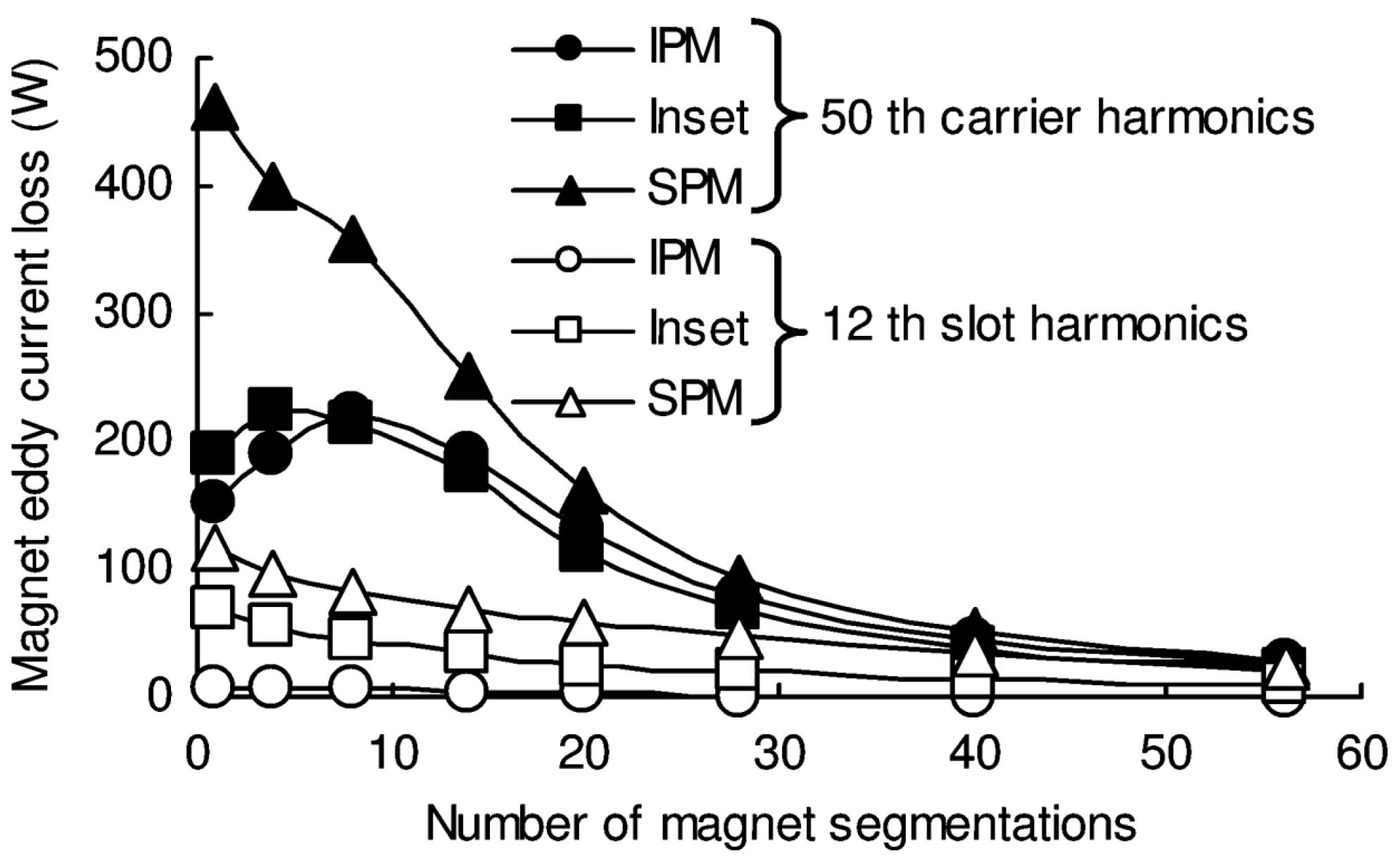
4. Segmentation Effects
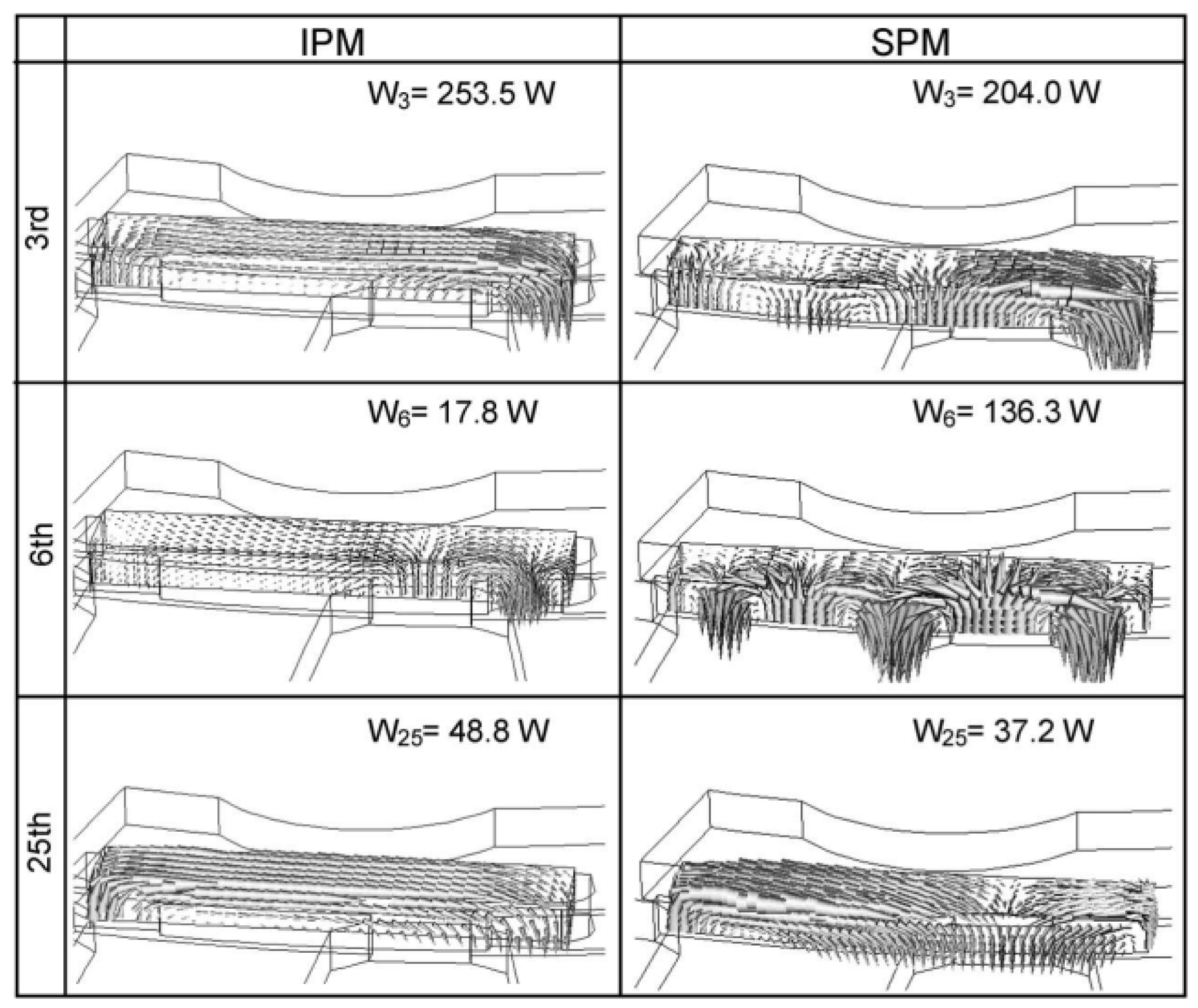
5. Rotor Types
6. Stator and Winding Type
7. Other Considerations in Loss Reduction
8. Validation and Tests
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, W.Y.; Bettayeb, A.; Kaczmarek, R.; Vannier, J.C. Optimization of magnet segmentation for reduction of eddy-current losses in permanent magnet synchronous machine. IEEE Trans. Energy Convers. 2010, 25, 381–387. [Google Scholar] [CrossRef]
- Aoyama, Y.; Miyata, K.; Ohashi, K. Simulations and experiments on eddy current in Nd-Fe-B magnet. IEEE Trans. Magn. 2005, 41, 3790–3792. [Google Scholar] [CrossRef]
- Ruoho, S.; Dlala, E.; Arkkio, A. Comparison of demagnetization models for finite-element analysis of permanent-magnet synchronous machines. IEEE Trans. Magn. 2007, 43, 3964–3968. [Google Scholar] [CrossRef]
- Petrov, I.; Egorov, D.; Link, J.; Stern, R.; Ruoho, S.; Pyrhönen, J. Hysteresis losses in different types of permanent magnets used in PMSMs. IEEE Trans. Ind. Electron. 2016, 64, 2502–2510. [Google Scholar] [CrossRef]
- Pyrhönen, J.; Ruoho, S.; Nerg, J.; Paju, M.; Tuominen, S.; Kankaanpää, H.; Stern, R.; Boglietti, A.; Uzhegov, N. Hysteresis losses in sintered NdFeB permanent magnets in rotating electrical machines. IEEE Trans. Ind. Electron. 2014, 62, 857–865. [Google Scholar] [CrossRef]
- Yamazaki, K.; Fukushima, Y. Effect of eddy-current loss reduction by magnet segmentation in synchronous motors with concentrated windings. IEEE Trans. Ind. Appl. 2011, 47, 779–788. [Google Scholar] [CrossRef]
- Sergeant, P.; Van den Bossche, A. Segmentation of magnets to reduce losses in permanent-magnet synchronous machines. IEEE Trans. Magn. 2008, 44, 4409–4412. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, J.; Liu, C.; Lei, G.; Guo, Y.; Zhu, J. Reduction of magnet eddy current loss in PMSM by using partial magnet segment method. IEEE Trans. Magn. 2019, 55, 8105105. [Google Scholar] [CrossRef]
- Kim, D.M.; Kim, J.H.; Lee, S.G.; Park, M.R.; Lee, G.H.; Lim, M.S. Estimation Method for Rotor Eddy Current Loss in Ultrahigh-Speed Surface-Mounted Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2020, 57, 8103205. [Google Scholar] [CrossRef]
- Hemeida, A.; Sergeant, P.; Vansompel, H. Comparison of methods for permanent magnet eddy-current loss computations with and without reaction field considerations in axial flux PMSM. IEEE Trans. Magn. 2015, 51, 8107511. [Google Scholar] [CrossRef]
- Wu, X.; Wrobel, R.; Mellor, P.H.; Zhang, C. A computationally efficient PM power loss mapping for brushless AC PM machines with surface-mounted PM rotor construction. IEEE Trans. Ind. Electron. 2015, 62, 7391–7401. [Google Scholar] [CrossRef]
- Zhang, P.; Sizov, G.Y.; He, J.; Ionel, D.M.; Demerdash, N.A. Calculation of magnet losses in concentrated-winding permanent-magnet synchronous machines using a computationally efficient finite-element method. IEEE Trans. Ind. Appl. 2013, 49, 2524–2532. [Google Scholar] [CrossRef]
- Gerlach, T.; Rabenstein, L.; Dietz, A.; Kremser, A.; Gerling, D. Determination of eddy current losses in permanent magnets of SPMSM with concentrated windings: A hybrid loss calculation method and experimental verification. In Proceedings of the 2018 Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 10–12 April 2018; pp. 1–8. [Google Scholar]
- Atallah, K.; Howe, D.; Mellor, P.H.; Stone, D.A. Rotor loss in permanent-magnet brushless AC machines. IEEE Trans. Ind. Appl. 2000, 36, 1612–1618. [Google Scholar]
- Ishak, D.; Zhu, Z.; Howe, D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole. IEEE Trans. Magn. 2005, 41, 2462–2469. [Google Scholar] [CrossRef]
- Toda, H.; Xia, Z.; Wang, J.; Atallah, K.; Howe, D. Rotor eddy-current loss in permanent magnet brushless machines. IEEE Trans. Magn. 2004, 40, 2104–2106. [Google Scholar] [CrossRef]
- Ding, X.; Mi, C. Modeling of eddy current loss in the magnets of permanent magnet machines for hybrid and electric vehicle traction applications. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 419–424. [Google Scholar]
- Jumayev, S.; Merdzan, M.; Boynov, K.; Paulides, J.; Pyrhönen, J.; Lomonova, E. The effect of PWM on rotor eddy-current losses in high-speed permanent magnet machines. IEEE Trans. Magn. 2015, 51, 8109204. [Google Scholar] [CrossRef]
- Balamurali, A.; Lai, C.; Mollaeian, A.; Loukanov, V.; Kar, N.C. Analytical investigation into magnet eddy current losses in interior permanent magnet motor using modified winding function theory accounting for pulsewidth modulation harmonics. IEEE Trans. Magn. 2016, 52, 8106805. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, Z.; Staton, D.; Popescu, M.; Hawkins, D. Analytical model for predicting magnet loss of surface-mounted permanent magnet machines accounting for slotting effect and load. IEEE Trans. Magn. 2011, 48, 107–117. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, Z.; Staton, D.; Popescu, M.; Hawkins, D. Analytical modeling and analysis of open-circuit magnet loss in surface-mounted permanent-magnet machines. IEEE Trans. Magn. 2011, 48, 1234–1247. [Google Scholar] [CrossRef]
- Ede, J.D.; Atallah, K.; Jewell, G.W.; Wang, J.B.; Howe, D. Effect of axial segmentation of permanent magnets on rotor loss in modular permanent-magnet brushless machines. IEEE Trans. Ind. Appl. 2007, 43, 1207–1213. [Google Scholar] [CrossRef]
- Wang, J.; Atallah, K.; Chin, R.; Arshad, W.; Lendenmann, H. Rotor eddy-current loss in permanent-magnet brushless AC machines. IEEE Trans. Magn. 2010, 46, 2701–2707. [Google Scholar] [CrossRef]
- Bellara, A.; Bali, H.; Belfkira, R.; Amara, Y.; Barakat, G. Analytical prediction of open-circuit eddy-current loss in series double excitation synchronous machines. IEEE Trans. Magn. 2011, 47, 2261–2268. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, Z.; Staton, D.; Popescu, M.; Hawkins, D. Analytical model of eddy current loss in windings of permanent-magnet machines accounting for load. IEEE Trans. Magn. 2012, 48, 2138–2151. [Google Scholar] [CrossRef]
- Amara, Y.; Reghem, P.; Barakat, G. Analytical prediction of eddy-current loss in armature windings of permanent magnet brushless AC machines. IEEE Trans. Magn. 2010, 46, 3481–3484. [Google Scholar] [CrossRef]
- Mukerji, S.K.; George, M.; Ramamurthy, M.; Asaduzzaman, K. Eddy currents in solid rectangular cores. Prog. Electromagn. Res. B 2008, 7, 117–131. [Google Scholar] [CrossRef]
- Pyrhonen, J.; Jussila, H.; Alexandrova, Y.; Rafajdus, P.; Nerg, J. Harmonic loss calculation in rotor surface permanent magnets—New analytic approach. IEEE Trans. Magn. 2012, 48, 2358–2366. [Google Scholar] [CrossRef]
- Dubas, F.; Espanet, C.; Miraoui, A. Field diffusion equation in high-speed surface mounted permanent magnet motors, parasitic eddy-current losses. In Proceedings of the ELECTROMOTION, Lausanne, Switzerland, 27–29 September 2005; pp. 1–6. [Google Scholar]
- Zhu, Z.; Ng, K.; Schofield, N.; Howe, D. Improved analytical modelling of rotor eddy current loss in brushless machines equipped with surface-mounted permanent magnets. IEE Proc.-Electr. Power Appl. 2004, 151, 641–650. [Google Scholar] [CrossRef]
- Markovic, M.; Perriard, Y. Analytical solution for rotor eddy-current losses in a slotless permanent-magnet motor: The case of current sheet excitation. IEEE Trans. Magn. 2008, 44, 386–393. [Google Scholar] [CrossRef]
- Yamazaki, K.; Shina, M.; Miwa, M.; Hagiwara, J. Investigation of eddy current loss in divided Nd–Fe–B sintered magnets for synchronous motors due to insulation resistance and frequency. IEEE Trans. Magn. 2008, 44, 4269–4272. [Google Scholar] [CrossRef]
- de la Barriere, O.; Hlioui, S.; Ahmed, H.B.; Gabsi, M. An analytical model for the computation of no-load eddy-current losses in the rotor of a permanent magnet synchronous machine. IEEE Trans. Magn. 2013, 52, 8103813. [Google Scholar] [CrossRef]
- Dubas, F.; Rahideh, A. Two-dimensional analytical permanent-magnet eddy-current loss calculations in slotless PMSM equipped with surface-inset magnets. IEEE Trans. Magn. 2013, 50, 54–73. [Google Scholar] [CrossRef]
- Nuscheler, R. Two-dimensional analytical model for eddy-current loss calculation in the magnets and solid rotor yokes of permanent magnet synchronous machines. In Proceedings of the 2008 18th International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008; pp. 1–6. [Google Scholar]
- Deng, F.; Nehl, T.W. Analytical modeling of eddy-current losses caused by pulse-width-modulation switching in permanent-magnet brushless direct-current motors. IEEE Trans. Magn. 1998, 34, 3728–3736. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Nair, S.S. An analytical method for predicting 3-D eddy current loss in permanent magnet machines based on generalized image theory. IEEE Trans. Magn. 2015, 52, 8103311. [Google Scholar] [CrossRef]
- Nair, S.S.; Wang, J.; Chen, L.; Chin, R.; Manolas, I.; Svechkarenko, D. Prediction of 3-D high-frequency eddy current loss in rotor magnets of SPM machines. IEEE Trans. Magn. 2016, 52, 8107910. [Google Scholar] [CrossRef]
- Zhu, Z.; Meng, Z. 3D analysis of eddy current loss in the permanent magnet coupling. Rev. Sci. Instrum. 2016, 87, 074701. [Google Scholar] [CrossRef]
- Mirzaei, M.; Binder, A.; Funieru, B.; Susic, M. Analytical calculations of induced eddy currents losses in the magnets of surface mounted PM machines with consideration of circumferential and axial segmentation effects. IEEE Trans. Magn. 2012, 48, 4831–4841. [Google Scholar] [CrossRef]
- Sahu, R.; Pellerey, P.; Laskaris, K. Eddy current loss model unifying the effects of reaction field and non-homogeneous 3-D magnetic field. IEEE Trans. Magn. 2020, 56, 7508404. [Google Scholar] [CrossRef]
- Rahideh, A.; Korakianitis, T. Analytical calculation of open-circuit magnetic field distribution of slotless brushless PM machines. Int. J. Electr. Power Energy Syst. 2013, 44, 99–114. [Google Scholar] [CrossRef]
- Pfister, P.D.; Perriard, Y. Slotless permanent-magnet machines: General analytical magnetic field calculation. IEEE Trans. Magn. 2011, 47, 1739–1752. [Google Scholar] [CrossRef]
- Song, Z.; Liu, C.; Chen, Y.; Huang, R. Air-gap Permeance and Reluctance Network Models for Analyzing Vibrational Exciting Force of In-wheel PMSM. IEEE Trans. Veh. Technol. 2022, 71, 7122–7133. [Google Scholar] [CrossRef]
- Mukundan, S.; Dhulipati, H.; Tjong, J.; Kar, N.C. Parameter determination of PMSM using coupled electromagnetic and thermal model incorporating current harmonics. IEEE Trans. Magn. 2018, 54, 8110505. [Google Scholar] [CrossRef]
- Hemeida, A.; Sergeant, P. Analytical modeling of surface PMSM using a combined solution of Maxwell–s equations and magnetic equivalent circuit. IEEE Trans. Magn. 2014, 50, 7027913. [Google Scholar] [CrossRef]
- Tariq, A.R.; Nino-Baron, C.E.; Strangas, E.G. Iron and magnet losses and torque calculation of interior permanent magnet synchronous machines using magnetic equivalent circuit. IEEE Trans. Magn. 2010, 46, 4073–4080. [Google Scholar] [CrossRef]
- Abbaszadeh, K.; Alam, F.R. On-load field component separation in surface-mounted permanent-magnet motors using an improved conformal mapping method. IEEE Trans. Magn. 2015, 52, 5200112. [Google Scholar] [CrossRef]
- Alam, F.R.; Abbaszadeh, K. Magnetic field analysis in eccentric surface-mounted permanent-magnet motors using an improved conformal mapping method. IEEE Trans. Energy Convers. 2015, 31, 333–344. [Google Scholar] [CrossRef]
- Pfister, P.D.; Yin, X.; Fang, Y. Slotted permanent-magnet machines: General analytical model of magnetic fields, torque, eddy currents, and permanent-magnet power losses including the diffusion effect. IEEE Trans. Magn. 2015, 52, 8103013. [Google Scholar] [CrossRef]
- Burress, T.; Coomer, C.; Campbell, S.; Seiber, L.; Marlino, L.D.; Staunton, R.; Cunningham, J. Evaluation of the 2007 Toyota Camry Hybrid Synergy Drive System; Technical Report; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2008. [Google Scholar]
- Zhang, H.; Wallmark, O. Limitations and constraints of eddy-current loss models for interior permanent-magnet motors with fractional-slot concentrated windings. Energies 2017, 10, 379. [Google Scholar] [CrossRef]
- Standard Specifications For Permanent Magnet Materials, No. 0100-00. Available online: https://www.datasheetarchive.com/whats_new/ba4f284c073012d3e2490a1b41e0e98c.html (accessed on 31 July 2022).
- Yamazaki, K.; Abe, A. Loss investigation of interior permanent-magnet motors considering carrier harmonics and magnet eddy currents. IEEE Trans. Ind. Appl. 2009, 45, 659–665. [Google Scholar] [CrossRef]
- Yamazaki, K.; Watari, S. Loss analysis of permanent-magnet motor considering carrier harmonics of PWM inverter using combination of 2-D and 3-D finite-element method. IEEE Trans. Magn. 2005, 41, 1980–1983. [Google Scholar] [CrossRef]
- Ou, J.; Liu, Y.; Liang, D.; Doppelbauer, M. Investigation of PM eddy current losses in surface-mounted PM motors caused by PWM. IEEE Trans. Power Electron. 2019, 34, 11253–11263. [Google Scholar] [CrossRef]
- Takahashi, N.; Shinagawa, H.; Miyagi, D.; Doi, Y.; Miyata, K. Analysis of eddy current losses of segmented Nd–Fe–B sintered magnets considering contact resistance. IEEE Trans. Magn. 2009, 45, 1234–1237. [Google Scholar] [CrossRef]
- Fukuma, A.; Kanazawa, S.; Miyagi, D.; Takahashi, N. Investigation of AC loss of permanent magnet of SPM motor considering hysteresis and eddy-current losses. IEEE Trans. Magn. 2005, 41, 1964–1967. [Google Scholar] [CrossRef]
- Yamazaki, K.; Fukushima, Y.; Sato, M. Loss analysis of permanent magnet motors with concentrated windings-variation of magnet eddy current loss due to stator and rotor shapes. In Proceedings of the 2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–8. [Google Scholar]
- Yamazaki, K.; Shina, M.; Kanou, Y.; Miwa, M.; Hagiwara, J. Effect of eddy current loss reduction by segmentation of magnets in synchronous motors: Difference between interior and surface types. IEEE Trans. Magn. 2009, 45, 4756–4759. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kitayuguchi, K. Teeth shape optimization of surface and interior permanent-magnet motors with concentrated windings to reduce magnet eddy current losses. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Korea, 10–13 October 2010; pp. 990–995. [Google Scholar]
- Choi, G.; Jahns, T.M. Reduction of eddy-current losses in fractional-slot concentrated-winding synchronous PM machines. IEEE Trans. Magn. 2016, 52, 8105904. [Google Scholar] [CrossRef]
- Chaithongsuk, S.; Takorabet, N.; Kreuawan, S. Reduction of eddy-current losses in fractional-slot concentrated-winding synchronous PM motors. IEEE Trans. Magn. 2015, 51, 8102204. [Google Scholar] [CrossRef]
- Dajaku, G.; Xie, W.; Gerling, D. Reduction of low space harmonics for the fractional slot concentrated windings using a novel stator design. IEEE Trans. Magn. 2013, 50, 8201012. [Google Scholar] [CrossRef]
- Wu, L.; Qu, R.; Li, D. Reduction of rotor eddy-current losses for surface PM machines with fractional slot concentrated windings and retaining sleeve. IEEE Trans. Magn. 2014, 50, 8205704. [Google Scholar] [CrossRef]
- Reddy, P.B.; El-Refaie, A.M.; Huh, K.K. Effect of number of layers on performance of fractional-slot concentrated-windings interior permanent magnet machines. IEEE Trans. Power Electron. 2014, 30, 2205–2218. [Google Scholar] [CrossRef]
- Chaithongsuk, S.; Takorabet, N.; Meibody-Tabar, F. On the use of pulse width modulation method for the elimination of flux density harmonics in the air-gap of surface PM motors. IEEE Trans. Magn. 2009, 45, 1736–1739. [Google Scholar] [CrossRef]
- Sato, D.; Itoh, J.i. Total loss comparison of inverter circuit topologies with interior permanent magnet synchronous motor drive system. In Proceedings of the 2013 IEEE ECCE Asia Downunder, Melbourne, VIC, Australia, 3–6 June 2013; pp. 537–543. [Google Scholar]
- Korta, P.; Kundu, A.; Balamurali, A.; Iyer, L.V.; Schlager, G.; Kar, N.C. A Novel Hybrid Modelling Approach Towards Comprehensive Drive Cycle Analysis of Si, SiC, and GaN based Electric Motor Drives. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 6331–6336. [Google Scholar]
- Kuenzler, M.; Werner, Q.; Schaefer, U. Multidisciplinary Analysis of Permanent Magnet Machines Considering Thermal Contact Resistance. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; Volume 1, pp. 940–946. [Google Scholar]
- Driesen, J.; Belmans, R.J.; Hameyer, K. Finite-element modeling of thermal contact resistances and insulation layers in electrical machines. IEEE Trans. Ind. Appl. 2001, 37, 15–20. [Google Scholar] [CrossRef]
- Joo, D.; Cho, J.H.; Woo, K.; Kim, B.T.; Kim, D.K. Electromagnetic field and thermal linked analysis of interior permanent-magnet synchronous motor for agricultural electric vehicle. IEEE Trans. Magn. 2011, 47, 4242–4245. [Google Scholar] [CrossRef]
- Zhao, N.; Zhu, Z.; Liu, W. Rotor eddy current loss calculation and thermal analysis of permanent magnet motor and generator. IEEE Trans. Magn. 2011, 47, 4199–4202. [Google Scholar] [CrossRef]
- Malloy, A.C.; Martinez-Botas, R.F.; Lampérth, M. Measurement of magnet losses in a surface mounted permanent magnet synchronous machine. IEEE Trans. Energy Convers. 2014, 30, 323–330. [Google Scholar] [CrossRef]
- Fratila, R.; Benabou, A.; Tounzi, A.; Mipo, J.C. A combined experimental and finite element analysis method for the estimation of eddy-current loss in NdFeB magnets. Sensors 2014, 14, 8505–8512. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Jassal, A.; Polinder, H.; Ferreira, J. Validation of eddy current loss models for permanent magnet machines with fractional-slot concentrated windings. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 678–685. [Google Scholar]


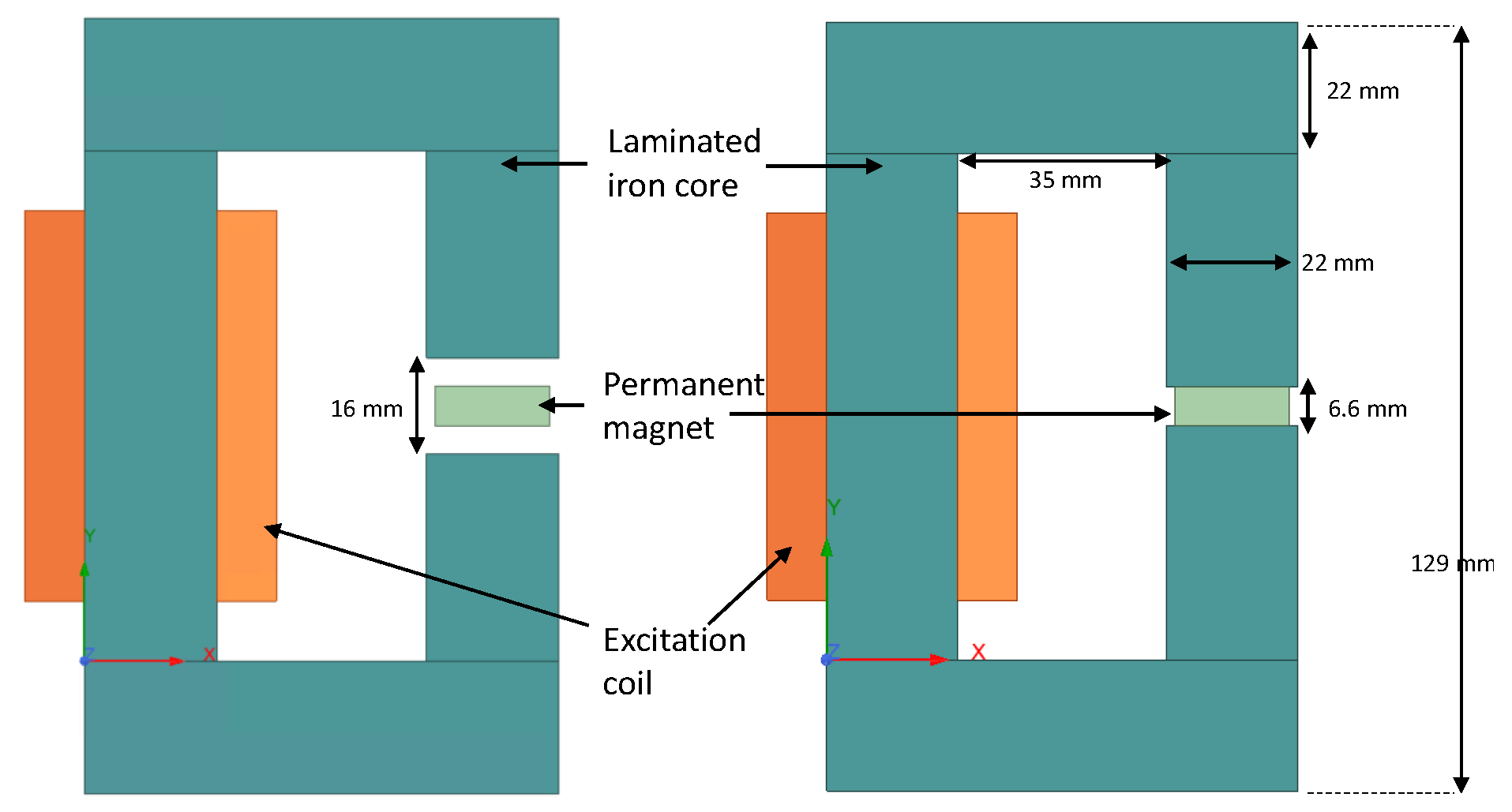
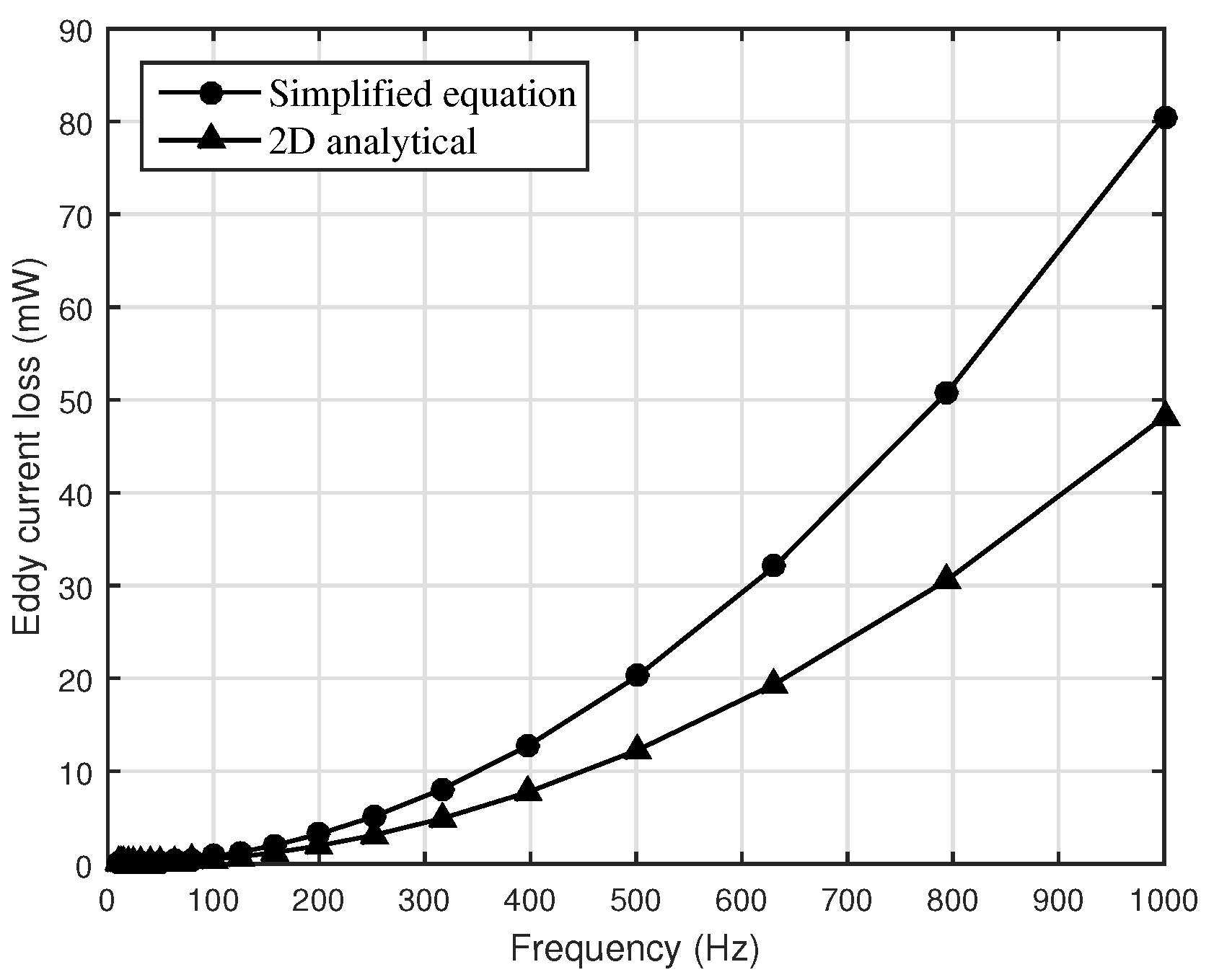
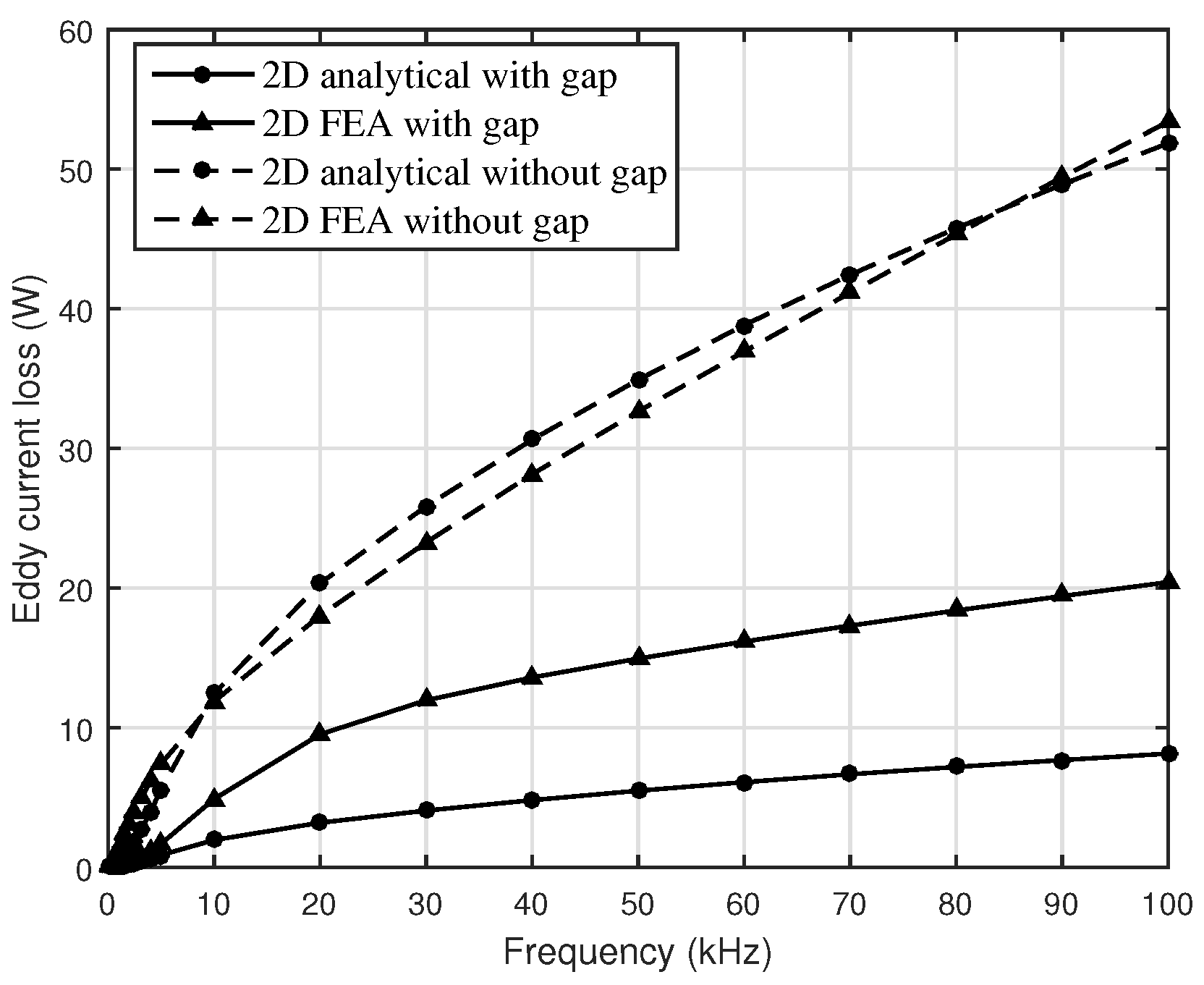

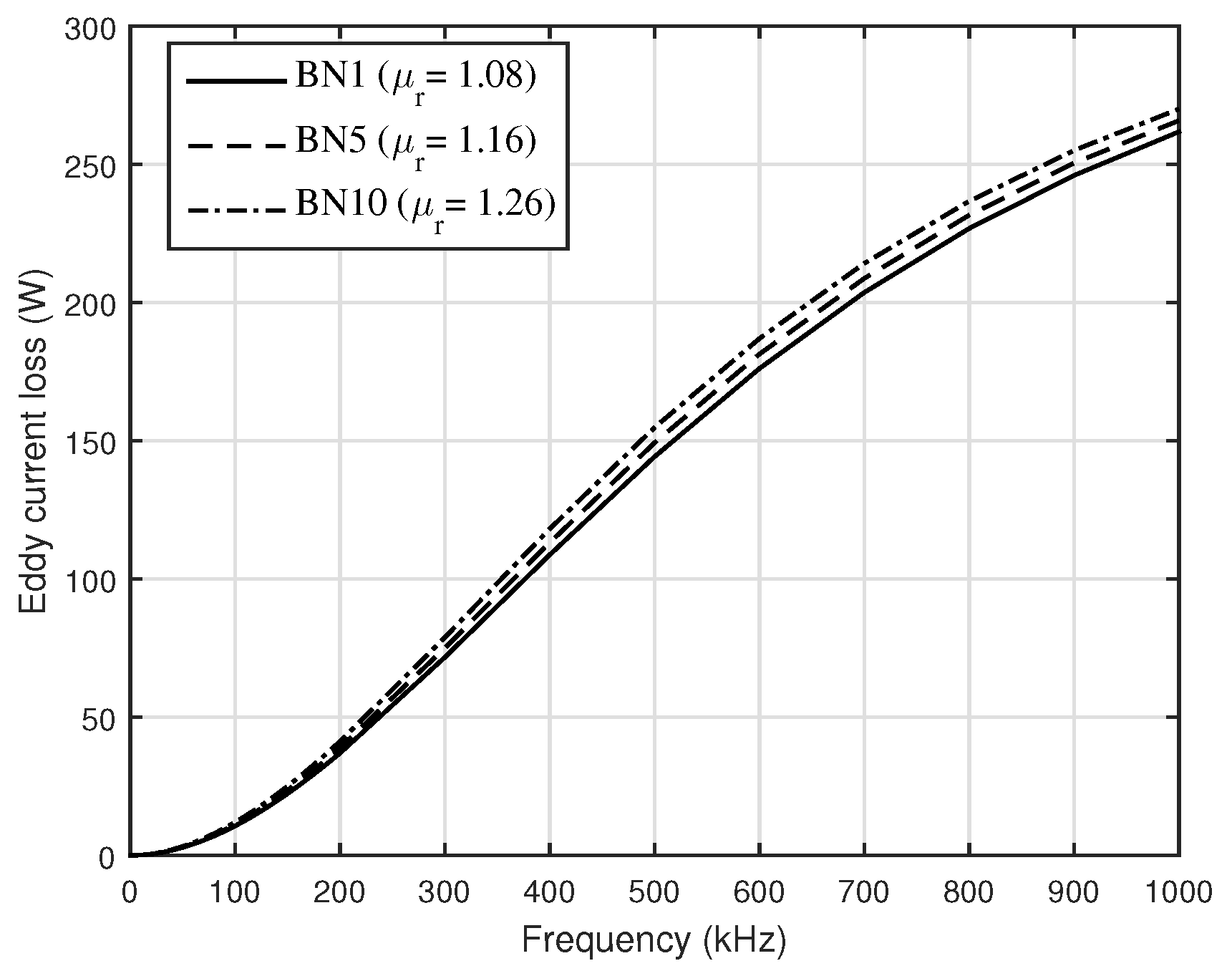
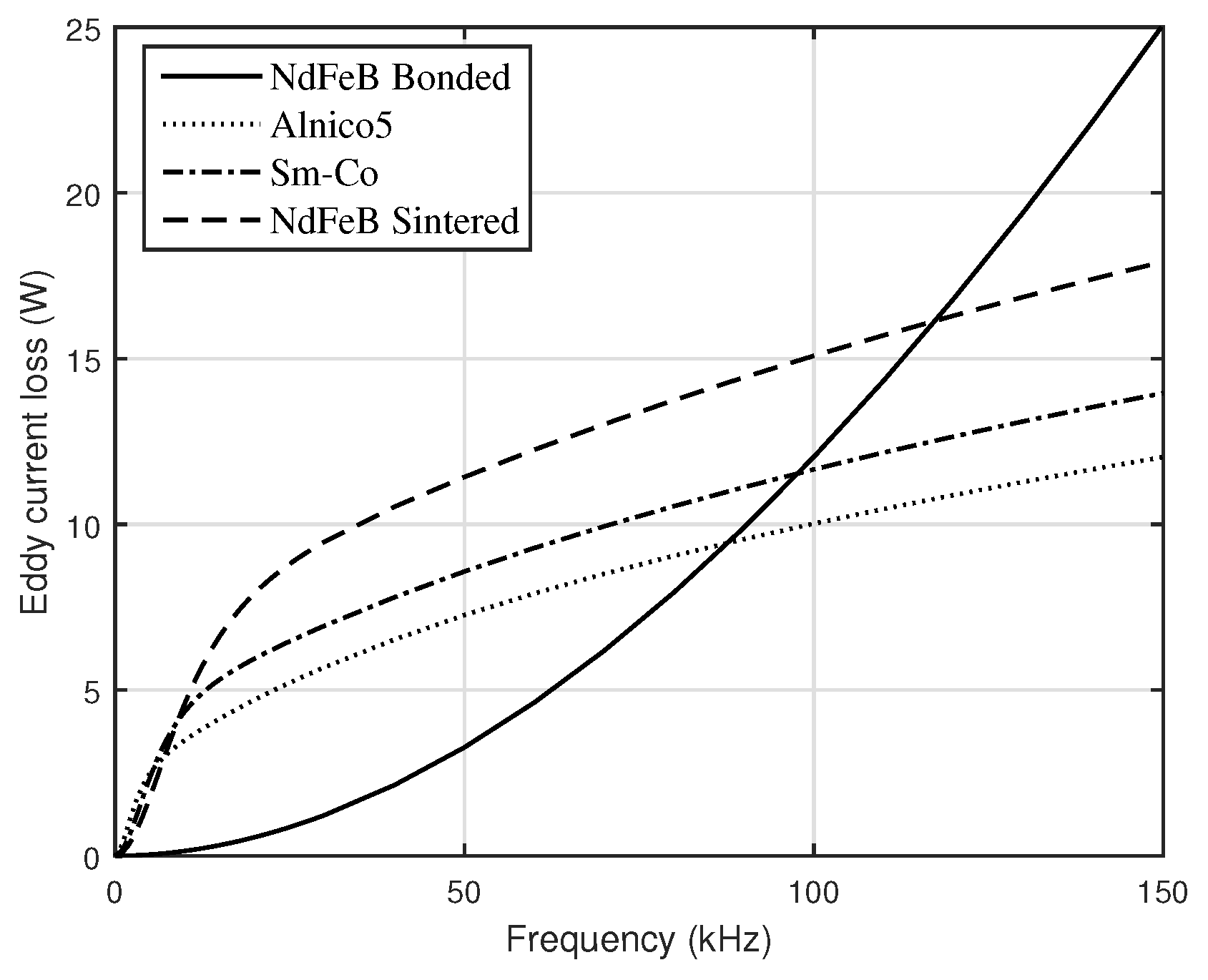

| Material | (MS/m) | (T) | |
|---|---|---|---|
| NdFeB Bonded (BN10) | 1.26 | 0.01 | 0.7 |
| Alnico 5 | 1.5 | 2 | 1.0 |
| Sm-Co | 1.1 | 1.16 | 0.8–1.15 |
| NdFeB Sintered | 1.05 | 0.66 | 1–1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sirimanna, S.; Balachandran, T.; Haran, K. A Review on Magnet Loss Analysis, Validation, Design Considerations, and Reduction Strategies in Permanent Magnet Synchronous Motors. Energies 2022, 15, 6116. https://doi.org/10.3390/en15176116
Sirimanna S, Balachandran T, Haran K. A Review on Magnet Loss Analysis, Validation, Design Considerations, and Reduction Strategies in Permanent Magnet Synchronous Motors. Energies. 2022; 15(17):6116. https://doi.org/10.3390/en15176116
Chicago/Turabian StyleSirimanna, Samith, Thanatheepan Balachandran, and Kiruba Haran. 2022. "A Review on Magnet Loss Analysis, Validation, Design Considerations, and Reduction Strategies in Permanent Magnet Synchronous Motors" Energies 15, no. 17: 6116. https://doi.org/10.3390/en15176116
APA StyleSirimanna, S., Balachandran, T., & Haran, K. (2022). A Review on Magnet Loss Analysis, Validation, Design Considerations, and Reduction Strategies in Permanent Magnet Synchronous Motors. Energies, 15(17), 6116. https://doi.org/10.3390/en15176116






