Simulation and Study of DC Corona Discharge Characteristics of Bar-Plate Gap

Abstract

In this paper, the corona discharge process of the bar-plate gap at −1 kV DC voltage is simulated using a two-dimensional axisymmetric plasma module. We analyze the variation of air negative corona discharge current, and the distribution morphology of microparticles in different discharge stages in detail. The significance of plasma chemical reactions at some typical time and the distribution characteristics of heavy particles are investigated according to reaction rates. Results show that, in the current rising stage, the collision ionization reactions (e.g., R₁ and R₂) and electron adsorption reaction (e.g., R₃) play a major role, which lead to the increase in charged particles and the formation of an electron avalanche. In the current drop stage, all reaction rates decreased, except for collision ionization and electron attachment, partial charge transfer reactions (e.g., R₈, R₁₀, R₁₁, and R₁₄), and composite reactions (e.g., R₁₆, R₁₇, and R₁₈), which come into play and gradually reduce the number of charged ions in the gap. In the current stabilizing stage, the main chemical reactions are composite reactions (e.g., R₁₆ and R₁₇), then the corona discharge ends. For the heavy particle distribution, O₂⁺ and O₄⁺ are the main positive ions, O₂⁻ is the most abundant negative ions, and the neutral particles are mainly O.

1. Introduction

Corona discharge is a partial discharge phenomenon occurring near the electrode with a small radius of curvature in an uneven electric field. When the electric field intensity exceeds the ionization field intensity, the air gap will be broken down, accompanied by electrical, acoustic, and optical phenomena [1]. The corona discharge will have an irreversible impact on the power system. First, the physical reactions in the discharge process will cause energy loss. Second, the appearance of corona will increase the gas temperature around the transmission equipment and reduce the thermal stability of the transmission equipment. Finally, in the radius of curvature at smaller places, the microparticles are accelerated by a strong field, and the electrode is subjected to force vibration and torsion, which will reduce the dynamic stability of the power transmission equipment. Therefore, the study of corona discharge characteristics has crucial practical significance [2,3,4].

In the microscopic process of corona discharge, various particles (such as ions, free radicals, and excited particles) will be produced, leading to further complex physical and chemical reactions. In early research, people simulated the gas discharge process by establishing a circuit model [5]. However, the plasma discharge process lacks an effective measurement method. Then, scientists began to choose the numerical simulation method to conduct in-depth research on the micro process of corona discharge [6,7].

The numerical simulation method can be used to obtain the variation of space/surface charge and local field distribution with time in the corona discharge process and realize the quantitative analysis of the interaction between charge distribution and discharge process [8]. In addition, numerical simulation can compensate for the deficiency of actual measurement when studying the micro-physical mechanism of the discharge process.

In the research of using a simulation model to analyze corona discharge characteristics, Chen et al. [9] built a three-species corona model coupled with gas dynamics in COMSOL Multiphysics, and calculated the mean current, Trichel pulse frequency and flow velocity. The ionic wind mechanism in the Trichel pulse stage was revealed. Gao et al. [10] used the fluid dynamic drift–diffusion theory of finite element simulation software COMSOL to simulate SF₆ gas negative corona discharge and obtained the space–time characteristics of the SF₆ gas Trichel pulse. They measured the distribution of charged particles and the total number of charged particles with time. In Reference [11], the characteristics of heavy particles in bar-plate DC positive corona discharge were studied. An improved, multicomponent, and 2D hybrid model was used in the simulation. The electric field distribution and net space charge distribution at typical times, and the composition and distribution of particles were analyzed. Peng et al. [12] built a global model of atmospheric pressure humid air discharge plasma and researched the variation of charged particles densities and chemical reaction rates with time. The key particles and chemical reactions reflecting the chemical process of atmospheric pressure discharge plasma in humid air were summarized. Based on the hydrodynamic model and the collision reaction model, Liao et al. [13] improved the bar-plate electrode negative corona discharge model. They analyzed the time–space development laws of electric field intensity, plasma chemical reaction rate, space charge density, and electron density distribution in the process of Trichel pulse. He et al. [14] researched the negative corona discharge pulse characteristics of the needle electrode structure of SF₆/N₂ gas mixture under DC voltage. They analyzed the effects of air pressure, gap distance, and content of N₂ on the initial voltage and pulse characteristic parameters. The results showed that the current pulse is mainly distributed irregularly with a small amplitude. To sum up, there are few reports on the plasma equations and heavy particle microscopic characteristics of DC negative corona bar-plate gap discharge.

This paper proposes a plasma simulation model based on the hydrodynamic model. The plasma chemistry model is established on the simulation software COMSOL Multiphysics, and the variation curve of the discharge current in the discharge channel is obtained. The distribution morphologies of the electric field intensity E, space charge density ρ, electron number density N_e, positive ion number density N_p, and negative ion number density N_n are analyzed at the typical times. Subsequently, this work summarizes the main chemical reactions in the plasma model according to the reaction rates and the distribution law of heavy particles at different times and analyzes the air negative corona discharge characteristics from the perspective of microparticles. The rest of this paper is arranged as follows. The corona discharge model of bar-plate gap is established in Section 2. The process of DC negative corona discharge is analyzed according to the pulse current curve and corona discharge topography in Section 3. Section 4 presents the importance of plasma chemical reactions and the distribution of heavy particles in air corona discharge. Finally, the conclusion is given in Section 5.

2. Corona Discharge Model of Bar-Plate Gap

2.1. Hydrodynamic Governing Equation

The hydrodynamic numerical simulation model is a commonly used model in the corona pulse simulation research, which mainly includes the continuity equation and Poisson equation [15]. To describe the microscopic physical process of corona discharge, the plasma chemical reaction model is added in this paper, and some additional terms are added based on the traditional governing equation.

We obtained the number density of charged particles by solving continuity Equations (1)–(3) and coupling with Poisson Equations (4) and (5). The number density of charged particles can reflect the movement of charged particles in the bar-plate gap, that is the generation and disappearance of particles [8,16,17]:

$$\frac{\partial n_e}{\partial t}+\nabla \left(-n_e{\mu }_e\overrightarrow{E}-D_e\nabla n_e\right)=\alpha n_e\left|{\mu }_e\overrightarrow{E}\right|-\eta n_e\left|{\mu }_e\overrightarrow{E}\right|-k_{ep}{n}_e{n}_p,$$

(1)

$$\frac{\partial n_p}{\partial t}+\nabla \left(n_p{\mu }_p\overrightarrow{E}-D_p\nabla n_p\right)=\alpha n_e\left|{\mu }_e\overrightarrow{E}\right|-k_{ep}{n}_e{n}_p,$$

(2)

$$\frac{\partial n_n}{\partial t}+\nabla \left(-n_n{\mu }_n\overrightarrow{E}-D_n\nabla n_n\right)=\eta n_e\left|{\mu }_e\overrightarrow{E}\right|-k_{np}{n}_n{n}_p,$$

(3)

$${\epsilon }_0{\epsilon }_r{\nabla }^2\varphi =-q\left(n_p-n_n-n_e\right),$$

(4)

$$\overrightarrow{E}=-\nabla \varphi ,$$

(5)

where n_e, n_p and n_n are the number densities of electrons, positive ions and negative ions, 1/m³; μ_e, μ_p, μ_n, D_e, D_p, and D_n are mobilities (m²/Vs) and diffusion coefficients (m²/s) of electrons, positive ions, and negative ions, respectively; $\overrightarrow{E}$ is the electric field vector, V/m; α is ionization coefficient, 1/m; η is the attachment coefficient, 1/m; k_ep is the recombination coefficients of electrons and positive ions, m³/s; k_np is the recombination coefficients of negative and positive ions, m³/s; ε₀ is the vacuum permittivity, F/m; ε_r is the relative permittivity, F/m; and φ is the potential, V.

In the above governing equations, the setting of each parameter has a direct influence on the final calculation result of a negative corona discharge. The air discharge parameters used in this paper are from the experimental parameters provided by Nikonov [18].

During corona discharge, electrons migrate and diffuse because of the action of the electric field force, and the electron number density in the gap changes correspondingly. The mobility and diffusion coefficient of electrons are differed from those of positive and negative ions, so the charge distribution in the gap will change.

2.2. Air Electrochemical Reaction Process

In this paper, the air plasma chemical reaction process mainly contains 12 particles, namely, e, N₂⁺, N₂, O₂, O₂⁻, O, O⁻, O₄⁺, N₄⁺, O₂⁺, N₂O₂⁺, and O₃. The specific reaction process and relevant data [7,19,20] are shown in

Table 1. Air plasma gas–phase reactions.

No.	Reaction Process	Rate Coefficient 1	ΔE 2
R1	N2 + e=>2e + N2+	f(ε)	15.6
R2	O2 + e=>2e + O2+	F(ε)	12.1
R3	2O2 + e=>O2 + O2−	6.0 × 10−39Te−1
R4	O4+ + e=>2O2	2.42 × 10−11Te−0.5
R5	O2+ + e=>2O	6.0 × 10−11Te−1
R6	N2 + +N2 + O2=>N4+ + O2	5.0 × 10−41
R7	N2+ + N2 + N2=>N4+ + N2	5.0 × 10−41
R8	N4+ + O2=>O2+ + 2N2	2.5 × 10−16
R9	N2+ + O2=>O2+ + N2	1.04 × 10−15T−0.5
R10	2N2 + O2+=>N2O2+ + N2	8.1 × 10−38T−2
R11	N2O2+ + N2=>O2+ + 2N2	14.8T−5.3exp(−2357/T)
R12	N2O2+ + O2=>O4+ + N2	1.0 × 10−15
R13	O2+ + O2 + O2=>O4+ + O2	2.04 × 10−34T−3.2
R14	O2+ + O2 + N2=>O4+ + N2	2.04 × 10−34T−3.2
R15	O4+ + O2−=>3O2	1.0 × 10−13
R16	O4+ + O2− + O2=>3O2 + O2	2.0 × 10−37
R17	O4+ + O2− + N2=>3O2 + N2	2.0 × 10−37
R18	O2+ + O2−+O2=>2O2 + O2	2.0 × 10−37
R19	O2+ + O2− + N2=>2O2 + N2	2.0 × 10−37
R20	O + O2 + O2=>O3 + O2	2.5 × 10−46
R21	O + O2 + N2=>O3 + N2	2.5 × 10−46
R22	e + N2+ + N2=>2N2	6.07 × 10−34Te−2.5
R23	N2+ + 2e=>N2 + e	5.651 × 10−27Te−0.8

¹ The units of two-body reaction-rates are m³/s, three-body reaction-rates are m⁶/s; T is environment temperature, T_e is electronic temperature, K. ² ΔE is the energy loss during electron collision, eV.

.

All surface reactions in the plasma model are shown in

Table 2. Air plasma surface reactions.

No.	Surface Reaction Process	Adhesion Coefficient
S1	O2+=>O2	1
S2	N2+=>N2	1
S3	N4+=>2N2	1
S4	N2O2+=>2N2+O2	1
S5	O4+=>2O2	1
S6	O2−=>O2	1
S7	O−=>0.5O2	1
S8	O=>0.5O2	1

. Charged and unstable neutral particles are assumed to return to the plasma where parent neutral molecules exist. The adhesion coefficient represents the influence of all excited neutral particles, free radicals, and ion types on the surface reactions.

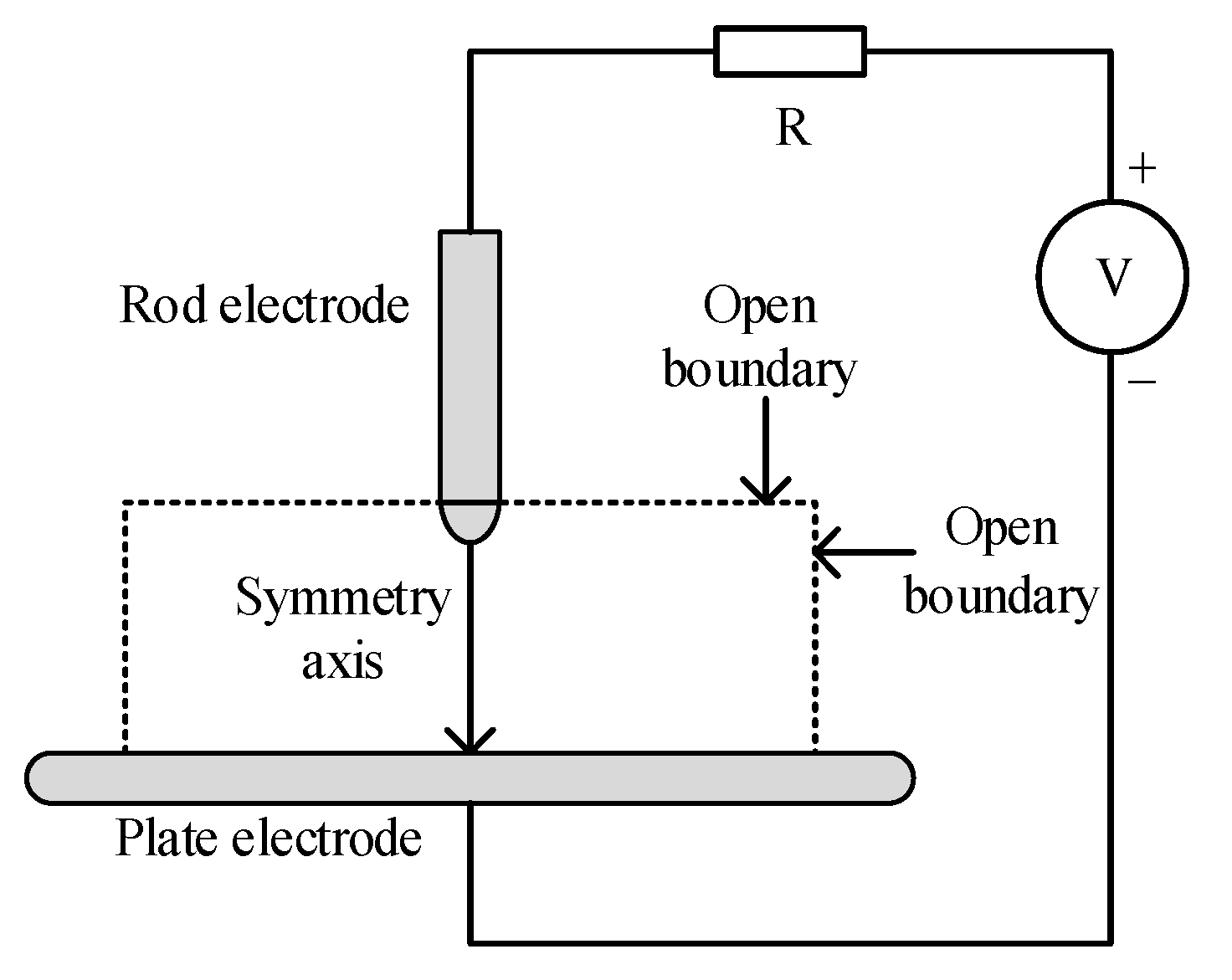
2.3. Boundary Conditions and Algorithm Model

In COMSOL Multiphysics, the two-dimensional axisymmetric plasma bar-plate corona discharge model is used for modeling and simulation. The model is solved by the plasma module of COMSOL Multiphysics software. The geometric structure is shown in Figure 1. The curvature radius of the rod electrode is 0.2 mm. The gap distance between the rod and plate is 5.5 mm. The solution domain width is 5 mm. The applied voltage is −1 kV. The computing time is 300 ns, and the step is 1 ns. The corona discharge belongs to a low-temperature discharge. The gas temperature is 293 K.

The meshing of the computational domain in the simulation is shown in Figure 2. Refinements are made at the reaction tip and in the region below, making the mesh very dense. In other areas with the weak responses, it does not need to be too dense, which can ensure accurate results and save calculation time.

In electron transport theory, the definition of boundary conditions is helpful for the convergence and accuracy of the results. Determining the appropriate boundary conditions according to the physical environment is essential when solving partial differential equations. Secondary electron emission is an important mechanism to maintain the further development of negative corona discharge. For corona discharge, especially negative corona discharge, the cathode boundary condition must consider the emission process of secondary electrons.

The specific boundary conditions are set as follows [21,22]:

Given the secondary emission process, the electrons move several times on the wall with average free travel, then dissipate, and the boundary conditions causing electron flux are expressed as:

$$n·{\Gamma }_e=\left(\frac{1}{2}{v}_{e,th}{n}_e\right)-{\displaystyle \sum }_i{\gamma }_i\left({\Gamma }_i·n\right)$$

(6)

The boundary conditions of electron energy flux at positive and negative electrodes are expressed as follows:

$$n·{\Gamma }_{\epsilon }=\left(\frac{5}{6}{v}_{e,th}{n}_{\epsilon }\right)-{\displaystyle \sum }_i{\gamma }_i{\epsilon }_i\left({\Gamma }_i·n\right)$$

(7)

where Γ_i is the ion density flux, 1/(m²·s). $v_{e,th}$ is the electron thermal rate,$v_{e,th}=\sqrt{8k_B{T}_e/\pi m_e}$, m/s. k_B is the Boltzmann constant, J/K. m_e is the electronic mass, kg. γ_i is the secondary electron emission coefficient caused by positive ion collision with cathode. ε_i is the average energy of the secondary electron.

For heavy particle substances, ions will be lost on the wall under the action of surface reactions, and the electric field will point directly to the wall.

The boundary conditions of positive and negative ions are expressed as follows:

$$n·{\Gamma }_i=\frac{1}{4}{v}_{i.th}{n}_i+\alpha n_i{\mu }_{i}E·n$$

(8)

where

$$v_{i.th}=\sqrt{8k_{B}T/\pi m_i}$$

(9)

$$\alpha =\{\begin{array}{cc}1& {\mu }_{i}E·n>0\\ 0& {\mu }_{i}E·n\le 0\end{array}$$

(10)

The second term of Equation (8) can be simplified by the boundary conditions of neutral particle flux at the positive and negative electrodes, that is,

$$n·{\Gamma }_i=\frac{1}{4}{v}_{i.th}{n}_i$$

(11)

where $v_{i,th}$ is the ion movement rate, m/s. T is the particle temperature, K. m_i is the mass of ions, kg. n_i is the ion number density, 1/m³. μ_i is the ion migration rate, m²/(V·s).

The density flux satisfied by all particles under open boundary conditions is

$$n·\nabla n_k=0$$

(12)

The boundary condition satisfied by the potential is expressed as follows:

$$n·\nabla \mathsf{\phi }=0$$

(13)

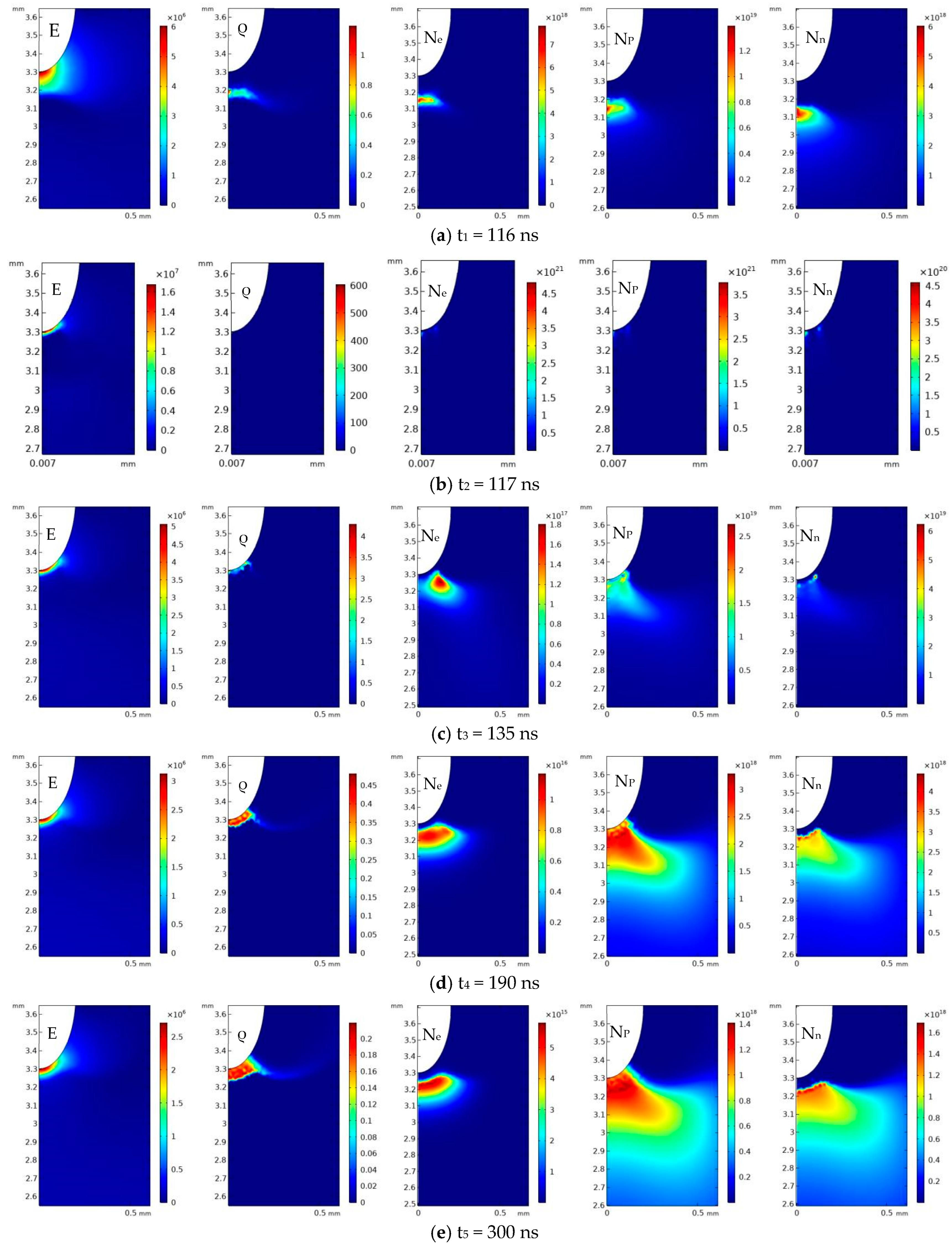
3. Air Negative Corona Discharge Morphology Analysis

The charge in the bar-plate gap moves directionally from a current due to the action of a strong field. According to the current calculation equation obtained from Sato’s research [23], the current is presented as follows:

$$I=\frac{e}{V_0}{\displaystyle \iint }2\pi r\left({\mu }_p{n}_p+{\mu }_e{n}_e+{\mu }_n{n}_n\right)\overrightarrow{E}·\overrightarrow{E_L}drdz$$

(14)

where V₀ is the applied voltage, V; $\overrightarrow{E_L}$ is the Laplace electric field, V/m; and μ_p, μ_n, and μ_e are the positive ion, negative ion, and electron mobility, m²/(V·s), respectively.

Through model construction and parameter setting, we can study the model. Based on the calculation of air corona discharge, the transient characteristics of plasma are studied in this model. After typing the time step, the system begins solving. Figure 3 shows the typical negative corona discharge current calculated by this model. The current waveform curve has five main stages: discharge starting time (t₁), current rising stage (t₁–t₂), current falling stage (t₂–t₃), current stabilizing stage (t₃–t₄), and current stabilizing stage (t₄–t₅). The current in the discharge starting stage is tiny (approximately 8 μA), and the current increases rapidly to 1.934 mA in t₁–t₂. In t₂–t₃, the current decrease slowly, the current in t₃–t₄ gradually tends to be stable, and the current remains approximately 10.5 μA stably in t₄–t₅.

Figure 4 shows the electric field intensity E, space charge density ρ, electron number density N_e, positive ion density N_P (N₂⁺, N₄⁺, O₄⁺, O₂⁺, and N₂O₂⁺), and negative ion density N_n (O₂⁻ and O⁻) at different times of each stage.

In the early stages of corona discharge development (t = 116 ns), the maximum rod field strength is 60 kV/cm, which is greater than the initial breakdown field strength of the air negative bar-plate gap. Next, the air ionizes positive ions and electrons rapidly under the action of an applied electric field, and the number density of positive ions and electrons in the gap increases gradually. The positive ions on the surface of the plate move to the rod, collide with the rod electrode, produce secondary electrons, and quickly form an electron avalanche. Due to the adsorption, some electrons are adsorbed by neutral molecules in the air to form negative ions. The negative ions and electrons migrate to the plate electrode under the action of electric field force. The electrons continue to adsorb to form negative ions in the process of migration, making the number of negative ions gradually increase. At 116 ns, the maximum number density of electrons is 7.8 × 10¹⁸ m⁻³, the positive and negative ions reach 1.4 × 10¹⁹ m⁻³ and 6.0 × 10¹⁸ m⁻³, and the space charge density reaches 1.2 C/m³.

With the development of discharge, the space electric field is distorted, and the air continues to ionize under the action of the distorted electric field. The number density of positive ions increases continuously, and the number of negative ions produce by electron adsorption also accumulates rapidly. Then the space charge density increases rapidly.

In the bar-plate gap, positive ions constantly move toward the rod electrode, electrons and negative ions move toward the plate electrode, forming a discharge current. The current value increases with the increase in electron and ion number density and reaches a peak of 1.934 mA at 117 ns. At this time, the number density of electrons, positive and negative ions reach the maximum values, which are 4.8 × 10²¹ m⁻³, 3.8 × 10²¹ m⁻³, and 5.5 × 10²⁰ m⁻³. The maximum space charge density increases to 605 C/m³. Then, the discharge enters the next stage.

In the current drop stage (t = 117–135 ns), some positive ions react with negative ions to gradually reduce the number of positive and negative ions. At the same time, negative ions and electron clusters diffuse to the plate electrode to form a large diffusion radius (Figure 4c). In the bar-plate gap, the original electric field intensity is weakened, the ionization rate is also reduced, and the electron number density and positive ion number density decrease accordingly. The weakened electron adsorption reduces the negative ion number density. When t = 135 ns, the number density of electron, positive ion, and negative ion are reduced to 1.8 × 10¹⁷ m⁻³, 2.7 × 10¹⁹ m⁻³, and 6.3 × 10¹⁹ m⁻³, and the space charge density decreases to 4.3 C/m³.

After that, the charge density becomes too low to distort the electric field. As a result, the electric field intensity decreases, and the electron production rate decreases. In the period of t = 190 ns to 300 ns, the electron number density decreases from 1.1 × 10¹⁶ m⁻³ to 5.8 × 10¹⁵ m⁻³, and the electron avalanche tends to end gradually. The number of positive and negative ions decreases and tends to be stable. The maximum number density of positive ions reduced from 3.3 × 10¹⁸ m⁻³ to 1.4 × 10¹⁸ m⁻³, and the negative ion declined from 4.4 × 10¹⁸ m⁻³ to 1.7 × 10¹⁸ m⁻³. The ion movement in the gap decreases, and the discharge current tends to be stable.

4. Research on Plasma Chemical Reaction

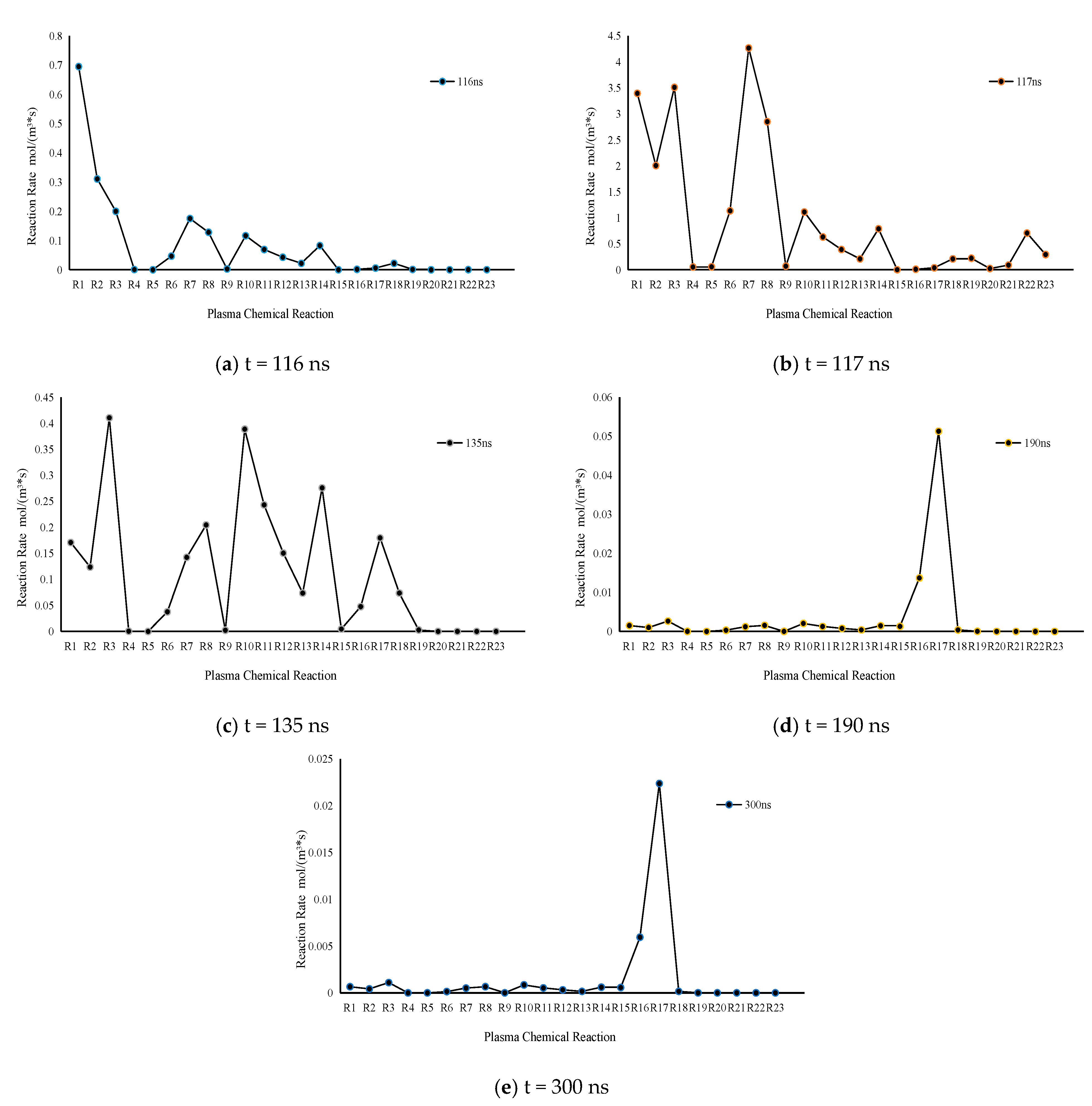
4.1. Importance Analysis of Chemical Reactions

This model has identified 23 plasma chemical reactions based on previous studies. Since the rate of collision reaction can reflect the intensity of the reaction process in air discharge [7], the reaction rates of plasma chemical reactions involved in different discharge periods are studied in this paper, and the plasma reactions that played a major role in several typical moments are obtained, as shown in Figure 5.

Collision ionization reactions, electron adsorption reactions, charge transfer reactions, and composite reactions are considered in the micro process of the corona discharge. The maximum reaction rate is used to characterize the importance of the reaction in the discharge process. We can see from Figure 5a that the first three major reactions at the initial stage of the discharge are R₁, R₂, and R₃, namely collision ionization and electron adsorption reactions. At this stage, positive ions and electrons are generated by gas collision ionization, and electrons are absorbed by neutral molecules to form negative ions. The number of charged particles begins to increase.

As shown in Figure 5b, when t = 117 ns, except for collision ionization reactions (e.g., R₁, R₂) and electron adsorption reaction (e.g., R₃), the charge transfer reactions (e.g., R₇ and R₈) begin to play a role, generating a large amount of O₂⁺. At this time, the rates of all reactions reach the maximum, the reactions are the most intense, and the number of charged particles reaches a peak.

In Figure 5c, when t = 135 ns, the rates of all reactions decrease. At this time, the major reactions are the electron adsorption reaction (e.g., R₃) and part of the charge transfer reactions (e.g., R₈, R₁₀, R₁₁, and R₁₄), and the number of positive and negative ions decreases. Meanwhile, the rate of composite reactions (e.g., R₁₆, R₁₇, and R₁₈) begins to increase gradually, resulting in declining charged particles in the gap and the end of the electron avalanche.

As shown in Figure 5d,e, during t = 190–300 ns, the main chemical reactions are composite reactions (e.g., R₁₆ and R₁₇). The reaction rates of the rest of the plasma are close to zero, indicating that the generation reaction of charged particles is basically over in this period. In the gap, the positive ion O₄⁺ and the negative ion O₂^- react and combine to generate the neutral particle O₂. The reaction becomes weaker and weaker, marking the end of the corona discharge.

Based on the above analysis, the primary plasma chemical reactions at each typical time are obtained according to the change in reaction rate, and the corresponding discharge current and changes in microparticles are further formed.

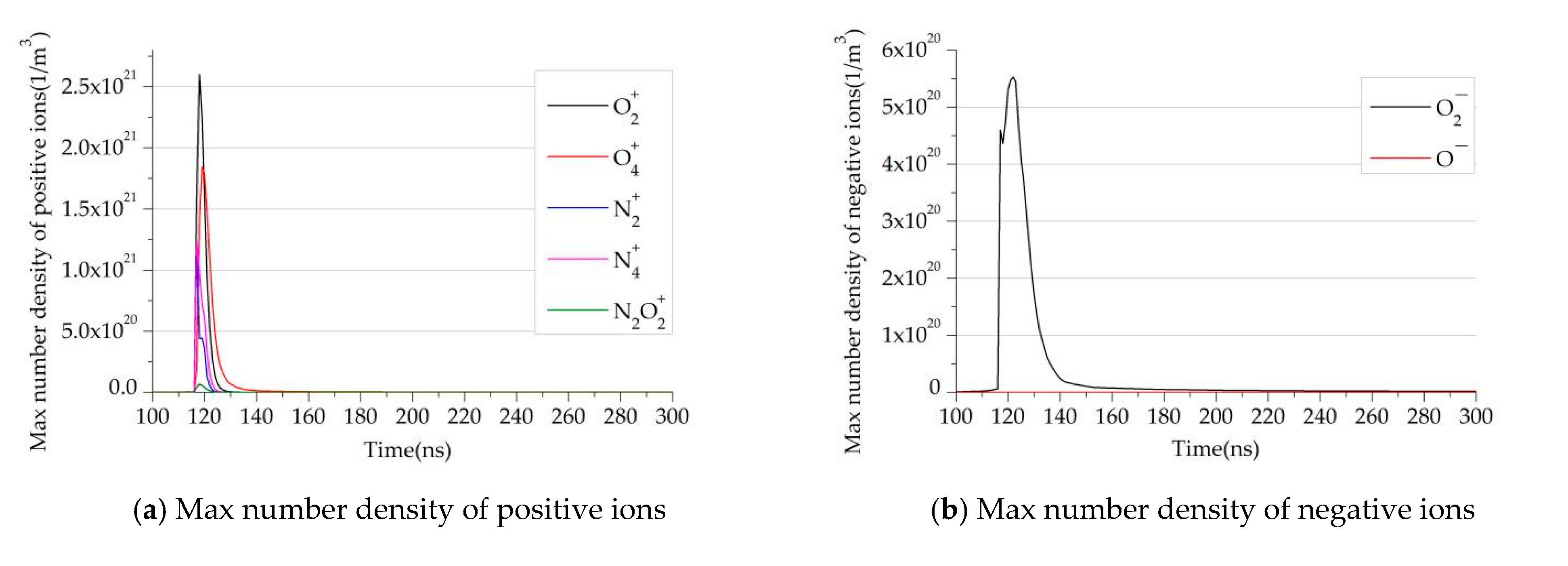
4.2. Distribution of Heavy Particles

To further study the discharge characteristics of air at DC voltage, the distribution characteristics of heavy particles at different discharge periods are discussed in this model, which is taken as a factor to describe the micro process of air discharge at the DC negative polarity bar-plate gap. The values and corresponding curves of the maximum number density of the spatial distribution of heavy particles at different times are shown in

Table 3. The number density of heavy particles at different times.

Particle	Maximum Number Density of Heavy Particles/m−3
	116 ns	117 ns	135 ns	190 ns	300 ns
O2+	5.7 × 1018	1.5 × 1021	8.8 × 1017	4.0 × 1016	1.5 × 1016
O4+	5.9 × 1018	1.8 × 1020	2.6 × 1019	3.3 × 1018	1.4 × 1018
N2+	3.3 × 1018	1.1 × 1021	8.3 × 1016	5.1 × 1015	1.9 × 1015
N4+	2.0 × 1018	1.2 × 1021	1.8 × 1017	9.5 × 1015	3.5 × 1015
N2O2+	1.5 × 1017	4.2 × 1019	2.3 × 1016	1.0 × 1015	3.9 × 1014
O−	6.1 × 108	6.2 × 108	4.7 × 1010	1.5 × 1010	5.3 × 109
O2−	6.0 × 1018	4.6 × 1020	6.2 × 1019	4.4 × 1018	1.7 × 1018
O	6.8 × 1011	1.1 × 1017	8.9 × 108	4.2 × 106	1.6 × 106
O3	5.3 × 1017	2.0 × 1021	8.4 × 1021	7.0 × 1021	4.9 × 1021

and Figure 6.

According to Table 3 and Figure 6, the number density of positive ions in the discharge process mainly depends on O₂⁺ and O₄⁺, and the number of positive ions that contain N is relatively small. This because, on the one hand, N₂⁺ and O₂⁺ mainly come from the collision ionization of N₂, O₂, and e. The collision ionization energy loss of O₂ is 12.1 eV, and the collision ionization energy loss of N₂ is 15.6 eV. Collision ionization of O₂ is relatively easy to occur. On the other hand, in the charge transfer reaction equations, N-containing ions are prone to charge transfer reaction to generate O-containing positive ions, and the reaction rate is fast, whereas O₄⁺ can be generated from O₂⁺ through the charge transfer reaction. Therefore, the number density of positive ions that contain O is higher than that of positive ions that contain N.

The number density of negative ions is mainly determined by O₂⁻, which is generated by the adsorption reaction of O₂ adsorbed free electrons. The number density of negative ions is lower than that of positive ions. The reason is that neutral particles are difficult to absorb fast-moving electrons, and the O₂⁻ generated will react with O₂⁺ or O₄⁺ to form neutral molecules. In corona discharge, collision ionization is dominant, which leads to a lower number density of negative ions. Neutral particles are mainly O, except N₂ and O₂. Neutral particles have minimal effects on the ionization reaction, and their role in corona discharge reaction does not need to be considered too much.

5. Conclusions

In this paper, the characteristics of negative corona discharge in the bar-plate gap are simulated, and the main conclusions are presented as follows:

(1)

A negative corona discharge model based on the plasma discharge model, in which collision ionization reaction, charge transfer reaction, recombination reaction, electron adsorption reaction, and surface reaction are considered, is proposed.

(2)

When the rod applied voltage is −1 kV, the discharge current curve shows a pulse change trend. Within a discharge pulse cycle, the curve can be divided into the current rising stage, the current falling stage, the current tending to stable stage, and the current stable stage. At the same time, the distribution morphology of particles at different stages of corona discharge is obtained, which is highly consistent with the literature results.

(3)

In the process of negative corona discharge, the maximum reaction rate indicates the importance of plasma reaction at each stage. The collision ionization reactions (e.g., R₁ and R₂) and electron adsorption reaction (e.g., R₃) play a primary role in the current rising period, resulting in an increase in charged particles and the formation of an electron avalanche. In the current drop phase, all reaction rates decreased. Except for collision ionization and electron attachment, partial charge transfer reactions (e.g., R₈, R₁₀, R₁₁, and R₁₄) and composite reactions (e.g., R₁₆, R₁₇, and R₁₈) begin to play their role, making the number of charged ions in the gap gradually decrease. Composite reactions (e.g., R₁₆ and R₁₇) are mainly present in the current stabilization stage, and the other reaction rates are almost zero. The corona discharge is over.

(4)

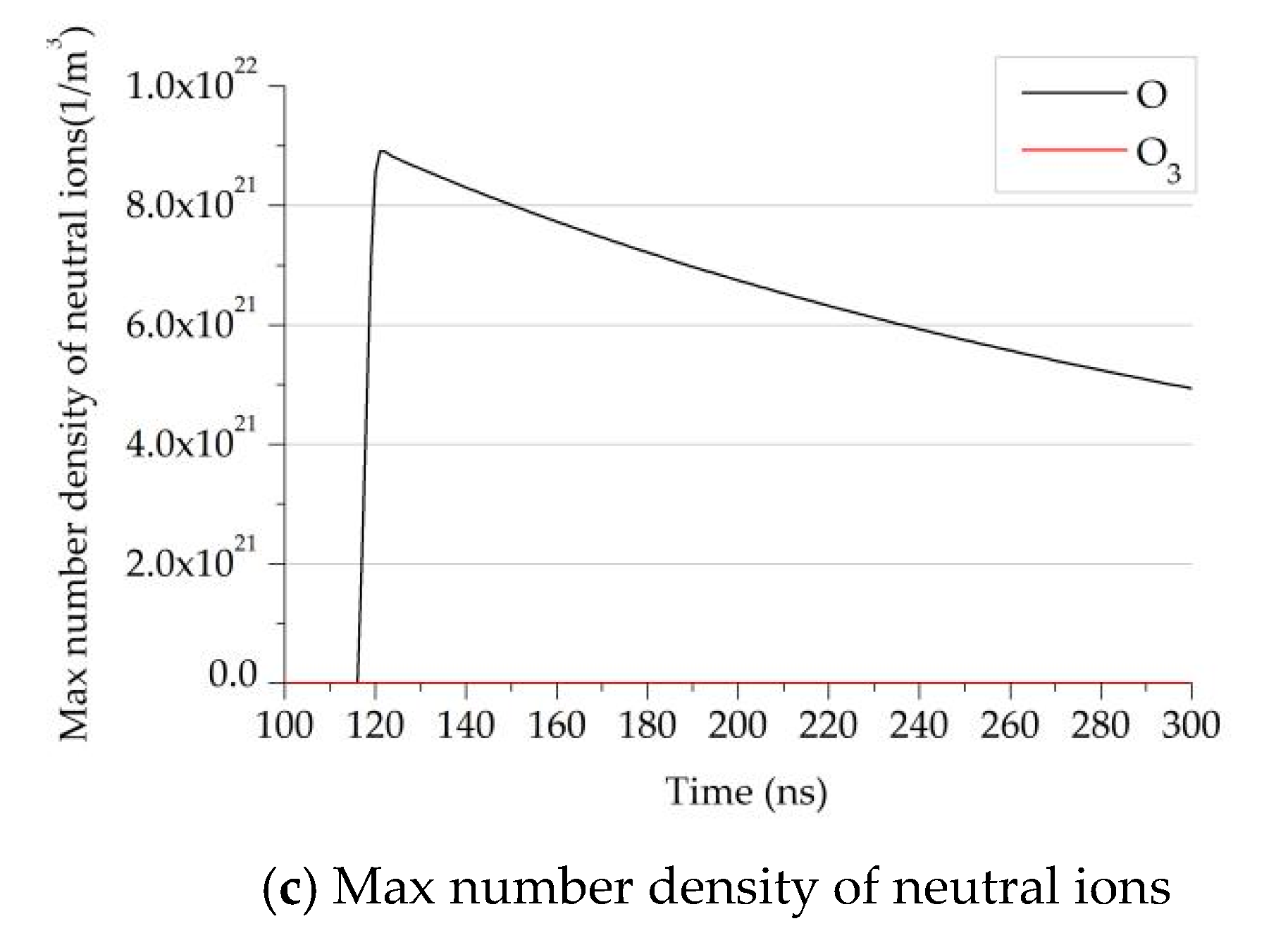
Among all the particles involved in the plasma reactions, the positive ion number density of O₂⁺ and O₄⁺ accounts for the most significant proportion of all positive ions, and the negative ion O₂⁻ is the most abundant particle. The neutral particle is mainly O except for N₂ and O₂. The neutral particles have little influence on the ionization reaction and corona discharge.