Measurement of Interfacial Characteristics of Horizontal and Inclined Oil–Water Flows by Using Wire-Mesh Sensor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Wire-Mesh Sensor System
2.2. Experiment of Oil–Water Two-Phase Flows
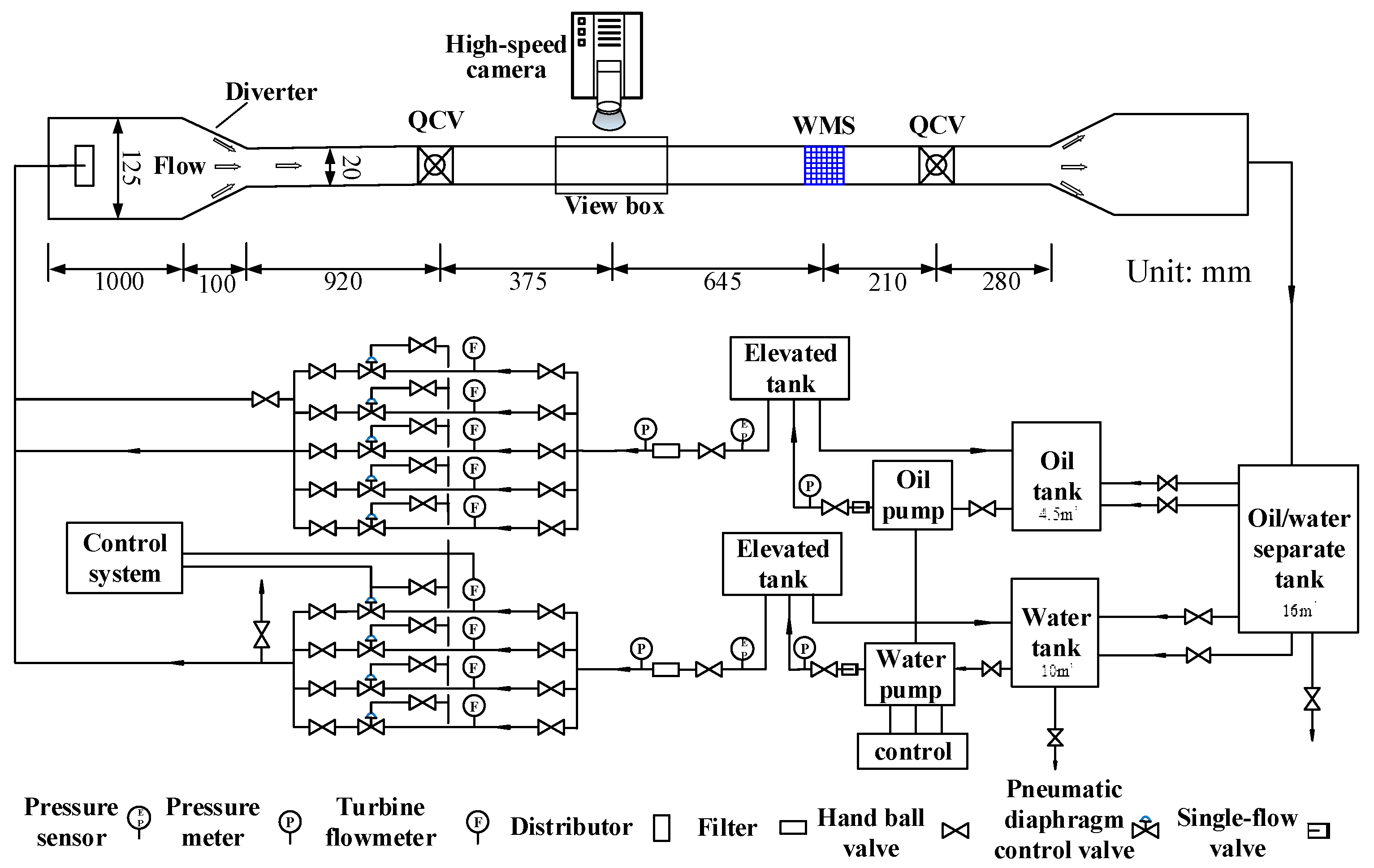
2.2.1. Experimental Setup
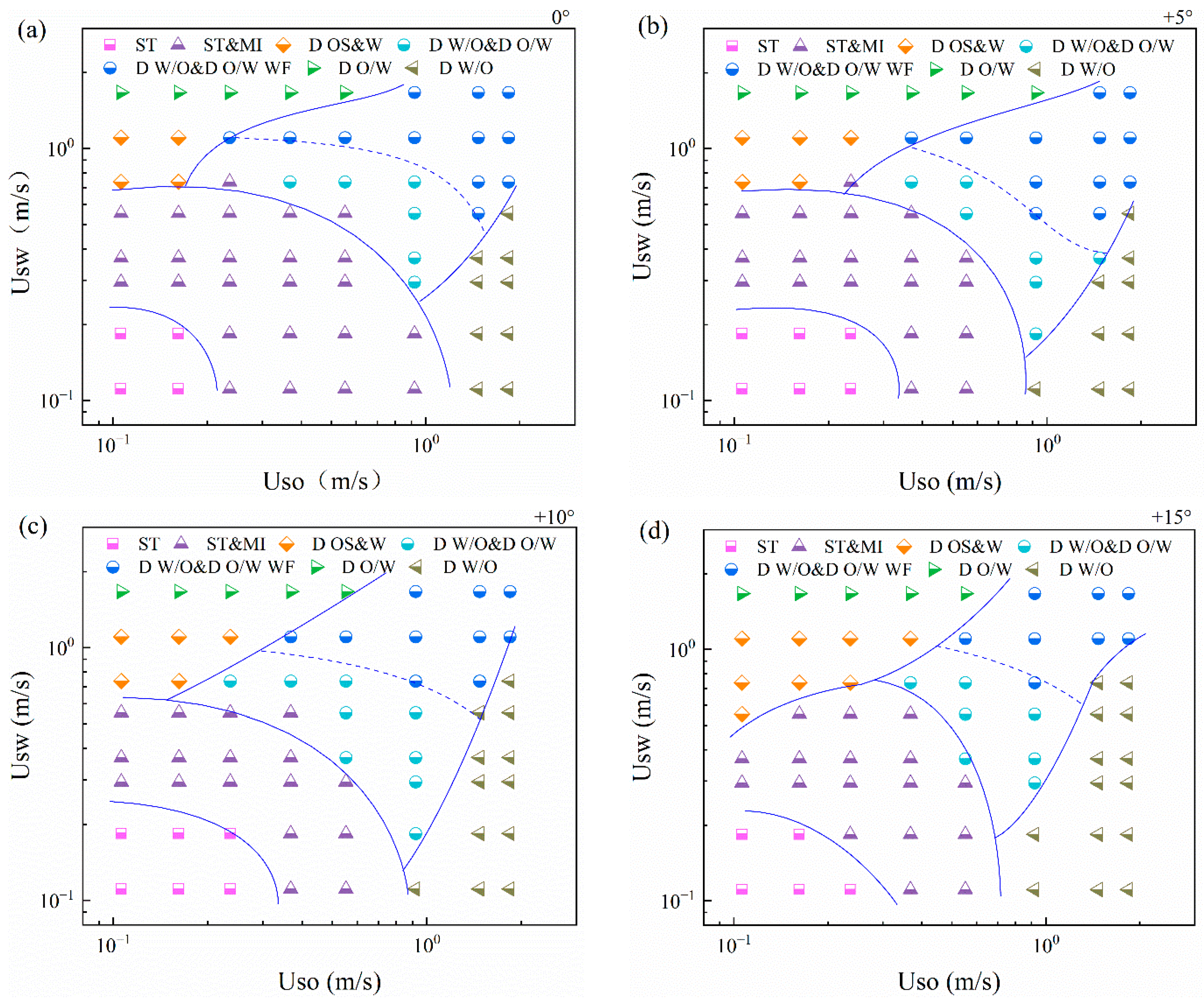
2.2.2. Flow Pattern Map
2.3. Processing of Data
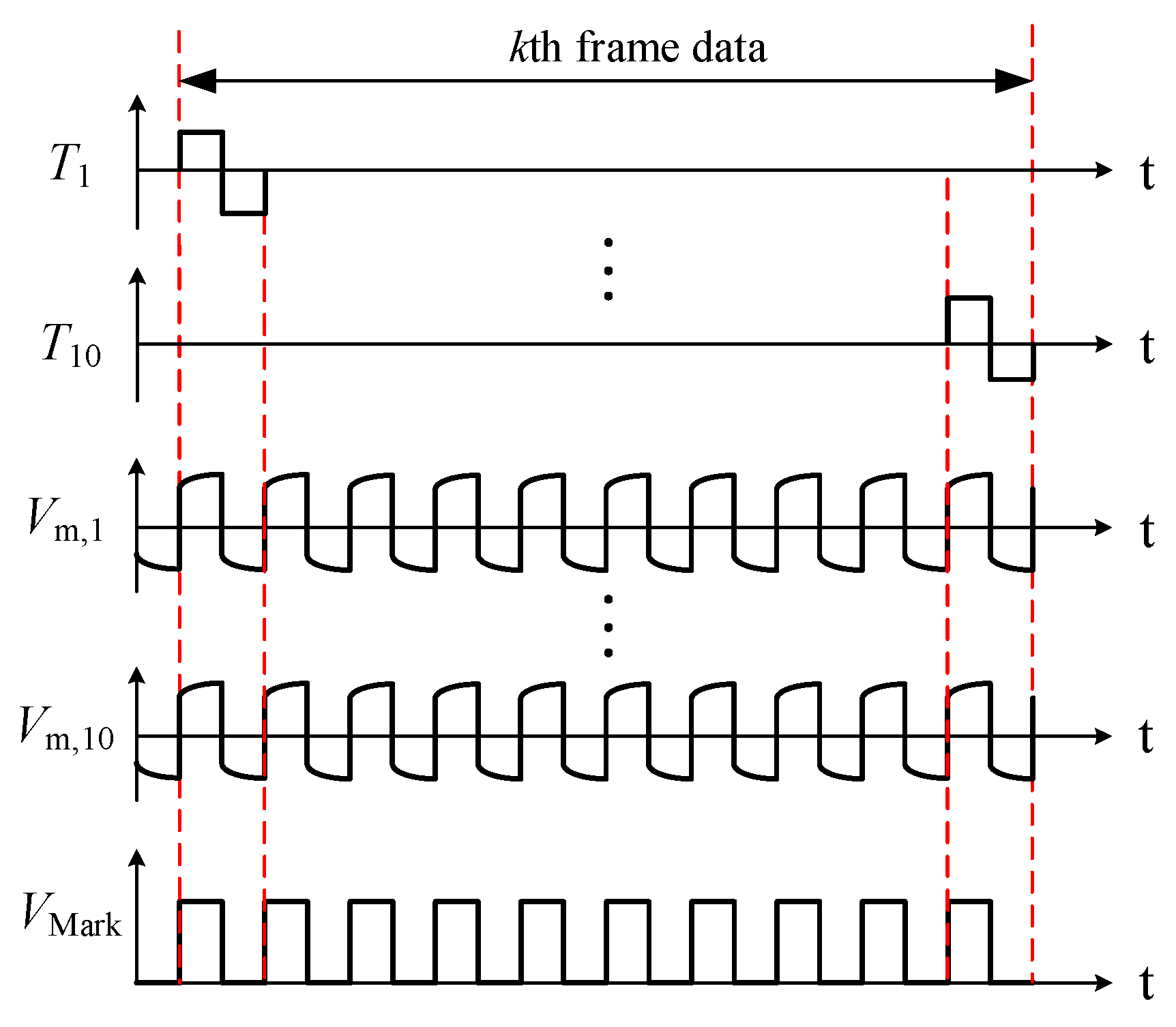
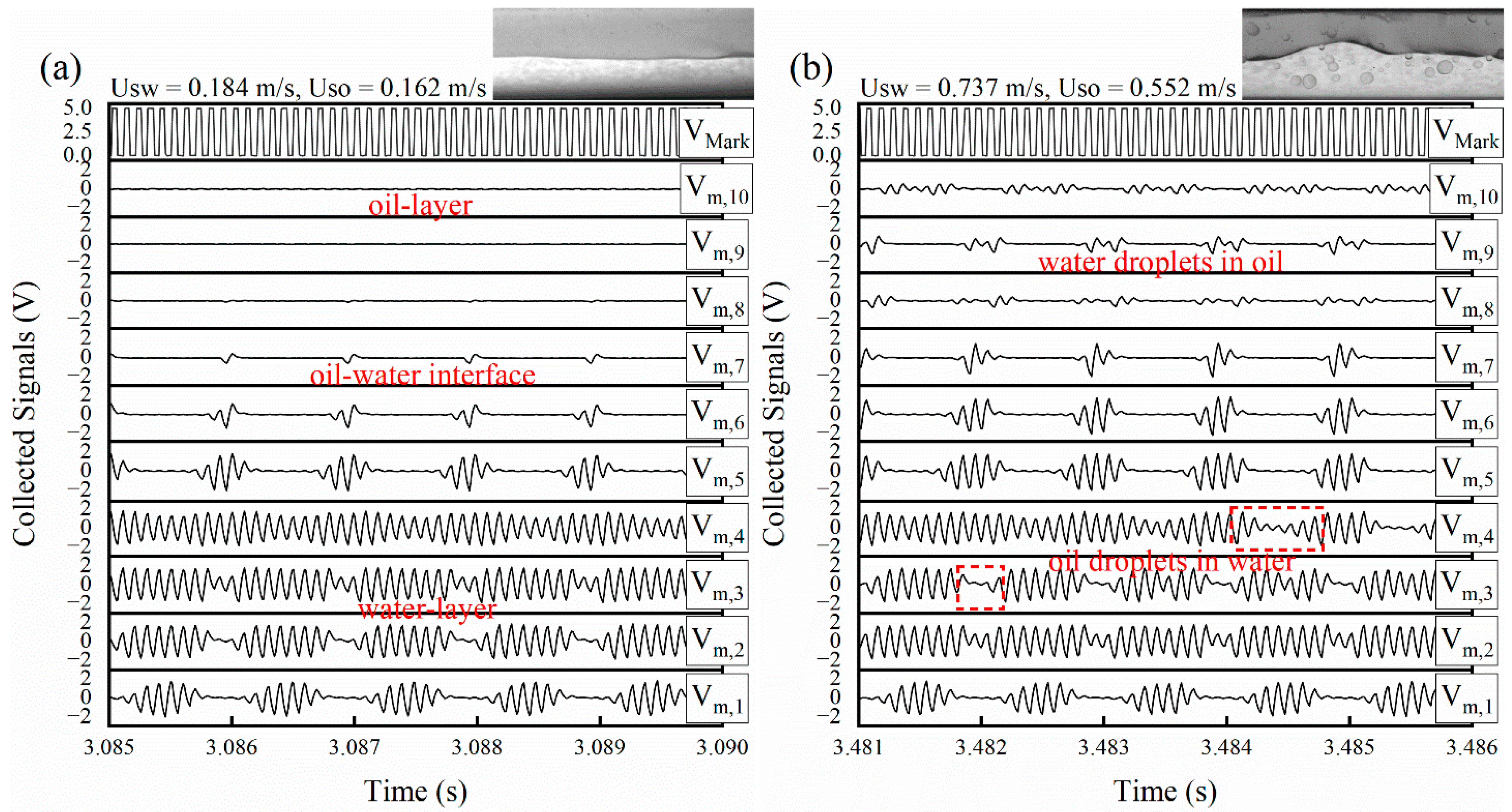
2.3.1. Wire-Mesh Sensor Responses
2.3.2. 3D Flow Visualization
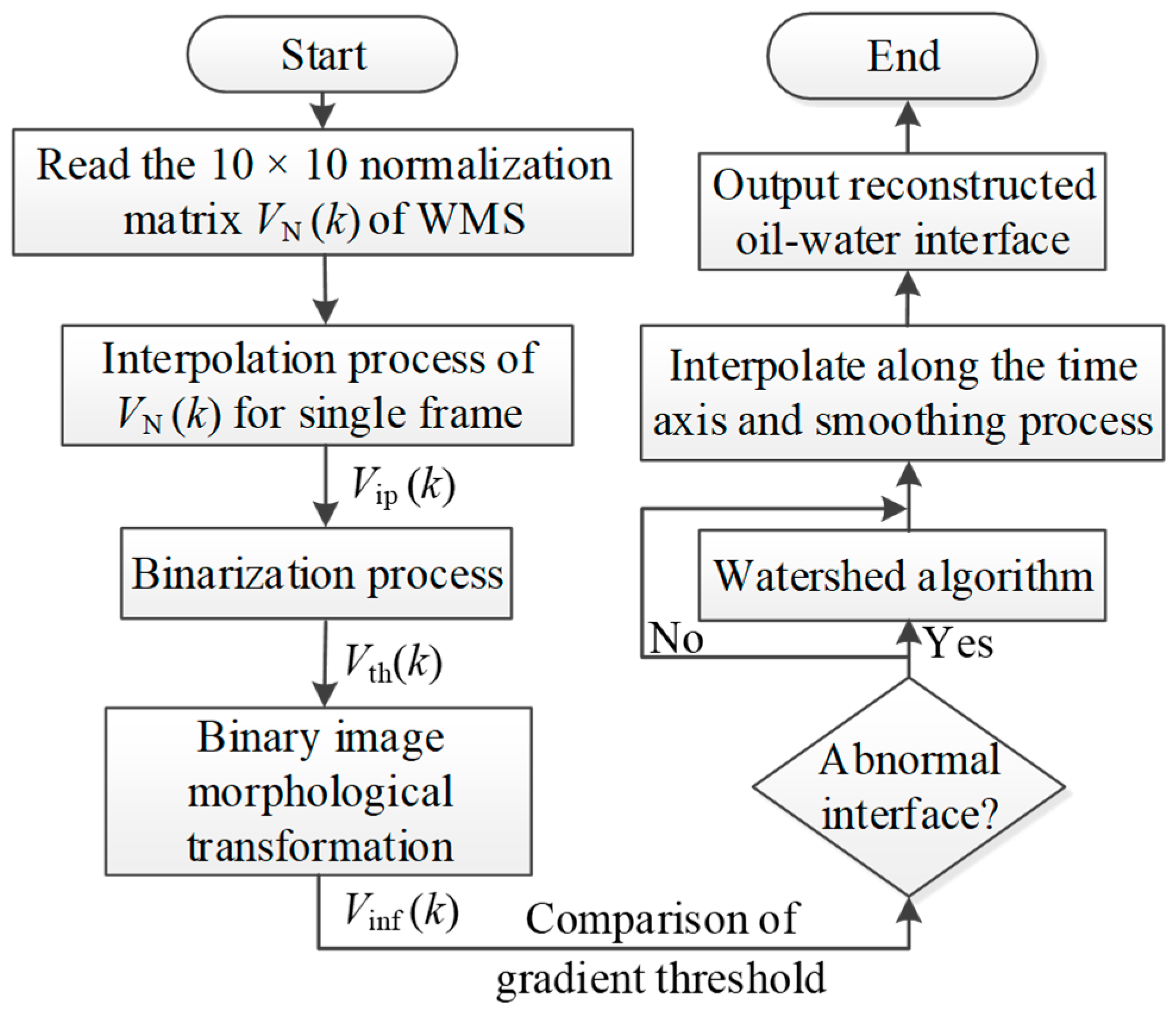
2.4. Reconstruction of Interface Structures
3. Results and Discussion
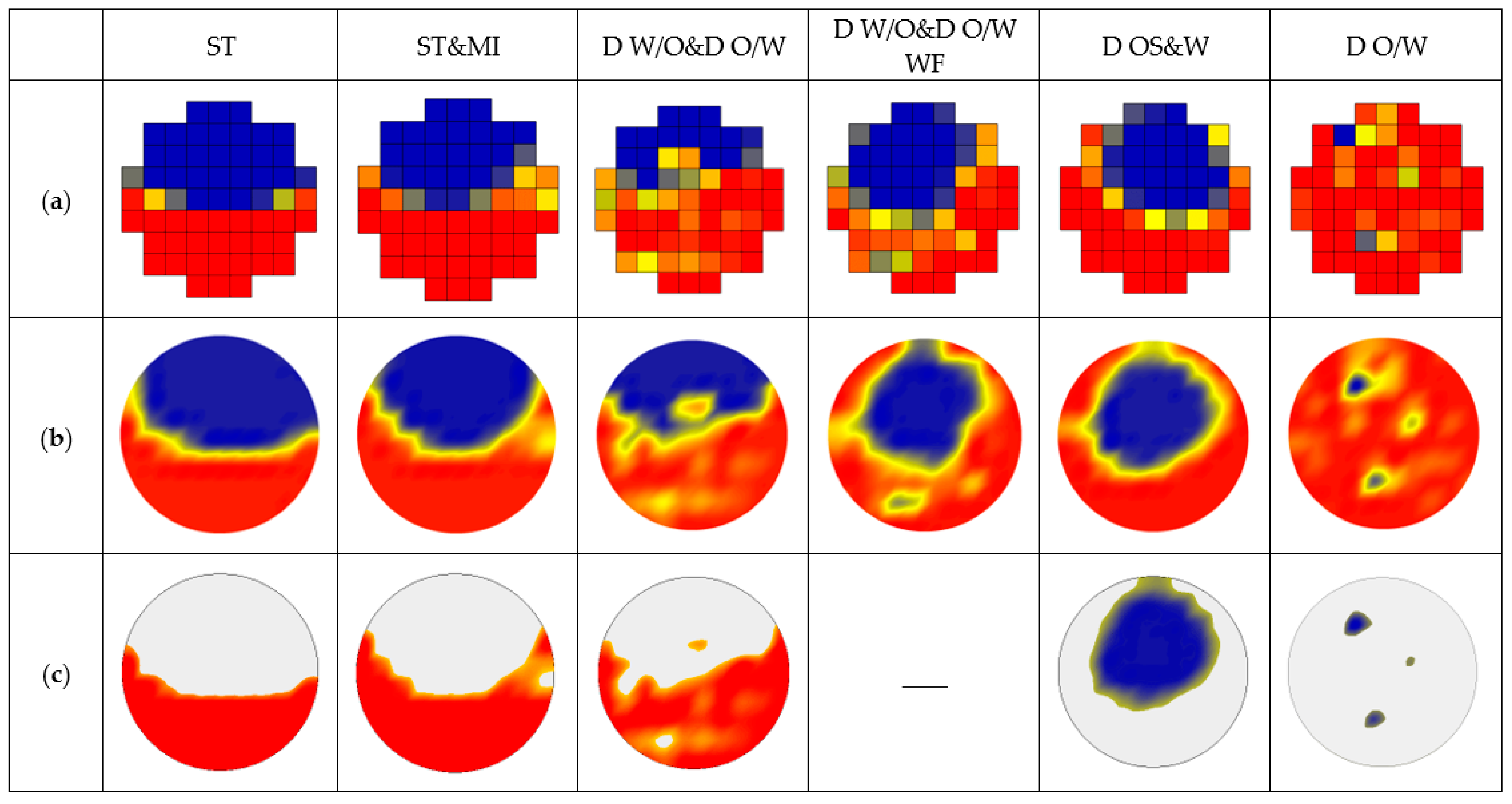
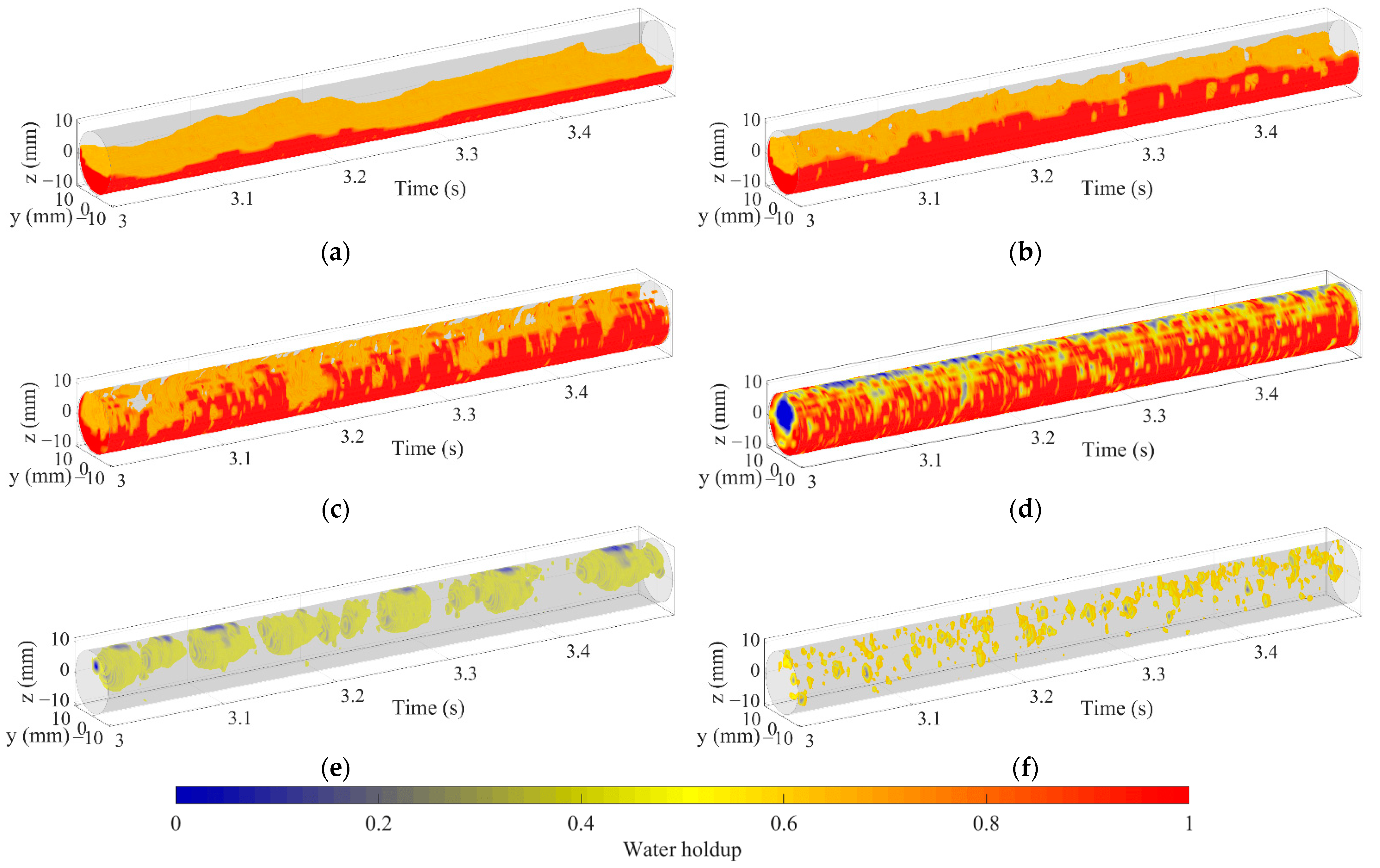
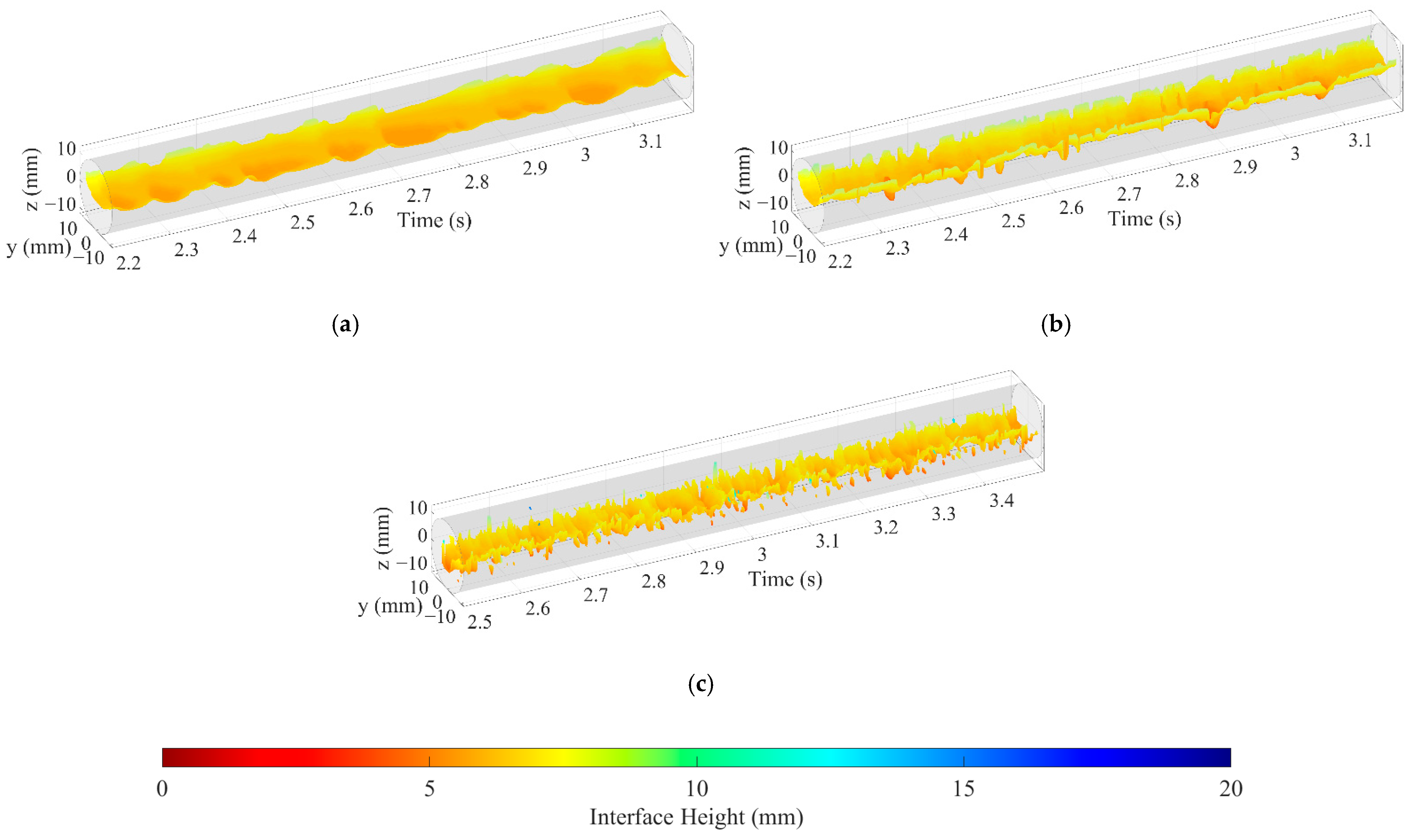
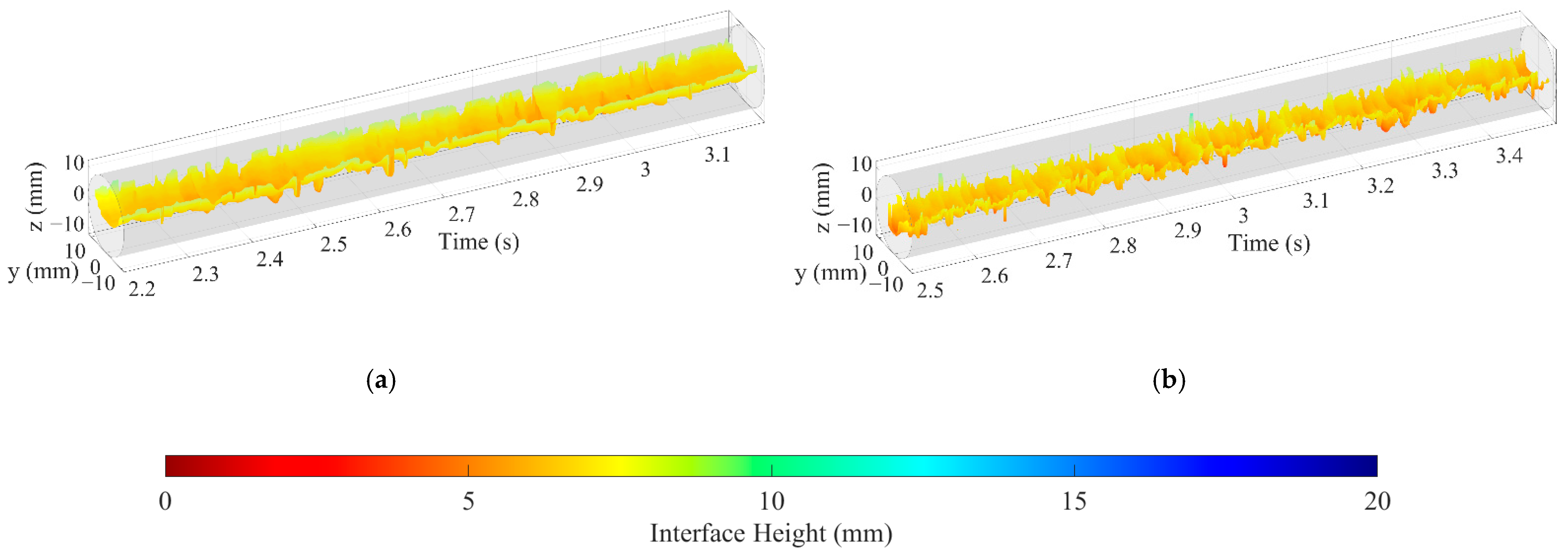
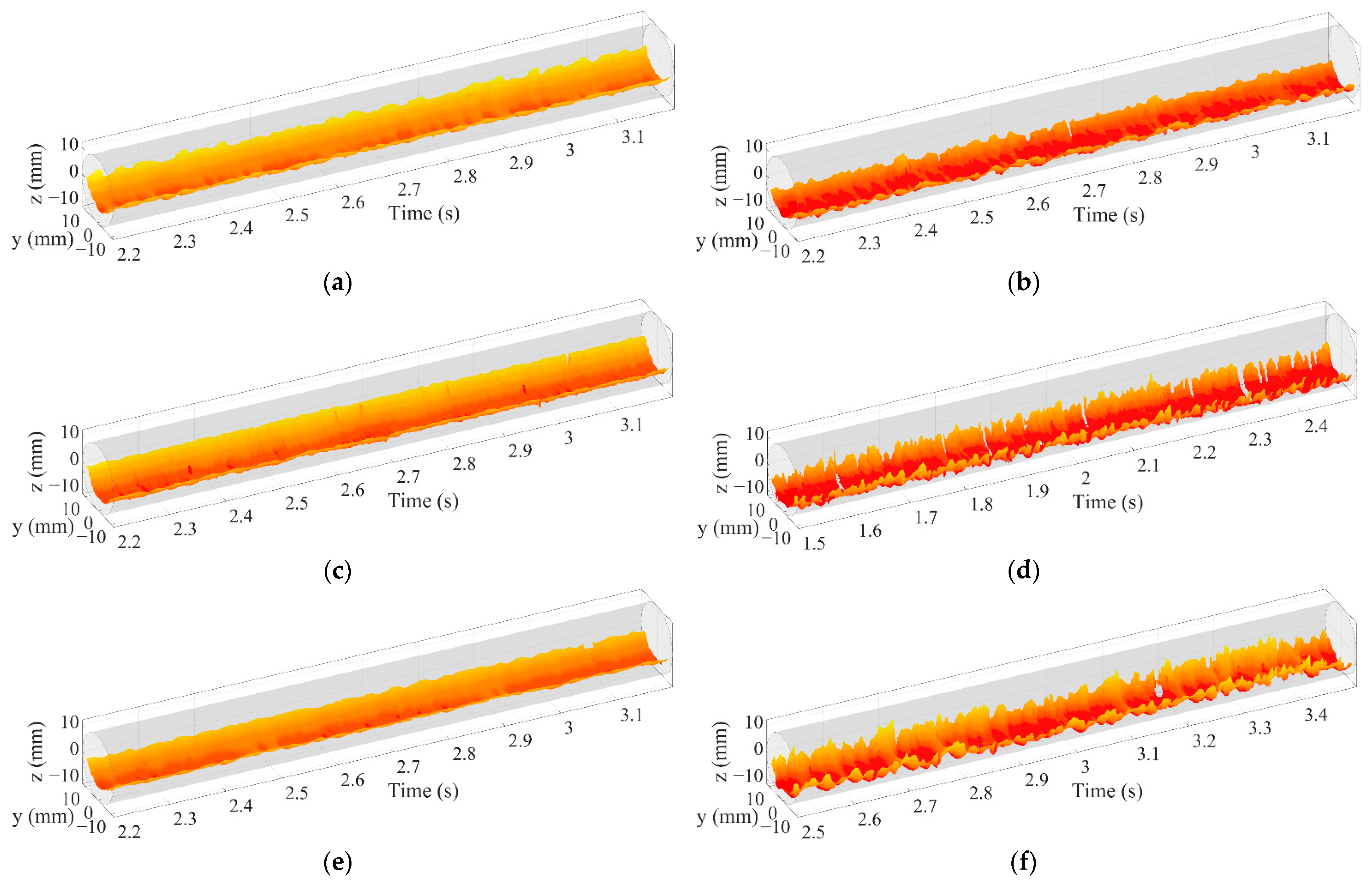
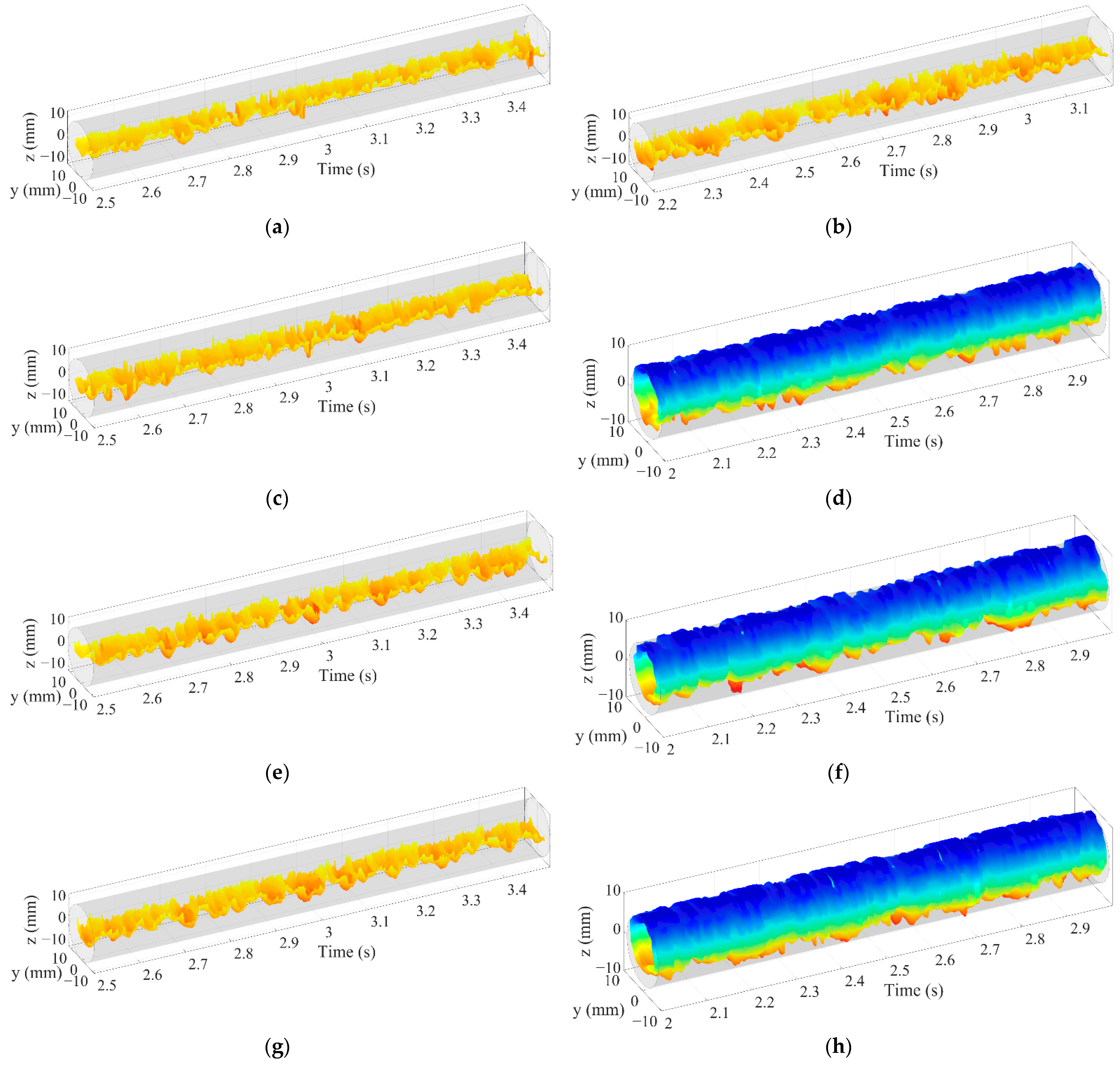
3.1. Interfacial Configuration
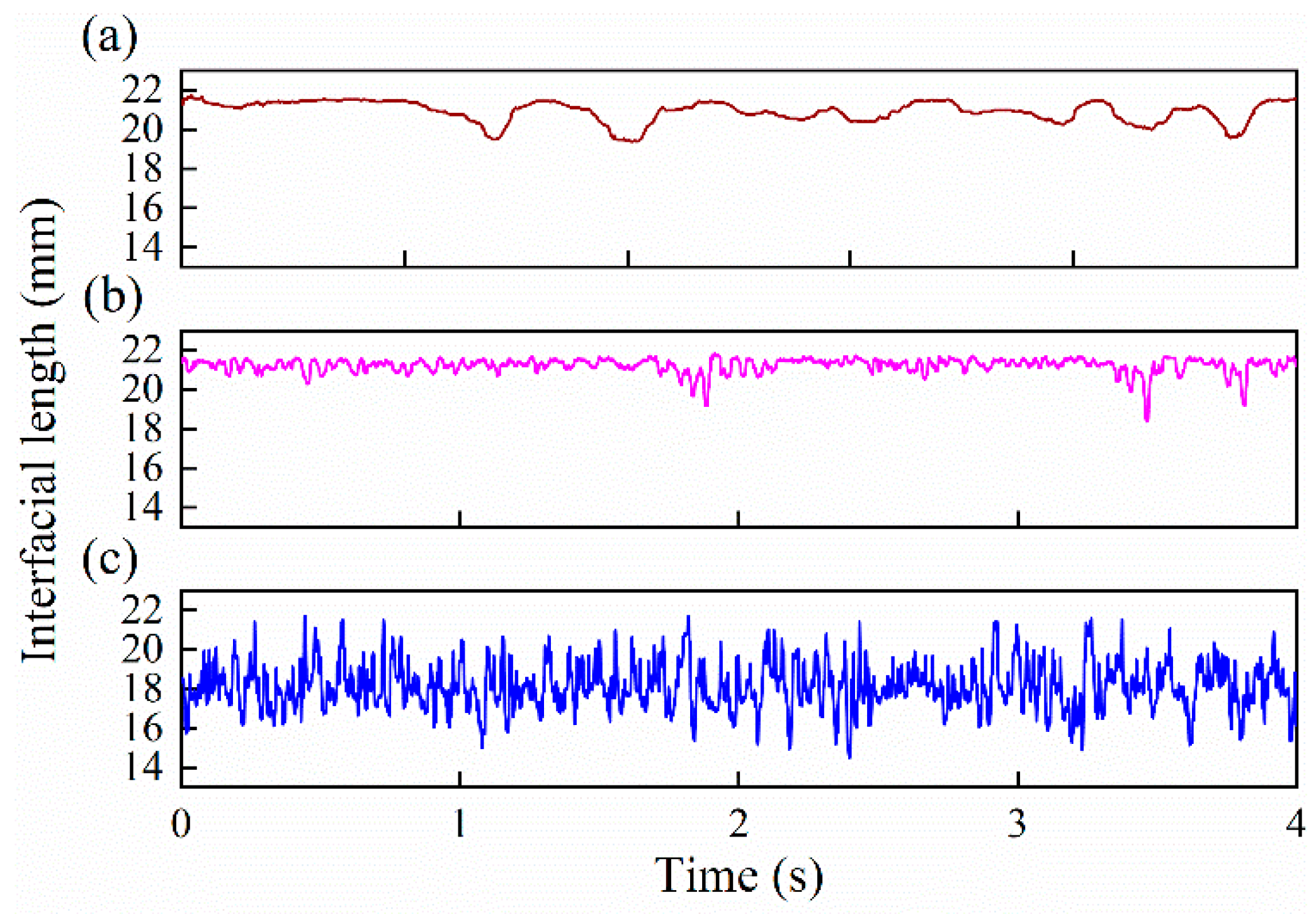
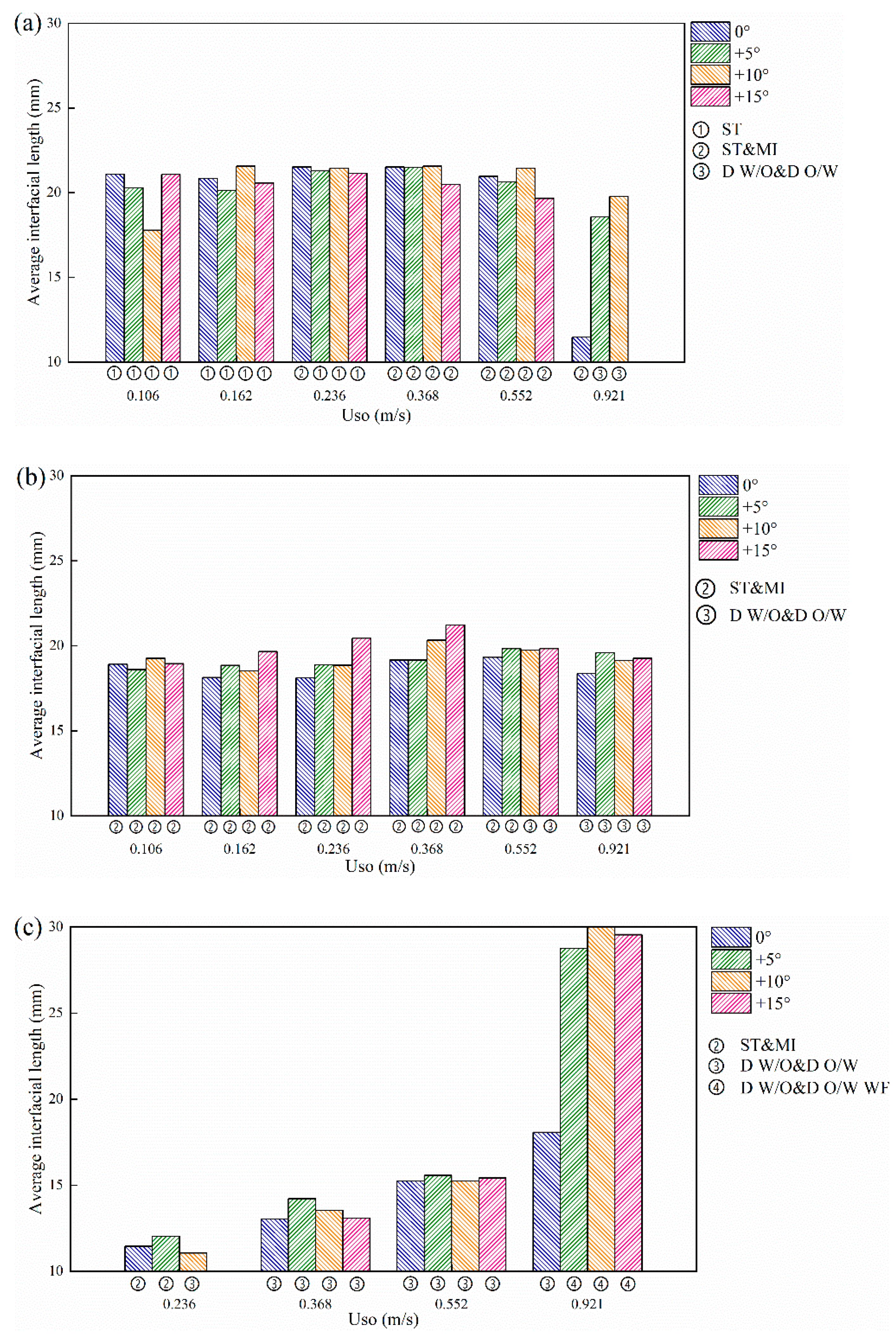
3.2. Interfacial Height and Length
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Trallero, J.L.; Sarica, C.; Brill, J.P. A Study of Oil/Water Flow Patterns in Horizontal Pipes. SPE Prod. Facil. 1997, 12, 165–172. [Google Scholar] [CrossRef]
- Angeli, P.; Hewitt, G.F. Flow structure in horizontal oil–water flow. Int. J. Multiph. Flow 2000, 26, 1117–1140. [Google Scholar] [CrossRef]
- Zhai, L.-S.; Jin, N.-D.; Zong, Y.-B.; Hao, Q.-Y.; Gao, Z.-K. Experimental flow pattern map, slippage and time–frequency representation of oil–water two-phase flow in horizontal small diameter pipes. Int. J. Multiph. Flow 2015, 76, 168–186. [Google Scholar] [CrossRef]
- Rodriguez, O.M.H.; Oliemans, R.V.A. Experimental study on oil–water flow in horizontal and slightly inclined pipes. Int. J. Multiph. Flow 2006, 32, 323–343. [Google Scholar] [CrossRef]
- Grassi, B.; Strazza, D.; Poesio, P. Experimental validation of theoretical models in two-phase high-viscosity ratio liquid–liquid flows in horizontal and slightly inclined pipes. Int. J. Multiph. Flow 2008, 34, 950–965. [Google Scholar] [CrossRef]
- Boostani, M.; Karimi, H.; Azizi, S. Heat transfer to oil-water flow in horizontal and inclined pipes: Experimental investigation and ANN modeling. Int. J. Therm. Sci. 2017, 111, 340–350. [Google Scholar] [CrossRef]
- Hanafizadeh, P.; Hojati, A.; Karimi, A. Experimental investigation of oil–water two phase flow regime in an inclined pipe. J. Petrol. Sci. Eng. 2015, 136, 12–22. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, H.; Rui, J.; Pan, Y.; Liu, X.; Shang, Z. Prediction model for the transition between oil–water two-phase separation and dispersed flows in horizontal and inclined pipes. J. Petrol. Sci. Eng. 2020, 192, 107161. [Google Scholar] [CrossRef]
- Paolinelli, L.D. A comprehensive model for stability of dispersed oil-water flow in horizontal and inclined pipes. Chem. Eng. Sci. 2020, 211, 115325. [Google Scholar] [CrossRef]
- Al-Wahaibi, T.; Smith, M.; Angeli, P. Transition between stratified and non-stratified horizontal oil–water flows. Part II: Mechanism of drop formation. Chem. Eng. Sci. 2007, 62, 2929–2940. [Google Scholar] [CrossRef]
- de Castro, M.S.; Pereira, C.C.; dos Santos, J.N.; Rodriguez, O.M.H. Geometrical and kinematic properties of interfacial waves in stratified oil–water flow in inclined pipe. Exp. Therm. Fluid Sci. 2012, 37, 171–178. [Google Scholar] [CrossRef]
- Perera, K.; Time, R.W.; Pradeep, C.; Kumara, A.S. Interfacial wave analysis of low viscous oil-water flow in upwardly inclined pipes. Chem. Eng. Sci. 2019, 196, 444–462. [Google Scholar] [CrossRef]
- Al-Wahaibi, T.; Angeli, P. Experimental study on interfacial waves in stratified horizontal oil–water flow. Int. J. Multiph. Flow 2011, 37, 930–940. [Google Scholar] [CrossRef]
- Zhai, L.; Zhang, H.; Yan, C.; Jin, N. Measurement of Oil-Water Interface Characteristics in Horizontal Pipe Using a Conductance Parallel-Wire Array Probe. IEEE Trans. Instrum. Meas. 2019, 68, 3232–3243. [Google Scholar] [CrossRef]
- Morgan, R.G.; Markides, C.N.; Hale, C.P.; Hewitt, G.F. Horizontal liquid–liquid flow characteristics at low superficial velocities using laser-induced fluorescence. Int. J. Multiph. Flow 2012, 43, 101–117. [Google Scholar] [CrossRef]
- Morgan, R.G.; Markides, C.N.; Zadrazil, I.; Hewitt, G.F. Characteristics of horizontal liquid–liquid flows in a circular pipe using simultaneous high-speed laser-induced fluorescence and particle velocimetry. Int. J. Multiph. Flow 2013, 49, 99–118. [Google Scholar] [CrossRef]
- Ibarra, R.; Matar, O.K.; Markides, C.N. Experimental investigations of upward-inclined stratified oil-water flows using simultaneous two-line planar laser-induced fluorescence and particle velocimetry. Int. J. Multiph. Flow 2021, 135, 103502. [Google Scholar] [CrossRef]
- Jia, J.; Wang, H.; Millington, D. Electrical Resistance Tomography Sensor for Highly Conductive Oil-Water Two-Phase Flow Measurement. IEEE Sens. J. 2017, 17, 8224–8233. [Google Scholar] [CrossRef]
- Hossain, M.S.; Abir, M.T.; Alam, M.S.; Volakis, J.L.; Islam, M.A. An Algorithm to Image Individual Phase Fractions of Multiphase Flows Using Electrical Capacitance Tomography. IEEE Sens. J. 2020, 20, 14924–14931. [Google Scholar] [CrossRef]
- Tompkins, C.; Prasser, H.-M.; Corradini, M. Wire-mesh sensors: A review of methods and uncertainty in multiphase flows relative to other measurement techniques. Nucl. Eng. Des. 2018, 337, 205–220. [Google Scholar] [CrossRef]
- Prasser, H.M.; Böttger, A.; Zschau, J. A new electrode-mesh tomograph for gas–liquid flows. Flow Meas. Instrum. 1998, 9, 111–119. [Google Scholar] [CrossRef]
- Furuya, M.; Kanai, T.; Arai, T.; Takiguchi, H.; Prasser, H.-M.; Hampel, U.; Schleicher, E. Three-dimensional velocity vector determination algorithm for individual bubble identified with Wire-Mesh Sensors. Nucl. Eng. Des. 2018, 336, 74–79. [Google Scholar] [CrossRef]
- Kickhofel, J.; Yang, J.; Prasser, H.-M. Designing a high temperature high pressure mesh sensor. Nucl. Eng. Des. 2018, 336, 122–128. [Google Scholar] [CrossRef]
- Dias, F.D.A.; Pipa, D.R.; Morales, R.E.M.; Silva, M.J.d. Wire-Mesh Sensor Super-Resolution Based on Statistical Reconstruction. IEEE Trans. Instrum. Meas. 2021, 70, 4503212. [Google Scholar] [CrossRef]
- Sharaf, S.; van der Meulen, G.P.; Agunlejika, E.O.; Azzopardi, B.J. Structures in gas–liquid churn flow in a large diameter vertical pipe. Int. J. Multiph. Flow 2016, 78, 88–103. [Google Scholar] [CrossRef]
- Kesana, N.R.; Parsi, M.; Vieira, R.E.; Azzopardi, B.; Schleicher, E.; McLaury, B.S.; Shirazi, S.A.; Hampel, U. Visualization of gas-liquid multiphase pseudo-slug flow using Wire-Mesh Sensor. J. Nat. Gas Sci. Eng. 2017, 46, 477–490. [Google Scholar] [CrossRef]
- Da Silva, M.J.; dos Santos, E.N.; Hampel, U.; Rodriguez, I.H.; Rodriguez, O.M.H. Phase fraction distribution measurement of oil–water flow using a capacitance wire-mesh sensor. Meas. Sci. Technol. 2011, 22, 104020. [Google Scholar] [CrossRef]
- Rodriguez, I.H.; Velasco Peña, H.F.; Bonilla Riaño, A.; Henkes, R.A.W.M.; Rodriguez, O.M.H. Experiments with a Wire-Mesh Sensor for stratified and dispersed oil-brine pipe flow. Int. J. Multiph. Flow 2015, 70, 113–125. [Google Scholar] [CrossRef]
- Zhang, H.; Xiao, Y.; Gu, H. A new method to determine conductivity distribution based on wire-mesh sensor by iteration. Ann. Nucl. Energy 2020, 143, 107443. [Google Scholar] [CrossRef]
- Prasser, H.-M.; Beyer, M.; Carl, H.; Gregor, S.; Lucas, D.; Pietruske, H.; Schütz, P.; Weiss, F.-P. Evolution of the structure of a gas–liquid two-phase flow in a large vertical pipe. Nucl. Eng. Des. 2007, 237, 1848–1861. [Google Scholar] [CrossRef]
- da Silva, M.J.; Hampel, U. Capacitance wire-mesh sensor applied for the visualization of three-phase gas–liquid–liquid flows. Flow Meas. Instrum. 2013, 34, 113–117. [Google Scholar] [CrossRef]
- Zhang, H.; Xiao, Y.; Gu, H.; Liu, D. Study on bubbly and cap-bubbly flow in a square channel using dual wire-mesh sensors. Int. J. Multiph. Flow 2020, 133, 103461. [Google Scholar] [CrossRef]
- Lee, J.; Kim, M.; Park, H. Single-layer wire-mesh sensor to simultaneously measure the size and rise velocity of micro-to-millimeter sized bubbles in a gas-liquid two-phase flow. Int. J. Multiph. Flow 2021, 139, 103620. [Google Scholar] [CrossRef]
- Zhai, L.; Wang, Y.; Yang, J.; Jin, N. Visualization of Vertical Oil–Water–Gas Flows Using Conductance Compensated Wire-Mesh Sensor. IEEE Trans. Instrum. Meas. 2022, 71, 7500516. [Google Scholar] [CrossRef]
- Beucher, S.; Meyer, F. The Morphological Approach to Segmentation: The Watershed Transformation. In Mathematical Morphology in Image Processing; CRC Press: Boca Raton, FL, USA, 1993; Volume 34, pp. 433–481. [Google Scholar]
- Tzotzi, C.; Andritsos, N. Interfacial shear stress in wavy stratified gas–liquid flow in horizontal pipes. Int. J. Multiph. Flow 2013, 54, 43–54. [Google Scholar] [CrossRef]
- Rodriguez, O.M.H.; Castro, M.S. Interfacial-tension-force model for the wavy-stratified liquid–liquid flow pattern transition. Int. J. Multiph. Flow 2014, 58, 114–126. [Google Scholar] [CrossRef]
- Al-Sarkhi, A.; Pereyra, E.; Mantilla, I.; Avila, C. Dimensionless oil-water stratified to non-stratified flow pattern transition. J. Petrol. Sci. Eng. 2017, 151, 284–291. [Google Scholar] [CrossRef]
- Rodriguez, O.M.H.; Baldani, L.S. Prediction of pressure gradient and holdup in wavy stratified liquid–liquid inclined pipe flow. J. Petrol. Sci. Eng. 2012, 96–97, 140–151. [Google Scholar] [CrossRef]
- Premanadhan, V.K.; Hernandez-Perez, V.; Teik, W.T.; Tam, N.D.; Bratland, O.; Loh, W.L. Experimental investigation of interfacial waves in stratified liquid-liquid flows in horizontal pipelines: Characteristics and pressure gradients. J. Petrol. Sci. Eng. 2019, 173, 20–36. [Google Scholar] [CrossRef]
- Zhai, L.; Zhang, H.; Jin, N. Prediction of pressure drop for segregated oil-water flows in small diameter pipe using modified two-fluid model. Exp. Therm. Fluid Sci. 2020, 114, 110078. [Google Scholar] [CrossRef]
- Sharma, A.; Al-Sarkhi, A.; Sarica, C.; Zhang, H.-Q. Modeling of oil–water flow using energy minimization concept. Int. J. Multiph. Flow 2011, 37, 326–335. [Google Scholar] [CrossRef]
- Guet, S.; Rodriguez, O.M.H.; Oliemans, R.V.A.; Brauner, N. An inverse dispersed multiphase flow model for liquid production rate determination. Int. J. Multiph. Flow 2006, 32, 553–567. [Google Scholar] [CrossRef]
- Al-Wahaibi, T.; Angeli, P. Predictive model of the entrained fraction in horizontal oil–water flows. Chem. Eng. Sci. 2009, 64, 2817–2825. [Google Scholar] [CrossRef]
- Hibiki, T.; Rassame, S. Analytical model for predicting oil fraction in horizontal oil–water two-phase flow. Exp. Comput. Multiph. Flow 2019, 1, 73–84. [Google Scholar] [CrossRef] [Green Version]










| NO. | Author | Measurement Object | Pipe Diameter (mm) | WMS Configuration | Spatial Resolution (mm) |
|---|---|---|---|---|---|
| 1 | Prasser et al. [21] | Air–water flow | 51.2 | 16 × 16 | 3.2 |
| 2 | Prasser et al. [30] | Air–water flow | 192 | 64 × 64 | 3 |
| 3 | Da Silva et al. [31] | Gas–liquid–liquid flow | 50 × 50 | 16 × 16 | 3.12 |
| 4 | Parsi et al. [26] | Air–water flow | 76.2 | 16 × 16 | 4.76 |
| 5 | Xiao et al. [32] | Air–water flow | 66 × 66 | 16 × 16 | 2.06 |
| 6 | Lee et al. [33] | Air–water flow | 60 × 60 | 5 × 5 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, L.; Qiao, J.; Wang, W.; Wang, Y. Measurement of Interfacial Characteristics of Horizontal and Inclined Oil–Water Flows by Using Wire-Mesh Sensor. Energies 2022, 15, 6638. https://doi.org/10.3390/en15186638
Zhai L, Qiao J, Wang W, Wang Y. Measurement of Interfacial Characteristics of Horizontal and Inclined Oil–Water Flows by Using Wire-Mesh Sensor. Energies. 2022; 15(18):6638. https://doi.org/10.3390/en15186638
Chicago/Turabian StyleZhai, Lusheng, Jiawei Qiao, Wenhao Wang, and Yuqing Wang. 2022. "Measurement of Interfacial Characteristics of Horizontal and Inclined Oil–Water Flows by Using Wire-Mesh Sensor" Energies 15, no. 18: 6638. https://doi.org/10.3390/en15186638
APA StyleZhai, L., Qiao, J., Wang, W., & Wang, Y. (2022). Measurement of Interfacial Characteristics of Horizontal and Inclined Oil–Water Flows by Using Wire-Mesh Sensor. Energies, 15(18), 6638. https://doi.org/10.3390/en15186638







