Effects of Radial and Circumferential Flows on Power Density Improvements of Tubular Solid Oxide Fuel Cells
Abstract
:1. Introduction
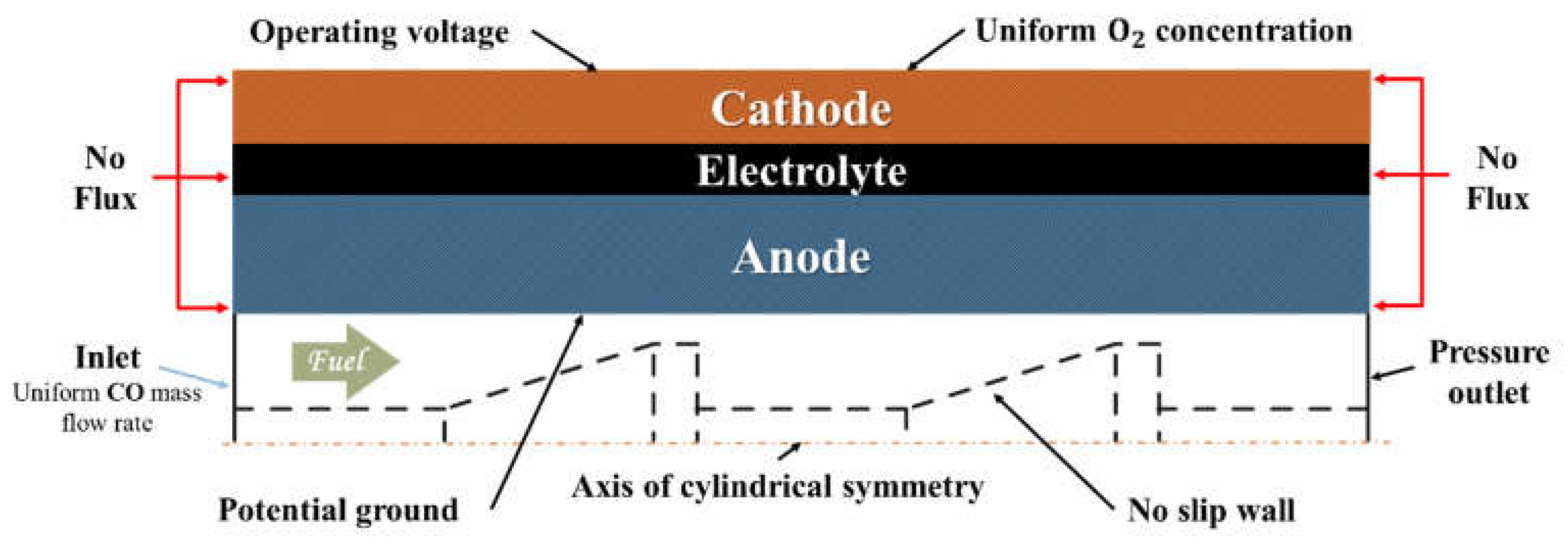
2. Model Description
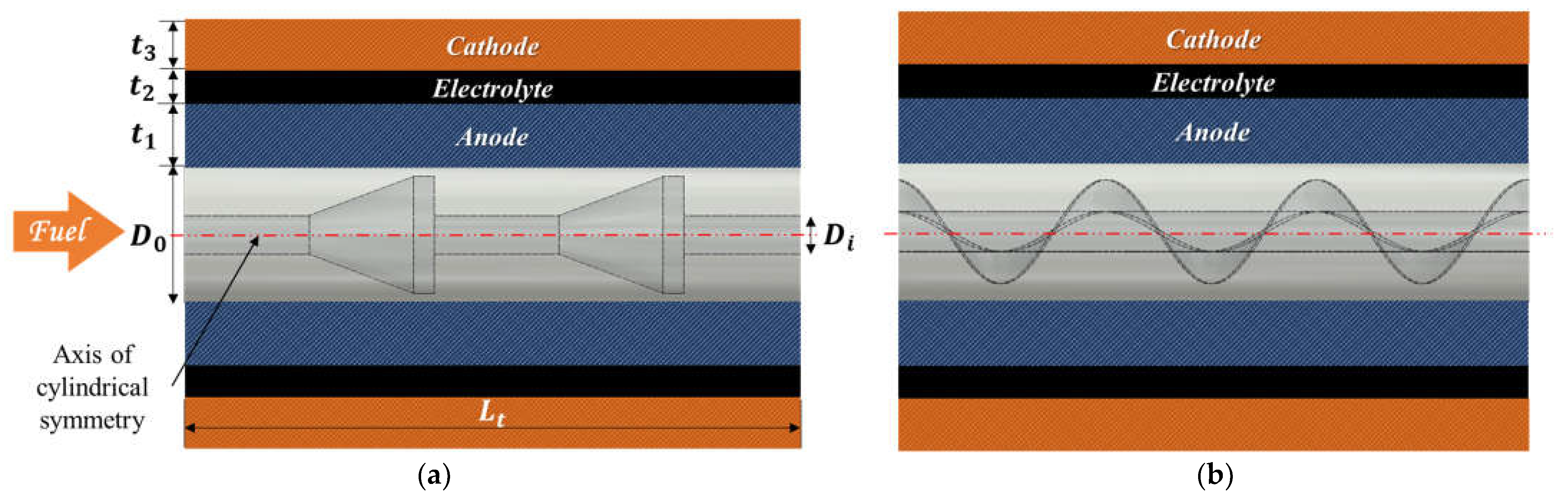
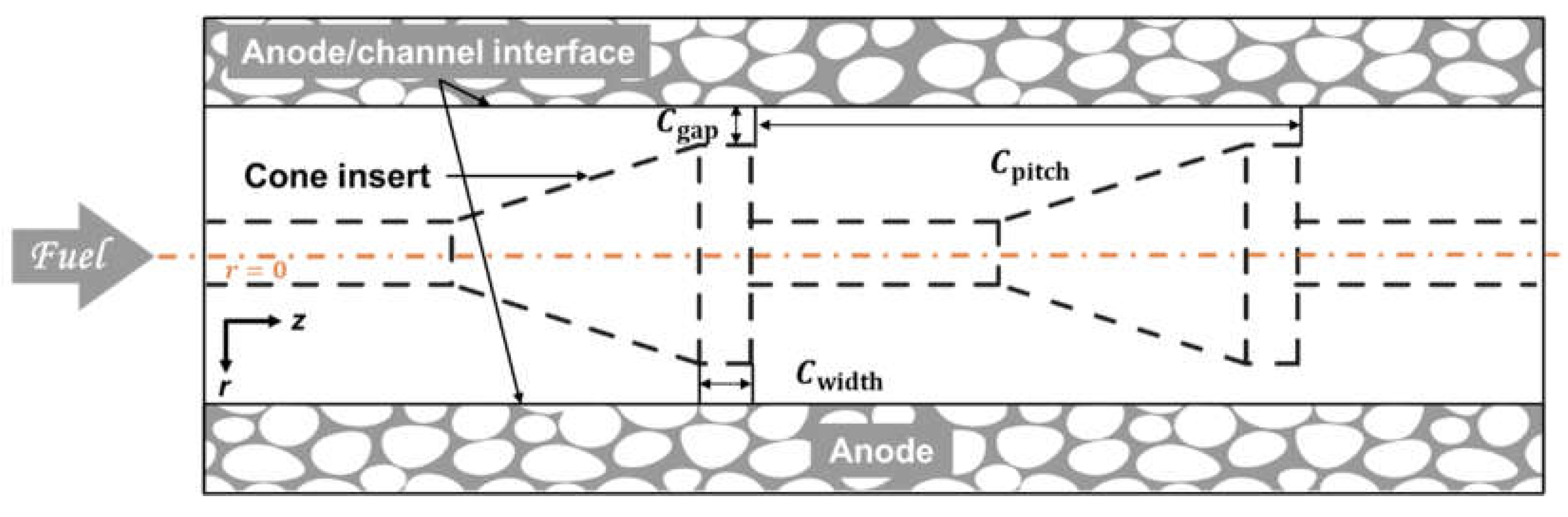
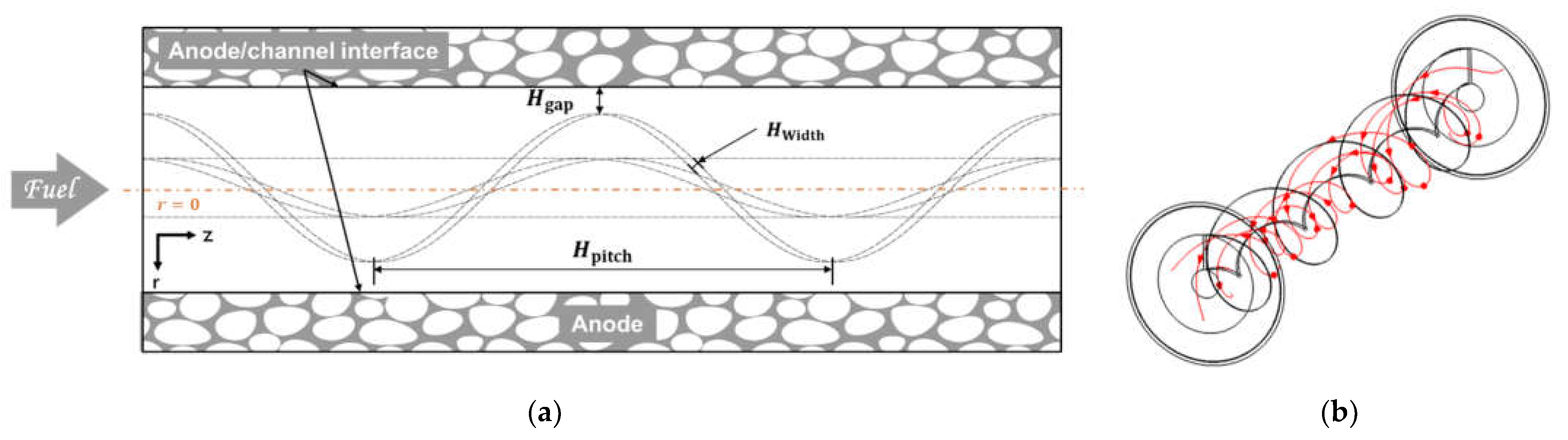
2.1. Geometry Description
2.2. Numerical Model
2.2.1. Electrochemical Reactions
2.2.2. Momentum Transport
2.2.3. Mass Transport
2.3. Numerical Model
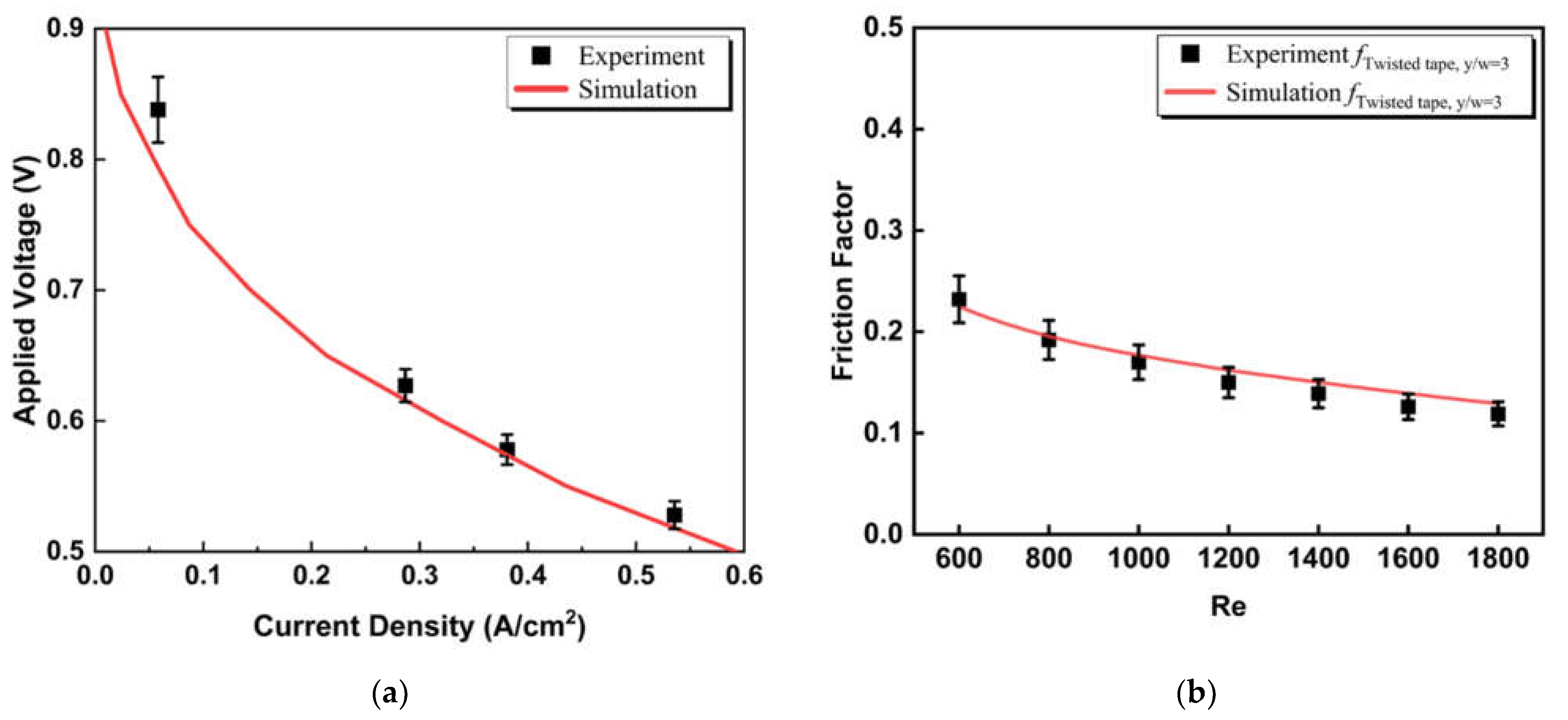
2.4. Model Validation
3. Results and Discussion
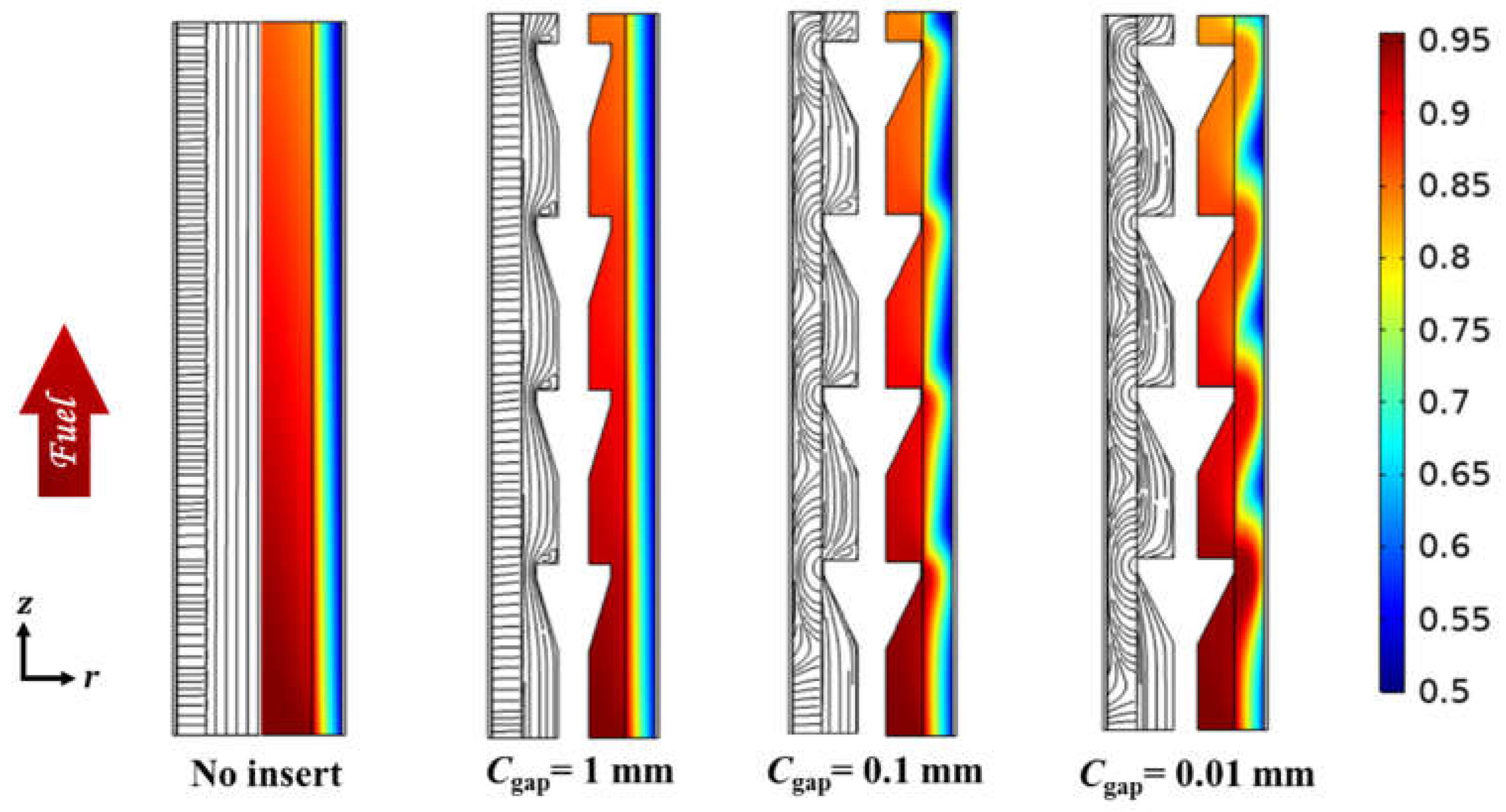
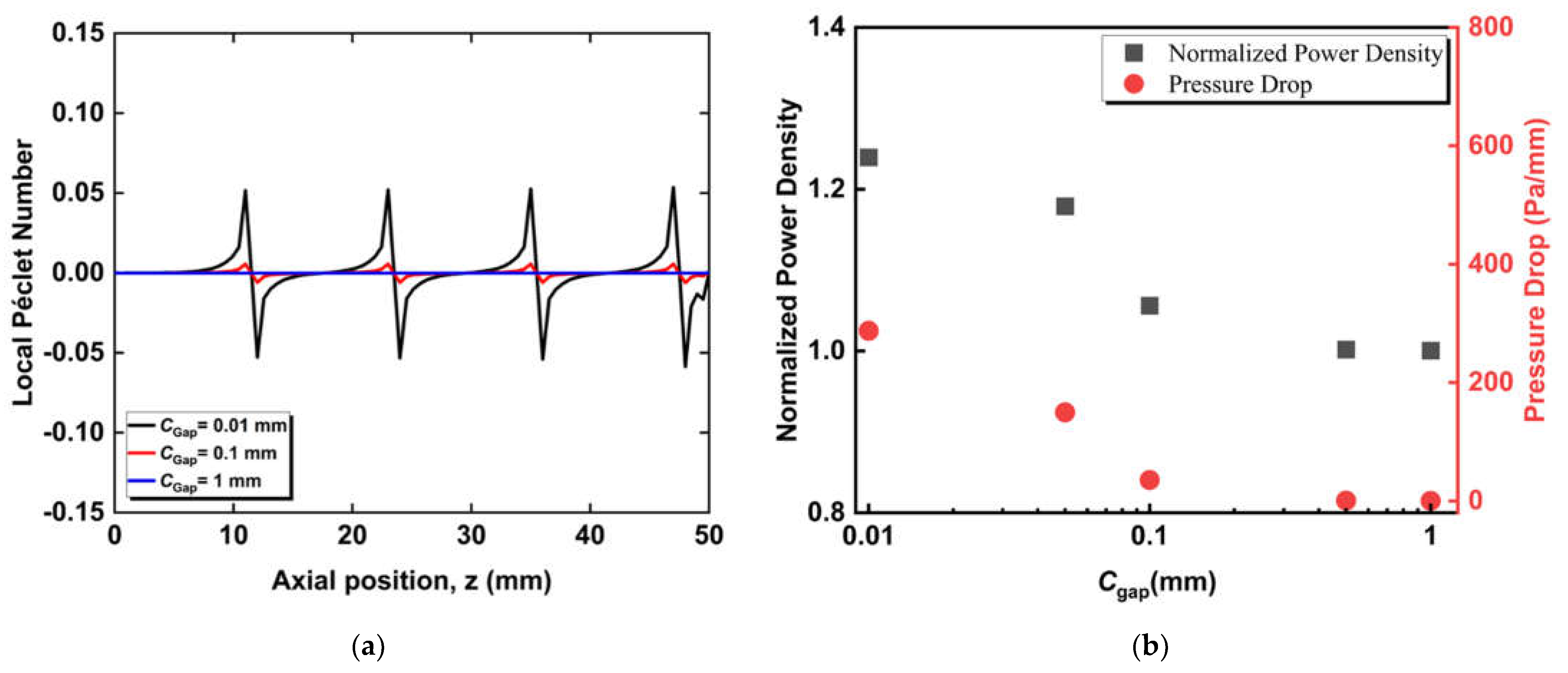
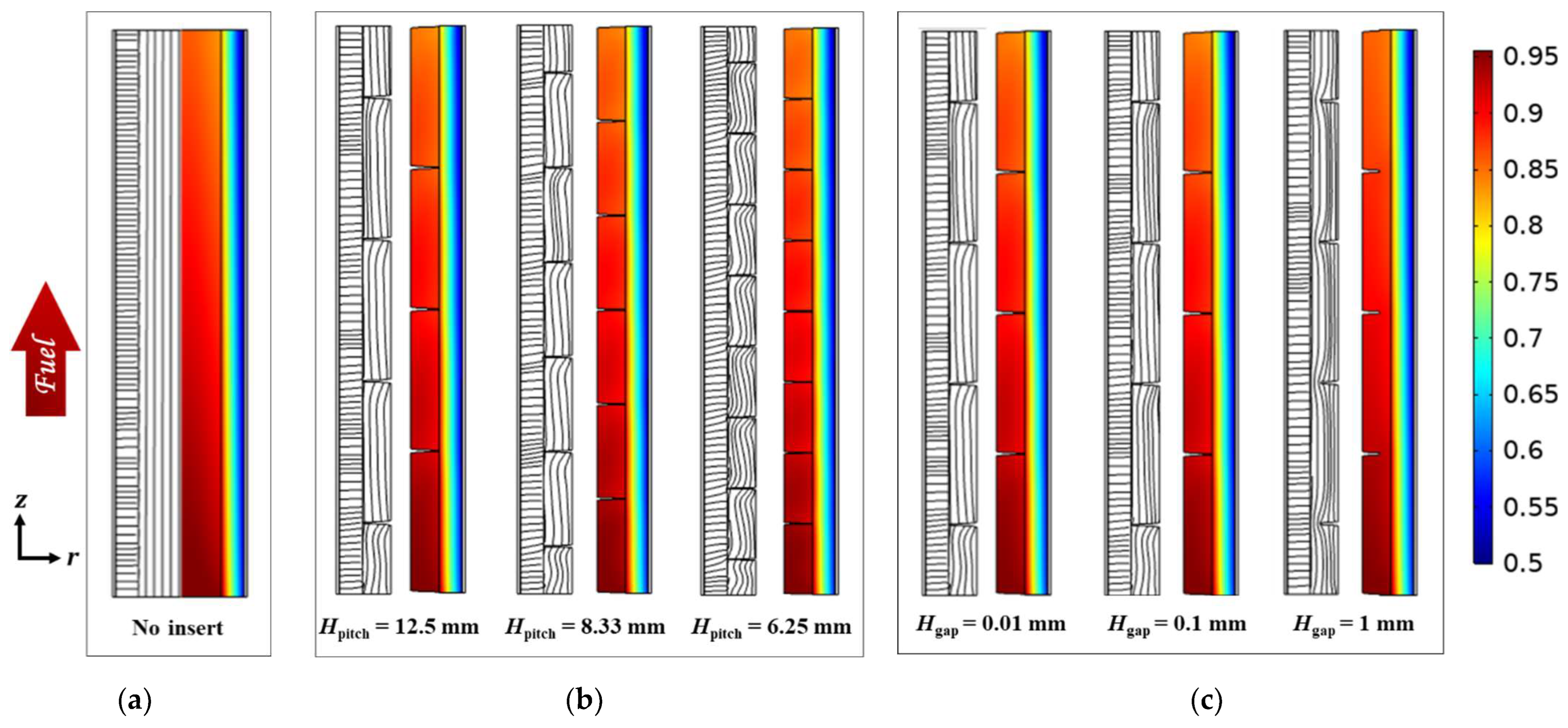
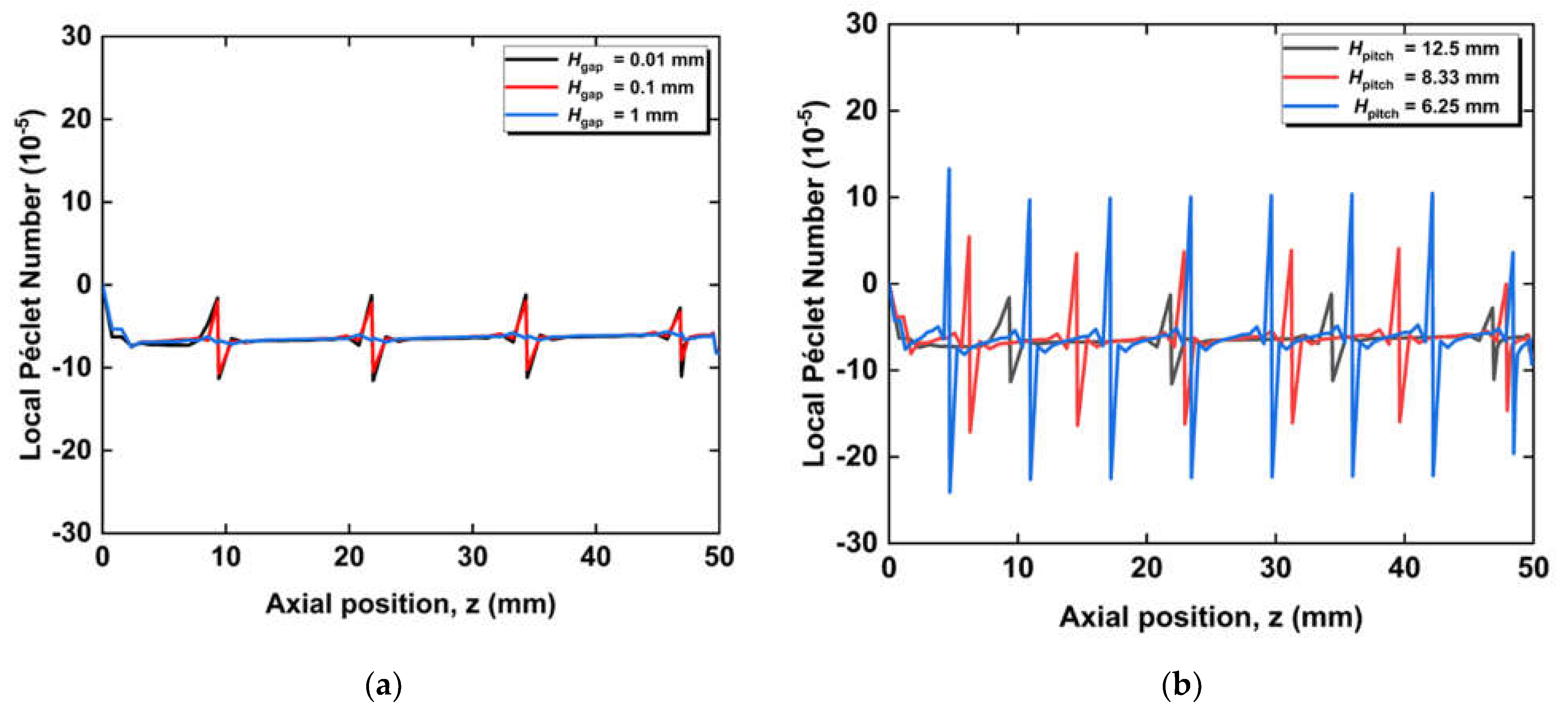
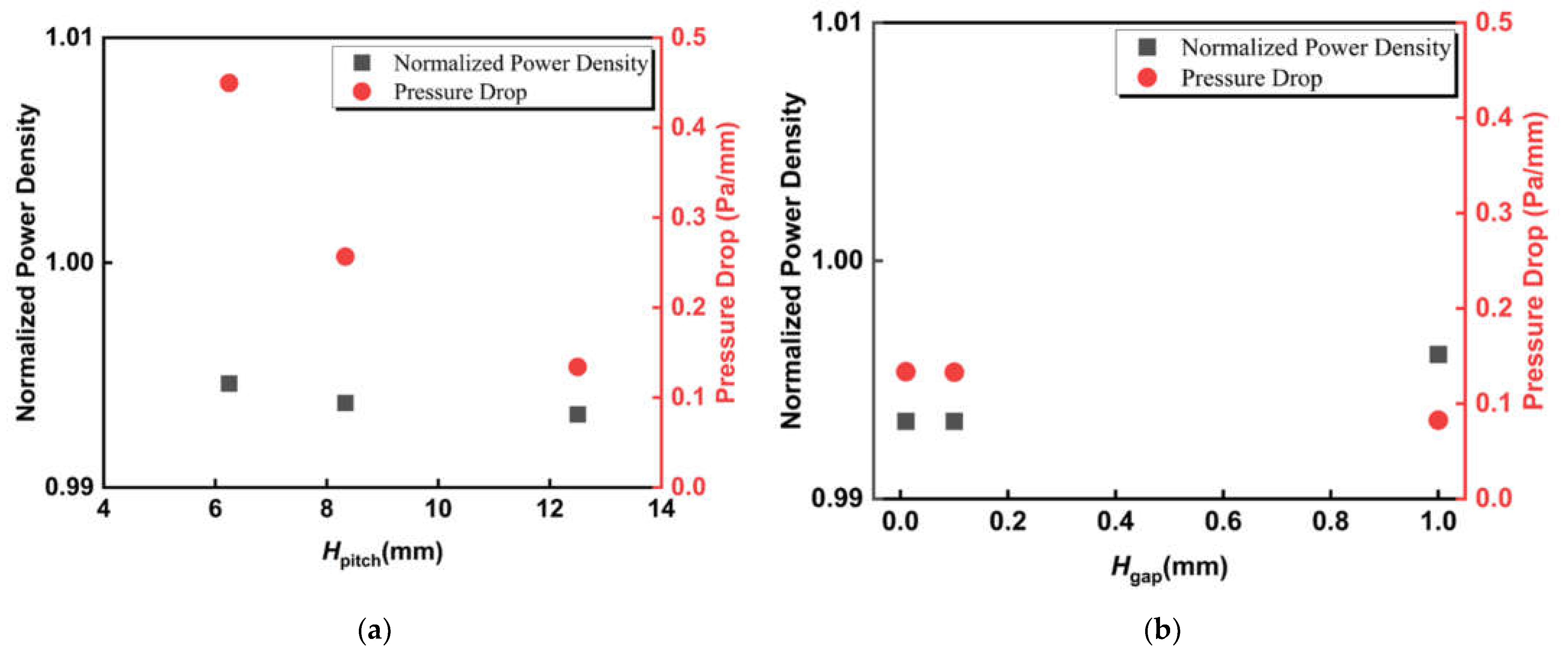
3.1. Effect of Radial Flows
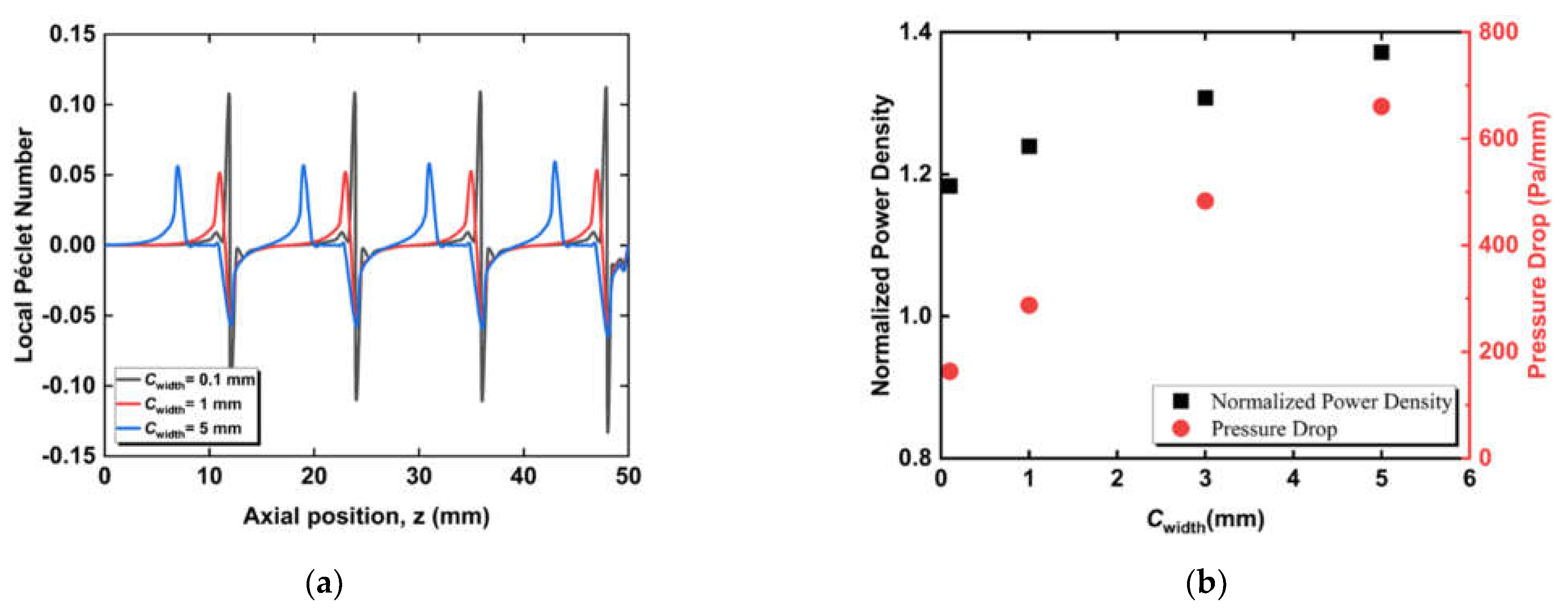
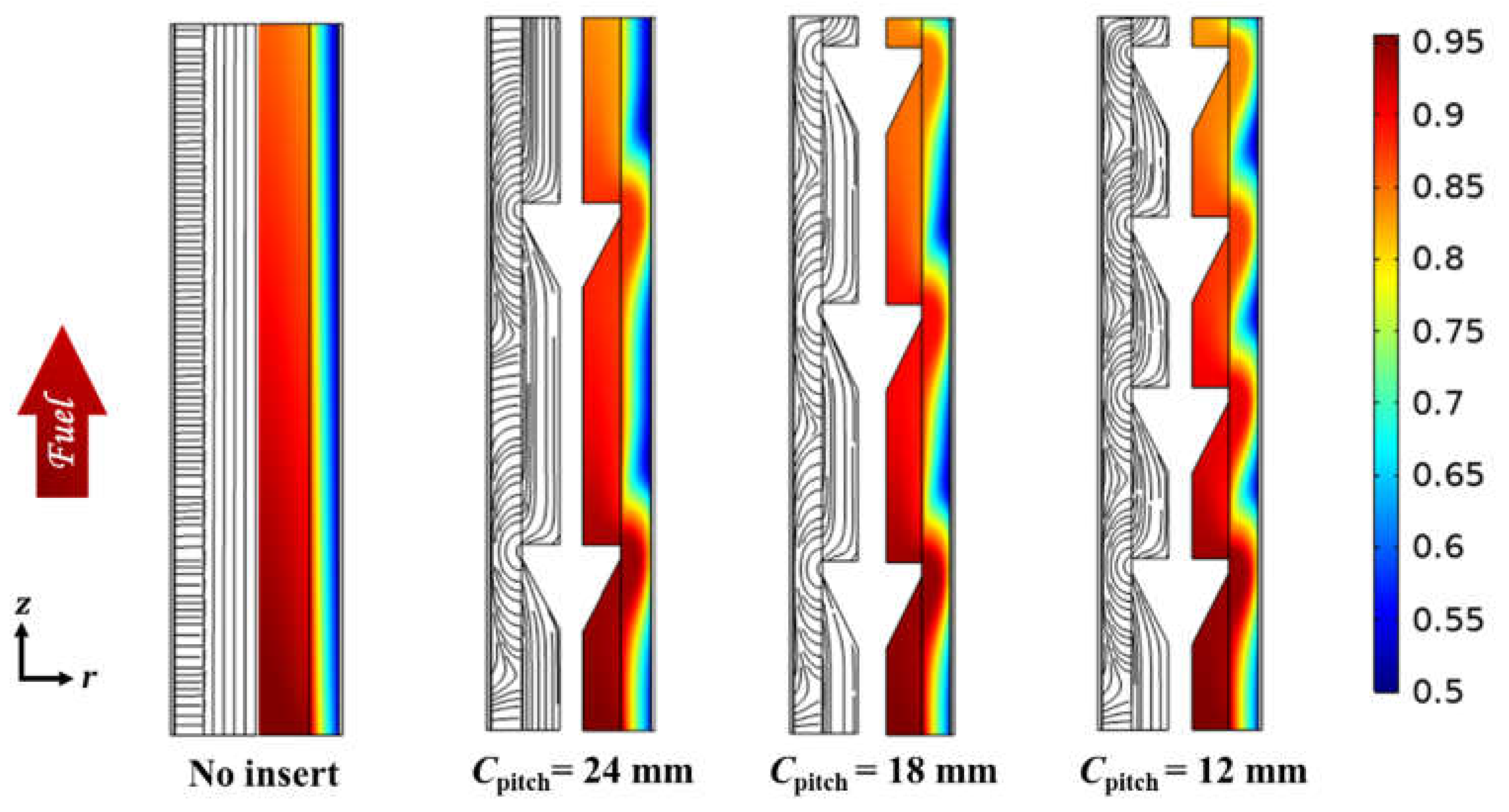
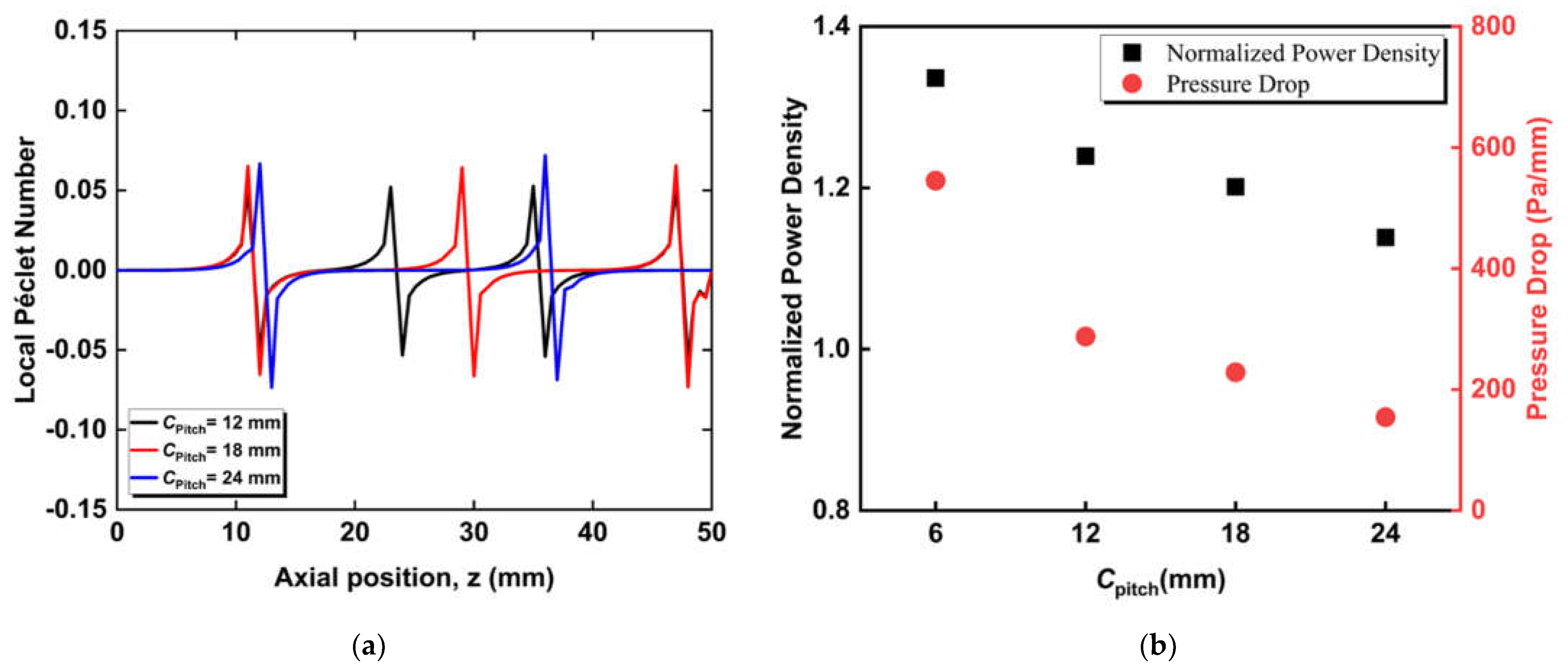
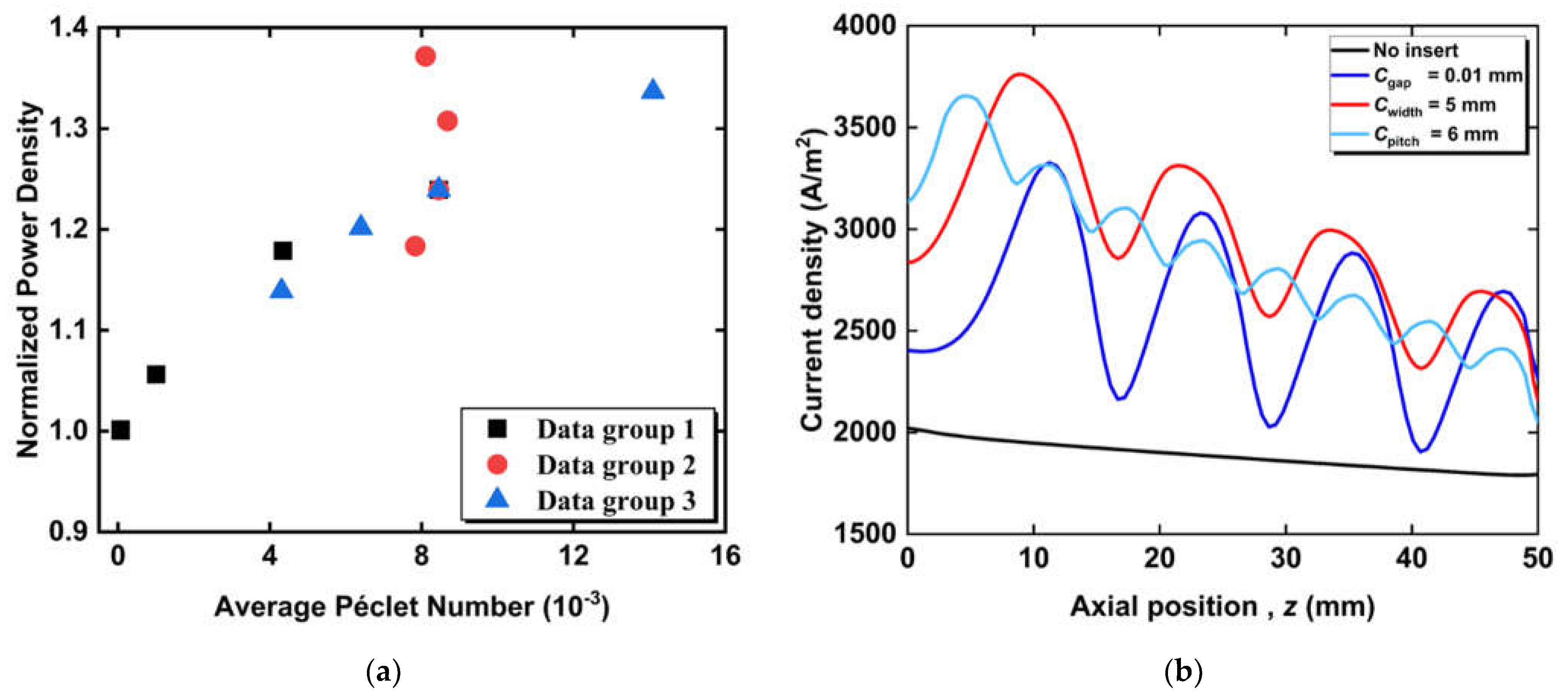
3.2. Effect of Circumferential Flow
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Dincer, I. Energy and Environmental Impacts: Present and Future Perspectives. Energy Sources 1998, 20, 427–453. [Google Scholar] [CrossRef]
- Stambouli, A.B.; Traversa, E. Solid Oxide Fuel Cells (SOFCs): A Review of an Environmentally Clean and Efficient Source of Energy. Renew. Sustain. Energy Rev. 2002, 6, 433–455. [Google Scholar] [CrossRef]
- Mekhilef, S. Comparative Study of Different Fuel Cell Technologies. Renew. Sustain. Energy Rev. 2012, 9, 981–989. [Google Scholar] [CrossRef]
- McLean, G.F.; Niet, T.; Prince-Richard, S.; Djilali, N. An Assessment of Alkaline Fuel Cell Technology. Int. J. Hydrogen Energy 2002, 20, 507–526. [Google Scholar] [CrossRef]
- Mulder, G.; Coenen, P.; Martens, A.; Spaepen, J. The Development of a 6 kW Fuel Cell Generator Based on Alkaline Fuel Cell Technology. Int. J. Hydrogen Energy 2008, 33, 3220–3224. [Google Scholar] [CrossRef]
- Kordesch, K.; Hacker, V.; Reichmann, K.; Cifrain, M.; Hejze, T.; Aronsson, R.R. The Safe and Economic Revival of Alkaline Hydrogen/Air Fuel Cells with Circulating Electrolytes, Recommended for Vehicles Using Battery Hybrid Systems and H2 from Ammonia Crackers. ECS Trans. 2008, 11, 167–185. [Google Scholar] [CrossRef]
- Lü, X.; Qu, Y.; Wang, Y.; Qin, C.; Liu, G. A Comprehensive Review on Hybrid Power System for PEMFC-HEV: Issues and Strategies. Energy Convers. Manag. 2018, 171, 1273–1291. [Google Scholar] [CrossRef]
- Cooper, N.J.; Smith, T.; Santamaria, A.D.; Park, J.W. Experimental Optimization of Parallel and Interdigitated PEMFC Flow-Field Channel Geometry. Int. J. Hydrogen Energy 2016, 41, 1213–1223. [Google Scholar] [CrossRef]
- Fernandes, A.; Woudstra, T.; van Wijk, A.; Verhoef, L.; Aravind, P.V. Fuel Cell Electric Vehicle as a Power Plant and SOFC as a Natural Gas Reformer: An Exergy Analysis of Different System Designs. Appl. Energy 2016, 173, 13–28. [Google Scholar] [CrossRef]
- Bessekon, Y.; Zielke, P.; Wulff, A.C.; Hagen, A. Simulation of a SOFC/Battery Powered Vehicle. Int. J. Hydrogen Energy 2019, 44, 1905–1918. [Google Scholar] [CrossRef]
- Luo, Y.; Shi, Y.; Cai, N. Chapter 4—High-Efficiency Hybrid Fuel Cell Systems for Vehicles and Micro-CHPs. In Hybrid Systems and Multi-energy Networks for the Future Energy Internet; Academic Press: Cambridge, MA, USA, 2021; Volume 27. [Google Scholar]
- Eguchi, K. Fuel Flexibility in Power Generation by Solid Oxide Fuel Cells. Solid State Ion. 2002, 152–153, 411–416. [Google Scholar] [CrossRef]
- Nehter, P.; Wildrath, B.; Bauschulte, A.; Leites, K. Diesel Based SOFC Demonstrator for Maritime Applications. ECS Trans. 2017, 78, 171–180. [Google Scholar] [CrossRef]
- Maru, H.C.; Singhal, S.C.; Stone, C.; Wheeler, D. 1–10 KW Stationary Combined Heat and Power Systems Status and Technical Potential: Independent Review. 2010. Available online: https://www.osti.gov/servlets/purl/993647 (accessed on 1 September 2022).
- Ellamla, H.R.; Staffell, I.; Bujlo, P.; Pollet, B.G.; Pasupathi, S. Current Status of Fuel Cell Based Combined Heat and Power Systems for Residential Sector. J. Power Sources 2015, 293, 312–328. [Google Scholar] [CrossRef]
- Zhu, B. Advantages of Intermediate Temperature Solid Oxide Fuel Cells for Tractionary Applications. J. Power Sources 2001, 93, 82–86. [Google Scholar] [CrossRef]
- Zhao, Y.; Jing, R.; Zhang, Z. Feasibility of Solid Oxide Fuel Cell Stationary Applications in China’s Building Sector and Relevant Progress. In Design and Operation of Solid Oxide Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2020; pp. 359–393. ISBN 978-0-12-815253-9. [Google Scholar]
- Winkler, W.; Lorenz, H. Design Studies of Mobile Applications with SOFC–Heat Engine Modules. J. Power Sources 2002, 6, 338–343. [Google Scholar] [CrossRef]
- Rechberger, J.; Kaupert, A.; Hagerskans, J.; Blum, L. Demonstration of the First European SOFC APU on a Heavy Duty Truck. Transp. Res. Procedia 2016, 14, 3676–3685. [Google Scholar] [CrossRef]
- Santarelli, M.; Cabrera, M.; Calì, M. Solid Oxide Fuel Based Auxiliary Power Unit for Regional Jets: Design and Mission Simulation With Different Cell Geometries. J. Fuel Cell Sci. Technol. 2010, 7, 021006. [Google Scholar] [CrossRef]
- Korean Researchers Create Miniaturised SOFC to Power Drones. Fuel Cells Bull. 2016, 2016, 5. [CrossRef]
- Kendall, K. Progress in Microtubular Solid Oxide Fuel Cells. Int. J. Appl. Ceram. Technol. 2010, 7, 1–9. [Google Scholar] [CrossRef]
- Leah, R.T.; Bone, A.; Hammer, E.; Selcuk, A.; Rahman, M.; Clare, A.; Mukerjee, S.; Selby, M. Development Progress on the Ceres Power Steel Cell Technology Platform: Further Progress Towards Commercialization. ECS Trans. 2017, 78, 87–95. [Google Scholar] [CrossRef]
- Mukerjee, S.; Leah, R.; Selby, M.; Stevenson, G.; Brandon, N.P. Life and Reliability of Solid Oxide Fuel Cell-Based Products. In Solid Oxide Fuel Cell Lifetime and Reliability; Elsevier: Amsterdam, The Netherlands, 2017; pp. 173–191. ISBN 978-0-08-101102-7. [Google Scholar]
- Kendall, K.; Dikwal, C.M.; Bujalski, W. Comparative Analysis of Thermal and Redox Cycling for Microtubular SOFCs. ECS Trans. 2019, 7, 1521–1526. [Google Scholar] [CrossRef]
- Campana, R.; Merino, R.I.; Larrea, A.; Villarreal, I.; Orera, V.M. Fabrication, Electrochemical Characterization and Thermal Cycling of Anode Supported Microtubular Solid Oxide Fuel Cells. J. Power Sources 2009, 192, 120–125. [Google Scholar] [CrossRef]
- Matus, Y.; Dejonghe, L.; Jacobson, C.; Visco, S. Metal-Supported Solid Oxide Fuel Cell Membranes for Rapid Thermal Cycling. Solid State Ion. 2005, 176, 443–449. [Google Scholar] [CrossRef]
- Yu, Z.; Xu, Y.; Hu, B.; Liu, S.; Zhang, X. Comparing the Air Flow Distribution Qualities Among Three Different Air Flow Path Configurations for Tubular Solid Oxide Fuel Cell Stacks. Int. J. Electrochem. Sci. 2016, 11, 9100–9109. [Google Scholar] [CrossRef]
- Chen, D.; Xu, Y.; Hu, B.; Yan, C.; Lu, L. Investigation of Proper External Air Flow Path for Tubular Fuel Cell Stacks with an Anode Support Feature. Energy Convers. Manag. 2018, 171, 807–814. [Google Scholar] [CrossRef]
- Saied, M.; Ahmed, K.; Nemat-Alla, M.; Ahmed, M.; El-Sebaie, M. Performance Study of Solid Oxide Fuel Cell with Various Flow Field Designs: Numerical Study. Int. J. Hydrogen Energy 2018, 43, 20931–20946. [Google Scholar] [CrossRef]
- Bi, W.; Chen, D.; Lin, Z. A Key Geometric Parameter for the Flow Uniformity in Planar Solid Oxide Fuel Cell Stacks. Int. J. Hydrogen Energy 2009, 34, 3873–3884. [Google Scholar] [CrossRef]
- Danilov, V.A.; Tade, M.O. A CFD-Based Model of a Planar SOFC for Anode Flow Field Design. Int. J. Hydrogen Energy 2009, 34, 8998–9006. [Google Scholar] [CrossRef]
- Yuan, H. Compare New Designed Flow Channels of Interconnect for Planar SOFCs with Typical Channels. 2009, p. 7. Available online: https://www.ht.energy.lth.se/fileadmin/ht/Kurser/TFRF05/09_project/Yung_Huang.pdf (accessed on 1 September 2022).
- Khazaee, I.; Rava, A. Numerical Simulation of the Performance of Solid Oxide Fuel Cell with Different Flow Channel Geometries. Energy 2017, 119, 235–244. [Google Scholar] [CrossRef]
- Liu, S.; Kong, W.; Lin, Z. Three-Dimensional Modeling of Planar Solid Oxide Fuel Cells and the Rib Design Optimization. J. Power Sources 2009, 194, 854–863. [Google Scholar] [CrossRef]
- Wei, S.-S.; Wang, T.-H.; Wu, J.-S. Numerical Modeling of Interconnect Flow Channel Design and Thermal Stress Analysis of a Planar Anode-Supported Solid Oxide Fuel Cell Stack. Energy 2014, 69, 553–561. [Google Scholar] [CrossRef]
- Christman, K.L.; Jensen, M.K. Solid Oxide Fuel Cell Performance With Cross-Flow Roughness. J. Fuel Cell Sci. Technol. 2011, 8, 024501. [Google Scholar] [CrossRef]
- Canavar, M.; Mat, A.; Celik, S.; Timurkutluk, B.; Kaplan, Y. Investigation of Temperature Distribution and Performance of SOFC Short Stack with/without Machined Gas Channels. Int. J. Hydrogen Energy 2016, 41, 10030–10036. [Google Scholar] [CrossRef]
- Zeng, Z.; Hao, C.; Zhao, B.; Qian, Y.; Zhuge, W.; Wang, Y.; Shi, Y.; Zhang, Y. Local Heat Transfer Enhancement by Recirculation Flows for Temperature Gradient Reduction in a Tubular SOFC. Int. J. Green Energy 2022, 19, 1132–1147. [Google Scholar] [CrossRef]
- Zhao, B.; Zeng, Z.; Hao, C.; Essaghouri, A.; Qian, Y.; Zhuge, W.; Wang, Y.; Shi, Y.; Zhang, Y. A Study of Mass Transfer Characteristics of Secondary Flows in a Tubular Solid Oxide Fuel Cell for Power Density Improvement. Int. J. Energy Res. 2022, 1–19. [Google Scholar] [CrossRef]
- Ni, M. Modeling of SOFC Running on Partially Pre-Reformed Gas Mixture. Int. J. Hydrogen Energy 2012, 37, 1731–1745. [Google Scholar] [CrossRef]
- Guidelli, R.; Compton, R.G.; Feliu, J.M.; Gileadi, E.; Lipkowski, J.; Schmickler, W.; Trasatti, S. Defining the Transfer Coefficient in Electrochemistry: An Assessment (IUPAC Technical Report). Pure Appl. Chem. 2014, 86, 245–258. [Google Scholar] [CrossRef]
- Mirahmadi, A.; Valefi, K. Study of Thermal Effects on the Performance of Micro-Tubular Solid-Oxide Fuel Cells. Ionics 2011, 17, 767–783. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001; ISBN 978-0-07-011682-5. [Google Scholar]
- Wesselingh, J.A.; Krishna, R.; Krishna, R. Mass Transfer in Multicomponent Mixtures, 1st ed.; VSSD: Delft, The Netherlands, 2006; ISBN 978-90-71301-58-2. [Google Scholar]
- Lemcoff, N.O.; Tweedie, M. CFD Modeling and Analysis of a Planar Anode Supported Intermediate Temperature Solid Oxide Fuel Cell. 2014, p. 7. Available online: https://www.semanticscholar.org/paper/CFD-Modeling-and-Analysis-of-a-Planar-Anode-Solid-Tweedie-Lemcoff/f87d81d31581cc90c8caaa1994beaed0b1cf1b6e (accessed on 1 September 2022).
- Nagata, S.; Momma, A.; Kato, T.; Kasuga, Y. Numerical Analysis of Output Characteristics of Tubular SOFC with Internal Reformer. J. Power Sources 2001, 101, 60–71. [Google Scholar] [CrossRef]
- Chen, B.; Xu, H.; Tan, P.; Zhang, Y.; Xu, X.; Cai, W.; Chen, M.; Ni, M. Thermal Modelling of Ethanol-Fuelled Solid Oxide Fuel Cells. Appl. Energy 2019, 237, 476–486. [Google Scholar] [CrossRef]
- Akhtar, N.; Decent, S.P.; Kendall, K. A Parametric Analysis of a Micro-Tubular, Single-Chamber Solid Oxide Fuel Cell (MT-SC-SOFC). Int. J. Hydrogen Energy 2011, 36, 765–772. [Google Scholar] [CrossRef]
- Williford, R.E.; Chick, L.A.; Maupin, G.D.; Simner, S.P.; Stevenson, J.W. Diffusion Limitations in the Porous Anodes of SOFCs. J. Electrochem. Soc. 2003, 150, A1067. [Google Scholar] [CrossRef]
- Chen, B.; Xu, H.; Ni, M. Modelling of SOEC-FT Reactor: Pressure Effects on Methanation Process. Appl. Energy 2017, 185, 814–824. [Google Scholar] [CrossRef]
- Todd, B.; Young, J.B. Thermodynamic and Transport Properties of Gases for Use in Solid Oxide Fuel Cell Modelling. J. Power Sources 2002, 110, 186–200. [Google Scholar] [CrossRef]
- Ni, M. Computational Fluid Dynamics Modeling of a Solid Oxide Electrolyzer Cell for Hydrogen Production. Int. J. Hydrogen Energy 2009, 34, 7795–7806. [Google Scholar] [CrossRef]
- Manglik, R.M.; Bergles, A.E. Heat Transfer and Pressure Drop Correlations for Twisted-Tape Inserts in Isothermal Tubes: Part I—Laminar Flows. J. Heat Transf. 1993, 115, 881–889. [Google Scholar] [CrossRef]

| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Fuel channel diameter | D0 | 7 | mm |
| Internal diameter | Di | 1 | mm |
| Total length | Lt | 50 | mm |
| Anode thickness | ta | 2 | mm |
| Electrolyte thickness | te | 50 | µm |
| Cathode thickness | tc | 250 | µm |
| Parameters | Symbols | Values | Units | Ref. |
|---|---|---|---|---|
| Activation energy for the anode reaction | Ea | 120 | kJ mol−1 | [47] |
| Activation energy for the cathode reaction | Ec | 130 | kJ mol−1 | [47] |
| Electrode porosity | ε | 0.35 | - | [43] |
| Specific surface area of the anode | Aυ,a | 2.33 × 105 | m−1 | [48] |
| Specific surface area of the cathode | Aυ,c | 2.46 × 105 | m−1 | [48] |
| Permeability | k | 1 × 10−11 | m2 | [49] |
| Electrode tortuosity | τ | 4 | - | [50] |
| Viscosity, CO | μCO | 4.1877 × 10−5 | Pa·s | [44] |
| Viscosity, O2 | μO2 | 5.1343 × 10−5 | Pa·s | [44] |
| Viscosity, CO2 | μCO2 | 4.1904 × 10−5 | Pa·s | [44] |
| Viscosity, N2 | μN2 | 4.3529 × 10−5 | Pa·s | [44] |
| Electrical conductivity, anode | σNi | 30,316 | S·m−1 | [51] |
| Electrical conductivity, cathode | σLSM | 12,793 | S·m−1 | [51] |
| Ionic conductivity, electrolyte | σYSZ | 2.2669 | S·m−1 | [51] |
| Diffusion volume, CO | υCO | 18.0 | cm3 | [52] |
| Diffusion volume, O2 | υO2 | 16.3 | cm3 | [52] |
| Diffusion volume, CO2 | υCO2 | 26.7 | cm3 | [52] |
| Diffusion volume, N2 | υN2 | 18.5 | cm3 | [52] |
| Effective radius of the pores | rp | 0.5 | µm | [53] |
| Ambient pressure | Patm | 101.325 | kPa | [41] |
| Inlet mass flow rate at the anode | Qfuel | 6.27 × 10−6 | kg s−1 | - |
| Inlet mole fraction, CO | xCO | 0.95 | - | - |
| Inlet mole fraction, O2 | xO2 | 0.21 | - | - |
| Reference temperature | Tref | 800 | °C | - |
| Operating potential | E | 0.6 | V | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Essaghouri, A.; Zeng, Z.; Zhao, B.; Hao, C.; Qian, Y.; Zhuge, W.; Zhang, Y. Effects of Radial and Circumferential Flows on Power Density Improvements of Tubular Solid Oxide Fuel Cells. Energies 2022, 15, 7048. https://doi.org/10.3390/en15197048
Essaghouri A, Zeng Z, Zhao B, Hao C, Qian Y, Zhuge W, Zhang Y. Effects of Radial and Circumferential Flows on Power Density Improvements of Tubular Solid Oxide Fuel Cells. Energies. 2022; 15(19):7048. https://doi.org/10.3390/en15197048
Chicago/Turabian StyleEssaghouri, Abdellah, Zezhi Zeng, Bingguo Zhao, Changkun Hao, Yuping Qian, Weilin Zhuge, and Yangjun Zhang. 2022. "Effects of Radial and Circumferential Flows on Power Density Improvements of Tubular Solid Oxide Fuel Cells" Energies 15, no. 19: 7048. https://doi.org/10.3390/en15197048
APA StyleEssaghouri, A., Zeng, Z., Zhao, B., Hao, C., Qian, Y., Zhuge, W., & Zhang, Y. (2022). Effects of Radial and Circumferential Flows on Power Density Improvements of Tubular Solid Oxide Fuel Cells. Energies, 15(19), 7048. https://doi.org/10.3390/en15197048








