Challenges Facing Pressure Retarded Osmosis Commercialization: A Short Review
Abstract
:1. Introduction
2. Modeling of PRO Process
2.1. Osmotic Processes
2.2. Solution Diffusion Model
2.2.1. Neglecting the Effect of Concentration Polarization
2.2.2. Lee’s Model
2.2.3. Solution Diffusion Model Development
Achilli’s Model
Yip’s Model
Touati’s Model
Comparison between Different Models
3. PRO Membranes and Modules
3.1. Plate-and-Frame Module
3.2. Spiral Wound Module (SWM)
4. First PRO Pilot Plant
5. PRO Challenges
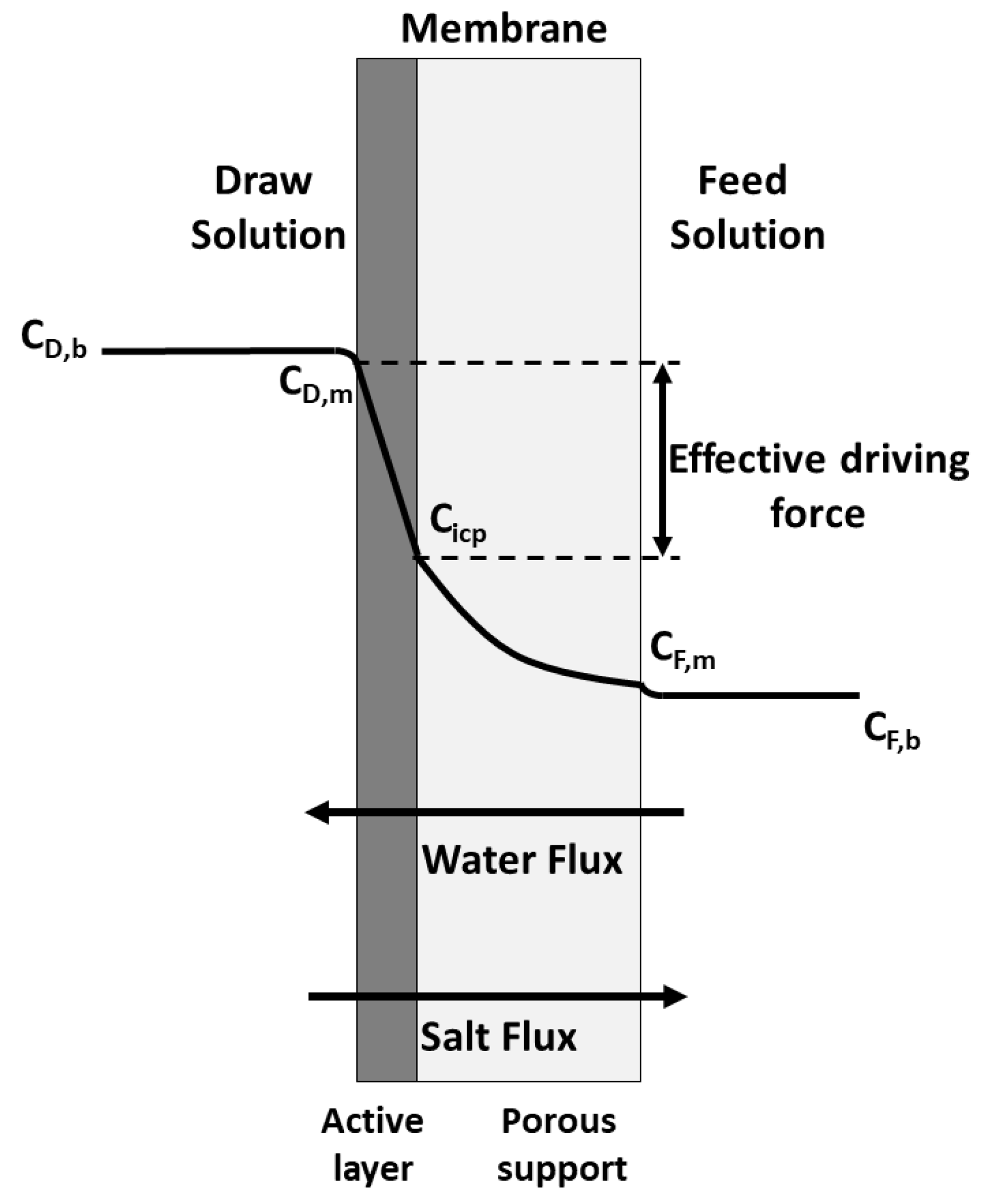
5.1. Concentration Polarization
5.2. Pressure Drop
5.3. Draw Pressure Effect on Feed Channel Hydrodynamics
5.4. Temperature Variation Effect
6. Conclusions and Recommendations
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Membrane water permeability | m/s·Pa |
| B | Membrane salt permeability | m/s |
| C | Concentration | g/kg |
| D | Diffusion coefficient | m2/s |
| J | Flow flux | m/s |
| K | Solute resistivity | s/m |
| k | Mass transfer coefficient | m/s |
| P | Hydraulic pressure | Pa |
| R | Universal gas constant | J/mol·K |
| S | Structure parameter | m |
| t | Membrane thickness | m |
| W | Power density | W/m2 |
| Greek symbols | ||
| β | van’t Hoff coefficient | - |
| ε | Porosity | - |
| π | Osmotic pressure | Pa |
| τ | Tortuosity | - |
| Subscripts | ||
| b | Bulk | |
| D | Draw solution | |
| F | Feed solution | |
| icp | Active–support layer interface | |
| m | Membrane surface | |
| s | Salt or solute | |
| w | Water | |
References
- Pattle, R.E. Production of Electric Power by mixing Fresh and Salt Water in the Hydroelectric Pile. Nature 1954, 174, 660. [Google Scholar] [CrossRef]
- Lee, C.; Chae, S.H.; Yang, E.; Kim, S.; Kim, J.H.; Kim, I.S. A comprehensive review of the feasibility of pressure retarded osmosis: Recent technological advances and industrial efforts towards commercialization. Desalination 2020, 491, 114501. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, B.; Song, S.; Fan, Y. Blue energy: Current technologies for sustainable power generation from water salinity gradient. Renew. Sustain. Energy Rev. 2014, 31, 91–100. [Google Scholar] [CrossRef]
- Chung, T.-S. Membrane Technology for Osmotic Power Generation by Pressure Retarded Osmosis, 1st ed.; CRC Press: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Hatzell, M.C.; Cusick, R.D.; Logan, B.E. Capacitive mixing power production from salinity gradient energy enhanced through exoelectrogen-generated ionic currents. Energy Environ. Sci. 2014, 7, 1159–1165. [Google Scholar] [CrossRef]
- Jones, A.; Finley, W. Recent development in salinity gradient power. In Proceedings of the Oceans 2003: Celebrating the Past—Teaming Toward the Future, San Diego, CA, USA, 22–26 September 2003; Volume 4, pp. 2284–2287. [Google Scholar] [CrossRef]
- Yip, N.Y.; Brogioli, D.; Hamelers, H.V.M.; Nijmeijer, K. Salinity Gradients for Sustainable Energy: Primer, Progress, and Prospects. Environ. Sci. Technol. 2016, 50, 12072–12094. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Das, P.P.; Chakraborty, A.; Purkait, M.K. Clean energy from salinity gradients using pressure retarded osmosis and reverse electrodialysis: A review. Sustain. Energy Technol. Assess. 2021, 49, 101687. [Google Scholar] [CrossRef]
- Yip, N.Y.; Elimelech, M. Comparison of Energy Efficiency and Power Density in Pressure Retarded Osmosis and Reverse Electrodialysis. Environ. Sci. Technol. 2014, 48, 11002–11012. [Google Scholar] [CrossRef]
- Helfer, F.; Lemckert, C.; Anissimov, Y.G. Osmotic power with Pressure Retarded Osmosis: Theory, performance and trends—A review. J. Membr. Sci. 2014, 453, 337–358. [Google Scholar] [CrossRef]
- Cath, T.Y.; Childress, A.E.; Elimelech, M. Forward osmosis: Principles, applications, and recent developments. J. Membr. Sci. 2006, 281, 70–87. [Google Scholar] [CrossRef]
- Sarp, S.; Li, Z.; Saththasivam, J. Pressure Retarded Osmosis (PRO): Past experiences, current developments, and future prospects. Desalination 2016, 389, 2–14. [Google Scholar] [CrossRef]
- Chung, T.-S.; Luo, L.; Wan, C.F.; Cui, Y.; Amy, G. What is next for forward osmosis (FO) and pressure retarded osmosis (PRO). Sep. Purif. Technol. 2015, 156, 856–860. [Google Scholar] [CrossRef] [Green Version]
- Bogler, A.; Lin, S.; Bar-Zeev, E. Biofouling of membrane distillation, forward osmosis and pressure retarded osmosis: Principles, impacts and future directions. J. Membr. Sci. 2017, 542, 378–398. [Google Scholar] [CrossRef]
- Altaee, A.; Sharif, A. Pressure retarded osmosis: Advancement in the process applications for power generation and desalination. Desalination 2015, 356, 31–46. [Google Scholar] [CrossRef]
- Abdelkader, B.A.; Sharqawy, M.H. Ecological Potential of Osmotic Power Generation by Pressure Retarded Osmosis in Ontario, Canada. In Proceedings of the 4th International Conference on Energy Harvesting, Storage, and Transfer (EHST’20), Ottawa, ON, Canada, 18–19 June 2019. [Google Scholar] [CrossRef]
- Zadeh, A.E.; Touati, K.; Mulligan, C.N.; McCutcheon, J.R.; Rahaman, S. Closed-loop pressure retarded osmosis draw solutions and their regeneration processes: A review. Renew. Sustain. Energy Rev. 2022, 159, 112191. [Google Scholar] [CrossRef]
- Yip, N.Y.; Elimelech, M. Thermodynamic and Energy Efficiency Analysis of Power Generation from Natural Salinity Gradients by Pressure Retarded Osmosis. Environ. Sci. Technol. 2012, 46, 5230–5239. [Google Scholar] [CrossRef]
- Loeb, S. Method and Apparatus for Generating Power Utilizing Pressure-Retarded-Osmosis. U.S. Patent US3906250A, 16 September 1975. [Google Scholar]
- Loeb, S. Large-scale power production by pressure-retarded osmosis, using river water and sea water passing through spiral modules. Desalination 2002, 143, 115–122. [Google Scholar] [CrossRef]
- Touati, K.; Tadeo, F.; Chae, S.H.; Kim, J.H.; Alvarez-Silva, O. Pressure Retarded Osmosis: Renewable Energy Generation and Recovery, 1st ed.; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Kim, J.; Jeong, K.; Park, M.J.; Shon, H.K.; Kim, J.H. Recent Advances in Osmotic Energy Generation via Pressure-Retarded Osmosis (PRO): A Review. Energies 2015, 8, 11821–11845. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Zubair, S.M.; Lienhard, J.H. Energy utilization from disposed brine of desalination plants. In Proceedings of the International Mechanical Engineering Congress & Exposition, Houston, TX, USA, 9–15 November 2012; pp. 1–9. [Google Scholar]
- Bajraktari, N.; Hélix-Nielsen, C.; Madsen, H.T. Pressure retarded osmosis from hypersaline sources—A review. Desalination 2017, 413, 65–85. [Google Scholar] [CrossRef]
- Kim, Y.C.; Elimelech, M. Potential of osmotic power generation by pressure retarded osmosis using seawater as feed solution: Analysis and experiments. J. Membr. Sci. 2013, 429, 330–337. [Google Scholar] [CrossRef]
- Kim, Y.C.; Elimelech, M. Adverse Impact of Feed Channel Spacers on the Performance of Pressure Retarded Osmosis. Environ. Sci. Technol. 2012, 46, 4673–4681. [Google Scholar] [CrossRef]
- She, Q.; Hou, D.; Liu, J.; Tan, K.H.; Tang, C.Y. Effect of feed spacer induced membrane deformation on the performance of pressure retarded osmosis (PRO): Implications for PRO process operation. J. Membr. Sci. 2013, 445, 170–182. [Google Scholar] [CrossRef]
- She, Q.; Jin, X.; Tang, C.Y. Osmotic power production from salinity gradient resource by pressure retarded osmosis: Effects of operating conditions and reverse solute diffusion. J. Membr. Sci. 2012, 401–402, 262–273. [Google Scholar] [CrossRef]
- Kim, Y.C.; Kim, Y.; Oh, D.; Lee, K.H. Experimental Investigation of a Spiral-Wound Pressure-Retarded Osmosis Membrane Module for Osmotic Power Generation. Environ. Sci. Technol. 2013, 47, 2966–2973. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, W.K. Progress in the Development of Osmotic Power. In Proceedings of the Quingdao International Conference on Desalination and Water Reuse, Qingdao, China, 20–23 June 2011. [Google Scholar]
- Kim, J.; Lee, J.; Kim, J.H. Overview of pressure-retarded osmosis (PRO) process and hybrid application to sea water reverse osmosis process. Desalin. Water Treat. 2012, 43, 193–200. [Google Scholar] [CrossRef]
- Fang, L.-F.; Cheng, L.; Jeon, S.; Wang, S.-Y.; Takahashi, T.; Matsuyama, H. Effect of the supporting layer structures on antifouling properties of forward osmosis membranes in AL-DS mode. J. Membr. Sci. 2018, 552, 265–273. [Google Scholar] [CrossRef]
- Yang, T.; Wan, C.F.; Xiong, J.Y.; Chung, T.-S. Pre-treatment of wastewater retentate to mitigate fouling on the pressure retarded osmosis (PRO) process. Sep. Purif. Technol. 2019, 215, 390–397. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, M.; Zhang, H.; Yang, F.; Tang, C.Y.; Dong, Y. Recent development of pressure retarded osmosis membranes for water and energy sustainability: A critical review. Water Res. 2020, 189, 116666. [Google Scholar] [CrossRef]
- Einarsson, S.J.; Wu, B. Thermal associated pressure-retarded osmosis processes for energy production: A review. Sci. Total Environ. 2020, 757, 143731. [Google Scholar] [CrossRef]
- NASA Earth Observatory. Sea Surface Temperatures. 2021. Available online: https://earthobservatory.nasa.gov/global-maps/MYD28M (accessed on 16 September 2022).
- Lee, K.; Baker, R.; Lonsdale, H. Membranes for power generation by pressure-retarded osmosis. J. Membr. Sci. 1981, 8, 141–171. [Google Scholar] [CrossRef]
- Achilli, A.; Cath, T.Y.; Childress, A.E. Power generation with pressure retarded osmosis: An experimental and theoretical investigation. J. Membr. Sci. 2009, 343, 42–52. [Google Scholar] [CrossRef]
- Elimelech, M.; Bhattacharjee, S. A novel approach for modeling concentration polarization in crossflow membrane filtration based on the equivalence of osmotic pressure model and filtration theory. J. Membr. Sci. 1998, 145, 223–241. [Google Scholar] [CrossRef]
- Gekas, V.; Hallström, B. Mass transfer in the membrane concentration polarization layer under turbulent cross flow: I. Critical literature review and adaptation of existing sherwood correlations to membrane operations. J. Membr. Sci. 1987, 30, 153–170. [Google Scholar] [CrossRef]
- Yip, N.Y.; Elimelech, M. Performance Limiting Effects in Power Generation from Salinity Gradients by Pressure Retarded Osmosis. Environ. Sci. Technol. 2011, 45, 10273–10282. [Google Scholar] [CrossRef] [PubMed]
- Touati, K.; Hänel, C.; Tadeo, F.; Schiestel, T. Effect of the feed and draw solution temperatures on PRO performance: Theoretical and experimental study. Desalination 2015, 365, 182–195. [Google Scholar] [CrossRef]
- Abdelkader, B.A.; Sharqawy, M.H. Temperature effects on salinity gradient energy harvesting and utilized membrane properties—Experimental and numerical investigation. Sustain. Energy Technol. Assess. 2021, 48, 101666. [Google Scholar] [CrossRef]
- Zhang, S.; Chung, T.-S. Minimizing the Instant and Accumulative Effects of Salt Permeability to Sustain Ultrahigh Osmotic Power Density. Environ. Sci. Technol. 2013, 47, 10085–10092. [Google Scholar] [CrossRef]
- Han, G.; Wang, P.; Chung, T.-S. Highly Robust Thin-Film Composite Pressure Retarded Osmosis (PRO) Hollow Fiber Membranes with High Power Densities for Renewable Salinity-Gradient Energy Generation. Environ. Sci. Technol. 2013, 47, 8070–8077. [Google Scholar] [CrossRef]
- Sun, S.-P.; Chung, T.-S. Outer-Selective Pressure-Retarded Osmosis Hollow Fiber Membranes from Vacuum-Assisted Interfacial Polymerization for Osmotic Power Generation. Environ. Sci. Technol. 2013, 47, 13167–13174. [Google Scholar] [CrossRef]
- Gonzales, R.R.; Park, M.J.; Bae, T.-H.; Yang, Y.; Abdel-Wahab, A.; Phuntsho, S.; Shon, H.K. Melamine-based covalent organic framework-incorporated thin film nanocomposite membrane for enhanced osmotic power generation. Desalination 2019, 459, 10–19. [Google Scholar] [CrossRef]
- Cui, Z.; Jiang, Y.; Field, R. Fundamentals of Pressure-Driven Membrane Separation Processes. Membr. Technol. 2010, 1–18. [Google Scholar] [CrossRef]
- Naguib, M.F.; Maisonneuve, J.; Laflamme, C.B.; Pillay, P. Modeling pressure-retarded osmotic power in commercial length membranes. Renew. Energy 2015, 76, 619–627. [Google Scholar] [CrossRef]
- Lee, S. Performance Comparison of Spiral-Wound and Plate-and-Frame Forward Osmosis Membrane Module. Membranes 2020, 10, 318. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.W.; Swaminathan, J.; Banchik, L.D.; Lienhard, J.H. Economic framework for net power density and levelized cost of electricity in pressure-retarded osmosis. Desalination 2018, 448, 13–20. [Google Scholar] [CrossRef] [Green Version]
- Chung, H.W.; Banchik, L.D.; Swaminathan, J. On the present and future economic viability of stand-alone pressure-retarded osmosis. Desalination 2017, 408, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Straub, A.P.; Yip, N.Y.; Elimelech, M. Raising the Bar: Increased Hydraulic Pressure Allows Unprecedented High Power Densities in Pressure-Retarded Osmosis. Environ. Sci. Technol. Lett. 2013, 1, 55–59. [Google Scholar] [CrossRef]
- Hickenbottom, K.L.; Vanneste, J.; Elimelech, M.; Cath, T.Y. Assessing the current state of commercially available membranes and spacers for energy production with pressure retarded osmosis. Desalination 2016, 389, 108–118. [Google Scholar] [CrossRef] [Green Version]
- Plata, S.L.; Childress, A.E. Limiting power density in pressure-retarded osmosis: Observation and implications. Desalination 2019, 467, 51–56. [Google Scholar] [CrossRef]
- Madsen, H.T.; Nissen, S.S.; Muff, J.; Søgaard, E.G. Pressure retarded osmosis from hypersaline solutions: Investigating commercial FO membranes at high pressures. Desalination 2017, 420, 183–190. [Google Scholar] [CrossRef]
- Maisonneuve, J.; Laflamme, C.B.; Pillay, P. Experimental investigation of pressure retarded osmosis for renewable energy conversion: Towards increased net power. Appl. Energy 2015, 164, 425–435. [Google Scholar] [CrossRef]
- Thorsen, T.; Holt, T. The potential for power production from salinity gradients by pressure retarded osmosis. J. Membr. Sci. 2009, 335, 103–110. [Google Scholar] [CrossRef]
- Manzoor, H.; Selam, M.A.; Rahman, F.B.A.; Adham, S.; Castier, M.; Abdel-Wahab, A. A tool for assessing the scalability of pressure-retarded osmosis (PRO) membranes. Renew. Energy 2019, 149, 987–999. [Google Scholar] [CrossRef]
- Abdelkader, B.; Sharqawy, M.H. Temperature Effects and Entropy Generation of Pressure Retarded Osmosis Process. Entropy 2019, 21, 1158. [Google Scholar] [CrossRef] [Green Version]
- Foreman, G.E.; Worsley, P.K. Spiral Wound Membrane Module for Direct Osmosis Separations. U.S. Patent US4033878A, 5 July 1977. [Google Scholar]
- Attarde, D.; Jain, M.; Chaudhary, K.; Gupta, S.K. Osmotically driven membrane processes by using a spiral wound module—Modeling, experimentation and numerical parameter estimation. Desalination 2015, 361, 81–94. [Google Scholar] [CrossRef]
- Achilli, A.; Prante, J.L.; Hancock, N.T.; Maxwell, E.B.; Childress, A.E. Experimental Results from RO-PRO: A Next Generation System for Low-Energy Desalination. Environ. Sci. Technol. 2014, 48, 6437–6443. [Google Scholar] [CrossRef] [PubMed]
- Kakihana, Y.; Jullok, N.; Shibuya, M.; Ikebe, Y.; Higa, M. Comparison of Pressure-Retarded Osmosis Performance between Pilot-Scale Cellulose Triacetate Hollow-Fiber and Polyamide Spiral-Wound Membrane Modules. Membranes 2021, 11, 177. [Google Scholar] [CrossRef]
- Xu, Y.; Peng, X.; Tang, C.Y.; Fu, Q.S.; Nie, S. Effect of draw solution concentration and operating conditions on forward osmosis and pressure retarded osmosis performance in a spiral wound module. J. Membr. Sci. 2010, 348, 298–309. [Google Scholar] [CrossRef]
- Matta, S.M.; Selam, M.A.; Manzoor, H.; Adham, S.; Shon, H.K.; Castier, M.; Abdel-Wahab, A. Predicting the performance of spiral-wound membranes in pressure-retarded osmosis processes. Renew. Energy 2022, 189, 66–77. [Google Scholar] [CrossRef]
- Altaee, A.; Cipolina, A. Modelling and optimization of modular system for power generation from a salinity gradient. Renew. Energy 2019, 141, 139–147. [Google Scholar] [CrossRef]
- Binger, Z.M.; Achilli, A. Forward osmosis and pressure retarded osmosis process modeling for integration with seawater reverse osmosis desalination. Desalination 2020, 491, 114583. [Google Scholar] [CrossRef]
- Hong, S.-S.; Ryoo, W.; Chun, M.-S.; Lee, S.O.; Chung, G.-Y. Numerical studies on the pressure-retarded osmosis (PRO) system with the spiral wound module for power generation. Desalin. Water Treat. 2013, 52, 6333–6341. [Google Scholar] [CrossRef]
- Skilhagen, S.E. Osmotic power—A new, renewable energy source. Desalin. Water Treat. 2010, 15, 271–278. [Google Scholar] [CrossRef]
- Gerstandt, K.; Peinemann, K.-V.; Skilhagen, S.E.; Thorsen, T.; Holt, T. Membrane processes in energy supply for an osmotic power plant. Desalination 2008, 224, 64–70. [Google Scholar] [CrossRef]
- Alsvik, I.L.; Hägg, M.-B. Pressure Retarded Osmosis and Forward Osmosis Membranes: Materials and Methods. Polymers 2013, 5, 303–327. [Google Scholar] [CrossRef] [Green Version]
- Reddy, D.; Moon, T.Y.; Reineke, C.E. Counter Current Dual-Flow Spiral Wound Dual-Pipe Membrane Separation. U.S. Patent US5034126A, 23 July 1991. [Google Scholar]
- Mcginnis, R.L. Spiral Wound Membrane Module for Forward Osmotic Use. U.S. Patent US20110036774A1, 17 February 2011. [Google Scholar]
- Uda, Y.; Kobuke, M. Spiral-Wound Forward Osmosis Membrane Element and Forward Osmosis Membrane Module. U.S. Patent US9861938B2, 9 January 2018. [Google Scholar]
- Herron, J.R. Forward Osmosis and Pressure Retarded Osmosis Spacer. WO2014107464A1, 10 July 2014. [Google Scholar]
- Sun, G.; Yang, Z. Spiral Wound Membrane Rolls and Modules. WO2018153978A1, 30 August 2018. [Google Scholar]
- Lee, S.Y.; Sim, Y.J.; Lee, J.H. Porous Outflow Pipe for Forward Osmosis or Pressure-Retarded Osmosis, and Forward Osmosis or Pressure-Retarded Osmosis Module Comprising Same. U.S. Patent US 11,020,705 B2, 1 June 2021. [Google Scholar]
- Benton, C.; Bakajin, O. Separation Systems, Elements, and Methods for Separation Utilizing Stacked Membranes and Spacers. U.S. Patent US 2020/0094193 A1, 17 August 2020. [Google Scholar]
- Revanur, R.; Roh, I.; Klare, J.E.; Noy, A.; Bakajin, O. Thin Film Composite Membranes for Forward Osmosis, and Their Preparation Methods. U.S. Patent US20120080378A1, 5 April 2012. [Google Scholar]
- Tang, C.; She, Q.; Ma, N.; Wei, J.; Sim, S.T.V.; Fane, A.G. Reinforced Membranes for Producing Osmotic Power in Pressure Retarded Osmosis. U.S. Patent US20150217238A1, 6 August 2015. [Google Scholar]
- Tawalbeh, M.; Al-Othman, A.; Abdelwahab, N.; Alami, A.H.; Olabi, A.G. Recent developments in pressure retarded osmosis for desalination and power generation. Renew. Sustain. Energy Rev. 2020, 138, 110492. [Google Scholar] [CrossRef]
- AlZainati, N.; Saleem, H.; Altaee, A.; Zaidi, S.J.; Mohsen, M.; Hawari, A.; Millar, G.J. Pressure retarded osmosis: Advancement, challenges and potential. J. Water Process Eng. 2021, 40, 101950. [Google Scholar] [CrossRef]
- Cath, T.Y.; Elimelech, M.; Mccutcheon, J.R.; Mcginnis, R.L.; Achilli, A. Standard methodology for evaluating membrane performance in osmotically driven membrane processes. Desalination 2013, 312, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Zimmerer, C.; Kottke, V. Effects of spacer geometry on pressure drop, mass transfer, mixing behavior, and residence time distribution. Desalination 1996, 104, 129–134. [Google Scholar] [CrossRef]
- Schock, G.; Miquel, A. Mass transfer and pressure loss in spiral wound modules. Desalination 1987, 64, 339–352. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Fane, A.G. Net-Type Spacers: Effect of Configuration on Fluid Flow Path and Ultrafiltration Flux. Ind. Eng. Chem. Res. 1994, 33, 1845–1851. [Google Scholar] [CrossRef]
- Haidari, A.; Heijman, S.; van der Meer, W. Visualization of hydraulic conditions inside the feed channel of Reverse Osmosis: A practical comparison of velocity between empty and spacer-filled channel. Water Res. 2016, 106, 232–241. [Google Scholar] [CrossRef] [Green Version]
- Kavianipour, O.; Ingram, G.D.; Vuthaluru, H.B. Investigation into the effectiveness of feed spacer configurations for reverse osmosis membrane modules using Computational Fluid Dynamics. J. Membr. Sci. 2017, 526, 156–171. [Google Scholar] [CrossRef] [Green Version]
- Abdelkader, B.A.; Sharqawy, M.H. Pressure drop across membrane spacer-filled channels using porous media characteristics and computational fluid dynamics simulation. Desalin. Water Treat. 2022, 247, 28–39. [Google Scholar] [CrossRef]
- Ruiz-García, A.; De la Nuez, I. Feed Spacer Geometries and Permeability Coefficients. Effect on the Performance in BWRO Spriral-Wound Membrane Modules. Water 2019, 11, 152. [Google Scholar] [CrossRef] [Green Version]
- Haidari, A.H.; Heijman, S.G.J.; van der Meer, W.G.J. Optimal design of spacers in reverse osmosis. Sep. Purif. Technol. 2018, 192, 441–456. [Google Scholar] [CrossRef]
- Da Costa, A.; Fane, A.; Fell, C.; Franken, A. Optimal channel spacer design for ultrafiltration. J. Membr. Sci. 1991, 62, 275–291. [Google Scholar] [CrossRef]
- Thomas, D.G. Forced Convection Mass Transfer in Hyperfiltration at High Fluxes. Ind. Eng. Chem. Fundam. 1973, 12, 396–405. [Google Scholar] [CrossRef]
- Schwinge, J.; Wiley, D.E.; Fletcher, D.F. Simulation of the Flow around Spacer Filaments between Channel Walls. 2. Mass-Transfer Enhancement. Ind. Eng. Chem. Res. 2002, 41, 4879–4888. [Google Scholar] [CrossRef]
- Kerdi, S.; Qamar, A.; Vrouwenvelder, J.S.; Ghaffour, N. Fouling resilient perforated feed spacers for membrane filtration. Water Res. 2018, 140, 211–219. [Google Scholar] [CrossRef]
- Schwinge, J.; Neal, P.R.; Wiley, D.E.; Fletcher, D.F.; Fane, A.G. Spiral wound modules and spacers: Review and analysis. J. Membr. Sci. 2004, 242, 129–153. [Google Scholar] [CrossRef]
- Fárková, J. The pressure drop in membrane module with spacers. J. Membr. Sci. 1991, 64, 103–111. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Fane, A.G.; Wiley, D.E. Spacer characterization and pressure drop modeling in spacer-filled channels.pdf. J. Membr. Sci. 1994, 87, 79–98. [Google Scholar] [CrossRef]
- Sagiv, A.; Xu, W.; Christofides, P.D.; Cohen, Y.; Semiat, R. Evaluation of osmotic energy extraction via FEM modeling and exploration of PRO operational parameter space. Desalination 2016, 401, 120–133. [Google Scholar] [CrossRef]
- Maisonneuve, J.; Pillay, P.; Laflamme, C.B. Pressure-retarded osmotic power system model considering non-ideal effects. Renew. Energy 2015, 75, 416–424. [Google Scholar] [CrossRef]
- Roy, Y.; Sharqawy, M.H.; Lienhard, J.H. Modeling of flat-sheet and spiral-wound nanofiltration configurations and its application in seawater nanofiltration. J. Membr. Sci. 2015, 493, 360–372. [Google Scholar] [CrossRef]
- Koutsou, C.; Yiantsios, S.; Karabelas, A. A numerical and experimental study of mass transfer in spacer-filled channels: Effects of spacer geometrical characteristics and Schmidt number. J. Membr. Sci. 2009, 326, 234–251. [Google Scholar] [CrossRef]
- Geraldes, V. Flow management in nanofiltration spiral wound modules with ladder-type spacers. J. Membr. Sci. 2002, 203, 87–102. [Google Scholar] [CrossRef]
- Gu, B.; Adjiman, C.S.; Xu, X.Y. The effect of feed spacer geometry on membrane performance and concentration polarisation based on 3D CFD simulations. J. Membr. Sci. 2017, 527, 78–91. [Google Scholar] [CrossRef]
- Santos, J.; Geraldes, V.; Velizarov, S.; Crespo, J. Investigation of flow patterns and mass transfer in membrane module channels filled with flow-aligned spacers using computational fluid dynamics (CFD). J. Membr. Sci. 2007, 305, 103–117. [Google Scholar] [CrossRef]
- Fimbres-Weihs, G.; Wiley, D. Review of 3D CFD modeling of flow and mass transfer in narrow spacer-filled channels in membrane modules. Chem. Eng. Process. Process Intensif. 2010, 49, 759–781. [Google Scholar] [CrossRef]
- Koutsou, C.P.; Karabelas, A.J. Shear stresses and mass transfer at the base of a stirred filtration cell and corresponding conditions in narrow channels with spacers. J. Membr. Sci. 2012, 399–400, 60–72. [Google Scholar] [CrossRef]
- Shakaib, M.; Hasani, S.; Mahmood, M. CFD modeling for flow and mass transfer in spacer-obstructed membrane feed channels. J. Membr. Sci. 2009, 326, 270–284. [Google Scholar] [CrossRef]
- Toh, K.; Liang, Y.; Lau, W.; Fletcher, D. CFD study of the effect of perforated spacer on pressure loss and mass transfer in spacer-filled membrane channels. Chem. Eng. Sci. 2020, 222, 115704. [Google Scholar] [CrossRef]
- Fimbres-Weihs, G.; Wiley, D. Numerical study of two-dimensional multi-layer spacer designs for minimum drag and maximum mass transfer. J. Membr. Sci. 2008, 325, 809–822. [Google Scholar] [CrossRef]
- Landslide damage to the Boar River water supply pipeline, Bromley Hill, Jamaica: Case study of a landslide caused by Hurricane Gilbert (1988): Ahmad, R.; Earle, A.H.; Hugues, P.; Maharaj, R.; Robinson, E. Int Assoc Engng Geol BullN47, April 1993, P59–70. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1994, 31, A46. [CrossRef]
- Wardeh, S.; Morvan, H. CFD simulations of flow and concentration polarization in spacer-filled channels for application to water desalination. Chem. Eng. Res. Des. 2008, 86, 1107–1116. [Google Scholar] [CrossRef]
- Schwinge, J.; Wiley, D.; Fletcher, D. A CFD study of unsteady flow in narrow spacer-filled channels for spiral-wound membrane modules. Desalination 2002, 146, 195–201. [Google Scholar] [CrossRef]
- Ahmad, A.; Lau, K.K.; Abu Bakar, M. Impact of different spacer filament geometries on concentration polarization control in narrow membrane channel. J. Membr. Sci. 2005, 262, 138–152. [Google Scholar] [CrossRef]
- Ranade, V.V.; Kumar, A. Fluid dynamics of spacer filled rectangular and curvilinear channels. J. Membr. Sci. 2006, 271, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Saeed, A.; Vuthaluru, R.; Yang, Y.; Vuthaluru, H.B. Effect of feed spacer arrangement on flow dynamics through spacer filled membranes. Desalination 2012, 285, 163–169. [Google Scholar] [CrossRef]
- Picioreanu, C.; Vrouwenvelder, J.; van Loosdrecht, M. Three-dimensional modeling of biofouling and fluid dynamics in feed spacer channels of membrane devices. J. Membr. Sci. 2009, 345, 340–354. [Google Scholar] [CrossRef]
- Li, Y.-L.; Tung, K.-L. CFD simulation of fluid flow through spacer-filled membrane module: Selecting suitable cell types for periodic boundary conditions. Desalination 2008, 233, 351–358. [Google Scholar] [CrossRef]
- Li, Y.-L.; Tung, K.-L.; Lu, M.-Y.; Huang, S.-H. Mitigating the curvature effect of the spacer-filled channel in a spiral-wound membrane module. J. Membr. Sci. 2009, 329, 106–118. [Google Scholar] [CrossRef]
- Vrouwenvelder, J.S.; Picioreanu, C.; Kruithof, J.C.; Van Loosdrecht, M.C.M. Biofouling in spiral wound membrane systems: Three-dimensional CFD model based evaluation of experimental data. J. Membr. Sci. 2010, 346, 71–85. [Google Scholar] [CrossRef]
- Karabelas, A.J.; Koutsou, C.P.; Sioutopoulos, D.C. Comprehensive performance assessment of spacers in spiral-wound membrane modules accounting for compressibility effects. J. Membr. Sci. 2018, 549, 602–615. [Google Scholar] [CrossRef]
- Jeon, J.; Jung, J.; Lee, S.; Choi, J.Y.; Kim, S. A simple modeling approach for a forward osmosis system with a spiral wound module. Desalination 2018, 433, 120–131. [Google Scholar] [CrossRef]
- Touati, K.; Tadeo, F.; Hänel, C.; Schiestel, T. Effect of the operating temperature on hydrodynamics and membrane parameters in pressure retarded osmosis. Desalin. Water Treat. 2015, 57, 10477–10489. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, Z.; Li, J.; Tang, Q.; Hu, Y. Investigation of the reduced specific energy consumption of the RO-PRO hybrid system based on temperature-enhanced pressure retarded osmosis. J. Membr. Sci. 2019, 581, 439–452. [Google Scholar] [CrossRef]
- Sivertsen, E.; Holt, T.; Thelin, W.R. Concentration and Temperature Effects on Water and Salt Permeabilities in Osmosis and Implications in Pressure-Retarded Osmosis. Membranes 2018, 8, 39. [Google Scholar] [CrossRef] [Green Version]
- Touati, K.; Tadeo, F.; Schiestel, T. Impact of Temperature on Power Recovery in Osmotic Power Production by Pressure Retarded Osmosis. Energy Procedia 2014, 50, 960–969. [Google Scholar] [CrossRef]








| Model | Model Expression | Assumptions |
|---|---|---|
| Lee et al. [37] | ||
| Achilli et al. [38] | ||
| Yip et al. [41] | ||
| Touati et al. [42] |
| Membrane Material | Membrane Area (m2) × 10−4 | Membrane Properties | Operating Conditions | Power Density (W/m2) | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|
| A (L/m2 hr bar) | B (L/m2 hr) | S (µm) | Concentration (Feed/Draw) | Hydraulic Pressure Difference (bar) | |||||
| Experimental investigations | CTA | 18.8 | 0.67 | 0.40 | 682 | DI/0.6 M NaCl | 9.7 | 2.7 | [38] |
| CTA | 18.8 | 0.67 | 0.40 | 682 | DI/1.026 M NaCl | 9.7 | 5.1 | [38] | |
| CTA | 140.0 | 0.37 | 0.28 | 590 | 0.01 M/1 M NaCl | 15.0 | 3.9 | [28] | |
| CTA | 140.0 | 0.44 | 0.07 | 1380 | 0.01 M/1 M NaCl | 14.0 | 3.0 | [28] | |
| CTA | 140.0 | 0.75 | 0.01 | 480 | 0.01 M/1 M NaCl | 12.0 | 4.5 | [28] | |
| CTA | 20.0 | 1.23 | 2.62 | 409 | 0.5 M/1 M NaCl | 12.5 | 0.9 | [25] | |
| CTA | 20.0 | 1.23 | 2.62 | 504 | 0.5 M/1.5 M NaCl | 12.5 | 2.8 | [25] | |
| CTA | 20.0 | 1.23 | 2.62 | 505 | 0.5 M/2 M NaCl | 12.5 | 4.7 | [25] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/0.6 M NaCl | 13.8 | 7.5 | [53] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/1 M NaCl | 20.7 | 14.1 | [53] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/2 M NaCl | 41.4 | 39.4 | [53] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/3 M NaCl | 48.3 | 59.7 | [53] | |
| TFC | 139.0 | 1.50 | 3.74 | 159 | DI/1 M NaCl | 10.5 | 7.0 | [54] | |
| TFC | 139.0 | 1.94 | 1.99 | 274 | DI/1 M NaCl | 10.5 | 6.8 | [54] | |
| TFC | 139.0 | 1.63 | 1.42 | 295 | DI/1 M NaCl | 21.0 | 8.3 | [54] | |
| TFC | 139.0 | 1.63 | 1.42 | 295 | DI/2 M NaCl | 35.0 | 11.5 | [54] | |
| TFC | 139.0 | 1.63 | 1.42 | 295 | DI/3 M NaCl | 41.0 | 15.5 | [54] | |
| CTA | 139.0 | 0.51 | 2.19 | 600 | DI/1 M NaCl | 19.0 | 3.8 | [54] | |
| TFC | 120.0 | 2.78 | 1.36 | 513 | DI/1.2 M NaCl | 21.0 | 15.3 | [55] | |
| TFC | 120.0 | 2.29 | 0.30 | 198 | DI/1.2 M NaCl | 21.0 | 12.5 | [55] | |
| CTA | 120.0 | 0.77 | 0.29 | 408 | DI/1.2 M NaCl | 21.0 | 9.8 | [55] | |
| CTA | 120.0 | 0.77 | 0.29 | 408 | DI/1.2 M NaCl | 12.0 | 6.9 | [55] | |
| TFC | 120.0 | 3.35 | 1.18 | 398 | DI/1.2 M NaCl | 12.0 | 7.9 | [55] | |
| CTA | 33.7 | 0.42 | 0.29 | 1028 | DI/3 M NaCl | 40.0 | 10.5 | [56] | |
| CTA | 33.7 | 0.76 | 0.44 | 655 | DI/3 M NaCl | 40.0 | 30.0 | [56] | |
| CTA | 33.7 | 0.69 | 0.34 | 707 | DI/3 M NaCl | 60.0 | 32.0 | [56] | |
| TFC | 33.7 | 1.25 | 0.19 | 471 | DI/3 M NaCl | 35.0 | 27.0 | [56] | |
| TFC | 33.7 | - | - | - | DI/3 M NaCl | 10.0 | 5.0 | [56] | |
| TFC | 87.5 | 4.21 | 1.43 | 267 | DI/0.51 M NaCl | 6.0 | 5.0 | [57] | |
| CTA | 10.0 | 0.13 | 0.02 | 800 | 0.008 M/0.6 M NaCl | 13.0 | 2.3 | [42] | |
| CTA | 10.0 | 0.38 | 0.09 | 1550 | 0.008 M/0.6 M NaCl | 13.0 | 3.0 | [42] | |
| CTA | 10.0 | 0.38 | 0.09 | 1550 | 0.008 M/1.026 M NaCl | 24.0 | 5.0 | [42] | |
| CA | 0.5 | 0.72 | 0.22 | 2500 | DI/0.4 M NaCl | 7.5 | 1.6 | [58] | |
| TFC | 0.5 | 2.56 | 0.40 | 670 | DI/0.48 M NaCl | 10.5 | 2.7 | [58] | |
| CTA | 20.0 | 1.23 | 2.62 | 689 | DI/0.5 M NaCl | 12.5 | 1.0 | [26] | |
| CTA | 20.0 | 1.23 | 2.62 | 689 | DI/1 M NaCl | 12.5 | 3.8 | [26] | |
| CTA | 20.0 | 1.23 | 2.62 | 689 | DI/2 M NaCl | 12.5 | 7.9 | [26] | |
| CTA | 140.0 | 0.8 | 0.41 | 652 | Tap water/0.17 M NaCl | 3.6 | 0.3 | [43] | |
| CTA | 140.0 | 0.8 | 0.41 | 652 | Tap water/0.34 M NaCl | 7.1 | 1.2 | [43] | |
| CTA | 140.0 | 0.8 | 0.41 | 652 | Tap water/0.51 M NaCl | 10.7 | 2.6 | [43] | |
| Numerical investigations | TFC | 139.0 | 1.63 | 1.42 | 295 | DI/1 M NaCl | 24.0 | 9.0 | [54] |
| TFC | 139.0 | 1.63 | 1.42 | 295 | DI/2 M NaCl | 52.5 | 26.0 | [54] | |
| TFC | 139.0 | 1.63 | 1.42 | 295 | DI/3 M NaCl | 87.0 | 44.0 | [54] | |
| CTA | 10.0 | 0.13 | 0.02 | 800 | 0.008 M/0.6 M NaCl | 13.0 | 2.5 | [42] | |
| CTA | 10.0 | 0.38 | 0.09 | 1550 | 0.008 M/0.6 M NaCl | 13.0 | 3.5 | [42] | |
| CTA | 10.0 | 0.38 | 0.09 | 1550 | 0.008 M/1.026 M NaCl | 24.0 | 5.5 | [42] | |
| CTA | 18.8 | 0.67 | 0.40 | 682 | DI/0.6 M NaCl | 13.0 | 2.9 | [38] | |
| CTA | 18.8 | 0.67 | 0.40 | 646 | DI/1.026 M NaCl | 23.0 | 8.0 | [38] | |
| CTA | 20.0 | 1.23 | 2.62 | 409 | 0.5 M/1 M NaCl | 10.0 | 1.0 | [25] | |
| CTA | 20.0 | 1.23 | 2.62 | 504 | 0.5 M/1.5 M NaCl | 22.0 | 3.2 | [25] | |
| CTA | 20.0 | 1.23 | 2.62 | 505 | 0.5 M/2 M NaCl | 34.0 | 6.8 | [25] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/0.6 M NaCl | 13.8 | 6.9 | [53] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/1 M NaCl | 24.0 | 15.0 | [53] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/2 M NaCl | 55.0 | 41.0 | [53] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/3 M NaCl | 95.0 | 75.0 | [53] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/1 M NaCl | 23.0 | 14.2 | [59] | |
| TFC | 20.0 | 2.49 | 0.39 | 564 | DI/3 M NaCl | 51.0 | 39.5 | [59] | |
| TFC | 20.0 | 1.23 | 2.62 | 689 | DI/1 M NaCl | 18.2 | 4.8 | [59] | |
| TFC | 20.0 | 1.23 | 2.62 | 689 | DI/0.5 M NaCl | 8.0 | 1.6 | [59] | |
| CTA | 10.0 | 0.38 | 0.09 | 1550 | 0.008 M/0.6 M NaCl | 12.0 | 2.5 | [60] | |
| CTA | 10.0 | 0.38 | 0.09 | 1550 | 0.008 M/1.2 M NaCl | 30.0 | 12.0 | [60] | |
| Membrane Material | Membrane Area (m2) | Membrane Properties | Operating Conditions | Power Density (W/m2) | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|
| A (L/m2 hr bar) | B (L/m2 hr) | S (µm) | Concentration (Feed/Draw) | Hydraulic Pressure Difference (bar) | |||||
| Experimental investigations | TFC | 29.0 | 0.72 | 0.28 | 645 | 0.001 M/0.6 M NaCl | 7.7 | 0.96 | [29] |
| TFC | 29.0 | 0.72 | 0.28 | 645 | 0.001 M/1.2 M NaCl | 15.6 | 2.10 | [29] | |
| TFC | 29.0 | 0.72 | 0.28 | 645 | 0.001 M/0.52 M NaCl | 9.8 | 0.82 | [29] | |
| TFC | 29.0 | 0.72 | 0.28 | 645 | 0.002 M/0.6 M NaCl | 9.8 | 1.00 | [29] | |
| TFC | 29.0 | 0.72 | 0.28 | 645 | 0.01 M/0.6 M NaCl | 9.8 | 0.91 | [29] | |
| TFC | 29.0 | 0.72 | 0.28 | 645 | 0.05 M/0.6 M NaCl | 9.8 | 0.49 | [29] | |
| TFC | 29.0 | 0.72 | 0.28 | 645 | 0.08 M/0.6 M NaCl | 9.8 | 0.08 | [29] | |
| CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/0.07 M NaCl | 1.0 | 0.02 | [62] | |
| CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/0.1 M NaCl | 2.3 | 0.07 | [62] | |
| CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/0.15 M NaCl | 3.4 | 0.15 | [62] | |
| CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/0.51 M NaCl | 4.0 | 0.56 | [62] | |
| CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/1.026 M NaCl | 4.0 | 1.10 | [62] | |
| CTA | 0.9 | - | - | - | DI/0.5 M NaCl | 4.5 | 0.40 | [65] | |
| TFC | 15.3 | - | - | - | Tap water/0.6 M NaCl | 12.0 | 1.40 | [64] | |
| TFC | 15.3 | - | - | - | Tap water/0.8 M NaCl | 12.0 | 1.64 | [64] | |
| TFC | 15.3 | - | - | - | Tap water/1.2 M NaCl | 16.0 | 2.33 | [64] | |
| TFC | 4.2 | 5.10 | 0.09 | 310 | DI/0.48 M NaCl | 4.5 | 1.12 * | [63] | |
| TFC | 4.2 | 5.10 | 0.09 | 310 | DI/0.48 M NaCl | 9.5 | 3.51 * | [63] | |
| Numerical investigations | CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/0.07 M NaCl | 1.5 | 0.03 | [62] |
| CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/0.1 M NaCl | 2.3 | 0.07 | [62] | |
| CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/0.15 M NaCl | 3.4 | 0.15 | [62] | |
| CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/0.51 M NaCl | 10.2 | 0.95 | [62] | |
| CTA | 0.5 | 0.63 | 0.42 | 496 | 0.008 M/1.026 M NaCl | 21.0 | 3.25 | [62] | |
| TFC | 4.2 | 5.10 | 0.09 | 310 | DI/0.48 M NaCl | 8.0 | 5.10 | [68] | |
| TFC | 4.2 | 5.10 | 0.09 | 310 | DI/0.48 M NaCl | 10.5 | 9.50 | [68] | |
| TFC | 4.2 | 5.10 | 0.09 | 310 | DI/0.48 M NaCl | 9.5 | 9.00 | [68] | |
| TFC | 4.2 | 5.10 | 0.09 | 310 | DI/0.48 M NaCl | 11.0 | 11.00 | [68] | |
| TFC | 4.2 | 5.10 | 0.09 | 310 | DI/0.48 M NaCl | 10.0 | 10.80 | [68] | |
| CTA | 30.0 | 0.40 | 0.30 | 702 | 0.6 M/2.74 M NaCl | 50.0 | 9.90 | [66] | |
| CTA | 30.0 | 0.40 | 0.30 | 702 | DI/0.5 M NaCl | 9.0 | 1.75 | [66] | |
| CTA | 8.4 | 3.42 | 0.31 | 350 | DI/0.6 M NaCl | 13.0 | 16.00 | [69] | |
| N/A | 24.0 | 1.23 | 2.60 | 167 | 0.02 M/1.2 M NaCl | 27.5 | 12.10 | [67] | |
| N/A | 24.0 | 1.23 | 2.60 | 167 | 0.02 M/0.6 M NaCl | 13.8 | 3.70 | [67] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelkader, B.A.; Sharqawy, M.H. Challenges Facing Pressure Retarded Osmosis Commercialization: A Short Review. Energies 2022, 15, 7325. https://doi.org/10.3390/en15197325
Abdelkader BA, Sharqawy MH. Challenges Facing Pressure Retarded Osmosis Commercialization: A Short Review. Energies. 2022; 15(19):7325. https://doi.org/10.3390/en15197325
Chicago/Turabian StyleAbdelkader, Bassel A., and Mostafa H. Sharqawy. 2022. "Challenges Facing Pressure Retarded Osmosis Commercialization: A Short Review" Energies 15, no. 19: 7325. https://doi.org/10.3390/en15197325
APA StyleAbdelkader, B. A., & Sharqawy, M. H. (2022). Challenges Facing Pressure Retarded Osmosis Commercialization: A Short Review. Energies, 15(19), 7325. https://doi.org/10.3390/en15197325






