Solar Thermochemical CO2 Splitting Integrated with Supercritical CO2 Cycle for Efficient Fuel and Power Generation
Abstract
:1. Introduction
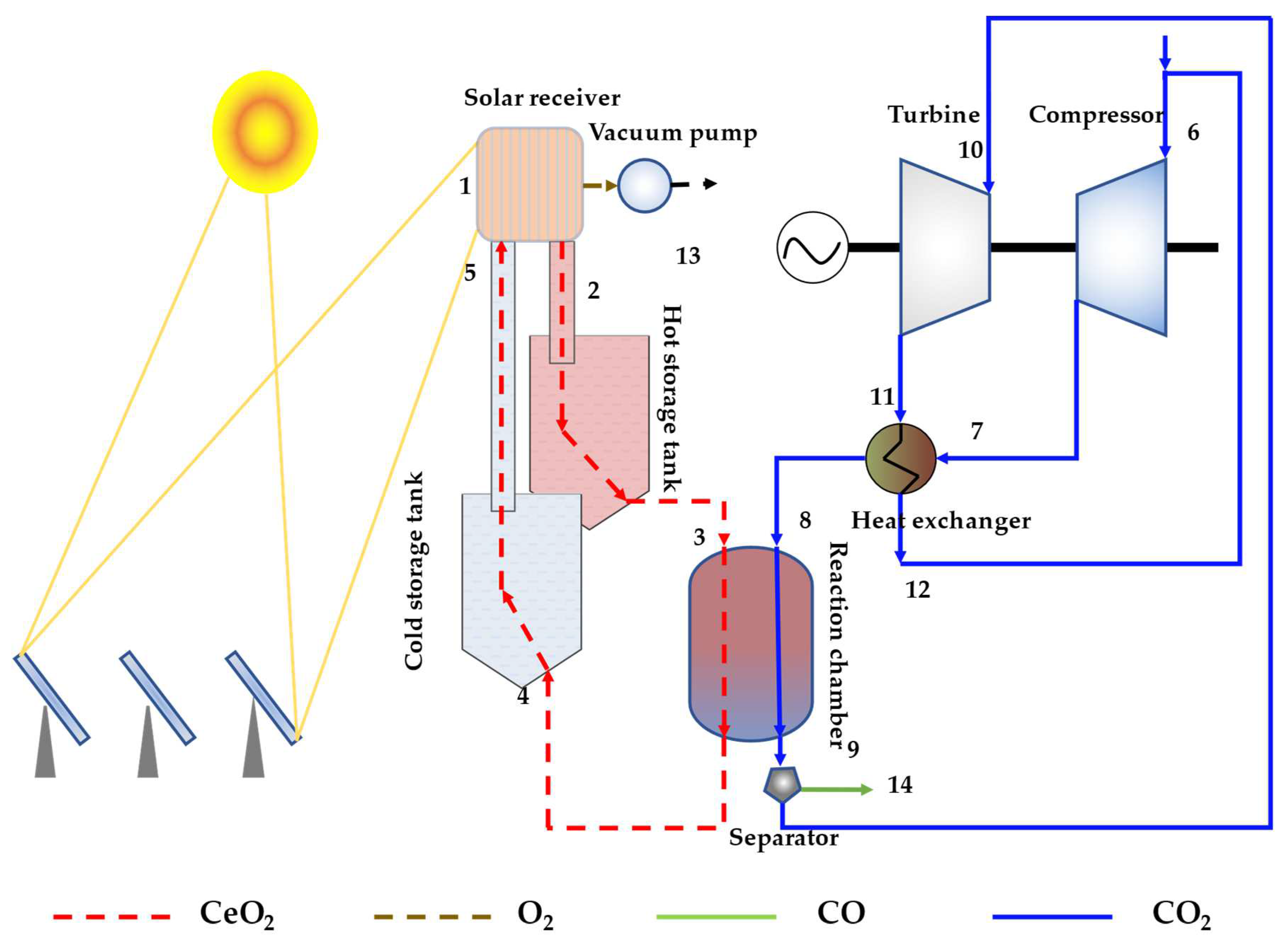
2. Thermodynamic Model
2.1. Thermodynamic Efficiency
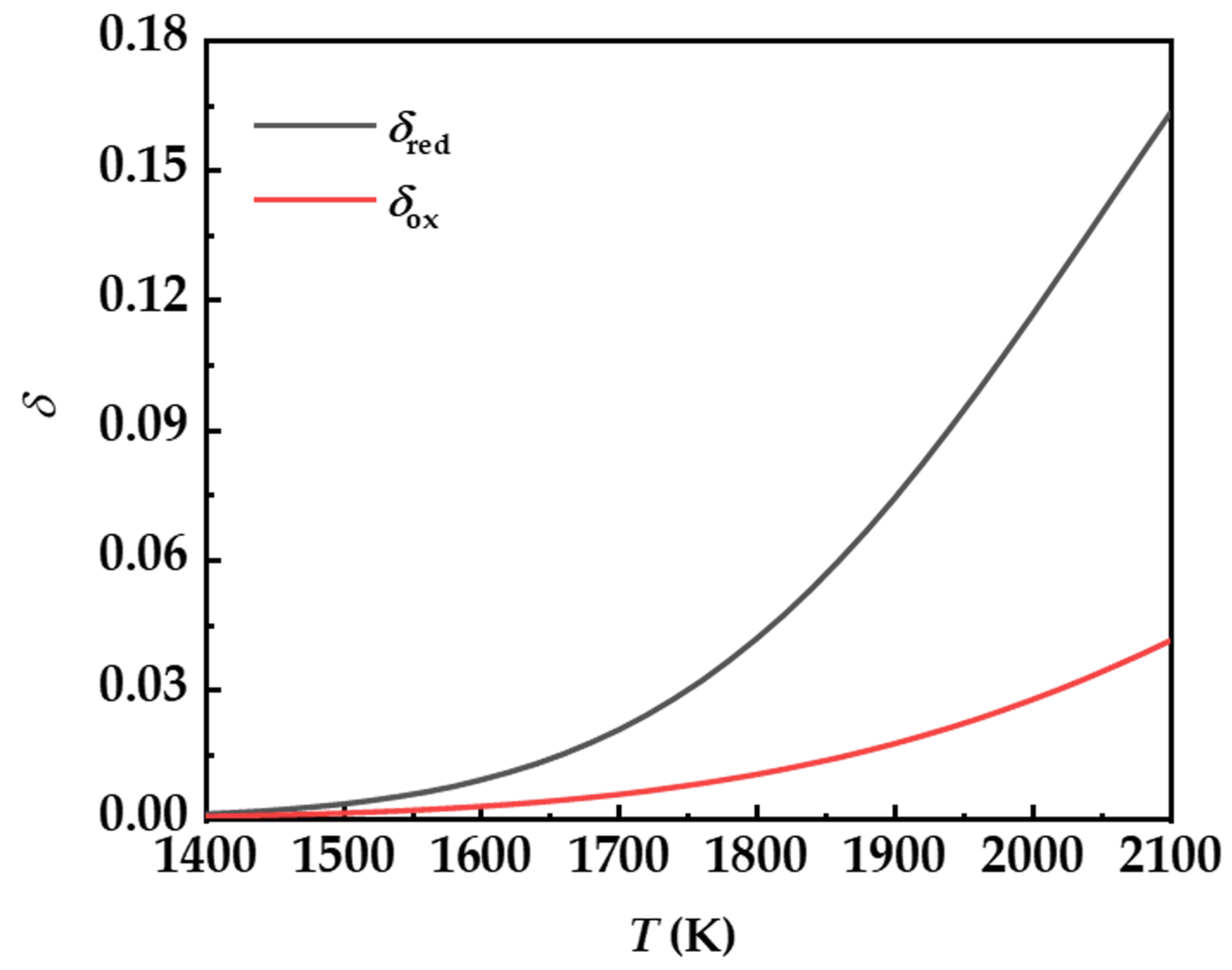
2.2. Ceria’s Reduction and Heating
2.3. Storage Tank and Reaction Chamber
2.4. Auxiliary Energy
2.5. System Efficiency
3. Results
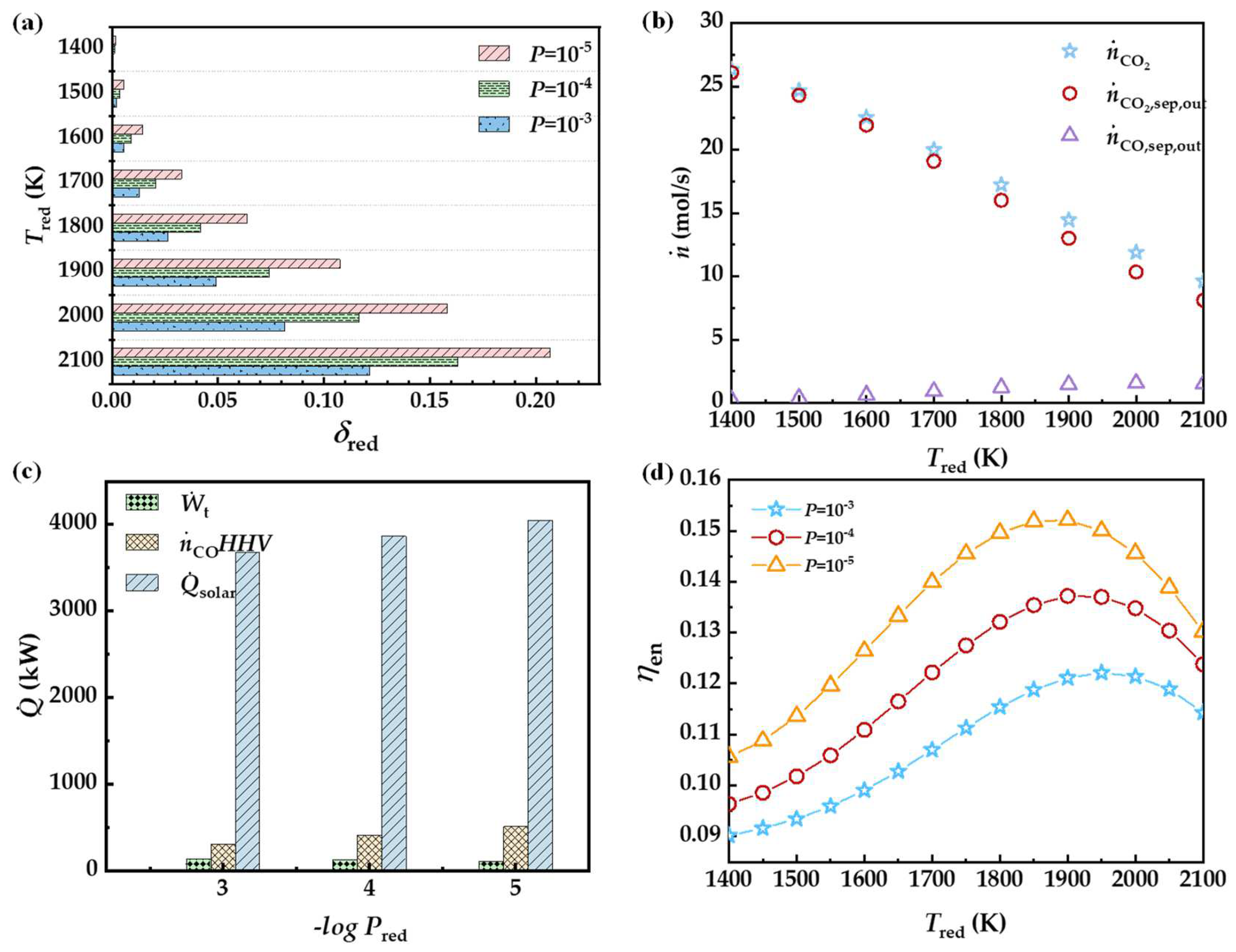
3.1. Oxygen Partial Pressure during Reduction
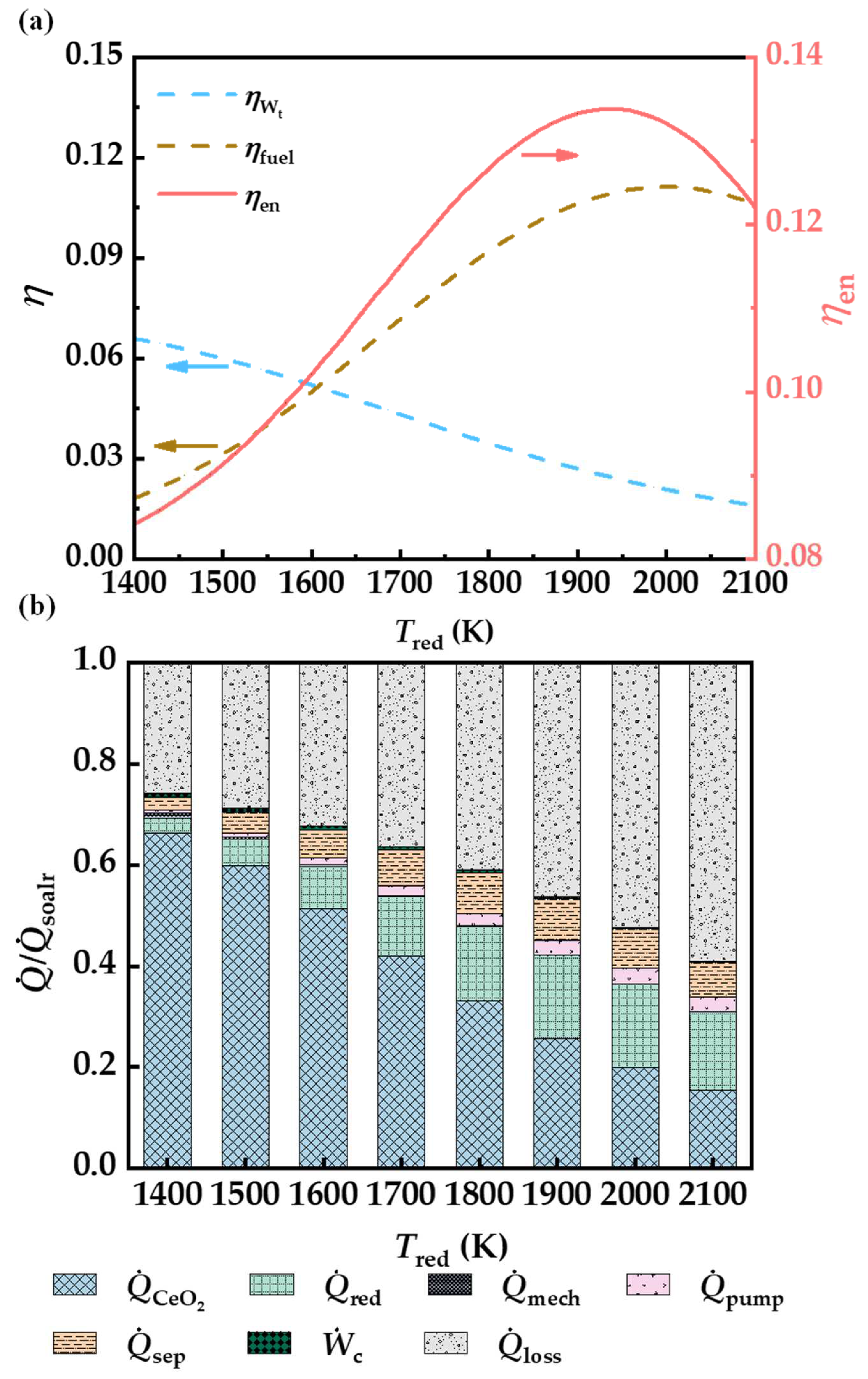
3.2. Reduction Temperature
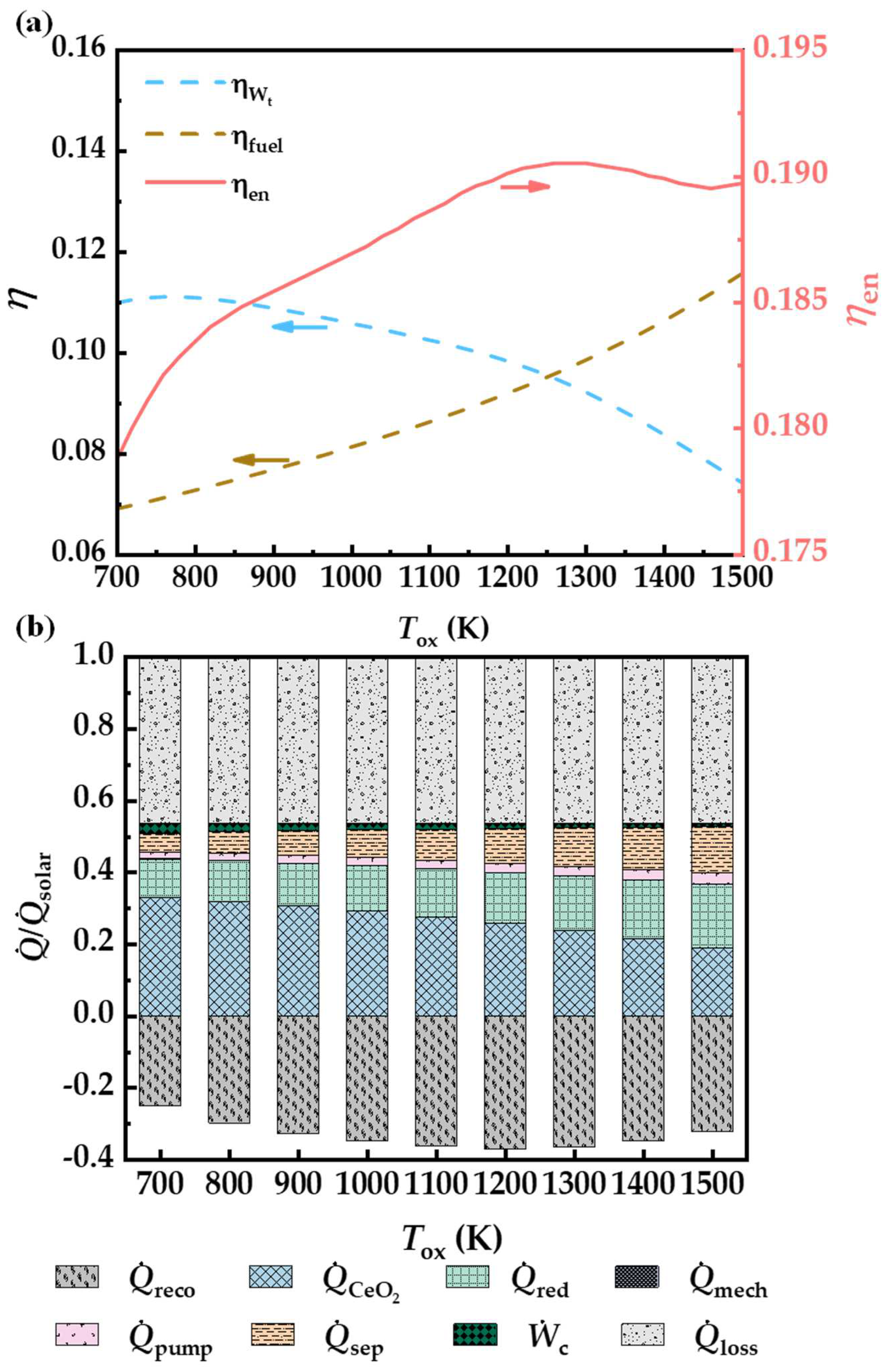
3.3. Oxidation Temperature
3.4. Heat Recovery
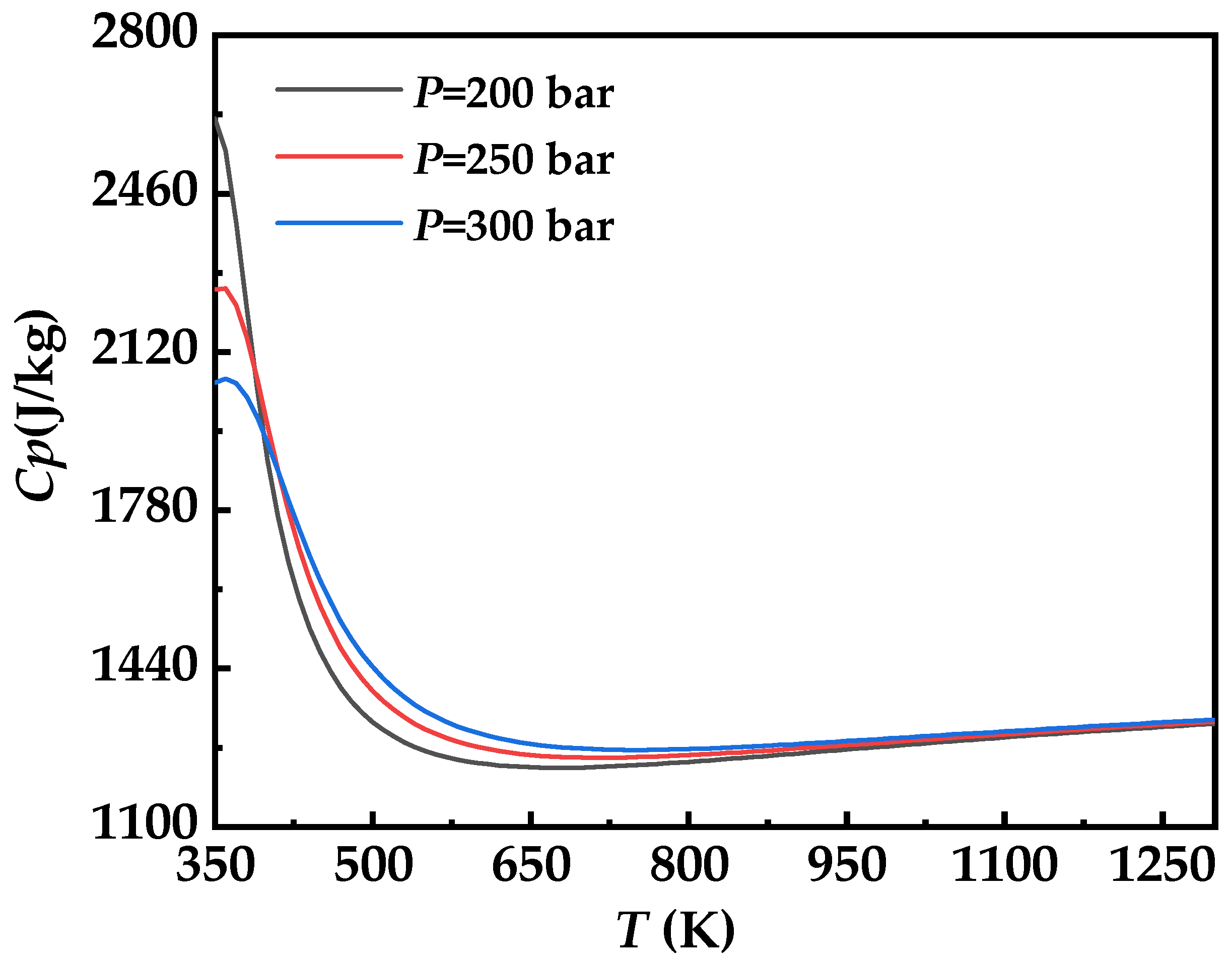
3.5. Cycle High Pressure
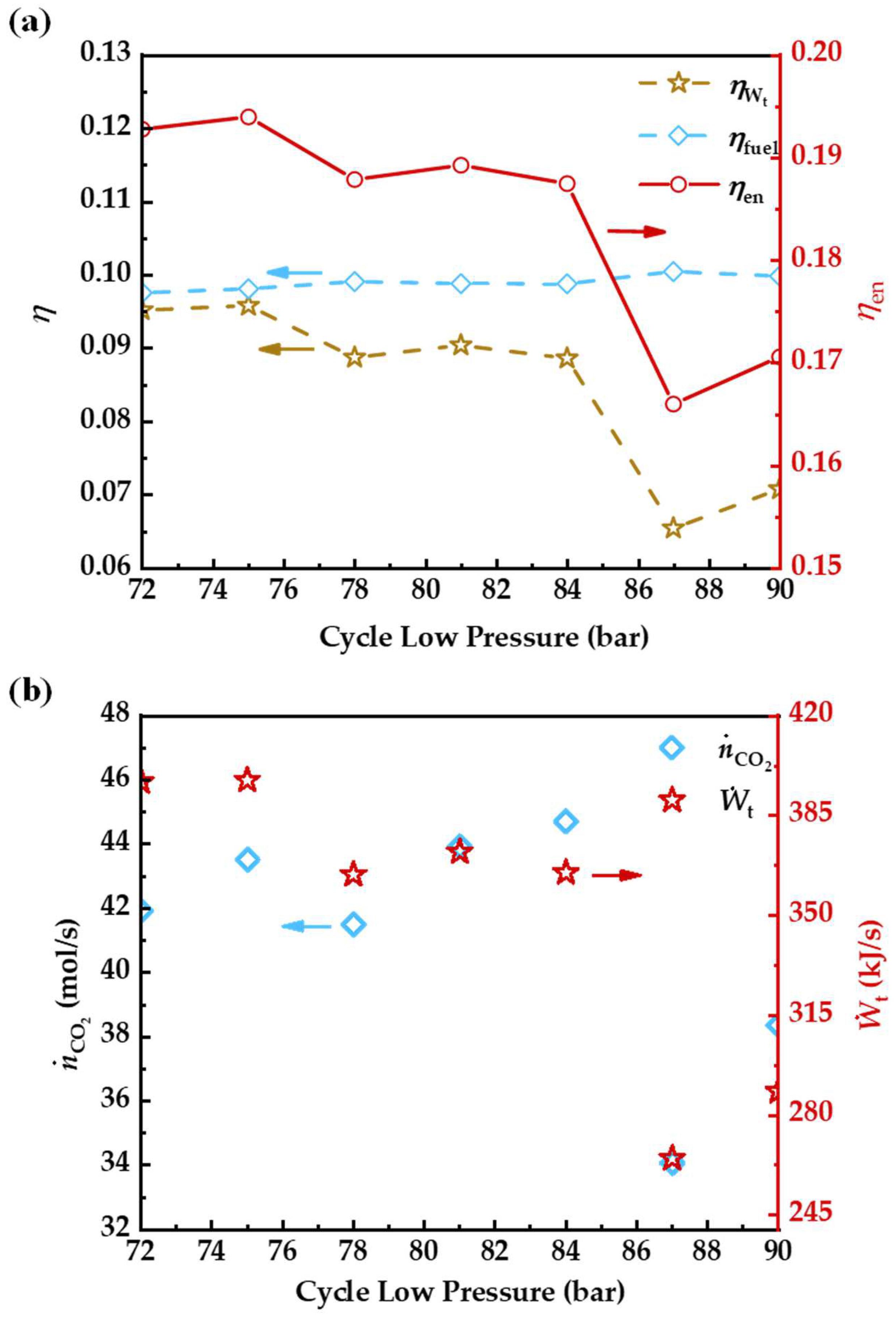
3.6. Cycle Low Pressure
3.7. Economic Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | area (m−2) |
| C | solar concentration |
| Cp | specific heat capacity (J mol−1 K−1) |
| Fr | view factor |
| h | specific enthalpy (kJ/mol) or heat |
| transfer coefficient (W m−2 K−1) | |
| H | height (m) |
| HHV | high heating value (kJ/mol) |
| I | solar radiation intensity (kW/m2) |
| mole flow rate (mol/s) | |
| P | pressure (bar) |
| heat rate (kW) | |
| R | universal gas constant |
| T | temperature (K) |
| work rate (kW) | |
| Greek | |
| α | fraction completed for oxidation reaction |
| δ | non-stoichiometric coefficient |
| Δδ | non-stoichiometric coefficient difference |
| ΔH | change in enthalpy or |
| ΔS | change in entropy |
| ε | emissivity or heat recovery effectiveness |
| η | efficiency |
| ρ | reflectivity |
| Subscripts | |
| 0 | ambient |
| 1,2, … | state point |
| abs | absorb |
| ape | aperture |
| c | compressor |
| conv | convection |
| en | energy |
| g | gas |
| hox | heat in exothermic oxidation reaction |
| in | inlet |
| mech | mechanically moving objects |
| out | outlet |
| ox | oxidation |
| pump | vacuum pump |
| rad | radiation |
| rec | receiver |
| reco | recovery |
| red | reduction |
| ref | reflection |
| sep | separation |
| surf | surface |
| t | turbine |
| tc | total |
| th | thermodynamic |
References
- NOAA Administration. Carbon Dioxide Now More Than 50% Higher Than Pre-Industrial Levels. Available online: www.noaa.gov (accessed on 11 July 2022).
- Haeussler, A.; Abanades, S.; Julbe, A.; Jouannaux, J.; Drobek, M.; Ayral, A.; Cartoixa, B. Remarkable performance of microstructured ceria foams for thermochemical splitting of H2O and CO2 in a novel high–temperature solar reactor. Chem. Eng. Res. Des. 2020, 156, 311–323. [Google Scholar] [CrossRef]
- Zang, G.; Sun, P.; Elgowainy, A.A.; Bafana, A.; Wang, M. Performance and cost analysis of liquid fuel production from H2 and CO2 based on the Fischer-Tropsch process. J. CO2 Util. 2021, 46, 101459. [Google Scholar] [CrossRef]
- Gong, W.; Ye, R.-P.; Ding, J.; Wang, T.; Shi, X.; Russell, C.K.; Tang, J.; Eddings, E.G.; Zhang, Y.; Fan, M. Effect of copper on highly effective Fe-Mn based catalysts during production of light olefins via Fischer-Tropsch process with low CO2 emission. Appl. Catal. B Environ. 2020, 278, 119302. [Google Scholar] [CrossRef]
- Sonal; Ahmad, E.; Upadhyayula, S.; Pant, K.K. Biomass-derived CO2 rich syngas conversion to higher hydrocarbon via Fischer-Tropsch process over Fe–Co bimetallic catalyst. Int. J. Hydrog. Energy 2019, 44, 27741–27748. [Google Scholar] [CrossRef]
- Li, D.; Kassymova, M.; Cai, X.; Zang, S.-Q.; Jiang, H.-L. Photocatalytic CO2 reduction over metal-organic framework-based materials. Coord. Chem. Rev. 2020, 412, 213262. [Google Scholar] [CrossRef]
- Xiong, X.; Mao, C.; Yang, Z.; Zhang, Q.; Waterhouse GI, N.; Gu, L.; Zhang, T. Photocatalytic CO2 Reduction to CO over Ni Single Atoms Supported on Defect-Rich Zirconia. Adv. Energy Mater. 2020, 10, 2002928. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, Y.; Wang, J.; Shen, Q.; Zhang, Y.; Ding, C.; Bai, Y.; Jiang, G.; Li, Z.; Gaponik, N. Boosting Photocatalytic CO2 Reduction on CsPbBr3 Perovskite Nanocrystals by Immobilizing Metal Complexes. Chem. Mater. 2020, 32, 1517–1525. [Google Scholar] [CrossRef]
- Huan, T.N.; Corte DA, D.; Lamaison, S.; Karapinar, D.; Lutz, L.; Menguy, N.; Foldyna, M.; Turren-Cruz, S.-H.; Hagfeldt, A.; Bella, F.; et al. Low-cost high-efficiency system for solar-driven conversion of CO2 to hydrocarbons. Proc. Natl. Acad. Sci. USA 2019, 116, 9735–9740. [Google Scholar] [CrossRef] [Green Version]
- Sriramagiri, G.M.; Ahmed, N.; Luc, W.; Dobson, K.D.; Hegedus, S.S.; Jiao, F. Toward a Practical Solar-Driven CO2 Flow Cell Electrolyzer: Design and Optimization. ACS Sustain. Chem. Eng. 2017, 5, 10959–10966. [Google Scholar] [CrossRef]
- Küngas, R. Review—Electrochemical CO2 Reduction for CO Production: Comparison of Low- and High-Temperature Electrolysis Technologies. J. Electrochem. Soc. 2020, 167, 044508. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, Q.; An, H.; Zhang, J.; Hao, S.; Li, X.; Cai, L.; Yu, W.; You, K.; Zhu, X.; et al. Platinum Group Metal Catalyst (RuOx, PtOx, and IrOx)-Decorated Ceria-Zirconia Solid Solution as High Active Oxygen Carriers for Solar Thermochemical CO2 Splitting. ACS Catal. 2022, 12, 7719–7736. [Google Scholar] [CrossRef]
- Riaz, A.; Kreider, P.; Kremer, F.; Tabassum, H.; Yeoh, J.S.; Lipiński, W.; Lowe, A. Electrospun Manganese-Based Perovskites as Efficient Oxygen Exchange Redox Materials for Improved Solar Thermochemical CO2 Splitting. ACS Appl. Energy Mater. 2019, 2, 2494–2505. [Google Scholar] [CrossRef]
- Liu, X.; Wang, T.; Gao, K.; Meng, X.; Xu, Q.; Song, C.; Zhu, Z.; Zheng, H.; Hao, Y.; Xuan, Y. Ca- and Ga-Doped LaMnO3 for Solar Thermochemical CO2 Splitting with High Fuel Yield and Cycle Stability. ACS Appl. Energy Mater. 2021, 4, 9000–9012. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, L.; Agrafiotis, C.; Vieten, J.; Roeb, M.; Sattler, C. Solar fuels production: Two-step thermochemical cycles with cerium-based oxides. Prog. Energy Combust. Sci. 2019, 75, 100785. [Google Scholar] [CrossRef]
- Xiao, L.; Wu, S.-Y.; Li, Y.-R. Advances in solar hydrogen production via two-step water-splitting thermochemical cycles based on metal redox reactions. Renew. Energy 2012, 41, 1–12. [Google Scholar] [CrossRef]
- Kodama, T.; Gokon, N. Thermochemical Cycles for High-Temperature Solar Hydrogen Production. Chem. Rev. 2007, 107, 4048–4077. [Google Scholar] [CrossRef]
- Yutaka, N.; Bernard, C. Production of Carbon Monoxide by Direct Thermal Splitting of Carbon Dioxide at High Temperature. Bull. Chem. Soc. Jpn. 1986, 59, 1997–2002. [Google Scholar]
- Smestad, G.P.; Steinfeld, A. Review: Photochemical and Thermochemical Production of Solar Fuels from H2O and CO2 Using Metal Oxide Catalysts. Ind. Eng. Chem. Res. 2012, 51, 11828–11840. [Google Scholar] [CrossRef]
- Kang, Y.; Han, Y.; Wei, C.; Liu, K.; Tian, M.; Huang, C.; Wang, C.; Lin, J.; Hou, B.; Pan, X.; et al. A novel carbon cycle process assisted by Ni/La2O3 catalyst for enhanced thermochemical CO2 splitting. J. Energy Chem. 2021, 61, 297–303. [Google Scholar] [CrossRef]
- Kong, H.; Kong, X.; Wang, H.; Wang, J. A strategy for optimizing efficiencies of solar thermochemical fuel production based on nonstoichiometric oxides. Int. J. Hydrog. Energy 2019, 44, 19585–19594. [Google Scholar] [CrossRef]
- Muhich, C.L.; Blaser, S.; Hoes, M.C.; Steinfeld, A. Comparing the solar-to-fuel energy conversion efficiency of ceria and perovskite based thermochemical redox cycles for splitting H2O and CO2. Int. J. Hydrog. Energy 2018, 43, 18814–18831. [Google Scholar] [CrossRef]
- Panlener, R.J.; Blumenthal, R.N.; Garnier, J.E. A thermodynamic study of nonstoichiometric cerium dioxide. J. Phys. Chem. Solids 1975, 36, 1213–1222. [Google Scholar] [CrossRef]
- Le Gal, A.; Abanades, S.; Flamant, G. CO2 and H2O Splitting for Thermochemical Production of Solar Fuels Using Nonstoichiometric Ceria and Ceria/Zirconia Solid Solutions. Energy Fuels 2011, 25, 4836–4845. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, Y.; Li, F. Reactivity of Ni, Cr and Zr doped ceria in CO2 splitting for CO production via two-step thermochemical cycle. Int. J. Hydrog. Energy 2018, 43, 13754–13763. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, Y. Reactivity and Efficiency of Ceria-Based Oxides for Solar CO2 Splitting via Isothermal and Near-Isothermal Cycles. Energy Fuels 2018, 32, 736–746. [Google Scholar] [CrossRef]
- Gao, K.; Liu, X.; Jiang, Z.; Zheng, H.; Song, C.; Wang, X.; Tian, C.; Dang, C.; Sun, N.; Xuan, Y. Direct solar thermochemical CO2 splitting based on Ca- and Al- doped SmMnO3 perovskites: Ultrahigh CO yield within small temperature swing. Renew. Energy 2022, 194, 482–494. [Google Scholar] [CrossRef]
- Kaneko, H.; Miura, T.; Fuse, A.; Ishihara, H.; Taku, S.; Fukuzumi, H.; Naganuma, Y.; Tamaura, Y. Rotary-Type Solar Reactor for Solar Hydrogen Production with Two-step Water Splitting Process. Energy Fuels 2007, 21, 2287–2293. [Google Scholar] [CrossRef]
- Johnson, T.A.; Hogan, J.; Roy, E.; McDaniel, A.H.; Siegel, N.P.; Dedrick, D.E.; Stechel, E.B.; Diver, J.; Richard, B.; Miller, J.E.; et al. Reimagining Liquid Transportation Fuels: Sunshine to Petrol; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2012; p. 33. [Google Scholar]
- Marxer, D.; Furler, P.; Scheffe, J.; Geerlings, H.; Falter, C.; Batteiger, V.; Sizmann, A.; Steinfeld, A. Demonstration of the Entire Production Chain to Renewable Kerosene via Solar Thermochemical Splitting of H2O and CO2. Energy Fuels 2015, 29, 3241–3250. [Google Scholar] [CrossRef]
- Farsi, A.; Dincer, I. Thermodynamic assessment of a hybrid particle-based concentrated solar power plant using fluidized bed heat exchanger. Sol. Energy 2019, 179, 236–248. [Google Scholar] [CrossRef]
- Alqahtani, B.J.; Patiño-Echeverri, D. Integrated Solar Combined Cycle Power Plants: Paving the way for thermal solar. Appl. Energy 2016, 169, 927–936. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; He, Y.-L. Thermodynamic analysis and optimization of a molten salt solar power tower integrated with a recompression supercritical CO2 Brayton cycle based on integrated modeling. Energy Convers. Manag. 2017, 135, 336–350. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Q.; Lei, J.; Han, W.; Jin, H. Investigation of thermodynamic performances for two-stage recompression supercritical CO2 Brayton cycle with high temperature thermal energy storage system. Energy Convers. Manag. 2018, 165, 477–487. [Google Scholar] [CrossRef]
- Pitz-Paal, R.; Botero, N.B.; Steinfeld, A. Heliostat field layout optimization for high-temperature solar thermochemical processing. Sol. Energy 2011, 85, 334–343. [Google Scholar] [CrossRef]
- Ehrhart, B.; Gill, D. Evaluation of Annual Efficiencies of High Temperature Central Receiver Concentrated Solar Power Plants with Thermal Energy Storage. Energy Procedia 2014, 49, 752–761. [Google Scholar] [CrossRef] [Green Version]
- Dähler, F.; Wild, M.; Schäppi, R.; Haueter, P.; Cooper, T.; Good, P.; Larrea, C.; Schmitz, M.; Furler, P.; Steinfeld, A. Optical design and experimental characterization of a solar concentrating dish system for fuel production via thermochemical redox cycles. Sol. Energy 2018, 170, 568–575. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A.; Worek, W.M. Solar Engineering of Thermal Processes. J. Sol. Energy Eng. 1994, 116, 67–68. [Google Scholar] [CrossRef]
- Li, X.; Kong, W.; Wang, Z.; Chang, C.; Bai, F. Thermal model and thermodynamic performance of molten salt cavity receiver. Renew. Energy 2010, 35, 981–988. [Google Scholar] [CrossRef]
- Ho, C.K.; Christian, J.M.; Yellowhair, J.; Armijo, K.; Kolb, W.J.; Jeter, S.; Golob, M.; Nguyen, C. Performance evaluation of a high-temperature falling particle receiver. In Energy Sustainability; ASME: New York, NY, USA, 2016. [Google Scholar]
- Liu, Y.; Wang, Y.; Huang, D. Supercritical CO2 Brayton cycle: A state-of-the-art review. Energy 2019, 189, 115900. [Google Scholar] [CrossRef]
- Xu, C.; Wang, Z.; Li, X.; Sun, F. Energy and exergy analysis of solar power tower plants. Appl. Therm. Eng. 2011, 31, 3904–3913. [Google Scholar] [CrossRef]
- Zinkevich, M.; Djurovic, D.; Aldinger, F. Thermodynamic modelling of the cerium–oxygen system. Solid State Ion. 2006, 177, 989–1001. [Google Scholar] [CrossRef]
- Bulfin, B.; Lowe, A.J.; Keogh, K.A.; Murphy, B.E.; Lübben, O.; Krasnikov, S.A.; Shvets, I.V. Analytical Model of CeO2 Oxidation and Reduction. J. Phys. Chem. C 2013, 117, 24129–24137. [Google Scholar] [CrossRef]
- Bader, R.; Venstrom, L.J.; Davidson, J.H.; Lipiński, W. Thermodynamic Analysis of Isothermal Redox Cycling of Ceria for Solar Fuel Production. Energy Fuels 2013, 27, 5533–5544. [Google Scholar] [CrossRef]
- Bulfin, B.; Call, F.; Lange, M.; Lübben, O.; Sattler, C.; Pitz-Paal, R.; Shvets, I.V. Thermodynamics of CeO2 Thermochemical Fuel Production. Energy Fuels 2015, 29, 1001–1009. [Google Scholar] [CrossRef]
- Bulfin, B.; Lange, M.; de Oliveira, L.; Roeb, M.; Sattler, C. Solar thermochemical hydrogen production using ceria zirconia solid solutions: Efficiency analysis. Int. J. Hydrog. Energy 2016, 41, 19320–19328. [Google Scholar] [CrossRef]
- Ricken, M.; Nölting, J.; Riess, I. Specific heat and phase diagram of nonstoichiometric ceria (CeO2−x). J. Solid State Chem. 1984, 54, 89–99. [Google Scholar] [CrossRef]
- Guo, J. Design analysis of supercritical carbon dioxide recuperator. Appl. Energy 2016, 164, 21–27. [Google Scholar] [CrossRef]
- PraveenKumar, S.; Agyekum, E.B.; Velkin, V.I.; Yaqoob, S.J.; Adebayo, T.S. Thermal management of solar photovoltaic module to enhance output performance: An experimental passive cooling approach using discontinuous aluminum heat sink. Int. J. Renew. Energy Res. 2021, 11, 1700–1712. [Google Scholar]
- Ma, Z.; Glatzmaier, G.C.; Mehos, M. Development of Solid Particle Thermal Energy Storage for Concentrating Solar Power Plants that Use Fluidized Bed Technology. Energy Procedia 2014, 49, 898–907. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, A.; Yokomine, T.; Nagafuchi, T. Development of gas–solid direct contact heat exchanger by use of axial flow cyclone. Int. J. Heat Mass Transf. 2004, 47, 4601–4614. [Google Scholar] [CrossRef]
- Ma, Z.; Martinek, J. Analysis of a Fluidized-Bed Particle/Supercritical-CO2 Heat Exchanger in a Concentrating Solar Power System. J. Sol. Energy Eng. 2020, 143, 031010. [Google Scholar] [CrossRef]
- Lin, M.; Haussener, S. Solar fuel processing efficiency for ceria redox cycling using alternative oxygen partial pressure reduction methods. Energy 2015, 88, 667–679. [Google Scholar] [CrossRef] [Green Version]
- Baloch, A.A.B.; Bahaidarah, H.M.S.; Gandhidasan, P.; Al-Sulaiman, F.A. Experimental and numerical performance analysis of a converging channel heat exchanger for PV cooling. Energy Convers. Manag. 2015, 103, 14–27. [Google Scholar] [CrossRef]
- Praveenkumar, S.; Gulakhmadov, A.; Agyekum, E.B.; Alwan, N.T.; Velkin, V.I.; Sharipov, P.; Safaraliev, M.; Chen, X. Experimental Study on Performance Enhancement of a Photovoltaic Module Incorporated with CPU Heat Pipe—A 5E Analysis. Sensors 2022, 22, 6367. [Google Scholar] [CrossRef]
- Agyekum, E.B.; PraveenKumar, S.; Alwan, N.T.; Velkin, V.I.; Shcheklein, S.E.; Yaqoob, S.J. Experimental Investigation of the Effect of a Combination of Active and Passive Cooling Mechanism on the Thermal Characteristics and Efficiency of Solar PV Module. Inventions 2021, 6, 63. [Google Scholar] [CrossRef]
- Agyekum, E.B.; PraveenKumar, S.; Alwan, N.T.; Velkin, V.I.; Adebayo, T.S. Experimental Study on Performance Enhancement of a Photovoltaic Module Using a Combination of Phase Change Material and Aluminum Fins—Exergy, Energy and Economic (3E) Analysis. Inventions 2021, 6, 69. [Google Scholar] [CrossRef]
- Falter, C.; Sizmann, A. Solar Thermochemical Hydrogen Production in the USA. Sustainability 2021, 13, 7804. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Z.; Duan, Y. Load matching and techno-economic analysis of CSP plant with S–CO2 Brayton cycle in CSP-PV-wind hybrid system. Energy 2021, 223, 120016. [Google Scholar] [CrossRef]


| Property | Value(s) |
|---|---|
| C | 3000 |
| Fr | 0.0757 |
| Tred | 1400–2100 K |
| Tox | 700–1500 K |
| P0 | 1 bar |
| Pc,in | 72–90 bar |
| Pt,in | 180–300 bar |
| ηmech | 0.1 |
| ηO2-rem | 0.15 |
| ηsep | 0.15 |
| ρ | 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Lian, W.; Gao, K.; Jiang, Z.; Tian, C.; Sun, N.; Zheng, H.; Wang, X.; Song, C.; Liu, X. Solar Thermochemical CO2 Splitting Integrated with Supercritical CO2 Cycle for Efficient Fuel and Power Generation. Energies 2022, 15, 7334. https://doi.org/10.3390/en15197334
Yu X, Lian W, Gao K, Jiang Z, Tian C, Sun N, Zheng H, Wang X, Song C, Liu X. Solar Thermochemical CO2 Splitting Integrated with Supercritical CO2 Cycle for Efficient Fuel and Power Generation. Energies. 2022; 15(19):7334. https://doi.org/10.3390/en15197334
Chicago/Turabian StyleYu, Xiangjun, Wenlei Lian, Ke Gao, Zhixing Jiang, Cheng Tian, Nan Sun, Hangbin Zheng, Xinrui Wang, Chao Song, and Xianglei Liu. 2022. "Solar Thermochemical CO2 Splitting Integrated with Supercritical CO2 Cycle for Efficient Fuel and Power Generation" Energies 15, no. 19: 7334. https://doi.org/10.3390/en15197334
APA StyleYu, X., Lian, W., Gao, K., Jiang, Z., Tian, C., Sun, N., Zheng, H., Wang, X., Song, C., & Liu, X. (2022). Solar Thermochemical CO2 Splitting Integrated with Supercritical CO2 Cycle for Efficient Fuel and Power Generation. Energies, 15(19), 7334. https://doi.org/10.3390/en15197334







