A Composite Control Method for Permanent Magnet Synchronous Motor System with Nonlinearly Parameterized-Uncertainties
Abstract
1. Introduction
- The proposed controller uses a non-recursive design framework, the stability analysis and controller design can be separated, and has a fixed architecture framework, that is easy to design and implement for engineering;
- The proposed controller adopts a one-step adaptive law to deal with parametric uncertainties of the PMSM system, which is an one-step designed adaptive mechanism which is more direct and effective;
- The proposed controller applied the nonsmooth control technique which has better convergence performances around the equilibrium points and greater robustness.
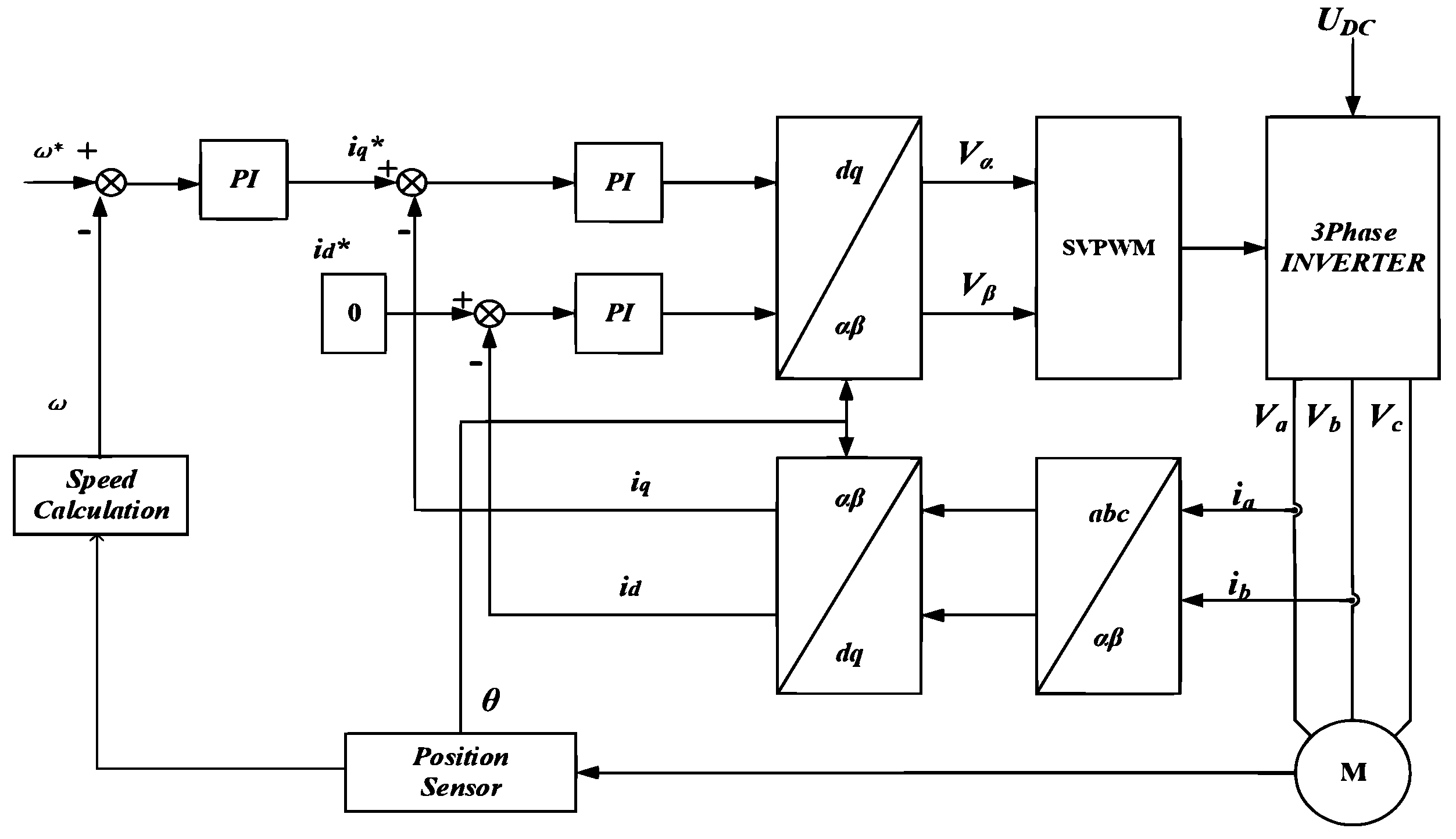
2. The Mathematical Model of PMSM
3. Analysis of Nonlinear Parameterized-Uncertainties
3.1. Nonlinear Parameterized-Uncertainties in PMSM
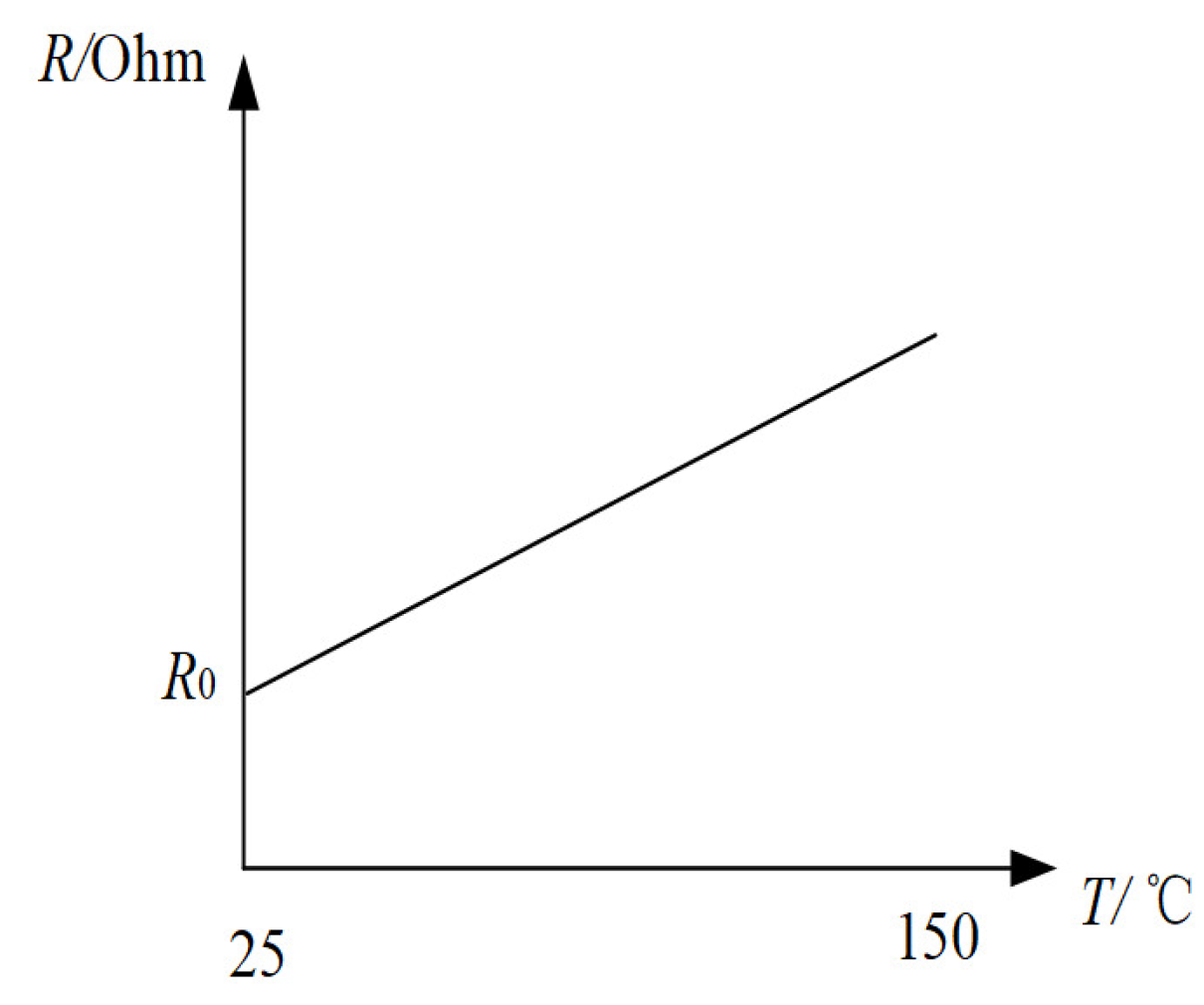
3.1.1. Temperature Change
Magnetism Loss and Coercivity
The Change of Stator Resistance
3.1.2. Friction Torque
3.2. Simulation of Nonlinearly Parameterized-Uncertainties in PMSM
3.2.1. Simulation of the Influence of Temperature Change
3.2.2. Simulation of the Influence of Friction Torque
3.2.3. Control Strategy
4. Composite Controller Design
4.1. Adaptive Controller Design
4.2. ESO Design
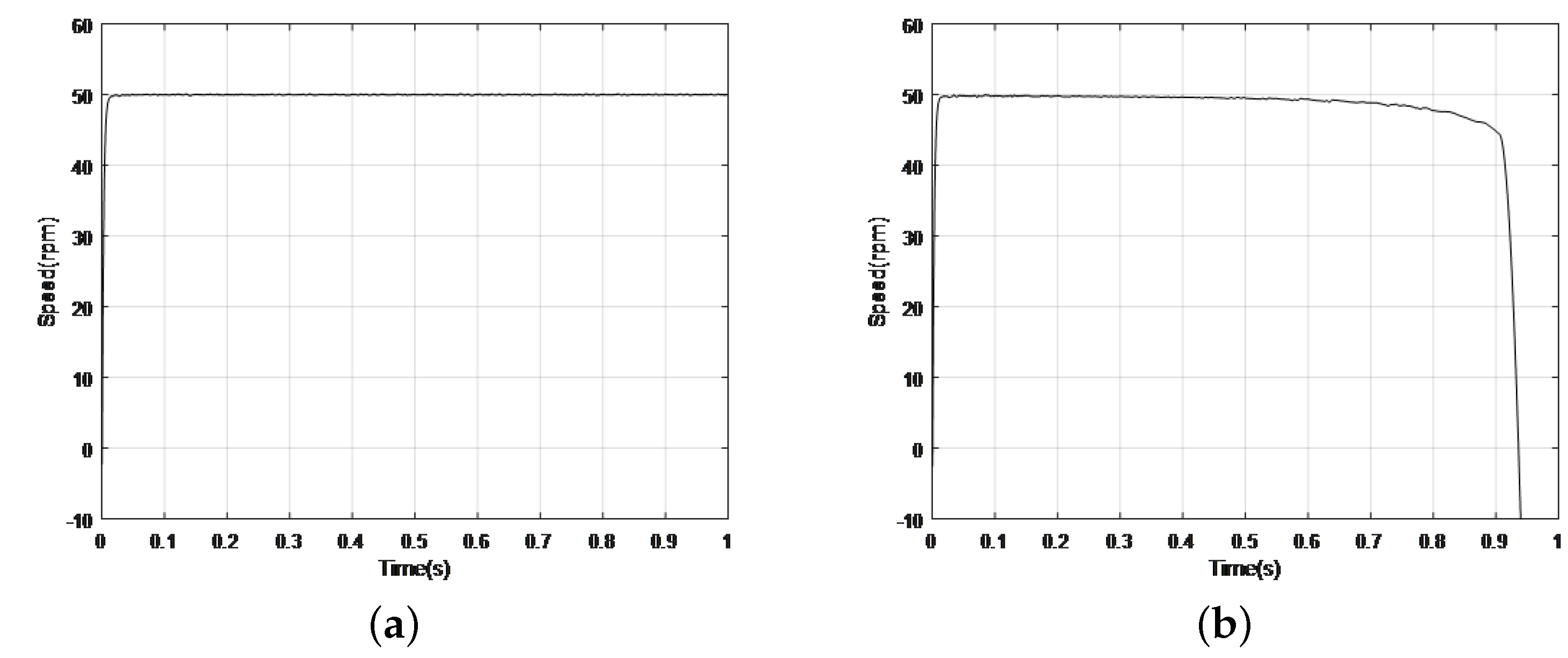
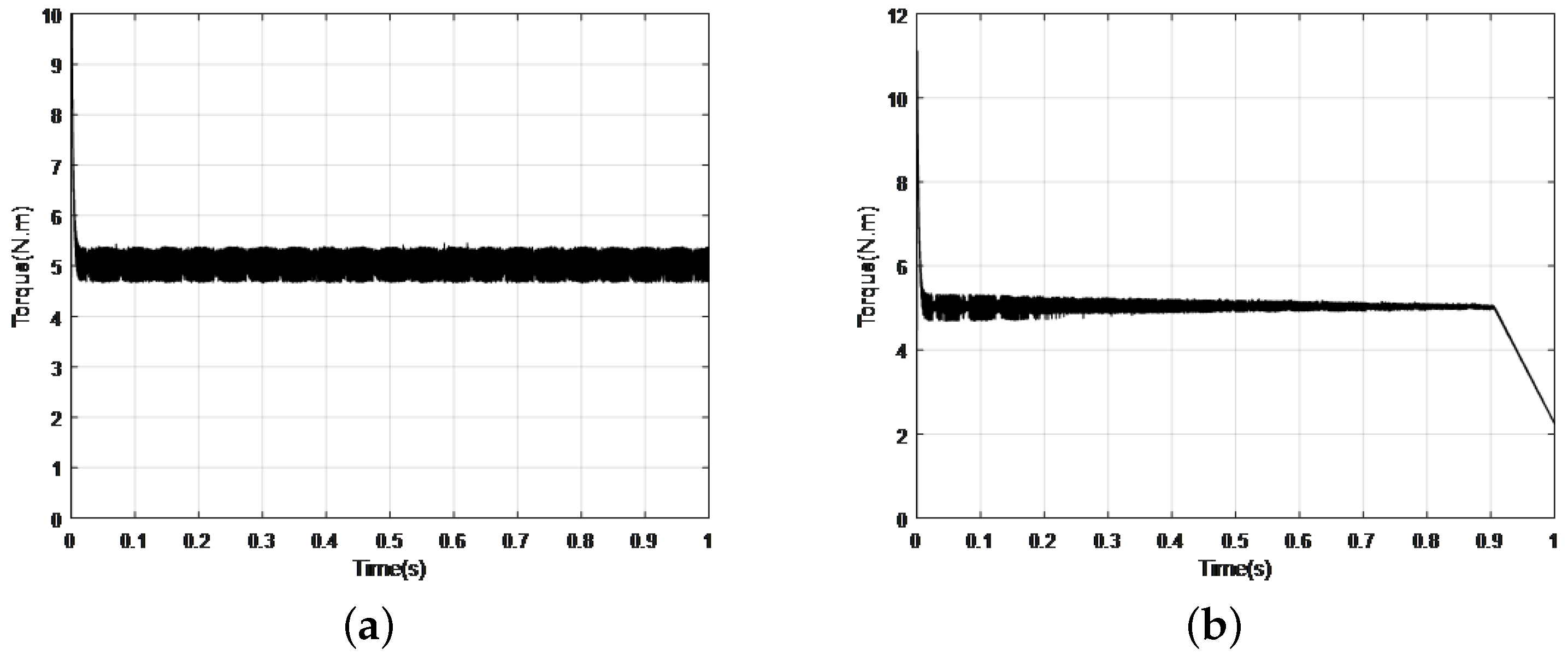
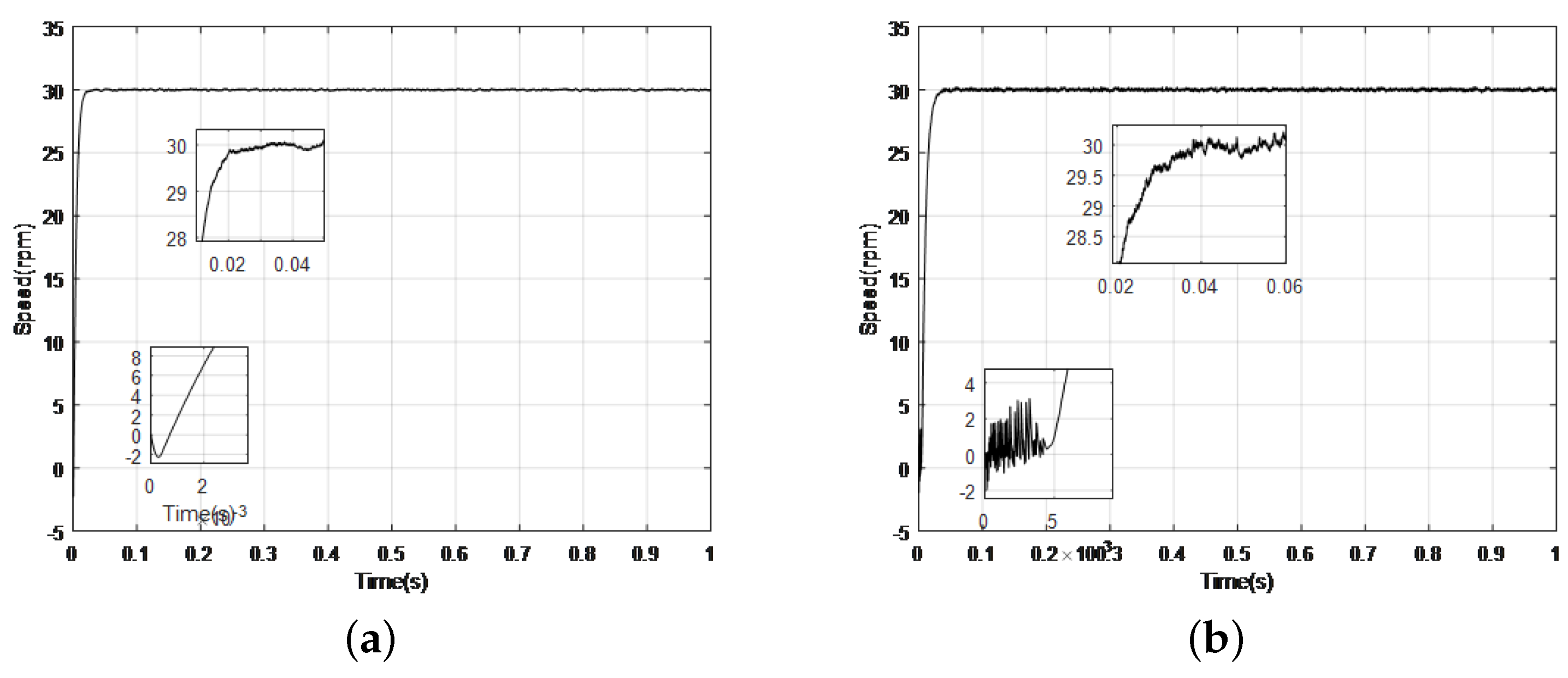
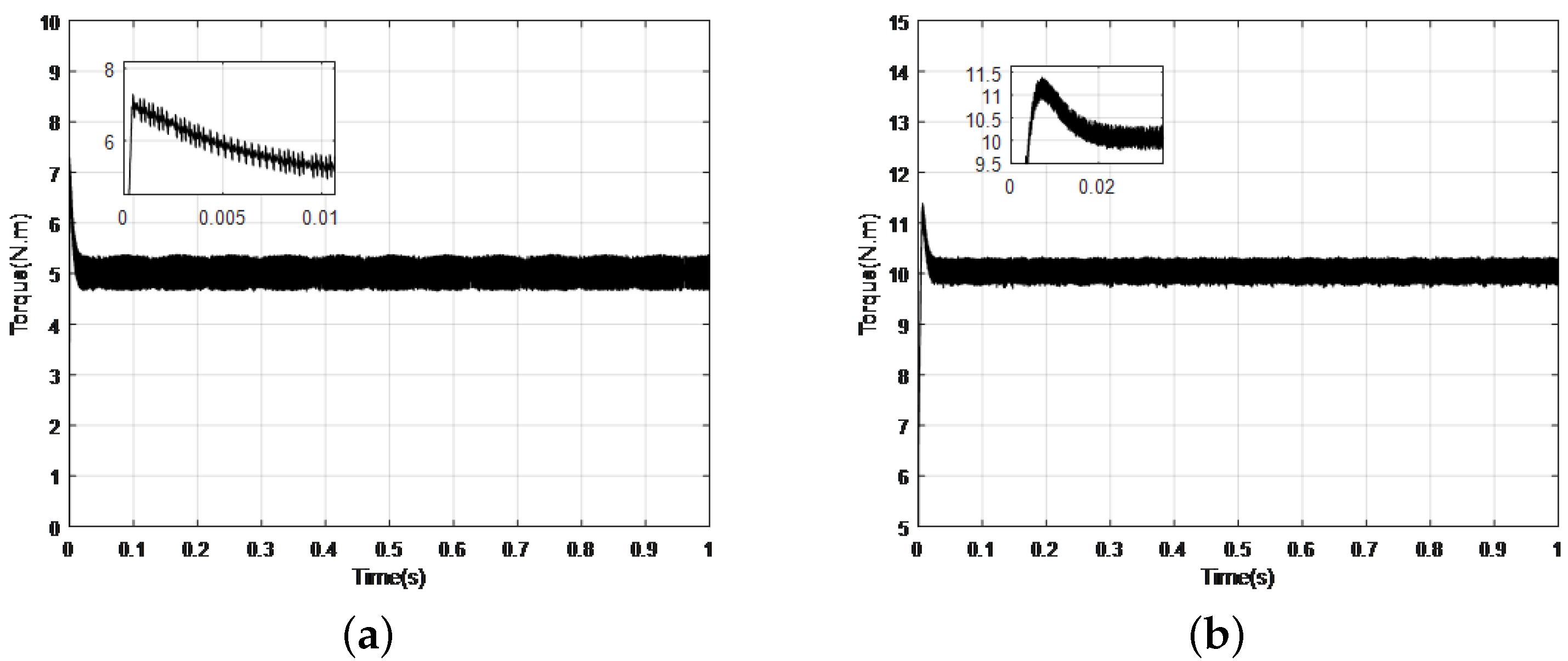
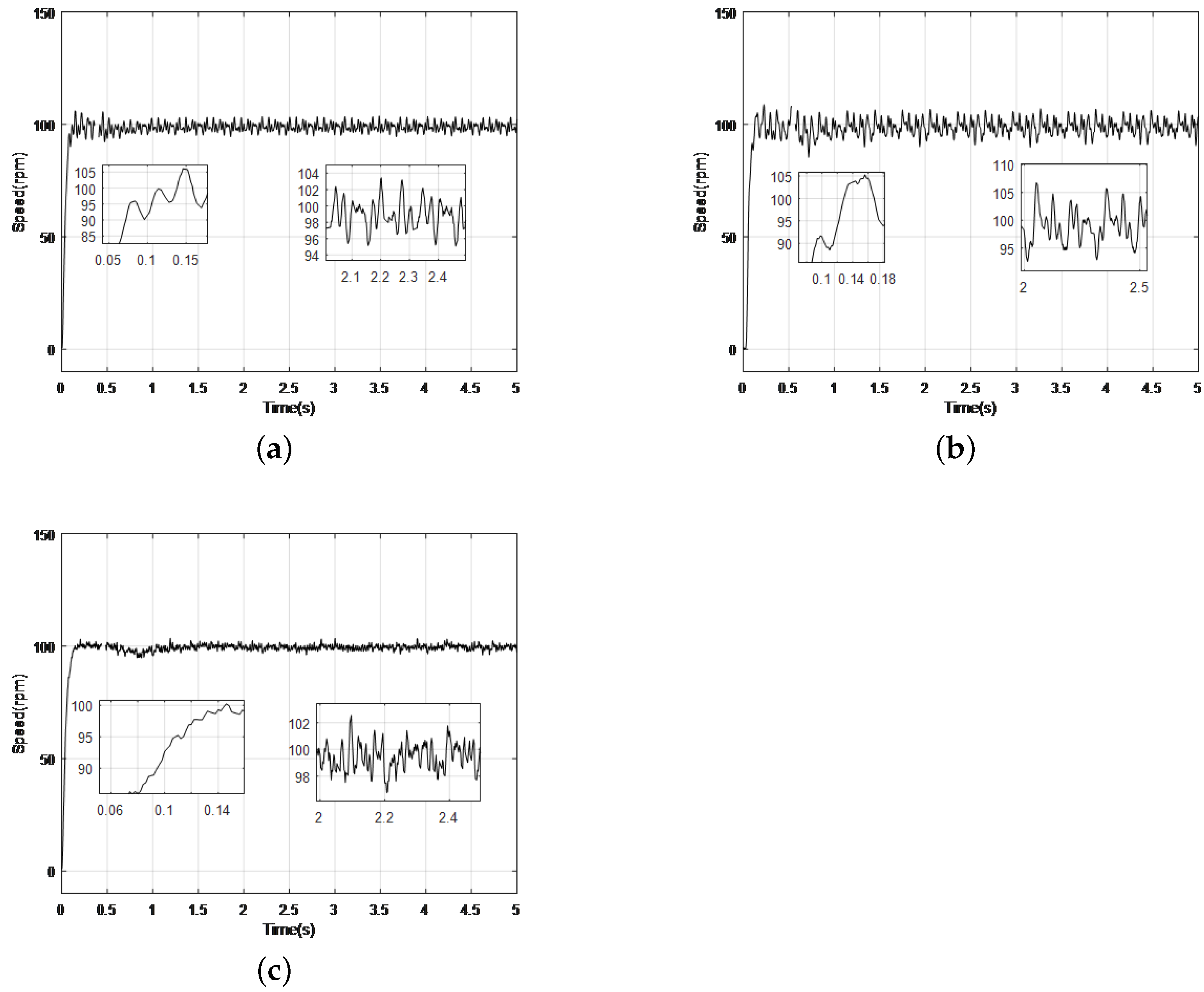
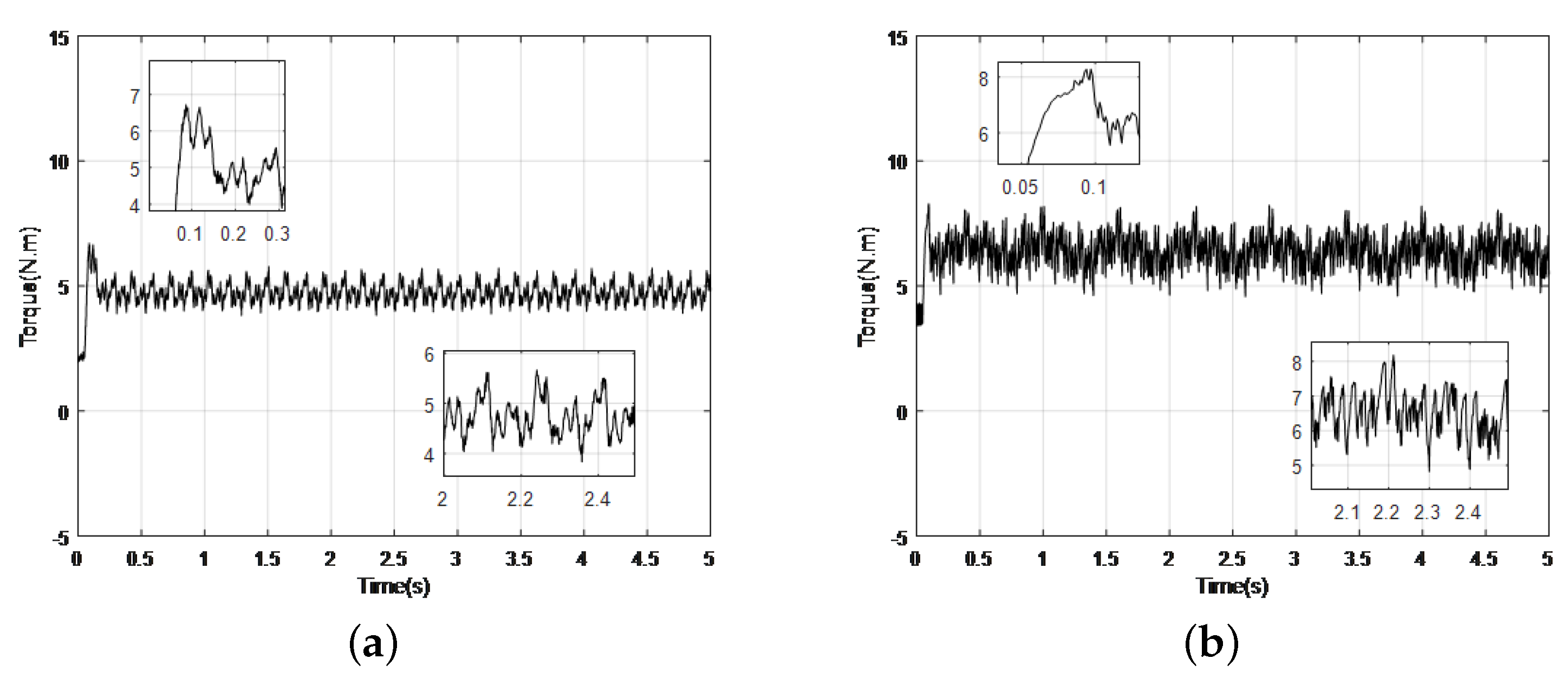
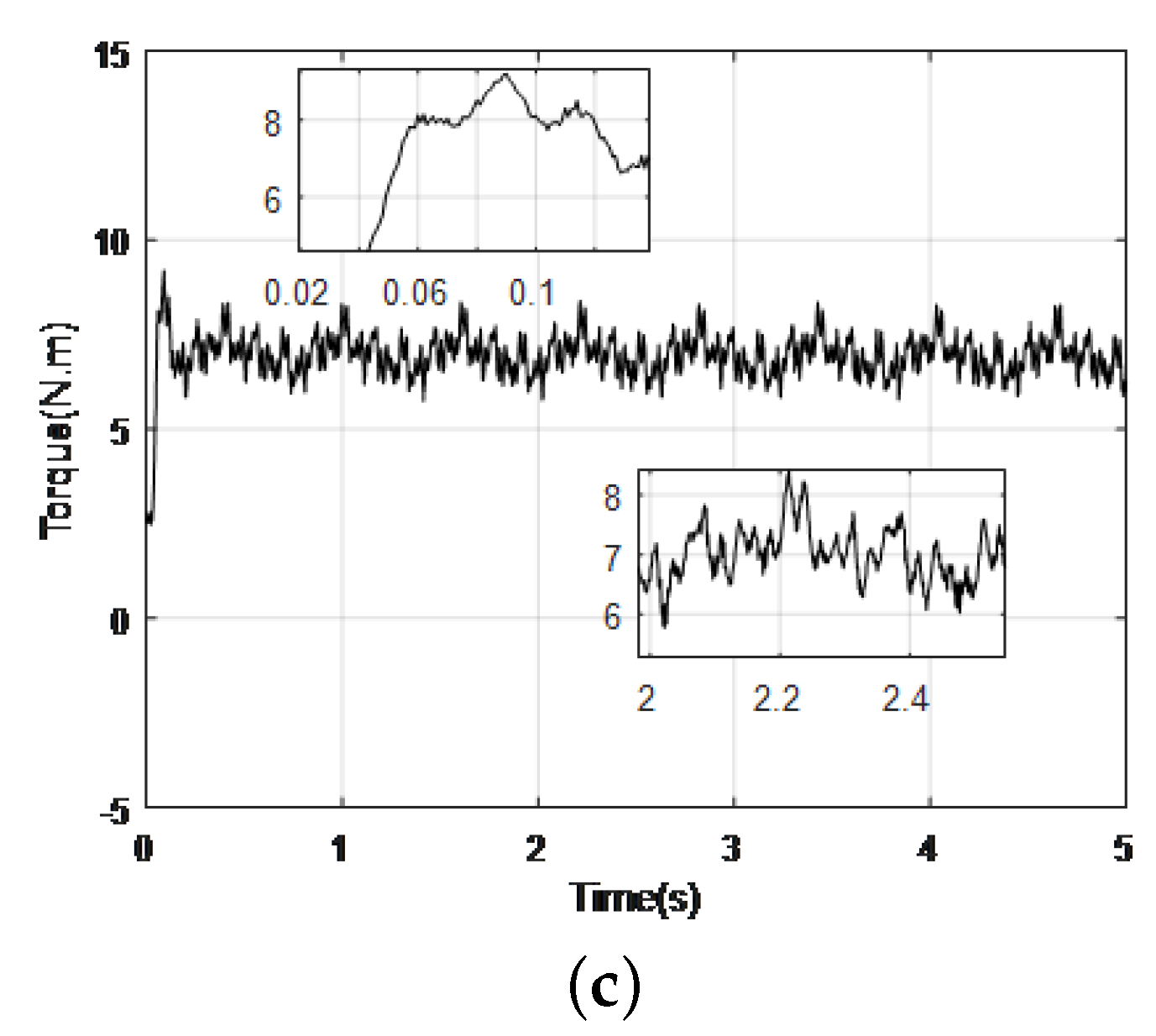
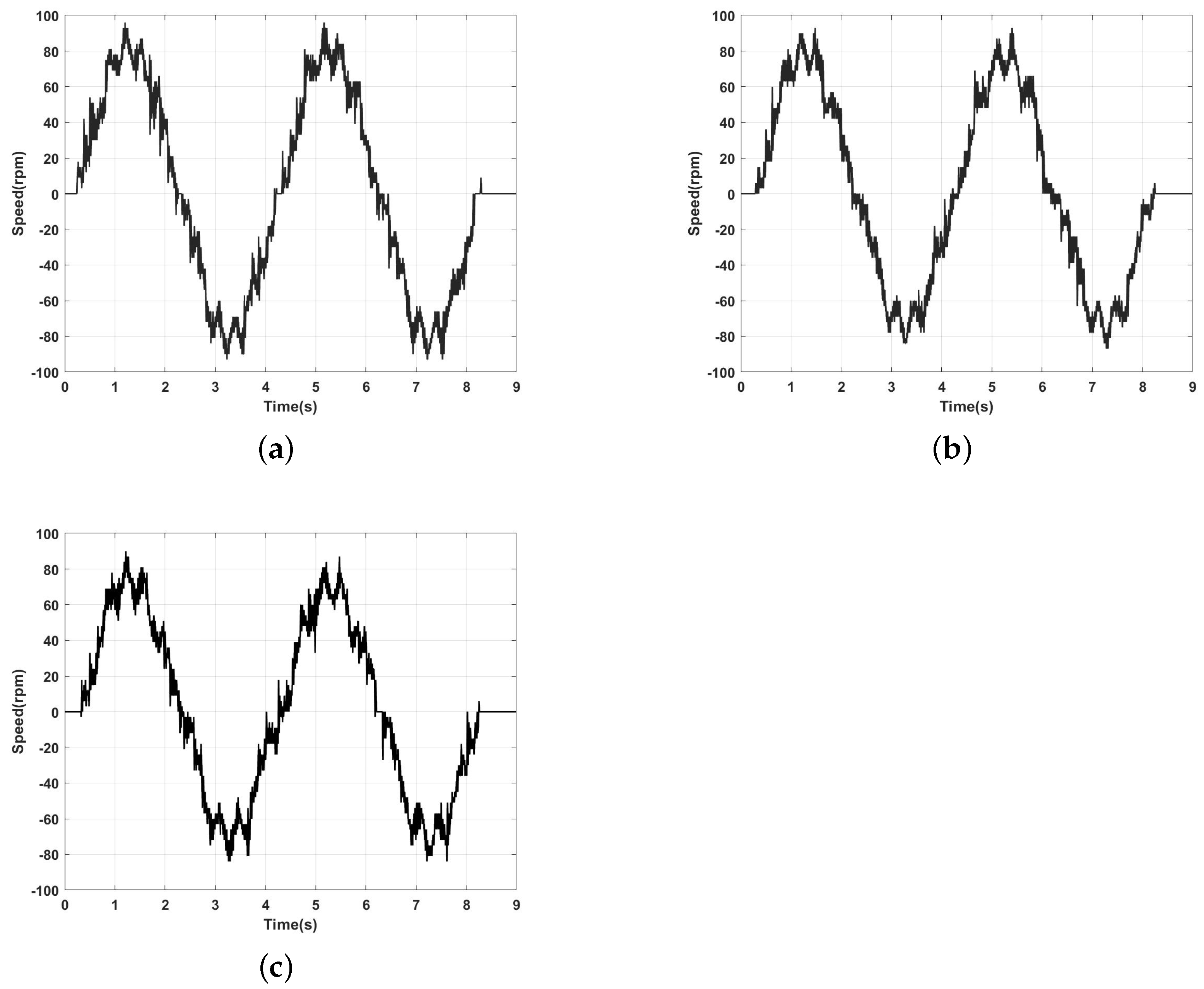
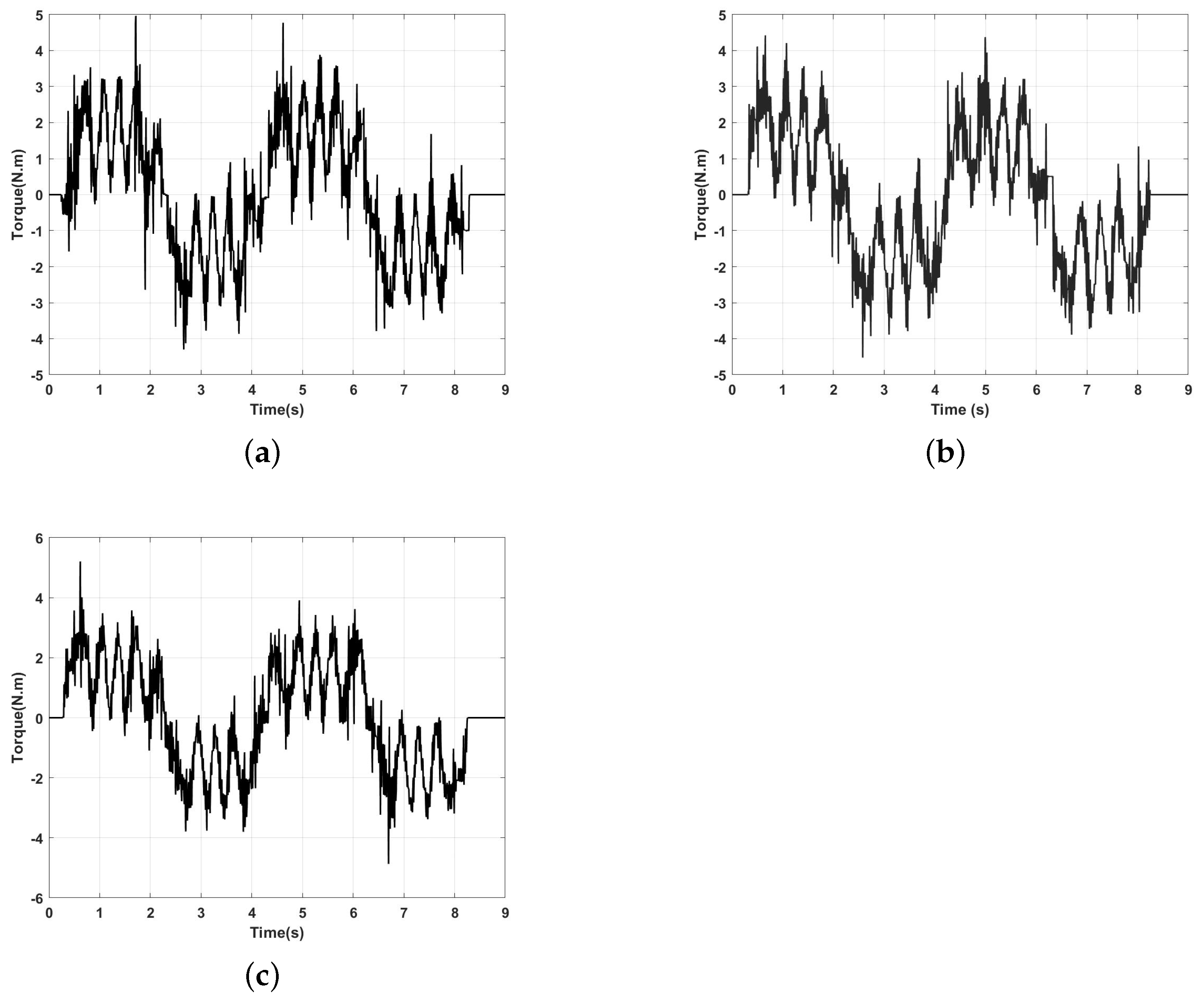
5. Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ni, R.; Xu, D.; Wang, G.; Gui, X.; Zhang, G.; Zhan, H.; Li, C. Efficiency enhancement of general AC drive system by remanufacturing induction motor with interior permanent-magnet rotor. Trans. Ind. Electron. 2015, 63, 808–820. [Google Scholar] [CrossRef]
- Ni, R.; Xu, D.; Wang, G.; Ding, L.; Zhang, G.; Qu, L. Maximum efficiency per ampere control of permanent-magnet synchronous machines. Trans. Ind. Electron. 2014, 62, 2135–2143. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, G.; Xu, D.; Zhao, N. ADALINE-network-based PLL for position sensorless interior permanent magnet synchronous motor drives. Trans. Power Electron. 2015, 31, 1450–1460. [Google Scholar] [CrossRef]
- Zhang, X.H.; Tang, Q.T. Adaptive backstepping control of interior permanent magnet synchronous motors considering parameter and load uncertainties. Control Decis. 2016, 31, 1509–1512. [Google Scholar]
- Yang, J.; Su, J.; Li, S.; Yu, X. High-order mismatched disturbance compensation for motion control systems via a continuous dynamic sliding-mode approach. Trans. Ind. Informatics 2013, 10, 604–614. [Google Scholar] [CrossRef]
- Zhu, Y. Multivariable process identification for MPC: The asymptotic method and its applications. J. Process Control 1998, 8, 101–115. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, B.; Mao, D. Robust sliding mode control of PMSM based on rapid nonlinear tracking differentiator and disturbance observer. Sensors 2018, 18, 1031. [Google Scholar] [CrossRef]
- Gutman, S. Uncertain dynamical systems—A Lyapunov min-max approach. IEEE Trans. Autom. Control 1979, 24, 437–443. [Google Scholar] [CrossRef]
- Corless, M.; Leitmann, G. Continuous state feedback guaranteeing uniform ultimate boundedness for uncertain dynamic systems. IEEE Trans. Autom. Control 1981, 26, 1139–1144. [Google Scholar] [CrossRef]
- Praly, L.; Jiang, Z.P. Linear output feedback with dynamic high gain for nonlinear systems. Syst. Control Lett. 2004, 53, 107–116. [Google Scholar] [CrossRef]
- Koo, M.S.; Choi, H.L.; Lim, J.T. Universal control of nonlinear systems with unknown nonlinearity and growth rate by adaptive output feedback. Automatica 2011, 47, 2211–2217. [Google Scholar] [CrossRef]
- Krishnamurthy, P.; Khorrami, F. Dynamic high-gain scaling: State and output feedback with application to systems with ISS appended dynamics driven by all states. Trans. Autom. Control 2011, 49, 2219–2239. [Google Scholar] [CrossRef]
- Lei, H.; Lin, W. Universal adaptive control of nonlinear systems with unknown growth rate by output feedback. Automatica 2006, 42, 1783–1789. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Continuous finite-time stabilization of the translational and rotational double integrators. Trans. Autom. Control 2006, 43, 678–682. [Google Scholar] [CrossRef]
- Xu, J.X.; Qu, Z. Robust iterative learning control for a class of nonlinear systems. Automatica 2006, 43, 983–988. [Google Scholar] [CrossRef]
- Chen, Q.; Yu, X.; Sun, M.; Wu, C.; Fu, Z. Adaptive repetitive learning control of PMSM servo systems with bounded nonparametric uncertainties: Theory and experiments. IEEE Trans. Ind. Electron. 2020, 68, 8626–8635. [Google Scholar] [CrossRef]
- Huang, M.; Deng, Y.; Li, H.; Shao, M.; Liu, J. Integrated Uncertainty/Disturbance Suppression Based on Improved Adaptive Sliding Mode Controller for PMSM Drives. Energies, 2021; 14, 6538. [Google Scholar]
- Choi, K.; Kim, Y.; Kim, S.K.; Kim, K.S. Current and position sensor fault diagnosis algorithm for PMSM drives based on robust state observer. IEEE Trans. Ind. Electron. 2020, 68, 5227–5236. [Google Scholar] [CrossRef]
- Ullah, K.; Guzinski, J.; Mirza, A.F. Critical review on robust speed control techniques for permanent magnet synchronous motor (PMSM) speed regulation. Energies 2022, 15, 1235. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, J.; Li, H.; Liu, J.; Tian, D. Adaptive sliding mode current control with sliding mode disturbance observer for PMSM drives. ISA Trans. 2019, 88, 113–126. [Google Scholar] [CrossRef]
- Xu, J.; Xu, J.X. Memory based nonlinear internal model: What can a control system learn. In Proceedings of the 4th Asia Control Conference, Singapore, 25–27 September 2002; pp. 446–451. [Google Scholar]
- Tan, Y.; Xu, J.X. Learning based nonlinear internal model control. In Proceedings of the IEEE 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Zhang, C.; Wen, C. A non-recursive C1 adaptive stabilization methodology for nonlinearly parameterized uncertain nonlinear systems. J. Frankin Inst. 2018, 355, 5099–5113. [Google Scholar] [CrossRef]
- Ohishi, K.; Nakao, M.; Ohnishi, K.; Miyachi, K. Microprocessor-controlled DC motor for load-insensitive position servo system. IEEE Trans. Ind. Electron. 1987, 34, 44–49. [Google Scholar] [CrossRef]
- Che, J.; Qian, X. Analysis of temperature effect in direct torque control system for permanent magnet synchronous motor. Mach. Tool Hydraul. 2013, 41, 54–57. [Google Scholar]
- De Wit, C.C.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Ran, M.; Li, J.; Xie, L. A new extended state observer for uncertain nonlinear systems. Automatica 1995, 131, 109772. [Google Scholar] [CrossRef]



| rated power | 426 W | pole pairs | 4 |
| rated voltage | 60 V | stator resistance | 0.36 Ohms |
| rated torque | 1.5 N·m | stator inductance | 0.4 mH |
| rated current | 7.1 A | rotor inertia | 3.75 kg·m |
| rated speed | 6000 rpm | back-EMF | 4.64 v/krpm |
| Traditional PID | Composite Controller | ||
|---|---|---|---|
| speed loop proportional gain | 25 | design parameter a | 0.5 |
| speed loop integral gain | 0.001 | design parameter b | 0.8 |
| speed loop differential gain | 0.01 | design parameter c | 1 |
| current loop / proportional gain | 0.04 | design parameter k / | 1.5 |
| current loop / integral gain | 0.02 | constant gain K | −0.5 |
| gain of ESO | 23 | ||
| gain of ESO | 4.5 | ||
| current loop / proportional gain | 0.04 | ||
| current loop / integral gain | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Sun, Z.; Shi, Y. A Composite Control Method for Permanent Magnet Synchronous Motor System with Nonlinearly Parameterized-Uncertainties. Energies 2022, 15, 7354. https://doi.org/10.3390/en15197354
Li S, Sun Z, Shi Y. A Composite Control Method for Permanent Magnet Synchronous Motor System with Nonlinearly Parameterized-Uncertainties. Energies. 2022; 15(19):7354. https://doi.org/10.3390/en15197354
Chicago/Turabian StyleLi, Shenghui, Zhenxing Sun, and Ying Shi. 2022. "A Composite Control Method for Permanent Magnet Synchronous Motor System with Nonlinearly Parameterized-Uncertainties" Energies 15, no. 19: 7354. https://doi.org/10.3390/en15197354
APA StyleLi, S., Sun, Z., & Shi, Y. (2022). A Composite Control Method for Permanent Magnet Synchronous Motor System with Nonlinearly Parameterized-Uncertainties. Energies, 15(19), 7354. https://doi.org/10.3390/en15197354








