Junction Temperature Prediction of Insulated-Gate Bipolar Transistors in Wind Power Systems Based on an Improved Honey Badger Algorithm
Abstract
1. Introduction
2. Review of the Literature
2.1. Junction Temperature Prediction of IGBTs in Wind Power Converters
2.2. Improved Honey Badger Algorithm—Extreme Learning Machine
2.3. The Method in This Study
3. Method
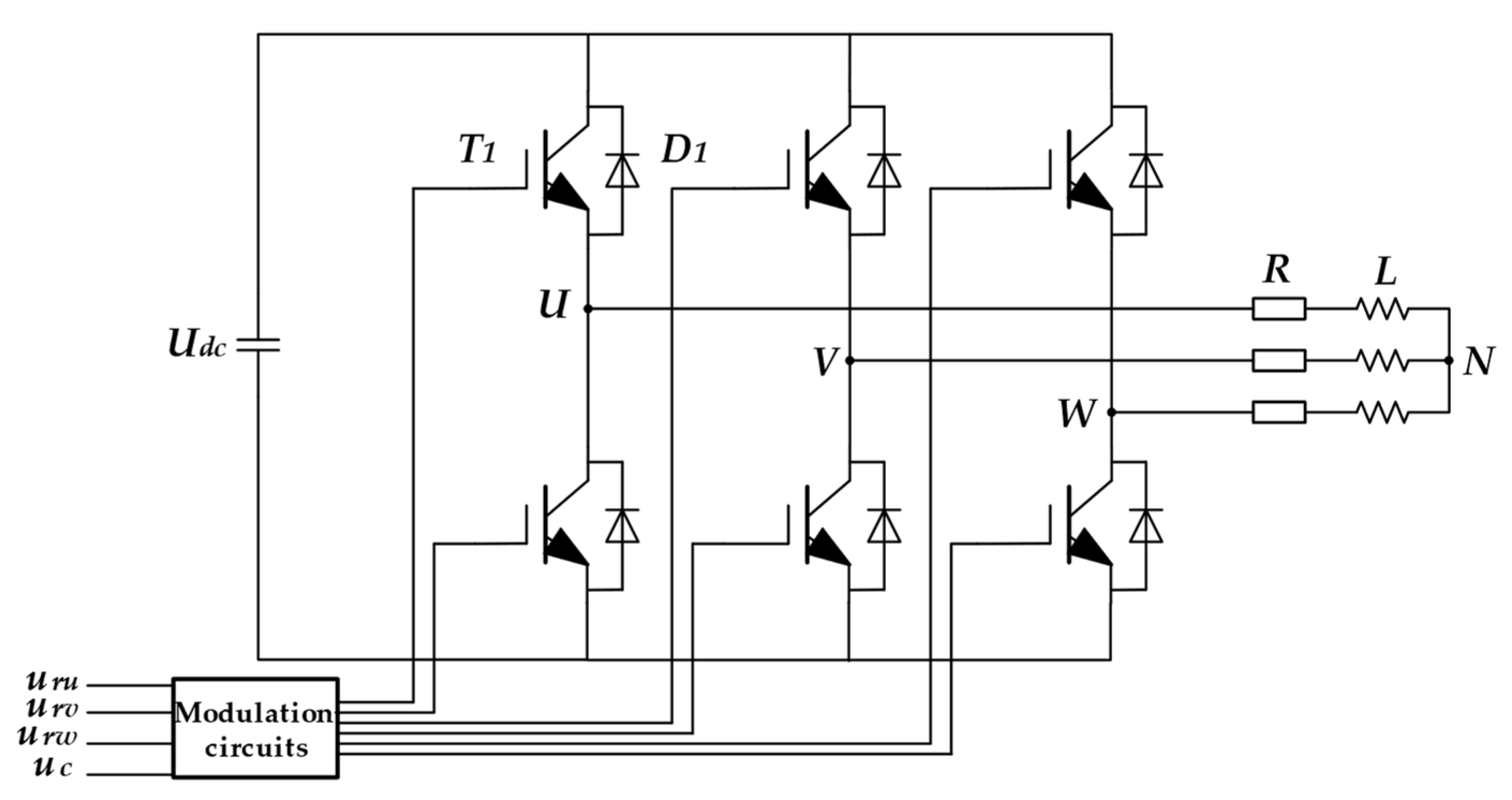
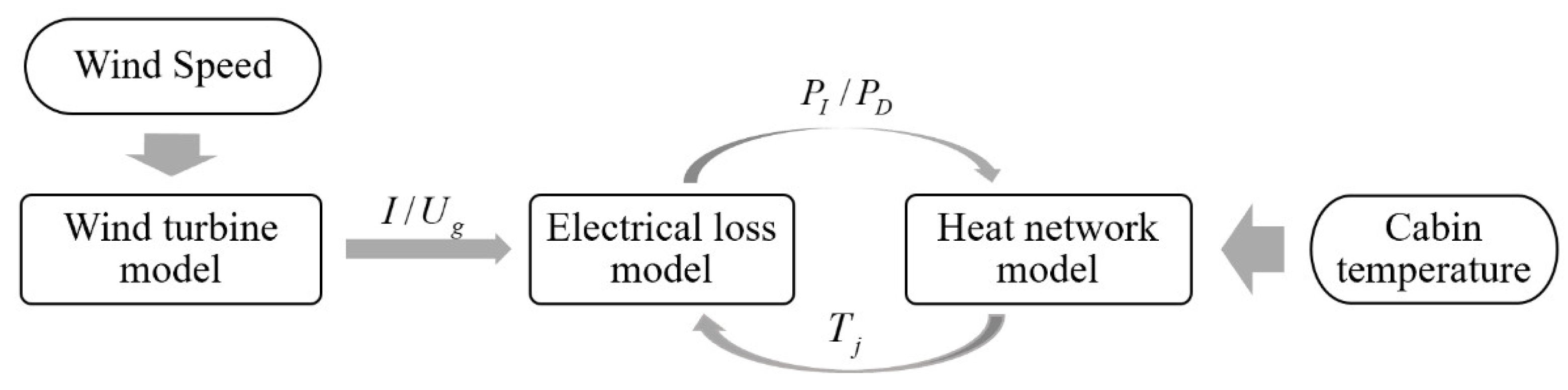
3.1. Principle of Electro-Heat Coupling Model Method
3.1.1. Electrical Loss Model
- 1.
- Equation (1) is utilized to obtain the loss of IGBT in the conduction state.
- 2.
- Equation (2) is utilized to obtain the loss of FWD in the conduction state.
- 3.
- Equation (3) is utilized to obtain the loss of IGBT in the switching state.
- 4.
- Equation (4) is utilized to obtain the loss of FWD in the switching state.
3.1.2. Heat Network Model
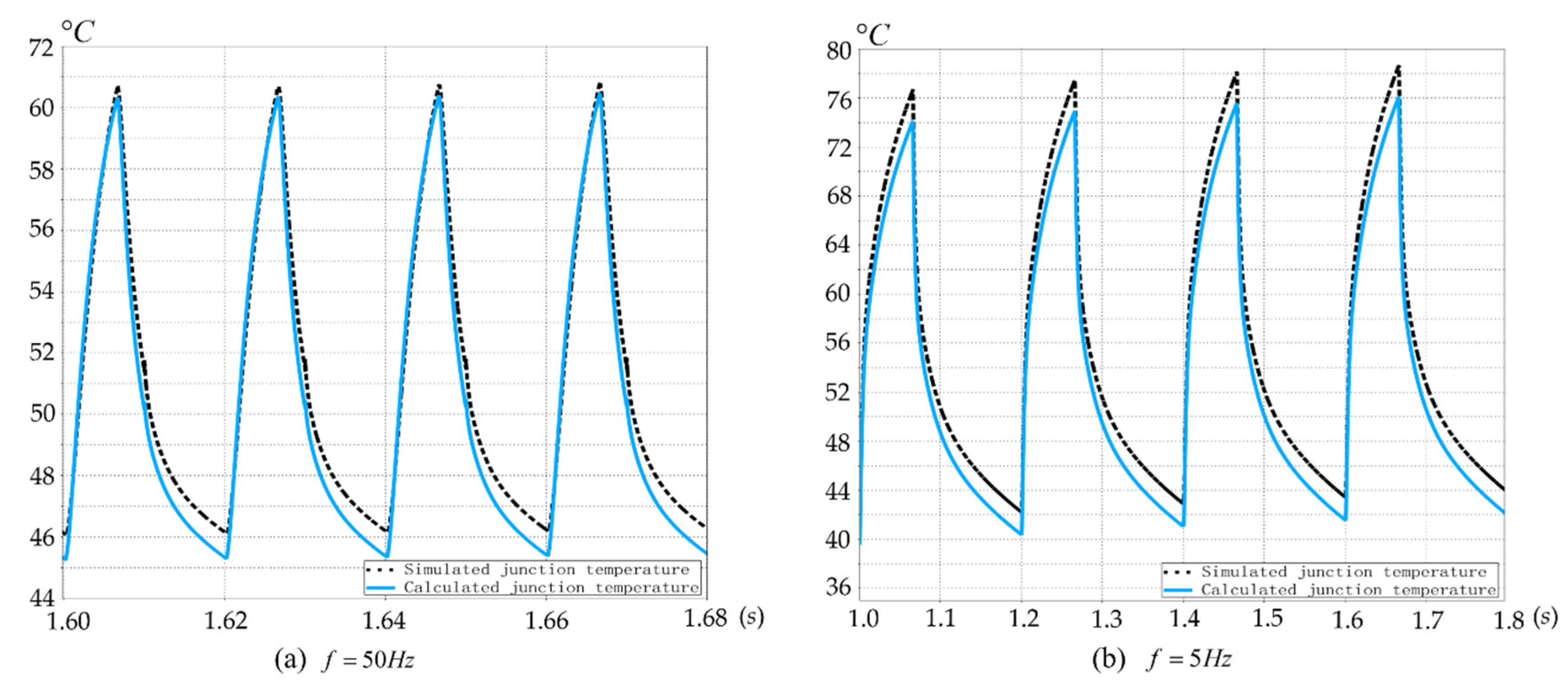
3.2. Simulation Validation
3.3. Example of Junction Temperature Calculation of IGBTs in Wind Power Converters
3.3.1. Wind Turbine Model
3.3.2. Junction Temperature Calculation Process
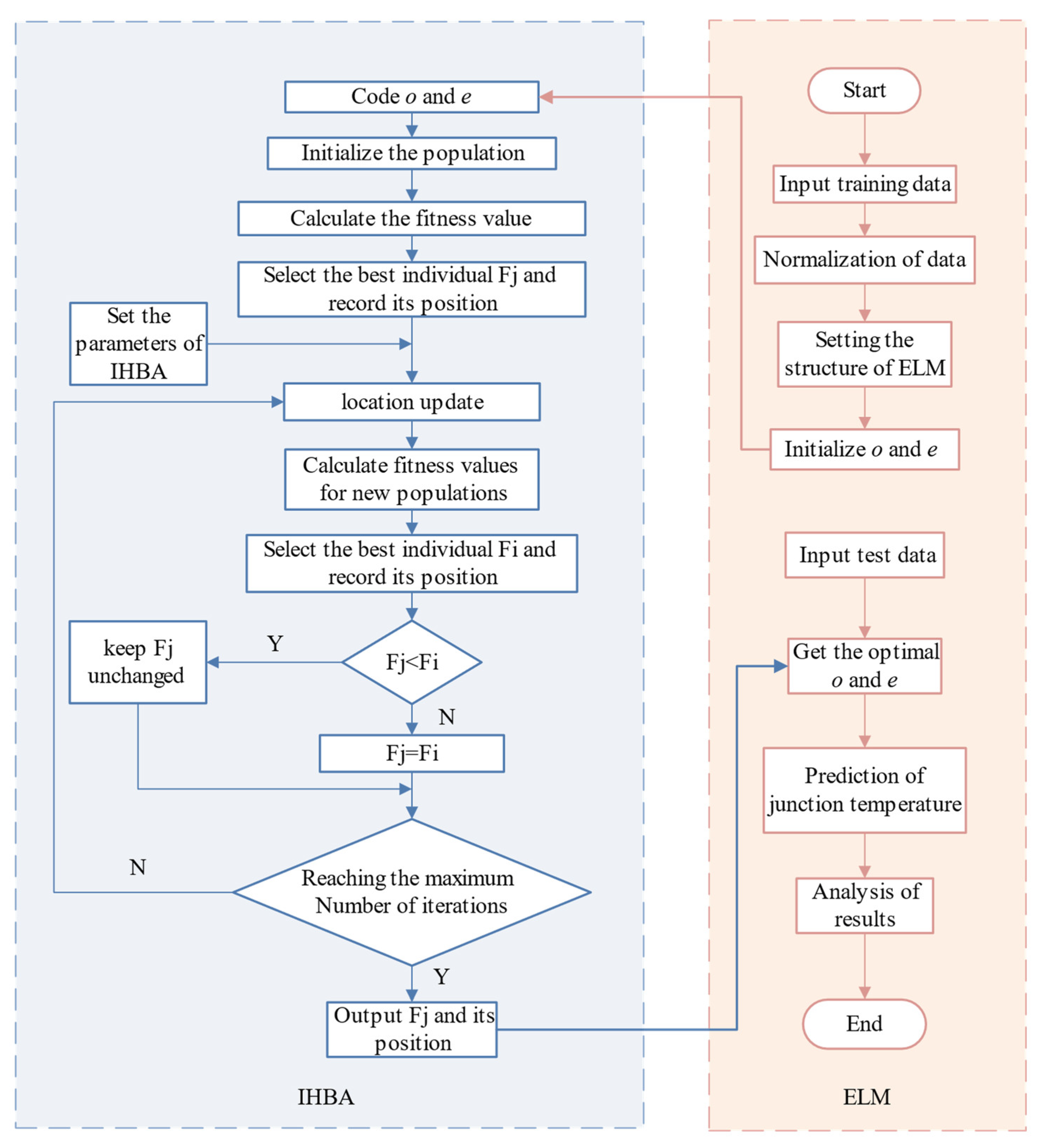
3.4. Modeling of Junction Temperature Prediction Based on IHBA-ELM
3.4.1. Principle of Extreme Learning Machine and Honey Badger Algorithm
- 1.
- Initialization of algorithm parameters. That is, set the problem’s dimension, the number of honey badgers and their initial position.
- 2.
- Calculate honey attractiveness. Honey attractiveness is the degree of attraction of the hive to honey badgers. Equation (15) is used to obtain it.
- 3.
- Update the location of honey badgers. There are two location update formulas. Let be a number that is located within at random. If , the location of the honey badger can be updated by Equation (16).
3.4.2. Improvement of the HBA
- 1.
- The initialization of the population was improved. To enhance the quality of the initial population and the diversity of population individuals, cubic chaotic mapping was introduced in this paper [51]. As shown in Equation (19).
- 2.
- The wave state adaptive weights were introduced. In the position update formula of the honey badger population, the coefficient in front of is 1, which could lead to local rigidity in position updates. Therefore, the wave state adaptive weights were introduced as coefficients of to improve the optimization ability.
- 3.
- The Gaussian variance function was introduced. In late iterations, the population diversity of the honey badger algorithm decreases; thus, the local optimum tends to be obtained. Therefore, the Gaussian variation function was introduced to make the population more prosperous. After obtaining the new population by Equation (16) or Equation (18). Let
3.4.3. The Process and Evaluation Index of IHBA-ELM
4. Results
5. Discussion
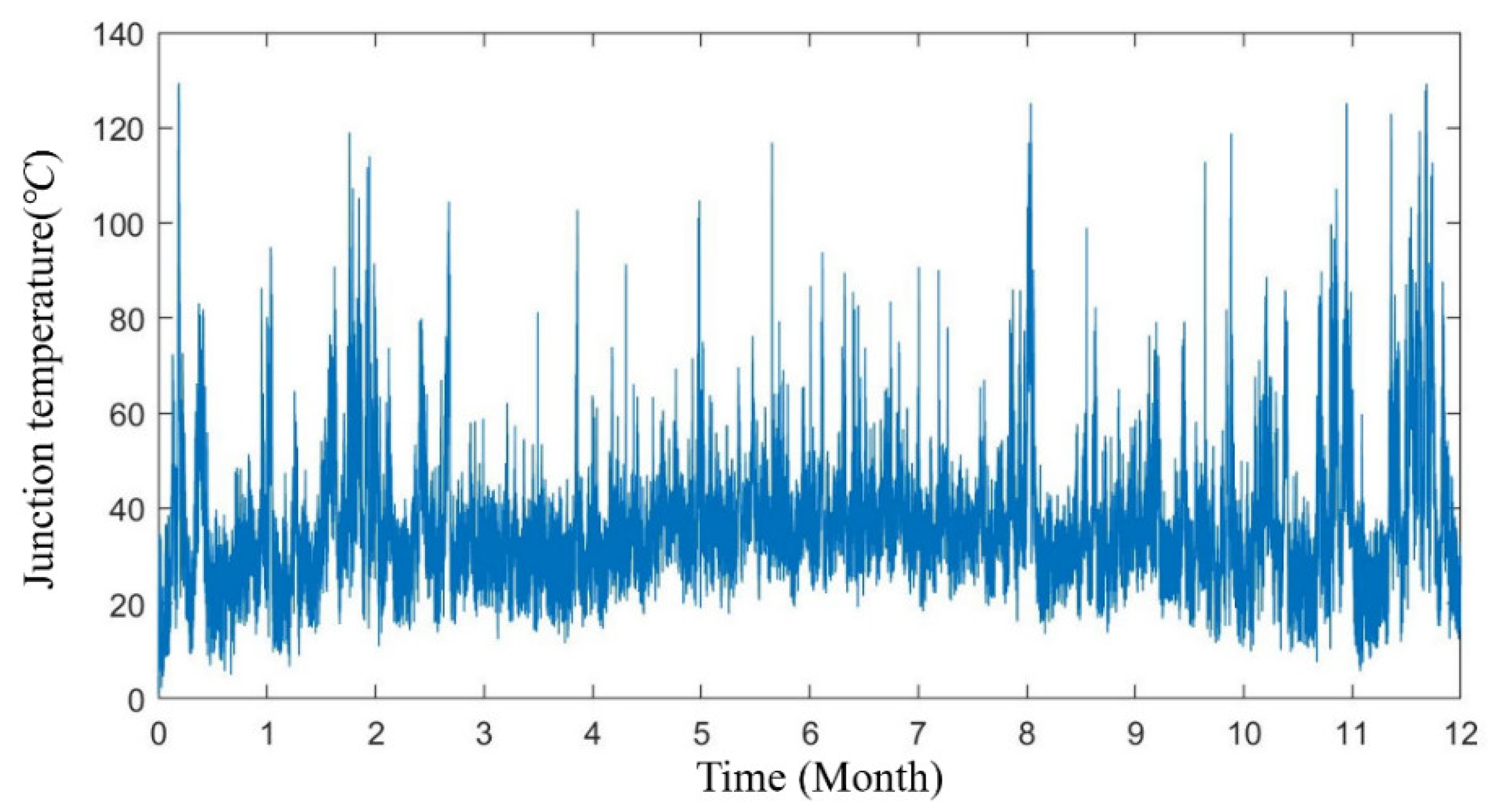
5.1. Junction Temperature Acquisition
- (1)
- Due to the thermal resistance, the energy loss of the IGBT power module can be converted into heat. If it cannot be dissipated in time, the heat will accumulate, which leads to an increase in junction temperature. Since the electro-heat coupling model is based on the principle of heat generation, the junction temperature obtained by this method is accurate.
- (2)
- (3)
- In Section 3, the accuracy of this method has been verified by simulation methods. PLECS is a professional system-level power electronic circuit simulation software. Therefore, the simulation circuit was built on PLECS, and the junction temperature of the IGBT was obtained by two methods. One method was to calculate the junction temperature using the electro-heat coupling model method, and the other was to measure the junction temperature directly, using the thermal simulation function of the software. The acquired junction temperature was imported to the oscilloscope. Then, the waveform can be obtained as shown in Figure 3. According to Figure 3, it can be seen that the fluctuations of the junction temperature obtained by these two methods are almost equal. This indicates that the calculation of the junction temperature by the electro-heat coupled model method is accurate.
5.2. Improved Honey Badger Algorithm—Extreme Learning Machine
- (1)
- In this study, the initialization strategy and iteration strategy of the HBA were improved with the cubic chaotic mapping, the wave state adaptive weights, and the Gaussian variance function, and the IHBA was obtained. The HBA, IHBA, GWO, and SOA were compared using six test functions, as shown in Table 1. The results prove that the IHBA has higher convergence accuracy and faster convergence speed.
- (2)
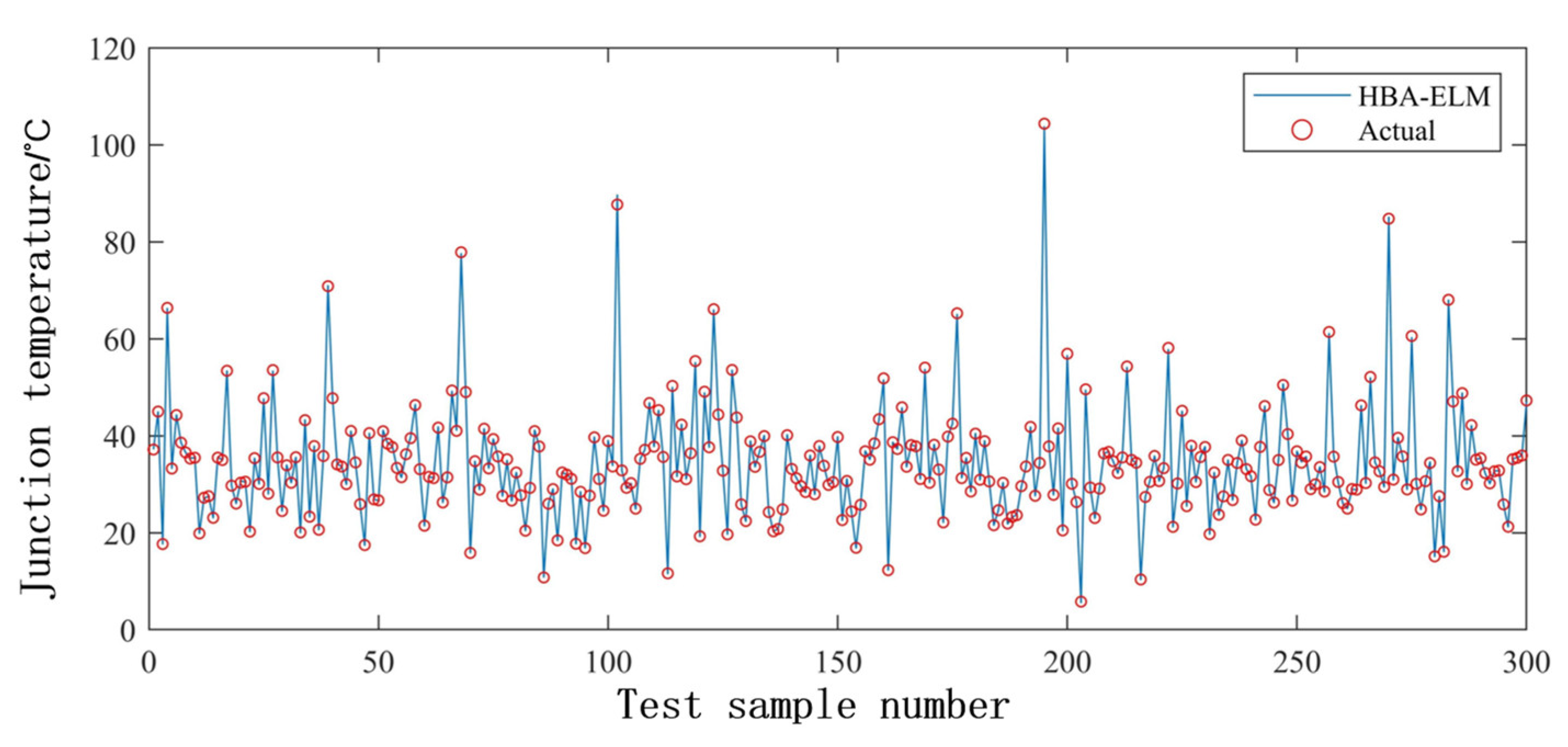
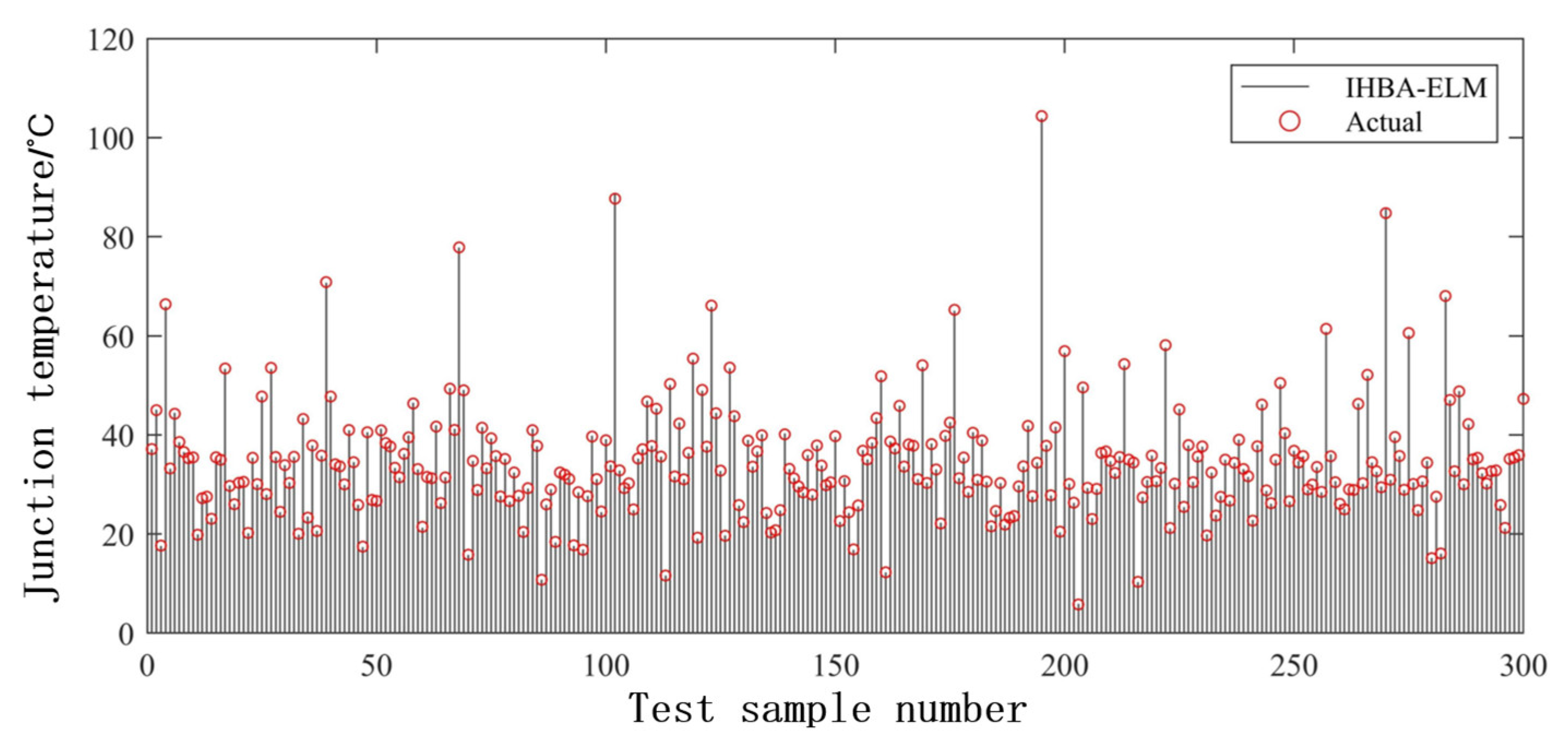
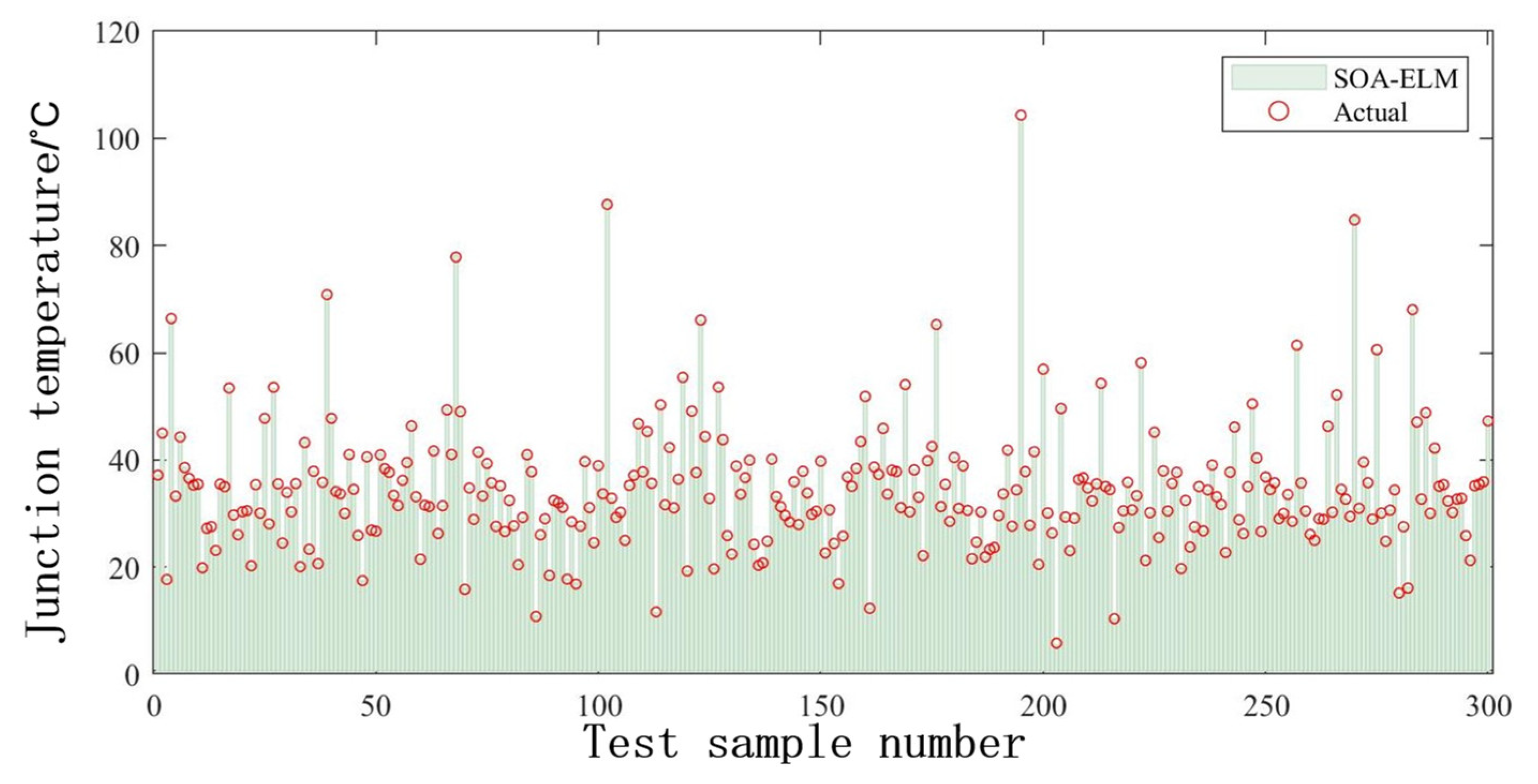
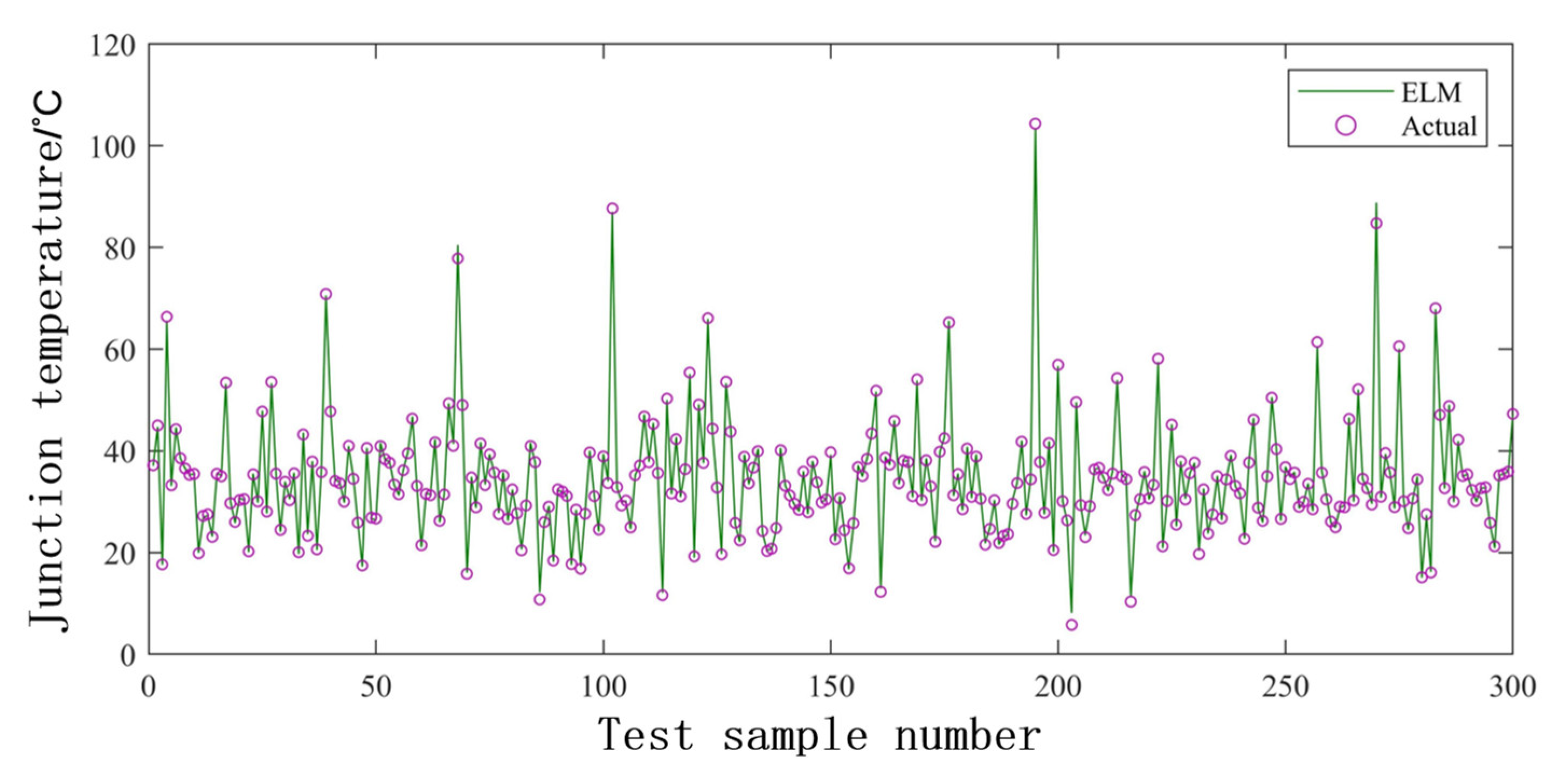
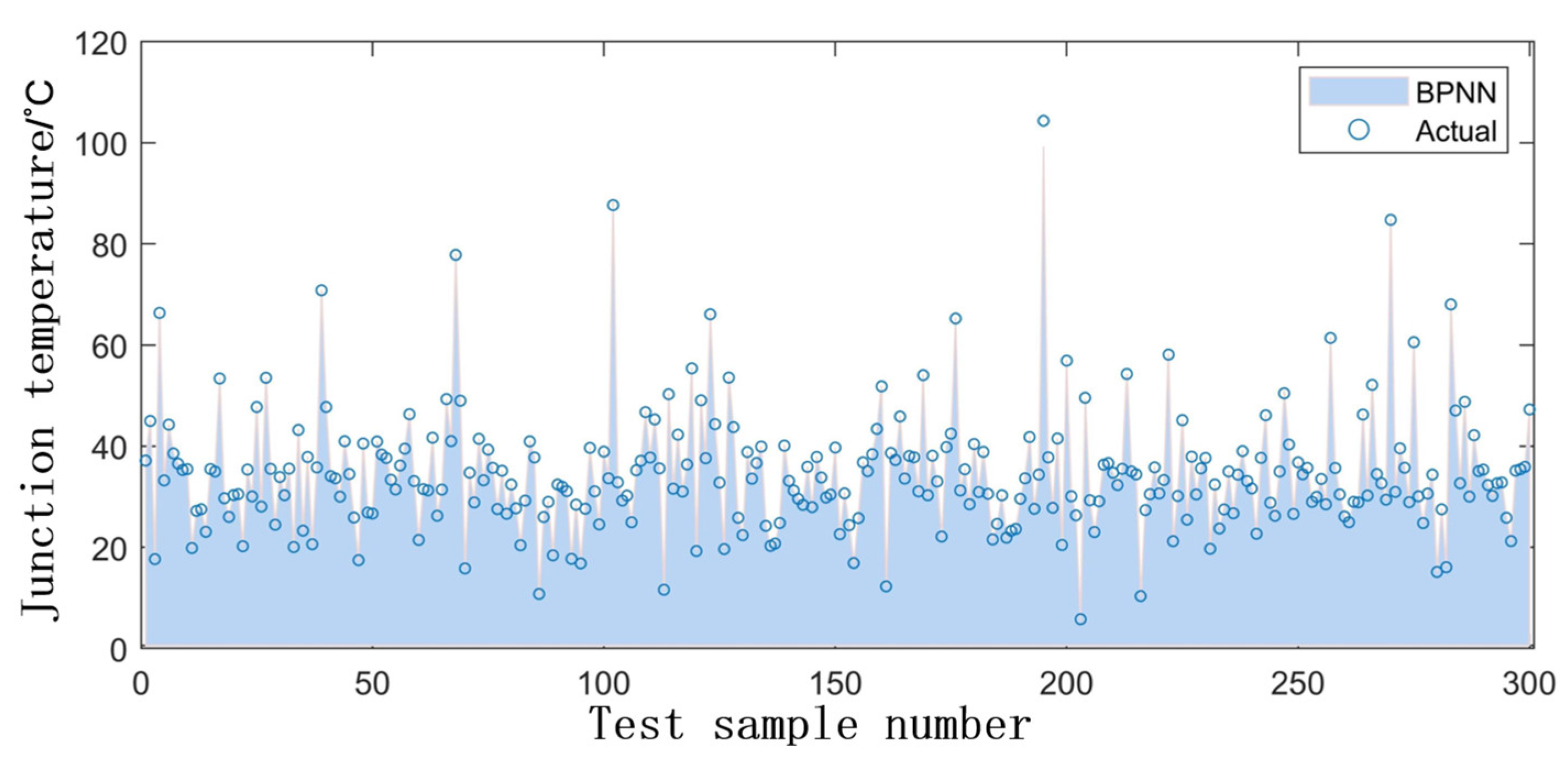
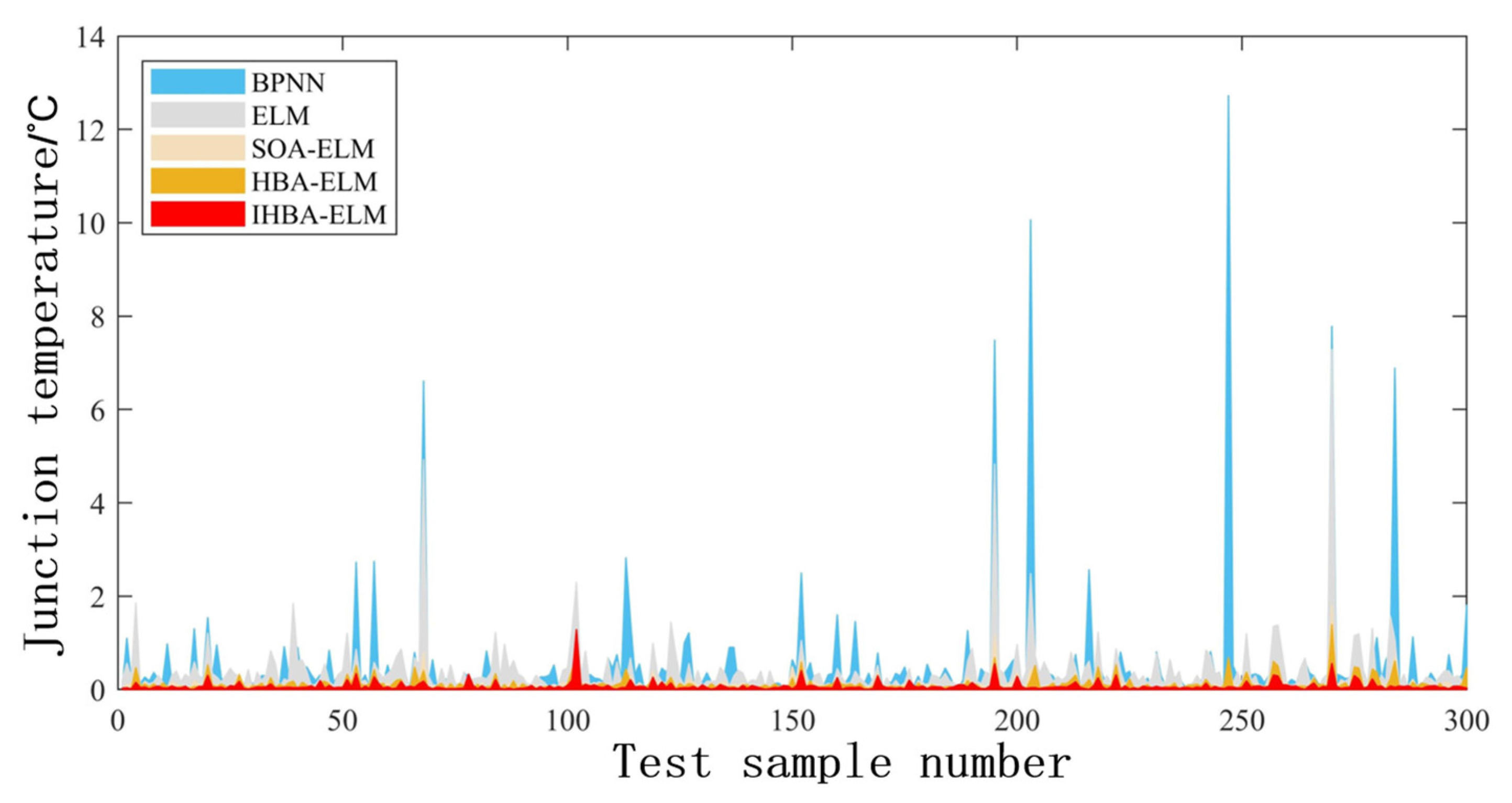
- The algorithm used for the BPNN is the gradient descent (GD) method, which requires several iterations and a long training time. Furthermore, the BPNN can easily fall into the local minimum, resulting in poor convergence accuracy. Compared with the BPNN, the ELM randomly generates the weight value joining the input layer to the hidden layer and the threshold of the hidden layer during the iteration, which does not need to be adjusted during the training process. Therefore, the ELM has faster convergence and better generalization ability than the BPNN. It has been proved that the MEA of ELM is lower than that of BPNN in this study. Therefore, ELM is more suitable for junction temperature prediction. In addition, good results have been achieved using artificial intelligence algorithms to optimize the ELM. The SOA-ELM, HBA-ELM, and IHBA-ELM all have lower MEA and RMSE than the ELM. This is because the artificial intelligence algorithm can find the best weights and thresholds, thus improving the accuracy of the ELM. The design principles of different artificial intelligence algorithms are different, and their search performance and computational efficiency also vary. However, there is no absolute superiority or inferiority between different intelligent algorithms. Each type of problem has its own best suited artificial intelligence algorithm. By comparing several models, it can be found that the IHBA-ELM model used in this study has higher accuracy in predicting the junction temperature of IGBTs in wind power systems.
- (3)
- Based on the IHBA-ELM, the junction temperature of the IGBT can be obtained by inputting the wind speed and the cabin temperature of the generator. Both wind speed and temperature can be easily measured. Therefore, the proposed method was easy to apply.
6. Conclusions
- (1)
- A junction temperature prediction model based on the IHBA-ELM was proposed. The model can effectively predict the junction temperature of IGBTs in wind power converters and ensure the stable operation of wind power systems.
- (2)
- Based on the proposed model, the junction temperature of the IGBT can be obtained by inputting the wind speed and the cabin temperature of the generator. The wind speed and the cabin temperature of the generator are easy to measure, and no additional sensors are needed.
- (3)
- Compared with other prediction models, the model proposed in this study is more suitable for junction temperature prediction of IGBTs in wind power systems.
- (4)
- The proposed IHBA-ELM model is not only suitable for junction temperature prediction of IGBTs in wind power systems, but also can provide reference for prediction in other fields.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shah, S.A.A.; Sayyad, M.H.; Khan, K.; Guo, K.; Shen, F.; Sun, J.; Tareen, A.K.; Gong, Y.; Guo, Z. Progress towards High-Efficiency and Stable Tin-Based Perovskite Solar Cells. Energies 2020, 13, 5092. [Google Scholar] [CrossRef]
- Lotfi, M.; Javadi, M.; Osorio, G.J.; Monteiro, C.; Catalao, J.P.S. A Novel Ensemble Algorithm for Solar Power Forecasting Based on Kernel Density Estimation. Energies 2020, 13, 216. [Google Scholar] [CrossRef]
- Zhou, F.; Tu, X.; Wang, Q. Research on offshore wind power system based on Internet of Things technology. Int. J. Low-Carbon Technol. 2022, 17, 645–650. [Google Scholar] [CrossRef]
- Rasool, S.; Muttaqi, K.M.; Sutanto, D.; Hemer, M. Quantifying the reduction in power variability of co-located offshore wind-wave farms. Renew. Energy 2021, 185, 1018–1033. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, S.; Zao, P.; Yu, Y.; Zou, L.; Liu, L.; Li, J. Experimental evaluation of a tree-shaped quad-rotor wind turbine on power output controllability and survival shutdown capability. Appl. Energy 2022, 309, 118350. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, G.; Zhang, D.; Kim, B.; Xu, F.; Xiao, Y. Aerodynamic Characteristics of a Square Cylinder with Vertical-Axis Wind Turbines at Corners. Appl. Sci. 2022, 12, 3515. [Google Scholar] [CrossRef]
- Srinivasan, P.; Jagatheeswari, P. Machine Learning Controller for DFIG Based Wind Conversion System. Intell. Autom. Soft Comput. 2023, 35, 381–397. [Google Scholar] [CrossRef]
- Pape, M.; Kazerani, M. A Generic Power Converter Sizing Framework for Series-Connected DC Offshore Wind Farms. IEEE Trans. Power Electron. 2022, 37, 2307–2320. [Google Scholar] [CrossRef]
- Choi, U.-M.; Blaabjerg, F.; Lee, K.-B. Study and Handling Methods of Power IGBT Module Failures in Power Electronic Converter Systems. IEEE Trans. Power Electron. 2015, 30, 2517–2533. [Google Scholar] [CrossRef]
- Luo, H.; Chen, Y.; Sun, P.; Li, W.; He, X. Junction Temperature Extraction Approach with Turn-Off Delay Time for High-Voltage High-Power IGBT Modules. IEEE Trans. Power Electron. 2016, 31, 5122–5132. [Google Scholar] [CrossRef]
- Hu, Y.; Shi, P.; Li, H.; Yang, C. Health Condition Assessment of Base-Plate Solder for Multi-Chip IGBT Module in Wind Power Converter. IEEE Access 2019, 7, 72134–72142. [Google Scholar] [CrossRef]
- Abuelnaga, A.; Narimani, M.; Bahman, A.S. A Review on IGBT Module Failure Modes and Lifetime Testing. IEEE Access 2021, 9, 9643–9663. [Google Scholar] [CrossRef]
- Tsai, H.-W.; Ker, M.-D. Layout Consideration and Circuit Solution to Prevent EOS Failure Induced by Latchup Test in a High-Voltage Integrated Circuits. IEEE Trans. Device Mater. Reliab. 2014, 14, 493–498. [Google Scholar] [CrossRef][Green Version]
- Hu, Z.; Ge, X.; Xie, D.; Zhang, Y.; Yao, B.; Dai, J.; Yang, F. An Aging-Degree Evaluation Method for IGBT Bond Wire with Online Multivariate Monitoring. Energies 2019, 12, 3962. [Google Scholar] [CrossRef]
- Wang, C.; He, Y.; Wang, C.; Li, L.; Wu, X. Multi-Chip IGBT Module Failure Monitoring Based on Module Transconductance with Temperature Calibration. Electronics 2020, 9, 1559. [Google Scholar] [CrossRef]
- Yang, J.; Che, Y.; Ran, L.; Du, M.; Jiang, H.; Xiao, M. Monitoring Initial Solder Layer Degradation in a Multichip IGBT Module via Combined TSEPs. IEEE Trans. Device Mater. Reliab. 2021, 22, 26–35. [Google Scholar] [CrossRef]
- Shao, L.; Xu, G.; Li, P. A Hybrid Model of Turn-Off Loss and Turn-Off Time for Junction Temperature Extraction. IEEE J. Electron Devices Soc. 2021, 10, 3–12. [Google Scholar] [CrossRef]
- Liu, Z.F.; Li, L.L.; Liu, Y.W.; Liu, J.Q.; Li, H.Y.; Shen, Q. Dynamic economic emission dispatch considering renewable energy generation: A novel multi-objective optimization approach. Energy 2021, 235, 121407. [Google Scholar] [CrossRef]
- Li, L.-L.; Liu, Z.-F.; Tseng, M.-L.; Zheng, S.-J.; Lim, M.K. Improved tunicate swarm algorithm: Solving the dynamic economic emission dispatch problems. Appl. Soft Comput. 2021, 108, 107504. [Google Scholar] [CrossRef]
- Wei, W.; Zhu, W.; Liu, T.; Xu, G. Junction Temperature Online Extraction Method for Power MOSFET by Current Fall Time. IEEE Trans. Electron Devices 2022, 69, 3811–3819. [Google Scholar] [CrossRef]
- Xu, C.Q.; Zhao, B.; Zhang, X.Y.; Chen, Z.Y.; Liu, J.P.; Zhou, W.P.; Zeng, R. Full-Time Junction Temperature Extraction of IGCT Based on Electrothermal Model and TSEP Method for High-Power Applications. IEEE Trans. Ind. Electron. 2020, 68, 47–58. [Google Scholar] [CrossRef]
- Polom, T.A.; Lorenz, R.D. Power Device Interface Characterization with Low-Cost Thermal System Identification. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 1342–1352. [Google Scholar] [CrossRef]
- Ji, B.; Song, X.; Cao, W.; Pickert, V.; Hu, Y.; Mackersie, J.W.; Pierce, G. In Situ Diagnostics and Prognostics of Solder Fatigue in IGBT Modules for Electric Vehicle Drives. IEEE Trans. Power Electron. 2014, 30, 1535–1543. [Google Scholar]
- Du, B.; Hudgins, J.L.; Santi, E.; Bryant, A.T.; Palmer, P.R.; Mantooth, H.A. Transient Electrothermal Simulation of Power Semiconductor Devices. IEEE Trans. Power Electron. 2009, 25, 237–248. [Google Scholar]
- Schmidt, R.; Scheuermann, U. Using the Chip as a Temperature Sensor—The Influence of Steep Lateral Temperature Gradients on the V-CE(T)-Measurement. Epe J. 2011, 21, 5–10. [Google Scholar] [CrossRef]
- Dupont, L.; Avenas, Y.; Jeannin, P.-O. Comparison of Junction Temperature Evaluations in a Power IGBT Module Using an IR Camera and Three Thermosensitive Electrical Parameters. IEEE Trans. Ind. Appl. 2013, 49, 1599–1608. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, P. A Novel Converter-Level IGBT Junction Temperature Estimation Method Based on the Bus Voltage Ringing. IEEE Trans. Power Electron. 2021, 37, 4553–4563. [Google Scholar] [CrossRef]
- Shao, L.; Hu, Y.; Xu, G. A High Precision On-Line Detection Method for IGBT Junction Temperature Based on Stepwise Regression Algorithm. IEEE Access 2020, 8, 186172–186180. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, F.; Wang, F. Junction Temperature Measurement of IGBTs Using Short-Circuit Current as a Temperature-Sensitive Electrical Parameter for Converter Prototype Evaluation. IEEE Trans. Ind. Electron. 2015, 62, 3419–3429. [Google Scholar] [CrossRef]
- Liu, B.; Chen, G.; Lin, H.-C.; Zhang, W.; Liu, J. Prediction of IGBT junction temperature using improved cuckoo search-based extreme learning machine. Microelectron. Reliab. 2021, 124, 114267. [Google Scholar] [CrossRef]
- Xu, D.W.; Lu, H.W.; Huang, L.P.; Azuma, S.S.; Kimata, M.H.; Uchida, R.H. Power loss and junction temperature analysis of power semiconductor devices. IEEE Trans. Ind. Appl. 2002, 38, 1426–1431. [Google Scholar]
- Li, H.; Liao, X.; Zeng, Z.; Hu, Y.; Li, Y.; Liu, S.; Ran, L. Thermal Coupling Analysis in a Multichip Paralleled IGBT Module for a DFIG Wind Turbine Power Converter. IEEE Trans. Energy Convers. 2016, 32, 80–90. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Wang, Z.; Yang, Y.; Blaabjerg, F. A Simplification Method for Power Device Thermal Modeling with Quantitative Error Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1649–1658. [Google Scholar] [CrossRef]
- Sang, B. Application of genetic algorithm and BP neural network in supply chain finance under information sharing. J. Comput. Appl. Math. 2020, 384, 113170. [Google Scholar] [CrossRef]
- Pan, Z.; Meng, Z.; Chen, Z.; Gao, W.; Shi, Y. A two-stage method based on extreme learning machine for predicting the remaining useful life of rolling-element bearings. Mech. Syst. Signal Process. 2020, 144, 106899. [Google Scholar] [CrossRef]
- Pan, L.; Xiong, Y.; Zhu, Z.; Wang, L.C. Research on variable pitch control strategy of direct-driven offshore wind turbine using KELM wind speed soft sensor. Renew. Energy 2022, 184, 1002–1017. [Google Scholar] [CrossRef]
- Kushwah, G.S.; Ranga, V. Detecting DDoS Attacks in Cloud Computing Using Extreme Learning Machine and Adaptive Differential Evolution. Wirel. Pers. Commun. 2022, 124, 2613–2636. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.S.; Rajaguru, H. Automatic Detection and Classification of Mammograms Using Improved Extreme Learning Machine with Deep Learning. Irbm 2022, 43, 49–61. [Google Scholar] [CrossRef]
- Han, E.R.; Ghadimi, N. Model identification of proton-exchange membrane fuel cells based on a hybrid convolutional neural network and extreme learning machine optimized by improved honey badger algorithm. Sustain. Energy Technol. Assess. 2022, 52, 106899. [Google Scholar] [CrossRef]
- Li, H.; Long, H.; Bai, P.; Zheng, M. Loss Calculation of Multi-chip IGBT Modular with the Influence of Stray Inductance. Power Electron. 2018, 52, 26–30. [Google Scholar]
- Ju, J.H.; Zhao, Z.M.; Shi, B.C.; Zhu, Y.C.; Yu, Z.J. Motor-Oriented Discrete State Event-Driven Method for Multitime-Scale Simulation of Power Traction Systems. IEEE Trans. Transp. Electrif. 2021, 7, 1652–1661. [Google Scholar] [CrossRef]
- Gorecki, P. Electrothermal Averaged Model of a Diode-IGBT Switch for a Fast Analysis of DC-DC Converters. IEEE Trans. Power Electron. 2022, 37, 13003–13013. [Google Scholar] [CrossRef]
- Hefner, A.R.; Diebolt, D.M. An experimentally verified IGBT model implemented in the Saber circuit simulator. In Proceedings of the 22nd Annual IEEE Power Electronics Specialists Conference (Pesc 91), Cambridge, MA, USA, 24–27 June 1991; pp. 10–19. [Google Scholar]
- Wang, X.; Li, Z.; Yao, F.; Tang, S. Simplified Estimation of Junction Temperature Fluctuation at the Fundamental Frequency for IGBT Modules Considering Mission Profile. IEEE Access 2019, 7, 149308–149317. [Google Scholar] [CrossRef]
- Khan, M.N.H.; Forouzesh, M.; Siwakoti, Y.P.; Li, L.; Kerekes, T.; Blaabjerg, F. Transformerless Inverter Topologies for Single-Phase Photovoltaic Systems: A Comparative Review. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 805–835. [Google Scholar] [CrossRef]
- Mansour, M.Z.; Me, S.P.; Hadavi, S.; Badrzadeh, B.; Karimi, A.; Bahrani, B. Nonlinear Transient Stability Analysis of Phased-Locked Loop-Based Grid-Following Voltage-Source Converters Using Lyapunov’s Direct Method. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2699–2709. [Google Scholar] [CrossRef]
- Gorecki, P.; Wojciechowski, D. Accurate Computation of IGBT Junction Temperature in PLECS. IEEE Trans. Electron Devices 2020, 67, 2865–2871. [Google Scholar] [CrossRef]
- Madhusoodhanan, S.; Mainali, K.; Tripathi, A.K.; Kadavelugu, A.; Patel, D.; Bhattacharya, S. Power Loss Analysis of Medium-Voltage Three-Phase Converters Using 15-kV/40-A SiC N-IGBT. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 902–917. [Google Scholar] [CrossRef]
- Xie, K.; Jiang, Z.; Li, W. Effect of Wind Speed on Wind Turbine Power Converter Reliability. IEEE Trans. Energy Convers. 2012, 27, 96–104. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Wang, C.; Di, Y.; Tang, J.; Shuai, J.; Zhang, Y.; Lu, Q. The Dynamic Analysis of a Novel Reconfigurable Cubic Chaotic Map and Its Application in Finite Field. Symmetry 2021, 13, 1420. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowledge-Based Syst. 2018, 165, 169–196. [Google Scholar] [CrossRef]

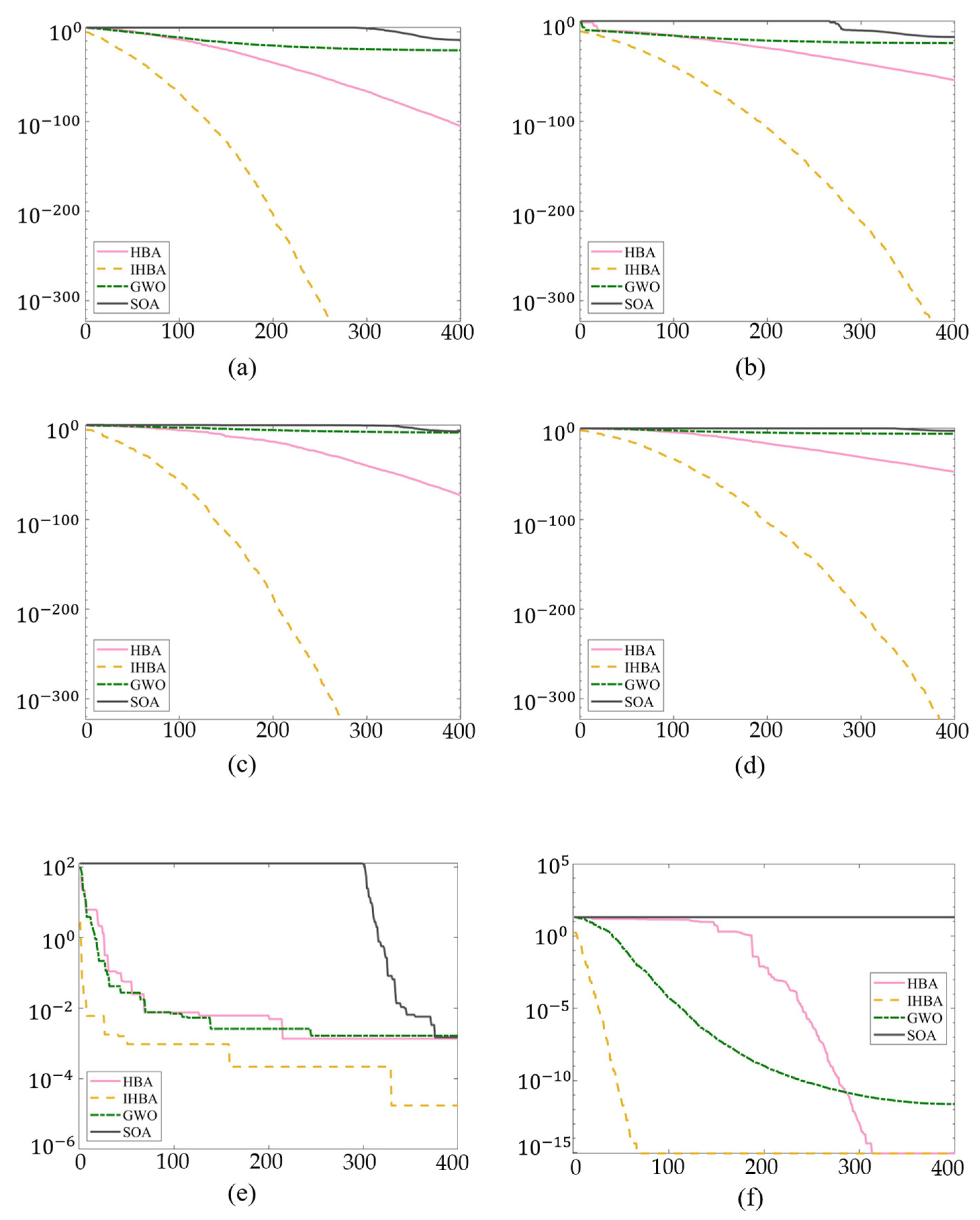
| Test Functions | Dimension | Upper Boundary | Lower Boundary | Optimum Value |
|---|---|---|---|---|
| 30 | 100 | −100 | 0 | |
| 30 | 10 | −10 | 0 | |
| 30 | 100 | −10 | 0 | |
| 30 | 100 | −100 | 0 | |
| 30 | 1.28 | −1.28 | 0 | |
| 30 | 32 | −32 | 0 |
| Test Functions | Algorithm | Worst Value | Best Value | Average Value | Variance |
|---|---|---|---|---|---|
| HBA | 6.50 × 10−101 | 1.91 × 10−110 | 3.59 × 10−102 | 1.73 × 10−202 | |
| IHBA | 0 | 0 | 0 | 0 | |
| GWO | 2.30 × 10−20 | 7.40 × 10−23 | 1.80 × 10−21 | 1.64 × 10−41 | |
| SOA | 2.41 × 10−54 | 2.29 × 10−70 | 1.36 × 10−55 | 2.32 × 10−109 | |
| HBA | 3.11 × 10−54 | 5.81 × 10−58 | 3.60 × 10−55 | 5.75 × 10−109 | |
| IHBA | 0 | 0 | 0 | 0 | |
| GWO | 8.86 × 10−13 | 1.00 × 10−13 | 4.34 × 10−13 | 4.18 × 10−26 | |
| SOA | 8.07 × 10−39 | 4.87 × 10−46 | 2.90 × 10−40 | 2.09 × 10−78 | |
| HBA | 3.03 × 10−71 | 1.41 × 10−84 | 1.87 × 10−72 | 3.94 × 10−143 | |
| IHBA | 0 | 0 | 0 | 0 | |
| GWO | 8.56 × 10−3 | 2.15 × 10−6 | 1.24 × 10−3 | 5.49 × 10−6 | |
| SOA | 9.64 × 104 | 1.99 × 104 | 5.03 × 104 | 2.91 × 108 | |
| HBA | 1.44 × 10−43 | 3.84 × 10−50 | 9.68 × 10−45 | 7.66 × 10−88 | |
| IHBA | 0 | 0 | 0 | 0 | |
| GWO | 1.64 × 10−4 | 6.46 × 10−6 | 2.68 × 10−5 | 9.41 × 10−10 | |
| SOA | 89.71 | 11.91 | 55.24 | 5.74e + 02 | |
| HBA | 1.45 × 10−3 | 7.08 × 10−5 | 5.49 × 10−4 | 1.53 × 10−7 | |
| IHBA | 3.45 × 10−4 | 5.54 × 10−6 | 1.07 × 10−4 | 9.75 × 10−9 | |
| GWO | 7.68 × 10−3 | 6.73 × 10−4 | 2.79 × 10−3 | 3.51 × 10−6 | |
| SOA | 1.55 × 10−2 | 7.34 × 10−5 | 3.61 × 10−3 | 2.09 × 10−5 | |
| HBA | 7.55 × 10−5 | 8.87 × 10−16 | 2.52 × 10−6 | 1.84 × 10−10 | |
| IHBA | 8.87 × 10−16 | 8.87 × 10−16 | 8.87 × 10−16 | 8.87 × 10−16 | |
| GWO | 2.78 × 10−11 | 2.38 × 10−12 | 9.71 × 10−12 | 4.02 × 10−23 | |
| SOA | 1.51 × 10−14 | 8.87 × 10−16 | 5.15 × 10−15 | 9.59 × 10−30 |
| Prediction Models | Evaluation Indicators | Maximum Value (°C) | Minimum Value (°C) | Average Value (°C) | Variance |
|---|---|---|---|---|---|
| HBA-ELM | MEA | 0.0793 | 0.0142 | 0.0339 | 1.0337 × 10−4 |
| RMSE | 0.0420 | 0.0086 | 0.0043 | 3.8752 × 10−7 | |
| R2 | 0.9999 | 0.9994 | 0.9998 | 5.3134 × 10−9 | |
| IHBA-ELM | MEA | 0.0526 | 0.0135 | 0.0303 | 7.0670 × 10−5 |
| RMSE | 0.0052 | 0.0027 | 0.0041 | 3.3057 × 10−7 | |
| R2 | 0.9999 | 0.9996 | 0.9998 | 3.6326 × 10−9 | |
| SOA-ELM | MEA | 0.0567 | 0.0180 | 0.0341 | 1.0939 × 10−4 |
| RMSE | 0.0056 | 0.0032 | 0.0043 | 4.4091 × 10−7 | |
| R2 | 0.9999 | 0.9996 | 0.9998 | 5.6227 × 10−9 | |
| ELM | MEA | 2.6834 | 0.0857 | 0.3637 | 0.3432 |
| RMSE | 0.0387 | 0.0069 | 0.0122 | 5.4236 × 10−5 | |
| R2 | 0.9994 | 0.9829 | 0.9976 | 1.3719 × 10−5 | |
| BPNN | MEA | 11.1554 | 0.0151 | 0.6791 | 4.0340 |
| RMSE | 3.3400 | 0.1230 | 0.5892 | 0.3434 | |
| R2 | 0.9999 | 0.9522 | 0.9964 | 7.4671 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Gao, B.; Yang, H.; Zhang, X.; Liu, J.; Li, L. Junction Temperature Prediction of Insulated-Gate Bipolar Transistors in Wind Power Systems Based on an Improved Honey Badger Algorithm. Energies 2022, 15, 7366. https://doi.org/10.3390/en15197366
Zhou C, Gao B, Yang H, Zhang X, Liu J, Li L. Junction Temperature Prediction of Insulated-Gate Bipolar Transistors in Wind Power Systems Based on an Improved Honey Badger Algorithm. Energies. 2022; 15(19):7366. https://doi.org/10.3390/en15197366
Chicago/Turabian StyleZhou, Chao, Bing Gao, Haiyue Yang, Xudong Zhang, Jiaqi Liu, and Lingling Li. 2022. "Junction Temperature Prediction of Insulated-Gate Bipolar Transistors in Wind Power Systems Based on an Improved Honey Badger Algorithm" Energies 15, no. 19: 7366. https://doi.org/10.3390/en15197366
APA StyleZhou, C., Gao, B., Yang, H., Zhang, X., Liu, J., & Li, L. (2022). Junction Temperature Prediction of Insulated-Gate Bipolar Transistors in Wind Power Systems Based on an Improved Honey Badger Algorithm. Energies, 15(19), 7366. https://doi.org/10.3390/en15197366






