Development of Monitoring and Forecasting Technology Energy Efficiency of Well Drilling Using Mechanical Specific Energy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Development of Algorithms for Association of Axial and Transverse Vibrations While Drilling
- The height of the bit indenter—h, the damping coefficient that combines the action of dissipative forces and controls the rate of damping of vibrations, the Young’s modulus of the string, the outer and inner diameters of the DS, its mass, length of the BHA, and the frequency of shocks generated at the bottom are set.
- The initial conditions are assumed as follows: the DS is lowered to the bottom, the rock is destroyed, and the first wave is simultaneously generated, which makes the following contribution to the effective acceleration of gravity acting on the DS, Equation (8).
- For the time in the specified range, the generation of new waves is calculated. New waves can be generated in two ways: (1) the wave, propagating at the speed of sound in steel, reaches the top of the BHA. The wave is reflected, which can be represented as an instantaneous damping of the incident wave with the generation of a secondary reflected wave in the opposite direction; (2) the DS is again lowered to the bottom, generating a wave when the indenter contacts the bottom rock.
- A graph of the total impact of waves is built for a given time, taking into account their attenuation, the decrement of which can be expressed as , where T—period, moreover , and .
- m—the mass of the BHA, kg.
- Ac—contact area proportional to the indenter area, m2.
- ω—the angular velocity of rotation of the bit, rad/s.
- I—the moment of inertia of the BHA, kg × m2.
- —cutting depth for rock breaking, m.
- n—rate of rotation, rpm.
2.2. Experimental Research of Longitudinal and Transverse Deformation of Rock Samples
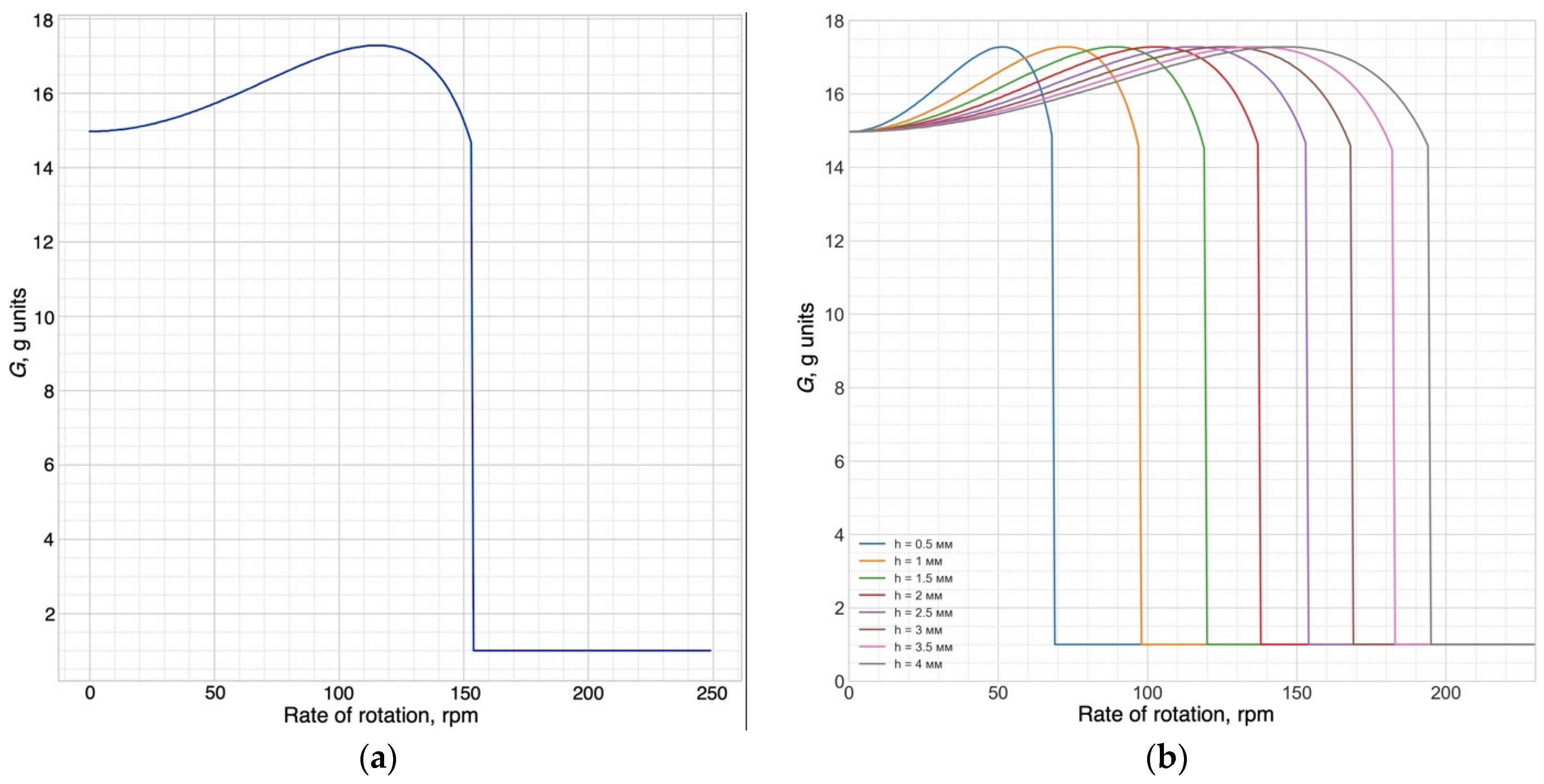
2.3. Simulation of the Dynamics of Directional Indention to Determine the Cutting Depth of the Drilling of Rocks
- —Young’s modulus of steel and rock, GPa.
- —density of steel and rock, respectively, kg/m3.
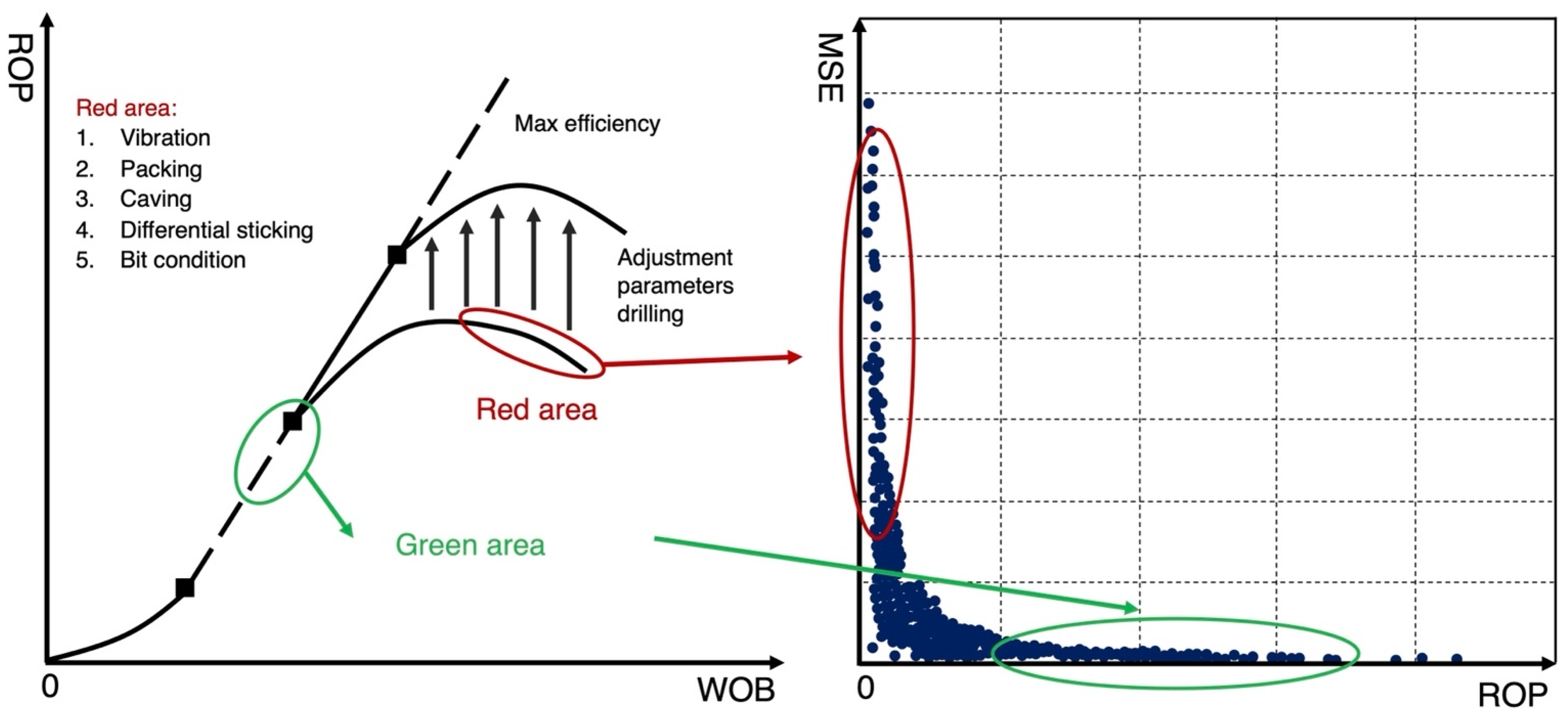
2.4. Analysis of the Drilling Process Performance
- N—number of rotations.
- Mb—torque on bit, N·m.
- M—torque on rotor, N·m.
- —bit sliding coefficient, units.
- —drill string sliding coefficient of friction, units.
- —zenith angle, rad.
- E—energy spent on rock destruction, J.
- V—volume of destroyed rock, m3.
- Sb—borehole cross-sectional area, m2.
- —Actual WOB at the bottom hole, N.
- —torque at the bottom hole, N × m.
- —bit sliding coefficient of friction, units.
- —drill string sliding coefficient of friction, units.
- —zenith angle, rad.
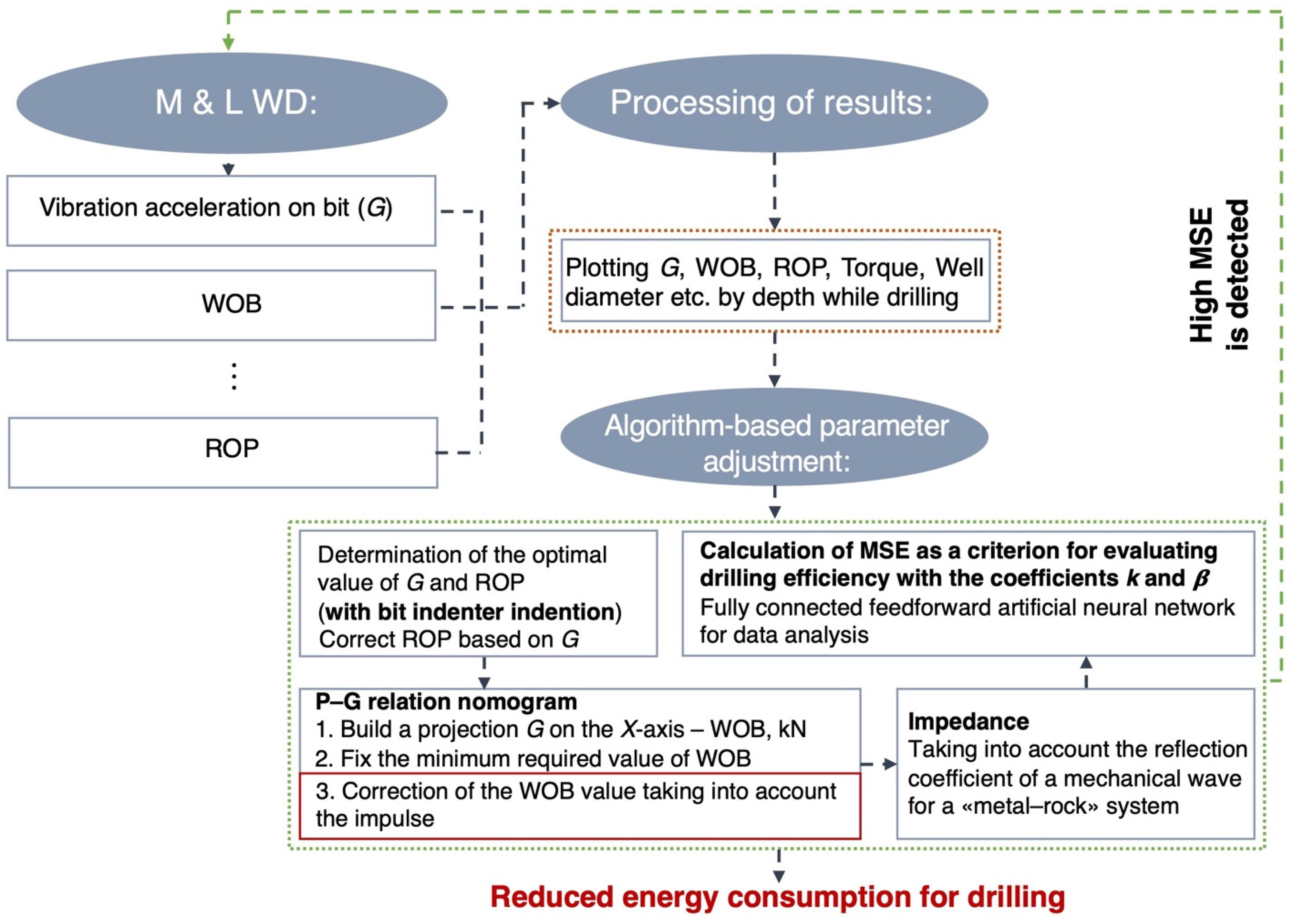
2.5. Algorithm for Predicting and Monitoring the Impulse and Determining the Most Efficient WOB While Drilling Directional Wells
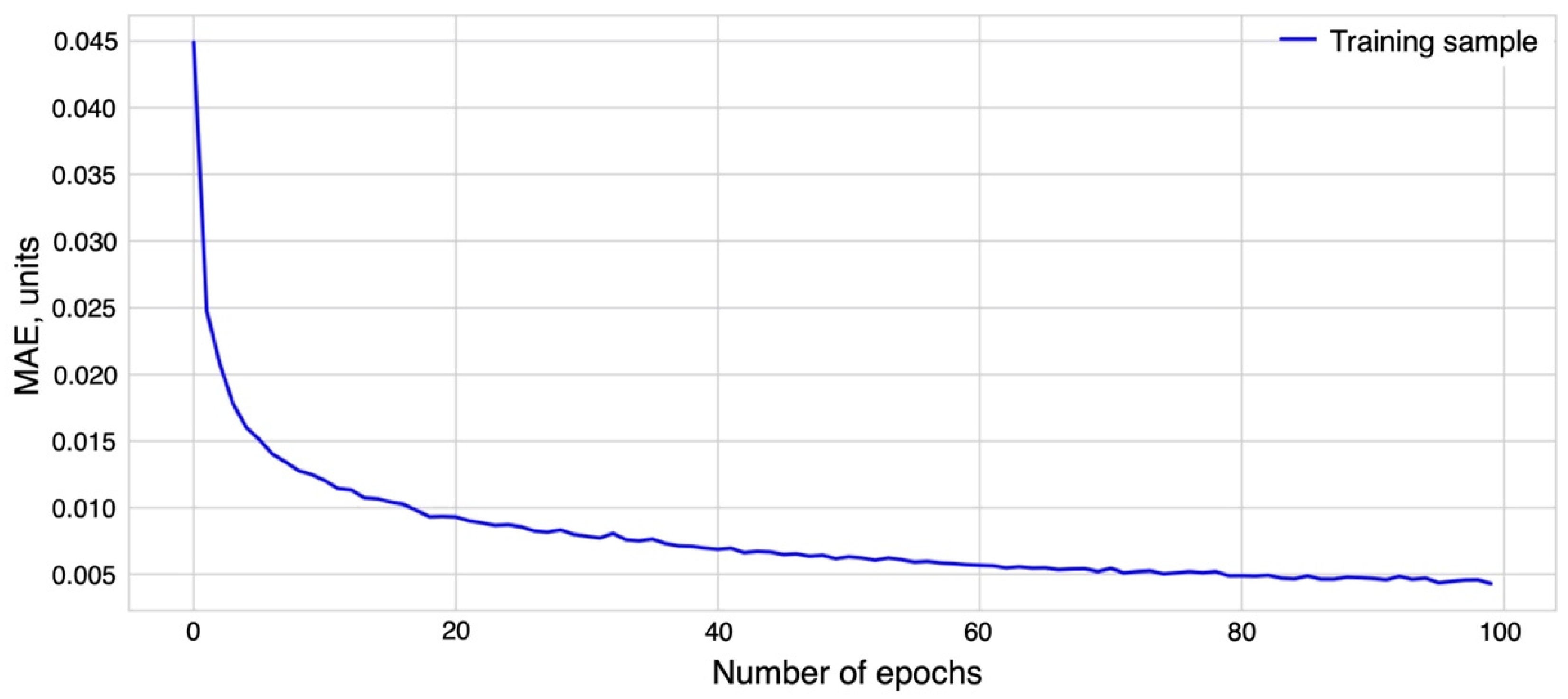
- y—the predicted value of the model.
- x—the real value.
- n—number of values.
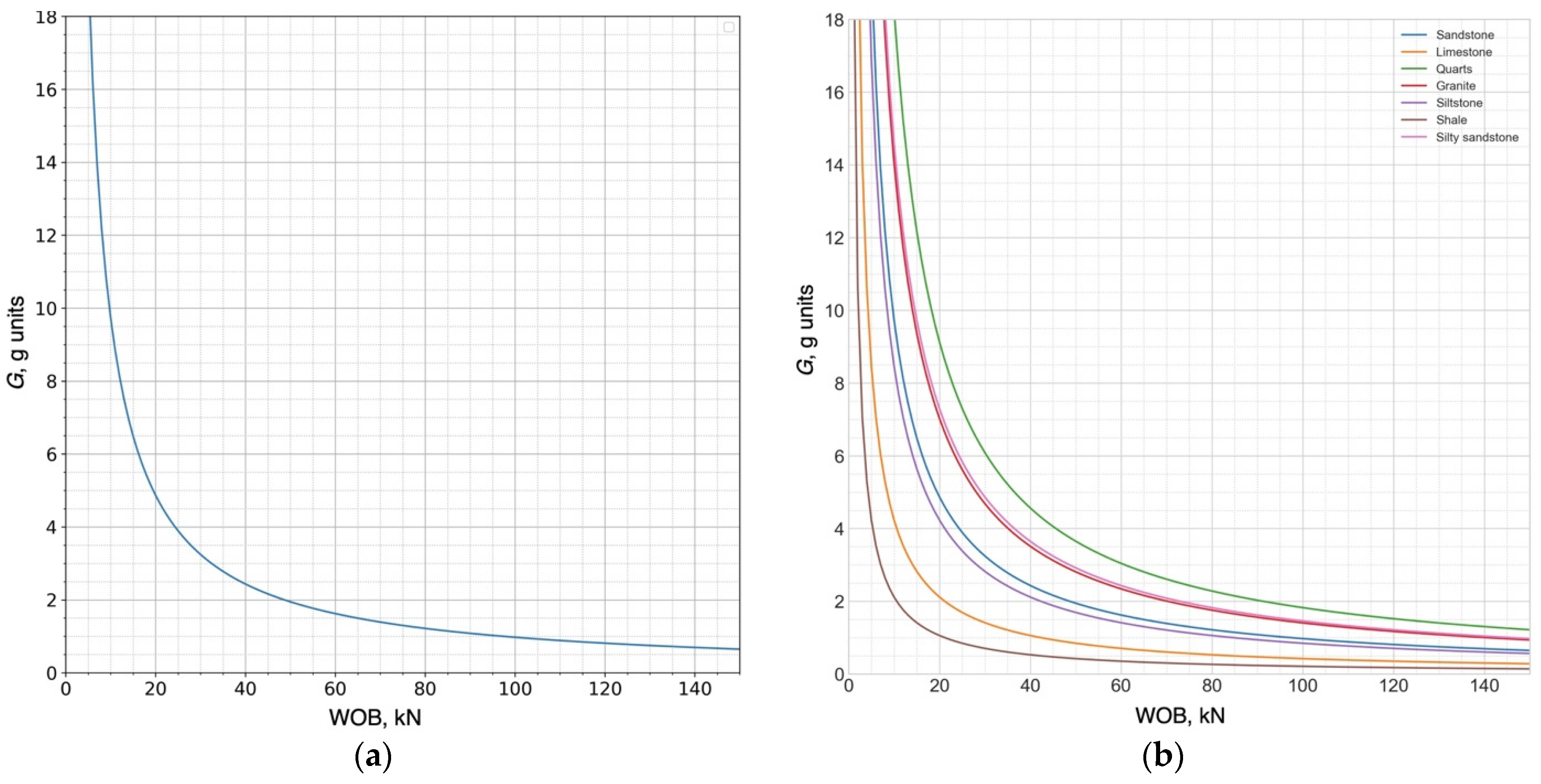
3. Results of Research and Analysis of Developed Algorithms
- The shock impulse is calculated according to (21):
- The shock time is determined by (23):
- The average magnitude of the shock reaction according to (24):
4. Discussion
5. Conclusions
- The necessity and expediency of monitoring and predicting BHA shock impulse, which is the basis for the formation of an energy-efficient WOB during well drilling, were theoretically substantiated and scientifically confirmed.
- Based on experimental studies of the physical and mechanical properties of rocks with a hardness of 60 to 170 MPa, a range of longitudinal and transverse deformations was established, which makes it possible to estimate the penetration depth of the PDC bit cutting structure for the determination of the BHA impact impulse and its prediction using the lithological and stratigraphic data of the well.
- A mathematical model was developed that enabled us to determine effective PDC WOB, represented by the introduced BHA unloading capacity coefficient, based on the discussed energy-efficient rock destruction theory.
- Based on the proposed algorithm for determination of the minimum resultant vibration acceleration of the BHA and the cut depth of the rock, which ensure the creation of its optimal shock impulse, a technology for monitoring and predicting energy-efficient PDC WOB was developed.
6. Patents
- Kunshin, A.A.; Starikov, V.V.; Buslaev G.V. Program for predicting possible complications while drilling in real time based on artificial neural networks and calculating the mechanical specific energy. Russia. Certificate No. 2021665628, 30 September 2021.
- Kunshin, A.A.; Dvoynikov, M.V. Program for determining the required WOB while drilling wells with vibration acceleration of the BHA. Russia. Certificate No. 2020616213, 11 June 2020.
- Kunshin, A.A.; Dvoynikov, M.V.; Polyansky, S.D. Program for determining vibration acceleration with damped axial vibrations of the drill string. Russia. Certificate No. 2020615753, 1 June 2020.
- Kunshin, A.A.; Sidorov, D.A.; Buslaev, G.V.; Dvoynikov, M.V. Downhole shock absorber. Russia. Patent No. 2749705 C1, 16 June 2021.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Islamov, S.; Grigoriev, A.; Beloglazov, I.; Savchenkov, S.; Gudmestad, O.T. Research Risk Factors in Monitoring Well Drilling—A Case Study Using Machine Learning Methods. Symmetry 2021, 13, 1293. [Google Scholar] [CrossRef]
- Alexandrov, V.; Kobulia, G. Optimization of the field economics. Vestn. McKinsey 2011, 24. Available online: http://vestnikmckinsey.ru/oil-ang-gas/optimizaciya-ehkonomiki-mestorozhdenij (accessed on 19 September 2022).
- Alyautdinov, R.T. Optimization of oil field development in modern conditions. Sustain. Dev. Sci. Educ. J. 2020, 4. [Google Scholar]
- Dvoynikov, M.V.; Budovskaya, M.E. Development of a hydrocarbon completion system for wells with low bottomhole temperatures for conditions of oil and gas fields in Eastern Siberia. J. Min. Inst. 2022, 253, 12–22. [Google Scholar] [CrossRef]
- Quanta, Z.; Zongming, Z.; Bing, H.; Linhu, M.; Jiaxiang, X. Downhole vibration causing a drill collar failure and solutions. Nat. Gas Ind. B 2017, 4, 73–80. [Google Scholar] [CrossRef]
- Mardashov, D.V.; Bondarenko, A.V.; Raupov, I.R. Technique for calculating technological parameters of non-Newtonian liquids injection into oil well during workover. J. Min. Inst. 2022, 1–14. [Google Scholar] [CrossRef]
- Al-AbdulJabbar, A.; Mahmoud, A.A.; Elkatatny, S.; Abughaban, M. A Novel Artificial Neural Network-Based Correlation for Evaluating the Rate of Penetration in a Natural Gas Bearing Sandstone Formation: A Case Study in a Middle East Oil Field. J. Sens. 2021, 2022, 9444076. [Google Scholar] [CrossRef]
- Gurina, E.; Klyuchnikov, N.; Antipova, K.; Koroteev, D. Forecasting the abnormal events at well drilling with machine learning. Appl. Intell. 2021, 52, 9980–9995. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, N.; Jiang, J.; Zhu, J.; Song, G.; Chen, X. The Application of Downhole Vibration Factor in Drilling Tool Reliability Big Data Analytics—A Review. ASME. ASME J. Risk Uncertain. Part B 2019, 5, 010801. [Google Scholar] [CrossRef] [Green Version]
- Golitsyna, M.; Semenikhin, A.; Chebuniaev, I.; Vasilyev, V.; Koryabkin, V.; Makarov, V.; Simon, I.; Baybolov, T.; Osmonalieva, O. Automatic Method for Anomaly Detection while Drilling. In Proceedings of the First EAGE Digitalization Conference and Exhibition, Vienna, Austria, 30 November–3 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Alley, S.D.; Sutherland, G.B. The Use of Real-Time Downhole Shock Measurements to Improve BHA Component Reliability. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991. [Google Scholar]
- Mitchell, R.F.; Allen, M.B. Lateral vibration: The key to BHA failure analysis. World Oil 1985, 200, 5103137. [Google Scholar]
- Dareing, D.W.; Livesay, J. Longitudinal and Angular Drill String Vibrations with Dampening; ASME—American Society of Mechanical Engineers: New York, NY, USA, 1968; pp. 671–679. [Google Scholar]
- Berro, M.J.; Reich, M. Laboratory investigations of a hybrid mud pulse telemetry (HMPT)—A new approach for speeding up the transmitting of MWD/LWD data in deep boreholes. J. Pet. Sci. Eng. 2019, 183, 106374. [Google Scholar] [CrossRef]
- Fjær, E.; Martin Holt, R.; Horsrud, P.; Raaen, A.M.; Risnes, R. Mechanical properties and in situ stresses from field data. Dev. Pet. Sci. 2021, 72, 429–459. [Google Scholar] [CrossRef]
- Lyagov, I.A.; Baldenko, F.D.; Lyagov, A.V.; Yamaliev, V.U.; Lyagova, A.A. Methodology for calculating technical efficiency of power sections in small-sized screw downhole motors for the «Perfobur» system. J. Min. Inst. 2019, 240, 694–700. [Google Scholar] [CrossRef]
- Galle, E.M.; Woods, H.B. Best Constant Weight and Rotary Speed for Rotary Rock Bits; AIME Drilling and Production Practice; American Petroleum Institute (API): Washington, DC, USA, 1963; pp. 48–55. [Google Scholar]
- Yigit, A.S.; Christoforou, A.P. Stick-Slip and Bit-Bounce Interaction in Oil-Well Drill strings. J. Energy Resour. Technol. 2006, 128, 268–274. [Google Scholar] [CrossRef]
- Simonyants, S.L.; Al Taee, M. Stimulation of the Drilling Process with the Top Driven Screw Downhole Motor. J. Min. Inst. 2019, 238, 438–442. [Google Scholar] [CrossRef] [Green Version]
- Spanos, P.D.; Sengupta, A.K.; Cunningham, R.A.; Paslay, P.R. Modeling of Roller Cone Bit Lift-Off Dynamics in Rotary Drilling. ASME J. Energy Resour. Technol. 1995, 117, 197–207. [Google Scholar] [CrossRef]
- Dawson, R.; Lin, Y.Q.; Spanos, P.D. Drill String Stick-Slip Oscillations. In Proceedings of the Conference of the Society for Experimental Mechanics, Houston, TX, USA, 14–19 June 1987; pp. 590–595. [Google Scholar]
- Batretdinov, T.V.; Yamaliev, V.U. Analysis of drill string vibrations and the use of damping devices. Sci. J. Oil Gas Bus. 2016, 6, 5–22. (In Russian) [Google Scholar] [CrossRef] [Green Version]
- Jia, B.; Xian, C.-G. Permeability measurement of the fracture-matrix system with 3D embedded discrete fracture model. Pet. Sci. 2022, 19, 1757–1765. [Google Scholar] [CrossRef]
- Han, G.; Liu, X.; Huang, J. Theoretical Comparison of Test Performance of Different Pulse Decay Methods for Unconventional Cores. Energies 2020, 13, 4557. [Google Scholar] [CrossRef]
- Jia, B.; Jin, L.; Mibeck, B.A.; Smith, S.A.; Sorensen, J.A. An integrated approach of measuring permeability of naturally fractured shale. J. Pet. Sci. Eng. 2019, 186, 106716. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, H.; Boudjatit, M. Matrix permeability measurement from fractured unconventional source-rock samples: Method and application. J. Contam. Hydrol. 2020, 233, 103663. [Google Scholar] [CrossRef] [PubMed]
- Kamatov, K.A.; Buslaev, G.V. Solutions for Drilling Efficiency Improvement in Extreme Geological Conditions of Timano-Pechora Region. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 26–28 October 2015. [Google Scholar] [CrossRef]
- Gospodarikov, A.P.; Zatsepin, M.A. Mathematical modeling of nonlinear boundary value problems in geomechanics. Gorn. Zhurnal 2019, 12, 16–20. [Google Scholar] [CrossRef]
- Leine, R.I.; Van Campen, D.H.; Keultjes, W.J. Stick-slip Whirl Interaction in Drill string Dynamics. J. Sound Acoust. 2002, 124, 209–220. [Google Scholar] [CrossRef] [Green Version]
- Navarro-Lopez, E.; Cortes, D. Sliding-mode of a multi-DOF oil well drill string with stick-slip oscillations. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 11–13 July 2007; pp. 3837–3842. [Google Scholar] [CrossRef] [Green Version]
- Saldivar, B.; Boussaada, I.; Mounier, H.; Mondié, S.; Niculescu, S.I. An Overview on the Modeling of Oilwell Drilling Vibrations. IFAC Proc. Vol. 2014, 47, 5169–5174. [Google Scholar] [CrossRef] [Green Version]
- Tucker, R.W.; Wang, C. On the effective control of torsional vibrations in drilling systems. J. Sound Vib. 1999, 224, 101–122. [Google Scholar] [CrossRef]
- Challamel, N. Rock destruction effect on the stability of a drilling structure. J. Sound Vib. 2000, 233, 235–254. [Google Scholar] [CrossRef]
- Saldivar, M.B.; Mondié, S. Drilling vibration reduction via attractive ellipsoid method. J. Frankl. Inst. 2013, 350, 485–502. [Google Scholar] [CrossRef]
- Bolobov, V.I.; Plaschinskiy, V.; Thanh, B.L. Crack propagation in rock upon impact. Obogashchenie Rud 2019, 5, 3–8. [Google Scholar] [CrossRef]
- Bolobov, V.I.; Chupin, S.A.; Bochkov, V.S.; Mishin, I.I. Increasing the service life of rock cutting tools by increasing the wear resistance of their holders by thermomechanical treatment. Gorn. Zhurnal 2019, 5, 67–71. [Google Scholar] [CrossRef]
- Zha, Y.; Pham, S. Monitoring downhole drilling vibrations using surface data through deep learning. In Proceedings of the SEG International Exposition and Annual Meeting, Anaheim, CA, USA, 15–20 September 2018. [Google Scholar] [CrossRef]
- Lykov, Y.V.; Gorelikov, V.G.; Gantulga, B. Analytical research and classification of mechanism of diamond drilling-bits contact with rocks during well sinking. IOP Conf. Ser. Earth Environ. Sci. 2017, 87, 022012. [Google Scholar] [CrossRef]
- Chen, X.; Gao, D.; Yang, J. Drilling Performance Optimization Based on Mechanical Specific Energy Technologies. Drilling 2018, 35, 133–161. [Google Scholar] [CrossRef] [Green Version]
- Richard, T.; Detournay, E.; Drescher, A.; Nicodeme, P.; Fourmaintraux, D. The scratch test as a means to measure strength of sedimentary rocks. In Proceedings of the EuRock’98 Conference (Rock Mechanics in Petroleum Engineering), Trondheim, Norway, 8–10 July 1998; Volume 2, pp. 15–22. [Google Scholar] [CrossRef]
- Zhang, H.; Shubin, L.; Hongjian, N. Numerical study on optimal impact angle of a single PDC cutter in impact rock cutting. Energy Rep. 2021, 7, 4172–4183. [Google Scholar] [CrossRef]
- Teale, R. The concept of specific energy in rock drilling. Int. J. Rock Mech. Min. Sci. Geomech. 1965, 2, 57–73. [Google Scholar] [CrossRef]
- Mazen, A.Z.; Rahmanian, N.; Mujtaba, I.M.; Hassanpour, A. Effective mechanical specific energy: A new approach for evaluating PDC bit performance and cutters wear 2021. J. Pet. Sci. Eng. 2020, 196, 108030. [Google Scholar] [CrossRef]
- Mohan, K.; Adil, F.; Samuel, R. Tracking drilling efficiency using hydro-mechanical specific energy. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, Amsterdam, The Netherlands, 17–19 March 2009. [Google Scholar] [CrossRef]
- Rashidi, B.; Hareland, G.; Fazaelizadeh, M.; Svigir, M. Comparative study using rock energy and drilling strength models. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S. Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Juan, L. Research on torque and drag in extended-reach horizontal wells and its application in Chenghai-1 area. Oil Drill. Prod. Technol. 2009, 31, 21–25. [Google Scholar]
- Dupriest, F.E.; Koederitz, W.L. Maximizing drill rates with real-time surveillance of mechanical specific energy. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 23–25 February 2005. [Google Scholar] [CrossRef]
- Chen, X.; Gao, D.; Guo, B.; Feng, Y. Real-time optimization of drilling parameters based on mechanical specific energy for rotating drilling with positive displacement motor in the hard formation. J. Nat. Gas Sci. Eng. 2016, 35 Part A, 686–694. [Google Scholar] [CrossRef]
- Pessier, R.C.; Fear, M.J. Quantifying common drilling problems with mechanical specific energy and a bit-specific coefficient of sliding friction. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992. [Google Scholar] [CrossRef]
- Kunshin, A.A.; Starikov, V.V.; Buslaev, G.V. Program for Predicting Possible Complications while Drilling in Real Time Based on Artificial Neural Networks and Calculating the Mechanical Specific Energy. Russia Certificate No. 2021665628, 30 September 2021. [Google Scholar]
- Liu, S.; Ni, H.; Wang, X.; Wang, P.; Li, N. Numerical study of the compound vertical and horizontal impact cutting with a single PDC cutter. Energy Rep. 2020, 6, 1520–1527. [Google Scholar] [CrossRef]
- Mahmoud, A.A.; Elkatatny, S.; Al Shehri, D. Application of Machine Learning in Evaluation of the Static Young’s Modulus for Sandstone Formations. Sustainability 2020, 12, 1880. [Google Scholar] [CrossRef] [Green Version]
- Equinor ASA. Available online: https://www.equinor.com/en/what-we-do/norwegian-continental-shelf-platforms/volve.html (accessed on 19 September 2022).
- Kunshin, A.A.; Dvoynikov, M.V. Program for Determining the Required WOB while Drilling Wells with Vibration Acceleration of the BHA. Russia Certificate No. 2020616213, 11 June 2020. [Google Scholar]
- Kunshin, A.A.; Dvoynikov, M.V.; Polyansky, S.D. Program for Determining Vibration Acceleration with Damped Axial Vibrations of the Drill String. Russia Certificate No. 2020615753, 1 June 2020. [Google Scholar]
- Abdelkrim, A.; Aissa, A.; Mostefa, B.; Abdelkader, D.; Mohammed, E.G. Fatigue life estimation of components with use a non-linear energy model coupled a finite element method. In Proceedings of the International Conference on Materials & Energy, Baku, Azerbaijan, 22–25 May 2020; p. 307. [Google Scholar] [CrossRef] [Green Version]
- Litvinenko, V.S.; Bowbrick, I.; Naumov, I.A.; Zaitseva, Z. Global guidelines and requirements for professional competencies of natural resource extraction engineers: Implications for ESG principles and sustainable development goals. J. Clean. Prod. 2022, 338, 130530. [Google Scholar] [CrossRef]
- Morenov, V.; Leusheva, E.; Lavrik, A.; Lavrik, A.; Buslaev, G. Gas-Fueled Binary Energy System with Low-Boiling Working Fluid for Enhanced Power Generation. Energies 2022, 15, 2551. [Google Scholar] [CrossRef]
- Zimin, R.Y.; Kuchin, V.N. Improving the Efficiency of Oil and Gas Field Development through the Use of Alternative Energy Sources in the Arctic. In Proceedings of the 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 6–9 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
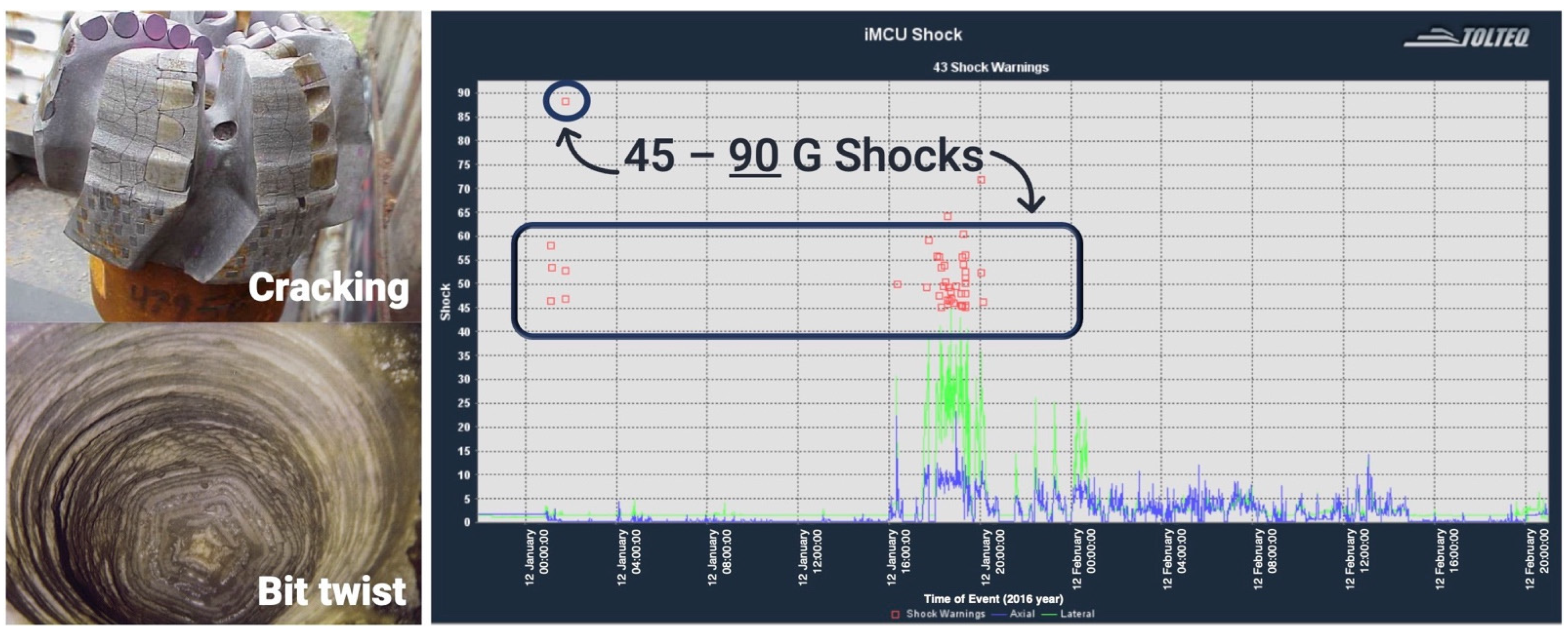
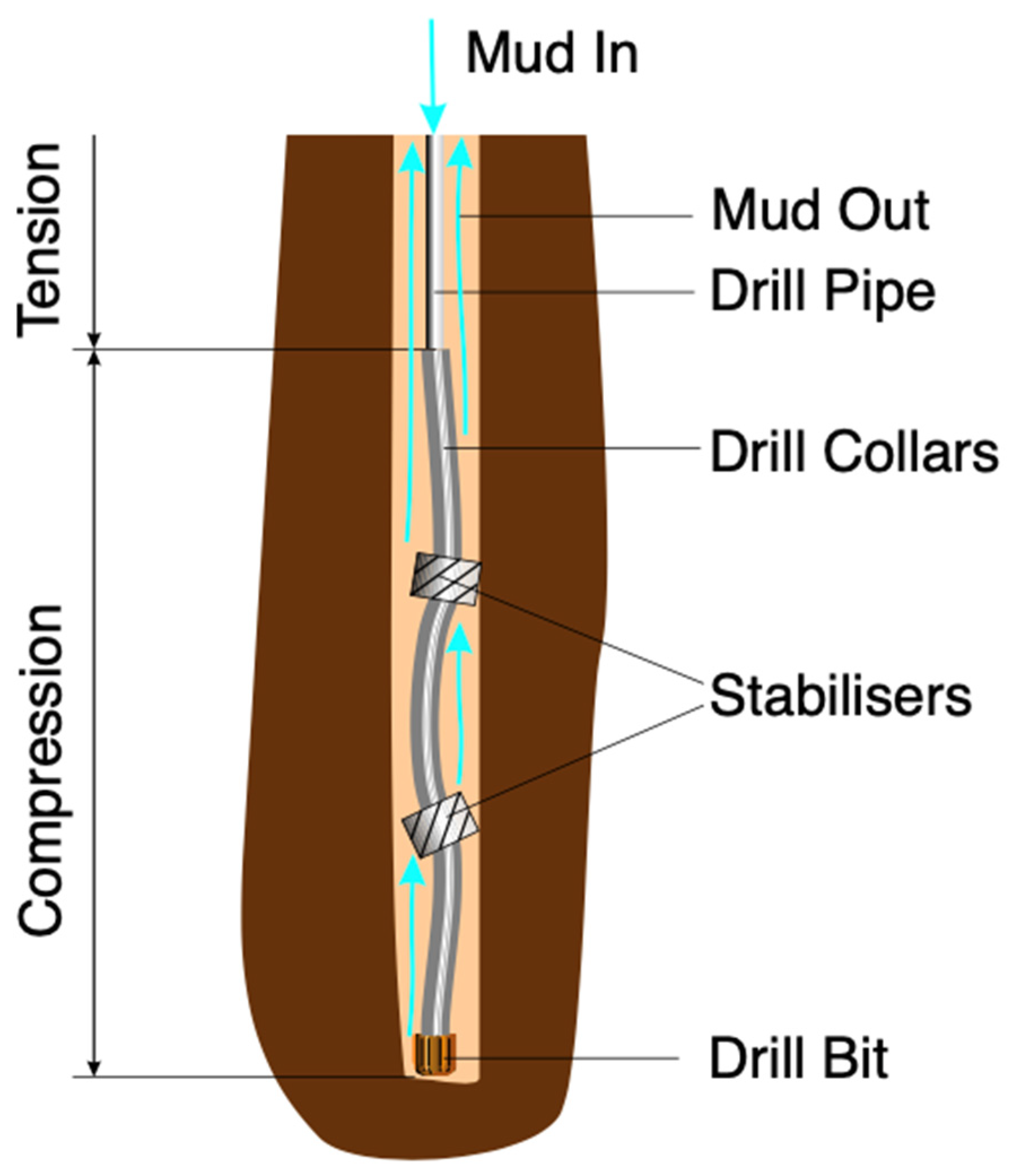
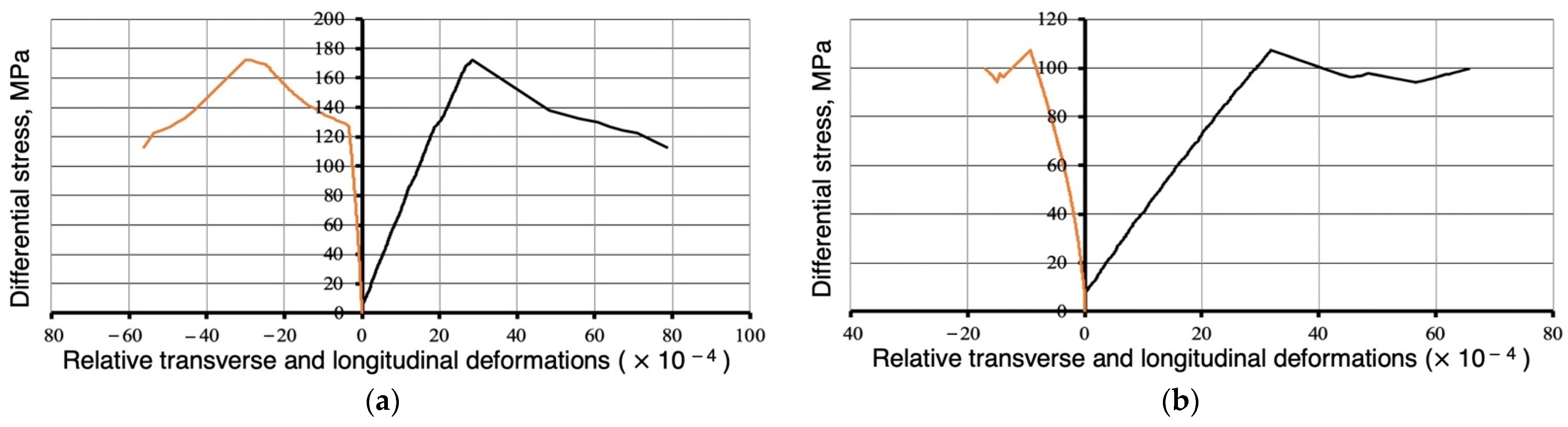
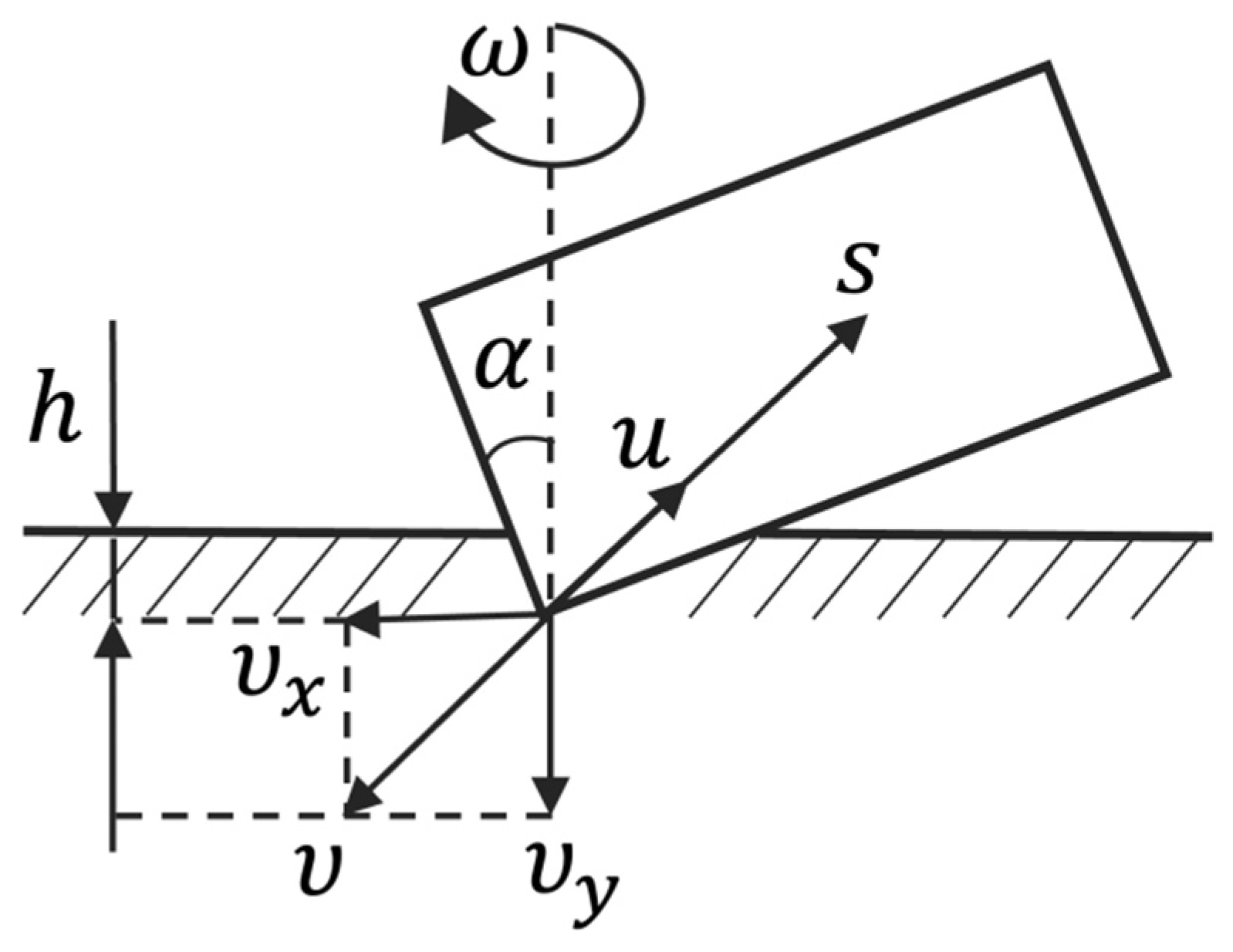





| Name of the Rock | Poisson’s Ratio | Differential Strength, MPa |
|---|---|---|
| Shale | 0.11 | 19.6 |
| Limestone | 0.32 | 50.0 |
| Siltstone | 0.35 | 107.22 |
| Granite | 0.27 | 166.0 |
| Silty sandstone | 0.28 | 172.4 |
| Quartz | 0.15 | 215.7 |
| Type of the Rock | k, Units | β, Units |
|---|---|---|
| Shale | 0.05–0.1 | 110–170 |
| Limestone | 0.03–0.06 | 300–900 |
| Siltstone | 0.04–0.08 | 170–650 |
| Granite | 0.03–0.05 | 300–550 |
| Silty sandstone | 0.05–0.08 | 170–420 |
| Quartz | 0.06–0.08 | 170–300 |
| Interval, m | 950–1000 | 1020–1100 | |
|---|---|---|---|
| Parameter | |||
| WOB, kN | 31 | 101.4 | |
| Well diameter, mm | 215.9 | 215.9 | |
| ROP, m/h | 16.8 | 51.0 | |
| Rate of rotation, rpm | 140.8 | 193.0 | |
| Torque, kN × m | 8470.0 | 8360.0 | |
| Zenith angle, degrees | 59.0 | 60.0 | |
| Friction coefficient «bit-rock» | 0.2 | 0.2 | |
| Friction coefficient «DS-wellbore» | 0.45 | 0.45 | |
| Strength strongest compression of sandstone, MPa | 115.0 | ||
| Sandstone density, kg/m3 | 2400.0 | ||
| Steel density, kg/m3 | 7800.0 | ||
| Young’s modulus (sandstone), GPa | 25.0 | ||
| Young’s modulus (steel), GPa | 200.0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kunshin, A.; Dvoynikov, M.; Timashev, E.; Starikov, V. Development of Monitoring and Forecasting Technology Energy Efficiency of Well Drilling Using Mechanical Specific Energy. Energies 2022, 15, 7408. https://doi.org/10.3390/en15197408
Kunshin A, Dvoynikov M, Timashev E, Starikov V. Development of Monitoring and Forecasting Technology Energy Efficiency of Well Drilling Using Mechanical Specific Energy. Energies. 2022; 15(19):7408. https://doi.org/10.3390/en15197408
Chicago/Turabian StyleKunshin, Andrey, Mikhail Dvoynikov, Eduard Timashev, and Vitaly Starikov. 2022. "Development of Monitoring and Forecasting Technology Energy Efficiency of Well Drilling Using Mechanical Specific Energy" Energies 15, no. 19: 7408. https://doi.org/10.3390/en15197408
APA StyleKunshin, A., Dvoynikov, M., Timashev, E., & Starikov, V. (2022). Development of Monitoring and Forecasting Technology Energy Efficiency of Well Drilling Using Mechanical Specific Energy. Energies, 15(19), 7408. https://doi.org/10.3390/en15197408





