Comparative Analysis of Riser Base and Flowline Gas Injection on Vertical Gas-Liquid Two-Phase Flow
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
2. Experimental Setup and Procedure
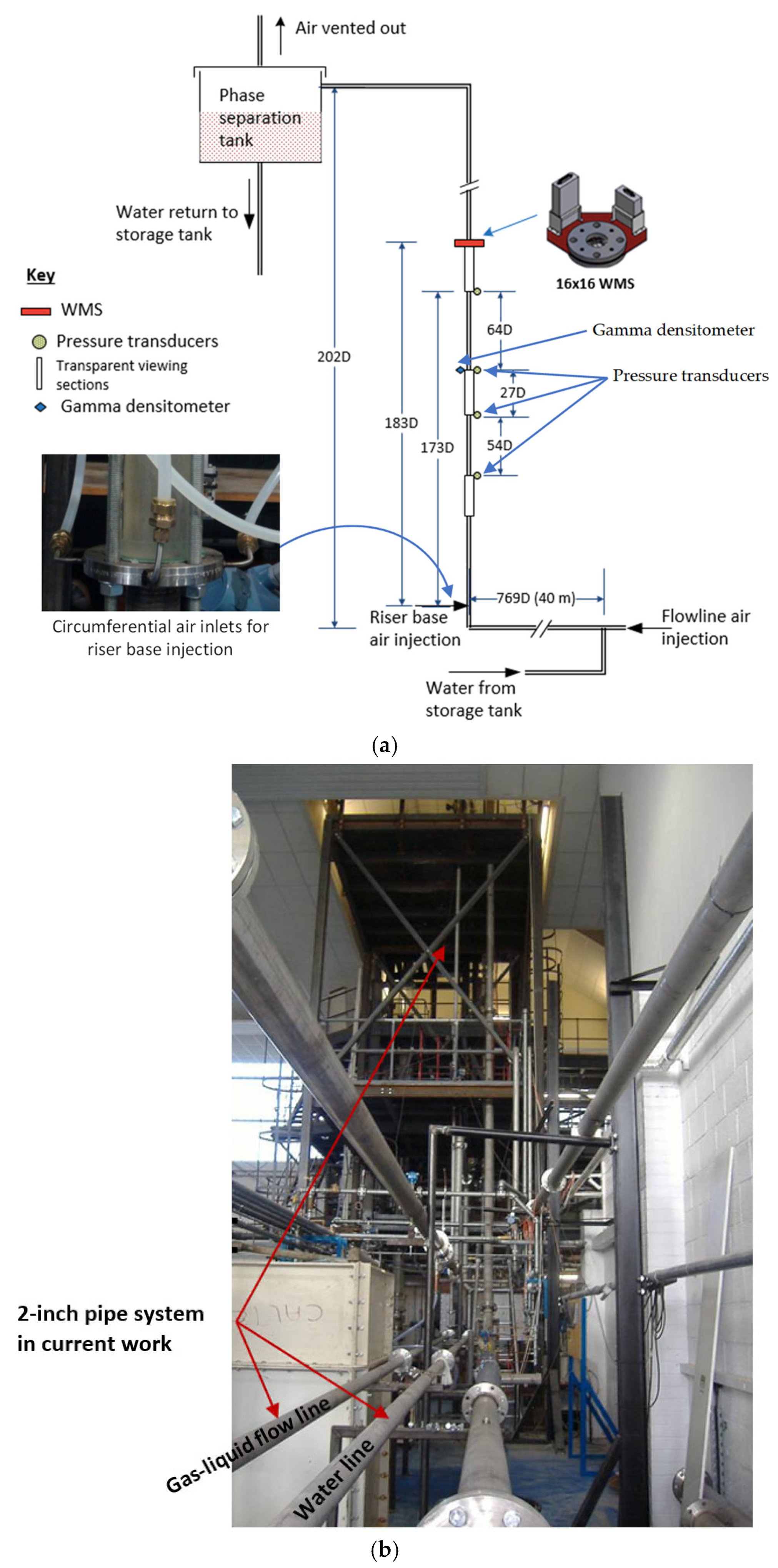
2.1. Experimental Rig
2.2. Instrumentation
2.2.1. Gamma Densitometer (GD)
2.2.2. Wire Mesh Sensor (WMS)
2.3. Experimental Procedure
3. Results and Discussion
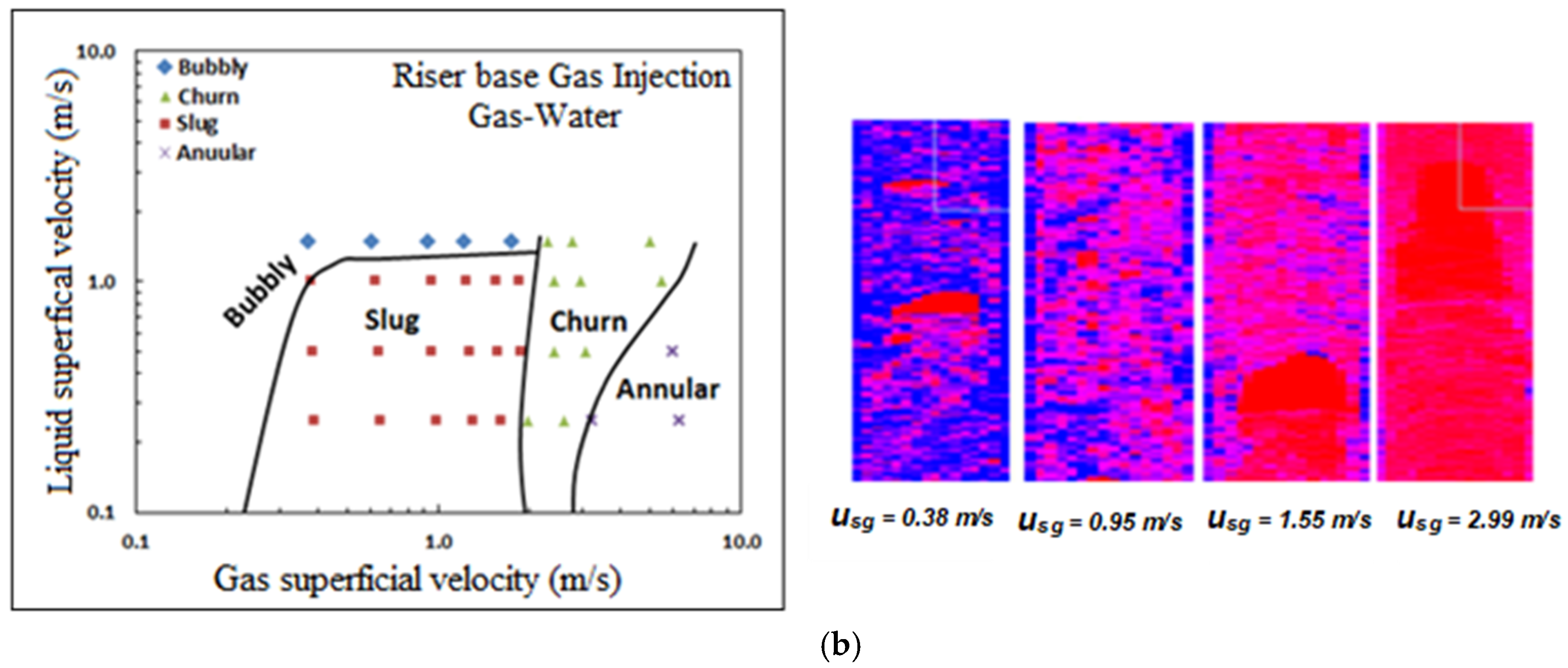
3.1. Flow Patterns
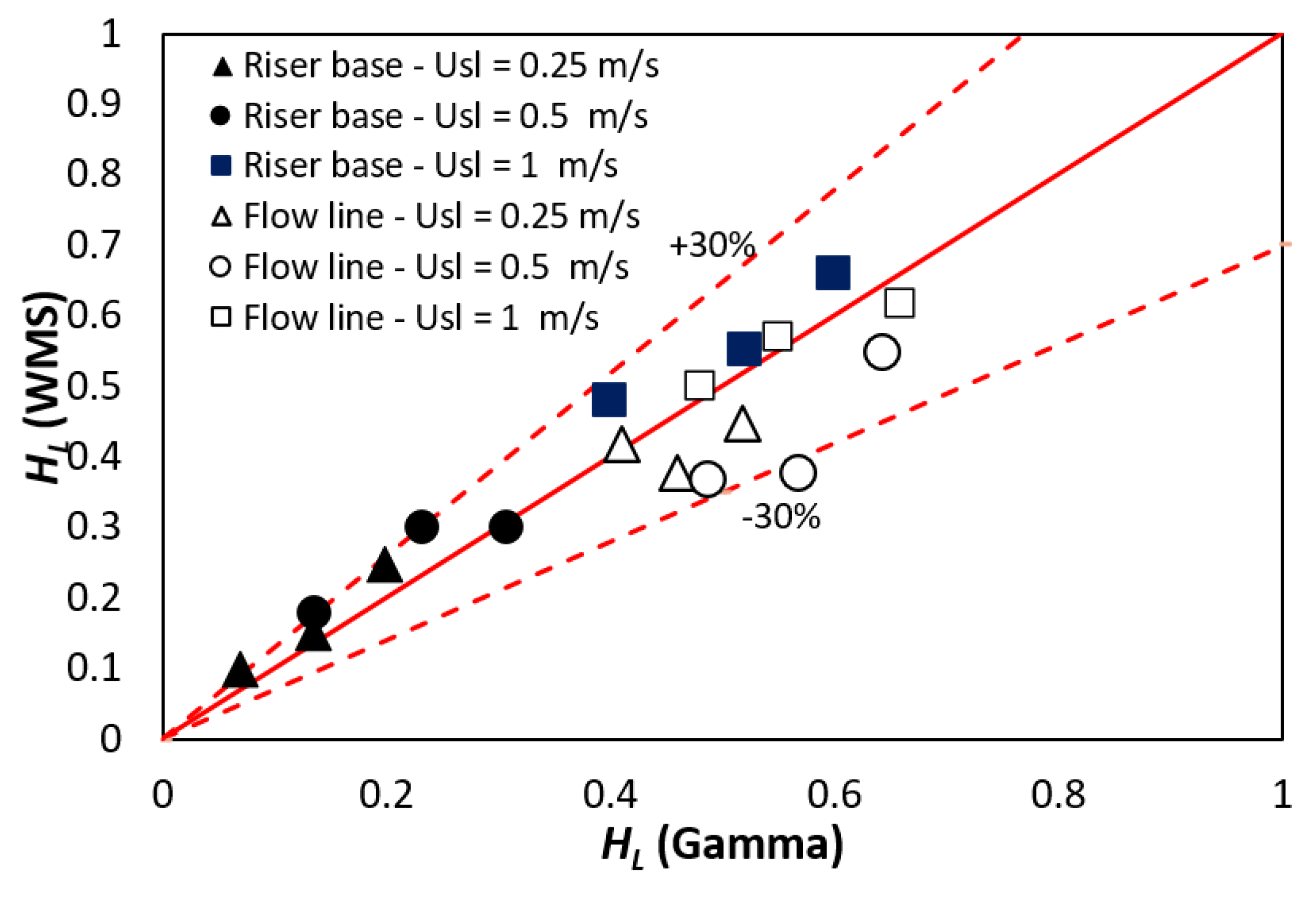
3.2. Probability Distribution Functions (PDFs) of Liquid Hold up Measurements
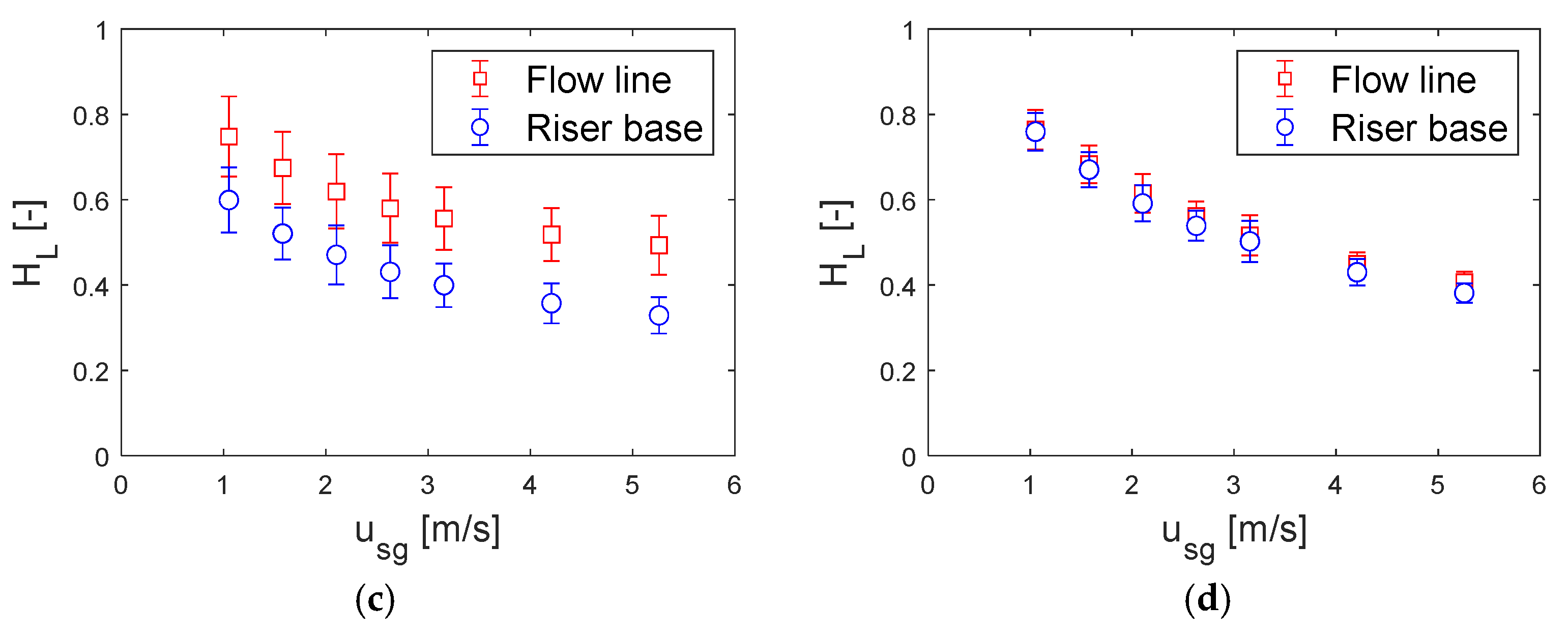
3.3. Effect of Superficial Gas Velocity and Injection Method on Holdup
3.4. Peaking Behaviour of Holdup
3.5. Analysis of Appropriate Correlations for Hold-Up Prediction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guet, S.; Rodriguez, O.; Oliemans, R.; Brauner, N. An inverse dispersed multiphase flow model for liquid production rate determination. Int. J. Multiph. Flow 2006, 32, 553–567. [Google Scholar] [CrossRef]
- Hagedorn, A.R.; Brown, K.E. The Effect of Liquid Viscosity in Two-Phase Vertical Flow. J. Pet. Technol. 1964, 16, 203–210. [Google Scholar] [CrossRef]
- Szalinski, L.; Abdulkareem, L.; Da Silva, M.; Thiele, S.; Beyer, M.; Lucas, D.; Perez, V.H.; Hampel, U.; Azzopardi, B. Comparative study of gas–oil and gas–water two-phase flow in a vertical pipe. Chem. Eng. Sci. 2010, 65, 3836–3848. [Google Scholar] [CrossRef]
- Vishnyakov, V.; Suleimanov, B.; Salmanov, A.; Zeynalov, E. Water altering gas injection. In Primer on Enhanced Oil Recovery; Elsevier: Amsterdam, The Netherlands, 2020; pp. 127–139. [Google Scholar] [CrossRef]
- Descamps, M.; Oliemans, R.; Ooms, G.; Mudde, R.; Kusters, R. Influence of gas injection on phase inversion in an oil–water flow through a vertical tube. Int. J. Multiph. Flow 2006, 32, 311–322. [Google Scholar] [CrossRef]
- Sami, N.A.; Turzo, Z. Computational fluid dynamic (CFD) modelling of transient flow in the intermittent gas lift. Pet. Res. 2020, 5, 144–153. [Google Scholar] [CrossRef]
- Rodrigues, H.T.; Almeida, A.R.; Barrionuevo, D.C.; Fraga, R.S. Effect of the gas injection angle and configuration in the efficiency of gas lift. J. Pet. Sci. Eng. 2020, 198, 108126. [Google Scholar] [CrossRef]
- Guerra, L.; Temer, B.; Loureiro, J.; Freire, A.S. Experimental study of gas-lift systems with inclined gas jets. J. Pet. Sci. Eng. 2022, 216, 110749. [Google Scholar] [CrossRef]
- Rosettani, J.; Ahmed, W.; Geddis, P.; Wu, L.; Clements, B. Experimental and numerical investigation of gas-liquid metal two-phase flow pumping. Int. J. Thermofluids 2021, 10, 100092. [Google Scholar] [CrossRef]
- Archibong-Eso, A.; Aliyu, A.M.; Yan, W.; Okeke, N.E.; Baba, Y.D.; Fajemidupe, O.; Yeung, H. Experimental Study on Sand Transport Characteristics in Horizontal and Inclined Two-Phase Solid-Liquid Pipe Flow. J. Pipeline Syst. Eng. Pract. 2020, 11, 04019050. [Google Scholar] [CrossRef]
- Fajemidupe, O.T.; Aliyu, A.M.; Baba, Y.D.; Archibong-Eso, A.; Yeung, H. Sand minimum transport conditions in gas–solid–liquid three-phase stratified flow in a horizontal pipe at low particle concentrations. Chem. Eng. Res. Des. 2019, 143, 114–126. [Google Scholar] [CrossRef] [Green Version]
- Fajemidupe, O.T.; Aliyu, A.M.; Baba, Y.D.; Archibong-Eso, A.; Yeung, H. Minimum sand transport conditions in gas-solid-liquid three-phase stratified flow in horizontal pipelines. Chem. Eng. Res. Des. 2019, 143, 114–126. [Google Scholar] [CrossRef] [Green Version]
- Lockhart, R.; Martinelli, R. Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Sci. 1949, 45, 39–48. [Google Scholar]
- Woldesemayat, M.A.; Ghajar, A.J. Comparison of void fraction correlations for different flow patterns in horizontal and upward inclined pipes. Int. J. Multiph. Flow 2007, 33, 347–370. [Google Scholar] [CrossRef]
- Zuber, N.; Findlay, J.A. Average Volumetric Concentration in Two-Phase Flow Systems. J. Heat Transf. 1965, 87, 453–468. [Google Scholar] [CrossRef]
- Almabrok, A.A.; Aliyu, A.M.; Baba, Y.D.; Lao, L.; Yeung, H.; Aliyu, A. Void fraction development in gas-liquid flow after a U-bend in a vertically upwards serpentine-configuration large-diameter pipe. Heat Mass Transf. 2017, 54, 209–226. [Google Scholar] [CrossRef] [Green Version]
- Gomez, L.; Shoham, O.; Taitel, Y. Prediction of slug liquid holdup: Horizontal to upward vertical flow. Int. J. Multiph. Flow 2000, 26, 517–521. [Google Scholar] [CrossRef]
- Pietrzak, M.; Płaczek, M. Void fraction predictive methods in two-phase flow across a small diameter channel. Int. J. Multiph. Flow 2019, 121, 103115. [Google Scholar] [CrossRef]
- Butterworth, D. A comparison of some void-fraction relationships for co-current gas-liquid flow. Int. J. Multiph. Flow 1975, 1, 845–850. [Google Scholar] [CrossRef]
- Huq, R.; Loth, J.L. Analytical two-phase flow void prediction method. J. Thermophys. Heat Transf. 1992, 6, 139–144. [Google Scholar] [CrossRef]
- Da Silva, M.J.; Thiele, S.; Abdulkareem, L.A.; Azzopardi, B.J.; Hampel, U. High-resolution oil–gas two-phase flow measurement with a new capacitance wire-mesh tomography. Flow Meas. Instrum. 2010, 21, 191–197. [Google Scholar] [CrossRef]
- Tesi, A. Multiphase Flow Measurement Using Gamma-Based Techniques. Ph.D. Thesis, Cranfield University, Bedford, UK, 2011. [Google Scholar]
- Abdulkadir, M.; Abdulahi, A.; Eastwick, C.N.; Azzopardi, B.J.; Smith, I.E.; Unander, T.E.; Mukhtar, A. Investigating the effect of pressure on a vertical two-phase upward flow with a high viscosity liquid. AIChE J. 2019, 66, e16860. [Google Scholar] [CrossRef]
- Abdulkadir, M.; Jatto, D.; Abdulkareem, L.; Zhao, D. Pressure drop, void fraction and flow pattern of vertical air–silicone oil flows using differential pressure transducer and advanced instrumentation. Chem. Eng. Res. Des. 2020, 159, 262–277. [Google Scholar] [CrossRef]
- Prasser, H.-M.; Misawa, M.; Tiseanu, I. Comparison between wire-mesh sensor and ultra-fast X-ray tomograph for an air–water flow in a vertical pipe. Flow Meas. Instrum. 2005, 16, 73–83. [Google Scholar] [CrossRef]
- Da Silva, M.J.; Schleicher, E.; Hampel, U. Capacitance wire-mesh sensor for fast measurement of phase fraction distributions. Meas. Sci. Technol. 2007, 18, 2245–2251. [Google Scholar] [CrossRef]
- Baba, Y.D.; Aliyu, A.M.; Archibong, A.-E.; Almabrok, A.A.; Igbafe, A.I.; Aliyu, A. Study of high viscous multiphase phase flow in a horizontal pipe. Heat Mass Transf. 2017, 54, 651–669. [Google Scholar] [CrossRef]
- Ahmed, S.K.B.; Aliyu, A.M.; Ehinmowo, A.; Yeung, H. Effect of riser base and flowline gas injection on the characteristics of gas-liquid two-phase flow in a vertical riser system. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Virtual, 11–13 August 2020; OnePetro: Houston, TX, USA, 2020. [Google Scholar] [CrossRef]
- Ahmed, S.K.B.; Lao, L.; Yeung, H. Liquid/gas flows and development on riser: Upstream effect. In Proceedings of the International Conference on Multiphase Flow, Jeju, Korea, 26–31 May 2013; pp. 1–10. [Google Scholar]
- Aliyu, A.M.; Baba, Y.D.; Lao, L.; Yeung, H.; Kim, K.C. Interfacial friction in upward annular gas–liquid two-phase flow in pipes. Exp. Therm. Fluid Sci. 2017, 84, 90–109. [Google Scholar] [CrossRef]
- Stahl, P.; von Rohr, P.R. On the accuracy of void fraction measurements by single-beam gamma-densitometry for gas–liquid two-phase flows in pipes. Exp. Therm. Fluid Sci. 2003, 28, 533–544. [Google Scholar] [CrossRef]
- Prasser, H.-M.; Häfeli, R. Signal response of wire-mesh sensors to an idealized bubbly flow. Nucl. Eng. Des. 2018, 336, 3–14. [Google Scholar] [CrossRef]
- Ogasawara, T.; Takagi, S.; Matsumoto, Y. Influence of local void fraction distribution on turbulent structure of upward bubbly flow in vertical channel. J. Phys. Conf. Ser. 2009, 147, 012027. [Google Scholar] [CrossRef]
- Nicklin, D.J.; Wilkes, J.C.; Davidson, J.F. Two-phase flow in vertical tubes. Trans. Inst. Chem. Eng. 1962, 40, 61–68. [Google Scholar]
- Aliyu, A.M. Vertical Annular Gas-Liquid Two-Phase Flow in Large Diameter Pipes. Ph.D. Thesis, Cranfield University, Bedford, UK, 2015. [Google Scholar]
- Aliyu, A.M.; Kim, Y.K.; Choi, S.H.; Ahn, J.H.; Kim, K.C. Development of a dual optical fiber probe for the hydrodynamic investigation of a horizontal annular drive gas/liquid ejector. Flow Meas. Instrum. 2017, 56, 45–55. [Google Scholar] [CrossRef]
- Lao, L.; Xing, L.; Yeung, H. Behaviours of elongated bubbles in a large diameter riser. In Proceedings of the 8th North American Conference on Multiphase Technology, Banff, AB, Canada, 20–22 June 2012; OnePetro: Houston, TX, USA, 2012; pp. 381–392. Available online: www.onepetro.org/conference-paper/BHR-2012-A026 (accessed on 15 January 2022).
- Omebere-Iyari, N.K. The effect of pipe diameter and pressure in vertical two-phase flow. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2006. [Google Scholar]
- Aliyu, A.M.; Seo, H.; Kim, H.; Kim, K.C. Characteristics of bubble-induced liquid flows in a rectangular tank. Exp. Therm. Fluid Sci. 2018, 97, 21–35. [Google Scholar] [CrossRef]
- Kaji, R.; Azzopardi, B. The effect of pipe diameter on the structure of gas/liquid flow in vertical pipes. Int. J. Multiph. Flow 2010, 36, 303–313. [Google Scholar] [CrossRef]








| Author(s) | Equation and Comments | Eqn. |
|---|---|---|
| Homogenous model (see Woldesemayat & Ghajar [14] and Pietrzak & Placzek [18]) | (2) | |
| Developed for low gas volume fraction dispersed phase where the slip with the continuous phase is small. It is pipe inclination independent. | ||
| Lockhart & Martinelli [13] (see Butterworth [19]) | (3) | |
| The Lockhart–Martinelli is one of the most-used empirical correlations for two-phase flows and pressure drop in pipes. Combinations of fluids used by Lockhart & Martinelli to generate their original model include air/water, air/various oils; and pipes of diameters that range between 1.5 and 25 mm. Butterworth [19] showed that the Lockhart–Martinelli parameter X can be used to derive Equation (3). | ||
| Huq & Loth [20] | (4) | |
| Huq & Loth’s analytical model is for predicting the lower limit of void fraction as a function of gas quality and system pressure in vertical pipes. | ||
| Almabrok et al. [16] | (5) | |
| Almabrok and co-workers obtained the void fraction equation from the regression of 347 data points from vertical large pipes of diameter 101.6, 127, 152, and 203 mm from air/water studies covering bubbly, churn, and annular flows. | ||
| Gomez et al. [17] | (6) | |
| where is the inclination angle and the equation is valid for . Total of 283 data points for horizontal and vertical pipes with diameters ranging from 51 to 203 mm. Fluid combinations include air/oil, air/kerosene, air/water, nitrogen/diesel, and Freon/water. | ||
| Woldesemayat & Ghajar [14] | (7) | |
| 2700 data points were used comprising horizontal, inclined and vertical flow, for air/water, air/kerosene mixtures. Pipe diameters ranged between 12- and 78-mm. Correlation was obtained by modifying Dix’s and others [21] correlation to account for operating pressure and pipe inclination. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, S.K.B.; Aliyu, A.M.; Baba, Y.D.; Abdulkadir, M.; Abdulhadi, R.O.; Lao, L.; Yeung, H. Comparative Analysis of Riser Base and Flowline Gas Injection on Vertical Gas-Liquid Two-Phase Flow. Energies 2022, 15, 7446. https://doi.org/10.3390/en15197446
Ahmed SKB, Aliyu AM, Baba YD, Abdulkadir M, Abdulhadi RO, Lao L, Yeung H. Comparative Analysis of Riser Base and Flowline Gas Injection on Vertical Gas-Liquid Two-Phase Flow. Energies. 2022; 15(19):7446. https://doi.org/10.3390/en15197446
Chicago/Turabian StyleAhmed, Salem K. Brini, Aliyu M. Aliyu, Yahaya D. Baba, Mukhtar Abdulkadir, Rahil Omar Abdulhadi, Liyun Lao, and Hoi Yeung. 2022. "Comparative Analysis of Riser Base and Flowline Gas Injection on Vertical Gas-Liquid Two-Phase Flow" Energies 15, no. 19: 7446. https://doi.org/10.3390/en15197446
APA StyleAhmed, S. K. B., Aliyu, A. M., Baba, Y. D., Abdulkadir, M., Abdulhadi, R. O., Lao, L., & Yeung, H. (2022). Comparative Analysis of Riser Base and Flowline Gas Injection on Vertical Gas-Liquid Two-Phase Flow. Energies, 15(19), 7446. https://doi.org/10.3390/en15197446








