Numerical Simulation of Effective Hole Cleaning by Using an Innovative Elliptical Drillpipe in Horizontal Wellbore
Abstract
:1. Introduction
2. Mathematical Model
2.1. Governing Equations
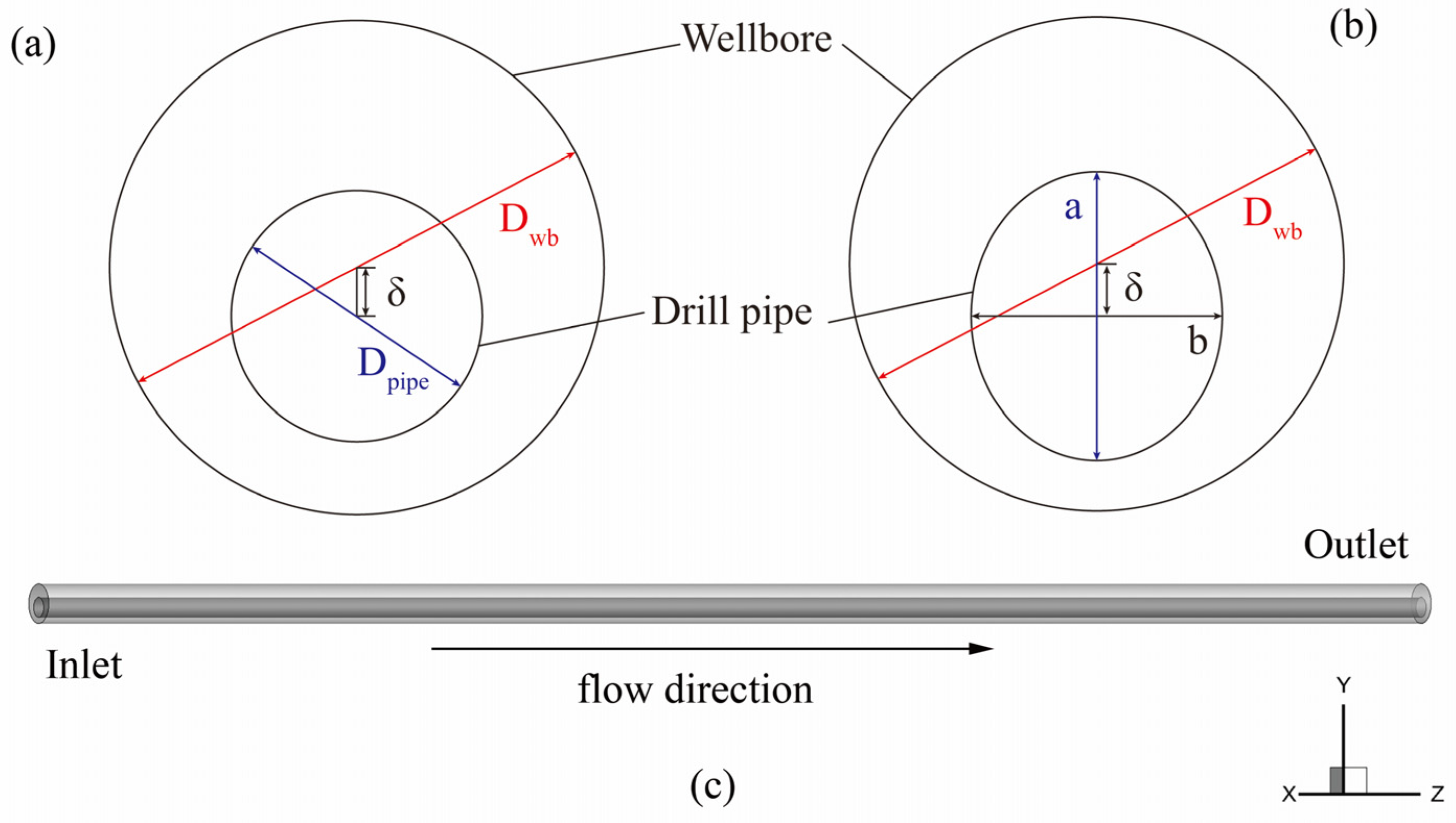
2.2. Numerical Model
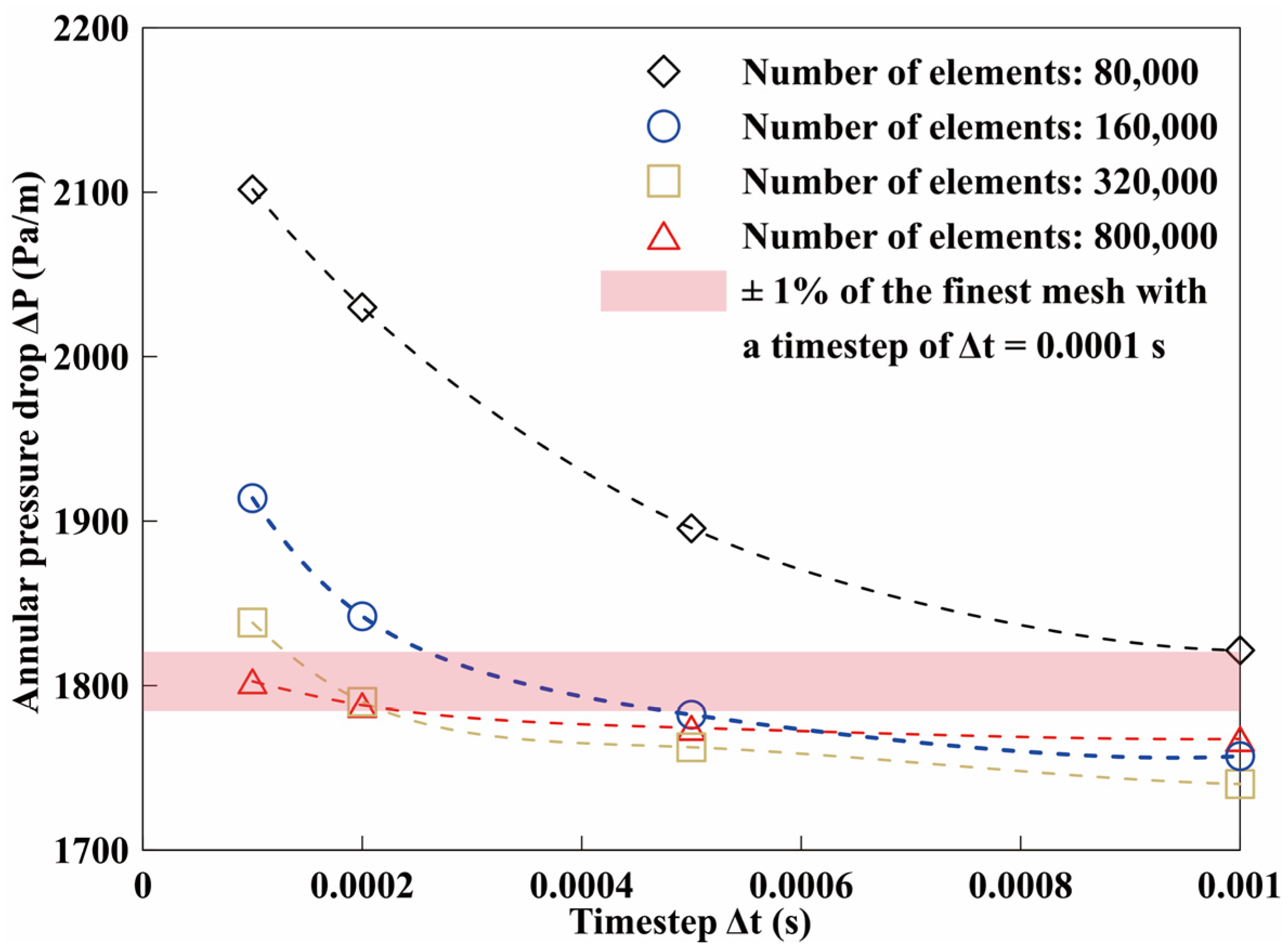
2.3. Boundary Conditions and Grid Independence Study
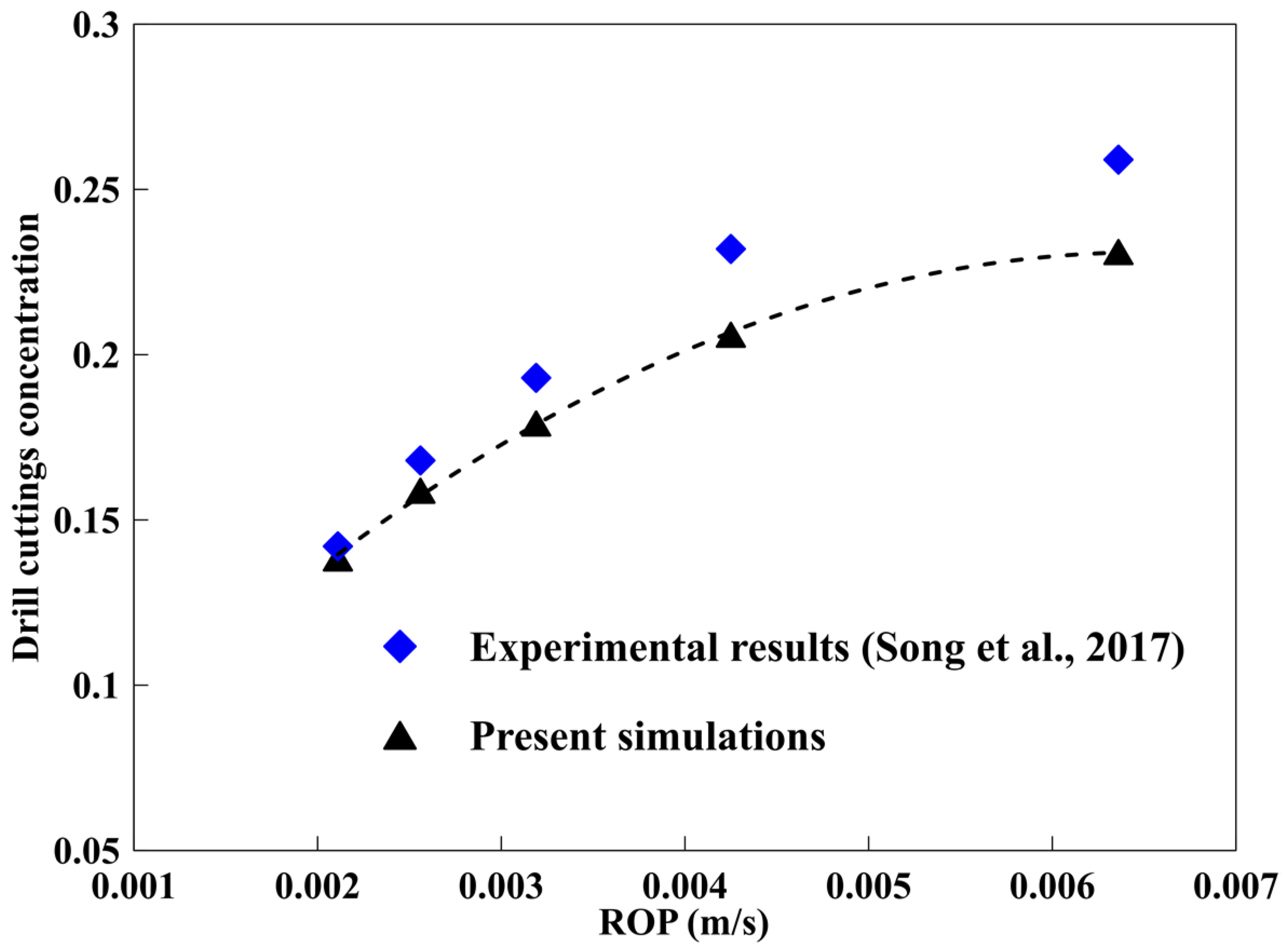
2.4. Verification of CFD-Based Simulation
3. Results and Discussion
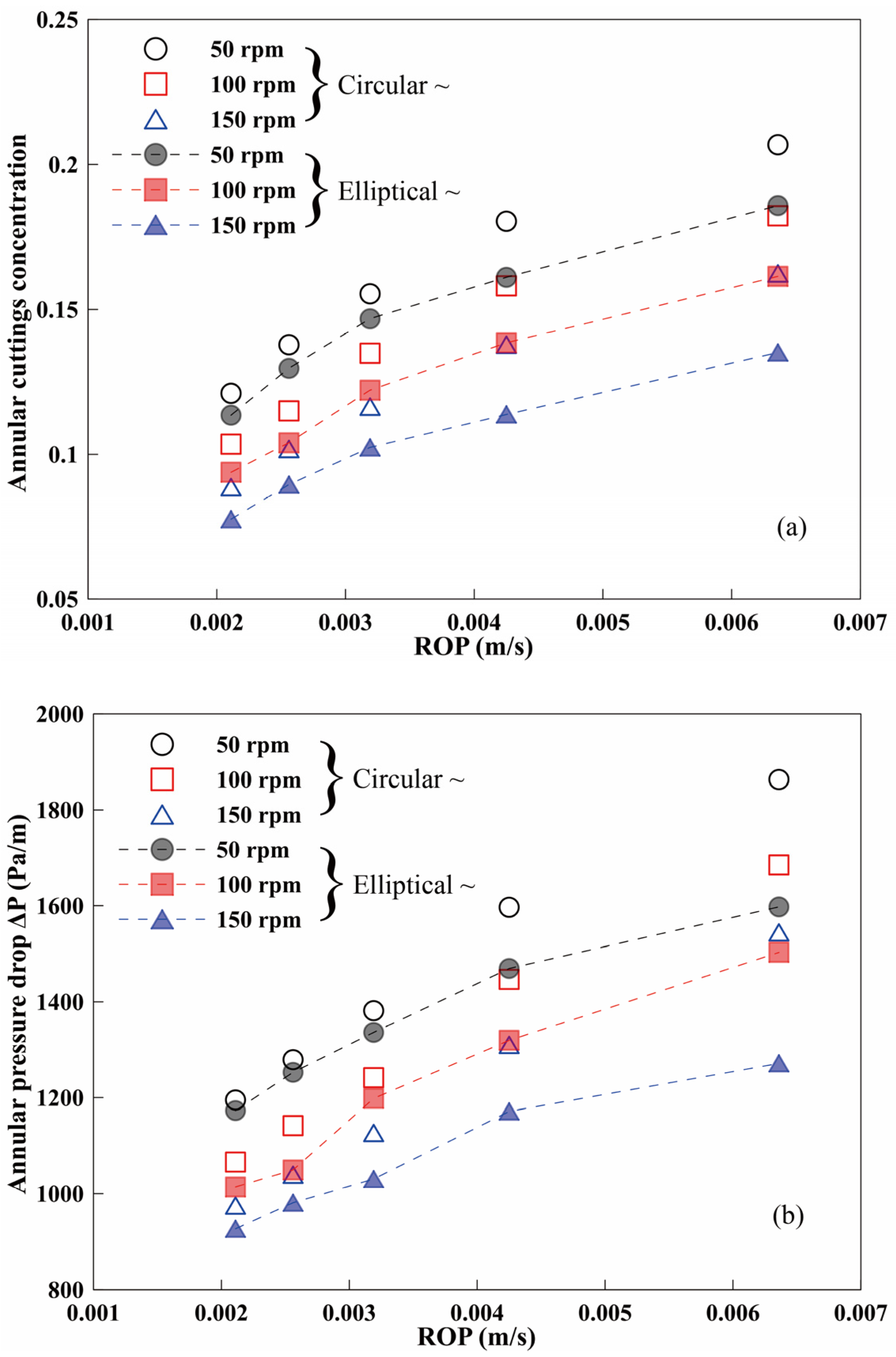
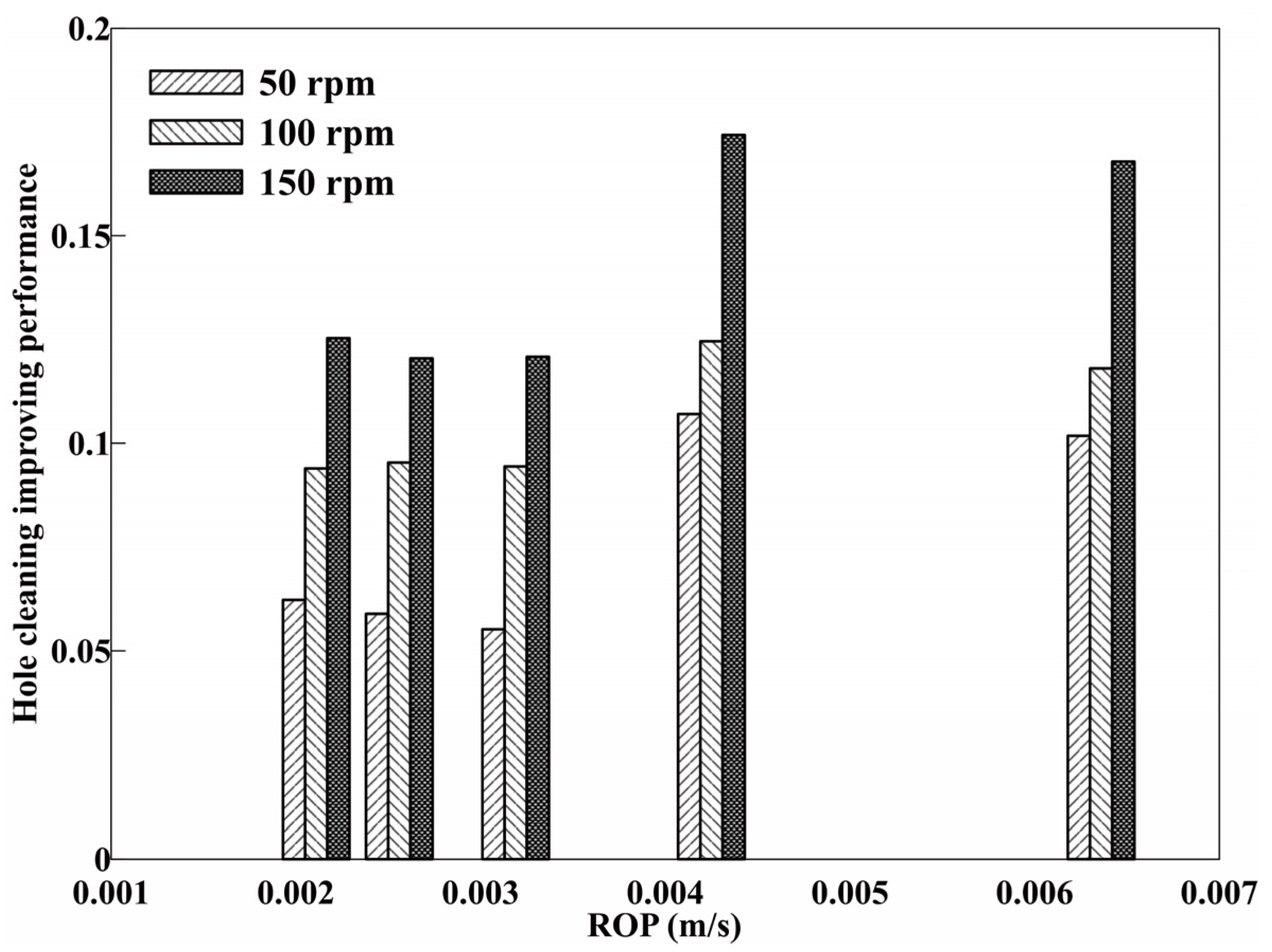
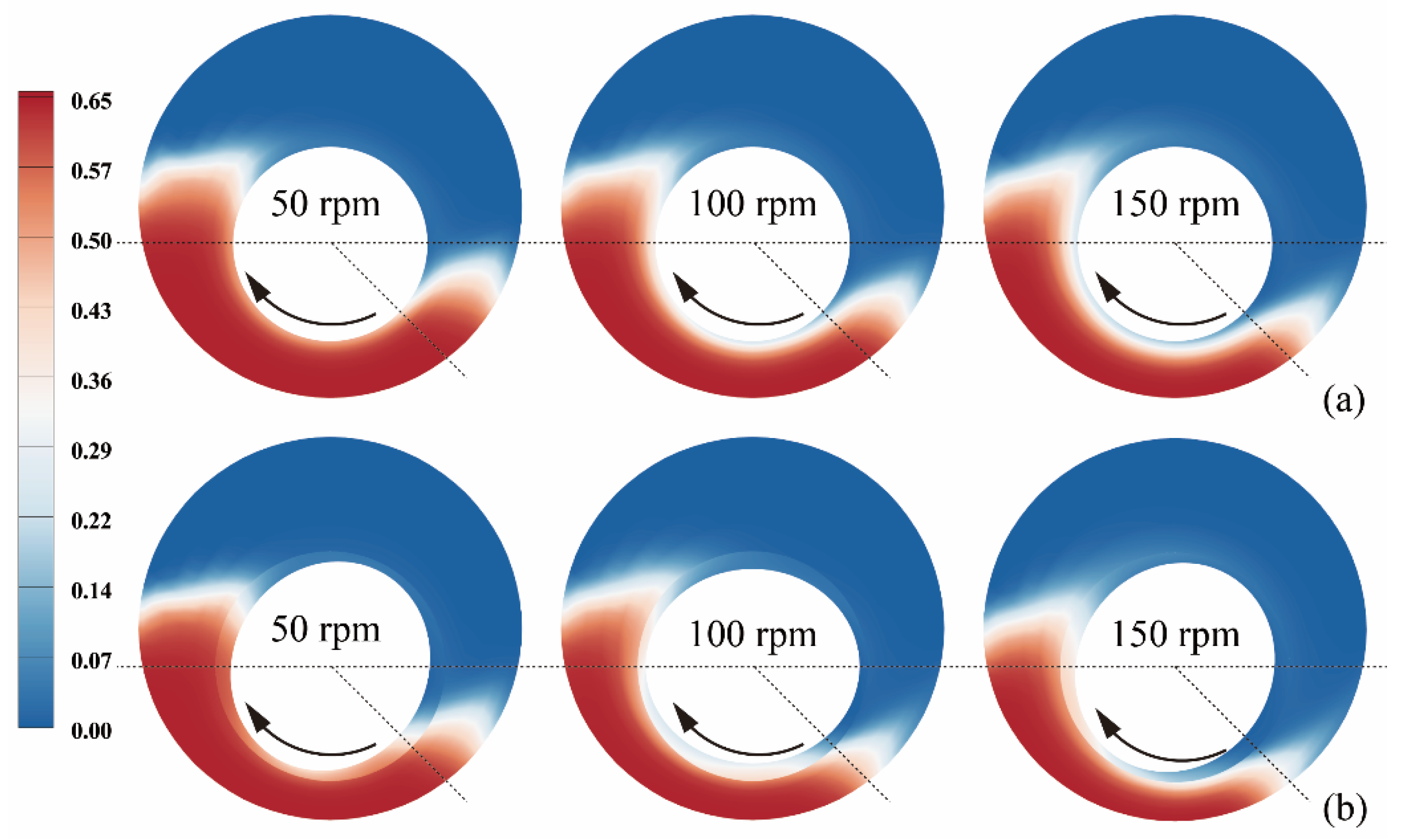
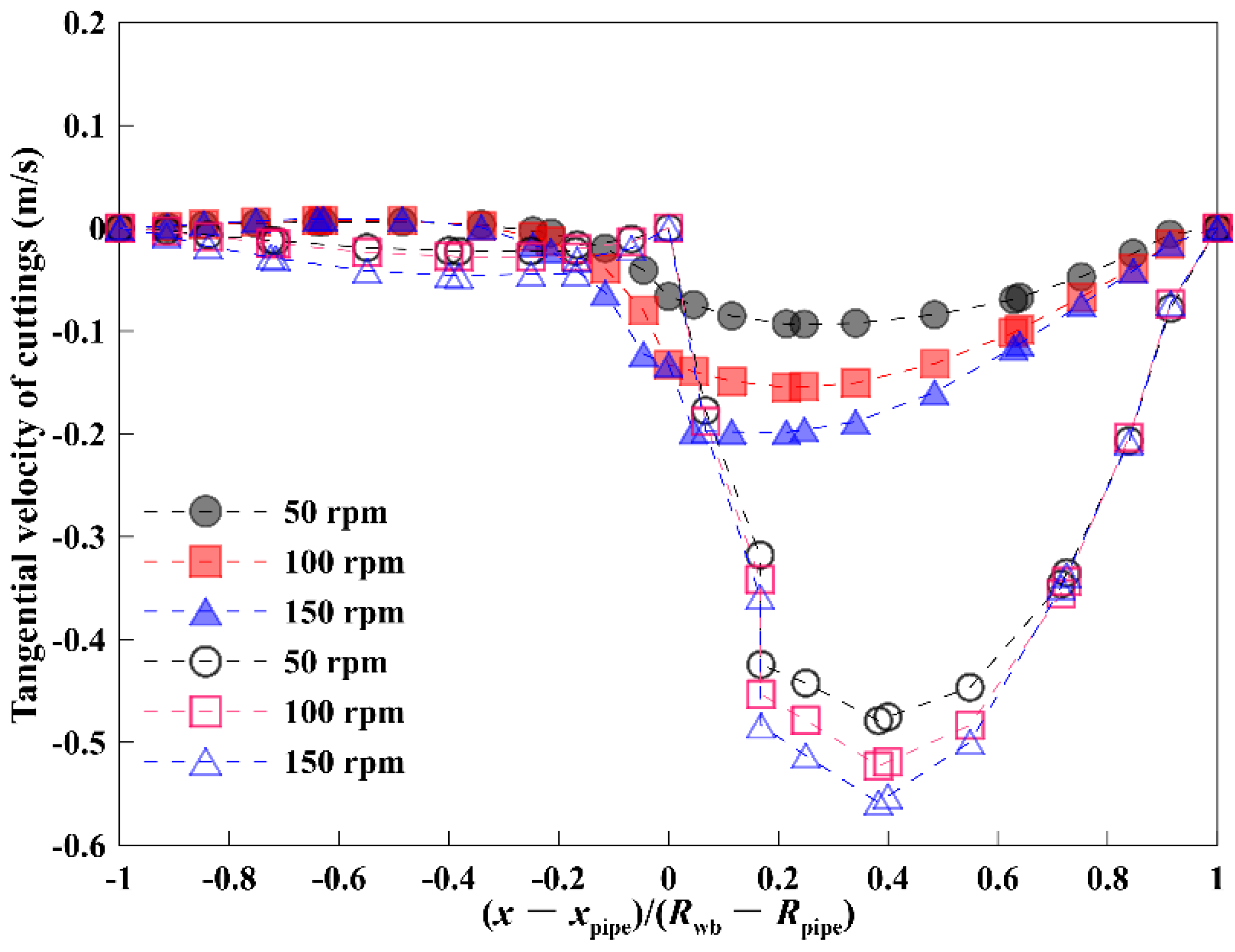
3.1. Effect of Drillpipe Rotation
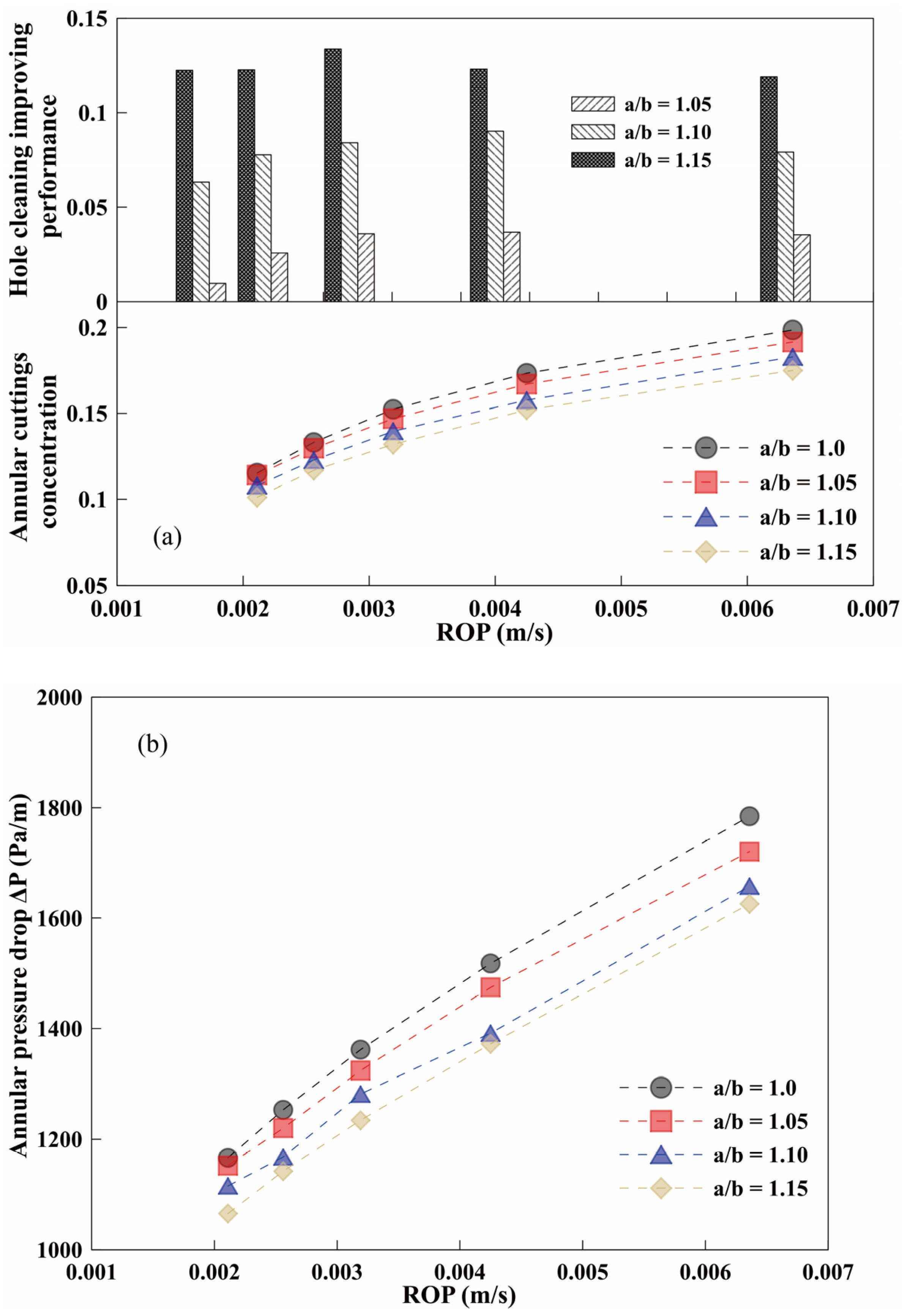
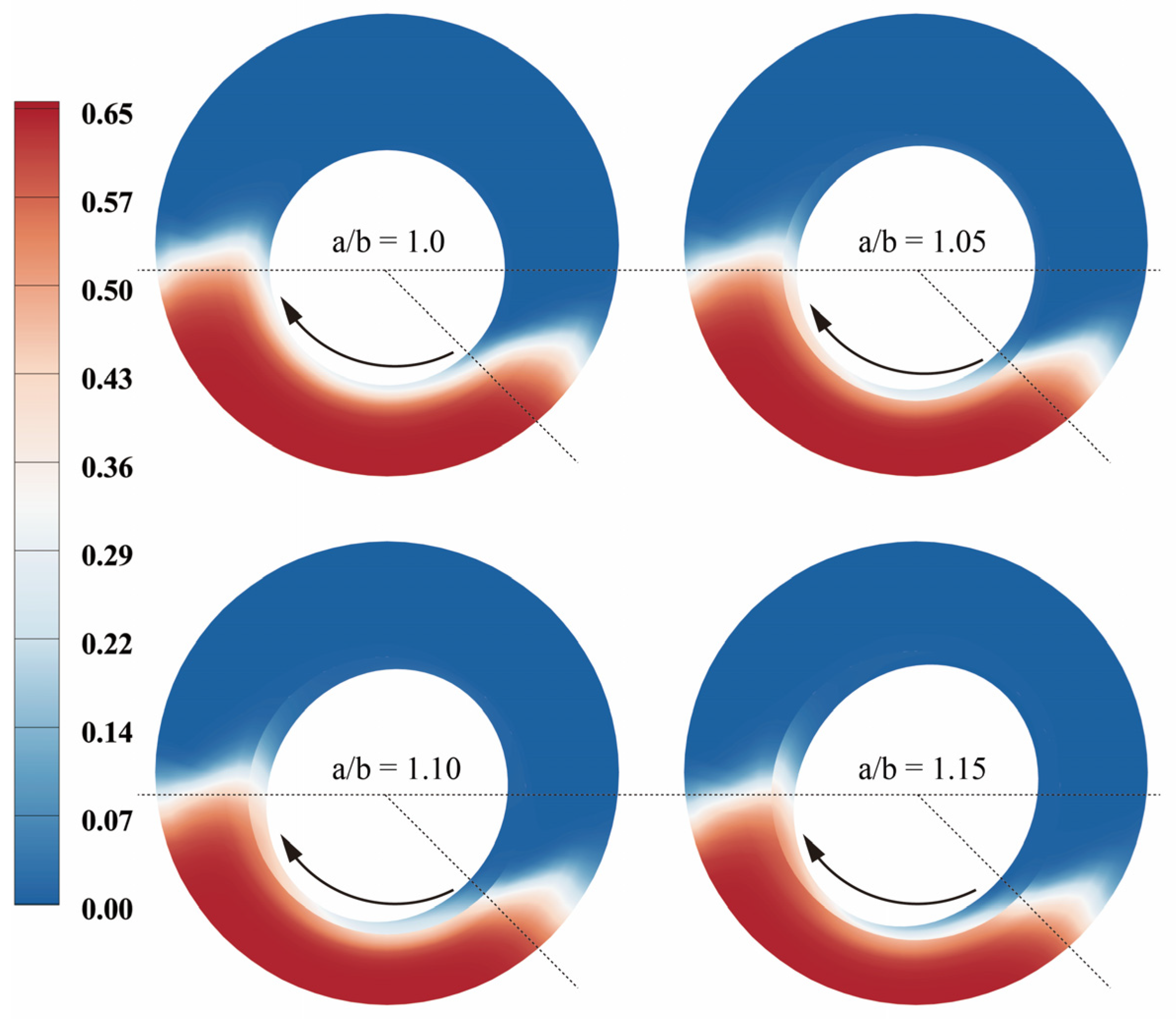
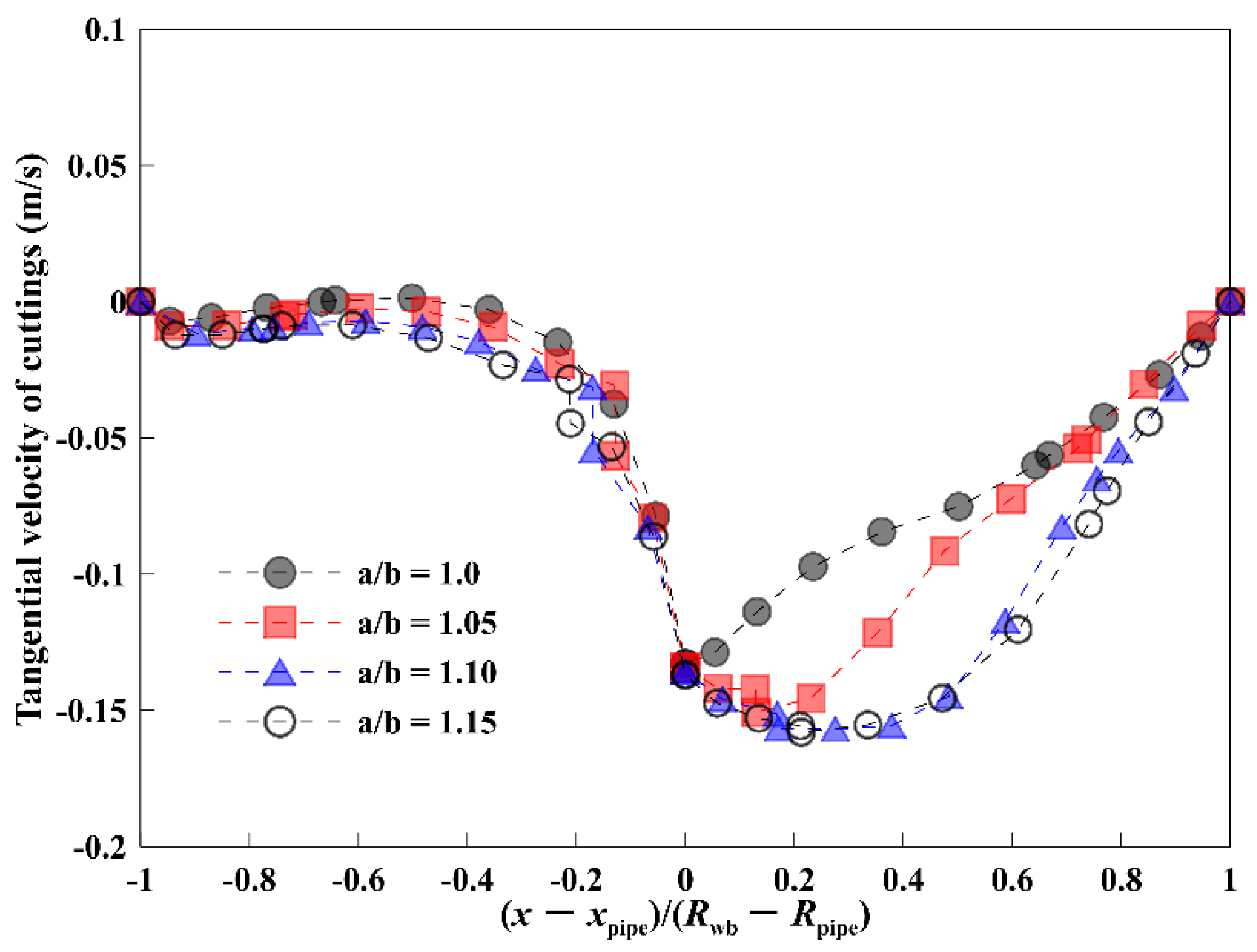
3.2. Effect of Major to Minor Axial Ratio a/b
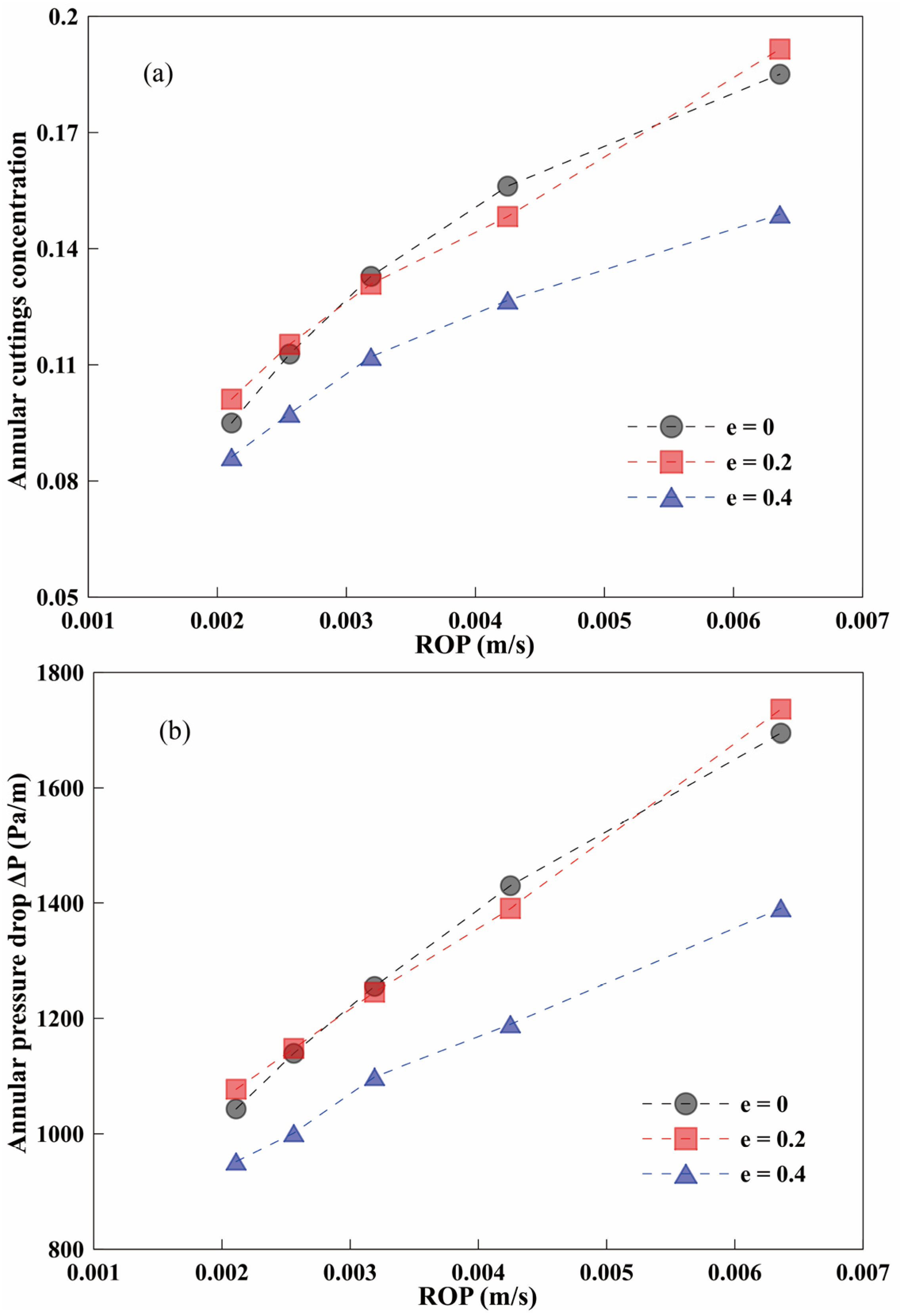
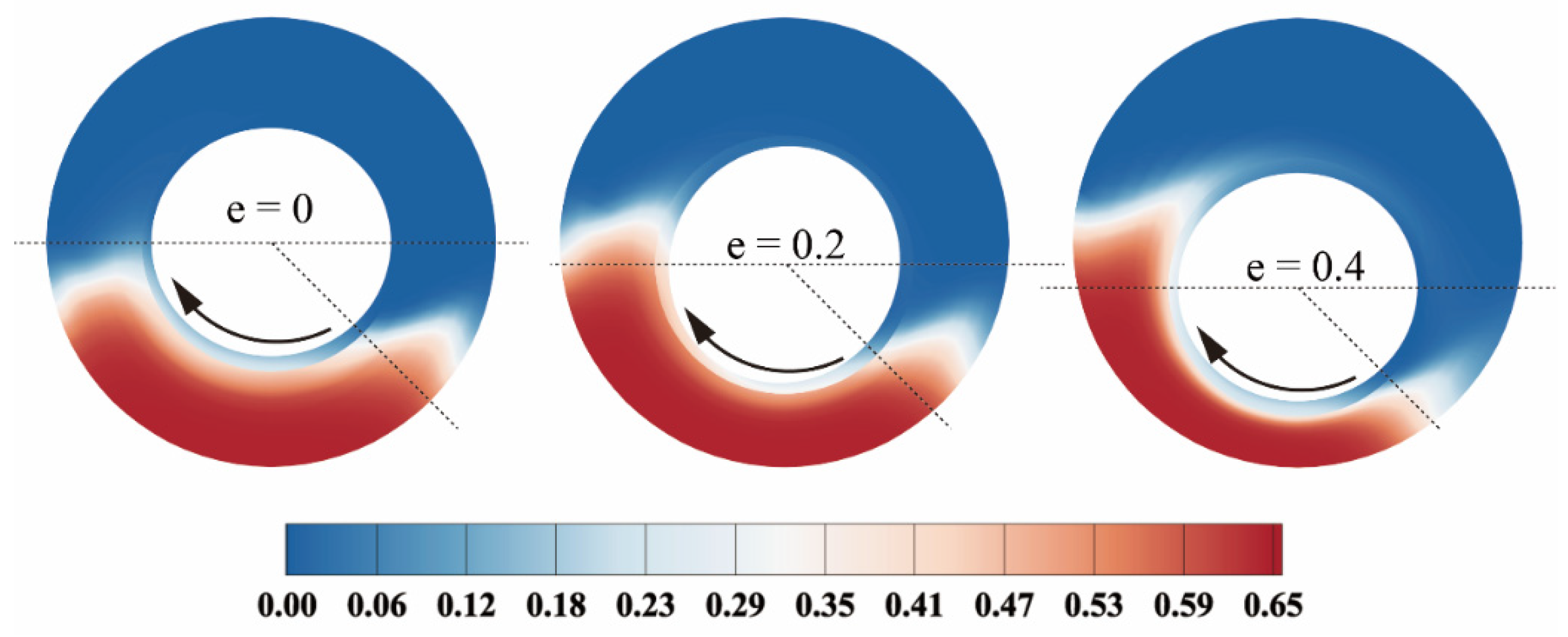
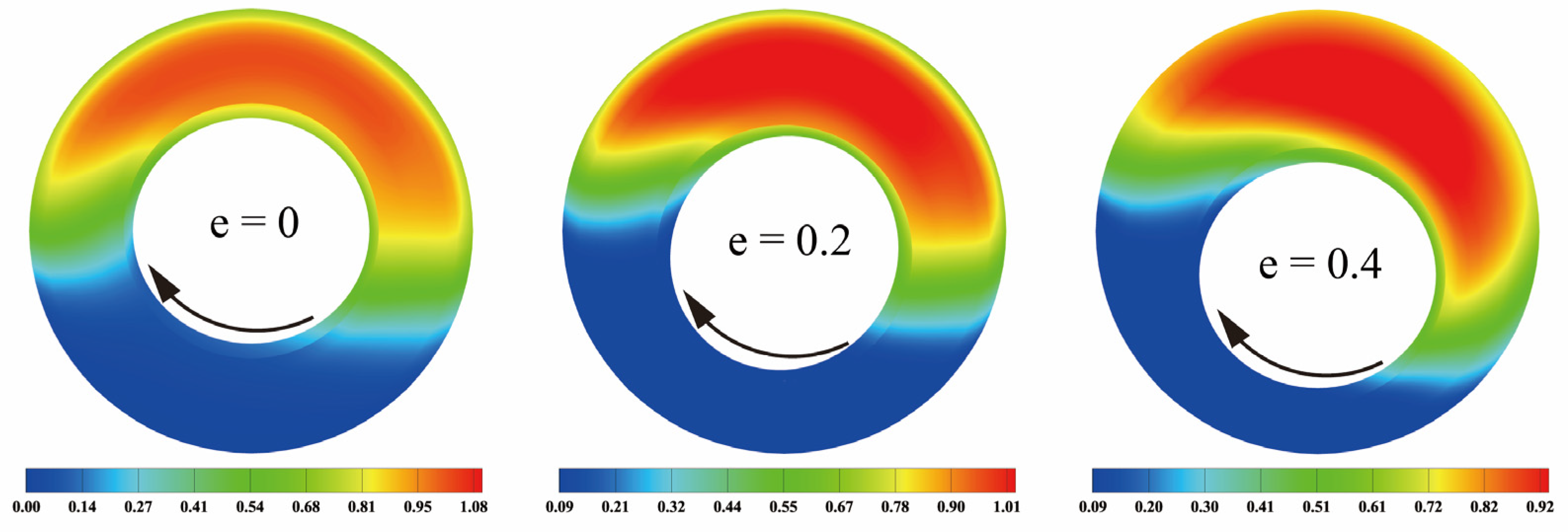
3.3. Effect of Eccentricity
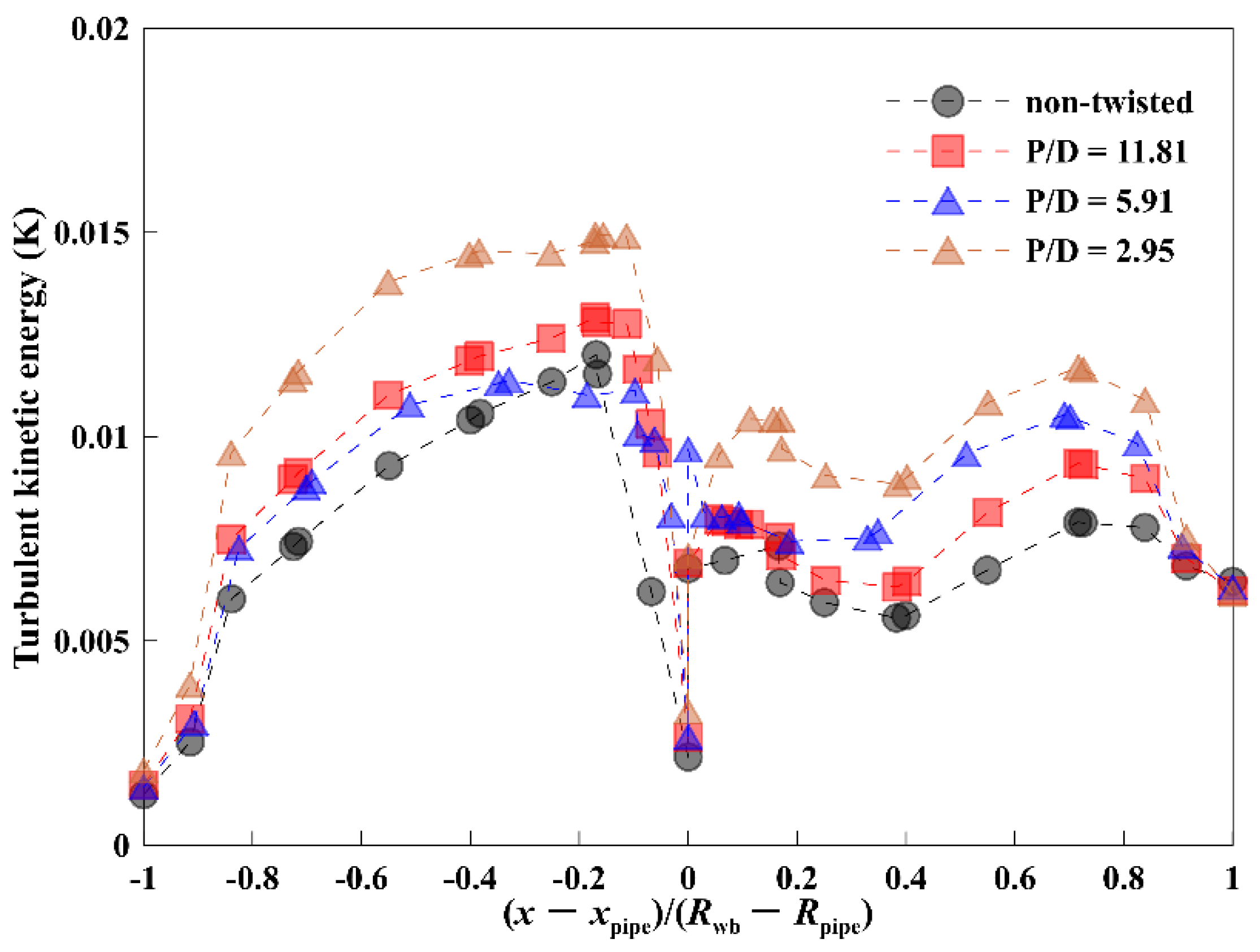
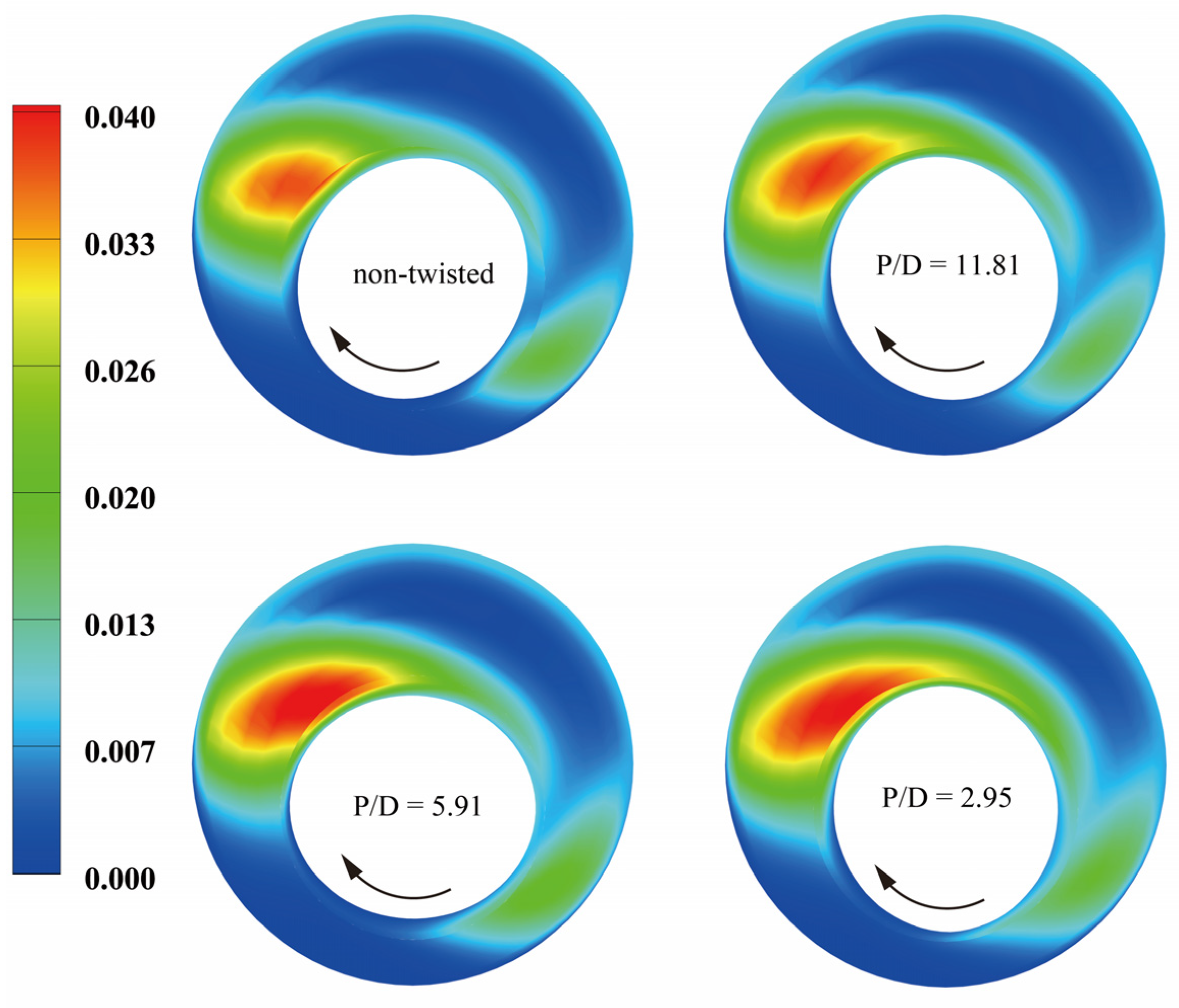
3.4. Effect of Pitch Length Ratio (P/Dpipe)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, W.; Xie, P.; Li, Y.; Teng, L.; Zhu, J. Hydrodynamic characteristics and mass transfer performance of rotating packed bed for CO2 removal by chemical absorption: A review. J. Nat. Gas Sci. Eng. 2020, 79, 103373. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Pan, Y.; Wang, X.; Yan, M.; Shi, X.; Zhou, X.; Li, H. Experiments and analysis on the influence of multiple closed cemented natural fractures on hydraulic fracture propagation in a tight sandstone reservoir. Eng. Geol. 2021, 281, 105981. [Google Scholar] [CrossRef]
- Mahmoud, H.; Hamza, A.; Nasser, M.S.; Hussein, I.A.; Ahmed, R.; Karami, H. Hole cleaning and drilling fluid sweeps in horizontal and deviated wells: Comprehensive review. J. Pet. Sci. Eng. 2020, 186, 106748. [Google Scholar] [CrossRef]
- Guan, Z.C.; Liu, Y.M.; Liu, Y.M.; Xu, Y.Q. Hole cleaning optimization of horizontal wells with the multi-dimensional ant colony algorithm. J. Nat. Gas Sci. Eng. 2016, 28, 347–355. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, L.; Zhu, Q. A quadruple-porosity model for transient production analysis of multiple-fractured horizontal wells in shale gas reservoirs. Environ. Earth Sci. 2015, 73, 5917–5931. [Google Scholar] [CrossRef]
- Heydari, O.; Sahraei, E.; Skalle, P. Investigating the impact of drillpipe’s rotation and eccentricity on cuttings transport phenomenon in various horizontal annuluses using computational fluid dynamics (CFD). J. Pet. Sci. Eng. 2017, 156, 801–813. [Google Scholar] [CrossRef]
- Movahedi, H.; Vasheghani Farahani, M.; Jamshidi, S. Application of Hydrated Basil Seeds (HBS) as the herbal fiber on hole cleaning and filtration control. J. Pet. Sci. Eng. 2017, 152, 212–228. [Google Scholar] [CrossRef]
- Van Puymbroeck, L.; El Bachiri, K.; Williams, H. New generation drill pipe to increase drilling performance in ERD wells. In Proceedings of the SPE/IADC Middle East Drilling Technology Conference & Exhibition, Dubai, United Arab Emirates, 7–9 October 2013; pp. 7–9. [Google Scholar]
- Duan, M.; Miska, S.Z.; Yu, M.; Takach, N.E.; Zettner, R.M.A.C.M. Critical Conditions for Effective Sand-Sized Solids Transport in Horizontal and High-Angle Wells. SPE Drill. Complet. 2009, 24, 229–238. [Google Scholar] [CrossRef]
- Han, S.M.; Woo, N.S.; Hwang, Y.K. Solid-liquid mixture flow through a slim hole annulus with rotating inner cylinder. J. Mech. Sci. Technol. 2009, 23, 569–577. [Google Scholar] [CrossRef]
- Ulker, E.; Sorgun, M. Comparison of computational intelligence models for cuttings transport in horizontal and deviated wells. J. Pet. Sci. Eng. 2016, 146, 832–837. [Google Scholar] [CrossRef]
- Epelle, E.I.; Gerogiorgis, D.I. CFD modelling and simulation of drill cuttings transport efficiency in annular bends: Effect of particle sphericity. J. Pet. Sci. Eng. 2018, 170, 992–1004. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Xu, Z.; Wang, M.; Li, G.; Shah, S.N.; Pang, Z. Experimental Study on the Wellbore-Cleaning Efficiency of Microhole-Horizontal-Well Drilling. SPE J. 2017, 22, 1189–1200. [Google Scholar] [CrossRef]
- Tomren, P.H. Experiment study of cuttings transport in Directional Wells. SPE Drill. Eng. 1986, 1, 43–56. [Google Scholar] [CrossRef]
- Epelle, E.I.; Gerogiorgis, D.I. A review of technological advances and open challenges for oil and gas drilling systems engineering. AIChE J. 2020, 66. [Google Scholar] [CrossRef]
- Yan, T.; Wang, K.; Sun, X.; Luan, S.; Shao, S. State-of-the-art cuttings transport with aerated liquid and foam in complex structure wells. Renew. Sustain. Energy Rev. 2014, 37, 560–568. [Google Scholar] [CrossRef]
- Boyou, N.V.; Ismail, I.; Wan Sulaiman, W.R.; Sharifi Haddad, A.; Husein, N.; Hui, H.T.; Nadaraja, K. Experimental investigation of hole cleaning in directional drilling by using nano-enhanced water-based drilling fluids. J. Pet. Sci. Eng. 2019, 176, 220–231. [Google Scholar] [CrossRef] [Green Version]
- Song, X.Z.; Li, G.S.; Huang, Z.W.; Wang, H.Z.; Tian, S.C.; Shi, H.Z. Experimental study on horizontal wellbore cleanout by rotating jets. J. Pet. Sci. Eng. 2010, 75, 71–76. [Google Scholar] [CrossRef]
- Allahvirdizadeh, P.; Kuru, E.; Parlaktuna, M. Experimental investigation of solids transport in horizontal concentric annuli using water and drag reducing polymer-based fluids. J. Nat. Gas Sci. Eng. 2016, 35, 1070–1078. [Google Scholar] [CrossRef]
- Busahmin, B.; Saeid, N.H.; Alusta, G.; Zahran, E.S.M.M. Review on hole cleaning for horizontal wells. ARPN J. Eng. Appl. Sci. 2017, 12, 4697–4708. [Google Scholar] [CrossRef]
- Keshavarz Moraveji, M.; Sabah, M.; Shahryari, A.; Ghaffarkhah, A. Investigation of drill pipe rotation effect on cutting transport with aerated mud using CFD approach. Adv. Powder Technol. 2017, 28, 1141–1153. [Google Scholar] [CrossRef]
- Yan, T.; Qu, J.; Sun, X.; Chen, Y.; Hu, Q.; Li, W.; Zhang, H. Numerical investigation on horizontal wellbore hole cleaning with a four-lobed drill pipe using CFD-DEM method. Powder Technol. 2020, 375, 249–261. [Google Scholar] [CrossRef]
- Kunlabud, S.; Chuwattanakul, V.; Kongkaitpaiboon, V.; Promthaisong, P.; Eiamsa-ard, S. Heat transfer in turbulent tube flow inserted with loose-fit multi-channel twisted tapes as swirl generators. Theor. Appl. Mech. Lett. 2017, 7, 372–378. [Google Scholar] [CrossRef]
- Tang, X.; Dai, X.; Zhu, D. International Journal of Heat and Mass Transfer Experimental and numerical investigation of convective heat transfer and fluid flow in twisted spiral tube. Int. J. Heat Mass Transf. 2015, 90, 523–541. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, D.; Ren, K.; Han, Y.; Zhu, Y.; Peng, X.; Deng, J.; Zhang, X. A comparative review of self-rotating and stationary twisted tape inserts in heat exchanger. Renew. Sustain. Energy Rev. 2016, 53, 433–449. [Google Scholar] [CrossRef]
- GhasemiKafrudi, E.; Hashemabadi, S.H. Numerical study on cuttings transport in vertical wells with eccentric drillpipe. J. Pet. Sci. Eng. 2016, 140, 85–96. [Google Scholar] [CrossRef]
- Mohammadzadeh, K.; Hashemabadi, S.H.; Akbari, S. CFD simulation of viscosity modifier effect on cutting transport by oil based drilling fluid in wellbore. J. Nat. Gas Sci. Eng. 2016, 29, 355–364. [Google Scholar] [CrossRef]
- Liang, C.; Jiang, H.; Lin, S.; Li, H.; Wang, B. Intelligent Generation of Evolutionary Series in a Time-Variant Physical System via Series Pattern Recognition. Adv. Intell. Syst. 2021, 3, 2000172. [Google Scholar] [CrossRef]
- Huilin, L.; Gidaspow, D.; Bouillard, J.; Wentie, L. Hydrodynamic simulation of gas-solid flow in a riser using kinetic theory of granular flow. Chem. Eng. J. 2003, 95, 1–13. [Google Scholar] [CrossRef]
- Ozbayoglu, E.M.; Osgouei, R.E.; Ozbayoglu, A.M.; Yuksel, H.E. Hole-cleaning performance of gasified drilling fluids in horizontal well sections. SPE J. 2012, 17, 912–923. [Google Scholar] [CrossRef]
- Amanna, B.; Khorsand Movaghar, M.R. Cuttings transport behavior in directional drilling using computational fluid dynamics (CFD). J. Nat. Gas Sci. Eng. 2016, 34, 670–679. [Google Scholar] [CrossRef]
- Jafari, M.; Dabiri, S.; Farhadi, M.; Sedighi, K. Effects of a three-lobe swirl generator on the thermal and flow fields in a heat exchanging tube: An experimental and numerical approach. Energy Convers. Manag. 2017, 148, 1358–1371. [Google Scholar] [CrossRef]
- Dewangan, S.K.; Sinha, S.L. Exploring the hole cleaning parameters of horizontal wellbore using two-phase Eulerian CFD approach. J. Comput. Multiph. Flows 2016, 8, 15–39. [Google Scholar] [CrossRef] [Green Version]


| Geometrical Parameters | Value |
|---|---|
| Annulus length (L), mm | 2000 |
| Wellbore diameter (Dwb), mm | 50 |
| Drillpipe diameter (Dpipe), mm | 24.6 |
| Minor axis (b) (equal to Dpipe), mm | 24.6 |
| Major to minor axis ratio (a/b) | 1.00; 1.05; 1.10; 1.15 |
| Eccentricity (e) | 0, 0.2, 0.4 |
| Pitch length ratio (P/Dpipe) | 2.95, 5.91, 11.81 |
| Inclination angle (θ), degrees | 90 |
| Physical Parameters | Value |
|---|---|
| Fluid density (ρl), kg/m3 | 998.2 |
| Fluid viscosity (μl), Pa.s | 0.001 |
| Cuttings density (ρs), kg/m3 | 2650 |
| Cuttings diameter (ds), mm | 1.2 |
| ROP, (m/s) | 0.00211; 0.00256; 0.00319; |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, G.; Yan, T.; Sun, X. Numerical Simulation of Effective Hole Cleaning by Using an Innovative Elliptical Drillpipe in Horizontal Wellbore. Energies 2022, 15, 399. https://doi.org/10.3390/en15020399
Ju G, Yan T, Sun X. Numerical Simulation of Effective Hole Cleaning by Using an Innovative Elliptical Drillpipe in Horizontal Wellbore. Energies. 2022; 15(2):399. https://doi.org/10.3390/en15020399
Chicago/Turabian StyleJu, Guoshuai, Tie Yan, and Xiaofeng Sun. 2022. "Numerical Simulation of Effective Hole Cleaning by Using an Innovative Elliptical Drillpipe in Horizontal Wellbore" Energies 15, no. 2: 399. https://doi.org/10.3390/en15020399
APA StyleJu, G., Yan, T., & Sun, X. (2022). Numerical Simulation of Effective Hole Cleaning by Using an Innovative Elliptical Drillpipe in Horizontal Wellbore. Energies, 15(2), 399. https://doi.org/10.3390/en15020399





