Hysteresis Control in Pump-Controlled Systems—A Way to Reduce Mode-Switch Oscillations in Closed and Open Circuits
Abstract
:1. Introduction
- One must be able to compensate for the difference in flow that an asymmetric cylinder causes. Note that asymmetric cylinders often are preferred because of their compactness compared to symmetrical cylinders.
- It is desirable to recuperate energy when possible, which means that the pump should work as a motor when desired. The switch between pumping and motoring modes can cause unwanted oscillations. Also, note that the conventional load-holding functionality must be replaced to allow energy recuperation.
1.1. State of the Art
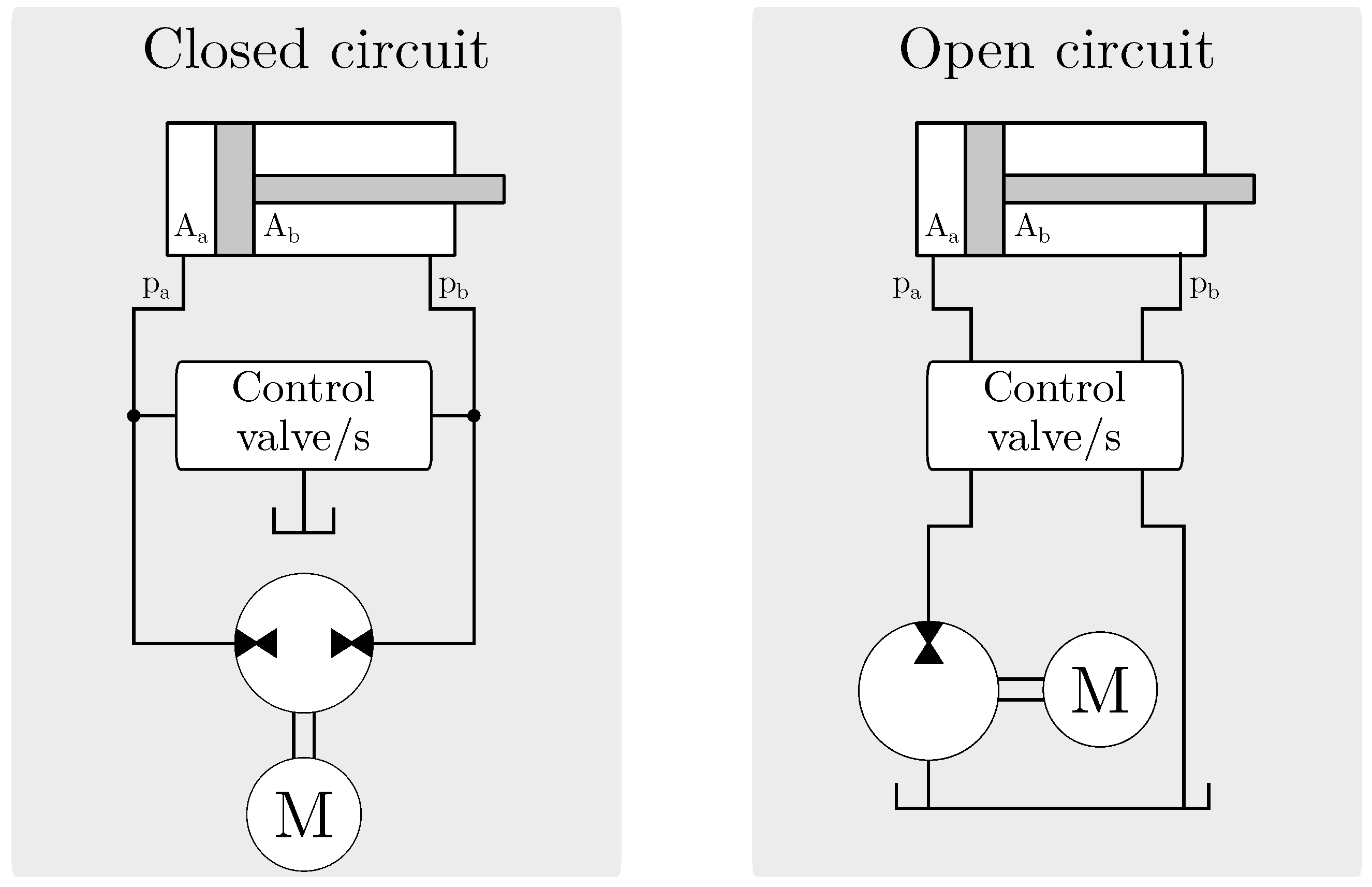
1.1.1. Closed Circuits
1.1.2. Open Circuits
1.2. Contributions
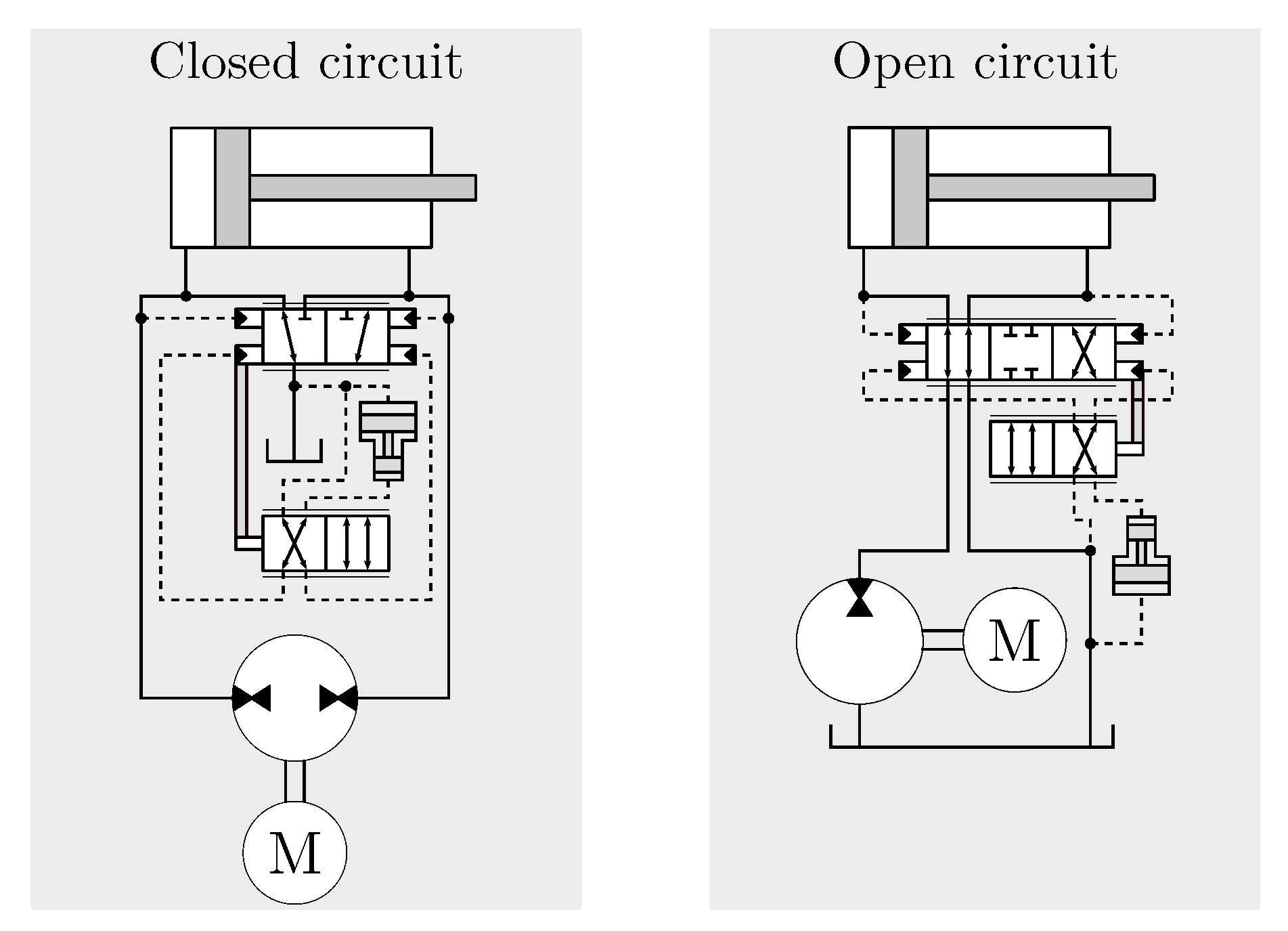
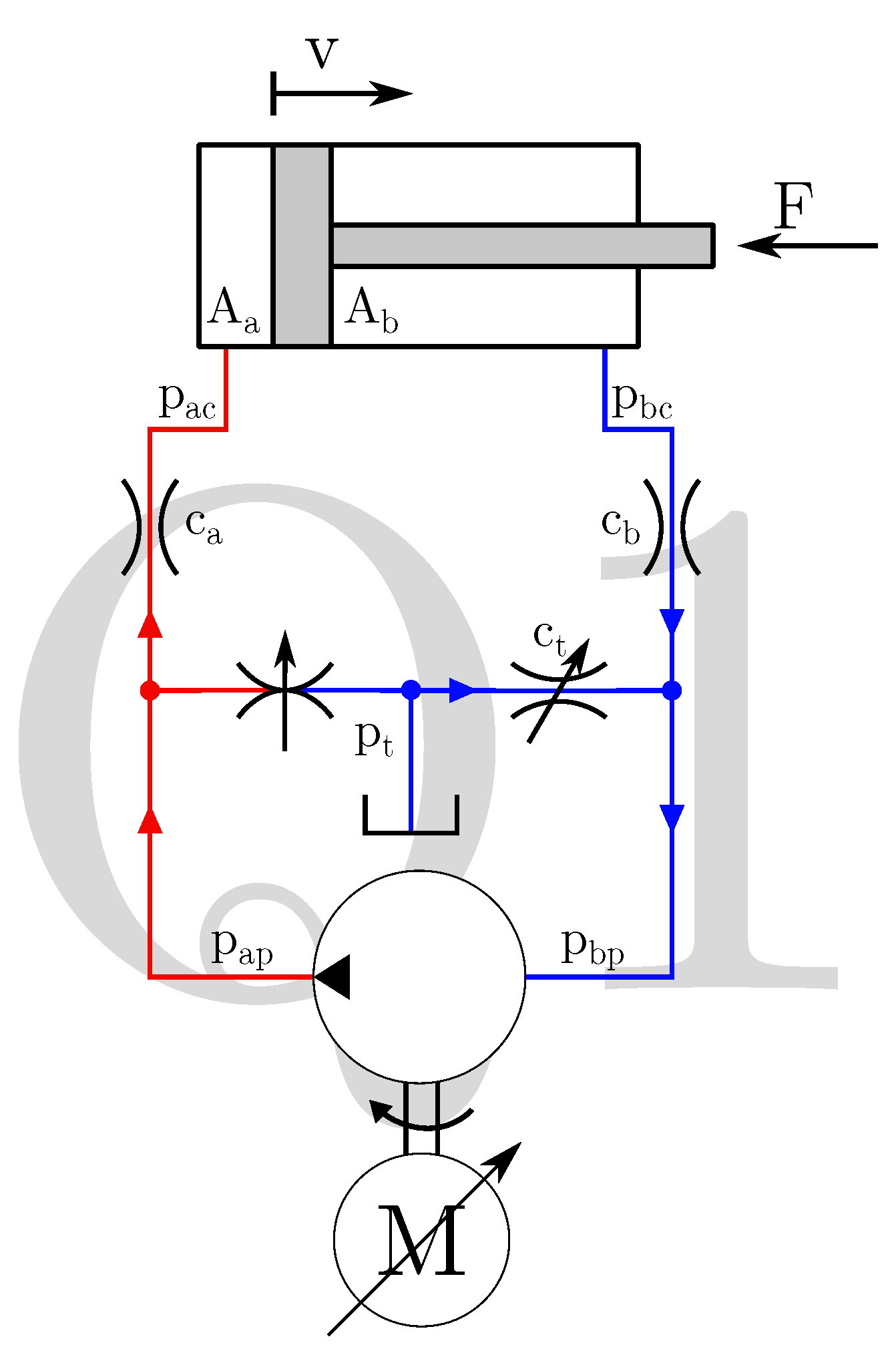
2. Considered Circuits
2.1. Circuit Requirements
2.1.1. Pressurised Reservoir
2.1.2. Filtering
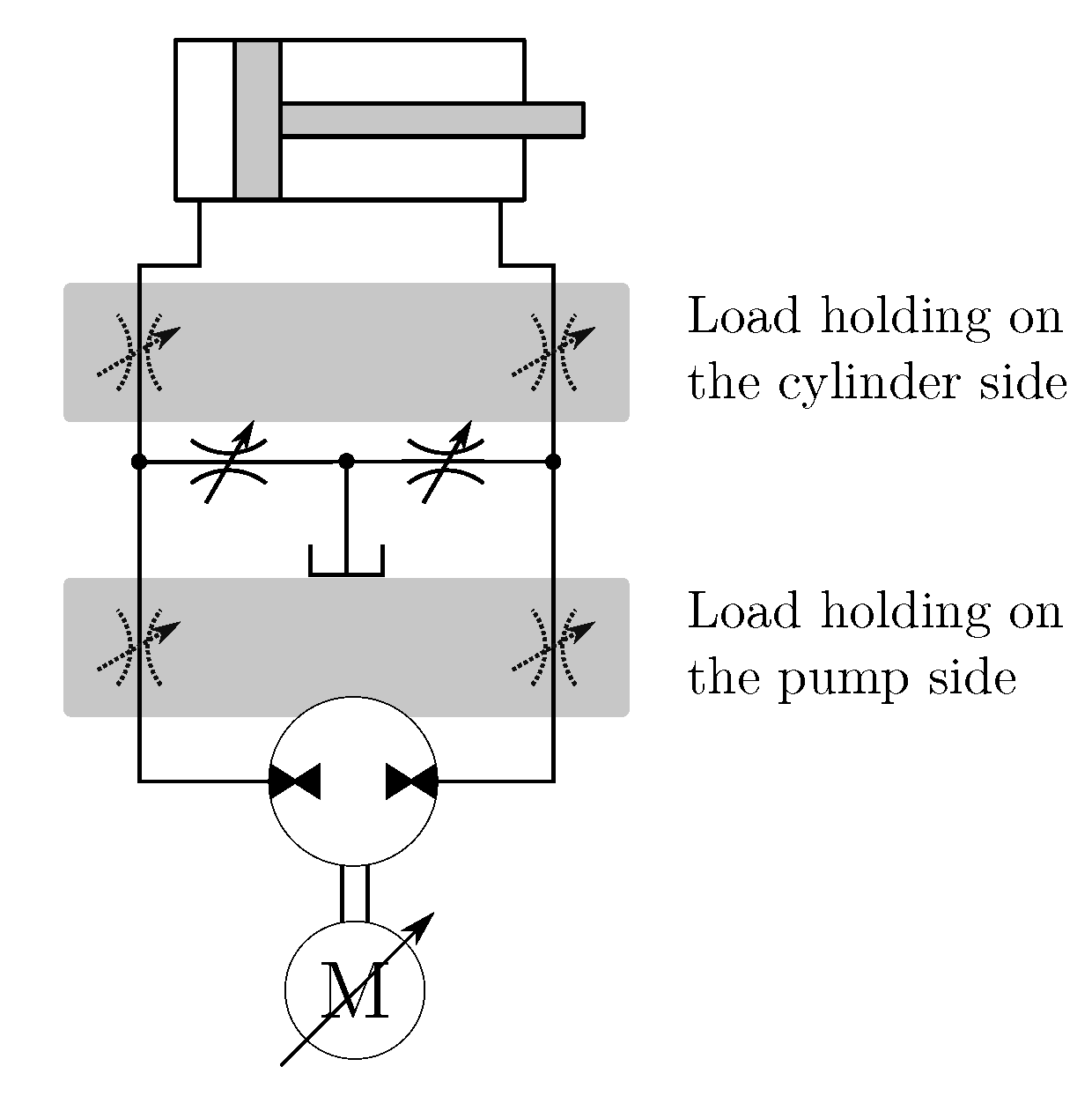
2.1.3. Load-Holding Functionality
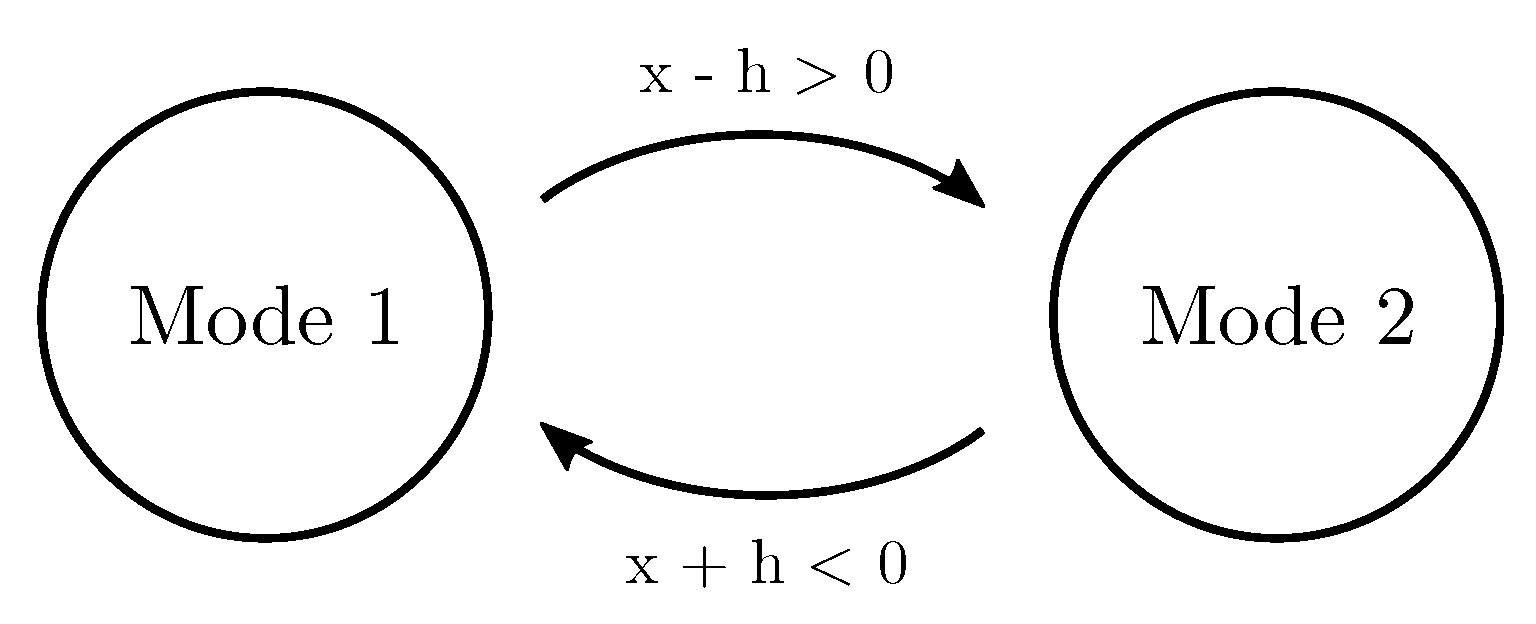
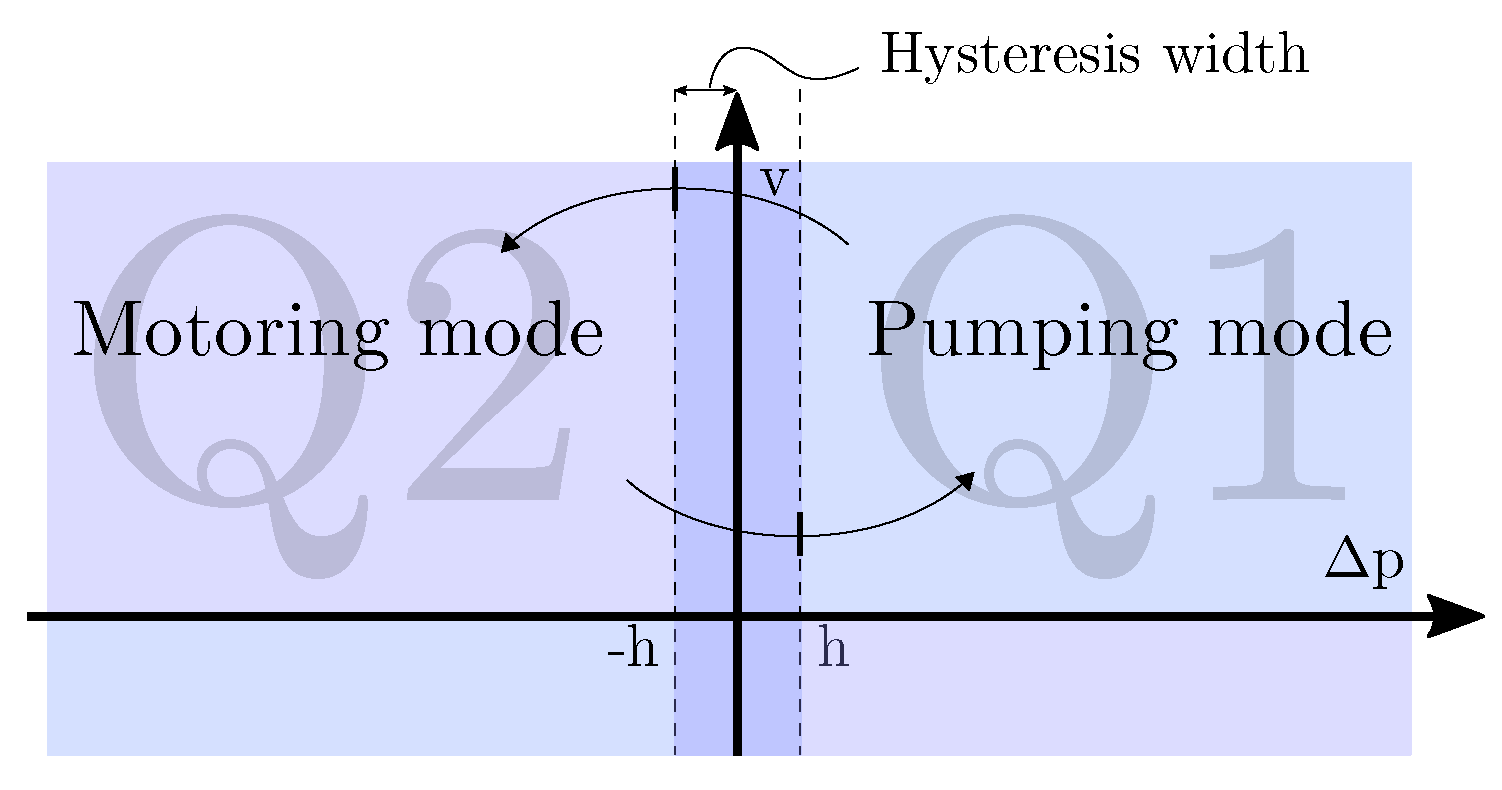
3. Hysteresis Control
3.1. Hysteresis Width Limitations
3.2. Implementation
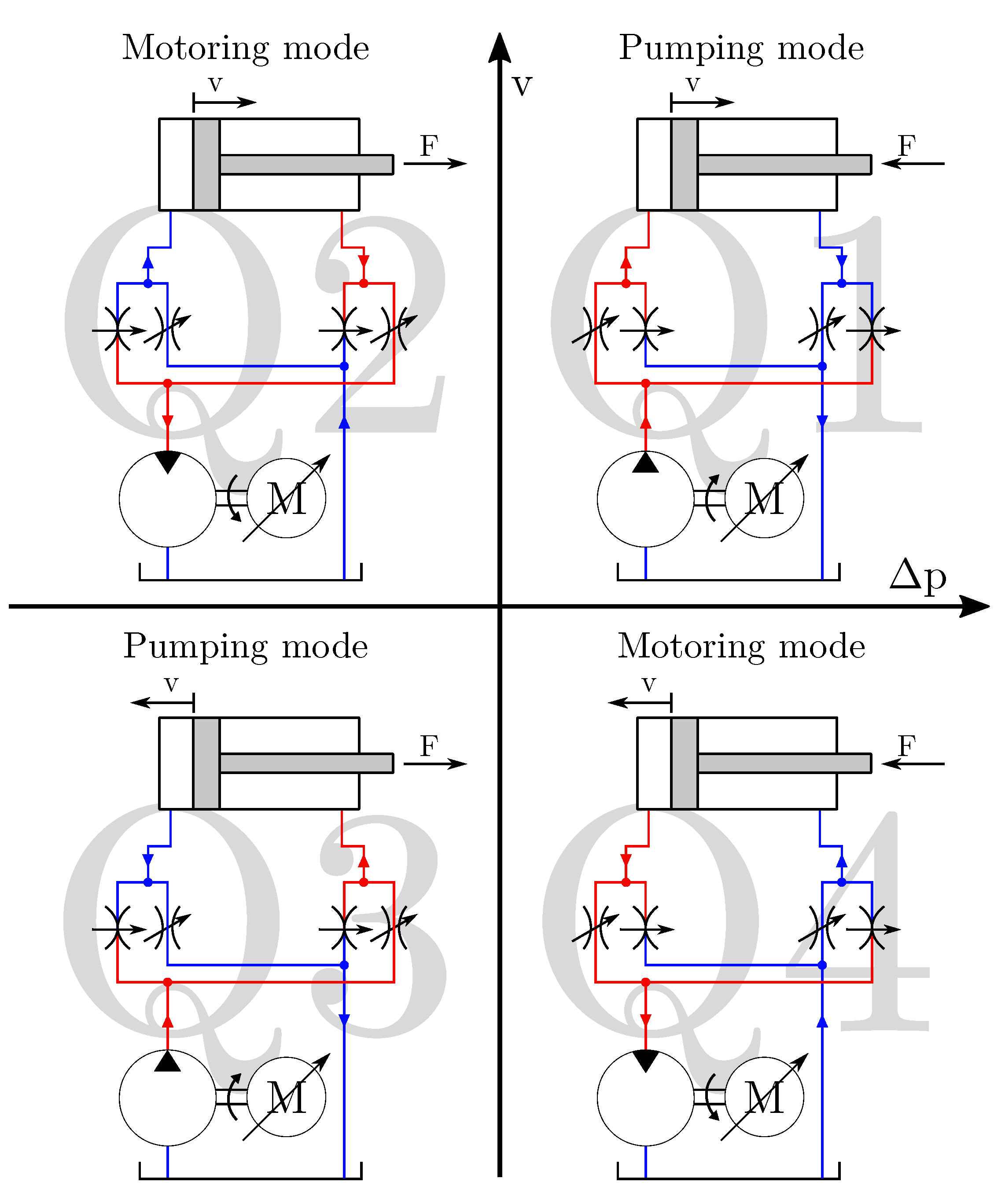
3.2.1. Active Hysteresis
3.2.2. Pressure-Drop Hysteresis
3.2.3. Hydro-Mechanical Hysteresis
3.2.4. Active Throttling
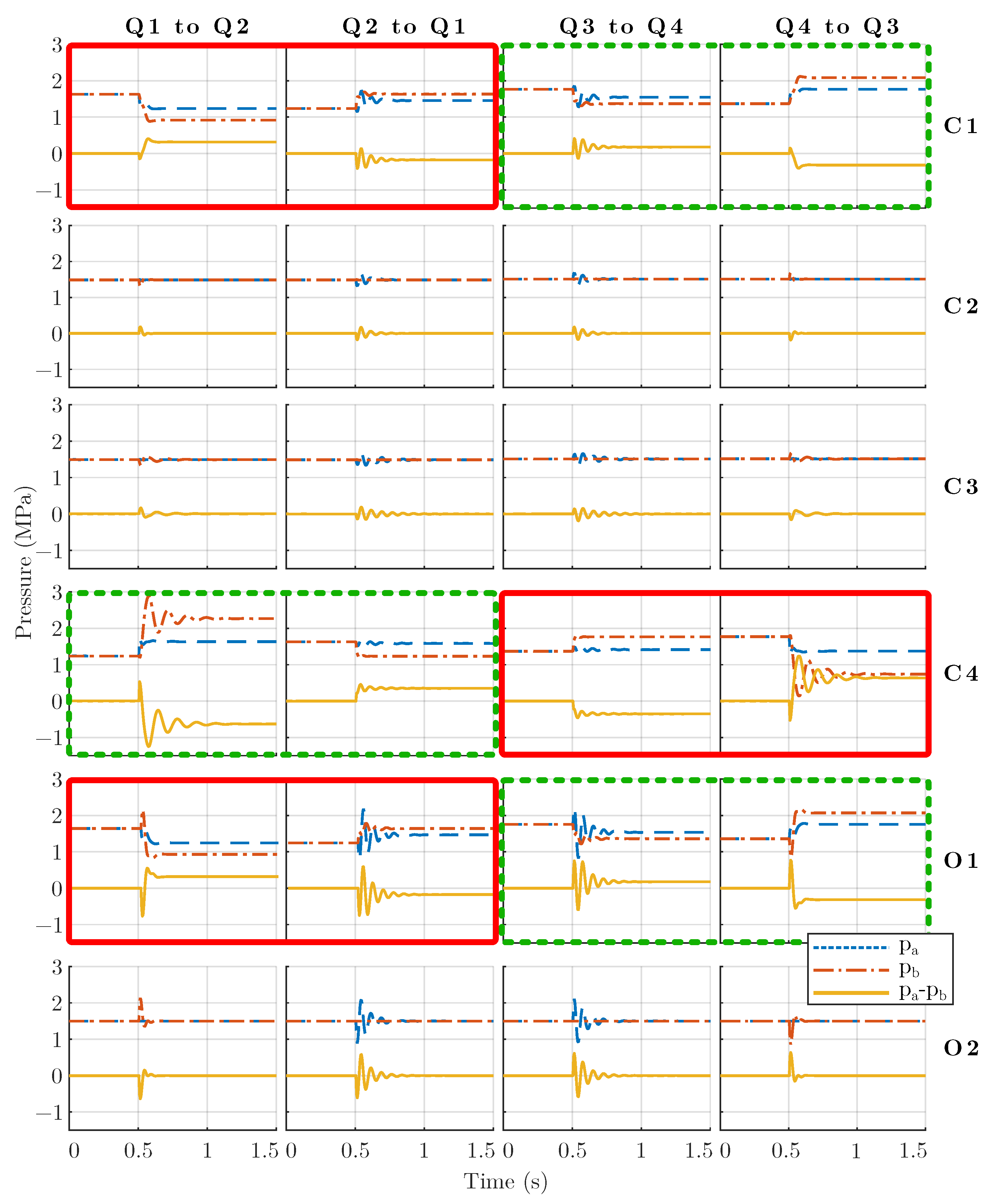
4. Where to Sense the Pressures
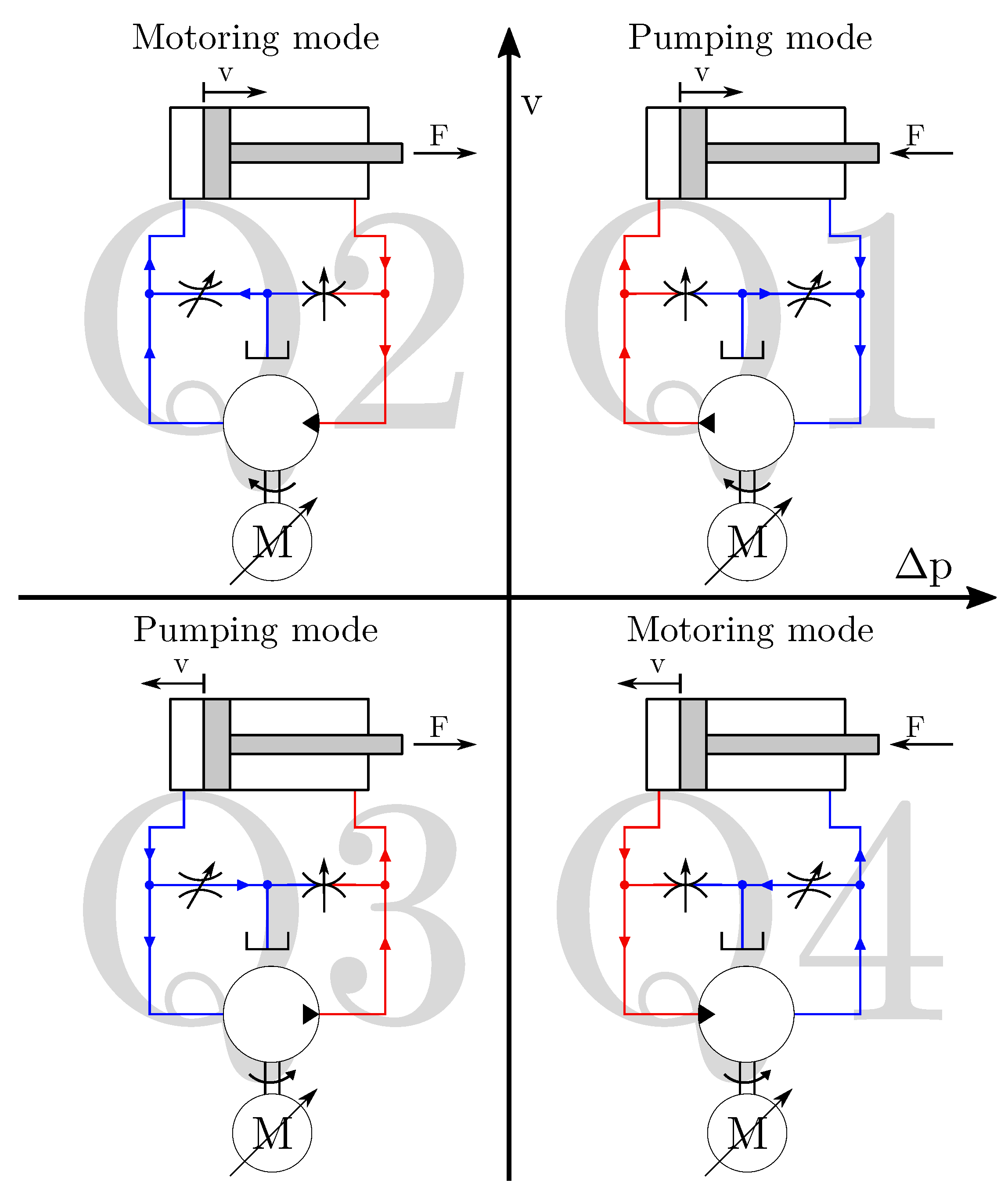
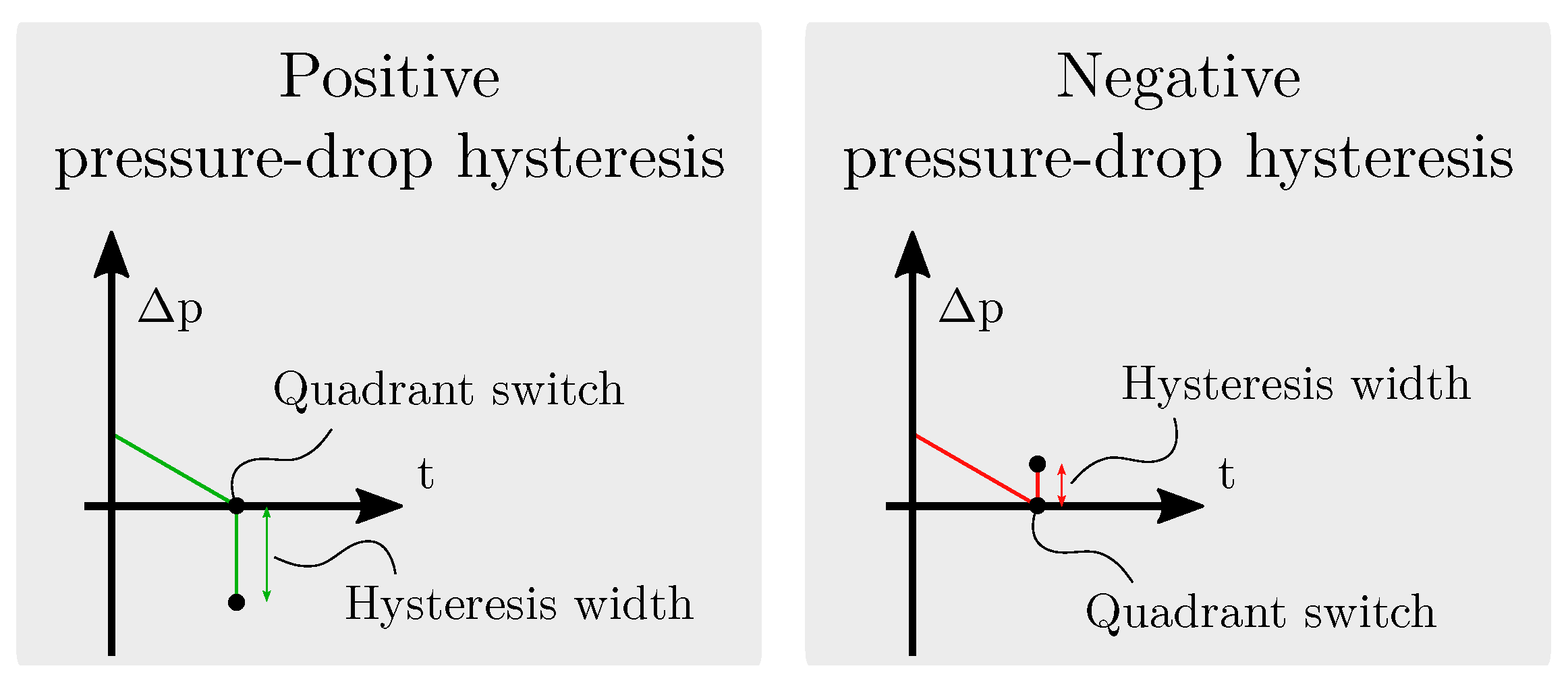
4.1. Positive and Negative Pressure-Drop Hysteresis
4.2. Pressure-Drop Hysteresis Calculations
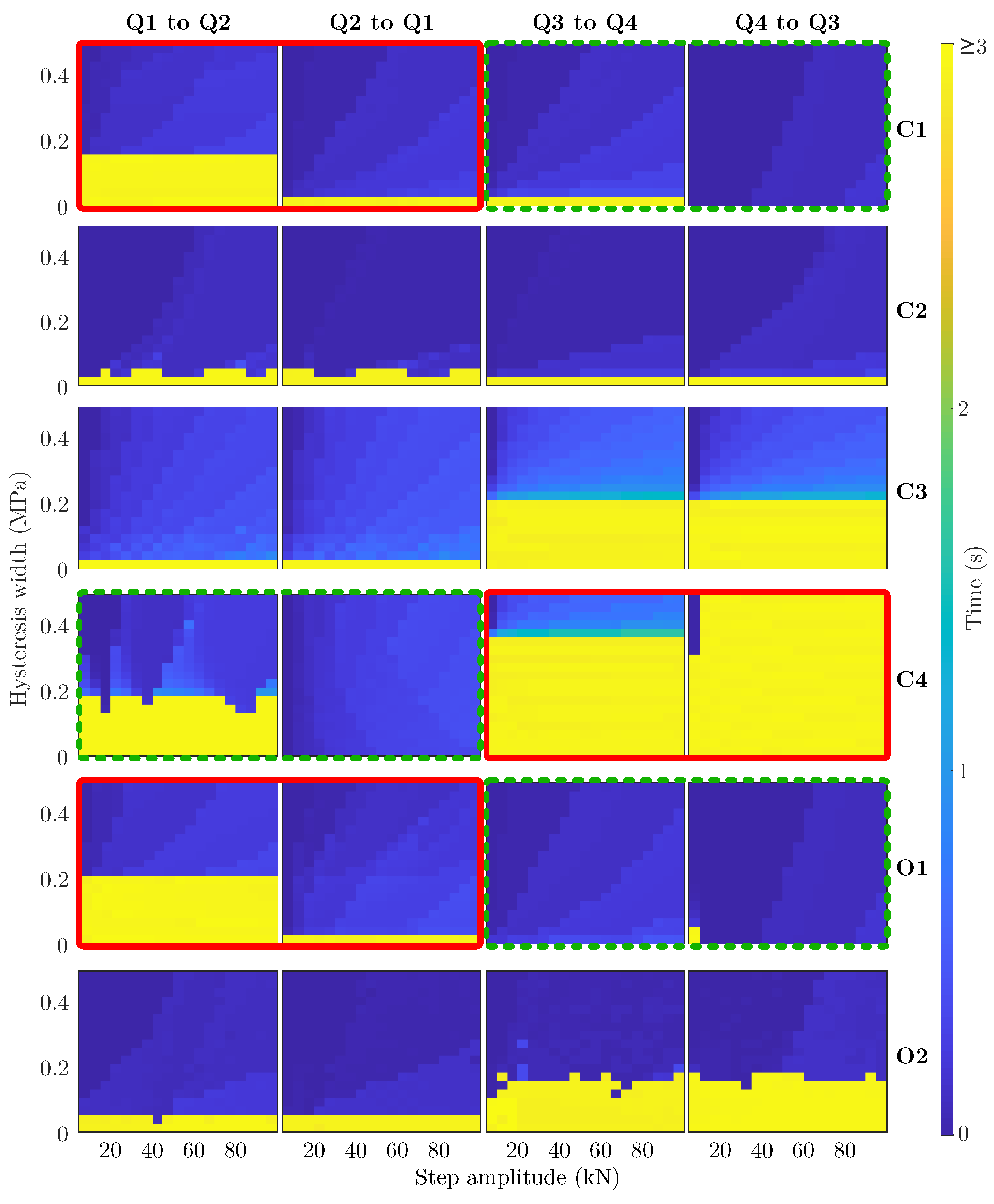
5. Dynamic Analysis
5.1. Valve and Motor Dynamics
5.2. Worst Case: External Force Considerations
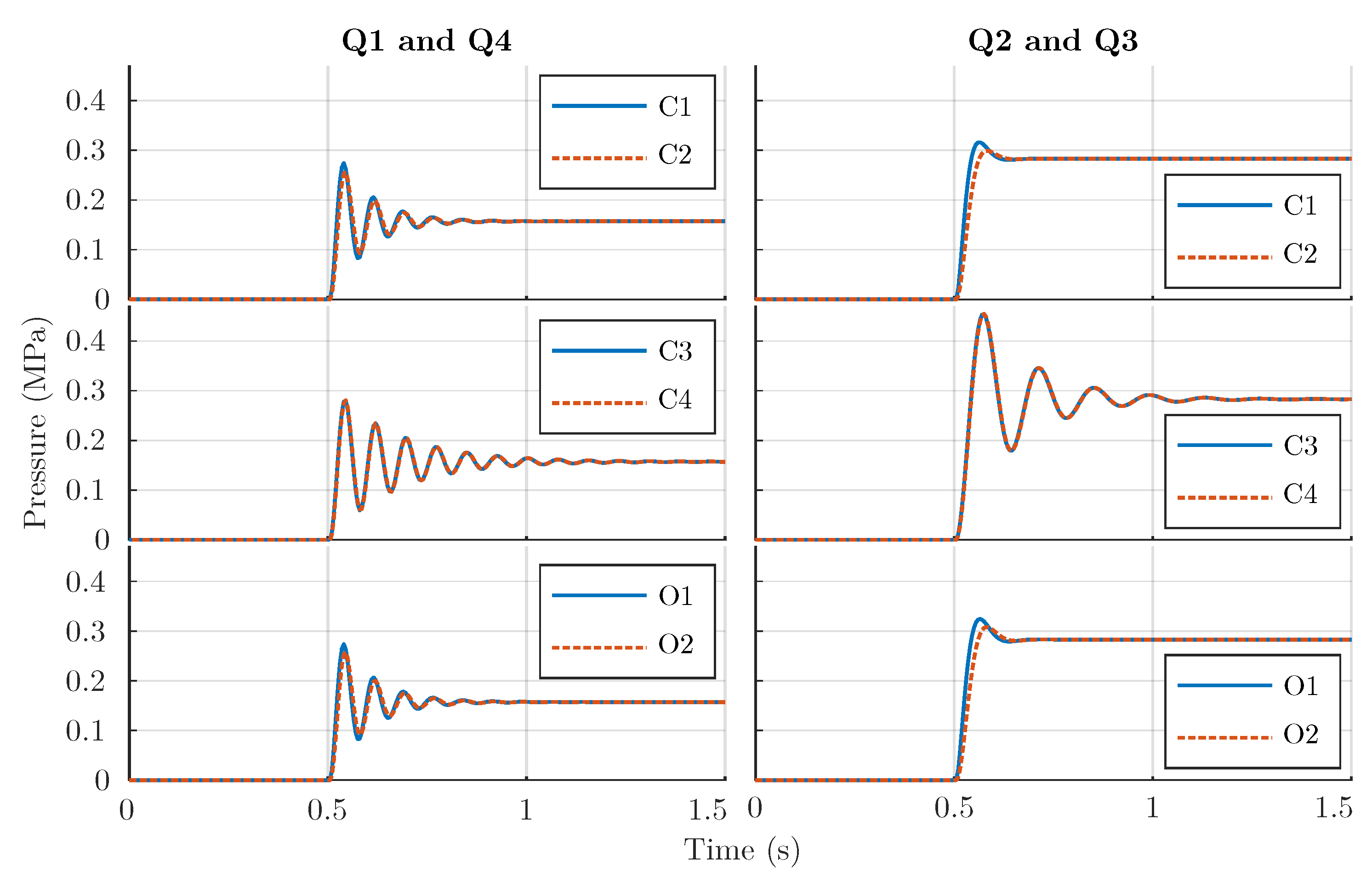
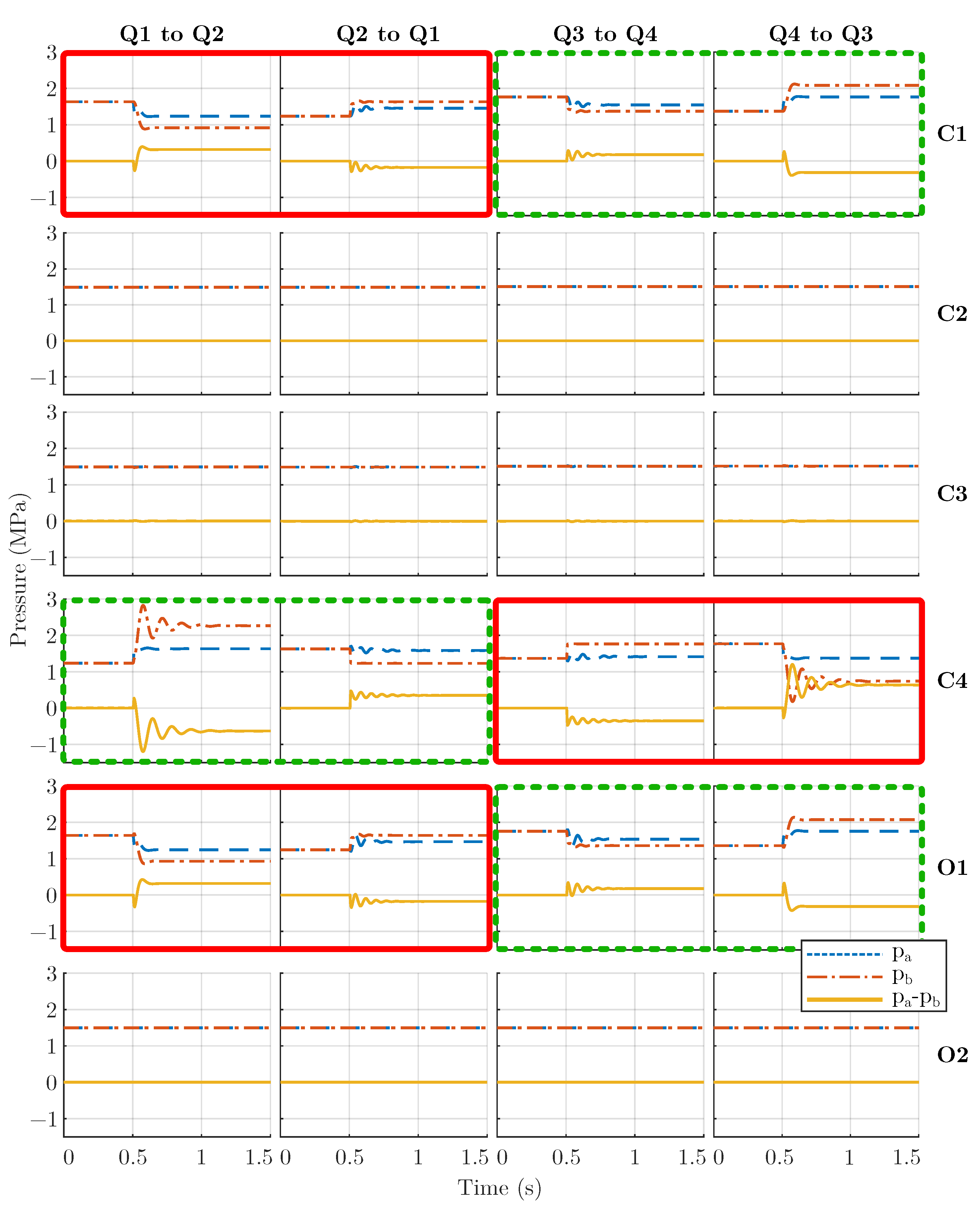
5.3. Open Loop Analysis: Switching without Pressure Feedback
5.4. Closed Loop Analysis: Switching with Pressure Feedback
6. Discussion
- They require pressurized reservoirs
- Their filtering systems must be able to handle flow in both directions
- Pump flow compensation is required to avoid a change in cylinder speed when switching between Q1 and Q2 or Q3 and Q4
- They can suffer from mode-switch oscillations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jalayeri, E.; Imam, A.; Tomas, Z.; Sepehri, N. A throttle-less single-rod hydraulic cylinder positioning system: Design and experimental evaluation. Adv. Mech. Eng. 2015, 7, 1687814015583249. [Google Scholar] [CrossRef] [Green Version]
- Jalayeri, E.; Imam, A.; Sepehri, N. A throttle-less single rod hydraulic cylinder positioning system for switching loads. Case Stud. Mech. Syst. Signal Process. 2015, 1, 27–31. [Google Scholar] [CrossRef] [Green Version]
- Rahmfeld, R.; Ivantysynova, M.; Eggers, B. Active Vibration Damping for Off-Road Vehicles Using Valveless Linear Actuators. In Proceedings of the SAE Commercial Vehicle Engineering Congress & Exhibition, Detroit, MI, USA, 8–11 March 2004; SAE International: Warrendale, PA, USA, 2004. [Google Scholar] [CrossRef]
- Williamson, C.; Ivantysynova, M. Pump mode prediction for four-quadrant velocity control of valueless hydraulic actuators. In Proceedings of the JFPS International Symposium on Fluid Power, Matsue, Japan, 28–31 October 2018; The Japan Fluid Power System Society: Tokyo, Japan, 2008; pp. 323–328. [Google Scholar] [CrossRef]
- Zakharov, V.; Minav, T. Analysis of Field Oriented Control of Permanent Magnet Synchronous Motor for a Valveless Pump-Controlled Actuator. Proceedings 2020, 64, 8491. [Google Scholar] [CrossRef]
- Bonato, C.; Minav, T.A.; Sainio, P.; Pietola, M. Position control of direct driven hydraulic drive. In Fluid Power Systems Technology; American Society of Mechanical Engineers: New York, NY, USA, 2014; Volume 45820, p. V001T05A007. [Google Scholar]
- Minav, T.A.; Sainio, P.; Pietola, M. Direct-driven hydraulic drive without conventional oil tank. In Fluid Power Systems Technology; American Society of Mechanical Engineers: New York, NY, USA, 2014; Volume 45974, p. V001T01A022. [Google Scholar]
- Lawrence, P.D.; Salcudean, S.; Sepehri, N.; Chan, D.; Bachmann, S.; Parker, N.; Zhu, M.; Frenette, R. Coordinated and force-feedback control of hydraulic excavators. In Experimental Robotics IV; Springer: Berlin/Heidelberg, Germany, 1997; pp. 181–194. [Google Scholar]
- Rahmfeld, R.; Ivantysynova, M. Displacement controlled linear actuator with differential cylinder—A way to save primary energy in mobile machines. In Proceedings of the ICFP 2001: Fifth International Conference on Fluid Power Transmission and Control, Hangzhou, China, 3–5 April 2001; pp. 296–301. [Google Scholar]
- Heybroek, K.; Palmberg, J.O. Evaluating a Pump Controlled Open Circuit Solution. In Proceedings of the International Exposition for Power Transmission, Nevada, USA: Proceedings of the 51st IFPE, Las Vegas, NV, USA, 12–14 March 2008; Omnipress: Madison, WI, USA, 2008; pp. 681–694. [Google Scholar]
- Ivantysyn, R.; Weber, J. Novel open circuit displacement control architecture in heavy machinery. In Proceedings of the 8th FPNI Ph. D Symposium on Fluid Power, Lappeenranta, Finland, 11–13 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Schneider, M.; Koch, O.; Weber, J. Green Wheel Loader–improving fuel economy through energy efficient drive and control concepts. In Proceedings of the 10th International Fluid Power Conference (10. IFK), Dresden, Germany, 8–10 March 2016; Volume 2, pp. 63–78. [Google Scholar]
- Schmidt, L.; Roemer, D.B.; Pedersen, H.C.; Andersen, T.O. Speed-Variable Switched Differential Pump System for Direct Operation of Hydraulic Cylinders. Fluid Power Syst. Technol. 2015, V001T01A042. [Google Scholar] [CrossRef]
- Qu, S.; Fassbender, D.; Vacca, A.; Busquets, E.; Neumann, U. A Closed Circuit Electro-Hydraulic Actuator with Energy Recuperation Capability. In Proceedings of the 12th International Fluid Power Conference, Online, 12–14 October 2020. [Google Scholar] [CrossRef]
- Fassbender, D.; Zakharov, V.; Minav, T. Utilization of electric prime movers in hydraulic heavy-duty-mobile-machine implement systems. Autom. Constr. 2021, 132, 103964. [Google Scholar] [CrossRef]
- Kärnell, S.; Fernlund, E.; Lagerstedt, F.; Ericson, L. Pump-Controlled Actuators with Dump Valves. In Proceedings of the 17th Scandinavian International Conference on Fluid Power, Linköping, Sweden, 1–2 June 2021. [Google Scholar] [CrossRef]
- Niraula, A.; Zhang, S.; Minav, T.; Pietola, M. Effect of zonal hydraulics on energy consumption and boom structure of a micro-excavator. Energies 2018, 11, 2088. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Minav, T.; Pietola, M.; Kauranne, H.; Kajaste, J. The effects of control methods on energy efficiency and position tracking of an electro-hydraulic excavator equipped with zonal hydraulics. Autom. Constr. 2019, 100, 129–144. [Google Scholar] [CrossRef]
- Ketelsen, S.; Padovani, D.; Andersen, T.O.; Ebbesen, M.K.; Schmidt, L. Classification and Review of Pump-Controlled Differential Cylinder Drives. Energies 2019, 12, 1293. [Google Scholar] [CrossRef] [Green Version]
- Hewett, A.J. Hydraulic Circuit Flow Control. US Patent 5,329,767, 19 July 1994. [Google Scholar]
- Rahmfeld, R. Energy saving hydraulic actuators for mobile machines. In Proceedings of the 1st Bratislavian Fluid Power Symposium, Casta-Pila, Slovakia, 2–3 June 1998; pp. 47–57. [Google Scholar]
- Williamson, C.; Ivantysynova, M. Stability and motion control of inertial loads with displacement controlled hydraulic actuators. In Proceedings of the 6th FPNI-PhD Symposium, West Lafayette, IN, USA, 15–19 June 2010; pp. 15–19. [Google Scholar]
- Michel, S.; Weber, J. Electrohydraulic compact-drives for low power applications considering energy-efficiency and high inertial loads. In Proceedings of the 7th FPNI PhD Symposium on Fluid Power, Reggio Emilia, Italy, 27–30 June 2012; pp. 27–30. [Google Scholar]
- Wang, L.; Book, W.J.; Huggins, J.D. A hydraulic circuit for single rod cylinders. J. Dyn. Syst. Meas. Control. 2012, 134, 011019. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Book, W.J. Using leakage to stabilize a hydraulic circuit for pump controlled actuators. J. Dyn. Syst. Meas. Control. 2013, 135, 061007. [Google Scholar] [CrossRef]
- Çalışkan, H.; Balkan, T.; Platin, B.E. A complete analysis and a novel solution for instability in pump controlled asymmetric actuators. J. Dyn. Syst. Meas. Control. 2015, 137, 091008. [Google Scholar] [CrossRef]
- Çalışkan, H.; Balkan, T.; Platin, B.E. A Complete Analysis for Pump Controlled Single Rod Actuators. In Proceedings of the 10th International Fluid Power Conference (10th IFK), Dresden, Germany, 8–10 March 2016. [Google Scholar]
- Imam, A.; Rafiq, M.; Jalayeri, E.; Sepehri, N. Design, Implementation and Evaluation of a Pump-Controlled Circuit for Single Rod Actuators. Actuators 2017, 6, 10. [Google Scholar] [CrossRef] [Green Version]
- Imam, A.; Rafiq, M.; Jalayeri, E.; Sepehri, N. A Pump-Controlled Circuit for Single-Rod Cylinders that Incorporates Limited Throttling Compensating Valves. Actuators 2018, 7, 13. [Google Scholar] [CrossRef] [Green Version]
- Imam, A.; Rafiq, M.; Zeljko, T.; Sepehri, N. Improving the Performance of Pump-Controlled Circuits for Single-Rod Actuators. Actuators 2019, 8, 26. [Google Scholar] [CrossRef] [Green Version]
- Costa, G.K.; Sepehri, N. Four-quadrant analysis and system design for single-rod hydrostatic actuators. J. Dyn. Syst. Meas. Control. 2019, 141, 021011. [Google Scholar] [CrossRef]
- Koury Costa, G.; Sepehri, N. A Critical Analysis of Valve-Compensated Hydrostatic Actuators: Qualitative Investigation. Actuators 2019, 8, 59. [Google Scholar] [CrossRef] [Green Version]
- Koury Costa, G.; Sepehri, N. A Critical Analysis of Flow-Compensated Hydrostatic Single Rod Actuators: Simulation Study. Actuators 2020, 9, 58. [Google Scholar] [CrossRef]
- Gøytil, P.H.; Padovani, D.; Hansen, M.R. A Novel Solution for the Elimination of Mode Switching in Pump-Controlled Single-Rod Cylinders. Actuators 2020, 9, 20. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Li, S.; Minav, T. Control and Performance Analysis of Variable Speed Pump-Controlled Asymmetric Cylinder Systems under Four-Quadrant Operation. Actuators 2020, 9, 123. [Google Scholar] [CrossRef]
- Heybroek, K.; Larsson, J.; Palmberg, J.O. Mode Switching and Energy Recuperation in Open-Circuit Pump Control. In Proceedings of the 10th Scandinavian International Conference on Fluid Power, Tampere, Finland, 21–23 May 2007; Tampere University of Technology: Tampere, Finland, 2007; pp. 197–209. [Google Scholar]
- Heybroek, K.; Palmberg, J.O. Applied Control Strategies for a Pump Controlled Open Circuit Solution. In Proceedings of the 6th IFK: International Fluid Power Conference, Dresden, Germany, 31 March–2 April 2008; Dresdner Verein zur Förderung der Fluidtechnik e.V.: Dresden, Germany, 2008; pp. 39–52. [Google Scholar]
- Qu, S.; Vacca, A.; Fassbender, D.; Busquets, E. Formulation, Design and Experimental Verification of an Open Circuit Electro-Hydraulic Actuator. In Proceedings of the 2020 IEEE Global Fluid Power Society PhD Symposium (GFPS), Online, 19–21 October 2020. [Google Scholar]
- Qu, S.; Fassbender, D.; Vacca, A.; Busquets, E. A high-efficient solution for electro-hydraulic actuators with energy regeneration capability. Energy 2021, 216, 119291. [Google Scholar] [CrossRef]
- ISO 15442: Cranes—Safety Requirements for Loader Cranes; International Organization for Standardization: Geneva, Switzerland, 2012.
- ISO 8643: Earth-Moving Machinery—Hydraulic Excavator and Backhoe Loader Lowering Control Device—Requirements and Tests; International Organization for Standardization: Geneva, Switzerland, 2017.
- Liberzon, D. Switching in Systems and Control; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
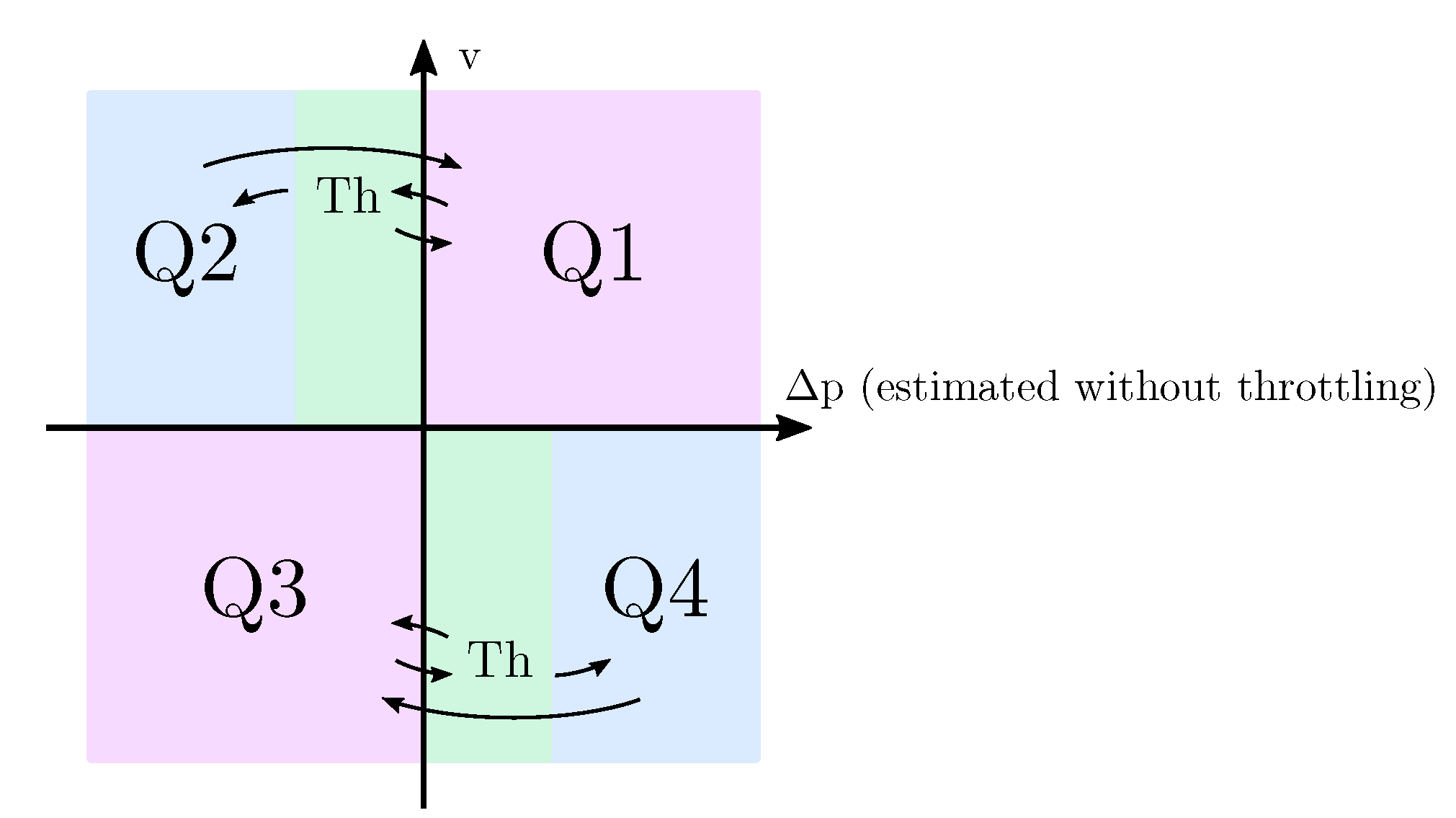


| Description | Denotation | Value | Unit |
|---|---|---|---|
| Reservoir pressure | Pa | ||
| Cylinder area, piston side | |||
| Cylinder area, rod side | |||
| Flow coefficient, piston side | |||
| Flow coefficient, rod side | |||
| Flow coefficient, tank | |||
| Cylinder velocity | v | ||
| Viscous friction | b | Ns/m |
| Denotation | LHV | p | Q1 to Q2 | Q2 to Q1 | Q3 to Q4 | Q4 to Q3 |
|---|---|---|---|---|---|---|
| Placement | Sensing | [MPa] | [MPa] | [MPa] | [MPa] | |
| C1 | Cylinder | Cylinder | 0.32 | −0.18 | 0.18 | −0.32 |
| C2 | Cylinder | Pump | 0 | 0 | 0 | 0 |
| C3 | Pump | Cylinder | 0 | 0 | 0 | 0 |
| C4 | Pump | Pump | −0.63 | 0.35 | −0.35 | 0.63 |
| O1 | - | Cylinder | 0.32 | −0.18 | 0.18 | −0.32 |
| O2 | - | Pump | 0 | 0 | 0 | 0 |
| Description | Denotation | Value | Unit |
|---|---|---|---|
| Pump volume, piston side | |||
| Pump volume, rod side | |||
| Cylinder volume, piston side | |||
| Cylinder volume, rod side | |||
| Bulk modulus | Pa | ||
| Inertial load | m | 1000 | kg |
| Pump leakage | 0 | ||
| Cylinder leakage | 0 | ||
| Motor resonance frequency (fast) | 1000 | Hz | |
| Motor resonance frequency (slow) | 20 | Hz | |
| Valve resonance frequency | 1000 | Hz | |
| Motor damping ratio (fast) | 1 | - | |
| Motor damping ratio (slow) | - | ||
| Valve damping ratio | 1 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kärnell, S.; Ericson, L. Hysteresis Control in Pump-Controlled Systems—A Way to Reduce Mode-Switch Oscillations in Closed and Open Circuits. Energies 2022, 15, 424. https://doi.org/10.3390/en15020424
Kärnell S, Ericson L. Hysteresis Control in Pump-Controlled Systems—A Way to Reduce Mode-Switch Oscillations in Closed and Open Circuits. Energies. 2022; 15(2):424. https://doi.org/10.3390/en15020424
Chicago/Turabian StyleKärnell, Samuel, and Liselott Ericson. 2022. "Hysteresis Control in Pump-Controlled Systems—A Way to Reduce Mode-Switch Oscillations in Closed and Open Circuits" Energies 15, no. 2: 424. https://doi.org/10.3390/en15020424
APA StyleKärnell, S., & Ericson, L. (2022). Hysteresis Control in Pump-Controlled Systems—A Way to Reduce Mode-Switch Oscillations in Closed and Open Circuits. Energies, 15(2), 424. https://doi.org/10.3390/en15020424






