Next Article in Journal
The Impact of Soil Hydrothermal Properties on Geothermal Power Generation (GPG): Modeling and Analysis
Previous Article in Journal
Numerical Study on the Homogeneous Reactions of Mercury in a 600 MW Coal-Fired Utility Boiler
Previous Article in Special Issue
A Multi-Scale Numerical Model for Investigation of Flame Dynamics in a Thermal Flow Reversal Reactor
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 15
Issue 2
10.3390/en15020447
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Design and Performance Investigation of a Compact Catalytic Reactor Integrated with Heat Recuperator

by
Qiang Chen
,
Mingming Mao
*,
Min Gao
,
Yongqi Liu
,
Junrui Shi
and
Jia Li
School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255000, China
*
Author to whom correspondence should be addressed.
Energies 2022, 15(2), 447; https://doi.org/10.3390/en15020447
Submission received: 9 December 2021 / Revised: 2 January 2022 / Accepted: 4 January 2022 / Published: 9 January 2022
(This article belongs to the Special Issue Combustion and Energy Conversion under Small Scales)
Browse Figures
Versions Notes

Abstract

:
The catalytic combustion has the advantage of lower auto-ignition temperature and helps to expand the combustible limit of lean premixed gas. However, the intake needs to be preheated to certain temperature commonly through an independent heat exchanger. Similar to the principles of non-catalytic RTO combustion, this paper presents a similar approach whereby the combustion chamber is replaced by a catalytic combustion bed. A new catalytic reactor integrated with a heat recuperator is designed to enhance the heat recirculation effect. Using a two-dimensional computational fluid dynamics model, the performance of the reactor is studied. The reaction performances of the traditional and compact reactors are compared and analyzed. Under the same conditions, the compact reactor has better reaction performance and heat recirculation effect, which can effectively decrease the ignition temperature of feed gas. The influences of the inlet velocity, the inlet temperature, the methane concentration, and the thermal conductivity of porous media on the reaction performance of integrated catalytic reactor are studied. The results show that the inlet velocity, inlet temperature, methane concentration, and thermal conductivity of porous media materials have important effects on the reactor performance and heat recirculation effect, and the thermal conductivity of porous media materials has the most obvious influence. Moreover, the reaction performance of multiunit integrated catalytic reactor is studied. The results show that the regenerative effect of multiunit integrated catalytic reactor is further enhanced. This paper is of great significance to the recycling of low calorific value gas energy and relieving energy stress in the future.

1. Introduction

At present, saving energy and protecting the environment are the focus of global concern. With the rapid development of human society, energy consumption intensifies, and environmental problems increase sharply. In China, low-calorific-value gas energy production is abundant, but a large number of low calorific value gas is not fully utilized. This gas has been directly discharged into the atmosphere, which not only causes environmental damage but also causes energy waste. Ventilation air produced by coal mining is a kind of low calorific value gas, and its main component is methane with the concentration ranging from 0.1% to 1%. Methane is both a greenhouse gas and a clean energy source [1,2]. China emits a large amount of methane into the atmosphere every year through ventilation air methane, with a greenhouse gas effect equivalent to about 200 million tons of CO2 [3,4]. It causes serious environmental pollution and energy waste. However, the use of traditional combustion technology needed to be in high-temperature conditions to carry out combustion. This method not only burns incompletely, but also produces harmful gases NOx [5]. The catalytic combustion technology can effectively reduce the combustion temperature and improve combustion efficiency. This book introduced the theory of catalytic combustion and selected examples of catalytic combustion for investigation [6]. Compared with traditional catalysts, monolithic catalysts have low pressure drop, high applicable space velocity, thin catalyst layer loaded on the pore, short diffusion distance, small diffusion resistance, and good thermal conductivity [7,8,9]. Brooks et al. [10] studied the microchannel reactor and the results showed that the microchannel reactor Ru–TiO2 catalyst coating had high activity and stability. Liu et al. [11] had demonstrated that Ni-based catalysts on microchannels exhibit excellent catalytic performance and long-term reliability during methanation reactions. The use of monolithic catalysts for low calorific value gases is a very promising technology. The efficient use of energy will effectively relieve environmental pressure and energy problems.
If the heat recirculation technology is used in the combustion of low calorific value gas, the combustion efficiency can be improved effectively. In recent years, a large number of researchers have studied the heat recirculation reactor. Min et al. [12] studied the honeycomb ceramic reactor with unidirectional flow, and the results showed that the peak temperature of the gas was greater than the adiabatic combustion temperature. Thus, the heat recirculation in the reactor was confirmed. Hashemi et al. [13] conducted a numerical study on the flame stability in a double-layer porous burner. Heat recirculation processes were investigated, and the amounts of heat transfer modes were quantified. Experimental studies on premixed combustion of ultra-low calorific gas in an axial and radial gradually-varied porous media burner with annular for heat recirculation were conducted [14]. The experiment proved that the combustion and flow characteristics could be improved by using an annular heat recirculation. Chen et al. [15] numerically studied the combustion stability in catalytic micro combustor with single-channel and heat recirculation. The results showed that heat recirculation can significantly improve the stability under materials with low thermal conductivity.
In this paper, a heat-recirculation catalytic reactor is designed, and the reactor and preheater are integrated. A two-dimensional computational model is used to study the performance and heat recirculation of the reactor. The performances of the traditional catalytic reactor and the integrated catalytic reactor were compared. Then, the effects of the inlet conditions and porous media materials on the performance and heat recirculation of the integrated catalytic reactor were analyzed. Moreover, the reaction performance of multiunit integrated catalytic reactor is studied.

2. Catalytic Experiment Reactor and Integrated Catalytic Reactor Design

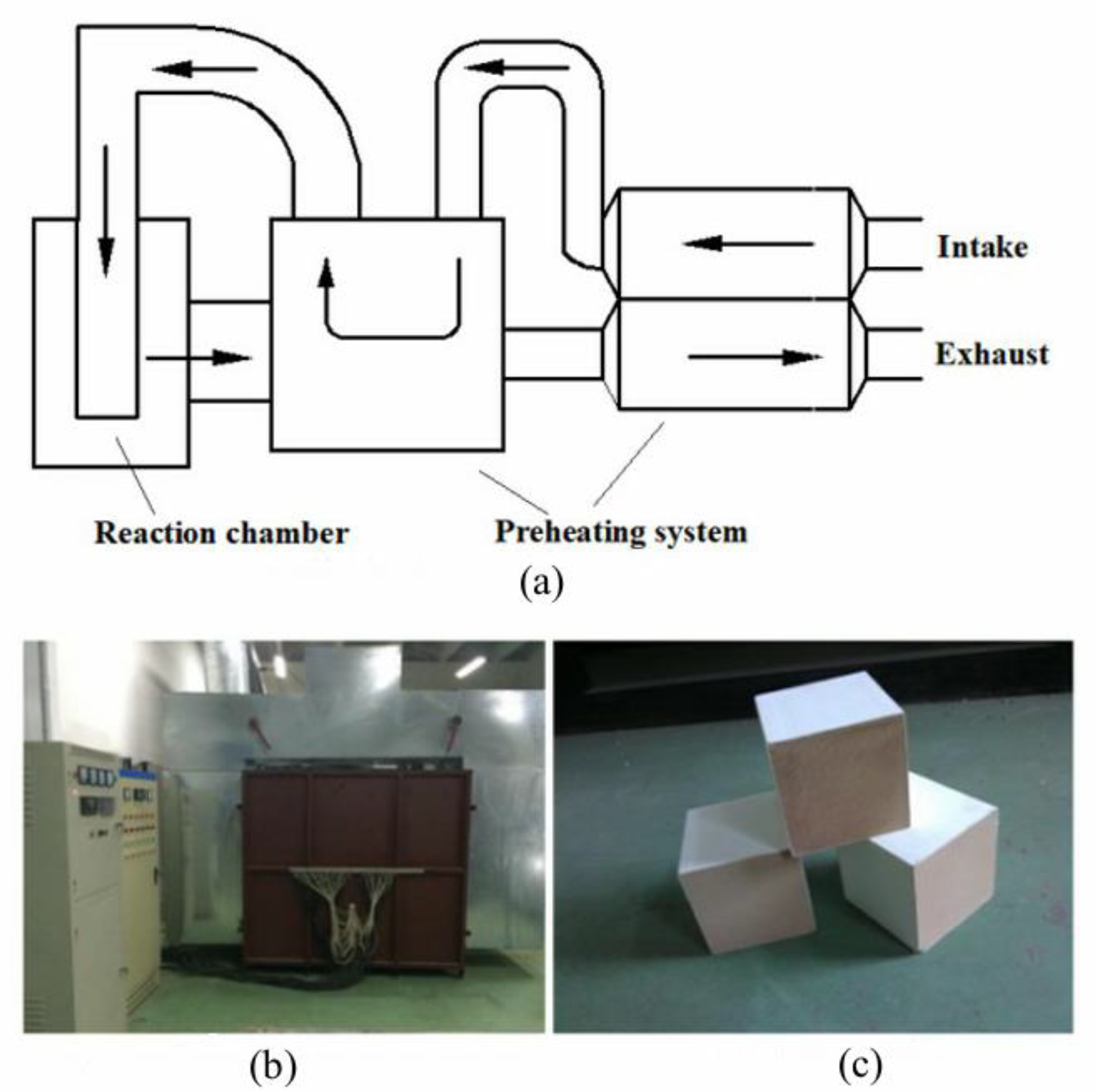
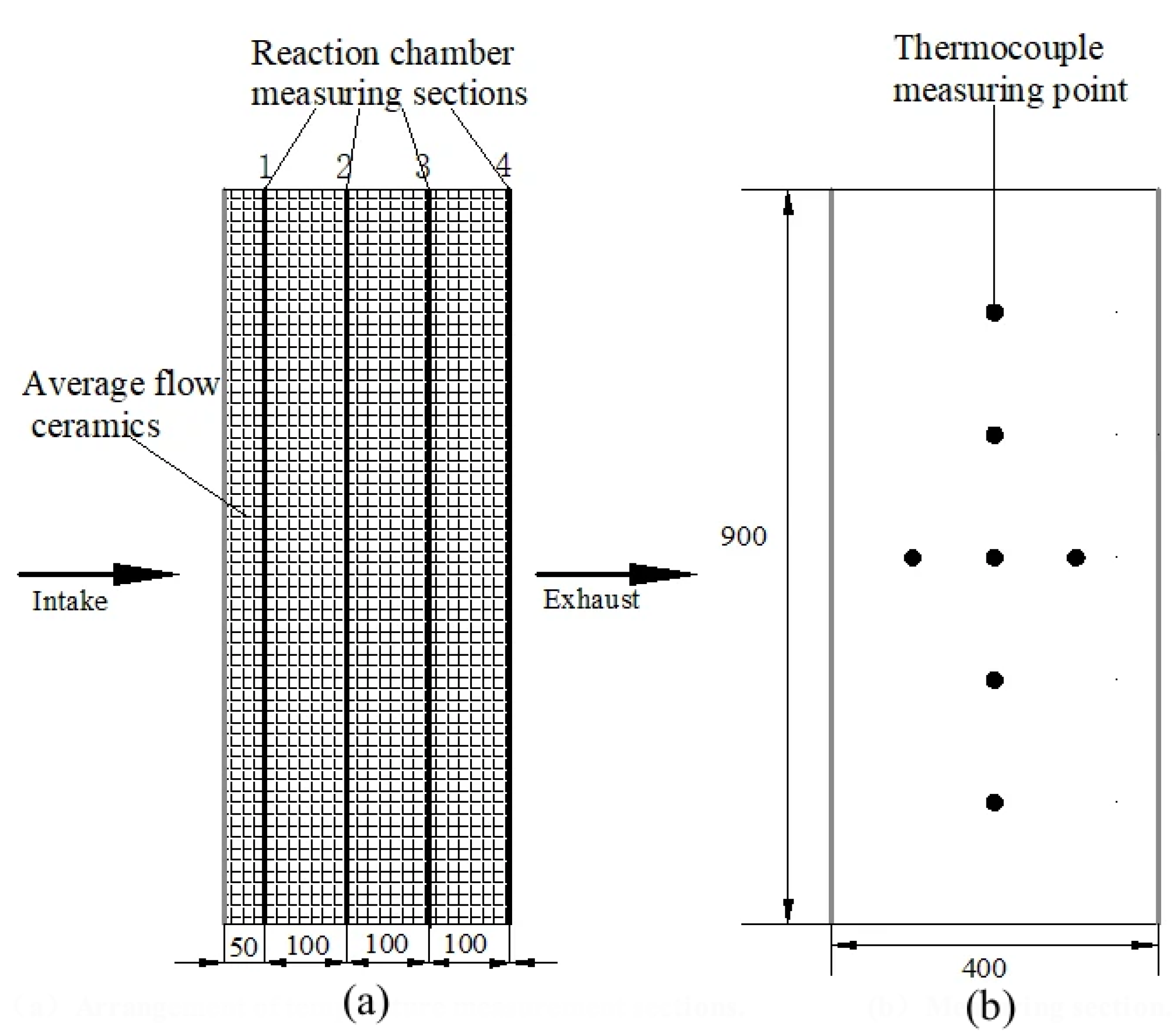
2.1. Introduction of Preheat Catalytic Reactor Test Rig

The catalytic combustion experiment is carried out in a two-chamber preheat catalytic reactor [16]. The schematic diagram and photos of the preheat catalytic reactor are shown in Figure 1a,b. The experimental system includes five parts: the gas supply system, the preheating system, the startup system, two reaction chambers, and the parameter acquisition system. The two reaction chambers are opposed. The lean methane mixture is supplied to the two reaction chambers from the outside intake pipes, and then the exhaust is discharged from the outlet. The two catalytic oxidation beds are installed in the two reaction chambers which are both composed of three catalytic ceramic layers and one inert ceramic layer. The section of the catalytic ceramic layer is 400 mm × 900 mm. Each catalytic ceramic layer is packed with catalytic honeycomb ceramics, whose size is 100 mm × 100 mm × 100 mm. The hole density is 300 CPSI (channels per square inch), and the hole is square. The picture of catalytic ceramics is shown in Figure 1c. The temperature parameters of the catalytic bed are measured by the data acquisition system. The construction of the catalytic packed bed ceramics and the distribution of the temperature measurement points in the packed bed are shown in Figure 2a,b.

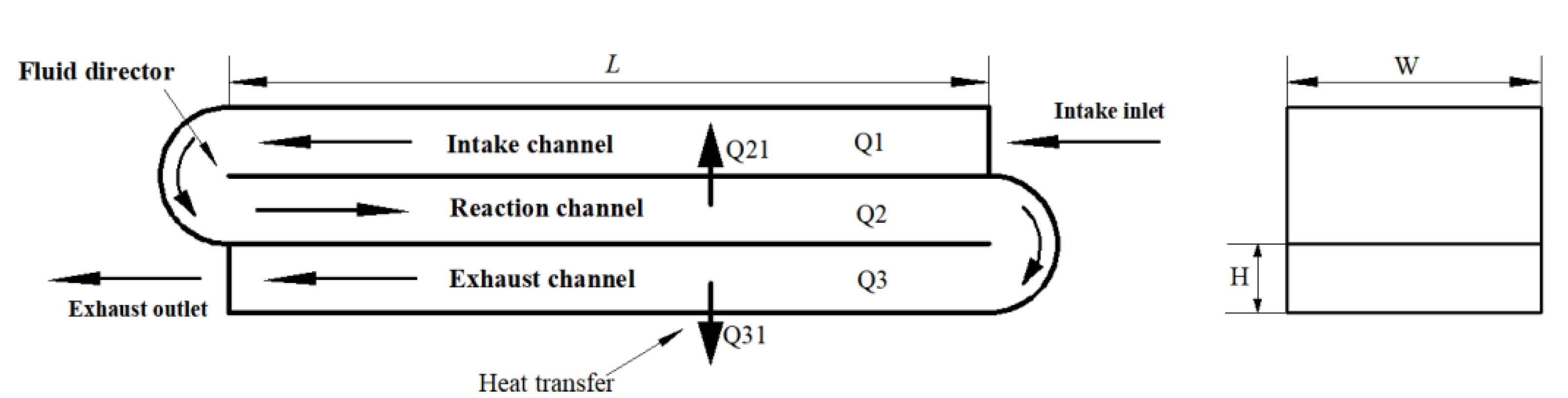
2.2. Integrated Catalytic Reactor Design

The design principle diagram of the integrated catalytic reactor is shown in Figure 3. In order to improve the efficiency of heat transfer and preheat the feed gas sufficiently, multiple reactor channels are piled up vertically in the design. A reactor unit consists of four parts: intake channel, reaction channel, exhaust channel, and fluid director. The feed gas is preheated in the intake channel, and then the preheated gas completes the catalytic oxidation reaction in the reaction channel. Finally, the exhaust gas is discharged from the exhaust channel. The deflector plays the role of connection and diversion between channels. Metal partitions are used between channels to ensure isolation and heat transfer.

2.3. Design Process

The design conditions are as follows. The inlet flow rate is 10 m3/h, the methane concentration at the inlet is 1 vol.%, the inlet temperature is 473 K, and the feed gas is preheated to 673 K in the intake channel. The outlet temperature is 743 K. It is assumed that the flue gas enters the exhaust channel with the temperature of 573 K. The specific surface area of the ceramics is 2000 m2/m3, the pore side length is 3 mm, and the porosity ε is 0.6. The reaction process is considered to be adiabatic. The diaphragm between channels adopts metallic material, ignoring the thermal resistance.
The detailed design process is shown in Appendix A.
Previous experiments showed that the length of the reaction channel should be at least 300 mm; otherwise, the methane could not fully react [17]. Thus, the length should be ensured at least 300 mm; otherwise, the heat transfer area will be magnified. The width of the reactor is tentatively set to 100 mm, and the following numerical simulation will verify its suitability. Then, the height of the channels is determined according to F. The main parameters of reactor design are shown in Table 1.

3. Numerical Models and Simulation Approach

3.1. Geometric Model

The two-dimensional models of the integrated catalytic reactor and the single-channel catalytic reactor are shown in Figure 4. The length and height of the three channels are all 300 mm and 27 mm. The porous media of honeycomb ceramics are fed into all three channels, and the catalyst with the main active component of Pd is coated in the ceramics of the reaction channel. The porous media of honeycomb ceramics are also fed into the single-channel catalytic reactor. The length and height of the single-channel catalytic reactor are 300 mm and 27 mm, respectively, and the same catalyst is coated in the ceramics of the channel. The diaphragms in the integrated catalytic reactor between the channels are made of 2-mm-thick stainless steel of 310S. The physical parameters of the porous media include porosity of 0.6, thermal conductivity of 3 W/m × K, density of 3800 kg/m3, and specific heat capacity of 1050 J/kg × K. The physical parameters of stainless steel 310S include thermal conductivity of 14.2 W/m × K, density of 7980 kg/m3, and specific heat capacity of 500 J/kg × K.

3.2. Numerical Models

In a study on the combustion of porous media, the processes including flow, heat transfer, and chemical reaction are very complex, and it is very difficult to simulate the complete combustion process. Thus, the hypotheses are used as follows to simplify the model.
The model assumptions and the specific form of the equations are shown in Appendix B.
The SIMPLE algorithm is used to solve the pressure–velocity coupling momentum equation [18]. The second-order upwind scheme is employed for discretization of the momentum and energy equations. All the equations are solved until a relative convergence of 10 × 10−6 is achieved.
The size of cell mesh has an important influence on the simulation results. In order to reduce the calculation amount, the calculations with different mesh sizes are carried out. In this work, Gambit is used to divide the two-dimensional model of the integrated catalytic reactor into three kinds of grids with coarse, medium, and fine grids. The total number of the grids is 6898, 9278, and 11,878, respectively. The grid number of 11,878 has the best goodness of fit with the experimental results, and the increase in grid number has little effect on the result. Thus, the third-grid division is used for calculation in this paper.

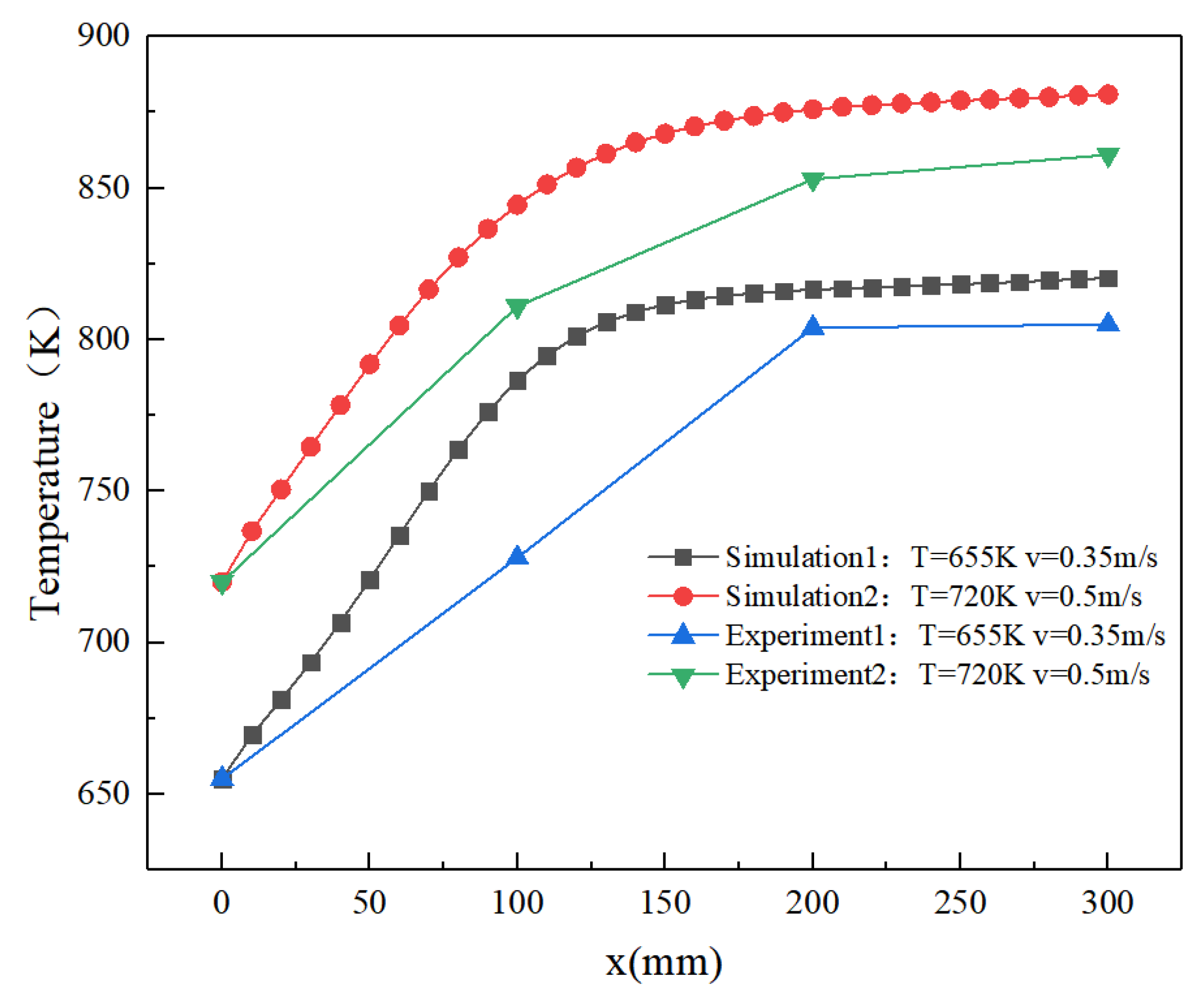
3.3. Model Validation

The accuracy of the catalytic combustion simulation is verified by comparing the experimental data with the simulation data. A single-channel model of 300 mm × 27 mm is adopted, and the temperature distribution on the porous media center line is compared with the preheat catalytic combustion experimental results under the conditions of inlet velocity of 0.35 m/s and 0.5 m/s, methane concentration of 1 vol.%, and inlet temperatures of 655 K and 720 K [16]. The temperature distribution of the experimental and simulated results along the channel centerline is shown in the Figure 5. The temperature obtained by numerical simulation is in good agreement with the experimental results, and the variation trend of temperature is basically consistent. The temperature of numerical results is higher than that of experimental results, with a maximum difference of about 50 K. This difference is because the wall is set adiabatic in the numerical simulation process. In fact, it is difficult to maintain an adiabatic state in the experiments and a certain heat loss is generated.

4. Results and Discussion

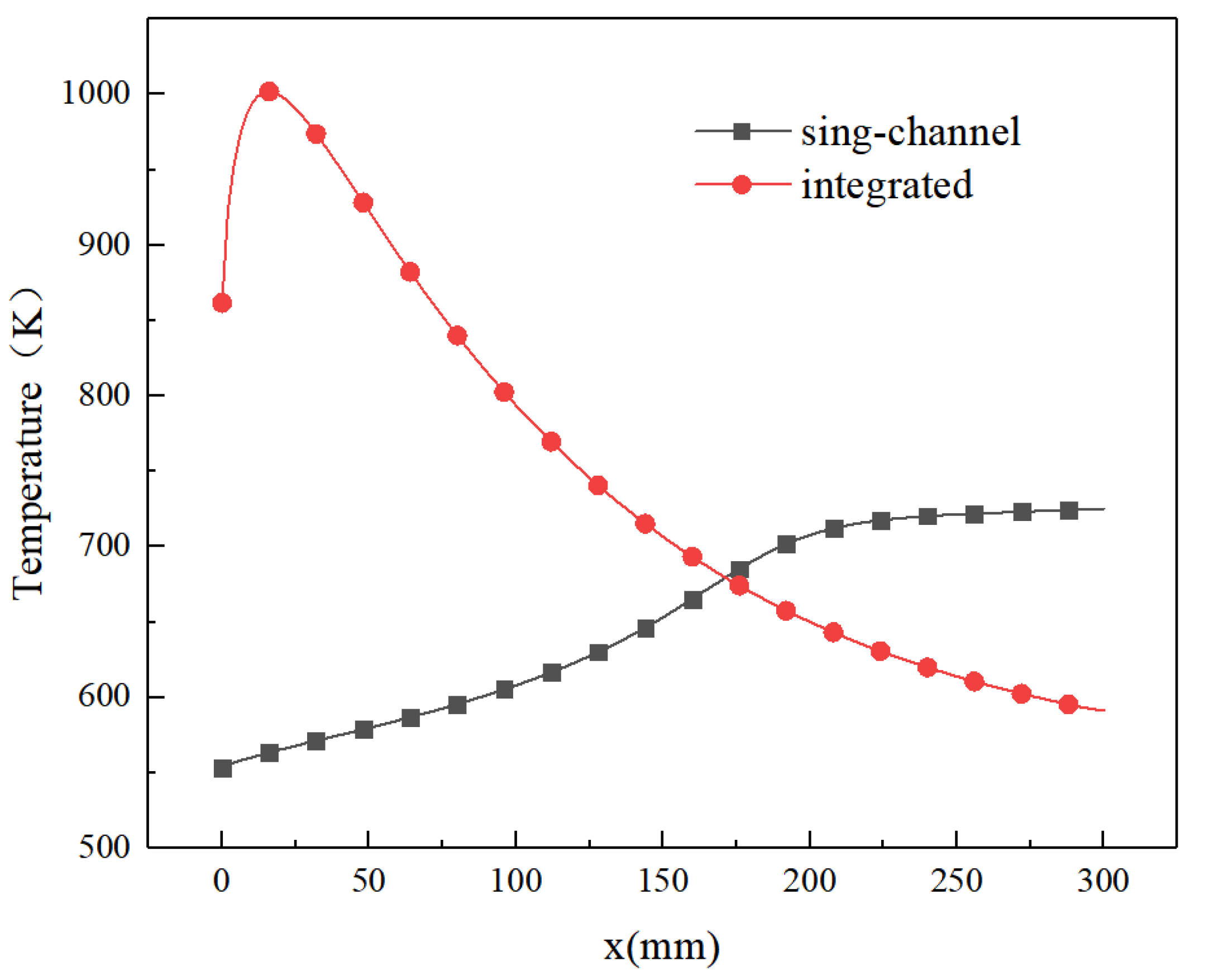
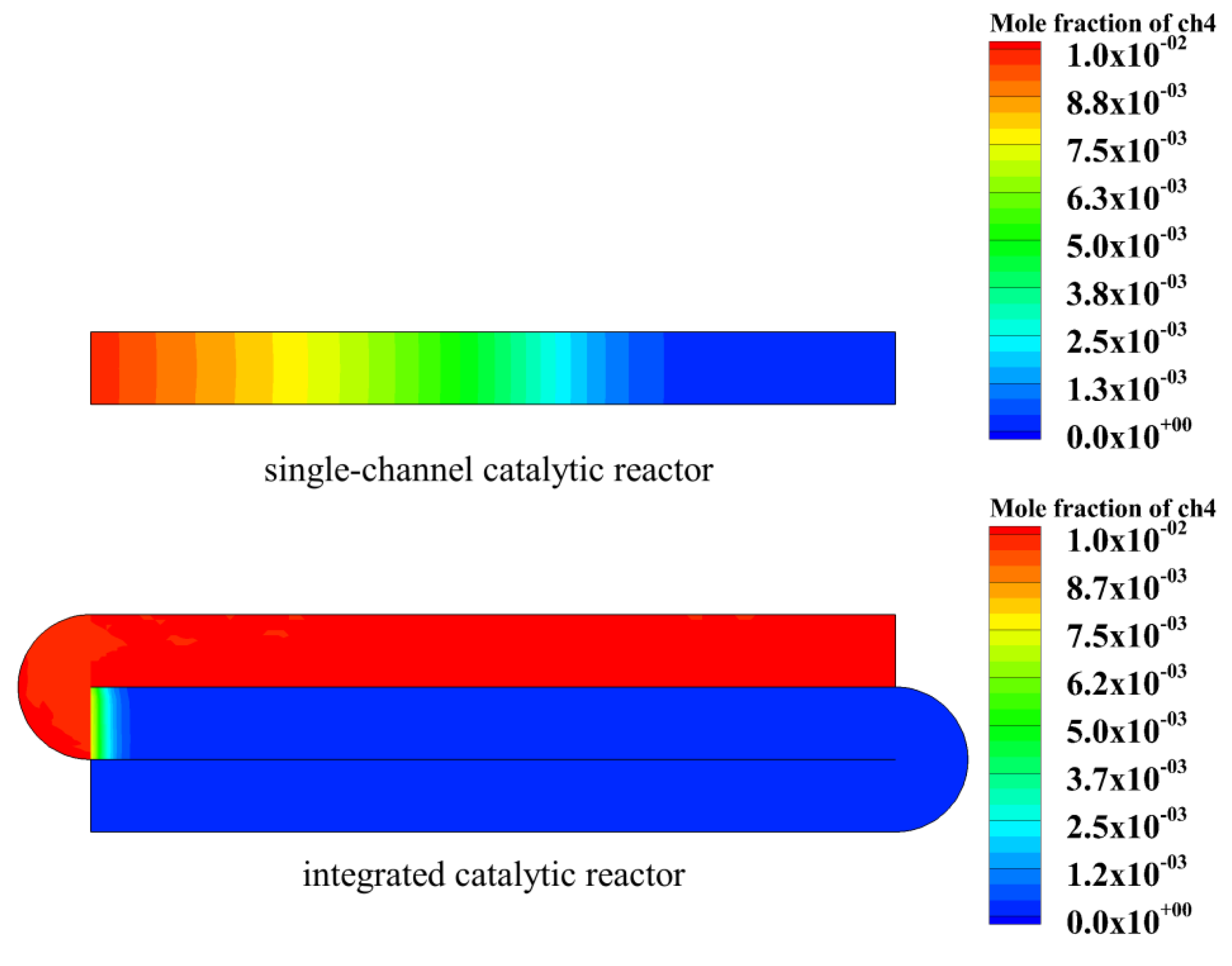
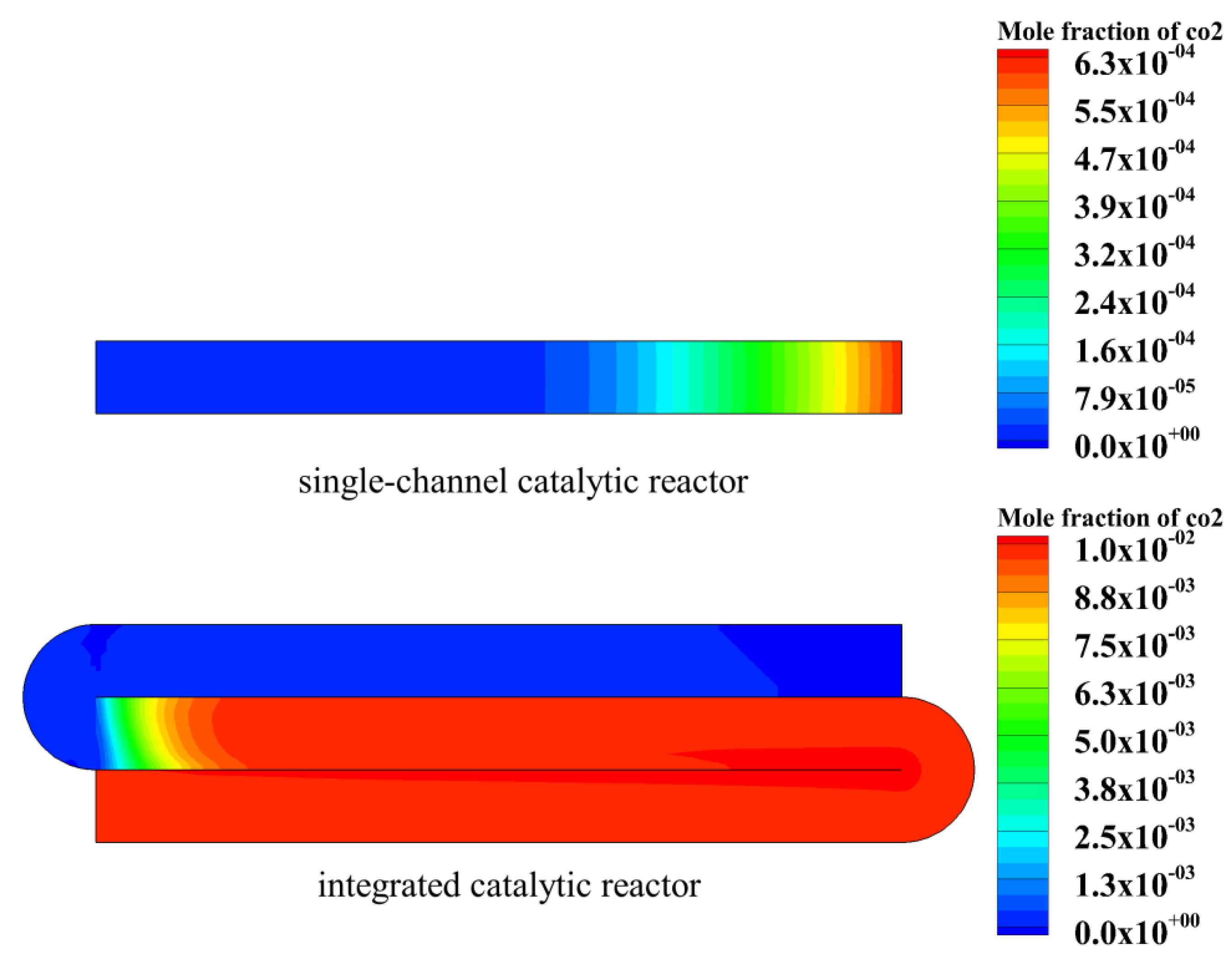
4.1. Performance Comparison between Single-Channel Catalytic Reactor and Integrated Catalytic Reactor

In order to study the heat recuperation performance of the integrated catalytic reactor, the integrated catalytic reactor and single-channel catalytic reactor are numerically simulated and compared under the same conditions. The methane concentration is 1 vol.%, the inlet temperature is 553 K, and the inlet velocity is 0.5 m/s. For igniting, the initial temperature field of 773 K is set in the porous media region of both models. The temperature distribution at the center of the reaction channel of the two reactors and the temperature distribution cloud of the two reactors are shown in Figure 6 and Figure 7. As can be seen from Figure 6 and Figure 7, the temperature of the single-channel catalytic reactor gradually increases from 553 K at inlet to 725 K at outlet. The temperature of the reaction channel of the integrated catalytic reactor reaches the maximum temperature at the front end of the reactor, and then the temperature decreases continuously. The maximum temperature of the integrated catalytic reactor is 1007 K, which is 282 K higher than that of the single-channel catalytic reactor. The main reason is that the temperature at the front end of the single-channel catalytic reactor is low and the reactants cannot react completely. With the increase in temperature, the methane reaction intensifies, so the temperature continues to rise. For the integrated catalytic reactor, the feed gas in the intake channel is fully preheated by the reaction channel. The temperature of the feed gas entering the reaction channel is very high. Methane reacts completely at the front end of the reaction channel, releasing a lot of heat, and the gas temperature in the reaction channel reaches the maximum. The temperature of the reaction channel decreases continuously because the gas in the intake channel absorbs the heat of the reaction channel.
Figure 8 is a cloud diagram of methane distribution in the single-channel catalytic reactor and the integrated catalytic reactor, respectively. The figure shows that the concentration distribution of methane in the single-channel catalytic reactor corresponds to the temperature distribution. The methane conversion rate gradually increases from the inlet to outlet, and the maximum methane conversion rate at the exhaust outlet is 90%. In the integrated catalytic reactor, methane has completely reacted in the front of the reaction channel. Figure 9 is a cloud diagram of carbon dioxide concentration distribution. It can be seen from the diagram that the carbon dioxide concentration in the single-channel catalytic reactor is very low, and the carbon dioxide concentration at outlet is 6.3%. In an integrated catalytic reactor, methane is completely converted to carbon dioxide. It is shown that the integrated catalytic reactor can completely convert methane to carbon dioxide with better reaction performance under the same inlet conditions.

4.2. Effect of Inlet Parameters on Performance of the Integrated Catalytic Reactor

4.2.1. The Effect of Inlet Temperature

Under the conditions of inlet velocity of 0.5 m/s and methane concentration of 1.0 vol.%, 0.9 vol.% and 0.8 vol.%, the effect of the inlet temperature on the reaction performance of integrated catalytic reactor is studied. Figure 10 shows the conversion of methane at different temperatures. It can be seen from the figure that the inlet temperature has an important impact on the conversion of methane. The conversion rate of methane grows with the increase in temperature. When the inlet temperature reaches a certain value, the conversion rate of methane rises rapidly. With the further increase in temperature, methane is finally completely converted. The lower concentration of methane, the higher the temperature is required for complete combustion of methane. When methane concentration is 1 vol.%, the inlet temperature required for complete transformation is 523 K. When methane concentration is 0.8 vol.%, the temperature required for complete transformation is 583 K. It shows that methane can be completely converted to carbon dioxide in the reactor only when the inlet temperature reaches a certain temperature.

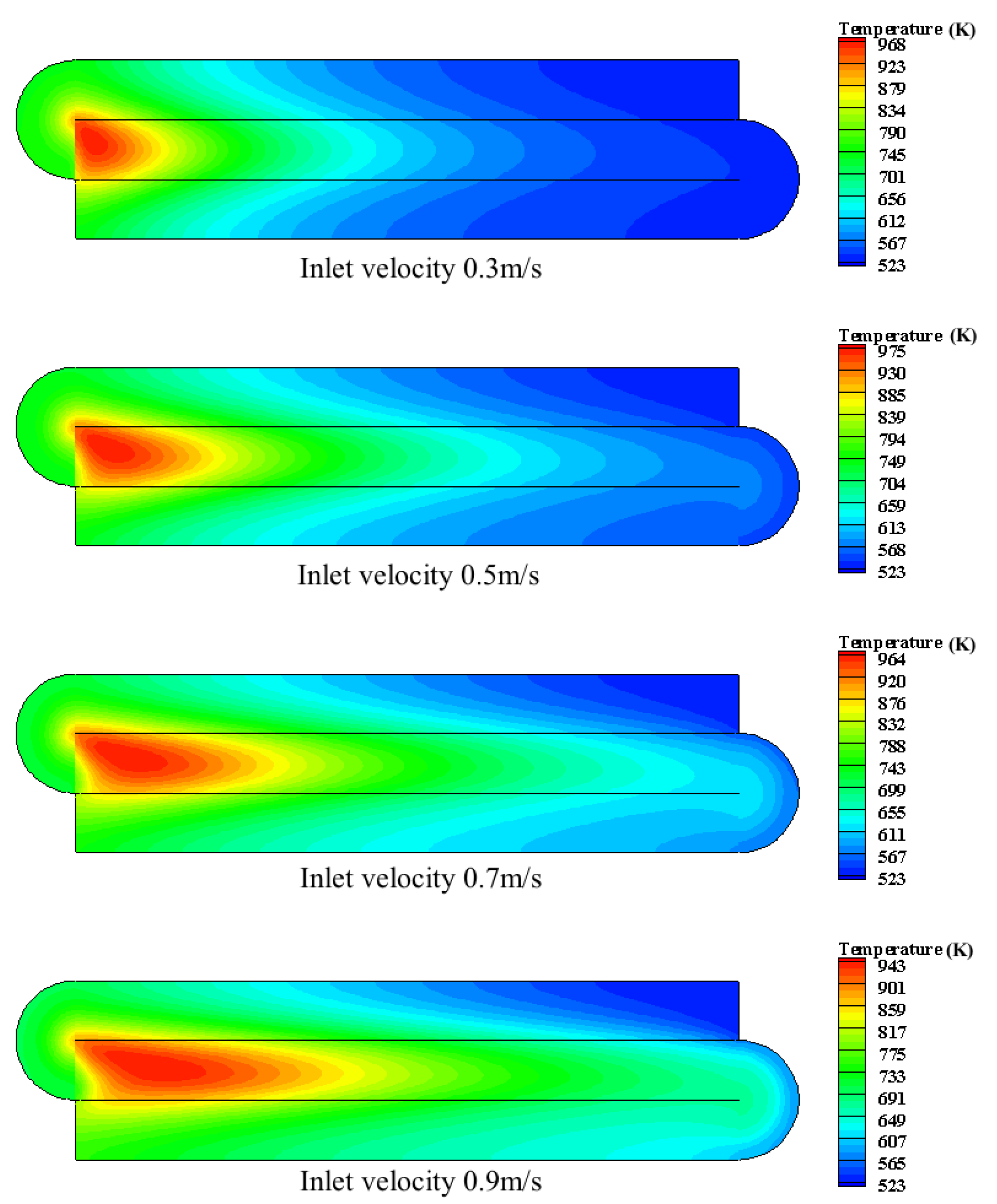
4.2.2. The Effect of Inlet Velocity

The effect of the inlet velocity on the reaction performance of the reactor is studied. The numerical simulation of the integrated catalytic reactor is carried out under the following conditions: an inlet temperature of 523 K, a methane concentration of 1 vol.%, and different inlet velocities. When the inlet velocity is 0.3 m/s, 0.5 m/s, 0.7 m/s, and 0.9 m/s, the conversion of methane is 99.76%, 99.63%, 99.37%, and 98.32%, respectively. Figure 11 shows the temperature distribution along the centerline of the reaction channel at different inlet velocities. It can be seen from the figure that the inlet velocity affects the temperature distribution of the reactor greatly. At different inlet velocities, the temperature peaks at the front end of the reaction channel, and then the temperature decreases along the flow direction. With the increase in inlet velocity, the peak temperature decreases and the temperature at the outlet of the reaction channel grows. When the inlet velocity is 0.3 m/s, the difference between the maximum temperature of the reaction channel and the outlet temperature of the reaction channel is 425 K. However, when the inlet velocity is 0.9 m/s, the temperature difference is 290 K. The reason is that when the inlet velocity is low, the high-temperature gas in the reaction channel has enough time for heat exchange to preheat the gas in the intake channel. If the heat exchange is insufficient when the inlet velocity is high, the outlet temperature of the reaction channel is higher.
Figure 12 is a temperature cloud picture of an integrated catalytic reactor at different inlet velocities. In general, it can be seen from the figure that an increase in inlet velocity extends the high-temperature zone (temperature greater than 900 K) in the reactor, but the peak temperature in the high-temperature zone decreases. The reason is that the smaller inlet velocity creates a more sufficient contact time between the reactant and the catalyst. Then, a complete reaction can be carried out within a small distance of the reaction channel. The larger inlet velocity, the shorter residence time of the reactant, and the longer required length of the reaction channel. However, when the inlet velocity is 0.5 m/s, the peak temperature is 975 K, i.e., the maximum under different inlet velocities. It shows that there is an optimal inlet velocity in a certain speed range, which makes the temperature of the reactor reach the maximum.

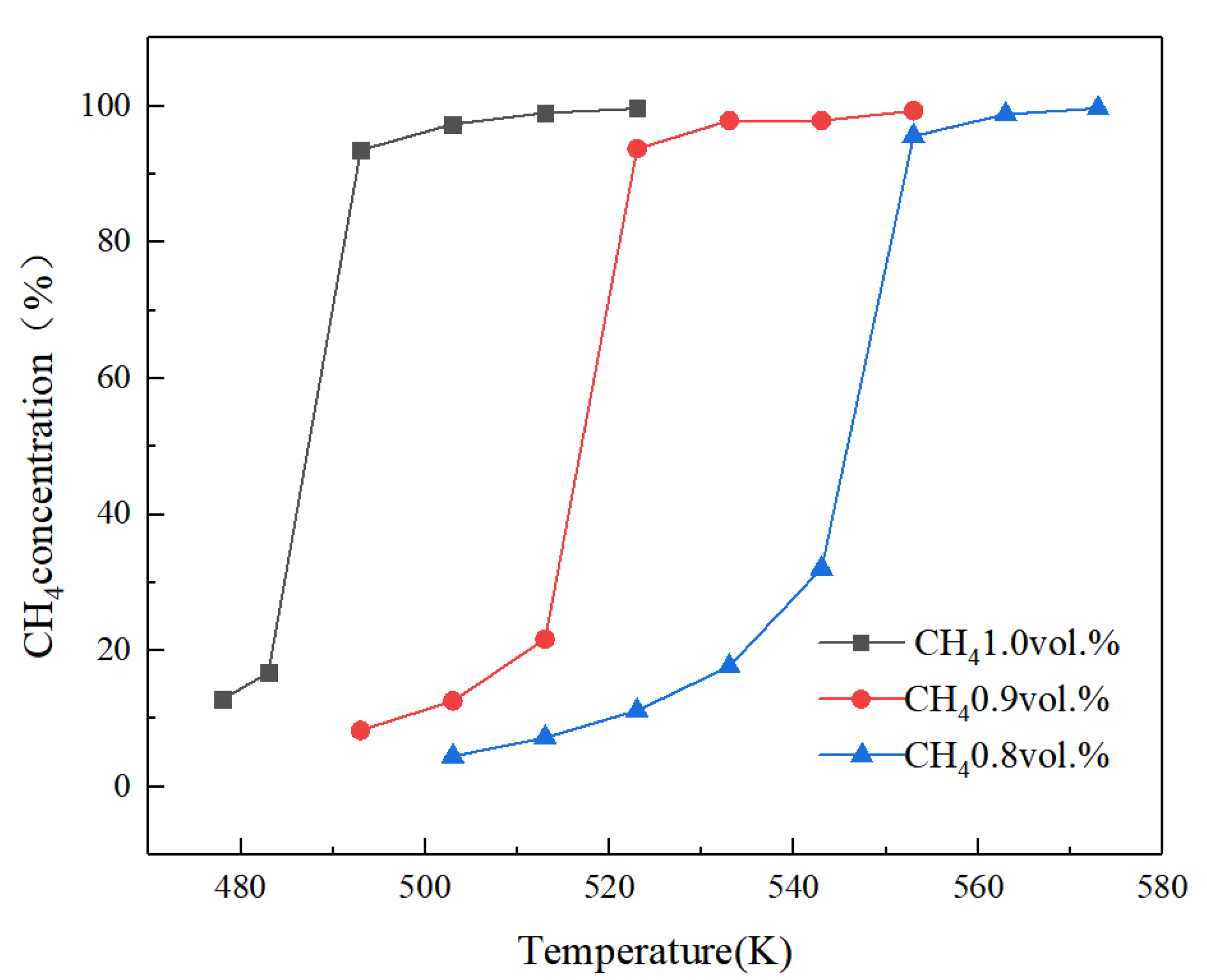
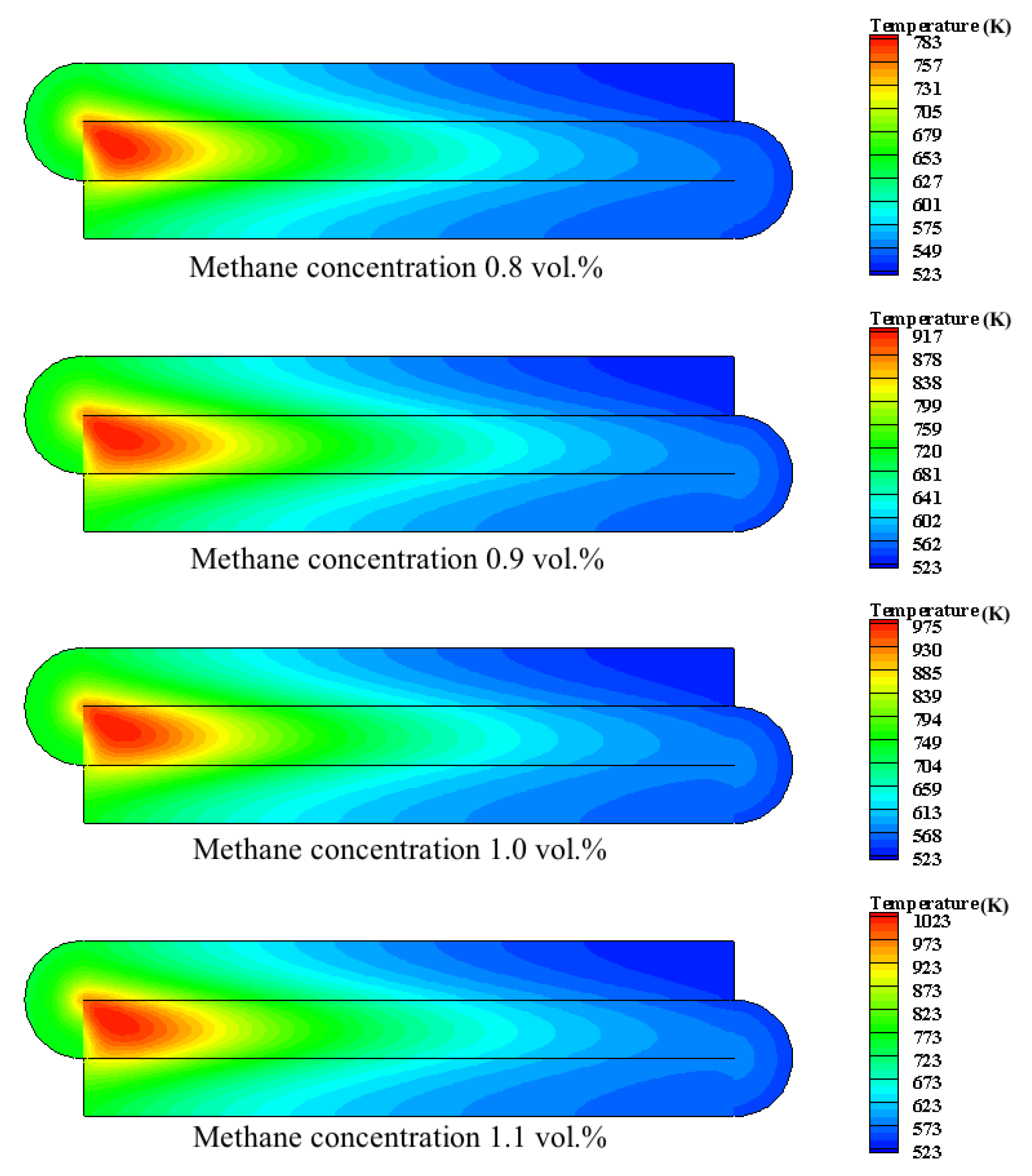
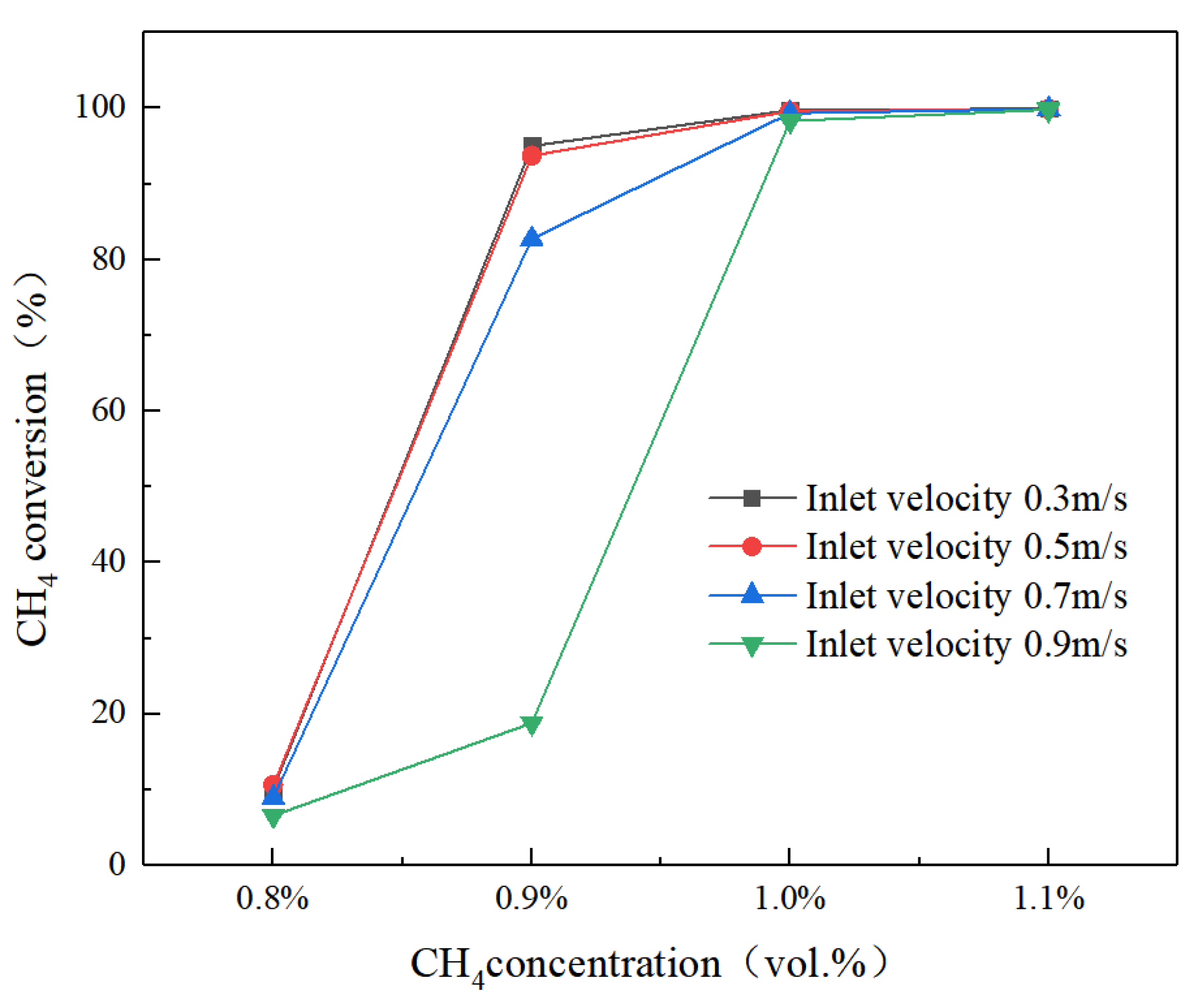
4.2.3. Effect of Feed Concentration

Figure 13 shows the temperature cloud diagram of the integrated catalytic reactor when the methane concentration is from 0.8 vol.% to 1.1 vol.%, the inlet velocity is 0.5 m/s, and the inlet temperature is 523 K. It is obvious that the methane concentration affects the temperature distribution of the catalytic integrated reactor. When the methane concentration is 0.8 vol.%, the maximum temperature of the integrated catalytic reactor is 783 K. Furthermore, when the methane concentration is 1.1 vol.%, the maximum temperature of the integrated catalytic reactor is 1023 K. With the increase in methane concentration, the peak temperature in the reaction channel of catalytic integrated reactor increases, and the preheating temperature of feed gas in the intake channel also increases. The reason is that a higher methane concentration leads to more heat released in the reaction channel. Thus, the peak temperature in the reaction channel increases. The high-temperature gas in the reaction channel fully preheats the feed gas in the intake channel.
Figure 14 shows the conversion of methane with different concentrations in the integrated catalytic reactor at different inlet velocities with an inlet temperature of 523 K. Generally, the conversion rate of methane grows with increasing methane concentration at different inlet velocities. When the methane concentration is 0.8 vol.%, the methane conversion rate is less than 20%. With the methane concentration increased to 1%, methane is almost completely converted. The conversion of methane is related to reaction channel temperature. The higher the methane concentration, the more heat released by the reaction and the higher reaction channel temperature. High temperature promotes the conversion of methane. This shows that high methane concentration is more favorable for the reaction.

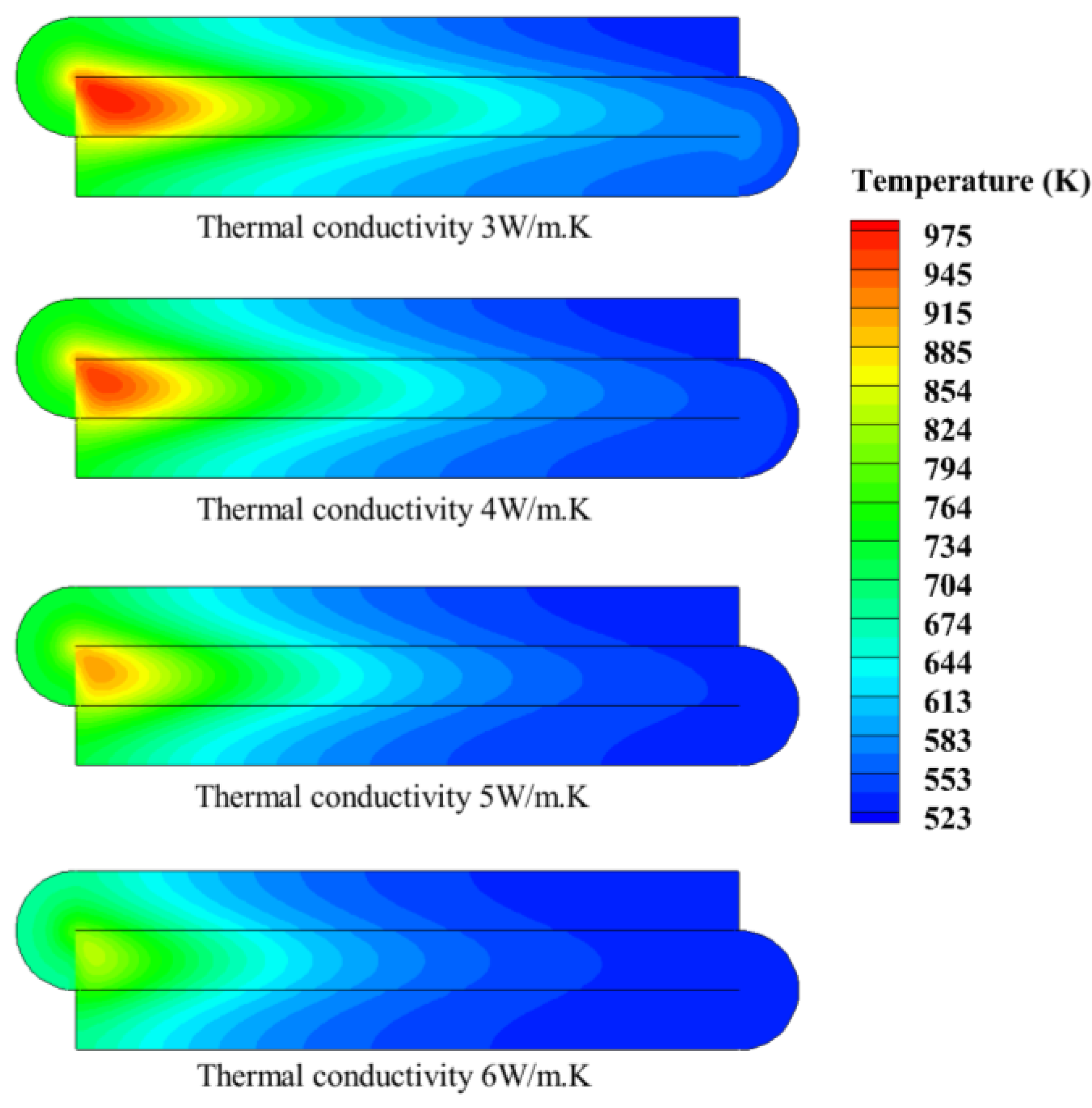
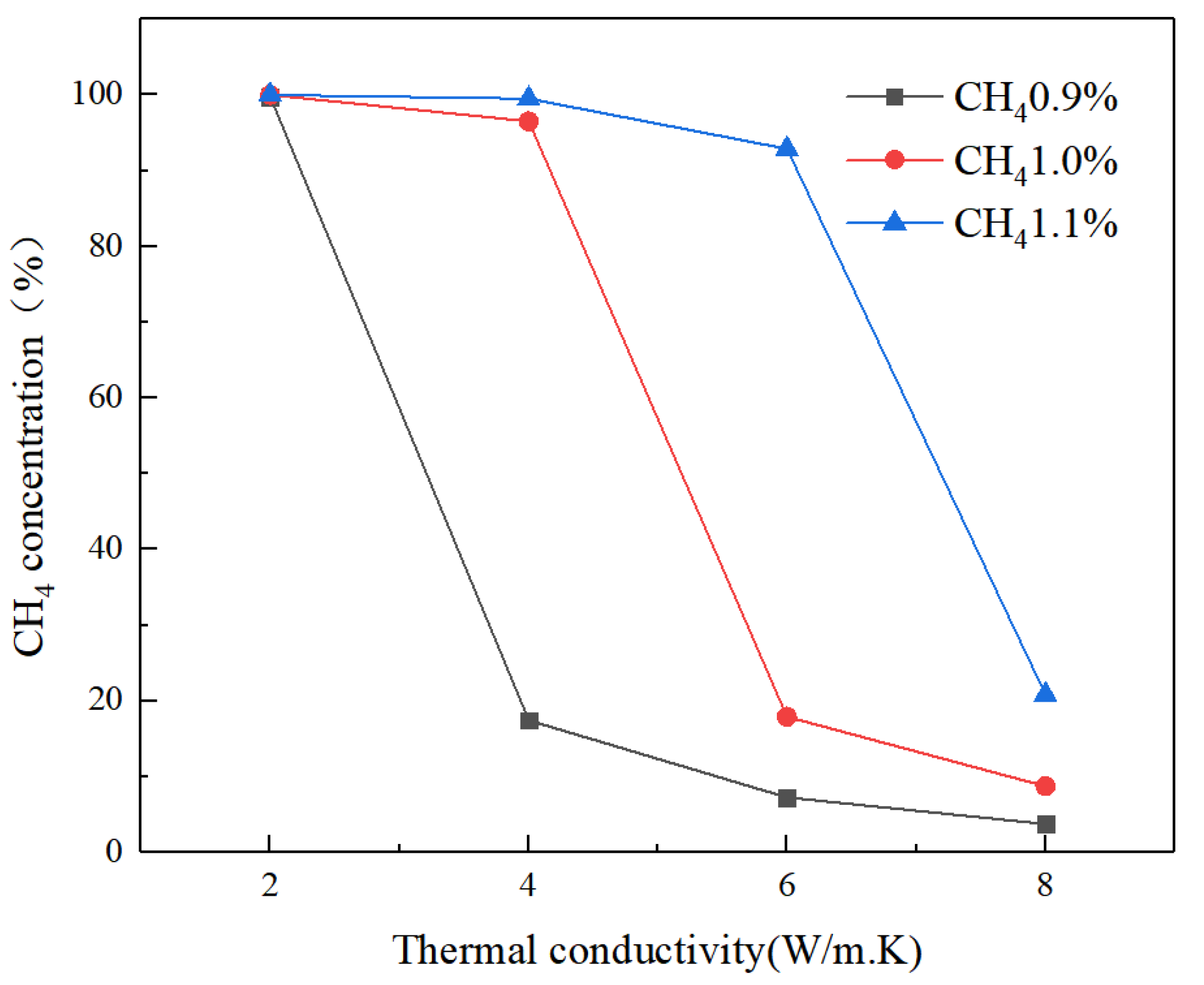
4.3. Effect of Thermal Conductivity of Porous Media

Thermal conductivity of the porous media is an important parameter affecting heat transfer, which is of great significance to study the reaction performance and heat recovery effect of reactors. The integrated catalytic reactor filled with porous media of thermal conductivity of 3, 4, 5, and 6 W/m × K is numerically simulated under the same inlet conditions. The inlet temperature is 523 K, the inlet velocity is 0.5 m/s, and the methane concentration is 1 vol.%. Figure 15 shows the temperature distribution cloud diagram of the integrated catalytic reactor with different thermal conductivity.
As can be seen from Figure 15, the thermal conductivity of porous media affects the temperature distribution of the reactor. When the thermal conductivity of porous media is 3 W/m × K, the maximum temperature in the reactor is 975 K. As the thermal conductivity of porous media is increased to 6 W/m × K, the maximum temperature of the reactor decreases to 832 K. The smaller thermal conductivity of porous media, the higher peak temperature in the integrated catalytic reactor. In addition, the size of the high-temperature zone above 900 K is larger, and the preheating temperature of feed gas in the intake channel is higher. With the increase in the thermal conductivity of porous media, the overall temperature of the integrated catalytic reactor decreases, and the high-temperature zone shrinks gradually and finally disappears.
Figure 16 shows the methane conversion at different methane concentrations when the reactor is filled with porous media with the thermal conductivity of 2, 4, 6, and 8 W/m × K. The inlet temperature is 523 K and inlet velocity is 0.5 m/s. It can be seen from the figure that, under different methane concentrations, methane conversion decreases with the increase in thermal conductivity of porous media. When the thermal conductivity of porous media is 2 W/m × K, methane can be completely converted. However, when the thermal conductivity of porous media increases to 8 W/m × K, the conversion rate of methane all decreases to less than 20%. The main reason is that when the thermal conductivity of porous media is low, the heat storage capacity of reaction channel is strong. Then, the temperature of catalytic ceramics is higher, which can promote the reaction. Therefore, methane can be completely converted and the overall temperature of the reactor is higher. When the thermal conductivity of porous media is high, the heat transfer from the reaction channel to the intake channel is intensified. Then, the heat of the reaction channel is reduced, and the catalytic combustion is weakened. As a result, the overall temperature of the reactor decreases and methane cannot be completely converted. It is shown that the lower thermal conductivity of the porous media facilitates the reaction.

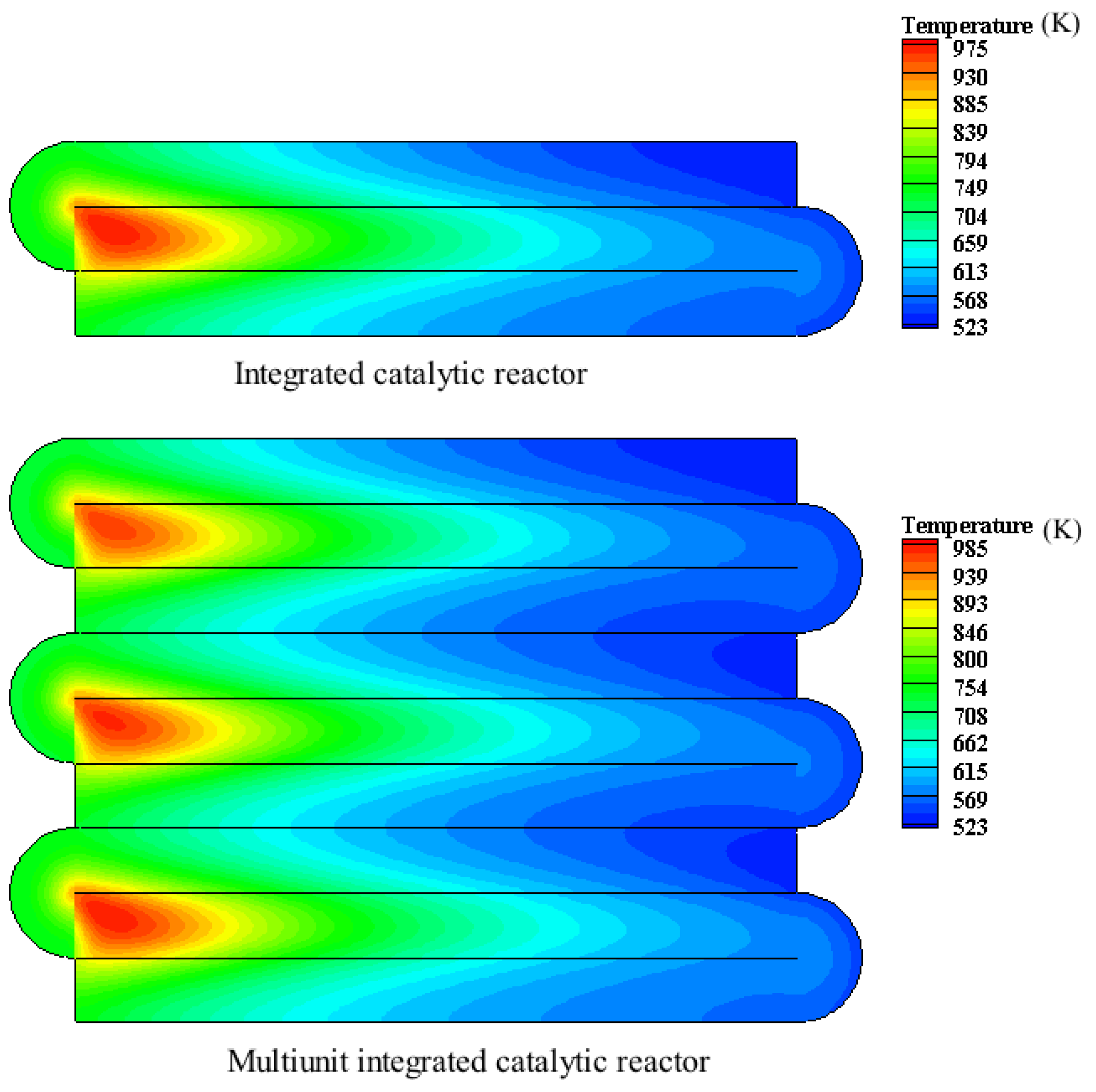
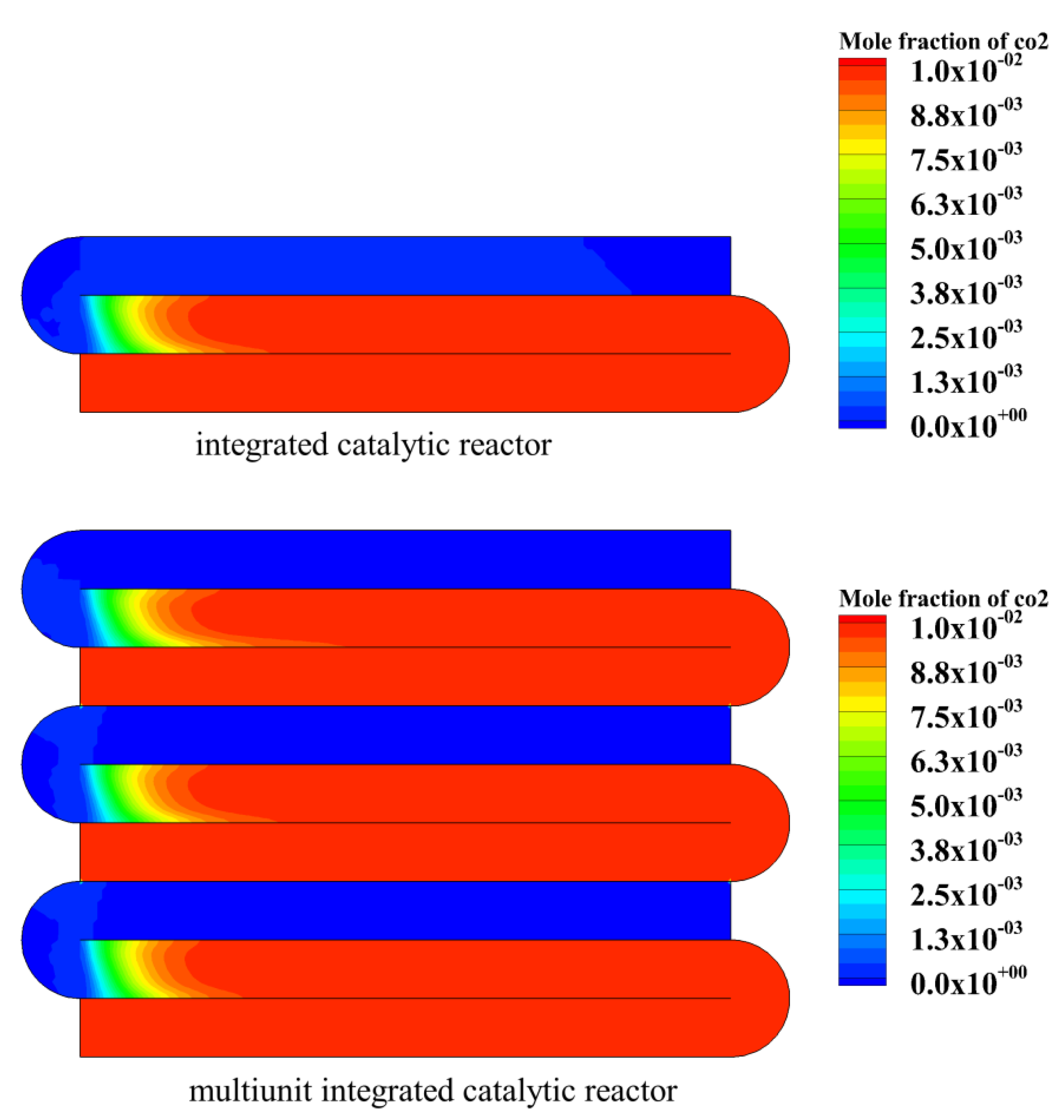
4.4. Study on the Performance of Multiunit Integrated Catalytic Reactor

In order to preheat the feed gas in the intake channel more sufficiently, multiple reactors are stacked vertically. Hence, the intake channel of the reactor can be preheated by the top exhaust channel and the bottom reaction channel at the same time, so as to improve the preheating efficiency. The principle structure diagram of the multiunit integrated catalytic reactor is shown in Figure 17. The multiunit integrated catalytic reactor consists of three integrated catalytic reactor units. To understand the reaction performance of the multiunit integrated catalytic reactor, the multiunit integrated catalytic reactor and integrated catalytic reactor are numerically studied and compared under the same conditions. The inlet conditions are an inlet temperature of 523 K, an inlet velocity of 0.5 m/s, and a methane concentration of 1 vol.%. The temperature and carbon dioxide distribution cloud diagrams of the two types of reactors are shown in Figure 18 and Figure 19.
It can be seen from Figure 18 that the maximum temperature of the catalytic integrated reactor is 975 K and that of the multiunit integrated catalytic reactor is 985 K. The peak temperature occurs in the reaction channel of the bottom unit of the multiunit integrated catalytic reactor. The maximum temperature of the multiunit integrated catalytic reactor is 10 K higher than that of the catalytic integrated reactor. The maximum temperature of the top reactor of the multiunit integrated catalytic reactor is 966 K, which is 9 K lower than that of the catalytic integrated reactor. However, the maximum temperature of the middle and bottom reactors of the multiunit integrated catalytic reactor are both greater than 975 K. The maximum temperature of the top unit reactor of the multiunit integrated catalytic reactor is low because the intake channel can only be preheated by the bottom reaction channel, and the heat transfer efficiency is low. However, the intake channel of the middle and bottom unit reactors can be preheated by the bottom reaction channel and the top exhaust channel at the same time, which enhances the heat transfer and effectively improves the preheating efficiency of the intake channel. It can be seen from the distribution of carbon dioxide in Figure 19 that the stacked reactors can completely convert methane. It is shown that the special structure of the multiunit integrated catalytic reactor further enhances the thermal cycle. Under the same intake concentration and velocity conditions, compared with the integrated catalytic reactor, the multiunit integrated catalytic reactor can achieve complete conversion of methane at a lower inlet temperature.

5. Conclusions

In order to understand the reaction performance and heat recuperation effect of integrated catalytic reactor, the catalytic combustion of methane air mixture over a pd-based catalyst is numerically studied. The reaction performance of an integrated catalytic reactor and single-channel catalytic reactor is compared and analyzed. Furthermore, the effects of the inlet conditions and porous media thermal conductivity of the integrated catalytic reactor are studied. The multiunit integrated catalytic reactor is also numerically simulated and compared with the integrated catalytic reactor to further enhance the regeneration performance. The main conclusions are summarized as follows.
  • Under the same inlet conditions, the integrated catalytic reactor enables efficient conversion of methane at lower inlet temperatures compared to a single-channel catalytic reactor.
  • The inlet temperature and inlet concentration of the integrated catalytic reactor have important effects on the conversion of methane. High inlet temperature and high methane concentration are more favorable for the conversion of methane; the inlet velocity affects the temperature distribution of the reactor and the preheating of the feed gas in the inlet channel.
  • When the thermal conductivity of porous media is low, thermal reflux promotes the intake preheat and catalytic combustion. However, when the thermal conductivity of porous media is too high, excessive heat dissipation weakens the catalytic combustion.
  • Under the same conditions, the maximum temperature of the multiunit integrated catalytic reactor is higher than that of the integrated catalytic reactor. The reason is that it further enhances the heat recovery efficiency.

Author Contributions

All of the authors contributed to publishing this paper. M.M. designed the reactor and put forward the modification suggestion to this paper. Q.C. performed the simulation and wrote the paper. M.G. and J.L. processed the simulation data. J.S. and Y.L. put forward the modification suggestion to this paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China, grant numbers 52106170.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The reactor design process is mainly divided into the following steps:
(1)
The calculation of the gas–solid heat exchange.
The heat Q1 for preheating feed gas in the intake channel can be expressed as
Q 1 = m ( C P 2 t 2 − C P 1 t 1 )
where m is the inlet feed gas mass flow, c p 1 and c p 2 are the average specific heat capabilities of the feed gas entering and exiting the intake channel, respectively, and are the corresponding temperatures at inlet and outlet of the intake channel.
The heat QR released from methane combustion in the reaction channel can be calculated as
Q R = V 1 ρ Q C H 4 M
where ρ is the density of methane, V1 is the flow rate of preheated gas. Q C H 4 is the heat of combustion for the methane of 1 mole, and M is the relative molecular mass of methane.
Q 2 = m ( c p 3 t 3 − c p 2 t 2 )
where c p 2 and c p 3 are the average specific heat capacities of the gas entering and the reaction channel, and t 2 and t 3 are the flue gas temperatures entering and leaving the reaction channel.
The absorbed heat in the exhaust channel is shown as follows:
Q 3 = m ( c p 4 t 4 − c p 3 t 3 )
where c p 4 is the average specific heat capacity of the flue gas exiting the exhaust channel. c p 3 and t 3 at the inlet of exhaust channel are the same values as those at the outlet of reaction channel.
In the process of heat transfer calculation, radiation heat transfer is ignored due to the low catalytic combustion temperature. No heat transfer between reaction channel and exhaust channel is considered for the low temperature difference between the two channels. Q21 represents the heat transfer from the reaction channel to the intake channel, and Q31 represents the heat transfer from the exhaust channel to the intake channel. Heat transfer has the following equations.
Q21 = QR − Q2
Q31 = Q3
Q1 = Q21 + Q31
(2)
The calculation of average temperature difference.
The average temperature difference Δ 12 between the intake channel and the reaction channel can be calculated as
Δ t 12 = ( t 3 − t 1 ) + ( t max − t 12 ) + ( t 2 − t 2 ) 3
where t max is maximum temperature of reaction in reaction channel, and t 12 is the average temperature in intake channel.
The average temperature difference Δ 13 between intake channel and exhaust channel can be calculated as
Δ 13 = ( t 4 − t 2 ) − ( t 3 − t 1 ) ln ( t 4 − t 2 ) ln ( t 3 − t 1 )
(3)
The calculation of comprehensive heat transfer coefficient.
The convective heat transfer coefficient of gas in the intake channel, reaction channel and exhaust channel can be calculated by the Equations (8) and (9) [19].
N u = K ⋅ d λ g
N u = 3.66 + 0.0668 ( d / L ) ⋅ R e ⋅ P r 1 + 0.04 [ ( d / L ) ⋅ R e ⋅ P r ] 2 / 3
where λ g is the thermal conductivity of gas; d is the single-channel hydraulic diameter; K is the convective heat transfer coefficient; L is the length of the porous medium region; and Nu, Re, and Pr are the Nusselt number, Reynolds number, and Prandtl number, respectively.
The calculation of comprehensive heat transfer coefficient K 12 between intake channel and reaction channel can be calculated as
K 12 = 1 2 ( K s 1 + K s 2 )
where K S 1 is the average convective heat transfer coefficient at the front end of the intake channel and the reaction channel, and K S 2 is the average convective heat transfer coefficient at the rear end of the intake channel and the reaction channel.
The calculation of comprehensive heat transfer coefficient K 13 between the intake channel and exhaust channel can be calculated as
K 13 = 1 2 ( K X 1 + K X 2 )
where K X 1 is the average convective heat transfer coefficient at the front end of the intake channel and the exhaust channel, and K X 2 is the average convective heat transfer coefficient at the rear end of the intake channel and the exhaust channel.
(4)
The calculation of size of reactor.
The heat transfer area A 12 between the intake channel and the reaction channel can be confirmed according to the following equation.
A 12 = Q 12 Δ t 12 K 12
The heat transfer area A 13 between the intake channel and the exhaust channel can be confirmed according to the following equation.
A 13 = Q 13 Δ t 13 K 13
The calculations of heat transfer areas of the intake channel, reaction channel, and exhaust channel ( A 1 , A 2 , and A 3 , respectively) are as follows.
A 1 = A 2 = A 3 = A 12 + A 13 3
The calculations of volumes of the intake channel, reaction channel, and exhaust channel ( V r 1 , V r 2 , and V r 3 , respectively) are as follows.
V r 1 = A 1 a V r 2 = A 2 a V r 3 = A 3 a
where a is the specific surface area.
The horizontal cross-sectional area F of the intake channel, reaction channel, and exhaust channel can be denoted as
F = V 1 a v 1
where v 1 , V1 are the mixed gas velocity and inlet flow rate in intake inlet.
The calculations of the length of the intake channel, reaction channel, and exhaust channel ( L 1 , L 2 , and L 3 , respectively).
L 1 = V r 1 F L 2 = V r 2 F L 3 = V r 3 F

Appendix B

  • The methane–air mixture and its products in the model are considered to be incompressible ideal gases.
  • The porosity of the porous media is constant.
  • The catalyst is evenly coated and the reaction on the surface of the catalyst is uniform.
  • The dispersion effect of gas in the porous media is ignored.
  • The heat radiation in the porous media is ignored.
  • The effect of gas gravity is ignored.
Although the reaction of methane in the reactor is complicated, it still follows the energy equation, momentum equation and continuity equation. The specific form of the equations are as follows.
Continuity equation:
∇ ⋅ ( ε ρ g u → ) = 0
where ρ g is the gas density, u → is the gas velocity, and ε is the porosity.
Momentum equation:
∇ ⋅ ( ε ρ g u ⋅ u → ) = ∇ ⋅ ( μ ∇ u ) + μ C 1 u + ρ g C 2 u 2 − ∇ P
where u is the gas velocity, and μ is the dynamic viscosity. C1 and C2 represent the permeability and the inertial resistance, respectively.
Energy equation:
∇ ⋅ ( u ρ g c g T ) = ∇ ⋅ ( λ e f f ∇ T g ) + ε ∑ i = 1 n w i W i h i
where λ e f f = ε λ g + ( 1 − ε ) λ s and T is the temperature. w i , W i , and h i are the reaction rate, molecular weight, and molar enthalpy of species i, respectively. g, s are the subscripts for gases and solids, respectively.
Species transport equation:
∇ ⋅ ( ε ρ g u Y i ) = − ∇ ⋅ ( ε ρ g D i ∇ Y i ) + ε w i W i
where Y i is the mass fraction of component i, and D i is the Diffusion coefficient of component i.
The multi-step surface reaction mechanism is used to describe the catalytic reaction of methane. In this paper, a palladium-based surface catalytic reaction mechanism containing 21-step elementary reactions proposed by Moallemi et al. [20,21] is adopted. The mechanism includes eight adsorption reactions, eight surface reactions, and dive analytical attachment reactions. A mechanism file in chemkin format is imported into fluent.
Ideal gas state equation:
ρ g = P R T g
where P is pressure.
For the inlet, the boundary conditions are given by:
T g = T g , i n , u = u 0 , v = 0 , X C H 4 = X C H 4 , i n , X O 2 = X O 2 , i n
where u is the velocity in the x direction, v is the velocity in the y direction, X C H 4 is the volume fraction of methane, and X O 2 is the volume fraction of oxygen.
For the outlet, it can be written as:
∂ T g ∂ x = ∂ T s ∂ x = ∂ Y i ∂ x = 0
The outer wall of the reactor, no-slip, impenetrability, and adiabatic conditions are defined as:
∂ u ∂ y = ∂ v ∂ y = ∂ T s ∂ y = ∂ T g ∂ y = ∂ Y i ∂ y = 0

References

  1. Gosiewski, K.; Pawlaczyk, A. Catalytic or thermal reversed flow combustion of coal mine ventilation air methane: What is better choice and when? Chem. Eng. J. 2014, 238, 78–85. [Google Scholar] [CrossRef]
  2. Karakurt, I.; Aydin, G.; Aydiner, K. Mine ventilation air methane as a sustainable energy source. Renew. Sustain. Energy Rev. 2010, 15, 1042–1049. [Google Scholar] [CrossRef]
  3. Pengfei, G. Development and present situation of utilization technology of Ventilation air methane (VAM) enrichment and utilization. IOP Conf. Ser. Earth Environ. Sci. 2019, 242, 022060. [Google Scholar] [CrossRef] [Green Version]
  4. Zhang, Y.; Doroodchi, E.; Moghtaderi, B. Utilization of ventilation air methane as an oxidizing agent in chemical looping combustion. Energy Convers. Manag. 2014, 85, 839–847. [Google Scholar] [CrossRef]
  5. Baiquan, L.; Huaming, D.; Chaoqun, W.; Qingzhao, L.; Ke, W.; Yuanzhen, Z. Combustion characteristics of low concentration coal mine methane in divergent porous media burner. Int. J. Min. Sci. Technol. 2014, 24, 671–676. [Google Scholar]
  6. Hayes, R.E.; Kolaczkowski, S.T. Introduction to Catalytic Combustion (1997); Routledge: London, UK, 2021. [Google Scholar]
  7. Irandoust, S.; Andersson, B. Monolithic Catalysts for Nonautomobile Applications. Catal. Rev. 1988, 30, 341–392. [Google Scholar] [CrossRef]
  8. Liu, H.; Zhao, J.; Li, C.; Ji, S. Conceptual design and CFD simulation of a novel metal-based monolith reactor with enhanced mass transfer. Catal. Today 2005, 105, 401–406. [Google Scholar] [CrossRef]
  9. Mei, H.; Li, C.; Liu, H. Simulation of heat transfer and hydrodynamics for metal structured packed bed. Catal. Today 2005, 105, 689–696. [Google Scholar] [CrossRef]
  10. Brooks, K.P.; Hu, J.; Zhu, H.; Kee, R.J. Methanation of carbon dioxide by hydrogen reduction using the Sabatier process in microchannel reactors. Chem. Eng. Sci. 2006, 62, 1161–1170. [Google Scholar] [CrossRef]
  11. Liu, Z.; Chu, B.; Zhai, X.; Jin, Y.; Cheng, Y. Total methanation of syngas to synthetic natural gas over Ni catalyst in a micro-channel reactor. Fuel 2012, 95, 599–605. [Google Scholar] [CrossRef]
  12. Min, D.K.; Shin, H.D. Laminar premixed flame stabilized inside a honeycomb ceramic. Int. J. Heat Mass Transf. 1991, 34, 341–356. [Google Scholar]
  13. Hashemi, S.M.; Hashemi, S.A. Flame stability analysis of the premixed methane-air combustion in a two-layer porous media burner by numerical simulation. Fuel 2017, 202, 56–65. [Google Scholar] [CrossRef]
  14. Song, F.; Wen, Z.; Dong, Z.; Wang, E.; Liu, X. Ultra-low calorific gas combustion in a gradually-varied porous burner with annular heat recirculation. Energy 2017, 119, 497–503. [Google Scholar] [CrossRef]
  15. Chen, J.; Yan, L.; Song, W.; Xu, D. Effect of heat recirculation on the combustion stability of methane-air mixtures in catalytic micro-combustors. Appl. Therm. Eng. 2017, 115, 702–714. [Google Scholar] [CrossRef]
  16. Zheng, B.; Liu, Y.; Sun, P.; Sun, J.; Meng, J. Oxidation of lean methane in a two-chamber preheat catalytic reactor. Int. J. Hydrog. Energy 2017, 42, 18643–18648. [Google Scholar] [CrossRef]
  17. Sun, J.; Liu, Y.; Sun, P.; Shi, Y. Oxidation characteristics of two-chamber lean methane preheat catalytic reactor. J. China Coal Soc. 2017, 42, 172–177. [Google Scholar]
  18. Moallemi, F.; Batley, G.; Dupont, V.; Foster, T.J.; Pourkashanian, M.; Williams, A. Chemical modelling and measurements of the catalytic combustion of CH4 /air mixtures on platinum and palladium catalysts. Catal. Today 1999, 47, 235–244. [Google Scholar] [CrossRef]
  19. Li, Q.; Bai, F.; Yang, B.; Wang, Y.; Xu, L.; Chang, Z.; Wang, Z.; Hefni, B.E.; Yang, Z.; Kubo, S.; et al. Dynamic simulations of a honeycomb ceramic thermal energy storage in a solar thermal power plant using air as the heat transfer fluid. Appl. Therm. Eng. 2018, 129, 3642–3649. [Google Scholar] [CrossRef]
  20. Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 787–1806. [Google Scholar] [CrossRef]
  21. Deutschmann, O.; Behrendt, F.; Warnatz, J. Modelling and simulation of heterogeneous oxidation of methane on a platinum foil. Catal. Today 1994, 21, 461–470. [Google Scholar] [CrossRef]
Energies 15 00447 g001 550
Figure 1. Schematic diagram and photos of preheat catalytic reactor. (a) Simplified flowsheet of preheat catalytic reactor. (b) General view of preheat catalytic reactor. (c) Catalytic ceramics.
Figure 1. Schematic diagram and photos of preheat catalytic reactor. (a) Simplified flowsheet of preheat catalytic reactor. (b) General view of preheat catalytic reactor. (c) Catalytic ceramics.
Energies 15 00447 g001
Energies 15 00447 g002 550
Figure 2. Temperature measuring points arrangement. (a) Arrangement of temperature measurement sections. (b) Measuring section.
Figure 2. Temperature measuring points arrangement. (a) Arrangement of temperature measurement sections. (b) Measuring section.
Energies 15 00447 g002
Energies 15 00447 g003 550
Figure 3. Integrated catalytic reactor design principal.
Figure 3. Integrated catalytic reactor design principal.
Energies 15 00447 g003
Energies 15 00447 g004 550
Figure 4. Schematic diagrams of reactor. (a) single-channel catalytic reactor. (b) integrated catalytic reactor.
Figure 4. Schematic diagrams of reactor. (a) single-channel catalytic reactor. (b) integrated catalytic reactor.
Energies 15 00447 g004
Energies 15 00447 g005 550
Figure 5. Comparison of the axial temperature distribution between simulation and experiment.
Figure 5. Comparison of the axial temperature distribution between simulation and experiment.
Energies 15 00447 g005
Energies 15 00447 g006 550
Figure 6. Comparison of the axial temperature distribution between integrated and single-channel catalytic reactors.
Figure 6. Comparison of the axial temperature distribution between integrated and single-channel catalytic reactors.
Energies 15 00447 g006
Energies 15 00447 g007 550
Figure 7. Temperature cloud picture of single-channel and integrated catalytic reactors.
Figure 7. Temperature cloud picture of single-channel and integrated catalytic reactors.
Energies 15 00447 g007
Energies 15 00447 g008 550
Figure 8. CH4 distribution cloud picture of single-channel reactor and integrated catalytic reactor.
Figure 8. CH4 distribution cloud picture of single-channel reactor and integrated catalytic reactor.
Energies 15 00447 g008
Energies 15 00447 g009 550
Figure 9. CO2 distribution cloud picture of a single-channel catalytic reactor and integrated catalytic reactor.
Figure 9. CO2 distribution cloud picture of a single-channel catalytic reactor and integrated catalytic reactor.
Energies 15 00447 g009
Energies 15 00447 g010 550
Figure 10. Methane conversion at different temperatures.
Figure 10. Methane conversion at different temperatures.
Energies 15 00447 g010
Energies 15 00447 g011 550
Figure 11. Temperature distribution of reaction channel centerline at different velocities.
Figure 11. Temperature distribution of reaction channel centerline at different velocities.
Energies 15 00447 g011
Energies 15 00447 g012 550
Figure 12. Temperature cloud picture of reactor at different inlet velocities.
Figure 12. Temperature cloud picture of reactor at different inlet velocities.
Energies 15 00447 g012
Energies 15 00447 g013 550
Figure 13. Temperature cloud picture of reactor at different CH4 concentrations.
Figure 13. Temperature cloud picture of reactor at different CH4 concentrations.
Energies 15 00447 g013
Energies 15 00447 g014 550
Figure 14. Conversion of different concentrations of methane at different inlet velocities at an inlet temperature of 523 K.
Figure 14. Conversion of different concentrations of methane at different inlet velocities at an inlet temperature of 523 K.
Energies 15 00447 g014
Energies 15 00447 g015 550
Figure 15. Temperature cloud diagram of reactor under different thermal conductivity.
Figure 15. Temperature cloud diagram of reactor under different thermal conductivity.
Energies 15 00447 g015
Energies 15 00447 g016 550
Figure 16. Conversion of different methane concentrations at different thermal conductivity with the inlet condition 0.5 m/s and 523 K.
Figure 16. Conversion of different methane concentrations at different thermal conductivity with the inlet condition 0.5 m/s and 523 K.
Energies 15 00447 g016
Energies 15 00447 g017 550
Figure 17. A physical model of the multiunit integrated catalytic reactor.
Figure 17. A physical model of the multiunit integrated catalytic reactor.
Energies 15 00447 g017
Energies 15 00447 g018 550
Figure 18. Temperature cloud diagram of integrated catalytic reactor and multiunit integrated catalytic reactor.
Figure 18. Temperature cloud diagram of integrated catalytic reactor and multiunit integrated catalytic reactor.
Energies 15 00447 g018
Energies 15 00447 g019 550
Figure 19. CO2 distribution cloud diagram of integrated catalytic reactor and multiunit integrated catalytic reactor.
Figure 19. CO2 distribution cloud diagram of integrated catalytic reactor and multiunit integrated catalytic reactor.
Energies 15 00447 g019
Table
Table 1. The main design results of reactor.
Table 1. The main design results of reactor.
ItemUnitRange/Value
Length of intake, reaction and exhaust channelsmm300
Height of intake, reaction and exhaust channelsmm27
Width of intake, reaction and exhaust channelsmm100
The flow rate of the mixed gasm3/h10
Inlet temperatureK473
Porosity/0.6
The specific surface aream2/m32000
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Chen, Q.; Mao, M.; Gao, M.; Liu, Y.; Shi, J.; Li, J. Design and Performance Investigation of a Compact Catalytic Reactor Integrated with Heat Recuperator. Energies 2022, 15, 447. https://doi.org/10.3390/en15020447

AMA Style

Chen Q, Mao M, Gao M, Liu Y, Shi J, Li J. Design and Performance Investigation of a Compact Catalytic Reactor Integrated with Heat Recuperator. Energies. 2022; 15(2):447. https://doi.org/10.3390/en15020447

Chicago/Turabian Style

Chen, Qiang, Mingming Mao, Min Gao, Yongqi Liu, Junrui Shi, and Jia Li. 2022. "Design and Performance Investigation of a Compact Catalytic Reactor Integrated with Heat Recuperator" Energies 15, no. 2: 447. https://doi.org/10.3390/en15020447

APA Style

Chen, Q., Mao, M., Gao, M., Liu, Y., Shi, J., & Li, J. (2022). Design and Performance Investigation of a Compact Catalytic Reactor Integrated with Heat Recuperator. Energies, 15(2), 447. https://doi.org/10.3390/en15020447

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop